1 Introduction

Premature infants come early into the world and they are born fragile, small and weighing less than full term infants. Many of the babies who survive face greater risks of significant health problems and disability throughout their lives (i.e, learning disabilities, visual and hearing problems, chronic lung disease and other long-term diseases) which translate into significant increased costs to healthcare, the economy and the broader society [27]. Premature is one of the major causes of infants’ death which is not an acute disease and compared to term infants experience more difficulty with feeding, blood glucose control, jaundice, temperature instability, respiratory distress and sepsis either singly or in combination [8].

Globally, an estimated 13 million infants are born before 37 completed weeks of gestation annually. Rates are generally highest in low and middle income countries and increasing in some middle and high income countries [17]. More than 1 in 10 of the world’s babies born in 2010 were born prematurely, making an estimated 15 million preterm births, of which more than 1 million died as a result of their prematurity [13]. Preterm birth accounts for 3.1% of all Disability Adjusted Life Years (DALYs) in the Global Burden of Disease, more than for HIV and malaria [21, 27]. Also, deaths constitute 28% of the 4 million annual new born deaths with 99% of these deaths occurring in developing countries [10]. Morbidity, mortality and prolonged hospital stay of preterm babies result in significant cost to the health sector, parents and the society [20].

In Ethiopia, according to report of United Nations of children fund [26], one of the main causes of neonatal death is preterm birth accounts for 23% of all other causes of neonatal death. Also, Ethiopian Demographic and Health Survey in 2011, high rate of neonatal mortality (37 deaths per 1000 live births) is reported and preterm birth is believed to be a major and direct cause of neonatal mortality. One in every 13 babies born in Ethiopia did not survive to celebrate its first birth day and one in every eight children died before its fifth birth day by Belaynew et al. [3].

Preterm birth has multiple factors whose solutions will not come through a single discovery but rather from an array of discoveries addressing multiple biological, clinical, and social behavioral risk factors. Causal factors linked to preterm birth include medical conditions of the mother or fetus, genetic influences, environmental exposure, infertility treatments, behavioral and socio-economic factors as well as iatrogenic prematurity [23]. Approximately 45–50% of preterm births are idiopathic, 30% are related to preterm rupture of membranes and another 15–20% result from medically indicated or elective preterm deliveries [11].

It is currently known that the study of risk factors for infant mortality is very important, as, particularly in the newborn, it can be considered one of the best quality indicators for health care, as well as an indicator for population social and economic welfare [24]. Neonatal death rate was overall 27.4%, which was significantly higher in gestational age subgroup of less than 28 weeks compared with other gestational age subgroups. The most prevalent etiologies of neonatal death were respiratory distress syndrome (73.8%), congenital abnormalities (13.8%) and sepsis (5.4%), respectively. Over 80% of all cases of death in the world are result of neonatology premature birth and the complications which are result of preterm birth are significant socioeconomic problem and the hyaline membrane disease (HMD) is in the leading place, in the field of prenatal medicine and neonatology are applied preventive treatments in order to reduce the risk of death of preterm newborns [1].

Even if premature birth is not an acute disease, it is one of the major causes of infants’ death and it continues to be significant public health burden. The average cost of medical care for a premature and low birth-weight baby for the first year of life is high in developing country like Ethiopia. These high medical expenses could burden the parents and family. In other case insurance coverage may provide additional benefits in the health plan in order to cover the medical cost incurred during the first year of preemies’ life and hence it helps to reduce the burden of the family.

The first 4 weeks of life carries one of the highest risks of death of any 4 weeks period in the human lifespan. Of the 130 million babies born every year, about 4 million die in the first 4 weeks of life in the wide world. Reducing Neonatal morbidity and mortality are now a major focus of child health strategies [16]. The study conducted in Fawzy Moaz Hospital in Egypt, were reported that 48% death of preterm infants admitted to NICU [9]. According to Ethiopian Demographic and Health Survey in 2011, in Ethiopia, high rate of neonatal mortality (37 deaths per 1000 live births)is reported and preterm birth is believe to be a major and direct cause of neonatal mortality [7] . A total of 225 neonates were admitted during the study period of Jan 2012 to Dec 2012 in JUSH. One of the main causes of admissions were found to be prematurity (30.7%) and the hospital neonatal mortality rate was 15.9%.The average length of hospital stay was 9.5 days with SD of 8.2 days using binary logistic regression analysis [25].

Parents’ awareness of premature birth and its consequences is still at a low level. Survival rates pattern or trend over the years is very important to give a sign to the parents whether their premature baby’s life is at a risky level or otherwise [27]. This study was intended to model the survival time of premature death of infants admitted to neonatal intensive care units (NICU) in Jimma University specialized hospital (JUSH) using survival analysis framework. The primary variable in survival analysis is survival time, time to death of infants admitted to NICU for this study. It was investigated the major risk factors of preterm death which will help to guide health professionals and health policy makers to identify indicators for monitoring preterm birth strategy and applying necessary preventive and appropriate measures to decrease preterm birth, and may ultimately it will helps to reduce infant mortality rate. The survival approach used for this, were non-parametric, semi-parametric and parametric survival with (exponential, weibull and log-logistic distribution) and the model best fit the data were selected using Akaikie information criteria (AIC).

2 Study Design and Procedure

2.1 Source of Data

All medical records of preterm infants those who were admitted to Neonatal Intensive Care Unit at Jimma University Specialized Hospital from January, 2013 to December, 2015 were retrospectively reviewed by medical professionals. The data consists of infants that admitted to Jimma University Specialized Hospital (Jimma, Ethiopia) with prematurity case. The total numbers of preterm infants admitted to NICU during this study were 552. Among the total of 552 of preterm registered in the given year, only 490 premature infants whose card had full information, satisfy inclusion criteria and hence are included in this study. Thus, Preterm infants admitted to NICU with a gestational age of 26 weeks or greater and less than 37 completed weeks were included and Term infants who born with in gestational age of greater than 37 weeks are excluded.

2.2 Study Population and Period

The study population includes all premature infants. All preterm infants those who were admitted to Neonatal Intensive Care Unit (NICU) at Jimma University Specialized Hospital from January, 2013 to December, 2015 G.C. were eligible to be included in the study

2.3 Data Collection Procedure

This study has an ethical approval from college of Natural Sciences, Jimma University, Research and Ethical Review board with number Ref. no RPG/132/08. Ethical permission was obtained from the neonatology department of JUSH. The hospital based data collected by trained enumerator and principal investigator. So this study incorporates secondary data and Data collection process was carried out in the time interval of 25/07/2008 to 15/08/2008 E.C.

2.4 Variables of the Study

The response (dependent) variable is continuous and describes the length of hospital stay time in days. The response variable for the ith individual is represented by \(Y_i\) and it measures duration to event and it is defined by status variable (event or censoring variable). Survival time measures the follow-up of time from a defined starting point to the occurrence of a given event. This observation time has two components, the beginning point of the study time and the observation of time to the end. In survival analysis, the outcome of interest (death in this study) is the duration of time until death occurs measured in days.

3 Method of Data Analysis

3.1 Non-parametric Survival Model

Kaplan–Meier Estimator

The Kaplan–Meier estimator of the survivorship function (or survival probability)

\(\hbox {S}(\hbox {t})=\hbox {P}(\hbox {T} \ge \hbox {t})\) is defined as:

(1)

where \(d_j \) is the number of individuals who experience the event at time \(t_j \) and \(n_j \) is the number of individuals who have not yet experienced the event at that time [12].

3.1.1 Comparison of Survivorship Function

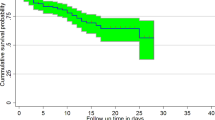
When comparing groups of subjects, it is always a good idea to begin with a graphical display of the data in each group. The figure in general shows the pattern of one survivorship if the function lying above another, it means the group defined by the upper curve lived longer, or had a more favorable survival experience than the group defined by the lower curve. The statistical question is whether the observed difference seen in the figure is significant.

The general form of this test statistic is given by:

(2)

where

figure a

\(n_{0i} \) is the number at risk at observed survival time \(t_{(i)} \).

In group 0, \(n_{1i} \) is the number at risk at observed survival time \(t_{(i)} \) in the group 1, \(d_{0i} \) is the number of observed deaths in group 0, \(d_{1i} \) is the number of observed deaths in group 1, \(n_i \) is the total number of individuals at risk before time \(t_{(i)} \) and \(d_i \) is the total number of deaths at \(t_{(i)} \). If weights \((w_i)\) equal to 1, i.e. \(w_i =1\), the Cochran–Mantel–Haenszel Log Rank test \((\hbox {Q}_{\mathrm{LR}})\) is used; otherwise if \(w_i =n_i \), the Generalized Wilcoxon test \((\hbox {Q}_{\mathrm{GWt}})\) is used.

(3)

3.2 Semi-parametric Survival Model

3.2.1 The Cox Proportional Hazard Model

The Cox Proportional Hazard (PH) Model is a multiple regression method and is used to evaluate the effect of multiple covariates on the survival [6]. This model gives an expression for the hazard at time t for an individual with a given specification of a set of explanatory variables denoted by X and it is generally given by:

$$\begin{aligned} h(t,x_t ,\beta )=h_0 (t)\exp (\beta ^{{\prime }}X_t ) \end{aligned}$$
(4)

where \(h_0 (t)\) is the baseline hazard function that characterizes how the hazard function changes as a function of survival time, \(X_i \) is the vector of values of the explanatory variables for the ith individual at time t and \(\upbeta \) is the vector of unknown regression parameters that are assumed to be the same for all individuals in the study, which measure the influence of covariate on the survival experience.

The cumulative hazard function is given by:\(H(t)=H_0 (t)\exp (\beta ^{{\prime }}X)\).

The survivor function is \(S(t,X,\beta )=S_0 (t)\exp (\beta ^{{\prime }}X)\). Where \(S_0 (t)\), is the baseline survival function.

3.2.2 Fitting Proportional Hazard Model

The maximum likelihood estimates of the cox model parameters are derived by maximizing a likelihood function usually denoted as L. The likelihood function is a mathematical expression which describes the joint probability of obtaining the data actually observed on the subjects in the study as a function of the unknown parameters (the \(\upbeta ^{{\prime }}\)s) in the model being considered. L is sometimes denoted as \(\hbox {L}(\upbeta )\) where \(\upbeta \) denotes the collection of unknown parameters.

The partial likelihood can be written as the product of several likelihoods, one for each of, say k failure times. Thus, at the jth failure time, \(l_j \) denotes the likelihood of failing at this time, given survival up to this time. Note that the set of individuals at risk at the jth failure time is called the “risk set,” \(R(t_{(j)} )\), and this set may changes and actually gets smaller in size as the failure time increases.

$$\begin{aligned} l(\beta )=\prod _{j=1}^k {l_j } \end{aligned}$$
(5)

In general sense, the partial likelihood is given by the expression

$$\begin{aligned} l_p (\beta )=\prod _{i=1}^m {\left[ {\frac{e^{x_i \beta }}{\sum \nolimits _{j\in R(t_i )} {e^{x_j \beta }} }} \right] } ^{c_i } \end{aligned}$$
(6)

where the summation in the denominator is over all subjects in the risk set at time \(t_i \) denoted by \(R(t_i )\), when there are no tied times, and it is often modified to exclude terms when \(\hbox {c}_{\mathrm{i}}=0\), yielding

$$\begin{aligned} l_p (\beta )= & {} \prod _{i=1}^m {\left[ {\frac{e^{x_i \beta }}{\sum \nolimits _{j\in R(t_i )} {e^{x_j \beta }} }} \right] } =\log (l_p (\beta ))\nonumber \\= & {} \sum _{i=1}^m {\left\{ {X_{(i)} \beta -\ln \left[ {\sum \limits _{j\in R(t_{(j)} )} {e^{X_j \beta }} } \right] } \right\} } \end{aligned}$$
(7)

where the product is over the m distinct ordered survival time and \(X_{(i)} \) denotes the value of the covariance for the subject with ordered survival times \(t_{(i)}\).

3.3 Parametric Regression Modeling

In previous topics it was focused entirely on the use of semi-parametric model of proportional hazards Cox regression model, in the analysis and prediction of the survival time of infants with prematurity. The basis of this method was to avoid having to specify the hazard function completely. However, there may be settings in which the distribution of the survival time is in specific parametric distribution that justifies the use of a fully parametric model to better address the goal of the analysis.

3.3.1 The Exponential Regression Model

For the time data and skewed to the right with exponential distribution, the time of survival for a set of covariate X, which is called, accelerated failure time is expressed as:

$$\begin{aligned} T=\exp (\beta ^{{\prime }}X+\varepsilon ) \end{aligned}$$
(8)

where, \(\varepsilon ^{{\prime }}\), is the error component.

The exponential model \((t\sim \exp (\alpha ))\) is the simplest parametric model and assumes a constant risk or hazard over time, which reflects the property of the distribution appropriately called “lack of memory” because the hazard function does not depend on time. Hence the probability of failure in a time interval \((\hbox {t}, \hbox {t}+\updelta \hbox {t})\) does not depend on previous interval. The survivorship function may be obtained by expressing in terms of time as: \(S(t,X,\beta )=\exp (-te^{-\beta ^{{\prime }}X})\) and the hazard function of the exponential regression model is \(h(t,X,\beta )=e^{-(\beta ^{{\prime }}X)}\). For the exponential regression survival model, the hazard ratio for the dichotomous covariate is \(HR(x=1,x=0)=e^{\beta _1 }\).

3.3.2 Weibull Regression Model

Survival time t is a positive random variable with weibull probability density function that can be expressed as:

$$\begin{aligned} f(t,\mu ,\alpha )=\frac{\alpha }{\mu }\left( {\frac{t}{\mu }} \right) ^{\alpha -1}\exp \left( {\left( {-\frac{t}{\mu }} \right) ^{\alpha }} \right) \end{aligned}$$
(9)

where, \(\mu >0\) and \(\alpha >0\) and the baseline hazard function of the distribution becomes:

$$\begin{aligned} h(t,\mu ,\alpha )=\frac{\alpha }{\mu }\left( {\frac{t}{\mu }} \right) ^{\alpha -1} \end{aligned}$$
(10)

This yield the following survivorship functions: \(S(t)=\exp \left[ {-\left( {\frac{t}{\mu }} \right) ^{\alpha }} \right] \) and the cumulative hazard function becomes: \(H(t)=\left( {\frac{t}{\mu }} \right) ^{\alpha }\) depending on the value of \(\alpha \), the hazard function can increase or decrease with increasing survival time. Hence the weibull model can yield an accelerated failure time model. Independent observations \((t_i ,\delta _i )\), \(\hbox {i}=1,{\ldots },\hbox {n}\) with survival time \(t_i \) and censoring indicator \(\delta _i \) which has value of one if ith observation is not censored and zero when the ith observation is censored and let \(\upbeta \) be the unknown parameter. The likelihood function is:

$$\begin{aligned} L(\beta )= & {} \prod _{i=1}^n {\left\{ {f(t_i )^{\delta _i }(S(t_i ))^{1-\delta _i }} \right\} }\nonumber \\= & {} \prod _{i=1}^n {\left\{ {\left( {\frac{f(t_i )}{S(t_i )}} \right) ^{\delta _i }S(t_i )} \right\} }\nonumber \\= & {} \prod _{i=1}^n {\left\{ {\left\{ {h(t_i )} \right\} ^{\delta _i }S(t_i )} \right\} } \nonumber \\= & {} \prod _{i=1}^n {\left\{ {\left( {\frac{\alpha }{\mu }\left( {\frac{t}{\mu }} \right) ^{\alpha -1}} \right) ^{\delta _i }\exp \left[ {-\left( {\frac{t}{\mu }} \right) ^{\alpha }} \right] } \right\} } \end{aligned}$$
(11)

Re-parameterizing the weibull distribution using \(\lambda =\mu ^{-\alpha }\) then \(h_0 (t)=\lambda \alpha t^{\alpha -1}\) will be the baseline hazard function. Now incorporate covariates X in the hazard function, the weibull regression models become:

$$\begin{aligned} h(t,X,\beta )=\lambda \alpha ^{\alpha -1}\exp (X\beta ^{{\prime }}) \end{aligned}$$
(12)

The model assumes that individual i and j with covariate \(\hbox {x}_{\mathrm{i}}\) and \(\hbox {x}_{\mathrm{j}}\) have proportional hazard function of the form \(\frac{h(t,x_i )}{h(t,x_j )}=\frac{\exp (x_i \beta )}{\exp (x_j \beta )}=\exp ((x_i -x_j )^{{\prime }}\beta )\)

A different parameterization is used with intercept \(\upsilon \) and scale parameter \(\upsigma \) and covariate effects \(\upgamma _{\mathrm{j}}\) having relationship with original parameterization as \(\beta _j =\frac{-\gamma _j }{\sigma },\alpha =\sigma ^{-1}\) and \(\mu =\exp (\upsilon )\).

3.3.3 The Log-Logistic Regression Model

Multiple covariate log-logistic accelerated failure time may be expressed as:

$$\begin{aligned} \ln (T)=\beta ^{{\prime }}X+\sigma \varepsilon \end{aligned}$$
(13)

where \(\upsigma \) is the scale parameter and \(\upvarepsilon \) is residual (unexplained) variation in the transformed survival times [5]. The survivorship function for the model (13) is: \(S(t,X,\beta ,\sigma )=\left[ {1+\exp (z)} \right] ^{-1}\) where z is the standardized log-time outcome variable that is; \(z=\frac{(y-\beta _0 -\beta _1 X)}{\sigma }\) and \(\hbox {y}=\ln (\hbox {t})\).

The odds of a survival time of at least t are, \(OR=\frac{S(t,X,\beta ,\sigma )}{1-S(t,X,\beta ,\sigma )}=\exp (-z)\), assumes that the covariate is dichotomous and coded 0 or 1. The odds-ratio at time t from the ratio the odds of a survival time evaluated at x \(=\) 0 and x \(=\) 1 is:

$$\begin{aligned} \textit{OR}(X=1,X=0)=\frac{\exp \left[ {-\frac{(y-\beta _0 -\beta _1 x1}{\sigma }} \right] }{\exp \left[ {-\frac{(y-\beta _0 -\beta _1 x0}{\sigma }} \right] }\quad = \exp \left( {\frac{\beta _1 }{\sigma }} \right) \end{aligned}$$
(14)

This is independent of time.

Then the hazard rate is given as follows:

$$\begin{aligned} \hbox {h}(\hbox {t}, \hbox {x},\upbeta )=\frac{\lambda pt^{p-1}\exp \left( {X\beta } \right) }{1+\lambda pt^{p}\exp \left( {X\beta } \right) } \end{aligned}$$
(15)

4 Result and Discussion

The medical cards of 490 premature infants were reviewed, 319 (65.1%) were discharged at the end of the follow up and 171 (34.9%) premature infants were died. Out of which 45.3% were female having death proportion of 15.5% lower than males (19.4%).

4.1 Comparison of Survival Experience

The mean survival time of premature infants who had Hyaline membrane disease were 12.319 days which is lower than infants who hadn’t hyaline membrane disease \((p<0.000)\). Both log-rank and Generalized Wilcoxon test for survival difference were highly significant. Log-rank showed that there is a significant difference of survival experience among groups of prenatal Asphyxia, hyaline membrane disease, sepsis, jaundice, Antenatal care visit, gestational age, respiratory distress syndrome and weight of infant. Similarly the results of Breslow (Generalized Wilcoxon) test also show that there were significant differences among premature infants survival experience of groups prenatal Asphyxia, hyaline membrane disease, sepsis, jaundice, gestational age, respiratory distress syndrome and weight of infant except for Antenatal care visit which means there is no differences in survival experience of premature infants whose mother had Antenatal care visit and had no Antenatal care visit have at the earlier phases where the number at risk is large (Tables 1, 2).

Table 1 Summary results of premature infants’ death by different demographic, health and risk behavior variables, at JUSH, during 2013–2015
Full size table
Table 2 Comparison of survival experience of premature infants using demographic, health and risk behavior variables at JUSH, during 2013–2015
Full size table

4.2 Multiple Covariate Analysis of Proportional Hazard Models

Survival of premature infants was significantly related with having sepsis, jaundice, prenatal asphyxia, hyaline membrane disease, respiratory distress syndrome, gestational Age at birth and temperature during admission. The values of the Wald-statistic for individual \(\beta \) coefficients support that the estimated values \(\beta _{i}'s\) are significantly different from zero at 5% level of significance. Hazard ratio having 95% CI for premature infants admitted to NICU who had Sepsis, Jaundice, Prenatal asphyxia, Hyaline membrane disease and Respiratory distress syndrome compared to those infants who hadn’t Sepsis, Jaundice, prenatal asphyxia,Hyaline membrane disease and Respiratory distress syndrome were 1.7763 (1.2234,2.5790), 2.3950 (1.7071,3.3603), 1.6399 (1.0495,2.5625), 1.8772 (1.2927,2.7261) and 2.2237 (1.5166,3.2605), respectively. That is, the risk of death for premature infants those who had Jaundice and Respiratory distress syndrome were 2.3950 and 2.2237 times higher than those infants without jaundice and Respiratory distress syndrome respectively. Premature infants who had Sepsis, Prenatal asphyxia and Hyaline membrane disease were 77.63, 63.99 and 87.72% more likely to die than those infants without Sepsis, Prenatal asphyxia and Hyaline membrane disease respectively. Also, the hazard ratio (95% CI) for premature infants admitted to NICU those who were born in between gestational age (28–30], (30–32], (32–34] and (34–37) weeks compared to those who were born at gestational age (26–28] were 0.598 (0.3232,1.1097), 0.5186 (0.2766,0.9725), 0.3787 (0.2042,0.7021) and 0.5528 (0.2940,1.0395), respectively. That is, Premature infants who were born in between gestational age (28–30], (30–32], (32–34] and (34–37) weeks were 40.2, 48.14,62.13 and 44.72% less likely to die than to those infants who were born in the interval (26–28] weeks of gestational age respectively.

Moreover, by letting other covariates constant, the hazard ratio (95% CI) of temperature at admission for premature infants were 0.8553 (0.7552,0.9687) at NICU. This means, the hazard ratio for a one unit increase in temperature is around 85.53%, so that increasing infants temperature,such that infants temperature goes up by one leads to a reduction in risk of death of 14.47% among premature infants admitted to NICU survivors. The remaining variables which were used in the single covariate analysis such as antenatal care visit of mother, weight of infants and Age at admission found to be non-significant. This implies that the covariates antenatal care visit of mother, weight of infants and Age at admission were no jointly effect on the time to death of premature infants admitted to NICU rather individual effect on the survival of preterm (Table 3).

Table 3 Results for the final Cox proportional hazard model for premature infant diagnosed
Full size table

4.3 Multiple Covariate Analysis of Log Logistic Regression Model

The relationship between covariates and survival probability of premature infants modeled by log logistic regression model are presented in Table 4 below. As can be seen from this table, survival of the infants was significantly related with having sepsis, Jaundice, prenatal Asphyxia, hyaline membrane disease, respiratory distress syndrome, with gestational age at birth and temperature at admission. Using the regression model of Eq. (15) and with the parameters found, the survival time of premature infants admitted to NICU have log logistic distribution. The log-logistic model has two parameter \(\lambda \) is the scale parameter and \(\rho \) is the shape parameter, which can be expressed as time \(\sim \)Log-logistic (\(\lambda ,\hbox { p}\)). The default output for parametric provide maximum likelihood estimates of intercept v, and scale parameter \(\updelta \), associated with the logistic distribution. The parameters of the underlying log logistic distribution are the functions of these extreme value parameters, \(\lambda =\exp (-\upmu /\hbox {p})=0.952245\) and \(\hbox {p}=1/\upalpha =1.248439\) where \(\upmu =\exp (\hbox {v})=0.06081\). Then time \(\sim \)log-logistic (0.952245,1.248439) have hazard rate of \(\hbox {h}_{\mathrm{o}}(\hbox {t}) =\frac{\lambda \rho t^{\rho -1}}{1+\lambda t^{\rho }}=\frac{1.18882t^{0.248439}}{1+0.952245t^{1.248439}}\). The log-logistic regression model that predicts the survival of premature infants admitted to neonatal intensive care unit with identical data settings were:

$$\begin{aligned} \hbox {h}(\hbox {t}, \hbox {x},\upbeta )=\frac{1.18882t^{0.248}\hbox {exp}\left( {X\beta } \right) }{1+0.952245t^{1.248\hbox {exp}(X\beta )^{{\prime }}}} \end{aligned}$$
(16)

In parametric settings, except for exponential regression models the baseline function is not proportional for all subjects as a case of cox regression model. For the log logistic regression model the base line hazard will vary with \(\hbox {h}_{\mathrm{o}}(\hbox {t})=\frac{\lambda \rho t^{\rho -1}}{1+\lambda t^{\rho }}\). So the base line hazard function of premature infants in every increase in time measured in days:

$$\begin{aligned} \hbox {h}_{0}(\hbox {t})=\frac{1.18882t^{0.248}}{1+0.952245t^{1.248}} \end{aligned}$$
(17)
Table 4 Parameter estimates, standard errors and the hazard ratios in the final log logistic regression model at JUSH, during 2013–2015
Full size table

4.4 Discussions

Results obtained in this study were found to be analogous with literature on the topic. The first factor that affects survival time of premature infant admitted to neonatal care unit is prenatal asphyxia of neonate. As it was indicated both in cox proportional hazard models and log-logistic regression models the hazard rate of premature infants admitted to NICU who had prenatal Asphyxia is about HR 1.6399 and OR 2.479 times higher than premature infants who had no prenatal Asphyxia respectively. This result is in accordance with the studies by Lawn et al. [15]. Other studies like studies of Black et al. [4].

Early onset of disease (Sepsis) of premature infants is a prognostic factor that significantly predicts survival of time to death of premature infants. The multiple covariate analysis of cox proportional hazard showed that, hazard rate of having Sepsis is 77.63% higher than premature infants who had no Sepsis and log logistic parametric model also indicates that the proportional odds of having sepsis is much higher for infants those had Sepsis (OR 2.072). The result is comparable with earlier study [4, 18] at global level. Sime et al. [25].

The results of this study suggested that hyaline membrane disease was significant predictive factor for time-to-death of premature infants. Infants who had hyaline membrane disease have hazard ratio 1.8772 (1.2927,2.7261), that is the risk of death for premature infants who had hyaline membrane disease was 87.72% higher than infants who hadn’t hyaline membrane disease. The log-logistic parametric regression model also suggested that the proportional odds of survival were 2.636 times higher odds of dying than premature infants who had no hyaline membrane disease (or 37.94% less likely of risk of dying for premature infants who had no hyaline membrane disease). This result supported by study carried out in ST. George, Germany on prevention of hyaline membrane disease in preterm infant conclude that Hyaline membrane disease is the leading cause of death for infants [1].

Jaundice disease is an important predictor of time to death of premature infants. Both cox proportional hazard and log logistic parametric models suggest that the jaundice disease have significantly associated with premature infants’ death. Premature infants who had jaundice have hazard rate of 2.395 (CI 1.7071,3.3603), higher than Premature infants who hadn’t jaundice disease. This is similar to reports by Khan et al. [14] in Karachi, Pakistan who reported jaundice and sepsis as the commonest morbidities in their preterm patients. However, Onwuanaku et al. [22] in Jos University Teaching Hospital Nigeria, reported sepsis as the commonest morbidity, followed by jaundice. They recommended that is an urgent need for the prevention and adequate management of jaundice in this vulnerable group.

In our study in both models, cox proportional and log-logistic regression models, the initial body temperature of infants was significantly associated with reducing the survival probability of premature infants. Cox proportional hazard and log-logistic parametric regression model were suggested the hazard ratio and odds ratio of 0.8553 and 0.811 respectively. This indicates that one unit increase in initial temperature of premature infants reduces the risk of death by 14.47 and 18.9% respectively. This result confirmed with study carried out by Merertu et al. [19] reported that Temperature at admission has strong association with survival in a multivariate model adjusted for gestational age and birth weight of neonatal and With the neonates whose temperature at admission was less than or equal to \(33\,{^{\circ }}\hbox {C}\) have a 5.43 times higher risk of death compared to those with \(\hbox {T}{^{\circ }}\) at admission between 36.50–37.5 \({^{\circ }}\hbox {C}\).

Respiratory distress syndrome is one of the potential risk factors that affect the survival time of premature infants. Results of cox proportional hazard and log-logistic parametric regression model showed that the respiratory distress syndrome disease have significantly associated with survival time of premature infants admitted to NICU. This study confirmed with the study carried out by Behnaz [2]; concluded that the death rate of respiratory distress syndrome (73.8%) is higher in premature infants who had the disease, which predict occurrences of death in premature infants.

5 Conclusions and Recommendations

5.1 Conclusions

Cox proportional hazard analysis showed that the major factors that affect the survival time of preterm are prenatal Asphyxia, Sepsis, hyaline membrane disease, jaundice, Gestational age, temperature and respiratory distress syndrome for time to death of premature infants. Preterm infants having prenatal asphyxia, Sepsis, Jaundice, Hyaline membrane and respiratory distress syndrome have higher death rate. Similarly, preterm with poor health indicators like lower gestational age (26–28) weeks and initial temperature, were less likely to survive.

To predict and model the survival time of premature infants, various baseline parametric regression models were applied. Among these, parametric model with log-logistic baseline distribution is best fitted to predict the survival time of the premature infants.

5.2 Recommendations

According to the results of this study the main predictive factors for the survival time of premature infants are more of clinical variables. So, health workers should be cautious when mother’s born preterm which has prenatal asphyxia, Sepsis, Jaundice, hyaline membrane disease and respiratory distress syndrome. The log-logistic regression model provides better predictions to the survival probability of premature infants’. So, future researchers could make use of this model. Future studies also need to assess the level of awareness, treatment and control of these risk factors.