Abstract
Scientists abstract hypotheses from observations of the world, which they then deploy to test their reliability. The best way to test reliability is to predict an effect before it occurs. If we can manipulate the independent variables (the efficient causes) that make it occur, then ability to predict makes it possible to control. Such control helps to isolate the relevant variables. Control also refers to a comparison condition, conducted to see what would have happened if we had not deployed the key ingredient of the hypothesis: scientific knowledge only accrues when we compare what happens in one condition against what happens in another. When the results of such comparisons are not definitive, metrics of the degree of efficacy of the manipulation are required. Many of those derive from statistical inference, and many of those poorly serve the purpose of the cumulation of knowledge. Without ability to replicate an effect, the utility of the principle used to predict or control is dubious. Traditional models of statistical inference are weak guides to replicability and utility of results. Several alternatives to null hypothesis testing are sketched: Bayesian, model comparison, and predictive inference (prep). Predictive inference shows, for example, that the failure to replicate most results in the Open Science Project was predictable. Replicability is but one aspect of scientific understanding: it establishes the reliability of our data and the predictive ability of our formal models. It is a necessary aspect of scientific progress, even if not by itself sufficient for understanding.


Similar content being viewed by others
Notes
For an insightful affirmative answer to this question, the serious reader should consult Jaynes and Bretthorst (2003).
According to the Neyman-Pearson approach, one cannot “reject the null” unless the p-value is smaller than a prespecified level of significance. With this approach, it is not kosher to report the actual p-value (Meehl, 1978). Following Fisher, however, one can report the p-value but not reject the null. Modern statistics in psychology are a bastard of these (see Gigerenzer, 1993, 2004). In all cases, it remains a logical fallacy to reject the null, as all of the above experts acknowledged.
The standard error of differences of means of independent groups is s\( \sqrt{2/n} \), explaining its appearance in the text.
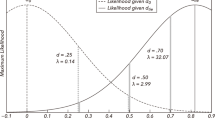
Thus illustrating the standard Bayesian complaint that p refers to the probability of obtaining data more extreme than what anyone has ever seen.
It increases from σ2/n1 to σ2(1/n1 + 1/n2). With n2= 1, that gives the formula in the text. When the data on the x-axis are effect sizes (d) rather than z-scores, the variance of d is approximately (n1+n2)/(n1n2) (Hedges & Olkin, 1985, p. 86). With equal ns in experimental and control, then s2d ≈ 2/n, which it is doubled for replication distributions. Because most stat-packs return the two-tailed p-value, that is halved in the above Excel formulae. In most replication studies there is an additive random effects variance of around 0.1 (Richard, Bond, & Stokes-Zoota, 2003), especially important to include in large-n studies.
References
Abikoff, H. (2009). ADHD psychosocial treatments. Journal of Attention Disorders, 13(3), 207–210. https://doi.org/10.1177/1087054709333385.
APS. (2017). Registered replication reports. Retrieved from https://www.psychologicalscience.org/publications/replication.
Ashby, F. G., & O'Brien, J. B. (2008). The p rep statistic as a measure of confidence in model fitting. Psychonomic Bulletin & Review, 15(1), 16–27. https://doi.org/10.3758/PBR.15.1.16.
Barlow, D. H., & Hayes, S. C. (1979). Alternating treatments design: one strategy for comparing the effects of two treatments in a single subject. Journal of Applied Behavior Analysis, 12(2), 199–210. https://doi.org/10.1901/jaba.1979.12-199.
Barlow, D. H., Nock, M., & Hersen, M. (2008). Single case research designs: strategies for studying behavior change (3rd ed.). New York, NY: Allyn & Bacon.
Bem, D. J. (2011). Feeling the future: experimental evidence for anomalous retroactive influences on cognition and affect. Journal of Personality & Social Psychology, 100(3), 407–425. https://doi.org/10.1037/a0021524.
Berry, K. J., Mielke Jr., P. W., & Johnston, J. E. (2016). Permutation statistical methods: an integrated approach. New York, NY: Springer.
Bolstad, W. M. (2004). Introduction to Bayesian statistics. Hoboken, NJ: Wiley.
Boomhower, S. R., & Newland, M. C. (2016). Adolescent methylmercury exposure affects choice and delay discounting in mice. Neurotoxicology, 57, 136–144. https://doi.org/10.1016/j.neuro.2016.09.016.
Brackney, R. J., Cheung, T. H., Neisewander, J. L., & Sanabria, F. (2011). The isolation of motivational, motoric, and schedule effects on operant performance: a modeling approach. Journal of the Experimental Analysis of Behavior, 96(1), 17–38. https://doi.org/10.1901/jeab.2011.
Branch, M. N. (1999). Statistical inference in behavior analysis: some things significance testing does and does not do. The Behavior Analyst, 22(2), 87–92.
Branch, M. N. (2014). Malignant side effects of null-hypothesis significance testing. Theory & Psychology, 24(2), 256–277.
Branch, M. N. (2018). The “reproducibility crisis”: might methods used frequently in behavior analysis research help? Perspectives on Behavior Science. https://doi.org/10.1007/s40614-018-0158-5.
Breland, K., & Breland, M. (1961). The misbehavior of organisms. American Psychologist, 16, 681–684. https://doi.org/10.1037/h0040090.
Burnham, K. P., & Anderson, D. R. (2002). Model selection and multimodel inference: a practical information-theoretic approach (2nd ed.). New York, NY: Springer.
Burnham, K. P., & Anderson, D. R. (2004). Multimodel inference: understanding AIC and BIC in model selection. Sociological Methods & Research, 33(2), 261–304. https://doi.org/10.1177/0049124104268644.
Button, K. S., Ioannidis, J. P. A., Mokrysz, C., Nosek, B. A., Flint, J., Robinson, E. S., & Munafò, M. R. (2013). Power failure: why small sample size undermines the reliability of neuroscience. Nature Reviews Neuroscience, 14(5), 365–376. https://doi.org/10.1038/nrn3475.
Cardeña, E. (2018). The experimental evidence for parapsychological phenomena: a review. American Psychologist, 73(5), 663–677. https://doi.org/10.1037/amp0000236.
Chaudhury, D., & Colwell, C. S. (2002). Circadian modulation of learning and memory in fear-conditioned mice. Behavioural Brain Research, 133(1), 95–108.
Church, R. M. (1979). How to look at data: a review of John W. Tukey’s Exploratory data analysis. Journal of the Experimental Analysis of Behavior, 31(3), 433–440.
Cohen, J. (1994). The earth is round (p < .05). American Psychologist, 49, 997–1003.
Colquhoun, D. (2017). The problem with p-values. Aeon. Retrieved from https://aeon.co/essays/it-s-time-for-science-to-abandon-the-term-statistically-significant?utm_source=Friends&utm_campaign=169df1a4dd.
Cumming, G. (2005). Understanding the average probability of replication: comment on Killeen (2005). Psychological Science, 16, 1002–1004. https://doi.org/10.1111/j.1467-9280.2005.01650.
Dallery, J., McDowell, J. J., & Lancaster, J. S. (2000). Falsification of matching theory’s account of single-alternative responding: Herrnstein's k varies with sucrose concentration. Journal of the Experimental Analysis of Behavior, 73, 23–43.
Davison, M. (2016). Quantitative analysis: a personal historical reminiscence. Retrieved from https://www.researchgate.net/profile/Michael_Davison2/publication/292986440_History/links/56b4614908ae5deb26587dbe.pdf.
DeHart, W. B., & Odum, A. L. (2015). The effects of the framing of time on delay discounting. Journal of the Experimental Analysis of Behavior, 103(1), 10–21.
Edgington, E., & Onghena, P. (2007). Randomization tests. Boca Raton, FL: Chapman Hall/CRC Press.
Estes, W. K. (1991). Statistical models in behavioral research. Mahwah, NJ: Lawrence Erlbaum Associates.
Fisher, R. A. (1959). Statistical methods and scientific inference (2nd ed.). New York, NY: Hafner.
Fitts, D. A. (2010). Improved stopping rules for the design of efficient small-sample experiments in biomedical and biobehavioral research. Behavior Research Methods, 42(1), 3–22. https://doi.org/10.3758/BRM.42.1.3.
Gigerenzer, G. (1993). The superego, the ego, and the id in statistical reasoning. In G. Keren & C. Lewis (Eds.), A handbook for data analysis in the behavioral sciences: methodological issues (pp. 311–339). Mahwah, NJ: Lawrence Erlbaum Associates.
Gigerenzer, G. (2004). Mindless statistics. Journal of Socio-Economics, 33, 587–606.
Gigerenzer, G. (2006). What’s in a sample? A manual for building cognitive theories. In K. Fiedler & P. Juslin (Eds.), Information sampling and adaptive cognition (pp. 239–260). New York, NY: Cambridge University Press.
Gigerenzer, G., & Marewski, J. N. (2015). Surrogate science: the idol of a universal method for scientific inference. Journal of Management, 41(2), 421–440.
Gilbert, D. T., King, G., Pettigrew, S., & Wilson, T. D. (2016). Comment on “Estimating the reproducibility of psychological science”. Science, 351(6277), 1037–1037. https://doi.org/10.1126/science.aad7243.
Harlow, H. F. (1949). The formation of learning sets. Psychological Review, 56(1), 51–65.
Harlow, L. L., Mulaik, S. A., & Steiger, J. H. (Eds.). (1997). What if there were no significance tests? Mawah, NJ: Lawrence Erlbaum Associates.
Hedges, L. V., & Olkin, I. (1985). Statistical methods for meta-analysis. New York, NY: Academic Press.
Herrnstein, R. J. (1970). On the law of effect. Journal of the Experimental Analysis of Behavior, 13, 243–266. https://doi.org/10.1901/jeab.1970.13-243.
Hoffmann, R. (2003). Marginalia: why buy that theory? American Scientist, 91(1), 9–11.
Hunter, I., & Davison, M. (1982). Independence of response force and reinforcement rate on concurrent variable-interval schedule performance. Journal of the Experimental Analysis of Behavior, 37(2), 183–197.
Ioannidis, J. P. A. (2005). Why most published research findings are false. PLoS Medicine, 2(8), e124. https://doi.org/10.1371/journal.pmed.0020124.
Irwin, R. J. (2009). Equivalence of the statistics for replicability and area under the ROC curve. British Journal of Mathematical & Statistical Psychology, 62(3), 485–487. https://doi.org/10.1348/000711008X334760.
Iverson, G., Wagenmakers, E.-J., & Lee, M. (2010). A model averaging approach to replication: The case of p rep. Psychological Methods, 15(2), 172–181. https://doi.org/10.1037/a0017182.
Iverson, G. J., Lee, M. D., & Wagenmakers, E.-J. (2009). p rep misestimates the probability of replication. Psychonomic Bulletin & Review, 16, 424–429. https://doi.org/10.3758/PBR.16.2.424.
Jaynes, E. T., & Bretthorst, G. L. (2003). Probability theory: the logic of science. Cambridge, UK: Cambridge University Press.
Jenkins, H. M., Barrera, F. J., Ireland, C., & Woodside, B. (1978). Signal-centered action patterns of dogs in appetitive classical conditioning. Learning & Motivation, 9(3), 272–296. https://doi.org/10.1016/0023-9690(78)90010-3.
Jiroutek, M. R., & Turner, J. R. (2017). Buying a significant result: do we need to reconsider the role of the P value? Journal of Clinical Hypertension, 19(9), 919–921.
Jones, L. V., & Tukey, J. W. (2000). A sensible formulation of the significance test. Psychological Methods, 5(4), 411–414.
Julious, S. A. (2005). Sample size of 12 per group rule of thumb for a pilot study. Pharmaceutical Statistics, 4(4), 287–291.
Killeen, P. R. (1978). Stability criteria. Journal of the Experimental Analysis of Behavior, 29(1), 17–25.
Killeen, P. R. (2001). The four causes of behavior. Current Directions in Psychological Science, 10(4), 136–140. https://doi.org/10.1111/1467-8721.00134.
Killeen, P. R. (2005a). Replicability, confidence, and priors. Psychological Science, 16, 1009–1012. https://doi.org/10.1111/j.1467-9280.2005.01653.x.
Killeen, P. R. (2005b). Tea-tests. General Psychologist, 40(2), 16–19.
Killeen, P. R. (2005c). An alternative to null hypothesis significance tests. Psychological Science, 16, 345–353. https://doi.org/10.1111/j.0956-7976.2005.01538.
Killeen, P. R. (2006a). Beyond statistical inference: a decision theory for science. Psychonomic Bulletin & Review, 13(4), 549–562. https://doi.org/10.3758/BF03193962.
Killeen, P. R. (2006b). The problem with Bayes. Psychological Science, 17, 643–644.
Killeen, P. R. (2007). Replication statistics. In J. W. Osborne (Ed.), Best practices in quantitative methods (pp. 103–124). Thousand Oaks, CA: Sage.
Killeen, P. R. (2010). P rep replicates: Comment prompted by Iverson, Wagenmakers, and Lee (2010); Lecoutre, Lecoutre, and Poitevineau (2010); and Maraun and Gabriel (2010). Psychological Methods, 15(2), 199–202.
Killeen, P. R. (2013). The structure of scientific evolution. The Behavior Analyst, 36(2), 325–344.
Killeen, P. R. (2015). P rep, the probability of replicating an effect. In R. L. Cautin & S. O. Lillenfeld (Eds.), The encyclopedia of clinical psychology (Vol. 4, pp. 2201–2208). Hoboken, NJ: Wiley.
Kline, R. B. (2004). Beyond significance testing: reforming data analysis methods in behavioral research. Washington, DC: American Psychological Association.
Krueger, J. I. (2001). Null hypothesis significance testing. On the survival of a flawed method. American Psychologist, 56(1), 16–26. https://doi.org/10.1037//0003-066X.56.1.16.
Krueger, J. I., & Heck, P. R. (2017). The heuristic value of p in inductive statistical inference. Frontiers in Psychology, 8, 908. https://doi.org/10.3389/fpsyg.2017.00908.
Kyonka, E. G. E. (2018). Tutorial: small-n power analysis. [e-article]. Perspectives on Behavior Science. https://doi.org/10.1007/s40614-018-0167-4.
Lau, B., & Glimcher, P. W. (2005). Dynamic response-by-response models of matching behavior in rhesus monkeys. Journal of the Experimental Analysis of Behavior, 84(3), 555–579.
Lecoutre, B., & Killeen, P. R. (2010). Replication is not coincidence: reply to Iverson, Lee, and Wagenmakers (2009). Psychonomic Bulletin & Review, 17(2), 263–269. https://doi.org/10.3758/PBR.17.2.263.
Lecoutre, B., Lecoutre, M.-P., & Poitevineau, J. (2010). Killeen’s probability of replication and predictive probabilities: how to compute and use them. Psychological Methods, 15, 158–171. https://doi.org/10.1037/a0015915.
Levy, I. M., Pryor, K. W., & McKeon, T. R. (2016). Is teaching simple surgical skills using an operant learning program more effective than teaching by demonstration? Clinical Orthopaedics & Related Research, 474(4), 945–955.
Macdonald, R. R. (2005). Why replication probabilities depend on prior probability distributions: a rejoinder to Killeen (2005). Psychological Science, 16, 1007–1008.
Maraun, M., & Gabriel, S. (2010). Killeen’s p rep coefficient: logical and mathematical problems. Psychological Methods, 15(2), 182–191. https://doi.org/10.1037/a0016955.
Masson, M. E. (2011). A tutorial on a practical Bayesian alternative to null-hypothesis significance testing. Behavior Research Methods, 43(3), 679–690. https://doi.org/10.3758/s13428-010-0049-5.
Maxwell, S. E. (2004). The persistence of underpowered studies in psychological research: causes, consequences, and remedies. Psychological Methods, 9(2), 147–163. https://doi.org/10.1037/1082-989X.9.2.147.
McDowell, J. J. (1986). On the falsifiability of matching theory. Journal of the Experimental Analysis of Behavior, 45(1), 63–74.
McDowell, J. J., & Dallery, J. (1999). Falsification of matching theory: changes in the asymptote of Herrnstein’s hyperbola as a function of water deprivation. Journal of the Experimental Analysis of Behavior, 72(2), 251–268.
Meehl, P. E. (1978). Theoretical risks and tabular asterisks: Sir Karl, Sir Ronald, and the slow progress of soft psychology. Journal of Consulting & Clinical Psychology, (46), 806–834.
Meehl, P. E. (1990). Why summaries of research on psychological theories are often uninterpretable. Psychological Reports, 66, 195–244.
Mill, J. S. (1904). A system of logic (8th ed.). London: Longmans, Green.
Miller, J. (2009). What is the probability of replicating a statistically significant effect? Psychonomic Bulletin & Review, 16(4), 617–640. https://doi.org/10.3758/PBR.16.4.617.
Myung, I. J. (2003). Tutorial on maximum likelihood estimation. Journal of Mathematical Psychology, 47, 90–100.
Nickerson, R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy. Psychological Methods, 5(2), 241–301. https://doi.org/10.1037/1082-989X.5.2.241.
Nickerson, R. S. (2015). Conditional reasoning: The unruly syntactics, semantics, thematics, and pragmatics of "if.". Oxford, UK: Oxford University Press.
Nuzzo, R. (2014). Scientific method, statistical errors: P values, the “gold standard” of statistical validity, are not as reliable as many scientists assume. Nature News. Retrieved from http://www.nature.com/news/scientific-method-statistical-errors-1.14700 , 506, 150–152.
Okrent, A. (2013). The Cupertino effect: 11 spell check errors that made it to press. Mental Floss. Retrieved from https://goo.gl/yQobXc.
Open Science Collaboration. (2015). Estimating the reproducibility of psychological science. Science, 349(6251), aac4716. https://doi.org/10.1126/science.aac4716.
Pant, P. N., & Starbuck, W. H. (1990). Innocents in the forest: forecasting and research methods. Journal of Management, 16(2), 433–460.
Peirce, C. S. (1955). Abduction and induction: philosophical writings of Peirce (Vol. 11). New York, NY: Dover.
Perone, M. (1999). Statistical inference in behavior analysis: experimental control is better. The Behavior Analyst, 22(2), 109–116.
Perone, M. (2018). How I learned to stop worrying and love replication failures. Perspectives on Behavior Science. https://doi.org/10.1007/s40614-018-0153-x.
Perone, M., & Hursh, D. E. (2013). Single-case experimental designs. APA handbook of behavior analysis (vol. 1, pp. 107–126).
Revusky, S. H. (1967). Some statistical treatments compatible with individual organism methodology. Journal of the Experimental Analysis of Behavior, 10(3), 319–330.
Richard, F. D., Bond Jr., C. F., & Stokes-Zoota, J. J. (2003). One hundred years of social psychology quantitatively described. Review of General Psychology, 7(4), 331–363. https://doi.org/10.1037/1089-2680.7.4.331.
Royall, R. (1997). Statistical evidence: a likelihood paradigm. London, UK: Chapman & Hall.
Royall, R. (2004). The likelihood paradigm for statistical evidence. In M. L. Taper & S. R. Lele (Eds.), The nature of scientific evidence: statistical, philosophical, and empirical considerations (pp. 119–152). Chicago, IL: University of Chicago Press.
Rubin, M. (2017). When does HARKing hurt? Identifying when different types of undisclosed post hoc hypothesizing harm scientific progress. Review of General Psychology, 21(4), 308–320. https://doi.org/10.1037/gpr0000128.
Sanabria, F., & Killeen, P. R. (2007). Better statistics for better decisions: rejecting null hypothesis statistical tests in favor of replication statistics. Psychology in the Schools, 44(5), 471–481. https://doi.org/10.1002/pits.20239.
Shadish, W. R., Cook, T. D., & Campbell, D. T. (2002). Experimental and quasi-experimental designs for generalized causal inference. New York, NY: Wadsworth Cengage Learning.
Shadish, W. R., & Haddock, C. K. (1994). Combining estimates of effect size. In H. Cooper & V. L. Hedges (Eds.), The handbook of research synthesis (pp. 261–281). New York, NY: Russell Sage Foundation.
Shadish, W. R., Rindskopf, D. M., & Hedges, L. V. (2008). The state of the science in the meta-analysis of single-case experimental designs. Evidence-Based Communication Assessment & Intervention, 2(3), 188–196.
Simmons, J. P., Nelson, L. D., & Simonsohn, U. (2018). False-positive citations. Perspectives on Psychological Science, 13(2), 255–259. https://doi.org/10.1177/1745691617698146.
Skinner, B. F. (1956). A case history in scientific method. American Psychologist, 11, 221–233.
Smith, J. D. (2012). Single-case experimental designs: a systematic review of published research and current standards. Psychological Methods, 17(4), 510–560. https://doi.org/10.1037/a0029312.
Trafimow, D. (2003). Hypothesis testing and theory evaluation at the boundaries: surprising insights from Bayes’s theorem. Psychological Review, 110, 526–535. https://doi.org/10.1037/0033-295X.110.3.526.
Trafimow, D., MacDonald, J. A., Rice, S., & Clason, D. L. (2010). How often is prep close to the true replication probability? Psychological Methods, 15(3), 300–307. https://doi.org/10.1037/a0018533.
Tryon, W. W. (1982). A simplified time-series analysis for evaluating treatment interventions. Journal of Applied Behavior Analysis, 15(3), 423–429.
Unicomb, R., Colyvas, K., Harrison, E., & Hewat, S. (2015). Assessment of reliable change using 95% credible intervals for the differences in proportions: a statistical analysis for case-study methodology. Journal of Speech, Language, & Hearing Research, 58(3), 728–739.
Urbach, P. (1987). Francis Bacon’s philosophy of science: an account and a reappraisal. LaSalle, IL: Open Court.
Van Dongen, H. P. A., & Dinges, D. F. (2000). Circadian rhythms in fatigue, alertness, and performance. In M. Kryger, T. Roth, & W. Dement (Eds.), Principles and practice of sleep medicine (Vol. 20, 3rd ed., pp. 391–399). Philadelphia, PA: Saunders.
Vandekerckhove, J., Rouder, J. N., & Kruschke, J. K. (2018). Editorial: Bayesian methods for advancing psychological science. Psychonomic Bulletin & Review, 25, 1–4. https://doi.org/10.3758/s13423-018-1443-8.
Wagenmakers, E.-J. (2007). A practical solution to the pervasive problems of p values. Psychonomic Bulletin & Review, 14(5), 779–804. https://doi.org/10.3758/BF03194105.
Wagenmakers, E.-J., & Grünwald, P. (2006). A Bayesian perspective on hypothesis testing: a comment on Killeen (2005). Psychological Science, 17, 641–642.
Weaver, E. S., & Lloyd, B. P. (2018). Randomization tests for single case designs with rapidly alternating conditions: an analysis of p-values from published experiments. Perspectives on Behavior Science. https://doi.org/10.1007/s40614-018-0165-6.
Wikipedia. (2017a). Replication crisis. Retrieved August 21, 2017, from https://en.wikipedia.org/w/index.php?title=Replication_crisis&oldid=795876147.
Wikipedia. (2017b). Scientific method. Retrieved July 22, 2018, from https://en.wikipedia.org/w/index.php?title=Scientific_method&oldid=795832022.
Winkler, R. L. (2003). An introduction to Bayesian inference and decision (2nd ed.). Gainseville, FL: Probabilistic Publishing.
Yong, E. (2015). How reliable are psychology studies. The Atlantic. https://www.theatlantic.com/science/archive/2015/08/psychology-studies-reliability-reproducability-nosek/402466/.
Author information
Authors and Affiliations
Corresponding author
Appendix : The Convoluted Logic of NHST
Appendix : The Convoluted Logic of NHST
All principles, laws, generalizations, models, and regularities (conjectures; when discussing logic and Bayes, rules; when discussing inferential statistics, hypotheses) may be stated as material implications: A implies B, or A ➔ B, or if A then B. It is easier to disprove such conditional rules than to prove them. If A is present and B absent (or “false”: ~B), then the rule fails. If A is absent and B present, no problem, as there are usually many ways to get a B (many sufficient causes of it). Indeed, if A is false or missing the implication is a “counterfactual conditional” in the presence of which both B and ~B are equally valid (“If wishes were autos then beggars would ride”). If A is present and B then occurs “in a case where this rule might fail”, it lends some support (generality) to the rule, but it cannot prove the rule, as B might still have occurred because of other sufficient causes—perhaps they were confounds in the experiment, or perhaps happenstances independent of it. This is a universal problem in the logic of science: no matter how effective at making validated predictions, we can never prove a general conjecture true (indeed, conjectures must be simplifications to be useful, so even in the best of cases they will be only sketches; something must always be left out). Newton’s laws sufficed for centuries before Einstein’s, and still do for most purposes. Falsified models, such as Newton’s, can still be productive: it was due to the failure of stars in the outer edges of the galaxy to obey Newtonian dynamics that caused dark matter to be postulated. Dark matter “saved the appearance” of Newtonian dynamics. Truth and falsity are paltry adjectives in the face of the rich implications of useful theories, even if some of their details aren’t right.
Conditional science. To understand the contorted logic of NHST requires further discussion of material implication. If the rule A ➔ B holds and A is present, then we can predict B. If B is absent (~B), then we can predict that A must also be absent: ~B ➔ ~A (if either prediction fails, the rule/model has failed and should be rejected). “If it were solid lead it would sink; it is not sinking. Therefore, it is not solid lead.” This process of inference is called modus tollens and plays a key role in scientific inference, and in particular NHST. Predict an effect not found then either the antecedent (A) is not in fact present, or the predictive model is wrong (for that context). All general conjectures/models are provisional. Some facts (which are also established using material implication; see Killeen, 2013) and conjectures that were once accepted have been undone by later research. Those with a lot going for them, such as Newton’s laws, are said to have high “verisimilitude.” They will return many more true predictions than false ones, and often that matters more than if they made one bad call.
An important but commonplace error in using conditionals such as material implication is, given A ➔ B, to assume that therefore B ➔ A. This common error has a number of names: illicit conversion, and the fallacy of affirming the consequent among them. If you are the president of the United States, then you are an American citizen. It does not follow that if you are an American citizen, then you are the president of the United States. Seems obvious, but it is a pervasive error in statistical inference. If A causes B, then A is correlated with B, for sure. But the conversion is illicit: If A is correlated with B, you may not infer that A causes B. Smoke is correlated with fire, but does not cause it.
Counterfactual conditionals play an important role in the social and behavioral sciences. Some sciences have models that make exact predictions: There are many ways to predict constants such as Avogadro’s number, or the fine-structure constant, to high accuracy. If your model gets them wrong, your model is wrong. But in other fields exact predictions are not possible; predictions are on the order of “If A, then B will be different than if ~ A.” If I follow a response with a reinforcer, the probability of the response in that context will increase. Precise magnitudes, and in many cases even directions, of difference cannot be predicted. What to do?
Absurd science. Caught in that situation, statisticians revert to a method known in mathematics and logic as a reductio ad absurdum: assume the opposite of what you are trying to prove. Say you are trying to prove A, and show that its opposite implies B, ~ A ➔ B, but if we know (or learn through experiment) that B is false, then (by modus tollens) we conclude that “not A” must also be false, and ~ ~ A ➔ A. Voila, like magic, we have proved A. Fisher introduced this approach to statistical analysis, to filter conjectures that might be worth pursuit from those that were not. Illegitimate versions of it are the heart of NHST (Gigerenzer, 1993, 2004).
Here is how it works in statistics. You have a new strain of knock-out mouse and want to see if the partial reinforcement extinction effect (PREE) holds for it. The PREE predicts that mice that receive food for every fifth response (FR5) will persist longer when food is withheld (experimental extinction) than when given for every response (FR1). You conduct a between group experiment with 10 mice in each group. What you would like to predict is A ➔ n(FR5) > n(FR1), where A is the PREE effect, and n(FR) is the number of responses in extinction. But you have two problems: Even if you found the predicted effect, you could not affirm the proposition A (illicit conversion; affirming the consequent); and you have no idea how much greater the number has to be to count as a PREE. Double the number? 5% more? So, you revert to reductio ad absurdum, and posit the opposite of what you want to prove: ~ A ➔ H0: n(FR5) = n(FR1). That is, not knowing what effect size to predict, predict 0 effect size: On the average, a zero difference between the mean extinction scores of the two groups. This prediction of “no effect” is the null hypothesis. If your data could prove the null hypothesis false, p(H0|D) = 0, you could legitimately reject the rejection of your proposition, and conclude that the new strain of mice showed the PREE! Statistical inference will give you the probability of the data that you analyzed (along with all bigger effects), given that the null hypothesis is true: p(D|H0). It is the area in Fig. 2 under the null distribution to the right of d1. What the above conditional needs in the reductio, alas, is the probability of the hypothesis given that the data are true: p(H0|D); not p(D|H0), which is what NHST gives! Unless you are a Bayesian (and even for them the trick is not easy; their “approximate Bayesian computations” require technical skill), you cannot convert one into the other without making the fallacy of illicit conversion. You cannot logically ever “reject the null hypothesis” even if your p < 0.001, any more than you can assume that all Americans are presidents. All you can do is say that the data would be unlikely had the null been true; you cannot say that the null is unlikely if the data are true; that is a statement about p(H0|D). You cannot use any of the standard inferential tools to make any statement about the probability of your conjecture/ hypothesis, on pain of committing a logical fallacy (Killeen, 2005b). Fisher stated this. Neyman and Pearson stated this. Many undergraduate stats text writers do not. You can never logically either accept or reject the null. Whiskey Tango Foxtrot! And the final indignity: even if you could generate a probability of the null from your experiment, material implication does not operate on probabilities, only on definitive propositions (Cohen, 1994). Is it surprising that we are said to be in a replication crisis when the very foundation of traditional statistical inference (NHST) in our field is fundamentally illogical, and its implementations so often flawed (Wagenmakers, 2007)? Even if you could make all these logical problems disappear, it is the nature of NHST to ignore the pragmatic utility of the results (the effect size), beyond its role in computing a p value. Even if it could tell you what is true, it cannot tell you what is useful.
Rights and permissions
About this article
Cite this article
Killeen, P.R. Predict, Control, and Replicate to Understand: How Statistics Can Foster the Fundamental Goals of Science. Perspect Behav Sci 42, 109–132 (2019). https://doi.org/10.1007/s40614-018-0171-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40614-018-0171-8