Material and particle size sensitivity analysis on coefficient of restitution in low-velocity normal impacts

Abstract

In many granular processes, impacts play a crucial role. These impacts are often described by the coefficient of restitution (COR). This COR does not only depend on impact velocity but also on the material pairing, the shape of impacting bodies, number of impacts, etc. This paper analyzes and compares the sensitivity of the COR for often seen material pairings metal–metal and metal–polymer. For experimental investigations, a steel sphere impacts different planar material probes in a defined manner, e.g., a sphere–wall contact is reproduced. While the metal–metal impacts show a significant dependency on impact velocity, the metal–polymer impacts show only little influence of the impact velocity. Also, repeated impacts onto the same spot have a significant influence on metal–metal impacts, while metal–polymer impacts are not affected. To gain insights not only about the macroscopic behavior of impacts but also about the microscopic behavior, finite element simulations are performed using an efficient 2D axisymmetric model and viscoelastic and elastic–viscoplastic material models. A good agreement between experiments and FEM simulations are achieved for the utilized material pairings. Then, the influence of the sphere’s size is studied. Afterward, a deeper look into the energy dissipation process during contact is investigated. Finally, the contact duration and normal force in the contact zone are studied experimentally.

1 Introduction

The dynamics of granular processes are mainly influenced by normal impacts of the granular material with each other and the surrounding walls. However, such impacts are very complicated events that depend on a variety of influence parameters, like impact velocity, material pairing, and shape of contact partners. These parameters significantly influence the contact duration, penetration depth, contact force, and energy dissipation of the contacting bodies [11]. In particular, the energy dissipation during such contacts is of big interest [11]. The energy dissipation comes, for instance, from elastic–viscoplastic deformations in metals or viscoelastic deformations in polymers [11, 25]. Additionally, kinetic energy of the rigid body action might be transformed during impact into wave propagation, especially in impacts involving slender bodies [20]. However, such slender bodies are not considered here, since the focus is on impacts that occur in granular materials. For the description of the global contact behavior, often a simplified description by the coefficient of restitution (COR) is used to summarize the energy dissipation during contact. The kinematic COR correlates the velocities before and after impact of both contact partners. It varies between zero and one. While a value of one implies no energy dissipation, a value of zero means maximum energy dissipation, i.e., both bodies move with the same velocity after impact [11].

The COR is a key simulation parameter of contact procedures that normally cannot be determined analytically. Therefore, in the past various numerical [1, 16, 19, 20, 28] and experimental [1, 7, 11, 16, 17, 19, 20, 24, 26] studies were performed. These studies might be further subdivided into different classes, like the used test apparatus, body materials, material models, shape of bodies, etc.

As test apparatus, often often drop-down tests [1, 17] or pendulum tests [20] are used. With the drop-down test, sphere–wall impacts are analyzed. A sphere is released from a certain height impacting the material probe at the bottom of the test apparatus. The rebound height of the sphere is measured using cameras. Thus, the COR can be easily extracted. Such a test apparatus is set up easily, but no information about contact duration and contact forces is gained. For the pendulum test, the contact partners are suspended by thin wires. By releasing one contact partner from an initial angle, a reproducible impact is achieved. Here, either sphere–sphere [24], sphere–rod [20], or sphere–wall impacts [11] have been analyzed. While Tatara [24] used the sphere’s rebound angle to determine the COR, nowadays often laser vibrometers are used to measure the bodies velocities directly [20]. This leads not only to very accurate results but also enables the analysis of contact force and contact duration, as will be shown later. Another special method for determining the COR is the idea of “listening” the COR [7]. The sound of impact can be measured accurately using technical equipment. The COR can then be extracted by this impact noise. Such measurements also enable the study of the sound radiation of impacts [14].

Due to their high importance for industrial applications, metal impacts are often analyzed experimentally by many authors [1, 16, 17, 20, 26]. However, also other materials like brass, glass, or polymers are investigated [11, 24, 25].

In the last decade, numerical analysis using the finite element method (FEM) gained more and more attention for impact analysis. These simulations enable a deeper understanding of the contact procedure and allow quick sensitivity analysis. Many different material models have been investigated so far. For instance, steel and aluminum might be described by elastic, elastic—plastic, or elastic–viscoplastic material models [16, 20]. It is shown that an accurate material model is very important for precise results as the material model has a major influence on the energy dissipation during contact and thus on the COR [20].

For materials showing a plastic behavior, repeated impacts are also of importance. Minamoto et al. [16], Weir [26], and Seifried [20] studied the COR for repeated impacts between metal contact partners. They found significant rises of the COR due to material hardening occurring in the contact zone.

While in the literature various influence parameters on the COR have been studied [1, 11, 24, 26], most of them are restricted to the analysis of the macromechanical behavior of impacts. Here, also the connection to micromechanical processes during impacts are performed. Hence, this paper presents an intensive analysis of impacts between a steel sphere and different wall materials using experiments and FEM simulations. The walls are made of steel, aluminum, or polymers. Thus, different but also accurate material models are necessary for the FEM simulations. Multiple influence parameters are studied, like impact velocity and sphere size. Using FEM simulations, deeper insights into the conversion of energy during the impacts are given. Thereby, the ratio of dissipated energy of sphere to wall is investigated. Additionally, contact duration and contact force are measured experimentally and compared for the different material pairings.

This paper is organized in the following way: First, in Sect. 2 the general impact procedure for a normal contact of two bodies is explained. In Sect. 3, the different material models for metals and polymer are presented. In Sect. 4 and Sect. 5, the experimental setup and the numerical model are introduced. A comprehensive overview of the results is given in Sect. 6, and finally, in Sect. 7 the conclusion is given.

2 Impact procedure—macromechanical considerations

An impact is characterized by a short contact duration of two or more bodies while a high force is exerted [11]. Figure 1 shows the general structure of a direct central impact problem. When two bodies collide on their line connecting their center of gravity, a central impact is achieved. As the resulting contact forces are only acting along this connecting line, the common center of gravity stays unaffected. However, due to possible dissipation losses during impact, the normal velocities of the collision partners might change. This ranges from fully elastic contacts—no energy loss, to fully inelastic contacts—both contact partners move with the same velocity afterward. Fully inelastic contacts are also referred as plastic contacts. However, a plastic contact does not necessarily imply plastic deformations, as this depends on the used materials [11].

Fig. 1

General central impact problem

Fig. 2

Contact force over time for a fully elastic, b partly plastic, and c fully plastic collision

The impact process is generally divided into two phases: compression and restitution phase. Both phases are described shortly in the following. See [11] for further information about this topic. The compression phase starts with the first contact of both bodies at $t=0$ and ends at $t=t^*$. At this time point, both bodies have the same rigid body normal velocity, i.e., zero relative movement. The contact force $F_\mathrm{{C}}$ raises first with time until it reaches its maximum value. If no wave propagation is present and the material behavior is rate-independent, this happens at $t=t^*$ [22]. The linear momentum of the compression phase is described by

$$\begin{aligned} p_\mathrm{{c}} = \int _{0}^{t^*} F_\mathrm{{C}}(t) \mathrm d t. \end{aligned}$$

(1)

After the compression phase, the restitution phase follows. Depending on occurring plastic deformations, the deformations will vanish or not. The contact force reduces from its maximum value down to zero at $t=t_\mathrm{{e}}$. The linear momentum follows to

$$\begin{aligned} p_\mathrm{{r}} = \int _{t^*}^{t_\mathrm{{e}}} F_\mathrm{{C}}(t) \mathrm d t. \end{aligned}$$

(2)

These two phases are visualized in Fig. 2 for the cases of a fully elastic, partly plastic and fully plastic collision. In case of a fully elastic contact, the linear momenta of compression and restitution phase are identical; hence, $p_\mathrm{{c}} = p_\mathrm{{r}}$. However, for partly plastic and plastic contacts this is no longer true. For partly plastic contacts, $p_\mathrm{{r}} < p_\mathrm{{c}}$, and for plastic contacts, $p_\mathrm{{r}} = 0$ holds.

The kinematic COR $\varepsilon$ is a widely used key indicator to describe the occurring velocity change. It designates the quotient between the velocities right after (1) and before (0) the impact for the bodies I and II as

$$\begin{aligned} \varepsilon = -\frac{v_\mathrm{{I}}^1 - v_\mathrm{{II}}^1}{v_\mathrm{{I}}^0 - v_\mathrm{{II}}^0}, \quad 0 \le \varepsilon \le 1 . \end{aligned}$$

(3)

For $\varepsilon = 1$, the impact is fully elastic, while for $\varepsilon = 0$ it is fully plastic. The linear momentum of the compression and restitution phase correlates as $p_\mathrm{{r}} = \varepsilon _\mathrm{{P}} p_\mathrm{{c}}$ with $\varepsilon _\mathrm{{P}}$ being the kinetic coefficient of restitution. For a central straight impact, kinematic and kinetic COR are identical [22].

If one of the impacting bodies is fixed, e.g., in case of a clammed wall, Eq. (3) simplifies to

$$\begin{aligned} \varepsilon = -\frac{v_\mathrm{{I}}^1}{v_\mathrm{{I}}^0} . \end{aligned}$$

(4)

3 Material models

Using FEM to describe the deformation behavior of a body, a meaningful material model is required. However, the choice does not only depend on the body’s material but also on the forces acting on it. Thus, the material model should be based on the expected deformation behavior. In this work, metals and polymers are used for impact analysis. Thus, high contact forces and high strain rates in the contact zone are expected. The material models should be able to reproduce this behavior.

3.1 Metals

Metals show at the beginning of loading first a linear–elastic material behavior, conforming to Hooke’s law

$$\begin{aligned} \sigma = E \epsilon , \end{aligned}$$

(5)

where $\sigma$ denotes the stress, $\epsilon$ the strain, and E the Young’s modulus. After reaching the yield stress, metals start to deform plastically. Also, the plastic flow might depend on the strain rate $\dot{\epsilon } = \frac{ \mathrm d \epsilon }{\mathrm d t}$ [13]. Thus, to describe metals accurately, an elastic–viscoplastic material model is necessary for impact problems [20]. Therefore, many different models have been developed, like the Bingham model, Perzyna model, Prager’s rule, or the Armstrong–Frederick kinematic hardening law [9]. Here, the widely used Perzyna model [18] is used [9]. This model relates the dynamic yield stress $\sigma _\mathrm{{d}}$ by a factor $\beta$ with the quasi-static yield stress $\sigma _\mathrm{{y}}$ and the effective plastic strain rate $\dot{\epsilon }_\mathrm{{p}}$ by

$$\begin{aligned} \sigma _\mathrm{{d}} = \beta \sigma _\mathrm{{y}} \text { with } \beta = 1 + \left( \frac{\dot{\epsilon }_\mathrm{{p}}}{\eta } \right) ^\lambda . \end{aligned}$$

(6)

The material viscosity parameter is denoted by $\eta$ and the strain rate hardening parameter by $\lambda$. Both parameters have to be obtained from the split Hopkinson pressure bar test [10]. For this test, the thin cylindrical test specimen is placed between two different long bars, named pressure and extension bar. By applying a pressure impulse to one end of the bars and measuring the other end’s displacement, the stress–strain curves of the specimen can be calculated. By varying the thickness of the specimen, different strain rates are obtained. From the different stress–strain curves, the dynamical yield stress $\sigma _\mathrm{{d}}$ is identified and the scaling factor $\beta$ determined. The parameters $\eta$ and $\lambda$ are found by minimizing the squared error between the scaling factors $\beta$ of the measurements and the Perzyna model.

Fig. 3

Piecewise linear approximations of quasi-static stress–strain curves for steel and aluminum [20]

Table 1 Material parameters and Perzyna coefficients obtained by the split Hopkinson pressure bar test [20]

In Fig. 3, the piecewise linear approximations of the quasi-static yield stress $\sigma _\mathrm{{y}}$ for the later used metals steel S235 and aluminum Al6060 are shown, which are taken from [20]. These curves are used in the later FEM simulations with the corresponding material data and Perzyna coefficients listed in Table 1. To give an impression about the dynamic yield stress, Fig. 4 shows the dynamical yield stress $\sigma _\mathrm {d}$ of S235 and Al6060 for different plastic strain rates using the Perzyna model, see Eq. (6). For both metals, the dynamical yield stress increases for higher strain rates. However, aluminum is showing only a little dependency on the strain rate. Only for the highest plotted strain rate of $\dot{\epsilon }_\mathrm{{p}} = {1000}\frac{1}{\hbox {s}}$ minor differences in the dynamical yield stress are visible. For steel instead, a high dependency is seen. At the plastic strain rate of $\dot{\epsilon }_\mathrm{{p}} = 1000\frac{1}{\hbox {s}}$, a factor of about three between dynamic and quasi-static yield stress is achieved.

Fig. 4

Stress–strain curves of steel S235 (blue –) and aluminum Al6060 (red –) for different strain rates by the Perzyna model

3.2 Polymers

The elastomeric material used in this study is a KRAIBON^® compound SAA9579-52 supplied by Gummiwerk KRAIBURG GmbH & Co. KG. Based on preliminary experimental investigations by the authors, this elastomer has not shown any dependence on the load amplitude and is therefore considered as isotropic and linear viscoelastic in this study. The time- and rate-dependent constitutive relation is expressed by

$$\begin{aligned} \tau \left( t \right) = \int _0^t G_\mathrm {R} \left( t-s \right) \dot{\gamma } \mathrm {d}s \end{aligned}$$

(7)

where $\tau$ represents the shear stress as the response to the uniaxial shear strain rate $\dot{\gamma }$. $G_\mathrm {R}$ is the time-dependent shear relaxation modulus. These as well as the following relations describing linear viscoelasticity can be found in [4] and [6]. A normalized relaxation shear modulus can be written as

$$\begin{aligned} g_\mathrm {R} \left( t \right) = \frac{G_\mathrm {R} \left( t \right) }{G_0} \end{aligned}$$

(8)

where $G_0$ describes the instantaneous linear elastic response of the material under infinitely fast loading. The relaxation function $g_\mathrm {R}$ is modeled using a generalized Maxwell model in terms of a Prony series

$$\begin{aligned} g_\mathrm {R} \left( t \right) = 1 - \sum _{i=1}^N g_i \left( 1 - e^{-\frac{t}{\tau _i}} \right) \end{aligned}$$

(9)

The material parameters $g_i$ and $\tau _i$ are determined from experimental dynamic mechanical analysis (DMA) tests described in [21]. Figure 5 shows the experimentally determined storage and loss modulus, and the Prony parameters are summarized in Table 2. The storage and loss moduli $G'$ and $G''$ are given by the Fourier transform of the relaxation modulus $G_\mathrm{{R}} (t)$ denoted as the complex shear modulus [4]

$$\begin{aligned} G^* (\omega ) = G'(\omega ) + \mathrm {i} G''(\omega ), \end{aligned}$$

(10)

with i being the complex number. Furthermore, the long-term relaxation modulus relates to the instantaneous modulus by

$$\begin{aligned} G_\infty = G_0 \left( 1 - \sum _{i=1}^N g_i \right) . \end{aligned}$$

(11)

The long-term shear modulus is calculated from the long-term Young’s modulus $E = 54.97\hbox { MPa}$ and Poisson’s ratio $\nu = 0.4477$.

Fig. 5

Storage modulus, loss modulus, and loss factor determined from experimental DMA tests

Table 2 Prony parameters determined from experimental DMA data

4 Experimental setup

In this paper, a pendulum testbed is developed to observe details of the impact, see Fig. 6. The utilized steel sphere of 30 mm diameter shall impact different planar material probes in the normal direction in a reproducible way. Thus, a sphere–wall impact is reproduced. The sphere is suspended by thin Kevlar wires impacting the material probe glued or fixed to a rigid steel block. Other authors also investigated this way sphere–sphere [15] and sphere–rod [20] impacts. The steel block is assumed to be fixed, as the armature is very stiff. In the initial position of the sphere, there is only a minimal gap to the wall probe. In the deflected state, the sphere is held by an electromagnet. Because the position of the electromagnet is variable, different initial impact velocities are achieved. The measurement range for this experimental setup is $v_\mathrm{{I}}^0 = 0.1\frac{m}{s} - 2.5\frac{m}{s}$. Repeated impacts on the same spot of the wall can be measured as well. After release, the velocity of the sphere is measured by a laser scanning vibrometer (LV) PSV-500 from Polytec with a sampling frequency of 250 kHz. The laser is adjusted in the initial state of the sphere on a reflection foil at the back of the sphere.

Fig. 6

Schematic representation a and picture b of test bed to determine the COR for a sphere–wall contact

Each measurement cycle consists of multiple impacts, i.e., the sphere is not caught after the first impact but the first three rebounds are measured as well. Hence, the effect of repeated impacts on the same spot can be investigated. The wall material probe is moved a bit after each cycle to get an undeformed spot of the material probe and the sphere is smoothed with sandpaper.

Due to the high sampling frequency of the LV, the contact process is measured very accurately. This makes it possible to compute the numerical derivative of the velocity signal by central finite differences, i.e., the acceleration a. This acceleration can then be used to calculate the contact force

$$\begin{aligned} F_\mathrm{C} = m a \end{aligned}$$

(12)

acting on the sphere with mass m. By numerical integration of the measured velocity signal, the sphere’s displacement and thus the local deformation $\delta$ are obtained. Thereby, it is assumed that all deformation occurs in the contact area.

5 Numerical setup

Besides the experimental analysis, finite element method (FEM) simulations are performed to determine the COR numerically.

Fig. 7

Schematic representation of the sphere–wall FEM impact model

5.1 Finite element method

The mathematical description of deformable systems, e.g., occurring in structural mechanics, leads to partial differential equations, which often cannot be solved analytically. The finite element method (FEM) is an important and powerful tool to find approximate solutions to such mathematical problems. There exists extensive literature of the foundations of FEM, see, for example, [3, 23, 27]. The idea of the FEM is to subdivide the solution domain, i.e., the deformable bodies, into finite elements of simple geometrical shape. Then a set of shape functions for the finite elements is used to find a solution of the underlying partial differential equation. The local equations of all finite elements are then assembled to a set of equations to describe the full body. Thus, the unknown quantities of the problem are described by discrete points (nodes) instead of continuous functions. Instead of solving the partial differential equations, now ordinary differential equations have to be solved. The solution of these equations delivers an approximate solution to the mathematical problem.

The analysis of impacts yields inherently nonlinear problems. Hence, the solution methods have to be adjusted to obtain efficient and robust algorithms; see, e.g., [27]. In this context, the unilateral contact can be modeled, e.g., using the penalty method or Lagrange multipliers. For details on treating unilateral contacts in FEM, see, e.g., [28]. For the impact problems considered in this research, also nonlinear material models as described in Sect. 3 have to be included. Aspects of nonlinear material models in FEM are given, e.g., in [8, 27].

5.2 Numerical model

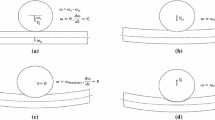
The commercial software program Abaqus is used for the simulations. A schematic representation of the sphere–wall model is shown in Fig. 7. The sphere is modeled with an initial radius of 5 mm. The wall is modeled as a cylinder with its diameter and length being the diameter of the sphere. The contour of the cylinder is completely clamped. As the contact zone during impact is much smaller as the spheres diameter, see [2], and due to the high length and diameter of the cylinder, the influence of the boundary condition is negligible and the wall can be seen as semi-infinite. Both bodies, i.e., sphere and cylinder, can be scaled for different sizes. This is done by multiplying the node coordinates by a constant scaling coefficient. The sphere consists of 5907 axisymmetric 2D elements, called CAX4R in Abaqus. The wall consists of 9019 CAX4R elements. The element size varies between 0.5 mm outside the contact zone and 0.015 mm inside the contact zone. As the cylinder, representing the wall, is clamped, the sphere is assigned with the impact velocity $v_\mathrm{{I}}^0$, see also Sect. 2.

The local deformation $\delta$ is calculated regarding the sphere’s center point, see Fig. 7. The kinematic COR is evaluated by the normal velocity of the sphere before and after the collision. The velocity before impact is known a priori. The velocity after impact is evaluated at the center point of the sphere. The mean value of the last few time steps is taken, as the velocity is oscillating a little bit due to mechanical vibrations of the sphere, which are induced through the collision. As different material pairings are used, the contact duration and thus the necessary simulation time can vary by multiple decays. This makes it important to approximate the contact duration. A formula based on Hertz theory [12] is used, see [2]. To remove the unnecessary overhead after contact, the simulation is stopped when the contact force turns zero.

The nonlinear material behavior of steel, aluminum, and polymer is here described by the relationships and data presented in Sect. 3. The metal behavior of steel and aluminum are implemented with the data of Table 1 and Fig. 3. The implementation of the SAA polymer is done with the so-called Prony series shown in Table 2.

6 Numerical and experimental results

In this section, experimental and numerical results are compared for steel–metal and steel–polymer contacts. Furthermore, sensitivity analyses on the sphere’s diameter and impact velocity are performed. Finally, the contact time and contact force are compared for the different material pairings to gain insights into the micromechanical processes during impact.

6.1 Steel–metal impacts

This section deals with pure metal–metal impacts. Hereby, a steel sphere impacts different planar metal walls of about 50 mm thickness. As wall material aluminum and steel are used in the following. These are often seen metals in technical applications and precise material models for FEM simulations are available, see also Sect. 3. It should be noted that the used metals are of the same type, but not from the same measurement charge.

6.1.1 Steel–steel impacts

For steel–steel impacts, the results of simulations and experiments of the COR for a sphere of 30 mm diameter are shown in Fig. 8. The simulation relates only to the first impact of the sphere against the wall. For the experiments, only the first impact, as well as an exponential fit, is plotted. As each impact velocity is measured five times, the mean values and their maximum deviation is shown. As every measurement cycle consists of multiple impacts on the same spot, those results are plotted as well in Fig. 8 labeled with “repeated impacts.”

Fig. 8

COR for impact of $30\hbox { mm}$-steel sphere against steel wall

Fig. 9

COR by FEM simulations for impact of steel sphere of different diameters against steel wall

A high dependency on impact velocity is observed in simulations and experiments. For very small impact velocities, which cannot be measured experimentally, the COR is close to one in the simulations. When the impact velocity increases the COR starts to decrease rapidly in simulations and experiments. For high impact velocities, the COR drops below 0.55 and converges to an almost constant value. For low impact velocities $v_\mathrm{{I}}^0 < 0.5\frac{m}{s}$, simulations and experiments match very well. For higher impact velocities, a slight difference of about 0.03 is seen in the COR. Hence, a good qualitative and quantitative agreement between experiment and simulation is achieved.

From the repeated impacts of the experiments, it can be seen that those have a higher COR than the first impacts. Thus, during the initial impact much energy dissipates by plastic deformations. At a repeated impact on the same spot, this cannot happen again in this amount due to the hardening of the contact zone. In consequence, the energy dissipation is lower, hence a higher COR results. See [16, 26] for further discussion on this topic.

The high CORs for low impact velocities can be explained by considering Hooke’s law. Only if the metal yield stress is exceeded, plastic deformations occur and thus energy is dissipated. For low impact velocities, this happens only in a very small area of the contact zone leading to low energy dissipation and thus to a high COR. For increasing impact velocity, the plastic deformations are becoming bigger, leading to a lower COR. For high impact velocities, the COR converges due to the elastic–viscoplastic material behavior of steel. This happens as the dynamical yield stress increases for higher strain rates, see Fig. 4. This leads to lower plastic deformations compared to a pure plastic material behavior and vanishes the effect of the increased contact area.

As the numerical model is suitable for calculating CORs of steel–steel impacts, it is used next for sensitivity analysis of the sphere’s diameter. The results are shown in Fig. 9 for sphere diameters between 1 mm to 50 mm. All COR curves show a similar progression but with an offset in the COR. As higher the sphere’s diameter, the lower the COR. Similar results were gained in [1] for a much smaller diameter range. Only for very low impact velocities, the COR seems to converge to the same high value. However, getting closer to the smallest/biggest sphere diameter the difference in the COR decreases. Thus, it is expected that even lower/higher sphere diameters do not have a significant influence on the COR anymore.

Next, the energy dissipation during impact can be analyzed in more detail using the simulation. In this study, the plastic deformation ALLPD (name in Abaqus) and the recoverable strain energy ALLSE are gathered from the simulation. Figure 10 shows the time course of those two energy types for an impact of a 30 mm sphere of $1\frac{\hbox {m}}{\hbox {s}}$ impact velocity. In addition to that, the time points of the maximum contact force, maximum indentation, and the end of impact are indicated.

Fig. 10

Time course of energy dissipation of a $1\frac{\hbox {m}}{\hbox {s}}$ impact between $30\hbox { mm}$-steel sphere and steel wall from simulation

At the beginning of impact, strain energy and plastic dissipation are quickly raising and showing then an almost constant slope. However, the plastic dissipation lags a bit in time. The strain energy reaches its maximum value approximately at the time of maximum contact force. The maximum indentation follows a little bit later ($5\,\upmu \hbox {s}$) as the maximum contact force. This can mainly be explained by the elastic–viscoplastic material behavior of steel. A pure elastic–plastic material model, i.e., if only the quasi-static yield stress is used, leads only to a time delay of $1\,\upmu \mathrm{s}$. Also, the time the compression wave needs to travel from the contact zone to the sphere’s center point will have a small effect. After the maximum contact force is exceeded, the slope of plastic dissipation reduces a lot. Shortly after the maximum indentation occurred the energy dissipated by plastic deformation reaches its maximum. Thus, the plastic dissipation takes mainly place in the compression phase. Throughout the restitution phase, the strain energy lowers drastically. At the end of the impact, there is still some strain energy left, which does not vanish. This happens due to permanent plastic deformations hindering a full strain release. Thus, this remaining strain energy can also be seen as energy dissipation.

Next, it is investigated in which part, e.g., sphere or wall, the energy is dissipated. Figure 11 shows the energy dissipation as relative distribution over different impact velocities for a 30 mm sphere. The dissipation is approximately fifty–fifty in both parts with only minor influence on impact velocity. Moreover, there is a negligible dependency on the sphere’s diameter, which is not shown in Fig. 11. Hence, the body’s geometry seems to be of negligible influence here.

Fig. 11

Location of energy dissipation between 30 mm steel sphere and steel wall

6.1.2 Steel–aluminum impacts

In this section, the impact of a steel sphere against an aluminum wall is treated. The results of the COR for experiments and simulations are shown in Fig. 12. The COR’s curve progression looks similar compared to the pure steel impacts, i.e., high CORs for low impact velocities with a high decrease at the beginning and converging to an almost constant value at high impact velocities of about 0.5. The experimental results show again only a small deviation within each impact velocity. A good qualitative agreement with a quantitative difference of about 0.05 is obtained to the simulations. From the repeated impacts of the experiments, it can be seen that those have again a higher COR than the first impacts.

Fig. 12

COR for impact of $30\hbox { mm}$-steel sphere against aluminum wall

Fig. 13

COR by FEM simulations for impact of steel sphere of different diameters against aluminum wall

Comparing steel–steel and steel–aluminum impacts, i.e., Figs. 8 and 12, the experimental COR values are very close to each other. The similar COR values might seem unintuitive as aluminum is a softer material than steel and one could thus expect more plastic deformations and energy dissipation and thus lower CORs. However, as will be shown later in Sect. 6.3, the contact force for steel–aluminum impacts is lower as for steel–steel impacts due to the lower Young’s modulus and lower weight of aluminum. Also, for steel–steel impacts, the energy dissipates equally in wall and sphere, see Fig. 11. For aluminum impacts, the energy dissipation is dominated by the aluminum wall, as shown in Fig. 15. Hence, the steel sphere shows almost no plastic deformations. In summary, this leads to a similar energy dissipation for steel–steel and steel–aluminum impacts. As the energy dissipation is concentrated to the aluminum wall, its contact zone is more hardened compared to pure steel–steel impacts. This might lead to the fact that the CORs of repeated impacts for aluminum are higher compared to pure steel impacts. For details on repeated impacts, see [16, 20, 26]. In consequence, general statements about the COR are only hardly possible for unknown metal material pairings.

In Fig. 13, the dependency of the sphere’s diameter regarding the COR is treated. Those curves look similar for steel–steel and steel–aluminum impacts, i.e., a lower sphere diameter leads to a higher COR, see Figs. 9 and 13. However, for steel–aluminum impacts the dependency on the sphere’s diameter is much less. This behavior might be due to a lower slope in the stress–strain curve at high strains for aluminum, see Fig. 3.

As explained in Sect. 6.1.1, the location of energy dissipation can be gathered from the FE analysis. The same is done for the steel–aluminum impacts and shown in Fig. 14. The time course of energy dissipation is qualitatively similar to the pure steel dissipation, compare Figs. 10 and 14. However, for the steel–aluminum impact the time delay between maximum contact force to maximum indentation is much lower with only $2.5\,\upmu \mathrm{s}$ to $5\,\upmu \mathrm{s}$ although the total contact time is higher ($133\,\upmu \mathrm{s}$ to $101\, \upmu \mathrm{s}$). This is due to the much lower dependency of the plastic flow on the strain rate of aluminum compared to steel. After the maximum indentation, i.e., during the restitution phase, almost no plastic dissipation occurs anymore.

Fig. 14

Time course of energy dissipation of a $1\frac{\hbox {m}}{\hbox {s}}$ impact between $30\hbox { mm}$-steel sphere and aluminum wall

Figure 15 shows, where the energy in both components dissipates relatively. It can be seen that approximately 90 % of the dissipated energy dissipates in the aluminum wall almost independent of impact velocity. Only for very low impact velocities, the dissipation ratio is a little bit lower. The difference to steel–steel is significantly, see Fig. 11. This effect can be explained by the lower yield stress of aluminum compared to steel. Thus, much more plastic deformations occur in the aluminum wall. This can also be observed after the experiments as the observable impact zone deformations on the aluminum block are much bigger than the ones on the steel block.

Fig. 15

Location of energy dissipation between $30\hbox { mm}$-steel sphere and aluminum wall

Table 3 Material data of used polymers

6.2 Steel–polymer impacts

In the previous sections, pure metal contacts are dealt with. Now, contacts between hybrid material combinations are investigated. The same steel sphere of $30\hbox { mm}$ diameter is used. As wall material, three different types of polymers are analyzed. However, due to missing material models, only one polymer is investigated numerically. The available material data are listed in Table 3. The Young’s modulus values can only be seen as rough approximations due to the viscoelastic material behavior of polymers. However, they give an impression about the material stiffness.

The first investigated polymer is a KRAIBON^® compound SAA9579-52. In the following, it is named SAA. Its viscoelastic material behavior is introduced in Sect. 3.2, i.e., this polymer is also investigated numerically. The second polymer is the widely used Polyvinyl chloride (PVC). The third one is a cold vulcanizing silicone rubber manufactured by Zhermack SpA (Badia Polesine, Italy) distributed through Troll Factory Rainer Habekost e.K. (Riede, Germany) under the name TFC Type 2. In the following, it is referred to T2. The polymer T2 is significantly softer than SAA and especially softer than PVC. The densities are on a similar scale.

6.2.1 Steel–SAA impacts

The used SAA probe is 2.4 mm thick and glued to the rigid steel block of the test armature. Due to this fact, the question arises whether the material thickness affects the COR. This will be investigated by FEM simulations later. In contrast to pure metal impacts, no effect of repeated impact is seen, i.e., repeated impacts have the same COR as corresponding first impacts. Thus, it is not differentiated between first or repeated impacts. As for each measurement cycle, the sphere rebounds until it comes to rest, the lowest measurable impact velocity reduces to about $0.01\frac{\hbox {m}}{\hbox {s}}$. This effect can be explained as the used polymer shows a viscoelastic material behavior. Hence, no or almost no plastic deformation occurs in the contact zone. Instead, the material fully recovers and no history-dependent behavior takes place.

In Fig. 16, the experimental and numerical results for the COR are shown. These are significantly different from the investigated steel–steel and steel–aluminum impacts, i.e., the dependency of the COR on impact velocity is recognizably smaller, compare with Figs. 8 and 12. However, the effect of higher CORs at lower velocities resembles. Already at the lowest impact velocity of $0.01\frac{\hbox {m}}{\hbox {s}}$ the COR has a value of $\varepsilon = 0.68$. The investigated metals have shown here a tendency to $\varepsilon = 1$. Additional, for the metals an exponential decay of the COR over impact velocity is observed on a large measurement range. Here, this is only up to impact velocities of $0.2\frac{\hbox {m}}{\hbox {s}}$ the case. Afterward, only a little almost linear decay is seen in the experiments.

In the following, two different simulation models are used, once with a 2.4 mm thick SAA layer on a semi-infinite steel wall (hybrid) and once only a semi-infinite SAA wall (non-hybrid). Both results are compared to the experiments in Fig. 16. It can be extracted that the difference between both simulation models is very small and a non-hybrid simulation can be used in the following. The COR values measured for impact velocities below $1\frac{\hbox {m}}{\hbox {s}}$ fit very well with the simulation results. Above this velocity, there is a notable difference. While in the experiments a small linear decay of the COR over impact velocity is seen, the simulations COR stays almost constant. A possible explanation for this behavior might be the way how the viscoelastic material data is gained from the experimental DMA tests [21]. Thus, the used simulation data might only fit for a specific range of impact velocities. Here, for impact velocities up to $1\frac{\hbox {m}}{\hbox {s}}$.

Fig. 16

COR for impact of $30\hbox { mm}$-steel sphere against $2.4\hbox { mm}$ SAA wall

Fig. 17

COR by FEM simulations for impact of steel sphere of different diameters against SAA wall

Likewise to the previous sections, for this kind of material pairing a parameter study regarding the diameter of the sphere is performed. As for high impact velocities experimental and numerical results begin to diverge, the analysis is limited to impact velocities up to $2\frac{\hbox {m}}{\hbox {s}}$. The results are shown in Fig. 17. The dependency on the sphere’s diameter is small. It is seen that bigger sphere diameters lead to higher CORs. This is vice versa to steel–steel (Fig. 9) and steel–aluminum (Fig. 13) impacts. However, for very small sphere diameters, like 1 mm and 2 mm, the convergence does not hold anymore as the COR values rise again. However, it is hard to judge the physical effect causing this behavior.

Next, the temporal evolution of energy dissipation is investigated. This is shown for an impact velocity of $1\frac{\hbox {m}}{\hbox {s}}$ in Fig. 18. In addition to the outputs mentioned in Sect. 6.1.1, for the viscoelastic SAA it is necessary to take the energy dissipation by viscoelasticity ALLCD into account.

Fig. 18

Time course of energy dissipation of a $1\frac{\hbox {m}}{\hbox {s}}$ impact between 30 mm steel sphere and SAA wall

Figure 18 displays that the energy stored in the material due to strain rises very fast at the beginning of contact, i.e., during the compression phase. During this phase, also the viscoelastic energy dissipation rises fast. Shortly before the strain energy reaches its maximum value, the maximum contact force occurs. Then, at about half the collision time, the maximum strain energy and afterward the maximum indentation is reached. The maximum strain energy lags behind the maximum contact force, due to the compression waves of both bodies. After the strain energies maximum, it decreases with a high slope. However, the gradient of viscoelastic dissipation is reduced. At the end of the contact, the strain energy is not zero but has still a negative slope. The viscoelastic dissipation increases the same amount as the strain energy decreases. This effect is also known as “elastic after effect” [5]. This is different to the steel–steel (Fig. 11) and steel–aluminum (Fig. 15) progressions, as these show a constant remaining strain energy after impact. The amount of energy dissipation due to plasticity in the steel sphere is negligibly small over the whole contact procedure.

The energy dissipation ratio between 30 mm steel sphere and SAA wall is shown in Fig. 19. It is seen that more than $99{\%}$ of energy dissipates in the SAA wall. The result does not surprise as already for aluminum, which is much softer than steel, $90{\%}$ of the dissipated energy is in the aluminum wall. The Young’s modulus of SAA is multiple decades lower than steel or aluminum. Due to this lower Young’s modulus, the strain in the SAA wall is much higher but the resulting contact forces are way lower. Consequently, the steel sphere shows almost no plastic deformation and most energy dissipates thru the viscoelasticity of the SAA.

Fig. 19

Location of energy dissipation between 30 mm steel sphere and SAA wall

6.2.2 Steel–PVC impacts and steel–T2 impacts – experimental results

The previous section has shown a much lower dependency of the COR on impact velocity for the polymer SAA than for pure metal impacts. To further investigate this behavior, two additional polymers PVC and T2 are analyzed next. However, due to missing material models, this is purely done experimentally. To prevent a slap through the materials during impact, both material probes have a high thickness of 8 mm (PVC) and 10 mm (T2).

Figure 20 shows the experimental results for the COR of both materials. It can be seen that there is only a minor dependency of the PVC COR on impact velocity. A little linear reduction of the COR to higher velocities is obtained. The COR starts at $\varepsilon = 0.92$ and reduces down to $\varepsilon = 0.87$. The deviations of the measurement results are very low.

The material T2 has an even lower dependency of the COR on the impact velocity. The COR is almost constant with values of $\varepsilon \approx 0.77$ and a small measurement deviation. Thus, all steel–polymer tests have shown a much lower dependency on impact velocity and a lower measurement deviation than the steel–metal impacts. Also, no damage of the material probes could be observed after tests, and the COR for first and repeated impacts does not change.

Fig. 20

COR for impact of 30 mm steel sphere against 8 mm PVC and 10 mm T2 wall

In the previous experiments, the material thickness was chosen high enough to prevent a slap through the material during impact. Next, this influence of material thickness shall be explored using the T2 material. The experiments are performed with multiple thicknesses, i.e., 0.65 mm, 1.5 mm, 2.5 mm, 3.2 mm, 4.0 mm, 4.9 mm, and 10 mm. In Fig. 21 the results are shown. For better readability, exponential function fits are inserted through the measurement points. The 10 mm probe can be seen as a reference because the effect of the steel block behind the wall material is not notable as will be shown later. While the 10 mm probe is showing an almost constant COR of $\varepsilon = 0.77$, all other probes exhibit an impact velocity-dependent behavior. For very small impact velocities, the COR is about $\varepsilon \approx 0.8$ for all thicknesses. However, a strong dependency on impact velocity is seen. As smaller the thickness the higher the velocity dependency. Conversely, the thicker the T2 wall gets, the more the curves seem to converge. This result surprises at first as it could be thought when the wall material is thinner the effect of the steel block behind increases. However, for low wall thicknesses the COR curves do not converge to the steel–steel curve, see Fig. 8. Instead, even lower COR values as for steel–steel impacts are achieved.

Fig. 21

COR for impact of 30 mm steel sphere against T2 wall with different probe thicknesses

To show the influence of the steel block behind the wall material probe when the probe thickness is small in Fig. 22 the sphere indentation into the wall is shown for an impact velocity of $2.5\frac{\hbox {m}}{\hbox {s}}$ and different probe thicknesses. The dashed vertical lines indicate the thickness of each wall probe in the same color. The curve for $0.65 \mathrm {mm}$ probe has quite a sharp kink at the beginning of the contact. This indicates that the effect of the steel block behind begins to predominate. This kink can also be seen for the thicknesses up to $4 \mathrm {mm}$ but in a weakened form. The $10 \mathrm {mm}$-probe does not have such a kink, hence it can rightfully be said that there is no serious effect of the steel block anymore. This wall is not a hybrid probe but a full polymer probe.

Performing the experiments, the very thin material probes show small circles in the impact zone or even visible damage. Due to the low wall thicknesses, higher stresses occur in the contact zone, leading to these plastic deformations. Thus, additional energy is dissipated in the polymer probes leading to a lower COR. Consequently, for impact applications, these little plastic deformations could reduce the long-term behavior of the material and should thus be avoided. On the other hand, for technical applications, the COR of such hybrid impact systems could be measured and used as an early indicator for the failure of the polymer.

Using the above insights, one might further explain the difference between simulations and experiments for the steel–SAA impacts of Sect. 6.2.1, shown in Fig. 16. Instead of changing the thickness of the SAA, the sphere’s diameter is varied. Hence, plastic deformations within the SAA should occur in a different amount. Indeed, experiments with a 20 mm instead of 30 mm diameter sphere (33 g to 110 g weight) have shown no significant differences in the COR. Thus, plastic deformations within the SAA are not the reason for the difference between simulations and experiments at high impact velocities.

6.3 Contact duration and contact force

As mentioned in Sect. 4, an advantage of using a laser vibrometer (LV) for measuring impacts is that the contact duration and contact force can be investigated. Figure 23 shows the results for the contact duration for all conducted experiments. A general observation is that for lower impact velocities, the contact duration increases in an exponential manner. For the pure metal impacts, this is in consistency with the Hertzian impact theory [12], but can also be applied to the polymer impacts.

The metal–metal contacts are in a region of one-tenth milliseconds and thus clearly shorter than metal–polymer contacts. Steel is harder than aluminum, so the duration is shorter. The same rationale can be applied to the polymer contacts since PVC is harder than SAA and T2. The PVC contact durations are in an area from 0.3–1.5 ms. SAA and T2 are in a region of 1–10 ms.

Fig. 22

Indentation of a 30 mm steel sphere into T2 wall for $2.5\frac{\hbox {m}}{\hbox {s}}$ impact velocity and different probe thicknesses. The dashed lines of the same color indicate the thickness of the wall probes

Fig. 23

Measured contact durations of a 30 mm steel sphere for different wall materials

Next, in Fig. 24 contact force profiles of impacts by a $30 \hbox { mm}$ steel sphere of $1\frac{\hbox {m}}{\hbox {s}}$ impact velocity against the different wall material probes are compared. As in Sect. 4 described, the accelerations and thus the contact forces are calculated by central finite differences of the velocity signal of the LV with a sampling frequency of 250 kHz. As expected, the maxima of the metal–metal impacts are much higher than those of metal–polymer contacts, i.e., 3027 N and 2180 N to 865 N, 388 N, and 50 N. The maxima are directly correlated with the Young’s modulus, i.e., higher Young’s modulus results in higher force peaks but lower contact times.

Fig. 24

Measured contact force profiles for $1\frac{\hbox {m}}{\hbox {s}}$ impact velocity of a 30 mm steel sphere for different wall materials

7 Conclusion

The analyzed steel–steel and steel–aluminum contacts show a high dependency on impact velocity. These start at high COR values for low impact velocities and show an exponential decay toward higher impact velocities. Due to plastic deformations, repeated impacts onto the same spot show a much higher COR. The contact times are short compared to steel–polymer impacts, which results in high contact forces and much higher noise emission. The finite element simulations are capable to reproduce the qualitative progression of the COR observed in experiments. However, small quantitative differences remain. Especially for steel–steel impacts, an effect of spheres diameter is observed. Bigger diameters lead to lower CORs. Indeed, a convergence to extreme diameters is visible. While for the steel–steel impacts the energy dissipation is distributed almost equally in sphere and wall, for steel–aluminum impacts this is dominated by the aluminum wall. Visible plastic deformations within the aluminum wall are observed after experiments.

Besides the metal–metal impacts, three different steel–polymer combinations are investigated. The used polymers can be roughly classified as soft, medium, and hard. The steel–polymer contacts show only little dependency on impact velocity. Often, only a little linear decrease of COR with impact velocity is observed. Also, the effect of repeated impacts vanishes, as no plastic deformations in the contact zone occur. The medium-stiff polymer is also analyzed numerically. A good agreement with experimental measurements is achieved for low impact velocities. At high impact velocities, bigger differences are seen. The effect of the sphere size is small for this polymer. The energy dissipation is completely dominated by the polymer wall and lasts even after contact has ended, due to the viscoelastic aftereffect of polymers.