1 Introduction

Particle impact is a common occurrence in numerous applications that involve handling and processing of powders. Depending on the impact details, it can have various implications for a process, e.g. it can affect the flow behaviour of powders due to kinetic energy dissipation [1] or influence the particle–particle and particle–substrate bonding mechanism, and consequently the quality of the final film in coating processes such as cold spraying and aerosol deposition [2, 3]. Thus, investigating the impact phenomenon is important for understanding and improving the efficiency of such processes.

Considering normal impact of an elastic-perfectly plastic spherical particle with another body, a fraction of the initial kinetic energy of the impact is stored in the contacting bodies as recoverable elastic strain energy. The remaining fraction is primarily dissipated by propagation of elastic waves and, if the initial kinetic energy is sufficiently high to induce yielding, plastic deformation. In light of this, inspection of energy loss during impact has long been a common approach to study the impact phenomenon. While elastic wave propagation is inherent in any impact regardless of the impact velocity, it has been shown experimentally and analytically that energy losses due to this mechanism are less than 3–4% of the initial kinetic energy [4,5,6,7]. However, at relatively high impact velocities, plastic deformation becomes the dominant mechanism for energy dissipation. There are various experimental [8,9,10,11,12,13,14,15,16,17,18,19] and analytical [20,21,22,23,24,25,26,27] studies that have investigated the energy dissipation during elastic–plastic impact of spheres. However, experimental investigation of particle impact is precarious as the event takes place in an extremely short span of time. Additionally, the available theoretical models are developed based on simplifying assumptions and need to be validated by experiments. Therefore, numerical simulations provide a great means for analysis of the phenomena taking place throughout impact.

Finite Element Method (FEM) and Discrete Element Method (DEM) are the most popular numerical methods used to date for simulation of particle impact. Specifically, DEM has been broadly explored over the past three decades for a wide range of particle-related problems. The accuracy of any DEM simulation depends on selecting an appropriate contact law as input, which can accurately account for deformation. Analytical contact laws have widely been adopted for DEM simulations. There are numerous models implemented in DEM that describe the normal elastic–plastic contact with [28,29,30,31,32] and without [21, 33, 34] adhesion. However, such models are based on simplifying assumptions and are currently only adequate for modelling problems that involve small strains, i.e. not accounting for extensive deformation.

As for FEM, there are several studies that model contact between an elastic–plastic sphere and a rigid surface [35,36,37,38,39,40,41]. However, these studies examine the aforementioned case in a quasi-static analysis. In fact, to the best of our knowledge, Wu et al.’s [42] work is the only study where the specific case of contact between an elastic–plastic sphere with a rigid surface is modelled in the dynamic framework, though there are several FEM studies that consider impact of an elastic sphere with an elastic–plastic substrate [22, 43, 44]. Wu et al. [42] have carried out two-dimensional FEM simulations of impact between an elastic-perfectly plastic sphere and a rigid wall. They conduct the simulations for different impact velocities and mechanical properties, to analyse the rebound behaviour of the sphere. This is done by investigating the coefficient of restitution, which is the ratio of rebound velocity to impact velocity, representing the energy loss during impact. Their results suggest that there is a critical velocity above which the sphere undergoes finite plastic deformation. At lower velocities, the coefficient of restitution is only dependent on the ratio of impact velocity to the yield velocity (Vi /Vy). However, at velocities higher than the critical value, the coefficient of restitution is not only dependent on (Vi /Vy), but also on the ratio of the effective Young’s modulus to yield strength (E*/Y) of the sphere. Based on these findings, Wu et al. propose equations for coefficient of restitution for both small deformation and finite plastic deformation regimes.

Nevertheless, it should be noted that although FEM is a well-established method, the problem of mesh distortion and element entanglement during large deformations affects the accuracy of the calculations. On the other hand, in recent years, a new method known as the Material Point Method (MPM) has been developed by Sulsky et al. [45] that overcomes this drawback. MPM discretises the material domain by a finite set of Lagrangian material points (integration points in FEM). Additionally, the space occupied by the body is discretised by an Eulerian background mesh. These material points are then tracked during the deformation process and each of them is assigned with a position and carries the state variables. The algorithm used in MPM is as follows: initially, information is mapped from the material points to the mesh nodes. Then, the solution to the momentum equations is calculated on the nodes. In the end, the nodal solution is mapped back to the material points to update their position and state variables [46]. The moving integration points naturally bypass the mesh distortion problems typical of FEM and provide a more convenient solution for problems concerning extensive deformation. There are few instances of MPM being used to study impact of materials that undergo plastic deformation [47,48,49]. The work of Li et al. [48] is of particular interest as it implements MPM to model impact of elastic-perfectly plastic disks of different mechanical properties on a rigid target. Their results show that the normalised contact law (force normalised by the contact force at yield and displacement normalised by radius of the particle) depends on and can be determined from E*/Y and Vi /Vy. Moreover, when the coefficient of restitution is expressed in terms of Vi /Vy, three distinct zones of deformation behaviour are identified: small deformation, full plasticity and large deformation. Li et al. suggest that the coefficient of restitution is only dependent on Vi /Vy in the first two zones and they express this dependency by formulating their own analytical expressions. For the third zone, their numerical results are in perfect agreement with Wu et al. [42] equation for coefficient of restitution.

Considering the drawbacks of the other methods and the fact that MPM has seldom been used for simulation of particle impact, it is timely to carry out a comprehensive study of the impact phenomenon by MPM, especially when large deformation is concerned. Following the approach of Wu et al. [42] and Li et al. [48], we analyse the effect of a much wider range of material properties, especially particle density, using three-dimensional MPM simulations to model high-velocity impact of single elastic-perfectly plastic particles on a rigid target. The analysis is focussed on the amount of energy dissipated through plastic deformation, and coefficient of restitution. Typically, the classical updated Lagrangian formulation of MPM (ULMPM) defines the reference configuration based on the configuration of the previous time step. This can lead to cell-crossing instability as the material points might not lie at an optimal position inside the background mesh elements. Moreover, the reference configuration is updated at each time step, which makes ULMPM relatively computationally expensive. Hence, the current study utilises the somewhat novel total Lagrangian formulation of MPM (TLMPM) to compensate for these drawbacks. In TLMPM, the reference configuration is fixed and the material points are always associated with their initial positions. This provides an efficient approach in terms of numerical stability and computational expenses.

2 Methodology

2.1 Explicit material point method

An implicit formulation of MPM coupled with Contact Dynamics (CD) method for treatment of frictional contact can be found in [50,51,52,53]. In this work, an explicit total Lagrangian formulation of MPM [46, 54] is coupled with a new implicit contact algorithm to model the particle.

To describe a continuum body in its initial configuration, a domain Ω0 is considered in ℝD, D being the domain dimension, with an external boundary \(\partial \) Ω0. The body is subjected to prescribed displacements and forces on its independent complementary parts of the boundary, i.e. the Dirichlet boundaries, \(\partial \) Ω0u and the Neumann boundaries, \(\partial \) Ω0f. The conservation of linear momentum of the body is expressed by Eq. (1) below:

$$ \nabla \cdot {\varvec{\varPi}}\left( {{\varvec{X}},t} \right) + {\varvec{b}}\left( {{\varvec{X}},t} \right) = \rho \left( {{\varvec{X}},t} \right){\varvec{a}}\left( {{\varvec{X}},t} \right)\,{\text{in}}\;\; \Omega_{0} , $$
(1)

where П(X,t), b(X,t), ρ(X,t) and a(X,t) are respectively the first Piola–Kirchhoff stress tensor, the body force, the density and the acceleration of a point at position X in its initial configuration at time t. The boundary conditions are described by:

$$ \left\{ {\begin{array}{*{20}l} {{\varvec{u}}\left( {{\varvec{X}},t} \right) = \hat{\user2{u}}\left( t \right)} \hfill & {{\text{on}} \;\;\partial \Omega_{0}^{u} ,} \hfill \\ {{\varvec{\varPi}}\left( {{\varvec{X}},t} \right).{\varvec{n}} = {\varvec{f}}\left( t \right)} \hfill & {{\text{on}} \;\;\partial \Omega_{0}^{f} ,} \hfill \\ \end{array} } \right. $$
(2)

where u(X,t) and û(t) are the displacement and the prescribed displacement fields, respectively. The terms f(t) and n respectively denote the prescribed load and the outward unit normal vector to \(\partial \) Ω0.

In the MPM, the body is divided into Np material points and mass is automatically conserved as each point is appointed with a fixed amount of mass. In order to solve Eq. (1), it is important to note that MPM is identical to FEM with the difference that the integration points (material points) are mobile. So, a weak form of Eq. (1), as described by Nezamabadi et al. [55] is first calculated using the relevant boundary conditions and is then discretized into Finite elements. Finally, MPM discretises the FEM integrals using a Dirac delta function and the resulting equation is shown by Eq. (3):

$${\varvec{M}}{\varvec{a}}_{{node}}\text{(}{{t}}{)}={\varvec{f}}_{{int}}{(}{{t}}{)}+{\varvec{f}}_{{ext}}{(}{{t}}{)}$$
(3)

where anode is the nodal acceleration and

\({\varvec{M}} = \mathop \sum \limits_{e = 1}^{{N_{e} }} \mathop \sum \limits_{p = 1}^{{N_{p}^{e} }} m_{p} {\varvec{N}}_{{p_{0} }}\) Lumped mass matrix,

\({\varvec{f}}_{{{int}}} (t) = \mathop \sum \limits_{e = 1}^{{N_{e} }} \mathop \sum \limits_{p = 1}^{{N_{p}^{e} }} {\varvec{G}}_{{p_{0} }}{\varvec{\varPi}}_{p} (t)V_{{p_{0} }}\) Internal force vector,

Sum of body forces and surface tractions, fS \({\varvec{f}}_{ext} (t) = \mathop \sum \limits_{e = 1}^{{N_{e} }} \mathop \sum \limits_{p = 1}^{{N_{p}^{e} }} {\varvec{N}}_{{p_{0} }} {\varvec{b}}_{p} (t) + {\varvec{f}}_{S} (t)\).

where Ne and Npe denote the number of the background mesh elements and that of the material points for an element, respectively. Also, mp and Vp0 are respectively the mass and volume of the material point in the reference (initial) configuration. Np0 is the shape function matrix (interpolation matrix) for a material point p and its function is to relate the quantities associated with the material points to the variables associated with the nodes of the element to which the material point belongs, at the reference configuration. Gp0 is the gradient of Np0. It should be noted that fS also includes the nodal contact forces, fC, between several bodies. In order to determine the nodal velocities vnode from the material point velocities vp, a weighted squares approach is used by solving the equation below:

$${\varvec{P}}_{{node}}{(}{{t}}{)}={\varvec{M}}{\varvec{v}}_{{node}}{(}{{t}}{)}=\sum_{{{e}}= {1} }^{{\varvec{N}}_{{e}}}\sum_{{{p}}= {1} }^{{\varvec{N}}_{{p}}^{{e}}}{{m}}_{{p}}{{{N}}}_{{{p}}_{0}}{\varvec{v}}_{{p}}{(}{{t}}{)}$$
(4)

where Pnode is the nodal momentum.

Equation (4) is solved using an explicit time integration procedure. Details of the algorithm used to update the material points position and state variables and the Contact Dynamics method to calculate the nodal contact forces can be found in detail in [56] and are not repeated here. An in-house MPM code is used for the current study.

2.2 Verification

In order to verify the method, the case of small deformation for impact of an elastic spherical particle is investigated through comparison with the analytical contact model provided by Johnson [20]. This is done by simulating normal impact of an elastic sphere at 1 m/s with a rigid wall placed 1.5 mm below it. The time step is set as 1 ns for the simulation. The sphere is discretised into 74,227 material points and 132,651 eight-node elements along with the cubic-spline shape function are used. The properties of the sphere are as follows: Radius, R = 12.5 mm, Young’s modulus, E = 4.9 MPa, Poisson’s ratio, υ = 0.25 and density, ρ = 1404 kg/m3.

According to Johnson [20], Hertz equation can be used as the contact law for impact of an elastic sphere undergoing small deformation, as shown by Eq. (5):

$$ F = \frac{4}{3}R^{1/2} E^{*} \delta^{3/2} $$
(5)

where F is the contact force, and δ is the displacement of the centre of the particle. E* is the effective Young’s modulus of the sphere defined as E* = E/(1–υ2). The relationship between δ and time t is given by:

$$ t = \frac{{\delta^{*} }}{{V_{i} }}\int {\frac{{d(\delta /\delta^{*} )}}{{\left[ {1 - (\delta /\delta^{*} )^{5/2} } \right]^{1/2} }}} $$
(6)

where:

$$ \delta^{*} = \left( {\frac{{15mV_{i}^{2} }}{{16R^{1/2} E^{*} }}} \right)^{2/5} $$
(7)

in which Vi is the impact velocity, δ* is the maximum displacement of the centre of the particle during impact and m is the mass of the particle. Deresiewicz [57] has evaluated Eq. (6) numerically, providing the values for δ/δ* and 2t/T, with T being the total contact time given by Johnson [20] according to Eq. (8):

$$T=\text{2.87}{\left(\frac{{{m}}^{2}}{{{R}}{{E}}^{{*}^{2}}{{V}}_{{i}}}\right)}^{1/5}$$
(8)

By calculating the maximum contact force, F*, from Eqs. (5) and (7), the change in contact force and displacement with time can be obtained in a dimensionless form. This is shown in Fig. 1 with the MPM results overlaid for comparison. It should be noted that the numerical total contact time is considered from the first instance the particle makes contact with the wall, to the time where contact is last detected. Considering Fig. 1, there is a good agreement between the analytical and the numerical results obtained from the MPM simulation, confirming the accuracy of the method.

Fig. 1
figure 1

Variation of contact force and displacement with time for impact of a sphere undergoing small elastic deformation; comparison between analytical [20] (dashed lines) and MPM results (discrete symbols)

Full size image

2.3 Case studies and simulation setup

As mentioned before, the current work aims to study the impact deformation behaviour of elastic-perfectly plastic particles having a wide range of material properties. Thus, four different densities of 1000, 2000, 4000 and 8000 kg/m3 are considered. As shown by Wu et al. [42] and Li et al. [48], the ratio of the effective Young’s modulus to yield strength of the material (E*/Y) plays an important role in the deformation behaviour of the particle. In the current work, three different values of 1, 10 and 100 GPa for Young’s modulus, and eight different values of 20, 40, 80, 160, 320, 640, 1280 and 2560 for the ratio of Young’s modulus to yield strength (E/Y) are investigated. This is done for the four different values of density, leading to a total of ninety six cases being studied. The values of yield strength corresponding to each case are shown in Table 1.

Table 1 The values of yield strength, Y, corresponding to each of the studied cases
Full size table

For all of the cases, particle radius is set as 250 μm and Poisson’s ratio as 0.35. For each case, the particle is normally impacting a wall placed 30 μm below it with an impact velocity of 50 m/s. After conducting a sensitivity analysis, a time step of 10 ps is selected and the particle is discretised into 74,227 material points. The mesh size is adjusted in a way that the ratio of the element size to the distance between the material points in each dimension is 1.5 for cases with a Young’s modulus of 100 GPa and 1.05 for cases with a Young’s modulus of 1 and 10 GPa. Damping is not applied.

3 Results and discussion

3.1 Extent of deformation

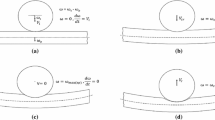
In order to display the diversity in the modelled extents of deformation, visualisations of the particle after rebound are shown in Fig. 2 for four different cases, as an example. Considering Fig. 2d, it is clear that the method allows for modelling very large deformation. However, it should be noted that for a number of the cases with a very low yield stress, as highlighted in the Appendix, the deformation is so extreme that no results are obtained.

Fig. 2
figure 2

Visualisation of the modelled particle after rebound for different cases: a ρ = 8000 kg/m3, E = 100 GPa, E/Y = 160; b ρ = 8000 kg/m3, E = 1 GPa, E/Y = 40; c ρ = 2000 kg/m3, E = 1 GPa, E/Y = 320 and d ρ = 1000 kg/m3, E = 1 GPa, E/Y = 1280. The orientation is chosen randomly to provide the best view of the extent of deformation

Full size image

3.2 Coefficient of restitution

The coefficient of restitution, e, is calculated using Eq. (9):

$${{e}} \, \text{=} \, \frac{{{V}}_{{r}}}{{{V}}_{{i}}}$$
(9)

where Vr and Vi are the absolute values of the rebound and impact velocity of the particle in the impact direction, respectively. In order to find Vr, the velocity of the particle in the impact direction is first calculated for each time step using the following equation:

$$\sum_{{{p}}= {1} }^{{{N}}_{{p}}}{{m}}_{{p}}{{{v}}}_{{p}}^{{z}}/\sum_{{{p}}= {1} }^{{{N}}_{{p}}}{{m}}_{{p}}$$
(10)

where vpz is the velocity of material point p in the impact direction (z axis here). Subsequently, the first instant at which the calculated velocity reaches a constant value after contact is lost is considered the rebound instant and the corresponding velocity is taken as the rebound velocity.

The coefficient of restitution obtained from Eq. (9) is plotted as a function of Vi /Vy for all the cases and presented in Fig. 3a, where Vy is the velocity required for the onset of plastic deformation, given by Johnson [20], as shown in Eq. (11). It should be noted that due to the high number of the case studies, no legends are displayed on any of the forthcoming graphs, and the reader is referred to Table 2 for the designation of the symbols.

$$ V_{y} = \left( {\frac{26Y}{\rho }} \right)^{1/2} \left( {\frac{Y}{{E^{*} }}} \right)^{2} $$
(11)
Fig. 3
figure 3

Coefficient of restitution, e, as a function of a Vi/Vy and b dimensionless group (Vi/Vy)/(E*/Y). The dashed line is the model of Wu et al. [42], shown by Eq. (12). For designation of the symbols, see Table 2. Note that the data points in each data set correspond to different densities

Full size image
Table 2 Symbol reference for all the graphs. NA denotes “not applicable”
Full size table

Considering Fig. 3a, when the coefficient of restitution is plotted as a function of Vi/Vy, a family of curves start to form where all the data points corresponding to a certain value of E/Y group together (in line with the findings of Wu et al. [42]). As a general trend, there is decrease in the coefficient of restitution with increase in Vi/Vy. Since Vi is the same for all the studied cases in the current work and the change in Vi /Vy is simply due to the change in Vy, this trend is expected; decrease in Y and increase in ρ, i.e. decrease in Vy translates to an earlier onset for plastic deformation, which in turn leads to a diminish in the recovered elastic energy. The trend is rapid for smaller values of E/Y (which generally correspond to small deformation) and slows down with further increase in E/Y. It should be noted that for the cases where the coefficient of restitution is less than 0.1, the trend becomes less orderly due to numerical errors, as the extreme deformation results in a lower number of material points per mesh cell.

According to Wu et al. [42], when (Vi/Vy)/(E*/Y)2 ≥ 0.008, the particle is considered to have undergone large deformation and the coefficient of restitution can be determined from Eq. (12).

$$ e_{ } = 0.62\left( {\frac{{V_{i} /V_{y} }}{{E^{*} /Y}}} \right)^{ - 1/2} $$
(12)

Consequently, the coefficient of restitution for the currently studied cases that fit this criterion (all cases except for three) is plotted as a function of (Vi/Vy)/(E*/Y) and shown in Fig. 3b, along with Wu et al. model superimposed for comparison. As seen in Fig. 3b, even though displaying e based on (Vi /Vy)/(E*/Y) unifies the data to a certain extent, Wu et al.’s model (dashed line) appears to deviate from the MPM simulation results for extensive deformations. This is due to the fact that only six different cases are considered in Wu et al. study (two and six different values for Young’s modulus and yield strength, respectively and one value for density), whereas the current work studies a much wider range of material properties. Moreover, the criterion suggested by Wu et al. to mark the boundary between small and large deformation is not deemed reasonable based on the results of the current work: there are multiple cases that fit the criterion yet their plastic strain in the impact direction is no more than 1% of the original particle diameter.

Whilst using the dimensionless group (Vi /Vy)/(E*/Y) does not fully unify the data for such a wide range of material properties, expressing the coefficient of restitution by the group [1-(2Yεp/ρVi2)]0.5 leads to better unification for the full range, as shown in Fig. 4. Here, εp is the equivalent plastic strain at the instant of rebound, calculated from Eq. (13) where εpij is the deviatoric plastic strain.

$$ \varepsilon_{p} = \sqrt {\frac{2}{3}\varepsilon_{ij}^{p} \varepsilon_{ij}^{p} } $$
(13)
Fig. 4
figure 4

Coefficient of restitution, e, as a function of the dimensionless group [1-(2Yεp/ρVi2)]0.5. For designation of the symbols, see Table 2

Full size image

With regards to Fig. 4, coefficient of restitution correlates well with the group 2Yεp/ρVi2 which describes the ratio of plastic work resulting from impact to the initial kinetic energy of an elastic-perfectly plastic particle. Moreover, presenting the data in this manner reveals that coefficient of restitution is not sensitive to Young’s modulus for elastic-perfectly plastic particles and the resultant decrease of e from unity is uniquely due to plastic deformation. Interestingly, the fitted line intercepts the x axis at about [1–(2Yεp/ρVi2)]0.5 = 0.2, suggesting that the particle will not rebound if more than 96% of the initial kinetic energy is dissipated by plastic deformation.

3.3 Plastic deformation

In order to probe the link between material properties and the plastic deformation induced by particle impact, the equivalent plastic strain, εp, is plotted against ρVi2/Y, as displayed in Fig. 5a. Considering the graph, εp increases with increase in ρVi2/Y which is expected as the increase in the latter is due to the decrease in the yield strength of the material or increase in the incident kinetic energy. Moreover, the data points remarkably unify and follow a common trajectory up to a certain point, after which they start to deviate from the common course. The unification is observed for data points corresponding to cases with relatively higher values of ρVi2 /Y. This suggests that for high-energy impact of highly deformable materials (large deformation), the extent to which an elastic-perfectly plastic particle undergoes plastic strain is only affected by the yield strength and the incident kinetic energy of the particle, with no sensitivity to Young’ modulus. Interestingly, when εp is expressed by the group (ρVi2 /Y)(E/Y)0.2, as shown in Fig. 5b, the data points corresponding to cases with relatively lower values of ρVi2 /Y unify only up to a certain value for the dimensionless group (approximately 0.1). This implies that for impact of elastic-perfectly plastic particles, if the yield strength of the material is relatively high or the incident kinetic energy is relatively low (small deformation), the plastic strain caused by impact is not only dependent on yield strength and the initial kinetic energy, but also on Young’s modulus of the material.

Fig. 5
figure 5

Equivalent plastic strain, εp, as a function of a ρVi2/Y and b dimensionless group (ρVi2/Y)(E/Y)0.2 for different cases. For designation of the symbols, see Table 2

Full size image

Considering the above discussion, a threshold value of 0.1 is chosen for the dimensionless group (ρVi2 /Y)(E/Y)0.2 to distinguish between these two regimes of behaviour: for cases with (ρVi2 /Y)(E/Y)0.2 < 0.1, the equivalent plastic strain is sensitive to Young’s modulus and can be obtained from the equation of the fitted line in Fig. 6a. As for cases with (ρVi2 /Y)(E/Y)0.2 > 0.1, plastic strain becomes independent of Young’s modulus, and the fitted line in Fig. 6b can be used for estimating the equivalent plastic strain. A summary is shown in Eq. (14).

$$ \varepsilon_{p} = \left\{ {\begin{array}{*{20}l} {0.32\left[ {\left( {\frac{{\rho V_{i}^{2} }}{Y}} \right)\left( \frac{E}{Y} \right)^{0.2} } \right]^{1.25} } \hfill & {{\text{if}} \left( {\frac{{\rho V_{i}^{2} }}{Y}} \right)\left( \frac{E}{Y} \right)^{0.2} < 0.1} \hfill \\ {0.47\left( {\frac{{\rho V_{i}^{2} }}{Y}} \right)^{1.03} } \hfill & {{\text{if}} \left( {\frac{{\rho V_{i}^{2} }}{Y}} \right)\left( \frac{E}{Y} \right)^{0.2} > 0.1} \hfill \\ \end{array} } \right. $$
(14)
Fig. 6
figure 6

Equivalent plastic strain, εp, as a function of a dimensionless group (ρVi2/Y)(E/Y)0.2 for cases with (ρVi2/Y)(E/Y)0.2 < 0.1 and b ρVi2/Y for cases with (ρVi2/Y)(E/Y)0.2 > 0.1. For designation of the symbols, see Table 2

Full size image

So as to further inspect the effect of material properties on plastic deformation of the impacting particle, the percentage of the initial kinetic energy dissipated by plastic deformation, Wp/Wi × 100, is plotted as a function of Vi/Vy and shown in Fig. 7a. Wp is the plastic work/energy, calculated, in simple terms, by deducting the recovered elastic energy from the total deformation energy for each time step. It should be noted that as damping is not considered in the system, after rebound, the recovered elastic energy is not dissipated. This results in fluctuations in the value of the elastic energy and consequently Wp, especially for soft particles. Thus, the values shown in Fig. 7a for Wp/Wi × 100 are average values, taken after rebound.

Fig. 7
figure 7

Percentage of the initial kinetic energy dissipated by plastic deformation, Wp/Wi × 100, as a function of a Vi /Vy and b dimensionless group (E/Y)1.5[ρ(Vi2–Vy2)/Y] for different cases. For designation of the symbols, see Table 2

Full size image

With regards to Fig. 7a, similar to what was observed for e, when Wp/Wi × 100 is expressed by Vi/Vy, a family of curves start to form based on E/Y, but the unification of data is poor. In general, there is increase in the percentage of the energy dissipated by plastic deformation with increase in Vi/Vy due to the decrease in Vy, i.e., the material getting more deformable. This trend is rapid and slows down as Vi/Vy is increased further. For the purpose of data unification, Wp/Wi × 100 is subsequently plotted against the dimensionless group (E/Y)1.5[ρ(Vi2–Vy2)/Y], as shown in Fig. 7b. In doing so, two regimes of behaviour can be recognised: for cases corresponding to small deformation, the percentage of the energy dissipated by plastic deformation is significantly affected by the combination of material properties expressed by the dimensionless group, where a rapid increase in Wp/Wi × 100 is observed with increase in (E/Y)1.5[ρ(Vi2–Vy2)/Y]. For this regime, a somewhat good unification is achieved up to the value of 40 for the dimensionless group, as shown in Fig. 8a. However, for the cases that undergo large deformation, Wp/Wi × 100 is less sensitive to (E/Y)1.5[ρ(Vi2–Vy2)/Y], suggesting that for extensive deformation, the amount of the induced plastic work as percentage of the initial kinetic energy cannot be fully described by this combination of material properties. It was previously observed that for the cases undergoing large deformation, the equivalent plastic strain is independent of Young’s modulus. Thus, as shown in Fig. 8b, Wp/Wi × 100 is alternatively expressed by ρ(Vi2–Vy2)/Y, for the cases which fit the criterion (E/Y)1.5[ρ(Vi2–Vy2)/Y] > 40, i.e. the data points that deviate from the common trajectory in Fig. 7b. Noting Fig. 8b, a better unification is achieved when the term (E/Y) is removed from the dimensionless group. This implies that for highly deformable materials, Young’s modulus has no influence on the percentage of the incident kinetic energy dissipated by plastic deformation of the particle during impact. However, it should be noted that the dependency of Wp/Wi × 100 on ρ(Vi2–Vy2)/Y for large deformation is still much weaker compared to that of Wp/Wi × 100 on (E/Y)1.5[ρ(Vi2–Vy2)/Y] for small deformation. This suggests that for extensively deformable materials (or very high-energy impacts), the deformation of the particle is potentially dominated by the rate of plastic flow. Nevertheless, the equations of the fitted lines in Fig. 8a and b can be used to get an approximate prediction for the percentage of the initial kinetic energy loss due to plastic deformation based on the material properties, as summarised in Eq. (15):

$$ \frac{{W_{p} }}{{W_{i} }} \times 100 = \left\{ {\begin{array}{*{20}l} {10.40\ln \left[ {\left( \frac{E}{Y} \right)^{1.5} \frac{{\rho \left( {V_{i}^{2} - V_{y}^{2} } \right)}}{Y}} \right] + 46.60 } \hfill & {{\text{if}} \left( \frac{E}{Y} \right)^{1.5} \left[ {\frac{{\rho \left( {V_{i}^{2} - V_{y}^{2} } \right)}}{Y}} \right] < 40} \hfill \\ {2.82\ln \left[ {\frac{{\rho \left( {V_{i}^{2} - V_{y}^{2} } \right)}}{Y}} \right] + 93.52 } \hfill & {{\text{if}} \left( \frac{E}{Y} \right)^{1.5} \left[ {\frac{{\rho \left( {V_{i}^{2} - V_{y}^{2} } \right)}}{Y}} \right] > 40} \hfill \\ \end{array} } \right. $$
(15)
Fig. 8
figure 8

Percentage of the initial kinetic energy dissipated by plastic deformation, Wp/Wi × 100, as a function of a dimensionless group (E/Y)1.5[ρ(Vi2–Vy2)/Y] for cases with (E/Y)1.5[ρ(Vi2–Vy2)/Y] < 40, and b ρ(Vi2–Vy2)/Y for cases with (E/Y)1.5[ρ(Vi2–Vy2)/Y] > 40. For designation of the symbols, see Table 2

Full size image

Another perspective from which plastic deformation can be studied is via investigating the extent to which the particle flattens due to impact. To this end, Hdeformed/H0, which describes the “flattening extent” of the particle, is plotted as a function of ρVi 2 /Y, as shown in Fig. 9. Hdeformed and H0 denote the length of the imaginary centre line that connects the top and bottom of the particle parallel to the impact direction, before and after impact, respectively (refer to Fig. 9). Consequently, decrease in Hdeformed/H0 implies an increase in the flattening extent. It should be mentioned that Hdeformed is measured after rebound as an average value, due to the fluctuations caused by the elastic waves in the particle.

Fig. 9
figure 9

Hdeformed /H0, as a function of ρVi2/Y for different cases. For designation of the symbols, see Table 2

Full size image

Considering Fig. 9, a master curve is obtained when Hdeformed /H0 is expressed by ρVi 2 /Y. Also, Hdeformed /H0 is intuitively decreasing with increase in ρVi 2 /Y, i.e. increase in the incident kinetic energy or decrease in the yield strength of the particle. The trend is initially slow when the material is less deformable, or the impact energy is low. However, the flattening extent increases at a faster rate for more deformable materials, or high-energy impacts. Figure 9 suggests that based on the value of yield strength and the incident kinetic energy, the flattening extent of the particle can be predicted. This is beneficial for high-velocity impact deposition techniques like cold spraying, where the particles experience extensive deformation, i.e. depending on the density and yield strength of the material, the impact velocity required to achieve a desired extent of flattening for the particles can be decided.

4 Conclusions

A numerical study of the impact phenomenon for elastic-perfectly plastic spherical particles has been carried out using MPM. The method is first verified through comparison with the analytical contact model of Johnson [20] for impact of an elastic sphere with a rigid wall. Subsequently, MPM is used to study the impact of an elastic-perfectly plastic particle with a rigid wall, covering a wide range of material properties and extents of deformation. The results show that for elastic-perfectly plastic particles with the studied range of material properties, the coefficient of restitution is not affected by Young’s modulus of the particle, but rather by the plastic flow. Additionally, it is found that for large deformation, the percentage of the initial kinetic energy loss due to plastic deformation, as well as the equivalent plastic strain are only affected by the particle yield strength and the impact energy. However, in the case of small deformation, the amount of the stored elastic energy also plays a role in the initial energy dissipation due to plastic deformation and the equivalent plastic strain. It is also shown that the extent to which the particle flattens due to impact correlates well with the incident kinetic energy and yield strength of the material. In the end, MPM proves to be a valuable tool for study of large deformation, compensating for the shortcomings of the other available methods.