Plasma effect in tape helix traveling-wave tube

Abstract

A linearized relativistic field theory of a plasma-loaded helix traveling-wave tube is presented for a configuration where a solid electron beam propagate through a sheath helix enclosed within a loss-free wall in which the gap between the helix and the outer wall is filled with a dielectric. Numerical study of the effect of plasma density on the phase velocity and growth rate has been done. Numerical results show that the plasma have different behaviors in different density limits.

Introduction

The relativistic traveling-wave tube (TWT) is an important high-power source of broad-band high-power microwave generation at centimeter wavelengths, developed over the last several decades [1–5]. One of the common features of a TWT is a slow-wave structure (SWS) such as a dielectric material, disk-loaded waveguide, or a helix [6–10]. The physical mechanism of operation is that the SWS reduces the phase velocity of the electromagnetic wave to synchronize it with the electron beam velocity, so that a strong interaction between the two can take place. This phenomenon of Cerenkov emission is the basis for all TWTs.

Pierce and his coworkers [11–13] employed the coupled-wave analysis in their pioneering work, and the analysis of TWT improved using linear theories based on the Maxwell’s equations in a sheath helix [14, 15]. The coupled-wave Pierce theory recovers the near-resonant limit. Both coupled-wave and field theories of TWT have discussed in [16] and [17]. Freund and coworkers developed the field theories of beam-loaded helix TWTs for tape helix model [18]. Freund and coworkers [19] described the numerical comparison between the complete dispersion equation and the Pierce model in helix TWT and shown that the coupled-wave theory breaks down for sufficiently high currents. The complete field theory is more exact than the coupled-wave theory. A common feature of all these theories is that they ignore the effects of any background plasma.

However, the residual gases in the container get ionized by the beam and plasma of sensible density is formed. It has been found experimentally that injection of plasma into the microwave devices may enhance the interaction and the output power. Plasma filling can also improve the transmission quality of electron beam, even make beam transmission without a guiding magnetic field [20, 21].

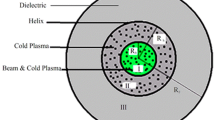
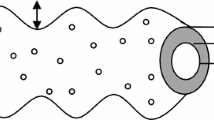
The specific geometry under study is illustrated in Fig. 1. A conducting waveguide of radius R_g encloses a hollow dielectric with an inner radius $R_{\text{h}}=R_{\text{d}}$. Background plasma with a uniform density distribution of radius $R_{\text{p}}$ is loaded inside the helix. The electron beam with radius $R_{\text{b}}<R_{\text{p}}$ propagates through the plasma.

Fig. 1

Cross-sectional view of the structure. The dielectric fills the region between R_h (helix radius) and R_g (conducting wall radius) and plasma fills the region between 0 and R_h. The relativistic electron beam along with the cold plasma fills the region between R = 0 and R_b

The purpose is to investigate the effects of dielectric constant, plasma density, axial guide magnetic field, and electron beam density on the phase velocity and growth rate. In this manuscript, we expand a complete self-consistent and relativistic field theory of the plasma-loaded helix TWT by solution of the relativistic fluid equation and Maxwell’s equations. The boundary condition includes three regions: (1) inside the beam that includes the electron beam and plasma, (2) between the beam and helix that includes the plasma, (3) between the helix and the wall that is dielectric.

The organization of the paper is as follows: “The model description” is determined in Sect. 2 through application of the appropriate boundary conditions upon the solution of Maxwell’s equations. In Sect. 3, we deal with “Numerical results and discussions” and finally some of the “Conclusions” are given in 4.

The model description

With the aid of the Maxwell and fluid equations the wave equations in regions I and II are given by Region I

$$({\mathrm{\nabla }}_{\perp }^2+{\mathit{\chi }}_{\pm ,\text{I},\text{bp}}^2)\mathit{\delta }{\widehat{E}}_z=0$$

(1)

$$({\mathrm{\nabla }}_{\perp }^2+{\mathit{\chi }}_{\pm ,\text{I},\text{bp}}^2)\mathit{\delta }{\widehat{B}}_z=0$$

(2)

Region II

$$({\mathrm{\nabla }}_{\perp }^2+{\mathit{\chi }}_{\pm ,\text{II},\text{p}}^2)\mathit{\delta }{\widehat{E}}_z=0$$

(3)

$$({\mathrm{\nabla }}_{\perp }^2+{\mathit{\chi }}_{\pm ,\text{II},\text{p}}^2)\mathit{\delta }{\widehat{B}}_z=0$$

(4)

$$\begin{array}{cc}\hfill {\mathit{\chi }}_{\pm ,\text{I},\text{bp}}=& {\left(2\left[1-\frac{{\mathit{\omega }}_{\text{b}}^2}{{\mathit{\gamma }}_{0\text{e}}^2\left(\mathit{\Delta }{\mathit{\omega }}^2-{\mathit{\Omega }}_{\text{ce}}^2\right)}+{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}Y3\right]\right)}^{-1}\hfill \\ \hfill & \times \left\{\left[1-\frac{{\mathit{\omega }}_{\text{b}}^2}{{\mathit{\gamma }}_{0\text{e}}^2\left(\mathit{\Delta }{\mathit{\omega }}^2-{\mathit{\Omega }}_{\text{ce}}^2\right)}+{\mathit{\Lambda }}_{sc}\left(1-2{\mathit{\alpha }}_{\text{b}}\right)\right]{\mathit{\chi }}_{}^2+{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}Y1\right\}\hfill \\ \hfill & \mp \left\{{\left[1-\frac{{\mathit{\omega }}_{\text{b}}^2}{{\mathit{\gamma }}_{0\text{e}}^2\left(\mathit{\Delta }{\mathit{\omega }}^2-{\mathit{\Omega }}_{\text{ce}}^2\right)}+{\mathit{\Lambda }}_{sc}\left(1-2{\mathit{\alpha }}_{\text{b}}\right)\right]}^2{\mathit{\chi }}_{}^4\right.\hfill \\ \hfill & +{\left({\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}Y1\right)}^2+2{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}Y1{\mathit{\chi }}_{}^2\left[1-\frac{{\mathit{\omega }}_{\text{b}}^2}{{\mathit{\lambda }}_{0\text{e}}^2\left(\mathit{\Delta }{\mathit{\omega }}^2-{\mathit{\Omega }}_{\text{ce}}^2\right)}+{\mathit{\Lambda }}_{\text{sc}}(1-2{\mathit{\alpha }}_{\text{b}})\right]\hfill \\ \hfill & {\left.-4{\mathit{\Lambda }}_{\text{sc}}{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}{\mathit{\chi }}_{}^4\left(1-\frac{{\mathit{\omega }}_{\text{b}}^2}{{\mathit{\gamma }}_{0\text{e}}^2\left(\mathit{\Delta }{\mathit{\omega }}^2-{\mathit{\Omega }}_{\text{ce}}^2\right)}\right)-4Y4{({\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}})}^2\right\}}^{1/2}\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathit{\chi }}_{\pm ,\text{II},\text{p}}=& {\mathit{\chi }}^2{\left(2\left[1-\frac{{\mathit{\omega }}_{\text{p}}^2{\mathit{\gamma }}_{0\text{e}}}{\left({\mathit{\omega }}^2-{({\mathit{\gamma }}_{0\text{e}}{\mathit{\Omega }}_{\text{ce}})}^2\right)}\right]\right)}^{-1}\hfill \\ \hfill & \times \left\{\left[1-\frac{{\mathit{\omega }}_{\text{p}}^2{\mathit{\gamma }}_{0\text{e}}}{\left({\mathit{\omega }}^2-{({\mathit{\gamma }}_{0\text{e}}{\mathit{\Omega }}_{\text{ce}})}^2\right)}+{\mathit{\Lambda }}_{\text{scp}}\left(1-2{\mathit{\alpha }}_{\text{p}}\right)\right]\right.\hfill \\ \hfill & \mp \left\{{\left[1-\frac{{\mathit{\omega }}_{\text{p}}^2{\mathit{\gamma }}_{0\text{e}}}{\left({\mathit{\omega }}^2-{({\mathit{\gamma }}_{0\text{e}}{\mathit{\Omega }}_{\text{ce}})}^2\right)}+{\mathit{\Lambda }}_{\text{scp}}(1-2{\mathit{\alpha }}_{\text{p}})\right]}^2\right.\hfill \\ \hfill & {\left.\left.-4{\mathit{\Lambda }}_{\text{scp}}{\mathit{\Lambda }}_{+\text{p}}{\mathit{\Lambda }}_{-\text{p}}\left(1-\frac{{\mathit{\omega }}_{\text{p}}^2{\mathit{\gamma }}_{0\text{e}}}{\left({\mathit{\omega }}^2-{({\mathit{\gamma }}_{0\text{e}}{\mathit{\Omega }}_{\text{ce}})}^2\right)}\right)\right\}\right\}}^{1/2}\hfill \\ \hfill {\mathit{\Lambda }}_{\text{sc}}=& 1-\frac{{\mathit{\omega }}_{\text{b}}^2}{\mathit{\Delta }{\mathit{\omega }}^2{\mathit{\gamma }}_{0\text{e}}^2},{\mathit{\Lambda }}_{\text{scp}}=1-\frac{{\mathit{\omega }}_{\text{p}}^2{\mathit{\gamma }}_{0\text{e}}}{{\mathit{\omega }}^2},\hfill \end{array}$$

$$\begin{array}{cc}\hfill Y_1& =-\frac{{\mathit{\chi }}^2{\mathit{\Lambda }}_{\text{sc}}(B_{\text{p}}+B_{\text{bp}})}{{\mathit{\Lambda }}_{\text{+ bp}}{\mathit{\Lambda }}_{-\text{bp}}}-\left(1+\frac{{\mathit{\alpha }}_{\text{b}}{\mathit{\Lambda }}_{0\text{b}}}{{\mathit{\Lambda }}_{\text{+ bp}}{\mathit{\Lambda }}_{-\text{bp}}}\right)\left(\frac{{\mathit{\chi }}^2{\mathit{\omega }}_{\text{p}}^2{\mathit{\gamma }}_{0\text{e}}}{{\mathit{\omega }}^2}\right)+\left(\frac{{\mathit{\chi }}^2{\mathit{\omega }}_{\text{p}}^2{\mathit{\gamma }}_{0\text{e}}}{{\mathit{\omega }}^2}\right)\left(\frac{\left(B_{\text{p}}+B_{\text{bp}}\right)}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\right)+\frac{\left(ck-\mathit{\omega }{\mathit{\beta }}_{0\text{e}}\right){\mathit{\chi }}^2{\mathit{\alpha }}_{\text{b}}}{\mathit{\Delta }{\mathit{\omega }}^2}\left\{\frac{\mathit{\Delta }\mathit{\omega }}{{\mathit{\Lambda }}_{+bp}{\mathit{\Lambda }}_{-bp}}(A_{\text{p}}\right.\hfill \\ \hfill & \left.+A_{\text{bp}})-\frac{i{\mathit{\Omega }}_{\text{ce}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}(D_{\text{p}}+D_{\text{bp}})\right\}+\frac{{\mathit{\chi }}^2{\mathit{\alpha }}_{\text{p}}(kc)}{{\mathit{\omega }}^2}{\overline{A}}_{\text{p},I,1}\hfill \end{array}$$

$$\begin{array}{cc}\hfill Y_3=& -\left\{1+\mathit{\Delta }{\mathit{\omega }}^{-2}{\mathit{\alpha }}_{\text{b}}{\left(ck-\mathit{\omega }{\mathit{\beta }}_{0\text{e}}\right)}^2\right.\hfill \\ \hfill & \times \left.\left[1+\frac{{\mathit{\alpha }}_{\text{b}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left({\mathit{\Lambda }}_{0\text{b}}+\frac{{\mathit{\Omega }}_{\text{ce}}^2}{\mathit{\Delta }{\mathit{\omega }}^2}\right)\right]\right\}\left(\frac{B_{\text{p}}+B_{\text{bp}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\right)\hfill \\ \hfill & +\left(1+\frac{{\mathit{\alpha }}_{\text{b}}{\mathit{\Lambda }}_{0\text{b}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\right)\left\{\frac{\left(ck-\mathit{\omega }{\mathit{\beta }}_{0\text{e}}\right){\mathit{\alpha }}_{\text{b}}}{\mathit{\Delta }{\mathit{\omega }}^2}\left\{\frac{\mathit{\Delta }\mathit{\omega }}{{\mathit{\Lambda }}_{\text{+ bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left(A_{\text{p}}+A_{\text{bp}}\right)\right.\right.\hfill \\ \hfill & \left.\left.-\frac{i{\mathit{\Omega }}_{\text{ce}}}{{\mathit{\Lambda }}_{\text{+ bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left(D_{\text{p}}+D_{\text{bp}}\right)\right\}+\frac{{\mathit{\alpha }}_{\text{p}}\left(kc\right)}{{\mathit{\omega }}^2}{\overline{A}}_{\text{p},I,1}\right\}\hfill \\ \hfill & +\left(\frac{B_{\text{p}}+B_{\text{bp}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\right)\left\{\frac{\left(ck-\mathit{\omega }{\mathit{\beta }}_{0\text{e}}\right){\mathit{\alpha }}_{\text{b}}}{\mathit{\Delta }{\mathit{\omega }}^2}\left\{\frac{\mathit{\Delta }\mathit{\omega }}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left(A_{\text{p}}+A_{\text{bp}}\right)\right.\right.\hfill \\ \hfill & \left.E_{\text{p}}-\frac{i{\mathit{\Omega }}_{\text{ce}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left(B_{\text{p}}+B_{\text{bp}}\right)\right]\hfill \\ \hfill & +\frac{i{\mathit{\alpha }}_{\text{b}}{\mathit{\Omega }}_{\text{ce}}\left(ck-\mathit{\omega }{\mathit{\beta }}_{0\text{e}}\right)}{\mathit{\Delta }{\mathit{\omega }}^2}\left[1+\frac{{\mathit{\alpha }}_{\text{b}}}{{\mathit{\Lambda }}_{\text{+ bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left(1+{\mathit{\Lambda }}_{0\text{b}}\right)\right]\left[\frac{D_{\text{p}}+D_{\text{bp}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\right]\hfill \\ \hfill & +\left\{\left[\frac{{\mathit{\alpha }}_{\text{b}}\left(ck-\mathit{\omega }{\mathit{\beta }}_{0\text{e}}\right)}{\mathit{\Delta }{\mathit{\omega }}^2}\right]\left[\frac{\mathit{\Delta }\mathit{\omega }}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\right.\right.\hfill \\ \hfill & \left.E_{\text{p}}-\frac{i{\mathit{\Omega }}_{\text{ce}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left(B_{\text{p}}+B_{\text{bp}}\right)\right]\hfill \\ \hfill & \left.+\frac{{\mathit{\alpha }}_{\text{p}}(kc)}{{\mathit{\omega }}^2}{\overline{A}}_{\text{p},I,2}\right\}\left\{\frac{i{\mathit{\alpha }}_{\text{b}}{\mathit{\Omega }}_{\text{ce}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\frac{\left(ck-\mathit{\omega }{\mathit{\beta }}_{0\text{e}}\right)}{\mathit{\Delta }{\mathit{\omega }}^2}\right\}\hfill \\ \hfill & +\left[\frac{D_{\text{p}}+D_{bp}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\right]\left\{\left[\frac{{\mathit{\alpha }}_{\text{b}}\left(ck-\mathit{\omega }{\mathit{\beta }}_{0\text{e}}\right)}{\mathit{\Delta }{\mathit{\omega }}^2}\right]\left[\frac{\mathit{\Delta }\mathit{\omega }}{{\mathit{\Lambda }}_{+bp}{\mathit{\Lambda }}_{-bp}}{E}_p-\frac{i{\mathit{\Omega }}_{\text{ce}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left(B_{\text{p}}+B_{\text{bp}}\right)\right]+\frac{{\mathit{\alpha }}_{\text{p}}\left(kc\right)}{{\mathit{\omega }}^2}{\overline{A}}_{\text{p},I,2}\right\}\hfill \end{array}$$

$$\begin{array}{cc}& Y_4=Y_3\left[{\mathit{\chi }}^4{\mathit{\Lambda }}_{\text{sc}}-{\mathit{\chi }}^4\frac{{\mathit{\omega }}_{\text{p}}^2{\mathit{\gamma }}_{0\text{e}}}{{\mathit{\omega }}^2}\right]-{\mathit{\chi }}^4\frac{{\mathit{\omega }}_{\text{p}}^2{\mathit{\gamma }}_{0\text{e}}}{{\mathit{\omega }}^2}\left[\left(1+\frac{{\mathit{\alpha }}_{\text{b}}{\mathit{\Lambda }}_{0\text{b}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\right)\right.\hfill \\ \hfill & \left\{1+{\mathit{\alpha }}_{\text{b}}{\left(ck-\mathit{\omega }{\mathit{\beta }}_{0\text{e}}\right)}^2\left[1+\frac{{\mathit{\alpha }}_{\text{b}}}{{\mathit{\Lambda }}_{\text{+ bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left({\mathit{\Lambda }}_{0\text{b}}+\frac{{\mathit{\Omega }}_{\text{ce}}^2}{\mathit{\Delta }{\mathit{\omega }}^2}\right)\right]/\mathit{\Delta }{\mathit{\omega }}^2\right\}\hfill \\ \hfill & \left.-\frac{{\mathit{\alpha }}_{\text{b}}^2{\mathit{\Omega }}_{\text{ce}}^2{\left(ck-\mathit{\omega }{\mathit{\beta }}_{0\text{e}}\right)}^2}{\mathit{\Delta }{\mathit{\omega }}^4{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left\{1+\frac{{\mathit{\alpha }}_{\text{b}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left(1+{\mathit{\Lambda }}_{0\text{b}}\right)\right\}\right]\hfill \\ \hfill \end{array}$$

$$\begin{array}{cc}& {\overline{B}}_{\text{p},II,1}=ck\left[1+\frac{{\mathit{\alpha }}_{\text{p}}}{{\mathit{\Lambda }}_{+\text{p}}{\mathit{\Lambda }}_{-\text{p}}}[{\mathit{\Lambda }}_{0\text{p}}+\frac{{({\mathit{\Omega }}_{\text{ce}}{\mathit{\gamma }}_{0\text{e}})}^2}{{\mathit{\omega }}^2}]\right],\hfill \\ \hfill & B_{\text{p},II,2}={\mathit{\Omega }}_{\text{ce}}{\mathit{\gamma }}_{0\text{e}}\left[1+\frac{{\mathit{\alpha }}_{\text{p}}}{{\mathit{\Lambda }}_{\text{+ p}}{\mathit{\Lambda }}_{-\text{p}}}[1+{\mathit{\Lambda }}_{0\text{p}}]\right].\hfill \end{array}$$

$$\begin{array}{cc}& {\overline{A}}_{\text{e},\text{I},1}=\left(kc-\mathit{\omega }{\mathit{\beta }}_{0\text{e}}\right)\left[1+\frac{{\mathit{\alpha }}_{\text{b}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left({\mathit{\Lambda }}_{0\text{b}}+\frac{{\mathit{\Omega }}_{\text{ce}}^2}{\mathit{\Delta }{\mathit{\omega }}^2}\right)\right]\hfill \\ \hfill & +\frac{\mathit{\Delta }\mathit{\omega }}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}[\left(A_{\text{p}}+A_{\text{bp}}\right]-\frac{i{\mathit{\Omega }}_{\text{ce}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}[(D_{\text{p}}+D_{\text{bp}}]\hfill \\ \hfill & {\overline{A}}_{\text{e},\text{I},2}=i{\mathit{\Omega }}_{\text{ce}}\left[1+\frac{{\mathit{\alpha }}_{\text{b}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left(1+{\mathit{\Lambda }}_{0\text{b}}\right)\right]\hfill \\ \hfill & +\frac{\mathit{\Delta }\mathit{\omega }}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}{E}_{\text{p}}-\frac{i{\mathit{\Omega }}_{\text{ce}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}[B_{\text{p}}+B_{\text{bp}}]\hfill \\ \hfill & {\overline{A}}_{\text{p},\text{I,}1}=kc+\frac{{\mathit{\alpha }}_{\text{b}}\left(kc-\mathit{\omega }{\mathit{\gamma }}_{0\text{e}}\right)}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left[\frac{\mathit{\omega }}{\mathit{\Delta }\mathit{\omega }}{\mathit{\Lambda }}_{0\text{b}}+\frac{{\mathit{\Omega }}_{\text{ce}}^2{\mathit{\gamma }}_{0e}}{\mathit{\Delta }{\mathit{\omega }}^2})\right]\hfill \\ \hfill & +\frac{\mathit{\omega }}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}[\left(A_{\text{p}}+A_{\text{bp}}\right]-\frac{i{\mathit{\Omega }}_{\text{ce}}{\mathit{\gamma }}_{0\text{e}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}[(D_{\text{p}}+D_{\text{bp}}]\hfill \\ \hfill & {\overline{A}}_{\text{p},\text{I},2}=i{\mathit{\Omega }}_{\text{ce}}{\mathit{\gamma }}_{0\text{e}}\left\{1+\frac{{\mathit{\alpha }}_{\text{b}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left[\frac{\mathit{\omega }}{\mathit{\Delta }\mathit{\omega }{\mathit{\gamma }}_{0\text{e}}}+{\mathit{\Lambda }}_{0\text{b}}\right]\right\}\hfill \\ \hfill & +\frac{\mathit{\omega }}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}{E}_p-\frac{i{\mathit{\Omega }}_{\text{ce}}{\mathit{\gamma }}_{0\text{e}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}[B_{\text{p}}+B_{\text{bp}}]\hfill \\ \hfill \end{array}$$

Having applied the boundary condition at the waveguide wall and edge of the beam, we obtain

$$\mathit{\delta }{\widehat{E}}_z=\left\{\begin{array}{c}A{J}_0\left({\mathit{\chi }}_{\pm ,I,\text{bp}}r\right),0\le r\le R_{\text{b}}\hfill \\ A\left[a^{\left(1\right)}{J}_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}r\right)+a^{\left(2\right)}{Y}_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}r\right)\right]+iF\left[c^{\left(1\right)}{J}_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}r\right)+c^{\left(2\right)}{Y}_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}r\right)\right],R_{\text{b}}<r\le R_{\text{h}}\hfill \\ DW\left(q{R}_{\text{g}},qr\right),R_{\text{h}}<r\le R_{\text{g}}\hfill \end{array}\right.$$

(5)

$$\mathit{\delta }{\widehat{B}}_z=\left\{\begin{array}{c}F{J}_0\left({\mathit{\chi }}_{\pm ,I,\text{bp}}r\right),0\le r\le R_{\text{b}}\hfill \\ F\left[b^{\left(1\right)}{J}_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}r\right)+b^{\left(2\right)}{Y}_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}r\right)\right]+iA\left[d^{\left(1\right)}{J}_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}r\right)+d^{\left(2\right)}{Y}_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}r\right)\right],R_{\text{b}}<r\le R_{\text{h}}\hfill \\ K{W}^{{}^{\prime }}(q{R}_{\text{g}},qr),R_{\text{h}}<r\le R_{\text{g}}\hfill \end{array}\right.$$

(6)

$$\begin{array}{cc}& q={(\mathit{\epsilon }{\mathit{\omega }}^2/c^2-k^2)}^{1/2}{a}^{\left(1\right)}=\frac{1}{G^{\left(2\right)}}\left[-J_0\left({\mathit{\chi }}_{\pm ,\text{I},\text{bp}}{R}_{\text{b}}\right){\mathit{\varsigma }}_{14}+Y_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right){\mathit{\varsigma }}_{12}\right],a^{\left(2\right)}=\frac{1}{G^{\left(2\right)}}\left[J_0\left({\mathit{\chi }}_{\pm ,\text{I},\text{bp}}{R}_{\text{b}}\right){\mathit{\varsigma }}_{13}-J_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right){\mathit{\varsigma }}_{12}\right],\hfill \\ \hfill & c^{\left(1\right)}=-\frac{1}{G^{\left(2\right)}}\left[Y_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right){\mathit{\varsigma }}_{11}\right],c^{\left(2\right)}=\frac{1}{G^{\left(2\right)}}\left[J_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right){\mathit{\varsigma }}_{11}\right],b^{\left(1\right)}=\frac{1}{G^{\left(1\right)}}\left[-J_0\left({\mathit{\chi }}_{\pm ,\text{I},\text{bp}}{R}_{\text{b}}\right){\mathit{\vartheta }}_{14}+Y_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right){\mathit{\vartheta }}_{12}\right],\hfill \\ \hfill & b^{\left(2\right)}=\frac{1}{G^{\left(1\right)}}\left[-J_0\left({\mathit{\chi }}_{\pm ,\text{I},\text{bp}}{R}_{\text{b}}\right){\mathit{\vartheta }}_{13}-J_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right){\mathit{\vartheta }}_{12}\right],d^{\left(2\right)}=-\frac{1}{G^{\left(1\right)}}\left[J_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right){\mathit{\vartheta }}_{11}\right],G^{\left(1\right)}=\left[Y_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right){\mathit{\vartheta }}_{13}-J_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right){\mathit{\vartheta }}_{14}\right],\hfill \\ \hfill & d^{\left(1\right)}=\frac{1}{G^{\left(1\right)}}\left[Y_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right){\mathit{\vartheta }}_{11}\right],G^{\left(2\right)}=\left[Y_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right){\mathit{\vartheta }}_{13}-J_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_b\right){\mathit{\vartheta }}_{14}\right],\hfill \\ \hfill & {\mathit{\vartheta }}_{11}=\frac{{\mathit{\chi }}_{\pm ,\text{II},\text{p}}}{{\mathit{\chi }}_{\pm ,\text{I},\text{bp}}}\left[\mathit{\Theta }7\frac{{\mathit{\chi }}_{\pm ,\text{II},\text{p}}}{{\mathit{\chi }}_{\pm ,\text{I,bp}}}{J}_0\left({\mathit{\chi }}_{\pm ,\text{I},\text{bp}}{R}_{\text{b}}\right)-S{J}_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right)\right]\left[\mathit{\Theta }4\mathit{\Theta }7-\mathit{\Theta }3\mathit{\Theta }8\right]-\frac{{\mathit{\chi }}_{\pm ,\text{II},\text{p}}}{{\mathit{\chi }}_{\pm ,\text{I},\text{bp}}}\left[\mathit{\Theta }7Y_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right)-\mathit{\Theta }8J_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right)\right]\hfill \\ \hfill & [P\mathit{\Theta }7-S\mathit{\Theta }3]\hfill \\ \hfill & {\mathit{\vartheta }}_{12}=\frac{{\mathit{\chi }}_{\pm ,\text{II},\text{p}}}{{\mathit{\chi }}_{\pm ,\text{I},\text{bp}}}\left[T{J}_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right)\right]\left[\mathit{\Theta }4\mathit{\Theta }7-\mathit{\Theta }3\mathit{\Theta }8\right]-[Q\mathit{\Theta }7+T\mathit{\Theta }3]\frac{{\mathit{\chi }}_{\pm ,\text{II},\text{p}}}{{\mathit{\chi }}_{\pm ,\text{I},\text{bp}}}\left[\mathit{\Theta }7Y_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)-\mathit{\Theta }8J_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right)\right]\hfill \\ \hfill & {\mathit{\vartheta }}_{13}={\left(\frac{{\mathit{\chi }}_{\pm ,\text{II},\text{p}}}{{\mathit{\chi }}_{\pm ,\text{I},\text{bp}}}\right)}^2\left[\mathit{\Theta }4\mathit{\Theta }7-\mathit{\Theta }3\mathit{\Theta }8\right]\left[\mathit{\Theta }5J_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_b\right)\right]-{\left(\frac{{\mathit{\chi }}_{\pm ,\text{II},\text{p}}}{{\mathit{\chi }}_{\pm ,\text{I},\text{bp}}}\right)}^2\left[\mathit{\Theta }7Y_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right)-\mathit{\Theta }8J_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right)\right][\mathit{\Theta }7\mathit{\Theta }1+\mathit{\Theta }5\mathit{\Theta }3]\hfill \\ \hfill & {\mathit{\vartheta }}_{14}={\left(\frac{{\mathit{\chi }}_{\pm ,\text{II},\text{p}}}{{\mathit{\chi }}_{\pm ,\text{I},\text{bp}}}\right)}^2\left[\mathit{\Theta }6J_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right)\right]\left[\mathit{\Theta }4\mathit{\Theta }7-\mathit{\Theta }3\mathit{\Theta }8\right]-{\left(\frac{{\mathit{\chi }}_{\pm ,\text{II},\text{p}}}{{\mathit{\chi }}_{\pm ,\text{I,bp}}}\right)}^2\left[\mathit{\Theta }7Y_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right)-\mathit{\Theta }8J_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right)\right][\mathit{\Theta }2\mathit{\Theta }7+\mathit{\Theta }6\mathit{\Theta }3]\hfill \\ \hfill & {\mathit{\varsigma }}_{11}=\frac{{\mathit{\chi }}_{\pm ,\text{II},\text{p}}}{{\mathit{\chi }}_{\pm ,\text{I},\text{bp}}}\left[\mathit{\Theta }5\frac{{\mathit{\chi }}_{\pm ,\text{II},\text{p}}}{{\mathit{\chi }}_{\pm ,\text{I},\text{bp}}}{J}_0\left({\mathit{\chi }}_{\pm ,\text{I},\text{bp}}{R}_{\text{b}}\right)-T{J}_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right)\right]\left[\mathit{\Theta }2\mathit{\Theta }5-\mathit{\Theta }1\mathit{\Theta }6\right]-\frac{{\mathit{\chi }}_{\pm ,\text{II},\text{p}}}{{\mathit{\chi }}_{\pm ,\text{I},\text{bp}}}\left[\mathit{\Theta }5Y_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right)-\mathit{\Theta }6J_0\left({\mathit{\chi }}_{\pm ,\text{II},\text{p}}{R}_{\text{b}}\right)\right]\hfill \\ \hfill & [Q\mathit{\Theta }5-T\mathit{\Theta }1]\hfill \\ \hfill & {\mathit{\varsigma }}_{12}=\frac{{\mathit{\chi }}_{\pm ,\text{II},\text{p}}}{{\mathit{\chi }}_{\pm ,\text{I,bp}}}\left[S{J}_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_b\right)\right]\left[\mathit{\Theta }2\mathit{\Theta }5-\mathit{\Theta }1\mathit{\Theta }6\right]-[P\mathit{\Theta }5+S\mathit{\Theta }1]\frac{{\mathit{\chi }}_{\pm ,\text{II,p}}}{{\mathit{\chi }}_{\pm ,\text{I,bp}}}[\mathit{\Theta }5Y_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_b\right)-\mathit{\Theta }6J_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)]\hfill \\ \hfill & {\mathit{\varsigma }}_{13}={\left(\frac{{\mathit{\chi }}_{\pm ,\text{II,p}}}{{\mathit{\chi }}_{\pm ,\text{I,bp}}}\right)}^2\left[\mathit{\Theta }2\mathit{\Theta }5-\mathit{\Theta }1\mathit{\Theta }6\right]\left[\mathit{\Theta }7J_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)\right]-{\left(\frac{{\mathit{\chi }}_{\pm ,\text{II,p}}}{{\mathit{\chi }}_{\pm ,\text{I,bp}}}\right)}^2\left[\mathit{\Theta }5Y_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)-\mathit{\Theta }6J_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)\right][\mathit{\Theta }3\mathit{\Theta }5+\mathit{\Theta }7\mathit{\Theta }1]\hfill \\ \hfill & {\mathit{\varsigma }}_{14}={\left(\frac{{\mathit{\chi }}_{\pm ,\text{II,p}}}{{\mathit{\chi }}_{\pm ,\text{I},\text{bp}}}\right)}^2\left[\mathit{\Theta }8J_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)\right]\left[\mathit{\Theta }2\mathit{\Theta }5-\mathit{\Theta }1\mathit{\Theta }6\right]-{\left(\frac{{\mathit{\chi }}_{\pm ,\text{II,p}}}{{\mathit{\chi }}_{\pm ,\text{I,bp}}}\right)}^2\left[\mathit{\Theta }5Y_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)-\mathit{\Theta }6J_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)\right][\mathit{\Theta }4\mathit{\Theta }5+\mathit{\Theta }1\mathit{\Theta }8]\hfill \\ \hfill \end{array}$$

$$\begin{array}{cc}& W\left(q{R}_{\text{g}},qr\right)=Y_0\left(q{R}_{\text{g}}\right)J_0\left(qr\right)-J_0\left(q{R}_{\text{g}}\right)Y_0\left(qr\right),W^{\prime }\left(q{R}_{\text{g}},qr\right)=Y_0^{{}^{\prime }}\left(q{R}_{\text{g}}\right)J_0\left(qr\right)-J_0^{{}^{\prime }}\left(q{R}_{\text{g}}\right)Y_0\left(qr\right).\hfill \\ \hfill & P=\frac{1}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left\{\left[{\mathit{\alpha }}_{\text{b}}{\mathit{\Lambda }}_{0\text{b}}\frac{\left(ck-\mathit{\omega }{\mathit{\beta }}_{0\text{e}}\right)}{\mathit{\Delta }\mathit{\omega }}+{\mathit{\alpha }}_{\text{p}}{\mathit{\Lambda }}_{0\text{p}}\frac{ck}{\mathit{\omega }}\right]J_{-1}\left({\mathit{\chi }}_{\pm ,\text{I},\text{bp}}{R}_{\text{b}}\right)-{\mathit{\alpha }}_{\text{b}}{\mathit{\alpha }}_{\text{p}}\left\{J_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,I,\text{bp}}{R}_{\text{b}}\right)\left\{\left(ck-\mathit{\omega }{\mathit{\beta }}_{0\text{e}}\right)\left[\frac{1}{\mathit{\Delta }{\mathit{\omega }}^2}+\frac{{\mathit{\Omega }}_{ce}{\mathit{\beta }}_{0\text{e}}}{\mathit{\omega }\mathit{\Delta }{\mathit{\omega }}^2}\right.\right.\right.\right.\hfill \\ \hfill & +\left.\left.\left.\left.\frac{{\mathit{\Omega }}_{\text{ce}}}{\mathit{\Delta }{\mathit{\omega }}^2}-\frac{{\mathit{\Omega }}_{\text{ce}}{\mathit{\beta }}_{0\text{e}}}{\mathit{\omega }\mathit{\Delta }\mathit{\omega }}\right]+ck\left[\frac{1}{{\mathit{\omega }}^2}+\frac{{\mathit{\Omega }}_{\text{ce}}}{\mathit{\Delta }\mathit{\omega }{\mathit{\omega }}^2}+\frac{{\mathit{\Omega }}_{\text{ce}}{\mathit{\beta }}_{0e}}{{\mathit{\omega }}^2}-\frac{{\mathit{\Omega }}_{\text{ce}}}{\mathit{\omega }\mathit{\Delta }\mathit{\omega }}\right]\right\}\right\}\right\}\hfill \\ \hfill \end{array}$$

$$Q=\left\{-J_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)+\frac{1}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left\{-[{\mathit{\alpha }}_{\text{b}}{\mathit{\Lambda }}_{0\text{b}}+{\mathit{\alpha }}_{\text{p}}{\mathit{\Lambda }}_{0\text{p}}]J_{-1}\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)+{\mathit{\Lambda }}_{\text{bp}}\left\{J_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)\left\{-\frac{2{\mathit{\Omega }}_{\text{ce}}^2{\mathit{\gamma }}_{0\text{e}}}{\mathit{\omega }\mathit{\Delta }\mathit{\omega }}+2\right\}\right\}\right\}\right\}$$

$$\begin{array}{cc}& \mathit{\Theta }1=-J_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)-R_p{J}_{-1}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right),\mathit{\Theta }2=Y_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)-R_{\text{p}}{Y}_{-1}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right),\mathit{\Theta }3=\frac{kc{R}_{\text{p}}}{\mathit{\omega }}{J}_{-1}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right),\hfill \\ \hfill & \mathit{\Theta }4=\frac{kc{R}_{\text{p}}}{\mathit{\omega }}{Y}_{-1}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right),\mathit{\Theta }5=\frac{\mathit{\omega }}{2ck}[\left({\mathit{\epsilon }}_{\text{+ p}}+2R_{\text{p}}{\mathit{\epsilon }}_{+\text{p}}-1\right)J_{-1}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)+({\mathit{\epsilon }}_{-\text{p}}-1)J_1\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)],\hfill \\ \hfill & \mathit{\Theta }6=\frac{\mathit{\omega }}{2ck}[\left({\mathit{\epsilon }}_{+\text{p}}+2R_{\text{p}}{\mathit{\epsilon }}_{\text{+ p}}-1\right)Y_{-1}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)+({\mathit{\epsilon }}_{-\text{p}}-1)Y_1\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)],\hfill \\ \hfill & \mathit{\Theta }7=J_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)+\frac{1}{2}[\left({\mathit{\epsilon }}_{+\text{p}}+2R_{\text{p}}{\mathit{\epsilon }}_{\text{+ p}}-1\right)J_{-1}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)-({\mathit{\epsilon }}_{-\text{p}}-1)J_1\left({\mathit{\chi }}_{\pm ,\text{II,}p}{R}_{\text{b}}\right)],\hfill \\ \hfill & \mathit{\Theta }8=Y_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)+\frac{1}{2}[\left({\mathit{\epsilon }}_{+\text{p}}+2R_{\text{p}}{\mathit{\epsilon }}_{+\text{p}}-1\right)Y_{-1}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)-({\mathit{\epsilon }}_{-\text{p}}-1)Y_1\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{b}}\right)],\hfill \\ \hfill & S=J_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)+\frac{\mathit{\omega }}{2ck}\frac{\left(ck-\mathit{\omega }{\mathit{\beta }}_{0\text{e}}\right)}{\mathit{\Delta }\mathit{\omega }}\left[{\mathit{\epsilon }}_{+\text{b}}+\frac{2{\mathit{\alpha }}_{\text{b}}{\mathit{\Lambda }}_{0\text{b}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}{\mathit{\epsilon }}_{+\text{b}}-1\right]J_{-1}\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)-\frac{1}{2}({\mathit{\epsilon }}_{-\text{b}}-1)J_1\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)+\frac{1}{2}\left\{\left[{\mathit{\epsilon }}_{+\text{p}}+\right.\right.\hfill \\ \hfill & \left.\left.\frac{2{\mathit{\alpha }}_{\text{p}}{\mathit{\Lambda }}_{0\text{p}}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}{\mathit{\epsilon }}_{+p}-1\right]J_{-1}\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)-({\mathit{\epsilon }}_{-\text{p}}-1)J_1\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)\right\}+FF1,\hfill \\ \hfill \end{array}$$

$$T=\frac{\mathit{\omega }}{2ck}[({\mathit{\epsilon }}_{+\text{b}}+\frac{2{\mathit{\alpha }}_{\text{b}}{\mathit{\Lambda }}_{0b}}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}{\mathit{\epsilon }}_{+b}-1)J_{-1}\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)+({\mathit{\epsilon }}_{-\text{b}}-1)J_1\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)]+\frac{\mathit{\omega }}{2ck}\left[\left({\mathit{\epsilon }}_{+\text{p}}+\frac{2{\mathit{\alpha }}_{\text{p}}{\mathit{\Lambda }}_{0\text{p}}}{{\mathit{\Lambda }}_{\text{+ bp}}{\mathit{\Lambda }}_{-\text{bp}}}{\mathit{\epsilon }}_{+\text{p}}-1\right)J_{-1}\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)+({\mathit{\epsilon }}_{-\text{p}}-1)J_1\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)\right]+FF2,$$

$$\begin{array}{cc}& FF1=\frac{\mathit{\omega }}{ck}\frac{1}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left\{-\frac{{\mathit{\omega }}_b^2}{{\mathit{\omega }}^2}\frac{\mathit{\Delta }\mathit{\omega }{\mathit{\alpha }}_{\text{p}}{\mathit{\Lambda }}_{0\text{p}}}{\left(\mathit{\Delta }\mathit{\omega }-{\mathit{\Omega }}_{\text{ce}}\right)}\frac{ck}{\mathit{\omega }}\frac{{\mathit{\omega }}_p^2{\mathit{\gamma }}_{0\text{e}}}{\mathit{\omega }}\frac{{\mathit{\alpha }}_b{\mathit{\Lambda }}_{0\text{b}}}{\left(\mathit{\omega }-{\mathit{\gamma }}_{0\text{e}}{\mathit{\Omega }}_{\text{ce}}\right)}\frac{\left(ck-\mathit{\omega }{\mathit{\beta }}_{0\text{e}}\right)}{\mathit{\Delta }\mathit{\omega }}\right\}{J}_{-1}\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)+\frac{\mathit{\omega }}{ck}({\mathit{\epsilon }}_{rr,I}R1+i{\mathit{\epsilon }}_{r\mathit{\theta },I}R2),\hfill \\ \hfill & FF2=\frac{\mathit{\omega }}{ck}\frac{1}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left\{-\frac{{\mathit{\omega }}_b^2}{{\mathit{\omega }}^2}\frac{\mathit{\Delta }\mathit{\omega }{\mathit{\alpha }}_{\text{p}}{\mathit{\Lambda }}_{0\text{p}}}{\left(\mathit{\Delta }\mathit{\omega }-{\mathit{\Omega }}_{\text{ce}}\right)}\frac{{\mathit{\omega }}_p^2{\mathit{\gamma }}_{0\text{e}}{\mathit{\alpha }}_{\text{b}}{\mathit{\Lambda }}_{0\text{b}}}{\mathit{\omega }\left(\mathit{\omega }-{\mathit{\gamma }}_{0\text{e}}{\mathit{\Omega }}_{\text{ce}}\right)}{J}_{-1}\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)+\frac{\mathit{\omega }}{ck}({\mathit{\epsilon }}_{rr,\text{I}}R3+i{\mathit{\epsilon }}_{r\mathit{\theta },\text{I}}R4)\right\},\hfill \\ \hfill & R1=\frac{1}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left\{J_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)A_{\text{bp}}\right.,\hfill \\ \hfill & R2=\frac{1}{{\mathit{\Lambda }}_{\text{+ bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left\{-i{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)D_{\text{bp}}-{\mathit{\alpha }}_{\text{b}}{\mathit{\alpha }}_{\text{p}}{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)\left\{\left(ck-\mathit{\omega }{\mathit{\beta }}_{0\text{e}}\right)\left[\frac{1}{\mathit{\Delta }{\mathit{\omega }}^2}+\frac{{\mathit{\gamma }}_{0\text{e}}{\mathit{\Omega }}_{\text{ce}}}{\mathit{\omega }\mathit{\Delta }{\mathit{\omega }}^2}\right]+ck\left[\frac{1}{{\mathit{\omega }}^2}+\frac{{\mathit{\Omega }}_{\text{ce}}}{{\mathit{\omega }}^2\mathit{\Delta }\mathit{\omega }}\right]\right\}\right\},\hfill \\ \hfill & R3=\frac{1}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\left\{-{\mathit{\alpha }}_{\text{b}}{\mathit{\alpha }}_{\text{p}}{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)\left[\frac{1}{\mathit{\Delta }\mathit{\omega }}+\frac{{\mathit{\gamma }}_{0\text{e}}{\mathit{\Omega }}_{\text{ce}}}{\mathit{\omega }\mathit{\Delta }\mathit{\omega }}+\frac{1}{\mathit{\omega }}+\frac{{\mathit{\Omega }}_{\text{ce}}}{\mathit{\omega }\mathit{\Delta }\mathit{\omega }}\right]\right\},\hfill \\ \hfill & R4=\frac{1}{{\mathit{\Lambda }}_{+\text{bp}}{\mathit{\Lambda }}_{-\text{bp}}}\{-B_{\text{bp}}{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{I,bp}}{R}_{\text{b}}\right)\},{\mathit{\epsilon }}_{\pm \text{b}}=1-\frac{{\mathit{\omega }}_{\text{b}}^2}{{\mathit{\omega }}^2}\frac{\mathit{\Delta }{\mathit{\omega }}_{\text{m}}}{\left(\mathit{\Delta }{\mathit{\omega }}_{\text{m}}\mp {\mathit{\Omega }}_{\text{ce}}\right)},{\mathit{\epsilon }}_{\pm \text{p}}=1-\frac{{\mathit{\omega }}_{\text{p}}^2{\mathit{\gamma }}_{0\text{e}}}{\mathit{\omega }\left(\mathit{\omega }\mp {\mathit{\Omega }}_{\text{ce}}{\mathit{\gamma }}_{0\text{e}}\right)},\hfill \\ \hfill \end{array}$$

By imposing the following conditions at the helix

$$\begin{array}{cc}\hfill \mathit{\delta }{\widehat{E}}_z\left(R_{\text{h}}-\mathit{\epsilon }\right)& =\mathit{\delta }{\widehat{E}}_z\left(R_{\text{h}}+\mathit{\epsilon }\right)\hfill \\ \hfill \mathit{\delta }{\widehat{E}}_{\mathit{\theta }}\left(R_{\text{h}}-\mathit{\epsilon }\right)& =\mathit{\delta }{\widehat{E}}_{\mathit{\theta }}(R_{\text{h}}+\mathit{\epsilon })\hfill \end{array}$$

(7)

$D$ and $K$ are given by

$$\begin{array}{cc}& D=\frac{1}{W\left(q{R}_{\text{g}},q{R}_{\text{h}}\right)}\left\{A\left[a^{\left(1\right)}{J}_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+a^{\left(2\right)}{Y}_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)\right]+iF\left[c^{\left(1\right)}{J}_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+c^{\left(2\right)}{Y}_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)\right]\right\}\hfill \\ \hfill & K=\frac{q{\mathit{\chi }}_{\pm ,\text{II,p}}}{{\mathit{\chi }}^2{W}^{{}^{\prime \prime }}(q{R}_{\text{g}},q{R}_{\text{h}})}[F{\mathit{\varphi }}^{\left(1\right)}+iA{\mathit{\varphi }}^{\left(2\right)}],\hfill \\ \hfill \end{array}$$

where

$$\begin{array}{cc}& {\mathit{\varphi }}^{\left(1\right)}=\left[b^{\left(1\right)}{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,II,p}{R}_h\right)+b^{\left(2\right)}{Y}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)\right]+\frac{ck{R}_{\text{p}}}{\mathit{\omega }}\left[c^{\left(1\right)}{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+c^{\left(2\right)}{Y}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)\right]+R_{\text{p}}[b^{\left(1\right)}{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+b^{\left(2\right)}\hfill \\ \hfill & Y_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)]\hfill \\ \hfill & {\mathit{\varphi }}_{\text{l,m}}^{\left(2\right)}=\left[d^{\left(1\right)}{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+d^{\left(2\right)}{Y}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)\right]-\frac{ck{R}_{\text{p}}}{\mathit{\omega }}\left[a^{\left(1\right)}{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+a^{\left(2\right)}{Y}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)\right]+R_{\text{p}}[d^{\left(1\right)}{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+d^{\left(2\right)}\hfill \\ \hfill & Y_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)]\hfill \\ \hfill \end{array}$$

To obtain the final dispersion relation we must employ the discontinuity conditions in the axial and azimuthal magnetic fields due to the helix current sheet as follows

$$\mathit{\delta }{B}_{\mathit{\theta }}\left(R_{\text{h}}+\mathit{\epsilon }\right)-\mathit{\delta }{B}_{\mathit{\theta }}\left(R_{\text{h}}-\mathit{\epsilon }\right)=\frac{4\mathit{\pi }}{c}\mathit{\delta }{J}_{\text{ll}}\mathit{\Delta }{R}_{\text{h}}sin\mathit{\phi }\text{and}\mathit{\delta }{\widehat{B}}_z\left(R_{\text{h}}-\mathit{\epsilon }\right)-\mathit{\delta }{\widehat{B}}_z\left(R_{\text{h}}+\mathit{\epsilon }\right)=\frac{4\mathit{\pi }}{c}\mathit{\delta }{\widehat{J}}_{\text{ll}}\mathit{\Delta }{R}_{\text{h}}cos\mathit{\phi },$$

(8)

By employing Eq. 8 and onerous manipulations, we get:

$$A=[-i{W}^{{}^{\prime \prime }}\left(q{R}_{\text{g}},q{R}_{\text{h}}\right)cos\mathit{\phi }{T}_3-i{\mathit{\chi }}_{}^{2}sin\mathit{\phi }{T}_1]/[c(T_1{T}_4+T_3{T}_2)],$$

(9)

$$F=4\mathit{\pi }\mathit{\delta }{J}_{\text{ll}}\mathit{\Delta }{R}_{\text{h}}[W^{{}^{\prime \prime }}\left(q{R}_{\text{g}},q{R}_{\text{h}}\right)cos\mathit{\phi }{T}_4-{\mathit{\chi }}^{2}sin\mathit{\phi }{T}_2][c(T_1{T}_4+T_3{T}_2)],$$

(10)

where $T_1,T_2,T_3,T_4$ are as follows:

$$\begin{array}{cc}& T_1=\left[b^{\left(1\right)}{J}_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+b^{\left(2\right)}{Y}_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)\right]W^{{}^{\prime \prime }}\left(q{R}_{\text{g}},q{R}_{\text{h}}\right)-\frac{q{\mathit{\chi }}_{\pm ,\text{II,p}}}{{\mathit{\chi }}_{}^2}{W}^{{}^{\prime }}\left(q{R}_{\text{g}},q{R}_{\text{h}}\right){\mathit{\varphi }}^{\left(1\right)}\hfill \\ \hfill & T_2=\left[d^{\left(1\right)}{J}_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+b^{\left(2\right)}{Y}_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)\right]W^{{}^{\prime \prime }}\left(q{R}_{\text{g}},q{R}_{\text{h}}\right)-\frac{q{\mathit{\chi }}_{\pm ,\text{II,p}}}{{\mathit{\chi }}_{}^2}{W}^{{}^{\prime }}\left(q{R}_{\text{g}},q{R}_{\text{h}}\right){\mathit{\varphi }}_{}^{\left(2\right)}\hfill \\ \hfill & T_3=+\frac{{\mathit{\chi }}^2\mathit{\epsilon }\mathit{\omega }}{cqW\left(q{R}_{\text{g}},q{R}_{\text{h}}\right)}[Y_0\left(q{R}_{\text{g}}\right)J_0^{{}^{\prime }}\left(q{R}_{\text{h}}\right)-J_0\left(q{R}_{\text{g}}\right)Y_0^{{}^{\prime }}\left(q{R}_{\text{h}}\right)][c^{\left(1\right)}{J}_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+c^{\left(2\right)}{Y}_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)]-\hfill \\ \hfill & \left[\frac{{\mathit{\chi }}_{\pm ,\text{II,p}}}{c}+k{R}_{\text{p}}\frac{ck}{\mathit{\omega }}{\mathit{\chi }}_{\pm ,\text{II,p}}\right][c^{\left(1\right)}{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+c^{\left(2\right)}{Y}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)]-k{R}_{\text{p}}{\mathit{\chi }}_{\pm ,\text{II,p}}[b^{\left(1\right)}{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+b^{\left(2\right)}{Y}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)]\hfill \\ \hfill & T_4=\frac{{\mathit{\chi }}^2\mathit{\epsilon }\mathit{\omega }}{cqW\left(q{R}_g,q{R}_h\right)}[Y_0\left(q{R}_{\text{g}}\right)J_0^{{}^{\prime }}\left(q{R}_{\text{h}}\right)-J_0\left(q{R}_{\text{g}}\right)Y_0^{{}^{\prime }}\left(q{R}_{\text{h}}\right)][a^{\left(1\right)}{J}_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+a^{\left(2\right)}{Y}_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)]-\left[\frac{{\mathit{\chi }}_{\pm ,\text{II,p}}\mathit{\omega }}{c}+k{R}_{\text{p}}\right.\hfill \\ \hfill & \left.\frac{ck}{\mathit{\omega }}{\mathit{\chi }}_{\pm ,\text{II,p}}\right]\left[a^{\left(1\right)}{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+a^{\left(2\right)}{Y}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)\right]\hfill \\ \hfill & +k{R}_{\text{p}}{\mathit{\chi }}_{\pm ,\text{II,p}}\left[d^{\left(1\right)}{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+d^{\left(2\right)}{Y}^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)\right]\hfill \\ \hfill \end{array}$$

The final condition says that the electric field parallel to the helix must be zero [18],

$$\left[\mathit{\delta }{E}_{z}sin\mathit{\phi }+\mathit{\delta }{E}_{z}cos\mathit{\phi }\right]=0,$$

(11)

The dispersion relation obtained by employing Eqs. (9)–(11).

$$\left\{{\mathit{\Psi }}^{(1)}+{\mathit{\Psi }}^{(2)}\right\}=0,$$

(12)

where

$$\begin{array}{cc}& {\mathit{\Psi }}^{(1)}=\frac{4\mathit{\pi }\mathit{\delta }{\widehat{J}}_{\Vert }\mathit{\Delta }{R}_h}{c}\left[\left[-i{W}^{{}^{\prime \prime }}\left(\mathit{\chi }{R}_{\text{g}},\mathit{\chi }{R}_{\text{h}}\right)cos\mathit{\phi }{T}_3-i{\mathit{\chi }}^{2}sin\mathit{\phi }{T}_1\right]/(T_1{T}_4+T_3{T}_2)\right]\left[\left[a^{\left(1\right)}{J}_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+a^{\left(2\right)}{Y}_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)\right]\right.\hfill \\ \hfill & sin\mathit{\phi }+\left[d^{\left(1\right)}{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+d^{\left(2\right)}{Y}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)\right]\left(\frac{\mathit{\omega }{\mathit{\chi }}_{\pm ,\text{II,p}}}{c{\mathit{\chi }}_{}^2}cos\mathit{\phi }[1+R_{\text{p}}\left(\mathit{\omega },k_{}\right)]\right)-\frac{k{\mathit{\chi }}_{\pm ,\text{II,p}}}{{\mathit{\chi }}_{}^2}{R}_{\text{p}}\left(\mathit{\omega },k\right)cos\mathit{\phi }[a^{\left(1\right)}{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)\hfill \\ \hfill & +\left.\left.a^{\left(2\right)}{Y}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)\right]\right],\hfill \end{array}$$

and

$$\begin{array}{cc}& {\mathit{\psi }}^{(2)}=\frac{i4\mathit{\pi }\mathit{\delta }{\widehat{J}}_{\Vert }\mathit{\Delta }{R}_{\text{h}}}{c}\left[\left[W^{{}^{\prime \prime }}\left(\mathit{\chi }{R}_{\text{g}},\mathit{\chi }{R}_{\text{h}}\right)cos\mathit{\phi }{T}_4-{\mathit{\chi }}^{2}sin\mathit{\phi }{T}_2\right]/(T_1{T}_4+T_3{T}_2)\right][\left[c^{\left(1\right)}{J}_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)c^{\left(2\right)}{Y}_0\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)\right]sin\mathit{\phi }-[\hfill \\ \hfill & b^{\left(1\right)}{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+b^{\left(2\right)}{Y}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)]\left(\frac{\mathit{\omega }{\mathit{\chi }}_{\pm ,\text{II,p}}}{c^2}cos\mathit{\phi }[1+R_{\text{p}}]\right)-\frac{k{\mathit{\chi }}_{\pm ,\text{II,p}}}{{\mathit{\chi }}^2}{R}_{\text{p}}cos\mathit{\phi }[c^{\left(1\right)}{J}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)+c^{\left(2\right)}{Y}_0^{{}^{\prime }}\left({\mathit{\chi }}_{\pm ,\text{II,p}}{R}_{\text{h}}\right)]],\hfill \\ \hfill \end{array}$$

Numerical results and discussion

We analyze the dispersion characteristics of the slow-wave structure from the numerical computation of the dispersion using (12). The nominal parameters of this system correspond to a helix with a period ${\mathit{\lambda }}_{\text{h}}$ = 1.966 cm a width ${\mathit{\xi }}_{\text{h}}$ = 0.764 cm, and a radius of $R_{\text{h}}$ = 1.4 cm enclosed within a wall of radius $R_{\text{w}}$ = 3.63 cm. Consider only the case in which m = 0. The growth rate is proportional to the Pierce gain parameter known in the theory of TWTs $C={(Z{I}_{\text{b}}/(4V_{\text{b}}))}^{1/3}$. Where $I_{\text{b}}$ is the electron beam current and Z is the coupling impedance of electrons to the wave, which depends on the transverse structure of the wave in the beam region. The coupling impedance of solid electron beam in the presence of plasma can be much larger than the vacuum case [22].

First, we consider the plasma density is weak. Figure 2 shows the variation of the plasma velocity as a function of the frequency for several values of plasma frequency. As seen in this figure, the plasma velocity decreases with frequency, and it remains constant with plasma density.

Fig. 2

Variation of the normalized phase velocity ($v_{\text{ph}}/c$) with frequency ($f$) for several values of the plasma density (low plasma density). The chosen parameters are as follows: ${\mathit{\omega }}_{\text{b}}=0.025$, ${\mathit{\Omega }}_{\text{ce}}=0.07$, and $\mathit{\epsilon }=1.75$

The plot of gain as a function of frequency for different values of plasma density is shown in Fig. 3. In accordance with Fig. 2, the growth rate is constant by increasing plasma density. This shows that the coupling impedance in the lower plasma density is weak and growth rate remains constant in this limit.

Fig. 3

Variation of the normalized growth rate ($I_{m}k/k_{\text{h}}$) with frequency ($f$) for several values of the plasma density (low plasma density). The chosen parameters are as follows: ${\mathit{\omega }}_{\text{b}}=0.025$, ${\mathit{\Omega }}_{\text{ce}}=0.07$, ${\mathit{\gamma }}_{0\text{e}}=1.005558$, $\mathit{\epsilon }=1.75$

Now, we consider the numerical solution for strong plasma density. Figure 4 shows the phase velocity as a function of frequency for several choice of plasma density. It is clear from Fig. 4 that the phase velocity increases with frequency, and the plasma density increases the phase velocity.

Fig. 4

Variation of the normalized phase velocity ($v_{\text{ph}}/c$) with frequency ($f$) for several values of the plasma density (high plasma density). The chosen parameters are as follows: ${\mathit{\omega }}_{\text{b}}=0.025$, ${\mathit{\Omega }}_{\text{ce}}=0.07$, and $\mathit{\epsilon }=1.75$

Figure 5 illustrates the variation of gain as a function of frequency for different values of plasma density. Figure 5 has a good agreement with Fig. 4. As seen in this figure, the effect of plasma is to enhance the gain in the strong plasma density limit. The presence of plasma should increase the growth rate of the electromagnetic wave. The presence of strong plasma is to increase the coupling impedance.

Fig. 5

Variation of the normalized growth rate ($I_{\text{m}}k/k_{\text{h}}$) with frequency ($f$) for several values of the plasma density (high plasma density). The chosen parameters are as follows: ${\mathit{\omega }}_{\text{b}}=0.025$, ${\mathit{\Omega }}_{\text{ce}}=0.07$, ${\mathit{\gamma }}_{0\text{e}}=1.005558$, R$\mathit{\epsilon }=1.75$

In the absence of the plasma the dispersion relation reduce to the final dispersion relation in the Ref. [18, 19]. The comparison of the growth rate in the absence and presence of the plasma is shown in Fig. 6. As seen in this figure, the effect of plasma is to increase the growth rate and frequency bandwidth.

Fig. 6

The comparison of the growth rate as a function of frequency in the presence and absence of the plasma. The chosen parameters are as: ${\mathit{\omega }}_{\text{b}}=0.025$, ${\mathit{\Omega }}_{\text{ce}}=0.07$, ${\mathit{\gamma }}_{0\text{e}}=1.005558$, $\mathit{\epsilon }=1.75$

Conclusion

Now, we can summarize the specific results of this project as:

• 1. In the lower plasma density, the effect of plasma on the growth rate and frequency bandwidth is not considerable.

• 2. The effect of strong plasma is to increase the growth rate and frequency bandwidth.

• 3. The coupling impedance is strong in the strong plasma density.

• 4. Presence of plasma in the system considerably increases the growth rate and bandwidth in comparison with the absence of the plasma.