Analysis of time delayed Rabies model in human and dog populations with controls

Abstract

Rabies is a fatal zoonotic disease caused by a virus through bites or saliva of an infected animal. Dogs are the main reservoir of rabies and responsible for most cases in humans worldwide. In this article, a delay differential equations model for assessing the effects of controls and time delay as incubation period on the transmission dynamics of rabies in human and dog populations is formulated and analyzed. Analysis from the model show that there is a locally and globally asymptotic stable disease-free equilibrium whenever a certain epidemiological threshold, the control reproduction number $\mathcal {R}_v$, is less than unity. Furthermore, the model has a unique endemic equilibrium when $\mathcal {R}_v$ exceed unity which is also locally and globally asymptotically stable for all delays. Time delay is found to have influence on the endemicity of rabies. Vaccination of humans and dogs coupled with annual crop of puppies are imposed to curtail the spread of rabies in the populations. Sensitivity analysis on the number of infected humans and dogs revealed that increasing dog vaccination rate and decreasing annual birth of puppies are more effective in human populations. However in dog populations, the vaccination and birth control of puppies, have equal effective measures for rabies control. Numerical experiments are conducted to illustrate the theoretical results and control strategies.

1 Introduction

Rabies is an acute and fatal zoonotic virus disease mainly affecting all species of mammals and other carnivores with dogs being the carrier for most human cases worldwide [6, 28, 32]. The rabies virus is mainly contained in the saliva of animals but may also be found in tears, urine, semen and other body fluids [2, 8]. The virus infects central nervous system and causes cerebral dysfunction in the brain, and once clinical symptoms developed, its mortality rate is certain [15, 34]. Moreover, Rabies has the highest case fatality rate of any conventional infectious disease, approaching the $100\%$ mark [7].

Dogs are the primary sources of rabies in humans, and the main transmission route is through bites or scratch, especially by infected dogs [5, 18, 34]. Rabies can also be transmitted through direct contact with wound or mucosal surface (e.g. mouth, nose, eye) that is contaminated with the saliva from a rabid dog [6]. Humans and other mammals can develop rabies from aerosol transmission or through transplantation of tissues and organs [2, 30]. At the early stage of infection, initial symptoms of rabies resemble flu-like which include fever with pain and unusual or unexplained tingling, hypersalivation, sore throat, cough, nausea and vomiting, pricking, or burning sensation (paraesthesia) at the site of animal bite [28, 32]. Thereafter, as the virus spreads to the central nervous system, progressive and fatal inflammation of the brain and spinal cord developed resulting in hyperactivity and paralysis [28].

The incubation period (the time between exposure to rabies virus and the development of symptoms) for most rabies cases in humans and dogs are generally between 20 days to 3 months but may vary from 1  week to 1 year, depending upon factors such as the location of virus entry and viral load [26, 31, 32]. In extreme cases, the incubation period can be up to 7 years [26, 28].

Rabies is still a very serious disease that exists with varying degrees of severity in practically all countries of the world except Antarctica and the Arctic. Islands such as New Zealand, Australia, Mauritius and the Seychelles, are helped by their natural isolations [8, 30]. In 2004, a young patient survived rabies in Wisconsin, but the reasons for this favorable outcome remain elusive [2]. Rabies is responsible for the death of 50,000 to 60,000 people annually and was responsible for 1.74 million disability adjusted life years (DALYs) losses each year [6, 17]. More than 99% of these death occur in the developing countries where the disease is endemic in domestic dog population [6, 33].

The World Health Organization (WHO) calls rabies a “$100\%$ vaccine-preventable disease” [6, 8]. Caroll et al. identified three most common control strategies for rabies namely epidemiological surveillance, dog mass vaccination and population control [5]. Other preventive measures for rabies include immediate thorough wound washing with soap and water after contact with a suspected rabid animal [32]. There are vaccines that are derived from a variety of tissue culture or chicken embryo origins used for treating rabies and can be administered before or after exposure [1]. Control of the disease is hampered by cultural, social and economic realities in which expenditure on treatment and control exceed $\$500$ million per annum [4, 15]. With widespread global movement of people and animals, it is inevitable that rabies will continue to be introduced into countries hitherto free of the disease.

Mathematical modelling in bioscience and indeed other field of study have provided insight towards better understanding of the mechanisms involved and can provide useful optimal strategies for control measures. Based on this facts, in recent years, mathematical rabies models have been developed towards achieving these goals, see for example [1, 5,6,7, 10, 34]. For instance, in [5], an SEIV (susceptible,exposed,infectious,vaccinated) continuous time compartmental model in dog populations was created to investigate the effects of rabies control using three control methods (vaccination, fertility control + vaccination and culling). Kwaku in [1], considered another rabies model in dog populations with vaccination as control strategy. The impact of the vaccine was shown by the increase in the number of recovered dogs. In order to explore the dynamics, effective control and prevention measures of rabies in China, Zhang et al. [34] used an SEIR (susceptible,exposed,infectious,recovered) deterministic model to describe the spread of rabies among dogs and from infectious dogs to humans. The model simulations agreed with the human rabies data reported by the Chinese Ministry of Health and predicted that the number of human rabies is decreasing but may reach another peak around 2030. Their study also demonstrated that reducing dog birth rate and increasing dog immunization coverage rate are the most effective methods for controlling rabies in China. In 2015, based on the model of Zhang et al. [34], Chen et al. in [7], proposed a multi-patch model to describe the transmission dynamics of rabies between dogs and humans in different provinces. Their study investigated how the movement of dogs affects the geographically inter-provincial spread of rabies in Mainland China. They found that immigration of dogs can make the disease endemic even if it dies out in each isolated patch (province). Chapwanya et al. in [6], formulated yet another SEI rabies model in human and dog populations with additional vaccinated compartment in humans. They proposed the discrete counterpart using the nonstandard finite difference scheme.

Introduction of time delay in mathematical modelling has shown significant impacts on dynamics of the system and disease burden. Research has shown the existence of time delay between infection to infectiousness [16]. Time delay can cause equilibria of models to change from stable to unstable or conditionally stable, thereby generating periodic solutions with delay as a bifurcating parameter [9, 14, 35, 36]. Furthermore, models with time delay are shown to decrease disease burden and more suitable for modelling severe acute respiratory syndrome (SARS) of 2003 than models without delay [25]. From the foregoing, an important reality (time delay), ought to be considered in model formulations looking at the wide range of the incubation period and the complexity involved before symptoms appeared. Motivated by the studies [6, 25, 34], in this article, we formulate and analyze a rabies model with infections from dogs to dogs, and dogs to humans by incorporating time delay as incubation period to form a system of delay differential equations. Furthermore, in order to reduce the menace of rabies in the populations of human and dog, we propose three control strategies; vaccination of humans and dogs, coupled with annual birth control of new born puppies. The main objectives are to study the effects of control strategies and time delay in both the model dynamical properties and the endemicity of rabies virus in the populations. The rest of the article is organized as follows. In Sect.  2, we present the model formulation with basic properties results, followed by existence and stability of equilibria in Sect. 3. Numerical simulations are presented in Sect. 4 and conclusion in Sect. 5.

2 Model formulation

The model consists of two populations: humans and dogs leaving in the same environment. At any time t, the human population is sub-divided into three sub-populations of susceptible humans ($S_h(t)$), infected humans ($I_h(t)$) and vaccinated humans ($V_h(t)$). Hence, the total population of humans denoted by $N_h(t)$, is given by

$$\begin{aligned} N_h(t)=S_h(t) + I_h(t) + V_h(t) \end{aligned}$$

Similarly, at any time t, the dog population is sub-divided into three sub-populations of susceptible dogs ($S_d(t)$), infected dogs ($I_d(t)$), and vaccinated dogs ($V_d(t)$) so that the total population of dogs is

$$\begin{aligned} N_d(t) = S_d(t) + I_d(t) + V_d(t). \end{aligned}$$

Fig. 1

Schematic diagram of the rabies delay model equations (2.1)–(2.5)

The susceptible human population is increased by the per capita growth rate ($\mu _hK_h$), where $\mu _h$ is birth/death rate (which is assumed to occur in all human compartments), while $K_h$ is humans annual birth population. It is decreased by administering vaccination (at a rate v, natural death and infection due to sufficient contact between susceptible humans and infected dogs at rate ($\beta _{hd}S_hI_d(t-\tau )e^{-\mu _d\tau }$). Here, $\tau > 0$, is the time lag (delay) that accounts for the time between infection and infected stage while $e^{-\mu _d\tau }$ is the probability that rabid dogs survived the natural death over the period $[0, \tau ]$, and $\beta _{hd}$ is transmission rate of rabies from dogs to humans.

The infected human class is increased by sufficient contact between susceptible humans and infected dogs (at a rate $\beta _{hd}S_hI_d(t-\tau )e^{-\mu _d\tau }$), and decreased by natural and rabies induced-death at rates $\mu _h$ and $\alpha _h$, respectively. The vaccinated human population is increased by vaccine dose administered to susceptibles (at rate v) and is decreased due to natural death (at rate $\mu _h$).

Similarly, susceptible dog population is increased by per capita growth (at a rate $\mu _dK_d$), where $\mu _d$ is birth/death rate (which is assumed to occur in other dog compartment), while $K_d$ is dogs annual birth rate of newborn puppies. It is decreased by natural death (at rate $\mu _d$), vaccination (at rate $kS_d$) and by infection when there is sufficient contact between susceptible dogs and infected dogs (at rate $\beta _{dd}S_dI_d(t-\tau )e^{-\mu _d\tau }$). The infected dogs population increase by infection after sufficient contact between susceptible dogs and infected dogs (at a rate $\beta _{dd}S_dI_d(t-\tau )e^{-\mu _d\tau }$), and is decreased by the rate at which the infected dogs die naturally (at rate $\mu _d$), and due to the rabies virus (at rate $\alpha _d$).

In the formulation of this model, we make the following assumptions:

• 1. there is no transmission of rabies virus between susceptible and infected humans;

• 2. there is no transmission between rabid humans and susceptible dogs;

• 3. there are vaccinations in human and dog populations with long time immunity so that vaccinated populations doesn’t revert to susceptibles.

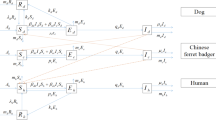
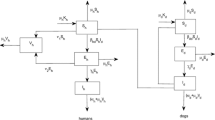
The human and dog populations dynamics in a uniform environment, that may be regarded as a single humans habitat site and single dogs breeding site, is represented by the following system of delay differential equations as illustrated in Fig. (1). The model variables and parameters are described in Table  (1).

$$\begin{aligned} \frac{dS_h}{dt}= & {} \mu _hK_h-(\mu _h + v)S_{h}-\beta _{hd}S_hI_d(t-\tau )e^{-\mu _d\tau }, \end{aligned}$$

(2.1)

$$\begin{aligned} \frac{dI_h}{dt}= & {} \beta _{hd}S_hI_d(t-\tau )e^{-\mu _d\tau } - (\mu _h+\alpha _h)I_h, \end{aligned}$$

(2.2)

$$\begin{aligned} \frac{dV_h}{dt}= & {} vS_h - \mu _hV_h, \end{aligned}$$

(2.3)

$$\begin{aligned} \frac{dS_d}{dt}= & {} \mu _dK_d -( \mu _d+k)S_d - \beta _{dd}S_dI_d(t-\tau )e^{-\mu _d\tau }, \end{aligned}$$

(2.4)

$$\begin{aligned} \frac{dI_d}{dt}= & {} \beta _{dd}S_dI_d(t-\tau )e^{-\mu _d\tau } - (\mu _d + \alpha _d)I_d, \end{aligned}$$

(2.5)

$$\begin{aligned} \frac{dV_d}{dt}= & {} kS_d - \mu _dV_d, \end{aligned}$$

(2.6)

with initial data,

$$\begin{aligned} \begin{aligned} ( S_h(t), ~I_h(t), ~V_h(t), ~S_d(t), ~I_d(t), ~V_d(t) ) =&( \Psi _{1}(t), ~\Psi _2(t), ~\Psi _3(t), ~\Psi _4(t), ~\Psi _5(t), ~\Psi _6(t) )\\&\,\text {for}\ t \in [-\tau ,~0], \end{aligned} \end{aligned}$$

(2.7)

where ($\Psi _{1}(t)$, $\Psi _2(t)$, $\Psi _3(t)$, $\Psi _4(t)$, $\Psi _5(t)$, $\Psi _6(t)$), $\in \mathcal {C}^+: \mathcal {C}^+([-\tau ,0],\mathbb {R}^6_+)$ is the space of continuous functions on the interval $[-\tau , ~0]$ equipped with maximum norm.

Table 1 Description of variables and parameters of model (2.1)–(2.6)

Description of variables and parameters of model (2.1)–(2.6)

2.1 Basic properties of the model

The basic dynamical features of the model (2.1)–(2.6) will now be explored. For the model to be epidemiologically meaningful, it is important to prove that all variables are non-negative for all time, a unique and bounded solution exist. The model (2.1)–(2.6) is basically divided into two regions; $\Omega _d=\begin{Bmatrix} S_d,&I_d,&V_d \end{Bmatrix} \in \mathbb {R}^3_+$ and $\Omega _h=\begin{Bmatrix} S_h,&I_h,&V_h \end{Bmatrix} \in \mathbb {R}^3_+$ , thus $\Omega = \Omega _h \times \Omega _d\,\in \,\mathbb {R}^6_+$.

Let $Y(t):[-\tau , \infty )\rightarrow \mathbb {R}_+^6$ be the humans and dogs valued function such that

$Y(t)=( S_h(t), I_h(t), V_h(t), S_d(t), I_d(t), V_d(t))$. The model system (2.1)–(2.6) can be written as

$$\begin{aligned} \frac{dY(t)}{dt}= & {} f(t,~Y_t) ,\quad t \ge 0. \end{aligned}$$

(2.8)

$$\begin{aligned} Y_t(\theta )= & {} Y(t+\theta ),\quad \text {for} \; \theta \in [-\tau , ~0], \end{aligned}$$

(2.9)

where $f : [-\tau , 0]\times \mathbb {R}_+^6 \rightarrow \mathbb {R}_+^6$ is a Lipschitz continuous function from $[-\tau , 0]\times \mathbb {R}_+^6$ into $\mathbb {R}_+^6$. From the assumed properties of the model, we can establish the following.

Theorem 1

The solution $( S_h(t), I_h(t), V_h(t), S_d(t), I_d(t), V_d(t))$ of the model (2.1)–(2.6) exists and is unique for all time.

Proof

Since f is continuous and Lipschitzian, it follows from Theorem  (2.2) in [13] that the delay differential equation system (2.1)–(2.6) has a unique solution given the initial data (2.7). $\square$

Theorem 2

The solution $( S_h(t), I_h(t), V_h(t), S_d(t), I_d(t), V_d(t))$ of model (2.1)–(2.6) is positive for all time $t>0$ and bounded in $\Omega$, given the initial data in (2.7) .

Proof

Suppose all the initial data in (2.7) are positive. Consider Eq. (2.1), with $\mu _hK_h>0$, we have

$$\begin{aligned} \frac{dS_h}{dt}\ge & {} \left[ -(\mu _h + v)-\beta _{hd}I_d(t-\tau )e^{-\mu _d\tau }\right] S_{h}, \; \text {so that}\\ S_h(t)\ge & {} S_h(0)\exp \left( - \int _0^t[(\mu _h + v)+\beta _{hd}I_d(u-\tau )e^{-\mu _d\tau }]du\right) \\> & {} 0. \end{aligned}$$

Hence $S_h(t)$ is positive. Similarly, from (2.4), having $\mu _dK_d>0$,

$$\begin{aligned} \frac{dS_d}{dt}\ge & {} - [(\mu _d + k)+\beta _{dd}I_d(t-\tau )e^{-\mu _d\tau }]S_{d}(t), \; \text {so}\\ S_d(t)\ge & {} S_d(0)\exp \left( - \int _0^t[(\mu _d + k)+\beta _{dd}I_d(u-\tau )e^{-\mu _d\tau }]du\right) \\> & {} 0. \end{aligned}$$

Therefore, $S_d(t)$ is also positive.

Now, with the positivity of $S_h(t)$ and $S_d(t)$ above, we can deduce from Eqs. (2.3) and (2.6) that

$$\begin{aligned} \frac{dV_h}{dt}\ge & {} - \mu _hV_h(t) \; \text {and}\\ \frac{dV_d}{dt}\ge & {} - \mu _dV_d(t), \; \text {respectively}. \end{aligned}$$

Therefore,

$$\begin{aligned} V_h(t)\ge & {} V_h(0)\exp (\mu _h t)>0 \; \text {and} \\ V_d(t)\ge & {} V_d(0)\exp (\mu _d t)>0. \end{aligned}$$

Therefore, $V_h(t)>0$ and $V_d(t)>0$.

For the other variables ($I_h(t)$ and $I_d(t)$), we use the method of contradiction using the approach in [11] as follows. Noting that $I_h(\theta )$ and $I_d(\theta )$ are positive for any $\theta \in [-\tau , ~0]$. Suppose that by contradiction, the variables are negative, then there exists a time $\hat{t}>0$ such that $I_h(\hat{t})=0, \;I_d(\hat{t})=0,$ and $S_h({t})>0, I_h({t})>0, V_h({t})>0, S_d({t})>0, I_d({t})>0, V_d({t})>0\; \text {for all }\; t\in [0,\hat{t})$ and $\frac{dI_h(\hat{t})}{dt}\le 0$, $\frac{dI_d(\hat{t})}{dt}\le 0$. It follows from (2.2),

$$\begin{aligned} \frac{dI_h(\hat{t})}{dt}= & {} \beta _{hd}S_h(\hat{t})I_d(\hat{t}-\tau )e^{-\mu _d\tau }>0, \end{aligned}$$

which contradicts our earlier assumption. Therefore, $I_h(t)$ is positive $\forall \ t>0$.

Similarly, from (2.5) we have,

$$\begin{aligned} \frac{dI_d(\hat{t})}{dt}= & {} \beta _{dd}S_d(\hat{t})I_d(\hat{t}-\tau )e^{-\mu _d\tau }>0, \end{aligned}$$

which also contradicts our earlier assumption. Hence, $I_d(t)$ is positive $\forall \ t>0$. This proves the first part of Theorem  2.

To show boundedness of solution, from the model equations in (2.1)–(2.6), adding the human subpopulations, we have

$$\begin{aligned} \begin{aligned} \frac{dN_h(t)}{dt}=\,&\mu _hK_h -\mu _hN_h(t) -\alpha _hI_h,\\ \le \,&\mu _hK_h -\mu _hN_h(t). \end{aligned} \end{aligned}$$

(2.10)

Using standard comparison theorem [29], one can show that

$$\begin{aligned} N_h(t)~ \le ~ N_h(0)e^{-\mu _h t} - K_h [ e^{-\mu _h t} - 1 ]. \end{aligned}$$

(2.11)

In particular,

$$\begin{aligned} N_h(t)~ \le ~ K_h \quad if ~~ N_h(0) \le K_h. \end{aligned}$$

(2.12)

Therefore, the feasible solution for the human population in the model (2.1)–(2.6) is in the region,

$$\begin{aligned} \Omega _h =\{ ( S_h(t), I_h(t), V_h(t) ) \in \mathbb {R}_+^3, N_h(t) \le K_h \}. \end{aligned}$$

(2.13)

Similarly, from the model Eqs. (2.1)–(2.6), the total subpopulations of dog at any time t is given as

$$\begin{aligned} \begin{aligned} \frac{dN_d(t)}{dt}&\,=\, \mu _dK_d + \mu _dN_d(t) - \alpha _dI_d,\\&\le \, \mu _dK_d + \mu _dN_d(t). \end{aligned} \end{aligned}$$

(2.14)

The solution of (2.13) can be obtained using standard comparison theorem [29] as

$$\begin{aligned} N_d(t)~ \le ~ N_d(0)e^{-\mu _d t} - K_d [ e^{-\mu _d t} - 1 ]. \end{aligned}$$

(2.15)

Hence,

$$\begin{aligned} N_d(t)~ \le ~ K_d ~~~ if ~~ N_d(0) \le K_d. \end{aligned}$$

(2.16)

Therefore, the feasible solution of dog population in the model is in the region

$$\begin{aligned} \Omega _d =\{ ( S_d(t), I_d(t), V_d(t) \in \mathbb {R}_+^3, N_d(t) \le K_d \}. \end{aligned}$$

(2.17)

Thus, $\Omega ~ = ~\Omega _h \times \Omega _d~ = \{ ( S_h +I_h+ V_h )\le K_h ; ~~( S_d+I_d +V_d) \le K_d \}$. Therefore, the model (2.1)–(2.6) is mathematically well-posed and epidemiologically meaningful. $\square$

3 Existence and stability of equilibria

The existence and asymptotic stability properties of the model will be explored in this section. At equilibrium, $I_d(t)=I_d(t-\tau )=I_d^*$, $S_h(t)=S_h^*$, $I_h(t)=I_h^*$, $V_h(t)=V_h^*$, $V_d(t)=V_d^*$.

At equilibrium, we set the right hand sides of Eqs.  (2.1)–(2.6) to zero. Thus,

$$\begin{aligned} \mu _hK_h-(\mu _h + v)S_h^*-\beta _{hd}S_h^*I_d^*e^{-\mu _d\tau }= & {} 0, \end{aligned}$$

(3.1)

$$\begin{aligned} \beta _{hd}S_h^*I_d^*e^{-\mu _d\tau } - (\mu _h+\alpha _h)I_h^*= & {} 0, \end{aligned}$$

(3.2)

$$\begin{aligned} vS_h^* - \mu _hV_h^*= & {} 0, \end{aligned}$$

(3.3)

$$\begin{aligned} \mu _dK_d -( \mu _d+k)S_d^* - \beta _{dd}S_d^*I_d^*e^{-\mu _d\tau }= & {} 0, \end{aligned}$$

(3.4)

$$\begin{aligned} \beta _{dd}S_d^*I_d^*e^{-\mu _d\tau } - (\mu _d + \alpha _d)I_d^*= & {} 0, \end{aligned}$$

(3.5)

$$\begin{aligned} kS_d^* - \mu _dV_d^*= & {} 0. \end{aligned}$$

(3.6)

From (3.5),

$$\begin{aligned}{}[\beta _{dd}S_d^*e^{-\mu _d\tau } - (\mu _d + \alpha _d)]I_d^*= & {} 0, \end{aligned}$$

(3.7)

which gives $I_d^* = 0$ or $\beta _{dd}S_d^*e^{-\mu _d\tau } - (\mu _d + \alpha _d)=0$.

The case where $I_d^* = 0$, gives the disease-free equilibrium by using appropriate substitutions in other equations, to get

$$\begin{aligned} \mathcal {E}_0 \equiv (S_h^0,~~ I_h^0,~~ V_h^0,~~ S_d^0,~~ I_d^0, ~~ V_d^0) =\left( \frac{\mu _h K_h}{\mu _h + v},~~ 0,~~\frac{vK_h}{\mu _h + v},~~\frac{\mu _dK_d}{\mu _d + k},~~0, ~~\frac{kK_d}{\mu _d + k}\right) . \end{aligned}$$

(3.8)

The basic control reproduction number denoted by $\mathcal {R}_v$ is defined as the expected number of secondary cases produced by introducing one infected in a completely susceptible population in the presence of intervention. According to the approaches in [37, 38], the next infection operator matrix is defined to be $\mathcal {M}_{0} = \begin{bmatrix} 0&{}\frac{\beta _{hd}S_h^0e^{-\mu _d\tau }}{(\mu _h + \alpha _h)}\\ \ \\ 0&{}\frac{\beta _{dd}S_d^0e^{-\mu _d\tau }}{(\mu _d + \alpha _d)}\\ \end{bmatrix}$.

Thus, the spectral radius of $\mathcal {M}_{0}$ gives the basic control reproduction number for the model as

$$\begin{aligned} \mathcal {R}_v = \frac{\beta _{dd}e^{-\mu _d\tau }\mu _dK_d}{(\mu _d+\alpha _d ) (\mu _d+k )}. \end{aligned}$$

(3.9)

Remark 3

It is worth noting here that, all the parameters of $\mathcal {R}_v$ are defined explicitly in terms of dog’s parameters including the time delay $\tau$. Thus for any meaningful control strategy, more attention should be directed towards these parameters as suggested in [6].

However, if $I_d^* \ne 0$, then from (3.7), $S_d^* = \frac{\mu _d + \alpha _d}{\beta _{dd}e^{-\mu _d\tau }}$.

Substituting $S_d^*$ in equation (3.6), we get $V_d^* = \frac{kS_d^*}{\mu _d}= \frac{k(\mu _d + \alpha _d)}{\mu _d\beta _{dd}e^{-\mu _d\tau }}$. Similarly, substituting $S_d^*$ in (3.4) and simplifying, $I_d^* =\frac{\mu _d + k}{\beta _{dd}e^{-\mu _d\tau }}\left[ \mathcal {R}_v-1\right]$, which holds only if $\mathcal {R}_v>1$. Continuing with these back substitutions, we get unique endemic equilibrium define as

$$\begin{aligned} \mathcal {E}_1 \equiv (S_h^{**},~~ I_h^{**},~~ V_h^{**},~~ S_d^{**},~~ I_d^{**},~~ V_d^{**}), \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} S_h ^{**}=~&\frac{\mu _h K_h}{ \beta _{hd}e^{-\mu _d\tau }I_d^{**} + (\mu _h + v)},\\ I_h^{**}~= ~&\frac{\beta _{hd}e^{-\mu _d\tau }S_h^{**}I_d^{**}}{ (\mu _h + \alpha _h)},\\ V_h ^{**}~= ~&\frac{v S_h^{**}}{\mu _h} ,\\ S_d^{**}~=~&\frac{\mu _d + \alpha _d}{\beta _{dd}e^{-\mu _d\tau }},\\ I_d^{**}~=~&\frac{\mu _d + k}{\beta _{dd}e^{-\mu _d\tau }}\left( \mathcal {R}_v-1\right) ,\\ V_d^{**}~=~&\frac{k(\mu _d + \alpha _d)}{\mu _d\beta _{dd}e^{-\mu _d\tau }}, \end{aligned} \end{aligned}$$

(3.10)

when $\mathcal {R}_v > 1$.

3.1 Stability of equilibria

To establish the local asymptotic stability of the equilibria, we linearize model (2.1)–(2.6) about an arbitrary equilibrium, to have

$$\begin{aligned} \frac{d Y(t)}{dt} = J_0 Y(t) + J_1Y{(t-\tau )} \end{aligned}$$

(3.11)

where, $Y(t)= (S_h(t),~~ I_h(t),~~ V_h(t),~~ S_d(t),~~ I_d(t)~~ V_d(t) )^{T}$, and $J_0= (a_{ij})$ is the Jacobian matrix with respect to Y(t), while $J_1=(b_{ij})$ is the Jacobian with respect to $Y( t - \tau )$ for $i, j = 1, 2, 3, 4, 5,6$, evaluated at any arbitrary equilibrium point so that

$$\begin{aligned} J_0 = \begin{pmatrix} -(\mu _h+v+\beta _{hd}I_{d}^*e^{-\mu _{d}\tau }) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \beta _{hd}I_{d}^*e^{-\mu _{d}\tau } &{} -(\mu _h+\alpha _h) &{} 0 &{} 0 &{} 0 &{} 0\\ v &{} 0 &{} -\mu _h &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} -(\mu _d+\beta _{dd}I_{d}^* e^{-\mu _d\tau }) &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} \beta _{dd}I_{d}^* e^{-\mu _d\tau } &{} -(\mu _d+\alpha _d) &{} 0\\ 0 &{} 0 &{} 0 &{} k &{} 0 &{} -\mu _d\\ \ \\ \end{pmatrix} \end{aligned}$$

and

$J_1 = \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} -\beta _{hd}S_h^*e^{-\tau (\lambda +\mu _d )}&{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \beta _{hd}S_h^*e^{-\tau (\lambda +\mu _d )}&{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} -\beta _{dd}S_d^* e^{-\tau (\lambda +\mu _d )}&{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \beta _{dd}S_d^* e^{-\tau (\lambda +\mu _d )}&{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \end{pmatrix}.$

Next, we seek a solution for the system (3.11) of the form

$$\begin{aligned} Y(t)= Ce^{ \lambda t}, \end{aligned}$$

(3.12)

where C is a constant matrix and $\lambda$ an eigenvalue. Substituting (3.12) into Eq. (3.11), rearranging and simplifying, for non-trivial solution of (3.11), gives the transcendental equation

$$\begin{aligned} G(\lambda ) = |\lambda I-J_0-J_1|=0, \end{aligned}$$

(3.13)

where I is a $6\times 6$ identity matrix.

3.1.1 Stability of disease-free equilibrium

Theorem 4

If $\mathcal {R}_v<1$, the disease-free equilibrium $\mathcal {E}_0$ is absolutely stable for all delay $\tau \ge 0$ and unstable if $\mathcal {R}_v>1$.

Proof

Substituting the disease-free equilibrium $\mathcal {E}_0$ in Eq. (3.13), we have the transcendental equation

$$\begin{aligned} \begin{aligned} G(\lambda )&=\,(\lambda + \mu _d)(\lambda + \mu _h+v)(\lambda + \mu _h+\alpha _h)(\lambda + \mu _h)(\lambda + \mu _d)g_1(\lambda ), \end{aligned} \end{aligned}$$

(3.14)

where

$$\begin{aligned} \begin{aligned} g_1(\lambda )&= \, \lambda +\mu _d + \alpha _d - \beta _{dd}S^0_d e^{-\tau (\lambda + \mu _d)}=0. \end{aligned} \end{aligned}$$

(3.15)

It can be seen that (3.14) has five negative roots ($\lambda =-\mu _d,\, \lambda =- (\mu _h+v),\, \lambda =-(\mu _h+\alpha _h),\, \lambda = -\mu _h, \,\lambda =- \mu _d$). Therefore the stability of $\mathcal {E}_0$ can now be determined by the distribution of roots for $g_1(\lambda )=0$. Now,

$$\begin{aligned} \begin{aligned} g_1(0)&=\, (\mu _d + \alpha _d)\left[ 1 - \frac{\beta _{dd}S^0_d e^{-\tau \mu _d}}{\mu _d + \alpha _d}\right] ,\\&=\, (\mu _d + \alpha _d)[1 - \mathcal {R}_v]. \end{aligned} \end{aligned}$$

If $\mathcal {R}_v>1$, then $g_1(0)<0$, and $g_1(+\infty ) = +\infty$, hence $g_1(\lambda )$ has at least one positive root, therefore $\mathcal {E}_0$ is unstable. This proved the last part of Theorem  4.

When $\tau = 0$, from (3.14),

$$\begin{aligned} \begin{aligned} \lambda&=\, \left[ \frac{\beta _{dd}S^0_d}{\mu _d + \alpha _d} - 1\right] , \\&< \, 0, \; \text {if} \; \mathcal {R}_v<1. \end{aligned} \end{aligned}$$

Hence, the root of (3.15) has negative real part.

When $\tau > 0$, according to Corollary 2.4 [24], for a stability switch (a root with positive (negative) real part to cross the imaginary axis) to necessarily occurs, there must be a root $\lambda = \pm iy_1$ for some $y_1\in \mathbb {R}^+$. We assume that $\lambda = iy_1$, is a root of Eq. (3.15). Substituting $\lambda = iy_1$ in (3.15), we get

$$\begin{aligned} \begin{aligned} g_1(iy_1) =&iy_1 +(\mu _d + \alpha _d) - \beta _{dd}S^0_d e^{-\tau \mu _d}(\cos y_1\tau - i\sin y_1\tau )=0. \end{aligned} \end{aligned}$$

Separating real and imaginary parts, squaring and adding we have

$$\begin{aligned} y^2_1= & {} (\beta _{dd}S^0_d e^{-\tau \mu _d})^2 -(\mu _d + \alpha _d)^2. \end{aligned}$$

Hence

$$\begin{aligned} y_1= & {} \sqrt{(\beta _{dd}S^0_d e^{-\tau \mu _d} +\mu _d + \alpha _d)[\beta _{dd}S^0_d e^{-\tau \mu _d} -(\mu _d + \alpha _d)]},\\= & {} \sqrt{(\beta _{dd}S^0_d e^{-\tau \mu _d} +\mu _d + \alpha _d)(\mu _d + \alpha _d)[\mathcal {R}_v - 1]}. \end{aligned}$$

If $\mathcal {R}_v<1$, there is no such $y_1\in \mathbb {R}^+$, which shows that (3.15) has no purely imaginary root. This implies that all roots of $g_1(\lambda )$ must have negative real parts (no stability switch). Therefore, the disease-free equilibrium $\mathcal {E}_0$, is absolutely stable when $\mathcal {R}_v<1$ for all delay $\tau \ge 0$. $\square$

In order to ensure total eradication of rabies infection in the populations irrespective of the initial population started with, we now prove the global stability of $\mathcal {E}_0$.

Theorem 5

The disease-free equilibrium, $\mathcal {E}_0$ is globally asymptotically stable for all delay $\tau \ge 0$, if $\mathcal {R}_v < 1.$

Proof

Here, we use the method of Lyapunov function in conjunction with Lasalle’s Invariance Principle as follows. Let $U(t) = (S_h(t), I_h(t), V_d (t), Sd (t), Id (t), V_d (t)) \in \mathbb {R}_+^6$ for $t>0$. Let $L(U)= \mu _d I_d(t)$ be the Lyapunov function. It can be seen clearly that $L(U)> 0$, for all $I_d(t) > 0$ and $L(U)= 0$ only if $I_d(t)=0$. To show that $\dot{L}<0,$ we differentiate along the solution of model (2.1)–(2.6) as follows

$$\begin{aligned} \begin{aligned} \dot{L}(U)=&~~ \mu _d \dot{I}_d(t), \\ =&~~\mu _d[\beta _{dd} S_d(t)I_d(t-\tau )e^{-\mu _d \tau } - (\mu _d + \alpha _d)I_d(t)], \\ \le&~~ \mu _d[\beta _{dd} S_d(t)e^{-\mu _d \tau } - (\mu _d + \alpha _d) ] I_d(t-\tau ), \; \\&\text {here} I_d(t) \text {is a decreasing function, so}\, I(t)\le I(t-\tau ),\\ \le&~~ \mu _d[\beta _{dd} K_de^{-\mu _d \tau } - (\mu _d + \alpha _d) ] I_d(t-\tau ), \\ \le&~~ \mu _d(\mu _d + \alpha _d) \left[ \frac{\beta _{dd} K_de^{-\mu _d \tau }}{\mu _d + \alpha _d} -1 \right] I_d(t-\tau ), \\ =&~~ \mu _d(\mu _d + \alpha _d)[\mathcal {R}_v -1] I_d(t-\tau ). \\ \end{aligned} \end{aligned}$$

Therefore

$$\begin{aligned} \begin{aligned} \dot{L}(U) \le&~~ \mu _d(\mu _d + \alpha _d)[\mathcal {R}_v -1] I_d(t-\tau ), \\<&~~ 0, ~~~\text { when} \mathcal {R}_v < 1 \text {with equality only at} \mathcal {E}_0. \\ \end{aligned} \end{aligned}$$

Therefore, L(U) is a Lyapunov function. According to Theorem 2.3.1 in [27] as applied in [11], if $\mathcal {R}_v < 1$, there exists the only disease free equilibrium $\mathcal {E}_0$ which is globally asymptotically stable (GAS) in $\Omega$ for all delay $\tau \ge 0$. Hence, proved. $\square$

3.1.2 Stability of the endemic equilibrium

Theorem 6

The endemic equilibrium $\mathcal {E}_1$ is locally asymptotically stable if $\mathcal {R}_v > 1$ for all delay $\tau \ge 0$.

Proof

Soppose $\mathcal {R}_v > 1$, then substituting the endemic equilibrium $\mathcal {E}_1$ in the arbitrary transcendental Eq. (3.13), we have

$$\begin{aligned} \begin{aligned} G_2(\lambda ) =&( \lambda + \mu _h+v+\beta _{hd}I_d^{**}e^{\mu _d \tau })(\lambda + \mu _h+\alpha _h)(\lambda + \mu _h)( \lambda + \mu _d+k+\beta _{dd}I_d^{**}e^{\mu _d \tau })\\&(\lambda + \mu _d)g_2(\lambda ) =0, \end{aligned} \end{aligned}$$

(3.16)

where $g_2(\lambda ) = \lambda + \mu _d+\alpha _d-\beta _{dd}S_d^{**}e^{-\tau (\lambda + \mu _d)}=0$. From (3.16), $G_2(\lambda )$ has five negative roots given as ($\lambda _1=- (\mu _h+v+\beta _{hd}I_d^{**}e^{\mu _d \tau }), \,\lambda _2=- (\mu _h+\alpha _h), \, \lambda _3 = -\mu _h, \, \lambda _4 = -(\mu _d+k+\beta _{dd}I_d^{**}e^{\mu _d \tau })\; \text {and}\, \lambda _5= -\mu _d$). Therefore the stability of $\mathcal {E}_1$ can be determined by the distribution of roots in $g_2(\lambda )=0$.

When $\tau =0$, we have

$$\begin{aligned} g_2(0)&\ge \,0\quad \text {and}\quad \lim _{\lambda \rightarrow \infty } g_2(\lambda )= +\infty . \end{aligned}$$

Hence there is no positive root of $g_2(\lambda )=0$ when $\tau =0$. Therefore $\mathcal {E}_1$ is stable.

When $\tau >0$, we assume there is a root $\lambda = iy_2$ for any $y_2\in \mathbb {R}^+$. Substituting $\lambda = iy_2$ in $g_2(\lambda )=0$, we have

$$\begin{aligned} \begin{aligned} g_2(iy) =&iy_2 +(\mu _d + \alpha _d) - \beta _{dd}S^{**}_d e^{-\tau \mu _d}(\cos y_2\tau - i\sin y_2\tau )=0. \end{aligned} \end{aligned}$$

Separating real and imaginary parts, squaring and adding the two parts, we get

$$\begin{aligned} y^2_2= & {} (\mu _d + \alpha _d)^2\left[ \frac{(\beta _{dd}S^{**}_d e^{-\tau \mu _d})^2}{(\mu _d + \alpha _d)^2}-1\right] . \end{aligned}$$

Therefore if $\mathcal {R}_v > 1$, there is no $y_2\in \mathbb {R}^+$ such that $\lambda = iy_2$ can be a root for $g_2(\lambda )=0$. From the general theory of transcendental equations, (see [3, 19]), we conclude that when $\mathcal {R}_v > 1$, then endemic equilibrium $\mathcal {E}_1$ is locally asymptotically stable for all delay $\tau \ge 0$.

$\square$

Next we look at the global attractiveness for $\mathcal {E}_1$.

Theorem 7

The endemic equilibrium $\mathcal {E}_1$ is globally asymptotically stable, if $\mathcal {R}_v > 1$ for all delay $\tau \ge 0$.

Proof

Let $\mathcal {R}_v>1$. Since $V_{h}$ and $V_{d}$ does not appear in the equations for $\frac{dS_{h}}{dt}$, $\frac{dI_{h}}{dt}$, $\frac{dS_{d}}{dt}$ and $\frac{dI_{d}}{dt}$, then model (2.1)–(2.6) can sufficiently be analyzed by dropping the equations of $\frac{dV_{h}}{dt}$ and $\frac{dV_{d}}{dt}$ with the same initial conditions. Hence we consider

$$\begin{aligned} \frac{dS_h}{dt}&= \,\mu _hK_h-(\mu _h + v)S_{h}-\beta _{hd}S_hI_d(t-\tau )e^{-\mu _d\tau }, \end{aligned}$$

(3.17)

$$\begin{aligned} \frac{dI_h}{dt}&= \,\beta _{hd}S_hI_d(t-\tau )e^{-\mu _d\tau } - (\mu _h+\alpha _h)I_h, \end{aligned}$$

(3.18)

$$\begin{aligned} \frac{dS_d}{dt}&= \,\mu _hK_d - (\mu _d+k)S_d - \beta _{dd}S_dI_d(t-\tau )e^{-\mu _d\tau }, \end{aligned}$$

(3.19)

$$\begin{aligned} \frac{dI_d}{dt}&=\, \beta _{dd}S_dI_d(t-\tau )e^{-\mu _d\tau } - (\mu _d + \alpha _d)I_d. \end{aligned}$$

(3.20)

The Lyapunov function we will consider for the global stability of the endemic equilibrium point $\mathcal {E}_1$ is of the same form as those used in [12, 14, 22, 23]. Thus we let the Lyaponuv function defined as

$$\begin{aligned} V(t)=( S_{h}-S_{h}^{**} \ln (S_{h})) + A (I_{h}-I_{h}^{**} \ln (I_{h})) + (S_{d}-S_{d}^{**} \ln (S_{d})) + B( I_{d}-I_{d}^{**} \ln (I_{d}) ), \end{aligned}$$

(3.21)

where A and B are constants to be determined. Differentiating (3.21) with the respect to time along the solution of (3.17)–(3.20), we have

$$\begin{aligned} \dot{ V(t)}= & {} \left( \dot{S_{h}}- \frac{S_{h}^{**} }{S_{h}}\dot{S_{h}}\right) + A \left( \dot{I_{h}}- \frac{I_{h}^{**} }{I_{h}}\dot{I_{h}}\right) + \left( \dot{S_{d}}- \frac{S_{d}^{**} }{S_{d}}\dot{S_{d}} \right) + B \left( \dot{I_{d}}- \frac{I_{d}^{**} }{I_{d}}\dot{I_{d}} \right) ,\nonumber \\ \end{aligned}$$

(3.22)

$$\begin{aligned}= & {} \left( 1- \frac{S_{h}^{**} }{S_{h}}\right) \dot{S_{h}} + A \left( 1 - \frac{I_{h}^{**} }{I_{h}}\right) \dot{I_{h}} + \left( 1 - \frac{S_{d}^{**} }{S_{d}} \right) \dot{S_{d}} + B \left( 1 - \frac{I_{d}^{**} }{I_{d}} \right) \dot{I_{d}}. \end{aligned}$$

(3.23)

At the endemic equilibrium it can be seen from (3.17)–(3.20) that

$$\begin{aligned} \mu _hK_h=&~ (\mu _h + v)S_{h}^{**} + \beta _{hd}S_{}^{**}I_{d}^{**}e^{-\mu _d\tau } \end{aligned}$$

(3.24)

$$\begin{aligned} (\mu _{h} + \alpha _{h}) =&~\frac{ \beta _{hd}S_{h}^{**}I_{d}^{**}e^{-\mu _{d}\tau }}{ I_{h}^{**}} \end{aligned}$$

(3.25)

$$\begin{aligned} \mu _hK_d =&~ (\mu _d +k)S_d^{**} + \beta _{dd}S_d^{**}I_d^{**}e^{-\mu _d\tau } \end{aligned}$$

(3.26)

$$\begin{aligned} (\mu _d + \alpha _d) =&~ \frac{\beta _{dd}S_d^{**}I_d^{**}e^{-\mu _d\tau }}{I_d^{**}} \end{aligned}$$

(3.27)

Substituting, the derivatives from (3.17)–(3.20) and further with the constants from (3.24)–(3.27), in Eq. (3.23), we have

$$\begin{aligned} \dot{ V(t)}= & {} \left( 1- \frac{S_{h}^{**} }{S_{h}}\right) \left[ (\mu _h + v)S_{h}^{**} + \beta _{hd}S_h{}^{**}I_{d}^{**}e^{-\mu _d\tau }-(\mu _h + v)S_{h}-\beta _{hd}S_hI_d(t-\tau )e^{-\mu _d\tau }\right] \nonumber \\&+ A \left( 1 - \frac{I_{h}^{**} }{I_{h}}\right) \left[ \beta _{hd}S_hI_d(t-\tau )e^{-\mu _d\tau } - \left( \frac{ \beta _{hd}S_{h}^{**}I_{d}^{**}e^{-\mu _{d}\tau }}{ I_{h}^{**}}\right) I_h\right] \nonumber \\&+ \left( 1 - \frac{S_{d}^{**} }{S_{d}} \right) \left[ (\mu _d +k)S_d^{**} + \beta _{dd}S_d^{**}I_d^{**}e^{-\mu _d\tau } - (\mu _d+k)S_d - \beta _{dd}S_dI_d(t-\tau )e^{-\mu _d\tau }\right] \nonumber \\&+ B \left( 1 - \frac{I_{d}^{**} }{I_{d}} \right) \left[ \beta _{dd}S_dI_d(t-\tau )e^{-\mu _d\tau } - \left( \frac{\beta _{dd}S_d^{**}I_d^{**}e^{-\mu _d\tau }}{I_d^{**}}\right) I_d\right] . \end{aligned}$$

(3.28)

Expanding and simplifying (3.28), we get

$$\begin{aligned} \dot{ V}(t)= & {} -(\mu _h + v) \frac{(S_{h}-S_{h}^{**})^2}{S_{h}} - (\mu _d +k) \frac{(S_{d} - S_{d}^{**})^2 }{S_{d}} \nonumber \\&+ \beta _{hd}S_{h}^{**}I_{d}^{**}e^{-\mu _{d}\tau }\left( 1- \frac{S_{h}^{**} }{S_{h}} - \frac{S_hI_d}{S_{h}^{**}I_{d}^{**}} + \frac{I_d}{I_{d}^{**}} + A \frac{S_{h}I_{d}}{S_{h}^{**} I_{d}^{**}}\right. \nonumber \\&\left. - A\frac{I_{h} }{I_{h}^{**}} \frac{S_{h}I_{d}}{S_{h}^{**} I_{d}^{**}} - A \frac{ I_{h}^{**}}{I_{h}} + A \right) \nonumber \\&+ \beta _{dd}S_d^{**}I_d^{**}e^{-\mu _d\tau } \left( 1- \frac{S_{d}^{**} }{S_{d}} - \frac{S_{d}I_{d}}{S_{d}^{**}I_{d}^{**}} + \frac{I_{d}}{I_{d}^{**}} + B \frac{S_dI_d}{S_{d}^{**}I_{d}^{**}}\right. \nonumber \\&\left. - B \frac{I_{d}^{**} }{I_{d}} \frac{S_dI_d}{S_{d}^{**}I_{d}^{**}} - B \frac{I_d}{I_{d}^{**}} + B \right) . \end{aligned}$$

(3.29)

Now choosing $A=B=1$, and initially, the number of infected dogs ($I_d(t)$) is less than or equal to $I_d^{**}$, then $\frac{I_{d}}{I_{d}^{**}}\le 1$. Hence

$$\begin{aligned} \begin{aligned} \dot{ V}(t)\le&-(\mu _h + v) \frac{(S_{h}-S_{h}^{**})^2}{S_{h}} - (\mu _d +k) \frac{(S_{d} - S_{d}^{**})^2 }{S_{d}} \\&+ \beta _{hd}S_{h}^{**}I_{d}^{**}e^{-\mu _{d}\tau }\left( 3 - \frac{S_{h}^{**} }{S_{h}} - \frac{I_{h}^{**} S_{h}}{I_{h}S_{h}^{**}} - \frac{ I_{h}^{**}}{I_{h}}\right) \\&+ \beta _{dd}S_d^{**}I_d^{**}e^{-\mu _d\tau } \left( 2- \frac{S_{d}^{**} }{S_{d}} - \frac{I_{d}^{**} S_d}{I_{d}S_{d}^{**}}\right) . \\ \end{aligned} \end{aligned}$$

(3.30)

From the last two terms in (3.30), using the fact that geometric mean is less than or equal to arithmetic mean, it implies

$$\begin{aligned} \begin{aligned} \dot{ V}(t)&\le 0. \end{aligned} \end{aligned}$$

(3.31)

Therefore, it follows that $~\dot{ V}(t)\le 0~$ and $~\dot{ V}(t)= 0~$ only at the endemic equilibrium point $\mathcal {E}_1$. Hence by LaSalle’s Invariance Principle [21], the only invariant set in

$\begin{Bmatrix} ( S_h, ~I_h,~ V_h,~ S_d, ~I_d,~ V_d~)~ \in ~\mathbb {R}_{+}^{6}&: ( S_h, ~I_h,~ V_h,~ S_d, ~I_d,~ V_d~) \rightarrow \mathcal {E}_1 \end{Bmatrix}$ is the singleton endemic equilibrium point $~\mathcal {E}_1~$. Thus any solution to model (2.1)–(2.6) which intersect the interior of $\mathbb {R}_{+}^{6}$ limits to $~\mathcal {E}_1$. Therefore, $~\mathcal {E}_1~$ is globally asymptotically stable in $\Omega$ whenever $\mathcal {R}_v > 1$ for all delay $\tau \ge 0$. $\square$

4 Numerical simulations

In this section, we present numerical simulations that support the theoretical results obtained in the previous sections. We use the parameter values in Table 2 that are mostly from published literature associated with rabies to illustrate our theoretical results. Moreover, the numerical experiments will be used to show the sensitivity of certain parameters as it affects the endemicity and control of the virus.

Table 2 Parameter values used in the numerical simulations of the model (2.1)–(2.6)

Fig. 2

Numerical simulations depicting the stability of equilibria in human subpopulations for the model (2.1)–(2.6) with parameter values in Table  2, except for (c) and (d), with $\beta _{hd} = 0.5$, $\beta _{dd} = 6.58 \times 10^{-3}$, $K_d =6000$ so that $\mathcal {R}_{v}=16.97>1$. In (a) time series of local stability for DFE, (b) 3D phase portrait for global asymptotic stability for DFE, (c) local asymptotic stability for EE (d) 3D phase portrait for global stability for EE

Figures 2 illustrate the asymptotic stabilities for equilibria ($\mathcal {E}_0$ and $\mathcal {E}_1$) in human population using parameter values in Table 2. In Figs.  2a, b, the local and global asymptotic stabilities for disease free equilibrium $\mathcal {E}_0$ are displayed using time series and 3D phase portrait respectively. Similarly, Fig. 2c, d, show the corresponding local and global asymptotic stabilities for endemic equilibrium $\mathcal {E}_1$ with parameter values from Table 2, except for $\beta _{hd} = 0.5$, $\beta _{dd} = 6.58 \times 10^{-3}$, $K_d =6000$ so that $\mathcal {R}_{v}=16.97>1$.

Fig. 3

Numerical simulations depicting the stability of equilibria in dog subpopulations for the model (2.1)–(2.6) with parameter values in Table  2, except for (c) and (d), with $\beta _{hd} = 0.5$, $\beta _{dd} = 6.58 \times 10^{-3}$, $K_d =6000$ so that $\mathcal {R}_{v}=16.97>1$. In (a) time series of local stability for DFE, (b) phase portrait for global asymptotic stability for DFE, (c) local asymptotic stability for EE (d) phase portrait for global stability for EE

Similarly, in Fig. 3, the asymptotic stabilities for equilibria ($\mathcal {E}_0$ and $\mathcal {E}_1$) in dog population are displayed. In Fig. 3a, b, the local and global asymptotic stabilities for disease free equilibrium $\mathcal {E}_0$ are shown with time series and 3D phase portrait respectively while Fig. 2c, d, show the corresponding local and global asymptotic stabilities for endemic equilibrium $\mathcal {E}_1$ in human subpopulations with parameter values as in Fig. 2c, d above. In both Figs.  2, 3a, b, the value of $\mathcal {R}_{v}$ is 0.67.

Fig. 4

Numerical simulations displaying the effects of vaccination in human and dog susceptible ubspopulations, and annual crop of new puppies using parameter values from Table 2, except for (a) $v= 0.01, 0.15, 0.45, 0.73, 1.98$, (b), (c) $k=0.02, 0.05, 0.07, 0.09, 0.2$ and (d) $K_d= 4500, 5000, 5500, 6000, 6500$

In order to explore the influence of control strategies on the numbers of infected humans and dogs, we varied the parameters of vaccination and annual crop of puppies as shown in Fig.  4a–d. From Fig. 4a, it can be seen that increasing the rate of human vaccination from $v = 0.01$ to $v=1.98$, the number of infected humans with rabies, after reaching highest peak of 80 people, decline to about 30 infected humans. It can further be observed in each case, the peak and number of infected cases are reducing as the vaccine rate increases. Although human vaccine reduces the infectivity of the virus, however, as shown from Fig. 4a, the rate of human vaccine for rabies must be very high for the basic reproduction number, $\mathcal {R}_{v}$ to be less than one. This suggest combine control strategy, especially from the dog population. In line with this and as remarked, we consider the sensitivity of vaccination in susceptible dog’s population. As observed from Figs.  4b, c, as k is increased from 0.02 to 0.2, the number of infected humans and dogs decreased to zero with value of $\mathcal {R}_{v}<1$. The implication of this control is that, the increase in dog vaccination rate can eradicate the disease in both human and dog populations. Another effective control strategy for rabies is to reduce the dog population by culling [20]. However, there are controversies associated with this control strategy ranging from critics by pet owners, animal activists to social factors [5]. For these reasons, we employ the method of reducing the birth rate of new born puppies annually by using immunocontraception as suggested in [5]. Thus, in Fig. 4d, as $K_d$ is reduced from 6500 to 4500, the number of infected dogs reduces to almost zero, hence bringing the value of $\mathcal {R}_{v}$ to below 1. In this case again, the disease can be eradicated in the population of the two organisms.

Fig. 5

Numerical simulations showing the effect of time delay as incubation period in both infected human and dog populations using parameter values in Table 2, except with $\tau = 0.33,\, 0.49, \, 0.58, \, 0.98, \, 1.5, \,2$ in (a) Infected humans and (b) infected dogs

Lastly, we consider the influence of time delay ($\tau$) as incubation period of rabies in dogs. As shown from Fig.  5a, b, as $\tau$ is increased from 0.33 to 2, there are rapid decrease in both the number and peaks in graphs of infected humans and dogs respectively. This suggest that if the incubation period can be elongated by any possible technique, the endemicity of rabies can be reduced.

5 Conclusion

In this article, we formulate and analyze a rabies model in co-population of humans and dogs by incorporating three control strategies (vaccination of dogs and humans coupled with annual birth of puppies) and time delay as incubation period to form a system of delay differential equations. This serves as an extension to several models proposed in [5, 6, 34] with respect to the control strategies and model dynamics. Basic properties of the model as par the theories of delay differential equations are established and the model is well-posed mathematically and biologically. The main findings of the study are summarized as follows:

• (i) Two equilibria are identified viz: disease free and endemic equilibria. Basic control reproduction number $\mathcal {R}_{v}$, is obtained and all parameters are defined in terms of dog population. Disease-free and endemic equilibria are shown to be both locally and globally asymptotically stable whenever $\mathcal {R}_{v}$ is less than/greater than unity and unstable otherwise, respectively, for any delay value. Thus in the former case, rabies can be eradicated if $\mathcal {R}_{v}$ can be reduced and maintained below one.

• (ii) Human vaccination for rabies is found to reduce the infectivity in humans, however, combining this with dog vaccination can eradicate the disease in humans.

• (iii) Similarly, administering vaccination on susceptible dogs can eradicate rabies in dog population in about 10 years.

• (iv) Decreasing the crop of new puppies annually using immunocontraception can also eliminate rabies in dog’s population within 10 years.

• (iv) Increasing time delay as incubation period is shown to decrease the infectivity of rabies in both human and dog populations.

• (vi) Numerical simulations, using MATLAB DDE23, are used to illustrate the theoretical results and sensitivity analysis of parameters associated with basic control reproduction number.