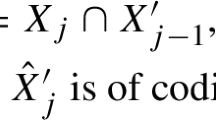Infinitesimal Torelli for weighted complete intersections and certain Fano threefolds

Abstract

We generalize the classical approach of describing the infinitesimal Torelli map in terms of multiplication in a Jacobi ring to the case of quasi-smooth complete intersections in weighted projective space. As an application, we prove that the infinitesimal Torelli theorem does not hold for hyperelliptic Fano threefolds of Picard rank 1, index 1, degree 4, and study the action of the automorphism group on cohomology. The results of this paper are used to prove Lang-Vojta’s conjecture for the moduli of such Fano threefolds in a follow-up paper.

1 Introduction

The Torelli problem asks the question if given a family of varieties, whether the period map is injective, i.e., if the variety is uniquely determined by its Hodge structure. This question has first been studied for curves; see Andreotti (1958). The infinitesimal Torelli problem is the related question that asks whether the period map has an injective differential. The problem can be formulated very concretely for a smooth projective variety X over ${{\mathbb {C}}}$ of dimension n. Namely, we say that X satisfies the infinitesimal Torelli theorem if the map

$$\begin{aligned} {{\,\textrm{H}\,}}^1(X,\Theta _X^1) \rightarrow \bigoplus _{p+q = n} \textrm{Hom}_{{\mathbb {C}}}\left( \textrm{H}^p(X,\Omega _X^q), \textrm{H}^{p+1}(X,\Omega _X^{q-1}) \right) \end{aligned}$$

induced by the contraction map is injective. In addition to curves, whether this holds has been studied among others for the following types of varieties:

• Hypersurfaces in projective space (Carlson et al. 1983; Donagi 1983)

• Hypersurfaces in weighted projective space (Saitō 1986)

• Complete intersections in projective space (Peters 1975, 1976; Terasoma 1990; Usui 1976)

• Zerosets of sections of vector bundles (Flenner 1986)

• Certain cyclic covers of a Hirzebruch surface (Konno 1985)

• Complete intersections in certain homogeneous Kähler manifolds (Konno 1986)

• Some weighted complete intersections (Usui 1977)

• Certain Fano quasi-smooth weighted hypersurfaces (Fatighenti et al. 2019)

• Some elliptic surfaces (Kii 1978; Kloosterman 2004; Saitō 1983)

The methods used in many of these studies have in common that they describe the cohomology groups relevant for the infinitesimal Torelli map as components of a so-called Jacobi ring and argue that the map can be interpreted as multiplication by some element in this ring. We generalize this method to the case of quasi-smooth complete intersections in weighted projective space. Following (Dolgachev 1982), we introduce the terminology:

Definition 1.1

Let k be a field. For $W=(W_0,\dots ,W_n) \in {{\mathbb {N}}}^{n+1}$ a tuple of positive integers, let $S_W = k[x_0,\dots ,x_n]$ be the graded polynomial algebra with $\deg (x_i) = W_i$. We define weighted projective space over k with weights W to be ${\mathbb {P}}(W) = {{\,\textrm{Proj}\,}}S_W.$ Given $d = (d_1,\dots ,d_c) \in {{\mathbb {N}}}^{c}$, $c \le n$, a closed subvariety $X \subseteq {\mathbb {P}}(W)$ is a complete intersection of degree d if it has codimension c and is given as the vanishing locus of homogeneous polynomials $f_1,\dots ,f_c \in S_W$ with $\deg (f_i)= d_i$. A weighted complete intersection $X = V(f_1,\dots ,f_c) \subseteq {\mathbb {P}}(W)$ is quasi-smooth if its affine cone $A(X) = {{\,\textrm{Spec}\,}}( S_W/(f_1,\dots ,f_c) ) \setminus \{0\}$ is smooth.

Given a quasi-smooth weighted complete intersection X over ${{\mathbb {C}}}$ as above, we can define generalized sheaves of differentials ${\tilde{\Omega }}^q_{X}$. One of the equivalent definitions of ${\tilde{\Omega }}^q_{X}$ is as the reflexive hull $\Omega _X^{**}$ of the usual sheaf of differentials; see Sect. 8 for details. There is a decomposition

$$\begin{aligned} \textrm{H}^{n-c}(X,{{\mathbb {C}}}) = \bigoplus _{p+q = n-c} \textrm{H}^p(X,{\tilde{\Omega }}_X^q) \end{aligned}$$

that coincides with the usual Hodge decomposition in case X is smooth; see Theorem 8.3. Consider the polynomial $F = y_1 f_1 + \dots + y_c f_c \in {{\mathbb {C}}}[x_0,\dots ,x_{n},y_1,\dots ,y_c]$, which is homogeneous with respect to the bigrading given by $\deg (x_i) = (0,W_i)$ and $\deg (y_j) = (1,-d_j)$. The Jacobi ring associated to the complete intersection X is the bigraded ring

$$\begin{aligned} R = {{\mathbb {C}}}[x_0,\dots ,x_{n},y_1,\dots ,y_c]/(\partial _{x_0}F,\dots ,\partial _{x_{n}}F,\partial _{y_1}F,\dots ,\partial _{y_c}F). \end{aligned}$$

1.1 Main results

Our first main result can be interpreted as giving an explicit description of the differential of the period map associated to a quasi-smooth weighted complete intersection in terms of its Jacobi ring.

Theorem 1.2

Let $X = V_+(f_1, \dots , f_c) \subseteq {\mathbb {P}}_{{\mathbb {C}}}(W_0,\dots ,W_n)$ be a quasi-smooth weighted complete intersection of degree $(d_1,\dots ,d_c)$ with tangent sheaf $\Theta _X^1$ of dimension $\dim (X) =n-c > 2$. Let R be the associated Jacobi ring. Let $\nu = \sum W_i - \sum d_j$. For all integers $p \in {{\mathbb {Z}}}$ with $0<p<n-c$ and $p\ne n-c-p$, there are isomorphisms

$$\begin{aligned} \textrm{H}^{n-c-p}(X,{\tilde{\Omega }}_X^p) \cong \textrm{Hom}_{{\mathbb {C}}}(R_{p,-\nu },{{\mathbb {C}}}) \end{aligned}$$

and

$$\begin{aligned} \textrm{H}^1(X,\Theta _X^1) \cong R_{1,0}. \end{aligned}$$

Under these isomorphisms, the contraction map

$$\begin{aligned} \textrm{H}^1(X,{\Theta }^1_X) \rightarrow \textrm{Hom}(\textrm{H}^{n-c-p}(X,{\tilde{\Omega }}_X^p),\textrm{H}^{n-c-p+1}(X,{\tilde{\Omega }}_X^{p-1})) \end{aligned}$$

is the map

$$\begin{aligned} R_{1,0} \rightarrow \textrm{Hom}(\textrm{Hom}_{{\mathbb {C}}}(R_{p,-\nu },{{\mathbb {C}}}),\textrm{Hom}_{{\mathbb {C}}}(R_{p-1,-\nu },{{\mathbb {C}}})) = \textrm{Hom}( R_{p-1,-\nu }, R_{p,-\nu }) \end{aligned}$$

that sends $\alpha \in R_{1,0}$ to the multiplication-by-$\alpha$ map.

Our second main result is an application of this theorem to prove the infinitesimal Torelli theorem for smooth Fano threefolds of Picard rank 1, index 1, and degree 4. In this paper all Fano threefolds are assumed to be smooth. By Iskovskikh’s classification, there are two types of such varieties; see (Iskovskih, 1979, Table 3.5). The varieties of the first type are smooth quartics in ${\mathbb {P}}^4$. For smooth hypersurfaces in projective space, the infinitesimal Torelli problem is completely understood. In particular, smooth quartic threefolds satisfy the infinitesimal Torelli theorem; see Carlson et al. (1983). The second type of Fano threefolds with Picard rank 1, index 1, degree 4 are called hyperelliptic; each such Fano threefold X is a double cover of a smooth quadric $Q \subseteq {\mathbb {P}}^4$ ramified along a smooth divisor of degree 8 in Q. Such a double cover comes naturally with an involution $\iota$ associated to the double cover. It turns out that such hyperelliptic Fano threefolds do not satisfy the infinitesimal Torelli theorem, i.e., the period map on the moduli of Fano threefolds of Picard rank 1, index 1, and degree 4 does not have an injective differential. However, the following result says that the “restricted” period map on the locus of hyperelliptic Fano threefolds does have an injective differential.

Theorem 1.3

(Infinitesimal Torelli problem for hyperelliptic Fano threefolds) Let X be a hyperelliptic smooth Fano threefold of Picard rank 1, index 1, and degree 4 over ${{\mathbb {C}}}$. Then X does not satisfy the infinitesimal Torelli theorem. However, if $\iota \in {{\,\textrm{Aut}\,}}(X)$ is the involution associated to the double cover, then the $\iota$-invariant part of the infinitesimal Torelli map

$$\begin{aligned} {{\,\textrm{H}\,}}^1(X,\Theta _X)^\iota \rightarrow \bigoplus _{p+q = 3} \textrm{Hom}_{{\mathbb {C}}}\left( \textrm{H}^p(X,\Omega _X^q), \textrm{H}^{p+1}(X,\Omega _X^{q-1}) \right) \end{aligned}$$

is injective.

As explained in (Javanpeykar and Loughran, 2018, Sect. 3.5), among the Fano threefolds of Picard number 1 and index 1, the infinitesimal Torelli theorem is satisfied if the degree is 2, 6 or 8, and it is known to fail for degrees 10 and 14. Our work deals with one of the remaining cases, namely that of degree 4.

Note that the failure of infinitesimal Torelli for Fano threefolds of Picard number 1, index 1, and degree 4 is analogous to the failure of infinitesimal Torelli for curves of genus $g\ge 3$. Such a curve satisfies the infinitesimal Torelli theorem if and only if it is not hyperelliptic [20], but the period map restricted to the hyperelliptic locus is an embedding (Landesman 2021).

It is natural to study the action of the automorphism group of a variety on its cohomology group; see for example (Cai et al. 2013; Javanpeykar and Loughran 2017; Kuznetsov et al. 2018). As an application of the explicit description of the cohomology groups of a Fano threefold with Picard rank 1, index 1, and degree 4 given by Theorem 1.2, we get the following result about the action of the automorphism group.

Theorem 1.4

Let X be a smooth Fano threefold of Picard rank 1, index 1, and degree 4 over ${{\mathbb {C}}}$. Then the following statements hold.

• 1. The automorphism group ${{\,\textrm{Aut}\,}}(X)$ acts faithfully on ${{\,\textrm{H}\,}}^1(X,\Theta _X)$.

• 2. If X is hyperelliptic, then the kernel $\ker \left( {{\,\textrm{Aut}\,}}(X) \rightarrow {{\,\textrm{Aut}\,}}(\textrm{H}^3(X,{{\mathbb {C}}}))\right)$ is isomorphic to ${{\mathbb {Z}}}/2{{\mathbb {Z}}}$ and generated by the involution $\iota$.

Additionally, it is known that if X is a smooth quartic threefold, then ${{\,\textrm{Aut}\,}}(X)$ acts faithfully on $\textrm{H}^3(X,{{\mathbb {C}}})$; see for example (Javanpeykar and Loughran, 2017, Proposition 2.12).

1.2 Ingredients of proof

For smooth complete intersections $X =V(f_1,\dots ,f_c)$ in usual projective space, similar results to Theorem 1.2 have been achieved by relating the IVHS of X to the IVHS of the hypersurface $V(F) \subseteq {\mathbb {P}}(E)$, with $E= \bigoplus {\mathcal {O}}_{{\mathbb {P}}^n}(d_i)$; see Terasoma (1990). To avoid problems of this geometric approach arising from the singular nature of the surrounding weighted projective space in our case, we will use another purely algebraic approach inspired by the calculations of Flenner; see (Flenner 1981, Sect. 8). We will construct resolutions of the sheaves ${\tilde{\Omega }}_X^p$ that will give us spectral sequences converging towards the cohomology groups of interest. The difficult part will be to make sure that the identification of the cohomology parts with the homogeneous components of the Jacobi ring is done in such a way that the contraction map can be identified with the ring-multiplication. To do this, we will extend the contraction pairing to a pairing of the resolutions and then to a pairing of the spectral sequences.

1.3 Arithmetic motivation

It is well-known that a variety admitting a quasi-finite period map is hyperbolic (Griffiths and Schmid 1969, Sect. 8-9), and therefore (by Lang-Vojta’s conjecture) should have only finitely many integral points, i.e., be “arithmetically hyperbolic”; see (Abramovich, 1997, § 0.3) or Javanpeykar (2020); Lang (1986). For evidence on Lang-Vojta’s arithmetic conjectures, see (Autissier 2009, 2011; Corvaja and Zannier 2006; Faltings 1994; Levin 2009; Javanpeykar 2021; Ullmo 2004).

We were first led to investigate the infinitesimal Torelli problem for these Fano threefolds when studying the arithmetic hyperbolicity of the moduli stack ${\mathcal {F}}$ of Fano threefolds of Picard rank 1, index 1, degree 4; see (Javanpeykar and Loughran, 2018, Sect. 2) for a definition of this stack. The property of a stack being arithmetically hyperbolic, i.e., having “only finitely many integral points” is formalized in Javanpeykar and Loughran (2021).

In Licht (2022), we prove the arithmetic hyperbolicity of this stack by first proving that the period map

$$\begin{aligned} p:{\mathcal {F}}^{an}_{{\mathbb {C}}}\rightarrow {\mathcal {A}}_{30}^{an} \end{aligned}$$

is quasi-finite and then using Faltings’s theorem (Faltings 1983) which says that the stack of principally polarized abelian varieties ${\mathcal {A}}_{30}$ is arithmetically hyperbolic. For the cases of Fano threefolds of Picard rank 1, index 1, and degree 2, 6 or 8, the quasi-finiteness of the period map is deduced from it being unramified, i.e. its differential, the infinitesimal Torelli map, being injective; see Javanpeykar and Loughran (2018). However, by our result in the degree 4 case, the infinitesimal Torelli map is not injective. We overcome this difficulty in Licht (2022) by showing that the moduli stack ${\mathcal {F}}$ has a natural two-step “stratification” and that on each stratum, the “restricted” period map is unramified. This then suffices to deduce the desired quasi-finiteness of the above period map.

2 Multigraded differential modules

In this section, we introduce multi-graded differential modules, which is a notion used for example in [41]. In particular, this notion describes single and double complexes and pages of spectral sequences.

Let R be a (commutative) ring or, more generally, the structure sheaf ${\mathcal {O}}_T$ of a scheme T. A differential d on an n-graded R-module $E = \bigoplus _{p \in {{\mathbb {Z}}}^n} E^{p}$ for us is always considered to be an R-linear self map that is homogeneous of a certain degree with $d \circ d = 0$. A bidifferential n-graded module is an n-graded module together with two commuting differentials.

Let $(E_1,d_1)$ and $(E_2, d_2 )$ be differential n-graded R-modules with homogeneous differentials of the same degree $a\in {{\mathbb {Z}}}^n$. Then the tensor product $E_1 \otimes E_2$ comes with an induced (2n)-grading

$$\begin{aligned} E_1 \otimes E_2 = \bigoplus _{(p,q)\in {{\mathbb {Z}}}^n \times {{\mathbb {Z}}}^n} E^p_1 \otimes E^{q}_2 \end{aligned}$$

and the two homogeneous differentials $d_1 \otimes {{\,\textrm{id}\,}}$ and ${{\,\textrm{id}\,}}\otimes d_2$, giving us a bidifferential 2n-graded R-module.

Definition 2.1

Let $n\in {{\mathbb {Z}}}_{>0}$ be a positive integer and let $(E,d_1,d_2)$ be a bidifferential 2n-graded R-module. Write the degree of $d_i$ as $(a_i,b_i)$ where $a_i,b_i \in {{\mathbb {Z}}}^n$. Suppose $a_1+b_1 = a_2+b_2$, then we define the associated total differential n-graded R-module of $(E,d_1,d_2)$ to be the n-graded module

$$\begin{aligned} {{\,\textrm{Tot}\,}}(E) = \bigoplus _{p \in {{\mathbb {Z}}}^n} {{\,\textrm{Tot}\,}}^p(E) \end{aligned}$$

where

$$\begin{aligned} {{\,\textrm{Tot}\,}}^p(E) = \bigoplus _{\begin{array}{c} s,t\in {{\mathbb {Z}}}^n \\ s+t = p \end{array}} E^{s,t} \end{aligned}$$

with homogeneous differential $d \in \text {End}({{\,\textrm{Tot}\,}}(E) )$ of degree $a_1+b_1 = a_2+b_2$ defined by $d\vert _{E^{s,t}} = d_1 + (-1)^{s_1} d_2.$

Example 2.2

Let $(K^{\bullet ,\bullet },d_1,d_2)$ be a double complex. Then $K = \bigoplus _{p,q\in {{\mathbb {Z}}}} K ^{p,q}$ is a bigraded module and $d_1$, $d_2$ define differentials of degree (1, 0), (0, 1) on K, thus giving K the structure of a bidifferential bigraded module. In fact, giving the data of a double complex is equivalent to defining a bigraded module with differentials of degree (1, 0) and (0, 1). Similarly, a complex $(L^\bullet ,d)$ can be identified with the differential graded module $(L = \bigoplus _{p\in {{\mathbb {Z}}}} L^p, d)$. Under these identifications, the total single complex associated to $K^{\bullet ,\bullet }$ and the total differential graded module associated to $K^{\bullet ,\bullet }$ are the same.

Example 2.3

For us, the total differential bigraded module associated to a tensor product of bigraded differential modules with differentials of the same degree $a\in {{\mathbb {Z}}}^2$ is of particular interest. So let $(E_1,d_1)$ and $(E_2, d_2 )$ be differential bigraded modules. Then the differentials $d_1 \otimes {{\,\textrm{id}\,}}$ and ${{\,\textrm{id}\,}}\otimes d_2$ on the quadgraded module $E_1 \otimes E_2$ have degrees $(a_1,a_2,0,0)$ and $(0,0,a_1,a_2)$. For $p,q \in {{\mathbb {Z}}}$, we have

$$\begin{aligned} {{\,\textrm{Tot}\,}}^{p,q}(E_1 \otimes E_2) = \bigoplus _{\begin{array}{c} s+t = p \\ u+v = q \end{array}} E^{s,u}_1 \otimes E^{t,v}_2. \end{aligned}$$

On $E^{s,u} \otimes E^{t,v}$ the differential is given as

$$\begin{aligned} d_{Tot}\vert _{E^{s,u} \otimes E^{t,v}} = d_1\vert _{E^{s,u}} \otimes {{\,\textrm{id}\,}}_{E^{t,v}} + (-1)^s {{\,\textrm{id}\,}}\vert _{E^{s,u}} \otimes d_2\vert _{E^{t,v}}. \end{aligned}$$

3 Pairings of filtered complexes

In this section, we explain how a pairing of filtered complexes induces a pairing of the associated homology complexes that respects the induced filtration. Let R be a ring or, more generally, the structure sheaf $R= {\mathcal {O}}_T$ of a scheme T. All modules are considered to be R-modules and all single (resp. double) complexes are considered to be single (resp. double) complexes of R-modules.

Let (K, d) , $( K^\bullet _1, d_1)$ and $( K^\bullet _2, d_2)$ be complexes. The total complex of the tensor product of $K^\bullet _1$ and $K^\bullet _2$, as introduced in Sect. 2, is given by

$$\begin{aligned} {{\,\textrm{Tot}\,}}^n( K^\bullet _1 \otimes K^\bullet _2) = \bigoplus _{p+q=n} K^{p}_1 \otimes K^{q}_2 \end{aligned}$$

with the differential given by

$$\begin{aligned} d_{Tot}\vert _{K_1^p\otimes K_2^q} = d_1 \otimes {{\,\textrm{id}\,}}\vert _{K_2^q} + (-1)^p {{\,\textrm{id}\,}}\vert _{K_1^p} \otimes d_2. \end{aligned}$$

Definition 3.1

A pairing of complexes from $( K^\bullet _1, d_1)$ and $( K^\bullet _2, d_2)$ to $(K^\bullet ,d)$ is a morphism of complexes

$$\begin{aligned} \phi :({{\,\textrm{Tot}\,}}^\bullet ( K^\bullet _1 \otimes K^\bullet _2) ),d_{Tot})\rightarrow (K^\bullet ,d). \end{aligned}$$

We write the components of $\phi$ as $\phi ^{p,q}:K^{p}_1 \otimes K^{q}_2 \rightarrow K^{p+q}$, for $p,q \in {{\mathbb {Z}}}$.

A pairing of complexes induces a pairing of the associated homology complexes.

Lemma 3.2

Let $(K^\bullet ,d)$, $( K^\bullet _1, d_1)$ and $( K^\bullet _2, d_2)$ be complexes and let

$$\begin{aligned} \phi :{{\,\textrm{Tot}\,}}^\bullet ( K^\bullet _1 \otimes K^\bullet _2) \rightarrow K^\bullet \end{aligned}$$

be a pairing of complexes. Then $\phi$ induces a pairing of the associated homology complexes (which are equipped with the zero differential)

$$\begin{aligned} {\overline{\phi }}:{{\,\textrm{Tot}\,}}^\bullet ( {{\,\textrm{H}\,}}^\bullet (K^\bullet _1,d_1) \otimes {{\,\textrm{H}\,}}^\bullet (K_2^\bullet , d_2) ) \rightarrow {{\,\textrm{H}\,}}^\bullet ({{\,\textrm{Tot}\,}}^\bullet ( K^\bullet _1 \otimes K^\bullet _2),d_{Tot}). \end{aligned}$$

Proof

There is a canonical graded map

$$\begin{aligned} {{\,\textrm{Tot}\,}}^\bullet ( {{\,\textrm{H}\,}}^\bullet (K^\bullet _1,d_1) \otimes {{\,\textrm{H}\,}}^\bullet (K_2^\bullet , d_2) ) \rightarrow {{\,\textrm{H}\,}}^\bullet ({{\,\textrm{Tot}\,}}^\bullet ( K^\bullet _1 \otimes K^\bullet _2),d_{Tot}) . \end{aligned}$$

We get ${\overline{\phi }}$ by composing this map with

$$\begin{aligned} \textrm{H}^\bullet (\phi ):{{\,\textrm{H}\,}}^\bullet ({{\,\textrm{Tot}\,}}^\bullet ( K^\bullet _1 \otimes K^\bullet _2),d_{Tot}) \rightarrow \textrm{H}^\bullet (K^\bullet ,d). \end{aligned}$$

A filtered complex is a triple $(K^\bullet ,d,F)$, where $K^\bullet$ is a complex with differential d, and F is a decreasing filtration on $K^\bullet$ compatible with the differential, i.e., for each $n\in {{\mathbb {Z}}}$, we have a decreasing filtration

$$\begin{aligned} K^n \supseteq \dots \supseteq F^{p} K^n \supseteq F^{p+1} K^n \supseteq \dots \end{aligned}$$

such that $d(F^{p} K^n) \subseteq F^{p} K^{n+1}$ for all $n,p \in {{\mathbb {Z}}}$. This means that $F^{p} K^\bullet$ becomes a subcomplex of $K^\bullet$ for every $p\in {{\mathbb {Z}}}$.

Given a filtered complex $(K^\bullet , d, F)$, there is an induced filtration on the homology complex $\textrm{H}^\bullet (K^\bullet ,d)$ given by

$$\begin{aligned} F^p \textrm{H}^n (K^\bullet ,d)) := {\text {im}}(\textrm{H}^n(F^p K^\bullet ) \rightarrow \textrm{H}^n(K^\bullet )) = \frac{\ker (d)\cap F^p K^n + {\text {im}}(d) \cap K^n}{{\text {im}}(d) \cap K^n}. \end{aligned}$$

For the associated graded pieces, we have

$$\begin{aligned} \textrm{gr}^p \textrm{H}^n(K^\bullet ) := \frac{F^p \textrm{H}^n (K^\bullet ,d))}{F^{p+1} \textrm{H}^n (K^\bullet ,d)} = \frac{\ker (d)\cap F^p K^n}{\ker (d)\cap F^{p+1} K^n + {\text {im}}(d) \cap F^p K^n}; \end{aligned}$$

(3.1)

see [The Stacks Project Authors 2022, Tag 0BDT].

Definition 3.3

Let R be a a ring (resp. let $R= {\mathcal {O}}_T$ be the structure sheaf of a scheme T). Let $(K^\bullet ,d,F)$,$( K^\bullet _1, d_1, F_1)$ and $( K^\bullet _2, d_2, F_2)$ be filtered complexes of R-modules. A pairing of complexes

$$\begin{aligned} \phi :{{\,\textrm{Tot}\,}}^\bullet ( K^\bullet _1 \otimes K^\bullet _2) \rightarrow K^\bullet \end{aligned}$$

is a pairing of filtered complexes if it is compatible with the filtrations, that is for all elements (resp. sections) $\alpha$ of $F^i_1 K^p_1$ and $\beta$ of $F^j_2 K^q_2$, we have that $\phi ^{p,q}(\alpha \otimes \beta )$ is an element (resp. section) of $F^{i+j} K^{p+q}$.

From the definition, it is evident that for each $p,q \in {{\mathbb {Z}}}$, such a pairing of filtered complexes induces a pairing of complexes

$$\begin{aligned} \phi :{{\,\textrm{Tot}\,}}^\bullet ( F^p_1 K^\bullet _1 \otimes F^{q}_2 K^\bullet _2) \rightarrow F^{p+q} K^\bullet . \end{aligned}$$

Hence the induced pairing of the homology complexes

$$\begin{aligned} {\overline{\phi }}:{{\,\textrm{Tot}\,}}^\bullet (\textrm{H}^\bullet ( K^\bullet _1, d_1 ) \otimes \textrm{H}^\bullet {( K^\bullet _2,d_2)}) \rightarrow \textrm{H}^\bullet (K^\bullet ,d) \end{aligned}$$

from Lemma 3.2 is compatible with the induced filtrations on the homology complexes. Therefore, for each $p,q,i,j \in {{\mathbb {Z}}}$, we get induced maps ${\overline{\phi }}^{p,q,i,j}$ and ${{\,\textrm{gr}\,}}^{p,q,i,j}(\phi )$ making the diagram

commute, where the maps $\alpha ^{a,b}$ denote the natural injections and the maps $\beta ^{a,b}$ denote the natural surjections.

4 Spectral pairing

In this section, we follow [The Stacks Project Authors 2022, Tag 012K] and explain how to construct the spectral sequence associated to a filtered complex. Building on this, we show that a pairing of filtered complexes induces a pairing of the associated spectral sequences.

Let R be a ring or, more generally, the structure sheaf $R= {\mathcal {O}}_T$ of a scheme T. All complexes are complexes of R-modules. A spectral sequence is given by the data

$$\begin{aligned} E = (E_r,d_r)_{r \in {{\mathbb {Z}}}_{\ge 0}} \end{aligned}$$

where $E_r = \bigoplus _{(p,q)\in {{\mathbb {Z}}}^2} E^{p,q}$ is a bigraded R-module and $d_r \in \text {End}(E_r)$ is a homogeneous differential of degree $(r,-r+1)$ such that

$$\begin{aligned} E_{r+1} = {{\,\textrm{H}\,}}(E_r,d_r) := \ker (d_r)/ {\text {im}}(d_r). \end{aligned}$$

All spectral sequences considered in this paper are bigraded. We can associate a spectral sequence to a filtered complex $(K^\bullet ,d,F)$ in the following way. We define

$$\begin{aligned} Z_r^{p,q}= & {} \frac{F^p K^{p+q}\cap d^{-1}(F^{p+r}K^{p+q+1})+F^{p+1}K^{p+q}}{F^{p+1}K^{p+q}}\\ B_r^{p,q}= & {} \frac{F^pK^{p+q}\cap d(F^{p-r+1}K^{p+q-1})+F^{p+1}K^{p+q}}{F^{p+1}K^{p+q}} \end{aligned}$$

and $E_r^{p,q} = Z_r^{p,q}/B_r^{p,q}$. Now set $B_r = \bigoplus _{p,q} B_r^{p,q}$, $Z_r = \bigoplus _{p,q} Z_r^{p,q}$ and $E_r = \bigoplus _{p,q} E_r^{p,q}$. Define the map $d_r:E_r \rightarrow E_r$ as the direct sum of the maps

$$\begin{aligned} d_r^{p,q}:E_r^{p,q} \rightarrow E_r^{p+r,q-r+1}:\quad {\overline{z}} \mapsto \overline{d(z)} \end{aligned}$$

where $z \in F^p K^{p+q}\cap d^{-1}(F^{p+r}K^{p+q+1})$. This defines the spectral sequence $(E_r,d_r)$ associated to the filtered complex $(K^\bullet ,d,F)$.

Definition 4.1

Let $( E_r,d_r), (\,^\prime E_r, \,^\prime d_r)$ and $(\,^{\prime \prime }E_r, \,^{\prime \prime }d_r)$ be spectral sequences. Let $\phi = (\phi _r)_{r \in {{\mathbb {Z}}}_{\ge 0}}$ be a collection of morphisms of bigraded differential modules

$$\begin{aligned} \phi _r:{{\,\textrm{Tot}\,}}^{\bullet ,\bullet }(\,^\prime E_r^{\bullet ,\bullet } \otimes \,^{\prime \prime }E_r^{\bullet ,\bullet }) \rightarrow E_r^{\bullet ,\bullet } \end{aligned}$$

that are homogeneous of degree 0. We write the components of $\phi _r$ as

$$\begin{aligned} \phi ^{s,t,u,v}_r:\,^\prime E_r^{s,u} \otimes \,^{\prime \prime }E_r^{t,v} \rightarrow E_r^{s+t,u+v}. \end{aligned}$$

The collection $\phi$ is called a pairing of spectral sequences if the diagram $\phi _{r+1}^{s,t,u,v}$ is induced by $\phi _r^{s,t,u,v}$ for all $r,s,t,u,v \in {{\mathbb {Z}}}$, $r \ge 0$. That means the diagram

commutes.

Form the definitions, we see:

Lemma 4.2

Let $((K^\bullet , d, F), (E_r,d_r))$, $((\, ^\prime K^\bullet , \,^\prime d , \,^\prime F), ( \,^\prime E_r,\,^\prime d_r))$ and $((\,^{\prime \prime } K^\bullet , \,^{\prime \prime } d , \,^{\prime \prime } F), (\,^{\prime \prime }E_r, \,^{\prime \prime }d_r))$ be pairs of filtered complexes with their associated spectral sequences. Any pairing of filtered complexes

$$\begin{aligned} \phi :{{\,\textrm{Tot}\,}}^\bullet ( ( \, ^\prime K^\bullet , \,^\prime d , \,^\prime F) \otimes (\,^{\prime \prime } K^\bullet , \,^{\prime \prime } d , \,^{\prime \prime } F) )\rightarrow (K^\bullet , d, F) \end{aligned}$$

induces a pairing of the associated spectral sequences ${\tilde{\phi }} = ({\tilde{\phi }}_r)_{r\in {{\mathbb {Z}}}_{\ge 0}}$,

$$\begin{aligned} {\tilde{\phi }}_r :{{\,\textrm{Tot}\,}}^{\bullet ,\bullet }((\,^\prime E_r^{\bullet ,\bullet }, \,^\prime d_r) \otimes (\,^{\prime \prime }E_r^{\bullet ,\bullet }, \,^{\prime \prime }d_r)) \rightarrow ( E_r^{\bullet ,\bullet },d_r). \end{aligned}$$

Proof

A computation shows that $\phi$ induces a map $\,^\prime Z_r^{s,u} \otimes \,^{\prime \prime }Z_r^{t,v} \rightarrow Z_r^{s+t,u+v}$ which maps both $\,^\prime B_r^{s,u} \otimes \,^{\prime \prime }Z_r^{t,v}$ and $\,^\prime Z_r^{s,u} \otimes \,^{\prime \prime }B_r^{t,v}$ to $B_r^{s+t,u+v}$. That ${\tilde{\phi }}_{r+1}^{s,t,u,v}$ is induced by ${\tilde{\phi }}_r^{s,t,u,v}$ follows from the fact that both maps are induced by $\phi$. For details see Licht (2022). $\square$

For a filtered complex $(K^\bullet ,d,F)$, we define

$$\begin{aligned} Z_\infty ^{p,q} = \bigcap _r Z_r^{p,q} = \bigcap _r \frac{F^p K^{p+q}\cap d^{-1}(F^{p+r}K^{p+q+1})+F^{p+1}K^{p+q}}{F^{p+1}K^{p+q}} \end{aligned}$$

and

$$\begin{aligned} B_\infty ^{p,q} = \bigcup _r B_r^{p,q} = \bigcup _r \frac{F^pK^{p+q}\cap d(F^{p-r+1}K^{p+q-1})+F^{p+1}K^{p+q}}{F^{p+1}K^{p+q}} \end{aligned}$$

and $E_\infty ^{p,q} = Z_\infty ^{p,q} / B_\infty ^{p,q}$. If we now suppose that the filtration is finite, i.e., for all $n \in {{\mathbb {Z}}}$, there are $l, m\in {{\mathbb {Z}}}$ such that $F^l K^n = K^n$ and $F^m K^n = 0$, then the chains

$$\begin{aligned} Z_0^{p,q} \supseteq \dots Z_r^{p,q} \supseteq Z_{r+1}^{p,q} \supseteq \dots \end{aligned}$$

and

$$\begin{aligned} B_0^{p,q} \subseteq \dots B_r^{p,q} \subseteq B_{r+1}^{p,q} \subseteq \dots \end{aligned}$$

become stationary and assume $Z_\infty ^{p,q}$ and $B_\infty ^{p,q}$ after finitely many steps. We have

$$\begin{aligned} Z_\infty ^{p,q} = \frac{F^p K^{p+q}\cap \ker (d) +F^{p+1}K^{p+q}}{F^{p+1}K^{p+q}} \end{aligned}$$

and

$$\begin{aligned} B_\infty ^{p,q} = \frac{F^p K^{p+q}\cap {\text {im}}(d) + F^{p+1}K^{p+q}}{F^{p+1}K^{p+q}}. \end{aligned}$$

If we now put $n=p+q$ and compare with Eq. (3.1), we get an identity

$$\begin{aligned} \textrm{gr}^p \textrm{H}^n(K^\bullet ) = \frac{\ker (d)\cap F^p K^n + F^{p+1} K^n}{{\text {im}}(d)\cap F^p K^n + F^{p+1} K^n} = E_\infty ^{p,q}. \end{aligned}$$

(4.1)

Theorem 4.3

Let $((K^\bullet , d, F), (E_r,d_r))$, $((\, ^\prime K^\bullet , \,^\prime d , \,^\prime F), ( \,^\prime E_r,\,^\prime d_r))$ and $((\,^{\prime \prime }K^\bullet , \,^{\prime \prime } d , \,^{\prime \prime } F), (\,^{\prime \prime }E_r, \,^{\prime \prime }d_r))$ be pairs of filtered complexes with their associated spectral sequences such that all the filtrations are finite, and let

$$\begin{aligned} \phi :{{\,\textrm{Tot}\,}}^\bullet (\,^\prime K^\bullet \otimes \,^{\prime \prime }K^\bullet ) \rightarrow K^\bullet \end{aligned}$$

be a pairing of filtered complexes. The induced pairing of the associated spectral sequences induces a pairing of bigraded modules

$$\begin{aligned} {\tilde{\phi }}_\infty :{{\,\textrm{Tot}\,}}^\bullet (\,^\prime E_\infty ^{\bullet ,\bullet } \otimes \,^{\prime \prime }E_\infty ^{\bullet ,\bullet }) \rightarrow E_\infty ^{\bullet ,\bullet } \end{aligned}$$

such that for all $i,j,p,q \in {{\mathbb {Z}}}$, the diagram

commutes.

Proof

By Lemma  4.2, the pairing of filtered complexes $\phi$ induces a pairing of spectral sequences

$$\begin{aligned} {\tilde{\phi }}_r :{{\,\textrm{Tot}\,}}^{\bullet ,\bullet }((\,^\prime E_r^{\bullet ,\bullet }, \,^\prime d_r) \otimes (\,^{\prime \prime }E_r^{\bullet ,\bullet }, \,^{\prime \prime }d_r)) \rightarrow ( E_r^{\bullet ,\bullet },d_r). \end{aligned}$$

For each ${i,j,p,q}\in {{\mathbb {Z}}}$ the modules $E_r^{i,p}$, $'E_r^{i,p}$ and $''E_r^{i,p}$ assume $E_\infty ^{i,p}$, $'E_\infty ^{i,p}$ and $''E_\infty ^{i,p}$ after finitely many pages. Hence the maps ${\tilde{\phi }}^{i,j,p,q}_r$ converge to a map

$$\begin{aligned} {\tilde{\phi }}^{i,j,p,q}_\infty :\,^\prime E_\infty ^{i,p} \otimes \,^{\prime \prime }E_\infty ^{j,q} \rightarrow E_\infty ^{i+j, p+q}. \end{aligned}$$

It coincides with ${{\,\textrm{gr}\,}}^{p+i,q+j,i,j} (\phi )$ as both maps are induced by $\phi$. $\square$

5 The contraction pairing on the affine cone

Let k be a field of characteristic zero and let $X = V_+(f_1,\dots ,f_c) \subseteq {\mathbb {P}}_k(W_0,\dots ,W_n)$ be a quasi-smooth weighted complete intersection of degree $(d_1,\dots ,d_c)$ with coordinate ring

$$\begin{aligned} A = S_W/(f_1,\dots ,f_c) \end{aligned}$$

and affine cone $U = Y \setminus \{0 \}$, where $Y = {{\,\textrm{Spec}\,}}A$. Let ${\mathcal {I}}\subseteq {\mathcal {O}}_{{\mathbb {A}}^{n+1}\setminus \{0\}}$ be the ideal sheaf of U in ${\mathbb {A}}^{n+1} \setminus \{0\}$. Let $\Omega _U^1$ be the sheaf of k-differentials on U and let $\Theta _U^1$ be its dual, namely the tangent sheaf. Let p be an integer satisfying $1 \le p \le n-c$. Building on Flenner’s calculations (Flenner 1981, Sect. 8), in this section we will construct free resolutions of the sheaves $\Omega _U^p$ and extend the contraction pairing

$$\begin{aligned} \Omega _U^p \otimes \Theta _U^1 \xrightarrow {\gamma } \Omega _U^{p-1} \end{aligned}$$

to these resolutions and their associated total Čech cohomology complexes.

5.1 The resolutions

The conormal sequence associated to the closed immersion of the smooth complete intersection U into ${\mathbb {A}}^{n+1}\setminus \{ 0 \}$, namely

$$\begin{aligned} 0 \rightarrow {\mathcal {I}}/{\mathcal {I}}^2 \rightarrow \Omega _{{\mathbb {A}}^{n+1}\setminus \{0\}}^1 \otimes {\mathcal {O}}_U \rightarrow \Omega _U^1 \rightarrow 0, \end{aligned}$$

is exact and $\Omega _U^1$ is locally free; see (Hartshorne, 1977, Theorem II.8.17). This uses the smoothness of U. The ${\mathcal {O}}_U$-module $\Omega _{{\mathbb {A}}^{n+1}\setminus \{0\}}^1 \otimes {\mathcal {O}}_U$ is free of rank $n+1$ and spanned by the elements $dx_0,\dots , dx_n$. The conormal sheaf ${\mathcal {I}}/{\mathcal {I}}^2$ of the complete intersection U is free of rank c and is generated by the elements $f_1,\dots ,f_c$. Hence the conormal sequence is described by the exact sequence

$$\begin{aligned} 0 \rightarrow F = \bigoplus \limits _{i\in \{1,\dots ,c\}} {\mathcal {O}}_{U}\cdot y_i \xrightarrow {\phi } G =\bigoplus \limits _{j \in \{ 0, \dots n\}} {\mathcal {O}}_{U}\cdot dx_j \xrightarrow {\pi } \Omega _U^1 \rightarrow 0 \end{aligned}$$

(5.1)

of ${\mathcal {O}}_{U}$-modules, where the $y_i$ are basis elements, the morphism $\phi$ is the ${\mathcal {O}}_{U}$-linear map with

$$\begin{aligned} \phi (y_i) = d(f_i) = \sum _{j=0}^n \partial _{j}(f_i) \cdot dx_j \end{aligned}$$

and $\pi$ is the natural surjection. Note, if we set $\deg (y_i) = d_i$ and $\deg (dx_i) = W_i$, then the induces morphisms $\phi _U: \Gamma (U,F) \rightarrow \Gamma (U,G)$ and $\pi _U: \Gamma (U,G) \rightarrow \Gamma (U,\Omega _U^1)$ are homogeneous of degree 0.

For any quasi-coherent ${\mathcal {O}}_U$-module N and $r\in {{\mathbb {Z}}}_{\ge 0}$, let $S^r(N)$ denote the r-th symmetric power of N. As the ${\mathcal {O}}_U$-module F is free with a basis $y_1,\dots ,y_c$, the symmetric power $S^r(F)$ is free with a basis formed by the elements

$$\begin{aligned} y^{ \lambda } := y_1^{ \lambda _1}\cdot \ldots \cdot y_c^{ \lambda _c} \end{aligned}$$

where $\lambda \in {{\mathbb {Z}}}_{\ge 0}^c$ with $\sum \lambda _i = r$. For the notation $y^{ \lambda }$, we will allow $\lambda \in {{\mathbb {Z}}}^c$. Namely, if $\lambda _i < 0$ for some i, then we set $y^{ \lambda } = 0$. Similarly to (Lebelt, 1977, example (ii)), for $1\le p \le n-c$, we define the complex $(K_p^\bullet ,d_{K_p}^\bullet )$ of ${\mathcal {O}}_{U}$-modules with components

$$\begin{aligned} K_p^q = S^{-q}(F) \otimes \bigwedge ^{p+q} (G) \end{aligned}$$

for $-p\le q \le 0$ and $K_p^q = 0$ otherwise and differential

$$\begin{aligned} K_p^q = S^{-q}(F) \otimes \bigwedge ^{p+q} (G) \rightarrow K_p^{q+1} = S^{-q-1}(F) \otimes \bigwedge ^{p+q+1} (G) \end{aligned}$$

given as the ${\mathcal {O}}_{U}$-linear map that sends $y^{\lambda } \otimes \omega$, where $\lambda \in {{\mathbb {Z}}}_{\ge 0}^c$ with $\sum _{i=c} \lambda _i = -q$ and $\omega = dx_{i_1}\wedge \dots \wedge dx_{i_{p+q}}$, to

$$\begin{aligned} \sum _{i=1}^c y^{\lambda -e_i} \otimes d(f_i) \wedge \omega , \end{aligned}$$

where $e_i \in {{\mathbb {Z}}}^c$ denotes the i-th standard basis vector.

By composing it with the natural surjection $K_p^0 = \bigwedge ^p (G) \rightarrow \Omega _U^p$, we get a complex

$$\begin{aligned} 0 \rightarrow K_p^{-p} \rightarrow \dots \rightarrow K_p^{0} \rightarrow \Omega _U^p \rightarrow 0. \end{aligned}$$

Note for $p = 1$, this is Sequence (5.1). By dualizing the exact sequence (5.1) of locally free sheaves, we get an exact sequence

$$\begin{aligned} 0 \rightarrow \Theta _U^1 \xrightarrow {\pi ^*} G^* = \bigoplus _{i=0}^n {\mathcal {O}}_{U}\cdot \delta _{i} \xrightarrow {\phi ^*} F^* = \bigoplus _{j=1}^c {\mathcal {O}}_{U}\cdot y_j^* \rightarrow 0, \end{aligned}$$

where the elements $\delta _0,\dots , \delta _n$ are the dual basis for $dx_0,\dots ,dx_n$ and the elements $y_1^*,\dots ,y_c^*$ are the dual basis for $y_1,\dots ,y_c$. The differential $\phi ^*$ maps $\delta _i$ to $\sum _{j=1}^c \partial _{x_i}(f_j) \cdot y_j^*$. Again, we set $\deg (\delta _i)= -w_i$ and $\deg (y_i^*) = -d_i$, so that the maps become homogeneous of degree 0 on global sections. We define the complex $(K_{-1}^\bullet ,d_{K_{-1}}^\bullet )$ with components $K_{-1}^0 = G^*$, $K_{-1}^1 = F^*$ and $K_{-1}^q = 0$ if $q\not \in \{0,1\}$ and differential $\phi ^*$. These complexes give the desired resolutions.

Theorem 5.1

In the situation above, for every $p \in \{1,\dots , n-c \}$, the complex of ${\mathcal {O}}_U$-modules

$$\begin{aligned} 0 \rightarrow K_{p}^{-p} \rightarrow \dots \rightarrow K_{p}^{0} \rightarrow \Omega _U^p \rightarrow 0 \end{aligned}$$

is exact. Furthermore the complex of ${\mathcal {O}}_U$-modules

$$\begin{aligned} 0\rightarrow \Theta _U^1 \rightarrow K_{-1}^0 \rightarrow K_{-1}^1 \rightarrow 0 \end{aligned}$$

is exact.

Proof

We have already proven the second statement and the first statement for $p=1$. Let $p>1$ and let $V = {{\,\textrm{Spec}\,}}B \subseteq U$ be any affine open subset such that the the B-module $M = \Gamma (V,\Omega _U^1)$ is free. Then M is m-torsion-free (see (Lebelt, 1977, Introduction) for definition) for any positive integer $m\in {{\mathbb {Z}}}_{>0}$. Hence by applying (Lebelt 1977, Satz 3.1) (note, since $\textrm{char}(k) = 0$, the ring B is a ${{\mathbb {Q}}}$-algebra and hence the divided powers used in that reference are isomorphic to symmetric powers) to M with the free resolution

$$\begin{aligned} 0 \rightarrow \Gamma (V,K_{1}^{-1}) \rightarrow \Gamma (V,K_{1}^{0}) \rightarrow M \rightarrow 0, \end{aligned}$$

we see that the complex

$$\begin{aligned} 0 \rightarrow \Gamma (V,K_{p}^{-p}) \rightarrow \dots \rightarrow \Gamma (V,K_{p}^{0}) \rightarrow \Gamma (V,\Omega _U^p) \rightarrow 0 \end{aligned}$$

is exact. Since $\Omega ^1_U$ is locally free, we can cover U with affine opens V such that the restriction is free. So we are done. $\square$

5.2 The pairing of resolutions

There are ${\mathcal {O}}_{U}$-bilinear contraction maps

$$\begin{aligned} {\tilde{\gamma }}_G:\quad \bigwedge ^q (G) \times G^*&\rightarrow \bigwedge ^{q-1} (G) \\ (dx_{i_1} \wedge \dots \wedge dx_{i_q} ,\theta )&\mapsto \sum _{j = 1}^q (-1)^j \theta (dx_{i_j}) dx_{i_1} \wedge \ldots \hat{dx_{i_j}} \ldots \wedge dx_{i_q} \end{aligned}$$

and

$$\begin{aligned} {\tilde{\gamma }}_F:S^{q}(F) \times F^*&\rightarrow S^{q-1}(F) \\ (y^{\lambda }, \mu )&\mapsto \sum _{i=1}^{r} y^{\lambda - e_i} \mu (y_i). \end{aligned}$$

These contraction maps induce morphisms

$$\begin{aligned} {{\,\textrm{id}\,}}_F \otimes {\tilde{\gamma }}_G:K_p^q \otimes K_{-1}^0 \rightarrow K_{p-1}^{q} \end{aligned}$$

and

$$\begin{aligned} {{\,\textrm{id}\,}}_G \otimes {\tilde{\gamma }}_F:K_p^q \otimes K_{-1}^{1} \rightarrow K_{p-1}^{q+1}. \end{aligned}$$

We define

$$\begin{aligned} {\tilde{\gamma }}^q:{{\,\textrm{Tot}\,}}^q\left( K_p^\bullet \otimes K_{-1}^\bullet \right) = K_p^{q-1} \otimes K_{-1}^1 \oplus K_p^q \otimes K_{-1}^0 \rightarrow K_{p-1}^{q} \end{aligned}$$

as

$$\begin{aligned} {\tilde{\gamma }}^q = {{\,\textrm{id}\,}}_G \otimes {\tilde{\gamma }}_F \oplus (-1)^{q} {{\,\textrm{id}\,}}_F \otimes {\tilde{\gamma }}_G. \end{aligned}$$

Lemma 5.2

The maps above define a pairing of complexes

$$\begin{aligned} {\tilde{\gamma }}:{{\,\textrm{Tot}\,}}^\bullet \left( K_p^\bullet \otimes K_{-1}^\bullet \right) \rightarrow K_{p-1}^\bullet \end{aligned}$$

and induce the contraction pairing, i.e., given sections $\theta$ of $\Theta _U^1$ and $\omega '$ of $\bigwedge ^p G$ with $\omega := \left( \bigwedge ^p\pi \right) (\omega ')$, we have

$$\begin{aligned} \gamma (\omega ,\theta ) = \left( \bigwedge ^{p-1}\pi \right) \circ {\tilde{\gamma }}(\omega ',\pi ^*(\theta )) \end{aligned}$$

where $\gamma :\Omega _U^p \otimes \Theta _U^1 \rightarrow \Omega _U^{p-1}$ is the contraction pairing.

For a proof, see (Licht 2022, Lemma 3.1.2).

5.3 The pairing of the total Čech complexes

Let ${\mathcal {U}}$ be an open affine covering of U. For $p\in \{-1,1,\dots , n-c \}$, let $\check{C}^\bullet ({\mathcal {U}}, K_p^\bullet )$ be the Čech double complex (as defined in [The Stacks Project Authors 2022,Tag 01FP]) and let

$$\begin{aligned} L_p^\bullet = {{\,\textrm{Tot}\,}}^\bullet \left( \check{C}^\bullet ({\mathcal {U}} , K_p^\bullet )\right) \end{aligned}$$

be the associated total complex. We consider the cup product map of complexes

$$\begin{aligned} \cup :{{\,\textrm{Tot}\,}}^\bullet (L_p^\bullet \otimes L_{-1}^\bullet ) \rightarrow {{\,\textrm{Tot}\,}}^\bullet (\check{C}^\bullet ({\mathcal {U}}, {{\,\textrm{Tot}\,}}^\bullet (K_p^\bullet \otimes K_{-1}^\bullet ) )) \end{aligned}$$

as defined in [The Stacks Project Authors 2022, Tag 07MB] and compose it with the map

$$\begin{aligned} {{\,\textrm{Tot}\,}}^\bullet (\check{C}^\bullet ({\mathcal {U}}, {{\,\textrm{Tot}\,}}^\bullet (K_p^\bullet \otimes K_{-1}^\bullet ) )) \rightarrow {{\,\textrm{Tot}\,}}^\bullet (\check{C}^\bullet ({\mathcal {U}}, K_{p-1}^\bullet )) \end{aligned}$$

induced by the pairing of complexes from Lemma 5.2 to obtain a pairing of complexes

$$\begin{aligned} {\bar{\gamma }}:{{\,\textrm{Tot}\,}}^\bullet (L_p^\bullet \otimes L_{-1}^\bullet ) \rightarrow L_{p-1}^\bullet . \end{aligned}$$

6 Cohomology for weighted complete intersections

In this section, we explain how to calculate the cohomology of certain coherent sheaves on weighted complete intersections. We give an overview of results on that matter found in Dolgachev (1982) and (Flenner, 1981, Sect. 8). We start with weighted projective space, where a similar statement can be found in Dolgachev (1982). The proof for the case of usual projective space, found in (Hartshorne, 1977, Theorem III.5.1), also works in the general case.

Lemma 6.1

Let k be a field, let $W\in {{\mathbb {N}}}^{n+1}$ be weights, let ${S_W} = k[x_0,\dots ,x_n]$ be the weighted polynomial algebra and let ${\mathbb {P}}= {\mathbb {P}}_k(W) = {{\,\textrm{Proj}\,}}{S_W}$ be weighted projective space. Then the following statements hold.

• 1. The natural map ${S_W} \rightarrow \bigoplus _{l\in {{\mathbb {Z}}}} H^0({\mathbb {P}},{\mathcal {O}}_{\mathbb {P}}(l))$ is an isomorphism of graded $S_W$-modules.

• 2. We have $\textrm{H}^q({\mathbb {P}},{\mathcal {O}}_{\mathbb {P}}(l)) = 0$ for $q \ne 0,n$ and $l \in {{\mathbb {Z}}}$.

• 3. In Čech cohomology with respect to the covering ${\mathcal {U}} = \{ D_+(x_i) \}$, the graded module $\bigoplus _{l\in {{\mathbb {Z}}}} \check{\textrm{H}}^n({\mathcal {U}},{\mathbb {P}},{\mathcal {O}}_{\mathbb {P}}(l))$ is the cokernel

  $$\begin{aligned} {{\,\textrm{coker}\,}}\left( k\langle x_0^{\alpha _0}\dots x_n^{\alpha _n} \, \vert \, \text { there exists } i \text { with } \alpha _i \ge 0 \rangle \rightarrow {S_W}[1/x_0,\dots ,1/x_n] \right) . \end{aligned}$$

To better handle the top cohomology, we introduce the k-dual module.

Definition 6.2

Let k be a field, let A be a k-algebra and let M be a graded A-module. We define the k-dual module of M to be the graded A-module $\textrm{D}(M) = \bigoplus _{l\in {{\mathbb {Z}}}} \textrm{D}(M)_l$ with $\textrm{D}(M)_l = \textrm{Hom}_k(M_{-l},k)$.

For example, if $A = {S_W}$ is a weighted polynomial algebra, then $\textrm{D}({S_W})_l = \textrm{Hom}_k(({S_W})_{-l},k)$. Here $({S_W})_{-l}$ is spanned by the monomials $x_0^{\alpha _0}\dots x_n^{\alpha _n}$ with $\sum \alpha _i W_i = - l$. We denote the corresponding dual basis elements by $\phi _{\alpha _0,\dots ,\alpha _n} \in \textrm{D}({{S_W}})_l$.

Note that $\textrm{D}$ defines a contravariant additive self-functor. If we assume A to be finitely generated over k (hence noetherian) and restrict $\textrm{D}$ to the category of finitely generated graded A-modules, then it is exact. This is because in that case, the homogeneous components $M_l$ are finite-dimensional k-vector spaces. In particular, under the application of $\textrm{D}$, injections become surjections, kernels become cokernels and vice versa.

Remark 6.3

Let $\vert W \vert = \sum W_i$. The k-vector space $\check{\textrm{H}}^n({\mathcal {U}},{\mathbb {P}}(W),{\mathcal {O}}_{{\mathbb {P}}(W)}(l))$ vanishes if $l > - \vert W \vert$. If $l \le - \vert W \vert$, then the vector space is spanned by the elements $x_0^{-1-\alpha _0}\dots x_n^{-1-\alpha _n}$ where $\alpha \in ({{\mathbb {Z}}}_{\ge 0})^{n+1}$ and $- \vert W \vert - \sum \alpha _i w_i = l$. The k linear map

$$\begin{aligned} \bigoplus _{l\in {{\mathbb {Z}}}} \check{\textrm{H}}^n({\mathcal {U}},{\mathbb {P}}(W),{\mathcal {O}}_{{\mathbb {P}}(W)}(l)) \rightarrow \textrm{D}(S) (\vert W \vert ) \end{aligned}$$

that maps $x_0^{-1-\alpha _0}\dots x_n^{-1-\alpha _n}$ to $\phi _{\alpha _0,\dots ,\alpha _n}$ defines an isomorphism of graded S-modules.

Consider a complete intersection $X = V(f_1,\dots ,f_c) \subseteq {\mathbb {P}}(W)$ of codimension c and degree $d_1,\dots ,d_c$ in ${\mathbb {P}}(W)$. The surjection of coordinate rings ${{S_W}} \rightarrow A = {{S_W}}/(f_1,\dots ,f_c)$ naturally induces an embedding $\textrm{D}(A) \subseteq \textrm{D}(S)$. For $r \in \{1,\dots ,c\}$ the scheme

$$\begin{aligned} X_r = {{\,\textrm{Proj}\,}}A_r, \quad A_r = {{S_W}}/(f_1,\dots ,f_r) \end{aligned}$$

is a weighted complete intersection of codimension r. We have a chain of closed immersions

$$\begin{aligned} X = X_c \subseteq \dots \subseteq X_0 := {\mathbb {P}}(W). \end{aligned}$$

For every $l \in {{\mathbb {Z}}}$ and $1 \le r \le c-1$, the ideal sheaf sequence

$$\begin{aligned} 0 \rightarrow {\mathcal {O}}_{X_r}(l-d_{r+1}) \xrightarrow {\cdot f_{r+1}} {\mathcal {O}}_{X_r}(l) \rightarrow {\mathcal {O}}_{X_{r+1}}(l) \rightarrow 0 \end{aligned}$$

is exact, as $f_1,\dots ,f_{r+1}$ is a regular sequence in $S_W$. Considering the associated long exact cohomology sequence and arguing inductively, we can prove the following lemma. (The induction starts with Lemma 6.1 and Remark 6.3.) For more details on the proof, we refer to Licht (2022).

Lemma 6.4

Let $l \in {{\mathbb {Z}}}$ and let X be a weighted complete intersection of codimension c as above. Let $\nu = \vert W \vert - \sum _{i=1}^c d_i$. Suppose $\dim (X) = n-c \ge 1$. Then

• 1. the natural map $A \rightarrow \bigoplus _{l\in {{\mathbb {Z}}}} \textrm{H}^0(X,{\mathcal {O}}_{X}(l))$ is an isomorphism of graded A-modules,

• 2. $\textrm{H}^q(X,{\mathcal {O}}_{X}(l)) = 0$ for $q \ne 0,n-c$ and $l \in {{\mathbb {Z}}}$, and

• 3. $\bigoplus _{l\in {{\mathbb {Z}}}} \textrm{H}^{n-c}(X,{\mathcal {O}}_{X}(l)) \cong \textrm{D}(A) \left( \nu \right)$.

Remark 6.5

If A is the coordinate ring of a weighted complete intersection X with affine cone $U = Y \setminus \{0\}$, where $Y= {{\,\textrm{Spec}\,}}A$, and M is a graded A-module, then there is a natural isomorphism of graded A-modules

$$\begin{aligned} \textrm{H}^q(U,M^{\sim }\vert _U) \cong \bigoplus \limits _{l\in {{\mathbb {Z}}}} \textrm{H}^q(X,(M(l))^\sim ), \end{aligned}$$

where M(l) denotes the module M with grading shifted by l, and $(\_)^\sim$ denotes the functor that associates to an A-module its associated ${\mathcal {O}}_Y$-module (respectively its associated graded ${\mathcal {O}}_X$-module). This isomorphism can be established by compairing the Čech cohomology with respect to the coverings $\{ D(x_i) \}$ for U and $\{ D_+(x_i) \}$ for X (see Licht 2022) or with methods of local cohomology (see (Flenner, 1981, Sect. 8)). We can use this identification to bring the results above in a more compact form. In particular, we have

$$\begin{aligned} \textrm{H}^q(U,{\mathcal {O}}_U) \cong \bigoplus _{l\in {{\mathbb {Z}}}} \textrm{H}^q(X,{\mathcal {O}}_{X}(l)). \end{aligned}$$

7 The Jacobi ring of a weighted complete intersection

In this section, we will introduce the Jacobi ring of a weighted complete intersection and explain how cohomology can be expressed in terms of it. Our methods build on Flenner’s calculation in (Flenner, 1981, Sect. 8). We continue with notations and conventions from Sect. 5. All components of the complexes $K_p^\bullet$ are free and hence quasi-coherent. So by Serre’s Criterion of affineness the higher cohomology groups vanish on any affine open subset. Hence, the homology of the associated total complex of the Čech double complexes with respect to the affine covering ${\mathcal {U}}$ calculates the hypercohomology of these complexes, i.e.,

$$\begin{aligned} {\mathbb {H}}^q(U,K_p^\bullet ) = \textrm{H}^q({{\,\textrm{Tot}\,}}^\bullet (\check{C}^\bullet ({\mathcal {U}} , K_p^\bullet ))) = \textrm{H}^q(L_p^{\bullet }); \end{aligned}$$

see [The Stacks Project Authors 2022, Tag 0FLH]. The total complex associated to a double complex comes with two filtrations $F_1$ and $F_2$ given by

$$\begin{aligned} F_1^r( L_p^q) = \bigoplus _{i+j=q, i\ge r} \check{C}^i({\mathcal {U}},K_p^j) \end{aligned}$$

and

$$\begin{aligned} F_2^r( L_p^q) = \bigoplus _{i+j=q, j\ge r} \check{C}^i({\mathcal {U}},K_p^j); \end{aligned}$$

see [The Stacks Project Authors 2022, Tag 012X]. The pairing ${\bar{\gamma }}$ is compatible with these filtrations. Hence, by Theorem 4.3, we get pairings of the associated spectral sequences, one for each filtration. We denote the spectral sequences associated to the filtered complex $(L_p^\bullet ,F_i)$ by $(E^{\bullet ,\bullet }_{i,p,r})_{r\in {{\mathbb {Z}}}_{\ge 0}}$. See Sect. 4 or [The Stacks Project Authors 2022, Tag 0130] for formulas for the computation of the pages of these spectral sequences. We first compute the pairing of spectral sequences associated to the filtration $F_1$. By Theorem 5.1, on the first page, we see

$$\begin{aligned} E_{1,p,1}^{s,t} = \textrm{H}^t(\check{C}^s({\mathcal {U}},K_p^\bullet )) = {\left\{ \begin{array}{ll} \check{C}^s ({\mathcal {U}},\Omega _U^p) &{} \text {if}\ t=0 \\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

if $p>0$ and

$$\begin{aligned} E_{1,-1,1}^{s,t} = \textrm{H}^t(\check{C}^s({\mathcal {U}},K_{-1}^\bullet )) = {\left\{ \begin{array}{ll} \check{C}^s ({\mathcal {U}},\Theta _U^1) &{} \text {if}\ t=0 \\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

Therefore, all spectral sequences converge on the second page with

$$\begin{aligned} E_{1,p,\infty }^{s,t} = E_{1,p,2}^{s,t} = {\left\{ \begin{array}{ll} \textrm{H}^s (U,\Omega _U^p)) &{} \text {if}\ t=0 \\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} E_{1,-1,\infty }^{s,t} = E_{1,-1,2}^{s,t} = {\left\{ \begin{array}{ll} \textrm{H}^s (U,\Theta _U^1) &{} \text {if}\ t=0 \\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

By Theorem 4.3, there is a pairing induced by ${\bar{\gamma }}$

$$\begin{aligned} {{\,\textrm{Tot}\,}}^\bullet (E_{1,p,\infty }^{\bullet ,\bullet } \otimes E_{1,-1,\infty }^{\bullet ,\bullet } ) \rightarrow E_{1,p-1,\infty }^{\bullet ,\bullet }. \end{aligned}$$

In particular, we obtain a pairing

$$\begin{aligned} \textrm{H}^{s_1}(U,\Omega _U^p) \otimes \textrm{H}^{s_2}(U,\Theta _U^1) \rightarrow \textrm{H}^{s_1+s_2}(U,\Omega _U^{p-1}). \end{aligned}$$

We note that it is the pairing induced by the contraction map $\gamma :\Omega _U^p \otimes \Theta _U^1 \rightarrow \Omega _U^{p-1}$ on cohomology, see Lemma 5.2. Now, we compute the pairing of spectral sequences associated to the filtration $F_2$. On the first page, we see

$$\begin{aligned} E_{2,p,1}^{s,t} = \textrm{H}^t(\check{C}^\bullet ({\mathcal {U}},K_p^s)) = \textrm{H}^t(U,K_p^s). \end{aligned}$$

All modules involved in the complex $K_p^\bullet$ are free. So by Lemma 6.4 and Remark 6.5, we see that the spectral sequence satisfies $E_{2,p,1}^{s,t} = 0$ if $t \ne 0,n-c$. Recall that the complex $K^\bullet _p$ is concentrated in degrees $-p,\dots ,0$, and we made the assumption that $p < n-c$. Hence, we see that the spectral sequences converge on page 2 since the differential never connects non-vanishing parts on later pages. We have

$$\begin{aligned} E_{2,p,\infty }^{s,t} = E_{2,p,2}^{s,t} = {\left\{ \begin{array}{ll} \textrm{H}^s(\textrm{H}^t(U,K_p^\bullet )) &{} \text {if } t \in \{0,n-c\} \\ 0 &{} \text {otherwise} \end{array}\right. }. \end{aligned}$$

The pairing

$$\begin{aligned} {{\,\textrm{Tot}\,}}^\bullet (E_{2,p,\infty }^{\bullet ,\bullet } \otimes E_{2,-1,\infty }^{\bullet ,\bullet } ) \rightarrow E_{2,p-1,\infty }^{\bullet ,\bullet } \end{aligned}$$

is the one induced by the pairing

$$\begin{aligned} {{\,\textrm{Tot}\,}}^\bullet (K_p^\bullet \otimes K_{-1}^\bullet ) \rightarrow K_{p-1}^\bullet \end{aligned}$$

on cohomology. Note that for both filtrations, all spectral sequences converge in such a way that for each integer m there is only one combination of (s, t) depending on m such that $s+t = m$ and

$$\begin{aligned} {{\,\textrm{gr}\,}}^s \textrm{H}^m(L_p^\bullet ) = E_{i,p,\infty }^{s,t} \ne 0; \end{aligned}$$

see Eq. (4.1). That means

$$\begin{aligned} F^q \textrm{H}^m(L_p^\bullet ) = {\left\{ \begin{array}{ll} 0 &{}\text {if } q > s \\ \textrm{H}^m(L_p^\bullet ) &{}\text {if } q \le s \end{array}\right. } \end{aligned}$$

and therefore in the diagram

$$\begin{aligned} \textrm{H}^m(L_p^\bullet ) \xleftarrow {\alpha ^{m,s}} F^s \textrm{H}^m(L_p^\bullet ) \xrightarrow {\beta ^{m,s}} {{\,\textrm{gr}\,}}^s \textrm{H}^m(L_p^\bullet ), \end{aligned}$$

the maps $\alpha ^{m,s}$ and $\beta ^{m,s}$ are both isomorphisms. We combine Diagram (3.2) for suitable choices of i and j with the diagram from Theorem 4.3 to get a commutative diagram

where the horizontal morphisms are isomorphisms. Thus, we have identified the pairings of spectral sequences for the filtrations $F_1$ and $F_2$ with each other. As shown above, the pairing

$$\begin{aligned} E_{1,p,\infty }^{n-c-p,0} \otimes E_{1,-1,\infty }^{1,0} \rightarrow E_{1,p-1,\infty }^{n-c-p+1,0} \end{aligned}$$

is identified with the contraction map

$$\begin{aligned} \textrm{H}^{n-c-p}(U,\Omega _U^p) \otimes \textrm{H}^{1}(U,\Theta _U^1) \rightarrow \textrm{H}^{n-c-p+1}(U,\Omega _U^{p-1}). \end{aligned}$$

On the other hand, the pairing

$$\begin{aligned} E_{2,p,\infty }^{-p,n-c} \otimes E_{2,-1,\infty }^{1,0} \rightarrow E_{1,p-1,\infty }^{1-p,n-c} \end{aligned}$$

is the pairing

$$\begin{aligned} \textrm{H}^{-p}(\textrm{H}^{n-c}(U,K_p^\bullet )) \otimes \textrm{H}^{1}(\textrm{H}^{0}(U,K_{-1}^\bullet )) \rightarrow \textrm{H}^{1-p}(\textrm{H}^{n-c}(U,K_{p-1}^\bullet )) \end{aligned}$$

induced by ${\tilde{\gamma }}$. We now explicitly calculate all the cohomology groups involved in this pairing. The group $\textrm{H}^{-p}(\textrm{H}^{n-c}(U,K_p^\bullet ))$ is the kernel of the map

$$\begin{aligned} \textrm{H}^{n-c}(U,K_p^{-p}) \rightarrow \textrm{H}^{n-c}(U,K_p^{1-p}). \end{aligned}$$

We compute:

$$\begin{aligned} \textrm{H}^{n-c}(U,K_p^{-p})= & {} \textrm{H}^{n-c}(U,S^p(F)) =\bigoplus \limits _{\sum \beta _j = p} \textrm{H}^{n-c}(U,{\mathcal {O}}_{U}) \cdot y^{\beta },\\ \textrm{H}^{n-c}(U,K_p^{1-p})= & {} \textrm{H}^{n-c}(U,S^{p-1}(F)\otimes G) = \bigoplus \limits _{\begin{array}{c} 0 \le i \le n, \\ \sum \beta _j = p-1 \end{array}} \textrm{H}^{n-c}(U,{\mathcal {O}}_{U}) \cdot y^{\beta } dx_i. \end{aligned}$$

We note that $\deg (y^{\beta }) = \sum \beta _j d_j$, and $\deg (dx_i) = W_i$. Hence, by Lemma 6.4 and Remark 6.5, we see that

$$\begin{aligned} \textrm{H}^{n-c}(U,K_p^{-p}) = \bigoplus \limits _{\sum \beta _j = p} \textrm{D}\left( A\left( -\nu +\sum \beta _j d_j \right) \right) \cdot y^{\beta }, \end{aligned}$$

and that

$$\begin{aligned} \textrm{H}^{n-c}(U,K_p^{-p}) = \bigoplus \limits _{\begin{array}{c} 0 \le i \le n, \\ \sum \beta _j = p-1 \end{array}} \textrm{D}\left( A\left( -\nu +W_i+\sum \beta _j d_j\right) \right) \cdot y^{\beta } dx_i. \end{aligned}$$

The kernel of the map $\textrm{H}^{n-c}(U,K_p^{-p}) \rightarrow \textrm{H}^{n-c}(U,K_p^{1-p})$ is the k-dual of the cokernel of the map

$$\begin{aligned} \alpha :\bigoplus \limits _{\begin{array}{c} 0 \le i \le n, \\ \sum \beta _j = p-1 \end{array}} A\left( -\nu +W_i+\sum \beta _j d_j\right) \cdot y^{\beta } dx_i \rightarrow \bigoplus \limits _{\sum \beta _j = p} A\left( -\nu +\sum \beta _j d_j \right) \cdot y^{\beta } \end{aligned}$$

that maps $y^{\beta }dx_i$ to $\sum _j \partial _{x_i}(f_j) y^{\beta +e_j}$. To describe the cokernel of this map, we introduce the Jacobi ring.

Definition 7.1

Let $X = V(f_1, \dots , f_c) \subseteq {\mathbb {P}}(W)$ be a weighted complete intersection of multidegree $(d_1,\dots ,d_c)$. Let $k[x_0,\dots ,x_n,y_1,\dots ,y_n]$ be the polynomial ring with bigrading $\deg (x_i) = (0,w_i)$, $\deg (y_j) = (1,-d_j)$. The polynomial $F = y_1f_1+ \dots + y_cf_c$ is bihomogeneous of degree (1, 0). We define the Jacobi ring of Y to be the bigraded ring

$$\begin{aligned} R = k[x_0,\dots ,x_n,y_1,\dots ,y_c]/(\partial _{x_0}(F),\dots ,\partial _{x_n}(F),\partial _{y_0}(F),\dots ,\partial _{y_c}(F)). \end{aligned}$$

We see that ${{\,\textrm{coker}\,}}(\alpha )$ is the part of R in which we fix the first degree to be p. In fact, if we view this part $R_{p,*}$ as a graded module via $\deg _2$, we get an isomorphism

$$\begin{aligned} {{\,\textrm{coker}\,}}(\alpha ) \cong R_{p,*}(-\nu ) \end{aligned}$$

of graded modules. This shows

$$\begin{aligned} \textrm{H}^{-p}(\textrm{H}^{n-c}(U,K_p^\bullet ))&= \ker (\textrm{H}^{n-c}(U,K_p^{-p}) \rightarrow \textrm{H}^{n-c}(U,K_p^{1-p}))\\&= \textrm{D}({{\,\textrm{coker}\,}}(\alpha )) \\ {}&= \textrm{D}(R_{p,*})(\nu ). \end{aligned}$$

Next we calculate $\textrm{H}^{1}(\textrm{H}^{0}(U,K_{-1}^\bullet ))$. It is the cokernel of the map

$$\begin{aligned} \textrm{H}^0(U,G^*) = \bigoplus _{i=0}^n A(W_i) \cdot \delta _{i} \xrightarrow {\phi ^*} \textrm{H}^0(U,F^*) = \bigoplus _{j=1}^c A(d_j) \cdot y_j^*, \end{aligned}$$

where the differential maps $\delta _i$ to $\sum _{j=1}^c \partial _{x_i}(f_j) \cdot y_j^*$. Hence, the cokernel is the $\deg _1 = 1$ part of the Jacobi ring, namely

$$\begin{aligned} \textrm{H}^{1}(\textrm{H}^{0}(U,K_{-1}^\bullet )) = R_{1,*}. \end{aligned}$$

For $x \in R_{1,*}$, let $m_x:R_{p-1,*} \rightarrow R_{p,*}$ be the multiplication by x. Now under these identifications, the pairing is explicitly given as

$$\begin{aligned} \textrm{D}(R_{p,*})(\nu ) \otimes R_{1,*} \rightarrow \textrm{D}(R_{p-1,*})(\nu ):\quad \varphi \otimes x \mapsto \varphi \circ m_x. \end{aligned}$$

We have proven the following.

Lemma 7.2

Let A be the coordinate ring of a quasi-smooth weighted projective complete intersection $X = V(f_1, \dots , f_c) \subseteq {\mathbb {P}}(W_0,\dots ,W_n)$ of degree $(d_1,\dots ,d_c)$ with affine cone U. Let $\nu = \sum W_i - \sum d_j$. There are isomorphisms $\textrm{H}^{n-c-p}(U,\Omega _U^p) \cong \textrm{D}(R_{p,*})(\nu )$ and $\textrm{H}^{1}(U,\Theta _U^1) \cong R_{1,*}$. Under theses isomorphisms the contraction pairing

$$\begin{aligned} \textrm{H}^{n-c-p}(U,\Omega _U^p) \otimes \textrm{H}^{1}(U,\Theta _U^1) \rightarrow \textrm{H}^{n-c-p+1}(U,\Omega _U^{p-1}) \end{aligned}$$

is the pairing

$$\begin{aligned} \textrm{D}(R_{p,*})(\nu ) \otimes R_{1,*} \rightarrow \textrm{D}(R_{p-1,*})(\nu ):\quad \varphi \otimes x \mapsto \varphi \circ m_x \end{aligned}$$

Remark 7.3

Giving the pairing

$$\begin{aligned} \textrm{H}^{n-c-p}(U,\Omega _U^p) \otimes \textrm{H}^{1}(U,\Theta _U^1) \rightarrow \textrm{H}^{n-c-p+1}(U,\Omega _U^{p-1}). \end{aligned}$$

is equivalent to giving a map

$$\begin{aligned} \textrm{H}^{1}(U,\Theta _U^1) \rightarrow \textrm{Hom}(\textrm{H}^{n-c-p}(U,\Omega _U^p), \textrm{H}^{n-c-p+1}(U,\Omega _U^{p-1} )). \end{aligned}$$

Under the identifications given in Lemma 7.2, this is the map

$$\begin{aligned} R_{1,*} \rightarrow \textrm{Hom}(\textrm{D}(R_{p,*})(\nu ),\textrm{D}(R_{p-1,*})(\nu )) = \textrm{Hom}(R_{p-1,*}(-\nu ),R_{p,*}(-\nu )) \end{aligned}$$

that sends a homogeneous element $x\in R_{1,*}$ to $m_x$.

8 Hodge structure on V-varieties

Following (Peters and Steenbrink 2008, Sect. 2.5), we recall some facts about almost Kähler V-varieties (e.g., quasi-smooth weighted complete intersections).

Definition 8.1

A complex analytic space X is an n-dimensional V-manifold if there is an open cover $X = \bigcup X_i$ such that $X_i = U_i/G_i$ is the quotient of an open subset $U_i \subseteq {{\mathbb {C}}}^n$ by a finite group $G_i$ acting holomorphically on $X_i$. A V-manifold X is almost Kähler if there exists a manifold Y that is bimeromorphic to a Kähler manifold and a proper modification $f:Y \rightarrow X$, i.e., a proper holomorphic map which is biholomorphic over the complement of a nowhere dense analytic subset.

There are generalized sheaves of differentials on almost Kähler V-manifolds.

Definition 8.2

Let X be a V-manifold. Let $i:X_{sm} \rightarrow X$ be the inclusion map of the smooth locus. Define

$$\begin{aligned} {\tilde{\Omega }}^p_X = i_* \Omega ^p_{X_{sm}}. \end{aligned}$$

The cohomology of these sheaves determines a Hodge structure, which coincides with the usual Hodge decomposition in the compact Kähler case; see (Peters and Steenbrink 2008 Theorem 2.43) and its proof.

Theorem 8.3

Let X be an almost Kähler V-manifold. Then, the complex ${\tilde{\Omega }}_X^\bullet$ is a resolution of the constant sheaf ${{\mathbb {C}}}_X$. Furthermore the spectral sequence in hypercohomology

$$\begin{aligned} E_1^{p,q} = \textrm{H}^q(X,{\tilde{\Omega }}^q_X) \Rightarrow \textrm{H}^{p+q}(X,{{\mathbb {C}}}) \end{aligned}$$

degenerates on page 1, and $\textrm{H}^l({X,{{\mathbb {Q}}}})$ admits a Hodge structure of weight l given by

$$\begin{aligned} \textrm{H}^l(X,{{\mathbb {Q}}}) \otimes {{\mathbb {C}}}= \textrm{H}^l(X,{{\mathbb {C}}}) = \bigoplus _{p+q=l} \textrm{H}^q(X,{\tilde{\Omega }}^q_X). \end{aligned}$$

As remarked in (Flenner 1981 Sect. 7) there are multiple equivalent ways of defining the ${\tilde{\Omega }}^p_X$. For us, the identification with the reflexive hull of the usual sheaf of differentials is relevant.

Lemma 8.4

Let k be an algebraically closed field, let X be a normal integral scheme of finite type over k, and let $i:X_{sm} \rightarrow X$ denote the inclusion of the smooth locus. Then there is a canonical isomorphism

$$\begin{aligned} (\Omega _X^p)^{**} \rightarrow i_* \Omega _{X_{sm}}^p . \end{aligned}$$

Proof

The restriction map $\Omega _X^p \rightarrow i_* \Omega _{X_{sm}}^p$ induces a map of the corresponding reflexive hulls $(\Omega _X^p)^{**} \rightarrow (i_*\Omega _{X_{sm}}^p)^{**}$. As $\Omega _{X_{sm}}^p$ is reflexive, there is a canonical isomorphism $(i_*\Omega _{X_{sm}}^p)^{**} \cong i_*\Omega _{X_{sm}}^p$. The induced map

$$\begin{aligned} (\Omega _X^p)^{**} \rightarrow i_*\Omega _{X_{sm}}^p \end{aligned}$$

is a map of reflexive sheaves that restricted to $X_{sm}$ is an isomorphism. Note since X is normal, the complement of the smooth locus $X\setminus X_{sm}$ has a codimension of at least 2. Hence it is an isomorphism by (Hartshorne 1980, Proposition 1.6). $\square$

Remark 8.5

If $X \subseteq {\mathbb {P}}_{{\mathbb {C}}}(W)$ is a quasi-smooth weighted projective variety, then X is normal; see (Dolgachev 1982 Proposition 1.3.3) for the case $X = {\mathbb {P}}_{{\mathbb {C}}}(W)$, the argument given there, namely that X is the quotient of its smooth (and hence normal) affine cone by a finite group, also applies in the general case. Hence by Lemma 8.4 the generalized sheaf of differentials ${\tilde{\Omega }}^p_X$ is canonically isomorphic to the reflexive hull $(\Omega _X^p)^{**}$. In particular, the tangent sheaf $\Theta ^1_X$ is therefore canonically isomorphic to the dual ${\tilde{\Theta }}^1_X := ({\tilde{\Omega }}^1_X)^*$ of ${\tilde{\Omega }}^1_X$.

9 Infinitesimal Torelli for weighted complete intersections

In this section, we proof Theorem 1.2. We continue with notations from Sect. 7. From now on we choose the base field $k={{\mathbb {C}}}$.

Let $X = V(f_1, \dots , f_c) \subseteq {\mathbb {P}}_{{\mathbb {C}}}(W_0,\dots ,W_n)$ be a weighted complete intersection of degree $(d_1,\dots ,d_c)$ with affine cone U. Let $A= S_W/(f_1,\dots ,f_c)$ be its coordinate ring. Let $Y = {{\,\textrm{Spec}\,}}A$, and let $U= Y \setminus \{0\}$ be the affine cone. Let $\Omega ^1_A$ be the sheaf of ${{\mathbb {C}}}$-differentials on A, and let $\Omega ^p_A = \bigwedge ^p \Omega _A^1$.

Definition 9.1

We define the Euler map as the A-linear morphism

$$\begin{aligned} \xi :\Omega _A^{p} \rightarrow \Omega _A^{p-1} \end{aligned}$$

that sends $dx_{i_1}\wedge \ldots \wedge dx_{i_p}$ to $\sum _{j=1}^p (-1)^j W_j x_j \cdot dx_{i_1}\wedge \ldots \hat{dx_{i_j}} \ldots \wedge dx_{i_p}$.

The associated ${\mathcal {O}}_Y$-module $(\Omega _A^p)^\sim$ is the sheaf of p-Forms on Y. Hence, we see that

$$\begin{aligned} (\Omega _A^p)^\sim \vert _U = \Omega ^p_Y\vert _U = \Omega _U^p. \end{aligned}$$

Therefore by Remark 6.5, there is a natural isomorphism

$$\begin{aligned} \textrm{H}^q(U,\Omega _U^p) \cong \bigoplus _{l\in {{\mathbb {Z}}}} \textrm{H}^q(X,(\Omega _A^p(l)^\sim ). \end{aligned}$$

(9.1)

In the following, we write $(\Omega _A^p(0))^\sim$ for the associated for the ${{\mathcal {O}}_{X}}$-module associated to the graded A-module $\Omega _A^p$ to avoid confusion with the associated ${\mathcal {O}}_Y$-module $(\Omega _A^p)^\sim$.

Lemma 9.2

(Flenner 1981, Lemma 8.9) For all integers $l\in {{\mathbb {Z}}}$, the complex $((\Omega _A^\bullet (l))^\sim ,\xi )$ of sheaves on X is exact and the kernel of

$$\begin{aligned} (\Omega _A^p(0))^\sim \xrightarrow {\xi } (\Omega _A^{p-1}(0))^\sim \end{aligned}$$

is canonically isomorphic to ${\tilde{\Omega }}_X^p$.

Lemma 9.2 gives us short exact sequences

$$\begin{aligned} 0 \rightarrow {\tilde{\Omega }}_X^p \rightarrow (\Omega _A^p(0))^\sim \xrightarrow {\xi } {\tilde{\Omega }}_X^{p-1} \rightarrow 0. \end{aligned}$$

(9.2)

There is the following vanishing result.

Lemma 9.3

(Flenner 1981, Lemma 8.10) In the situation above, the following statements hold.

• 1. We have $\textrm{H}^q(U,((\Omega _A^p(l))^\sim ) = 0$, if $p+q \ne n-c, n-c+1$ and $0< q < n-c$.

• 2. The map $\textrm{H}^0(X,(\Omega _A^p(0))^\sim ) \xrightarrow {\xi } \textrm{H}^0(X, {\tilde{\Omega }}_X^{p-1})$ is surjective if $p \ge 2$ and has cokernel isomorphic to ${{\mathbb {C}}}$ if $p=1$.

These results allow us to calculate the relevant cohomology groups.

Lemma 9.4

Let X be a weighted complete intersection as above of dimension $n-c>2$. Then, the following identities hold.

• 1. For $0<p<n-c$:

  $$\begin{aligned} \textrm{H}^q(X,{\tilde{\Omega }}^p_X) = {\left\{ \begin{array}{ll} 0 &{}\text {if } 0<q< n-c-p, q \ne p \\ {{\mathbb {C}}}&{}\text {if } 0<q < n-c-p, q = p \\ \textrm{Hom}_{{\mathbb {C}}}(R_{p,-\nu },{{\mathbb {C}}}) &{}\text {if } q = n-c-p, q \ne p \\ {{\mathbb {C}}}\oplus \textrm{Hom}_{{\mathbb {C}}}(R_{p,-\nu },{{\mathbb {C}}}) &{}\text {if } q = p = n-c-p. \end{array}\right. } \end{aligned}$$
• 2.
  $$\begin{aligned} \textrm{H}^1(X,{\Theta }_X^{1}) = R_{1,0}. \end{aligned}$$

Proof

We first prove (1). We argue by induction on p. In each step we consider the long exact cohomology sequences associated to the short exact Sequence (9.2) and use Lemmata 6.4, 7.2, 9.3 and Isomorphism 9.1 to compute certain cohomology groups. Let $p=1$. We know ${\tilde{\Omega }}_X^0 = {A}^\sim$. Hence, it follows Lemma 6.4 that $\textrm{H}^q(X,{\tilde{\Omega }}_X^0) = 0$ for $0<q<n-c$. The long exact sequence is

The assertion for $p=1$ immediately follows. Now assume that $2\le p < n-c-p$ and that the result holds for $p-1$. We see the assertion is also true for p by considering the long exact sequence

Similarly the result is verified in case $p \ge n-c-p$.

Now we prove (2). If we dualize Sequence (9.2) for $p=1$ and consider the associated long exact sequence, we get

$$\begin{aligned} \textrm{H}^1(X,\Theta ^0_X) \rightarrow \textrm{H}^1(X,\Theta _U^1)_0 \rightarrow \textrm{H}^1(X,\Theta _X^{1}) \rightarrow \textrm{H}^2(X,\Theta ^0_X); \end{aligned}$$

see Remark 8.5. Under the assumption that $2 < n-c$, we have $\textrm{H}^1(X,\Theta ^0_X) = \textrm{H}^2(X,\Theta ^0_X) = 0$ and therefore

$$\begin{aligned} \textrm{H}^1(X,{\Theta }_X^{1}) = \textrm{H}^1(X,\Theta _U^1))_0 = R_{1,0}. \end{aligned}$$

This proves the lemma. $\square$

Proof of Theorem 1.2

The statement is a combination of Lemma 9.4, Lemma 7.2, and Remark 7.3. $\square$

10 Infinitesimal Torelli for hyperelliptic Fano threefolds of type (1,1,4)

In this section, we will prove Theorem 1.3 and Theorem 1.4. Any hyperelliptic Fano threefold of Picard rank 1, index 1, and degree 4 over ${{\mathbb {C}}}$ is a weighted complete intersection

$$\begin{aligned} X = V_+(z^2-f,g) \subset {\mathbb {P}}_{{\mathbb {C}}}(1,1,1,1,1,2) = {{\,\textrm{Proj}\,}}{{\mathbb {C}}}[x_0,\dots ,x_4,z] \end{aligned}$$

with $f,g\in {{\mathbb {C}}}[x_0,\dots ,x_4]$, $\deg (g)=2$, $\deg (f)=4$; see (Iskovskih, 1979, Theorem II.2.2.ii). It is a double cover of the smooth quadric $V(g) \subseteq {\mathbb {P}}^4$ with ramification along the smooth surface $V(f,g) \subseteq {\mathbb {P}}^4$. Since V(g) is a smooth quadric, after a change of coordinates, we may assume $g = x_0^2+ \dots + x_4^2$. Write $h_i = \partial _{x_i}(f)/2$. Then the Jacobi ring of X is given by

$$\begin{aligned} R = {{\mathbb {C}}}[x_0,\dots ,x_4,z,y_2,y_4]/(f-z^2,g,y_2 x_0 - y_4 h_0, \dots , y_2 x_4 - y_4 h_4, y_4 \cdot z). \end{aligned}$$

We apply Theorem 1.2 to a complete intersection of this type. We calculate $\nu = 7-6=1$ and therefore

$$\begin{aligned} \textrm{H}^1(X,\Theta _X)&\cong R_{1,0},\, \\ \textrm{H}^{1}(X,{\tilde{\Omega }}_X^2)&\cong \textrm{Hom}_{{\mathbb {C}}}(R_{2,-1},{{\mathbb {C}}}),\, \\ \textrm{H}^{2}(X,{\tilde{\Omega }}_X^1)&\cong \textrm{Hom}_{{\mathbb {C}}}(R_{1,-1},{{\mathbb {C}}}). \end{aligned}$$

There are surjections

$$\begin{aligned}&y_2 \cdot {{\mathbb {C}}}[x_0,\dots ,x_4,z]_2 \oplus y_4 \cdot {{\mathbb {C}}}[x_0,\dots ,x_4,z]_4 \rightarrow R_{1,0}, \\&y_2 \cdot {{\mathbb {C}}}[x_0,\dots ,x_4,z]_1 \oplus y_4 \cdot {{\mathbb {C}}}[x_0,\dots ,x_4,z]_3 \rightarrow R_{1,-1}, \\&y_2^2 \cdot {{\mathbb {C}}}[x_0,\dots ,x_4,z]_3 \oplus y_2y_4 \cdot {{\mathbb {C}}}[x_0,\dots ,x_4,z]_5 \oplus y_4^2 \cdot {{\mathbb {C}}}[x_0,\dots ,x_4,z]_7 \rightarrow R_{2,-1}. \end{aligned}$$

Let $B = {{\mathbb {C}}}[x_0,\dots ,x_4]/(f,g)$. Using the relations $y_2 x_i = y_4 h_i$ and $y_4 z = 0$, we see

$$\begin{aligned} R_{1,0}&\cong {{\mathbb {C}}}\cdot y_2 z \oplus y_4 B_4, \\ R_{1,-1}&\cong y_4 B_3, \\ R_{2,-1}&\cong y_4^2 B_7. \end{aligned}$$

Note that there are injections

$$\begin{aligned} T_1 := y_2 B_2 \oplus {{\mathbb {C}}}\cdot y_2 z \rightarrow R_{1,0} \end{aligned}$$

and

$$\begin{aligned} T_2 := y_2 B_1 \rightarrow R_{1,-1}. \end{aligned}$$

We will need the following Lemma to prove Theorem 1.4.

Lemma 10.1

If $\varphi \in {{\,\textrm{Aut}\,}}(X)$, then there are linear polynomials $\lambda _i \in k[x_0,\dots ,x_4]_1$ and $b\in {{\mathbb {C}}}^*$ such that, for all $(x_0:\dots :x_4:z) \in X({{\mathbb {C}}})$, we have

$$\begin{aligned} \varphi (x_0:\dots :x_4:z) = (\lambda _0:\dots :\lambda _4:bz). \end{aligned}$$

Proof

The anticanonical bundle of X is isomorphic to ${\mathcal {O}}_{X}(1)$; see (Dolgachev, 1982, Theorem 3.3.4). The cohomology group $\textrm{H}^0(X,{\mathcal {O}}_{X}(1))$ is a 5-dimensional vector space generated by $x_0,\dots ,x_4$, and $\textrm{H}^0(X,{\mathcal {O}}_{X}(2))$ is a 15-dimensional vector space generated by $x_0^2,x_0x_1,\dots ,x_4^2,z$. Any automorphism $\varphi \in {{\,\textrm{Aut}\,}}(X)$ induces an automorphism of these cohomology groups. Hence $\varphi$ is of the form

$$\begin{aligned} \varphi (x_0,\dots ,x_4,z) = (\lambda _0,\dots ,\lambda _4,bz+q), \end{aligned}$$

where $\lambda _i \in k[x_0,\dots ,x_4]_1$, $b\in {{\mathbb {C}}}^*$ and $q\in {{\mathbb {C}}}[x_0,\dots ,x_4]_2.$ Note if $g(x_0,\dots ,x_4)=0$, then there is a $z\in {{\mathbb {C}}}$ such that $(x_0,\dots ,x_4,z) \in X$. This shows that $g(\lambda _0,\dots ,\lambda _4)$ vanishes on $V_+(g)\subseteq {\mathbb {P}}^4$. By Hilbert’s Nullstellensatz, $g(\lambda _0,\dots ,\lambda _4) = \nu g$ for some $\nu \in {{\mathbb {C}}}^*$. Furthermore, again by Hilbert’s Nullstellensatz, we see

$$\begin{aligned} (bz+q)^2-f(\lambda _0,\dots ,\lambda _4) \in (z^2-f,g). \end{aligned}$$

Hence, there are $a_1,a_2 \in {{\mathbb {C}}}$ and $p \in {{\mathbb {C}}}[x_0,\dots ,x_4]_2$ such that

$$\begin{aligned} b^2z^2 + 2b q z + q^2 - f(\lambda _0,\dots ,\lambda _4) = a_1(z^2-f) + a_2gz + pg. \end{aligned}$$

Comparing the z-terms, we see that g and q are the same up to a scalar multiple. As q vanishes on $V_+(g)$, we can put $q=0$. $\square$

Note that the involution coming from the double cover is given by

$$\begin{aligned} \iota :X \rightarrow X:\quad (x_0,\dots ,x_4,z) \mapsto (x_0,\dots ,x_4,-z). \end{aligned}$$

Proof of Theorem 1.4

(1): Consider an automorphism $\varphi \in {{\,\textrm{Aut}\,}}(X)$ as in Lemma 10.1. If $\varphi$ operates trivially on $\textrm{H}^1(X,\Theta _X^1)$, then it operates trivially on $T_1$. Therefore, we have $b=1$ and $\varphi (x_ix_j) = x_ix_j$ for all i, j. This shows that either $\lambda _i = x_i$ for all i or $\lambda _i = -x_i$ for all i. Note in ${\mathbb {P}}_{{\mathbb {C}}}(1,1,1,1,1,2)$, the coordinates $(x_0:\ldots :x_4,z)$ and $(-x_0:\ldots :-x_4,z)$ define the same point. Hence $\varphi = {{\,\textrm{id}\,}}$. (2): As mentioned in the introduction, this is already proven; see (Javanpeykar and Loughran, 2017, Proposition 2.12).

(3): If $\varphi$ acts trivially on $\textrm{H}^3(X,{{\mathbb {C}}})$, then it acts trivially on $\textrm{H}^{2,1}$. In particular, such a $\varphi$ then operates trivially on $T_2$. Hence, we have $\lambda _i = x_i$ for $i\in \{0,\dots ,4\}$. As $\varphi$ has to preserve the equation $z^2-f$, we see $b \in \{1,-1\}$. This implies $\varphi \in \{{{\,\textrm{id}\,}},\iota \}$. $\square$

Proof of Theorem 1.3

From the explicit descriptions above, we calculate that

$$\begin{aligned} \textrm{H}^1(X,\Theta _X) \cong (R_{1,0}) \cong y_4 B_4 \oplus {{\mathbb {C}}}\cdot y_2 z. \end{aligned}$$

The map $R_{1,-1} \rightarrow R_{2,-1}$ that multiplies by $y_2 z$ is the zero map. Hence by Theorem 1.2 the infinitesimal Torelli map is not injective.

We also see that the involution invariant part $H^1(X,\Theta _X)^\iota$ is

$$\begin{aligned} (R_{1,0})^\iota \cong y_4 B_4. \end{aligned}$$

Hence by Theorem 1.2, the involution invariant infinitesimal Torelli map can be identified with the map

$$\begin{aligned} B_4 \rightarrow \textrm{Hom}\left( B_3,B_7\right) . \end{aligned}$$

The sequence f, g is regular as these polynomials define a complete intersection in ${\mathbb {P}}^4$. We can find polynomials $h_1,h_2,h_3$ such that $f,g,h_1,h_2,h_3$ is regular. Note that we can choose these polynomials of arbitrarily large degrees. Now, by Macaulay’s theorem (Voisin 2007, Corollary 6.20), the map

$$\begin{aligned} \left( \frac{{{\mathbb {C}}}[x_0,\dots ,x_4]}{(f,g,h_1,h_2,h_3)}\right) _4 \rightarrow \textrm{Hom}\left( \left( \frac{{{\mathbb {C}}}[x_0,\dots ,x_4]}{(f,g,h_1,h_2,h_3)}\right) _3,\left( \frac{{{\mathbb {C}}}[x_0,\dots ,x_4]}{(f,g,h_1,h_2,h_3)}\right) _7\right) \end{aligned}$$

is injective. $\square$