Skip to main content
SpringerLink
Log in

On the Expected Number of Equilibria in a Multi-player Multi-strategy Evolutionary Game

  • Published:
Dynamic Games and Applications Aims and scope Submit manuscript

Abstract

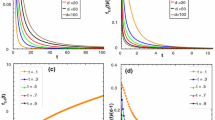
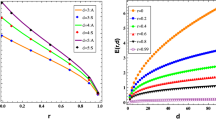
In this paper, we analyze the mean number \(E(n,d)\) of internal equilibria in a general \(d\)-player \(n\)-strategy evolutionary game where the agents’ payoffs are normally distributed. First, we give a computationally implementable formula for the general case. Next, we characterize the asymptotic behavior of \(E(2,d)\), estimating its lower and upper bounds as \(d\) increases. Then we provide a closed formula for \(E(n,2)\). Two important consequences are obtained from this analysis. On the one hand, we show that in both cases, the probability of seeing the maximal possible number of equilibria tends to zero when \(d\) or \(n\), respectively, goes to infinity. On the other hand, we demonstrate that the expected number of stable equilibria is bounded within a certain interval. Finally, for larger \(n\) and \(d\), numerical results are provided and discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Abel NH (1824) Mémoire sur les équations algébriques, où l’on démontre l’impossibilité de la résolution de l’équation générale du cinquiéme degré. Abel’s Ouvres 1:28–33

    Google Scholar 

  2. Altenberg L (2010) Proof of the Feldman–Karlin conjecture on the maximum number of equilibria in an evolutionary system. Theor Popul Biol 77(4):263–269

    Article  Google Scholar 

  3. Broom M, Cannings C, Vickers GT (1993) On the number of local maxima of a constrained quadratic form. Proc R Soc Lond A 443:573–584

    Article  MathSciNet  MATH  Google Scholar 

  4. Broom M, Cannings C, Vickers GT (1994) Sequential methods for generating patterns of ESS’s. J Math Biol 32(6):597–615

    Article  MathSciNet  MATH  Google Scholar 

  5. Broom M, Cannings C, Vickers GT (1997) Multi-player matrix games. Bull Math Biol 59(5):931–952

    Article  MATH  Google Scholar 

  6. Broom M, Rychtar J (2013) Game-theoretical models in biology. CRC Press, Boca Raton

    MATH  Google Scholar 

  7. Edelman A, Kostlan E (1995) How many zeros of a random polynomial are real? Bull Am Math Soc (N.S.) 32(1):1–37

    Article  MathSciNet  MATH  Google Scholar 

  8. Fudenberg D, Harris C (1992) Evolutionary dynamics with aggregate shocks. J Econ Theory 57:420–441

    Article  MathSciNet  MATH  Google Scholar 

  9. Gross T, Rudolf L, Levin SA (2009) Generalized models reveal stabilizing factors in food webs. Science 325:747–750

    Article  Google Scholar 

  10. Gokhale CS, Traulsen A (2010) Evolutionary games in the multiverse. Proc Natl Acad Sci USA 107(12):5500–5504

    Article  Google Scholar 

  11. Haigh J (1988) The distribution of evolutionarily stable strategies. J Appl Probab 25(2):233–246

    Article  MathSciNet  MATH  Google Scholar 

  12. Haigh J (1989) How large is the support of an ESS? J Appl Probab 26(1):164–170

    Article  MathSciNet  MATH  Google Scholar 

  13. Hardin G (1968) The tragedy of the commons. Science 162:1243–1248

    Article  Google Scholar 

  14. Hauert C, De Monte S, Hofbauer J, Sigmund K (2002) Replicator dynamics for optional public good games. J Theor Biol 218:187–194

    Article  MathSciNet  Google Scholar 

  15. Han TA, Pereira LM, Lenaerts T (2015) Avoiding or restricting defectors in public goods games? J R Soc Interface 12(103). doi:10.1098/rsif.2014.1203

  16. Hart S, Rinott Y, Weiss B (2008) Evolutionarily stable strategies of random games, and the vertices of random polygons. Ann Appl Probab 18(1):259–287

    Article  MathSciNet  MATH  Google Scholar 

  17. Hofbauer J, Sigmund K (1998) Evolutionary games and population dynamics. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  18. Han TA, Traulsen A, Gokhale CS (2012) On equilibrium properties of evolutionary multi-player games with random payoff matrices. Theor Popul Biol 81(4):264–272

    Article  Google Scholar 

  19. Karlin S (1980) The number of stable equilibria for the classical one-locus multiallele selection model. J Math Biol 9:189–192

    Article  MathSciNet  MATH  Google Scholar 

  20. Karlin S, Feldman MW (1970) Linkage and selection: two locus symmetric viability model. Theor Popul Biol 1:39–71

    Article  MathSciNet  MATH  Google Scholar 

  21. Kostlan E (1993) On the distribution of roots of random polynomials. In: From topology to computation: proceedings of the smalefest (Berkeley., CA, 1990), Springer, New York, pp 419–431

  22. Kostlan E (2002) On the expected number of real roots of a system of random polynomial equations. In: Foundations of computational mathematics (Hong Kong, 2000). World Scientific Publishing, River Edge, pp 149–188

  23. Kontogiannis SC, Spirakis PG (2009) On the support size of stable strategies in random games. Theor Comput Sci 410(8):933–942

    Article  MathSciNet  MATH  Google Scholar 

  24. Levin SA (2000) Multiple scales and the maintenance of biodiversity. Ecosystems 3:498–506

    Article  Google Scholar 

  25. McLennan A, Berg J (2005) Asymptotic expected number of Nash equilibria of two-player normal form games. Games Econ Behav 51(2):264–295

    Article  MathSciNet  MATH  Google Scholar 

  26. McLennan A (2005) The expected number of Nash equilibria of a normal form game. Econometrica 73(1):141–174

    Article  MathSciNet  MATH  Google Scholar 

  27. Maynard-Smith J (1982) Evolution and the theory of games. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  28. Nowak MA (2006) Evolutionary dynamics. Harvard University Press, Cambridge

    MATH  Google Scholar 

  29. Packer C, Caro TM (1997) Foraging costs in social carnivores. Animal behaviour 54(5):1317–1318

    Article  Google Scholar 

  30. Pacheco JM, Santos FC, Souza MO, Skyrms B (2009) Evolutionary dynamics of collective action in n-person stag hunt dilemmas. Proc R Soc B 276:315–321

    Article  Google Scholar 

  31. Sigmund K (2010) The calculus of selfishness. Princeton University Press, Princeton

    Book  MATH  Google Scholar 

  32. Schuster P, Sigmund K (1983) Replicator dynamics. J Theo Biol 100:533–538

    Article  MathSciNet  Google Scholar 

  33. Santos FC, Santos MD, Pacheco JM (2008) Social diversity promotes the emergence of cooperation in public goods games. Nature 454:213–216

    Article  Google Scholar 

  34. Stander PE (1992) Cooperative hunting in lions: the role of the individual. Behav Ecol Sociobiol 29(6):445–454

    Article  Google Scholar 

  35. Taylor PD, Jonker L (1978) Evolutionary stable strategies and game dynamics. Math Biosci 40:145–156

    Article  MathSciNet  MATH  Google Scholar 

  36. Tao T, Vu V (2014) Local universality of zeroes of random polynomials. Int Math Res Not 16(2). doi:10.1093/imrn/rnu084

  37. Vickers GT, Cannings C (1988) On the number of equilibria in a one-locus, multi allelic system. J theor Biol 131:273–277

    Article  MathSciNet  Google Scholar 

  38. Vickers GT, Cannings C (1988) Patters of ESS’s I. J theor Biol 132:387–408

    Article  MathSciNet  Google Scholar 

  39. Vickers GT, Cannings C (1988) Patters of ESS’s II. J theor Biol 132:409–420

    Article  MathSciNet  Google Scholar 

  40. Wu B, Traulsen A, Gokhale CS (2013) Dynamic properties of evolutionary multi-player games in finite populations. Games 4(2):182–199

    Article  MathSciNet  MATH  Google Scholar 

  41. Zeeman EC (1980) Population dynamics from game theory. Lect Notes Math 819:471–497

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

We would like to thank members of the WMS seminar at the CASA at Eindhoven University of Technology, especially Dr. R. van Hassel and Prof. A. Blokhuis for useful discussion. Part of this work was done under the support of the F.W.O. Belgium (TAH, postdoctoral fellowship 05_05 TR 7142).

Author information

Authors and Affiliations

  1. Mathematics Institute, Zeeman Building, University of Warwick, Coventry, CV4 7AL, UK

    Manh Hong Duong

  2. School of Computing, Teesside University, Borough Road, Middlesbrough, TS1 3BA, UK

    The Anh Han

Authors
  1. Manh Hong Duong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. The Anh Han
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to The Anh Han.

Appendix

Appendix

1.1 Properties of \(a_k\)

In the following, we prove that \(a_{2d-4-k} = a_k\) for all \(0 \le k \le 2d-4\), i.e., (22). First, we transform \(a_k\) as follows

$$\begin{aligned} a_k&=\sum \limits _{\begin{array}{c} 0\le i\le d-1\\ 0\le j\le d-2\\ i+j=k \end{array}}\begin{pmatrix} d-1\\ i \end{pmatrix}^2\begin{pmatrix} d-2\\ j \end{pmatrix}^2-\sum \limits _{\begin{array}{c} 0\le i'\le d-2\\ 0\le j'\le d-2\\ i'+j'=k-1 \end{array}}\begin{pmatrix} d-2\\ i' \end{pmatrix}\begin{pmatrix} d-1\\ i'+1 \end{pmatrix}\begin{pmatrix} d-2\\ j' \end{pmatrix}\begin{pmatrix} d-1\\ j'+1 \end{pmatrix} \\&= \begin{pmatrix} d-2 \\ k \end{pmatrix}^2 + \sum \limits _{\begin{array}{c} 0\le i\le d-2\\ 0\le j\le d-2\\ i+j=k-1 \end{array}}\begin{pmatrix} d-1\\ i+1 \end{pmatrix}^2\begin{pmatrix} d-2\\ j \end{pmatrix}^2-\sum \limits _{\begin{array}{c} 0\le i'\le d-2\\ 0\le j'\le d-2\\ i'+j'=k-1 \end{array}}\begin{pmatrix} d-2\\ i' \end{pmatrix}\begin{pmatrix} d-1\\ i'+1 \end{pmatrix}\begin{pmatrix} d-2\\ j' \end{pmatrix}\begin{pmatrix} d-1\\ j'+1 \end{pmatrix}\\&= \begin{pmatrix} d-2 \\ k \end{pmatrix}^2 + \sum \limits _{\begin{array}{c} 0\le i\le d-2\\ 0\le j\le d-2\\ i+j=k-1 \end{array}}\begin{pmatrix} d-1\\ i+1 \end{pmatrix}\begin{pmatrix} d-2\\ j \end{pmatrix}\left( \begin{pmatrix} d-1\\ i+1 \end{pmatrix}\begin{pmatrix} d-2\\ j \end{pmatrix} - \begin{pmatrix} d-2\\ i \end{pmatrix}\begin{pmatrix} d-1\\ j+1 \end{pmatrix} \right) \\&= \begin{pmatrix} d-2 \\ k \end{pmatrix}^2 + \sum \limits _{\begin{array}{c} 0\le i \le j \le d-2\\ i+j=k-1 \end{array}}\left( \begin{pmatrix} d-1\\ i+1 \end{pmatrix}\begin{pmatrix} d-2\\ j \end{pmatrix} - \begin{pmatrix} d-2\\ i \end{pmatrix}\begin{pmatrix} d-1\\ j+1 \end{pmatrix} \right) ^2 \end{aligned}$$

Now we prove that \(a_{2d-4-k} = a_{k}\). Indeed, we have

$$\begin{aligned} a_{2d - 4 - k}&= \begin{pmatrix} d-2 \\ 2d - 4 - k \end{pmatrix}^2 + \sum \limits _{\begin{array}{c} 0\le i \le j \le d-2\\ i+j=2d-k-5 \end{array}}\left( \begin{pmatrix} d-2\\ i+1 \end{pmatrix}\begin{pmatrix} d-2\\ j \end{pmatrix} - \begin{pmatrix} d-2\\ i \end{pmatrix}\begin{pmatrix} d-1\\ j+1 \end{pmatrix} \right) ^2 \\&\quad \text {(we use here the transformations i = d-3 - i and j = d-3 - j)}\\&= \begin{pmatrix} d-2 \\ 2d - 4 - k \end{pmatrix}^2 + \sum \limits _{\begin{array}{c} -1\le j \le i \le d-3\\ i+j=k-1 \end{array}}\left( \begin{pmatrix} d-1\\ i+1 \end{pmatrix}\begin{pmatrix} d-2\\ j+1 \end{pmatrix} - \begin{pmatrix} d-2\\ i+1 \end{pmatrix}\begin{pmatrix} d-1\\ j+1 \end{pmatrix} \right) ^2 \\&= \begin{pmatrix} d-2 \\ 2d - 4 - k \end{pmatrix}^2 + \sum \limits _{\begin{array}{c} -1\le j \le i \le d-3\\ i+j=k-1 \end{array}}\left( \begin{pmatrix} d-1\\ i+1 \end{pmatrix}\begin{pmatrix} d-2\\ j \end{pmatrix} - \begin{pmatrix} d-2\\ i \end{pmatrix}\begin{pmatrix} d-1\\ j+1 \end{pmatrix} \right) ^2. \\ \end{aligned}$$

Since for \(j = -1\) and \(i = k\), we have

$$\begin{aligned} \left( \begin{pmatrix} d-1\\ i+1 \end{pmatrix}\begin{pmatrix} d-2\\ j \end{pmatrix} - \begin{pmatrix} d-2\\ i \end{pmatrix}\begin{pmatrix} d-1\\ j+1 \end{pmatrix} \right) ^2 = \begin{pmatrix} d-1 \\ k \end{pmatrix}^2, \end{aligned}$$

and for \(j = d-2\) and \(i = k-1 - (d-2)\), we have

$$\begin{aligned} \left( \begin{pmatrix} d-1\\ i+1 \end{pmatrix}\begin{pmatrix} d-2\\ j \end{pmatrix} - \begin{pmatrix} d-2\\ i \end{pmatrix}\begin{pmatrix} d-1\\ j+1 \end{pmatrix} \right) ^2&= \left( \begin{pmatrix} d-1\\ k-(d-2) \end{pmatrix}- \begin{pmatrix}d-2\\ k-1-(d-2) \end{pmatrix} \right) ^2 \\&= \begin{pmatrix} d-2\\ k-(d-2) \end{pmatrix}^2 \\&= \begin{pmatrix} d-2\\ 2d-4-k \end{pmatrix}^2 , \end{aligned}$$

it follows that \(a_{2d-4-k} = a_k\) for all \(0 \le k \le 2d-4\).

1.2 Detailed Computation of \(f(1)\)

We use the following identities involving the square of binomial coefficients.

$$\begin{aligned}&M_d(1)=\sum \limits _{k=0}^{d-1}\begin{pmatrix} d-1\\ k \end{pmatrix}^2=\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix},\\&A_d(1)=(d-1)^2M_{d-1}(1)=(d-1)^2\begin{pmatrix} 2(d-2)\\ d-2 \end{pmatrix},\\&B_d(1)=\sum \limits _{k=1}^{d-1}k\begin{pmatrix} d-1\\ k \end{pmatrix}^2=\frac{d-1}{2}\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}. \end{aligned}$$

Therefore, we have

$$\begin{aligned} f(1)&=\frac{1}{\pi }\frac{\sqrt{A_d(1)M_d(1)-B_d(1)^2}}{M_d(1)}\\&=\frac{1}{\pi }\frac{\sqrt{(d-1)^2\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}\left[ \begin{pmatrix} 2(d-2)\\ d-2 \end{pmatrix}-\frac{1}{4}\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}\right] }}{\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}}\\&=\frac{d-1}{\pi }\times \sqrt{\frac{\begin{pmatrix} 2(d-2)\\ d-2 \end{pmatrix}}{\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}}-\frac{1}{4}}\\&=\frac{d-1}{\pi }\times \sqrt{\frac{d-1}{2(2d-3)}-\frac{1}{4}}\\&=\frac{d-1}{2\pi \sqrt{2d-3}}, \end{aligned}$$

where we have used the identity \(\begin{pmatrix} 2(n+1)\\ n+1 \end{pmatrix}=\frac{n+1}{2(2n+1)}\begin{pmatrix}2n\\ n \end{pmatrix}.\)

1.3 Alternative Proof of the Fifth Property in Lemma 2

We show here an alternative proof of the fifth property without using the first one in Lemma 2.

Since \(M_d\left( \frac{1}{t}\right) =t^{2(1-d)M_d(t)}\), we have

$$\begin{aligned} M_d'\left( \frac{1}{t}\right)&=-t^{3-2d}\left[ 2(1-d)M_d(t)+tM_d'(t)\right] ,\\ M_d''\left( \frac{1}{t}\right)&=t^{4-2d}\left[ 2(3-2d)(1-d)M_d(t) +2(3-2d)tM_d'(t)+t^2M_d''(t)\right] . \end{aligned}$$

Therefore, from (26), we have

$$\begin{aligned} B_d\left( \frac{1}{t}\right) =\frac{1}{2}M_d'\left( \frac{1}{t}\right) =-t^{3-2d}\left[ (1-d)M_d(t)+\frac{1}{2}tM_d'(t)\right] , \end{aligned}$$

and

$$\begin{aligned} A_d\left( \frac{1}{t}\right)&=\frac{t}{4}\left[ M_d'\left( \frac{1}{t}\right) +\frac{1}{t}M_d''\left( \frac{1}{t}\right) \right] \\&=\frac{1}{4}t^{4-2d}\left[ 4(1-d)^2+(5-4d)tM_d'(t)+t^2M_d''(t)\right] . \end{aligned}$$

Hence,

$$\begin{aligned} A_d\left( \frac{1}{t}\right) M_d\left( \frac{1}{t}\right) -B_d\left( \frac{1}{t} \right) ^2&=\frac{1}{4}t^{6-2d}\left[ 4(1-d)^2M_d(t)^2+(5-4d)tM_d'(t)M_d(t)\right. \\&\qquad \left. +t^2M_d''(t)M_d(t)\right] -t^{6-4d}\left[ (1-d)M_d(t)+\frac{1}{2}tM_d'(t)\right] ^2\\&=\frac{1}{4}t^{6-2d}\left[ tM_d(t)M_d'(t)+t^2M_d(t)M_d''(t) -t^2M_d'(t)^2\right] \\&=\frac{1}{4}t^{8-2d}\left[ \frac{1}{t}M_d(t)M_d'(t) +M_d(t)M_d''(t)-M_d'(t)^2\right] . \end{aligned}$$

Therefore,

$$\begin{aligned} f\left( \frac{1}{t}\right)&=\frac{1}{\pi }\frac{\sqrt{A_d\left( \frac{1}{t} \right) M_d\left( \frac{1}{t}\right) -B_d\left( \frac{1}{t}\right) ^2}}{M_d \left( \frac{1}{t}\right) }\\&=\frac{1}{\pi }\frac{t^{4-2d}\sqrt{\frac{1}{4t}\left[ M_d(t)M_d'(t) +tM_d(t)M_d''(t)-tM_d'(t)^2\right] }}{t^{2-2d}M_d(t)}\\&=t^2\frac{1}{\pi }\frac{\sqrt{\frac{1}{4t}\left[ M_d(t)M_d'(t)+ tM_d(t)M_d''(t)-tM_d'(t)^2\right] }}{M_d(t)}\\&=t^2f(t). \end{aligned}$$

1.4 Proof of Lemma 3

Denoting \(\varSigma = 1+\sum _{k=1}^{n-1} t_k^2\), we have

$$\begin{aligned} \det L&= \frac{1}{\varSigma ^{2(n-1)}} \det \begin{pmatrix} \varSigma -t_1^2 &{} -t_1 t_2&{} \dots &{} -t_1 t_{n-1} \\ -t_2 t_1&{} \varSigma -t_2^2 &{} \dots &{} -t_2 t_{n-1} \\ \dots &{} \dots &{} \dots &{} \dots \\ -t_{n-1} t_1&{} -t_{n-1} t_2 &{} \dots &{}\varSigma -t_{n-1}^2 \end{pmatrix}\\&= \frac{1}{t_1 \dots t_{n-1}} \frac{1}{\varSigma ^{2(n-1)}} \det \begin{pmatrix} t_1(\varSigma -t_1^2) &{} -t_1 t_2^2&{} \dots &{} -t_1 t_{n-1}^2 \\ -t_2 t_1^2&{} t_2( \varSigma -t_2^2) &{} \dots &{} -t_2 t_{n-1}^2 \\ \dots &{} \dots &{} \dots &{} \dots \\ -t_{n-1} t_1^2&{} -t_{n-1} t_2^2 &{} \dots &{}t_{n-1}(\varSigma -t_{n-1}^2) \end{pmatrix}\\&= \frac{1}{t_1 \dots t_{n-1}} \frac{1}{\varSigma ^{2(n-1)}} \det \begin{pmatrix} t_1 &{} -t_1 t_2^2&{} \dots &{} -t_1 t_{n-1}^2 \\ t_2 &{} t_2( \varSigma -t_2^2) &{} \dots &{} -t_2 t_{n-1}^2 \\ \dots &{} \dots &{} \dots &{} \dots \\ t_{n-1} &{} -t_{n-1} t_2^2 &{} \dots &{}t_{n-1}(\varSigma -t_{n-1}^2) \end{pmatrix}\\&= \frac{1}{\varSigma ^{2(n-1)}}\det \begin{pmatrix} 1 &{} - t_2^2&{} \dots &{} - t_{n-1}^2 \\ 1 &{} \varSigma -t_2^2 &{} \dots &{} - t_{n-1}^2 \\ \dots &{} \dots &{} \dots &{} \dots \\ 1 &{} - t_2^2 &{} \dots &{}\varSigma -t_{n-1}^2 \end{pmatrix}\\&=\frac{1}{\varSigma ^{2(n-1)}} \det \begin{pmatrix} 1 &{} - t_2^2&{} \dots &{} - t_{n-1}^2 \\ 0 &{} \varSigma &{} \dots &{} 0 \\ \dots &{} \dots &{} \dots &{} \dots \\ 0 &{} 0 &{} \dots &{}\varSigma \end{pmatrix}\\&= \frac{1}{\varSigma ^n}. \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Duong, M.H., Han, T.A. On the Expected Number of Equilibria in a Multi-player Multi-strategy Evolutionary Game. Dyn Games Appl 6, 324–346 (2016). https://doi.org/10.1007/s13235-015-0148-0

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13235-015-0148-0

Keywords

Search

Navigation