On the Expected Number of Internal Equilibria in Random Evolutionary Games with Correlated Payoff Matrix

Abstract

The analysis of equilibrium points in random games has been of great interest in evolutionary game theory, with important implications for understanding of complexity in a dynamical system, such as its behavioural, cultural or biological diversity. The analysis so far has focused on random games of independent payoff entries. In this paper, we overcome this restrictive assumption by considering multiplayer two-strategy evolutionary games where the payoff matrix entries are correlated random variables. Using techniques from the random polynomial theory, we establish a closed formula for the mean numbers of internal (stable) equilibria. We then characterise the asymptotic behaviour of this important quantity for large group sizes and study the effect of the correlation. Our results show that decreasing the correlation among payoffs (namely, of a strategist for different group compositions) leads to larger mean numbers of (stable) equilibrium points, suggesting that the system or population behavioural diversity can be promoted by increasing independence of the payoff entries. Numerical results are provided to support the obtained analytical results.

1 Introduction

1.1 Motivation

Evolutionary Game Theory (EGT) was originally introduced in 1973 by Maynard Smith and Price [41] as an application of classical game theory to biological contexts, providing explanations for odd animal behaviours in conflict situations. Since then, it has become one of the most diverse and far reaching theories in biology, finding further applications in various fields such as ecology, physics, economics and computer science [3, 9, 34, 35, 40, 45, 49, 55]. For example, in economics, it has been used to make predictions in settings where traditional assumptions about agents’ rationality and knowledge may not be justified [24, 55]. In computer science, EGT has been used extensively to model dynamics and emergent behaviour in multiagent systems [29, 66]. Furthermore, EGT has helped explain the evolution and emergence of cooperative behaviours in diverse societies, one of the most actively studied and challenging interdisciplinary problems in science [10, 35, 45, 46].

Similar to the foundational concept of Nash equilibrium in classical game theory [42], the study of equilibrium points and their stability in EGT has been of significant importance and extensive research [4, 10, 12, 14, 15, 27, 28, 36]. They represent population compositions where all the strategies have the same average fitness, thus predicting the coexistence of different strategic behaviours or types in a population. The major body of such EGT literature has focused on equilibrium properties in EGT for concrete games (i.e. games with well-specified payoff structures) such as the coordination and the public goods games. For example, the maximal number of equilibria, the stability and attainability of certain equilibrium points in concrete games have been well established; see for example [4, 11, 50, 56, 62].

In contrast to the equilibrium analysis of concrete games, a recent body of works investigates random games where individual payoffs obtained from the games are randomly assigned [10, 14, 15, 25, 27, 28, 36]. This analysis has proven useful to provide answers to generic questions about a dynamical system such as its overall complexity. Using random games is useful to model and understand social and biological systems in which very limited information is available, or where the environment changes so rapidly and frequently that one cannot predict the payoffs of their inhabitants [20, 26, 36, 39]. Moreover, even when randomly generated games are not directly representative for real-world scenarios, they are valuable as a null hypothesis that can be used to sharpen our understanding of what makes real games special [25]. In general, an important question posed in these works is what is the expected number, E(d), of internal equilibria in ad-player game. An answer to the question provides important insights into the understanding of the expected levels of behavioural diversity or biodiversity one can expect in a dynamical system [27, 38, 64]. It would allow us to predict the level of biodiversity in multiplayer interactions, describing the probability of which a certain state of biodiversity may occur. Moreover, computing E(d) provides useful upper-bounds for the probability $p_m$ that a certain number m of equilibria is attainted, since [36]: $p_{m}\le E(d)/m$. Of particular interest is such an estimate for the probability of attaining the maximal of internal equilibria, i.e. $p_{d-1}$, as in the Feldman–Karlin conjecture [2].

Mathematically, to find internal equilibria in a d-player game with two strategies A and B, one needs to solve the following polynomial equation for $y>0$ (see Eq. 5 and its derivation in Sect. 2),

$$\begin{aligned} P(y):=\sum \limits _{k=0}^{d-1}\beta _k\begin{pmatrix} d-1\\ k \end{pmatrix}y^k=0, \end{aligned}$$

(1)

where $\beta _k=a_k-b_k$, with $a_k$ and $b_k$ being random variables representing the payoff entries of the game payoff matrix for A and B, respectively. Therefore, calculating E(d) amounts to the computation of the expected number of positive zeros of the (random) polynomial P. As will be shown in Sect. 2, the set of positive roots of P is the same as that of the so-called gain function which is a Bernstein polynomial. Thus, one can gain information about internal equilibria of a multiplayer game via studying positive roots of Bernstein polynomials. For deterministic multiplayer games, this has already been carried out in the literature [48]. One of the main goals of this paper is to extend this research to random multiplayer games via studying random polynomials.

In [27, 28, 36], the authors provide both numerical and analytical results for games with a small number of players ($d\le 4$), focusing on the probability of attaining a maximal number of equilibrium points. These works use a direct approach by solving Equation (1), expressing the positivity of its zeros as domains of conditions for the coefficients and then integrating over these domains to obtain the corresponding probabilities. However, in general, a polynomial of degree five or higher is not analytically solvable [1]. Therefore, the direct approach cannot be generalised to larger d. More recently, in [14, 15] the authors introduce a novel method using techniques from random polynomials to calculate E(d) with an arbitrary d, under the assumption that the entries of the payoff matrix are independent normal random variables. More precisely, they derive a computationally implementable formula for E(d) for arbitrary d and prove the following monotonicity and asymptotic behaviour of E(d):

$$\begin{aligned} \frac{E(d)}{d-1}~\text {is decreasing and}~ \lim _{d\rightarrow \infty }\frac{\ln E(d)}{\ln (d-1)}=\frac{1}{2}. \end{aligned}$$

(2)

However, the requirement that the entries of the payoff matrix are independent random variables is rather restricted from both mathematical and biological points of view. In evolutionary game theory, correlations may arise in various scenarios particularly when there are environmental randomness and interaction uncertainty such as in games of cyclic dominance [59], coevolutionary multigames [58] or when individual contributions are correlated to the surrounding contexts (e.g. due to limited resource) [60], see also recent reviews [16, 57] for more examples. One might expect some strategies to have many similar properties and hence yield similar results for a given response of the respective opponent [5]. Furthermore, in a multiplayer game (such as the public goods games and their generalisations), a strategy’s payoffs, which may differ for different group compositions, can be expected to be correlated given a specific nature of the strategy [30,31,32,33, 47, 64]. Similarly, different strategies’ payoffs may be correlated given the same group composition. From a mathematical perspective, the study of real zeros of random polynomials with correlated coefficients has attracted substantial attention, see e.g. [13, 21,22,23, 51].

In this paper, we remove the assumption on the dependence of the coefficients. We will study the expected number of internal equilibria and its various properties for random evolutionary games in which the entries of the payoff matrix are correlated random variables.

1.2 Summary of Main Results

We now summarise the main results of this paper. More detailed statements will be presented in the sequel sections. We consider d-player two-strategy random games in which the coefficients $\beta _k$ ($k\in \{0,\ldots ,d-1\}$) can be correlated random variables, satisfying that $\mathrm {corr}(\beta _i,\beta _j)=r$ for $i\ne j$ and for some $0\le r\le 1$ (see Lemma 1 about this assumption).

The main result of the paper is the following theorem which provides a formula for the expected number, E(r, d), of internal equilibria, characterises its asymptotic behaviour and studies the effect of the correlation.

Theorem 1

(On the expected number of internal equilibria)

• (1) (Computational formula for E(r, d))

  $$\begin{aligned} E(r,d)=2\int _0^1 f(t;r,d)\,dt, \end{aligned}$$

  (3)

  where the density function f(t; r, d) is given explicitly in (8).

• (2) (Monotonicity of E(r, d) with respect to r) The function $r\mapsto E(r,d)$ decreases for any given d.

• (3) (Asymptotic behaviour of E(r, d) for large d) We perform formal asymptotic computations to get

  $$\begin{aligned} E(r,d){\left\{ \begin{array}{ll}\sim \frac{\sqrt{2d-1}}{2}\sim \mathcal {O}(d^{1/2})\quad \text {if}~~ r=0,\\ \sim \frac{d^{1/4}(1-r)^{1/2}}{2\pi ^{5/4}r^{1/2}}\frac{8\varGamma \left( \frac{5}{4}\right) ^{2}}{\sqrt{\pi }}\sim \mathcal {O}(d^{1/4})\quad \text {if}~~ 0<r<1,\\ =0\quad \text {if}~~ r=1. \end{array}\right. } \end{aligned}$$

  (4)

  We compare this asymptotic behaviour numerically with the analytical formula obtained in part 1.

This theorem clearly shows that the correlation r has a significant effect on the expected number of internal equilibria E(r, d). For sufficiently large d, when r increases from 0 (uncorrelated) to 1 (identical), E(r, d) reduces from $\mathcal {O}(d^{1/2})$ at $r=0$, to $\mathcal {O}(d^{1/4})$ for $0<r<1$ and to 0 at $r=1$. This theorem generalises and improves the main results in [15] for the case $r=0$: the asymptotic behaviour, $E(r,d)\sim \frac{\sqrt{2d-1}}{2}$, is stronger than (2). In addition, as a by-product of our analysis, we provide an asymptotic formula for the expected number of real zeros of a random Bernstein polynomial as conjectured in [18], see Sect. 6.7.

1.3 Methodology of the Present Work

We develop further the connections between EGT and random/deterministic polynomials theory discovered in [14, 15]. The integral representation (3) is derived from the theory of [19], which provides a general formula for the expected number of real zeros of a random polynomial in a given domain, and the symmetry of the game, see Theorem 2; the monotonicity and asymptotic behaviour of E(r, d) are obtained by using connections to Legendre polynomials, which were described in [15], see Theorems 3 and  1.

1.4 Organisation of the Paper

The rest of the paper is organised as follows. In Sect. 2, we recall the replicator dynamics for multiplayer two-strategy games. In Sect. 3, we prove and numerically validate the first and the second parts of Theorem 1. Section 4 is devoted to the proof of the last part of Theorem 1 and its numerical verification. Section 5 provides further discussion, and finally, “Appendix 6” contains detailed computations and proofs of technical results.

2 Replicator Dynamics

A fundamental model of evolutionary game theory is the replicator dynamics [35, 45, 63, 65, 69], describing that whenever a strategy has a fitness larger than the average fitness of the population, it is expected to spread. From the replicator dynamics, one then can derive a polynomial equation that an internal equilibrium of a multiplayer game satisfies . To this end, we consider an infinitely large population with two strategies, A and B. Let x, $0 \le x \le 1$, be the frequency of strategy A. The frequency of strategy B is thus $(1-x)$. The interaction of the individuals in the population is in randomly selected groups of d participants, that is, they play and obtain their fitness from d-player games. The game is defined through a $(d-1)$-dimensional payoff matrix [27], as follows. Let $a_k$ (respectively, $b_k$) be the payoff of an A strategist (respectively, a B strategist) obtained when interacting with a group of $d-1$ other players containing k A strategists (i.e. $d-1-k$ B strategists). In this paper, we consider symmetric games where the payoffs do not depend on the ordering of the players. Asymmetric games will be studied in a forthcoming paper. In the symmetric case, the average payoffs of A and B are, respectively

$$\begin{aligned} \pi _A= \sum \limits _{k=0}^{d-1}a_k\begin{pmatrix} d-1\\ k \end{pmatrix}x^k (1-x)^{d-1-k},\quad \pi _B = \sum \limits _{k=0}^{d-1}b_k\begin{pmatrix} d-1\\ k \end{pmatrix}x^k (1-x)^{d-1-k}. \end{aligned}$$

Internal equilibria are those points that satisfy the condition that the fitnesses of both strategies are the same $\pi _A=\pi _B$, which gives rise to $g(x)=0$ where g(x) is the so-called gain function given by [6, 48]

$$\begin{aligned} g(x)=\sum \limits _{k=0}^{d-1}\beta _k \begin{pmatrix} d-1\\ k \end{pmatrix}x^k (1-x)^{d-1-k}, \end{aligned}$$

where $\beta _k = a_k - b_k$. Note that this equation can also be derived from the definition of an evolutionary stable strategy (ESS), see, e.g. [4]. As also discussed in that paper, the evolutionary solution of the game (such as the set of ESSs or the set of stable rest points of the replicator dynamics) involves not only finding the roots of the gain function g(x) but also determining the behaviour of g(x) in the vicinity of such roots. We also refer the reader to [65, 69] and references therein for further discussion on relations between ESSs and game dynamics. Using the transformation $y= \frac{x}{1-x}$, with $0< y < +\infty$, and dividing g(x) by $(1-x)^{d-1}$, we obtain the following polynomial equation for y

$$\begin{aligned} P(y):=\sum \limits _{k=0}^{d-1}\beta _k\begin{pmatrix} d-1\\ k \end{pmatrix}y^k=0. \end{aligned}$$

(5)

As in [14, 15, 27], we are interested in random games where $a_k$ and $b_k$ (thus $\beta _k$), for $0\le k\le d-1$, are random variables. However, in contrast to these papers where $\beta _k$ are assumed to be independent, we analyse here a more general case where they are correlated. In particular, we consider that any pair $\beta _i$ and $\beta _j$, with $0\le i\ne j \le d-1$, have a correlation r ($0\le r \le 1$). In general, $r = 0$ means $\beta _i$ and $\beta _j$ are independent, while when $r = 1$ they have a (perfectly) linear correlation, and the larger r is the stronger they are correlated. It is noteworthy that this type of dependency between the coefficients is common in the literature on evolutionary game theory [5, 25] as well as random polynomial theory [13, 23, 51].

The next lemma shows how this assumption arises naturally from simple assumptions on the game payoff entries. To state the lemma, let $\mathrm {cov}(X,Y)$ and $\mathrm {corr}(X,Y)$ denote the covariance and correlation between random variables X and Y, respectively; moreover, $\mathrm {var}(X)=\mathrm {cov}(X,X)$ denotes the variance of X.

Lemma 1

Suppose that, for $0\le i\ne j\le d-1$,

• $\mathrm {var}(a_i)=\mathrm {var}(b_i)=\eta ^2$,

• $\mathrm {corr}(a_i,a_j)=r_a$, $\mathrm {corr}(b_i,b_j)=r_b$,

• $\mathrm {corr}(a_i,b_j)=r_{ab}$, $\mathrm {corr}(a_i,b_i)=r'_{ab}$.

Then, the correlation between $\beta _i$ and $\beta _j$, for $1\le i\ne j\le d-1$, is given by

$$\begin{aligned} \mathrm {corr}(\beta _i,\beta _j)=\frac{r_a+r_b-2r_{ab}}{2(1-r'_{ab})}, \end{aligned}$$

(6)

which is a constant. Clearly, it increases with $r_a$, $r_b$ and $r'_{ab}$ while decreasing with $r_{ab}$. Moreover, if $r_a+r_b=2r_{ab}$, then $\beta _i$ and $\beta _j$ are independent. Also, if $r_{ab} = r'_{ab} = 0$, i.e. when payoffs from different strategists are independent, we have: $\mathrm {corr}(\beta _i,\beta _j)=\frac{r_a+r_b}{2}$. If we further assume that $r_a = r_b = r$, then $\mathrm {corr}(\beta _i,\beta _j)= r$.

Proof

See “Appendix 6.1”. $\square$

The assumptions in Lemma 1 mean that a strategist’s payoffs for different group compositions have a constant correlation, which in general is different from the cross-correlation of payoffs for different strategists. These assumptions arise naturally for example in a multiplayer game (such as the public goods games and their generalisations), since a strategist’s payoffs, which may differ for different group compositions, can be expected to be correlated given a specific nature of the strategy (e.g. cooperative vs. defective strategies in the public goods games). These natural assumptions regarding payoffs’ correlations are just to ensure the pairs $\beta _i$ and $\beta _j$, $0\le i\ne j\le d-1$, have a constant correlation. Characterising the general case where $\beta _i$ and $\beta _j$ have varying correlations would be mathematically interesting but is out of the scope of this paper. We will discuss further this issue particularly for other types of correlations in Sect. 5.

3 The Expected Number of Internal Equilibria E(r, d)

We consider the case where $\beta _k$ are standard normal random variables but assume that all the pairs $\beta _i$ and $\beta _j$, for $0\le i\ne j\le d-1$, have the same correlation $0 \le r \le 1$ (cf. Lemma 1).

In this section, we study the expected number of internal equilibria E(r, d). The starting point of the analysis of this section is an improper integral to compute E(r, d) as a direct application of the Edelman–Kostlan theorem [19], see Lemma 2. We then further simplify this formula to obtain a more computationally tractable one (see Theorem 2) and then prove a monotone property of E(r, d) as a function of the correlation r, see Theorem 3.

3.1 Computations of E(r, d)

Lemma 2

Assume that $\beta _k$ are standard normal random variables and that for any $i\ne j$, the correlation between $\beta _i$ and $\beta _{j}$ is equal to r for some $0 \le r \le 1$. Then, the expected number of internal equilibria, E(r, d), in a d-player random game with two strategies is given by

$$\begin{aligned} E(r,d)=\int _0^\infty f(t; r,d)\,dt, \end{aligned}$$

(7)

where

$$\begin{aligned}{}[\pi \,f(t; r,d)]^2= & {} \frac{(1-r)\sum \nolimits _{i=0}^{d-1}i^2\begin{pmatrix} d-1\\ i \end{pmatrix}^2t^{2(i-1)}+r (d-1)^2(1+t)^{2(d-2)}}{(1-r)\sum \nolimits _{i=0}^{d-1}\begin{pmatrix} d-1\\ i \end{pmatrix}^2t^{2i}+r(1+t)^{2(d-1)}} \nonumber \\&-\left[ \frac{(1-r)\sum \nolimits _{i=0}^{d-1}i\begin{pmatrix} d-1\\ i \end{pmatrix}^2t^{2i-1}+r(d-1)(1+t)^{2d-3}}{(1-r)\sum \nolimits _{i=0}^{d-1}\begin{pmatrix} d-1\\ i \end{pmatrix}^2t^{2i}+r(1+t)^{2(d-1)}}\right] ^2.\qquad \end{aligned}$$

(8)

Proof

According to [19] (see also [14, 15]), we have

$$\begin{aligned} E(r,d)=\int _0^\infty f(t;r,d)\,\mathrm{d}t, \end{aligned}$$

where the density function f(t; r, d) is determined by

$$\begin{aligned} f(t;r,d)=\frac{1}{\pi }\left[ \frac{\partial ^2}{\partial x\partial y}\Big (\log v(x)^T\mathcal { C}v(y)\Big )\Big \vert _{y=x=t}\right] ^\frac{1}{2}, \end{aligned}$$

(9)

with the covariance matrix $\mathcal { C}$ and the vector v given by

$$\begin{aligned} \mathcal { C}_{ij}={\left\{ \begin{array}{ll} \begin{pmatrix} d-1\\ i \end{pmatrix}^2,\quad \text {if}~~ i=j\\ r\begin{pmatrix} d-1\\ i \end{pmatrix}\begin{pmatrix} d-1\\ j \end{pmatrix},\quad \text {if}~~i\ne j. \end{array}\right. } \quad \text {and} \quad v(x)=\begin{pmatrix} 1\\ x\\ \vdots \\ x^{d-1} \end{pmatrix}. \end{aligned}$$

(10)

Let us define

$$\begin{aligned} H(x,y)&:=v(x)^T \mathcal { C}v(y)\nonumber \\&=\sum \limits _{i=0}^{d-1}\begin{pmatrix} d-1\\ i \end{pmatrix}^2x^iy^i+r\sum _{i\ne j=0}^{d-1}\begin{pmatrix} d-1\\ i \end{pmatrix}\begin{pmatrix} d-1\\ j \end{pmatrix}x^iy^j\nonumber \\&=(1-r)\sum \limits _{i=0}^{d-1}\begin{pmatrix} d-1\\ i \end{pmatrix}^2x^iy^i+r\left( \sum _{i=0}^{d-1}\begin{pmatrix} d-1\\ i \end{pmatrix}x^i\right) \left( \sum _{j=0}^{d-1}\begin{pmatrix} d-1\\ j \end{pmatrix}y^j\right) . \end{aligned}$$

(11)

Then, we compute

$$\begin{aligned} \frac{\partial ^2}{\partial _x\partial _y}(\log v(x)^T\mathcal { C}v(y))=\frac{\partial ^2}{\partial _x\partial _y} \log H(x,y)=\frac{\partial ^2_{xy}H(x,y)}{H(x,y)}-\frac{\partial _x H(x,y)\partial _y H(x,y)}{H(x,y)^2}. \end{aligned}$$

Particularly, for $y=x=t$, we obtain

$$\begin{aligned} \frac{\partial ^2}{\partial _x\partial _y}(\log v(x)^T\mathcal { C}v(y))\Big \vert _{y=x=t}&=\left( \frac{\partial ^2_{xy}H(x,y)}{H(x,y)}-\frac{\partial _x H(x,y)\partial _y H(x,y)}{H(x,y)^2}\right) \Big \vert _{y=x=t} \\&=\frac{\partial ^2_{xy}H(x,y)\big \vert _{y=x=t}}{H(t,t)}-\left( \frac{\partial _x H(x,y)\big \vert _{y=x=t}}{H(t,t)}\right) ^2. \end{aligned}$$

Using (11), we can compute each term on the right-hand side of the above expression explicitly

$$\begin{aligned}&H(t,t)=(1-r)\sum \limits _{i=0}^{d-1}\begin{pmatrix} d-1\\ i \end{pmatrix}^2t^{2i}+r\left( \sum \limits _{i=0}^{d-1}\begin{pmatrix} d-1\\ i \end{pmatrix}t^i\right) ^2, \end{aligned}$$

(12a)

$$\begin{aligned}&\partial _x H(x,y)\big \vert _{y=x=t}=(1-r)\sum \limits _{i=0}^{d-1}i\begin{pmatrix} d-1\\ i \end{pmatrix}^2t^{2i-1}\nonumber \\&\quad +r\left( \sum _{i=0}^{d-1}i\begin{pmatrix} d-1\\ i \end{pmatrix}t^{i}\right) \left( \sum _{j=0}^{d-1}\begin{pmatrix} d-1\\ j \end{pmatrix}t^{j-1}\right) , \end{aligned}$$

(12b)

$$\begin{aligned}&\partial ^2_{xy}H(x,y)\big \vert _{y=x=t}=(1-r)\sum \limits _{i=0}^{d-1}i^2\begin{pmatrix} d-1\\ i \end{pmatrix}^2t^{2(i-1)}+r\left( \sum \limits _{i=0}^{d-1}i\begin{pmatrix} d-1\\ i \end{pmatrix}t^{i-1}\right) ^2. \end{aligned}$$

(12c)

We can simplify further the above expressions using the following computations which are attained from the binomial theorem and its derivatives

$$\begin{aligned}&\left( \sum _{i=0}^{d-1}\begin{pmatrix} d-1\\ i \end{pmatrix}t^i\right) ^2=(1+t)^{2(d-1)}, \end{aligned}$$

(13a)

$$\begin{aligned}&\left( \sum \limits _{i=0}^{d-1}i\begin{pmatrix} d-1\\ i \end{pmatrix}t^{i-1}\right) ^2=\left( \frac{d}{\mathrm{d}t}\sum _{i=0}^{d-1}\begin{pmatrix} d-1\\ i \end{pmatrix}t^i\right) ^2=\left( \frac{d}{\mathrm{d}t}(1+t)^{d-1}\right) ^2 \nonumber \\&\quad =(d-1)^2 (1+t)^{2(d-2)},\end{aligned}$$

(13b)

$$\begin{aligned}&\left( \sum _{i=0}^{d-1}i\begin{pmatrix} d-1\\ i \end{pmatrix}t^{i}\right) \left( \sum _{j=0}^{d-1}\begin{pmatrix} d-1\\ j \end{pmatrix}t^{j-1}\right) =\frac{1}{2}\frac{d}{\mathrm{d}t}\left( \sum _{i=0}^{d-1}\begin{pmatrix} d-1\\ i \end{pmatrix}t^i\right) ^2\nonumber \\&\quad =\frac{1}{2}\frac{d}{\mathrm{d}t}(1+t)^{2(d-1)}=(d-1)(1+t)^{2d-3}. \end{aligned}$$

(13c)

Substituting (12) and (13) back into (9), we obtain (8) and complete the proof. $\square$

Next, we will show that, as in the case $r=0$ studied in [14, 15], the improper integral (7) can be reduced to a definite integral from 0 to 1. A crucial property enables us to do so is the symmetry of the strategies. The main result of this section is the following theorem (cf. Theorem 1–(1)).

Theorem 2

• (1) The density function f(t; r, d) satisfies that

  $$\begin{aligned} f(1/t; r,d)=t^2 f(t;r,d). \end{aligned}$$

  (14)

• (2) (Computable formula for E(r, d)). E(r, d) can be computed via

  $$\begin{aligned} E(r,d)=2\int _0^1\, f(t)\mathrm{d}t=2\int _1^\infty f(t)\,\mathrm{d}t. \end{aligned}$$

  (15)

Proof

The proof of the first part is lengthy and is given in “Appendix 6.2”. Now, we prove the second part. We have

$$\begin{aligned} E(r,d)=\int _0^\infty f(t;r,d)\,\mathrm{d}t=\int _0^1 f(t;r,d)\,\mathrm{d}t+\int _1^\infty f(t;r,d)\,\mathrm{d}t. \end{aligned}$$

(16)

By changing of variables $t:=\frac{1}{s}$, the first integral on the right-hand side of (16) can be transformed as

$$\begin{aligned} \int _0^1 f(t;r,d)\,\mathrm{d}t=\int _{1}^\infty f(1/s;r,d)\frac{1}{s^2}\,\mathrm{d}s=\int _1^\infty f(s;r,d)\,\mathrm{d}s, \end{aligned}$$

(17)

where we have used (14) to obtain the last equality. The assertion (15) is then followed from (16) and (17). $\square$

As in [15], we can interpret the first part of Theorem 2 as a symmetric property of the game. We recall that $t=\frac{y}{1-y}$, where y and $1-y$ are, respectively, the fractions of strategies 1 and 2. We write the density function f(t; r, d) in terms of y using the change of variable formula as follows.

$$\begin{aligned} f(t;r,d)\,\mathrm{d}t=f\Big (\frac{y}{1-y};r,d\Big )\frac{1}{(1-y)^2}\,dy:=g(y;r,d)\,dy, \end{aligned}$$

where

$$\begin{aligned} g(y;r,d):=f\Big (\frac{y}{1-y};r,d\Big )\frac{1}{(1-y)^2}. \end{aligned}$$

(18)

The following lemma expresses the symmetry of the strategies. (Swapping the index labels converts an equilibrium at y to one at $1-y$.)

Corollary 1

The function $y\mapsto g(y;r,d)$ is symmetric about the line $y=\frac{1}{2}$, i.e.

$$\begin{aligned} g(y;r,d)=g(1-y;r,d). \end{aligned}$$

(19)

Proof

The equality (19) is a direct consequence of (14). We have

$$\begin{aligned} g(1-y;r,d)=f\Big (\frac{1-y}{y};r,d\Big )\frac{1}{y^2}&\overset{(14)}{=}f\Big (\frac{y}{1-y};r,d\Big )\frac{y^2}{(1-y)^2}\frac{1}{y^2} \\&=f\Big (\frac{y}{1-y};r,d\Big )\frac{1}{(1-y)^2}=g(y;r,d). \end{aligned}$$

$\square$

3.2 Monotonicity of $r\mapsto E(r,d)$

In this section, we study the monotone property of E(r, d) as a function of the correlation r. The main result of this section is the following theorem on the monotonicity of $r\mapsto E(r,d)$ (cf. Theorem 1–(2)).

Theorem 3

The function $r\mapsto f(t;r,d)$ is decreasing. As a consequence, $r\mapsto E(r,d)$ is also decreasing.

Proof

We define the following notations:

$$\begin{aligned}&M_1=M_1(t;r,d)=\sum _{i=0}^{d-1}\begin{pmatrix} d-1\\ i \end{pmatrix}^2t^{2i}, \quad M_2=M_2(t;r,d)=(1+t)^{2(d-1)}, \\&A_1=A_1(t;r,d)=\sum \limits _{i=0}^{d-1}i^2\begin{pmatrix} d-1\\ i \end{pmatrix}^2t^{2(i-1)}, \quad A_2=A_2(t;r,d)=(d-1)^2(1+t)^{2(d-2)}, \\&B_1=B_1(t;r,d)=\sum \limits _{i=0}^{d-1}i\begin{pmatrix} d-1\\ i \end{pmatrix}^2t^{2i-1}, \quad B_2=B_2(t;r,d)=(d-1)(1+t)^{2d-3}, \\&M=(1-r)M_1+ r M_2, \quad A=(1-r) A_1+r A_2, \quad B=(1-r)B_1+ r B_2. \end{aligned}$$

Then, the density function f(t; r, d) in (8) can be written as

$$\begin{aligned} (\pi f(t;r,d))^2=\frac{A M-B^2}{M^2}. \end{aligned}$$

(20)

Taking the derivation with respect to r of the right-hand side of (20), we obtain

$$\begin{aligned}&\frac{\partial }{\partial r}\left( \frac{A M-B^2}{M^2}\right) \\&\quad =\frac{(A^\prime M + M^\prime A -2 B B^\prime ) M^2 - 2 (A M -2 B^2 ) M M^\prime }{M^4} \\&\quad =\frac{(A^\prime M + M^\prime A -2 B B^\prime ) M - 2 (A M - B^2 ) M^\prime }{M^3} \\&\quad =\frac{2 B (B M^\prime - B^\prime M) - M (A M^\prime -M A^\prime ) }{M^3} \\&\quad \overset{(*)}{=}\frac{2 B (B_1 M_2 - M_1 B_2 ) - M (A_1 M_2 - M_1 A_2 ) }{M^3} \\&\quad =\frac{2 B \left( B_1 (1+t)^{2(d-1)} - M_1 (d-1)(1+t)^{2d-3} \right) - M \left( A_1 (1+t)^{2(d-1)} - M_1 (d-1)^2(1+t)^{2(d-2)} \right) }{M^3} \\&\quad =\frac{ (1+t)^{2d-4}\left\{ 2(t+1)B \left[ B_1(1+t) - M_1 (d-1) \right] - M \left[ A_1 (1+t)^2 - M_1 (d-1)^2\right] \right\} }{M^3}. \end{aligned}$$

Note that to obtain (*) above we have used the following simplifications

$$\begin{aligned} B M^\prime - B^\prime M&= \left[ B_1 + r (B_2 - B_1)\right] (M_2 - M_1) - (B_2 - B_1) \left[ M_1 + r (M_2 - M_1)\right] \\&= B_1 (M_2-M_1) - (B_2 - B_1) M_1 \\&= B_1 M_2 - M_1 B_2, \end{aligned}$$

and similarly,

$$\begin{aligned} A M^\prime - A^\prime M = A_1 M_2 - M_1 A_2. \end{aligned}$$

Since $M>0$ and according to Proposition 2,

$$\begin{aligned} 2(t+1)B \Big [B_1(1+t) - M_1 (d-1) \Big ] - M \Big [A_1 (1+t)^2 - M_1 (d-1)^2\Big ]\le 0, \end{aligned}$$

it follows that

$$\begin{aligned} \frac{\partial }{\partial r}\left( \frac{A M-B^2}{M^2}\right) \le 0. \end{aligned}$$

The assertion of the theorem is then followed from this and (20). $\square$

As a consequence, we can derive the monotonicity property of the number of stable equilibrium points, denoted by SE(r, d). It is based on the following property of stable equilibria in multiplayer two-strategy evolutionary games, which has been proved in [36, Theorem 3] for payoff matrices with independent entries. We provide a similar proof below for matrices with exchangeable payoff entries. We need the following auxiliary lemma whose proof is presented in “Appendix 6.3”.

Lemma 3

Let X and Y be two exchangeable random variables, i.e. their joint probability distribution $f_{X,Y}(x,y)$ is symmetric, $f_{X,Y}(x,y)=f_{X,Y}(y,x)$. Then, $Z=X-Y$ is symmetrically distributed about 0, i.e. its probability distribution satisfies $f_Z(z)=f_Z(-z)$. In addition, if X and Y are iid, then they are exchangeable.

Theorem 4

Suppose that $a_k$ and $\beta _k$ are exchangeable random variables. For d-player evolutionary games with two strategies, the following holds

$$\begin{aligned} SE(r,d) = \frac{1}{2} E(r,d). \end{aligned}$$

(21)

Proof

The replicator equation in this game is given by [27, 32]

$$\begin{aligned} {\dot{x}} = x(1-x)\sum _{k = 0}^{d-1} \beta _k \ \genfrac(){0.0pt}1{d-1}{k} \ x^k (1-x)^{d-1-k}. \end{aligned}$$

(22)

Suppose $x^*\in (0,1)$ is an internal equilibrium of the system and h(x) is the polynomial on the right-hand side of the equation. Since $x^*$ is stable if and only if $h^\prime ( x^*) < 0$ which can be simplified to [36]

$$\begin{aligned} \sum _{k = 1}^{d-1} k \beta _k \ \genfrac(){0.0pt}1{d-1}{k}{y^*}^{k-1} < 0, \end{aligned}$$

(23)

where $y^*= \frac{x^*}{1-x^*}$. As a system admits the same set of equilibria if we change the sign of all $\beta _k$ simultaneously, and for such a change the above inequality would change the direction (thus the stable equilibrium $x^*$ would become unstable), all we need to show for the theorem to hold is that $\beta _k$ has a symmetric density function. This is guaranteed by Lemma 3 since $\beta _k=a_k-b_k$ where $a_k$ and $b_k$ are exchangeable. $\square$

Corollary 2

Under the assumption of Theorem 4, the expected number of stable equilibrium points SE(r,d) is a decreasing function with respect to r.

Proof

This is a direct consequence of Theorems 3 and 4. $\square$

3.3 Monotonicity of E(r, d): Numerical Investigation

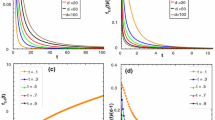
In this section, we numerically validate the analytical results obtained in the previous section. In Fig. 1, we plot the functions $r\mapsto E(r,d)$ for several values of d (left panel) and $d\mapsto E(r,d)$ for different values of r using formula 7 (right panel). In the panel on the left, we also show the value of E(r, d) obtained from samplings. That is, we generate $10^6$ samples of $\beta _k (0\le k\le d-1)$ where $\beta _k$ are normally distributed random variables satisfying that $\mathrm {corr}(\beta _i,\beta _j)=r$ for $0\le i\ne j\le d-1$. For each sample, we solve Eq. (5) to obtain the corresponding number internal equilibria (i.e. the number of positive zeros of the polynomial equation). By averaging over all the $10^6$ samples, we obtain the probability of observing m internal equilibria, ${\bar{p}}_m$, for each $0\le m\le d-1$. Finally, the mean or expected number of internal equilibria is calculated as $E(r,d)=\sum _{m=0}^{d-1}m\cdot {\bar{p}}_m$. The figure shows the agreement of results obtained from analytical and sampling methods. In addition, it also demonstrates the decreasing property of $r\mapsto E(r,d)$, which was proved in Theorem 3. Additionally, we observe that E(r, d) increases with the group size, d.

Note that to generate correlated normal random variables, we use the following algorithm that can be found in many textbooks, for instance [43, Section 4.1.8].

Algorithm 5

Generate n correlated Gaussian distributed random variables ${\mathbf {Y}}\!=\!(Y_1,\ldots , Y_n)$, ${\mathbf {Y}}\sim \mathcal {N}(\mu ,\Sigma )$, given the mean vector $\mu$ and the covariance matrix $\Sigma$.

• Step 1. Generate a vector of uncorrelated Gaussian random variables, ${\mathbf {Z}}$,

• Step 2. Define ${\mathbf {Y}}=\mu + C {\mathbf {Z}}$ where C is the square root of $\Sigma$ (i.e. $C C^T=\Sigma$).

The square root of a matrix can be found using the Cholesky decomposition. These two steps are easily implemented in Mathematica.

Fig. 1

(Left) Plot of $r\mapsto E(r,d)$ for different values of d. The solid lines are generated from analytical (A) formulas of E(r, d) as defined in Eq. (7). The solid diamonds capture simulation (S) results obtained by averaging over $10^6$ samples of $\beta _k$ ($1 \le k \le d-1$), where these $\beta _k$ are correlated, normally standard random variables. To generate correlated random variables, the algorithm described in Algorithm 5 was used. (Right) Plot of $d\mapsto E(r,d)$ for different values of r. We observe that E(r, d) decreases with respect to r but increases with respect to d

4 Asymptotic Behaviour of E(r, d)

4.1 Asymptotic Behaviour of E(r, d): Formal Analytical Computations

In this section we perform formal asymptotic analysis to understand the behaviour of E(r, d) when d becomes large.

Proposition 1

We have the following asymptotic behaviour of E(r, d) as $d\rightarrow \infty$

$$\begin{aligned} E(r,d){\left\{ \begin{array}{ll}\sim \frac{\sqrt{2d-1}}{2}\quad \text {if}~~ r=0,\\ \sim \frac{d^{1/4}(1-r)^{1/2}}{2\pi ^{5/4}r^{1/2}}\frac{8\varGamma \left( \frac{5}{4}\right) ^{2}}{\sqrt{\pi }}\quad \text {if}~~ 0<r<1,\\ =0\quad \text {if}~~ r=1. \end{array}\right. } \end{aligned}$$

Proof

We consider the case $r=1$ first. In this case, we have

$$\begin{aligned}&M(t)=M_2(t)=(1+t)^{2(d-1)}, A(t)=A_2(t)=(d-1)^2(1+t)^{2(d-2)},\\&B(t)=B_2(t)=(d-1)(1+t)^{2d-3}. \end{aligned}$$

Since $A_2(t)M_2(t)-B_2^2(t)=0$, we obtain $f(t;1,d)=0$. Therefore $E(1,d)=0$.

We now deal with the case $0\le r<1$. According to [7, Example 2, page 229], [68], for any $x>1$

$$\begin{aligned} P_d(x)=\frac{1}{\sqrt{2d\pi }}\frac{(x+\sqrt{x^2-1})^{d+1/2}}{(x^2-1)^{1/4}}+\mathcal {O}(d^{-1})\quad \text {as}~~ d\rightarrow \infty . \end{aligned}$$

Therefore,

$$\begin{aligned}&M_1=(1-t^2)^{d-1}P_{d-1}\left( \frac{1+t^2}{1-t^2}\right) \sim \frac{1}{\sqrt{4\pi (d-1)t}}(1+t)^{2d-1}, \\&M\sim (1-r)\frac{1}{\sqrt{4\pi (d-1)t}}(1+t)^{2d-1}+r(1+t)^{2d-2}. \end{aligned}$$

Using the relations between $A_1, B_1$ and $M_1$ in (27), we obtain

$$\begin{aligned}&A\sim (d-1)^{2}r(t+1)^{2(d-2)}+\frac{(2d-1)(t+1)^{2d-2}}{8t\sqrt{\pi }\sqrt{(d-1)t}}-\frac{(d-1)(t+1)^{2d-1}}{16t\sqrt{\pi }((d-1)t)^{3/2}}\\&\quad +\frac{1}{4}\bigg (\frac{(2d-2)(2d-1)(t+1)^{2d-3}}{2\sqrt{\pi }\sqrt{(d-1)t}}-\frac{(d-1)(2d-1)(t+1)^{2d-2}}{2\sqrt{\pi }((d-1)t)^{3/2}}\\&\quad +\frac{3(d-1)^{2}(t+1)^{2d-1}}{8\sqrt{\pi }((d-1)t)^{5/2}}\bigg ),\\&B\sim (d-1)r(t+1)^{2d-3}+\frac{1}{2}(1-r)\left( \frac{(2d-1)(t+1)^{2d-2}}{2\sqrt{\pi }\sqrt{(d-1)t}}-\frac{(d-1)(t+1)^{2d-1}}{4\sqrt{\pi }((d-1)t)^{3/2}}\right) . \end{aligned}$$

Therefore, we get

$$\begin{aligned} f^2&=\frac{1}{\pi ^2}\frac{AM-B^2}{M^2}\\&\sim \frac{(1-r)\left( 2(1-2d)(r-1)t(t+1)+\sqrt{\pi }r(t(8d+t-6)+1)\sqrt{(d-1)t}\right) }{8\pi ^{2}t^{2}(t+1)\left( (r-1)(t+1)-2\sqrt{\pi }r\sqrt{(d-1)t}\right) ^{2}}. \end{aligned}$$

Denote the expression on the right-hand side by $f_a^2$. If $r=0$, we have

$$\begin{aligned} f_a^2=\frac{2(2d-1)t(t+1)}{8\pi ^2t^2(t+1)(t+1)^2}=\frac{2d-1}{4\pi ^2 t(t+1)^2}, \end{aligned}$$

which means

$$\begin{aligned} f_a=\frac{\sqrt{2d-1}}{2\pi \sqrt{t} (t+1)}. \end{aligned}$$

Therefore

$$\begin{aligned} E\sim E_a:=2\int _0^1 f_a \,\mathrm{d}t=2 \int _0^1 \frac{\sqrt{2d-1}}{2\pi t^{1/2}(1+t)}\,\mathrm{d}t=\frac{\sqrt{2d-1}}{2}=\mathcal {O}(d^{1/2}). \end{aligned}$$

It remains to consider the case $0< r < 1$. As the first asymptotic value of E we compute

$$\begin{aligned} E_1=2\int _0^1 f_a(t)\,\mathrm{d}t. \end{aligned}$$

(24)

However, this formula is still not explicit since we need to take square root of $f_a$. Next we will offer another explicit approximation. To this end, we will further simplify $f_a$ asymptotically. Because

$$\begin{aligned} \left( 2(1-2d)(r-1)t(t+1)+\sqrt{\pi }r(t(8d+t-6)+1)\sqrt{(d-1)t}\right) \sim \sqrt{\pi }rt8d\sqrt{\mathrm{d}t} \end{aligned}$$

and

$$\begin{aligned} \left( (r-1)(t+1)-2\sqrt{\pi }r\sqrt{(d-1)t}\right) ^{2}\sim 4\pi r^{2}\mathrm{d}t \end{aligned}$$

we obtain

$$\begin{aligned} f_a^{2}&=\frac{(1-r)\left( 2(1-2d)(r-1)t(t+1)+\sqrt{\pi }r(t(8d+t-6)+1)\sqrt{(d-1)t}\right) }{8\pi ^{2}t^{2}(t+1)\left( (r-1)(t+1)-2\sqrt{\pi }r\sqrt{(d-1)t}\right) ^{2}}\\&\sim \frac{(1-r)\sqrt{\pi }rt8d\sqrt{\mathrm{d}t}}{8\pi ^{2}t^{2}(t+1)4\pi r^{2}\mathrm{d}t}=\frac{\sqrt{d}(1-r)}{4\pi ^{5/2}rt^{3/2}(t+1)}, \end{aligned}$$

which implies that

$$\begin{aligned} f_{a}\sim \frac{d^{1/4}(1-r)^{1/2}}{2\pi ^{5/4}r^{1/2}t^{3/4}(t+1)^{1/2}}.\\ \end{aligned}$$

Hence, we obtain another approximation for E(r, d) as follows.

$$\begin{aligned} E(r,d) \sim E_2&:=\int _{0}^{1}\frac{d^{1/4}(1-r)^{1/2}}{2\pi ^{5/4}r^{1/2}t^{3/4}(t+1)^{1/2}}\mathrm{d}t\nonumber \\&=\frac{d^{1/4}(1-r)^{1/2}}{2\pi ^{5/4}r^{1/2}}\int _{0}^{1}\frac{1}{t^{3/4}(t+1)^{1/2}}\mathrm{d}t \nonumber \\&=\frac{d^{1/4}(1-r)^{1/2}}{2\pi ^{5/4}r^{1/2}}\frac{8\varGamma \left( \frac{5}{4}\right) ^{2}}{\sqrt{\pi }}. \end{aligned}$$

(25)

$\square$

The formal computations clearly show that the correlation r between the coefficients $\{\beta \}$ significantly influences the expected number of equilibria E(r, d):

$$\begin{aligned} E(r,d)={\left\{ \begin{array}{ll} \mathcal {O}(d^{1/2}), \quad \text {if}~~ r=0,\\ \mathcal {O}(d^{1/4}), \quad \text {if}~~ 0<r<1,\\ 0, \text {if}~~ r=1. \end{array}\right. } \end{aligned}$$

In Sect. 4.2 we will provide numerical verification for our formal computations.

Corollary 3

The expected number of stable equilibrium points SE(r,d) follows the asymptotic behaviour

$$\begin{aligned} SE(r,d)={\left\{ \begin{array}{ll} \mathcal {O}(d^{1/2}), \quad \text {if}~~ r=0,\\ \mathcal {O}(d^{1/4}), \quad \text {if}~~ 0<r<1,\\ 0, \quad \text {if}~~ r=1. \end{array}\right. } \end{aligned}$$

Proof

This is a direct consequence of Theorems 3 and 1. $\square$

Fig. 2

Plot of $E_1/E(r,d)$ (left), and $E_2/E(r,d)$ (right). The figure shows that these ratios all converge to 1 when d becomes large. We also notice that $E_{2}$ approximates E better when r is close to 1 while $E_{1}$ approximates E better when r is small

Table 1 $\Big |\frac{E_{1}}{E}-1\Big |$

Table 2 $\Big |\frac{E_{2}}{E}-1\Big |$

Remark 1

In “Appendix 6.4”, we show the following asymptotic formula for f(1; r, d)

$$\begin{aligned} f(1;r,d)\sim \frac{(d-1)^{1/4}(1-r)^{1/2}}{2\sqrt{2}\pi ^{5/4}r^{1/2}}. \end{aligned}$$

It is worth noticing that this asymptotic behaviour is of the same form as that of E(r, d).

4.2 Asymptotic Behaviour of E(r, d): Numerical Investigation

In this section, we numerically validate the asymptotic behaviour of E(r, d) for large d that is obtained in the previous section using formal analytical computations. In Fig. 2, Tables 1 and 2 we plot the ratios of the asymptotically approximations of E(r, d) obtained in Sect. 4 with itself, i.e. $E_1/E(r,d)$ and $E_2/E(r,d)$, for different values of r and d. We observe that: for $r=0$ the approximation is good; while for $0<r<1$: $E_{1}$ (respectively, $E_2$) approximates E(r, d) better when r is small (respectively, when r is close to 1).

5 Conclusion

In this paper, we have studied the mean value, $E(r,d)$, of the number of internal equilibria in d-player two-strategy random evolutionary games where the entries of the payoff matrix are correlated random variables (r is the correlation). We have provided analytical formulas for $E(r,d)$ and proved that it is decreasing as a function of r. That is, our analysis has shown that decreasing the correlation among payoff entries leads to larger expected numbers of (stable) equilibrium points. This suggests that when payoffs obtained by a strategy for different group compositions are less correlated, it would lead to higher levels of strategic or behavioural diversity in a population. Thus, one might expect that when strategies behave conditionally on or even randomly for different group compositions, diversity would be promoted. Furthermore, we have shown that the asymptotic behaviour of $E(r,d)$ (and thus also of the mean number of stable equilibrium points, $SE(r,d)$), i.e. when the group size d is sufficiently large, is highly sensitive to the correlation value r. Namely, $E(r,d)$ (and $SE(r,d)$) asymptotically behave in the order of $d^{1/2}$ for $r = 0$ (i.e. the payoffs are independent for different group compositions), of $d^{1/4}$ for $0< r < 1$ (i.e. non-extreme correlation), and 0 when $r = 1$ (i.e. the payoffs are perfectly linear). It is also noteworthy that our numerical results showed that $E(r,d)$ increases with the group size d. In general, our findings might have important implications for the understanding of social and biological systems given the important roles of social and biological diversities, e.g. in the evolution of cooperative behaviour and population fitness distribution [37, 47, 60].

Moreover, we have explored further connections between EGT and random polynomial theory initiated in our previous works [14, 15]. The random polynomial P obtained from EGT (cf. (5)) differs from three well-known classes of random polynomials, namely Kac polynomials, elliptic polynomials and Weyl polynomials, that are investigated intensively in the literature. We elaborate further this difference in Sect. 6.6. In addition, as will be explained in Sect. 6.7, the set of positive roots of P is the same as that of a Bernstein random polynomial. As a result, our work provides an analytical formula and asymptotic behaviour for the expected number of Bernstein random polynomials proving [18, Conjecture 4.7]. Thus, our work also contributes to the literature of random polynomial theory and to further its existing connection to EGT.

Although the expected number of internal equilibria provides macroscopic (average) information, to gain deeper insights into a multiplayer game such as possibilities of different states of biodiversity or the maintenance of biodiversity, it is crucial to analyse the probability distribution of the number of (stable) internal equilibria [27, 37, 61]. Thus a more subtle questions is: what is the probability, $p_m$, with $0\le m\le d-1$, that a d-player two-strategy game attains m internal equilibria? This question has been addressed for games with a small number of players [27, 36]. We will tackle this more intricate question for arbitrary d in a separate paper [17]. We expect that our work in this paper as well as in [17] will open up a new exciting avenue of research in the study of equilibrium properties of random evolutionary games. We discuss below some directions for future research.

Other types of correlations. In this paper we have assumed that the correlations $corr (\beta _i,\beta _j)$ are constants for all pairs $i\ne j$. This is a fairly simple relation. Generally $\mathrm {corr}(\beta _i,\beta _j)$ may depend on i and j as showing in Lemma 1. Two interesting cases that are commonly studied in interacting particle systems are: (a) exponentially decay correlations, $\mathrm {corr}(\beta _i,\beta _j)=\rho ^{|i-j|}$ for some $0<\rho <1$, and (b) algebraically decay correlations, $\mathrm {corr}(\beta _i,\beta _j)=(1+|i-j|)^{-\alpha }$ for some $\alpha >0$. These types of correlations have been studied in the literature for different types of random polynomials [13, 22, 53].

Universality phenomena. Recently, in [67] the authors proved, for other classes of random polynomials (such as Kac polynomials, Weyl polynomials and elliptic polynomials, see Sect. 6.6), an intriguing universal phenomenon: the asymptotic behaviour of the expected number of zeros in the non-gaussian case matches that of the gaussian case once one has performed appropriate normalizations. Further research is demanded to see whether this universality phenomenon holds true for the random polynomial (1).

Appendix: Detailed Proofs and Computations

This appendix consists of detailed proofs and computations of some lemmas and theorems in the main text.

1.1 Proof of Lemma 1

We have

$$\begin{aligned} \mathrm {cov}(\beta _i, \beta _j)&= \mathrm {cov}(a_i-b_i, a_j - b_j) \\&= \mathrm {cov}(a_i, a_j) + \mathrm {cov}(b_i, b_j) - \mathrm {cov}(a_i, b_j) - \mathrm {cov}(b_i, a_j) \\&= r_a \eta ^2 +r_b \eta ^2 -2 r_{ab} \eta ^2 \\&= (r_a +r_b -2 r_{ab}) \eta ^2. \end{aligned}$$

Similarly,

$$\begin{aligned} \mathrm {var}(\beta _i)=\mathrm {var}(a_i-b_i) = \mathrm {cov}(a_i-b_i,a_i-b_i) = 2\eta ^2 - 2 r^\prime _{ab} \eta ^2 = 2 (1-r^\prime _{ab}) \eta ^2. \end{aligned}$$

Hence, the correlation between $\beta _i$ and $\beta _j$ is

$$\begin{aligned} \mathrm {corr}(\beta _i, \beta _j) = \frac{\mathrm {cov}(\beta _i, \beta _j)}{\sqrt{\mathrm {var}(\beta _i) \mathrm {var}(\beta _j) }} = \frac{(r_a + r_b - 2r_{ab})\eta ^2}{2(1-r^\prime _{ab})\eta ^2} = \frac{r_a + r_b - 2r_{ab}}{2(1-r^\prime _{ab})}. \end{aligned}$$

1.2 Proof of Theorem 2–(1)

We prove (14). We recall the following notations that have been used in the proof of Theorem 3.

$$\begin{aligned}&M_1=M_1(t,d)=\sum _{i=0}^{d-1}\begin{pmatrix} d-1\\ i \end{pmatrix}^2t^{2i}, \quad M_2=M_2(t,d)=(1+t)^{2(d-1)}, \\&A_1=A_1(t,d)=\sum \limits _{i=0}^{d-1}i^2\begin{pmatrix} d-1\\ i \end{pmatrix}^2t^{2(i-1)}, \quad A_2=A_2(t,d)=(d-1)^2(1+t)^{2(d-2)} \\ {}&B_1=B_1(t,d)=\sum \limits _{i=0}^{d-1}i\begin{pmatrix} d-1\\ i \end{pmatrix}^2t^{2i-1}, \quad B_2=B_2(t,d)=(d-1)(1+t)^{2d-3}, \\ {}&M=M(t;r,d)=(1-r)M_1+ r M_2, \quad A=A(t;r,d)=(1-r) A_1+r A_2, \\ {}&B=B(t;r,d)=(1-r)B_1+ r B_2. \end{aligned}$$

Then the density function f(t; r, d) is expressed in terms of M, A and B as (for simplicity of notation we drop r, d in f in the following)

$$\begin{aligned} f(t)=\frac{1}{\pi }\frac{\sqrt{AM-B^2}}{M}. \end{aligned}$$

(26)

Next, we compute f(1 / t). According to [15], we have the following relations, where $'$ denotes a derivative with respect to t,

$$\begin{aligned}&A_1(t)=\frac{1}{4t}(tM_1'(t))'=\frac{1}{4t}(M_1'(t)+tM_1''(t)),\quad B_1(t)=\frac{1}{2}M_1'(t),\nonumber \\&M_1(1/t)=t^{2-2d}M_1(t),\nonumber \\&A_1(1/t)=\frac{t}{4}\Big [M_1'(1/t)+\frac{1}{t}M_1''(1/t)\Big ]\nonumber \\&\quad =\frac{1}{4}t^{4-2d}\left[ 4(d-1)^2M_1(t)+(5-4d)tM_1'(t)+t^2M_1''(t)\right] ,\nonumber \\&B_1(1/t)=\frac{1}{2}M_1'(1/t)=-t^{3-2d}\left[ (1-d)M_1(t)+\frac{1}{2}tM_1'(t)\right] . \end{aligned}$$

(27)

Using the relations between $A_1, B_1$ and $M_1$ in (27), we transform further $A_1(1/t)$ and $B_1(1/t)$

$$\begin{aligned} A_1(1/t)&=\frac{1}{4}t^{4-2d}\Big [4(d-1)^2M_1(t)+4(1-d)tM_1'(t)+t(M_1'(t)+tM_1''(t))\Big ] \\&=t^{4-2d}\Big [4(d-1)^2M_1(t)+4(1-d)tM_1'(t)+t^2 A_1(t)\Big ], \\ B_1(1/t)&=-t^{3-2d}\left[ (1-d)M_1(t)+\frac{1}{2}tM_1'(t)\right] =t^{2-2d}\Big [(d-1)M_1(t)-tB_1(t)\Big ]. \end{aligned}$$

Using explicit formulas of $M_2, A_2$ and $B_2$, we get

$$\begin{aligned} M_2(1/t)=t^{2-2d}M_2(t), \quad A_2(1/t)=t^{4-2d} A_2(t), \quad B_2(1/t)=t^{3-2d}B_2(t). \end{aligned}$$

(28)

Therefore, we obtain

$$\begin{aligned} M(1/t)&= (1-r)M_1(1/t)+ rM_2(1/t)\\&\quad =t^{2-2d}[(1-r)M_1(t)+rM_2(t)]=t^{2-2d}M(t),\\ A(1/t)&=t^{4-4d}\left[ (1-r)\Big ((d-1)^2 M_1(t)+(1-d)tM_1'(t)+t^2 A_1(t)\Big )+r A_2(t)\right] ,\\ B(1/t)&=t^{3-2d}\left[ (1-r)\Big ((d-1)M_1(t)-tB_1(t)\Big )+rB_2(t)\right] ,\\ M(1/t)A(1/t)&=t^{6-4d}\Bigg [(1-r)^2\Big ((d-1)^2 M_1(t)+(1-d)tM_1'(t)+t^2 A_1(t)\Big )M_1(t)\\&\qquad +r(1-r)\bigg (\Big ((d-1)^2 M_1(t)+(1-d)tM_1'(t)+t^2 A_1(t)\Big )M_2(t)\\&\qquad +A_2(t)M_1(t)\bigg )+r^2A_2(t)M_2(t)\Bigg ],\\ B(1/t)^2&=t^{6-4d}\Bigg [(1-r)^2\Big ((d-1)M_1(t)-tB_1(t)\Big )^2\\&\qquad +2r(1-r)\Big ((d-1)M_1(t)-tB_1(t)\Big ) B_2(t)+r^2B_2(t)^2\Bigg ]. \end{aligned}$$

So we have

$$\begin{aligned}&M(1/t)A(1/t)-B(1/t)^2\nonumber \\&\quad =t^{6-4d}\Bigg [(1-r)^2\Big ((1-d)tM_1(t)M_1'(t)+t^2A_1(t)M_1(t)+2(d-1)M_1(t)B_1(t)\Big )\nonumber \\&\qquad -t^2B_1(t)^2+ r(1-r)\bigg ((d-1)^2M_1(t)M_2(t)+(1-d)tM_1'(t)M_2(t)\nonumber \\&\qquad +t^2A_1(t)M_2(t)+A_2(t)M_1(t)-2\Big ((d-1)M_1(t)-tB_1(t)\Big )B_2(t)\bigg )\nonumber \\&\qquad + r^2(A_2(t)M_2(t)-B_2(t)^2)\Bigg ]. \end{aligned}$$

(29)

Using the relations (27) and explicit formulas of $A_2, B_2, M_2$ we get

$$\begin{aligned}&A_2(t)M_2(t)-B_2^2(t)=0, \\&(1-d)tM_1(t)M_1'(t)+2(d-1)M_1(t)B_1(t)=(d-1)M_1(t)\Big [2B_1(t)-M_1'(t)\Big ]=0, \\&(d-1)^2M_1(t)M_2(t)+A_2(t)M_1(t)-2(d-1)M_1(t)B_2(t) \\&\quad =M_1(t)\Big ((d-1)M_2(t)+A_2(t)-2(d-1)B_2(t)\Big ) \\&\quad =t^2 M_1(t)A_2(t), \\&(1-d)tM_1'(t)M_2(t)+2tB_1(t)B_2(t)=2(1-d)tB_1(t)M_2(t)+2tB_1(t)B_2(t) \\&\quad =B_1(t)\Big (2(1-d)tM_2(t)+2tB_2(t)\Big ) \\&\quad =-2t^2B_1(t)B_2(t). \end{aligned}$$

Substituting these computations into (29), we obtain

$$\begin{aligned}&M(1/t)A(1/t)-B(1/t)^2 \\&\quad =t^{8-4d}\Bigg [(1-r)^2\Big (A_1(t)M_1(t)-B_1(t)^2\Big )+r(1-r)\Big (M_1(t)A_2(t)\\&\qquad +M_2(t)A_1(t)-2B_1(t)B_2(t)\Big )\Bigg ] \\&\quad =t^{8-4d}\Bigg [\Big ((1-r)M_1(t)+rM_2(t)\Big )\Big ((1-r)A_1(t)+rA_2(t)\Big )\\&\qquad -\Big ((1-r)B_1(t)+rB_2(t)\Big )^2\Bigg ] \\&\quad =t^{8-4d}\Big (M(t)A(t)-B(t)^2\Big ). \end{aligned}$$

Finally, we get

$$\begin{aligned} f(1/t)&=\frac{1}{\pi }\frac{\sqrt{A(1/t)M(1/t)-B(1/t)^2}}{M(1/t)}=\frac{1}{\pi }\frac{t^{4-2d}\sqrt{A(t)M(t)-B^2(t)}}{t^{2-2d}M(t)}\\&=\frac{1}{\pi }t^2\frac{\sqrt{A(t)M(t)-B^2(t)}}{M(t)}=t^2f(t). \end{aligned}$$

1.3 Proof of Lemma 3

The probability distribution, $f_Z$, of $Z=X-Y$ can be found via the joint probability distribution $f_{X,Y}$ as

$$\begin{aligned} f_{Z}(z)=\int _{-\infty }^{\infty } f_{X,Y}(x,x-z)\,dx=\int _{-\infty }^{\infty } f_{X,Y}(y+z,y)\,dy. \end{aligned}$$

Therefore, using the symmetry of $f_{X,Y}$ we get

$$\begin{aligned} f_Z(-z)=\int _{-\infty }^{\infty } f_{X,Y}(x,x+z)\,dx=\int _{-\infty }^{\infty } f_{X,Y}(x+z,x)\,dx=f_Z(z). \end{aligned}$$

If X and Y are iid with the common probability distribution f, then

$$\begin{aligned} f_{X,Y}(x,y)=f(x)f(y), \end{aligned}$$

which is symmetric with respect to x and y, i.e. X and Y are exchangeable.

1.4 Computations of f(1; r, d)

Substituting $t=1$ into expressions of A, B, M at the beginning of the proof of Theorem 2, we obtain

$$\begin{aligned} M(1;r,d)&=(1-r)\sum \limits _{k=0}^{d-1}\begin{pmatrix} d-1\\ k \end{pmatrix}^2+r\, 2^{2(d-1)}=(1-r)\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}+r\, 2^{2(d-1)}, \\A(1;r,d)&=(1-r)(d-1)^2M(1;r,d-1)+r(d-1)^22^{2(d-2)} \\ {}&=(1-r)(d-1)^2\begin{pmatrix} 2(d-2)\\ d-2 \end{pmatrix}+r(d-1)^22^{2(d-2)}, \\B(1;r,d)&=(1-r)\sum \limits _{k=1}^{d-1}k\begin{pmatrix} d-1\\ k \end{pmatrix}^2+r(d-1)2^{2d-3)} \\ {}&=(1-r)\frac{d-1}{2}\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}+r(d-1)2^{2d-3}. \end{aligned}$$

Therefore,

$$\begin{aligned} AM-B^2&=(1-r)^2(d-1)^2\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}\left[ \begin{pmatrix} 2(d-2)\\ d-2 \end{pmatrix}-\frac{1}{4}\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}\right] \\&\quad +r(1-r)(d-1)^22^{2(d-2)}\left[ 4\begin{pmatrix} 2(d-2)\\ d-2 \end{pmatrix}+\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}-2\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}\right] \\ {}&=(1-r)^2(d-1)^2\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}\left[ \begin{pmatrix} 2(d-2)\\ d-2 \end{pmatrix}-\frac{1}{4}\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}\right] \\&\quad +r(1-r)(d-1)^22^{2(d-1)}\left[ \begin{pmatrix} 2(d-2)\\ d-2 \end{pmatrix}-\frac{1}{4}\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}\right] \\&=(1-r)(d-1)^2\left[ \begin{pmatrix} 2(d-2)\\ d-2 \end{pmatrix}-\frac{1}{4}\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}\right] \\&\quad \left[ (1-r)\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}+r 2^{2d-1}\right] . \end{aligned}$$

Substituting this expression and that of M into (26), we get

$$\begin{aligned} f(1;r,d)&=\frac{1}{\pi }\frac{\sqrt{AM-B^2}}{M}\\&=\frac{1}{\pi }(d-1)\sqrt{1-r}\times \sqrt{\frac{\begin{pmatrix} 2(d-2)\\ d-2 \end{pmatrix}-\frac{1}{4}\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}}{(1-r)\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}+r\, 2^{2(d-1)}}}\\&=\frac{1}{\pi }(d-1)\sqrt{1-r}\times \sqrt{\frac{\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}\frac{1}{4(2d-3)}}{(1-r)\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}+r\, 2^{2(d-1)}}}\\&=\frac{1}{\pi }\frac{d-1}{2\sqrt{2d-3}}\sqrt{\frac{(1-r)\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}}{(1-r)\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}+r\, 2^{2(d-1)}}}. \end{aligned}$$

If $r=1$ then $f(1;r,d)=0$. If $r<1$ then

$$\begin{aligned} f(1;r,d)=\frac{1}{\pi }\frac{d-1}{2\sqrt{2d-3}}\sqrt{\frac{1}{1+\alpha }}\quad \text {where}\quad \alpha =\frac{r}{1-r}\frac{2^{2(d-1)}}{\begin{pmatrix} 2(d-1)\\ d-1 \end{pmatrix}}. \end{aligned}$$

By Stirling formula, we have

$$\begin{aligned} \begin{pmatrix} 2n\\ n \end{pmatrix}\sim \frac{4^n}{\sqrt{\pi n}} \quad \hbox { for large}\ n. \end{aligned}$$

It implies that for $0< r<1$ and for large d, $\alpha \sim \frac{r}{1-r}\sqrt{\pi (d-1)}$, from which we obtain

$$\begin{aligned} f(1;r,d)\sim \frac{1}{\pi }\frac{d-1}{2\sqrt{2d-3}}\sqrt{\frac{1}{1+\frac{r}{1-r}\sqrt{\pi (d-1)}}}\sim \frac{(d-1)^{1/4}(1-r)^{1/2}}{2\sqrt{2}\pi ^{5/4}r^{1/2}}. \end{aligned}$$

1.5 Some Technical Lemmas Used in Proof of Theorem 3

We need the following proposition.

Proposition 2

The following inequality holds

$$\begin{aligned} 2(t+1)B\Big [B_1(1+t)-M_1(d-1)\Big ]<M\Big [A_1(1+t)^2-M_1(d-1)^2\Big ]. \end{aligned}$$

(30)

To prove Proposition 2, we need several auxiliary lemmas. We note that throughout this section

$$\begin{aligned} x=\frac{1+t^2}{1-t^2}, \quad 0<t<1, \end{aligned}$$

and $P_d(z)$ is the Legendre polynomial of degree d which is defined through the following recurrent relation

$$\begin{aligned} (2d+1) z P_d(z)=(d+1) P_{d+1}(z)+d\, P_{d-1}(z); \quad P_0(z)=1, \quad P_1(z)=z. \end{aligned}$$

(31)

We refer to [15] for more information on the Legendre polynomial and its connections to evolutionary game theory.

Lemma 4

It holds that

$$\begin{aligned} \lim _{d\rightarrow \infty }\frac{P_d(x)}{P_{d+1}(x)}=x-\sqrt{x^2-1}. \end{aligned}$$

Note that $x=\frac{1+t^2}{1-t^2}$, we can write the above limit as

$$\begin{aligned} \lim _{d\rightarrow \infty }\frac{P_d(x)}{P_{d+1}(x)}=\frac{1-t}{1+t}. \end{aligned}$$

(32)

Proof

According to [15, Lemma 4], we have

$$\begin{aligned} P_d(x)^2\le P_{d+1}(x) P_{d-1}(x). \end{aligned}$$

Since $P_d(x)>0$, we get

$$\begin{aligned} x\ge \frac{1}{x} = \frac{P_{0}(x)}{P_{1}(x)}\ge \frac{P_1(x)}{P_2(x)} \ge \cdots \ge \frac{P_{d-1}(x)}{P_{d}(x)} \ge \frac{P_{d}(x)}{P_{d+1}(x)}\ge 0. \end{aligned}$$

(33)

Therefore, there exists a function $0\le f(x)\le \frac{1}{x}$ such that

$$\begin{aligned} \lim _{d\rightarrow \infty }\frac{P_d(x)}{P_{d+1}(x)}=f(x). \end{aligned}$$

From the recursive relation (31), we have

$$\begin{aligned} (2d+1)x=(d+1)\frac{P_{d+1}(x)}{P_d(x)}+d\frac{P_{d-1}(x)}{P_d(x)}, \end{aligned}$$

which implies that

$$\begin{aligned} \frac{d+1}{d}=\frac{\frac{P_{d-1}(x)}{P_d(x)}-x}{x-\frac{P_{d+1}(x)}{P_d(x)}}. \end{aligned}$$

Taking the limit $d\rightarrow \infty$ both sides, we obtain

$$\begin{aligned} 1=\frac{f(x)-x}{x-\frac{1}{f(x)}}. \end{aligned}$$

Solving this equation for f(x), requiring that $0\le f(x)\le \frac{1}{x}\le x$ we obtain $f(x)=x-\sqrt{x^2-1}$. $\square$

Lemma 5

The following inequalities hold

$$\begin{aligned} (1-t)^2 \le (1-t^2) \frac{P_{d}(x)}{P_{d+1}(x)} \le 1+t^2. \end{aligned}$$

(34)

Proof

By dividing by $1-t^2$, the required inequalities are equivalent to (recalling that $0<t<1$)

$$\begin{aligned} \frac{1-t}{1+t} \le \frac{P_{d}(x)}{P_{d+1}(x)} \le x, \end{aligned}$$

which are true following from (32) and (33). $\square$

Lemma 6

The following equality holds

$$\begin{aligned} 2(d-1)t \left[ B_1(1+t) - M_1 (d-1) \right] = (t-1) \left[ A_1 (1+t)^2 - M_1 (d-1)^2\right] . \end{aligned}$$

(35)

Proof

The stated equality is simplified to

$$\begin{aligned} A_1 (t^2 - 1) + M_1 (d-1)^2 - 2(d-1) t \, B_1 = 0. \end{aligned}$$

(36)

We use the following results from [15, Lemma 3 & Section 6.2]

$$\begin{aligned} A_1(t,d)&= (d-1)^2 M_1(t,d-1) = (d-1)^2 (1-t^2)^{d-2}P_{d-2}(x), \end{aligned}$$

(37)

$$\begin{aligned} M_1&= (1-t^2)^{d-1}P_{d-1}(x),\nonumber \\ B_1&= \frac{M_1^\prime }{2} \nonumber \\&= M_1 \left( \frac{-t\,(d-1)}{1-t^2}+\frac{2t}{(1-t^2)^2}\frac{P_{d-1}'}{P_{d-1}}\left( x\right) \right) \nonumber \\&= M_1 \left( \frac{-t\,(d-1)}{1-t^2}+\frac{2t}{(1-t^2)^2} \frac{(d-1)(1-t^2)^2}{4t^2}\left( \frac{1+t^2}{1-t^2}-\frac{P_{d-2}(x)}{P_{d-1}(x)}\right) \right) \nonumber \\&= M_1 \left( \frac{-t\,(d-1)}{1-t^2}+ \frac{d-1}{2t}\left( \frac{1+t^2}{1-t^2}-\frac{P_{d-2}(x)}{P_{d-1}(x)}\right) \right) \nonumber \\&= (d-1)\bigg (-t(1-t^2)^{d-2} P_{d-1}(x)\nonumber \\&\quad + \frac{(1+t^2)(1-t^2)^{d-2} P_{d-1}(x) - (1-t^2)^{d-1} P_{d-2}(x) }{2t} \bigg ). \end{aligned}$$

(38)

Substituting these expressions into the left-hand side of (36), we obtain 0 as required. $\square$

Lemma 7

The following inequality holds

$$\begin{aligned}&(t -1) \left[ B_1(1+t) - M_1 (d-1) \right] \ge 0, \end{aligned}$$

(39)

$$\begin{aligned}&(t^2-1)B_1 - (d-1) t \, M_1 \le 0 , \end{aligned}$$

(40)

$$\begin{aligned}&(t^2-1)(B_2-B_1) - (d-1)t (M_2-M_1) \le 0. \end{aligned}$$

(41)

Proof

We prove (39) first. Since $M_1 > 0$, (39) is simplified to

$$\begin{aligned} (t^2-1)\frac{B_1}{M_1} - (d-1)(t -1) \ge 0. \end{aligned}$$

Using the relation (38) between $B_1$ and $M_1$, we obtain

$$\begin{aligned}&(t^2-1)\frac{B_1}{M_1} - (d-1)(t -1) \\&\quad =(t^2-1)\frac{M_1^\prime }{2 M_1} - (d-1)(t -1) \\&\quad =(t^2-1)\Bigg [\frac{-\,t\,(d-1)}{1-t^2}+\frac{2t}{(1-t^2)^2}\frac{P_{d-1}'}{P_{d-1}}\left( \frac{1+t^2}{1-t^2}\right) \Bigg ]-(d-1)(t -1) \\&\quad =(d-1) + \frac{2t}{t^2-1}\frac{P_{d-1}'}{P_{d-1}}\left( x \right) . \end{aligned}$$

Now using the following relation [15, Eq. (49)]

$$\begin{aligned} \frac{P_{d-1}'(x)}{P_{d-1}(x)}=\frac{d-1}{x^2-1}\left( x-\frac{P_{d-2}(x)}{P_{d-1}(x)}\right) =\frac{(d-1)(1-t^2)^2}{4t^2}\left( \frac{1+t^2}{1-t^2}-\frac{P_{d-2}(x)}{P_{d-1}(x)}\right) ,\qquad \end{aligned}$$

(42)

we obtain

$$\begin{aligned} (t^2-1)\frac{B_1}{M_1} - (d-1)(t -1)&=(d-1)\left( 1-\frac{1+t^2}{2t} - \frac{t^2-1}{2t}\frac{P_{d-2}(x)}{P_{d-1}(x)} \right) \\&=-\frac{d-1}{2t}\Big [(1-t)^2-(1-t^2)\frac{P_{d-1}}{P_{d-1}}(x)\Big ] \\&\ge 0, \end{aligned}$$

where the last inequality follows from Lemma 5. This establishes (39).

Next, we prove (40), which can be simplified to

$$\begin{aligned} (d-1)\left( -\frac{1+t^2}{2t} - \frac{t^2-1}{2t}\frac{P_{d-2}(x)}{P_{d-1}(x)} \right) \le 0, \end{aligned}$$

which is in turn equivalent to

$$\begin{aligned} (1-t^2)\frac{P_{d-2}(x)}{P_{d-1}(x)} \le 1 + t^2. \end{aligned}$$

This has been proved in Lemma 5.

Finally, we prove (41). First, we simplify

$$\begin{aligned} (t^2-1)B_2- (d-1)t \,M_2= & {} (d-1)(t^2-1)(1+t)^{2d-3} - (d-1) t (1+t)^{2d-2}\\= & {} - (d-1) (1+t)^{2d-2}. \end{aligned}$$

Thus, (41) is equivalent to

$$\begin{aligned} (d-1)\left( \frac{1+t^2}{2t} + \frac{t^2-1}{2t}\frac{P_{d-2}(x)}{P_{d-1}(x)} - (1+t)^{2d-2} \right) \le 0. \end{aligned}$$

This clearly holds because $t \ge 0$ and from the proof of the first inequality we already know that

$$\begin{aligned} \frac{1+t^2}{2t} + \frac{t^2-1}{2t}\frac{P_{d-2}(x)}{P_{d-1}(x)} - 1 \le 0. \end{aligned}$$

Thus, we finish the proof of the lemma. $\square$

We are now ready to provide a proof of Proposition 2.

Proof (Proof of Proposition 2)

From Lemma 6, since $M_1, A_1 and B_1$ are polynomials (of t) with integer coefficients, there exists a polynomial S(t) such that

$$\begin{aligned} B_1(1+t) - M_1 (d-1) = (t-1) S(t) \quad \text {and}\quad A_1 (1+t)^2 - M_1 (d-1)^2 = 2(d-1) t \ S(t) \end{aligned}$$

If follows from (39) that $S(t)\ge 0$. Next, we will prove that

$$\begin{aligned}&2(t+1)B_1 \left[ B_1(1+t) - M_1 (d-1) \right] \le M_1 \left[ A_1 (1+t)^2 - M_1 (d-1)^2\right] , \end{aligned}$$

(43)

$$\begin{aligned}&2(t+1)(B_2-B_1) \left[ B_1(1+t) - M_1 (d-1) \right] \le (M_2 - M_1) \left[ A_1 (1+t)^2 - M_1 (d-1)^2\right] . \end{aligned}$$

(44)

Indeed, these inequalities can be rewritten as

$$\begin{aligned}&2S(t) \left[ (t^2-1)b_1 - (d-1) t \, m_1 \right]< 0,\\&2S(t) \left[ (t^2-1)(b_2-b_1) - (d-1)t (m_2-m_1) \right] < 0, \end{aligned}$$

which hold due to Lemma 7. Multiplying (44) with $r>0$ and adding with (43) yield the assertion of Proposition 2. $\square$

1.6 Comparison with Known Results for Other Classes of Random Polynomials

The distribution and expected number of real zeros of a random polynomial has been a topic of intensive research dating back to 1932 with Block and Pólya [8], see for instance the monograph [13] for a nice exposition and [44, 67] for recent results and discussions. The most general form of a random polynomial is given by

$$\begin{aligned} \mathcal {P}_d(z)=\sum _{i=0}^{d} c_i\,\xi _i\,z^i, \end{aligned}$$

(45)

where $c_i$ are deterministic coefficients which may depend on both d and i, and $\xi _i$ are random variables. The most three well-known classes of polynomials are

• (i) Kac polynomials: $c_i:=1$,

• (ii) Weyl (or flat) polynomials: $c_i:=\frac{1}{i!}$,

• (iii) Elliptic (or binomial) polynomials: $c_i:=\sqrt{\begin{pmatrix} d\\ i \end{pmatrix}}$.

The expected number of real zeros of these polynomials when $\{\xi _i\}$ are i.i.d standard normal variables is, respectively, $E_K\sim \frac{2}{\pi }\log d$, $E_{W}\sim \frac{2}{\pi }\sqrt{d}$ and $E_E=\sqrt{d}$, see, e.g. [67] and references therein. Random polynomials in which $\xi _i$ are correlated random variables have also attracted considerable attention, see, e.g. [13, 21,22,23, 51,52,53,54] and references therein. Particularly, when $\{\xi _i\}$ satisfy the same assumption as in this paper, it has been shown, in [51] for the Kac polynomial that $E_K\sim \frac{2}{\pi }\sqrt{1-r^2}\log d$, and in [23] for elliptic polynomials that $E_E\sim \frac{\sqrt{d}}{2}$.

The random polynomial P arising from evolutionary game theory in this paper, see Equation (1), corresponds to $c_i=\begin{pmatrix} d-1\\ i \end{pmatrix}$; thus it differs from all the above three classes. In Sect. 6.7, we show that a root of P is also a root of the Bernstein polynomial. Therefore, we also obtain an asymptotic formula for the expected number of real zeros of the random Bernstein polynomial. We anticipate that evolutionary game theory and random polynomial theory have deeply undiscovered connections in different scenarios. We shall continue this development in a forthcoming paper.

1.7 On the Expected Number of Real Zeros of a Random Bernstein Polynomial of Degree d

Similarly as in [15, Corollary 2], as a by-product of Theorem 1, we obtain an asymptotic formula for the expected number of real zeros, $E_{\mathcal { B}}$, of a random Bernstein polynomial of degree d

$$\begin{aligned} \mathcal { B}(x)=\sum \limits _{k=0}^{d}\beta _k\begin{pmatrix} d\\ k \end{pmatrix}x^k\,(1-x)^{d-k}, \end{aligned}$$

where $\beta _k$ are i.i.d. standard normal distributions. Indeed, by changing of variables $y=\frac{x}{1-x}$ as in Sect. 2, zeros of $\mathcal { B}(x)$ are the same as those of the following random polynomial

$$\begin{aligned} {\tilde{\mathcal { B}}}(y)=\sum \limits _{k=0}^{d}\beta _k\begin{pmatrix} d\\ k \end{pmatrix}y^k. \end{aligned}$$

As a consequence of Theorem 1, the expected number of real zeros, $E_{\mathcal { B}}$, of a random Bernstein polynomial of degree d is given by

$$\begin{aligned} E_{\mathcal { B}}=2E(0,d+1)\sim \sqrt{2d+1}. \end{aligned}$$

(46)

This proves Conjecture 4.7 in [18]. Connections between EGT and Bernstein polynomials have also been discussed in [48].