Outlier robust extreme learning machine to simulate discharge coefficient of side slots

Abstract

As the first time, this paper attempts to recreate the discharge coefficient (DC) of side slots by another artificial intelligence procedure named "Outlier Robust Extreme Learning Machine (ORELM)". Accordingly, at first, the variables affecting the DC comprising the ratios of the flow depth to the side slot length (Y_m/L), the side slot crest elevation to the side slot length (W/L), the main channel width to the side slot length (B/L), as well as the Froude number (F_r) are determined and subsequently five ORELM models (ORELM 1 to ORELM 5) are created utilizing these variables. From that point forward, laboratory measurements are arranged into two datasets comprising training (70%) and testing (30%). At the subsequent stage, the best model alongside the most affecting input variables is presented by executing a sensitivity examination. The most impressive model (i.e., ORELM 3) reproduces DC values as far as B/L, W/L and F_r. It is worth focusing on that ORELM 3 forecasts DC values with worthy precision. For instance, the correlation coefficient (R), the scatter index (SI) and the Nash–Sutcliffe effectiveness (NSC) for ORELM 3 are acquired in the examination state to be 0.936, 0.049 and 0.852, independently. Examining the outcomes yielded from the simulation demonstrates that W/L and F_r are the most impacting factors to reproduce the DC. Besides, the findings of the sensitivity examination uncover that ORELM 3 acts in an underestimated way. Finally, a computer code is put forward to compute the DC of side slots.

Introduction

Side slots are commonly placed on main channel walls to conduct and control excess water in drainage networks and irrigation canals. To increase efficiency of a side slot, the detection of parameters affecting discharge volume is crucially important. It is worth focusing on that the DC is the most effective variable for the optimal design of a side slot. This coefficient is a function of different hydraulic and geometric variables and determining the importance of each of them plays a crucial role in optimal designing of this sort of flow divert structures. Because of the significance of side slots, many experiments have been done on the properties of the flow passing through side slots and their coefficient of discharge. For example, Carballada (1978), Ramamurthy et al. (1986), Gill (1987), Ramamurthy et al. (1987), Swamee (1992) and Swamee et al. (1993) performed several experiments on the flow around side slots and their discharge coefficient. In addition, Ojha and Subbaiah (1997) investigated the flow field as well as the coefficient of discharge of side slots through a laboratory work. Utilizing a numerical method, they approximated the side slot discharge and compared the values computed by this technique with experimental data. They finally concluded that the error computed by this method was almost equal to 10%. Moreover, Oliveto et al. (1997) by carving a slot on the bed of circular channels experimentally evaluated the flow pattern near such divert structures. They demonstrated that the Froude number was the most affecting variable on the mechanism of the flow. Additionally, Ghodsian (2003) solved the dynamic equation of spatial variable flows nearby side gates to suggest an equation for the estimation of the coefficient of discharge. This author expressed the DC of side gates as a function of the flow hydraulic properties as well as geometric properties of the laboratory model. Hussain et al. (2010) executed a laboratory test to assess the flow behavior alongside the DC of the flow passing through circular-shaped side orifices. By examining the findings acquired from the examination, they established a regression relation for computing the coefficient of discharge. Swamee and Swamee (2010) managed to analyze experimental results to provide an explicit relationship computing the DC of circular side orifices. They stated that the DC of side orifices is a function of viscosity and flow potential. Through a test, Hussain et al. (2011) studied the DC of rectangular-shaped side orifices. They meticulously studied the flow pattern around the side orifice and presented a relation to approximate the coefficient. Moreover, Hussain et al. (2014) presented a relation for computing the DC of rectangular-shaped side orifices as the conclusion of an analytical study. They showed that the blunder of the provided model was almost equal to 5%. Furthermore, Hussain et al. (2016) experimentally investigated the flow pattern inside circular side orifices in both free and submerged conditions. According to their findings, the Froude number was the most influencing variable on the flow jet. In last decades, the application of artificial intelligence (AI) procedures and also soft computing approaches such as the adaptive neuro-fuzzy inference system (ANFIS), artificial neural network (ANN), the gene expression programming (GEP), the group method of data handling (GMDH) and the extreme learning machine (ELM) have dramatically increased thanks to their ability in modeling nonlinear phenomena and complex systems. Such models act fast in simulating various phenomena and are acceptably flexible. Because of these advantages, different examines have been done on the recreation of the DC of side weirs, side orifices and side slots by artificial intelligence models. For instance, Ebtehaj et al. (2015a) reproduced the DC of weirs set on rectangular canals through the GMDH model. By examining the simulation outcomes, they presented an equation to approximate the DC. Moreover, Ebtehaj et al. (2015b) forecasted the DC of rectangular-shaped side orifices via the GMDH model. As the result of a sensitivity analysis, they presented the most powerful model as well as the most influencing factor on the DC. Khoshbin et al. (2016) established a coupled model for ascertaining the DC of rectangular side weirs. For recreating the DC, they integrated the genetic algorithm (GA), ANFIS and singular vector decomposition (SVM) models. Besides, Azimi et al. (2017a) computed the DC of rectangular side orifices by utilizing a computational fluid dynamics (CFD) model and also a hybrid artificial intelligence technique. These scholars indicated that the artificial intelligence model showed higher exactness in modeling the DC. Akhbari et al. (2017) using an ANN model and the M5’ model managed to recreate this coefficient for triangular-shaped weirs. They provided several relations for estimating the DC. Additionally, Azimi et al. (2019) predicted the DC of rectangular weirs arranged on trapezoidal canals via the vector machine (SVM) model. By executing a sensitivity analysis, they introduced the most powerful model and most influencing variable and managed to develop a matrix with the ability of computing the coefficient.

Bagherifar et al. (2020), Huang et al. 2004) modeled the three dimensional flow field within a circular conduit along with a side weir using the FLOW-3D model. The authors applied the RNG k–ε turbulence model and volume of fluid (VOF) scheme so as to reconstruct the flow turbulence and free surface.

Examining the previous works shows that the DC of divert structures such as side weirs, side orifices and side slots is crucially important as the most influencing parameter in choosing an optimal scheme. Moreover, various artificial intelligence techniques have been broadly utilized for recreating of the DC of this type of flow divert structures.

Accordingly, as the first time, this paper attempts to recreate the discharge coefficient (DC) of side slots by another artificial intelligence procedure named " Outlier Robust Extreme Learning Machine (ORELM)". The basic objective of this research is to present the most powerful model and the most impacting input variable via the analysis of the ORELM model results. Initially, five ORELM models are specified by implementing the factors impacting on the coefficient of discharge. At the next step, the best ORELM model alongside the most affecting parameter are specified via a sensitivity examination and the ORELM outcomes are contrasted with the ELM. Besides, an uncertainty examination is conducted on the ORELMs. It ought to be noticed that as the final task of the research, a partial derivative sensitivity analysis is also done on the ORELM. Lastly, a computer code is presented to compute the DC.

Methodology

Extreme learning machine

High speed modeling despite the large number of parameters which should be initialized prior to modeling and also trapping in local minima are common issues of learning the feed-forward neural network (FFNN) by gradient algorithms such as back propagation (BP). To conquer such troubles, Bagherifar et al. (2020), Huang et al. (2004, 2006) presented the extreme learning machine (ELM) algorithm. Converting the nonlinear problem to a linear form, as the most significant achievement of this approach, significantly reduces the modeling process time so that the modeling process is completed in few seconds. The structure of this model is a single layer FFNN (SLFFNN). In this technique, the matrix interfacing the input layer to the hidden layer (the input weight matrix) and hidden layer biases are haphazardly initialized, while the matrix which associates the hidden layer to the output layer (i.e., the output weight matrix) is computed by processing a linear problem. Using the defined structure significantly reduces the modeling time compared to time-consuming methods such as BP. The results of the previous studies demonstrate that in addition to the surprising modeling speed, this method has higher generalizability than other gradient algorithms (Azimi and Shiri 2021; Azimi et al. 2021; Azimi et al. 2017b).

Given N samples in the form of datasets with several inputs ($x_{i} \in R^{n}$) and one output($y_{i} \in R$) as $\left\{ {(x_{i} ,y_{i} )} \right\}_{i = 1}^{N}$ and considering L neurons within the hidden layer and the activation function g(x), the structure of the ELM model for establishing mapping between the considered inputs and output is expressed as follows (Azimi et al. 2017b):

$$ y_{j} = \sum\limits_{i = 1}^{L} {\beta_{i} g({\mathbf{w}}_{i} \cdot {\mathbf{x}}_{j} + b_{i} )} ,\quad j = 1,2, \ldots ,N $$

(1)

In this relationship, ${\mathbf{w}}_{i} = (w_{i1} ,w_{i2} , \ldots ,w_{in} )\,(i = 1:L)$ is the matrix interfacing input neurons to the ith hidden layer neuron, b_i represents the bias related to the ith hidden layer neuron and β_i denotes the weight matrix associating the ith hidden layer neuron to the output neuron. Among the three defined matrices, w_i and b_i are randomly initialized, while the matrix β_i is computed during solving the interested problem via the ELM. Also, N denotes the number of input variables of the problem. The output node in the mathematical expression specified for the ELM is linear and ${\mathbf{w}}_{i} .{\mathbf{x}}_{j}$ represent the inner outcome related to matrices of the input weight and problem variables, respectively. Rewriting this formula as a matrix forms Eq. (2) (Azimi et al. 2017b):

$$ {\mathbf{H}}\beta = {\mathbf{y}} $$

(2)

where $\beta = [\beta_{1} , \ldots ,\beta_{N} ]^{{\text{T}}}$, $\beta = [\beta_{1} , \ldots ,\beta_{N} ]^{{\text{T}}}$ and H denotes the hidden layer output matrix which is solved in the following way:

$$ {\mathbf{H}}({\mathbf{w}}_{{\mathbf{1}}} ,{\mathbf{w}}_{{\mathbf{2}}} , \ldots ,{\mathbf{w}}_{{\mathbf{L}}} ,{\mathbf{x}}_{{\mathbf{1}}} ,{\mathbf{x}}_{{\mathbf{2}}} , \ldots ,{\mathbf{x}}_{{\mathbf{L}}} , \ldots ,b_{1} ,b_{2} , \ldots ,b_{L} ) = \left[ {\begin{array}{*{20}c} {g{(}{\mathbf{w}}_{{\mathbf{1}}} \cdot {\mathbf{x}}_{{\mathbf{1}}} + b_{1} {)}} & \cdots & {g{(}{\mathbf{w}}_{{\mathbf{L}}} \cdot {\mathbf{x}}_{{\mathbf{1}}} + b_{1} {)}} \\ \vdots & \ddots & \vdots \\ {g{(}{\mathbf{w}}_{{\mathbf{1}}} \cdot {\mathbf{x}}_{{\mathbf{N}}} + b_{1} {)}} & \cdots & {g{(}{\mathbf{w}}_{{\mathbf{1}}} \cdot {\mathbf{x}}_{{\mathbf{N}}} + b_{L} {)}} \\ \end{array} } \right] $$

(3)

As discussed before, among the three defined matrices, w and b are randomly initialized and β is calculated analytically. Thus, the only remaining unknown is the matrix β which is calculated by means of a linear relationship. Since the matrix H in Eq. 2 is non-square, solving this equation is not as simple as solving a linear equation. Thus, the loss function value is minimized through the solution process by the least square technique (i.e.,$\min \left\| {{\mathbf{y}} - {\mathbf{H}}\beta } \right\|$). Therefore, the result is obtained through the optimization process by minimizing l₂-norm (Azimi et al. 2017b).

$$ \hat{\beta } = {\mathbf{H}}^{ + } {\mathbf{y}} $$

(4)

where H⁺ is the Moore–Penrose generalized inverse (MPGI) (Rao and Mitra 1971) of H. For modeling by the ELM, the hidden layer nodes number should be less than training samples (L < N) otherwise, overfitting occurs. So, the above relationship is rewritten as follows (Azimi et al. 2017b):

$$ \hat{\beta } = ({\mathbf{H}}^{{\text{T}}} {\mathbf{H}}{)}^{ - 1} {\mathbf{H}}^{{\text{T}}} {\mathbf{y}} $$

(5)

Outlier robust ELM (ORELM)

Considering that in solving complex nonlinear problems via AI-based algorithms, the existence of outliers which is because of the nature of the problem and should not be considered as outliers, will have a noticeable influence on the modeling outcomes. Thus, a significant percent of the modeling error (e) is related to the existence of outliers. To take into account this issue in modeling nonlinear problems using the ELM, Zhang and Luo (2015) defined the existence of outliers by sparsity. Knowing that l₀-norm acts better in reflecting sparsity than l₂-norm, instead of using l₂-norm, they defined the training model error (e) as follows:

$$ \mathop {\min }\limits_{\beta } \,C\left\| {\mathbf{e}} \right\|\,_{0} + \left\| \beta \right\|_{2}^{2} \,\,\,\,\,\,\text{subject\,to}\,\,{\mathbf{y}} - {\mathbf{H}}\beta = {\mathbf{e}} $$

(6)

Zhang and Luo (2015) to solve this non-convex programming problem, modified it in a tractable convex relaxation form without loss of the sparsity characteristic problem. Using l₁-norm instead of l₀-norm in the following equation not only guarantees the presence of sparse characteristics but comes with minimization convex:

$$ \mathop {\min }\limits_{\beta } \left\| {\mathbf{e}} \right\|\,_{1} + \frac{1}{C}\left\| \beta \right\|_{2}^{2} \quad \text{subject\,to}\;{\mathbf{y}} - {\mathbf{H}}\beta = {\mathbf{e}} $$

(7)

This formula is a constrained convex optimization problem in such a way that fits completely the suitable domain of the Augmented Lagrangian (AL) multiplier approach. Therefore, the function AL is provided as:

$$ L_{\mu } ({\mathbf{e}},\beta ,\lambda ) = \left\| {\mathbf{e}} \right\|_{1} + \frac{1}{C}\left\| \beta \right\|_{2}^{2} + \lambda^{2} ({\mathbf{y}} - {\mathbf{H}}\beta - {\mathbf{e}}) + \frac{\mu }{2}\left\| {{\mathbf{y}} - {\mathbf{H}}\beta - {\mathbf{e}}} \right\|_{2}^{2} $$

(8)

Here, $\lambda \in R^{n}$ is the vector of the Lagrangian multiplier and $\mu = = 2N/\left\| {\mathbf{y}} \right\|_{1}$ (Yang and Zhang 2011) demonstrates the penalty parameter. The optimal answer of finding e, β and λ is achieved through the iterative process for minimizing the function AL:

$$ \left\{ \begin{gathered} ({\mathbf{e}}_{k + 1} ,\beta_{k + 1} ) = \arg \,\mathop {\min }\limits_{{{\mathbf{e}},\beta }} L_{\mu } ({\mathbf{e}},\beta ,\lambda )\quad (\text{a}) \hfill \\ \lambda_{k + 1} = \lambda_{k} + \mu ({\mathbf{y}} - {\mathbf{H}}\beta_{k + 1} - {\mathbf{e}}_{k + 1} )\quad \;\;\;(\text{b}) \hfill \\ \end{gathered} \right\} $$

(9)

Physical models

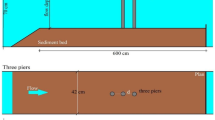
In this paper, the experimental data reported by Ojha and Subbaiah (1997) and Hussain et al. (2011) are used for approving the AI models. The rectangular-shaped channel used in Ojha and Subbaiah's model is assumed to be 4.5 m in length, 0.4 m in width and 0.5 m in height. A side slide gate with a width of 0.2 m installed at 2.5 m from the channel entrance has been installed on this model. However, the rectangular channel utilized in Hussain et al. (2011) model is assumed to be 9.15 m in length, 0.5 m in width and 0.6 m in height. Additionally, a rectangular side gate is situated at a 5 m distance from the entrance of the channel. The experimental data were utilized on rectangular gates for three widths comprising 0.044 m, 0.089 m and 0.133 m for this model. Figure 1 depicts the layouts of these laboratory models.

Fig. 1

Layout of experimental models reported by Ojha and Subbaiah (1997) and Hussain et al. (2011)

DC of side slot

Generally, the DC of side slots is a function of the following parameters (Hussain et al. 2011; Azimi et al. 2018):

$\left( L \right)$ = length of side slot, $\left( b \right)$ = height of side slot, $\left( B \right)$ = width of main channel, $\left( W \right)$ = height of the side slot bed from the main channel bed, $\left( {V_{1} } \right)$ = flow velocity in the main channel, $\left( {Y_{m} } \right)$ = the flow depth in the main channel, $\left( \rho \right)$ = fluid density, $\left( \mu \right)$ = flow viscosity, $\left( g \right)$ = gravitational acceleration

$$ C_{d} = f_{1} \left( {L,b,B,W,V_{1} ,Y_{m} ,\rho ,\mu ,g} \right) $$

(10)

Given that the flow Froude number is $F_{r} = \frac{{V_{1} }}{{\sqrt {g.Y_{m} } }}$ and density, viscosity and gravitational acceleration remain constant, while $B$, $W$ and $Y_{m}$ become dimensionless, thus Eq. (10) is rewritten as:

$$ C_{d} = f_{2} \left( {\frac{B}{L},\frac{W}{L},\frac{{Y_{m} }}{L},F_{r} } \right) $$

(11)

Hence, in this investigation, the impact of the factors of Eq. (11) on the DC of side slots is considered. The range of the variables reported by Ojha and Subbaiah (1997) and Hussain et al. (2011) for developing the ORELM models are given in Table 1.

Table 1 Range of the dimensionless parameters reported by Ojha and Subbaiah (1997) and Hussain et al. (2011) for developing ORELM models

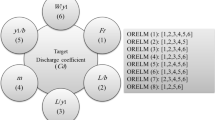
The integrations of the dimensionless parameters related to relation (11) used for developing the ORELM models are shown in Fig. 2. It merits referencing that 70% of the laboratory data are employed for learning the models, while the remaining (i.e., 30%) are utilized for examining them.

Fig. 2

Integrations of input variables for ORELM models

Goodness of fit

To test the precision of the presented mathematical models, several statistical indices comprising the correlation coefficient (R), variance accounted for (VAF), root-mean-square error (RMSE), scatter index (SI), mean absolute error (MAE) and Nash–Sutcliffe efficiency (NSC) are utilized (Azimi et al. 2022):

$$ R = \frac{{\sum\nolimits_{i = 1}^{n} {\left( {F_{i} - \overline{F} } \right)\left( {O_{i} - \overline{O} } \right)} }}{{\sqrt {\sum\nolimits_{i = 1}^{n} {\left( {F_{i} - \overline{F} } \right)^{2} \sum\nolimits_{i = 1}^{n} {\left( {O_{i} - \overline{O} } \right)^{2} } } } }} $$

(12)

$$ {\text{VAF}} = \left( {1 - \frac{{{\text{var}} \left( {F_{i} - O_{i} } \right)}}{{{\text{var}} \left( {F_{i} } \right)}}} \right) \times 100 $$

(13)

$$ {\text{RMSE}} = \sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left( {F_{i} - O_{i} } \right)^{2} } } $$

(14)

$$ {\text{SI}} = \frac{{{\text{RMSE}}}}{{\overline{O} }} $$

(15)

$$ {\text{MAE}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {F_{i} - O_{i} } \right|} $$

(16)

$$ {\text{NSC}} = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {\left( {O_{i} - F_{i} } \right)^{2} } }}{{\sum\nolimits_{i = 1}^{n} {\left( {O_{i} - \overline{O}} \right)^{2} } }} $$

(17)

where $O_{i}$ = observed measurements, $F_{i}$ = values recreated by models, $\overline{O}$ = average of observed measurements, n = number of observed measurements.

Next, different activation functions are tested. After that, the most powerful model alongside the most affecting input parameter is specified by performing a sensitivity analysis(SA). Additionally, the ORELM most efficient model is contrasted with the ELM. Besides, an uncertainty analysis (UA) as well as a partial derivative sensitivity analysis (PDSA) are conducted on the best model. Finally, a computer code is provided for the estimation of the DC of side slots.

Results and discussion

Hidden layer neurons number

This part evaluates and determines the hidden layer neurons number (HLNN). Figure 3 depicts the changes of HLNN versus different statistical indices in the training mode. To choose the most optimal HLNN, a neuron is initially specified for the hidden layer; then by increasing the number to 30, the numerical model results are compared with the experimental values. The modeling exactness improves with increasing the HLNN, but from one particular stage onwards, the increase in the number of neurons has no noticeable impact on the modeling exactness. The most optimal HLNN in the training mode is considered equal to 14. For this HLNN, the scatter index value and the correlation coefficient, respectively, are computed to be 0.052 and 0.927. Furthermore, for the model with HLNN = 14, the MAE, VAF and NSC are estimated to be 0.018, 85.923 and 0.836, individually.

Fig. 3

Variations of NHLN versus different statistical indices in training mode

Moreover, the changes of HLNN in the testing mode versus different statistical indices are depicted in Fig. 4. In the testing mode, the most optimal HLNN is considered to be 14 as well. For the model with HLNN = 14, the RMSE, R and MAE are computed to be 0.029, 0.925 and 0.019, separately. It should be reminded that for this model, NSC, VAF and SI are equal to 0.851, 87.468 and 0.049, separately.

Fig. 4

Changes of NHLN versus different statistical indices in testing mode

Figure 5 shows a comparison between the simulated DC with the experimental data for hidden layer neurons equal to 14 in both modes (i.e., training and testing). The modeling exactness in both the training and testing modes is in an acceptable range. So, in the modeling process of the DC by the ORELM, the HLNN is assumed to be 14.

Fig. 5

Comparison of simulated coefficient of discharge with experimental data for NHLN equal to 14 in both training and testing modes

Activation function

The ORELM model owns five activation functions(AF) named “sig,””sin,” “hardlim,” “tribas” and “radbas.” This section studies different activation functions and their influences on the outcomes of modeling the coefficient of discharge by the ORELM model. Also, in Fig. 6 different statistical indices calculated for five different AFs in both modes are illustrated. For sig, MAE, R, and VAF in the testing state are computed to be 0.019, 0.935, and 87.468, separately. For the training mode of sin, the estimations of RMSE, NSC and R are also acquired to be 0.081, 0.328 and 0.373, individually. Additionally, VAF, R and MAE for the training mode of hardlim are estimated to be 1.519, 0.015 and 0.068, separately. Additionally, SI, NSC and RMSE for tribas in the testing state are yielded to be 0.621, − 0.222 and 0.364, individually. Moreover, MAE, R and VAF for radbas, respectively, are obtained to be 0.125, 0.0001 and − 416.193.

Fig. 6

Outcomes of statistical indices acquired in both modes for different activation functions

Figure 7 depicts a comparison between the DC values simulated by different AFs in both modes with the experimental data. According to the simulation outcomes, the activation function sig exhibits better performance compared to the other functions. This activation function models the DC data in both modes with reasonable exactness. Thus, this activation function is chosen to model the DC by the ORELM model.

Fig. 7

Comparison of coefficient of discharge simulated by different AFs in both modes

Sensitivity Analysis

A sensitivity analysis (SA) is performed in this section for different ORELM models. The outcomes of the statistical indices computed for different ORELM models in both modes are presented in Fig. 8. It should be noted that ORELM1 is a function of all inputs which recreates the DC data in terms of B/L, W/L,Y_m/L and F_r. This model computes SI, VAF and NSC in the training state, respectively, equal to 0.052, 85.923 and 0.836.

Fig. 8

Outcomes of statistical indices computed for ORELM models in both modes

In contrast, four models (i.e., ORELM2 to ORELM5) simulate the DC values in terms of three inputs. For instance, ORELM2 estimates RMSE, MAE and R in the testing state, respectively, equal to 0.031, 0.019 and 0.924 and the impact of the Froude number is eliminated for it. Also, ORELM3 estimates values of the target function in terms of B/L, W/L and F_r and the influence of Y_m/L is neglected for it. It should be noted that R, SI and NSC for the testing mode of the ORELM3 are, respectively, acquired to be 0.936, 0.049 and 0.852. Furthermore, the impact of W/L is omitted for ORELM4 and this model recreates the DC data in terms of the input variables such as B/L, Y_m/L and F_r. Besides, NSC, VAF and RMSE for ORELM4 in the testing state, respectively, are computed to be 0.836, 85.794 and 0.031. Furthermore, ORELM5 recreates the target function values in terms of W/L,Y_m/Land F_r and the influence of the dimensionless parameter B/Lis disregarded for this model. Moreover, MAE, SI and VAF for ORELM5 in the training state are, respectively, acquired to be 0.019, 0.053 and 85.518.

Figure 9 shows the comparison of the DC computed by ORELM models with the observed data in both modes. According to the sensitivity analysis, the ORELM 3 model forecasts the coefficient of discharge data in both modes with higher exactness than the other defined models. Thus, this model is chosen as the best model. In contrast, ORELM 4 is also identified as the worst artificial intelligence model. It is worth mentioning that by eliminating the parameters W/L and F_r, the modeling accuracy is dramatically reduced. So, these two dimensionless parameters are specified as the most effective input variables on the ORELM model.

Fig. 9

Comparison of coefficient of discharge computed by ORELM models with observed data in both modes

Comparison with ELM

The outcomes of the best model (ORELM 3) are compared with the ELM in this section. Figure 10 depicts indices computed for ORELMs and ELMs in both states. As shown, the ORELM model generates the coefficient of discharge data with higher exactness than the ELM. It should be noted that the correlation of this model with the experimental data is reasonably high. For example, the NSC, SI and MAE for the training state of the ELM model are equal to 0.833, 0.052 and 0.018, separately. Moreover, R, VAF and RMSE for the ELM testing state are, respectively, achieved to be 0.845, 85.320 and 0.031.

Fig. 10

Statistical indices obtained for ORELM and ELM models in both modes

Figures 11 and 12 present the comparison of the outcomes acquired by the ORELM and ELM models with the observed measurements alongside their scatter plots in both modes. Based on the results, the ORELM acts better than the ELM. In both modes, the ORELM model has less error and higher correlation compared to the experimental DC values.

Fig. 11

Comparison of outcomes acquired by ORELM and ELM models with observed data in both modes

Fig. 12

Scatter plots of ORELM and ELM models in both modes

Uncertainty analysis

This step discusses about the uncertainty analysis (UA) accomplished for testing the efficiency of the most powerful models. The UA is basically an efficient task conducted for the evaluation of the efficiency of numerical models (Azimi et al. 2019; Azimi et al. 2018). Therefore, the UA is done to assess errors forecasted via numerical models and examine the efficiency of this sort of models. Additionally, the blunder forecasted via the model is generally equivalent to values reproduced using the model (P_i) minus observed data (O_i) $\left( {e_{i} = P_{i} - O_{i} } \right)$. Moreover, $\overline{e} = \sum\nolimits_{i = 1}^{n} {e_{i} }$ represents the average of the forecasted error. Besides, $S_{e} = \sqrt {\sum\nolimits_{i = 1}^{n} {\left( {e_{i} - \overline{e} } \right)^{2} /n - 1} }$ yields the standard deviation of predicted errors. It is worth mentioning that the negative sign of $\overline{e}$ demonstrates the underestimated efficiency of the model has, while the positive sign proves the overestimated efficiency. Moreover, the utilization of the parameters $\overline{e}$ and $S_{e}$ forms a confidence bound around errors forecasted through the Wilson score approach without the continuity correction. Thus, the use of ± 1.64S_e, prompts a 95% confidence bound. The UA variables of the best models are given in Table 2. In addition, the width of uncertainty bound and the 95% prediction error interval are denoted in this table by WUB and 95% PEI, separately. By considering the conducted UA outcomes, ORELM 1, ORELM 2, ORELM 4 and ORELM 5 own an overestimated efficiency, while the efficiency of the ORELM3 model is underestimated. Furthermore, for the GMDH and GSGMDH models, the WUB are, respectively, computed to be ± 0.002 and ± 0.007. Furthermore, for the GMDH, 95% PEI is acquired between − 0.002 and 0.002, while for the GSGMDH, this value is acquired to be between − 0.007 and 0.007. It is worth mentioning that the standard deviation belonging to the predicted error values for the ORELM2, ORELM4 and ORELM% models are equal to 0.0310, 0.033 and 0.031, respectively. Moreover, the WUB for the ORELM1, ORELM2 and ORELM3 models are estimated to be ± 0.004, ± 0.004 and ± 0.003, independently. Moreover, the 95%PEI for ORELM3 is between -0.003 to 0.003.

Table 2 UA results for ORELM models

Box 1 MATLAB code for Cd calculation

Partial derivative sensitivity analysis (PDSA)

This step attempts to execute a partial derivative sensitivity analysis (PDSA) for the most powerful ORELM model (i.e., ORELM 3). Basically, the PSDA is done for the identification of the impact of input variables on the target parameter. However, the PSDA is defined as an approach introducing the changing pattern of the goal variable based on the input variables. In the case where the PSDA is in the positive state, it is concluded that implies that the target function (i.e., the DC) is expanding, while its negative state reveals that the target function is diminishing. Moreover, the relative derivative of each input variable in this technique is computed based on the target function (Azimi et al. 2017c). According to the PDSA outcomes, when the parameter B/L is increasing, the PSDA also increases and part of the PDSA outcomes have a positive sign and the other part have a negative sign. Furthermore, the increased parameter W/L, the decreased PSDA and almost all the PSDA outcomes are computed positive for this parameter, while the increased the Froude number, the increased the PSDA (Fig. 13).

Fig. 13

Results of PSDA for superior model (ORELM3)

Superior ORELM model

According to the outcomes obtained from reproducing the DC of side slots through the ORELM technique, ORELM 3 is introduced as the most powerful model. This model reproduces DC values in terms of B/L, W/L and F_r with acceptable accuracy. A computer code shown in Box 1 is provided to compute the DC of side slots for this artificial intelligence model.

Conclusion

The coefficient of discharge is the most crucial parameter for the design of a side slot. As the main goal, this paper attempted to reproduce the discharge coefficient (DC) of side slots installed on rectangular channels for the first time via a new machine learning (ML) model named “Outlier Robust Extreme Learning Machine (ORELM).” To do this, the variables affecting the DC were initially specified and five distinctive models were developed by utilizing them. Two different datasets were employed for validating the artificial intelligence models. Moreover, 70% of the laboratory measurements were implemented for training the ORELM model and the rest (i.e., 30%) for examining them. It merits referencing that the most optimal number of hidden layer neurons for this ML model was selected to be 14. Besides, the activation function sigmoid was detected as the most efficient activation function of this study. Then, the best ORELM model was specified by performing a sensitivity analysis. This model estimated the DC in terms of F_r, B/L, and W/L. In both modes (i.e., training and testing), this model had acceptable exactness. For instance, the RMSE, VAF, and SI for the training mode were estimated to be 0.029, 86.778 and 0.050, respectively. The outcomes of the sensitivity analysis exhibited that W/L and F_r were the most important input variables for recreating the DC of side slots using the ORELM model. Moreover, the ORELM model outcomes were contrasted with the ELM results and it was proved that the ORELM has a better performance in both modes. It should be noted that an uncertainty analysis was executed for the ML model to exhibit that the ORELM had an underestimated efficiency. Furthermore, as the result of executing a partial derivative sensitivity analysis, it was concluded that increased the parameter W/L, increased the target function value with the same discharge coefficient. Lastly, a computer code was presented for engineers to estimate the coefficient of discharge of side slots using the ORELM model.