1 Introduction

The predator–prey interaction among the population is well known to be one of the most difficult inquiry areas for the biology and ecology population. Many ecologists, mathematicians, and biologists have studied this during the last few decades [1,2,3,4,5,6]. The differential and difference equations are used to explain the majority of dynamic population models. When populations have non-overlapping generations, the discrete-time models are more reasonable than the continuous-time models [2, 7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. Due to its universal existence and importance, a large number of investigations have already examined the predator–prey models (see [24,25,26,27,28,29,30,31,32,33,34,35], for examples). Volterra established a model in 1931 to represent the connection between predators and their preys in an ecological system by developing a system of two autonomous ordinary differential equations [36]. Based on linear per capita growth rates, the Volterra system is the simplest model of predator–prey interactions. The following system of ordinary differential equations represents the famous Volterra prey–predator model.

$$\begin{aligned} \left. \begin{array}{l} {\dot{X}}=a X-b X Y \\ {\dot{Y}}=-c Y+d X Y \end{array}\right\} \end{aligned}$$

where X stands for the number of prey and Y stands for the number of predators. Furthermore, the parameters a, b, c, and d are all positive. It has been demonstrated that in the absence of predators, the number of prey increases exponentially, while the number of predators declines exponentially in the absence of a prey population. The terms bXY and dXY describe predator–prey interactions that are beneficial to predators but deadly to prey. A good update for this model is to replace the term aX by the logistic growth \(aX(1-X)\) where population’s per capita growth rate decreases as population size approaches a maximum imposed by limited resources. Stability, bifurcations and chaos control of the improved system studied by [37]. However, we are quite interested in studying the effect of using Ricker map \(r\,X_{n}\,e^{1-\frac{X_{n}}{k}}\) instead of the logistic map to describe the dynamics of preys. In Ricker map, the population growth is virtually exponential; but, as population size grows, the instantaneous growth rate decreases linearly; and finally, population size plateaus and fluctuates around a mean.

The outline of this paper is as follows: The construction of the model is discussed in Sect. 2. Section 3 investigates the existence of equilibria and local stability of the model (5) with various topological types. We explore the existence of bifurcations around equilibria in Sect. 4. Numerical simulations using MATLAB are applied in Sect. 5 to support the theoretical analysis and visualize the newly observed complex dynamics of the system. Section contains the conclusion and discussion.

2 Derivation of the model

This paper deals with the study of stability and bifurcations of a discrete-time predator–prey model. Let \(X_{n}\) and \(Y_{n}\) represent the population density of prey and predator at time n, respectively. We impose the following assumptions to formulate the difference equations which describe the required system.

Assumption 1

In the absence of predator Y, the population of prey X would grow in a classical discrete Ricker population map manner.

$$\begin{aligned} X_{n+1}=r\,X_{n}\,e^{1-\frac{X_{n}}{k}}, \end{aligned}$$
(1)

where \(r\,>\,0\) is per-capita birth or growth rate in absence of predators r is the prey finite rate of increase in the absence of predators and \(k>0\) is the carrying capacity parameter.

Assumption 2

The population of prey X will drop in the presence of the predator Y. If we suppose that the interaction between the prey and the predator has the mass action principle response due to the prey’s defensive ability, then Eq. (1) can be expressed as

$$\begin{aligned} \displaystyle {X_{n+1}=r\,X_{n}\,e^{1-\frac{X_{n}}{k}}-b\,X_{n}\,Y_{n}}, \end{aligned}$$
(2)

where \(b>0\) is the biomass conversion parameter.

Assumption 3

Prey X are favourite food for predator Y, the population density of predator Y will increase following the mass action principle response manner in the presence of favourite food. Hence we have

$$\begin{aligned} Y_{n+1}=d\,X_{n}\,Y_{n}, \end{aligned}$$
(3)

where \(d>0\) denotes the predator’s biomass conversion efficiency.

Hence the proposed model is from Eqs. (1)–(3)

$$\begin{aligned} \begin{aligned} X_{n+1}&=r\,X_{n}\,e^{1-\frac{X_{n}}{k}} -b\,X_{n}\,Y_{n}, \\ Y_{n+1}&=d\,X_{n}\,Y_{n}, \end{aligned} \end{aligned}$$
(4)

with positive initial condition \(X_{0}>0\) and \(Y_{0}>0\). Let \(X_{n}=k\,x_{n}\) and \(Y_{n}=\frac{y_{n}}{b}\). We rewrite model Eq. (4) as

$$\begin{aligned} \begin{aligned} x_{n+1}&=r x_{n}\,e^{1-x_{n}}-x_{n}\,y_{n}, \\ y_{n+1}&=\alpha x_{n} y_{n}, \end{aligned} \end{aligned}$$
(5)

where \(\alpha = d\,k\,>0.\)

3 Fixed points: existence and stability

In this section, we study the existence and stability of fixed points of the system (5) in \({\mathbb {R}}_{+}^{2}\). Results about the existence of fixed points are summarized as follows:

Proposition 1

For model (5), we can have at most three fixed points:

  1. (i)

    The trivial fixed point \(E_{0}(0, 0)\) always exists;

  2. (ii)

    The predator-free fixed point \(E_{1}\left( 1+\ln {(r)},0\right) \) exists if \( r\,>\,\mathrm {e}^{-1}\);

  3. (iii)

    The interior fixed \(E_{2}\left( \frac{1}{\alpha },r\,\mathrm {e}^{\frac{\alpha -1}{\alpha }}-1\right) \) exists if \(r\,>\, \mathrm {e}^{\frac{1-\alpha }{\alpha }}\).

Proof

The fixed points correspond to the steady states of the model population (5) can be obtained by solving the algebraic system

$$\begin{aligned} x&=r\,x\,\mathrm {e}^{1-x}-x\,y, \\ y&=\alpha \,x\,y, \end{aligned}$$

then all non-negative fixed points of the system (5) are \(E_{0}(0, 0),\) \(E_{1}\left( 1+\ln {(r)},0\right) , \) which is positive if \( r\,>\,\mathrm {e}^{-1}\) and \(E_{2}\left( \frac{1}{\alpha },r\,\mathrm {e}^{\frac{\alpha -1}{\alpha }}-1\right) ,\) which is positive if \(r\,>\,\mathrm {e}^{\frac{1-\alpha }{\alpha }}\). \(\square \)

The Jacobian matrix J(x, y) of the model (5) about the fixed point (x, y) is given by

$$\begin{aligned} J(x,y)=\left( \begin{array}{cc} r\,(1-x)\,\mathrm {e}^{1-x}-y &{} -x \\ \alpha \,y &{} \alpha \,x \end{array} \right) . \end{aligned}$$
(6)

Its characteristic equation is

$$\begin{aligned} {\mu }^{2}+ \left( y-\alpha \,x+r\,\left( x-1 \right) \,{\mathrm{e}^{1-x}} \right) \mu +\alpha \,r\,x \left( 1-x \right) \,{\mathrm{e}^{1-x}}=0. \end{aligned}$$
(7)

The biological interruption for three fixed points is as follows: The fixed point \(E_{0}\) represents a situation in which there is no prey and no predators. The fixed point \(E_{1}\) reflects the case where there is prey but no predators. \(E_{2}\) refers to the coexistence of fixed nonzero numbers of prey and predators.

3.1 Dynamic behavior of the model

Now we will study the behavior of the solutions of (5) about \( E_{0} \), \(E_{1}\) and \(E_{2}\). To do this we recall the following definitions:

Definition 1

Let E(x, y) be a fixed point of (5) and let \(\mu _1\) and \(\mu _2\) are the eigenvalues of (7).

  1. (i)

    E is called a sink (locally asymptotic stable) if \(\mid \mu _1\mid < 1\) and \(\mid \mu _2\mid < 1\);

  2. (ii)

    E is called a source if \(\mid \mu _1\mid > 1\) and \(\mid \mu _2\mid > 1\). A source is locally unstable;

  3. (iii)

    E is called a saddle if \(\mid \mu _1\mid < 1\) and \(\mid \mu _2\mid > 1\) (or \(\mid \mu _1\mid > 1\) and \(\mid \mu _2\mid < 1\));

  4. (iv)

    E is called non-hyperbolic if either \(\mid \mu _1\mid =1\) and \(\mid \mu _2\mid = 1\).

The relations between roots and coefficients of the quadratic equation is given by the following Lemma.

Lemma 1

Let \(R(\mu ) = \mu ^2 + A\mu + B\). Suppose that \(R(1) > 0\), \(\mu _1\) and \(\mu _2\) are the roots of \(R(\mu ) = 0\). Then

  1. (i)

    \(\mid \mu _1\mid < 1\) and \(\mid \mu _2\mid < 1\) if and only if \(R(-1) > 0\) and \(B < 1\);

  2. (ii)

    \(\mid \mu _1\mid < 1\) and \(\mid \mu _2\mid > 1\) (or \(\mid \mu _1\mid > 1\) and \(\mid \mu _2\mid < 1\)) if and only if \(R(-1) < 0\);

  3. (iii)

    \(\mid \mu _1\mid > 1\) and \(\mid \mu _2\mid > 1\) if and only if \(R(-1) > 0\) and \(B > 1\);

  4. (iv)

    \(\mu _1 =-1\) and \(\mid \mu _2\mid \ne 1\) if and only if \(R(-1) = 0\) and \(B \ne 0,2\);

  5. (v)

    \(\mu _1\) and \(\mu _2\) are complex and \(\mu _1 =\mid \mu _2\mid = 1\) if and only if \(A^2-4B < 0\) and \(B = 1\). \(\square \)

The following Proposition confirms the stability of fixed points of system (5) under some conditions.

Proposition 2

For the fixed point \(E_{0}\) of the system (5), the following statements are true:

  1. (i)

    \(E_{0}\) is sink if \(0\,<\,r\,<\,{\mathrm {e}^{-1}}\);

  2. (ii)

    \(E_{0}\) is never a source;

  3. (iii)

    \(E_{0}\) is an unstable saddle if \(r\,>\,{\mathrm {e}^{-1}}\);

  4. (iv)

    \(E_{0}\) is non-hyperbolic if \(r\,=\,\mathrm {e}^{-1}\).

Proof

The Jacobian matrix associated with (5) at \(E_{0}\) is \(J\left( E_{0}\right) \) and is given by

$$\begin{aligned} J(E_{0})=\left( \begin{array}{cc} r\,\mathrm {e} &{} 0 \\ 0 &{} 0 \end{array} \right) , \end{aligned}$$

the eigenvalues of \(J\left( E_{0}\right) \) are \(\lambda _{1}=0\) and \(\lambda _{2}=r\,\mathrm {e}\). So, the fixed point

  1. (i)

    \(E_{0}\) is a sink if and only if \(0\,<\,r\,<\,\mathrm {e}^{-1}\);

  2. (ii)

    \(E_{0}\) is never a source since one of the eigenvalues is always zero;

  3. (iii)

    \(E_{0}\) is a saddle if and only if \(r\,>\,\mathrm {e}^{-1}\);

  4. (iv)

    \(E_{0}\) is non-hyperbolic if only if \(r\,=\,\mathrm {e}^{-1}\). \(\square \)

Proposition 3

The fixed point \(E_{0}\) of the system (5) is globally asymptotically stable if \(0\,<\,r\,<\,{\mathrm {e}^{-1}}\).

Proof

It was shown in Proposition 2 that \(E_{0}\) is locally asymptotically stable if \(0\,<\,r\,<\,{\mathrm {e}^{-1}}\). So, proving that \(\lim _{n\rightarrow \infty } x_{n}=0\) and \(\lim _{n\rightarrow \infty } y_{n}=0\) is sufficient to prove the global stability of \(E_{0}\).

It follows from the first equation of system (5) that

$$\begin{aligned} \begin{aligned} x_{n+1}&=r x_{n}\,\mathrm {e}^{1-x_{n}}-x_{n}\,y_{n} \\&\le r \mathrm {e} x_{n}\,\mathrm {e}^{-x_{n}}\\&\le r \mathrm {e} x_{n}. \end{aligned} \end{aligned}$$

Then

$$\begin{aligned} \begin{aligned} x_{n}\le (r \mathrm {e})^{n} x_{0}, \quad n= 1, 2, ... \end{aligned} \end{aligned}$$
(8)

Then

$$\begin{aligned} \begin{aligned} \lim _{n\rightarrow \infty } x_{n}=0. \end{aligned} \end{aligned}$$

Note that

$$\begin{aligned} \begin{aligned} x_{n+1}\ge 0&\iff x_{n}(r \mathrm {e} \,\mathrm {e}^{-x_{n}}-\,y_{n}) \ge 0\\&\iff r \mathrm {e} \,\mathrm {e}^{-x_{n}} \ge y_{n}\\&\iff r \mathrm {e} \ge y_{n} \mathrm {e}^{x_{n}}. \end{aligned} \end{aligned}$$

Since \(x < \mathrm {e}^{x}\) for all \(x \ge 0\), then \(x_{n}y_{n}< y_{n} \mathrm {e}^{x_{n}} < r \mathrm {e}\). Then it follows from second equation of system (5) that \( y_{n+1} \le \alpha r \mathrm {e}\). That is \(y_{n}\) is bounded from above. Again we see from the second equation of system (5) and Eq. (8) that

$$\begin{aligned} \begin{aligned} y_{n+1}=\alpha x_{n} y_{n} \le \alpha (r \mathrm {e})^{n} x_{0} y_{n}, \quad n= 1, 2, ... \end{aligned} \end{aligned}$$

Thus

$$\begin{aligned} \begin{aligned} y_{n} \le (r \mathrm {e})^{n} \alpha ^{n} x_{0}^{n} y_{0}. \end{aligned} \end{aligned}$$

Since \(y_{n}\) is bounded and \(r \mathrm {e}<1\) therefore

$$\begin{aligned} \begin{aligned} \lim _{n\rightarrow \infty } y_{n}=0. \end{aligned} \end{aligned}$$

Then the proof is completed. \(\square \)

Proposition 4

For the fixed point \(E_{1}\) of the system (5), the following statements are true:

  1. (i)

    \(E_{1}\) is sink if \(\mathrm {e}^{-1}\,<\,r\,<\,\min \{\mathrm {e},\mathrm {e}^{\frac{1-\alpha }{\alpha }}\}\);

  2. (ii)

    \(E_{1}\) is a source if \(r\,>\,\max \{\mathrm {e},\mathrm {e}^{\frac{1-\alpha }{\alpha }}\}\);

  3. (iii)

    \(E_{1}\) is an unstable saddle point if \(\min \{\mathrm {e},\mathrm {e}^{\frac{1-\alpha }{\alpha }}\}\,<\,r\,<\,\max \{\mathrm {e},\mathrm {e}^{\frac{1-\alpha }{\alpha }}\}\);

  4. (iv)

    \(E_{1}\) is non-hyperbolic if \(r\in \{\mathrm {e},\mathrm {e}^{-\frac{\alpha -1}{\alpha }}\}\).

Proof

In the same manner as in Proposition (2). The Jacobian matrix associated with (5) at \(E_{1}\) is \(J\left( E_{1}\right) \) and is given by

$$\begin{aligned} J(E_{1})=\left( \begin{array}{cc} -\ln (r) &{} -\ln (r)-1 \\ 0 &{} \alpha \,(\ln (r)+1) \end{array} \right) , \end{aligned}$$

hence, the eigenvalues of \(J\left( E_{1}\right) \) are \(\lambda _{1}=-\ln (r)\) and \(\lambda _{2}=\alpha \,(1+\ln (r))\). Then, by using Lemma (1) we get the results of Proposition (4). \(\square \)

We are interested to analyze the dynamical behavior of the system around interior fixed point \(E_{2}\) for its importance. In order to determine conditions that guarantee that the characteristic roots of Jacobian matrix about \(E_{2}\) are inside the unit disk one can use Lemma (1).

Proposition 5

The positive equilibrium point \(E_{2}\) of the model (5) is sink if and only if the following conditions hold:

  1. (i)

    \(\mathrm {e}^{\frac{1-\alpha }{\alpha }}\,<\,r<\,\frac{3\,\alpha }{2-\alpha }\,\mathrm {e}^{\frac{1-\alpha }{\alpha }}\) and \(\frac{1}{2}< \alpha \,\le \frac{5}{4}\);

  2. (ii)

    \(\mathrm {e}^{\frac{1-\alpha }{\alpha }}\,<\,r<\,\frac{\alpha }{\alpha -1}\,\mathrm {e}^{\frac{1-\alpha }{\alpha }}\) and \( \alpha \,>\,\frac{5}{4}\);

Proof

The Jacobian matrix (6) at \(E_{2}\) reads as

$$\begin{aligned} J(E_{2})=\left( \begin{array}{cc} 1-\frac{r}{\alpha } \mathrm {e}^{\frac{\alpha -1}{\alpha }}&{} -\frac{1}{\alpha } \\ \alpha \,r \mathrm {e}^{\frac{\alpha -1}{\alpha }}-\alpha &{} 1 \end{array} \right) , \end{aligned}$$

and the characteristic equation of \(J(E_{2})\) is

$$\begin{aligned} \mu ^{2}+P \mu +Q=0, \end{aligned}$$

where

$$\begin{aligned} P=\frac{r}{\alpha }\,\mathrm {e}^{\frac{\alpha -1}{\alpha }}-2, \qquad and \qquad Q=\frac{r(\alpha -1)}{\alpha }\,\mathrm {e}^{\frac{\alpha -1}{\alpha }}, \end{aligned}$$

according to Lemma (1), the positive equilibrium point \(E_{2}\) is locally asymptotically stable if

  1. (i)

    \(1+P+Q>0\) and this means \(r>\mathrm {e}^{\frac{1-\alpha }{\alpha }}\);

  2. (ii)

    \(1-P+Q>0\) and this means \(r\,(2-\alpha )\mathrm {e}^{\frac{\alpha -1}{\alpha }}<3\alpha \); and

  3. (iii)

    \(Q<1\) and this means \(r(\alpha -1)\mathrm {e}^{\frac{\alpha -1}{\alpha }}<\alpha \),

or, equivalently

  1. (i)

    \(\mathrm {e}^{\frac{1-\alpha }{\alpha }}\,<\,r<\,\frac{3\,\alpha }{2-\alpha }\,\mathrm {e}^{\frac{1-\alpha }{\alpha }}\) and \(\frac{1}{2}< \alpha \,\le \frac{5}{4}\);

  2. (ii)

    \(\mathrm {e}^{\frac{1-\alpha }{\alpha }}\,<\,r<\,\frac{\alpha }{\alpha -1}\,\mathrm {e}^{\frac{1-\alpha }{\alpha }}\) and \( \alpha \,>\,\frac{5}{4}\).\(\square \)

The nonhyperbolic fixed point case is more involved. According to the eigenvalues of 1 or \(-\,1\), there are several scenarios. It is common to use centre manifold theory to determine the stability of the fixed point when one of the eigenvalues is on the unit circle and the other eigenvalue is inside the unit circle [38,39,40]. In order to determine conditions that guarantee that the characteristic roots in the unit circle, one can use Theorem 4.5 (Elaydi [40], p. 203). \(\square \)

Proposition 6

\(E_{2}\) loses stability:

  1. (i)

    via a flip point when \(1 / 2<\alpha <5 / 4\) and \(r=\frac{3 \alpha }{ 2-\alpha }e^{\frac{1-\alpha }{\alpha }}\);

  2. (ii)

    via a Neimark–Sacker point when \(5/ 4<\alpha \) and \(r=\frac{ \alpha }{ \alpha -1}e^{\frac{1-\alpha }{\alpha }}\);

  3. (iii)

    via a branch point when \(\alpha >1 / 2\) and \(r=e^{\frac{1-\alpha }{\alpha }}\).

Proof

By Proposition (4) the stability boundary of \(E_{2}\) consists of parts of three curves, namely,

  1. (1)

    Curve 1: \(r=\frac{3 \alpha }{2-\alpha }e^{\frac{1-\alpha }{\alpha }}\),

  2. (2)

    Curve 2:\(r=\frac{ \alpha }{\alpha -1}e^{\frac{1-\alpha }{\alpha }}\),

  3. (3)

    Curve 3: \(r=e^{\frac{1-\alpha }{\alpha }}\), the points of Curve 1 on the stability boundary of \(E_{2}\) meet \(1+p+q=0\), implying that they have an eigenvalue of \(-1\) and are hence period doubling points. The points on the stability boundary of Curve 2 satisfy \(q=1\), i.e. they have two eigenvalues with product 1 and are hence Neimark–Sacker points. Curve 3 points on the stability boundary satisfy \(1-p+q=0\), implying that they have an eigenvalue of 1. It is simple to verify that \(E_{2}\) then branches to \(E_{1}\). When this is combined with Proposition (4), the interior points of the boundary parts of Curves 1,2, and 3 form the sets specified in Proposition (4) parts (i), (ii), and (iii) respectively. \(\square \)

Fig. 1
figure 1

Stability regions in (\(\alpha ,r\))-space

Full size image

4 Bifurcations analysis

The existence of bifurcations about equilibria is investigated in this section, which is based on theoretical studies in Sect. 3. It is well known that the classification of bifurcation types depends mainly on the natural of the eigenvalues about the equilibrium points. The following is a summary of the presence of related bifurcations around the equilibria \(E_{0}\), \(E_{1}\), and \(E_{2}\):

  1. (i)

    From Proposition (2), we can find out that when \(r =\mathrm {e}^{-1}\), one of the eigenvalues about the equilibrium \(E_{0}\) is 1. So when the parameter varies in the small neighborhood of \(r =\mathrm {e}^{-1}\), a fold bifurcation may occur.

  2. (ii)

    From Proposition (2), we can see that if \(r = \mathrm {e}^{\frac{1-\alpha }{ \alpha }}\) holds then one of the eigenvalues about \(E_{1}\) is 1 . So a fold bifurcation may occurs when the parameter varies in a small neighborhood of \( r = \mathrm {e}^{\frac{1-\alpha }{\alpha }}\). And we denote the parameters satisfying \(r = \mathrm {e}^{\frac{1-\alpha }{\alpha }}\) as

    $$\begin{aligned} F_{E_{1}}=\left\{ \left( \alpha , r\right) : r = \mathrm {e}^{\frac{1-\alpha }{ \alpha }}, \alpha , r>0\right\} . \end{aligned}$$
  3. (iii)

    If (i) holds in Proposition (6), we can observe that one of the eigenvalues of \(J_{E_{2}}\) about \(E_{2}\) is \(-1\), while the other is neither 1 nor \(-1\) . As a result, a period-doubling bifurcation exists due to parameter variation in a small neighborhood of \(r=\frac{3\alpha }{2-\alpha }\mathrm {e}^{ \frac{1-\alpha }{\alpha }}\). More precisely we can also represent the parameters satisfying \(r=\frac{3\alpha }{2-\alpha }\mathrm {e}^{\frac{1-\alpha }{ \alpha }}\) as

    $$\begin{aligned} P_{E_{2}}=\left\{ \left( \alpha , r\right) : r=\frac{3\alpha }{2-\alpha }\mathrm {e} ^{\frac{1-\alpha }{\alpha }}\quad \text {and} \quad \frac{1}{2}<\alpha <\frac{5}{ 4} \right\} . \end{aligned}$$
  4. (iv)

    If (ii) holds in Proposition (6), we see that the eigenvalues of \(J_{E_{2}}\) about \(E_{2}\) are a pair of complex conjugate with modulus 1 . So a Neimark–Sacker bifurcation exists by the variation of parameter in a small neighborhood of \(r=\frac{\alpha }{\alpha -1}\mathrm {e}^{\frac{1-\alpha }{\alpha } } \). Precisely we represent the parameters satisfying \(r=\frac{\alpha }{ \alpha -1}\mathrm {e}^{\frac{1-\alpha }{\alpha }} \) as

$$\begin{aligned} N_{E_{2}}=\left\{ \left( \alpha , r\right) : r=\frac{\alpha }{\alpha -1}\mathrm {e} ^{\frac{1-\alpha }{\alpha }} \text{ and } \alpha >\frac{5}{4}\right\} . \end{aligned}$$

The stability regions (i), (ii) and (iii) of \(E_{2}\) obtained in Proposition 3 are depicted as \(\Omega _{E 2}^{S}\) in Fig. 1. \(\Omega _{E 0}^{S}\) and \(\Omega _{E 1}^{S}\) in Fig. 1 represent the stability regions of \(E_{0}\) and \(E_{1}\), respectively.The following is the biological interpretation of Fig. 1. For all parameter values, the situation with no prey and no predators exists, but it is only stable in \(\Omega _{E 0}^{S}\), that is, for \(r<\frac{1}{e}\). For every \(r>\frac{1}{e}\), the situation with a fixed number of prey but no predators exists, but only in \(\Omega _{E 2}^{S}\) is stable. When \(r>\frac{1}{ e}\) and \(\alpha >\frac{1}{1+\ln (r)}\), coexistence of fixed nonzero numbers of prey and predators is possible, but only in \(\Omega _{E 2}^{S}\) is stable.

4.1 Neimark–Sacker bifurcation about \(E_{2}\)

We first discuss the Neimark–Sacker bifurcation of the model (5) about \(E_{2}\). Consider the parameter r in a neighborhood of \(r^{*}\), i.e., \(r=r^{*}+\epsilon \) where \(\epsilon \ll 1\), then the model (5) becomes

$$\begin{aligned} \begin{aligned} x_{n+1}&=\left( r^{*}+\epsilon \right) x_{n}e^{1-x_{n}}-x_{n} y_{n}, \\ y_{n+1}&=\alpha x_{n} y_{n}, \end{aligned} \end{aligned}$$
(9)

the characteristic equation of \(J_{E_{2}(\frac{1}{\alpha },(r^{*}+\epsilon ) \mathrm {e}^{\frac{\alpha -1}{\alpha }}-1)}\) about \(E_{2}(\frac{1}{\alpha } ,(r^{*}+\epsilon )\mathrm {e}^{\frac{\alpha -1}{\alpha }}-1)\) of the model (9) is

$$\begin{aligned} \lambda ^{2}-p(\epsilon ) \lambda +q(\epsilon )=0, \end{aligned}$$

where

$$\begin{aligned} p(\epsilon )=-\frac{(r^{*}+\epsilon )\mathrm {e}^{\frac{\alpha -1}{\alpha } }-2\alpha }{\alpha }, \quad q(\epsilon )=\frac{(r^{*}+\epsilon )(\alpha -1) \mathrm {e}^{\frac{\alpha -1}{\alpha }} }{\alpha }, \end{aligned}$$

the roots of characteristic equation of \(J_{E_{2}(\frac{1}{\alpha } ,(r^{*}+\epsilon )\mathrm {e}^{\frac{\alpha -1}{\alpha }}-1)}\) about \(E_{2}( \frac{1}{\alpha },(r^{*}+\epsilon )\mathrm {e}^{\frac{\alpha -1}{\alpha }}-1)\) are

$$\begin{aligned} \begin{aligned} \lambda _{1,2}&=\frac{p(\epsilon ) \pm \iota \sqrt{4 q(\epsilon )-p^{2}(\epsilon )}}{2}, \\&=-\frac{(r^{*}+\epsilon )\mathrm {e}^{\frac{\alpha -1}{\alpha }}-2\alpha }{2\alpha } \pm \frac{\iota }{2} \sqrt{\frac{-(r+\epsilon )^{2}\left( \mathrm {e}^\frac{\alpha -1}{\alpha } \right) ^{2}+4 \alpha ^{2}(r+\epsilon ) \mathrm {e}^{\frac{\alpha -1}{\alpha }}-4 \alpha ^{2}}{\alpha ^{2}}},\\ \left| \lambda _{1,2}\right|&=\sqrt{q(\epsilon )}=\sqrt{\frac{(r^{*}+\epsilon )( \alpha -1)\mathrm {e}^{\frac{\alpha -1}{\alpha }} }{\alpha }}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \left. \quad \frac{d\left| \lambda _{1,2}\right| }{d \epsilon } \right| _{\epsilon =0}=\sqrt{\frac{\alpha -1}{4 \alpha r}}e^{(\frac{\alpha -1}{ 2\alpha })}>0, \end{aligned}$$

additionally, we required that when \(\epsilon =0, \lambda _{1,2}^{m} \ne 1, m=1,2,3,4\), which corresponds to \(p(0) \ne -2,0,1,2\), which is true by computation.Let \(u_{n}=x_{n}-x^{*}, v_{n}=y_{n}-y^{*}\) then the equilibrium \(E_{2}\) of the model (5) transforms into O(0, 0).By manipulation, one gets

$$\begin{aligned} \begin{aligned} u_{n+1}&=\left( r^{*}+\epsilon \right) \left( u_{n}+x^{*}\right) \left( e^{1-u_{n}-x^{*}}\right) -\left( u_{n}+x^{*}\right) \left( v_{n}+y^{*} \right) -x^{*}, \\ v_{n+1}&=\alpha \left( u_{n}+x^{*}\right) \left( v_{n}+y^{*}\right) -y^{*}, \end{aligned} \end{aligned}$$
(10)

where \(x^{*}=\frac{1}{\alpha }\), \( y^{*}=r\mathrm {e}^{\frac{\alpha -1}{\alpha }}-1\). Hereafter when \(\epsilon =0\), the normal form of system (10) is studied. Expanding (10) up to third order about \(\left( u_{n}, v_{n}\right) =(0,0)\) by Taylor series, we get

$$\begin{aligned} \left. \begin{array}{l} u_{n+1}=\Lambda _{11} u_{n}+\Lambda _{12} v_{n}+\Lambda _{13} u_{n}^{2}+\Lambda _{14} u_{n} v_{n} + O(|u_{n}|^3), \\ v_{n+1}=\Lambda _{21} u_{n}+\Lambda _{22} v_{n}+\Lambda _{23} u_{n} v_{n}, \end{array} \right\} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{l} \Lambda _{11}=r^{*}e^{1- x^{*}}\left( 1- x^{*}\right) -y^{*}, \quad \Lambda _{12}=-x^{*}, \quad \Lambda _{13}=r^{*}e^{1- x^{*}}\left( \frac{1}{2} x^{*}-1\right) , \quad \Lambda _{14}=-1, \\ \Lambda _{21}=\alpha y^{*}, \quad \Lambda _{22}=\alpha x^{*}, \quad \Lambda _{23}=\alpha . \end{array} \end{aligned}$$

Now, let

$$\begin{aligned} \begin{array}{l} \eta =-\frac{(r^{*}+\epsilon )\mathrm {e}^{\frac{\alpha -1}{\alpha }}-2\alpha }{ 2\alpha }, \\ \zeta =\frac{1}{2}\sqrt{\frac{(r^{*}+\epsilon )\mathrm {e}^\frac{\alpha -1}{ \alpha }\left[ 4 \alpha ^2 - (r^{*}+\epsilon )\mathrm {e}^\frac{\alpha -1}{\alpha } \right] -4 \alpha ^{2}}{\alpha ^{2}}}, \end{array} \end{aligned}$$

and the invertible matrix T defined by

$$\begin{aligned} T=\left( \begin{array}{cc} \Lambda _{12} &{} 0 \\ \eta -\Lambda _{11} &{} -\zeta \end{array} \right) . \end{aligned}$$

Using the following translation:

$$\begin{aligned} \left( \begin{array}{l} u_{n} \\ v_{n} \end{array} \right) =\left( \begin{array}{cc} \Lambda _{12} &{} 0 \\ \eta -\Lambda _{11} &{} -\zeta \end{array} \right) \left( \begin{array}{l} X_{n} \\ Y_{n} \end{array} \right) , \end{aligned}$$

(10) gives

$$\begin{aligned} \left( \begin{array}{l} X_{n+1} \\ Y_{n+1} \end{array} \right) =\left( \begin{array}{cc} \eta &{} -\zeta \\ \zeta &{} \eta \end{array} \right) \left( \begin{array}{l} X_{n} \\ Y_{n} \end{array} \right) +\left( \begin{array}{c} \Phi \left( X_{n}, Y_{n}\right) \\ \Psi \left( X_{n}, Y_{n}\right) \end{array} \right) , \end{aligned}$$
(11)

where

$$\begin{aligned} \begin{aligned} \Phi \left( X_{n}, Y_{n}\right)&=\Pi _{11} X_{n}{ }^{2}+\Pi _{12} X_{n} Y_{n}+\Pi _{13} X_{n}^{3}+O(|X_{n}|^4), \\ \Psi \left( X_{n}, Y_{n}\right)&=\Pi _{21} X_{n}{ }^{2}+\Pi _{22} X_{n} Y_{n}+\Pi _{23} X_{n}^{3}+O(|X_{n}|^4), \end{aligned} \end{aligned}$$
(12)

and

$$\begin{aligned} \begin{array}{l} \Pi _{11}=\Lambda _{12} \Lambda _{13}+\Lambda _{14}\left( \eta -\Lambda _{11}\right) , \\ \Pi _{12}=-\zeta \Lambda _{14}, \\ \Pi _{13}= \Lambda _{14}\Lambda _{12}^{2}, \\ \Pi _{21}=\frac{-\Lambda _{23}}{\zeta }\left[ \Lambda _{12}\left( \Lambda _{13}- \Lambda _{23}\right) +\Lambda _{14}\left( \eta -\Lambda _{11}\right) \right] , \\ \left. \Pi _{22}=\Lambda _{12} \Lambda _{23}-\Lambda _{14}\left( \eta -\Lambda _{11}\right) \right) , \\ \Pi _{23}= \frac{1}{\zeta } \left( (\eta -\Lambda _{11})\Lambda _{14}\Lambda _{12}^{2}\right) . \\ \end{array} \end{aligned}$$

In addition,

$$\begin{aligned} \left. \Phi _{X_{n} X_{n}}\right| _{(0,0)}=2 \Pi _{11},\left. \quad \Phi _{X_{n} Y_{n}}\right| _{(0,0)}=\Pi _{12},\left. \quad \Phi _{Y_{n} Y_{n}}\right| _{(0,0)}=0, \\ \left. \Phi _{X_{n} X_{n} X_{n}}\right| _{(0,0)}=6\Pi _{13},\quad \left. \Phi _{X_{n} X_{n} Y_{n}}\right| _{(0,0)}=\left. \Phi _{X_{n} Y_{n} Y_{n}}\right| _{(0,0)}=\left. \Phi _{Y_{n} Y_{n} Y_{n}}\right| _{(0,0)}=0, \end{aligned}$$

and

$$\begin{aligned} \begin{array}{l} \left. \Psi _{X_{n} X_{n}}\right| _{(0,0)}=2 \Pi _{21},\left. \quad \Psi _{X_{n} Y_{n}}\right| _{(0,0)}=\Pi _{22},\left. \quad \Psi _{Y_{n} Y_{n}}\right| _{(0,0)}=0, \\ \left. \Psi _{X_{n} X_{n} X_{n}}\right| _{(0,0)}=6 \Pi _{23},\quad \left. \Psi _{X_{n} X_{n} Y_{n}}\right| _{(0,0)}=\left. \Psi _{X_{n} Y_{n} Y_{n}}\right| _{(0,0)}=\left. \Psi _{Y_{n} Y_{n} Y_{n}}\right| _{(0,0)}=0 . \end{array} \end{aligned}$$

In order for (11) to undergo a Neimark–Sacker bifurcation, it is mandatory that the following discriminatory quantity, i.e., \(\chi \ne 0\) (see [38, 40, 41]),

$$\begin{aligned} \chi =-{Re}\left[ \frac{(1-2 {\bar{\lambda }}) {\bar{\lambda }}^{2}}{1-\lambda } \tau _{11} \tau _{20}\right] -\frac{1}{2}\left\| \tau _{11}\right\| ^{2}-\left\| \tau _{02}\right\| ^{2}+{Re}\left( {\bar{\lambda }} \tau _{21}\right) , \end{aligned}$$

where

$$\begin{aligned} \begin{array}{l} \tau _{02}=\left. \frac{1}{8}\left[ \Phi _{X_{n} X_{n}}-\Phi _{Y_{n} Y_{n}}+2 \Psi _{X_{n} Y_{n}}+\iota \left( \Psi _{X_{n} X_{n}}-\Psi _{Y_{n} Y_{n}}+2 \Phi _{X_{n} Y_{n}}\right) \right] \right| _{(0,0)}, \\ \tau _{11}=\left. \frac{1}{4}\left[ \Phi _{X_{n} X_{n}}+\Phi _{Y_{n} Y_{n}}+\iota \left( \Psi _{X_{n} X_{n}}+\Psi _{Y_{n} Y_{n}}\right) \right] \right| _{(0,0)}, \\ \tau _{20}=\left. \frac{1}{8}\left[ \Phi _{X_{n} X_{n}}-\Phi _{Y_{n} Y_{n}}+2 \Psi _{X_{n} Y_{n}}+\iota \left( \Psi _{X_{n} X_{n}}-\Psi _{Y_{n} Y_{n}}-2 \Phi _{X_{n} Y_{n}}\right) \right] \right| _{(0,0)}, \\ \tau _{21}=\frac{1}{16}\left[ \Phi _{X_{n} X_{n} X_{n}}+\Phi _{X_{n} Y_{n} Y_{n}}+\Psi _{X_{n} X_{n} Y_{n}}+\Psi _{Y_{n} Y_{n} Y_{n}}\right. \\ \left. \qquad \qquad +\iota \left( \Psi _{X_{n} X_{n} X_{n}}+\Psi _{X_{n} Y_{n} Y_{n}}-\Phi _{X_{n} X_{n} Y_{n}}-\Phi _{Y_{n} Y_{n} Y_{n}}\right) \right] \left. \right| _{(0,0)}, \end{array} \end{aligned}$$

after calculating, we get

$$\begin{aligned} \begin{array}{l} \tau _{02}=\frac{1}{4}\left[ \Pi _{11}+\Pi _{22}+\iota \left( \Pi _{21}+\Pi _{12} \right) \right] , \\ \tau _{11}=\frac{1}{2}\left[ \Pi _{11}+\iota \Pi _{21}\right] , \\ \tau _{20}=\frac{1}{4}\left[ \Pi _{11}+\Pi _{22}+\iota \left( \Pi _{21}-\Pi _{12} \right) \right] , \\ \tau _{21}=\frac{3}{8}\left[ \Pi _{13}+\iota \left( \Pi _{23}\right) \right] . \end{array} \end{aligned}$$

Based on this analysis and the Neimark–Sacker bifurcation Proposition discussed in [38, 42,43,44,45], we arrive at the following Proposition.

Proposition 6

If \(\chi \ne 0\) then the model (5) undergoes a Neimark–Sacker bifurcation about \(E_{2}\) as \(\left( r, \alpha \right) \) go through \(N_{E_{2}} .\) Additionally, an attracting (resp. repelling) closed curve bifurcates from \(E_{2}\) if \(\chi <0(\) resp. \(\chi >0)\).

Remark

According to bifurcation theory discussed in [43], the bifurcation is called a supercritical Neimark–Sacker bifurcation if the discriminatory quantity \(\chi <0 .\) In the following section, numerical simulations guarantee that a supercritical Neimark–Sacker bifurcation occurs for the model (5).

4.2 Period-doubling bifurcation

Here we study the period-doubling bifurcation of model (5) at \(E_{2}\) when parameters vary in a small neighborhood of \( P_{E_{2}}\). Select arbitrary parameters \(\left( r^{*},\alpha \right) \) from \( P_{E_{2}}\). We consider the parameter \(r^{*}\) as a new dependent variable, and we can get

$$\begin{aligned} \begin{aligned} x_{n+1}&=\left( r+r^{*}\right) x_{n}\left( e^{1-x_{n}}\right) -x_{n} y_{n}, \\ y_{n+1}&=\alpha x_{n} y_{n}, \end{aligned} \end{aligned}$$
(13)

let \(u_{n}=x_{n}-x^{*}\), \(v_{n}=y_{n}-y^{*}\) then the equilibrium \(E_{2}\) of the discrete-time model (13) transforms into O(0, 0). By calculating we get

$$\begin{aligned} \left. \begin{array}{l} u_{n+1}=\widehat{\Lambda _{11}} u_{n}+\widehat{\Lambda _{12}} v_{n}+\widehat{ \Lambda _{13}} u_{n}^{2}+\widehat{\Lambda _{14}} u_{n} v_{n}+\Upsilon _{01} u_{n} r^{*}+\Upsilon _{02} u_{n}^{2} r^{*}+O\left( \left| u_{n}\right| ,\left| r^{*}\right| \right) ^{4}, \\ v_{n+1}=\widehat{\Lambda _{21}} u_{n}+\widehat{\Lambda _{22}} v_{n}+\widehat{ \Lambda _{23}} u_{n} v_{n}, \end{array} \right\} \nonumber \\ \end{aligned}$$
(14)

where

$$\begin{aligned} \begin{aligned}&\widehat{\Lambda _{11}}=r(1-x^{*})e^{1-x^{*}}-y^{*}, \quad \widehat{\Lambda _{12}}=-x^{*}, \quad \widehat{\Lambda _{13}}=\frac{r(x-2)e^{1-x}}{2}, \quad \widehat{\Lambda _{14}}=-1, \\&\Upsilon _{01}=(1-x)e^{1-x}, \quad \Upsilon _{02}=\frac{(x-2)e^{1-x}}{2}, \\&\widehat{\Lambda _{21}}=\alpha y^{*}, \quad \widehat{\Lambda _{22}}=\alpha x^{*}, \quad \widehat{\Lambda _{23}}=\alpha . \end{aligned} \end{aligned}$$

Now, construct an invertible matrix T

$$\begin{aligned} T=\left( \begin{array}{cc} \widehat{\Lambda _{12}} &{} \widehat{\Lambda _{12}} \\ -1-\widehat{\Lambda _{11}} &{} \lambda _{2}-\widehat{\Lambda _{11}} \end{array} \right) , \end{aligned}$$

and use the translation

$$\begin{aligned} \left( \begin{array}{c} u_{n} \\ v_{n} \end{array} \right) =\left( \begin{array}{cc} \widehat{\Lambda _{12}} &{} \widehat{\Lambda _{12}} \\ -1-\widehat{\Lambda _{11}} &{} \lambda _{2}-\widehat{\Lambda _{11}} \end{array} \right) \left( \begin{array}{c} X_{n} \\ Y_{n} \end{array} \right) , \end{aligned}$$

(14) gives

$$\begin{aligned} \left( \begin{array}{c} X_{n+1} \\ Y_{n+1} \end{array} \right) =\left( \begin{array}{cc} -1 &{} 0 \\ 0 &{} \lambda _{2} \end{array} \right) \left( \begin{array}{l} X_{n} \\ Y_{n} \end{array} \right) +\left( \begin{array}{l} {\widehat{\Phi }}\left( u_{n}, v_{n}, r^{*}\right) \\ {\widehat{\Psi }}\left( u_{n}, v_{n}, r^{*}\right) \end{array} \right) , \end{aligned}$$
(15)

where

$$\begin{aligned} {\widehat{\Phi }}(u_{n}, v_{n}, r^{*})= & {} \frac{\widehat{\Lambda _{13}}(\lambda _{2}-\widehat{\Lambda _{11}} )}{{\widehat{\Lambda _{12}}(1+\lambda _{2})}} u_{n}^{2}+\frac{\widehat{\Lambda _{14}}(\lambda _{2}-\widehat{ \Lambda _{11}})-\widehat{\Lambda _{12}} \widehat{\Lambda _{23}}}{\widehat{\Lambda _{12}}(1+\lambda _{2})} u_{n} v_{n} \\&+\frac{\Upsilon _{01}(\lambda _{2}-\widehat{\Lambda _{11}})}{ \widehat{\Lambda _{12}}(1+\lambda _{2})} u_{n} r^{*}+\frac{\Upsilon _{02}(\lambda _{2}-\widehat{\Lambda _{11}})}{ \widehat{\Lambda _{12}}(1+\lambda _{2})} u_{n}^{2} r^{*} +O(|u_{n}|,|r^{*}|)^{4}, \\ {\widehat{\Psi }}(u_{n}, v_{n}, r^{*})= & {} \frac{\widehat{\Lambda _{13}}(1+\widehat{\Lambda _{11}})}{\widehat{ \Lambda _{12}}(1+\lambda _{2})} u_{n}^{2}+\frac{\widehat{\Lambda _{14}}(1+\widehat{\Lambda _{11}})+ \widehat{\Lambda _{12}} \widehat{\Lambda _{23}}}{\widehat{\Lambda _{12}}(1+\lambda _{2})} u_{n} v_{n} \\&+\frac{\Upsilon _{01}(1+\widehat{\Lambda _{11}})}{\widehat{ \Lambda _{12}}(1+\lambda _{2})} u_{n} r^{*} +\frac{\Upsilon _{02}(1+\widehat{\Lambda _{11}})}{\widehat{ \Lambda _{12}}(1+\lambda _{2})} u_{n}^{2} r^{*}, \\ u_{n}^{2}= & {} \widehat{\Lambda _{12}}^{2}\left( X_{n}^{2}+2 X_{n} Y_{n}+Y_{n}^{2}\right) , \\ u_{n}v_{n}= & {} -\widehat{\Lambda _{12}}(1+\widehat{\Lambda _{11}}) X_{n}^{2}\\&\quad +\left( \widehat{\Lambda _{12}}(\lambda _{2}-\widehat{ \Lambda _{11}})-\widehat{\Lambda _{12}}(1+\widehat{\Lambda _{11}}) \right) X_{n} Y_{n} +\widehat{\Lambda _{12}}\left( \lambda _{2}-\widehat{\Lambda _{11}}\right) Y_{n}^{2}, \\ u_{n} r^{*}= & {} \widehat{\Lambda _{12}} X_{n} r^{*}+\widehat{\Lambda _{12}} Y_{n} r^{*}, \\ u_{n}^{2} r^{*}= & {} \widehat{\Lambda _{12}}^{2}\left( X_{n}^{2} r^{*}+2 X_{n} Y_{n} r^{*}+Y_{n}^{2} r^{*}\right) , \end{aligned}$$

hereafter we determine the center manifold \(W^{c}(0,0)\) of (15) about (0, 0) in a small neighborhood of \(r^{*}\) [6, 38, 43, 46]. By center manifold theorem, there exists a center manifold \(W^{c}(0,0)\) that can be represented as follows:

$$\begin{aligned} W^{c}(0,0)=\left\{ \left( X_{n}, Y_{n}\right) : Y_{n}=c_{0} r^{*}+c_{1} X_{n}^{2}+c_{2} X_{n} r^{*}+c_{3} (r^{*})^{ 2}+O\left( \left( \left| X_{n}\right| ,\left| r^{*}\right| \right) ^{3}\right) \right\} , \end{aligned}$$

where \(O\left( \left( \left| X_{n}\right| +\left| r^{*}\right| \right) ^{3}\right) \) is a function with order at least three in their variables \(\left( X_{n}, r^{*}\right) \), and

$$\begin{aligned} \begin{aligned}&c_{0}=0, \\&c_{1}=\frac{-\widehat{\Lambda _{23}} \widehat{\Lambda _{12}}^2+(1+\widehat{\Lambda _{11}})\left( \widehat{\Lambda _{14}}(1+\widehat{\Lambda _{11}})-\widehat{ \Lambda _{12}} (\widehat{\Lambda _{13}}-\widehat{\Lambda _{24}})\right) }{\lambda _{2}^{2}-1}, \\&c_{2}=-\frac{\Upsilon _{01}(1+\widehat{\Lambda _{11}})}{(1+ \lambda _{2})^{2}}, \\&c_{3}=0. \end{aligned} \end{aligned}$$

Therefore, we consider the map (15) restricted to \(W^{c}(0,0)\) as follows:

$$\begin{aligned} f\left( X_{n}\right) =-X_{n}+h_{1} X_{n}^{2}+h_{2} X_{n} r^{*}+h_{3} X_{n}^{2} r^{*}+h_{4} X_{n} (r^{*})^{2}+h_{5} X_{n}^{3}+O\left( \left( \left| X_{n}\right| ,\left| r^{*}\right| \right) ^{4} \right) , \end{aligned}$$
(16)

where

$$\begin{aligned} \begin{aligned} h_{1}=&\frac{1}{1+\lambda _{2}}\left[ \widehat{\Lambda _{11}}^{2}\widehat{ \Lambda _{14}}+\left( (\widehat{\Lambda _{23}}-\widehat{\Lambda _{13}}) \widehat{\Lambda _{12}}-\widehat{\Lambda _{14}}\left( \lambda _{2}-1\right) \right) \widehat{\Lambda _{11}}+(\lambda _{2}\widehat{\Lambda _{13}}+\widehat{ \Lambda _{23}}) \widehat{\Lambda _{12}}-\lambda _{2} \widehat{\Lambda _{14}}\right] , \\ h_{2}=&\frac{1}{1+\lambda _{2}}\left[ \Upsilon _{01}(\lambda _{2}-\widehat{ \Lambda _{11}})\right] , \\ h_{3}=&\frac{\widehat{\Lambda _{11}}^{2} \widehat{\Lambda _{14}}+\big ((\widehat{\Lambda _{23}}-\widehat{ \Lambda _{13}}) \widehat{\Lambda _{12}}-2 \lambda _{2} \widehat{\Lambda _{14}}\big )\widehat{\Lambda _{11}}+(\lambda _{2} \widehat{\Lambda _{13}}+\widehat{\Lambda _{23}}) \widehat{\Lambda _{12}}+\lambda _{2}^{2} \widehat{\Lambda _{14}}\big )(1+\widehat{\Lambda _{11}}) \Upsilon _{01}}{\left( \lambda _{2}-1\right) \left( \lambda _{2}+1\right) ^{2}} \\&+\frac{\Upsilon _{02} \widehat{\Lambda _{12}}\left( \lambda _{2}-1\right) \left( \lambda _{2}+1\right) (\lambda _{2}-\widehat{\Lambda _{11}})}{\left( \lambda _{2}-1\right) \left( \lambda _{2}+1\right) ^{2}},\\ h_{4}=&\frac{\Upsilon _{01}^{2} (\lambda _{2}-\widehat{\Lambda _{11}})(1+\widehat{ \Lambda _{11}})}{\left( \lambda _{2}^{2}-1\right) \left( \lambda _{2}+1 \right) },\\ h_{5}=&\frac{\Big (\widehat{\Lambda _{14}}\widehat{\Lambda _{11}}+(\widehat{\Lambda _{23}}-\widehat{\Lambda _{13}}) \widehat{\Lambda _{12}}+\widehat{\Lambda _{14}}\Big )(1+\widehat{ \Lambda _{11}})}{\Big (\lambda _{2}-1\Big )\Big (\lambda _{2}+1\Big )^{2}}\Big [ 2 \widehat{\Lambda _{11}}^{2} \widehat{\Lambda _{14}}+\Big (2( \widehat{\Lambda _{23}}- \widehat{\Lambda _{13}}) \widehat{\Lambda _{12}}+(1-3\lambda _{2})\widehat{\Lambda _{14}}\Big ) \widehat{\Lambda _{11}}\\&+\Big ((2 \widehat{\Lambda _{13}}-\widehat{\Lambda _{23}}) \lambda _{2}+\widehat{\Lambda _{23}}\Big ) \widehat{\Lambda _{12}}+\lambda _{2}\widehat{\Lambda _{14}}(\lambda _{2}-1 )\Big ], \end{aligned} \end{aligned}$$

in order for the map (16) to undergo a period-doubling bifurcation, we require that the following discriminatory quantities are non-zero:

$$\begin{aligned} \begin{aligned}&\Lambda _{1}=\left. \left( \frac{\partial ^{2} f}{\partial X_{n} \partial r^{*}}+\frac{1}{2} \frac{\partial f}{\partial r^{*}} \frac{\partial ^{2} f}{\partial X_{n}^{2}}\right) \right| _{(0,0)}, \\&\Lambda _{2}=\left. \left( \frac{1}{6} \frac{\partial ^{3} f}{\partial X_{n}^{3}}+\left( \frac{1}{2} \frac{\partial ^{2} f}{\partial X_{n}^{2}}\right) ^{2}\right) \right| _{(0,0)}, \end{aligned} \end{aligned}$$

after calculating we obtain

$$\begin{aligned} \Lambda _{1}=h_{2}+\frac{1}{2}h_{3}, \end{aligned}$$

and

$$\begin{aligned} \Lambda _{2}=h_{5}+h_{1}^{2}, \end{aligned}$$

from the above analysis in [37] and theorem in [38, 42,43,44,45] ,we have the following Proposition

Proposition 7

If \(\Lambda _{2} \ne 0\), the map (13) undergoes a period-doubling bifurcation about the unique positive equilibrium \(E_{2}\) when \(r^{*}\) varies in a small neighborhood of O(0, 0) . Moreover, if \( \Lambda _{2}>0\left( \right. \) resp \(\left. . \Lambda _{2}<0\right) \), then the period-2 points that bifurcate from \(E_{2}\) are stable (resp. unstable).

5 Numerical simulations

We use numerical simulations to create bifurcation diagrams and the phase portraits of model (5) to support the previous theoretical analysis and highlight new complicated dynamical behaviors. We will use the MATCONTM package [43, 47] to carry out the numerical continuation of equilibria in order to obtain bifurcation curves of system (5) for different sets of parameters and locate points of interest. The bifurcation parameters are considered in the following four cases.

Fig. 2
figure 2

Phase portrait of equilibrium point \(E_{0}\) and its bifurcating to \(E_{1}\)

Full size image

Case 1 Choosing \(r=0.2, \alpha =1\), with initial value \(\left( x_{0}, y_{0}\right) =(0.1,0.1)\), We see that model (5) has stable equilibrium point \(E_{0}(0,0)\), there are no prey or predator in the area. Figure 2 shows the correctness of discussion about equilibrium \(E_{0}=(0,0)\) in Sect. 3. From Fig. 2d we see that equilibrium \(E_{0}=(0,0)\) loses its stability and bifurcates to \(E_{1}\) when \(r = \mathrm {e}^{-1}\). The MATCONTM report is

$$\begin{aligned} label =\mathrm {BP}, \mathrm {x}=\left( \begin{array}{lll}0.000000&0.000000&0.367879\end{array}\right) . \end{aligned}$$

Case 2 Choosing \(r=1, \alpha =0.4\), with initial value \(\left( x_{0}, y_{0}\right) =(0.5,0.2)\), model (5) has stable equilibrium point \(E_{1}(1,0)\). It can be observed from Fig. 3a that the prey density x is fixed at 1 but the predator population y quickly reduces to zero. In stability region of \(E_{1}\) with r free, we can see that \(E_{1}\) is stable when \(\mathrm {e}^{-1}<r<\mathrm {e}\). It loses its stability via a supercritical period doubling point (PD) when \(r=\mathrm {e}\), and via a branch point when \(r=\mathrm {e}^{-1}\) (see Fig. 3b). Figure 3 demonstrates the correctness of discussion about equilibrium \(E_{1}\left( 1+\ln {r},0\right) \) in Sect. 3. The MATCONTM report is

$$\begin{aligned} \begin{aligned}&label =\mathrm {BP}, \mathrm {x}=\left( \begin{array}{lll}0.000000&0.000000&0.367879\end{array}\right) ,\\&label =\mathrm {PD}, \mathrm {x}=\left( \begin{array}{lll} 2.000000&0.000000&2.718281\end{array}\right) ,\\&\text {Normal form coefficient of PD }=1.666667 e-01.\\ \end{aligned} \end{aligned}$$
Fig. 3
figure 3

Phase portraits of equilibrium point \(E_{1}\) and its bifurcation curve

Full size image

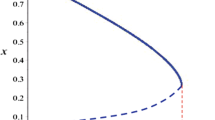
Case 3 Varying \(\alpha \) in range \(1.2 \le \alpha \le 1.54\) and fixing \( r=2.1\). When \(1.2 \le \alpha < 1.513333\) model (5) has a unique positive stable equilibrium point. By calculating, we see that this unique equilibrium point is (0.7142857143, 1.794495614) for \(\left( \alpha , r\right) =(1.4,2.1)\). The corresponding phase portraits for various values of \(\alpha \) in this range are shown in Fig. 4. Neimark–Sacker bifurcation occurs at \(\alpha =1.513333\), as shown in Fig. 5f, with \(\sqrt{\frac{\alpha -1}{4 \alpha r}}e^{(\frac{\alpha -1}{2\alpha } )}=0.2380951456>0\) hold. Moreover, for \(\alpha =1.513333\) the eigenvalues of \( J_{E_{2}}\) about \(E_{2}\) are

$$\begin{aligned} \lambda _{1,2}= 0.02597415076\pm 0.999662226\iota , \end{aligned}$$
(17)

after some calculations from Maple one gets

$$\begin{aligned} \begin{array}{l} \tau _{02}=0.0761055464 + 0.5739851115\iota , \\ \tau _{11}=0.1651982395 + 0.6481391100\iota , \\ \tau _{20}=0.0380527732 + 0.03707699925\iota , \\ \tau _{21}=-0.1637427475 - 0.1595435351\iota , \end{array} \end{aligned}$$
(18)

in view of (17) and (18) the value of the discriminatory quantity is \(\chi =-0.4373638855<0\). Therefore if \(\alpha =1.52>1.51333\) the model (5) undergoes a supercritical Neimark–Sacker bifurcation and a stable invariant close curve appears, which is presented in Fig. 5. The MATCONTM report is

$$\begin{aligned} \begin{aligned}&label =\mathrm {BP}, \mathrm {x}=\left( \begin{array}{lll}1.7419370&.000000&0.574073\end{array}\right) ,\\&label =\mathrm {NS}, \mathrm {x}= \left( \begin{array}{lll}0.6607931&1.9480521&1.513333\end{array}\right) ,\\&\text {normal form coefficient of } \mathrm {NS}=-6.713373 \mathrm {e}-01. \end{aligned} \end{aligned}$$
(19)
Fig. 4
figure 4

Phase portraits for various values of \(\alpha \) from 1.2 to 1.51

Full size image
Fig. 5
figure 5

Phase portraits for various values of \(\alpha \) from 1.5142 to 1.54

Full size image
Fig. 6
figure 6

Phase portraits for various values of r from 2.3 to 3.89

Full size image

The numerical solution in Figs. 4 and 5 reveals that the stable fixed point \(E_{2}\) becomes unstable, allowing preys and predators to coexist by a persistent positive periodic oscillation as time passes.Case 4 Varying r in range \(2.3 \le r \le 3.89\) and fixing \(\alpha =0.63\). Figure 6 shows that prey and predator densities are fixed at the stable equilibrium point \(E_{2}\) for \(r<2.482007420\), and \(E_{2}\) loses its stability when \(r=2.482007420\). Further, when \(r>2.482007420\), the numbers of prey and predator oscillate in a stable period-2 orbit then period 4-orbit and so on, that is a period-doubling bifurcation. Moreover, a chaotic set is emerged with the increasing of r.

6 Conclusion

The dynamical behaviors of model (5) is discussed in this study. Model (5) contains two boundary equilibria, \(E_{0}, E_{1}\), and a positive equilibria \(E_{2}\) when \(r>max\{\mathrm {e}^{-1}, \mathrm {e}^{\frac{1-\alpha }{\alpha }}\}\). We explored local stability along topological types about \(E_{0}\), \(E_{1}\) and \( E_{2}\) by using the linearization method. From the discussion in Sect. 4.2, we know there is period-doubling bifurcation and chaos near equilibria \(E_{2}\) as the parameter r varies in the small neighbourhood of \(r=2.5\). Moreover, if \( \alpha \) varies in the small neighborhood when \((a, r) \in N_{E_{2}}\), there exists Neimark–Sacker bifurcation.Numerical simulations have shown not only the correctness of the theoretical results but also the complexity of the behavior of the model (5) such as the period-2, -4, and -8 orbits. Comparing with the discrete-time model (4) in [37] where the author used the logistic growth \(rX_{n}(1-X_{n})\) in the first equation of the model. This logistic map has the unrealistic fact that the parabola drops below the horizontal axis as we move off to the right. A more reasonable choice would be the Ricker map \(r X_{n}\left( e^{1-X_{n}}\right) \) which produces very small, but still positive, values as \(X_{n}\) becomes very large [2]. The global qualitative analysis of model(5) has not been obtained yet, we will leave it for our future work.