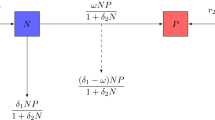
Abstract
In this paper, the dynamical behaviors of a discrete-time prey–predator model with Allee effect on the prey population are investigated. The existence and topological classification of the fixed points of the model are analyzed. It is shown that the model can undergo a Neimark–Sacker bifurcation at the unique positive fixed point by choosing a as a bifurcation parameter. The conditions of the existence for Neimark–Sacker bifurcation and the direction of bifurcation via bifurcation theory are presented. Also, some numerical simulations are presented to support of the analytical finding. Then bifurcation diagrams and phase portraits of the model are given.
Similar content being viewed by others
1 Introduction
The predator–prey models have a theoretical and practical significance. So many authors have studied the dynamics of these models. The Lotka–Volterra model is the first and the simplest model of predator–prey interactions. The model was developed independently by Lotka [1] and Volterra [2]. The Lotka–Volterra model assumes that the prey consumption rate by a predator is directly proportional to the prey abundance. This means that predator feeding is limited only by the amount of prey in the environment. While this may be realistic at low prey densities, it is certainly an unrealistic assumption at high prey densities where predators are limited, for example, by time and digestive constraints. So a number of changes in the model have been presented by researchers to include Holling type functional responses and density-dependent prey growth. Another way of modification of the Lotka–Volterra model can be considered by introducing the Allee effect. It is well known that the introduction of the Allee effect into the system is more realistic in modeling the prey–predator interaction.
The Allee effect is a crucial phenomenon that has drawn considerable attention from both theoretical and applied ecologists [3,4,5,6,7,8,9]. The Allee effect was first described by Allee in 1931 [10]. It describes a positive correlation between any measure of species fitness and population numbers. The main causes of the Allee effect are the difficulty in finding mates, inbreeding depression, social dysfunction at small population sizes, predator avoidance and food exploitation [11,12,13,14]. Empirical evidence of the Allee effect has been observed in many natural species, for example, plants [15], insects [16], marine invertebrates [17], birds and mammals [18]. Recent studies have shown that the Allee effect has important dynamical effects on the stability analysis of population models. The system with Allee effect shows either destabilization [11] or stabilization [19]. The local stability of a positive fixed point may be changed from stable to unstable or vice versa. In prey–predator systems, Allee effect may change the dynamics of the system in unexpected ways and induce complex dynamics. So, many authors have investigated the stabilizing or destabilizing effects on the predator–prey models with the Allee effect. But the bifurcation analysis of these systems with the Allee effect has been rarely performed. So, in this paper, a predator–prey system on which is imposed an Allee effect is considered.
In [20], the author has considered the following discrete-time predator–prey model which was proposed by Smith et al. [21]:
where \(X_{t}\) and \(Y_{t}\) denotes the numbers of prey and predator respectively. The parameters α, β are positive real numbers. They have studied stability and Neimark–Sacker bifurcation of a discrete-time predator–prey model. The analysis of bifurcations has already received much attention during the last few years [20, 22,23,24,25,26,27,28,29]. Bifurcation and stability analysis are examined in detail in [20, 22,23,24, 30,31,32,33,34,35,36,37,38,39,40,41].
In this paper, modification of the model (1) is considered by introducing the Allee effect for the prey population as follows:
where \(\frac{X}{m+X}\) is term for the Allee effect. \(m>0\) can be defined as Allee effect constant [11,12,13]. α and β are the growth rates of the prey and predator, respectively.
The aim of this paper is to investigate the dynamics of a modified a discrete-time predator–prey model with Allee effect on prey population by using bifurcation theory. The rest of the paper is organized as follows: In Sect. 2, the existence conditions and stability of the fixed points are discussed. In Sect. 3, choosing a parameter as bifurcation parameter, Neimark–Sacker bifurcation analysis is studied. Furthermore, by using normal form theory direction of Neimark–Sacker bifurcation is obtained. Finally, these theoretical results are supported by some numerical simulations.
2 The fixed points: existence and stability
In this section, we will study the existence of the fixed points of the discrete system with Allee effect and analyze the stability of these fixed points. To find the fixed points of the system (2), we can write
in the model (2)
It is clear that the fixed points of the model (2) satisfy Eq. (4).
Lemma 1
-
(i)
The system (2) always has an axial fixed point \(E_{1}= ( 0,0 ) \).
-
(ii)
The system (2) has an axial fixed point \(E_{2}= ( \frac{a-1}{a},0 ) \) if \(a>1\).
-
(iii)
The system (2) has a unique positive fixed point \(E _{\ast }= ( \beta ,\frac{(\beta +m)(a(1-\beta )-1)}{\beta } ) \) if \(a>\frac{1}{1-\beta }\) and \(\beta <1\).
In order to analyze the stability of the fixed points of the model (2), we give Definition 1 and Lemma 2 as follows:
Definition 1
A fixed point \((N,P)\) is called
-
(i)
sink if \(\vert \lambda _{1} \vert <1\) and \(\vert \lambda _{2} \vert <1\), and it is locally asymptotically stable,
-
(ii)
source if \(\vert \lambda _{1} \vert >1\) and \(\vert \lambda _{2} \vert >1\), and it is locally unstable,
-
(iii)
saddle if \(\vert \lambda _{1} \vert <1\) and \(\vert \lambda _{2} \vert >1\) or (\(\vert \lambda _{1} \vert >1\) and \(\vert \lambda _{2} \vert <1\)),
-
(iv)
non-hyperbolic if either \(\vert \lambda _{1} \vert =1\) or \(\vert \lambda _{2} \vert =1\).
To investigate the stability of the one nontrivial fixed point of the system (2), we give Lemma 2.
Lemma 2
Assume \(F(\lambda )=\lambda ^{2}+B\lambda +C\), where B and C are two real constants and let \(F(1)>0\). Suppose \(\lambda _{1}\) and \(\lambda _{2}\) are two roots of \(F ( \lambda ) =0\). Then the following statements hold.
-
(i)
\(\vert \lambda _{1} \vert <1\) and \(\vert \lambda _{2} \vert <1\) if and only if \(F(-1)>0\) and \(C<1\);
-
(ii)
\(\vert \lambda _{1} \vert >1\) and \(\vert \lambda _{2} \vert >1\) if and only if \(F(-1)>0\) and \(C>1\);
-
(iii)
\(\vert \lambda _{1} \vert <1\) and \(\vert \lambda _{2} \vert >1\), or \(\vert \lambda _{1} \vert >1\) and \(\vert \lambda _{2} \vert <1\), if and only if \(F(-1)<0\);
-
(iv)
\(\lambda _{1}\) and \(\lambda _{2}\) are a pair of conjugate complex roots and \(\vert \lambda _{1} \vert = \vert \lambda _{2} \vert =1\) if and only if \(B ^{2}-4C<0\) and \(C=1\);
-
(v)
\(\lambda _{1}=-1\) and \(\vert \lambda _{2} \vert \neq 1\) if and only if \(F(-1)=0\) and \(B\neq 0,2\).
Now we will discuss the topological classification of the fixed points of the model (2) and we will apply Lemma 2 to prove the following lemmas.
The Jacobian matrix of the planar map in (2) evaluated at any point \((x,y)\) is given by
and we have
Lemma 3
For the fixed point \(E_{1}(0,0)\), following topological classification holds:
-
(i.1)
\(E_{1}(0,0)\) is a sink if \(a<1\).
-
(i.2)
\(E_{1}(0,0)\) is a saddle if \(a>1\).
-
(i.3)
\(E_{1}(0,0)\) is a non-hyperbolic if \(a=1\).
Lemma 4
Assume that \(a>1\). For the fixed point \(E_{2}= ( \frac{a-1}{a},0 ) \), the following topological classification holds:
-
(ii.1)
\(E_{2}= ( \frac{a-1}{a},0 ) \) is a sink if \(1< a<\min \{\frac{1}{1-\beta },3\}\) and \(0<\beta <1\),
-
(ii.2)
\(E_{2}= ( \frac{a-1}{a},0 ) \) is a saddle if (\(\frac{1}{1-\beta }< a<3\) and \(0<\beta < \frac{2}{3}\)) or (\(3< a<\frac{1}{1-\beta }\) and \(\frac{2}{3}<\beta <1\)),
-
(ii.3)
\(E_{2}= ( \frac{a-1}{a},0 ) \) is a source if \(a>\max \{3,\frac{1}{1-\beta }\}\), \(0<\beta <1\),
-
(ii.4)
\(E_{2}= ( \frac{a-1}{a},0 ) \) is a non-hyperbolic if \(a=3\) or (\(a=\frac{1}{1-\beta }\), \(0< \beta <1\)).
The characteristic equation of matrix \(J(E_{\ast })\) can be written as follows:
From Lemma 2, we have
Since \(a>\frac{1}{1-\beta }\), \(F(1)>0\).
Lemma 5
Assume that \(a>\frac{1}{1-\beta }\) and \(\beta <1\) then for the unique positive fixed point \(E_{\ast }\) of the system (2) the following holds true.
-
(iii1)
\(E_{\ast }\) is sink fixed point if the following condition holds:
$$\begin{aligned}& \frac{1}{1-\beta }< a< \min \biggl\{ \frac{1}{1-2\beta -m} ,\frac{3\beta +5m}{3\beta ^{2}+\beta m+m-\beta }\biggr\} , \end{aligned}$$ -
(iii2)
\(E_{\ast }\) is source fixed point if the following condition holds:
$$\begin{aligned}& \frac{1}{1-2\beta -m}< a< \frac{3\beta +5m}{3\beta ^{2}+ \beta m+m-\beta }, \end{aligned}$$ -
(iii3)
\(E_{\ast }\) is saddle fixed point if the following condition holds:
$$\begin{aligned}& a>\frac{1}{1-2\beta -m}, \end{aligned}$$ -
(iii4)
non-hyperbolic fixed point if the following conditions hold:
$$\begin{aligned}& a=\frac{3\beta +5m}{3\beta ^{2}+\beta m+m-\beta }\quad \textit{and} \quad m \neq \frac{4}{5}- \frac{9}{5}\beta , \end{aligned}$$ -
(iii5)
the roots of Eq. (7) are complex with modules one if and only if
$$\begin{aligned}& a=\frac{1}{1-2\beta -m}\quad \textit{and} \quad m< \frac{4}{5}- \frac{9}{5} \beta . \end{aligned}$$
Example 1
For the parameter values \(a=2.5\), \(m=0.25\), \(\beta =0.23\) and initial condition \(( x_{0},y_{0} ) =(0.15,2.5)\), the positive fixed point of the model (2) is obtained: \(( x ^{\ast },y^{\ast } ) =(0.23,1.930434783)\). Figure 1 is shown that the fixed point \(( x^{\ast },y^{\ast } ) \) of the model (2) is local asymptotically stable where blue and red graphs represent \(x(t)\) and \(y(t)\) population, respectively.
A stable fixed point for the system (2) for \(a=2.5\), \(m=0.25\), \(\beta =0.23\) and initial condition \(( x_{0},y_{0} ) =(0.15,2.5)\)
3 Bifurcation analysis
3.1 Neimark–Sacker bifurcation at the point \(E_{\ast }\)
In this section we investigate the conditions for existence of the Neimark–Sacker bifurcation for unique positive fixed point \(E_{\ast }= ( \beta ,\frac{(\beta +m)(a(1-\beta )-1)}{\beta } ) \) of the model (2). Also, direction of Neimark–Sacker bifurcation is evaluated. We will take a as bifurcation parameter.
Let us consider the term of \(\varOmega _{NSB_{E^{\ast }}}\) as follows:
When the parameters change in small neighborhood of \(\varOmega _{NSB_{E^{\ast }}}\), two eigenvalues of \(J ( E^{\ast } ) \) are complex having magnitude one and Neimark–Sacker bifurcation can go out from the fixed point \(E^{\ast }\). The eigenvalues of Eq. (2) under these conditions are given by
It is easy to see that
From the transversality condition, we get
Moreover, the nonresonance condition \(B=-trJ_{E^{\ast }} ( a _{NS} ) \neq 0,1\) leads to
then we have
Assume that \(q,p\in \mathbb{C} ^{2}\) are two eigenvectors of \(J ( \varOmega _{NSB_{E^{\ast }}} ) \) and transposed matrix \(J^{T} ( \varOmega _{NSB_{E^{\ast }}} ) \) corresponding to λ and λ̅, respectively. We have
and
To achieve the normalization \(\langle p,q\rangle =1\), where \(\langle\, ,\,\rangle \) means the standard scalar product in \(C^{2}\), we can take the normalized vectors as
where \(S_{1}= ( -\frac{-5m-9\beta +4+\sqrt{4-5m-9\beta }\sqrt{m+ \beta }i}{2(-4+5m+9\beta )} ) \).
Using the transformation
the fixed point \(E^{\ast }\) is shifted to the point \(( 0,0 ) \). From a Taylor expansion, the system (2) converts to
where
The system (19) can be expressed as
where and are symmetric multilinear vector functions of \(x,y,u\in R ^{2}\). These functions are defined as follows:
\(\forall X\in \mathbb{R} ^{2}\) can be uniquely represented near \(a_{1}\) by
for some \(z\in \mathbb{C} \). The explicit formula of z is determined as \(z=\langle p,X\rangle \).
The system (19) can be transformed for all sufficiently small \(\vert a \vert \) into the form
where \(\lambda ( a ) = ( 1+\varphi ( a ) ) e^{i\arctan ( a ) }\) with \(\varphi (a_{NS})=0\) and \(g ( z,\overline{z},a ) \) is smooth complex-valued function. After taking the Taylor expression of g with respect to \(( z, \overline{z} )\), we obtain
By symmetric multilinear vector functions, the Taylor coefficients \(g_{kl}\) can be expressed by the formulas
The coefficient \(\beta _{2}(a_{NS})\), which determines the direction of the appearance of the invariant curve in a generic system exhibiting the Neimark–Sacker bifurcation, can be calculated via
where \(e^{i\arctan ( a_{NS} ) }=\lambda ( a_{NS} ) \).
We state the following theorem on the Neimark–Sacker bifurcation.
Theorem 1
Suppose that \(E_{\ast }\) is positive fixed point of the model (2). If (13) holds, \(1-2\beta -m\neq 0\), \(\beta _{2} ( a _{NS} ) \neq 0\) and the parameter a changes its value in small vicinity of \(\varOmega _{NSB_{E^{\ast }}}\), then the model (2) passes through a Neimark–Sacker bifurcation at only fixed point \(E_{\ast }\). Moreover, if \(\beta _{2} ( a_{NS} ) <0\) (resp., \(\beta _{2} ( a_{NS} ) >0\)), then the Neimark–Sacker bifurcation of model (2) at \(a=a_{NS}\) is supercritical (resp., subcritical) and there exists a unique closed invariant curve bifurcation from \(E_{\ast }\) for \(a=a_{NS}\), which is attracting (resp., repelling).
4 Numerical simulations
In this section, our aim is to present numerical simulations to validate the above theoretical results, especially the bifurcation diagrams and phase portraits for system (2) around fixed point \(E_{\ast }\). We will choose a as the bifurcation parameter. The Neimark–Sacker bifurcation point as \(a_{NS}=3.448275862\) is obtained. By taking the parameters values \(a_{NS}=3.448275862\), \(m=0.25\) and \(\beta =0.23\), the positive fixed point of the model (2) is evaluated as \(E_{\ast }= ( 0.23,3.454150957 ) \).
Using the above the parameters, we get the jacobian matrix as follows:
The eigenvalues are evaluated as follows:
Let \(q,p\in C^{2}\) be complex eigenvectors corresponding to \(\lambda _{1,2}\), respectively.
and
To obtain the normalization \(\langle p,q \rangle =1\), we can take normalized vectors as
and
Because of computing the coefficients of normal form, we transform the point \(( 0,0 ) \) to the fixed point \(E_{\ast }\) by a change of variables,
So, we can compute the coefficients of the normal of the system by using Eq. (24) as follows:
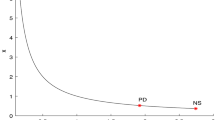
From (25), the critical part is obtained: \(\beta _{2} ( a _{NS} ) =-8.214126411<0\). Therefore, the Neimark–Sacker bifurcation is supercritical and it shows the correctness of Theorem 1. The bifurcation diagram and the phase portrait of the system (2) is shown in Figs. 2 and 3.
Bifurcation diagram for the system (2) for values of \(m=0.25\), \(\beta =0.23\), \(a=3.3:0.0001:3.4\) and initial value \(( x_{0},y_{0} ) =(0.2,3.4)\)
Phase portraits of the system (2) for different values of a
The bifurcation diagrams shown in Fig. 2 show that the stability of \(E_{\ast }\) holds for \(a<3.4482\) and loses its stability at \(a=3.4482\) and an attracting invariant curve appears if \(a>3.4482\).
The phase portraits of bifurcation diagrams in Fig. 2 for different values of a are displayed in Fig. 3, which clearly depicts the process of how a smooth invariant circle bifurcates from the stable fixed point \(E_{\ast }= ( 0.23,3.454150957 ) \). When a exceeds 3.448275862 there appears a circular curve enclosing the fixed point \(E_{\ast }\), and its radius becomes larger with respect to the growth of a.
5 Discussions
This paper is about to stability and bifurcation analysis of a discrete-time predator–prey model with Allee effect on prey population. We showed that the system (2) has three fixed points namely \(E_{1}\), \(E_{2}\) and \(E_{\ast} \). The topological classifications of these fixed points were given. By bifurcation theory [39,40,41] we showed that the system (2) undergoes a Neimark–Sacker bifurcation at unique coexistence fixed point if a varies around the set \(\varOmega _{NSB_{E_{\ast } }}\). The parametric conditions for existence and direction of Neimark–Sacker bifurcation in positive fixed point \(E_{\ast }\) were given. Also, we verified the theoretical results by presenting some numerical simulations and phase portrait diagrams using MATLAB. We displayed that when the bifurcation parameter a passes a critical bifurcation value, stability of the coexistence equilibrium point of the model (2) changes from stable to unstable and Neimark–Sacker bifurcation occurs at this critical value. Therefore, we can say that the parameter a has a strong effect on the stability of the system so as control two populations.
References
Lotka, A.J.: Elements of Mathematical Biology. Williams & Wilkins, Baltimore (1925)
Volterra, V.: Variazioni e fluttuazioni del numero di’ individui in specie animali conviventi. Mem. R. Accad. Naz. Dei Lincei, Ser. VI 2, 31–113 (1926)
Birkhead, T.R.: The effect of habitat and density on breeding success in the common guillemot. J. Anim. Ecol. 46, 751–764 (1977)
Dennis, B.: Allee effect: population growth, critical density, and the chance of extinction. Nat. Resour. Model. 3, 481–538 (1989)
McCarthy, M.A., Lindenmayer, D.B., Dreschler, M.: Extinction debts and risks faced by abundant species. Conserv. Biol. 11, 221–226 (1997)
Amarasekare, P.: Interactions between local dynamics and dispersal: insights from single species models. Theor. Popul. Biol. 53, 44–59 (1998)
Drake, J.M.: Allee effects and the risk of biological invasion. Risk Anal. 24, 795–802 (2004)
Shi, J., Shivaji, R.: Persistence in reaction diffusion models with weak Allee effect. J. Math. Biol. 52, 807–829 (2006)
Taylor, C.M., Hastings, A.: Allee effects in biological invasions. Ecol. Lett. 8, 895–908 (2005)
Allee, W.C.: Animal Aggretions: A Study in General Sociology. University of Chicago Press, Chicago (1931)
Zhou, S., Liu, Y., Wang, G.: The stability of predator–prey systems subject to the Allee effects. Theor. Popul. Biol. 67, 23–31 (2005)
Kangalgil, F., Ak Gümüş, Ö.: Allee effect and stability in a discrete-time host-parasitoid model. J. Adv. Res. Appl. Math. 7, 1–6 (2016)
Kangalgil, F., Ak Gümüş, Ö.: Allee effect in a new population model and stability analysis. Gen. Math. Notes (2016)
Duman, O., Merdan, H.: Stability analysis of continuous population model involving predation and Allee effect. Chaos Solitons Fractals 41, 1218–1222 (2009)
Groom, M.J.: Allee effects limit population viability of an annual plant. Am. Nat. 151, 487–496 (1998)
Kuussaari, M., Saccheri, I., Camara, M., Hanski, I.: Allee effect and population dynamics in the glanville fritillary butterfly. Oikos 82, 384–392 (1998)
Stoner, A.W., Ray-Culp, M.: Evidence for Allee effects in an over-harvested marine gastropod: density-dependent mating and egg production. Mar. Ecol. Prog. Ser. 202, 297–302 (2000)
Courchamp, F., Grenfell, B.T., Clutton-Brock, T.H.: Impact of natural enemies on obligately cooperative breeders. Oikos 91, 311–322 (2000)
Scheuring, I.: Allee effect increases the dynamical stability of populations. J. Theor. Biol. 199, 407–414 (1999)
Khan, A.Q.: Neimark–Sacker bifurcation of a two-dimensional discrete-time predator–prey model. SpringerPlus 5, 126 (2016)
Smith, J.: Mathematical Ideas in Biology. Cambridge Press, Cambridge (1968)
Kartal, S.: Multiple bifurcations in an early brain tumor model with piecewise constant arguments. Int. J. Biomath. 11(4), 1850055 (2018)
Kartal, S., Gurcan, F.: Global behaviour of a predator–prey like model with piecewise constant arguments. J. Biol. Dyn. 9(1), 157–171 (2015)
Elabbasy, E.M., Elsadany, A.A., Zhang, Y.: Bifurcation analysis and chaos in a discrete reduced Lorenz system. Appl. Math. Comput. 228, 184–194 (2014)
Zhang, J., Deng, T., Chu, Y., Qin, S., Du, W., Luo, H.: Stability and bifurcation analysis of a discrete predator–prey model with Holling type III functional response. J. Nonlinear Sci. Appl. 9, 6228–6243 (2016)
Liu, X., Xiao, D.: Complex dynamics behaviors of a discrete-time predator–prey system. Chaos Solitons Fractals 32, 80–94 (2007)
Rana, S.M., Kulsum, U.: Bifurcation analysis and chaos control in a discrete-time predator–prey system of Leslie type with simplified Holling type IV functional response. Discrete Dyn. Nat. Soc. 2017, Article ID 9705985 (2017)
Hu, Z., Teng, Z., Zhang, L.: Stability and bifurcation analysis of a discrete predator–prey model with nonmonotonic functional response. Nonlinear Anal., Real World Appl. 12, 2356–2377 (2011)
Du, W., Zhang, J., Qin, S., Yu, J.: Bifurcation analysis in a discrete SIR epidemic model with the saturated contact rate and vertical transmission. J. Nonlinear Sci. Appl. 9, 4976–4989 (2016)
Din, Q.: Neimark–Sacker bifurcation and chaos control in Hassel–Varley model. J. Differ. Equ. Appl. 23(4), 741–762 (2016)
Din, Q.: Complexity and choas control in a discrete-time prey–predator model. Commun. Nonlinear Sci. Numer. Simul. 49, 113–134 (2017)
Din, Q.: Bifurcation analysis and chaos control in a host–parasitoid model. Math. Methods Appl. Sci. 40, 5391–5406 (2017)
Din, Q.: A novel chaos control strategy for discrete-time brusselator models. J. Math. Chem. (2018). https://doi.org/10.1007/s10910-018-0931-4
Din, Q.: Stability, bifurcation analysis and chaos control for a predator–prey system. J. Vib. Control (2018). https://doi.org/10.1177/1077546318790871
Din, Q.: Bifurcation analysis and chaos control in a second-order rational difference equation. Int. J. Nonlinear Sci. Numer. Simul. 19(1), 53–68 (2018)
Din, Q.: Bifurcation analysis and chaos control in discrete-time glycolysis models. J. Math. Chem. 56(3), 904–931 (2018)
Din, Q., Hussain, M.: Controlling chaos and Neimark–Sacker bifurcation in a host-parasitoid model. Asian J. Control 21(4), 1–14 (2019)
Din, Q.: Controlling chaos in a discrete-time prey–predator model with Allee effects. Int. J. Dyn. Control https://doi.org/10.1007/s40435-017-0347-1
Kuznetsov, Y.A.: Elements of Applied Bifurcation Theory, 2nd edn. Springer, New York (1998)
Wiggins, S.: Introduction to Applied Nonlinear Dynamical System and Chaos, vol. 2. Springer, New York (2003)
Elaydi, S.N.: An Introduction to Difference Equations. Springer, New York (1996)
Acknowledgements
The authors would like to thank the referee and the editor for their valuable comments, which led to improvement of this work.
Availability of data and materials
Not applicable.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kangalgil, F. Neimark–Sacker bifurcation and stability analysis of a discrete-time prey–predator model with Allee effect in prey. Adv Differ Equ 2019, 92 (2019). https://doi.org/10.1186/s13662-019-2039-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2039-y