Tractable circula densities from Fourier series

Abstract

This article proposes an approach, based on infinite Fourier series, to constructing tractable densities for the bivariate circular analogues of copulas recently coined ‘circulas’. As examples of the general approach, we consider circula densities generated by various patterns of nonzero Fourier coefficients. The shape and sparsity of such arrangements are found to play a key role in determining the properties of the resultant models. The special cases of the circula densities we consider all have simple closed-form expressions involving no computationally demanding normalizing constants and display wide-ranging distributional shapes. A highly successful model identification tool and methods for parameter estimation and goodness-of-fit testing are provided for the circula densities themselves and the bivariate circular densities obtained from them using a marginal specification construction. The modelling capabilities of such bivariate circular densities are compared with those of five existing models in a numerical experiment, and their application illustrated in an analysis of wind directions.

1 Introduction

A direction observed in the plane $\mathbb {R}^2$ can be represented by an angle, $\Theta$, typically in $[0,2\pi )$ or $[-\pi ,\pi )$, measured in a specified direction from a specified origin. The natural support for such directions is the circumference of the unit circle, $\mathbb {S}^1$, data on them being referred to as circular. The natural support for a bivariate circular random vector with angular coordinates $(\Theta _1, \Theta _2)$ is the unit torus $\mathbb {T}^2=\mathbb {S}^1\times \mathbb {S}^1$, data on such vectors sometimes being referred to as ‘toroidal’.

Early constructions used to obtain models for toroidal data included maximum (Shannon) entropy characterization (or, equivalently, exponential family distributions, Mardia and Jupp 1999, p. 43), wrapping (Johnson and Wehrly 1977) and projection (Saw 1983). The latter two approaches can be applied to any bivariate distribution defined on $\mathbb {R}^2$, although the resulting toroidal densities generally cannot be expressed in closed-form or are highly convoluted.

Perhaps the best-known exponential family toroidal model is the eight-parameter bivariate von Mises distribution of Mardia (1975). Four of its parameters control the dependence between $\Theta _1$ and $\Theta _2$, but not in easily interpreted ways. Its submodels include the six-parameter model of Rivest (1988) and the latter’s five-parameter sine, cosine and hybrid submodels, the properties of which are studied at length in Mardia and Frellsen (2012). Such five-parameter models are, to some extent, toroidal analogues of the bivariate normal distribution, with four of their parameters controlling the locations and concentrations of the marginal distributions, and the fifth the dependence between $\Theta _1$ and $\Theta _2$. However, their concentration and dependence parameters also control the unimodality/bimodality of their densities. Like the bivariate normal, the densities of their unimodal cases have contours that are elliptical around the mode. Their normalizing constants must be computed numerically. Their conditional distributions are von Mises, but their marginal distributions are generally not and, for some parameter values, can be bimodal.

More recently, Navarro et al. (2017) conditioned a multivariate normal distribution to obtain the twelve-parameter bivariate generalized von Mises model of order 2 (BGvM$_2$), whose conditional distributions are second-order generalized von Mises (GvM$_2$), see, for example, Gatto (2008), while Hassanzadeh and Kalaylioglu (2018) used a conditional specification approach to obtain a toroidal model with one of its marginal distributions being GvM$_2$. GvM$_2$ densities can be symmetric or asymmetric and unimodal or bimodal. A highly flexible family of toroidal models obtained by normalizing time series spectra was proposed by Taniguchi et al. (2020). In general, the interpretation of the parameters of these various models is difficult, and their normalizing constants must be computed numerically.

Ameijeiras-Alonso and Ley (2022) extended the sine-skewing approach of Umbach and Jammalamadaka (2009) and Abe and Pewsey (2011) to generate models for mildly asymmetric toroidal data, focussing explicitly on sine-skewed extensions of the bivariate uniform, sine, cosine and wrapped Cauchy models. An appealing property of such models is that their normalizing constants are the same as those of the base models to which sine-skewing is applied.

The construction underpinning the proposal made here is a highly flexible marginal specification approach incorporating the circular analogues of bivariate copulas recently termed ‘circulas’ by Jones et al. (2015). Briefly put, circulas are copulas that are rescaled by $1/(2\pi )$ and satisfy periodicity constraints. Let $(\Theta _1,\Theta _2)$ be a bivariate random vector of continuous circular random variables and F its distribution function on $[0,2\pi )^2$ defined by $F(\theta _1,\theta _2) = P( \Theta _1 \in (\omega _1, \omega _1+\theta _1] , \Theta _2 \in (\omega _2, \omega _2 + \theta _2])$ $(0 \le \theta _1,\theta _2 < 2 \pi )$, where $0 \le \omega _1,\omega _2 < 2 \pi$ are arbitrary reference points. Define the marginal distribution function of $\Theta _j$ on $[0,2\pi )$ by $F_j(\theta _j) = P( \Theta _j \in (\omega _j, \omega _j+\theta _j])$ $(0 \le \theta _j < 2\pi )$ for $j=1,2$. Then, an analogous result to Sklar’s theorem states that the distribution function F can be related to the marginal distribution functions, $F_{1}$ and $F_{2}$, through the circula $C_\circ$ as

$$\begin{aligned} F(\theta _1,\theta _2)=C_\circ (2\pi F_{1}(\theta _1),2\pi F_{2}(\theta _2)) \quad (0 \le \theta _1,\theta _2 < 2 \pi ). \end{aligned}$$

$C_\circ$ is itself a bivariate circular distribution function, but with the specific reference points $\omega _1=\omega _2=0$ and marginal distributions for $\Psi _1=2\pi F_{1}(\Theta _1)$ and $\Psi _2=2\pi F_{2}(\Theta _2)$ that are circular uniform rather than the (linear) uniform ones of their copula counterparts. Taking partial derivatives, the density of $(\Theta _1,\Theta _2)$ is given by

$$\begin{aligned} f(\theta _1,\theta _2)=4\pi ^2 f_{1}(\theta _1)f_{2}(\theta _2)c_\circ (2\pi F_{1}(\theta _1),2\pi F_{2}(\theta _2)), \end{aligned}$$

(1)

where $f_{1}$ and $f_{2}$ are the marginal densities of $\Theta _1$ and $\Theta _2$, and $c_\circ$ is the circula density corresponding to $C_\circ$. Clearly, $c_\circ$ controls the dependence between $\Theta _1$ and $\Theta _2$, the circula density for independence being $c_\circ (\psi _1,\psi _2)=1/(4\pi ^2)$ for any $\psi _1,\psi _2 \in [0,2\pi )$, where $\psi _1=2\pi F_{1}(\theta _1)$ and $\psi _2=2\pi F_{2}(\theta _2)$. The domain of $c_\circ$ is extended to $\mathbb {R}^2$ through the assumption $c_\circ (\psi _1\pm 2\pi k , \psi _2 \pm 2\pi l) = c_\circ (\psi _1,\psi _2)\ (k,l =0,1,\ldots )$. In addition, $c_\circ$ is usually assumed to be continuous at $(2\pi k,\psi _2)$ and $(\psi _1,2\pi l)$ for any $\psi _1,\psi _2 \in [0,2\pi )$ as well as all other points on the torus.

Jones et al. (2015) provided an in-depth treatment of the Wehrly and Johnson (1980) class of circulas, with density

$$\begin{aligned} c_\circ (\psi _1,\psi _2)=\frac{1}{2\pi }g(\psi _1\pm \psi _2), \end{aligned}$$

(2)

where g is a circular density. See Jones et al. (2015) for details of the evolution of this class, Shieh and Johnson (2005) and Kato and Pewsey (2015) for special cases, and Pewsey and Kato (2016) for work on goodness-of-fit testing. The wider copula-related literature is summarized in Jones et al. (2015), and generalizations of copulas to other compact Riemannian manifolds have been considered in Jupp (2015); see also Jupp and Kume (2020).

Here we propose a general, Fourier series-based, approach to constructing tractable circula densities for use within (1) that includes (2) as a special case and focus on $c_\circ$ generated using five basic patterns of Fourier coefficients. The construction is attractive because: (i) various new circula models can be generated having simple closed-form expressions for their densities and flexible forms of dependence structure controlled by relatively few parameters; (ii) three well-known circular dependence measures are simple functions of just two of the Fourier coefficients; (iii) the conditional mean directions and mean resultant lengths depend only on a limited number of Fourier coefficients; (iv) methods for simulation, model identification, parameter estimation and testing goodness-of-fit and independence are available for both the $c_\circ$ and the bivariate circular distributions generated from using them within (1).

Although any forms of $f_1$ and $f_2$ can be employed within (1) to generate bivariate circular distributions, throughout the paper we illustrate the construction’s application using marginal circular densities from the Kato and Jones (2015) family. The latter is the most flexible four-parameter family of unimodal circular densities presently available, has closed-form expressions for both its density and distribution functions, and all four of its parameters have clear interpretations. As we shall see, most of the conditional distributions of the specific circula densities considered in Sect. 3 are also members of the Kato–Jones family. We note that the $c_\circ$ that we explore here might also be used in a semiparametric approach to modelling in which kernel density estimates and empirical distribution functions are used in place of $f_1$, $f_2$, $F_1$ and $F_2$ in (1). Such an approach would inherit the tractable and interpretable parametric modelling of dependence.

We stress that the approach based on infinite Fourier series introduced here differs in important ways from previously proposed constructions incorporating truncated (or partial) Fourier series. Fernández-Durán (2007) considered bivariate circular models based on (1), the Wehrly and Johnson (1980) circula density (2) and non-negative trigonometric sum densities (i.e. truncated Fourier series constrained to be non-negative) for $f_1$, $f_2$ and g. More generally, Pertsemlidis et al. (2005) and Fernández-Durán and Gregorio-Domínguez (2014) proposed toroidal densities obtained from truncated bivariate Fourier series, the latter constrained to be non-negative. When fitted to toroidal data, such models generally include large numbers of parameters that are difficult to interpret (Mardia et al. 2007) and, due to harmonic artefacts, manifest modes, sometimes multiple, unsupported by the data (see, for example, Fig. 4 of Fernández-Durán and Gregorio-Domínguez 2014). In contrast, our tractable $c_\circ$, as well as the toroidal models generated by using them within (1) in combination with the highly flexible unimodal circular marginal densities of Kato and Jones (2015), have relatively few parameters, all of which have clear interpretations, and closed-form expressions for their densities which involve no computationally demanding normalizing constants. As an important consequence of the latter property, numerically implemented maximum likelihood estimation is swift. While truncated bivariate Fourier series with Fourier coefficients satisfying the constraints in (6) and (4) to follow might be used as circulas, they will generally not be as tractable as the ones based on infinite Fourier series that we propose here.

The rest of the article is organized as follows. In Sect. 2, we provide the details of our proposed construction together with general results for three circular dependence measures and the conditional mean directions and mean resultant lengths of circulas generated using it. In Sect. 3, we consider $c_\circ$ generated using five basic patterns of Fourier coefficients within the proposed construction and provide details of their basic properties. In Sect. 4, we explain how model identification, parameter estimation and goodness-of-fit testing can be performed, for both the considered $c_\circ$ and the models for toroidal data derived from using them within (1). The results from a numerical experiment, designed to compare the large-sample modelling capabilities of such toroidal models with those of five existing bivariate circular models, are presented in Sect. 5. In Sect. 6, a new Wehrly and Johnson (1980) circula density and our proposed inferential methods are applied in the analysis of wind directions. Lastly, we offer some concluding remarks in Sect. 7. All equations, figures and tables with numbers preceded by the letter S are contained in an accompanying online supplementary materials document.

2 Circula densities from Fourier series

2.1 Circula densities

It is well known (Mardia and Jupp 1999, Sect. 3.3.2) that any continuous circular density, f, can be expressed in the form of a Fourier series as

$$\begin{aligned} f(\theta ) = \frac{1}{2\pi } \sum _{m=-\infty }^{\infty } \phi (m) \, e^{-i m \theta } \quad (-\pi \le \theta < \pi ), \end{aligned}$$

where $i=\sqrt{-1}$, for appropriately chosen Fourier coefficients $\phi (m) \ (m \in \mathbb {Z})$. Now consider the family of continuous distributions on the torus whose density can be expressed analogously as

$$\begin{aligned} f(\theta _1,\theta _2) = \frac{1}{4\pi ^2} \sum _{m,n=-\infty }^{\infty } \phi (m,n) \, e^{-i (m \theta _1 + n \theta _2)} \quad (-\pi \le \theta _1,\theta _2 < \pi ), \end{aligned}$$

(3)

where the Fourier coefficients $\phi (m,n) \in \mathbb {C} \ (m,n \in \mathbb {Z})$ are appropriately defined so that $f(\theta _1,\theta _2) \ge 0$ and $\int _{-\pi }^{\pi }\int _{-\pi }^{\pi } f(\theta _1,\theta _2)\text {d}\theta _1\text {d}\theta _2 = 1$.

Proposition 1

The following hold for density (3).

• (i) If a random vector $(\Theta _1,\Theta _2)$ has density (3) then

  $$\begin{aligned} E \left\{ e^{i (m \Theta _1 + n \Theta _2)} \right\} = \phi (m,n) \quad (m,n \in \mathbb {Z}). \end{aligned}$$

• (ii) A density in family (3) is a circula density if and only if

  $$\begin{aligned} \phi (m,0) = \left\{ \begin{array}{ll} 1, &{}\quad m=0, \\ 0, &{}\quad m \ne 0, \end{array} \right. \quad \phi (0,n) = \left\{ \begin{array}{ll} 1, &{}\quad n=0, \\ 0, &{}\quad n \ne 0, \end{array} \right. \quad (m,n \in \mathbb {Z}). \end{aligned}$$

  (4)

Proof

(i) It is clear from the following well-known equation that (i) holds:

$$\begin{aligned} \int _{-\pi }^{\pi } e^{i t \theta } \text {d}\theta = \left\{ \begin{array}{ll} 2\pi , &{}\quad t=0, \\ 0, &{}\quad t \in \mathbb {Z} {\setminus } \{0 \}. \end{array} \right. \end{aligned}$$

(5)

(ii) If $\phi (m,n)$ satisfies (4), the marginal density $f_1(\theta _1)$ can be expressed as

$$\begin{aligned} f_1(\theta _1) = \int _{-\pi }^{\pi } f(\theta _1,\theta _2) \text {d}\theta _2 = \frac{1}{2\pi } \sum _{m=-\infty }^{\infty } \phi (m,0) e^{-i m \theta _1} = \frac{1}{2\pi }. \end{aligned}$$

The second equality follows from (5). Similarly, $f_2(\theta _2)=1/(2\pi )$, and thus (3) is a circula density. Next, assume that a density in family (3) is a circula density. Since this assumption implies that each marginal density of (3) is the circular uniform density, the equations in (4) follow from (i). $\square$

It follows from Proposition 1(i) that, for any $\phi (m,n)$ in (3),

$$\begin{aligned} \overline{\phi (m,n)} = \phi (-m,-n), \quad |\phi (m,n)| \le 1, \quad \phi (0,0)=1, \end{aligned}$$

(6)

where $\overline{z}$ denotes the complex conjugate of z. The circula densities of Proposition 1(ii) can be expressed as

$$\begin{aligned} c_\circ (\psi _1,\psi _2)&= \frac{1}{4\pi ^2} \Biggl [ 1 + 2 \, \text{ Re } \biggl \{ \sum _{m=1} ^{\infty } \sum _{ \scriptstyle {\begin{array}{c} n= -\infty \\ \scriptstyle n \ne 0 \end{array}}}^{\infty } \phi (m,n) \, e^{-i (m \psi _1 + n \psi _2)} \biggr \} \Biggr ] \nonumber \\&= \frac{1}{4\pi ^2} \Biggl [ 1 + 2 \, \text{ Re } \biggl \{ \sum _{n=1}^{\infty } \sum _{ \scriptstyle {\begin{array}{c} m= -\infty \\ \scriptstyle m \ne 0 \end{array}}}^{\infty } \phi (m,n) \, e^{-i (m \psi _1 + n \psi _2)} \biggr \} \Biggr ]. \end{aligned}$$

(7)

If $\phi (m,n) =0$ for all $m,n \ne 0$, the density is that of the bivariate circular uniform distribution. Circula densities of the form (7) are the main focus of the paper.

2.2 Circular dependence measures

Here we provide general results for three signed circular dependence measures when applied to circula densities of the form (7). Let $(\Theta _1,\Theta _2)$ be a bivariate circular random vector. Then, the dependence measures of Fisher and Lee (1983), Jammalamadaka and Sarma (1988) and, for a circula, that of Rivest (1982) are defined as

$$\begin{aligned} \rho _{\text {FL}}= & {} \frac{\text{ det } \{ E ( X_1 X_2^T) \}}{[ \text{ det } \{ E ( X_1 X_1^T) \} \text{ det } \{ E( X_2 X_2^T) \} ]^{1/2}},\\ \rho _{\text {JS}}= & {} \frac{E \{ \sin (\Theta _1 - \mu _1) \sin (\Theta _2 - \mu _2) \}}{ [ E \{ \sin ^2 (\Theta _1-\mu _1) \} E \{ \sin ^2 (\Theta _2 - \mu _2) \} ]^{1/2}}, \\ \rho _{\text {R}}= & {} 2 \lambda _2, \end{aligned}$$

respectively, where, for $j=1,2$, $X_j = (\cos \Theta _j, \sin \Theta _j)^T$, $\mu _j$ is the mean direction of $\Theta _j$, and $\lambda _2$ denotes the smallest singular value of $E(X_1 X_2^T)$.

For circula densities (7), it can easily be shown that the dependence measures between the circular uniform random variables $\Psi _1$ and $\Psi _2$ reduce to

$$\begin{aligned} \rho _{\text {R}} = \rho _{\text {JS}} = |\phi (1,-1)|-|\phi (1,1)|, \quad \rho _{\text {FL}}=|\phi (1,-1)|^2- |\phi (1,1)|^2. \end{aligned}$$

Clearly, when only one of $\phi (1,-1)$ and $\phi (1,1)$ is nonzero, then $\rho _{\text {R}}$, $\rho _{\text {JS}}$ and $\rho _{\text {FL}}$ are simple functions of either $\phi (1,-1)$ or $\phi (1,1)$.

2.3 Conditional mean directions and resultant lengths

The first trigonometric moment of $\Psi _1|\Psi _2=\psi _2$ for a circula density of the form (7) can be expressed as

$$\begin{aligned} E (e^{i\Psi _1}|\psi _2) = \int _{-\pi }^{\pi } e^{i \psi _1} c_{1|2}(\psi _1|\psi _2) \text {d}\psi _1= \sum _{n=-\infty }^{\infty } \phi (1,n) e^{-i n \psi _2}, \end{aligned}$$

(8)

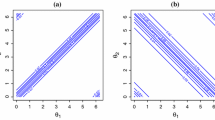
where $c_{1|2}(\psi _1|\psi _2)$ denotes the conditional density of $\Psi _1|\Psi _2=\psi _2$. Expression (8) implies that, in order to calculate the mean direction and mean resultant length of $\Psi _1|\Psi _2=\psi _2$, it suffices to focus on the nonzero Fourier coefficients in the $m=1$ column of a plot of the $\{ \phi (m,n) \}_{m,n \in \mathbb {Z}}$. Figure 1 provides examples of such plots. It then follows that:

• (a) If all the coefficients in the $m=1$ column are zero, the mean resultant length of the conditional distribution of $\Psi _1|\Psi _2=\psi _2$, $R(\Psi _1|\psi _2)\,\equiv \,| E(e^{i\Psi _1}|\psi _2)|$, is zero;

• (b) If there is only one nonzero coefficient in the $m=1$ column, say at $(m,n)=(1,d)$, the mean direction of the conditional distribution of $\Psi _1|\Psi _2=\psi _2$, $M(\Psi _1|\psi _2)$ $\equiv \,\arg ( E(e^{i\Psi _1}|\psi _2))$, is $-d \psi _2$ and $R(\Psi _1|\psi _2)=|\phi (1,d)|$;

• (c) If there are two or more nonzero coefficients in the $m=1$ column, $M(\Psi _1|\psi _2)$ is nonlinear and $R(\Psi _1|\psi _2)$ is in general heteroscedastic.

Analogous results hold for the conditional distribution of $\Psi _2|\Psi _1=\psi _1$.

Fig. 1

The nonzero Fourier coefficients of Patterns 1–5 with $q=-1$ and $m,n\in \{0,1,\ldots ,6\}$. The values of m appear on the horizontal axes, and those for n on the vertical axes. The area of a dot at (m, n) is proportional to the value of $\phi (m,n)$. The panels for the five patterns are ordered from top left to bottom right, reading from left to right

3 Circula models generated by five patterns of Fourier coefficients

3.1 Preliminaries

In this section we consider examples of (7) generated by five simple patterns of nonzero Fourier coefficients and provide details of the basic properties of certain specific models. Given the constraints on the Fourier coefficients in (6) and (4) , unless explicitly stated otherwise, we consider circula densities defined through nonzero Fourier coefficients on the $\mathbb {Z}^+\times (\mathbb {Z}^+\cup \mathbb {Z}^-)$ lattice. Figure 1 illustrates the five patterns of nonzero Fourier coefficients. We emphasize the parametric specification of these coefficients. In particular, the specific models generated by Patterns 2–5 are derived using geometric series of nonzero Fourier coefficients which have the added benefit of generating circulas with closed-form expressions for their densities. In order to obtain circula densities exhibiting pointwise symmetry about the origin, all of the nonzero Fourier coefficients are assumed to be real.

Since all of the patterns we consider have at most one of $\phi (1,-1)$ and $\phi (1,1)$ which is nonzero, we only quote values of $\rho _{\text {R}}$, those for $\rho _{\text {JS}}$ and $\rho _{\text {FL}}$ following from the relations identified in Sect. 2.2. The conditional mean directions and resultant lengths of all of the models we consider can be easily calculated using the results presented in Sect. 2.3; see Appendix A of the supplementary materials document. It follows that the conditionals of the models considered afford uniform, linear-homoscedastic, or nonlinear-heteroscedastic circular–circular regression. These properties and expressions for modes and antimodes of the circula densities we consider can be found in Table 1.

Appendix B of the supplementary materials document explains how data from any $c_\circ$ or bivariate circular density of the form (1) can be simulated.

Table 1 Some properties of six Fourier-based circula models. Formulae for regression quantities can be found in Appendix A

3.2 Pattern 1: single (nonzero) point

Let

$$\begin{aligned} \phi (m,n) = \left\{ \begin{array}{ll} \gamma , &{}\quad (m,n)=(1,-q ), \\ 0, &{}\quad \text{ otherwise }, \end{array} \right. \end{aligned}$$

where $0 \le \gamma \le 1/2$ and, here and henceforth, $q \in \{-1,1\}$. Thus, this pattern includes just a single nonzero real-valued Fourier coefficient. In this case, the circula density (7) reduces to

$$\begin{aligned} c_\circ (\psi _1,\psi _2)= \frac{1}{4\pi ^2} \left\{ 1 + 2 \gamma \cos (\psi _1-q \psi _2) \right\} . \end{aligned}$$

(9)

Figure 2 portrays a planar contour plot of density (9) when $q=1$ and $\gamma =0.3$. For this model, and all but one of the other models in this section, $\rho _{\text {R}}=q\gamma$ (see Table 1). The strength of dependence between $\Psi _1$ and $\Psi _2$ is thus controlled by $\gamma$, and its sign by q. The conditional distributions of $\Psi _1|\Psi _2=\psi _2$ and $\Psi _2|\Psi _1=\psi _1$ are cardioid distributions on the circle.

Fig. 2

Planar contour plot of circula density (9) with parameter vector $(q,\gamma ) = (1,{0.3})$. Here and in all other planar contour plots, the horizontal axis represents $\psi _1$ and the vertical axis $\psi _2$. The cross identifies $(\psi _1,\psi _2)=(0,0)$

3.3 Pattern 2: diagonal line

Consider circula densities generated using nonzero Fourier coefficients on a diagonal of the $\mathbb {Z}^+\times (\mathbb {Z}^+\cup \mathbb {Z}^-)$ lattice. Specifically, let

$$\begin{aligned} \phi (m,n) = \left\{ \begin{array}{ll} \varphi (m), &{}\quad n=-qm, \\ 0, &{}\quad n \ne -qm, \end{array} \right. \end{aligned}$$

where the $\varphi (m)$ are the Fourier coefficients of any circular distribution, for which $\varphi (0)=1$. Then, the circula density is of the form

$$\begin{aligned} c_\circ (\psi _1,\psi _2) = \frac{1}{2\pi } g (\psi _1 - q \psi _2), \end{aligned}$$

(10)

where $g(\psi )= (2\pi )^{-1} [ 1+ 2 \text{ Re } \{ \sum _{m=1}^{\infty } \varphi (m) e^{-i m \psi } \}]$ is a density on the unit circle. This is the Wehrly and Johnson (1980) class of circula densities discussed in Jones et al. (2015). For all but the case when g is circular uniform, (10) has linear contours parallel to the $q\pi /4$ diagonal. Density (10) reduces to (9) when $\varphi (1)=\gamma$ and $\varphi (m)=0$ otherwise, and $0 \le \gamma \le 1/2$.

When $\varphi (m)=\gamma \rho ^{m-1} \ (m =1,2,\ldots , 0 \le \gamma<1, \ 2\gamma -1 \le \rho <1)$, density (10) can be expressed in closed form as

$$\begin{aligned} c_\circ (\psi _1,\psi _2) = \frac{1}{4\pi ^2} \left\{ 1 + 2 \gamma \, \frac{\cos (\psi _1-q \psi _2) - \rho }{1+\rho ^2-2 \rho \cos (\psi _1 - q \psi _2)} \right\} . \end{aligned}$$

(11)

For this model, all three parameters, $\gamma = \phi (1,-q)=\varphi (1)$, $\rho$ and q, affect the dependence between $\psi _1$ and $\psi _2$ although, as elsewhere, $\rho _{\text {R}} = q\gamma$. Figure S8 presents planar contour plots of density (11) for $q=-1$, $\gamma =0.7$ and three values of $\rho$. The parameter $\rho$ regulates the concentration of the wrapped Cauchy-like distribution. Both conditional distributions are special cases of the unimodal circular distributions of Kato and Jones (2015) which are two component mixtures with circular uniform and wrapped Cauchy components.

3.4 Pattern 3: vertical line

Consider the pattern formed by nonzero Fourier coefficients on the vertical line of the $\mathbb {Z}^+\times (\mathbb {Z}^+\cup \mathbb {Z}^-)$ lattice given by

$$\begin{aligned} \phi (m,n) = \left\{ \begin{array}{ll} \varphi (n), &{}\quad m=1, \ q n \le -1, \\ 0, &{}\quad \text{ otherwise }, \end{array} \right. \end{aligned}$$

for some nonzero Fourier coefficients $\varphi$.

For example, if $\varphi (n)=\gamma \rho ^{|n|-1}$ $(0 \le \gamma \le 1/2, \ 0 \le \rho \le 1-2\gamma )$, then

$$\begin{aligned} c_\circ (\psi _1,\psi _2) = \frac{1}{4\pi ^2} \left\{ 1 + 2 \gamma \frac{\cos (\psi _1 -q \psi _2) - \rho \cos \psi _1}{1+\rho ^2 - 2\rho \cos \psi _2} \right\} . \end{aligned}$$

(12)

Panels (a) and (b) of Fig. S3 present planar contour plots of density (12) with $q=1$ and two $(\gamma ,\rho )$ combinations. The dependence between $\Psi _1$ and $\Psi _2$ is clearly regulated by all three parameters: $q, \gamma$ and $\rho$. In particular, $\gamma$ regulates the strength of the dependence between $\Psi _1$ and $\Psi _2$, and $\rho$ the degree of deformation of the density’s shape around the main diagonal. The conditional distribution of $\Psi _1|\Psi _2=\psi _2$ is a cardioid distribution and that of $\Psi _2 |\Psi _1=\psi _1$ is a special case of the Kato–Jones family.

Generalizations of Patterns 1–3, for which the nonzero Fourier coefficients are positioned more generically, are considered in Appendix C of the supplementary materials document.

3.5 Pattern 4: square

Now consider a square pattern of nonzero Fourier coefficients. As an attractive three-parameter example of this, let

$$\begin{aligned} \phi (m,n) = \left\{ \begin{array}{ll} \gamma \rho _1^{m-1} \rho _2^{|n|-1}, &{}\quad m,-qn \in \mathbb {Z}^+, \\ 0, &{}\quad \text{ otherwise }, \end{array} \right. \end{aligned}$$

where $0< \rho _1,\rho _2 < 1$. Density (7) then becomes

$$\begin{aligned} c_\circ (\psi _1,\psi _2) = \frac{1}{4 \pi ^2} \left\{ 1 + 2 \gamma \frac{\cos (\psi _1 -q \psi _2) - \rho _2 \cos \psi _1 - \rho _1 \cos \psi _2 + \rho _1 \rho _2}{(1+\rho _1^2-2\rho _1 \cos \psi _1) (1+\rho _2^2-2\rho _2 \cos \psi _2) } \right\} , \end{aligned}$$

(13)

where the range of $\gamma \, (\ge 0)$ is $\gamma \le \rho _1 \rho _2 / [ \{(1-\rho _1^2)(1-\rho _2^2) \}^{-1} -1 ]$ if $|\rho _1 - \rho _2| \le \rho _1 \rho _2$, $\gamma \le (1-\rho _1) (1+\rho _2)/2$ if $|\rho _1 - \rho _2| > \rho _1 \rho _2$ and $\rho _1 > \rho _2$, and $\gamma \le (1+\rho _1)(1-\rho _2)/2$ if $|\rho _1 - \rho _2| > \rho _1 \rho _2$ and $\rho _1 < \rho _2$. Figure S9 presents a contour plot of the maximum value of $\gamma$ as a function of $\rho _1$ and $\rho _2$. The maximum of $\gamma$ tends to 0.5 as $(\rho _1,\rho _2)\rightarrow (0,0)$.

The mode of density (13) occurs at $(\psi _1,\psi _2)=(0,0)$. If $|\rho _1 - \rho _2| > \rho _1 \rho _2$, then there is only one antimode of (13) which occurs at $(\psi _1,\psi _2)=(0,-\pi )$ for $\rho _1>\rho _2$ and $(\psi _1,\psi _2)=(-\pi ,0)$ for $\rho _1 < \rho _2$. When $|\rho _1 - \rho _2| \le \rho _1 \rho _2$, there are two antimodes which occur at $(\psi _1,\psi _2)= \pm (\alpha _1, -q \alpha _2)$, where $\alpha _j=\arg \{\rho _j + (1-\rho _j^2)/(\rho _j+e^{i x_j})\} = \text{ atan2 } \{ - (1-\rho _j^2) \sin x_j , 2 \rho _j + (1+\rho _j^2) \cos x_j \}$, $x_j=\arccos \{ (\rho _j^2 - \rho _j^2 \rho _k^2 -\rho _k^2) /(2 \rho _j \rho _k^2) \}$ $(j,k=1,2, \ j \ne k)$ and $\text {atan2}(y,x)$ returns the angle measured anticlockwise from the x-axis to the vector connecting the origin with (x, y). The conditional densities of $\Psi _1|\Psi _2=\psi _2$ and $\Psi _2|\Psi _1=\psi _1$ are special cases of the Kato–Jones family.

Fig. 3

Planar contour plots of circula density (13) with $q=1$ and $(\rho _1,\rho _2,\gamma )$ equal to: a (0.2, 0.2, 0.470); b (0.2, 0.5, 0.300); c (0.5, 0.5, 0.321). For each panel, the value of $\gamma$ corresponds to the upper bound of its parameter space

Planar contour plots of circula density (13) designed to illustrate the roles of $\rho _1$ and $\rho _2$ are displayed in Fig. 3. When $\rho _1=\rho _2$, the density is symmetric about the main diagonal and increasingly concentrated in the neighbourhood of the origin as $\rho _1=\rho _2$ increases. For a fixed value of $\rho _1$, as $\rho _2$ increases the main axis of the central elliptical contour tilts increasingly away from the main diagonal towards $\psi _2=0$ and the dispersion increases in the neighbourhood of $(-\pi ,-\pi )=(\pi ,\pi )$. Due to the symmetry of (13), for a fixed value of $\rho _2$ the main axis tilts increasingly towards $\psi _1=0$ as $\rho _1$ increases.

3.6 Pattern 5: triangle

As a final basic pattern, consider an arrangement of nonzero Fourier coefficients forming a triangular pattern. In particular, the pattern of nonzero Fourier coefficients underpinning circula density (11) can be extended to

$$\begin{aligned} \phi (m,n) = \left\{ \begin{array}{ll} \gamma \rho ^{m-1} \lambda ^{-(m+qn)}, &{}\quad 1 \le m \le -qn, \\ 0, &{}\quad \text{ otherwise }, \end{array} \right. \end{aligned}$$

where $0< \rho< 1, \ 0 \le \lambda <1$ . The constraints on $\gamma \,(\ge 0)$ are $\gamma \le \rho (1-\rho ^2)(1-\lambda ^2)/[1-\rho ^2(1-\lambda ^2)]$ if $\lambda \ge (1-\rho )/\rho$ and $\gamma \le (1-\lambda ) (1+\rho )/2$ otherwise. A contour plot of the maximum value of $\gamma$ as a function of $\rho$ and $\lambda$ is presented in Fig. S10. The maximum of $\gamma$ tends to 1 as $(\rho ,\lambda )\rightarrow (1,0)$. For this model, the circula density is

$$\begin{aligned} c_\circ (\psi _1,\psi _2) = \frac{1}{4\pi ^2} \left[ 1 + 2 \gamma \frac{\cos (\psi _1 -q \psi _2) - \lambda \cos \psi _1 + \rho \lambda \cos \psi _2 - \rho }{ \{1+\rho ^2-2\rho \cos (\psi _1-q \psi _2)\} (1+\lambda ^2-2\lambda \cos \psi _2) } \right] . \end{aligned}$$

(14)

The mode of the density is located at $(\psi _1,\psi _2)=(0,0)$, and the antimode(s) at $(\psi _1,\psi _2)=(-\pi ,0)$ if $\lambda < (1-\rho )/\rho$ or at $(\psi _1,\psi _2)=\pm (\alpha _1,-q \alpha _2)$ if $\lambda \ge (1-\rho )/\rho$. Here $\alpha _1 = - \alpha _2 + \text{ atan2 } \{ (1-\rho ^2) \sin x_1 , \rho (2+\rho \cos x_1) \}$, $\alpha _2 = \text{ atan2 } \{ -(1-\lambda ^2) \sin x_2 , 2 \lambda + (1+\lambda ^2) \cos x_2 \}$, $x_1=\arccos \{ (-1-\rho ^2+\rho ^2 \lambda ^2)/(2 \rho )\}$, and $x_2=\arccos \{ (1-\rho ^2-\rho ^2 \lambda ^2)/(2 \rho ^2 \lambda )\}$. The conditional distribution of $\Psi _1|\Psi _2=\psi _2$ is a special case of the Kato–Jones family, while that of $\Psi _2|\Psi _1=\psi _1$ does not seem to be a well-known distribution in general.

Fig. 4

Planar contour plots of circula density (14) for $q=1$, $\rho =0.6$ and $(\lambda ,\gamma )$ equal to: a (0, 0.8); b (0.4, 0.48); c (0.8, 0.16). For each panel, the value of $\gamma$ corresponds to the upper bound of its parameter space

Figure 4 presents planar contour plots of circula density (14) for $q=1$, $\rho =0.6$ and three combinations of $\lambda$ and $\gamma$. When $\lambda =0$ the contours are straight lines because (14) reduces to (11). As $\lambda$ increases, the axis of the central elliptical contour tilts increasingly away from the main diagonal towards $\psi _2=0$ and the other contours tend to be increasingly asymmetric about the main diagonal. Although the conditional distribution of $\Psi _2|\Psi _1=\psi _1$ can have more than one mode, the joint distribution of $(\Psi _1,\Psi _2)$ with this unique dependence structure, as well as the conditional distribution of $\Psi _1|\Psi _2=\psi _2$, is always unimodal.

Appendix D of the supplementary materials document briefly discusses the shapes of bivariate circular densities obtained using (1) with circula densities generated by Patterns 2 and 5.

4 Model fitting

4.1 Circula densities

Let $\{(\psi _{1k},\psi _{2k}); k=1,\ldots ,n\}$ denote an i.i.d. sample of random vectors from a circula density $c_\circ$ where, from here onwards, n denotes sample size. If the form of $c_\circ$ is unknown and n is moderate to large, an inspection of a planar scatterplot of the data will usually be sufficient to identify q and provide insight as to the form of $c_\circ$. However, the absolute values of the empirical Fourier coefficients, $\tilde{\phi }(r,-qs)=\frac{1}{n}\sum _{k=1}^ne^{i(r\psi _{1k}-qs\psi _{2k})}$, for $r,s=1,2,\ldots ,6,$ say, represented graphically in a level plot, will generally prove more revealing, showing patterns, like those in Fig. 1, indicative of the structure of the Fourier coefficients of $c_\circ$. Computation of the empirical Fourier coefficients is extremely fast. In practice, a range of potential $c_\circ$’s might be explored and the best fitting model established using information criteria, model reduction based on likelihood ratio testing and formal goodness-of-fit testing.

All of the densities of the five specific circula models in Sect. 3 have, by design, relatively simple closed-form expressions involving no computationally demanding normalizing constants, so computation of their log-likelihood functions is straightforward. Maximum likelihood (ML) estimation is then conducted using standard constrained optimization techniques. Method of moments (MM) estimates, calculated sequentially using the relations in Table 2, $q=\text {sgn}(|\phi (1,-1)|-|\phi (1,1)|)$, and $\tilde{\phi }(r,-qs)$ substituted for $\phi (r,-qs)$, can be used as starting values.

Table 2 Relations between parameters and Fourier coefficients for five specific models

The distribution function of a circula can be represented as $C_\circ (\psi _1, \psi _2)= C_{1|2}(\psi _1| \psi _2)$ $C_2(\psi _2)$, where $C_2(\psi _2)=\psi _2/(2\pi )$ is the marginal, uniform, distribution function of $\Psi _2$ and $C_{1|2}$ is the conditional distribution function of $\Psi _1|\Psi _2=\psi _2$. It follows that $\Psi _2$ and $2\pi C_{1|2}(\Psi _1 |\Psi _2=\psi _2)$ are independent and follow circular uniform distributions. Similar results hold for $\Psi _1$ and $2\pi C_{2|1}(\Psi _2 |\Psi _1=\psi _1)$. When the parameters of the conditional distributions are estimated, $\{(\psi _{2k}, 2\pi \hat{C}_{1|2}(\psi _{1k}|\psi _{2k})); k=1,\ldots ,n\}$ and $\{(\psi _{1k}, 2\pi {\hat{C}}_{2|1}(\psi _{2k}|\psi _{1k})); k=1,\ldots ,n\}$ will be samples of pseudo-uniform vectors on the torus. Systematic patterns in scatterplots of such samples are indicative of lack-of-fit. To test goodness-of-fit, we apply the obvious adaptation of the parametric bootstrap approach described in Sect. 3.2 of Pewsey and Kato (2016) to the two pseudo-uniform samples.

4.2 Bivariate circular densities

The shapes of the bivariate circular densities obtained using density (1) depend on the reference points from which the marginal densities are integrated in the definitions of the marginal distribution functions $F_1$ and $F_2$. Traditionally, the reference point used has been the origin, 0. However, for this choice, changes in the location parameters of the marginal distributions result in shape changes, not just location shifts, in the densities obtained using Eq. (1). To avoid such shape changes, we define $F_j(\theta ) \ (j=1,2)$ as $F_j(\theta )=\int _{\omega ^{A}_{j}}^{\theta }f_j(\varphi )\text {d}\varphi \ (\omega ^{A}_{j} \le \theta < \omega ^{A}_{j}+2\pi ),$ where $\omega ^{A}_{j}$ denotes the antimode of the circular density $f_j$.

We advocate the following sequential approach to modelling i.i.d. samples of random vectors $\{(\theta _{1k},\theta _{2k}); k=1,\ldots ,n\}$ exploiting the three-component structure of density (1). If the distributional forms of the marginal densities, $f_1$ and $f_2$, are not specified beforehand, histograms and/or kernel density estimates can provide insight into forms for them. Then, their parameters are initially estimated separately using ML. Denoting the marginal distribution functions corresponding to those parameter estimates by $\hat{F}^\text {s}_1$ and $\hat{F}^\text {s}_2$, next the ‘pseudo-sample’ $\{(\hat{\Psi }^\text {s}_{1k}, \hat{\Psi }^\text {s}_{2k}); k=1,\ldots ,n\} = \{(2\pi \hat{F}^\text {s}_1(\theta _{1k}), 2\pi \hat{F}^\text {s}_2(\theta _{2k})); k=1,\ldots ,n\}$ is computed. The procedures described in Sect. 4.1 are then applied to this pseudo-sample to obtain initial estimates of the form of the underlying circula density and its parameters. Finally, the estimates from the previous two stages are used as starting values in the maximization of the full log-likelihood function derived from (1). We denote the marginal distribution functions corresponding to the parameter estimates obtained in this final estimation stage by $\hat{F}_1$ and $\hat{F}_2$.

When the parameters of (1) are estimated as above, the samples $\{(2\pi \hat{F}_2(\theta _{2k}), 2\pi \hat{C}_{1|2}(2\pi \hat{F}_1(\theta _{1k})| 2\pi \hat{F}_2(\theta _{2k}))) ; k=1,\ldots ,n\}$ and $\{(2\pi \hat{F}_1(\theta _{1k}), 2\pi \hat{C}_{2|1}(2\pi \hat{F}_2(\theta _{2k})| 2\pi \hat{F}_1(\theta _{1k}))) ; k=1,\ldots ,n\}$ will be pseudo-uniformly distributed on the torus, and the goodness-of-fit of the fitted bivariate circular density can be tested using the parametric bootstrap approach referred to in Sect. 4.1.

Appendix E of the supplementary materials document explains how data from a circula density or a bivariate circular density of the form (1) can be tested for independence using the permutation approach proposed in Sect. 3.3 of Kato and Pewsey (2015).

5 Numerical experiment

As part of our investigations into the performance of the modelling approach based on (1) and our proposed circula densities, we performed an experiment designed to compare its large-sample modelling capabilities with those of five existing bivariate circular models. We simulated single samples of size $n=2000$ from each of the six models in Table 3, ranging from the 6-parameter pointwise symmetric model of Rivest (1988) to models capable of describing very varied distributional shapes. The parameter values in the same table were selected to produce representative unimodal cases of each model.

For each simulated sample we fitted all six models by ML, without pursuing model reduction, using R code developed by us and the CircNNTSR package of Fernández-Durán and Gregorio-Domínguez (2016) to fit the bivariate non-negative trigonometric sum (BNNTS) models. Table 4 contains the results obtained, the AIC values for the BNNTS models being those for the BIC-adjudged best fits, BIC being the model selection criterion advocated by Fernández-Durán and Gregorio-Domínguez (2014).

Table 3 Densities and parameter values of the six models used in simulations: Rivest (R); sine-skewed Sine (SsS); full bivariate von Mises (FBvM); bivariate generalized von Mises of order 2 (BGvM$_2$); (1) with Kato–Jones $f_j(\theta _j)$ and (14) as circula density (KJ$^2$(14)); bivariate non-negative trigonometric sum of order (1,2) (BNNTS(1,2)). Throughout, $c_{j}=\cos (\theta _j-\mu _j)$, $s_{j}=\sin (\theta _j-\mu _j)$ and $j=1,2$. The models are ordered, from top to bottom, by increasing number of parameters

Table 4 AIC (top) and BIC (bottom) values of the specified fitted models for samples of size $n=2000$ simulated using the model and parameter combinations in Table 3. The lowest off-diagonal values are highlighted in bold. The circula density of the best-fitting case of (1) with Kato–Jones marginal densities and one of our proposed circula densities (KJ$^2$Circ) is identified as (cd). The number of (free) parameters (np) for each fitted BNNTS model is that for the BIC-adjudged best fit

Using the column-wise sum of the ranks of the off-diagonal row-wise BIC values in Table 4 as a simple measure of overall performance, the following ordering, from best to worst, is obtained, with the sums of the ranks appearing between square brackets: BGvM$_2$ [7], BNNTS [15], FBvM [15 ], KJ$^2$Circ [16], R [18], SsS [19]. The analogous ordering for the AIC values is: BGvM$_2$ [7], BNNTS [11], FBvM [16], KJ$^2$Circ [17], R [19], SsS [20]. Both orderings identify the BGvM$_2$ model as having the best overall performance. The BIC-based measure identifies the KJ$^2$(13) model as having an overall performance similar to those of the BNNTS and FBvM models, with a marginally better overall performance than the R and SsS models. According to the AIC measure, BNNTS models perform second best, with the KJ$^2$(13) model performing similarly to the FBvM model and, again, marginally better than the R and SsS models.

We note that, for the samples from all five alternative models, the best-fitting case of (1) with Kato–Jones marginal densities and one of our proposed circula densities (KJ$^2$Circ) was the one incorporating circula model (13) (KJ$^2$(13)). This fact indicates that the circula structure underpinning the five alternative models can be approximately matched using just one of the circula models considered. Figures S11 and S12 present planar scatterplots of the six simulated data sets with contour plots of the best-fitting alternative and KJ$^2$Circ densities superimposed. They provide insight into the ability of the KJ$^2$Circ models to mimic the alternative models, and vice versa.

As the number of parameters of the underlying model increases, the performance of the KJ$^2$Circ and BNNTS models becomes increasingly competitive, although the latter generally have far more parameters than their KJ$^2$Circ counterparts. Also, while the interpretation of the parameters of KJ$^2$Circ models is straightforward, the interpretation of BNNTS parameters is generally impossible. The percentage increase in BIC for the best-fitting KJ$^2$(13) model above that for the best-fitting alternative model is largest for the sample from Rivest’s 6-parameter pointwise symmetric model (4.6%) and lowest for the data from the 10-(free)parameter BNNTS(1,2) model (0.6%).

6 Illustrative application

In contrast with the large sample size employed in Sect. 5, our illustrative analysis considers a much smaller sample of $n=80$ pairs of wind directions, $\{(\theta _{1k},\theta _{2k}), k=1,\ldots ,n\}$, recorded daily at a Milwaukee meteorological station at 4am and 6am, respectively, during the last three months of 2020. (This analysis was inspired by a related data analysis in Wehrly and Johnson (1980), which we have updated and expanded.) The data were extracted from the vast Milwaukee Met Data Archive series for 2020 available at https://www.glerl.noaa.gov/metdata/mil/archive/mil2020.01t.txt, and files containing them are included in the zip file linked to the supplementary materials document. Note that the archive does not include pairs of observations for the other 12 days of the trimester.

Given the two-hour separation between the measurements in each pair, one would expect them to be correlated. However, as the pairs span a trimester, it is not necessarily obvious what form of relation might exist between the pairs, nor what shapes the marginal distributions might exhibit. For the univariate time series, the only sample autocorrelation coefficient identified as being significantly different from 0 using the randomization version of the approach of Fisher (1993, Sect. 7.2.2) was the lag 1 coefficient for the 6am series, with an estimated p-value of 0.03 based on 9999 randomizations. However, the value of that autocorrelation coefficient is low (0.11) and in our analysis of the pairs of observations we treat them as forming an i.i.d. sample of toroidal data. Figure 5 includes a planar scatterplot of the data converted to radians in $[-\pi ,\pi )$, and Fig. 6a linear histograms of the $\theta _{1}$ and $\theta _{2}$ values. In the latter, the superimposed circular densities are those of Kato–Jones ML fits.

Fig. 5

Planar scatterplot of $\{(\theta _{1k},\theta _{2k}), k=1,\ldots ,n\}$ superimposed on a contour plot of the ML-fitted density for the full model (1) with marginal Kato–Jones densities and the circula density (11) with $q=1$

The pseudo-sample $\{(2\pi \hat{F}^\text {s}_1(\theta _{1k}), 2\pi \hat{F}^\text {s}_2(\theta _{2k})) ; k=1,\ldots ,n\}$ is portrayed in Fig. 6b. From an inspection of it, the dependence between the pseudo-circular uniform variates is positive, i.e. $q=1$. Figure 6c is a level plot of the absolute values of the empirical Fourier coefficients for that pseudo-sample and $q=1$. The largest absolute values can be seen to form a diagonal pattern, indicative of circula density (11) as a potential model for the underlying $c_\circ$. Figure 6d presents a planar scatterplot of $\{(2\pi \hat{F}_1(\theta _{1k}), 2\pi \hat{F}_2(\theta _{2k})); k=1,\ldots ,n\}$ superimposed upon a contour plot of the circula density from the fitted KJ$^2$(11) model.

The point estimates from the different stages of the fitting process are given in Table 5. Table 6 contains the AIC and BIC values for the KJ$^2$(11) model and the five alternative bivariate circular models employed in Sect. 5. Both criteria select the KJ$^2$(11) model, a member of the Wehrly and Johnson (1980) class with Kato and Jones (2015) circular marginal distributions and circula density (11), as being best. Contour plots of all six fitted densities are presented in Fig. S13. The densities of the models with the highest BIC-values, SsS and BNNTS, are bimodal.

The contour plot of the ML-fitted KJ$^2$(11) density included in Fig. 5 appears to describe the distribution of the observations well, and the scatterplots of the pseudo-toroidal uniform values in panels (e) and (f) provide little evidence of systematic departures from toroidal uniformity. Also, the goodness-of-fit testing approach of Pewsey and Kato (2016), using the Bingham-type test statistic for toroidal uniformity of Wellner (1979) and $B=999$ parametric bootstrap samples, returned a test statistic value of 2.63 and an estimated p-value of 0.33. Thus, there is no significant evidence against the KJ$^2$(11) model being a good model for the data.

Fig. 6

a Linear histograms of the wind directions with ML-fitted Kato–Jones circular densities (dashed curves) superimposed. Planar scatterplots of: b $\{{(2\pi \hat{F}^\text {s}_1(\theta _{1k}), 2\pi \hat{F}^\text {s}_2(\theta _{2k}))} ; k=1,\ldots ,n\}$, d $\{{(2\pi \hat{F}_1(\theta _{1k}), 2\pi \hat{F}_2(\theta _{2k}))}; k=1,\ldots ,n\}$ superimposed on a contour plot of the fitted circula density (11) from the full model fit, e $\{(2\pi \hat{F}_2(\theta _{2k}), 2\pi \hat{C}_{1|2}(2\pi \hat{F}_1(\theta _{1k})| 2\pi \hat{F}_2(\theta _{2k}))); k=1,$ $\ldots , n\}$, f $\{(2\pi \hat{F}_1(\theta _{1k}), 2\pi \hat{C}_{2|1}(2\pi \hat{F}_2(\theta _{2k})| 2\pi \hat{F}_1(\theta _{1k}))); k=1,\ldots ,n\}$. c Level plot of the absolute values of the empirical Fourier coefficients for the pseudo-sample in b and $q=1$

Table 5 Components of model (1) fitted to the wind direction data, parameters of the two marginal Kato–Jones densities and the circula density (11), MM and ML estimates for the parameters of the Kato–Jones densities fitted separately to the $\theta _1$ and $\theta _2$ values (MM$_\text {s}$ and ML$_\text {s}$), MM and ML likelihood estimates for the parameters of the circula density (11) with $q=1$ fitted to the values of $\{(2\pi {\hat{F}^\text {s}_1}(\theta _{1k}), 2\pi {\hat{F}^\text {s}_2}(\theta _{2k})) ; k=1,\ldots ,n\}$ (MM$_{c_\circ }$ and ML$_{c_\circ }$), and ML estimates for the full model (ML$_\text {f}$)

Table 6 AIC (top) and BIC (bottom) values of the specified fitted models for the $n=80$ pairs of wind directions. The number of (free) parameters (np) for the BNNTS model is that for the BIC-adjudged best fit. The lowest values are highlighted in bold

The KJ$^2$(11) model identified in our structured sequential analysis postulates the underlying marginal circular distributions of the wind directions at 4am and 6am to be symmetric cases of the unimodal Kato–Jones family with very similar parameter values. Given the 2-hour separation between the two wind direction measurements, the similarity between the marginal distributions is perhaps to be expected. The fitted model also postulates that the positive dependence between the pairs of wind directions can be modelled using a circula with density (11) and $q=1$. From the results in Jones et al. (2015), this implies that $\Psi _2=2\pi F_2(\Theta _2)$ is the result of a random rotation, $\Omega$, from $\Psi _1=2\pi F_1(\Theta _1)$, $\Omega$ being independent of $\Psi _1$ and having circular density $g(\omega )=2\pi \times$(11) with $\psi _1-\psi _2=\omega$.

7 Conclusion

As the specific models introduced in Sect. 3 illustrate, the proposed general Fourier series construction provides a means of generating tractable parametric circula densities with simple closed-form expressions and wide-ranging distributional shapes. Moreover, when combined with Kato and Jones (2015) circular densities through (1) they provide highly flexible models for toroidal data for which the marginal distributions are unimodal. Multimodal toroidal data can be modelled using mixtures of such models.

The flexibility of the circula densities can be further enhanced by allowing the Fourier series coefficients to be complex. The main effect of such an extension is to skew the circula distributions in various ways.

Stationary Markov models for circular time series can be defined from our circula densities using an analogous approach to that of Wehrly and Johnson (1980).

In principle, our bivariate circula construction can be extended to produce d-dimensional circula densities using the multivariate analogue of (3) and patterns of nonzero Fourier coefficients distributed in d dimensions. Another possibility is, as mentioned in Jones et al. (2015), to model multivariate circular data using the circular analogues of pair copulas.

Our proposed methodology makes use of level plots of the absolute values of empirical Fourier coefficients computed from pseudo-samples as a highly successful model identification tool. We stress again that such plots are generally easier to interpret than scatterplots of the pseudo-samples themselves because they usually provide insight into the structure of the Fourier coefficients of the underlying circula density.

The advantage of the modelling approach based on (1) is that it facilitates the separate modelling of the circular marginals and a circula density in a structured sequential way. Also, as we have illustrated, it accommodates formal goodness-of-fit testing, an issue neglected in the literature related to the application of existing models for toroidal data.