1 Introduction

Latent class analysis (LCA) (Goodman , 1974; Lazarsfeld and Henry , 1968), a statistical technique for model-based clustering, is widely used in the field of social and behavioral science. LCA identifies classes of people that are homogenous with respect to their scores on a set of indicators. Covariates can be related to class membership, for instance, by using multinomial logistic regression (Bandeen-roche et al. 1997; Dayton and Macready 1988). More recently, LCA is becoming more popular in medical research, for instance, to asses health-related quality of life (HRQOL) based on patient reported outcome measures (PROMS) (Clouth et al. 2020; Kelly et al. 2018; Larsen et al. 2017; Miaskowski et al. 2015). Furthermore, the effect of a certain treatment strategy on such HRQOL classes might be of interest. Such treatment effects can be assessed with randomized controlled trials (Greenland et al. 1999; Twisk et al. 2018). However, randomization into treatment and control groups is not always possible or there is an explicit choice for observational studies with a non-randomized design. Under the identifiability conditions of consistency, exchangeability, and positivity, causal inference techniques such as inverse propensity weighting (IPW) can be used to identify average treatment effects (ATE) (Imbens , 2000). Lanza et al. (2013) presented one approach for using IPW and matching on the propensity score in LCA and several extensions have been proposed thereafter (Bartolucci et al. 2016; Suk and Kim 2019; Tullio and Bartolucci 2019). In this paper, we will discuss a conceptual problem with this approach and propose an alternative strategy for including IPW in LCA.

In randomized controlled trials, assignment into treatment vs. control groups is randomized with the effect that both groups will, at baseline, be balanced on their covariates such as demographics and clinical characteristics. However, when randomization into intervention groups is not possible, causal inference techniques allow for the identification of the ATE based on observational data under previously mentioned identifiability conditions (Hernán and Robins , 2006). Traditionally, researchers used to estimate the conditional treatment effect. Here, the treatment effect is adjusted for the observational design by including all relevant observed confounders in a regression model. However, more recently, researchers prefer to use methods to estimate the marginal treatment effect. Most commonly, direct matching (Rosenbaum 1999), matching on the propensity score (Austin 2011), IPW (Imbens , 2000; Robins et al. , 1995), subclassification (Rosenbaum and Rubin 1984), and doubly robust methods (Bang and Robins 2005) are used. The common idea behind these methods is to generate synthesized data as if it comes from a randomized controlled trial. Then, any difference in the outcome between the two groups represents the marginal treatment effect. Both, from a conceptual and practical point of view, many researchers prefer these methods for estimating the marginal treatment effect as they separate the adjustment for confounding from the estimation of the treatment effect. For an extensive discussion on this see Austin (2011).

When data is observational rather than randomized, the selection into a treatment group vs. control group usually follows clinical indication. E.g., for low-stage prostate cancer patients, immediate treatment such as the resection of the tumor is not always necessary as this particular type of cancer progresses very slowly. For many of these patients, an active surveillance strategy is a beneficial alternative to a cancer treatment with considerable risks of severe side effects (Mohler et al. 2019). However, patients with a high Gleason score indicating an aggressive tumor, will usually receive treatment (Cher et al. 2017). As for these patients also a worse outcome is to be expected, the effect of the received treatment when comparing these two groups will be confounded by the Gleason score. The idea of the previously mentioned causal inference methods is to control for this confounding. For propensity score methods, a model for predicting the probability of receiving treatment is estimated based on all observed confounding variables. This propensity score reduces each individual’s set of covariates to a single score (Imbens 2000). Most commonly, logistic or probit regression models are used but more complex machine learning algorithms are recently explored for this purpose as well (Austin 2011). For instance, each patient that received treatment can be matched with a patient that did not receive treatment if that patient has a similar propensity score. Alternatively, each patient can be weighted with an individual weight based on the inverse of the propensity score (Imbens 2000). A patient with a low probability of receiving treatment that actually received treatment (hence, a combination that is rather uncommon in the data) will be up-weighted while a patient with a high probability of receiving treatment that actually received treatment (hence, a common combination) will be down-weighted. Under the identifiability conditions, both strategies will achieve a synthesized data set where the treatment group and the control group are balanced on the observed confounders (Austin 2011). Any difference in outcome between these groups can, hence, be attributed to the difference in treatment. In real-life applications, there might be a substantial number of confounding variables and, naturally, not all of them will be observed. This is a well-known problem in the causal inference literature and will not be discussed here.

These causal inference methods are easily combined with standard statistical models such as generalized linear models or survival analysis. However, often the outcome of interest is not directly observable and a measurement model for the outcome is needed. In cancer survivorship research, patient reported outcome measures (PROMS) such as the European Organisation for Research and Treatment of Cancer (EORTC) Quality of Life Questionnaire (Sprangers et al. 1993) or the EuroQol 5D (The EuroQol Group 1990) are widely used tools to asses a patient’s HRQOL. One obvious research question in this case is to identify the effect of a certain cancer treatment on the survivors’ HRQOL. PROMS use items to measure the construct of HRQOL and when assessed in an observational study, a combination of LCA and causal inference techniques is needed.

To include propensity score methods in LCA, Lanza et al. (2013) introduced an analysis strategy consisting of variable selection, a multiple imputation step for missing covariates, estimation of the propensity scores, calculation of weights or matching based on the propensity score, assessing balance, conducting LCA with treatment as a covariate, and pooling of the results from the imputation steps. Crucially, this approach consist of weighting or matching the full data set and then conducting LCA on this weighted or matched data in one step. While this strategy should, in theory, achieve the correct estimation of the treatment effect, it is problematic for two reasons.

First, it is unknown how using IPW as proposed by these authors affects the measurement model estimates in LCA. The authors indicated that by conducting a LCA on a weighted or matched data set, they are able to deal with the fact that the measurement model parameters, i.e., the item response probabilities, may be affected by the confounders used to construct the propensity scores. That is, they seem to claim to be able to deal with measurement non-invariance (MNI) or differential item functioning (DIF). However, it is unclear whether using IPW or matching resolves MNI, since the state-of-art approach is to include covariates causing DIF in the LCA and allow them to have direct effects on the indicators (Kankaraš et al. 2010). Second, when estimating the LCA model on weighted or matched data, the classes can no longer be interpreted as being based on the indicators alone as all confounders included in a propensity score model may also affect the estimates. In fact, it is unknown how the use of IPW affects the measurement model estimates in LCA. In their illustrative application of the their method, the authors showed that the use of IPW can alter the measurement model parameters substantially even in terms of the number of classes (Lanza et al. 2013), which is problematic for the interpretation of the ATE too as it may no longer represent the effect on class membership reflecting the outcome of interest. Furthermore, in LCA, selecting the right number of classes is an important and far from straight forward process. Information criteria such as the Bayes information criteria (BIC) (Schwarz , 1978) or the Akaike information criteria (AIC) (Akaike , 1974) and significance testing approaches such as the bootstrap likelihood ratio test (BLRT) (Tekle et al. 2016) are frequently used. However, these criteria are often in disagreement with each other and domain knowledge needs to be used to decide on the optimal number of classes. When conducting LCA with covariates, the recommended strategy is to perform model selection on the latent class model without covariates (thus, the measurement model) and, in a second step, include the covariates in the LCA with the pre-defined number of classes (Nylund-Gibson and Masyn , 2016). Using IPW or matching complicates this process further. As both alter the original data set, the model selection process may result in a different number of classes when performed on the weighted or matched data set.

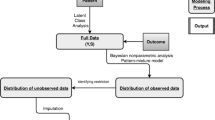
We propose an alternative strategy for incorporating IPW in LCA in which the estimation of the measurement model is fully separated from the estimation of the ATE. Our approach is based on a modification of the three-step approach proposed by Vermunt (2010) by using IPW in the third step. First, the measurement model, that is, the LCA without covariates, is estimated on the unweighted data and model selection is performed in the usual way. Second, observations are classified based on their posterior class membership probabilities obtained in step one and the resulting classification error probabilities for each class are calculated. Third, treatment as the only covariate is related to the assigned classes, where the classification errors are included as part of the model to obtain unbiased estimates for the treatment effects. For our approach, we introduce a weight, the inverse of the propensity score, in this last step. This stepwise approach not only simplifies model selection but also resolves several of the conceptual problems associated with the approach by Lanza et al. and therefore allowing for a clearer interpretation of the classes and the treatment effect.

In the following sections, we describe the new three-step approach which includes IPW for determining treatment effects, investigate its performance in a simulation study, and illustrate its use in a real data application. We end with a discussion and conclusion section.

2 Three-step LCA with IPW

In this section, we first present the three steps of a bias-adjusted three-step LCA with covariates, after which we show how this approach can be extended to include IPW weighting in the third step.

2.1 Bias-adjusted three-step LCA

Let \(Y_{ij}\) denote the response of individual i on the \(j_{th}\) categorical response variable, J the number of response variables, and \(R_{j}\) the number of categories of the \(j_{th}\) response variable. Moreover, let X represent the discrete latent variable, t a particular latent class, and T the number of classes. A latent class model for the response vector \(Y_{i}\) of individual i can be defined using the following mixture equation:

$$\begin{aligned} P(Y_{i})=\sum _{t=1}^{T}P(X=t) P(Y_{i} | X=t), \end{aligned}$$
(1)

with the fundamental local independence assumption stating that responses are independent given class membership:

$$\begin{aligned} P(Y_{i} | X=t)=\prod _{j=1}^{J}P(Y_{ij} | X=t)=\prod _{j=1}^{J}\prod _{r=1}^{R_{j}}\alpha _{tjr}^{\delta _{ijr}}. \end{aligned}$$
(2)

Here, \(\alpha _{tjr}\) is the probability of response r on the item j given membership in class t and \(\delta _{ijr}\) is an indicator variable for individual i on this response. For nominal responses, alpha can be estimated with an unrestricted multinomial logistic regression model whereas for ordinal responses, a restricted model is used. Class proportions \(\varTheta _{t}=P(X=t)\) and item response probabilities \(\alpha _{tjr}=P(Y_{ij}=r | X=t)\) can be estimated by maximum likelihood.

Estimation of the measurement model described in equations  1 and  2 defines the first step of a three-step LCA (Vermunt 2010). In the second step, the class memberships of the individuals are determined using their posterior class membership probabilities \(P(X=t | Y_{i})\). The most common methods are modal and proportional class assignment, which involve assigning individuals to the class with the largest posterior probability and to all classes with weights equal to the posterior probabilities, respectively. We refer to the resulting class assignments as W. Essential to the bias-adjusted three-step approach is the identification of the (imperfect) relationship between the assigned class memberships W and the true class memberships X. The classification error probabilities \(P(W=s | X=t)\) can be easily obtained as follows:

$$\begin{aligned} P(W=s | X=t)=\frac{\sum _{i=1}^{N}P(X=t | Y_{i})P(W_{i}=s | Y_{i})}{N*P(X=t)}. \end{aligned}$$
(3)

Here, \(P(W_{i}=s | Y_{i})\) depends on the classification rule. Under modal assignment, it equals 1 for the class with the highest posterior class membership probability and 0 for all other classes, while under proportional assignment, it equals the posterior class membership probability itself (Dias and Vermunt , 2008; McLachlan and Peel , 2000).

In the third step, the relationship between class membership and covariates is investigated. For this purpose, the class membership probabilities are modelled by means of a multinomial logistic (MNL) regression:

$$\begin{aligned} P(X=t | \mathbf{Z }_{i})=\varTheta _{t | \mathbf{Z }_{i}}=\frac{exp(\gamma _{0t}+\sum _{q=1}^{Q}\gamma _{qt}Z_{iq})}{\sum _{t=1}^{T}exp(\gamma _{0t}+\sum _{q=1}^{Q}\gamma _{qt}Z_{iq})}, \end{aligned}$$
(4)

with \(Z_{iq}\) being one of Q covariates and \(\gamma 's\) representing free parameters. Key of the bias-adjusted three-step approach is that this regression equation can be estimated using the class assignments W. More specifically, Bolck et al. (2004) showed that \(P(W=s | \mathbf{Z }_{i})\) is related to \(P(X=t | \mathbf{Z }_{i})\) as follows:

$$\begin{aligned} P(W=s | \mathbf{Z }_{i})=\sum _{t=1}^{T}P(X=t | \mathbf{Z }_{i})P(W=s | X=t). \end{aligned}$$
(5)

As pointed out by Vermunt (2010), the model parameters of this model can be obtained by maximizing the following log-likelihood function:

$$\begin{aligned} logL_{W}=\sum _{i=1}^{N}\sum _{s=1}^{T}P(W_{i}=s | Y_{i})ln\left\{ \sum _{t=1}^{T}\varTheta _{t | \mathbf{Z }_{i}}P(W=s | X=t)\right\} , \end{aligned}$$
(6)

where the \(P(W_{i}=s | Y_{i})\) serve as weights which as discussed above depend on the classification rule. The \(P(W=s | X=t)\) are obtained as shown in Eq. 3 and do not need to be estimated anymore. Optimizing 6 will yield the \(\gamma \) parameters appearing in the MNL regression of \(\varTheta _{t | \mathbf{Z }_{i}}\) (see Eq. 4).

2.2 Modification of the third step for the estimation of a treatment effect

Let us now look at how to modify the third step of a three-step LCA for the estimation the ATE using IPW. Here, we define the ATE as the difference between the class membership probabilities of a certain class when receiving treatment vs. being in the control group. First of all, we need to obtain propensity scores, typically denoted by \({\hat{\pi }}\), that reflect the probability of receiving a treatment conditional on a set of measured confounders C. In this study, we derive propensity scores using logistic regression:

$$\begin{aligned} {\hat{\pi }}_{i}=\frac{exp(\beta _{0}+\sum _{q=1}^{Q}\beta {q}C_{iq})}{1+exp(\beta _{0}+\sum _{q=1}^{Q}\beta {q}C_{iq})}. \end{aligned}$$
(7)

However, as alternatives probit regression and machine learning algorithms are frequently used (Austin , 2011). The weights for IPW equal \(ipw_{i}=1/{\hat{\pi }}_{i}\) for individuals that received treatment and \(ipw_{i}=1/1-{\hat{\pi }}_{i}\) for individuals that did not receive treatment. While these weights are used for estimating the ATE for the entire population, alternatively weights yielding estimates of the ATE among the treated could be used. To derive causal relations from the estimates, it is crucial to check for assumptions underlying these causal inference techniques such as overlap of propensity scores and balance on the confounders for the treatment and control group (Austin , 2011). Note that the estimation of the propensity scores and the construction of the weights are an additional step and being done separately from the estimation of the third step.

The inverse propensity weights \(ipw_{i}\) can be included as fixed weights in the estimation of the third step of a three-step LCA by rewriting the pseudo-log-likelihood function as:

$$\begin{aligned} logL_{W}=\sum _{i=1}^{N}\sum _{s=1}^{T}ipw_{i}P(W_{i}=s | Y_{i})ln\left\{ \sum _{t=1}^{T}\varTheta _{t | \mathbf{Z }_{i}}P(W=s | X=t)\right\} . \end{aligned}$$
(8)

Note that the MNL model for \(\varTheta _{t | \mathbf{Z }_{i}}\) now contains the treatment variable as the single predictor. As can be seen, the modification compared to Eq. 6 is that the weights used in the estimation of the parameters in \(\varTheta _{t | \mathbf{Z }_{i}}\) are now a product of the \(ipw_{i}\) and the class assignment weights \(P(W_{i}=s | Y_{i})\). As in Eq. 6, this third step represents a latent class model where the class assignment W serves as a single indicator and the error probabilities \(P(W=s|X=t)\) are known. The estimates for the treatment effect \(\varTheta _{t | \mathbf{Z }_{i}}\) are obtained by maximizing the log likelihood function in Eq. 8. As in a standard step-three LCA, cluster robust standard errors (Colin Cameron and Miller , 2015) can be used to account for the weighting and in the case of proportional assignment also for the fact that each person has T observations. However, in this step-wise procedure, both the inverse propensity weights as well as the classification error probabilities are treated as being known while they are actually estimated. Standard errors might therefore be slightly underestimated.

3 Simulation study

We conducted a simulation study to compare the performance of our newly proposed “three-step” method with the “one-step” method proposed by Lanza et al. (2013) (Fig. 1b) and with a “regression-adjusted” method (Fig. 1c) for estimating the ATE. The “regression-adjusted” method consists of a one-step LCA where the two confounders are entered in the model as covariates additional to the treatment variable. This "regression-adjusted" method represents the regression adjustment for estimating the conditional treatment effect. Essentially, it estimates the direct paths of the treatment and the confounders on the outcome. It, therefore, represents the data-generating model while ignoring the effect of the confounders on treatment allocation. However, this does not affect the estimate of the treatment effect. In this simulation study, the "regression-adjusted" method can be regarded the "gold standard". The performance was assessed based on the parameter bias and variation of the ATE for varying sample sizes, strength of the ATE, and strength of the confounding.

Fig. 1
figure 1

Graphical depiction of a the data generating model used in the simulation study, b the one-step and three-step method using IPW, and c the regression-adjustment method

Full size image
Table 1 Class membership probabilities for the control and treatment group and resulting average treatment effects (ATE) for varying levels of effect size (\(\gamma _{Z}\))
Full size table
Fig. 2
figure 2

Bias of the estimate of the average treatment effect (ATE) for the regression-adjusted, one-step, and three-step method, averaged over 1000 replications, respectively. Results are presented for three levels of effect size, confounding, and sample size, respectively

Full size image

3.1 Design

As the population model (Fig. 1a), we used a latent class model with 3 classes, 6 dichotomous indicators (high/ low), one treatment variable Z (0 = control, 1 = treatment), and two categorical confounders (−.5; .5 for \(C_{1}\) and −2; −1; 0; 1; 2 for \(C_{2}\)). Class 1 was most likely to give a high response on all 6 indicators (item response probability of .8) and class 3 was most likely to give a low response on all 6 indicators (item response probability of .2). Class 2 was most likely to give a high response on the first 3 indicators (item response probability of .8) and most likely to give a low response the last 3 indicators (item response probability of .2). These values were taken from the simulation setup in Vermunt (2010) and refer to moderate class separation and a pseudo \(R^{2}\) of .63. We choose this setting because moderate class separation is the situation in which the bias adjustment in the third step is most useful, but at the same time has been found to be challenging for the three-step approach. With very good class separation, the three-step approach always performs very well, while with very poor class separation, it is questionable whether it makes sense to look at covariate effects (here the treatment effects) on class membership in the first place.

The effect of the treatment and the confounders on the classes were modeled using logistic regression with class 1 as the reference category:

$$\begin{aligned} logit(X | C_{1}, C_{2}, Z)=.5+1*C_{1}+1*C_{2}+\gamma _{Z}*Z \end{aligned}$$
(9)

with \(logit(P) = log(P/1-P)\) where \(\gamma _{Z}\) was kept constant for class 2 (\(\gamma _{Z}\)=1) and varied for class 3 (\(\gamma _{Z}\)=[1;2;3]). The effect of the confounders on the treatment assignment was also modeled using logistic regression:

$$\begin{aligned} logit(Z | C_{1}, C_{2})=0+\beta _{1}*C_{1}+1*C_{2} \end{aligned}$$
(10)

where \(\beta _{1}\) took the values 1, 2, and 3.

The ATE can then be defined as the average difference in class proportions between the treatment and the control group across values of \(C_{1}\) and \(C_{2}\) (Table  1). As \(\gamma _{Z}\) was varied for class 3, we compared the performance of the three methods on the parameter for the ATE of class 3. Therefore, the effect of \(\gamma _{Z}\)=1 relates to class proportions of 34.7% for individuals who did not receive treatment and 41.3% for individuals who did receive treatment and an ATE of 6.6%. For \(\gamma _{Z}\)=2, the ATE is 30.2% and for \(\gamma _{Z}\)=3, the ATE is 48.2%. Note that the three levels for the \(\gamma _{Z}\) parameter yield a non-linear increase in the ATE. Furthermore, a large ATE also yields more unequal class proportions (class 3 becomes larger). The bias of the ATE for class 3 is defined as the difference between the estimate of the ATE and the true ATE. The variation of the estimate was assessed by the standard deviation (SD) of the ATE over 1000 replications. Furthermore, the standard error averaged over all replications was compared to the SD of the estimate to asses bias in the SE. We used sample sizes of 500, 1000, and 2500.

3.2 Results

Figures 2 and 3 present the average bias and the SD of the estimates of the ATE averaged over 1000 replications for the nine conditions investigated (\(\gamma _{Z}\)=[1,2,3] and \(\beta _{1}\)=[1,2,3]) for sample sizes of 500, 1000 and 2500.

Fig. 3
figure 3

Standard deviation (SD) of the estimate of the average treatment effect (ATE) for the regression-adjusted, one-step, and three-step method over 1000 replications, respectively. Results are presented for three levels of effect size, confounding, and sample size, respectively

Full size image
Fig. 4
figure 4

Bias of the standard error (SE) of the estimate of the average treatment effect (ATE) for the regression-adjusted, one-step, and three-step method, averaged over 1000 replications, respectively. Results are presented for three levels of effect size, confounding, and sample size, respectively

Full size image

For a small effect size, all methods produce parameter estimates with almost no bias. For larger effect sizes, this is also true for a large sample size of N = 2500. For smaller sample sizes and large effect sizes, the three-step approach underestimates the ATE. However, note that the largest ATE relates to a difference of 48.2 percentage points between the treatment and the control group. A bias of about two percentage points might, therefore, be regarded as small. The strength of the confounding only has a small effect for N = 500.

Both, the three-step and the one-step method, are less efficient (show larger variability) than the regression-adjusted method. This loss of efficiency is a well-documented finding for estimating methods that make use of weighting of observations. Furthermore, the variability of the estimates is mainly affected by sample size. However, while the regression-adjusted method is unaffected by varying levels of confounding, both, the one-step and the three-step method, show higher variability for larger effects of confounding (when more unequal weighting is needed). Effect size does not affect the variability of the estimates. Overall, the SEs (Fig. 4) are returned without noticeable bias for large sample sizes and with small bias for small sample sizes.

4 Real-world application using prostate cancer treatment data

Prostate cancer is the most prevalent cancer in men in the Western countries (Siegel et al. 2020). Patients newly diagnosed with localized prostate cancer can choose between several treatment options (such as surgical resection of the tumor, external beam radiotherapy, brachytherapy, and active surveillance) that have equivalent outcomes in survival but differ in their risk of adverse side effects and long-term HRQOL (Mols et al. 2009, 2006; Thong et al. 2010). Active surveillance refers to the systematic monitoring of patients with low-risk prostate cancer who choose against curative treatment at diagnosis. When the tumor shows signs of progression or the patient decides to change treatment, patients receive subsequent curative treatment (Cher et al. 2017). While active surveillance is the least invasive treatment option it has been found to be associated with higher levels of anxiety and feelings of uncertainty (Dall’Era et al. 2012). In this section, we demonstrate how our newly proposed method can be used to estimate the ATE of receiving curative treatment vs. active surveillance for a sample of low-risk prostate cancer patients.

Fig. 5
figure 5

Bayesian Information Criterion (BIC) for models with 1–10 classes estimated with the one-step method and the three-step method, respectively

Full size image
Fig. 6
figure 6

Profiles of the three classes estimated with the three-step method. Per class, the average score on all 15 dimensions of the EORTC QLQ-C30 are presented. Abbreviations: ql global quality of life score, pf physical functioning, rf role functioning, ef emotional functioning, cf cognitive functioning, sf social functioning, fa fatigue, nv nausea/vomiting, pa pain, dy dyspnea, sl insomnia, ap appetite loss, co constipation, di diarrhea, fi financial problems

Full size image

4.1 Settings and participants

In 2011, a random selection of patients diagnosed with prostate cancer between 2006 and 2009 in 7 hospitals in the south of the Netherlands were invited by their medical specialist for participation in a study. In total, 999 participants were approached and 697 patients agreed to participate (70% response rate).

Data were collected in October 2011 within Patient Reported Outcomes Following Initial Treatment and Long-Term Evaluation of Survivorship (PROFILES) (van de Poll-Franse et al. 2011). PROFILES is linked directly to clinical data from the Netherlands Cancer Registry. Urologists sent their (former) patients a letter to inform them about the study and to invite them to complete an online questionnaire. On request, patients received a paper questionnaire that could be returned in a pre-stamped envelope. A reminder was send within two months to non-respondents. For this analysis, only patients with tumor stage I or II were included as only for this group of patients it is reasonable to assume both treatment strategies to be realistic options.

The study was approved by the Medical Ethics Committee of the Maxima Medical Centre, the Netherlands.

4.2 Data collection

Socio-demographic data was collected by means of questionnaires. Clinical data was extracted from the Eindhoven Cancer Registry. HRQOL was assessed through the European Organization for Research and Treatment of Cancer Quality of Life Questionnaire(QLQ)-C30 (Niezgoda and Pater , 1993). The EORTC QLQ-C30 includes 30 items, divided in five functional scales (physical, role, emotional, social and cognitive functioning), three symptom scales (fatigue, pain and nausea/vomiting) and seven single items resulting in 15 dimensions. Scores were linearly transformed to a 0-100 scale, with higher scores representing better HRQOL/functioning (Fayers et al. 2001).

4.3 Analysis strategy

First, a LCA without covariates was estimated using the 15 EORTC QLQ-C30 dimension scores as ordinal indicators. Models with 1 to 10 classes were estimated and the BIC was used to determine the optimal number of classes. Second, propensity scores for all patients were estimated using logistic regression. Confounders included in this model were age (in categories of 5 year intervals), tumor stage, and the Gleason score (in categories, <7, 7 and 8–10). For these confounders, missing values were included as an additional category. Subsequently, overlap of the propensity scores and balance on the included confounders between the treatment and active surveillance group were assessed (Table 2). Other possible confounders such as BMI, smoking, and alcohol consumption were included in subsequent sensitivity analyses but did not show any improvement for achieving balance between the treatment groups. Lastly, the effect of receiving curative treatment on class membership was estimated using the new three-step method. Additionally, the treatment effect was estimated with the one-step and the regression-adjusted method. Data preparation and estimation of the propensity score model were conducted in R version 3.6.0 (R Core Team , 2019) and the latent class models were estimated using LatentGOLD version 6.0 (Vermunt and Magidson , 2020) and the code is freely available at GitHub (Clouth , 2021). The data can be made available upon request.

Fig. 7
figure 7

Overlap of the propensity scores for the treatment and the active surveillance group

Full size image
Table 2 Descriptive statistics before and after weighting for the three confounders used to estimate the propensity scores
Full size table

4.4 Results

In total 496 prostate cancer patients were included in this analysis. In this sample, about 50% of the male patients were between 65 and 75 years old, 59% had a tumor stage I, 41% tumor stage II, 60% had a Gleason score <7, 25% had a Gleason score of 7, and 12% had a Gleason score of 8-10 (3% missing values).

Figure 5 shows the BIC for the 1 to 10 class models. The 3 class solution yielded the lowest BIC and was selected. Note that for the approach proposed by Lanza and colleagues, the BIC on this data was inconclusive indicating >10 classes. With 46% the biggest class, class 1 is characterized by very good overall HRQOL. Class 2 (39%) is characterized by moderate to good HRQOL and class 3 (15%) is characterized by low to moderate HRQOL (Fig. 6).

Propensity scores for the treatment and active surveillance group show sufficient overlap (Fig. 7). Table 2 shows the standardized mean differences (SMD) on confounders before and after weighting. With almost all SMD below .1 in absolute value, there is evidence that balance was achieved using IPW.

Fig. 8
figure 8

Class membership probabilities for the treatment and the active surveillance group estimated with the three-step, one-step, and regression-adjusted method

Full size image

Figure  8 represents the effect of receiving curative treatment vs. active surveillance on the probability of class membership estimated with our proposed three-step method. Additionally, the figure shows the same parameters estimated with the one-step and regression-adjusted method. For the three-step method, the probability of class membership in class 1 (44% vs. 40%) was slightly higher for the treatment group than for the active surveillance group. For class 2, this probability was almost the same for both groups (40% vs. 39%) and for class 3, it was higher for the active surveillance group (16% vs. 21%). The results for the one-step method were similar in the direction of the effect, however, the differences in class membership probabilities between the treatment and active surveillance group were larger (48% vs. 40% for class 1, 39% vs 41% for class 2, and 14% vs. 20% for class 3). In contrast, for the regression-adjusted method, the effect of initial treatment vs. active surveillance pointed in opposite directions (45% vs. 46% for class 1, 37% vs. 46% for class 2, and 19% vs. 8% for class 3). Furthermore, the treatment effects presented here did not yield statistically significant differences.

4.5 Discussion

According to the effect sizes estimated with the one-step and three-step IPW methods, prostate cancer patients seemed to experience slightly lower HRQOL when following an active surveillance regime. However, the sample size in this sample was too small to generalize this treatment effect to the population of stage I-II prostate cancer patients. A limitation of both IPW methods that also became apparent in this application is the possibility of a few patients receiving extremely large weights. That is, the largest weight observed in this study was about 36 which corresponds to about 9% of the sample size. Single observations receiving such a great weight increases the variance of the estimate. Trimming (Stürmer et al. 2000) of these weights can increase the efficiency of the estimate, however, in this application, trimming also decreased the balancing property of IPW to an unacceptable extent (results not presented). Using stabilized weights (Robins et al. 2000) decreases variance without affecting balance and yielded similar results as presented in this application. Furthermore, a problem with using the regression adjustment method in LCA became apparent in this application. When using several categorical confounders for adjustment, some of the category combinations might only have few or none observations. In the presence of a rather small class, a class of 10% of the sample size is not uncommon in LCA, this scenario is even more likely and can lead to severe problems in estimation. The effect size showing in the opposite direction in this application, although not significant, can, therefore, not be trusted.

5 Discussion

In this study, we proposed a novel approach of incorporating IPW in LCA to estimate ATEs by adjusting for confounding in observational data. This method is based on the three-step approach (Vermunt , 2010) and separates the estimation of the measurement model from the estimation of the ATE. We compared this new approach to the existing one-step approach by Lanza and colleagues (Lanza et al. , 2013) and a regression-adjusted approach in which the confounders are entered in the model as covariates in a simulation study and a real data application investigating the effect of treatment vs. active surveillance on HRQOL classes in prostate cancer patients. Both, the one-step and the three-step approach, performed reasonably well with a bias of mainly below one percentage point. This result is to be expected as weighting generally does not induce bias if the model for the weights is correctly specified. That IPW in the one-step approach also affects the measurement model does not change this as, overall, the average of all patient specific measurement models reflects a measurement model that would have been estimated without weighting. Compared to the three-step approach, this shows that altering the measurement model on average still leads to the correct estimation of the ATE. For large effect sizes, the three-step method may underestimate the ATE. This slightly higher bias, especially for small sample sizes, is to be expected as well, as introducing an additional step of accounting for the classification errors (additional to the IPW) when estimating the ATE may cause additional bias. Note, that we used a simulation setting with moderate class separation because this setting is known to be challenging for the three-step approach. With better class separation, the ATE will be less underestimated and with worse separation, it is questionable if covariates should be related to class membership in the first place. However, IPW does not seem to increase this problem as long as the model for the propensity scores is correctly specified. Introducing IPW, as introducing weights of any kind, increases the variation of the estimates. As the one-step approach also uses the differential weighting for the estimation of the measurement model, an additional source of variation is introduced compared to the three-step approach where the measurement model is estimated without weighting.

The one-step and the three-step approach use the same conceptual framework for estimating the ATE. In both cases, weights based on the probability of receiving treatment are used to achieve a data set that is balanced on observed confounders at baseline and the models for estimating these propensity scores are identical. The only difference between the two approaches is the order in which the estimation is conducted. In the one-step approach, the data set is weighted first and the ATE is estimated simultaneously with the measurement model of the LCA. In the three-step approach, the measurement model is estimated first and IPW is only used to estimate the ATE in a separate step. This difference has a major practical implication when the data contains missing values on the observed confounders. As the propensity score model does not allow for missing values in the predictors, an additional step of conducting multiple imputation is needed. However, since also the measurement model needs to be estimated for each imputed data set, model selection might be ambiguous as different sets might show different results for the optimal number of classes. Even with the same number of classes, there is no guarantee that the classes have the same interpretation over the imputed sets. As a consequence, it is impossible to obtain a meaningful result for the ATE when pooling estimates over the imputed data sets. The three-step approach prevents this issue by estimating the measurement model before the missing values need to be imputed.

There are some limitations to our study worth mentioning. To draw valid conclusions from results obtained with causal inference tools, a set of assumptions needs to be met. In our simulation study, we did not investigate any consequences of violating these assumptions. However, in our real data application, we observed different results obtained with the IPW methods compared to the regression-adjusted method. It is possible that these differences are due to violations of these assumptions. Furthermore, we investigated the scenario of the confounders affecting the treatment and the class membership but not the item response probabilities. While it is, in principal, possible to include direct effects to account for measurement non-invariance in our three-step method, the consequences of such effects need further research. Lastly, in this simulation study, we assumed no missingness in the confounders. While it is possible to include multiple imputation for the propensity score model in the three-step method, the effect of missing information was not investigated.

6 Conclusion

In this study, we proposed a method for incorporating IPW in LCA using the three-step approach. This approach separates the estimation of the measurement model from the estimation of the ATE, which among others allows for using multiple imputation in the propensity score model. The simulation study showed a good performance of our three-step method and we recommend its use when estimating ATEs from observational data. Further research on possible interesting extensions of this new approach is needed, such as its application in the context of latent Markov models for longitudinal data (Bartolucci et al. 2016) and its modification to deal with situations in which there is measurement non-invariance (Vermunt and Magidson 2020).