Instability of SRPT, SERPT and SJF multiclass queueing networks

Abstract

We provide two examples of strictly subcritical multiclass queueing networks which are unstable under the shortest remaining processing time (SRPT) service protocol. Both of them are reentrant lines with two servers and eight customer classes. The customer service times in our first system are deterministic, yielding an example of an unstable shortest remaining expected processing time (SERPT) network. In the second one, the service times in one customer class are randomized. Both our examples show also system instability under the shortest job first (SJF) discipline. A simulation study of robustness of our results with respect to changes in the customer interarrival and service times is also provided. Our results indicate that size-based service policies may not use the available resources efficiently in a multiserver network setting and in fact cause instability effects. This is in sharp contrast with their satisfactory performance for single-server queues.

1 Introduction

Following Serfozo [40], by a stochastic network we mean a system in which customers move among stations where they receive services; there may be queueing for services, and customer routing and service times may be random. In many cases, we consider so-called multiclass networks in which stations can process more than one class of customers (jobs). Typical examples include computer and telecommunications networks, manufacturing and equipment maintenance networks, parallel simulation and distributed processing systems or logistics and supply chain networks.

A fundamental question in the theory of multiclass queueing networks is whether a given network is stable, i.e., the corresponding Markov process is positive Harris recurrent. The intuitive meaning of network stability is that the system performs well under reasonable workload: the queue lengths do not grow linearly with time and do not oscillate; there is no mutual blocking and forced idleness of the servers when work is present in the system. Stability of a network is a basic indicator of its proper design. Apparently, there is no general criterion for this behavior. It is well known that the usual necessary condition that the network be strictly subcritical (i.e., the traffic intensity $\rho _j$ be less than 1 at each station j) is not sufficient. However, the condition $\rho _j<1$ for all j is sufficient for generalized Jackson networks [35] and multiclass networks with some disciplines, including first-in-first-out (FIFO) in networks of Kelly type [11], head-of-the-line proportional processor sharing (HLPPS) [12], first-buffer-first-served and last-buffer-first-served [18, 21], as well as earliest-deadline-first (EDF) [14, 29, 31]. Dai [18], generalizing and systematizing earlier work of Rybko and Stolyar [37], provided a general framework for proving such stability results by showing stability of the corresponding fluid model, a deterministic analog of the network under consideration.

On the other side of the spectrum, we have unstable, strictly subcritical multiclass networks. Following Bramson [15], p. 53, we say that a queueing system is unstable if, for some initial state, the number of jobs in the network tends to infinity with positive probability as the time parameter $t\rightarrow \infty$. First examples of such systems were given in a deterministic setting. Kumar and Seidman [33] showed instability of a clearing policy in two nonacyclic networks. Lu and Kumar [34] provided an example (suggested by Seidman) of an unstable reentrant line with a preemptive static buffer priority (SBP) discipline. Recall that under an SBP protocol, customer classes are assigned a strict ranking and jobs of higher ranked classes are always served before tasks of lower ranked classes, while within a class, the jobs are served in the FIFO order (see, for example, Bramson [15], p. 12). A random counterpart of the Lu–Kumar network was later analyzed in Bramson [15], Sect. 3.1. To our knowledge, the first example of an unstable stochastic network was a preemptive SBP system due to Rybko and Stolyar [37], with the same topology as one of the clearing systems considered by Kumar and Seidman [33]. Subsequently, it was found that even strictly subcritical FIFO queueing networks might be unstable. Examples of such systems were given by Seidman [39] and Bramson [9, 10] in the deterministic and random case, respectively. Further examples of unstable queueing networks may be found in Dai and Weiss [21], Dumas [24], Bramson [13], Bacelli and Bonald [4] or Dai et al. [19, 20].

So far, most of the work in this area has been concentrated on the investigation of head-of-the-line (HL) disciplines, in which only the first job in each class may receive service, and hence, the tasks are served in the FIFO order within each class. In particular, little attention has been devoted to stability of multiclass queueing networks with size-based scheduling policies, in which the order of service is established on the basis of the customer service times (either initial, remaining or attained). Service policies of this type have been investigated thoroughly in the single-server setting; see the last three chapters in [28] and the references given there. Interest in such protocols stems from the fact that a proper size-based scheduling policy can substantially improve the performance of a queueing system. In particular, a classic result of Schrage [38] assures that the shortest remaining processing time (SRPT) policy, giving preemptive priority to the job which can be completed first, minimizes the queue length in a single-server system at each point in time.

It is natural to ask how well size-based disciplines perform in multiclass, multiserver networks. To our knowledge, there are few rigorous results in this area. Verloop et al. [41] investigated this issue in resource sharing networks. An essential difference between the latter systems and multiclass queueing networks is that jobs in a resource sharing network need access to all the resources on their routes simultaneously, while customers of a multiclass queueing network visit different servers along their routes in succession. Verloop et al. [41] found that linear, strictly subcritical resource sharing networks with Poisson arrivals and generally distributed document sizes, working under the SRPT, shortest expected remaining processing time (SERPT) and the least attained service (LAS) scheduling, may be unstable. Brown [16] investigated a packet level model (as opposed to flow level models used in [41]) and obtained stability conditions for some aged-based policies, including LAS, in data networks. Gieroba and Kruk [25] investigated some pathwise minimality properties associated with the SRPT protocol in resource sharing networks. Grosof et al. [27] provided bounds for the mean response time in the M/G/k queue under the SRPT and showed asymptotic optimality of this mean response time in the heavy-traffic limit. Recently, Dong and Ibrahim [22] investigated the multiserver M/G/k+G queue with impatient customers under the SRPT protocol and showed that, in the many-sever overloaded regime, its performance is asymptotically equivalent in steady state to a preemptive two-class priority queue. They also proved that in this setting, the SRPT discipline asymptotically maximizes the system throughput.

In the context of multiclass queueing networks, Banks and Dai [5] provided a simulation study demonstrating that a three station reentrant line with nine customer classes can be unstable under the SERPT protocol. Moreover, their simulations suggested that a variant of the Rybko–Stolyar (Kumar–Seidman) network may be unstable under the shortest mean remaining processing time first discipline, an analog of SERPT in which the priority of a customer class is established on the basis of the sum of the mean remaining processing times along its path rather than the mean processing time for this class. Chen and Yao [17], Section 8.6, presented a simulation indicating that a variant of the Rybko-Stolyar (Kumar-Seidman) network may not be stable under the preemptive SERPT discipline. They also stated, without providing any details, that both the simulation and the analysis of Sections 8.1-8.3 in [17] indicated that the above-mentioned network might not be stable under SRPT. Recently, Kruk [32] provided an example of a strictly subcritical multiclass network unstable under the LAS service protocol.

In this paper, we provide two examples of strictly subcritical multiclass queueing networks which are unstable under the SRPT service protocol. The first of them is a reentrant line with two servers and eight customer classes which may be regarded, in a suitable sense, as a variant of the Lu–Kumar network [34]. The customer service times in this system are deterministic, yielding an example of an unstable SERPT network. Moreover, we show that in this network no customer is ever preempted, so this example shows also the system instability under the shortest job first (SJF) discipline, a non-preemptive variant of SRPT.

Due to deterministic service times and the lack of preemption, in the network from our first example, the SRPT protocol implies fixed priorities between classes. This setup was chosen in order to maximally simplify our counterexample and the corresponding arguments. It is clear that further examples of unstable multiclass queueing networks in which SRPT does not coincide with fixed priorities may be given, at the expense of increased proof complexity. As an illustration of this fact, we provide an example of a similar unstable SRPT system, with the same network topology, in which the service times in one of the customer classes are randomized. While the proof of its instability proceeds along similar lines as in the previous case, additional technical difficulties arise, making the corresponding analysis notably more complicated. In our latter system, preemption may occur with positive probability, and hence, the SRPT and SJF service disciplines do not coincide. Nevertheless, a careful analysis of our argument shows that the network under consideration is unstable under the SJF protocol as well.

We conclude with a simulation study of the effects of changing the interarrival and/or service time distributions, while keeping the arrival and service rates unaltered, in the SRPT network from our first example and its more complex variant with two servers and 122 customer classes. It turns out that while the network’s qualitative behavior does not seem to be very sensitive to the distribution of the arrival process, it can apparently change from instability to stability after the change of the underlying service time distributions. This intriguing phenomenon does not seem to be easy to analyze and it deserves further studies.

Together with the findings of [32, 41], our results indicate that size-based service policies may not use the available resources efficiently in a multiserver network setting and in fact cause instability effects. This is in sharp contrast with their satisfactory performance for single-server queues. Accordingly, an implementation of the idea of Aalto and Ayesta [1] to use SRPT (or other size-based protocol) only within a single customer class, with class priorities arbitrated by another discipline, known to be stable in the multiclass network context (for example, HLPPS), might be advisable.

This paper is organized as follows: In Sect. 2, in order to motivate our further developments, we briefly recall the Lu–Kumar network. In Sect. 3, we provide our examples of unstable SRPT networks. The proofs of their instability are given in Sects. 4 and 5, respectively. In Sect. 6, we describe the simulation study illustrating our results. Section 7 concludes.

1.1 Notation

The following notation will be used throughout the paper: Let $\mathbb {N}=\{ 1,2,\ldots \}$ and let $\mathbb {R}$ denote the set of real numbers. We write $\lfloor a\rfloor$ for the largest integer less than or equal to a. For a vector $a=(a_1,...,a_n)\in \mathbb {R}^n$, let $|a| \triangleq \sum _{i=1}^n |a_i|$. We also denote the indicator of a measurable set B by $\mathbb {I}_{B}$.

2 The Lu–Kumar network

Fig. 1

Lu–Kumar network

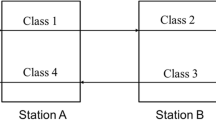
Consider the network depicted in Fig. 1, consisting of two single-server stations, indexed by $j=1,2$, with two customer (job, call) classes, or buffers at each station. It is a reentrant line. Customers follow a deterministic route, first visiting station 1 after entering the network, next visiting station 2 twice and then visiting station 1 a second time, before exiting the network. We order the customer classes according to their appearance along the route. The system evolves according to a preemptive SBP discipline, where class 4 jobs have priority over class 1 at the first server and class 2 jobs have priority over class 3 at the second one.

To our knowledge, this network topology was first considered by Kumar and Seidman [33], with a clearing service discipline. The SBP discipline defined above was introduced in the paper by Lu and Kumar [34], and hence, following Bramson [15], we call it the Lu–Kumar network.

It was shown in [34] that the Lu–Kumar network with periodic arrivals at the times 0, 1, 2, ... and deterministic service times $m_1=m_3=0$, $m_2=m_4=2/3$ is unstable. More generally, it may be shown that this network with rate-1 Poisson arrivals and independent, exponentially distributed service times having means $m_k>0$, $k=1,...,4$, satisfying

$$\begin{aligned} m_2+m_4>1, \end{aligned}$$

(1)

is unstable ([15], Theorem 3.2).

3 Networks unstable under SRPT

3.1 Models

Fig. 2

Network unstable under SRPT

We will now define two somewhat different strictly subcritical multiclass networks, with the same topology, which will be analyzed in the sequel. In the first one, the customer service times are deterministic. In the second one, the service times in one of the customer classes are randomized. Both of them turn out to be unstable under the SRPT and SJF protocols, while the first one is also unstable under SERPT (coinciding with SRPT for deterministic service times). Below, we first provide the information that is common for both networks. In Sect. 3.2, we define the first network model, while in Sect. 3.3, we describe the second one. Then, in Sect. 3.4, we state our main results.

Let $(\Omega , {\mathcal {F}},\mathbb {P})$ be a probability space on which all the random objects to follow will be defined. Consider a network topology depicted in Fig. 2. As in the previous case, it is a reentrant line consisting of two single-server stations, indexed by $j=1,2$, but now with four classes at each station. Customers follow a deterministic route, first visiting station 1 after entering the network, next visiting station 2 four times and then finally visiting station 1 three more times, before exiting the network. We order the customer classes according to their appearance along the route.

Intuitively, the above network topology is a variant of the Lu–Kumar system in which both the second and the fourth services of each job are split into three subtasks, executed by the same server. The number of jobs in the buffer k at time $t\ge 0$, $k=1,...,8$, (including the one currently served, if any) will be denoted by $Q_{k}(t)$. In particular, the numbers $Q_{k}(0)$, $k=1,...,8$, specify the initial condition (state) of the network.

The customer interarrival times are a sequence of strictly positive, independent, identically distributed (i.i.d.) random variables u(n), $n=1,2,\dots$, with unit expectation and moment-generating function that is finite in some neighborhood of zero, i.e., such that, for each $n\in \mathbb {N}$,

$$\begin{aligned} \mathbb {E}u(n)\;=\; 1, \qquad \quad \qquad \end{aligned}$$

(2)

$$\begin{aligned} \mathbb {E}e^{\beta u(n)}\;<\; \infty \quad \text{ for } \text{ some } \beta >0. \end{aligned}$$

(3)

The arrival time of the n-th customer to the system (i.e., to the buffer 1) is given by $U(n)=\sum _{l=1}^{n} u(l)$, $n=1,2,...$. For convenience, put $U(0)=0$. For $i=1,2$, let $N(t)=\max \{n\ge 0:U(n)\le t\}$ be the number of external arrivals of customers in the time interval (0, t]. By (2), the customer arrival rate equals $\alpha =1/\mathbb {E}u(n)=1$.

Customers are served at each station according to the SRPT discipline. That is, the customer with the shortest remaining processing time, regardless of class, is selected for service at each station. Preemption occurs when a customer more urgent than the customer in service arrives (we assume preempt–resume). There is no set up, switch-over or other type of overhead. As it is customary in the SRPT case, we assume that in case of a tie, FIFO is used as a tie-breaking rule.

3.2 Network with deterministic service times

In addition to the assumptions already made in Sect. 3.1, we require that the customer interarrival time distribution is supported on the set $0.3 *\mathbb {N}:=\{0.3 \cdot i, i\in \mathbb {N}\}$, i.e., such that, for each $n\in \mathbb {N}$,

$$\begin{aligned} \sum _{i=1}^\infty \mathbb {P}[u(n)=0.3 \cdot i] \,=\; 1. \end{aligned}$$

(4)

Simple examples of distributions satisfying (2), (4) are

$$\begin{aligned} \mathbb {P}[ u(n)=0.9] = \frac{2}{3}, \quad \mathbb {P}[ u(n)=1.2] = \frac{1}{3}, \quad n=1,2,\dots , \end{aligned}$$

(5)

and

$$\begin{aligned} \mathbb {P}[ u(n)=0.3] = \frac{5}{12}, \quad \mathbb {P}[ u(n)=1.5] = \frac{7}{12}, \quad n=1,2,\dots . \end{aligned}$$

(6)

Of course, many more examples may be given, including some distributions with unbounded support.

We assume that the service time of each job at class k is deterministic, given by a constant $m_{k}$, $k=1,...,8$. We take

$$\begin{aligned}&m_{1}=m_{5}=0.3, \qquad m_{2}=m_{6}=0.21, \end{aligned}$$

(7)

$$\begin{aligned}&m_{3}=m_{7}=0.2, \qquad m_{4}=m_8 =0.19. \end{aligned}$$

(8)

In particular, the network is strictly subcritical, since

$$\begin{aligned} \rho _1=\rho _2= \alpha (m_{1} + m_{6}+m_{7}+m_8) = 0.9 <1. \end{aligned}$$

Note that if we put $m_2:=m_2+m_3+m_4$, $m_4:=m_6+m_7+m_8$, i.e., “glue together” classes 2, 3, 4 (resp. 6, 7, 8) into a single class 2 (resp. 4), we get parameters satisfying (1), providing further support for the idea that our network is, in some sense, the Lu–Kumar system in which the second and the fourth services of each job are split into three subtasks. This suggests that the qualitative behavior of these two networks should be similar, so it is reasonable to expect that our system is unstable.

In what follows, the queueing system defined above will be referred to as Network 1.

3.3 Network with randomized service times of one class

In addition to the assumptions already made in Sect. 3.1, here we require that the customer interarrival time distribution is supported on the set $0.1 *\mathbb {N}:=\{0.1 \cdot i, i\in \mathbb {N}\}$, i.e., such that for each $n\in \mathbb {N}$,

$$\begin{aligned} \sum _{i=1}^\infty \mathbb {P}[u(n)=0.1 \cdot i] \,=\; 1. \qquad \end{aligned}$$

(9)

Clearly, every distribution satisfying (4), satisfies (9) as well. We also assume that for $n\ge 1$,

$$\begin{aligned} \mathbb {P}[u(n)\ge 0.9]=1. \end{aligned}$$

(10)

Note that, for example, the distribution (5) satisfies (10), while the distribution (6) does not. Furthermore, the service time of each job at class $k\ne 4$ is deterministic, given by a constant $m_{k}$, $k=1,...,3,5,...,8$, defined by (7) and

$$\begin{aligned} m_3=m_8=0.19, \qquad m_7=0.2. \end{aligned}$$

(11)

The service times of class 4 jobs, however, are i.i.d. random variables v(n), $n=1,2,...$, with distribution

$$\begin{aligned} \mathbb {P}[v(n)=0.2 ] = 1- \delta , \qquad \mathbb {P}[v(n)=0.4] = \delta , \quad n=1,2,..., \end{aligned}$$

(12)

where $\delta$ is small (say, $\delta =0.0001$¹). This is a small random perturbation of the constant service time 0.2. We assume that the sequences $\{u(n)\}$ and $\{v(n)\}$ are mutually independent. Under both the SRPT and SJF service protocols, class 4 jobs with service times 0.2 have priority over class 5 customers who have not received any service, while (unserved) class 4 jobs with service times 0.4 do not. Consequently, in general we do not have fixed class priorities in this system, even between unserved tasks. Let

$$\begin{aligned} \mu = \mathbb {E}v(n) = 0.2+0.2\delta . \end{aligned}$$

The network under consideration is again strictly subcritical, with $\rho _1=0.9$ as before and

$$\begin{aligned} \rho _2=\alpha (m_2+m_3+m_5+\mu )=0.9+0.2\delta . \end{aligned}$$

The intuition here is that the system just defined is a small perturbation of Network 1, so it should be unstable as well.

In what follows, the queueing system described in this subsection will be referred to as Network 2.

3.4 Main results

The following theorems are the main results of this paper.

Theorem 1

The SRPT Network 1 is unstable.

Theorem 1 follows from the following induction step which is justified in Sect. 4.

Proposition 1

Suppose that, in the SRPT Network 1, we have

$$\begin{aligned} Q_{1}(0)=M, \qquad \quad Q_{k}(0)=0, \quad k=2,...,8. \end{aligned}$$

(13)

Then, for some $\epsilon >0$, the constant M large enough and an appropriate random time $T=T(M)<\infty$, supported on $0.3 * \mathbb {N}$,

$$\begin{aligned}&\mathbb {P}\left[ Q_1(T)\ge \frac{7}{5} M, \; Q_k(T)=0, \; k=2,...,8\right] \ge 1-e^{-\epsilon M}, \end{aligned}$$

(14)

$$\begin{aligned}&\mathbb {P}[|Q(t)|\ge M\;\; \forall t\in [0,T] ] \ge 1-e^{-\epsilon M}, \qquad \end{aligned}$$

(15)

and, moreover, none of the class 1 customers present in the system at time T has received any service by that time.

Proof of Theorem 1

Consider the SRPT Network 1 with the initial condition (13), where M is large enough for Proposition 1 to hold. Let $T_1=T(M)$, where T(M) is as in the statement of Proposition 1, and let

$$\begin{aligned} A_1= \left[ Q_1(T_1)\ge \frac{7}{5} M, \; Q_k(T_1)=0, \; k=2,...,8\right] \cap [|Q(t)|\ge M\;\; \forall t\in [0,T_1] ]. \end{aligned}$$

By Proposition 1, for a suitable $\epsilon >0$, we have

$$\begin{aligned} \mathbb {P}(A_1)\ge 1-2 e^{-\epsilon M}. \end{aligned}$$

(16)

Using Proposition 1 again for the network restarted at the time $T_1$ (i.e., with the arrival process $N'(t)=N(t+T_1)-N(T_1)$ and the queue length process $Q'(t)=Q(t+T_1)$, $t\ge 0$, conditioned on the value $M'=Q'_1(0)=Q_1(T_1)\ge 7M/5$, we get the existence of a random time $T_2'=T'(M')$ supported on $0.3 * \mathbb {N}$ such that

$$\begin{aligned} \mathbb {P}(A_2|Q_{1}'(0)=M',Q_{k}'(0)=0,k=2,...,8] \ge 1-2 e^{-\epsilon M'} \ge 1-2 e^{-\epsilon 7M/5}, \end{aligned}$$

(17)

where

$$\begin{aligned} A_2= \left[ Q_1'(T_2')\ge \frac{7}{5} Q_{1}'(0), \; Q_k'(T_2')=0, \; k=2,...,8\right] \cap [|Q'(t)|\ge Q_{1}'(0)\;\; \forall t\in [0,T_2'] ]. \end{aligned}$$

(Note that $N'$ is, in general, a delayed renewal process, with the distribution of the first arrival time $u'(1)$ not necessarily equal to the distribution of u(n), although stochastically dominated by it. However, since $\mathbb {P}[T_1\in 0.3 * \mathbb {N}]=1$, the renewals corresponding to $N'$ are supported on $0.3* \mathbb {N}$ and it may be checked that the proof of Proposition 1 given below still works in this case). By (16), (17), we have $\mathbb {P}(A_1\cap A_2)\ge 1-2 e^{-\epsilon M} - 2 e^{-\epsilon 7M/5}.$ Moreover, conditioned on the set $A_1\cap A_2$, we have

$$\begin{aligned} |Q(t)|\ge M, \quad t\in [0,T_1], \qquad \qquad |Q(t)|\ge 7 M/5, \quad t\in [T_1,T_2], \end{aligned}$$

(18)

where $T_2=T_1+T_2'=T_1+T'(Q_1(T_1))$. By construction, $T_2$ is supported on $0.3* \mathbb {N}$.

Using Proposition 1 one more time for the network restarted at the time $T_2$, we obtain a random time $T_3$ supported on $0.3* \mathbb {N}$ and a set

$$\begin{aligned} A_3 = \left[ Q_1(T_3)\ge \frac{7}{5} Q_1(T_2), \; Q_k(T_3)=0, \; k=2,...,8\right] \cap [|Q(t)|\ge Q_{1}(T_2)\;\; \forall t\in [T_2,T_3] ], \end{aligned}$$

with $\mathbb {P}(A_1\cap A_2\cap A_3)\ge 1-2 e^{-\epsilon M} - 2 e^{-\epsilon 7M/5} - 2 e^{-\epsilon M(7/5)^2},$ such that conditioned on $A_1\cap A_2\cap A_3$, we have (18) and $|Q(t)|\ge M(7/5)^2$ for $t\in [T_2,T_3]$. Proceeding in this way, by repeated applications of Proposition 1 we get the estimate

$$\begin{aligned} \mathbb {P}\left[ \lim _{t\rightarrow \infty } |Q(t)| =\infty \right] \ge 1 - 2 \sum _{i=0}^\infty e^{-\epsilon M (\frac{7}{5})^i }, \end{aligned}$$

with the right-hand side converging to 1 as $M\rightarrow \infty$, and hence strictly positive for M large enough. $\square$

Theorem 2

The SRPT Network 2 is unstable.

The proof of Theorem 2 is similar to the argument justifying Theorem 1, with Proposition 1 replaced by

Proposition 2

Suppose that, in the SRPT Network 2, we have (13). Then, for some $\epsilon >0$, the constant M large enough and an appropriate random time $T=T(M)<\infty$, supported on $0.1 *\mathbb {N}$, the inequalities (14), (15) hold and, moreover, none of the class 1 customers present in the system at time T has received any service by that time.

The proof of Proposition 2 is provided in Sect. 5.

4 Proof of Proposition 1

Throughout this section, Network 1 will be considered. In order to show Proposition 1, we need several lemmas. The first one says that, roughly speaking, we can treat services of a customer at classes 2, 3 and 4 (resp., 6, 7 and 8) as one uninterrupted service period at station 2 (resp., 1) of length 0.6.

Lemma 1

If a customer enters service at buffer 2 at time $\tau$, then he finishes service at buffer 4 at time $\tau +0.6$. Similarly, if a customer enters service at buffer 6 at time $\eta$, then he finishes service at buffer 8 at time $\eta +0.6$.

Proof

Suppose that a customer, labeled by n, previously not served (even partially) by station 2, enters service at buffer 2 at time $\tau$. By (7), his remaining service time at this moment equals 0.21. Since the network protocol is SRPT, we must have $Q_3(\tau )=Q_4(\tau )=0$, because class 3 and 4 customers have service times less than 0.21, and hence, they have priority over a new task of class 2. Similarly, if $Q_5(\tau )>0$, then the customers present in the buffer 5 at time $\tau$ have remaining service times at least 0.21 at this time, and hence, they cannot preempt any customer of classes 2, 3, 4. Finally, every incoming class 2 customer has service time 0.21, so he cannot preempt any customer of classes 2, 3, 4, either. These facts, together with the network topology, assure that the customer n finishes service at buffer 2 at time $\tau +0.21$, moving immediately to the empty buffer 3, where his service time equals 0.2, while buffer 4 remains empty. By a similar argument, he finishes uninterrupted service at 3 at the time $\tau +0.41$, moving to the empty buffer 4, with the service time 0.19, and finally, he leaves buffer k at time $\tau +0.6$. The proof of the second claim is similar. $\square$

Motivated by Lemma 1, we define a moving event as a time at which either an external arrival to the system or a service completion at one of the buffers 1, 4, 5 or 8 takes place. Let us number consecutive moving events by $l=1,2,3,...$, and let $\theta _l$ be the (random) time of the l-th event. In general, more than one moving event may happen at the same time. If this is the case, to fix ideas, we list the external arrival (if any) first and then the departure events in the order of the buffers left. Accordingly, it may happen that $\theta _l=\theta _{l+1}$ for some l. The following lemma is a key to our analysis.

Lemma 2

Suppose that $Q_k(0)=0$ for $k=2,...,8$. Then, for every $l\ge 1$, we have

$$\begin{aligned} \mathbb {P}[\theta _l \in 0.3 * \mathbb {N}] =1. \end{aligned}$$

(19)

Proof

Fix $\omega \in \Omega$. For the remainder of the proof, all the random objects under consideration are evaluated at this $\omega$. We proceed by induction on l.

Let $l=1$. If $\theta _1$ is an arrival event, then (19) follows from (4). Otherwise, it must be the first service completion at buffer 1, so $\theta _1=m_1=0.3$, so again (19) holds.

Assume (19) for $l=1,...,n$. If the event $n+1$ is an external arrival, then (19) for $l=n+1$ follows from (4). If it is a service completion at buffer 4 (and hence arrival at buffer 5), then, by Lemma 1, the corresponding customer started his service at station 2 at time $\tau =\theta _{n+1}-0.6$. However, by the network topology, $\tau$ is either the arrival time of this customer at buffer 2 (i.e., its departure from 1), or a departure time of a customer from class 4 or 5. In any case, $\tau =\theta _l$ for some $l\le n$, so $\tau \in 0.3 *\mathbb {N}$ by the inductive assumption, and hence, $\theta _{n+1}\in 0.3 *\mathbb {N}$. The analysis for the case of the event $n+1$ being a service completion at buffer 8 is similar.

Suppose that the event $n+1$ is a departure from buffer 1. If the service of the corresponding customer at class 1 was uninterrupted, then $\theta _{n+1}=m_1+\tau =0.3+\tau$, where $\tau$, the starting time of his service at buffer 1, is either the arrival of this customer to the network, or a departure of a previous customer from buffer 1 or 8. In both cases, $\tau =\theta _l$ for some $l\le n$, so $\theta _{n+1}\in 0.3 *\mathbb {N}$ by the inductive assumption.

Now assume that there was an interruption in the service of the customer departing from buffer 1 at time $\theta _{n+1}$. As before, let $\tau$ denote the time of his entering into service. As before, we get $\tau \in 0.3 *\mathbb {N}$. By the network topology, the only event that can result in a preemption of a class 1 customer is an arrival of a customer to buffer 6, i.e., a departure from buffer 5. By the inductive assumption, this can only happen at a time $\theta _{l}\in 0.3 *\mathbb {N}$, $\tau<\theta _l<\theta _{n+1}$. Hence, $\theta _l-\tau \in 0.3 *\mathbb {N}$, and consequently, $\theta _l-\tau \ge 0.3=m_1$. This means that there is no preemption and the class 1 customer entering service at time $\tau$ finishes it at $\theta _{n+1}=\tau +m_1=\tau +0.3 \in 0.3*\mathbb {N}$.

Finally, the case of the event $n+1$ being a service completion at buffer 5 is similar to the latter one. $\square$

Corollary 1

Suppose that $Q_k(0)=0$ for $k=2,...,8$. Then, no customer of our SRPT network ever gets preempted.

Indeed, in the proof of Lemma 2 we have seen that a customer of class 1 (and similarly 5) cannot experience preemption. By (7), (8) and Lemma 1, customers of other classes do not get preempted, either.

Lemma 3

Let $u_1,u_2,...$ be i.i.d. random variables, with the same distribution as the interarrival times u(n), and let $S_n=\sum _{i=1}^n u_i$, $n\ge 1$. Then, for every $a>0$, there exists $\epsilon =\epsilon (a)>0$ such that, for all $n\ge 1$,

$$\begin{aligned} \mathbb {P}\left[ \frac{1}{n} |S_n-n| >a \right] \le e^{-\epsilon n}. \end{aligned}$$

(20)

This is an elementary large deviations estimate, following from (2), (3) by an application of Markov’s inequality to the moment generating function of $S_n$.

We are now ready to show Proposition 1. The main idea of its proof may be described as follows: By (7), (8), under the SRPT protocol, customers of classes 2, 3, 4 have priority over unserved class 5 customers. Therefore, a customer of class 5 may get into service only if the buffers 2, 3, 4 are empty. Accordingly, until the random time $\tau _1$ defined by (25), to follow, queues 6, 7, 8 are empty and station 1 serves only class 1 customers. Consequently, under the initial condition (13), with high probability we have more than 2.4M unserved class 5 customers at the time $\tau _1$. In the absence of newcoming class 1 customers at (or just before) the time $\tau _1$, when class 5 customers start receiving service, they get into classes 6-8, blocking service entry for fresh class 1 arrivals until they are served to completion and leave the system. When all of them leave at a random time T, after at least $(m_6+m_7+m_8) \cdot 2.4M = 1.44M$ time units of work at server 2, with high probability we have at least 1.4M unserved class 1 customers and all the other buffers empty. This behavior is similar to that of the unstable Lu–Kumar network from Sect. 2.

If incoming class 1 customers enter the network close to the time $\tau _1$, the situation is more complicated. Namely, this may introduce synchronized service at classes 1, 5 and 2-4, 6-8, respectively, leading to full utilization of both the servers. However, we argue that this only delays the system’s clogging observed in the previous case for some finite period of time, after which we have behavior analogous to that described above.

Proof of Proposition 1

Consider the dynamics of the SRPT Network 1 with the initial state (13), where M is large. At the time $t_1=m_{1}=0,3$, the first type 1 customer, after being served to completion at station 1, leaves the buffer 1, moves to the empty buffer 2 and starts receiving service there immediately. Then, subsequent initial customers receive service at class 1, after which they move to the second server, receiving service at buffers 2, 3 and 4. At the time

$$\begin{aligned} t_2=t_1+(m_2+m_3+m_4)M=0.3+0.6 M \end{aligned}$$

(21)

the last initial customer finishes service at the buffer 4 (see Lemma 1). Note that under the SRPT service protocol, no class 5 customer gets service in the time interval $[0,t_2]$, hence $Q_5(t_2)=M$ and

$$\begin{aligned} Q_6(t)=Q_7(t)=Q_8(t)=0, \qquad \qquad t\in [0,t_2]. \end{aligned}$$

(22)

By (21) and Lemma 3, for M large enough,

$$\begin{aligned} \mathbb {P}[N(t_2)\le 0.59 M ]= & {} \mathbb {P}[U(\lfloor 0.59 M \rfloor +1 )>t_2] \qquad \nonumber \\\le & {} \mathbb {P}\left[ \frac{|U(\lfloor 0.59 M \rfloor +1 ) - \lfloor 0.59 M \rfloor -1|}{\lfloor 0.59 M \rfloor +1} > \frac{1}{100}\right] \nonumber \\\le & {} e^{-\epsilon _1 M}, \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \;\; \end{aligned}$$

(23)

where $\epsilon _1 = \epsilon (1/100)/2$. Accordingly,

$$\begin{aligned} \mathbb {P}[N(t_2)> 0.59 M]\ge 1-e^{-\epsilon _1 M}. \end{aligned}$$

(24)

The busy period of station 2 associated with the service of customers from buffers 2, 3, 4 starting at time $t_1$ ends at the (random) time

$$\begin{aligned} \tau _1 = \min \{t\ge t_1: Q_{2}(t)+Q_{3}(t)+Q_4(t)=0\}. \end{aligned}$$

(25)

Under the SRPT service protocol, no class 5 customer gets service in the time interval $[0,\tau _1)$ so (22) can be generalized to

$$\begin{aligned} Q_6(t)=Q_7(t)=Q_8(t)=0, \qquad \qquad t\in [0,\tau _1]. \end{aligned}$$

(26)

In what follows, we will need the fact that $Q_5(\tau _1)>2.4 M$ with large probability, cf. (33), (34). In order to demonstrate this, we use the following iterative argument.

The customers entering the network in the time interval $(0, t_2]$ get served at station 1, devoted exclusively to the buffer 1 in this period (see (22)), and move to the buffer 2. Their service at the buffers 2, 3, 4 of the second station starts at the time $t_2$ and ends at

$$\begin{aligned} t_3=t_2+ (m_2+m_3+m_4) N(t_2)=t_2+0.6N(t_2). \end{aligned}$$

(27)

Now we shall prove the existence of a constant $\epsilon _2>0$ such that, for large M,

$$\begin{aligned} \mathbb {P}[N(t_2)> 0.59 M, \; N(t_3)-N(t_2)\le (0.59)^2M] \; \le \; e^{-\epsilon _2 M}. \end{aligned}$$

(28)

To this end, first note that

$$\begin{aligned} N(t_{3} ) - N(t_{2} )= & {} N(t_{3} ) - N(U(N(t_{2} ))) \ge N(U(N(t_{2} )) + t_{3} - t_{2} ) - N(U(N(t_{2} ))) \\= & {} N(U(N(t_{2} )) + 0.6N(t_{2} )) - N(U(N(t_{2} ))). \end{aligned}$$

Thus,

$$\begin{aligned}&\mathbb {P}[N(t_2)> 0.59 M, \; N(t_3)-N(t_2)\le (0.59)^2M] \qquad \qquad \qquad \qquad \qquad \qquad \qquad \nonumber \\&\quad \le \; \mathbb {P}[N(U(N(t_2))+0.6 \cdot 0.59 M)- N(U(N(t_2))) \le (0.59)^2M] \nonumber \\&\quad = \; \mathbb {P}[ N(0.6 \cdot 0.59 M) \le (0.59)^2M], \qquad \qquad \qquad \qquad \qquad \;\;\; \end{aligned}$$

(29)

where the equality follows from the fact that a renewal process “starts afresh” after each renewal. Proceeding similarly as in (23), we can find a constant $\epsilon _2>0$ such that, for large M,

$$\begin{aligned} \mathbb {P}[ N(0.6 \cdot 0.59 M) \le (0.59)^2M] \; \le \; e^{-\epsilon _2 M}, \end{aligned}$$

which, together with (29), justifies (28).

From (24) and (28), for large M we get

$$\begin{aligned} \mathbb {P}[N(t_2)> 0.59 M, \; N(t_3)-N(t_2)> (0.59)^2M] \; \ge \; 1-e^{-\epsilon _1 M}-e^{-\epsilon _2 M}. \end{aligned}$$

Iterating, for large M we get

$$\begin{aligned} \mathbb {P}[N(t_2)> 0.59 M, \; N(t_{i+1})-N(t_i)> (0.59)^iM,\; i=2,...,7] \; \ge \; 1-\sum _{i=1}^7 e^{-\epsilon _i M}, \nonumber \\ \end{aligned}$$

(30)

where $\epsilon _i>0$, $i=1,...,7$, are constants and

$$\begin{aligned} t_{i+1} = t_i +0.6(N(t_i)-N(t_{i-1})), \qquad i=3,...,8, \end{aligned}$$

(31)

is the time when the service at the buffers 2, 3, 4 of the customers entering the network in the time interval $(t_{i-1},t_i]$ ends. In particular, (30) implies that

$$\begin{aligned} \mathbb {P}[N(t_8)> (c-1) M] \; \ge \; 1-\sum _{i=1}^7 e^{-\epsilon _i M}, \quad \end{aligned}$$

(32)

where

$$\begin{aligned} c=\sum _{i=0}^7 (0.59)^i=2.403211514....>2.4. \end{aligned}$$

(33)

Moreover, for $\tau _1$ defined by (25), we have $\tau _1\ge t_9$, so the above construction implies that $Q_5(\tau _1)\ge M+N(t_8)$. Consequently, for large M the estimate (32) yields

$$\begin{aligned} \mathbb {P}[ Q_5(\tau _1)> cM] \; \ge \; 1-\sum _{i=1}^7 e^{-\epsilon _i M}. \end{aligned}$$

(34)

At time $\tau _1$, the first customer enters service at buffer 5. He finishes it without interruption at time $\tau _2=\tau _1+0.3$ (see Corollary 1), moving to the buffer 6, where his service starts immediately. Indeed, even if $Q_1(\tau _2)\ge 1$, then, by Lemma 2, every residual service time of a class 1 customer equals $m_1=0.3$, and hence, under the SRPT protocol, class 6 has priority over class 1. Consequently, by Lemma 1, the first departure from the system takes place at the time $\tau _3=\tau _2+0.6=\tau _1+0.9$. In particular, by (13),

$$\begin{aligned} |Q(t)|\ge |Q(0)|=M, \qquad \qquad 0\le t <\tau _3. \end{aligned}$$

(35)

For the reader’s convenience, the meanings of the random times $\tau _i$, as well as the times $\sigma _i$, $\eta$ defined below, are collected in Table 1.

Table 1 Key random times in the proof of Proposition 1

The definition of $\tau _1$ implies that $Q_1(\tau _1-0.3)=0$. Indeed, if $Q_1(\tau _1-0.3)\ge 1$, then, by (26) and Lemma 2, at the time $\tau _1$ a customer leaves buffer 1 and arrives into buffer 2, resulting in $Q_2(\tau _1)\ge 1$, which contradicts (25). Thus, by (4), we have $Q_1(\tau _1)\le 1$. Accordingly, the subsequent analysis is divided into two cases.

I. If $Q_1(\tau _1)=0$, then $Q_2(\tau _2)=Q_3(\tau _2)=Q_4(\tau _2)=0$, and hence, at time $\tau _2$ the second customer from buffer 5 enters service, finishing it and moving to the buffer 6. Under the SRPT protocol, as long as $Q_6(t)+Q_7(t)+Q_8(t)>0$, the incoming buffer 1 customers do not get any service. Accordingly, all the customers queued at the buffer 5 at time $\tau _1$ are processed by the first server in the time interval $[\tau _2,\tau _4]$, where

$$\begin{aligned} \tau _4= \tau _2 + (m_6+m_7+m_8)Q_5(\tau _1)=\tau _2 + 0.6 Q_5(\tau _1), \end{aligned}$$

(36)

leaving the system by that time. We have

$$\begin{aligned} Q_1(\tau _4)= N(\tau _4)-N(\tau _1), \qquad Q_k(\tau _4)=0, \;\; k=2,...,8. \end{aligned}$$

(37)

By (34) and (36), for large M

$$\begin{aligned} \mathbb {P}[ \tau _4 - \tau _1> 0.3+0.6cM] \ge 1-\sum _{i=1}^7 e^{-\epsilon _i M}, \end{aligned}$$

so (37) and another application of Lemma 3 yield the existence of a constant $\epsilon _8>0$ such that

$$\begin{aligned} \mathbb {P}[ Q_1(\tau _4) > 1.4 M] \; \ge \; 1-\sum _{i=1}^8 e^{-\epsilon _i M} \end{aligned}$$

for M suitably large. Together with the second statement of (37), this implies (14) for large M with $T=\tau _4$ and, say, $\epsilon =\min \{\epsilon _1,...,\epsilon _8\}/2$. The relation $\mathbb {P}[T\in 0.3 * \mathbb {N}]=1$ and the last claim of the proposition follow from the definition of T as a departure time $\tau _4$ of a customer from server 1, together with Lemma 2 and (13), Corollary 1, respectively.

It remains to establish (15). Until the time

$$\begin{aligned} \sigma _1=\tau _2+0.6 \cdot 1.4M=\tau _2+ .84M, \end{aligned}$$

(38)

there are less than 1.4M customers which have already left the system. Similarly, until the time

$$\begin{aligned} \sigma _2=\tau _2+0.6 \cdot 1.8M=\sigma _1+ .24M \end{aligned}$$

(39)

we have less than 1.8M customers which have already left the system. Conditioned on the set $[ Q_5(\tau _1)> cM]$,

$$\begin{aligned} |Q(t)|\ge |Q(\tau _1)|-1.4M>M, \qquad t\in [\tau _3,\sigma _1). \end{aligned}$$

(40)

Two more applications of Lemma 3 yield the existence of constants $\epsilon _9,\epsilon _{10}>0$ such that, for large M,

$$\begin{aligned} \mathbb {P}[N(\sigma _1)-N(\tau _1)>0.8M,\; N(\sigma _2)-N(\sigma _1)>0.2M] \; \ge \; 1-e^{-\epsilon _9 M}-e^{-\epsilon _{10} M}. \nonumber \\ \end{aligned}$$

(41)

Conditioned on the set $[ Q_5(\tau _1)> cM]$, for $t\in [\sigma _1,\sigma _2)$, we have

$$\begin{aligned} |Q(t)|\ge |Q(\tau _1)|-1.8M + N(\sigma _1)-N(\tau _1) >0.6M + N(\sigma _1)-N(\tau _1), \quad \end{aligned}$$

(42)

while

$$\begin{aligned} |Q(t)|\ge N(\sigma _2)-N(\tau _1), \; \qquad \ t\in [\sigma _2,\tau _4], \end{aligned}$$

(43)

(the latter estimate follows from the fact that no customer coming to the system after time $\tau _1$ gets service at the first buffer by time $\tau _4$; compare (37)). Let

$$\begin{aligned} A\;=\; [ Q_5(\tau _1)> cM, \;N(\sigma _1)-N(\tau _1)>0.8M,\; N(\sigma _2)-N(\sigma _1)>0.2M ]. \end{aligned}$$

(44)

By (34) and (41),

$$\begin{aligned} \mathbb {P}(A) \; \ge \; 1-\sum _{i=1}^{10} e^{-\epsilon _i M}. \end{aligned}$$

(45)

Conditioned on the set A, we have $|Q(t)|\ge M$ for each $t\in [0,\tau _4]$. Indeed, this fact follows from (35), (40), (42) and (43) for t belonging to $[0,\tau _3)$, $[\tau _3,\sigma _1)$, $[\sigma _1,\sigma _2)$ and $[\sigma _2,\tau _4]$, respectively. This, together with (45), implies (15) for large M with $T=\tau _4$ and, say, $\epsilon =\min \{\epsilon _1,...,\epsilon _{10}\}/2$.

II. The case of $Q_1(\tau _1)=1$ is slightly more delicate. Under this assumption, the customer at buffer 1 enters service at the time $\tau _1$ and moves to class 2 at time $\tau _2$. Recall that the first class 5 customer receives service in the time interval $[\tau _1,\tau _2)$ and moves to the buffer 6 at time $\tau _2$. Next, the former class 1 customer gets service at buffers 2, 3, 4, while class 5 customers are blocked, and then, he moves to class 5 at time $\tau _3$. In this time period, the customer of class 6 gets served, moving to buffers 7, 8, and finally leaving the network at time $\tau _3$. Note that the entry of newcoming class 1 customers into service is blocked in the time interval $[\tau _2,\tau _3]$. Summarizing, the first customers of classes 1 and 5 at time $\tau _1$ get synchronized in the time interval $[\tau _1,\tau _3]$, fully utilizing both servers. Note that

$$\begin{aligned} Q_5(\tau _3)=Q_5(\tau _1), \qquad Q_k(\tau _3)=0, \quad k\ne 1,5. \end{aligned}$$

(46)

If $Q_1(\tau _3)=0$, then the above “synchronization period” ends and the subsequent network dynamics follow those from case I (with time shifted by 0.9). Otherwise, the next two customers of classes 1 and 5 enter service at time $\tau _3$ and get service, perfectly synchronized, until the first one gets to class 5 and the other one leaves the network. This synchronization period finally ends at the time

$$\begin{aligned} \eta = \min \{t\ge \tau _1: Q_1(t)+Q_{2}(t)+Q_{3}(t)+Q_4(t)=0\}. \end{aligned}$$

It is easy to see that $\mathbb {P}[\eta <\infty ]=1$. Indeed, let $\zeta =\eta -\tau _1$ be the length of the synchronization period. Clearly, $\zeta =0.9 n_0$, where $n_0$ is the number of synchronized customer pairs served in this time period and $0.9=\tau _3-\tau _1$ is the service time of one such pair. In particular, for each $0\le n \le n_0-1$, in the time interval $(\tau _1,\tau _1+0.9 n]$ of length 0.9n we have at least n external arrivals. Hence, for $n\ge 1$,

$$\begin{aligned} \mathbb {P}[\zeta> 0.9 n]=\mathbb {P}[n_0>n] \le \mathbb {P}[ N(\tau _1+0.9n)- N(\tau _1)\ge n]. \end{aligned}$$

(47)

By (25), $\tau _1$ is a departure time of a customer from class 4, so $\mathbb {P}[\tau _1\in 0.3 *\mathbb {N}]=1$ by Lemma 2. On the other hand, $Q_1(\tau _1-0.3)=0<1=Q_1(\tau _1)$ by the case assumption. Consequently, by (4), $\tau _1$ is an external arrival time, so the process N “starts afresh” after $\tau _1$, and hence, by (47) and Lemma 3,

$$\begin{aligned} \mathbb {P}[\zeta > 0.9 n] \le \mathbb {P}[ N(0.9n)\ge n] = \mathbb {P}[U(n) \le 0.9 n] \le e^{-\epsilon n}, \qquad n\ge 1, \end{aligned}$$

(48)

with $\epsilon =\epsilon (0.05)$, so $\mathbb {P}[\eta<\infty ]=\mathbb {P}[\zeta <\infty ]=1$.

The display (46) generalizes to

$$\begin{aligned} Q_5(\eta )=Q_5(\tau _1), \qquad Q_k(\eta )=0, \quad k\ne 5, \end{aligned}$$

(49)

compare (25), (26). From this point, we follow the analysis of the first case, with $\eta$ in place of $\tau _1$. For the proof of (15), we additionally note that $|Q(t)|\ge Q_5(\tau _1)$ for $t\in [\tau _1, \eta )$, due to the synchronization process described above. $\square$

Remark 1

Probably the easiest way of showing instability of the random Lu–Kumar network satisfying (1) is the observation, going back to Botvich and Zamyatin [8], that after a suitable random time, jobs in the classes 2 and 4 are almost surely not served simultaneously (see [15], Lemma 3.3). This approach cannot be adapted directly to our SRPT network because of the “synchronization periods,” described in the case II, which may occur for arbitrarily large times.

Corollary 2

The Network 1 is unstable under the SERPT and SJF service protocols.

This follows immediately from Theorem 1, Corollary 1 and the fact that the service times in our network are deterministic.

5 Proof of Proposition 2

Throughout this section, the Network 2 will be considered. For the sake of the proof of Proposition 2, we introduce the following additional notation: Recall the distribution (12) of the class 4 service times. For $t\ge 0$, the number of jobs in the buffer 4 with service times equal to 0.2 (0.4) will be denoted by $Q^q_4(t)$ (resp., $Q^s_4(t)$). Here, the superscripts q and s stand for “quick” and “slow” class 4 customers, respectively, and this is how we shall refer to these two customer types in the sequel. In particular, if $v(n)=0.2$ (0.4), the customer n will be called a “quick” (resp., “slow”) class 4 customer even if he is currently not at the buffer 4.

Due to the presence of “slow” class 4 customers, Lemma 1 does not hold for the system under consideration. However, its weaker version, to follow, holds, with a similar proof.

Lemma 4

If a “quick” class 4 customer enters service at buffer 2 at time $\tau$, then he finishes service at buffer 4 at time $\tau +0.6$. Similarly, if a customer enters service at buffer 6 at time $\eta$, then he finishes service at buffer 8 at time $\eta +0.6$. Finally, if a “slow” class 4 customer enters service at buffer 2 at time $\tau$, then he finishes service at buffer 3 at time $\tau +0.4$.

Motivated by Lemma 4, we now define a moving event as a time at which either an external arrival to the system, or a service completion at one of the buffers 1, 3, 4, 5 or 8 takes place. As in the previous sections, we number consecutive moving events by $l=1,2,3,...$, and we denote by $\theta _l$ the (random) time of the l-th event. By Lemma 4, if a customer enters service at buffer 2 at time $\tau$, then he finishes service at buffer 3 at time $\tau +0.4$, so Lemma 2 no longer holds in our current setting. However, due to (7), (9) and (11), (12), the following natural counterpart of Lemma 2 is valid.

Lemma 5

Suppose that $Q_k(0)=0$ for $k=2,...,8$. Then, for every $l\ge 1$, we have

$$\begin{aligned} \mathbb {P}[\theta _l \in 0.1 * \mathbb {N}] =1. \end{aligned}$$

Proof

We follow the proof of Lemma 2, with obvious modifications. The only case that requires additional attention is the event $n+1$ being a departure of a “slow” customer from buffer 4. As before, let $\tau$ denote the starting time of his service. Note that $Q_2(\tau )=Q_3(\tau )=Q_4^q(\tau )=Q_5(\tau )=0$. By the network topology, $\tau$ is either a departure from 3 of a “slow” class 4 customer, or a departure from 5. Hence, by the inductive assumption, $\tau \in 0.1 *\mathbb {N}$. If the customer under consideration is served without preemption, then $\theta _{n+1}=\tau +0.4\in 0.1 *\mathbb {N}$. On the other hand, the only event that can result in his preemption is an arrival of a customer to buffer 2, i.e., a departure from buffer 1. By the inductive assumption, this can only happen at a time $\theta _{l}\in 0.1 *\mathbb {N}$, $\tau<\theta _l<\theta _{n+1}$. Hence, $\theta _l-\tau \in 0.1 *\mathbb {N}$, and consequently, the residual service time of the “slow” class 4 customer upon preemption equals $0.4-(\theta _l-\tau ) \in \{0.1, 0.2,0.3\}$. However, the service time of the incoming class 2 customer equals $m_2=0.21$. This means that under the SRPT protocol, the residual service time of the preempted “slow” class 4 customer equals 0.3. Let $\tau '$ be the time of his service resumption. Repeating the above argument, with $\tau '$ and 0.3 in the place of $\tau$ and 0.4, respectively, we conclude that $\tau ' \in 0.1 *\mathbb {N}$ and our customer does not get preempted again, so $\theta _{n+1}=\tau '+0.3 \in 0.1 *\mathbb {N}$. $\square$

From Lemmas 4, 5 and the proof of the latter result, we get the following counterpart of Corollary 1.

Corollary 3

Suppose that $Q_k(0)=0$ for $k=2,...,8$. Then, only “slow” class 4 customers may experience preemption in the SRPT Network 2. Moreover, each such customer gets preempted at most once and preemption does not take place in classes other than 4.

We will also need the following variant of Lemma 3, which can be justified by the same argument.

Lemma 6

Let $v_1,v_2,...$ be i.i.d. random variables, with the same distribution as the class 4 service times v(n), and let $S_n=\sum _{i=1}^n \mathbb {I}_{[v_i=0.2]}$, $n\ge 1$. Then, for every $a>0$, there exists $\epsilon =\epsilon (a)>0$ such that, for all $n\ge 1$,

$$\begin{aligned} \mathbb {P}\left[ \frac{1}{n} |S_n-(1-\delta ) n| >a \right] \le e^{-\epsilon n}. \end{aligned}$$

(50)

Corollary 4

Under the assumptions of Lemma 6, for every $a>0$, there exist $\tilde{\epsilon }=\tilde{\epsilon }(a)>0$ such that, for M sufficiently large,

$$\begin{aligned} \mathbb {P}\left( \bigcup _{n=M}^\infty [|S_n-(1-\delta ) n| >an ] \right) \le e^{-\tilde{\epsilon } M}. \end{aligned}$$

(51)

Proof

Let $\epsilon =\epsilon (a)$ be as in the statement of Lemma 6. Then, by (50),

$$\begin{aligned} \mathbb {P}\left( \bigcup _{n=M}^\infty [|S_n-(1-\delta ) n|>an ] \right)\le & {} \sum _{n=M}^\infty \mathbb {P}[|S_n-(1-\delta ) n| >an ] \\\le & {} \sum _{n=M}^\infty e^{-\epsilon n} \; =\; \frac{e^{-\epsilon M}}{1-e^{-\epsilon }}. \end{aligned}$$

Taking $\tilde{\epsilon }=\epsilon /2$ and M satisfying the inequality $e^{-\epsilon M/2}\le 1-e^{-\epsilon }$, we get (51). $\square$

We shall now prove Proposition 2. The main idea here is that the Network 2 is a small random perturbation of the Network 1, and hence, with high probability, the behavior of these two networks should be similar. Indeed, the proof of Proposition 2 follows the outline analogous to that for Proposition 1, although technical details of the argument are unavoidably more complicated.

Proof of Proposition 2

Consider the dynamics of the SRPT Network 2 with the initial state (13), where M is large. At the time $t_1=m_{1}=0.3$, the first type 1 customer, after being served to completion at station 1, leaves the buffer 1, moving to the empty buffer 2 and beginning to receive service there immediately. At the time $m_1+m_2+m_3=0.7$, he finishes service at the buffer 3, moving to the class 4. If $v(1)=0.2$, he immediately starts receiving service there, moving to the class 5 at the time 0.9, otherwise he waits at class 4, while the next class 2 customer starts receiving service.

The busy period of station 2 associated with the service of customers from buffers 2, 3 and “quick” buffer 4 customers starting at time $m_1$ ends at the random time

$$\begin{aligned} \tau _1 = \min \{t\ge m_1: Q_{2}(t)+Q_{3}(t)+Q_4^q(t)=0\}. \end{aligned}$$

(52)

Due to the SRPT service protocol, in the time interval $[t_1,\tau _1)$, “slow” class 4 customers and class 5 customers do not get any service. In particular, (26) holds.

For the reader’s convenience, the meanings of the key random times appearing in this proof are collected in Table 2.

Table 2 Key random times in the proof of Proposition 2

Our first aim is to show that

$$\begin{aligned} \mathbb {P}[N(\tau _1)> (c-1)M ] \ge 1-\sum _{i=1}^7 e^{-\epsilon _i M}, \end{aligned}$$

(53)

with c given by (33) and suitable $\epsilon _1,...,\epsilon _7>0$. To this end, we will use a modification of the argument leading to (32) from the proof of Proposition 1.

In what follows, we use $\delta =0.0001$. Let

$$\begin{aligned} t_2=0.3+ 0.4M + 0.2(1-2 \delta )M=0.3+ (0.6 - 0.4\delta ) M. \end{aligned}$$

(54)

Using the time $t_2$ given by (54), rather than (21), and proceeding as in (23), we get (24). Next, take

$$\begin{aligned} t_3=t_2+ 0.4 N(t_2) + 0.2 (1-2 \delta ) N(t_2) =t_2+ (0.6 - 0.4\delta ) N(t_2). \end{aligned}$$

(55)

Using the time $t_3$ given by (55), rather than (27), and proceeding as in the proof of Proposition 1, we get (28). Iterating, for large M we get (30), where $\epsilon _i>0$, $i=1,...,7$, are constants and

$$\begin{aligned} t_{i+1} = t_i +(0.6 - 0.4\delta )(N(t_i)-N(t_{i-1})), \qquad i=3,...,7, \end{aligned}$$

(56)

compare (31), (55). Relabeling $\epsilon _i$ as $\epsilon _i'$, we rewrite (30) as

$$\begin{aligned} \mathbb {P}(A) \; \ge \; 1-\sum _{i=1}^7 e^{-\epsilon _i' M}, \end{aligned}$$

(57)

where

$$\begin{aligned} A=[N(t_2)> 0.59 M, \; N(t_{i+1})-N(t_i)> (0.59)^iM,\; i=2,...,7]. \end{aligned}$$

(58)

For $n\ge 1$, let $S^q(n) = \sum _{i=1}^n \mathbb {I}_{[v(n)=0.2]}$ denote the number of “quick” class 4 tasks associated with the first n customers in the network. The initial customers finish their service in the buffers 2, 3, 4 prior to time $\tau _1$ (i.e., excluding the service at class 4 of “slow” initial customers) at the (random) time

$$\begin{aligned} \vartheta _1=m_1 + (m_2+m_3) M +0.2 S^q(M) = 0.3+0.4 M+0.2 S^q(M). \end{aligned}$$

(59)

Letting $a=\delta$ in Lemma 6 and using independence of the interarrival times and the service times, we get

$$\begin{aligned} \mathbb {P}[S^q(M)\ge (1-2 \delta )M|A]=\mathbb {P}[S^q(M)\ge (1-2 \delta )M] \ge 1- e^{-\tilde{\epsilon }_1 M}, \end{aligned}$$

and hence,

$$\begin{aligned} \mathbb {P}[\vartheta _1\ge t_2|A] \ge 1- e^{-\tilde{\epsilon }_1 M}, \end{aligned}$$

(60)

with $t_2$, A given by (54), (58), respectively, and $\tilde{\epsilon }_1=\epsilon (\delta )$.

If $t_2\le \vartheta _1$ (and hence $t_2\le \tau _1$), then the customers entering the network in the time interval $(0, t_2]$ get served at station 1, devoted exclusively to the buffer 1 in this period, and move to the buffer 2. Their service at the buffers 2, 3, 4, excluding the service at class 4 of “slow” customers, starts at the time $\vartheta _1$ and ends at

$$\begin{aligned} \vartheta _2= \vartheta _1+ 0.4 N(t_2) + 0.2 (S^q(M+N(t_2))-S^q(M)), \end{aligned}$$

(61)

compare (59). Conditioning on the set A, on which $N(t_2)>0.59M$, and using Corollary 4, we get

$$\begin{aligned} \mathbb {P}[\vartheta _2-\vartheta _1\ge t_3-t_2|A] \ge 1- e^{-\tilde{\epsilon }_2 M}, \end{aligned}$$

(62)

for M large enough, where $\tilde{\epsilon }_2=\tilde{\epsilon }(\delta )$. Similarly, for

$$\begin{aligned} \vartheta _i&= \vartheta _{i-1}+ 0.4 (N(t_i)-N(t_{i-1})) + 0.2 (S^q(M+N(t_i))-S^q(M+N(t_{i-1}))),\\&\quad i=3,...,7, \end{aligned}$$

by Corollary 4, we get

$$\begin{aligned} \mathbb {P}[\vartheta _i-\vartheta _{i-1}\ge t_{i+1}-t_i|A] \ge 1- e^{-\tilde{\epsilon }_2 M}, \qquad i=3,...,7, \end{aligned}$$

(63)

(compare (61), (62)). Note that $\vartheta _i$ is the ending time of service at the buffers 2, 3, 4 of customers entering the network in the time interval $(t_{i-1},t_i]$, excluding the service at class 4 of the corresponding “slow” tasks, provided that $t_l\le \vartheta _{l-1}$, $l=2,...,i$. Consequently, if $t_{i+1}\le \vartheta _{i}$, $i=1,...,7$, then $\vartheta _7\le \tau _1$, and hence $t_8 \le \tau _1$. Using this observation, together with (33), (57), (58), (60) and (62), (63), for large M we get

$$\begin{aligned} \mathbb {P}[N(\tau _1)> (c-1)M ]\ge & {} \mathbb {P}[N(t_8)> (c-1)M,\tau _1>t_8 ] \\\ge & {} \mathbb {P}[A\cap [\vartheta _i\ge t_{i+1},i=1,...,7]]\\= & {} \mathbb {P}[[\vartheta _i\ge t_{i+1},i=1,...,7]|A] \; \mathbb {P}(A) \\\ge & {} \Big ( 1- e^{-\tilde{\epsilon }_1 M} -6e^{-\tilde{\epsilon }_2 M} \Big ) \Big ( 1-\sum _{i=1}^7 e^{-\epsilon _i' M}\Big ) \\\ge & {} 1-\sum _{i=1}^7 e^{-\epsilon _i M}, \end{aligned}$$

with $\epsilon _1=\min \{\tilde{\epsilon }_1,\epsilon _1' \}/2$, $\epsilon _i=\min \{\tilde{\epsilon }_2,\epsilon _i' \}/2$, $i=2,...,7$, and (53) follows.

As in the proof of Proposition 1, at the time $\tau _1$, the first customer enters service at buffer 5, finishes it at time $\tau _2=\tau _1+0.3$ and moves to the buffer 6.

The definition of $\tau _1$ implies that $Q_1(\tau _1-0.3)=0$. Indeed, if $Q_1(\tau _1-0.3)\ge 1$, then, because of (26), by the time $\tau _1$ a customer leaves buffer 1 arriving into buffer 2, resulting in $Q_2(\tau _1)+Q_3(\tau _1)\ge 1$, which contradicts (52). Thus, by (10), we have $Q_1(\tau _1)\le 1$. The following analysis is divided into several cases.

I. If $Q_1(\tau _1)=0$, then $Q_2(\tau _2)=Q_3(\tau _2)=Q_4^q(\tau _2)=0$, and hence, at time $\tau _2$ the second customer from buffer 5 enters service, finishing it and moving to the buffer 6. If, additionally, $N(\tau _1+0.2)=N(\tau _1)$ (i.e., there are no external arrivals to the system after the time $\tau _1$, but before $\tau _2$), then the service of the first customer at buffer 6 starts immediately at the time $\tau _2$ of his arrival to the buffer. Thus, by Lemma 4, the first departure from the system takes place at the time $\tau _3=\tau _2+0.6=\tau _1+0.9$ and (35) holds. Recall that as long as $Q_6(t)+Q_7(t)+Q_8(t)>0$, the incoming buffer 1 customers do not get any service. Accordingly, all the customers in class 5 at time $\tau _1$ are served there in the time interval $[\tau _1, \gamma _1)$, where

$$\begin{aligned} \gamma _1=\tau _1+0.3 Q_5(\tau _1). \end{aligned}$$

(64)

After moving to classes 6, and subsequently to 7, 8, these customers are processed by the first server in the time interval $[\tau _2,\tau _4]$, where $\tau _4$ is defined by (36), leaving the system by that time. Between the times $\tau _2$ and $\tau _4$, no class 1 customers get service, and hence, there are no arrivals to class 2.

If $Q^s_4(\tau _1)=Q^s_4(\tau _2)=Q^s_4( \gamma _1)>0$ then, starting at time $\gamma _1$, consecutive “slow” class 4 customers are processed by the second server, first at class 4, and then at 5, finally moving to class 6. Let

$$\begin{aligned} \gamma _2=\gamma _1+(0.4+m_5)Q^s_4(\tau _1)= \gamma _1+0.7Q^s_4(\tau _1). \end{aligned}$$

(65)

Note that if $\gamma _2 \le \tau _4$, then all the former “ slow” class 4 customers who entered the network by the time $\tau _1$ enter class 6 by the time $\tau _4$ and then leave the network by the time

$$\begin{aligned} \tau _5=\tau _4+0.6 Q^s_4(\tau _1). \end{aligned}$$

(66)

In the meantime, no service is allotted to class 1, so still no arrivals to class 2 take place.

We will now show that, for a suitable $\epsilon _8>0$,

$$\begin{aligned} \mathbb {P}[ \gamma _2 \le \tau _4]\ge 1- e^{-\epsilon _8 M}. \end{aligned}$$

(67)

Indeed, by (36) and (64), (65), we have

$$\begin{aligned}{}[3 Q_4^s(\tau _1) \le Q_5(\tau _1)]\subseteq [ \gamma _2 \le \tau _4]. \end{aligned}$$

(68)

By (26), (52) and the case assumption, we have

$$\begin{aligned} Q_4^s(\tau _1) + Q_5(\tau _1) =M+N(\tau _1). \end{aligned}$$

(69)

This, together with (53), implies that

$$\begin{aligned} \mathbb {P}[Q_4^s(\tau _1) + Q_5(\tau _1)> cM ] \ge 1-\sum _{i=1}^7 e^{-\epsilon _i M}. \end{aligned}$$

(70)

Moreover,

$$\begin{aligned} Q_5(\tau _1) =S^q(M+N(\tau _1)), \end{aligned}$$

(71)

because all the “slow” customers who have entered the network by the time $\tau _1$ are still at class 4 by time $\tau _1$, while all the “quick” customers are already at class 5 by that time. By Corollary 4, for $\epsilon _8=\tilde{\epsilon }(\delta )$, we have

$$\begin{aligned} \mathbb {P}[S^q(M+N(\tau _1)) \ge (1-2\delta ) (M+N(\tau _1))] \ge 1- e^{-\epsilon _8 M}. \qquad \qquad \;\;\; \end{aligned}$$

(72)

The relations (69) and (71), (72) imply that

$$\begin{aligned} \mathbb {P}\left[ Q_5(\tau _1) \ge \frac{1-2\delta }{2\delta } Q_4^s(\tau _1) \right] = \mathbb {P}[Q_5(\tau _1) \ge (1-2\delta ) (Q_4^s(\tau _1) + Q_5(\tau _1))] \ge 1- e^{-\epsilon _8 M}. \end{aligned}$$

From this, recalling that $\delta =0.0001$, we get $\mathbb {P}[Q_5(\tau _1) \ge 3 Q_4^s(\tau _1) ] \ge 1- e^{-\epsilon _8 M},$ which, together with (68), implies (67).

In the following argument, we condition on the set $[ \gamma _2\le \tau _4]$. As was mentioned below (64) and (66), there is no service for class 1 customers in the time interval $[\tau _2,\tau _5]$. This, together with the case assumption, yields

$$\begin{aligned} Q_1(\tau _5) = N(\tau _5) - N(\tau _1), \end{aligned}$$

(73)

while, by the above discussion,

$$\begin{aligned} Q_k(\tau _5) = 0, \quad k=2,...,8, \end{aligned}$$

(74)

compare (37) from the proof of Proposition 1. By (66), (36) and (69),

$$\begin{aligned} \tau _5= \tau _4+0.6 Q^s_4(\tau _1) = \tau _2+0.6 Q_5(\tau _1)+0.6 Q^s_4(\tau _1) =\tau _2+0.6 ( M+N(\tau _1)). \end{aligned}$$

This, together with (53) and (67), yields

$$\begin{aligned} \mathbb {P}[ \tau _5 - \tau _1> 0.3+0.6cM] \ge 1-\sum _{i=1}^8 e^{-\epsilon _i M}, \end{aligned}$$

so (73) and another application of Lemma 3 yield the existence of a constant $\epsilon _9>0$ such that

$$\begin{aligned} \mathbb {P}[ Q_1(\tau _5) > 1.4 M] \; \ge \; 1-\sum _{i=1}^9 e^{-\epsilon _i M} \end{aligned}$$

for M suitably large. Together with (74), this implies (14) for large M with $T=\tau _5$ and, say, $\epsilon =\min \{\epsilon _1,...,\epsilon _9\}/2$. The relation $\mathbb {P}[T\in 0.1 * \mathbb {N}]=1$ and the last claim of the proposition follow similarly as in the proof of Proposition 1.

The justification of (15) is similar to the corresponding argument from the proof of Proposition 1, with $\sigma _1$, $\sigma _2$ defined by (38), (39) as before, (70) in place of (34), relabeling of $\epsilon _9$ there as $\epsilon _{11}$, conditioning on the set $[Q_4^s(\tau _1) + Q_5(\tau _1)> cM ]$ instead of $[Q_5(\tau _1)> cM ]$, the set A from (44) replaced by

$$\begin{aligned}{}[Q_4^s(\tau _1) + Q_5(\tau _1)> cM, \;N(\sigma _1)-N(\tau _1)>0.8M,\; N(\sigma _2)-N(\sigma _1)>0.2M ], \end{aligned}$$

the counterpart of (43) valid for all $t\in [\sigma _2,\tau _5]$ and $\epsilon = \min \{\epsilon _1,...,\epsilon _{11} \}/2$.

II. If $Q_1(\tau _1)=0$, but $N(\tau _1+0.2)>N(\tau _1)$ (i.e., we have an external arrival to the system after the time $\tau _1$, but before $\tau _2$), only a minor adjustment to the above analysis is required. By (52), $\tau _1$ is a service completion time at either the buffer 3, or 4, and hence, by Lemma 5, $\mathbb {P}[\tau _1\in 0.1 *\mathbb {N}]=1$. By (10) and the case assumption, there is a single arrival to the system at a time $\tilde{t} \in (\tau _1,\tau _1+0.2]$, so by (9) we have $\tilde{t}\in \{\tau _1+0.1,\tau _1+0.2\}$. Because the first server is empty before the time $\tilde{t}$, this arrival is processed immediately and the corresponding customer moves to class 2 at the time $\tilde{t}+0.3>\tau _2$. Accordingly, the first class 6 customer waits until the newcomer leaves station 1, and then, he enters service at the first station, finishing it at the time $\tau _3=(\tilde{t}+0.3)+0.6=\tilde{t}+0.9$ and leaving the system. In particular, (35) holds.

As in the previous case, at time $\tau _2$ the second customer from buffer 5 enters service, finishing it and moving to the buffer 6 at time $\tau _2+0.3$. He starts service there at the time $\tau _3$, leaving the system at $\tau _3+0.6$. Between the times $\tilde{t}+0.3$ and $\tau _3+0.6$, the service for incoming class 1 customers is blocked.

The customer coming to class 2 at time $\tilde{t}+0.3$ enters service there at the time $\tau _2+0.3$. Accordingly, at the time $\tau _2+0.7$ he moves to class 4. If he is a “slow” class 4 customer, he stays at this class; otherwise, he enters service at class 4 immediately, finishing it and moving to class 5 at the time $\tau _2+0.9$. Note that

$$\begin{aligned} \tau _2+0.9 =\tau _1 +1.2 <\tilde{t}+1.2 = \tau _3+0.3, \end{aligned}$$

so by the time $\tau _2+0.9$, the third class 5 customer enters service, finishing it by the time $\tau _2+1.2<\tau _3+0.6$ and moving to class 6. This extends the blocking period for class 1 customers by an additional 0.6 time units, while the next class 5 customers are being processed and move to class 6, and so on.

From this moment, we can follow the proof for the case I, with only minor changes. For example, we replace (64) by

$$\begin{aligned} \gamma _1=\tau _1+0.3Q_5(\tau _1) +0.4 + 0.5 \mathbb {I}_{[v(N(\tau _1+0.2))=0.2]}, \end{aligned}$$

where $0.4=m_2+m_3$ is the sum of the service times of the customer coming to the network at the time $\tilde{t}$ in classes 2, 3 and the last term is the sum of his service times in classes 4 and 5, added when this customer is “quick.” Similarly, we now have $\tau _4= \tau _2+0.6(Q_5(\tau _1) + \mathbb {I}_{[v(N(\tau _1+0.2))=0.2]})$, $\gamma _2=\gamma _1+0.7(Q^s_4(\tau _1)+ \mathbb {I}_{[v(N(\tau _1+0.2))=0.4]})$, $\tau _5= \tau _4 + 0.6 (Q^s_4(\tau _1)+ \mathbb {I}_{[v(N(\tau _1+0.2))=0.4]})$; the relation (68) should be replaced, for example, by $[3 Q_4^s(\tau _1) +6 \le Q_5(\tau _1)]\subseteq [ \gamma _2\le \tau _4]$, etc..

III. If $Q_1(\tau _1)=1$, we have a synchronization period in the work of both servers, similar to the one from case II in the proof of Proposition 1, but somewhat more involved, due to the presence of “slow” class 4 customers.

Suppose that $v(N(\tau _1))=0.2$, i.e., the customer in the first queue at time $\tau _1$ is “quick.” If $\tau _1$ is his arrival time to the system, then he gets synchronized with the first class 5 customer in the time interval $[\tau _1,\tau _3]$, where $\tau _3=\tau _1+0.9$, as described in the proof of Proposition 1. If he arrived at the time $\tau _1-0.1$ ($\tau _1-0.2$), his service in class 1 starts immediately and ends at the time $\tau _1+0.2$ ($\tau _1+0.1$). He then goes to class 2, where he waits 0.1 (resp. 0.2) time units for the end of service of the first class 5 customer at the time $\tau _2$. Then, since $Q_1(\tau _2)=0$ by (10), the customers in classes 2 and 6 get synchronized again as before. In particular, we get the following counterpart of (46):

$$\begin{aligned} Q_4^s(\tau _3)=Q_4^s(\tau _1), \;\; Q_5(\tau _3)=Q_5(\tau _1), \quad Q_4^q(\tau _3)=0, \;\; Q_k(\tau _3)=0, \; k\ne 1,4,5.\nonumber \\ \end{aligned}$$

(75)

If $Q_1(\tau _3)=0$, the synchronization period ends and we proceed further as in the case I or II. Otherwise, the next two customers from classes 1, 5 get synchronized.

The synchronization with a “slow” arriving customer is somewhat more complicated. Assume that $v(N(\tau _1))=0.4$. If the corresponding customer arrived at the system at time $\tau _1$, we have a synchronization as before until the time $\tau _1+0.7$ when the “slow” customer joins the queue at class 4 and the next class 5 customer enters service. As in the previous case, if the new “slow” customer arrived at the time $\tau _1-0.1$ ($\tau _1-0.2$), then his service in class 1 starts immediately and ends at $\tau _1+0.2$ ($\tau _1+0.1$). He then goes to class 2, where he waits 0.1 (resp. 0.2) time units for the end of service of the first class 5 customer, and then they get synchronized again as before, until $\tau _1+0.7$. At the time $\tau _3=\tau _1+0.9$, the first class 8 customer leaves the system. However, instead of (75), we now have

$$\begin{aligned} Q_4^s(\tau _3)=Q_4^s(\tau _1)+1, \;\; Q_5(\tau _3)=Q_5(\tau _1)-1, \;\; Q_4^q(\tau _3)=Q_k(\tau _3)=0, \; k\ne 1,4,5.\nonumber \\ \end{aligned}$$

(76)

The customer of class 5 who has entered service at $\tau _1+0.7$ goes to class 6 at time $\tau _1+1=\tau _3+0.1$. If $Q_1(\tau _3)=0$, he starts service at the second server immediately (even if there is an external arrival at the time $\tau _1+1$) and the synchronization period ends. Otherwise, the next class 1 customer enters service at time $\tau _3$, ending it at $\tau _3+0.3$, when he goes to class 2 and the customer at class 6 enters service, so that we have another synchronized pair of customers, and so on.

Let

$$\begin{aligned} \eta = \min \{t\ge m_1: Q_1(t)+Q_{2}(t)+Q_{3}(t)+Q_4^q(t)=0\} \end{aligned}$$

be the end of the synchronization period and let $\zeta =\eta -\tau _1$ be its length. It is clear from the above analysis that $\zeta =0.9 n_0$, where $n_0$ is the number of synchronized customer pairs served in this time period and $0.9=\tau _3-\tau _1$ is the service time of one such pair. If there are no “slow” arrivals in the period $[\tau _1-0.2,\eta ]$, then, by iterating the above analysis for a “quick” arrival, (75) can be generalized to

$$\begin{aligned} Q_4^s(\eta )=Q_4^s(\tau _1), \;\;\; Q_5(\eta )=Q_5(\tau _1), \quad Q_4^q(\eta )=0, \;\;\; Q_k(\eta )=0, \; k\ne 4,5. \end{aligned}$$

From this point, we proceed further as in the case I or II, with $\eta$ in place of $\tau _1$. However, as it is clear from (76), any “slow” arrival in the time period $[\tau _1-0.2,\eta ]$ changes the proportion between the numbers of “slow” class 4 and class 5 customers in the system, which is important in the above proof for the cases I and II; see (68). Hence, in general, to conclude this argument as in the previous cases, an upper bound on $\zeta$ or, equivalently, on $n_0$ (and hence on the number of “slow” arrivals in the period $[\tau _1-0.2,\eta ]$) is necessary. It can be derived similarly as in the proof of Proposition 1; see (48). However, due to our additional assumption (10), we can now provide a simpler, more direct bound; see (78) below.

It follows from the above analysis that for $0\le n \le n_0-1$, there is an external arrival between $\tau _1+0.9(n-1)$ and $\tau _1+0.9n$, so that $Q_1(\tau _1+0.9n)=1$ and there is a class 1 job at the beginning of the synchronization period of the $n+1$-th pair of customers. In particular, by (2) and (10), $n_0$ is stochastically dominated by a random variable which is geometrically distributed with parameter $p=\mathbb {P}[u(n)>0.9]>0$. Let $n^s$ be the number of “slow” arrivals in the time period $[\tau _1-0.2,\eta ]$. Clearly, $0\le n^s\le n_0$. Reasoning as in (75), (76), we get

$$\begin{aligned}&Q_4^s(\eta )=Q_4^s(\tau _1)+n^s, \;\; Q_5(\eta )=Q_5(\tau _1)-n^s, \quad \nonumber \\&Q_4^q(\eta )=0, \;\; Q_k(\eta )=0, \; k\ne 4,5. \end{aligned}$$

(77)

Moreover, for large M,

$$\begin{aligned} \mathbb {P}[n^s> \delta M] \le \mathbb {P}[n_0> \delta M] \le \sum _{i\ge \lfloor \delta M \rfloor +1} (1-p)^{i-1} p = (1-p)^{\lfloor \delta M \rfloor } \le e^{-\epsilon _{12} M},\nonumber \\ \end{aligned}$$

(78)

with, say, $\epsilon _{12}= - \delta \log (1-p)/2$. (One can easily improve this estimate to $\epsilon _{12}= - \log (1-p)/2$, since $n^s \approx \delta n_0$, but any $\epsilon _{12}>0$ is sufficient for our purposes).

From this point, we follow the proofs for the cases I and II, with $\eta$ in place of $\tau _1$, subject to suitable minor changes, additionally conditioning on the set $[n^s\le \delta M]$, using (77), (78) and finally letting $\epsilon = \min \{\epsilon _1,...,\epsilon _{12} \}/2$. $\square$

Remark 2

Corollary 3, together with a careful examination of the above proof, shows that, with probability at least $1-e^{-\epsilon M}$, there is no preemption up to time T in the system under consideration, where $M,T,\epsilon$ are as in the statement of Proposition 2. Therefore, the Network 2 is unstable also under the SJF service discipline.

Fig. 3

A simulated sample path of the unstable SRPT Network 1

Fig. 4

A simulated sample path of the unstable SRPT Network 2 with $\delta =0.01$

Fig. 5

A simulated sample path of the unstable SRPT Network 2 with $\delta =0.1$

Fig. 6

A simulated sample path of an unstable SRPT network with Poisson arrivals and deterministic service times

Fig. 7

A simulated sample path of an unstable SRPT network with Poisson arrivals and uniform service times

Fig. 8

A simulated sample path of an apparently stable SRPT network with Poisson arrivals and exponential service times

Fig. 9

A simulated sample path of an apparently unstable SRPT network with 122 customer classes, Poisson arrivals and exponential service times

Fig. 10

A simulated sample path of an apparently stable SRPT network with Poisson arrivals and Pareto service times

6 Simulation

The customer interarrival and service times in our models, satisfying either (4), (7), (8), or (7), (9), (12), are rather special. They have been chosen in this way in order to simplify the corresponding arguments, for example, to assure validity of Corollary 1. It is natural to ask about robustness of our results when the interarrival and service time distributions are altered.

In order to get some insight into this issue, we have conducted a simulation study. First, we have simulated the SRPT Network 1, with the customer interarrival distribution given by (5). The initial condition was set to (13) with $M=100$. We have found that the queue lengths in this system oscillate with increasing magnitude; see Fig. 3. This qualitative behavior is typical for unstable multiclass networks, confirming and illustrating Theorem 1.

We have also simulated the SRPT Network 2, with the customer interarrival distribution given by (5) and the initial condition (13) with $M=200$. In (12), we took $\delta =0.01$, instead of 0.0001 used in our proofs, in order to increase the impact of the service time variability. The qualitative image of the queue length dynamics is the same as before, in line with Theorem 2; see Fig. 4. Moreover, enlarging $\delta$ to 0.1 does not seem to stabilize the network, either; see Fig. 5.

We repeated our simulation of the Network 1 with the constant service times given by (7), (8), changing the interarrival time distribution to the exponential one with unit rate, making $N(\cdot )$ the standard Poisson process. In this case, the observed system behavior is qualitatively similar to the previous ones; see Fig. 6. This suggests that altering the arrival process to a nonlattice one might not notably change the system’s performance.

Next, retaining Poisson arrivals from the previous case, we have changed the deterministic customer service times for each class to i.i.d. uniform random variables with means given by (7), (8) and the support $[m_k-0.03,m_k+0.03]$ for the class k service time distribution for each k. Again, the simulated network appears to be unstable; see Fig. 7. This suggests that small oscillations of the service times around their means might not significantly change the system’s long time behavior, at least if the supports of class 1 (5) service time distributions are disjoint with the supports of the corresponding distributions for classes 6, 7, 8 (resp. 2, 3, 4).

Fig. 11

A simulated sample path of an apparently stable SRPT network with 122 customer classes, Poisson arrivals and Pareto service times

Fig. 12

A simulated sample path of an apparently stable SRPT network with Poisson arrivals and Weibull service times

Fig. 13

A simulated sample path of an apparently stable SRPT network with 122 customer classes, Poisson arrivals and Weibull service times

Then, retaining Poisson arrivals from the previous two cases, we have altered the customer service times for each class to i.i.d. exponential random variables with means given by (7), (8). Somewhat surprisingly, the latter system appears to be stable; see Fig. 8. It seems that stochastic variability of the exponential service times “smooths out” the underlying SRPT network’s performance to the point of stabilizing its long time behavior. This finding is in line with existing results showing that even in the G/G/1 case, the asymptotic SRPT system’s performance is very sensitive to variations in the underlying service time distributions (compare, for example, the limits in [6, 26, 36]). If our simulated network is indeed unstable, we have a phenomenon opposite, in some sense, to the one reported in [20], where a deterministic two-station reentrant line with static buffer priorities was stable, while its exponential counterpart was not. In order to start seeing numerical indications of the SRPT network instability in the case of exponential interarrival and service times, we had to “split the second and the fourth server in the Lu–Kumar system into sixty parts,” i.e., simulate a reentrant line with two stations, 122 customer classes and mean service times $m_1=m_{62}=0.3$, $m_2=...=m_{61}=m_{63}=...=m_{102}=0.01$, with classes 1, 63, ..., 102 served at the first station and 2, ..., 62 at the second one (see Fig. 9).

Finally, we have repeated the latter two experiments with the same interarrival distribution and mean service times, but with i.i.d. Pareto and Weibull service time distributions, respectively, instead of the exponential ones. Somewhat surprisingly, we have not found convincing indications of the resulting system instability, even in the case of 102 customer classes, although the network with 102 classes and Pareto service times exhibits much more queue length variability than the remaining ones (see Figs. 10, 11, 12, 13).

Summarizing, the issue of multiclass SRPT network stability/instability seems to depend heavily on the corresponding service time distributions (rather than merely on the interarrival and service rates), as well as on the underlying network topology. Consequently, providing general results addressing this issue and characterizing the corresponding fluid limits is likely to be challenging.

7 Discussion and conclusion

We have provided two examples of strictly subcritical multiclass queueing networks, with the same topology, which are unstable under both the SRPT and SJF service protocols. The service times in the first of them are deterministic, making it unstable also under the SERPT discipline. In the second one, the service times in one customer class are randomized.

It is natural to expect that the service times in other customer classes of our network can be (moderately) randomized as well, without changing its qualitative behavior, at the expense of further increase in the proof complexity. We would like to note, however, that randomizing service times in some customer classes seems to introduce more difficulties to the corresponding arguments than randomizing others. For instance, if we modify the second example by randomizing the service times in class 2, rather than 4, then the counterpart of the random time $\tau _1$ defined by (52) can actually be of the order O(1), rather than O(M), with non-negligible probability. To proceed as before, one would have to additionally argue that, with large probability, at least one of the network “work cycles,” similar to [0, T] from our Propositions 1, 2, has length O(M). Since the main goal of the present paper is to present counterexamples for stability of SRPT, SERPT and SJF multiclass queueing networks, we have not complicated our systems (and our analysis) any further.

Our findings are in sharp contrast with stability of EDF multiclass queueing networks, with or without preemption [14, 29, 31]. In a single-server queue setting, there is a deep relation between the EDF and SRPT scheduling strategies. To our knowledge, their similarity was first noticed by Bender et al. [7] and then, more explicitly, by Down et al. [23]. Atar et al. [2] proposed a unified framework for the analysis of single-server systems with various scheduling disciplines, including EDF, SJF and SRPT. Recently, Atar and Shadmi [3] extended the scope of this method to generalized Jackson networks working under the EDF protocol with hard or soft deadlines. Our instability results, together with different behavior of linear strictly subcritical resource sharing networks under the SRPT and EDF service disciplines [30, 41], suggest that it might be difficult to further extend the approach of [2] to the general multiserver setting. On the other hand, the above-mentioned EDF stability results suggest using the EDF protocols, with the customer initial lead times equal to large multiples of their service times, as stable proxies of SRPT and SJF in multiserver networks. See [30], Section 8 for more details.