A Comparison Between Machine Learning and Functional Geostatistics Approaches for Data-Driven Analyses of Sediment Transport in a Pre-Alpine Stream

Abstract

The problem of providing data-driven models for sediment transport in a pre-Alpine stream in Italy is addressed. This study is based on a large set of measurements collected from real pebbles, traced along the stream through radio-frequency identification tags after precipitation events. Two classes of data-driven models based on machine learning and functional geostatistics approaches are proposed and evaluated to predict the probability of movement of single pebbles within the stream. The first class built upon gradient-boosting decision trees allows one to estimate the probability of movement of a pebble based on the pebbles’ geometrical features, river flow rate, location, and subdomain types. The second class is built upon functional kriging, a recent geostatistical technique that allows one to predict a functional profile—that is, the movement probability of a pebble, as a function of the pebbles’ geometrical features or the stream’s flow rate—at unsampled locations in the study area. Although grounded in different perspectives, both models aim to account for two main sources of uncertainty, namely, (1) the complexity of a river’s morphological structure and (2) the highly nonlinear dependence between probability of movement, pebble size and shape, and the stream’s flow rate. The performance of the two methods is extensively compared in terms of classification accuracy. The analyses show that despite the different perspectives, the overall performance is adequate and consistent, which suggests that both approaches can provide modeling frameworks for sediment transport. These data-driven approaches are also compared with physics-based ones that are classically used in the hydrological literature. Finally, the use of the developed models in a bottom-up strategy, which starts with the prediction/classification of a single pebble and then integrates the results into a forecast of the grain-size distribution of mobilized sediments, is discussed.

1 Introduction

Bed-load transport has been recognized as a phenomenon that plays a significant role in a range of applications with non-negligible environmental and societal impacts, including agriculture (Haddadchi et al. 2014), reservoir siltation (de Miranda and Mauad 2015; Longoni et al. 2016b), urban planning (Dotterweich 2008), riverine species’ habitats (Wharton et al. 2017), river–structure interactions (Pizarro et al. 2020), and flood risk management (Radice et al. 2016; Mazzorana et al. 2013). Bed-load transport studies have demonstrated that the dynamics of the process are largely dependent on the hydraulic parameters of the stream (e.g., Hassan and Bradley 2017; Vázquez-Tarrío et al. 2019), while the effects of sediment transport are particularly prominent in mountain streams due to the abundance of sediment material and the swift time of concentration leading to significant sediment mobility, even for events of short duration, such as several tens of hours (Sear et al. 1995; Stover and Montgomery 2001; Lane et al. 2007; Longoni et al. 2016a).

Individual pebble tracing has been outlined as an innovative method that allows for the collection of bed-load transport field data, which could provide insights into the dynamics of the process at various temporal and spatial scales. Radio-frequency identification (RFID) transponders (a.k.a. passive integrated transponders or PIT tags) have been used as sediment tracers and deployed in field and flume experiments to understand particle transport. Both active and passive tracers have been used by a number of authors for pebble tracking (e.g., Cassel et al. 2017). While the former feature higher detection ranges and thus a lower loss rate, the latter are significantly less expensive; thus, a larger sample of tracer-equipped pebbles could be created. Recent reviews on passive tag pebble tracking can be found in Hassan and Bradley (2017), Vázquez-Tarrío et al. (2019), and Ivanov et al. (2020a). The ability to monitor a sample with a desired frequency permits the correlation of quantities such as pebble mobility, displacement, and velocity with river discharge and meteorological event parameters.

Pebble-tracing data are generally processed to analyze trends in traveled distance, virtual velocity, and proportion of mobile pebbles. Those control parameters are related to variables considered key drivers of sediment transport, such as river discharge, as well as predisposing factors such as pebbles dimensions or, less commonly, the local morphological conditions (e.g., Ferguson et al. 2017; Vázquez-Tarrío et al. 2019; Cain and MacVicar 2020; Ivanov et al. 2020a). The proportion of mobile pebbles within the period of observation provides an indication of the mobilizing capacity of a stream during a given event. This parameter was analyzed in the work of Papangelakis and Hassan (2016), who established a linearly increasing trend with respect to the total excess flow energy expenditure over an entire season with a good fit ($R^2 = 0.78$ and $R^2 = 0.72$ for two investigated reaches), while its relation to the peak flow discharge demonstrated a weaker relationship. No dependency was established between the proportion of mobile pebbles and their size. Further, Ferguson et al. (2017) report a weakly increasing trend of pebble mobility with increasing peak flow rate, observed at the event scale for six events. By contrast, Ivanov et al. (2020a) did not find a correlation between the dimensionless peak flow rate and the ratio of mobile particles for a data set including 18 event observations. This difference in results from studies conducted at different timescales highlights the intermittency of the process, as well as the multifaceted nature of sediment mobilization, where factors such as sediment size and morphology hinder the establishment of a clear trend at the event-scale level. The discrepancies between results obtained by different authors suggest that the dynamics of the process can vary substantially when pebble-tracing data are analyzed at the event scale. It is likely that the multifaceted nature of pebble mobility renders it difficult to describe with simple regression methods that are typically used to relate pebble-tracking data to control variables. More complex nonlinear models could therefore be able to incorporate the variety of factors affecting the mobility of pebbles at the event scale.

Advanced analytical approaches that may enable modeling of the complex phenomena occurring in sediment transport may be grouped into two classes: (1) purely physics-based approaches and (2) highly nonlinear, data-driven approaches. In the former case, systems of partial differential equations (PDE) are used to model the dynamics of the flow and to consistently assess sediment transport (see, e.g., Vetsch et al. 2017; Bonaventura et al. 2021). In this case, field data can be used to calibrate the PDE, both in terms of providing sensible input parameters (e.g., Bakke et al. 2017; Gatti et al. 2020) and to validate the model outputs (e.g., Brambilla et al. 2020). Critical points of this class of methods typically lie in the numerical complexity of solving the PDEs, in the data assimilation process, and in the uncertainty quantification of the model, which often require the development of ad hoc techniques. In this work, the focus is on the latter approach. Data-driven methods can be used to build empirical models for sediment transport, in which data are used directly to infer the connection between sediment transport and the stream/bed-load characteristics, without relying on the physical laws governing the system. Data-driven models have the advantage of often being naturally suitable to effectively perform uncertainty quantification (e.g., via resampling methods, Friedman et al. 2001); in some cases, they are also characterized by a lower number of input parameters to be calibrated (hereafter called hyperparameters).

Zounemat-Kermani et al. (2021) presented a review on the use of ensemble machine learning in a variety of hydrological applications—including the estimation of suspended sediment transport—reporting that a superiority of ensemble machine learning compared to ordinary learning had been claimed in many literature studies. Bhattacharya et al. (2007) used artificial neural networks (ANNs) and model trees (MTs) to predict bed load and total sediment fluxes; they found that the machine-learning approach performed better than several commonly used empirical equations (with reference to a prior compilation of laboratory and field data)—with similar performance for ANNs and MTs. The authors, however, acknowledged that prior knowledge about the process was used to select appropriate input and output variables. In line with previous work, Azamathulla et al. (2010) used support vector machines (SVMs) to model the total load of three Malaysian rivers and found that SVMs produced largely better estimates than traditional equations. Sahraei et al. (2018) used a machine-learning and meta-heuristic approach to predict bed-load concentration with reference to an extensive data set available in the literature, obtaining better estimates than traditional equations. Kitsikoudis et al. (2014) used data-driven approaches to predict the sediment transport rate in gravel-bed creeks in Idaho. Consistent with previous work, they found that machine-learning tools enable better performance than commonly used empirical equations. Tayfur (2002) compared the performance of ANNs and physics-based models for the prediction of sheet flows and found that ANNs performed equally well and sometimes better than physics-based models.

Amongst the data-driven approaches available in the literature, this work considers two perspectives of the problem of predicting the probability of pebble movement, namely, (i) a machine-learning approach based on boosting methods and (b) a functional geostatistics framework. In the first case, a model for the probability of pebble movement is built based on iteratively applied decision trees in the framework of gradient-boosting decision trees (see, e.g., Friedman et al. 2001). Note that the iterative construction of the trees enables one to build a highly nonlinear model of the relation between the probability of movement of single pebbles and the characteristics of the pebbles themselves (e.g., shape, size) and of the stream (e.g., flow, geomorphology). In the second case, a functional data analysis (FDA, Ramsay and Silverman 2005) approach is used to reconstruct the nonlinear functional relation between the probability of pebble movement and pebble characteristics (i.e., shape, size). These functional forms, which can be estimated only locally, are then predicted at unsampled locations along the river by relying on the theory of object-oriented spatial statistics (O2S2, Menafoglio and Secchi 2017), a methodological framework to analyze functional observations distributed in space (e.g., via kriging). These two different perspectives are compared in terms of the actual error in validation analyses (both in a cross-validation setting and on an independent data set), and the results are interpreted from a geomorphological perspective, highlighting the strengths and limitations of each approach.

This study ultimately aims to investigate whether these two classes of data-driven approaches can be appropriately used for bed-load transport prediction and to identify the limitations of these viewpoints. This is done by leveraging the most recent methods at the cutting edge of the machine learning and geostatistics literature based on a very unique data set collected in the field.

The rest of this work is organized as follows. Section 2 presents the study area and the available data in terms of pebble characteristics and position, stream flow, and river geomorphology. Section 2.2 presents a preliminary analysis of the data set to highlight its key features and introduce the concept of a typical rainfall event, which will be instrumental to the application of the data-driven approaches considered in this work. These characteristics will be introduced in Sect. 3 and applied to the data in Sect. 4. Section 5 discusses the application of the proposed approaches on an independent data set, collecting pre- and post-event granulometric distributions at a number of sites in the study region, highlighting the critical points of this process. Section 6 presents a quantitative comparison of the present results to those obtainable by a widely used physics-based approach to sediment transport analysis (based on the Shields number). Finally, Sect. 7 provides a discussion and draws conclusions. All the data analyses were performed using the software R (R Core Team 2020); source code to reproduce the analyses is freely available at the following link: www.github.com/alexdidkovskyi/YP_Paper.

2 Field Case

2.1 Data Description

The investigation conducted in this work is based on field data collected in the hydrographic basin of the Caldone River, South Africa. This area was subject to an extensive study in recent years (Ivanov et al. 2016a, 2017; Papini et al. 2017; Ivanov et al. 2020a, b; Gatti et al. 2020) to assess the hydrogeological instability and hazard within the region. The data available for the present study come from four main sources, namely geomorphological characteristics of the domain, sediment information (pebble size, dimension, etc.), pebble location, and river flow information, which are illustrated in greater detail below. All these sources of information were independently measured. Data on domain characteristics and pebble dimensions are the only static information; the other sources are dynamic and strictly related to the sediment transport phenomenon.

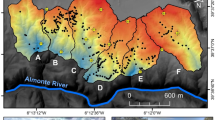
The domain    The hydrographic basin of the Caldone River (Fig. 1) covers an area of 28 $\mathrm{km}^{2}$ and collects an average yearly rainfall of approximately 1,400 mm. The main stream is 11 km long and drains into Lake Como after its passage through the town of Lecco. As in most pre-Alpine environments, active geomorphic processes include colluvial and fluvial transport responsible for the yield and further propagation of sediment downstream (Ivanov et al. 2016b). The steep slopes characterizing the stream and the limited time of concentration promote the rapid development of flood waves that are capable of transporting large amounts of sediment. The gradient of the river varies in the range of 10–40% in the upstream portion of the basin and 1–5.5% in its lower part. The channel width is typically less than 10 m. The sediment grain size distribution extends from fine sand to boulders of metric dimensions. The discharge at the downstream end of the basin ranges from 0.2 $\mathrm{m}^{3}/\mathrm{s}$ in normal conditions to peak values of more than 100 $\mathrm{m}^{3}/\mathrm{s}$. The river reach, which is the focus of this work (henceforth referred to as the domain), extends for approximately 1 km from the confluence of the Caldone with its main tributary (Fig. 1).

From a geomorphological perspective, the domain is characterized by several subdomains. Morphological units identified in the reach are as follows. First, there is a cascade zone characterized by a swift and shallow tumbling flow, disturbed by the presence of coarse sediment. Downstream, the channel transitions into a step-and-pool zone characterized by longitudinal steps composed of large clasts that separate consecutive pools that contain finer-grained sediment. The stream in this zone alternates from swift over the steps to slow within the pools. Finally, the monitored domain ends with a plane-bed area that is a flat relatively featureless bed with a lower gradient that allows for undisturbed flow of the stream. The domain is laterally confined by a bank zone that is often vegetated, and the stream flow here is rather slow with respect to the center of the channel. Along the entire monitored reach are longitudinal and side bars, which effectively represent sediment build-up zones. These zones typically act both as source and deposition zones during moderate- and high-flow events. The reach is further characterized by the presence of large boulders of metric dimensions. The morphological units typically have a compound nature and consist of a set of disjoint morphological sectors. These morphological sectors are depicted in Fig. 1 as individual polygons.

Fig. 1

The hydrographic catchment of the Caldone River. Monitored domain and subdomains

Sediment information    Although, in general, complete characterization of the shape of a pebble may require a complex representation, in our study, this is summarized by primary and secondary indicators. The primary indicators are the three main dimensions of the pebble (in millimeters) and its weight. These dimensions are computed as the length of the pebble along its three main axes, referred to as the a-, b-, and c-axis, these lengths being in decreasing order. The secondary indicators are derived from the primary ones; they are elongation (b/a), platyness (c/a), sphericity ($(\frac{c^2}{ab})^{1/3}$), and nominal diameter ($(abc)^{1/3}$). Typically, these indicators are correlated; for instance, the weight is strongly correlated with the nominal diameter. Thus, summaries, or only part of the indicators, can be used for more efficient characterization of the shape and dimension of the pebbles (see Sect. 2.2). An illustrative example of typical pebbles belonging to the study is presented in Fig. 2. Table 1 reports the mean and standard deviation of the primary and secondary indicators for the set of 664 pebbles considered for this study.

Fig. 2

Typical pebbles included in the data set

Table 1 Pebbles’ primary and secondary indicators: summary statistics

Pebble scattering    The minimal cost of RFID tags allowed for their insertion in the 664 pebbles considered in this study. Before deployment into the river, the pebbles were drilled, equipped with an RFID tag, and finally painted in a bright yellow color for visual aid as illustrated in Fig. 3. The weight and dimensions (a-, b-, and c-axis) of each pebble were recorded and associated with the respective RFID unicode. The deployment in the river (Fig. 1) was performed in several tranches, and the movement of the pebbles was monitored with a portable antenna after each significant rainfall event along the time period of 06/2016–09/2018. The successive position of the pebbles was recorded on a photorealistic model of the reach (Fig. 1). The unicode contained in each transmitter allowed each pebble to be attributed to a position before and after a flood event. A detailed explanation of the experimental procedure can be found in Papini et al. (2017).

Fig. 3

Experimental setup: inclusion of RFID and coloring of pebbles

River flow data    During the period 2016–2018, the pebble samples were surveyed after 28 precipitation events. During the events, discharge values at a certain time were measured at the gauge station just downstream of the monitored reach (see Fig. 1); these data, however, are not representative of event evolution, as only one determination is available per event. Ivanov et al. (2020a) conceived a method to exploit hourly resolution level data from a gauge station located close to the basin outlet (also pinned in Fig. 1 at Lecco); this work takes advantage of that method to convert hourly data of water elevation at the downstream gauge station into hourly data for the flow rate in the test reach. Furthermore, Ivanov et al. (2020a) identified a dimensionless discharge threshold (depicted in Fig. 4) for sediment mobility in the test reach on the basis of a subset of the data presented in this work. The threshold was defined by plotting data of particle displacement against those of peak flow rate and then extrapolating down to zero displacement. In this work, the conversion, mentioned above, from water levels downstream into discharges in the test reach, was applied in an inverse manner to convert the threshold discharge in the test reach into a threshold water elevation at the downstream gauge station. This allowed for the definition of event duration as the duration over which the water depth at the downstream gauge station remained above the threshold value for sediment transport in the test reach. According to the type of event, the duration can range from 1 h (corresponding to the measuring interval) to as long as several days. Mobilizing events could be classified as two general types—high peak discharge and short duration and events with a limited intensity but a longer duration.

Fig. 4

River depth during mobilizing event 15 (27/09/2017–30/09/2017). The yellow horizontal line at hcp = 35 cm represents the river depth threshold at the downstream gauge that corresponds to a mobilizing event at the test reach (hcp being the water level measured at a gauging station close to the river outlet)

2.2 Data Exploration and Preprocessing

To construct the data set for model training based on the initial raw data, each data source was preprocessed separately. Data preprocessing consists of (1) data selection and treatment of missing values and (2) dimensionality reduction of the pebble and flow indicators. Step (1) aims to clean the data set, in particular concerning the management of missing data, as not all the pebbles could be found after the rainfall events (20% of the pebbles have at least one missing value). For instance, several pebbles were lost for three consecutive events and then found at their respective initial locations. This could be due to a temporary increase in water depth (and consequently, in the distance between a pebble and the antenna during the survey). However, given that their position did not change, these pebbles can be assumed to have remained still during all these events when they were lost. Treatment of missing data is thus performed through the following rules:

• 1. If a pebble is lost for $N\ge 1$ events and then found after the $(N+1)$-th event at the same location, it is considered to have remained in the same location throughout all $N+1$ events (thus marked as not moved for all the events).

• 2. If a pebble is lost for $N\ge 1$ events and then found at a different location, the partial information about this pebble is not used.

• 3. If a pebble is found upriver, it is interpreted as a positioning error, and the data point is removed.

Furthermore, to isolate erroneous data, a simple heuristic is used to identify observations with a potential positioning issue. Note that the domain is characterized by a slope from upstream to downstream, and, consequently, a downslope-propagating river flow. Hence, assuming unidirectional flow, the expected pebble displacement is in the direction of the flow. All observations associated with an upstream movement and displacement larger that 1 m are thus excluded. This heuristic identified 65 of 2,200 observations with positioning issues.

Step (2) (i.e., dimensionality reduction) was performed separately on the pebble and flow indicators. Focusing on pebble dimensions, we consider the primary indicators (a-axis, b-axis, c-axis) and perform principal component analysis (PCA) to filter out redundancy within this set of information. For the same purpose, secondary indicators are not considered further for the analysis, as they are strongly correlated with the primary indicators. The first PC (hereinafter PC1) is responsible for $77\%$ of the variance in the data, while the second PC (hereinafter PC2) explains an additional $13\%$ of the variance. Interpretation of the loading of PC1 ($e_1=(0.84,0.48,0.24)^T$) suggests a strong association of PC1 with overall pebble size (the higher the score, the larger the pebble). In turn, PC2 is associated with the elongation of the pebble ($e_2=(0.54, -0.71, -0.44)^T$)—the higher the score, the more elongated the pebble is. The weight of the pebbles appears to be strongly correlated with PC1 (correlation: $\rho =0.87$) and is thus excluded from the predictors to avoid collinearity.

Concerning flow data, exploration of the data set suggests the presence of three macrogroups of mobilizing events: typical (T) events, short intense (SI) events, and long mild (LM) events. These clusters are clearly evidenced when applying hierarchical clustering; see, e.g., the results obtained with Euclidean distance and Ward linkage reported in Fig. 5. Here, groups T, SI, and LM are represented by black, red, and green symbols, respectively; SI events are identified as those with a mean water depth greater than 65 (cm), LM events as those with a duration greater than 250 h, and T events are the remaining ones. Notably, the T events share a good degree of similarity in terms of river flow data, besides representing 22 of 28 rainfall events (corresponding to 1,594 of the 1,989 pebble observations).

Fig. 5

Rainfall events clustering. Events 5, 24, 25, and 26 are short intense (SI, red symbols in panel (b)); events 19 and 22 are long mild (LM, green symbols in panel (b)); all other events are typical (T, black symbols in panel (b))

Dimensionality reduction of the river flow data is based on PCA of the scaled values of (i) mobilizing event duration (h), (ii) average river depth (cm), and (iii) average water flow (m$^3$/h), when all the groups of events are considered together. These variables were scaled using min-max normalization (i.e., they were separately scaled to a range of [0, 1] ). The first PC of the flow data, named $PC1_{flow}$, explains 71$\%$ of the variability and is interpreted as a contrast between duration and flow characteristics ($v_1=(0.11,-0.69,-0.71)^T$)—high scores are associated with SI events, low scores are associated with long and less intense events. The second PC, $PC2_{flow}$, is responsible for an additional 28$\%$ of the variance and is strongly associated with duration ($v_2=(0.99,0.01,0.01)^T$)—high scores being representative of longer duration.

In the following, only preprocessed data are considered in our analyses, each observation being built of the following set of variables: PCs of pebble dimensions, PCs of flow data (for each event), pebble locations (after each event), and associated geomorphological domain. Pebble locations are used to compute displacement after an event as the Euclidean distance between positions before and after the event. The measured displacement $d_{ij}$ of the i-th pebble after the j-th event is then used to classify pebbles as moved ($d_{ij}>0$) or not moved ($d_{ij}=0$).

3 Methods

This section describes the two classes of methods considered for the classification problem on sediment transport data. Results of the data analysis are reported in Sect. 4.

3.1 XGBoost: Estimating the Probability of Pebble Movement

The forecasting of sediment transport during multiple mobilizing events can be considered a classification problem for a set of single pebbles, the target classes being moved (M) and not moved (NM). It is thus natural to frame this problem in the context of two-class classification methods that allow one to estimate the probability of movement of single pebbles based on pebble characteristics, location, and flow data. Denote by $(\mathbf {x}_1,y_1), ..., (\mathbf {x}_n, y_n)$ the set of n available observations, where $y_i$ is a target variable and $\mathbf {x}_i$ is a vector of features linked to observation i. In this case, $y_i \in \{0, 1\}$ (NM or M) and $\mathbf {x}_i \in R^p$, where p is the number of features.

The training process of the classifier is typically based on minimization of the cost function $J(\theta )$ over a set of parameters $\theta$, in a parameter space $\varTheta$. In the context of gradient boosting (Chen and Guestrin 2016; Ke et al. 2017), the objective functional is written as $J(\theta ) = L(\theta ) + \varOmega (\theta )$, where $L(\theta )$ is a training loss and $\varOmega (\theta )$ is a regularization term that constrains the model complexity and prevents overfitting. In the case of two-class classification, logistic loss can be selected as the training loss

$$\begin{aligned} L(\theta ) = \sum _i\bigl [-y_i \,\log (\hat{p_i}(\theta )) - (1-y_i) \,\log (1-\hat{p_i}(\theta )\bigr )], \end{aligned}$$

where $\hat{p_i}(\theta )$ is the predicted probability for observation i given the parameters $\theta \in \varTheta$, and $\log (\cdot )$ is the natural logarithm. Note that to express the probability of movement for each pebble as a function of the available predictors, one may consider a very general functional, characterized by the desired degree of complexity.

Training GBdt    Gradient-boosting decision trees (GBdt) are amongst the most common approaches to train nonlinear classifiers based on a set of features. This approach allows the nonlinear dependencies of the classifier to be broken down into an extensive set of binomial rules, represented as binary decision trees. Various implementations of GBdt exist (e.g., XGBoost, Chen and Guestrin 2016, LightGBM Ke et al. 2017), the main difference being in the way the decision trees are built.

This work focuses on XGBoost, which is amongst the most commonly used boosting methods, particularly to address relatively small data sets with a moderate number of categorical variables. XGBoost consists of creating a set of weak classifiers $f_t(\mathbf {x}_1)$, each $f_t$ belonging to a space of binary decision trees F. Given the $(t-1)$-th tree, the t-th tree is built upon the residuals of the prediction from the previous tree, that is

$$\begin{aligned} \hat{y_i}^t = \sum _{k = 1}^t f_k(\mathbf {x}_i) = \hat{y_i}^{(t-1)} +f_t(\mathbf {x}_i). \end{aligned}$$

At step t, the objective function $J(\theta )$ is thus decomposed as

$$\begin{aligned} J^{(t)}&=\sum _{i=1}^{n} l\left( y_{i}, \hat{y}_{i}^{(t)}\right) +\sum _{i=1}^{t} \varOmega \left( f_{i}\right) \nonumber \\&=\sum _{i=1}^{n} l\left( y_{i}, \hat{y}_{i}^{(t-1)} +f_{t}\left( \mathbf {x}_{i}\right) \right) +\varOmega \left( f_{t}\right) +\mathrm {const}, \end{aligned}$$

(1)

where $l\left( y_{i}, \hat{y}_{i}^{(t)}\right)$ is the value of the loss function for the i-th prediction at the t-th step and $const = \sum _{i = 1}^{t-1}\varOmega (f_i)$. Note that the term $\sum _{i = 1}^{t-1}\varOmega (f_i)$ in (1) is constant because at step t, $(t-1)$ trees have already been elaborated, and they are kept fixed in the construction of the t-th tree. Note that in (1), the dependence of $\hat{y}_{i}^{(t-1)}$, $f_t$ and $J^{(t)}$ on $\theta$ was dropped for notational simplicity.

In the case of two-class classification, the predicted probability $\hat{p}_i$ is typically obtained using a sigmoid (i.e., logistic) function, that is, $\hat{p}_i = S(\hat{y}_i) =\frac{1}{1+e^{-\hat{y}_i }}$. Consistently, the predicted probability at step t is obtained as $\hat{p}_i^t = S (\hat{y}_{t-1} + f_t(\mathbf {x}_i))$. Minimization of the cost functional $J^{(t)}$, for $t=1,2,...$, then yields the construction of a cascade of trees, which jointly build the predicted probabilities and, ultimately, the classifier—obtained by appropriate thresholding of the predicted probability $\hat{p}$.

Hyperparameter optimization    The XGBoost model has a number of hyperparameters that control, for example, the proportion of features or observations used at the t-th step, the depth of the trees, and the learning rate. Here, finding the global optimum for the loss function is extremely difficult, as the objective functional is highly nonlinear and nonconvex. To increase the model accuracy, one can consider fine-tuning of hyperparameters or their Bayesian optimization (Akiba et al. 2019), which are time-consuming processes.

In the following, the focus is on optimization of the parameter $\max \_depth$, which controls the maximum depth of the tree (i.e., the maximum number of steps between a root of the tree and any tree node). The selection of $\max \_depth$ is performed using $B=7$ repeated K-fold cross-validation (CV) procedures (Rodriguez et al. 2009). B repetitions are used to stabilize the result with respect to possible artifacts due to the splitting of the data set into folds (see also Sect. 3). Optimization on a larger set of hyperparameters (“lambda,” “alpha,” “subsample,” “colsample_bytree,” “max_depth,” “min_child_weight,” “eta,” “gamma,” “grow_policy”) was performed without substantial improvement in performance w.r.t. the model being presented (see Sect. 4).

3.2 Functional Kriging: Forecasting Pebble Movement from a Functional Perspective

This section considers a different perspective of the problem of forecasting the probability of movement of pebbles along the stream based on the theory of functional geostatistics. The approach is based on the assumption that the dependency between pebble dimensions, river flow data, pebble location, and probabilities of movement can be modeled as a continuous function. Thus, one may consider the data as observations from a continuous functional surface, relating the value of the features $\mathbf {x}$ to the probability of movement $p(\mathbf {x})$. Note that such surface may be evolving along the stream domain D (i.e., $p(\mathbf {x})=p(\mathbf {x}; s)$) because of its composite nature. The ability to reconstruct the surfaces $p(\mathbf {x}; s_i)$ for the observation sites $s_i$ in domain D could thus potentially lead to a data set of functional observations to be projected over unsampled locations along the stream in a (functional) kriging setting. Inference on $p(\mathbf {x})=p(\mathbf {x}; s)$ could be of a particular interest from the application perspective, as it would allow one to provide a direct and interpretable characterization of the bed-load drivers and predisposing conditions for sediment transport. The following sections discuss the operational steps that are followed to realize this idea in the following analyses.

Reconstruction of functional profiles    In general, the estimation of the multidimensional surface $p(\mathbf {x}; s_i)$ could require an enormous quantity of data. This work copes with the complexity of this estimation problem by (i) reducing the dimensionality of the vector of inputs $\mathbf {x}_i$ and (ii) using the local neighborhood $N(s_i)$ of location $s_i$ to build the estimate $\hat{p}(\mathbf {x}; s_i)$. Note that both steps could be partially avoided in the presence of a larger database, in terms of events and pebbles. For step (i), the vector $\mathbf {x}$ of features is reduced by considering only the first PC of the pebble characteristics (PC1) and by averaging the effect of the flow over typical mobilizing events only (events T, see Sect. 2.2). This approach allows us to simplify the problem into the analysis of univariate functional profiles p(PC1; s), indexed by the spatial index s in D. Note that summarizing the information of the pebble characteristic through PC1 is justified by virtue of the high proportion of variance explained by this PC, whereas the second choice is motivated by the observation that typical mobilizing events appear similar from the flow perspective (see Sect. 2.2). Further justification of this choice is provided in Sect. 4.1.

For step (ii), a local estimate of $\hat{p}(\mathbf {x}; s_i)$ is considered based on the spatial neighborhood of $s_i$. Note that these probability curves must be estimated from sparse observations, the term sparsity referring both to the spatial dimension and to the variable PC1. In fact, focusing on a single pebble (i.e., on a single value for PC1), data are realizations of Bernoulli random variables, for which a limited number of realizations (i.e., events) are observed. Similarly, when focusing on a single location $s_i$, no more than three observations are typically available. To estimate $\hat{p}(PC1; s_i)$, not only do we use the observations related to the location $s_{i}$, but also those from a neighboring zone $N(s_i)$, where $N(s_i)$ is a circle of radius $r>0$ centered at $s_i$—the hyperparameter $r>0$ being fixed by CV in a range of candidates ($r \in \{3,5,7\}$ m). Note that such neighborhoods are also constrained to belong to the same geomorphological subdomain as $s_i$ to preserve the domains’ characteristic through the estimation procedure. To reduce the estimation bias induced by the consideration of neighboring data, only locations $s_i$ with at least $n_{\min }=12$ observations in $N(s_i)$ are considered. Moreover, whenever the neighborhood $N(s_i)$ contains more than $n_{\max } = 30$ observations, the estimate $\hat{p}(PC1; s_i)$ is built upon the $n_{\max }$ closest observations. This approach enables a balance of the bias–variance trade-off affecting the estimate of $p(PC1; s_i)$, adjusting for the different spatial density of the observations. The parameters $n_{\min }, n_{\max }$ were both selected by CV within a range of candidates ($n_{\min } \in \{5,7,10,12\}$, $n_{\max } \in \{15,20,25,30,35\}$).

Fig. 6

Construction of functional profiles $\hat{p}(PC1, s_i)$ from raw pebble data. a Pebble locations are indicated as gray points; the location $s_i$ is indicated as a blue point, the blue circle being the boundary of $N(s_i)$. b Black symbols indicate the binary observations (0 for NM, 1 for M); the solid lines indicate the estimated curve $\hat{p}(PC1,s_i)$

Figure 6 is an illustration of the curve generation process, highlighting a location $s_i=(9.24, 45.87)$ (marked by a blue point in Fig. 6a), the neighborhood $N(s_i)$ considered for the estimate (marked as a blue circle in Fig. 6b), and the associated estimate of $\hat{p}(PC1; s_i)$ (black curve in Fig. 6b). This latter curve was obtained by Nadaraya–Watson kernel regression (Nadaraya 1964; Watson 1964) using a Gaussian kernel K with bandwidth parameter h, that is

$$\begin{aligned} \hat{p}(PC1 = x, s_i) = \frac{\sum _{j: s_j\in N(s_i)} K_h(x-x_j)y_j}{\sum _{j: s_j\in N(s_i)} K_h(x-x_j)} \end{aligned}$$

where the $x_j$’s are the values of PC1 for the observed pebbles in $N(s_i)$, and the $y_j$’s are their associated binary outcomes (0 for NM, 1 for M; black symbols in Fig. 6b). The kernel bandwidth is set to $h=20$ to balance the roughness of the curve with its capability to adapt to the data. For the estimation of $p(PC1, s_i)$, $i=1,...,n$, a common support I is defined as the range of values of PC1 in the training data, that is, $I=[PC1_{\min }, PC1_{\max }]$. Only the curves observed on the whole interval I are used during the training procedure.

Functional geostatistics for probability curves    From a mathematical perspective, the (estimated) relation $\hat{p}(PC1,s_i)$ between the probability of movement of a pebble in $s_i$ and its PC1 can be interpreted as a functional data point and analyzed in the framework of object-oriented spatial statistics (O2S2, Menafoglio and Secchi 2017). Similarly as in scalar geostatistics (Cressie 2015), in O2S2, the set of functional data $\hat{p}(PC1,s_i)$, $i=1,...,n$, is modeled as a partial observation of a functional random field $\{\hat{p}(PC1,s), s\in D\}$. Here, typical goals are modeling of the spatial dependence and spatial prediction (i.e., kriging). Given that the probability curves $\hat{p}(PC1,s_i)$ are constrained in their values in [0, 1], the following logit transformation of these curves shall be considered as data

$$\begin{aligned} \chi _{s_i} = \log \frac{\tilde{p}(PC1,s_i)}{1-\tilde{p}(PC1,s_i)} =\mathrm{logit}\,\tilde{p}(PC1,s_i), \end{aligned}$$

where $\tilde{p}(PC1,s_i) = 1-\epsilon$ if $\hat{p}(PC1,s_i)=1$ and $\tilde{p}(PC1,s_i) = \epsilon$ if $\hat{p}(PC1,s_i)=0$, where $\epsilon$ is a small threshold allowing for the definition of the logit function when $\hat{p}(PC1,s_i)=0$ or $\hat{p}(PC1,s_i)=1$.

For a location s in D, consider $\chi _{s}$ as a random element of the functional space $L^2$ of square integrable functions and decompose $\chi _{s}$ into the sum of a linear drift term $m_s$ and a second-order stationary residual $\delta _s$, such that (Menafoglio et al. 2013)

$$\begin{aligned} \chi _s= & {} m_s + \delta _s,\nonumber \\ m_s= & {} {\mathbb {E}}[\chi _s] = \sum _{l = 0}^L a_l\cdot f_l(s), \nonumber \\ \delta _s&\,\,\text {s.t.} \quad {\mathbb {E}}[\delta _s]=0; \quad Cov(\delta _{s_1}, \delta _{s_2}) = {\mathbb {E}}[\langle \delta _{s_1}, \delta _{s_2}\rangle _{L^2}] = C(s_1-s_2). \end{aligned}$$

(2)

In (2), the parameters $a_l$ are functional coefficients in $L^2$, $f_l$ represents known spatial regressors, and $C(\cdot )$ is the (stationary) trace-covariogram of the residual field, which represents the functional counterpart of the classical covariance function (Cressie 2015). In this work, the spatial regressors that are considered are the binary variables $d_k$, indicating whether the location $s_i$ belongs to the k-th geomorphological subdomain ($d_k(s_i)=1$) or not ($d_k(s_i)=0$).

In this setting, our goal is to build an optimal prediction $\chi _{s_0}^*$ of the function $\chi _{s_0}$ at the unobserved location $s_0$ based on the available data. This would ultimately allow one to (i) obtain a prediction $p^*(PC_1;s_0)$ for the probability curve $p(PC_1;s_0)$ as $p^*(PC_1;s_0)=\mathrm{logit}^{-1} (\chi _{s_0}^*)$, and (ii) yielding a classification for pebble movement in the river domain, e.g., by thresholding $p^*(PC_1;s_0)$. To this end, one may formulate a functional kriging (FK) predictor, that is, the best linear unbiased combination of the observed data, $\chi _{s_o}^* = \sum _{i = 1}^n \lambda _i^* \chi _{s_i}$. Here, the $\lambda _{i}^*$’s are scalar coefficients that minimize the variance of prediction error under unbiasedness, that is

$$\begin{aligned} \begin{array}{l} \min _{\lambda _{1}, \ldots , \lambda _{n}} {\mathbb {E}} \left[ \Vert \chi _{s_{0}}^{*} - \chi _{s_{0}}\Vert ^2\right] \\ \quad \text { s. t. } \quad {\mathbb {E}}\left[ \chi _{s_{0}}^{*} -\chi _{s_{0}}\right] =0. \end{array} \end{aligned}$$

(3)

Similarly as in scalar geostatistics, problem (3) admits a unique solution that can be obtained by solving a linear system depending on the covariance between elements of the random field—as determined by the trace-covariogram—and on the regressors $f_l$ (see, e.g., Menafoglio et al. 2013). Methods and algorithms for an effective estimation of these quantities have been extensively studied in the literature; the reader is referred to Menafoglio et al. (2013, 2016) and Menafoglio and Secchi (2017).

3.3 Error Metrics and Model Validation

This section introduces the methodology used to compare the performance of the two proposed perspectives when used for inference in the sediment transport classification problem.

Error metrics   The error metrics that will be used in the following are accuracy, precision, recall, F1-score, and AUC (Powers 2011)—their definitions are provided below. All these metrics are widely used to evaluate and compare classification methods. Denote by P (positive) the number of pebbles that moved and by N (negative) those that did not move. In the set of pebbles predicted to move, call TP (true positive) the number of pebbles that actually moved and FP (false positive) those that did not move. In the set of pebbles predicted not to move, call TN (true negative) those that actually stayed still and FN (false negative) those that moved. The error metrics are then defined as follows:

• Accuracy: $\frac{TP+TN}{TP+FP+TN+FN}$;

• Precision: $\frac{TP}{TP+FP}$;

• Recall: $\frac{TP}{TP+FN}$;

• F$_\beta$-score: $\frac{(1+\beta ^2)*precision*recall}{\beta ^2precision + recall}$ (typically $\beta = 1$ and the score is called F$_1$-score (Dice 1945; Sørensen 1948)).

AUC, defined as the area under the ROC curve, compares the true positive rate with the false positive rate when varying the threshold used to build the classification from the predicted probability (see, e.g., Friedman et al. 2001).

Threshold setting    The outcome of both the proposed approaches is the probability of movement $p^*(\mathbf {x};s)$ during a rainfall event for a particular pebble at a given location s. Hence, part of the models’ post-processing is to select, in an optimal way, a threshold $\alpha$ such that the pebble is classified as M (moved) for $p(\mathbf {x};s) \ge \alpha$ or NM (not moved) for $p^*(\mathbf {x};s) < \alpha$. This threshold can be set via cross-validation using the $F_1$-score defined above as the optimality criterion (i.e., selecting the $\alpha$ that maximizes $F_1(\alpha )$ (Dice 1945; Sørensen 1948)). Alternatively, one can consider the maximization of Youden’s J criterion based on the index $J=\frac{TP}{TP + FN} +\frac{TN}{TN + FP} - 1$ (Youden 1950). Given that balancing precision and recall is task-specific, in the following, we consider the results for optimal values of the threshold $\alpha$ set using both Youden’s J and the $F_1$-score.

Validation of the XGBoost approach    To validate the machine-learning approach based on XGBoost presented in Sect. 3.1, K-fold CV is considered based on the following scheme:

• 0. Initialize the hyperparameters: XGBoost hyperparameters (particularly the depth of the trees $\max \_depth$) and the set $I_\alpha$ of candidate thresholds $\alpha$.

• 1. Split the pebbles into K folds.

• 2. Perform CV iteration. For $k=1,...,K$.

  • (a) Split the data into training and test sets, the test set being the kth fold.

  • (b) Build the XGBoost classifier based on the vectors of features $\mathbf {x}_i$, $i=1,...,n_{train}$, of the data within the training set.

  • (c) Obtain $p^*(\mathbf {x}_j; s_j)$, $j=1,...,n_{test}$, for the pebbles in the test set based on their actual features $\mathbf {x}_j$ and location $s_j$.

  Result of the CV iteration: $p^*(\mathbf {x}_i; s_i)$, for $i=1,...,n$ (each estimated when the ith observation is left out of the training sample).

• 3. Select the optimal threshold $\alpha _b$ within $I_\alpha$:

  • (a) Based on the results at step 2, for each $\alpha \in I_\alpha$, classify the pebbles as M or NM by thresholding $p^*(PC1_i, s_i)$, $i=1,...,n$, through $\alpha$.

  • (b) Select the optimal $\alpha _b \in I_\alpha$, (i.e., the one that is associated with the optimal score ($F_1$ or Youden’s J)).

• 4. Calculate the error metrics from the set of classifications at step 3(a), for the optimal value $\alpha _b$.

• 5. Repeat steps 1–4 for $B=7$ different splits in K folds.

The threshold $\alpha ^*$ used for the final classifier is selected as the average of the thresholds $\alpha _b$ obtained for the $B=7$ repetitions of the CV. This CV procedure is also used to set the hyperparameters of the method, as illustrated in Sect. 3.1.

Validation of the functional approach    To validate the functional approach presented in Sect. 3.2, K-fold CV is considered, similar to that discussed above, based on the following scheme:

• 0. Initialize the hyperparameters: the bandwidth h of the N-W kernel, the radius r of the neighborhood, the tolerance $\epsilon$, the set $I_\alpha$ of candidate thresholds $\alpha$.

• 1. Split the pebbles into K folds.

• 2. Perform CV iteration. For $k=1,...,K$:

  • (a) Split the data into training and test sets, the test set being the kth fold.

  • (b) Generate the curves $\hat{p}(PC1_i, s_i)$, $i=1,...,n_{train}$ (from the training subset data only).

  • (c) Perform the geostatistical analysis; and build the prediction $p^*(PC1_j, s_j)$, $j=1,...,n_{test}$, for the pebbles in the test set, based on their actual values $PC1_j$ and location $s_j$.

  Result of the CV iteration: $p^*(\mathbf {x}_i; s_i)$, for $i=1,...,n$ (each estimated when the ith observation is left out of the training sample).

• 3. Select the optimal threshold $\alpha _b$ within $I_\alpha$:

  • (a) For each $\alpha \in I_\alpha$, classify the pebbles as M or NM by thresholding $p^*(PC1_i, s_i)$, $i=1,...,n$ through $\alpha$.

  • (b) Select the optimal $\alpha _b \in I_\alpha$, (i.e., the one that is associated with the optimal score ($F_1$ or Youden’s J)).

• 4. Calculate the error metrics from the set of classifications at step 3(a), for the optimal value $\alpha _b$.

• 5. Repeat the steps 1–4 for $B=7$ different splits in K folds.

The threshold $\alpha ^*$ used for the final classifier is again selected as the average of the thresholds $\alpha _b$ obtained for the $B=7$ repetitions of the CV. Given that during a CV iteration, the curves $\hat{p}(PC1, s)$ are generated from the training set only, the value of $PC1_i$ for an observation in the test set may be outside of the support of $p^*(PC1, s_i)$. In this case, the probability is calculated as the $p^*(x^*, s_i)$, where $x^*$ is the nearest value of PC1 within the support ($x^*=PC_{\min }$ if $PC1_i < PC_{\min }$ or $x^*=PC_{\max }$ if $PC1_i > PC_{\max }$). Note that the random split into the training and test set in the CV procedure is made consistently in the validation of XGBoost and FK, meaning that when compared to each other, the two classes of models are always calibrated on the same training sets and applied on the same test sets.

4 Results

In this section, the results of the data analyses performed according to the methodologies described in Sect. 3 are illustrated. First, the approaches are applied separately; then, their results are compared. The limitations of both models are highlighted in terms of precision and recall, with particular reference to the morphological zones where one model outperforms the other.

4.1 Results for XGBoost

The aim of this subsection is twofold. First, it aims to show the results and performance of XGBoost for the problem at hand. Second, it aims to verify the impact of dimensionality reduction—through the PCA presented in Sect. 2—on the performance of the classifier. To do so, the results are distinguished in terms of (i) the type of rainfall event (all events or typical events T) and (ii) the dimensionality of the feature vector. In the latter case, the focus is on two options, obtained by including within the model (i) all the pebble features, their locations, and flow data (named all features) or (ii) only the pebble locations and the data PCs (named PCs): PC1, PC2, $PC1_{flow}$, $PC2_{flow}$ (see Sect. 2). This set of analyses also serves as a support to the dimensionality reduction needed to develop the functional approach discussed in Sect. 4.2. All the results presented in this section were obtained using the R package fdagstat (Grujic and Menafoglio 2017).

All events    Based on a fivefold CV analysis repeated $B=7$ times, the maximum depth of the trees is set to $\max \_depth = 7$ when all the features are used and $\max \_depth = 6$ when PCs are used instead.

The error metrics for XGBoost are presented in Table 2. Tables 3 and 4 report the average confusion matrices of the XGBoost model based on all the features (Table 3) or only the PCs (Table 4). Here, the threshold $\alpha$ for the classification was built by optimization of the $F_1$ metric (see Sect. 3.3)—the average being $\alpha ^* = 0.643$ for the case of all the features and $\alpha ^* =0.544$ for the PCs only. Notably, the PCs case appears to be associated with a higher accuracy and precision. In general, the all-features case presents a lower number of FPs but a higher number of FNs, thus yielding a general slight overestimation of the sediment transport w.r.t. the PCs case. These analyses suggest that representing the features through the PCs only does not result in a significant loss of information for the purpose of classification. Note that the average CV accuracy of a model when optimizing a set of eight hyperparameters is 0.87, which is substantially equivalent to the values reported in Table 2.

Table 2 Results of XGBoost when all the rainfall events are considered

Table 3 All features: average confusion matrix across CV repetitions

Table 4 PCs: average confusion matrix across CV repetitions

Typical events    The aim is now to study the impact of the flow data ($PC1_{flow}$ and $PC2_{flow}$) on XGBoost models when calibration is based on typical events only. Note that typical events appear to be similar in terms of flow (see Sect. 2). Therefore, one may argue that it is reasonable to suppose that, in this setting, exclusion of $PC1_{flow}$ and $PC2_{flow}$ should not significantly affect the prediction power of the models. Two models are compared, one obtained by training XGBoost either on PCs data (PC1, PC2, $PC1_{flow}$, and $PC2_{flow}$) and the other trained on PC1 only, with both models considering the location and the subdomain binary features (i.e., $d_k(s)$).

Similarly as in the previous paragraph, the optimal depth of both models was selected using $B=7$ repetitions of K-fold CV with $K=5$. The results of the procedure are $\max \_depth = 6$ for the model trained on PCs and $\max \_depth = 5$ in the second case. The $F_1$ thresholds estimated for the two models are, in both cases, $\alpha ^*=0.663$, suggesting that the balance between FP and FN is preserved. The error metrics of both models are reported in Table 5. Notably, the model based on PCs attains better results, although the difference in performance is limited compared to the significant reduction in the input dimensionality. The main source of the improvement in accuracy for the first model is the number of FNs. According to Tables 6 and 7, the average absolute difference between FNs ($\varDelta FN = 277.1-188 = 89.1$) in the two models is more than 3.5 times larger than the absolute difference in terms of FPs ($\varDelta FP = 96.1 - 70.7 = 25.4$). Reducing the dimensionality of the inputs thus results in overestimation of the incidence of the NM class (i.e., the model tends to underestimate the amount of mobilized sediment). This tendency is confirmed by the results of the functional approach, which are discussed in the next section.

Table 5 Results of XGBoost when typical rainfall events are considered

Table 6 PCs: average confusion matrix across CV repetitions

Table 7 PC1: average confusion matrix across CV repetitions

4.2 Results for the Functional Case

In this subsection, the results of the analyses based on the functional perspective described in Sect. 3.2 are presented. Recall that the functional approach is based on the consideration of just the feature PC1 and the observations related to typical (T) events. Moreover, the main hyperparameters for the method are (see also Sect. 3.2) the minimum/maximum number of points to generate a curve, set to $n_{\min } = 12$; $n_{\max } = 30$; the support of the curves, set to $[PC1_{\min }; PC1_{\max }] =[-50, 50]$; the tolerance, set to $\epsilon = 0.01$; and the kernel bandwidth, set to $h = 20$. Moreover, in the following, a Bessel model for the calibration of the variogram is considered. All the results presented in this section were obtained using the R package “fdagstat” (Grujic and Menafoglio 2017).

A fivefold CV analysis run as described in Sect. 3.3 indicates that the radius of the neighborhoods should be set to $r = 5$. This parameter setting allowed us to estimate the curves $\hat{p}(PC1; s_i)$ for the sample location $s_i$, $i=1,...,n$. A subset of this data set of functional profiles is reported in Fig. 7. One may observe notable variability in the shape of the curves, suggesting a highly nonlinear dependence between the probability of movement and the pebble characteristics, which varies over space in a nontrivial fashion. Figure 7b displays the means $\overline{p}(PC1; D_k)$ of the probability curves within the geomorphological subdomains $D_k$, $k=1,...,7$. More precisely, these curves were computed by back-transforming the sample mean of the logit transformations of the curves $\hat{p}(PC1; s_i)$, that is

$$\begin{aligned} \overline{p}(PC1; D_k) = \mathrm{logit}^{-1}\left( \frac{1}{n} \sum _{s_i\in D_k} \mathrm{logit}\,\tilde{p}(PC1; s_i) \right) , \end{aligned}$$

the transformation $\mathrm{logit}$ and $\tilde{p}(PC1,s_i)$ being defined as in Sect. 3.2. Such curves are thus representative of the mean values $m_s$ assumed by the object $\chi _s = logit(\tilde{p}(\cdot ;s))$ within the subdomains. One may note relatively high variability across groups, which suggests consideration of the binary variables $d_{k}(s)$ ($d_{k}(s)=1$ if $s\in D_k$, $d_{k}(s)=0$ otherwise) in the model for the drift term. However, CV analyses suggest that slightly better performance is obtained when using a stationary approach instead, which is discussed later. For the sake of completeness, Fig. 8 reports the variograms of the residuals (estimated as described in Sect. 3.2) when these refer to a stationary drift term (i.e., $m_s$ is spatially constant; Fig. 8a) or to a drift dependent on the geomorphological subdomains through the variables $d_k(s)$’s (Fig. 8b). Both variograms are compatible with the residuals’ stationarity; selection of the stationary model is thus based on the CV results.

Fig. 7

Estimated probability curves: data and mean within groups. In panel (b), the scale on the y-axis is set to [0.6, 1] to better appreciate the difference in $\overline{p}(PC1; D_k)$ between groups

Table 8 Results for the functional approach when setting the optimal threshold according to the $F_1$-score

Fig. 8

Estimated variograms of the residuals for two different forms of the drift term: a spatially constant and b spatially nonconstant

Table 9 reports the confusion matrix of the method (averaged over the CV repetitions), which suggests that the classifier built via the functional approach tends to be associated with a higher number of false positives (FPs: 250 of 1,594 pebbles), which is consistent with those associated with XGBoost based on PC1 for typical events, as discussed in Sect. 4.1. The next section provides further discussion and comparison between these approaches.

4.3 Comparison of the Two Perspectives

A comparative analysis between XGBoost and FK results is presented herein. For the purpose of coherency between the information used for training, the XGBoost model trained on typical events only (as presented in Sect. 4.1) is compared with the FK model calibrated on the same data (see Sect. 4.2). The CV folds that are used to estimate the error metrics are the same for both the XGBoost and FK models.

Table 9 Results of the functional approach: average confusion matrix across CV repetitions

Table 10 Results for the functional approach and XGBoost when setting the optimal threshold according to the $F_1$-score or Youden’s J

First, a comparison of the models is performed based on PC1 only, which is representative of the performance of the methods based on similar inputs. The first two lines of Table 10 report the classification performance, assessed by $B=7$ repetitions of fivefold CV, of the functional predictor. Here, the first line corresponds to a threshold $\alpha ^*$ set by optimization of the $F_1$ criterion ($\alpha ^*=0.613$), whereas the second line refers to the optimization of Youden’s J ($\alpha ^*=0.604$). The last two lines of Table 10 refer to the analogous quantities related to the XGBoost model trained on PC1 only, which are associated with a threshold $\alpha ^* = 0.663$ (approximately the same $\alpha ^*$ set for both Youden’s J and F1 criteria). The results in Table 10 suggest that all four settings are practically equivalent in terms of accuracy (approximately 76%) and precision (approximately 65%). The main differences are related to the AUC, which is slightly better in the XGBoost case (87%) than in FK (84%), indicating an overall better ordering of probabilities. Moreover, recall is higher in XGBoost than in FK (84% vs. 77%), indicating better performance for the former in terms of FPs, which is also observed in Tables 7, and 9. A comparison of the performance by subdomains is presented in Table 11. XGBoost has better performance overall, e.g., in the bars zone, although FK proves better in a number of subdomains, e.g., within the step/pool zone. Notably, the number of pebble locations in the bars zone is more than twice that in the step/pool zones, consistent with the observed differences in the absolute values of the FPs and FNs.

Table 11 XGBoost vs. FK: misclassified pebbles for each subdomain

Finally, the methods are compared in terms of local CV errors in Figs. 9 and 10. Both figures display visualizations of the results of seven-repetition CV. Figure 9 represents the CV results for each pebble separately; the colors are associated with the number of times a single pebble was correctly classified along the $B=7$ repetitions of the fivefold CV. Figure 9 displays the average accuracy within the subdomains $D_k$ identified according to the local morphology of the riverbed. Graphical inspection of Fig. 9 suggests that, although the two models appear similar in terms of the error metrics, slightly different patterns are observed in their errors. For instance, XGBoost is associated with noticeably fewer correct predictions for the left bottom corner, while, on average, its predictions are of high quality in the central and upper part of the domain. Similarly, observing Fig. 10, one may note that the main difference between the two models appears in the center left of the domain and in the bottom-left part.

Although the comparison of the models based on PC1 suggests overall consistency of the results obtained with the two approaches, when using all the PCs, improved results were obtained with XGBoost (see Sect. 4.1). This suggests that the input simplification needed to build the data set of probability profiles prior to FK may have induced a loss of predictive power with respect to a scalar approach based on state-of-the-art machine-learning methods. On the other hand, the functional approach clearly allows for direct interpretation of the relation between the tendency of pebbles to move and their characteristics, as further highlighted in Sect. 4.4. This is a clear advantage of XGBoost, whose interpretability still appears to be limited. Finally, additional analyses on the same data set—not discussed here for the sake of brevity—showed that FK outperforms other standard statistical methods, such as general liner models (GLM), thereby supporting the validity of the approach in the framework of model-based statistical classification.

4.4 A Geomorphological Interpretation of the Results

From a geomorphological perspective, the zones where the predictive models encounter difficulties in correctly classifying the probability of movement appear to be the banks and cascade, with approximately $30\%$ of observations misclassified by both models. A particular concentration of misclassified cases is found in the central section of the reach under investigation. This zone is characterized by a complex morphology, where the presence of a large boulder forces the stream into a rapid s-curve trajectory, unlike the surrounding environment. The upstream end of the reach is also characterized by a high concentration of misclassified cases. This area is close to the location of a large number of pebbles. Hence, this result could be attributed to the effect of the initial pebble deployment, which would likely behave differently with respect to sediment that has already undergone some settlement. The concentration of misclassified cases in the banks zone is also not surprising. Those zones are marginally affected by the flow rate during low- to moderate-flow rate events, and a slight increase/decrease in water depth could determine whether a pebble is affected by the flow. The definition of the boundaries of those zones is somewhat ambiguous due to, e.g., the presence of vegetation in summer and its absence in winter.

Fig. 9

CV error maps

Fig. 10

CV: Average accuracy by morphological sector

As a result of the functional kriging approach, the probability of pebble movement was obtained as a function of the pebble dimensions in the different morphological units (Fig. 10). This outcome illustrates a general similarity between banks, bars, and cascade zones, while there is a considerable difference in the predicted values for plane bed, run/rapid, and step and pool zones. For the former three subdomains, very small and very large pebbles tend to have a similar probability of movement, while average-sized ones are slightly less likely to be mobilized. This difference is also present in the case of the step and pool zone, although it is much more pronounced in the former cases. The effect of pebble size on mobility has often been considered by authors, arguing that the sediment mobility could be independent of the sediment dimensions in some morphological conditions. For instance, according to Liedermann et al. (2013), coarser particles are harder to mobilize, yet once mobilized, they may travel even farther than smaller ones. Ferguson et al. (2017) attributed the size selectiveness of the sediment mobility to the different types of channel morphology—a finding that is consistent with the results in the present work. For instance, the probability of pebble movement in a plane bed morphological unit appears to be entirely independent of sediment size, while in a run/rapid local morphology area, strong size dependency is observed, where smaller particles are characterized by a lower probability of movement. Church and Hassan (1992) noted that smaller particles are characterized by a higher likelihood of being trapped when the stream channel is composed of large grains, which could strongly influence the dependency of the sediment mobility on the grain size. The estimated mean probability of movement is greater than $50\%$ in all cases, which indicates that during moderate-flow events, the bed-load mobility is pronounced in the presented range of pebble dimensions.

5 Application to an Independent Data Set

To enrich the comparison between the two considered approaches, they are applied to an independent data set that was not included in the training process in the previous sections. Here, a Eulerian approach was adopted to observe the mobility of pebbles in a fixed spatial reference, as opposed to the Lagrangian approach used to track each single sediment particle along the river course.

Red pebble data    The observation zones represent 30 cm $\times$ 30 cm squares within which the riverbed was painted in red. The observation zones were captured before and after a flood event to identify the number of mobilized pebbles and their size. The size of the individual pebbles was estimated from the images using the automatic object detection software Basegrain (Detert et al. 2012), which allowed us to estimate the size of the a- and b-axes of each detected pebble. Figure 11 illustrates the steps of the tracking process. The available data set consists of seven sets of observations that were gathered during three events (events 11, 14, and 16, which occurred during the year 2017,¹) which can be considered typical in terms of the associated flow. In addition to assessing the capability of the proposed methods to address this type of data, this case is used to illustrate a potential approach to the application of the models to sets of sediment particles (instead of single particles).

Fig. 11

a Red pebbles painted before an event, b post-event image of the same area, c estimation of the dimensions of the remaining pebbles

Limitations of RP data    A technical limitation of this measurement campaign is the difficulty in finding a dry portion of the riverbed that can be painted, typically during low flow. Moreover, in the case of “red pebbles” (RPs), all the pebbles from the outlined zones were considered for the measurements, while in the “yellow pebbles” (YPs) case, only the particles large enough for insertion of an RFID tag were used. This inevitably results in selection bias for both cases, which renders the two analyses only partially comparable. In fact, some substantial differences are present between the grain size distributions of the two data sets. For instance, the RPs are, in general, much smaller than the YPs used to calibrate the models, the nominal diameters of the latter being, on average, 70 mm smaller than the diameters of the former (see Table 12).

Table 12 Summary of red pebble (RP) data

Another limitation is the fact that the estimation of RP measurements is based on 2D projections of the original 3D objects (see Fig. 11c). This hinders the computation of the three axes (a-,b-,c-axes) since one of the axes (presumably the c-axis) remains covered. In fact, the estimate of the two visible axes may itself be associated with non-negligible uncertainty. Moreover, the visible dimensions of RPs gathered before mobilizing events may not correspond to those after the events because pebbles tend to rotate or move—even without location change—due to the flow. Hence, these data cannot be used to find a one-to-one correspondence between particles before and after the events and to verify whether they moved or not, but rather they can be used to assess joint summaries about the set of particles (e.g., granulometric distributions).

Applicability of the models    Application of XGBoost and FK models on the RP data should take into account the specific features (and limitations) of this database. For instance, concerning FK, only $3\%$ of the red pebbles have a PC1 larger than $-50$ (when estimating the c-axis as 3/4 of the b-axis). Hence, the remaining $97\%$ of the data would be given the prediction $p^*(-50,s)$, which is associated with all the particles with a size leading to $PC1<-50$ (see Sect. 3.2). In fact, application of our models to RP data requires particular care, as one must pay close attention when testing models out of the range of the training data, no matter the approach being used. For the purpose of this study, a slight modification of the models described in Sect. 4 is considered to render the features of the YP training set as compatible as possible with those of the RP test set by using the pebble diameter.

A classification approach based on particle diameter    To cope with the lack of correspondence between pre-mobilizing and post-mobilizing event data, this work considers a variant of the classifiers built in Sect. 4 based on the nominal diameter, defined as $d_i = \sqrt{a_i*b_i}$. Note that the range of $d_i$ for YPs is [43.87, 160.16]; the range of diameters for RPs is found in Table 12. Partial overlap is attained between the diameters of YPs and RPs. In XGBoost, this variable is considered as the input, together with the location of the pebbles and the flow data—the model is trained on typical events only. In the functional approach, the probability profile $p(d_i;s)$ is estimated at the sampled locations and then projected via functional kriging at unknown sites along the river domain.

Fig. 12

Locations of red pebble (RP) data

The application of the model to the RP data is performed as follows. Given a square region $R_j$ and a mobilizing event e, $j\in \{1,2,4,5,6,8,9\}$, $e\in \{11,14,16\}$, call $S^{-}_{je}=\{S_{1},...,S_{n_{je}^-}\}$ the set of $n_{je}^-$ red pebbles in $R_j$ before the event e, and $S_{je}^{+}=\{S_{1},...,S_{n_{je}^+}\}$ the set of $n_{je}^+$ red pebbles that are still in $R_j$ after the event e. Table 12 reports the values of $n_{je}^-$ for the regions and events available in the data set. Considering a single pebble $S_i\in S^{-}_{je}$, one may estimate its probability $p^*_{i}$ of movement based on the set of features associated with the considered pebble and one of the calibrated models (XGBoost or FK). To describe the joint probability of movement of the set of pebbles in $S^{-}_{je}$, one can then consider their joint law, which under independence reads $\mathbf {p}_{je}^* = \prod _{i=1}^{n_{je}^-}p^*_i$. This approach enables simulation of a set of realizations from such a distribution to be compared with the actual observations in $S_{je}^{+}$. Comparison of the empirical distribution of the particle diameters—a.k.a. particle-size distributions (PSDs)—with the actual PSD after the events enables evaluation of the capability of the models to adapt to this type of data.

Results and comparison    As an example, Fig. 13 displays a set of $M=100$ empirical cumulative distribution functions (ECDFs) of the diameters of the particles found in location $R_6$ after event 16 (gray lines). These are compared with the ECDF of the PSD estimated from the pebbles in $P_{6,16}^{+}$, depicted as black lines.

Fig. 13

Sampled ECDFs of distributions of pebbles that did not move, and actual PSD, at location $R_6$

Graphical inspection of Fig. 13 suggests that both methodologies fail to correctly represent the displacement of pebbles with relatively small diameters (between 8 and 30 mm), possibly due to the partial incompatibility of the data in the YP and RP data sets. In particular, both models appear to be associated with underestimation of the mobility of small particles and overestimation of that of large particles (see also Table 13). Nevertheless, the XGBoost approach seems to be associated with a slightly higher variability of the estimated PSDs, particularly for relatively large diameters. The cloud of simulated PSDs is thus closer to the actual observation than that for FK. The results in Table 13 suggest that, overall, both approaches result in considerable overestimation of the proportion of stationary pebbles, particularly for R4 and R5.

An overall quantitative comparison between the simulated and actual PSDs can be obtained by computing the Wasserstein distance (see, e.g., Villani 2008) between these distributions, which is obtained as

$$\begin{aligned} d({\mathscr {P}}_{m},{\mathscr {P}}_{obs}) =\left( \int _0^1 ({\mathscr {P}}_{m}^{-1}(t) - {\mathscr {P}}_{obs}^{-1}(t))^2 dt \right) ^{1/2}, \end{aligned}$$

${\mathscr {P}}_{m}$,${\mathscr {P}}_{obs}$ being the PSD of the mth simulation (cumulative distribution functions), $m=1,...,100$, and the observed post-event PSD, respectively, and ${\mathscr {P}}_{m}^{-1}, {\mathscr {P}}_{obs}^{-1}$ the respective quantile functions. Table 13 reports the average Wasserstein distance, that is, $1/m\sum _{m=1}^M d({\mathscr {P}}_{m},{\mathscr {P}}_{obs})$, for the observed regions $R_j$. One may note a small discrepancy between the approaches—XGBoost performs only slightly better than FK.

In addition to the efforts made to render the YP and RP data sets compatible, these analyses suggest that the YP data are only partially informative on the phenomenon described by the RP data. This reflects the poorer performance of the models calibrated on the former data set when applied to the latter one. Moreover, the limitations highlighted within the section may point to directions of improvement for future investigations, if these are intended to support the construction of models better representative of the joint behavior of sediment particles within the region’s $R_j$’s.

Table 13 Comparison between XGBoost and FK on the red pebble data

6 A Quantitative Comparison between Data-Driven and Physics-Based Approaches

Bed-load transport in rivers is frequently predicted using empirical formulae developed from experimental data (obtained from laboratory installations or field campaigns). Depending on which formula is employed for the prediction, a preliminary assessment of threshold conditions may be necessary. In this context, the determination of incipient particle motion may rely on the traditional approach attributed to Shields (1936), which refers to a critical value of dimensionless shear stress at the riverbed.

The data presented in this manuscript are related to the mobilization of individual pebbles rather than sediment transport flux. The motion/stillness of a particle, related to the threshold conditions for sediment motion, is thus particularly relevant. To compare the results obtained by the data-driven approach with those obtained in a more traditional way, simple numerical simulations of a reach of the Caldone River were performed, with the objective of determining bed shear stress values corresponding to the flow rates measured during the events. The simulations were run with a highly simplified channel geometry because only a few sections were available for the 1-km reach. Within the latter, our test reach was represented by only two sections and resulted as a single-slope one; in other words, it was impossible to incorporate the step/pool geometry that characterizes the reach in terms of its geometric description, with a consequent need to account for it with a suitable value for the Manning coefficient. Furthermore, the simulations were run with a steady flow to determine the critical sediment size (minimum size of a pebble that remains still under a certain flow) at peak discharge. Finally, even if the attention is focused on the test reach, the extended 1-km reach was used in the hydraulic simulations to reduce the effect of boundary conditions.

The data-driven and physics-based approaches clearly work from different perspectives, each characterized by its own simplifying assumptions. Indeed, the hydrodynamic computation for incipient sediment motion considers the sediment to be distributed over a flat, rough surface, and is unable to distinguish particles from each other (except for size variability). Here, the parameters are the Manning roughness coefficient of the river and a chosen threshold value of the Shields number (usually between 0.03 and 0.06 in the fully turbulent regime). The data-driven approach does not account for the physics of the process and again considers each pebble individually; estimation of the classification rule is based on the training data set, which is also used to calibrate the model hyperparameters.

In the following, a twofold comparison is performed between the results of the data-driven and physics-based approaches. On the one hand, with reference to the data for the yellow pebbles (Sect. 2), the accuracy of the models is compared in terms of the prediction of the number of particles moved during an event. On the other hand, with reference to the data for the red pebbles (Sect. 5), the critical sediment size is compared. In this study, calibration of the two parameters characterizing the physics-based approach is not performed (because of the lack of data on the depth values in the test reach needed to calibrate the roughness coefficient), but a sensitivity analysis is performed. A set of 21 pairs of parameter values was considered, obtained by combining seven values for the Manning coefficient (ranging from 0.04 to 0.10—every 0.01— $\mathrm{s}/\mathrm{m}^{1/3}$, following the classic description provided by Chow (1959)) and three values for the threshold Shields number (0.03, 0.045, and 0.06). For each pair of parameters, the model was used to compute the critical diameter in a single event and, in turn, the number of yellow particles predicted to move, eventually obtaining 21 results for these outputs (one for each pair of parameters). Following the stress decomposition method (e.g., Chanson 1999), a skin roughness coefficient $n_{skin}$ was used to estimate the portion of the total shear stress contributing to the bed-load ($\tau _{skin}$). The set of equations used for the computations is as follows

$$\begin{aligned} n_{skin} = \frac{d_{90}^{1/6}}{26}; \quad \tau _{skin} = \gamma R_H \frac{n_{skin}^2 V^2}{R_H^{4/3}}; \quad d_{crit} = \frac{\tau _{skin}}{\gamma (s-1) \tau ^*_c} \end{aligned}$$

where $d_{90}$ is a sediment size corresponding to 90% in the granulometric distribution (a value of 150 mm was used here according to field measurements); $\gamma$ is the specific weight of water; $R_H$ and V are the hydraulic radius and bulk velocity of the flow, respectively, returned by the numerical simulation with assigned discharge; $d_{crit}$ is the critical diameter; s is the ratio of the sediment to water density; and $\tau ^*_c$ is the critical value of the Shields number (the Shields number for any particle size d is $\tau ^* = \tau _{skin}/(\gamma (s-1) d)$).

Yellow pebbles A comparison of the accuracy of the methods for the yellow pebbles is given in Fig. 14. The accuracy of the physics-based approach is quite sensitive to the parameter values. Furthermore, for two groups of events (9 to 12 and 20 onwards) it may jump from 0 to 1, changing the value of a parameter (these are the events with a binary behavior, with all the pebbles moving or being still). Generally, the XGB method presents larger accuracy (always larger than 0.6) and a similar behavior throughout all the events.

Fig. 14

Accuracy of model prediction for the yellow pebble data. For the physical approach, the Manning coefficient ranges in 0.04 (a), 0.06, (b) 0.08 (c), and 0.10 $\mathrm{s}/\mathrm{m}^{1/3}$ (d), while the critical values of the Shields number appear in the legends

Red pebbles A comparison of model performance exploiting the data for the red pebbles is presented in Fig. 15. Recall that these data are available for a set of locations and events, as shown in Table 12, and refer to observed granulometric distributions within a square area before and after an event. For consistency with Fig. 13, the results are shown for location R6 after event 16. The XGB method returns a good estimate of the critical diameter (that is conceptually the sediment size at 0%) while underestimating the sediment sizes of the distribution. The physics-based approach returns variable estimates of the critical diameter, with those intercepting the starting values of the actual PSD for 0.10–0.045 and 0.09–0.06 as couples of Manning coefficient and critical Shields number, respectively (the plots include only some combinations to avoid confusion between too many lines). Furthermore, the values of the estimated critical diameter correspond to an abrupt rise in the actual PSD (which is an alternative proxy for the critical diameter) for couples 0.08–0.03, 0.07–0.045, and 0.06–0.06. The results for other locations, not shown in the paper, confirm that relatively high values of the Manning coefficient and critical Shields number may better represent the field determinations. The need for a high Manning coefficient is explained by the poor geometric description used in the hydraulic model, which requires the step/pool morphology to be mimicked by an increased roughness. Furthermore, using a larger value of the critical Shields number corresponds to hindering the transport of particles. A best value of the critical Shields number relates to a need to parameterize, in the physics-based approach, several triggering or damping factors for sediment transport beyond the shear stress (exposure/damping conditions, collective entrainment, peripheral location on the river with low velocity, etc.).

Fig. 15

Sampled ECDFs of distributions pebbles that did not move, actual PSD, and estimated critical diameter by a physics-based approach at location R6. a XGB; b FK. The legends indicate the values of the Manning coefficient in $\mathrm{s}/\mathrm{m}^{1/3}$ and of the critical Shields number

7 Discussion and Conclusions

This work compared two methodological approaches to the prediction of sediment transport in a pre-Alpine region. To this end, state-of-the-art machine-learning and geostatistical methods, namely, XGBoost (Chen and Guestrin 2016) and functional kriging (FK,Menafoglio and Secchi 2017), were considered. Results on real data suggest that both approaches have good performance, with XGBoost having slightly better predictive power than FK. Nonetheless, FK yields more interpretable results since it allows for an explicit prediction of the probability of movement of a single pebble at a site s as a function of its dimensions (characterized by PC1). These results are in agreement with the general advantages and disadvantages evidenced in the comparison between machine-learning and model-based statistical methods, where the former often outperform the latter in terms of prediction power, while the latter are typically associated with higher interpretability.

However, the methods developed in this work are subject to a number of limitations that should be considered when applying the calibrated models to independent data. In addition to the limitations on the use of the models for independent data only partially compatible with our training set (e.g., for RP data, see Sect. 5), one should note that not all the regions of the spatial domain are densely covered by the observations, which results in spatially varying uncertainty in the predictions. Analyses have shown that the pebble location is indeed informative of its probability to move. For instance, if one trains the XGBoost model without the feature $s_i$, a relevant decrease in accuracy and AUC would be observed (on all the events, with all the other features: AUC = 0.915, accuracy = 0.815, $F_1$ = 0.758, compared with the results in Table 2). As such, higher degrees of uncertainty are associated with the areas of the domains where data are sparse. Note that FK is associated with a measure of prediction uncertainty (named kriging variance; see, e.g., Menafoglio et al. 2013), which also accounts for the data sparsity. This is not the case for XGBoost, where measures of uncertainty are only indirectly available (e.g., through CV analyses).

To enrich the comparison between the two approaches, a block CV was run using the R package BlockCV (Valavi et al. 2019). As expected, the accuracy of XGB was estimated to be lower than that in the nonspatial case, with an accuracy of 0.68 (average across CV repetitions). Similarly, FK showed worse performance, with lower accuracy than XGB (0.58). The discrepancy between this result and that reported in the manuscript is likely due to the strong local variability of the probability of movement, which has a detrimental effect on the prediction accuracy in the extrapolation. This additional validation further confirms the complex local nature of the probability of movement, which, in turn, is associated with the morphological structure of the Caldone River domain.

Another aspect worth mentioning concerns the river flow data. In XGBoost models, flow data are used as features and appear to be associated with improved accuracy (see Table 2). However, flow data are available only after the end of a rainfall event. To use the model in a real-world application to forecast sediment transport, one should thus consider predicted flow data or perform a scenario-based analysis. In both cases, the additional degree of uncertainty would affect the final sediment transport forecast. In this sense, although the fact that FK does not account for flow data may appear to be a limitation of the approach—resulting in decreased accuracy—this may not really be the case in the actual application of the model.

Nevertheless, an intrinsic limitation of FK is the need to estimate the functional profile $p(\mathbf {x},s)$ from raw data, which in turn imposes a limitation on the dimensionality of the feature vector $\mathbf {x}$. This aspect led us to assume all the typical events to be similar from the flow perspective and to work in an average flow scenario. In this respect, larger databases may allow for a higher dimensionality of $\mathbf {x}$ than that considered in this work to partially account for the dynamics of the event being considered. Indeed, even if the average characterizations of mobilizing events are similar, the dynamics of events could vary drastically, with a possible impact on the actual probability of movement of sediment particles.

The outcome of the comparisons between the data-driven approach explored in this manuscript and a traditional physics-based approach supports the claim that machine-learning approaches provide better estimates, as suggested by several previous works (e.g., Bhattacharya et al. 2007; Azamathulla et al. 2010; Sahraei et al. 2018). Those works were, however, related to the estimation of sediment transport fluxes, while the present study addresses the mobility of individual clasts. Furthermore, a key issue emerges, in line with the statement Kitsikoudis et al. (2014) that machine-learning approaches perform well if data are abundant. We revisit this statement considering the representativeness of the data. In fact, a crucial consideration is that the data-driven approach outperforms the physics-based approach in relation to the investigated pebble samples. Therefore, the outcome of an estimate based on, for example, XGB will provide a good representation of the river system only if the pebble sample selected for the analysis accurately represents the whole sediment population. In the present study, it was unfortunately impossible to assess the representativeness of the considered sediment samples with reference to the entire riverbed. It can be reasonably argued that two characteristics may affect this issue, namely, the sediment size and the geomorphological units. For the yellow pebbles, the sample spans a variety of units, but the sediment sizes explored were limited by the need to insert passive tags into the pebbles (see Fig. 3). Additionally, the yellow pebbles may have represented the largest sizes in the granulometric distributions, as shown by Ivanov et al. (2020a). By contrast, the samples for the red pebbles included a wider range of particle sizes, but each sample was limited to a single morphological unit (Table 12). Finally, the physics-based approach cannot consider local features (particle hiding/exposure, morphological unit, etc.) while returning a judgment of motion/stillness for a single pebble, but, as we acknowledge, may be more representative of the behavior of the entire sediment bed. However, it is difficult to assess this issue in a robust quantitative manner, and this consideration deserves further investigation in follow-up studies.

Notably, the majority of mobilizing events are characterized by moderate flow, that is, events that are sufficiently energetic to provoke sediment mobility, but not exceptional. While the data set includes observations of pebble mobility during high-flood events, these data are limited to four events, effectively participating in the XGBoost analysis through the PCA on river flow data, but excluded from the FK analysis due to its abovementioned limitations. The estimation of the probability of pebble movement presented here suggests that, during moderate-flow events, the mobilized YP sample is, on average, between $50\%$ and $100\%$, depending on the morphological unit, while looking at RPs—characterized by a considerably smaller grain size distribution—the proportion of mobile pebbles is over $90\%$ with the exception of bars, where this value is around $55\%$. While those two parameters are obtained through different methodologies and based on different (only partially comparable) data sets, they effectively correspond to the same conceptual quantity—the ratio of moving particles, as discussed by Ivanov et al. (2020a). The combination of those two parameters indicates that (i) there appears to be a general dependency of pebble mobility on grain size, and (ii) moderate-flow or “typical” events contribute significantly to the dynamics of bed-load transport. A further step in the investigation would be to try to quantify this effect in terms of the distances traveled by the pebbles, as well as their velocity (or virtual velocity). Analyses in this direction are currently ongoing, and will be the scope of future work.