Estimating distribution of length of stay in a multi-state model conditional on the pathway, with an application to patients hospitalised with Covid-19

Abstract

Multi-state models are used to describe how individuals transition through different states over time. The distribution of the time spent in different states, referred to as ‘length of stay’, is often of interest. Methods for estimating expected length of stay in a given state are well established. The focus of this paper is on the distribution of the time spent in different states conditional on the complete pathway taken through the states, which we call ‘conditional length of stay’. This work is motivated by questions about length of stay in hospital wards and intensive care units among patients hospitalised due to Covid-19. Conditional length of stay estimates are useful as a way of summarising individuals’ transitions through the multi-state model, and also as inputs to mathematical models used in planning hospital capacity requirements. We describe non-parametric methods for estimating conditional length of stay distributions in a multi-state model in the presence of censoring, including conditional expected length of stay (CELOS). Methods are described for an illness-death model and then for the more complex motivating example. The methods are assessed using a simulation study and shown to give unbiased estimates of CELOS, whereas naive estimates of CELOS based on empirical averages are biased in the presence of censoring. The methods are applied to estimate conditional length of stay distributions for individuals hospitalised due to Covid-19 in the UK, using data on 42,980 individuals hospitalised from March to July 2020 from the COVID19 Clinical Information Network.

1 Introduction

Multi-state models are used to describe how individuals transition through different states over time. The simplest multi-state model is the illness-death model, depicted in Fig. A. Quantities of interest in multi-state modelling analyses include rates of transition from one state to another, the probability of being in a given state at a given time after entering another state, and the expected length of time spent in a given state. Analysis methods include non-parametric methods, including the Aalen-Johansen estimator, and methods that enable estimation of the impact of predictors on these quantities, including extensions to the Cox model, and fully-parametric methods. Andersen and Keiding (2002) and Putter et al. (2007) provide overviews of multi-state modelling methods, and details of the underlying theory are provided in the books by Andersen et al. (1993) and Aalen et al. (2008).

In this paper we consider descriptive analysis of multi-state systems, with a focus on estimating the distribution of the time spent in different states in a multi-state model, which is often referred to as ‘length of stay’, or ‘state occupation time’. Beyersmann and Putter (2014) described non-parametric methods for estimating expected length of stay in multi-state models. Our interest is in the distribution of the time spent in different states conditional on the complete pathway taken through the states, which we refer to as conditional length of stay. In the illness-death model depicted in Fig. 1A there are two possible complete pathways through the states: the pathway from state 1 to state 3, and the pathway from state 1 to state 2 to state 3. In the illness-death model therefore, conditional length of stay provides information about: (i) time spent in the healthy state among individuals who do not transition through the illness state (complete pathway: state 1 to state 3), (ii) time spent in the healthy state among individuals who do transition through the illness state (complete pathway: state 1 to state 2 to state 3), (iii) time spent in the illness state.

The concept of conditional length of stay involves conditioning on future events, which is rarely appropriate in analyses of times-to-event (Andersen and Keiding 2012). If our aim was to investigate causal effects of exposures on rates of transition between states, or other causal estimands, or if the aim was to develop a prognostic model, then conditioning on the patient’s future pathway would not be appropriate for addressing the research question. Our consideration of conditional length of stay was motivated by questions about length of stay in hospital wards and intensive care units (ICU) among patients hospitalised due to Covid-19. Conditional length of stay estimates were of interest for two goals: (1) providing inputs to mathematical models which are used to inform resource requirements that are determined by patients’ length of stay in different states; (2) providing a more comprehensive description of the multi-state system taking into account patient pathways, alongside unconditional length of stay estimates. The motivating example is described in more detail in Sect. 2.

Conditional length of stay has not, to our knowledge, been considered previously in the multi-state modelling literature. In this paper we describe non-parametric methods for estimating conditional length of stay distributions in a multi-state model, including the conditional expected length of stay in a given state (CELOS). These methods take into account that censoring can occur in every state. We also consider conditional length of stay distributions restricted to a particular time horizon, which are relevant when the full distribution of transition times is not observed in the data at hand due to limited follow-up. To describe the statistical methods we begin by focusing on an illness-death model (Sect. 3). The methods are evaluated using a simulation study in Sect. 4. In Sect. 5 we extend the methods to the more complex multi-state model setting of the motivating example and apply them to estimate conditional length of stay in hospital and ICU for patients hospitalised with Covid-19 in the UK, using data from the ISARIC WHO CCP-UK COVID19 Clinical Information Network (CO-CIN) (Docherty et al. 2020). R code for implementing the methods is provided at https://github.com/ruthkeogh/lengthofstay.

2 Motivating example: patients hospitalised with Covid-19

The outbreak of Covid-19, caused by the novel severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), was characterized as a pandemic by the World Health Organization on 11 March 2020 (World Health Organisation 2020). According to UK government statistics (UK Government 2021), as of 3 April 2021 in the UK, 4,354,344 individuals had received a positive test for Covid-19, and a total of 458,868 hospitalisations and 126,955 deaths had been recorded (within 28 days of a positive Covid-19 test). Many patients require intensive care and, in the period up to 25 March 2021, 35,708 admissions to an intensive care unit (ICU) were recorded among patients in England, Wales and Northern Ireland with confirmed Covid-19 (Intensive 2021).

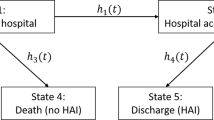
Figure  illustrates a multi-state model for patients hospitalised with Covid-19 in the UK. The states are: (1) hospital ward; (2) intensive care unit (ICU); (3) hospital ward post-ICU; (4) Death in hospital; (5) Discharged from hospital. State 4 is an absorbing state. We also consider state 5 as an absorbing state—although patients can be discharged and readmitted, we did not consider this aspect. There are six possible complete pathways starting from state 1. Some individuals can start in state 2 (ICU), from which there are four possible complete pathways.

There were two main motivators for obtaining estimates of conditional length of stay in this study. The original motivator was a request to provide conditional length of stay estimates as inputs to mathematical models used in planning hospital capacity requirements. Molenberghs et al. (2020) discussed the importance of providing estimates of how long individuals require care in hospital and in ICU for planning hospital capacity requirements during the Covid-19 pandemic. Mathematical models are widely used to estimate hospital capacity requirements under different scenarios, for example varying the number of infected individuals and their age distribution. This is typically done using a simulation approach. One approach would be simulate how patients progress through the states of the multi-state model (Fig. 2), using estimates of transition intensities. Expected lengths of stay in different states could then be estimated. However, this is computer intensive. Another approach, which is less computationally intensive, is to assign simulated patients at the time of hospital admission to one of the possible ‘complete pathways’ in the multi-state model with a given probability. This was the approach taken by Leclerc et al. (2021) from the London School of Hygiene & Tropical Medicine’s Centre for Mathematical Modelling of Infectious Diseases group, for whom we provided estimates. They aimed to investigate how estimates of overall length of stay are influenced by the ‘hospital bed pathways’ taken by a patient, which may differ by region depending on the local patient population and local resource availability. It was concluded that national estimates of expected overall length of stay may not be appropriate for local forecasts of bed occupancy for COVID-19 (Leclerc et al. 2021).

A second motivator for this work was to show how we can provide descriptive information to the medical and scientific community and the general public about how long people hospitalised due to Covid-19 will be expected to spend receiving different levels of treatment in the hospital. Expected length of stay in hospital or ICU provides an overall summary, but conditional length of stay provides more detailed information that has also been of interest. Stays in the hospital ward (before a potential transfer to ICU) can end with death, discharge or a transfer to ICU. Conditional length of stay provides separate information on how long a patient requires in the hospital to recover and get discharged, and how long it takes for people in the hospital ward to become life-threatening ill and require intensive care. It also provides separate information on how long it takes for an individual admitted to ICU to recover, and how long a patient spends in ICU prior to death.

If all individuals in a given data set available for estimating length of stay had completed their stay, that is if their complete pathway was known, then expected lengths of stay and conditional expected lengths of stay in different states could be estimated empirically using observed averages. However, when the follow-up time of individuals is subject to censoring, empirical estimates based on the subset of individuals whose complete pathway is known will be biased. A number of authors have presented estimates of length of stay and conditional lengths of stay in different hospitalised states for Covid-19 patients (Vekaria et al. 2020; Rieg et al. 2020; Rees et al. 2020; Liu et al. 2018; Hazard et al. 2020). However, several have used empirical estimates (i.e. not accounting for censoring), and in other papers the approach taken was unclear. In this paper we show how traditional non-parametric multi-state modelling methods can be used to enable estimation of conditional lengths of stay. We discuss similarities and differences between our approach and that of other authors in Sect. 6.

3 Methods: illness-death model

3.1 Notation

We begin by considering the illness-death model depicted in Fig. 1. The multi-state model is depicted in two different ways in Fig. 1A and B. Figure 1A shows three states: (1) healthy state, (2) illness, (3) death. In Fig. 1B the absorbing state of death is divided into two components: $3^{(1)}$—death directly from the healthy state, $3^{(2)}$—death from the illness state. These are two representations of the same model. In Fig. 1B there is only one arrow going into any given state, in contrast with Fig. 1A where there are two arrows going into state 3. Below it will be shown how the representation in Fig. 1B is helpful for estimating conditional length of stay, and subsequent notation will refer to the model representation in Fig. 1B.

Using standard notation for multi-state models we let X(t) denote the state occupied at time t after entering state 1. We let $P_{1k}(s,t)=\Pr (X(t)=k|X(s)=1)$ denote the probability of being in state k ($k=1,2,3^{(1)},3^{(2)}$) at time t conditional on having been in state 1 at time s. The intensities of transitions from state 1 to state k ($k=2,3^{(1)}$) at time t are denoted $\lambda _{1k}(t)$. For transitions out of state 2 we assume a clock-reset (i.e. semi-Markov) approach and let $X^{(2)}(t)$ denote the state occupied at time t after entering state 2. We define the transition probability $P_{2k}(s,t)=\Pr (X^{(2)}(t)=k|X^{(2)}(s)=2)$ as the probability of being in state ($k=2,3^{(2)}$) at time t after entering state 2, having been in state 2 at time s after entering state 2. The transition intensity from state 2 to state $3^{(2)}$ at time t after entering state 2 is denoted $\lambda ^{(2)}_{23^{(2)}}(t)$. In the motivating example, a clock-reset approach for the ICU and hospital-post-ICU states was considered most reasonable.

There are two possible complete pathways through the multi-state system: $1\rightarrow 3^{(1)}$, $1\rightarrow 2 \rightarrow 3^{(2)}$. We may also allow people to start in state 2, and the only possible pathway for those people is $2 \rightarrow 3^{(2)}$. Let $P_{k|p}(t)$ denote the probability that the time spent in state k is $\ge t$, conditional on the complete pathway being p. We are interested in the distribution of time spent in state 1 conditional on the complete pathway being $1\rightarrow 3^{(1)}$ or $1\rightarrow 2 \rightarrow 3^{(2)}$, defined by the probabilities $P_{1|13^{(1)}}(t)$ and $P_{1|123^{(2)}}(t)$ respectively. We are also interested in the distribution of time spent in state 2 conditional on the complete pathway being equivalently $1\rightarrow 2 \rightarrow 3^{(2)}$, defined by the probabilities $P_{2|123^{(2)}}(t)$. For those people who start in state 2 we are interested in $P_{2|23^{(2)}}(t)$. For the purposes of describing the methods, we assume that $P_{2|123^{(2)}}(t)=P_{2|23^{(2)}}(t)$, meaning that the distribution of time spent in state 2 (conditional on entering state 2) does not depend on whether the person started in state 1 or state 2. This assumption could be relaxed by estimating $P_{2|123^{(2)}}(t)$ and $P_{2|23^{(2)}}(t)$ separately. Below we consider estimation of $P_{1|13^{(1)}}(t)$, $P_{1|123^{(2)}}(t)$, $P_{2|123^{(2)}}(t)$, and $P_{2|23^{(2)}}(t)$.

We assume that data are available on a cohort of individuals and we let ${\mathcal {T}}_1=\{t_1,\ldots ,t_{J_1}\}$ denote the set of ordered observed times of transition out of state 1 (to state 2 or to state $3^{(1}$). Similarly, ${\mathcal {T}}_2=\{t_1^{(2)},\ldots ,t_{J_2}^{(2)}\}$ denotes the set of ordered observed times of transition from state 2 to state $3^{(2)}$.

3.2 Conditional distribution of time spent in state 1

By using the illness-death model in the format as depicted in Fig. 1B we can express the probabilities $P_{1|p}(t)$ in terms of the multi-state transition probabilities $P_{1k}(s,t)$. First, $P_{1|13^{(1)}}(t)$ can be written

$$\begin{aligned} \begin{aligned} P_{1|13^{(1)}}(t)=&\Pr (X(t)=1|X(\infty )=3^{(1)})\\ =&\frac{\Pr (X(\infty )=3^{(1)}|X(t)=1)\Pr (X(t)=1)}{\Pr (X(\infty )=3^{(1)})}\\ =&\frac{P_{13^{(1)}}(t,\infty )P_{11}(0,t)}{P_{13^{(1)}}(0,\infty )} \end{aligned} \end{aligned}$$

(1)

Similarly, we can write

$$\begin{aligned} \begin{aligned} P_{1|123^{(2)}}(t)=&\Pr (X(t)=1|X(\infty )=3^{(2)})\\ =&\frac{\Pr (X(\infty )=3^{(2)}|X(t)=1)\Pr (X(t)=1)}{\Pr (X(\infty )=3^{(2)})}\\ =&\frac{P_{13^{(2)}}(t,\infty )P_{11}(0,t)}{P_{13^{(2)}}(0,\infty )} \end{aligned} \end{aligned}$$

(2)

Using established results for multi-state models (Aalen et al. 2008, Ch.3) we can write the transition probabilities $P_{11}(s,t)$, $P_{13^{(1)}}(s,t)$ and $P_{13^{(2)}}(s,t)$ as functions of the transition intensities as follows:

$$\begin{aligned} P_{11}(s,t)= & {} \Pr (X(t)=1|X(s)=1)\nonumber \\= & {} e^{-\int _{s}^{t}(\lambda _{12}(x)+\lambda _{13^{(1)}}(x))dx} \end{aligned}$$

(3)

$$\begin{aligned} P_{13^{(1)}}(s,t)= & {} \Pr (X(t)=3^{(1)}|X(s)=1)\nonumber \\= & {} \int _{s}^{t}P_{11}(s,u^{-})P_{13^{(1)}}(u^{-},u)du \nonumber \\= & {} \int _{s}^{t}e^{-\int _{s}^{u^{-}}(\lambda _{12}(x)+\lambda _{13^{(1)}}(x))dx}\lambda _{13^{(1)}}(u)du \end{aligned}$$

(4)

$$\begin{aligned} P_{13^{(2)}}(s,t)= & {} \Pr (X(t)=3^{(2)}|X(s)=1)\nonumber \\= & {} \int _{s}^{t}\int _{0}^{t-u}P_{11}(s,u^-)P_{12}(u^-,u)P^{(2)}_{22}(0,v^-)P^{(2)}_{23^{(2)}}(v^-,v)dv du \nonumber \\= & {} \int _{s}^{t}\int _{0}^{t-u}\!e^{-\int _{s}^{u^{-}}(\lambda _{12}(x)+\lambda _{13^{(1)}}(x))dx}\lambda _{12}(u) e^{-\int _{0}^{v^{-}}\lambda ^{(2)}_{23^{(2)}}(x)dx}\lambda ^{(2)}_{23^{(2)}}(v)dv du\nonumber \\ \end{aligned}$$

(5)

The transition intensities $\lambda _{1k}(t)$ ($k=2,3^{(1)},3^{(2)}$) can be estimated non-parametrically using $\hat{\lambda }_{1k}(t)=d_{1k}(t)/n_{1}(t)$, where $d_{1k}(t)$ denotes the number of transitions from state 1 to state k at time t, and $n_{1}(t)$ denotes the number at risk of transitioning to state 1 from state k at time t, i.e. the number of individuals observed to be in state 1 just before time t. Note that $\hat{\lambda }_{13^{(1)}}(t_j)=0$ for times $t_j\in {\mathcal {T}}_1$ that are times of transition from state 1 to state 2 but not times of transition from state 1 to state $3^{(1)}$, and similarly ${\hat{\lambda }}_{12}(t_j)=0$ for times $t_j\in {\mathcal {T}}_1$ that are times of transition from state 1 to state $3^{(1)}$ but not times of transition from state 1 to state 2.

Suppose first that the full distribution of transition times out of state 1 and state 2 is observed in the data. Note that this does not preclude the presence of censoring. In Sect. 3.4 we discuss estimation of $P_{k|p}(t)$ when the full distribution of transition times is not observed. The probabilities in (3), (4), and (5) can be estimated using

$$\begin{aligned} {\widehat{P}}_{11}(s,t)= & {} \prod _{s<t_j\le t} \left( 1-{\hat{\lambda }}_{12}(t_j)-{\hat{\lambda }}_{13^{(1)}}(t_j)\right) \end{aligned}$$

(6)

$$\begin{aligned} {\widehat{P}}_{13^{(1)}}(s,t)= & {} \sum _{s<t_j\le t}{\hat{\lambda }}_{13^{(1)}}(t_j)\prod _{s<u< t_j} \left( 1-{\hat{\lambda }}_{12}(u)-{\hat{\lambda }}_{13^{(1)}}(u)\right) . \end{aligned}$$

(7)

$$\begin{aligned} {\widehat{P}}_{13^{(2)}}(s,t)= & {} \sum _{s<t_j\le t}\sum _{0<t_j^{(2)}<t-t_j}\left( \prod _{s<u<t_j} \left( 1-{\hat{\lambda }}_{12}(u)-{\hat{\lambda }}_{13^{(1)}}(u)\right) \right) {\hat{\lambda }}_{12}(t_j)\nonumber \\{} & {} \quad \times \left( \prod _{0<v<t_j^{(2)}} \left( 1-{\hat{\lambda }}_{23^{(2)}}(v)\right) \right) {\hat{\lambda }}^{(2)}_{23^{(2)}}(t_j^{(2)}) \end{aligned}$$

(8)

It follows from the above that $P_{1|13^{(1)}}(t)$ (Eq. 1) can be estimated using

$$\begin{aligned} \begin{aligned} {\widehat{P}}_{1|13^{(1)}}(t)=\frac{\sum _{t_j>t}{\hat{\lambda }}_{13^{(1)}}(t_j)\prod _{u< t_j} \left( 1-{\hat{\lambda }}_{12}(u)-{\hat{\lambda }}_{13^{(1)}}(u)\right) }{\sum _{t_j\in {\mathcal {T}}_1} {\hat{\lambda }}_{13^{(1)}}(t_j)\prod _{u< t_j} \left( 1-{\hat{\lambda }}_{12}(u)-{\hat{\lambda }}_{13^{(1)}}(u)\right) } \end{aligned} \end{aligned}$$

(9)

and $P_{1|123^{(2)}}(t)$ (Eq. 2) can be estimated using

$$\begin{aligned} \begin{aligned} {\widehat{P}}_{1|123^{(2)}}(t)=\frac{\sum _{t_j>t}{\hat{\lambda }}_{12}(t_j)\prod _{u< t_j} \left( 1-{\hat{\lambda }}_{12}(u)-{\hat{\lambda }}_{13^{(1)}}(u)\right) }{\sum _{t_j\in {\mathcal {T}}_1} {\hat{\lambda }}_{12}(t_j)\prod _{u< t_j} \left( 1-{\hat{\lambda }}_{12}(u)-{\hat{\lambda }}_{13^{(1)}}(u)\right) } \end{aligned} \end{aligned}$$

(10)

3.3 Conditional distribution of time spent in state 2

The probability of being in state 2 for time t or longer (conditional on reaching state 2) conditional on the pathway being $1\rightarrow 2 \rightarrow 3^{(2)}$ or $2 \rightarrow 3^{(2)}$ can be written

$$\begin{aligned} \begin{aligned} P_{2|123^{(2)}}(t)=&\Pr (X^{(2)}(t)=2|X^{(2)}(\infty )=3^{(2)})\\ =&\frac{\Pr (X^{(2)}(\infty )=3^{(2)}|X^{(2)}(t)=2)\Pr (X^{(2)}(t)=2)}{\Pr (X^{(2)}(\infty )=3^{(2)})}\\ =&\frac{P_{23^{(2)}}(t,\infty )P_{22}(0,t)}{P_{23^{(2)}}(0,\infty )} \end{aligned} \end{aligned}$$

(11)

where $P_{23^{(2)}}(0,\infty )=1$ and $P_{23^{(2)}}(t,\infty )=1$. The transition probabilities $P_{22}(s,t)$ can be written

$$\begin{aligned} P_{22}(s,t)=e^{-\int _{s}^{t}\lambda _{23^{(2)}}(x)dx}. \end{aligned}$$

(12)

If the full distribution of transition times is observed, these probabilities can be estimated for any s and t using

$$\begin{aligned} {\widehat{P}}_{22}(s,t)=\prod _{s<t^{(2)}_j\le t}\left( 1-{\hat{\lambda }}^{(2)}_{23^{(2)}}(t_j^{(2)})\right) \end{aligned}$$

(13)

Therefore $P_{2|123^{(2)}}(t)$ can be estimated using

$$\begin{aligned} {\widehat{P}}_{2|123^{(2)}}(t)=\prod _{0<t^{(2)}_j\le t}\left( 1-{\hat{\lambda }}^{(2)}_{23^{(2)}}(t_j^{(2)})\right) \end{aligned}$$

(14)

This is simply the Kaplan-Meier estimate, because once a person reaches state 2 there is only one subsequent state to which they can transition. The transition intensity $\lambda ^{(2)}_{23^{(2)}}(t)$ can be estimated by ${\hat{\lambda }}^{(2)}_{23^{(2)}}(t)=d_{2k}(t)/n_{2}(t)$, where $d_{2k}(t)$ denotes the number of transitions from state 2 to state $3^{(2)}$ at time t after entering state 2, and $n_{2}(t)$ denotes the number at risk of transitioning to state 2 from state $3^{(2)}$ at time t after entering state 2.

3.4 Estimation when the full distribution of transition times is not observed

Above we assumed for estimation that the full distributions of transition times out of state 1 and state 2 were observed in the data. Suppose instead that there is censoring in the observed data in such a way that the full distributions of transition times are not observed. This means that the last observed time of censoring or transition out of a given state (state 1 or state 2) will be a censoring time rather than a transition time. In this case it is not possible to estimate the probabilities $P_{1|13^{(1)}}(t)$ and $P_{1|123^{(2)}}(t)$. We note that this problem does not arise if the data are only subject to uninformative censoring prior to the last transition time, but rather is specific to ‘late’ censoring which results in the full distribution of transition times not being observed. In this situation, we can consider instead $P_{1|13^{(1)}}^{\tau }(t)$—the probability of spending time t or longer in state 1 conditional on transitioning to state $3^{(1)}$ before time $\tau$, and $P_{1|123^{(2)}}^{\tau }(t)$—the probability of spending time t or longer in state 1 conditional on transitioning to state 2 before time $\tau$ (because subsequent transition to state $3^{(2)}$ is then inevitable). The probabilities $P_{1|13^{(1)}}^{\tau }(t)$ and $P_{1|123^{(2)}}^{\tau }(t)$ can be estimated for times $\tau \le t^*_{J_1}$, where $t^*_{J_1}$ denotes the latest observed follow-up time in state 1 (including both transition times and censoring times). To estimate $P_{1|13^{(1)}}^{\tau }(t)$ and $P_{1|123^{(2)}}^{\tau }(t)$, the results in Eqs. (9) and (10) can be applied, with the sums in the denominators changed from $\sum _{t_j\in {\mathcal {T}}_1}$ to $\sum _{t_j\le \tau }$.

For time spent in state 2, $P_{2|123^{(2)}}(t)$ can be estimated for any $t\le t^*_{J_2}$, where $t^*_{J_2}$ denotes the latest observed follow-up time in state 2 (including both transition times and censoring times). We may also be interested in $P_{2|123^{(2)}}^{\tau }(t)$, which we define at the probability of spending time t or longer in state 2 conditional on transitioning to state $3^{(2)}$ before time $\tau$, which can be written $P_{2|123^{(2)}}^{\tau }(t)=\frac{P_{23^{(2)}}(t,\tau )P_{22}(0,t)}{P_{23^{(2)}}(0,\tau )}$, and estimated using

$$\begin{aligned} {\widehat{P}}_{2|123^{(2)}}^{\tau }(t)=\frac{\sum _{t<t^{(2)}_j\le \tau }{\hat{\lambda }}^{(2)}_{23^{(2)}}(t_j^{(2)})\prod _{u<t^{(2)}_j}\left( 1-{\hat{\lambda }}^{(2)}_{23^{(2)}}(u)\right) }{\sum _{0<t^{(2)}_j\le \tau }{\hat{\lambda }}^{(2)}_{23^{(2)}}(t_j^{(2)})\prod _{u<t^{(2)}_j}\left( 1-{\hat{\lambda }}^{(2)}_{23^{(2)}}(u)\right) } \end{aligned}$$

(15)

3.5 Conditional expected length of stay (CELOS)

Above we focused on the distribution of conditional lengths of stay. The expected time spent in a given state conditional on the pathway is one way of summarising the distribution. We refer to this as conditional expected length of stay (CELOS) and let $\textrm{CELOS}_{k|p}$ denote the expected length of stay in state k conditional on the complete pathway being p. The (unconditional) expected length of stay in state k can be written in terms of the state occupation probability: $E_k=\int _{0}^{\infty }\Pr (X(t)=k)dt$ (Beyersmann and Putter 2014). It follows that $\textrm{CELOS}_{k|p}$ can be written

$$\begin{aligned} \textrm{CELOS}_{k|p}=\int _{0}^{\infty }P_{k|p}(t)dt \end{aligned}$$

(16)

The conditional expected length of stay in state 1 among those who do not transition to state 2, denoted $\textrm{CELOS}_{1|13^{(1)}}$, can therefore be estimated using

$$\begin{aligned} \widehat{\textrm{CELOS}}_{1|13^{(1)}}=\sum _{t_j \in {\mathcal {T}}_1}(t_j-t_{j-1})\times \widehat{P}_{1|13^{(1)}}(t_{j-1}) \end{aligned}$$

(17)

where $t_0=0$ and $P_{1|13^{(1)}}(t_{0})=1$. $\textrm{CELOS}_{1|13^{(1)}}$ can equivalently be estimated using $\widehat{\textrm{CELOS}}_{1|13^{(1)}}=\sum _{t_j \in {\mathcal {T}}_1}t_{j}\times (\widehat{P}_{1|13^{(1)}}(t_{j+1})-\widehat{P}_{1|13^{(1)}}(t_{j}))$. The expression in (17) is similar to that used by Beyersmann and Putter (2014) for restricted expected length of stay. Similarly, $\widehat{\textrm{CELOS}}_{1|123^{(2)}}=\sum _{t_j \in {\mathcal {T}}_1} (t_j-t_{j-1})\times \widehat{P}_{1|123^{(2)}}(t_{j-1})$ and $\widehat{\textrm{CELOS}}_{2|123^{(2)}}=\sum _{t_j \in {\mathcal {T}}_2}(t_j-t_{j-1})\times \widehat{P}_{2|123^{(2)}}(t_{j-1})$.

In studies where there is censoring such that the full distribution of transition times is not observed, we discussed above that the conditional probabilities $P_{1|13^{(1)}}(t)$ and $P_{1|123^{(2)}}(t)$ cannot be estimated, and $P_{2|123^{(2)}}(t)$ can only be estimated for times t up to the latest observed transition time. Beyersmann and Putter (2014) discussed restricted expected length of stay in the multi-state modelling context, defined as $E_k^{\tau }=\int _{0}^{\tau }\Pr (X(t)=k)dt$, which is the expected time spent in state k up to time $\tau$. This is an extension to the multi-state setting of restricted mean survival time (RMST), proposed by Irwin (1949) (see also Royston and Parmar (2013) for example), which is the mean survival up to a particular time horizon.

We define restricted conditional expected length of stay (RCELOS) as the expected length of stay in a given state up to time $\tau$ conditional on the pathway taken up to time $\tau$:

$$\begin{aligned} \text {RCELOS}^{\tau }_{k|p}=\int _{0}^{\tau }P_{k|p}(t)dt. \end{aligned}$$

(18)

$\text {RCELOS}^{\tau }_{1|13^{(1)}}$ and $\text {RCELOS}^{\tau }_{1|123^{(2)}}$ can be estimated using

$$\begin{aligned} \widehat{\textrm{RCELOS}}^{\tau }_{1|13^{(1)}}=\sum _{t_j\in {\mathcal {T}}_1, t_j\le \tau }(t_j-t_{j-1})\times \widehat{P}^{\tau }_{1|13^{(1)}}(t_{j-1}) \end{aligned}$$

and

$$\begin{aligned} \widehat{\textrm{RCELOS}}^{\tau }_{1|123^{(2)}}=\sum _{t_j\in {\mathcal {T}}_1, t_j\le \tau }(t_j-t_{j-1})\times \widehat{P}^{\tau }_{1|123^{(2)}}(t_{j-1}). \end{aligned}$$

$\textrm{RCELOS}^{\tau }_{2|123^{(2)}}$ is the same as the restricted (unconditional) length of stay in state 2 and is estimated using $\widehat{\textrm{RCELOS}}^{\tau }_{2|123^{(2)}}=\sum _{t^{(2)}_j\in {\mathcal {T}}_2, t^{(2)}_j\le \tau }(t^{(2)}_j-t^{(2)}_{j-1})\times \widehat{P}_{2|123^{(2)}}(t^{(2)}_{j-1})$. We may also be interested in

$$\begin{aligned} \widehat{\textrm{RCELOS}}^{\tau *}_{2|123^{(2)}}=\sum _{t^{(2)}_j\in {\mathcal {T}}_2, t^{(2)}_j\le \tau }(t^{(2)}_j-t^{(2)}_{j-1})\times \widehat{P}^{\tau }_{2|123^{(2)}}(t^{(2)}_{j-1}) \end{aligned}$$

which estimates the expected length of stay in state 2 conditional on transitioning to state $3^{(2)}$ before time $\tau$ after entering state 2.

3.6 Software

The conditional state occupation probabilities $P_{k|p}(t)$ and $\textrm{CELOS}_{k|p}$, and the restricted equivalents $P^{\tau }_{k|p}(t)$ and $\text {RCELOS}^{\tau }_{k|p}$ can be estimated ‘manually’ by obtaining estimates of the transition intensities $\lambda _{1k}(t)$ ($k=2,3^{(1)}$) and $\lambda ^{(2)}_{23^{(2)}}(t)$, and applying the formulae given above. In the illness-death setting that we have considered so far, it is also possible to make use of some of the features of the mstate package in R (De Wreede et al. 2011; Putter et al. 2020), notably the probtrans function which can provide an estimate of the probability of having entered state 2. However, the probtrans function does not currently allow a clock-reset approach, which we assume here, which means that it cannot be used without modification beyond the illness-death setting.

4 Simulation study

We conducted a simulation study with the primary aims of checking the results in Sect. 3 and of demonstrating the bias if a naive analysis is used, in which empirical probabilities and means are calculated from the data ignoring censoring. The simulation also aims to illustrate some of the considerations needed when estimating restricted length of stay. R code is provided at https://github.com/ruthkeogh/lengthofstay, enabling the simulation results to be replicated.

4.1 Simulating data

Data were generated from the multi-state model depicted in Fig. 1 for $N=1000$ individuals. We consider three scenarios. In scenario (1) transition times were generated from exponential distributions using constant transition intensities $\lambda _{12}=0.005$, $\lambda _{13^{(1)}}=0.1$, $\lambda ^{(2)}_{23^{(2)}}=0.3$. In the motivating example transition times are recorded in terms of dates, resulting in ties. To mimic this discrete time setting of the motivating example, all times were rounded up to the next whole number in this scenario. In scenario (2) transition times were generated from Weibull hazard models of the form $\lambda (t)=\kappa \gamma t^{\kappa -1}$ for each transition, where $\kappa$ is the shape parameter and $\gamma$ is the rate parameter. For $\lambda _{12}(t)$, $\lambda _{13^{(1)}}(t)$, and $\lambda ^{(2)}_{23^{(2)}}(t)$ we used $(\kappa =0.75,\gamma =0.05)$, $(\kappa =0.75,\gamma =0.1)$, and $(\kappa =1.25,\gamma =0.3)$ respectively. In practice, there is likely to be heterogeneity of transition intensities between individuals. We therefore considered a scenario (3) in which we incorporated individual frailties. This was done using Weibull transition hazards as in scenario (2), and individual frailties generated from a log-normal distribution with mean 0 and variance 1 and independently across transitions.

In all three scenarios censoring times were generated from an exponential model with hazard $\lambda _0$. We consider situations with no censoring ($\lambda _0=0$) and with substantial censoring ($\lambda _0=0.2$) designed to result in the full distribution of transition times not being observed. In the situation with censoring, the choice of $\lambda _0$ resulted in an average of 53% of individuals having their transition out of state 1 censored in scenario (1), 67% in scenario (2), and 60% in scenario (3).

There are 6 scenarios in total: scenarios (1), (2) and (3), each with and without censoring. We generated 1000 simulated data sets under each scenario.

4.2 Estimands

The estimands of interest were the CELOS ($\textrm{CELOS}_{1|13^{(1)}}$, $\textrm{CELOS}_{1|123^{(2)}}$, $\textrm{CELOS}_{2|123^{(2)}}$) and the RCELOS ($\textrm{RCELOS}^{\tau }_{1|13^{(1)}}$, $\textrm{RCELOS}^{\tau }_{1|123^{(2)}}$, $\textrm{RCELOS}^{\tau }_{2|123^{(2)}}$, $\textrm{RCELOS}^{\tau ^*}_{2|123^{(2)}}$) for a time horizon of $\tau =5$. We note that the RCELOS with a large $\tau$ correspond to the CELOS. For the RCELOS we present results for a time horizon of $\tau =5$ because the maximum observed times spent in states 1 and 2 in the simulated data sets was typically greater than 5 in all scenarios, meaning that we expect to be able to obtain unbiased estimate of the RCELOS with $\tau =5$ in situations with and without censoring. In practice, the time horizon may be selected as the maximum observed transition or censoring time in each state.

For scenario (1), where transition times are integers, we also obtained estimates of the probabilities $P_{1|13^{(1)}}(t)$, $P_{1|123^{(2)}}(t)$ and $P_{2|123^{(2)}}(t)$ (corresponding to the CELOS) and $P^{\tau }_{1|13^{(1)}}(t)$, $P^{\tau }_{1|123^{(2)}}(t)$ and $P^{\tau }_{2|123^{(2)}}(t)$ for $\tau =5$ (corresponding to the RCELOS).

4.3 Methods and true values

We applied the multi-state analysis methods described in Sect. 3. We also calculated the empirical (“naive”) estimates in each simulated data set. For example, the naive estimate of $\textrm{CELOS}_{1|13^{(1)}}$ was calculated as the mean observed time of entering state $3^{(1)}$ in those who transition to that state, excluding individuals who were censored. The naive estimate of $\textrm{RCELOS}^{\tau }_{1|13^{(1)}}$ was calculated as the mean observed time of entering state $3^{(1)}$ in those who transition to that state and who do so before time $\tau$, excluding individuals who were censored. The naive estimates of $P_{1|13^{(1)}}(t)$ and $P^{\tau }_{1|13^{(1)}}(t)$ were calculated as the proportion of individuals who transitioned to state $3^{(1)}$ whose time of transition to $3^{(1)}$ was $\ge t$ (and $\le \tau$ for $P^{\tau }_{1|13^{(1)}}(t)$), excluding individuals who were censored.

In scenarios without censoring we expect the estimates of the CELOS to be (asymptotically) unbiased using both the naive approach and using our formulae. In scenarios with censoring the CELOS cannot always be estimated. Given the quite substantial censoring generated in the censoring scenarios, we expect the estimates of the CELOS to be biased both under the naive approach and using our formulae.

The true values of the estimands were approximated by simulating a data set of one million individuals for scenarios (1), (2) and (3) without censoring and calculating the empirical values, as in the naive approach.

For each estimand, we present the mean estimate across the 1000 simulated data sets and the empirical standard deviation. We also present the bias using the mean difference between the 1000 estimates and the true value, and corresponding Monte-Carlo standard error, which is calculated as the empirical standard deviation of the estimates divided by $\sqrt{1000}$ (the square-root of the number of simulated data sets). In scenario (1), averages of probability estimates at a given time t are obtained only from those simulated data sets in which t was an observed transition time.

4.4 Results

Simulation results for the CELOS and RCELOS estimates for Scenarios (1), (2) and (3) are summarised in Tables ,   and .

When there is no censoring, the naive estimates of the CELOS and RCELOS are identical to those obtained from the multi-state analysis, as we would expect. The estimates are (approximately) unbiased, with very small bias in some values (according to the MCE) being attributed to the finite sample size.

When there is censoring the CELOS estimates are biased both using the naive approach and the multi-state analysis. Again, this is what we expect to see. The censoring induced by the data generating mechanisms results in the latest observed transition or censoring time typically being a censoring time. The bias from the multi-state analysis does not arise because there is a problem with the method, but because the conditional mean cannot be estimated when the full distribution of transition times in not observed, highlighting that restricted estimates are required in this situation. We note that the bias is smaller from the multi-state analysis than from the naive analysis, but it is still substantial in all three scenarios. The bias is in the direction of under-estimating the conditional expected length of stay. We chose a high hazard for censoring in this simulation. The bias due to ignoring censoring will clearly depend strongly on the extent and distribution of censoring. In the motivating example shown later, the amount of censoring is much lower.

Estimates of the RCELOS obtained using the multi-state analysis are (approximately) unbiased in all three scenarios, including when there is censoring. The naive estimates are unbiased only when there is no censoring. When there is censoring the naive analysis results in estimates that are biased downwards, i.e. under-estimating the RCELOS.

Supplementary Figures 1–4 show plots of the estimated distribution of time spent in different states conditional on the pathway taken in scenario (1), for situations without censoring and with censoring. These demonstrate clearly how bias arises in the naive approach when there is censoring, with small values of t being over-represented relative to large values of t due to incomplete follow-up, resulting in an underestimate of the CELOS and RCELOS.

5 Application to hospitalisation for Covid-19

5.1 Data

The International Severe Acute Respiratory and emerging Infections Consortium WHO Clinical Characterisation Protocol UK (ISARIC WHO CCP-UK) study was established in the wake of the influenza A H1N1 pandemic (2009) and the emergence of Middle East respiratory syndrome coronavirus (2012). Further details about ISARIC WHO CCP-UK can be found at https://isaric4c.net. A key component of the ISARIC WHO CCP-UK study is the COVID19 Clinical Information Network (CO-CIN), which has collected clinical care data in near-real time from 208 hospitals in England, Scotland, and Wales on patients admitted to hospital since January 2020. Data were collected by clinical research nurses and administrators from clinical notes and entered into an online database. The clinical features of patients in this cohort have been described previously (Docherty et al. 2020).

We used CO-CIN data on individuals with proven or a high likelihood of infection with SARS-CoV-2 leading to COVID-19 disease with hospital admission from 10 March to 19 July 2020 (130 days). Information recorded includes patient characteristics, level of care (ward based, high dependency unit, or intensive care unit), complications, and dates of entering the following states: admission to hospital ward, admission to ICU (defined as high dependency unit or intensive care unit), stepping down from ICU to the general ward, death in hospital, and discharge. We include patients who had been admitted for a separate condition but had tested positive for SARS-CoV-2 during their hospital stay. A small proportion of individuals whose age or sex was not recorded were excluded.

The majority of individuals start in the hospital ward state, and the remainder start in the ICU admission state. The “discharge” state included individuals recorded with the outcomes “discharged alive” or “palliative discharge”. Individuals with the outcomes “hospitalized” or “transfer to other facility” were assumed alive and still in hospital or ICU at their outcome date. Some individuals have no outcome recorded because they were still within their care episode at the date of data extraction. These individuals were censored at the last date at which they had any information recorded in the data. When more than one event/transition was recorded on the same date for a given individual, we assumed the events occurred in quick succession and modified the data. For example if an individual was recorded as having been admitted to ICU on the same date as hospital admission, and then recorded as dying on the same date, the time of ICU admission was considered to be 0.25 days and the time of death 0.5 days.

5.2 Methods

Figure 2A illustrates the multi-state model for the more complex motivating example, in which there are 5 states. For patients starting in state 1 (hospital ward) there are 6 possible pathways. In the data, some individuals are observed to be admitted directly to ICU and therefore start in state 2. Therefore, we are also interested in the three possible pathways than a patient can follow if they start in state 2. The probabilities $P_{k|p}(t)$ for this setting are summarised in Table . In Fig. 2B the two absorbing states of discharge (state 4) and death (state 5) depicted in Fig. 2A are each divided into three states. State 4 is divided into states $4^{(1)}$ for people who are discharged from the hospital ward, state $4^{(2)}$ for people who are discharged from ICU, and $4^{(3)}$ for people who are discharged from the ward after ICU. Similarly state 5 is divided into states $5^{(1)}$, $5^{(2)}$, $5^{(3)}$, depending on the state from which an individual transitions to the death state.

The methods outlined for the simpler illness-death model can be extended to this more complex multi-state model and details are provided in the Supplementary Materials.

5.3 Results

The data contained the records of a total of 74,722 individuals. After restricting to those with a proven or a high likelihood of infection with SARS-CoV-2 and admitted to hospital between 10 March and 19 July 2020 there remain 43,256 individuals for analysis. We excluded 270 individuals with missing data on age or sex. The sample used for the analysis contains 42,980 individuals, including 24,776 males (58%) and 18,204 females (42%). Table  summarises the numbers of observed transitions between states. The majority of individuals start in the hospital ward state (39571, 92%), with the remainder starting in ICU. A total of 7816 (18%) of individuals entered the ICU state (including those who start in that state), of whom the majority (89%) went back to the hospital ward after ICU, prior to death or discharge. There were 12,058 deaths (28%) and 24,456 (57%) individuals were discharged, with the remaining 15% of patients being censored.

We began by summarising how patients transition through the multi-state model using plots of state occupation probabilities, estimated non-parametrically. Figure  shows the resulting estimated state occupation probabilities. These show that the majority of transitions out of the hospital ward (pre ICU) have occurred by around 40 days. There are longer tails on the state occupation estimates after entering the ICU state. After entering the hospital ward after being in ICU, the plot shows that individuals who then die tend to do so quickly and the majority of deaths and discharges occurred within 10 days. The maximum time of transition out of state 1 (hospital ward pre-ICU) was 103 days, the maximum time of transition out of state 2 (ICU) was 107 days and the the maximum time of transition out of state 3 (hospital ward after ICU) was 89 days.

The (unconditional) expected lengths of stay in the hospital ward, in ICU and in the hospital ward after entering ICU were estimated using the methods of Beyersmann and Putter (2014), using the ELOS function from the mstate package in R. For individuals admitted go the hospital ward, the expected length of stays are: 8.99 days (95% CI 8.87, 9.11) in the hospital ward, 12.36 days (11.99, 12.77) in ICU, and 9.44 days (8.65, 10.20) in the hospital ward after ICU. For individuals admitted directly to ICU, the expected length of stays are: 14.36 days (13.79, 14.89) in ICU, and 9.26 days (8.37, 10.12) in the hospital ward after ICU.

We applied the methods described in Sect. 5.2 to estimate the conditional length of stay distributions (Table 4) and corresponding CELOS. Preliminary investigations indicate that the length of follow-up available in this data set captures almost the full distribution of time spent in each state, and therefore permits estimation of the CELOS (as opposed to RCELOS). For comparison, we also calculated the naive estimates of the CELOS, which exclude the 15% of patients who were censored. Bootstrapping (percentile method) was used to estimate 95% confidence intervals (CI) for the CELOS estimates.

CELOS estimates are shown in Table  and the corresponding full conditional distributions in Figs.   and . We focus on the results obtained for individuals who started their stay in the hospital ward, as opposed to in ICU. Individuals who were discharged at the end of their stay tend to spend longer in any given state (1, 2 or 3) compared with patients who die at the end of their stay. Among patients who did not go to the ICU, the expected time spent in hospital was 8.07 days in those who died at the end of their stay and 10.23 days in those who were discharged. Figure 4 (first panel) shows the long tail on the distributions. Time spent in the hospital ward (pre-ICU) was much shorter in those who transition to ICU, being just over 4 days. Figure 4 (first panel) shows a large drop off in the curves after 1 day for the curves corresponding to pathways through ICU. Because we have assumed a clock-reset approach, the time spent in hospital conditional on going to ICU does not depend on the states entered after ICU.

Patients who went to ICU followed by the hospital ward were estimated to spend an average of 12.38 days in ICU. Time spent in ICU was slightly shorter in those who did not subsequently return to the hospital ward (CELOS 7.71 days for those die in ICU and 9.76 days for those who are discharged directly from ICU), but these estimates are based on small numbers and the confidence intervals are wide. In those who go to ICU and then return to the hospital ward, the time spent in the hospital ward after ICU tended to be very short in patients who died (CELOS 1.03 days), suggesting that some individuals are returned to the ward from ICU when it is known that they are close to death. The expected time spent in the hospital ward after ICU was 10.77 days in those who were subsequently discharged. Figure 4 (third panel) shows a very large drop off in the distribution after 1 day for individuals who die. The distribution of time spent in states 2 and 3 was similar for patients who started in state 1 and patients who started in state 2 (i.e. were admitted directly to ICU).

The estimates of conditional length of stay using the naive analysis (excluding censored observations) tend to underestimate the true values (Table 6), which we expect from the simulation results and from theory.

6 Discussion

We have presented methods for estimating distributions of length of stay in a multi-state model conditional on the pathway taken through the states in the model. We also showed how the conditional length of stay distribution can be summarised in terms of a conditional expected length of stay (CELOS) or restricted CELOS (RCELOS), which is appropriate when there is censoring such that the last observed time in the state of interest is a censoring time rather than a transition time. The methods are non-parametric and do not rely on distributional assumptions. We described the methods for the widely used illness-death multi-state model and also provided details of the extension to the more complex multi-state model relevant for transitions of hospitalised Covid-19 patients. We assumed a clock-reset approach in which the transition intensities in a given state depend on time since entering that state, but not on previous states visited or duration spent in previous states. Extensions to our approach could relax this assumption, for example by specifying Cox models for the transition intensities and including previous state and time spent in previous states as covariates.

The methods were assessed using a simulation study based on an illness-death model. The results show that in situations with censoring such that the full distribution of transition times is not observed, the naive estimates of the conditional length of stay distributions are biased, giving under estimates of the RELOS due to small transition times being over-represented in the data and higher transition times not being observed. The proposed multi-state approach gives approximately unbiased estimates. The results highlight that care should be taken when interpreting expected length of stay results when there is censoring and in finite samples—in these situations the restricted conditional length of stay (RCELOS) (up to a chosen time horizon $\tau$) is an appropriate summary measure. We have also provided example R code for creating a simulated data set and for implementing the methods.

Alongside describing new methods, we applied the methods to estimate conditional length of stay in different states in patients hospitalised with Covid-19 in the UK using data on 42980 patients. Results were presented in terms of distributions and conditional expected length of stay in the hospital ward, in ICU, and in the hospital ward after ICU. The CELOS in the hospital ward in patients not admitted to ICU was 9.58 days, CELOS in ICU (among those admitted to ICU) was 12.38 days (in those who stepped down to the hospital ward after ICU, which was the majority), and the CELOS in the hospital ward after ICU (in those who entered that state) was 6.88 days, though this differed considerably between patients who subsequently died and those who were discharged.

Conditional length of stay in a state of a multi-state model involves conditioning on what happens to an individual in the future, which is usually best avoided in time-to-event analyses (Andersen and Keiding 2012). However, our estimands were carefully defined as conditional on the pathway, and we have shown that they enable a nuanced description of the multi-state system, as well as providing inputs that can be used in mathematical models. A different aim in a multi-state model could be to provide information about the risk of certain transitions occurring for an individual given their characteristics, or to estimate how certain covariates are associated with rates of transition. In that case conditioning on the pathway taken, or on any other future information, would be in appropriate for the question at hand. In the Covid-19 literature, multi-state modelling methods have been used by a number of authors to investigate time spent in different states in the context of patients hospitalised with Covid-19, and both unconditional and conditional lengths of stay have been estimated. Vekaria et al. (2020) estimated conditional lengths of stays using data on 6208 Covid-19 patients in the UK observed in the COVID-19 Hospitalisation in England Surveillance System (CHESS) from March to May 2020. They took a parametric modelling approach and fitted Weibull models for each transition in a multi-state model, which was combined with a simulation procedure to obtain conditional length of stay estimates. Their estimates are in line with ours. They estimated a mean of 4 days spent in hospital prior to ICU admission (our estimate: 4.23 days). In those who did not go to ICU the expected time to death was 8.8 days (our estimate: 8.07 days) and the expected time to discharge 11.3 days (our estimate: 10.23 days). Among individuals who stepped down to the hospital ward after ICU, the expected time to discharge was 6.2 days (our estimate: 10.77 days). The expected time from ICU admission to death was 17.4 days (we did not obtain an equivalent estimate). They stated that they did not observe any individuals who stepped down from ICU to the hospital ward and then died. We observed individuals who transitioned from ICU to the hospital ward, however our results showed that a high proportion of these individuals died a short time after returning to the ward, suggesting that it may be appropriate to class some of these deaths as deaths in ICU. Data on the reason for a patient going to the Ward after ICU would facilitate this. There may have been different ways of recording death after ICU admission in the CHESS and CO-CIN data sets.

Rieg et al. (2020) performed multi-state modelling using data on 213 patients admitted to a German hospital (February–May 2020). They considered the following states: regular ward, ICU (without mechanical ventilation), mechanical ventilation, extracorporeal membrane oxygenation (ECMO), death and discharge. In those admitted to the regular ward, the expected length of stay in the regular ward was 13.6 days, and expected length of stay in ICU was 0.8 days—this appears not be be conditional on actually going to ICU and so has a different interpretation than our estimates. In patients admitted directly to ICU the expected length of stay in ICU was 5.6 days. Hazard et al. (2020) used non-parametric multi-state modelling analysis to estimate restricted expected length of stay in ventilated and non-ventilated Covid-19 patients admitted to ICU using data from two small published data sets from the US (n = 24) and the US, Europe and Japan (n = 53). The estimated total length of stay in ICU up to 28 days was 15.05 days (95% CI 9.29–21.66) in the larger study, which involved patients treated with remdesivir.

Rees et al. (2020) conducted a systematic review of estimated length of stay in Covid-19 patients based on studies published up to 12 April 2020. They identified 52 studies, most of which were from China. In studies from China the median length of stay in hospital was 14 days (interquartile range 10–19 days), and in studies outside of China the median length of stay in hospital was 5 days (interquartile range 3–9 days). Median length of stay in ICU was 8 days in studies from China, and 7 days outside of China. We estimated the full distribution of length of stay in different states and the means. For use in planning capacity requirements, means are more appropriate than medians as summary measures. Rees et al. (2020) noted that patients discharged alive tended to have longer length of stay compared with those who died, which we also found. In a study of trajectories among patients hospitalised with Covid-19 in France, Boelle et al. (2020) found that the median time to death in those who went to ICU was 20 days, and the median time to discharge from ICU was 17 days. In those who did not go to ICU, the median time to death was 9 days, and median time to discharge was also 9 days. They used parametric modelling methods, though it was not entirely clear how they estimated the length of stay. In a study from Australia, Liu et al. (2018) found that the median time spent in hospital was 9 days and the median time spent in ICU was 6 days; their results appear to be based on patients with death or discharge observed.

The methods described in this paper are non-parametric and do not incorporate covariates. The methods could be applied to subsets of patients defined by characteristics such as age group and sex. In further work it is of interest to extend the methods to incorporate several covariates simultaneously. This could be done, for example, by using semi-parametric Cox models for the transition intensities, and it should be straightforward to implement this using the mstate package in R. It would also be of interest to investigate extensions of the work of Klinten Grand and Putter (2016) who used pseudo–observations to construct regression models for expected length of stay in multi-state models, which enables estimation of associations between covariates and length of stay to be quantified.

Fig. 1

Illness-death multistate model

Fig. 2

Multi-state model for patients hospitalised due to Covid-19

Table 1 Simulation results for scenario (1) (exponential data generating model)

Table 2 Simulation results for scenario (2) (Weibull data generating model)

Table 3 Simulation results for scenario (3) (Weibull data generating model with individual frailty)

Table 4 Summary of possible pathways for the multistate model in Fig. 2, and notation for distribution of time spent in a given state k conditional on a given pathway p, $P_{k|p}(t)$

Table 5 Number (%) of transitions between states and censorings among 42,980 patients in the CO-CIN data

Fig. 3

Estimated state occupation probabilities up to 100 days after entering each state, applied to Covid-19 hospitalised patients using the CO-CIN data. For individuals admitted to the hospital ward. See Supplementary Figure 1 for corresponding plots for individuals admitted directly to ICU

Table 6 Conditional expected length of stay (CELOS) in states 1 (hospital ward), 2 (ICU) and 3 (ward after ICU) for Covid-19 hospitalised patients using the CO-CIN data: Naive estimates (excluding censored observations) and estimates obtained using the multi-state analysis

Fig. 4

Summary of the distribution of time spent in the hospital ward (pre-ICU), in ICU, and in the hospital ward after ICU conditional on the pathway taken, for patients who are admitted to the hospital ward. The plots how the probability that the time spent in state k is $\ge t$ days conditional on the pathway p: $P_{k|p}(t)$

Fig. 5

Summary of the distribution of time spent in ICU, and in the hospital ward after ICU conditional on the pathway taken, for patients who are admitted directly to ICU. The plots how the probability that the time spent in state k is $\ge t$ days conditional on the pathway p: $P_{k|p}(t)$. Estimated distribution of time spent in the ICU and hospital ward after ICU conditional on the pathway taken