Abstract
We study inexact fixed-point proximity algorithms for solving a class of sparse regularization problems involving the \(\ell _0\) norm. Specifically, the \(\ell _0\) model has an objective function that is the sum of a convex fidelity term and a Moreau envelope of the \(\ell _0\) norm regularization term. Such an \(\ell _0\) model is non-convex. Existing exact algorithms for solving the problems require the availability of closed-form formulas for the proximity operator of convex functions involved in the objective function. When such formulas are not available, numerical computation of the proximity operator becomes inevitable. This leads to inexact iteration algorithms. We investigate in this paper how the numerical error for every step of the iteration should be controlled to ensure global convergence of the inexact algorithms. We establish a theoretical result that guarantees the sequence generated by the proposed inexact algorithm converges to a local minimizer of the optimization problem. We implement the proposed algorithms for three applications of practical importance in machine learning and image science, which include regression, classification, and image deblurring. The numerical results demonstrate the convergence of the proposed algorithm and confirm that local minimizers of the \(\ell _0\) models found by the proposed inexact algorithm outperform global minimizers of the corresponding \(\ell _1\) models, in terms of approximation accuracy and sparsity of the solutions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Sparse learning plays a pivotal role in today’s era of big data due to its capacity for significantly decreasing the computational burden through sparse solution representation. Natural images or data streams are often inherently sparse in certain bases or dictionaries, under which they can be approximately expanded by only few significant elements carrying the most relevant information [7, 31, 42, 49]. Sparsity-promoting regularization is a common and powerful tool to capture the most important features hidden in the enormous data. Such a technique has been successfully applied in many areas, for example, compressed sensing [4, 14], image processing [15, 20, 24, 32, 38], and machine learning [27, 40].
The most intuitive choice of the regularization term for promoting sparsity is the \(\ell _0\)-norm which counts the number of the nonzero components of a vector. The geometric viewpoint of the \(\ell _0\)-norm has been explored in [50], demonstrating that the \(\ell _0\) regularization term results in lifting the graph of the target function according to the level of sparsity. Nevertheless, it is challenging to develop an efficient algorithm to solve the \(\ell _0\)-norm based regularization problem due to the discontinuity and non-convexity of the \(\ell _0\) norm. This challenge has been discussed in [6, 18, 33] that finding a global minimizer of the \(\ell _0\)-norm based regularization problem is an NP-hard problem. A widely adopted approach to address this issue is replacing the \(\ell _0\)-norm by the \(\ell _1\)-norm which transfers a non-convex problem to a convex one. There are plenty of feasible algorithms from convex optimization for solving the \(\ell _1\)-norm based regularization problem [8, 24, 32]. However, the \(\ell _1\) norm whose proximity operator is the well-known soft thresholding operator, could bring up unnecessary bias on the components of the solution even if some of them are dominant [16, 53] and such a bias may jeopardize the performance of the solution, especially the accuracy on the data. The mentioned disadvantage of the \(\ell _1\)-norm in fact can be avoided by the \(\ell _0\)-norm, which takes the hard thresholding operator as its proximity operator and potentially elevates the accuracy of the solution applying to the data. Consequently, there arises a need to devise algorithms that directly address the challenge of solving the \(\ell _0\)-norm based regularization problem.
Recently, there was notable advancement in the development of convergent algorithms designed for the \(\ell _0\)-norm based regularization problem. It was proposed in [37] a fixed-point proximity algorithm in the context of image inpainting, with guaranteed convergence to a local minimizer of the objective function involving the \(\ell _0\)-norm. Its proof reveals that the support of the sequence generated by the algorithm remains unchanged after a finite number of iterations, and thus on the fixed support the non-convex optimization problem is reduced to a convex one. This idea has also been applied to the problems of the seismic wavefield modeling [48] and medical image reconstruction [52]. Moreover, the numerical examples provided in [37, 48, 52] affirm that solutions obtained from the \(\ell _0\)-norm based regularization model exhibit superior performance compared to those from the \(\ell _1\)-norm based regularization model. The algorithm studied in [37, 48] usually requires the evaluation of the proximity operator of the composition of a convex function and a matrix for each iteration. The precise value of that proximity operator is difficult to obtain except for the case of the matrix having some special property, such as the matrix being reduced to be an identity matrix or having circulant blocks structure [20]. This requirement significantly constrains the applicability of the algorithm in some areas, for example, regression and classification problems in machine learning and deblurring problems in image processing. The fixed-point iterative algorithms proposed in [24, 32] facilitate computing the proximity operator of a convex function composite with a general matrix, in which errors are unavoidable with a finite number of iterations. This motivates us to consider an inexact version of the algorithm proposed in [37, 48], namely the inexact fixed-point proximity algorithm.
In the field of optimization, inexact methods have attracted considerable attention. Inexact methods for solving convex optimization problems related to monotone operators and the proximal point algorithm were developed in [35]. Moreover, the inexact forward–backward algorithm, the inexact variant of the Krasnosel’skiĭ-Mann iteration, and the inexact implicit fixed-point proximity algorithm were proposed in [11, 29, 34, 39, 44], respectively. In [1], inexact descent methods were developed for non-convex optimization problems with the objective function satisfying the Kurdyka-Łojasiewicz (KL) property [21, 30] and their convergence to a critical point of the objective function was established.
The goal of this paper is to propose an inexact fixed-point proximity algorithm to solve the \(\ell _0\)-norm based regularization problem and prove its convergence to a local minimizer of the objective function without assuming the KL property. Specifically, we show that the proposed algorithm first pursues the support of a sparse solution of the non-convex model involving the \(\ell _0\)-norm and then searches for the solution on the resulting support set, and based on this understanding, we establish the convergence result. We apply the inexact fixed-point proximity algorithm to three application problems including regression and classification and image deblurring. The convergence and effectiveness of the proposed algorithm are confirmed by numerical experiments.
This paper is organized in six sections. In Sect. 2, we describe the \(\ell _0\)-norm based regularization model and characterize a solution of the model as the fixed-point problem. In Sect. 3, we propose the inexact fixed-point proximity algorithm to solve the \(\ell _0\)-norm based regularization model and demonstrate its feasibility. Section 4 is devoted to convergence analysis of the proposed inexact algorithm. In Sect. 5 we apply the proposed algorithm to solve regression, classification and image deblurring problems and demonstrate the performance of the proposed algorithm. Our conclusions are drawn in Sect. 6.
2 Sparse Regularization Model
In this section, we describe the sparse regularization model and present a necessary condition for a global minimizer of the resulting minimization problem.
Many application problems may be modeled as sparse regularization problems. The sparsity of a vector is naturally measured by the number of its nonzero components. Specifically, for \(\textbf{x}\in \mathbb {R}^n\), \({\left\| {\textbf{x}}\right\| }_0\) counts the number of nonzero components of \(\textbf{x}\) and we call \({\left\| { \textbf{x}}\right\| }_0\) the \(\ell _0\)-norm of \(\textbf{x}\), even though it is not really a norm. A sparse regularization problem may be described as
where the function \(\psi :\mathbb {R}^p\rightarrow \mathbb {R}\) is proper, convex, continuously differentiable, and bounded below, \({{\textbf{B}}}\in {{\mathbb {R}}}^{p \times m}\), \({{\textbf{D}}}\in {{\mathbb {R}}}^{n \times m}\) are matrices, and \(\lambda \) is a positive regularization parameter. The matrix \({{\textbf{D}}}\) appearing in (2.1) is often a redundant system chosen as a mathematical transformation, such as a discrete cosine transform [41], a wavelet transforms [13, 28, 31], or a framelet transform [9, 36], depending on specific applications. In this paper, we are mainly interested in the case of \({{\textbf{D}}}\) being a discrete tight framelet system, that is, \({{\textbf{D}}}^{\top }{{\textbf{D}}}= {{\textbf{I}}}\) with \({{\textbf{D}}}^{\top }\) being the transpose of \({{\textbf{D}}}\) and \({{\textbf{I}}}\) the identity matrix.
The discontinuity and non-convexity of the \(\ell _0\)-norm are major barriers to developing efficient algorithms for solving the optimization problem (2.1). Practically the \(\ell _0\)-norm in the model (2.1) is often replaced by the \(\ell _1\)-norm [8, 24, 32] which is both continuous and convex. The resulting model is
Model (2.2) is a special case of the model in [8, 24], which may be solved by the first-order primal–dual algorithm [8] and multi-step fixed-point proximity algorithm [24]. Both of these algorithms are required to compute the proximity operator of \(\lambda {\left\| {\textbf{D}\textbf{v}}\right\| }_1\), which often has no closed-form. Alternatively, one may introduce an auxiliary variable \(\textbf{u}\) to free \(\textbf{D}\textbf{v}\) from the non-differentiable norm \({\left\| {\cdot }\right\| }_1\) and add the difference between \(\textbf{u}\) and \(\textbf{D}\textbf{v}\) as a penalized term. This yields the model
This falls into the quadratic penalty approach which can be tracked back to [12] and has been widely used in image reconstruction [43, 45, 51]. However, the \(\ell _1\)-norm may promote biases [16]. For this reason, we prefer using the \(\ell _0\)-norm by overcoming difficulties brought by it. Specifically, we adopt the quadratic penalty approach to free \(\textbf{D}\textbf{v}\) from \({\left\| {\cdot }\right\| }_0\). This leads to the following two variables \(\ell _0\)-norm based regularization problem
where \(\gamma >0\) is the envelope parameter. We remark that the sum of the last two terms in (2.4) approaches to \({\left\| {{{\textbf{D}}}\textbf{v}}\right\| }_0\) as \(\gamma \) goes to zero. For notation simplicity, we let
In this notation, problem (2.4) may be restated as
We next present a necessary condition for a solution of (2.6). To this end, we recall the definition of the proximity operator [2]. For a proper, lower semi-continuous function \(f:{{\mathbb {R}}}^m\rightarrow {{\mathbb {R}}}\cup \{\infty \}\) and a positive number t, the proximity operator \(\text {prox}_{tf}: {{\mathbb {R}}}^m \rightarrow {{\mathbb {R}}}^m \) at \(\textbf{y}\in {{\mathbb {R}}}^{m}\) is defined as
We remark that the proximity operator \(\text {prox}_{tf}\) defined by (2.7) is set-valued and if f is further assumed to be convex, the corresponding proximity operator will be single-valued. In particular, if f is continuously differentiable and convex, then
The remaining part of this section is to establish a necessary condition for a solution of (2.6) in the form of a fixed-point of the proximity operators. To prepare for this, we present three technical lemmas.
Lemma 1
If \(\textbf{a}, \textbf{b}\in {{\mathbb {R}}}^m\) and \(q\in [0,1]\), then
Proof
A direct computation confirms that
This establishes the desired inequality (2.8). \(\square \)
Lemma 2
Suppose that \(f:\mathbb {R}^n\rightarrow \mathbb {R} \cup \left\{ \infty \right\} \) is a proper, lower semi-continuous function. If \(p>0\) and \(\textbf{x}^*, \textbf{y}^*\in \mathbb {R}^n\) such that
then for all \(q\in [0,1]\),
Proof
From the definition of the proximity operator, it suffices to prove that
By employing inequality (2.8) of Lemma 1 with \(\textbf{a}:=\textbf{x}- \textbf{y}^*\) and \(\textbf{b}:= \textbf{x}^*-\textbf{y}^*\), we obtain that
Combining (2.11) with the assumption (2.9) leads to estimate (2.10). \(\square \)
Lemma 3
If \({{\textbf{D}}}\in {{\mathbb {R}}}^{n \times m}\) such that \({{\textbf{D}}}^{\top }{{\textbf{D}}}= {{\textbf{I}}}\), then
Proof
We prove (2.12) by direct computation. Since by assumption \({{\textbf{D}}}^\top {{\textbf{D}}}={{\textbf{I}}}\), we may expand \({\left\| {\textbf{u} - {{\textbf{D}}}\textbf{v}}\right\| }_2^2\) as
and \({\left\| {\textbf{v} - {{\textbf{D}}}^{\top } \textbf{u}}\right\| }_2^2\) as
Subtracting (2.14) from (2.13) yields that
which leads to equation (2.12). \(\square \)
The next proposition presents a necessary condition for a solution of (2.6) as a fixed-point of the proximity operator. For notation simplicity, we define the operator \(\mathscr {S}: {{\mathbb {R}}}^m \rightarrow {{\mathbb {R}}}^m\) as
Proposition 1
If the pair \((\textbf{u}^*, \textbf{v}^*) \in {{\mathbb {R}}}^n \times {{\mathbb {R}}}^m\) is a global minimizer of problem (2.6), then for any \(\alpha \in (0, 1]\),
Proof
Since \((\textbf{u}^*, \textbf{v}^*)\) is a global minimizer of (2.6), we obtain that
By noting the definition of F and choosing \(\textbf{v}:= \textbf{v}^*\) in (2.18), we obtain that
Applying Lemma 2 with \(p:=\frac{\lambda }{2\gamma }\), \(q:=\alpha \), \(\textbf{x}^*:= \textbf{u}^*\), \(\textbf{y}^*:= {{\textbf{D}}}\textbf{v}^*\) and \(f:=\lambda \Vert \cdot \Vert _0\) and employing the definition of the proximity operator, we get (2.16). We next take \(\textbf{u}:= \textbf{u}^*\) in (2.18) and find that
It follows from Lemma 3 that
and
Substituting (2.21) and (2.22) into (2.20) yields the inequality
Inequality (2.23) is equivalent to the equation \(\textbf{v}^* = \textrm{prox}_{\frac{\gamma }{\lambda }\psi \circ {{\textbf{B}}}}\left( {{\textbf{D}}}^{\top } \textbf{u}^*\right) \), which is reduced to \(\textbf{v}^* = \mathscr {S}\left( {{\textbf{D}}}^{\top }\textbf{u}^*\right) \) due to the continuous differentiability of \(\frac{\gamma }{\lambda }\psi \circ {{\textbf{B}}}\). \(\square \)
The necessary condition for a global minimizer of optimization problem (2.6) presented in Proposition 1 suggests an inexact fixed-point proximity algorithm for solving (2.6), which will be discussed in the next section.
3 Inexact Fixed-Point Proximity Algorithm
In this section, we first describe an exact fixed-point proximity algorithm for the model (2.6), and discuss a computational issue of the exact algorithm. We then propose an inexact fixed-point proximity algorithm to address the computational issue.
The fixed-point equations (2.16)–(2.17) introduced in Proposition 1 suggest an exact fixed-point proximity algorithm for model (2.6). That is,
where \(\alpha \in (0, 1]\). The exact fixed-point proximity algorithm (3.1)–(3.2) has been introduced in [51] for \(\alpha \in (0, 1)\).
Comments for the case \(\alpha = 1\) are in order. In this case, iteration (3.1) reduces to
The sequence \(\left\{ \left( \textbf{u}^k, \textbf{v}^k\right) \right\} _{k=1}^{\infty }\) generated from (3.3) and (3.2) is well-defined. Moreover, it can be verified from inequalities (2.25) and (2.28) of [51] that the sequence of objective function values \(\left\{ F(\textbf{u}^k, \textbf{v}^k)\right\} _{k=1}^{\infty }\) is non-increasing, indicating convergence of the sequence \(\left\{ F(\textbf{u}^k, \textbf{v}^k)\right\} _{k=1}^{\infty }\), when the function \(\psi \) has a lower bound. Furthermore, for the special case where \(\psi (\textbf{B}\textbf{v}) = \frac{1}{2}{\left\| {\textbf{B}\textbf{v} - \textbf{r}}\right\| }_2^2\) for a given \(\textbf{r} \in {{\mathbb {R}}}^p\), with \(\textbf{B}\) satisfying \(\textbf{B}\textbf{B}^{\top } = \textbf{I}\), and \(\textbf{D} = \textbf{I}\), the sequence \(\left\{ \left( \textbf{u}^k, \textbf{v}^k\right) \right\} _{k=1}^{\infty }\) generated by algorithm (3.3) and (3.2) was proved in [48] to be convergent under the condition \(0<\frac{\gamma }{\lambda }<\frac{\sqrt{5}-1}{2}\). However, it remains uncertain whether the sequence \(\left\{ \left( \textbf{u}^k, \textbf{v}^k\right) \right\} _{k=1}^{\infty }\) generated by algorithm (3.3) and (3.2) in general is convergent.
One may apply the alternating direction method of multipliers (ADMM) to solve optimization problem (2.1). ADMM was originally proposed for solving convex optimization [5, 17, 19], and was later extended to solving nonconvex nonsmooth optimization [46]. Convergence of ADMM was established in [46] by requiring that the augmented Lagrangian function be of Kurdyka-Łojasiewicz and that the penalty parameter \(\lambda /\gamma \) in the augmented Lagrangian function defined by (3.5) below be sufficiently large.
To describe ADMM for (2.1), we rewrite problem (2.1) in an equivalent form
where \((\textbf{u}, \textbf{v}) \in {{\mathbb {R}}}^{n} \times {{\mathbb {R}}}^{m}\). We then define the augmented Lagrangian function for (3.4) as
where \(\textbf{w} \in {{\mathbb {R}}}^n\) is a dual variable. ADMM minimizes the augmented Lagrangian function (3.5) with respect to variables \(\textbf{u}\) and \(\textbf{v}\) alternatively and then updates the dual variable \(\textbf{w}\), leading to the following iteration scheme
Note that the gradient of the augmented Lagrangian function L with respect to the dual variable \(\textbf{w}\) is given by \(\textbf{D}\textbf{v} - \textbf{u}\). ADMM employs the gradient ascent method to update the dual variable \(\textbf{w}\), utilizing a fixed step-size \(\frac{\lambda }{\gamma }\). Consequently, for each iteration, the function value \(L(\textbf{u}, \textbf{v}, \textbf{w})\) decreases when updating the primal variables \(\textbf{u}\) and \(\textbf{v}\) and increases when updating the dual variable \(\textbf{w}\). In other words, the gradient ascent step that updates the dual variable in ADMM may lead to oscillations in values of the augmented Lagrange function. As such, ADMM may fail to converge for the augmented Lagrangian function L involving the \(\ell _0\) norm, since due to the non-convexity of the \(\ell _0\) norm, ensuring the monotonic decreasing behavior of the objective function at every iteration step is crucial for its convergence. Unlike ADMM, the exact fixed-point proximity algorithm (3.1)–(3.2) consists only the \(\textbf{u}\)-minimization step (3.1) and \(\textbf{v}\)-minimization step (3.2). It was proved in Theorem 2.1 of [51] that the objective function F defined by (2.5) is monotonically decreasing at every iteration step of (3.1)–(3.2), leading to its convergence. For this reason, we prefer minimizing the objective function F defined by (2.5) rather than the augmented Lagrangian function L. Our goal is to develop a convergence guaranteed inexact fixed-point algorithm to solve the optimization problem (2.6) without requiring the objective function to be a Kurdyka-Łojasiewicz function and the penalty parameter \(\frac{\lambda }{\gamma }\) to be sufficiently large, as required in [46].
We now consider the implementation of the exact fixed-point proximity algorithm (3.1)–(3.2). It is well-known that for \(\textbf{u} \in {{\mathbb {R}}}^n\), the proximity operator of the \(\ell _0\)-norm is given by
with \(t>0\), where
Note that \(\text {prox}_{t|\cdot |_0}\) is the hard thresholding operator. The closed-form formula (3.9) facilitates the implementation of (3.1). However, the implementation of (3.2) encounters a computational issue of evaluating the operator \(\mathscr {S}\). We assume that the operator \(\left( {{\textbf{I}}}+ \lambda /\gamma \nabla \psi \right) ^{-1}\) has a closed form, which is true in many problems of practical importance. In the special case when the matrix \({{\textbf{B}}}\) in (3.2) satisfies \({{\textbf{B}}}{{\textbf{B}}}^{\top } = {{\textbf{I}}}\), the operator \(\mathscr {S}\) also has a closed form. It is known (for example, Theorem 6.15 of [3]) that if \({{\textbf{B}}}{{\textbf{B}}}^{\top } = {{\textbf{I}}}\), then for any \(\textbf{x} \in {{\mathbb {R}}}^m\),
In this case, the update \(\textbf{v}^{k+1}\) in (3.2) can be computed exactly by using the above formula and a closed-form formula of \(\left( {{\textbf{I}}}+ \gamma /\lambda \nabla \psi \right) ^{-1}\). For general cases where \({{\textbf{B}}}{{\textbf{B}}}^{\top } \ne {{\textbf{I}}}\), there is no closed form for \(\mathscr {S}\) and thus, the update \(\textbf{v}^{k+1}\) in (3.2) cannot be computed exactly. According to [32], the operator \(\mathscr {S}\) may be computed by solving a fixed-point equation. Therefore, we can only obtain approximate values of \(\textbf{v}^{k+1}\). This leads to an inexact fixed-point approach: Suppose that \({\tilde{{\varvec{\varepsilon }}}}^{k+1} \in {{\mathbb {R}}}^{m}\) is a predetermined error and \(\alpha \in (0, 1]\). Assuming that \({\tilde{\textbf{u}}}^k\) and \({\tilde{\textbf{v}}}^k\) are given, we find
where
and define \({\tilde{\textbf{v}}}^{1}_{*}:= {\tilde{\textbf{v}}}^1\). The equation (3.12) is uncomputable since it is not feasible to calculate \({\tilde{\textbf{v}}}^{k+1}_*\) exactly. In practice, computing an approximation of \({\tilde{\textbf{v}}}^{k+1}_*\) requires an inner loop, which leads to an inexact algorithm.
We now describe a specific algorithm to compute an approximation of \({\tilde{\textbf{v}}}_*^{k+1}\) at the \((k+1)\)-step, which will serve as an inner loop for the inexact algorithm for solving model (2.6). By Theorem 3.1 of [32], for an \(\textbf{x}\in {{\mathbb {R}}}^m\), we have that
where \(\textbf{w}\) satisfies the fixed-point equation
for any positive parameter q. Note that introduction of the parameter q allows us to choose its values so that the corresponding fixed-point algorithm for finding \(\textbf{w}\) converges. When \({\tilde{\textbf{u}}}^{k+1}\) is available, we can find an update \(\tilde{\textbf{v}}^{k+1}\) via employing the Fixed-Point Proximity Algorithm (FPPA) proposed in [24, 32] to solve equations (3.14) and (3.15) numerically. For given positive constants p, q and initial points \({\tilde{\textbf{v}}}^{k+1}_1\), \({\tilde{\textbf{w}}}^{k+1}_1\), the FPPA is described as
From [24, 32], iteration (3.16) converges if \(\Vert \textbf{B}\Vert _2^2<pq\). Computing an exact value of the proximity operator of \(\psi \circ {{\textbf{B}}}\) requires executing infinite times of iteration (3.16). While, in practical implementation, iteration (3.16) can only be executed finite number of times. This means that we can only obtain an approximate surrogate of \({\tilde{\textbf{v}}}^{k+1}_*\). The error between \({\tilde{\textbf{v}}}^{k+1}_*\) and the approximation will influence the global error and thus appropriately choosing a stopping criterion for the inner loop is essential.
We next motivate the choice of the stopping criterion for the inner loop. To this end, we define
Note that for fixed \({\tilde{\textbf{u}}}^{k+1}\), \(H(\cdot ; {\tilde{\textbf{u}}}^{k+1})\) is a continuously differentiable convex function. From the definition of operator \(\mathscr {S}\), we observe that \(\tilde{\textbf{v}}_*^{k+1}\) is equal to
It is advantageous to have an equivalent form of (3.18). Recalling the definition of F, we define the optimization problem
For the sake of simplicity, we introduce the similarity notation of two functions. We say two functions f and g are similar if their difference is a constant and we write it as \(f \sim g\). Hence, if \(f \sim g\), then
Two minimization problems are said to be equivalent if they have the same set of global minimizers.
Lemma 4
The minimization problems (3.18) and (3.19) are equivalent.
Proof
From Lemma 3, the difference between \({\left\| {{\tilde{\textbf{u}}}^{k+1} - {{\textbf{D}}}\textbf{v}}\right\| }_2^2\) and \( {\left\| {\textbf{v} - {{\textbf{D}}}^{\top } {\tilde{\textbf{u}}}^{k+1}}\right\| }_2^2\) is \(\left( {\tilde{\textbf{u}}}^{k+1}\right) ^{\top }({{\textbf{I}}}- {{\textbf{D}}}{{\textbf{D}}}^{\top }) {\tilde{\textbf{u}}}^{k+1}\), which is a constant with respect to \(\textbf{v}\). Notice that the term \(\lambda {\left\| {\tilde{\textbf{u}}^{k+1}}\right\| }_0\) is also a constant with respect to \(\textbf{v}\). Hence,
By the definition of F, the minimization problems (3.18) and (3.19) are equivalent. \(\square \)
We next review the notion of the strictly convex function (see, for example, Chapters 8 and 11 of [2]). Let \(f: {{\mathbb {R}}}^d \rightarrow {{\mathbb {R}}}\cup \left\{ \infty \right\} \) be a proper function. A function f is strictly convex if
It is well-known that the minimizer of a proper strictly convex function is unique. We use \(\mathbb {N}\) to denote the set of all positive integers.
Lemma 5
Suppose that \(\alpha \in (0, 1]\) and \(\left\{ \left( \tilde{\textbf{u}}^{k}, {\tilde{\textbf{v}}}^{k}, \tilde{\textbf{v}}^{k}_{*}\right) \right\} _{k=1}^{\infty }\) is the sequence defined by (3.11)–(3.13). Let \(k\in {{\mathbb {N}}}\) be fixed.
-
(a)
If \({\left\| {{\tilde{\textbf{u}}}^{k+1} - {\tilde{\textbf{u}}}^{k}}\right\| }_2^2 + {\left\| {\nabla H({\tilde{\textbf{v}}}^{k}; {\tilde{\textbf{u}}}^{k+1})}\right\| }_2^2 = 0\), then \(({\tilde{\textbf{u}}}^k, {\tilde{\textbf{v}}}^k)\) is a fixed-point of (2.16)–(2.17).
-
(b)
If \({\left\| {{\tilde{\textbf{u}}}^{k+1} - {\tilde{\textbf{u}}}^{k}}\right\| }_2^2 + {\left\| {\nabla H({\tilde{\textbf{v}}}^{k}; {\tilde{\textbf{u}}}^{k+1})}\right\| }_2^2 > 0\), then either \({\left\| {{\tilde{\textbf{u}}}^{k+1} - \tilde{\textbf{u}}^{k}}\right\| }_2^2 >0\) or \({\left\| {{\tilde{\textbf{u}}}^{k+1} - \tilde{\textbf{u}}^{k}}\right\| }_2^2 = 0\) and
$$\begin{aligned} F({\tilde{\textbf{u}}}^{k+1}, {\tilde{\textbf{v}}}^k) > F({\tilde{\textbf{u}}}^{k+1}, {\tilde{\textbf{v}}}^{k+1}_*). \end{aligned}$$(3.20)
Proof
We first prove (a). The hypothesis of (a) is equivalent to \({\tilde{\textbf{u}}}^{k+1} = {\tilde{\textbf{u}}}^k\) and \(\nabla H({\tilde{\textbf{v}}}^k; {\tilde{\textbf{u}}}^{k+1}) = 0\). It follows from (3.11) with \({\tilde{\textbf{u}}}^{k+1} = {\tilde{\textbf{u}}}^k\) that
Since \(H(\cdot ; {\tilde{\textbf{u}}}^{k+1} )\) is a continuously differentiable convex function and \(\nabla H({\tilde{\textbf{v}}}^k; {\tilde{\textbf{u}}}^{k+1})=0\), we observe that \({\tilde{\textbf{v}}}^{k}\) is the global minimizer of problem (3.18). Since \(\psi \circ {{\textbf{B}}}\) is continuously differentiable, we have that \( {\tilde{\textbf{v}}}^k = \mathscr {S}\left( {{\textbf{D}}}^{\top } \tilde{\textbf{u}}^{k+1} \right) \). This together with \({\tilde{\textbf{u}}}^{k+1} = {\tilde{\textbf{u}}}^k\) yeilds that
Equations (3.21) and (3.22) show that \(({\tilde{\textbf{u}}}^k, \tilde{\textbf{v}}^k)\) is a fixed-point of (2.16)–(2.17).
We next establish (b). It suffices to show that \({\left\| {{\tilde{\textbf{u}}}^{k+1} - {\tilde{\textbf{u}}}^k}\right\| }_2^2 = 0\) implies the inequality (3.20). The hypothesis of (b) together with \({\left\| {{\tilde{\textbf{u}}}^{k+1} - \tilde{\textbf{u}}^k}\right\| }_2^2 = 0\) leads to \(\nabla H({\tilde{\textbf{v}}}^k; {\tilde{\textbf{u}}}^{k+1}) \ne 0\). On the other hand, \(\tilde{\textbf{v}}^{k+1}_*\) is the global minimizer of (3.18). Therefore, \(\nabla H({\tilde{\textbf{v}}}^{k+1}_*; \tilde{\textbf{u}}^{k+1}) = 0\), which implies that \({\tilde{\textbf{v}}}^{k+1}_{*} \ne {\tilde{\textbf{v}}}^k\). We next show (3.20). Noting that \({\tilde{\textbf{v}}}^{k+1}_*\) is the global minimizer of (3.18), Lemma 4 ensures that \( {\tilde{\textbf{v}}}^{k+1}_* = \text {argmin} \left\{ F({\tilde{\textbf{u}}}^{k+1}, \textbf{v}): \textbf{v} \in {{\mathbb {R}}}^m\right\} . \) By employing the identity in Lemma 3, we observe that
The convexity of \(\psi \) ensures that \(F({\tilde{\textbf{u}}}^{k+1}, \cdot )\) is strictly convex for any fixed \({\tilde{\textbf{u}}}^{k+1}\). Hence, the minimizer of \(F({\tilde{\textbf{u}}}^{k+1}, \cdot )\) is unique. Therefore, the fact \({\tilde{\textbf{v}}}^k \ne \tilde{\textbf{v}}^{k+1}_* \) leads to (3.20). \(\square \)
Now, we provide insights leading to the stopping criterion for the inner loop in the inexact algorithm to be described. Let \(\alpha \in (0, 1]\) and \(\left\{ \left( {\tilde{\textbf{u}}}^{k}, \tilde{\textbf{v}}^{k}, {\tilde{\textbf{v}}}^{k}_{*}\right) \right\} _{k=1}^{\infty }\) be the sequence defined by (3.11)–(3.13). We define a subset of \({{\mathbb {N}}}\) by
Lemma 6
Suppose that \(\alpha \in (0, 1]\), \(\left\{ \left( \tilde{\textbf{u}}^{k}, {\tilde{\textbf{v}}}^{k}, \tilde{\textbf{v}}^{k}_{*}\right) \right\} _{k=1}^{\infty }\) is the sequence defined by (3.11)–(3.13). Let \(\rho '\) be a given positive constant and \(\left\{ e^k\right\} _{k=1}^{\infty }\) a given sequence of positive numbers. If for each \(k \in \mathbb {K}\), \(\left\{ \textbf{x}^{k+1}_l\right\} _{l=1}^{\infty }\) is a sequence convergent to \({\tilde{\textbf{v}}}^{k+1}_*\), then there exists a positive integer \(L_{k}\) such that for all \(l \ge L_k\),
and
Proof
Let \(k\in \mathbb {K}\) be fixed. We first show inequality (3.24). Since \(\psi \) is continuous, so is \(F\left( {\tilde{\textbf{u}}}^{k+1}, \cdot \right) \). Because \(\left\{ \textbf{x}^{k+1}_l\right\} _{l=1}^{\infty }\) is a sequence convergent to \({\tilde{\textbf{v}}}^{k+1}_*\), we find that
From (b) of Lemma 5, we need to show (3.24) by considering two cases: (i) \({\left\| {{\tilde{\textbf{u}}}^{k+1} - {\tilde{\textbf{u}}}^k}\right\| }_2^2 >0\) and (ii) \({\left\| {{\tilde{\textbf{u}}}^{k+1} - \tilde{\textbf{u}}^k}\right\| }_2^2 = 0\) with (3.20). For case (i), by (3.26), there exists a positive integer \(L_{k,1}\) such that for all \(l \ge L_{k,1}\),
Since \({\tilde{\textbf{v}}}^{k+1}_*\) is the global minimizer of (3.18), it follows from Lemma 4 that
Adding the above inequality to inequality (3.27) yields inequality (3.24) for all \(l \ge L_{k_1}\). For case (ii), inequality (3.24) is equivalent to
It suffices to show (3.28) for all l greater than some positive integer. From inequality (3.20), \(F({\tilde{\textbf{u}}}^{k+1}, {\tilde{\textbf{v}}}^{k}) - F({\tilde{\textbf{u}}}^{k+1}, {\tilde{\textbf{v}}}^{k+1}_*)\) is positive. Therefore, equation (3.26) ensures that there exists a positive integer \(L_{k, 2}\) such that
for all \(l\ge L_{k, 2}\). This is equivalent to inequality (3.28) for all \(l \ge L_{k,2}\), which completes the proof of inequality (3.24).
We next show inequality (3.25). Since \({\tilde{\textbf{v}}}^{k+1}_*\) is the global minimizer of (3.18), \(\nabla H\left( {\tilde{\textbf{v}}}^{k+1}_*; {\tilde{\textbf{u}}}^{k+1}\right) = 0\). Noting that \(\psi \) is continuously differentiable, we conclude that \(\nabla H\left( \cdot ; {\tilde{\textbf{u}}}^{k+1}\right) \) is continuous. Again, because \(\left\{ \textbf{x}^{k+1}_l\right\} _{l=1}^{\infty }\) is a sequence convergent to \({\tilde{\textbf{v}}}^{k+1}_*\), we have that \(\lim _{l \rightarrow \infty }{\left\| {\nabla H\left( \textbf{x}^{k+1}_l; \tilde{\textbf{u}}^{k+1}\right) }\right\| }_2 = 0\). Consequently, the positivity of \(e^{k+1}\) ensures that there exists a positive integer \(L_{k,3}\) such that for all \(l\ge L_{k,3}\), inequality (3.25) holds true.
The proof is completed by choosing \(L_k:= \max \{L_{k,1}, L_{k,3}\}\) if \({\left\| {{\tilde{\textbf{u}}}^{k+1} - {\tilde{\textbf{u}}}^k}\right\| }_2^2 > 0\) and \(L_k:= \max \{L_{k,2}, L_{k,3}\}\) if \({\left\| {\tilde{\textbf{u}}^{k+1} - {\tilde{\textbf{u}}}^k}\right\| }_2^2 = 0\). \(\square \)
Inequalities (3.24) and (3.25) in Lemma 6 may be used as a stopping criterion for the inner loop iteration (3.16). Combining (3.11)–(3.12), iteration (3.16) for finding the proximity operator of \(\psi \circ {{\textbf{B}}}\), with the stopping criterion provided by Lemma 6, we obtain an executable inexact fixed-point proximity algorithm, for model (2.6). We summarize it in Algorithm 1.
Inexact fixed-point proximity algorithm for problem (2.6)
The next proposition confirms that Algorithm 1 is executable in the sense that it will generate a sequence \(\left\{ \left( {\tilde{\textbf{u}}}^k, \tilde{\textbf{v}}^k\right) \right\} _{k=1}^{\infty }\).
Proposition 2
Suppose that \(\psi \) is a proper, continuously differentiable, and bounded below convex function, \({{\textbf{B}}}\) is a \(p\times m\) matrix, \({{\textbf{D}}}\) is an \(n\times m\) matrix, and \(\lambda , \gamma \) are positive constants. If \(\alpha \in (0, 1]\) and \(\rho '\) is a positive constant, \(\left\{ e^k\right\} _{k=1}^{\infty }\) is a positive sequence, and \(pq > {\left\| {{{\textbf{B}}}}\right\| }_2^2\), then Algorithm 1 is executable.
Proof
To show the executability of Algorithm 1, it suffices to establish that for each \(k \in \mathbb {N}\), given \(\left( {\tilde{\textbf{u}}}^{k}, {\tilde{\textbf{v}}}^{k}\right) \), the pair \(({\tilde{\textbf{u}}}^{k+1}, {\tilde{\textbf{v}}}^{k+1})\) can be obtained within a finite number of iteration steps. Since the proximity operator of \({\left\| {\cdot }\right\| }_0\) has a closed form, \({\tilde{\textbf{u}}}^{k+1}\) in Line 2 of Algorithm 1 can be computed directly. If \({\left\| {{\tilde{\textbf{u}}}^{k+1} - {\tilde{\textbf{u}}}^{k}}\right\| }_2^2 + {\left\| {\nabla H({\tilde{\textbf{v}}}^{k}; {\tilde{\textbf{u}}}^{k+1})}\right\| }_2^2 > 0\), then Algorithm 1 will enter the do-while inner loop. Since \(pq > {\left\| {{{\textbf{B}}}}\right\| }_2^2\), it follows from Theorem 6.4 of [24] that the sequence \(\left\{ \tilde{\textbf{v}}^{k+1}_{l}\right\} _{l=1}^{\infty }\) generated by the inner loop converges to \({\tilde{\textbf{v}}}^{k+1}_*\). Hence, according to Lemma 6, we conclude that conditions (3.24) and (3.25) with \(\textbf{x}_l^{k+1}:=\tilde{\textbf{v}}_l^{k+1}\) are satisfied within a finite number l of steps. Therefore, \({\tilde{\textbf{v}}}^{k+1}\) can be computed within a finite number of the inner iterations. If \({\left\| {{\tilde{\textbf{u}}}^{k+1} - {\tilde{\textbf{u}}}^{k}}\right\| }_2^2 + {\left\| {\nabla H({\tilde{\textbf{v}}}^{k}; {\tilde{\textbf{u}}}^{k+1})}\right\| }_2^2 = 0\), then from Line 12 of Algorithm 1 we have that \({\tilde{\textbf{v}}}^{k+1} = {\tilde{\textbf{v}}}^k\). Thus, Algorithm 1 is executable. \(\square \)
Proposition 2 guarantees that Algorithm 1 will generate a sequence \(\left\{ \left( {\tilde{\textbf{u}}}^k, \tilde{\textbf{v}}^k\right) \right\} _{k=1}^{\infty }\), which is for sure to satisfy the conditions
and
These two inequalities will play a crucial role in convergence analysis, of Algorithm 1, which will be provided in the next section.
4 Convergence Analysis
In this section we analyze the convergence of the inexact fixed-point proximity algorithm. Specifically, we will show that a sequence \(\left\{ \left( {\tilde{\textbf{u}}}^k, \tilde{\textbf{v}}^k\right) \right\} _{k=1}^{\infty }\) generated by Algorithm 1 converges to a local minimizer of (2.6). Since the sequence \(\left\{ (\tilde{\textbf{u}}^{k}, {\tilde{\textbf{v}}}^{k})\right\} _{k=1}^{\infty }\) generated from Algorithm 1 is a sequence defined by (3.11)–(3.12) satisfying conditions (3.29) and (3.30), we shall study the convergence property of sequences defined by (3.11) and (3.12). For this purpose, we reformulate the iterations (3.11) and (3.12) as an inexact Picard sequence of a nonlinear map. We then show their convergence by studying the property of the map. Finally, we show the convergence property of inexact fixed-point proximity algorithm (Algorithm 1) based on the convergence of iterations (3.11) and (3.12).
We first state the main results of this section.
Theorem 1
Suppose that \(\psi \) is a proper, continuously differentiable, and bounded below convex function, \(\textbf{B}\) is a \(p \times m\) matrix, \(\textbf{D}\) is an \(n \times m\) matrix satisfying \(\textbf{D}^{\top }\textbf{D} = \textbf{I}\), \(\lambda \) and \(\gamma \) are positive constants, \(\alpha \in (0, 1)\), and the operator \(\mathscr {T}\) defined in (4.11) has at least one fixed-point. If \(p>0, q>0\), \(pq > {\left\| {{{\textbf{B}}}}\right\| }_2^2\), \(\rho ' \in \left( 0, \frac{\lambda }{\gamma }\frac{1 - \alpha }{\alpha }\right) \) and \(\sum _{k=1}^{\infty }e^{k+1}<\infty \), then \(\left\{ (\tilde{\textbf{u}}^k, {\tilde{\textbf{v}}}^k)\right\} _{k = 1}^{\infty }\) generated from Algorithm 1 converges to a local minimizer \((\textbf{u}^*, \textbf{v}^*)\) of problem (2.6).
This section is devoted to providing a proof for Theorem 1. To this end, we establish a number of preliminary results. Throughout this section, we assume without further mentioning that \(\psi : {{\mathbb {R}}}^p \rightarrow {{\mathbb {R}}}\) is a proper, continuously differentiable, and bounded below convex function, \({{\textbf{B}}}\) is a \(p \times m\) matrix, \({{\textbf{D}}}\) is an \(n \times m\) matrix satisfying \(\textbf{D}^{\top }\textbf{D} = \textbf{I}\), \(\lambda \) and \(\gamma \) are positive constants, and \(\alpha \in (0, 1)\).
Note that in Theorem 1, we assume that \(\alpha \in (0,1)\) even though Algorithm 1 may still converge for \(\alpha \) equal to 1 or slightly bigger than 1, see the numerical examples presented in Sect. 5. For \(\alpha \ge 1\), convergence of Algorithm 1 is not guaranteed since the technical proof presented in this section requires \(\alpha \in (0,1)\). Moreover, there are examples exhibiting divergence of Algorithm 1 when \(\alpha >1\).
We prepare for the proof of Theorem 1. The iterations (3.11) and (3.12) have two stages. Its first stage basically searches the support of the candidate sparse vectors \(\textbf{u}\), in model (2.6), which involve the \(\ell _0\)-norm. Once it is obtained, the support will remain unchanged in future iterations and thus, the original non-convex optimization problem (2.6) reduces to one with \(\textbf{u}\) restricted to the fixed support. The restricted optimization problem becomes convex since the term \(\lambda \Vert \textbf{u}\Vert _0\) reduces to a fixed number independent of \(\textbf{u}\). For this reason, the second stage of the iterations is to solve the resulting convex minimization problem.
We now show that the first N steps of iterations (3.11) and (3.12), for certain positive integer N, is to pursue a support of the sparse vector \(\textbf{u}\). By the definition of the proximity operator, the right hand side of (3.11) is
We establish an equivalent form of (4.1). To this end, we consider the optimization problem
Lemma 7
The minimization problems (4.1) and (4.2) are equivalent.
Proof
Expanding the quadratic term in the objective function of minimization problem (4.1), we have that
Note that multiplying an objective function by a constant will not change its minimizer. Recalling the definition of F, we find that the minimization problems (4.1) and (4.2) are equivalent. \(\square \)
We next investigate the sequence generated by (3.11)–(3.12) with inequality (3.29) satisfied.
Lemma 8
If the sequence \(\left\{ \left( {\tilde{\textbf{u}}}^k, \tilde{\textbf{v}}^k\right) \right\} _{k=1}^{\infty }\) generated by (3.11)–(3.12) satisfies inequality (3.29) with \(\rho ' \in \left( 0, \frac{\lambda }{\gamma }\frac{1-\alpha }{\alpha } \right) \), then
-
(a)
\(F\left( {\tilde{\textbf{u}}}^{k+1}, {\tilde{\textbf{v}}}^{k+1}\right) \le F\left( {\tilde{\textbf{u}}}^{k}, {\tilde{\textbf{v}}}^{k}\right) \) and \(\lim _{k \rightarrow \infty }F\left( {\tilde{\textbf{u}}}^k, \tilde{\textbf{v}}^k\right) \) exists;
-
(b)
\(\lim _{k \rightarrow \infty } {\left\| {{\tilde{\textbf{u}}}^{k+1} - \tilde{\textbf{u}}^k}\right\| }_{2} = 0\).
Proof
By the definition of the proximity operator, \(\tilde{\textbf{u}}^{k+1}\) is a global minimizer of (4.1). It follows from Lemma 7 that
Adding the above inequality to inequality (3.29) yields that
Noting that \(\lambda , \gamma \) are positive, \(\alpha \in (0, 1)\), and \(\rho ' \in \left( 0, \frac{\lambda }{\gamma }\frac{1-\alpha }{\alpha }\right) \), the second term on the left hand side of the above inequality is non-negative, which implies the inequality in part (a). Since F is bounded below, the inequality of part (a) leads to the existence of \(\lim _{k \rightarrow \infty }F\left( {\tilde{\textbf{u}}}^k, {\tilde{\textbf{v}}}^k\right) \). This completes the proof of part (a).
It remains to show part (b). The second statement of part (a) ensures that \(\lim _{k\rightarrow \infty }\left[ F({\tilde{\textbf{u}}}^k, {\tilde{\textbf{v}}}^k)-F({\tilde{\textbf{u}}}^{k+1},\tilde{\textbf{v}}^{k+1})\right] =0\). This together with (4.3) and the assumption \(\frac{\lambda }{\gamma }\frac{1- \alpha }{\alpha } - \rho '>0\) yields part (b). \(\square \)
Next, we show that the support of the inexact sequence \(\left\{ {\tilde{\textbf{u}}}^k\right\} _{k=1}^{\infty }\) will remain unchanged after a finite number of steps, which reduces finding a local minimizer of the non-convex optimization problem to solving a constrained convex optimization problem. We first review the support of a vector. For a positive integer n, let \(\mathbb {N}_n:=\{1, 2, \ldots , n\}\). For \(\textbf{x} \in {{\mathbb {R}}}^n\), we use \(S(\textbf{x})\) to denote the support of \(\textbf{x}\), which is defined as
Clearly, \(S(\textbf{x})\) is a subset of \(\mathbb {N}_n\). It is empty if all components of \(\textbf{x}\) are zeros and it is equal to \(\mathbb {N}_n\) if all components of \(\textbf{x}\) are nonzeros. It is known (for example, Lemma 3 of [37]) that if \(\textbf{u} \in \text {prox}_{t\Vert \cdot \Vert _0}(\textbf{x})\), \(\textbf{v} \in \text {prox}_{t\Vert \cdot \Vert _0}(\textbf{y})\), for \(\textbf{x}, \textbf{y} \in {{\mathbb {R}}}^n\), then
Proposition 3
If \(\left\{ \left( {\tilde{\textbf{u}}}^k, \tilde{\textbf{v}}^k\right) \right\} _{k = 1}^{\infty }\) is the sequence generated by (3.11)–(3.12) satisfying the condition (3.29) with \(\rho ' \in \left( 0, \frac{\lambda }{\gamma }\frac{1-\alpha }{\alpha } \right) \), then there exists a positive integer N such that \(S\left( \tilde{\textbf{u}}^k\right) = S\left( {\tilde{\textbf{u}}}^{N}\right) \) for all \(k\ge N\).
Proof
From Lemma 8, we have that \(\lim _{k \rightarrow \infty }{\left\| {{\tilde{\textbf{u}}}^{k+1} - \tilde{\textbf{u}}^{k}}\right\| }_2 = 0. \) Hence, there exists an integer N, such that
The above inequality together with (4.4) leads to \(S\left( {\tilde{\textbf{u}}}^{k+1}\right) = S\left( \tilde{\textbf{u}}^{k}\right) \) for all \(k\ge N\). This further ensures that \(S\left( {\tilde{\textbf{u}}}^k\right) = S\left( \tilde{\textbf{u}}^{N}\right) \) for all \(k\ge N\). \(\square \)
Proposition 3 reveals that the support of \({\tilde{\textbf{u}}}^k\) remains unchanged when \(k\ge N\) and it turns out that the influence of \({\left\| {\cdot }\right\| }_0\) does not exist anymore when \(k\ge N\). Throughout this section, we use \(C \subseteq \mathbb {N}_{n}\) to denote the unchanged support. Accordingly, the non-convex optimization problem (2.6) reduces to a convex one. To describe the resulting convex optimization problem, we need the notion of the indicator function. For a given index set \(\Lambda \subseteq \mathbb {N}_n\), we define the subspace of \({{\mathbb {R}}}^n\) by letting
and define the indicator function \(\delta _{\Lambda }: {{\mathbb {R}}}^n \rightarrow {{\mathbb {R}}}\cup \left\{ \infty \right\} \) as
We define a convex function by
Proposition 3 implies that when \(k\ge N\), the non-convex optimization problem (2.6) boils down to the convex optimization problem
Specifically, we have the next result which follows directly from Theorem 4.8 of [50].
Proposition 4
Suppose that \(\left( \textbf{u}^*, \textbf{v}^*\right) \in {{\mathbb {R}}}^n \times {{\mathbb {R}}}^m\) and \(S(\textbf{u}^*) = C\). The pair \(\left( \textbf{u}^*, \textbf{v}^*\right) \) is a local minimizer of minimization problem (2.6) if and only if \(\left( \textbf{u}^*, \textbf{v}^*\right) \) is a global minimizer of minimization problem (4.7).
From Proposition 4, finding a local minimizer of optimization problem (2.6) is equivalent to finding a global minimizer of optimization problem (4.7).
We now turn to showing that the inexact sequence \(\left\{ ({\tilde{\textbf{u}}}^k, {\tilde{\textbf{v}}}^k)\right\} _{k= N}^{\infty }\) converges to a local minimizer of optimization problem (2.6). To this end, we reformulate the sequence as an inexact Picard sequence of a nonlinear operator and then show the nonlinear operator has certain favorable property that guarantees convergence of a sequence generated from the operator. For a given index set \(\Lambda \subseteq \mathbb {N}_n\), we define the projection operator \(\mathscr {P}_{\Lambda }: {{\mathbb {R}}}^n \rightarrow \textbf{B}_{\Lambda }\) as
and the diagonal matrix \({{\textbf{T}}}_{\Lambda } \in {{\mathbb {R}}}^{n \times n}\) as
From the definition of the operator \(\mathscr {P}_{\Lambda }\) and the matrix \({{\textbf{T}}}_{\Lambda }\), we have that
We next express the proximity operator of the \(\ell _0\)-norm in terms of the linear transformation \({{\textbf{T}}}_C\). To this end, we recall that for \(\textbf{x}, \textbf{z} \in {{\mathbb {R}}}^n\), if \(\textbf{x} \in \text {prox}_{t{\left\| {\cdot }\right\| }_0}(\textbf{z})\), then \(\textbf{x} = \mathscr {P}_{S(\textbf{x})}(\textbf{z})\) (see, Lemma 5 of [48]).
Lemma 9
If \(k \ge N\) and \({\tilde{\textbf{u}}}^{k+1} \in \textrm{prox}_{\alpha \gamma {\left\| {\cdot }\right\| }_0}(\textbf{z}^k)\) where \(\textbf{z}^k:=(1 - \alpha ) {\tilde{\textbf{u}}}^{k} + \alpha {{\textbf{D}}}{\tilde{\textbf{v}}}^{k}\), then \({\tilde{\textbf{u}}}^{k+1} ={{\textbf{T}}}_{C}(\textbf{z}^k)\).
Proof
By the hypothesis of this lemma, according to Lemma 5 of [48], we see that \({\tilde{\textbf{u}}}^{k+1} = \mathscr {P}_{S({\tilde{\textbf{u}}}^{k+1})} (\textbf{z}^k)\). From Proposition 3, we have that \(S({\tilde{\textbf{u}}}^{k+1}) = C\) for all \(k\ge N\). Hence, \( {\tilde{\textbf{u}}}^{k+1} = \mathscr {P}_{C} (\textbf{z}^k). \) Combining this equation with (4.10) completes the proof of this lemma. \(\square \)
We next reformulate iterations (3.11)–(3.12) as an inexact Picard sequence of a nonlinear operator for \(k \ge N\). We define operator \(\mathscr {T}:{{\mathbb {R}}}^n\rightarrow {{\mathbb {R}}}^n\) by
Proposition 5
If \(\left\{ \left( {\tilde{\textbf{u}}}^k, \tilde{\textbf{v}}^k\right) \right\} _{k=N}^{\infty }\) is a sequence generated by (3.11)–(3.12), then
Proof
Suppose that sequence \(\left\{ \left( {\tilde{\textbf{u}}}^k, {\tilde{\textbf{v}}}^k\right) \right\} _{k=N}^{\infty }\) satisfies (3.11)–(3.12). It follows from (3.12) and (3.13) that
Since \(\left\{ \left( {\tilde{\textbf{u}}}^k, \tilde{\textbf{v}}^k\right) \right\} _{k=N}^{\infty }\) satisfies (3.11), according to Lemma 9, we obtain that
Substituting (4.13) into the right hand side of (4.14) and using the linearity of \({{\textbf{T}}}_{C}\), we observe that
We complete the proof by calling the definition of \(\mathscr {T}\). \(\square \)
The next proposition identifies the relation between a global minimizer of minimization problem (4.7) and a fixed-point of the operator \(\mathscr {T}\). We first review the notion of subdifferential [2]. The subdifferential of a convex function \(f:\mathbb {R}^d\rightarrow {{\mathbb {R}}}\cup \left\{ \infty \right\} \) at \(\textbf{x} \in {{\mathbb {R}}}^d\) is defined by
If f is a convex function on \({{\mathbb {R}}}^d\) and \(\textbf{x} \in {{\mathbb {R}}}^d\), then \(y \in \partial f(\textbf{x})\) if and only if \(\textbf{x} = \textrm{prox}_{f}(\textbf{x}+\textbf{y})\) (see, Proposition 2.6 of [32]). The proximity operator of the indicator function \(\delta _C\) defined in (4.5) may be expressed as the projection operator, that is,
Proposition 6
Suppose a pair \((\textbf{u}^*, \textbf{v}^*) \in {{\mathbb {R}}}^{n} \times {{\mathbb {R}}}^m\) is given. Then \((\textbf{u}^*, \textbf{v}^*)\) is a global minimizer of (4.7) if and only if \(\textbf{u}^*\) is a fixed-point of \(\mathscr {T}\) and
Proof
This proof is similar to that of Theorem 2.1 in [24]. From Proposition 16.8 and Corollary 16.48 of [2], for \(\textbf{u} \in {{\mathbb {R}}}^n, \textbf{v}\in {{\mathbb {R}}}^m\), we have that
The Fermat rule (see, Theorem 16.3 of [2]) yields that \((\textbf{u}^*, \textbf{v}^*)\) is a global minimizer of (4.7) if and only if
From the definition of the indicator function \(\delta _{C}\), we notice that
Hence, (4.17) is equivalent to
for the quantity \(\alpha \) appearing in (3.11). We then rewrite (4.19) as \( -\alpha (\textbf{u}^* - {{\textbf{D}}}\textbf{v}^*) \in \partial \delta _{C}(\textbf{u}^*), \) which is equivalent to \(\textbf{u}^* = \text {prox}_{\delta _{C}}\left( (1 - \alpha )\textbf{u}^* + \alpha {{\textbf{D}}}\textbf{v}^*\right) \), according to Proposition 2.6 of [32]. It follows from equations (4.15), (4.10) and the linearity of \({{\textbf{T}}}_C\) that
Simplifying the relation (4.18) and solving for \(\textbf{v}^*\), we can obtain (4.16). We then substitute (4.16) into the right hand side of (4.20) and get that
Thus, by the definition of \(\mathscr {T}\), \(\textbf{u}^*\) is a fixed-point of \(\mathscr {T}\). \(\square \)
According to Proposition 6, obtaining a global minimizer of problem (4.7) is equivalent to finding a fixed-point of \(\mathscr {T}\). We turn to considering the fixed-point of \(\mathscr {T}\). Proposition 5 shows that the sequence \(\left\{ {\tilde{\textbf{u}}}^k\right\} _{k = N}^{\infty }\) generated from iteration (4.12) is an inexact Picard sequence of \(\mathscr {T}\). Convergence of inexact Picard iterations of a nonlinear operator, studied in [11, 29, 35], may be guaranteed by the averaged nonexpansiveness of the nonlinear operator. Our next task is to show the operator \(\mathscr {T}\) is averaged nonexpansive.
We now review the notion of the averaged nonexpansive operators which may be found in [2]. An operator \(\mathscr {P}:{{\mathbb {R}}}^d\rightarrow {{\mathbb {R}}}^d\) is said to be nonexpansive if
An operator \(\mathscr {F}:{{\mathbb {R}}}^d\rightarrow {{\mathbb {R}}}^d\) is said to be averaged nonexpansive if there is \(\kappa \in (0, 1)\) and a nonexpansive operator \(\mathscr {P}\) such that \(\mathscr {F}= \kappa \mathscr {I} + (1 - \kappa ) \mathscr {P}\), where \(\mathscr {I}\) denotes the identity operator. We also say that \(\mathscr {F}\) is \(\kappa \)-averaged nonexpansive. It is well-known that for any proper lower semi-continuous convex function \(f:\mathbb {R}^d\rightarrow \mathbb {R} \cup \left\{ \infty \right\} \), its proximity operator \(\text {prox}_{f}\) is nonexpansive.
We now recall a general result, which concerns the convergence of the inexact Picard sequence
for \(\mathscr {F}:{{\mathbb {R}}}^d\rightarrow {{\mathbb {R}}}^d\). Its proof may be found in [11, 29]. See [35] for a special case.
Lemma 10
Suppose that \(\mathscr {F}:{{\mathbb {R}}}^d\rightarrow {{\mathbb {R}}}^d\) is averaged nonexpansive and has at least one fixed-point, \(\left\{ \textbf{z}^{k}\right\} _{k=1}^{\infty }\) is the sequence defined by (4.21), and \(\left\{ e^{k+1}\right\} _{k=1}^{\infty }\) is a positive sequence of numbers. If \({\left\| {\varvec{\varepsilon }^{k+1}}\right\| }_2 \le e^{k+1}\) for \(k \in \mathbb {N}\) and \(\sum _{k=1}^{\infty }e^{k+1} < \infty \), then \(\left\{ \textbf{z}^k\right\} _{k=1}^{\infty }\) converges to a fixed-point of \(\mathscr {F}\).
We next show that the operator \(\mathscr {T}\) defined by (4.11) is averaged nonexpansive. To this end, we make the following observation.
Lemma 11
The operator \(\mathscr {S} \circ {{\textbf{D}}}^{\top }\) is nonexpansive.
Proof
Since \(\frac{\gamma }{\lambda }\psi \circ {{\textbf{B}}}\) is continuously differentiable and convex, we have that
It follows from the convexity of \(\frac{\gamma }{\lambda }\psi \circ {{\textbf{B}}}\) that the operator \(\textrm{prox}_{\frac{\gamma }{\lambda }\psi \circ {{\textbf{B}}}}\) is nonexpansive. Therefore, the operator \(\mathscr {S}\) is also nonexpansive. That is, for \(\textbf{u}_1, \textbf{u}_2 \in {{\mathbb {R}}}^n\),
Using the fact that \({\left\| {{{\textbf{D}}}^{\top }}\right\| }_2 = 1\), we have that
The above two inequalities ensure that the operator \(\mathscr {S} \circ {{\textbf{D}}}^{\top }\) is nonexpansive. \(\square \)
Proposition 7
The operator \(\mathscr {T}\) defined by (4.11) is \(\frac{1-\alpha }{2}\)-averaged nonexpansive.
Proof
We write \(\mathscr {T}= \frac{1-\alpha }{2} \mathscr {I}+ \frac{1+\alpha }{2}\mathscr {T}_1\) with
and show that \(\mathscr {T}_1\) is nonexpansive. The definition of \(\mathscr {T}\) leads to that
Then, for any \(\textbf{u}_1, \textbf{u}_2\in \mathbb {R}^n\), it follows from the triangle inequality that
Since the matrix \(\textbf{T}_C\) is diagonal with diagonal entries being either 1 or 0, we find that the matrix \(2\textbf{T}_C- \textbf{I}\) is also diagonal with diagonal entries being either 1 or \(-1\). Therefore,
Noting that \({\left\| {{{\textbf{T}}}_C}\right\| }_2 \le 1\) and \({\left\| {{{\textbf{D}}}}\right\| }_2 = 1\), we obtain from (4.23)–(4.24) and Lemma 11 that
which proves that \(\mathscr {T}_1\) is nonexpansive. \(\square \)
We next establish convergence of the inexact fixed-point iterations (3.11)–(3.12) satisfying condition (3.29).
Proposition 8
Suppose that \(\left\{ \tilde{\varvec{\varepsilon }}^{k+1}\right\} _{k=1}^{\infty }\) is a predetermined sequence in \(\mathbb {R}^m\), \(\left\{ \left( {\tilde{\textbf{u}}}^k, \tilde{\textbf{v}}^k\right) \right\} _{k = 1}^{\infty }\) is the sequence generated by (3.11)–(3.12) satisfying condition (3.29) with \(\rho ' \in \left( 0, \frac{\lambda }{\gamma }\frac{1 - \alpha }{\alpha }\right) \), and the operator \(\mathscr {T}\) has at least one fixed-point. Let \(\left\{ e^{k+1}\right\} _{k=1}^{\infty }\) be a positive sequence of numbers. If \({\left\| { \tilde{\varvec{\varepsilon }}^{k+1}}\right\| }_2 \le e^{k+1}\) for \(k \in \mathbb {N}\) and \(\sum _{k= 1}^{\infty } e^{k+1} < \infty \), then \(\left\{ \left( {\tilde{\textbf{u}}}^k, \tilde{\textbf{v}}^k\right) \right\} _{k = 1}^{\infty }\) converges to a local minimizer \((\textbf{u}^*, \textbf{v}^*)\) of optimization problem (2.6) and \(S(\textbf{u}^*) = C\).
Proof
It suffices to show the convergence of \(\left\{ \left( \tilde{\textbf{u}}^k, {\tilde{\textbf{v}}}^k\right) \right\} _{k = N}^{\infty }\), where N is determined in Proposition 3. Proposition 5 recasts the sequence \(\left\{ \tilde{\textbf{u}}^k\right\} _{k = N}^{\infty }\) as an inexact Picard sequence (4.12) of \(\mathscr {T}\). By Proposition 7, \(\mathscr {T}\) is \(\frac{1-\alpha }{2}\)-averaged nonexpansive. Since \(\alpha \in (0, 1)\), \(\left\| {{\textbf{T}}}_{C}\right\| _2 \le 1\), and \(\left\| {{\textbf{D}}}\right\| _2 = 1\), we obtain that \(\left\| \alpha {{\textbf{T}}}_C{{\textbf{D}}}\tilde{\varvec{\varepsilon }}^k \right\| _2 \le \left\| {\tilde{\varvec{\varepsilon }}}^k \right\| _2\). Noting that the operator \(\mathscr {T}\) has at least one fixed-point, Lemma 10 ensures that \(\left\{ {\tilde{\textbf{u}}}^k\right\} _{k = N}^{\infty }\) converges to a fixed-point \(\textbf{u}^*\) of \(\mathscr {T}\), that is,
We next prove that \(\left\{ \tilde{\textbf{v}}^k\right\} _{k=N}^{\infty }\) converges to \(\mathscr {S}\left( {{\textbf{D}}}^{\top } \textbf{u}^{*} \right) \). Notice that by the triangle inequality, for each \(k\in \mathbb {N}\),
Combining definition (3.12) of \({\tilde{\textbf{v}}}^k\), Lemma 11, and the above inequality, we have that
According to the assumption that \({\left\| {\tilde{\varvec{\varepsilon }}^{k+1}}\right\| }_2 \le e^{k+1}\) for \(k \in \mathbb {N}\) and \(\sum _{k= 1}^{\infty } e^{k+1} < \infty \), we obtain that \(\lim _{k\rightarrow \infty }\left\| {\tilde{ \varvec{\varepsilon } }}^k\right\| _2=0\). This together with (4.25) and (4.26) yields that
That is, \(\left\{ {\tilde{\textbf{v}}}^k\right\} _{k=N}^{\infty }\) converges to \(\mathscr {S}\left( {{\textbf{D}}}^{\top } \textbf{u}^{*} \right) \).
According to Proposition 6, \((\textbf{u}^*, \textbf{v}^*)\) is a global minimizer of optimization problem (4.7). Proposition 3 shows that \(S({\tilde{\textbf{u}}}^k) = C\), for all \(k \ge N\). Hence, \(S( \textbf{u}^*) = C\). This combined with Proposition 4 guarantees that \((\textbf{u}^*, \textbf{v}^*)\) is a local minimizer of optimization problem (2.6). \(\square \)
Proposition 8 requires the condition \({\left\| {{\tilde{\varvec{\varepsilon }}}^{k+1}}\right\| }_2=\Vert \tilde{\textbf{v}}^{k+1}-{\tilde{\textbf{v}}}^{k+1}_*\Vert _2 \le e^{k+1}\), which is difficult to verify in general. This condition may be replaced by (3.30) due to the known estimate (see, Proposition 3 of [35])
Finally, we present the proof for Theorem 1.
Proof of Theorem 1
Note the sequence \(\left\{ ({\tilde{\textbf{u}}}^{k}, \tilde{\textbf{v}}^{k})\right\} _{k=1}^{\infty }\) generated from Algorithm 1 is a sequence defined by (3.11)–(3.12) satisfying conditions (3.29) and (3.30). The condition (3.30) together with inequality (4.27) implies
Noting that \(\lambda , \gamma \) are positive constants, we have that
Therefore, all conditions of Proposition 8 are satisfied. Hence, \(\left\{ \left( {\tilde{\textbf{u}}}^k, \tilde{\textbf{v}}^k\right) \right\} _{k = 1}^{\infty }\) converges to a local minimizer of optimization problem (2.6) and \(S(\textbf{u}^*) = C\). \(\square \)
5 Numerical Experiments
In this section, we present numerical experiments to demonstrate the effectiveness of the proposed inexact algorithm for solving the \(\ell _0\) models for three applications including regression, classification, and image deblurring. The numerical results verify the convergence of Algorithm 1 and explore the impact of the inner iterations within the algorithm. Furthermore, the numerical results validate the superiority of the solution obtained from the \(\ell _0\) model (2.6) solved by the proposed algorithm when compared to the solution from the \(\ell _1\) model (2.2), across all three examples.
All the experiments are performed on the First Gen ODU HPC Cluster with Matlab. The computing jobs are randomly placed on an X86_64 server with the computer nodes Intel(R) Xeon(R) CPU E5-2660 0 @ 2.20 GHz (16 slots), Intel(R) Xeon(R) CPU E5-2660 v2 @ 2.20 GHz (20 slots), Intel(R) Xeon(R) CPU E5-2670 v2 @ 2.50 GHz (20 slots), Intel(R) Xeon(R) CPU E5-2683 v4 @ 2.10 GHz (32 slots).
For the regression and classification models, we need a kernel as described in [25, 26]. In the two examples to be presented, we choose the kernel as
where \(\sigma \) will be specified later.
We will use Algorithm 1 to solve model (2.6) for the three examples. The model (2.2) has a convex objective function, and hence, it can be efficiently solved by many optimization algorithms. Here, we employ Algorithms 2 and 3 (described below) to solve (2.2) with \({{\textbf{D}}}\) being the identity matrix and \({{\textbf{D}}}\) being the tight framelet matrix [37] (or the first order difference matrix [32]), respectively.
Fixed-point proximity scheme for problem (2.2) with \({{\textbf{D}}}\) being identity matrix
Inexact fixed-point proximity scheme for problem (2.2)
Note that Algorithm 2 was proposed in [24, 32] and Algorithm 3 was introduced in [34]. According to [34], the sequence \(({\tilde{\textbf{v}}}^{k}, {\tilde{\textbf{w}}}^{k})\) generated from Algorithm 3 converges to a global minimizer of problem (2.2) if the condition \(\sum _{k=1}^{\infty }e^{k+1} < \infty \) is satisfied.
We choose the parameter in Algorithm 1
with \(\alpha , \lambda \), and \(\gamma \) to be specified. The parameter \(\lambda \) serves as the regularization parameter in models (2.6) and (2.2). If this parameter is set too large, it can lead to a decrease in prediction accuracy. Conversely, if it is set too small, the resulting solution may lack sparsity, potentially leading to overfitting. Thus, identifying an appropriate range for \(\lambda \) is crucial. Similarly, the parameter p in Algorithm 1 and Algorithm 2, where \(\frac{1}{p}\) serves as the step size, affects the speed of the algorithm. It is crucial to choose an appropriate step size in both algorithms for optimal performance.
The impact of the choice of the parameter \(\alpha \) in the exact fixed-point proximity algorithm (3.1)–(3.2) was numerically investigated in [37], revealing its influence on the convergence speed of the algorithm. We will also explore the effect of the parameter \(\alpha \) for the inexact fixed-point proximity algorithm (Algorithm 1). For the regression, classification, and Gaussian noise image deblurring problems, we test Algorithm 1 with different values of \(\alpha \), even those with which the algorithm is not guaranteed to converge (\(\alpha \ge 1\)). In the instances where the value of \(\alpha \) is greater than or equal to 1, we set the corresponding \(\rho '\) to be 0. Moreover, to explore the impact of the inner iteration in Algorithm 1, we design its two variants. In the first variant, the inner iteration is performed for only one iteration. In this variant, the generated sequence may not satisfy the conditions (3.29) and (3.30). We will use several sets of parameters to explore the convergence of this case. In the second variant, we increase the value of \(\rho '\) of Algorithm 1 in a way that it fails to satisfy the condition of Theorem 1. We will use a single set of parameters \(\lambda ,\gamma \) and only increase the value of \(\rho '\), testing it at 10, 100, and 1000 times the choice (5.2).
We adopt the following stopping criterion for all iteration algorithms tested in this study. For a sequence \(\left\{ \textbf{x}^k\right\} _{k=1}^{\infty }\) generated by an algorithm performed in this section, iterations are terminated if
where \(\textrm{TOL}\) denotes a prescribed tolerance value.
5.1 Regression
In this subsection, we consider solving the regression problem by using the \(\ell _0\) model. Specifically, we explore the convergence behavior of Algorithm 1 and the impact of its inner iterations and compare the numerical performance of the \(\ell _0\) model with that of the \(\ell _1\) model.
In our numerical experiment, we use the benchmark dataset “Mg” [10] with 1385 instances, each of which has 6 features. Among the instances, we take \(m:=1000\) of them as training samples and the remaining 385 instances as testing samples.
We describe the setting of regression as follows. Our goal is to obtain a function that regresses the data set \(\left\{ (\textbf{x}_j, y_j): j\in \mathbb {N}_m\right\} \subset \mathbb {R}^6 \times \mathbb {R}\) by using the kernel method detailed in [25, 26], where \(\textbf{x}_j\) is the input features and \(y_j\) is the corresponding label. In this experiment, we choose the kernel K as defined in (5.1) with \(\sigma := \sqrt{10}\) and \(d:=6\). The regression function \(f: {{\mathbb {R}}}^6 \rightarrow {{\mathbb {R}}}\) is then defined as
The coefficient vector \(\textbf{v} \in {{\mathbb {R}}}^m\) that appears in (5.4) is learned by solving the optimization problem
where \(\lambda , \gamma \) are positive constants and the fidelity term \(L_{\textbf {y}}: {{\mathbb {R}}}^m \rightarrow {{\mathbb {R}}}\) is defined as
Optimization problem (5.5) may be reformulated in the form of (2.6) by choosing
\(\textbf{B}:=\textbf{K}:=[K(\textbf{x}_j, \textbf{x}_k):j,k\in \mathbb {N}_m]\) and \(\textbf{D}:=\textbf{I}_{m}\).
The \(\ell _0\) model (2.6) and the \(\ell _1\) model (2.2) are solved by Algorithm 1 and Algorithm 2, respectively. For both of these algorithms, the parameters p and \(\lambda \) are varied within the range of \([10^{-1}, 10^3]\) and \([10^{-7}, 10^{-2}]\), respectively, and \(q: =(1+10^{-6}){\left\| {\textbf{B}}\right\| }_2^2/p\). In addition, for Algorithm 1, the parameter \(\gamma \) is varied within the range \([10^{-7}, 10^{-3}]\) and \(e^{k+1}:= M/k^2\) with \(M:=10^{16}\). The stopping criterion for Algorithm 1 (resp. Algorithm 2) is either when (5.3) is satisfied with \(\textbf{x}^k:= {\tilde{\textbf{u}}}^k\) (resp. \(\textbf{x}^k:= \textbf{v}^k\)) and \(\textrm{TOL}:=10^{-6}\), or when the maximum iteration count of \(10^{5}\) is reached.
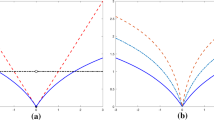
We first explore the effect of the parameter \(\alpha \) in convergence of Algorithm 1 by testing different values of \(\alpha \). Values of the objective function of model (2.6) against the number of iterations for the outer loop of Algorithm 1 with different values of \(\alpha \) are displayed in Fig. 1. We observe from Fig. 1a that for \(\alpha \in (0, 2]\), Algorithm 1 with a larger value of \(\alpha \) trends to produce a smaller value of the objective function. This suggests that for \(\alpha \in (0, 2]\), increasing the value of \(\alpha \) can accelerate the speed of convergence when implementing Algorithm 1. However, for \(\alpha > 2\), as shown in Fig. 1b, Algorithm 1 diverges. In the remaining part of this example, we choose \(\alpha :=0.99\) so that the hypothesis of Theorem 1 on the range of \(\alpha \) is satisfied, which guarantees convergence of Algorithm 1.
We then apply Algorithm 1 and its two variants to test their convergence for the \(\ell _0\) model. We use four sets of parameters for Algorithm 1 and the first variant, and a single set of parameters for the second variant. Figure 2a–c display values of the objective function generated from Algorithm 1, the first variant, and the second variant, respectively. Figure 2a confirms convergence of Algorithm 1 and Fig. 2b reveals divergence of the first variant. From Fig. 2c, we observe that a slight increase in \(\rho '\) maintains a convergence trend in the objective function value, but a significant increase, for example, changing it to \(1000 \times \rho '\), leads to divergence. These results demonstrate that the inclusion of the inner iteration is essential for effectively solving the \(\ell _0\) model. One conceivable explanation for this phenomenon could be that in the regression problem, the norm of \({{\textbf{B}}}\) in the objective function (2.5) is as large as 863, and thus even slight variations in the input variable can have a significant impact on the resulting objective function value. Therefore, the inner iteration is critical for controlling the error for each inexact step.
The effect of choices of parameter \(\alpha \) on convergence of Algorithm 1 for regression
Convergence of Algorithm 1 vs its first and second variants for regression: (a), (b) and (c) display objective function values generated from Algorithm 1, the first variant, and the second variant, respectively. In (c), we set \(\lambda , \gamma \), and p the values \(1.0\times 10^{-5}, 6.0\times 10^{-6} \), and 0.85, respectively
In Table 1, we compare the number of nonzero (NNZ) components of the solutions obtained by the \(\ell _0\) model and the \(\ell _1\) model, when they have comparable testing accuracy. It is clear from Table 1 that when the mean squared error on the testing dataset (\(\textrm{TeMSE}\)) falls within varying intervals, the \(\ell _0\) model consistently generates solutions sparser than those generated by the \(\ell _1\) model, with comparable mean squared errors on the training dataset (\(\textrm{TrMSE}\)).
5.2 Classification
In this subsection, we consider solving the classification problem by using the \(\ell _0\) model. Specifically, we investigate the convergence behavior and the impact of inner iterations on Algorithm 1 and compare the numerical performance of the \(\ell _0\) model with that of the \(\ell _1\) model.
In our numerical experiment, we use the handwriting digits from the MNIST database [22], which is composed of 60, 000 training samples and 10, 000 testing samples of the digits “0” through “9”. We consider classifying two handwriting digits “7” and “9” taken from MNIST. Handwriting digits “7” and “9” are often easy to cause obfuscation in comparison to other pairs of digits. We take \(m:=5,000\) instances as training samples and 2, 000 as testing samples of these two digits from the dataset. Specifically, we consider training data set \(\left\{ (\textbf{x}_j, y_j): j\in \mathbb {N}_m\right\} \subset \mathbb {R}^d \times \left\{ -1, 1\right\} \), where \(\textbf{x}_j\) are images of the digit 7 or 9.
The setting of classification is described as follows. Our goal is to find a function that separates the training data into two groups with label \(y_j:= 1\) (for digit 7) and \(y_j:=-1\) (for digit 9). We employ the kernel method to derive such a function, as detailed in [49]. We choose the kernel K as defined in (5.1) with \(\sigma :=4\) and \(d:=784\). The classification function \(f: {{\mathbb {R}}}^{784} \rightarrow \left\{ -1, 1\right\} \) is then defined as
where \(\text {sign}\) denotes the sign function, assigning \(-1\) for negative inputs and 1 for non-negative inputs. The coefficient vector \(\textbf{v} \in {{\mathbb {R}}}^m\) that appears in (5.7) is learned by solving the optimization
where \(\lambda , \gamma \) are positive constants and the fidelity term \(L_{\textbf {y}}: {{\mathbb {R}}}^m \rightarrow {{\mathbb {R}}}\) is defined as
Optimization problem (5.8) may be reformulated in the form of (2.6) by choosing
\(\textbf{D}:=\textbf{I}_{m}\) and \(\textbf{B}:=\textbf{Y}\textbf{K}\) where \(\textbf{K}:=[K(\textbf{x}_j,\textbf{x}_k):j,k\in \mathbb {N}_m]\) and \(\textbf{Y}:=\textrm{diag}(y_j:j\in \mathbb {N}_m)\).
The \(\ell _0\) model (2.6) and the \(\ell _1\) model (2.2) are solved by Algorithms 1 and 2, respectively.
For both of these algorithms, the parameter p is varied within the range [1, 100] and \(q:=(1+10^{-6}){\left\| {\textbf{B}}\right\| }_2^2/p\). For Algorithm 1, the parameters \(\lambda \) are varied within the range of [0.001, 1], while for Algorithm 2, it varies within [0.01, 5]. In addition, we vary the parameter \(\gamma \) within the range \([10^{-6}, 1]\) and fix \(e^{k+1}:= M/k^2\) with \(M:= 10^{16}\) for Algorithm 1.
We first investigate the impact of the parameter \(\alpha \) on convergence of Algorithm 1 by testing it with various values of \(\alpha \) and display the results in Fig. 3. When \(\alpha \) falls within the range (0, 1), increasing its value accelerates the algorithm’s convergence speed. However, for \(\alpha \in (1, 2)\), speed-up of convergence when further increasing \(\alpha \) becomes limited. Notably, Algorithm 1 diverges when \(\alpha \ge 3.5\). To adhere the theoretical requirement \(\alpha \in (0, 1)\) as established in Theorem 1, the same as in the regression problem, we set \(\alpha :=0.99\) in the rest of this example.
The effect of choices of parameter \(\alpha \) on convergence of Algorithm 1 for classification
We then apply Algorithm 1 and its two variants to solve the \(\ell _0\) model for classification, maintaining the same stopping criterion as used in the previous subsection. Figure 4a–c display objective function values generated from Algorithm 1, the first variant, and the second variant, respectively. The observed behavior closely resembles that of the previous example, with the key distinction that for the first variant, the objective function value converges for certain parameters and diverges for others. The numerical results demonstrate the critical importance of the inner iteration in solving the \(\ell _0\) model, primarily due to the norm of \({{\textbf{B}}}\) being 592.
We compare the solution of the \(\ell _0\) model solved by Algorithm 1 with that of the \(\ell _1\) model solved by Algorithm 2. The stopping criteria for both of these algorithms remains consistent with that in the previous subsection, except for adjusting \(\textrm{TOL}\) to \(10^{-4}\) and setting a maximum iteration count of \(5\times 10^4\). In Table 2, we compare NNZ and the accuracy on the training dataset (TrA) of the solutions obtained from the \(\ell _0\) model and the \(\ell _1\) model when they have the same accuracy on the testing dataset (TeA). We observe from Table 2 that the solutions of the \(\ell _0\) model have almost half NNZ compared to those of the \(\ell _1\) model, and the \(\ell _0\) model produces a higher TrA value compared to the \(\ell _1\) model. In Table 3, we compare TeA and TrA of the solutions obtained from the \(\ell _0\) model and the \(\ell _1\) model when they have comparable NNZ. We see from Table 3 that the solution of the \(\ell _0\) model has slightly better accuracy on the testing set and about one percent superior on the training set.
Convergence of Algorithm 1 vs its first and second variants for classification: (a), (b) and (c) display objective function values generated from Algorithm 1, the first variant, and the second variant, respectively. In (c), we set \(\lambda , \gamma \), and p the values \(9.0\times 10^{-3}, 1.0\times 10^{-3} \), and 1, respectively
5.3 Image Deblurring
In this subsection, we consider the \(\ell _0\) model solved by Algorithm 1 applied to image deblurring. Specifically, we compare performance of models (2.6) and (2.2) for image deblurring for images contaminated with two different types of noise: the Gaussian noise and the Poisson noise. We present numerical results obtained by using the \(\ell _0\) model with those obtained by using two \(\ell _1\) models, which will be described precisely later. Again, we study the impact of the inner iteration on Algorithm 1 when applied to image deblurring. In this regard, we present only the Gaussian noise case since the Poisson noise case is similar.
In our numerical experiments, we choose six clean images of “clock” with size \(200 \times 200\), “barbara” with size \(256 \times 256\), “lighthouse”, “airplane”, and “bike” with size \(512 \times 512\), and “zebra” with size \(321 \times 481\), shown in Fig. 5. Each tested image is converted to a vector \(\textbf{v}\) via vectorization. The blurred image is modeled as
where \(\textbf{x}\) denotes the observed corrupted image, \({{\textbf{K}}}\) is the motion blurring kernel matrix, and \(\mathscr {P}\) is the operation that describes the nature of the measurement noise and how it affects the image acquisition. The matrix \({{\textbf{K}}}\) is generated by the MATLAB function “fspecial” with the mode being motion, the angle of the motion blurring being 45 and the length of the motion blurring (“MBL”) varying from 9, 15, 21 and all blurring effects are generated by using the MATLAB function “imfilter” with symmetric boundary conditions [20]. We choose the operator \(\mathscr {P}\) as the Gaussian noise or the Poisson noise. The quality of a reconstructed image \(\widetilde{ \textbf{v}}\) obtained from a specific model is evaluated by the peak signal-to-noise ratio (PSNR)
Clean images
5.3.1 Gaussian Noise Image Deblurring
In this case, we choose the operation \(\mathscr {P}\) as the Gaussian noise, and model (5.10) becomes
where \(\mathscr {N}(\varvec{\mu }, \sigma ^2 \textbf{I})\) denotes the Gaussian noise with mean \(\varvec{\mu }\) and covariance matrix \(\sigma ^2 \textbf{I}\). The clean images are first blurred by the motion blurring kernel matrix and then contaminated by the Gaussian noise with standard deviation \(\sigma := 3\). The resulting corrupted images are shown in Fig. 6. Given an observed image \(\textbf{x} \in {{\mathbb {R}}}^m\), the function \(\psi \) in all three models is chosen to be
The matrix \({{\textbf{B}}}\) appearing in both models (2.6) and (2.2) is specified as the motion blurring kernel matrix \({{\textbf{K}}}\). Models (2.6) and (2.2) with \({{\textbf{D}}}\) being the tight framelet matrix constructed from discrete cosine transforms of size \(7\times 7\) [37] are respectively referred to as “L0-TF” and “L1-TF”. Model (2.2) with \({{\textbf{D}}}\) being the first order difference matrix [32] is referred to as “L1-TV”.
Corrupted images with MBL being 21 and Gaussian noise
The L0-TF model is solved by Algorithm 1, while both the L1-TF and L1-TV models are solved by Algorithm 3. In all three models, the parameter \(\lambda \) is adjusted within the interval [0.01, 2]. For the L0-TF model, we vary the parameter \(\gamma \) within the interval [0.1, 6], while maintaining fixed values of \(p:= 0.1\), \(q:=(1+10^{-6}) \times 4 /p\), and \(e^{k+1}:= M/k^2\) with \(M:= 10^{6}\) in Algorithm 1. For both the L1-TF and L1-TV models, the parameter \(p_1 = p_2\) is varied within the interval [0.01, 1] and \(q_2:=(1+10^{-6}) \times 4/p_2\), while \(q_1:=(1+10^{-6})/p_1\) for the L1-TF model and \(q_1:=(1+10^{-6}) \times 8 /p_1\) for the L1-TV model. Additionally, we set \(e^{k+1}:= M/k^2\) in Algorithm 3, where \(M:= 10^{8}\) for the L1-TF model and \(M:=10^{7}\) for the L1-TV model. The stopping criterion for both algorithms is when (5.3) is satisfied with \(\textbf{x}^k:= {\tilde{\textbf{v}}}^k\) and \(\textrm{TOL}:=10^{-5}\).
The effect of choices of parameter \(\alpha \) on convergence of Algorithm 1 for the Gaussian noise image deblurring problem of the image “clock” (a) and “barbara” (b)
We explore the effect of \(\alpha \) in Algorithm 1 for images ‘clock’ and ‘barbara’ by testing different values of \(\alpha \) and display the results in Fig. 7. As observed in Fig. 7, when the value of \(\alpha \) is close to 1, Algorithm 1 tends to yield smaller objective function values over the same number of iterations. Figure 8 provides zoomed-in views of values of the objective function for the last 800 iterations for the images of ‘clock’ and ‘barbara’, with \(\alpha :=1.00, 1.01\). While Algorithm 1 converges for both the \(\alpha \) values for the image ‘clock’, it appears that it converges for \(\alpha :=1\) but diverges for \(\alpha :=1.01\) for the ‘barbara’ image. These numerical results confirm the condition \(\alpha \in (0, 1)\) for convergence of Algorithm 1 established in Theorem 1. Consequently, we set \(\alpha :=0.99\) in the rest of this example to ensure convergence of Algorithm 1.
Zoomed-in views of the objective function values generated by Algorithm 1 with \(\alpha :=1.00, 1.01\) for the Gaussian noise image deblurring problem of the image “clock” (a, b) and “barbara” (c, d)
We then apply Algorithm 1 and the first variant to solve the L0-TF model. Figure 9a and b depict objective function values generated from Algorithm 1 and its first variant, respectively, while Fig. 9c and d illustrate the PSNR values of images reconstructed by Algorithm 1 and its first variant, respectively. Figure 9a confirms convergence of Algorithm 1 for all six tested images with values of parameters \(\lambda \) and \(\gamma \) displayed. Figure 9b shows that the objective function values generated from the first variant exhibit significant oscillation for the first 90 steps of iteration, followed by a convergence trend. These observations are also reflected in the PSNR value as depicted in Fig. 9c and d. The numerical results show that the significance of the inner iteration is limited for image deblurring problems, due to the fact that the norm of matrix \(\textbf{B}\) is not greater than 2.
We list in Table 4 the highest PSNR values for each of the reconstructed images, with the corresponding values of parameters \(\lambda \), \(\gamma \), p and \(p_1\) showed in Table 5. The results in Table 4 consistently demonstrate that the L0-TF model achieves the highest PSNR-value, surpassing the second-highest value by approximately 1 dB. For visual comparison, we display the deblurred images in Figs. 10 and 11. One can see that the L0-TF model is more powerful to suppress noise on smooth areas compared to the L1-TF and L1-TV models. In Fig. 12, comparison of two specific local areas in the zebra image is presented. We observe from Fig. 12 that the deblurred images obtained from the L0-TF model preserve finer details and edges more effectively than those obtained from the other two models.
Exploring the convergence of Algorithm 1 for image deblurring problems. (a) and (b) depict the function values, while (c) and (d) illustrate the PSNR values for Algorithm 1 and its first variant, respectively
Gaussian noise image deblurring: Deblurred images (clock, barbara, lighthouse) from corrupted images with MBL being 21
Gaussian noise image deblurring: Deblurred images (airplane, bike, zebra) from corrupted images with MBL being 21
Gaussian noise image deblurring: Deblurred local zebra images from the corrupted images with MBL being 21. The second, third, and fourth columns correspond to the deblurred local zebra images obtained from L0-TF, L1-TF, and L1-TV, respectively
5.3.2 Poisson Noise Image Deblurring
In this case, we choose the operation \(\mathscr {P}\) as Poisson noise [23, 47, 52], and model (5.10) becomes
where \(\text {Poisson}(\textbf{c})\) denotes a Poisson distributed random vector with mean \(\textbf{c}\). We generate a corrupted image in three steps: First, we scale a clean image to achieve a preset peak value, denoted as \(\text {MAX}_{\textbf{v}}\), which determines the level of Poisson noise. Second, we apply a motion blurring kernel to the scaled image. Third, we introduce Poisson noise to the blurred image. In this experiment, we set \(\text {MAX}_{\textbf{v}}\) to be 255. The resulting six corrupted images are shown in Fig. 13. Given an observed corrupted image \(\textbf{x} \in {{\mathbb {R}}}^{p}\), the function \(\psi \) appearing in (2.6) is chosen as
We specify the matrix \({{\textbf{B}}}\) appearing in both models (2.6) and (2.2) to be the motion blurring kernel matrix \({{\textbf{K}}}\). Models (2.6) and (2.2) with \({{\textbf{D}}}\) being the same tight framelet matrix constructed from discrete cosine transforms of size \(7\times 7\) [37] are respectively referred to as “L0-TF” and “L1-TF”. Model (2.2) with \({{\textbf{D}}}\) being the first order difference matrix [32] is referred to as “L1-TV”.
Corrupted images with MBL being 21 and Poisson noise
Poisson noise image deblurring: Deblurred images (clock, barbara, lighthouse) with MBL being 21
Poisson noise image deblurring: Deblurred images (airplane, bike, zebra) with MBL being 21
Poisson noise image deblurring: Deblurred local zebra images from the corrupted images with MBL being 21. The second, third, and fourth columns correspond to the restored local zebra images obtained from L0-TF, L1-TF, and L1-TV, respectively
The L0-TF model is solved by Algorithm 1, while both the L1-TF and L1-TV models are solved by Algorithm 3. In all the three models, the parameter \(\lambda \) is adjusted within the range [0.001, 1]. For the L0-TF model, we vary the parameter \(\gamma \) within the range [0.01, 10] and p within the range [0.0001, 0.1], while set q to \((1+10^{-6}) \times 4 /p\) and \(\alpha \) to 0.99 in Algorithm 1. For both the L1-TF and L1-TV models, the parameter \(p_1 = p_2\) is varied within the range [0.001, 1] and \(q_2:=(1+10^{-6}) \times 4/p_2\), while \(q_1:=(1+10^{-6})/p_1\) for L1-TF model and \(q_1:=(1+10^{-6}) \times 8 /p_1\) for L1-TV model. Additionally, we set \(e^{k+1}:= M/k^{1.01}\) in both algorithms with \(M=10^{8}\). The stopping criterion for the two algorithms is when (5.3) is satisfied with \(\textbf{x}^k:= {\tilde{\textbf{v}}}^k\) and \(\textrm{TOL}:=10^{-5}\), or when the maximum iteration counts of 2000 is attained.
We show in Table 6 the highest PSNR values for each of the reconstructed images, with the corresponding values of parameters \(\lambda \), \(\gamma \), p and \(p_1\) listed in Table 7. The results in Table 6 demonstrate that the L0-TF model achieves the highest PSNR-value, surpassing the second-highest value by approximately 0.6 dB expect for the ‘barbara’ image, where the PSNR-values of the L0-TF model are comparable with those of the L1-TF model. For visual comparison, we display the deblurred images in Figs. 14 and 15. One can see that the L0-TF model is more powerful to suppress noise on smooth areas compared with the L1-TF and L1-TV models. In Fig. 16, we compare performance of the three models on two specific local areas in the zebra image and observe that the images restored from the L0-TF model preserve finer details and edges more effectively than those from the other two models.
In summary, the numerical experiments presented above all confirm the convergence of the proposed inexact algorithm and demonstrate the superiority of the \(\ell _0\) regularization over the \(\ell _1\) regularization, in both approximation accuracy and sparsity. The numerical results also confirm that the importance of the inner iteration in the proposed inexact algorithm depends on the magnitude of the norm of the matrix \(\textbf{B}\) that appears in the objective function (2.5). In the case of regression and classification problems, inner iterations are crucial due to the norm of matrix \(\textbf{B}\) exceeding 500, while in deblurring problems, the significance of inner iterations is limited as the norm of matrix \(\textbf{B}\) is not greater than 2. The numerical results consistently verified that increasing the value of \(\alpha \) can speed up convergence of the proposed algorithm when \(\alpha \) falls within the range (0, 1), which is guaranteed by Theorem 1. While for \(\alpha >1\), the impact of \(\alpha \) on the algorithm varies depending on a specific application.
6 Conclusion
The theoretical study and numerical experiments conducted in this paper have shown that the proposed inexact fixed-point proximity algorithms are effective for solving sparse regularization models involving the \(\ell _0\)-norm. The proposed inexact algorithm incorporates an inner iteration for the evaluation of the proximity operator of a convex function composed with a linear transformation. We have shown convergence of the proposed inexact algorithm to a local minimizer of the \(\ell _0\) model under the hypothesis that the sequence of the numerical errors of the inner iteration is \(\ell _1\) summable. The analysis is performed through analyzing the convergence of the related convex optimization problem, constrained on the support of the sparse solution, with applying the theory of non-expansive operators.
We have applied the proposed algorithm to solve the problems of regression, classification, and image deblurring. Numerical experiments show that the proposed inexact fixed-point proximity algorithm can effectively solve the \(\ell _0\) models, leading to convergent solutions, which exhibit either higher sparsity or accuracy than those obtained from solving the related \(\ell _1\) models. In particular, numerical results for the regression problem demonstrate that the local minimizer obtained using our proposed algorithm for the \(\ell _0\) model has higher sparsity while maintaining similar accuracy, compared to the global minimizer of the related \(\ell _1\) model. The inexact algorithm for the \(\ell _0\) models displays elevated sparsity and accuracy for the classification problem, and improved image restoration quality for the image deblurring problem, when compared to the related \(\ell _1\) models. The numerical examples also demonstrate that the inner iteration plays a crucial role in regression and classification problems, while it has a limited impact on image deblurring problems, depending on the magnitude of the norm of the matrix \(\textbf{B}\) in the objective function.
The proposed algorithm significantly broadens the applicability of the exact fixed-point proximity algorithm. The convergence analysis methodology employed in this study may be extendable to other sparse regularization problems involving the \(\ell _0\) norm.
Data Availability
The computer codes that generate the numerical results presented in this paper can be found in the following website: https://github.com/msyan2023/InexactFPPA-L0.
References
Attouch, H., Bolte, J., Svaiter, B.F.: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward–backward splitting, and regularized Gauss–Seidel methods. Math. Program. 137, 91–129 (2013). https://doi.org/10.1007/s10107-011-0484-9
Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. Springer, New York (2011)
Beck, A.: First-Order Methods in Optimization. SIAM, Philadelphia (2017)
Boche, H., Calderbank, R., Kutyniok, G., Vybíral, J.: A survey of compressed sensing. In: Compressed Sensing and its Applications, pp. 1–39. Springer, New York (2015)
Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 3(1), 1–122 (2011). https://doi.org/10.1561/2200000016
Candes, E., Tao, T.: Decoding by linear programming. IEEE Trans. Inf. 51, 4203–4215 (2005). https://doi.org/10.1109/TIT.2005.858979
Candes, E.J., Tao, T.: Near-optimal signal recovery from random projections: Universal encoding strategies? IEEE Trans. Inf. 52, 5406–5425 (2006). https://doi.org/10.1109/TIT.2006.885507
Chambolle, A., Pock, T.: A first-order primal–dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 40, 120–145 (2011). https://doi.org/10.1007/s10851-010-0251-1
Chan, R.H., Riemenschneider, S.D., Shen, L., Shen, Z.: Tight frame: an efficient way for high-resolution image reconstruction. Appl. Comput. Harmon. Anal. 17, 91–115 (2004). https://doi.org/10.1016/j.acha.2004.02.003
Chang, C.C., Lin, C.J.: LIBSVM: a library for support vector machines. ACM Trans. Intell. 2, 1–27 (2011). https://doi.org/10.1145/1961189.1961199
Combettes*, P.L.: Solving monotone inclusions via compositions of non-expansive averaged operators. Optimization 53, 475–504 (2004). https://doi.org/10.1080/02331930412331327157
Courant, R.: Variational methods for the solution of problems of equilibrium and vibrations. Bull. Am. Math. 49, 1–23 (1943). (https://api.semanticscholar.org/CorpusID:16547277)
Daubechies, I.: Ten Lectures on Wavelets. SIAM, Philadelphia (1992)
Donoho, D.L.: Compressed sensing. IEEE Trans. Inf. 52, 1289–1306 (2006). https://doi.org/10.1109/TIT.2006.871582
Elad, M., Aharon, M.: Image denoising via learned dictionaries and sparse representation. In: 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), vol. 1, pp. 895–900. IEEE (2006). https://doi.org/10.1109/CVPR.2006.142
Fan, J., Li, R.: Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 96, 1348–1360 (2001). https://doi.org/10.1198/016214501753382273
Gabay, D., Mercier, B.: A dual algorithm for the solution of nonlinear variational problems via finite element approximation. Comput. Math. Appl. 2(1), 17–40 (1976)
Garey, M.R., Johnson, D.S.: Computers and intractability. A guide to the theory of NP-completeness. J. Symb. Log. 48 (1983). https://doi.org/10.2307/2273574
Glowinski, R., Marroco, A.: Sur l’approximation, par éléments finis d’ordre un, et la résolution, par pénalisation-dualité d’une classe de problèmes de dirichlet non linéaires. Revue française d’automatique, informatique, recherche opérationnelle. Analyse numérique 9(R2), 41–76 (1975)
Hansen, P.C., Nagy, J.G., O’leary, D.P.: Deblurring Images: Matrices, Spectra, and Filtering. SIAM, Philadelphia (2006)
Kurdyka, K.: On gradients of functions definable in o-minimal structures. In: Annales de l’institut Fourier, vol. 48, pp. 769–783 (1998)
LeCun, Y., Bottou, L., Bengio, Y., Haffner, P.: Gradient-based learning applied to document recognition. Proc. IEEE. 86, 2278–2324 (1998). https://doi.org/10.1109/5.726791
Lefkimmiatis, S., Unser, M.: Poisson image reconstruction with Hessian Schatten-norm regularization. IEEE Trans. Image Process. 22(11), 4314–4327 (2013)
Li, Q., Shen, L., Xu, Y., Zhang, N.: Multi-step fixed-point proximity algorithms for solving a class of optimization problems arising from image processing. Adv. Comput. Math. 41, 387–422 (2015). https://doi.org/10.1007/s10444-014-9363-2
Li, Z., Song, G., Xu, Y.: A fixed-point proximity approach to solving the support vector regression with the group lasso regularization. Int. J. Numer. Anal. Model. 15, 154–169 (2018)
Li, Z., Song, G., Xu, Y.: A two-step fixed-point proximity algorithm for a class of non-differentiable optimization models in machine learning. J. Sci. Comput. 81, 923–940 (2019). https://doi.org/10.1007/s10915-019-01045-7
Li, Z., Xu, Y., Ye, Q.: Sparse support vector machines in reproducing kernel Banach spaces. In: Contemporary Computational Mathematics—A Celebration of the 80th Birthday of Ian Sloan, pp. 869–887. Springer (2018)
Lian, Q., Shen, L., Xu, Y., Yang, L.: Filters of wavelets on invariant sets for image denoising. Appl. Anal. 90, 1299–1322 (2011). https://doi.org/10.1080/00036811.2010.490524
Liang, J., Fadili, J., Peyré, G.: Convergence rates with inexact non-expansive operators. Math. Program. 159, 403–434 (2016). https://doi.org/10.1007/s10107-015-0964-4
Lojasiewicz, S.: Une propriété topologique des sous-ensembles analytiques réels. Les équations aux dérivées partielles 117, 87–89 (1963)
Mallat, S.: A Wavelet Tour of Signal Processing. Elsevier, Amsterdam (1999)
Micchelli, C.A., Shen, L., Xu, Y.: Proximity algorithms for image models: denoising. Inverse Probl. 27, 045009 (2011). https://doi.org/10.1088/0266-5611/27/4/045009
Natarajan, B.K.: Sparse approximate solutions to linear systems. SIAM J. Comput. 24, 227–234 (1995)
Ren, J., Xu, Y.: Inexact fixed-point iterations with applications to convex optimization (2023, preprint)
Rockafellar, R.T.: Monotone operators and the proximal point algorithm. SIAM J. Control. Optim. 14, 877–898 (1976). https://doi.org/10.1137/0314056
Ron, A., Shen, Z.: Affine systems in\({L}_2(\mathbb{R} ^d)\): the analysis of the analysis operator. J. Funct. Anal. 148, 408–447 (1997). https://doi.org/10.1006/jfan.1996.3079
Shen, L., Xu, Y., Zeng, X.: Wavelet inpainting with the \(\ell _0\) sparse regularization. Appl. Comput. Harmon. Anal. 41, 26–53 (2016). https://doi.org/10.1016/j.acha.2015.03.001
Shen, L., Xu, Y., Zhang, N.: An approximate sparsity model for inpainting. Appl. Comput. Harmon. Anal. 37(1), 171–184 (2014). https://doi.org/10.1016/j.acha.2013.11.002
Solodov, M.V., Svaiter, B.F.: A hybrid approximate extragradient-proximal point algorithm using the enlargement of a maximal monotone operator. Set-Valued Anal. 7, 323–345 (1999). https://doi.org/10.1023/A:1008777829180
Song, G., Zhang, H., Hickernell, F.J.: Reproducing kernel Banach spaces with the \(\ell _1\) norm. Appl. Comput. Harmon. Anal. 34, 96–116 (2013)
Strang, G.: The discrete cosine transform. SIAM Rev. 41, 135–147 (1999)
Suter, B.W.: Multirate and Wavelet Signal Processing. Academic Press, San Diego (1998)
Tan, Z., Eldar, Y.C., Beck, A., Nehorai, A.: Smoothing and decomposition for analysis sparse recovery. IEEE Trans. Signal Process. 62(7), 1762–1774 (2014). https://doi.org/10.1109/TSP.2014.2304932
Villa, S., Salzo, S., Baldassarre, L., Verri, A.: Accelerated and inexact forward–backward algorithms. SIAM J. Optim. 23, 1607–1633 (2013). https://doi.org/10.1137/110844805
Wang, Y., Yang, J., Yin, W., Zhang, Y.: A new alternating minimization algorithm for total variation image reconstruction. SIAM J. Imaging Sci. 1(3), 248–272 (2008)
Wang, Y., Yin, W., Zeng, J.: Global convergence of ADMM in nonconvex non-smooth optimization. J. Sci. Comput. 78, 29–63 (2019)
Willett, R.M., Harmany, Z.T., Marcia, R.F.: Poisson image reconstruction with total variation regularization. In: 2010 Proceedings of the IEEE International Conference on Image Processing, pp. 4177–4180. IEEE (2010)
Wu, T., Xu, Y.: Inverting incomplete Fourier transforms by a sparse regularization model and applications in seismic wavefield modeling. J. Sci. Comput. 92, 1–35 (2022)
Xu, Y.: Sparse machine learning in Banach spaces. Appl. Numer. Math. 187, 138–157 (2023). https://doi.org/10.1016/j.apnum.2023.02.011
Xu, Y.: Sparse regularization with the \(\ell _0\) norm. Anal. Appl. 21, 901–929 (2023). https://doi.org/10.1142/S0219530522500105
Zeng, X., Shen, L., Xu, Y.: A convergent fixed-point proximity algorithm accelerated by FISTA for the \(\ell _0\) sparse recovery problem. In: International Conference on Imaging. Vision and Learning Based on Optimization and PDEs, pp. 27–45. Springer, New York (2016)
Zheng, W., Li, S., Krol, A., Schmidtlein, C.R., Zeng, X., Xu, Y.: Sparsity promoting regularization for effective noise suppression in SPECT image reconstruction. Inverse Probl. 35(11), 115011 (2019). https://doi.org/10.1088/1361-6420/ab23da
Zou, H.: The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 101, 1418–1429 (2006). https://doi.org/10.1198/016214506000000735
Funding
Y. Xu is supported in part by the US National Science Foundation under Grants DMS-1912958 and DMS-2208386, and by the US National Institutes of Health under Grant R21CA263876.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fang, R., Xu, Y. & Yan, M. Inexact Fixed-Point Proximity Algorithm for the \(\ell _0\) Sparse Regularization Problem. J Sci Comput 100, 58 (2024). https://doi.org/10.1007/s10915-024-02600-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-024-02600-7
Keywords
- Inexact fixed-point proximity algorithm
- Non-convex optimization
- The \(\ell _0\) norm
- Sparse regularization