Double Negation as Minimal Negation

Abstract

N. Kamide introduced a pair of classical and constructive logics, each with a peculiar type of negation: its double negation behaves as classical and intuitionistic negation, respectively. A consequence of this is that the systems prove contradictions but are non-trivial. The present paper aims at giving insights into this phenomenon by investigating subsystems of Kamide’s logics, with a focus on a system in which the double negation behaves as the negation of minimal logic. We establish the negation inconsistency of the system and embeddability of contradictions from other systems. In addition, we attempt at an informational interpretation of the negation using the dimathematical framework of H. Wansing.

1 Introduction

In Kamide (2017) introduced the systems IP and CP, which are variants of the intuitionistic system of constructible falsity N4 (Almukdad & Nelson, 1984) and its classical extension B$^{\rightarrow }_{4}$ (Odintsov, 2005). The difference between these systems is that a doubly negated formula $\mathord {\sim }\mathord {\sim }A$ in IP and CP corresponds to the intuitionistic/classically negated formula $\lnot A$, instead of A. In this sense, the negation $\mathord {\sim }$ is closely related to a type of connective called demi-negation, introduced by Humberstone (1995). The negation is also studied algebraically by Paoli (2019), who introduced another system with $\mathord {\sim }$ in a different language. Later, it was pointed out by Omori and Wansing (2018, 2022) that these systems prove a formula A as well as its negation $\mathord {\sim }A$. That is to say, IP and CP contain provable contradictions. Consequently, they are negation inconsistent but non-trivial systems. Their paper also offers a defence of reading $\mathord {\sim }$ as negation, by referring to A. Avron’s view (Avron, 2005) that a negation represents the falsehood in the sense that a negated formula is true iff its negand is false. In addition, Omori and Wansing suggest that the double negation can be understood as representing the phenomenon of negative concord in natural languages.

Given this kind of view, Kamide’s systems appear to be of interest from both formal and philosophical perspectives. When it comes to the former aspect, one essential task is to identify the source of negation inconsistency of the systems. One natural methodology for this would be to look into subsystems of IP in which the negation has more restricted properties.

In this paper, we shall first observe that the negation inconsistency still holds when the double negation is made to correspond to the negation of minimal logic (Johansson, 1937), with a system we shall call MP. In addition, we shall see that provable contradictions in CP can be embedded to provable contradictions in the weak system. We then investigate further the method of obtaining provable contradictions via translation, by turning our attention into P. Ruet’s quarter turn operation (Ruet, 1996).

This is followed by the observation concerning some subsystems of MP. We will observe the effects of restricting axiom schemata into rules on negation inconsistency.

Finally, we shall attempt at giving an interpretation of the negation in MP which complements the interpretation in Omori and Wansing (2018) for IP and CP. One characteristic of minimal negation is that it behaves like an implication to a propositional variable that does not have to exhibit a ‘negative’ property such as never being forced in a world of a Kripke model. This lack of a ‘negative’ flavour gives a more philosophical motivation to consider a negation whose double negation behaves as a minimal negation. It allows an interpretation of the double negation that is more ‘positive’, and so closer to usual kinds of negations which are better understood. We shall in particular attempt to understand MP from a more constructive and informational point of view, by employing the dimathematic perspective of Wansing (Wansing, 2022). For this purpose, we shall give a ‘positive’ interpretation of the double negation, according to which the support of falsity of $\mathord {\sim }A$ is equated with the regularity that the support of truth of A must be a strong one. We shall also discuss a modification to the semantic clause motivated by this interpretation, and how it fares with the negation inconsistency.

2 Minimal Variant of IP

Let $\textsf{PROP}=\{p_{i}:i\in {\mathbb {N}}\}$ be a set of propositional variables, and $()^{'}$ be a mapping which assigns for each $p_{i}$ another propositional variable $(p_{i})'$ in such a way that $\textsf{PROP}':=\{(p_{i})':i\in {\mathbb {N}}\}$ is a set distinct from $\textsf{PROP}$. We shall use $p,q,r,\ldots$ and $p',q',r',\ldots$ as the metavariables of the elements of $\textsf{PROP}$ and $\textsf{PROP}'$. In what follows, we shall use the next three propositional languages.

We shall use $\equiv$ for the literal identity of formulas. The first language $\mathcal {L}_{\mathord {\sim }}$ is the main language we shall consider. $\mathcal {L}_{\lnot }$ is a language with intuitionistic/minimal negation as well as duplicate propositional variables, which will be used for some arguments via translation. $\mathcal {L}_{\mathord {\circlearrowleft }}$ will be used for systems with the quarter turn operator. In each of the languages, we will use the abbreviations $A\leftrightarrow B$ for $(A\rightarrow B)\wedge (B\rightarrow A)$, $\circ ^{i+1} A$ for $\circ (\circ ^{i}A)$ and $\circ ^{0}A$ for A where $\circ \in \{\mathord {\sim },\lnot ,\mathord {\circlearrowleft }\}$. The complexity $\vert A\vert$ of formulas is inductively defined as follows:

where $\circ \in \{\wedge ,\vee ,\rightarrow \}$.

2.1 Sequent Calculi

The systems CP and IP are introduced in Kamide (2017) as sequent calculi. We introduce our system MP following the paradigm of these systems. One point to notice in these calculi is that $\Gamma ,\Delta ,\ldots$ will denote finite sets of formulas, rather than finite multisets as is often the case with sequent calculi.

Definition 1

(MP) The system MP in $\mathcal {L}_{\mathord {\sim }}$ is defined by the following rules.

where $i\in \{1,2\}.$

We shall write $\textbf{MP}\vdash \Gamma \Rightarrow C$ when a sequent $\Gamma \Rightarrow C$ is derivable following the rules of MP. In particular, we shall write $\textbf{MP}\vdash \ \Rightarrow C$ when $\Gamma =\emptyset$. Similar conventions apply for other systems in the paper.

For a system L and a rule (R), L-(R) will denote the system obtained by eliminating (R) from the rules of L. We say a rule is admissible in L, if the derivability of the premises in L implies that of the conclusion. In particular, a rule is derivable if a derivation of the conclusion is obtainable by continuing from any derivations of the premises.

We can readily check that $\textbf{MP}\text {-(Cut)}\vdash A,\Gamma \Rightarrow A$. Also, the system IP is defined in the following way.

Definition 2

(IP) The system IP is definable from MP by (i) replacing ($\mathord {\sim }\mathord {\sim }1$) and ($\mathord {\sim }\mathord {\sim }2$) with (L$\mathord {\sim }\mathord {\sim }$), (R$\mathord {\sim }\mathord {\sim }$) below; (ii) adding the next structural rule (RW).

Proposition 1

If $\textbf{MP}\vdash \Gamma \Rightarrow C$ then $\textbf{IP}\vdash \Gamma \Rightarrow C$.

Proof

It suffices to check that ($\mathord {\sim }\mathord {\sim }1$) and ($\mathord {\sim }\mathord {\sim }2$) are derivable in IP. The former case is immediate, and for the latter case, if $\textbf{IP}\vdash A,\Gamma \Rightarrow \mathord {\sim }\mathord {\sim }A$ then by applying (L$\mathord {\sim }\mathord {\sim }$), (R$\mathord {\sim }\mathord {\sim }$) to A, (L$\mathord {\sim }\mathord {\sim }$) and finally (R$\mathord {\sim }\mathord {\sim }$) to $\mathord {\sim }^{4}A$, we obtain $\textbf{IP}\vdash \Gamma \Rightarrow \mathord {\sim }^{6} A$. Also, $\textbf{IP}\vdash \mathord {\sim }^{6}A\Rightarrow \mathord {\sim }\mathord {\sim }A$ by a similar argument. Thus by (Cut) $\textbf{IP}\vdash \Gamma \Rightarrow \mathord {\sim }\mathord {\sim }A$. $\square$

In order to establish some results later, we need to look into minimal logic as well. For the sequent calculus formalisation of minimal logic, we shall use the following system, based on Bílková and Colacito (2020) and Colacito et al. (2017, Proposition 2) but again using finite sets rather than finite multisets.

Definition 3

(LM) The system LM in $\mathcal {L}_{\lnot }$ is defined by (Ax),¹ (Cut)–(R$\rightarrow$) and the following rules.

Theorem 2

(Cut) is admissible in IP-(Cut) and LM-(Cut).

Proof

Respectively see Kamide (2017, Theorem 11) and Colacito (2020, Theorem 4.1). In the latter case, it is not difficult to check that the difference in the presentation, namely that the antecedent of sequents is a finite set rather than a finite multiset, does not affect the structure of the argument. $\square$

Then the admissibility of (Cut) for MP-(Cut) can be obtained similarly to that of IP-(Cut), using an argument via translation.

Definition 4

We define a translation f of formulas in $\mathcal {L}_{\mathord {\sim }}$ into those of $\mathcal {L}_{\lnot }$ by the following clauses:

where $\circ \in \{\wedge ,\vee ,\rightarrow \}$.

This translation justifies the view that a double negation in MP represents minimal negation. In what follows, given a finite set $\Gamma$ we shall use the notation $f(\Gamma )$ for the set $\{f(A):A\in \Gamma \}$: similar conventions apply for later translations as well.

Theorem 3

The following statements hold.

• 1. $\textbf{MP}\vdash \Gamma \Rightarrow A$ if and only if $\textbf{LM}\vdash f(\Gamma )\Rightarrow f(A)$.

• 2. MP-(Cut)$\vdash \Gamma \Rightarrow A$ if and only if $\textbf{LM}\text {-(Cut)}\vdash f(\Gamma )\Rightarrow f(A)$.

• 3. (Cut) is admissible in $\textbf{MP}$-(Cut).

Proof

Analogous to Kamide (2017, Theorem 1–3). $\square$

One corollary of this theorem is the disjunction property, which indicates the constructivity of the system.

Corollary 4

If $\textbf{MP}\vdash \ \Rightarrow A\vee B$ then either $\textbf{MP}\vdash \ \Rightarrow A$ or $\textbf{MP}\vdash \ \Rightarrow B$.

Proof

Consider a proof of $\Rightarrow A\vee B$ in MP-(Cut). Then the last rule applied must be (R$\vee$), whose premise has either the form $\Rightarrow A$ or $\Rightarrow B$. $\square$

2.2 Hilbert-Style System and Semantics

We next introduce a Hilbert-style system for MP, which is obtained simply by combining the ones for IP (Omori & Wansing, 2018) and minimal logic.

Definition 5

(H-MP) The following axiomatisation defines the calculus H-MP.

where $i\in \{1,2\}$. A derivation of A from a set of formulas $\Gamma$ is a finite sequence $B_{1},\ldots , B_{n}\equiv A$, where each $B_{i}$ is either an element of $\Gamma$, an instance of one of the axiom schemata, or obtained from the preceding entries by a rule (in this case, (MP)). The derivability of A from $\Gamma$ in H-MP is denoted by $\Gamma \vdash _{h} A$. Then by straightforwardly modifying (Omori & Wansing, 2018, Proposition 3.11, 3.12), we can show the following.

Theorem 5

Let $\Gamma$ be a finite set. Then $\Gamma \vdash _{h} A$ if and only if $\textbf{MP}\vdash \Gamma \Rightarrow A$.

For semantics, a Kripke semantics for MP is obtained from those of IP (Kamide, 2017; Omori & Wansing, 2018) and minimal logic by Segerberg (1968).

Definition 6

(Kripke semantics for MP) We define a frame to be a triple $(W,\le ,Q)$ where W is a non-empty set, $\le$ is a partial ordering on W, and $Q\subseteq W$ is an upward closed set, i.e. $w\in Q$ and $w'\ge w$ implies $w'\in Q$.

A model then is a pair $(\mathcal {F},\mathcal {V})$ where $\mathcal {F}$ is a frame and $\mathcal {V}$ assigns a pair of upward closed sets $\mathcal {V}^{+}(p)$ and $\mathcal {V}^{-}(p)$ to each propositional variable p. $\mathcal {V}$ is extended to forcings ($\Vdash ^{+}, \Vdash ^{-}$) of all formulas by the next clauses.

We write $\Gamma \vDash A$ if for any model and $w\in W$, $w\Vdash ^{+} B$ for all $B\in \Gamma$ implies $w\Vdash ^{+} A$.

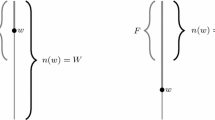
The last equivalence might appear mysterious; in fact, the right hand side just mirrors the condition for negation in minimal logic. Later in section 7, we shall discuss how the use of Q in MP enables an informal interpretation of the negation that is not available in IP.

Lemma 6

(upward closure) For $*\in \{+,-\}$, if $w\Vdash ^{*}A$ and $w'\ge w$ then $w'\Vdash ^{*}A$.

Proof

By induction on the complexity of A. In particular, if A is $\mathord {\sim }B$ and $w'\ge w$, then $w\Vdash ^{-}\mathord {\sim }B$ implies $x\Vdash ^{+}B\Rightarrow x\in Q$ for all $x\ge w$ and a fortiori for all $x\ge w'$. Thus $w'\Vdash ^{-}\mathord {\sim }B$. $\square$

Then the relationship between the Hilbert-style system and the semantics can be established in a standard manner.

Theorem 7

(completeness) $\Gamma \vdash _{h} A$ if and only if $\Gamma \vDash A$.

Proof

The left-to-right direction is shown by induction on the depth of derivations. For the converse direction, the outline is as in the case for IP (Omori & Wansing, 2018, Theorem 3.9).² We can likewise construct a canonical model $((W,\le ,Q),\mathcal {V})$, where:

• $(W,\le )$ is a set of collections of formulas ordered by $\le :=\{(\Sigma ,\Delta )\in W\times W:\Sigma \subseteq \Delta \}$, and each $\Sigma \in W$ satisfies:

  • there is A such that $A\notin \Sigma$

  • if $\Sigma \vdash _{h} A$ then $A\in \Sigma$.

  • if $A\vee B\in \Sigma$ then $A\in \Sigma$ or $B\in \Sigma$.

• $Q=\{\Sigma :\mathord {\sim }^{2} A,\mathord {\sim }^{4} A\in \Sigma \text { for some }A.\}$.

• $\Sigma \in \mathcal {V}^{+}(p)$ iff $p\in \Sigma$.

• $\Sigma \in \mathcal {V}^{-}(p)$ iff $\mathord {\sim }p\in \Sigma$.

It is immediate that Q is upward closed. We also have to check that:

$$\begin{aligned} \Sigma \Vdash ^{+}A&\text { if and only if }&A\in \Sigma .\\ \Sigma \Vdash ^{-}A&\text { if and only if }&\mathord {\sim }A\in \Sigma . \end{aligned}$$

Here we consider the latter equivalence for the case A is $\mathord {\sim }B$. By I.H. $\Sigma \Vdash ^{-}\mathord {\sim }B$ if and only if $\forall {\Delta \ge \Sigma }(B\in \Delta \Rightarrow \exists {C}(\mathord {\sim }^{2}C,\mathord {\sim }^{4}C\in \Delta ))$. We need to check this is equivalent to $\mathord {\sim }\mathord {\sim }B\in \Sigma$. For the forward direction, we show the contrapositive. If $\mathord {\sim }\mathord {\sim }B\notin \Sigma$, then $B\rightarrow \mathord {\sim }\mathord {\sim }B\notin \Sigma$. Now we can argue along (Omori & Wansing, 2018, Lemma 3.8) to conclude that there is $\Delta \in W$ s.t. $\Delta \supseteq \Sigma$, $B\in \Delta$ and $\mathord {\sim }\mathord {\sim }B\notin \Delta$. But then, using the fact that $\vdash _{h}(D\wedge \mathord {\sim }^{2}D)\rightarrow \mathord {\sim }^{2}E$ follows from $\vdash _{h}D\rightarrow (E\rightarrow D)$ and $\vdash _{h}(E\rightarrow D)\rightarrow (\mathord {\sim }^{2}D\rightarrow \mathord {\sim }^{2}E)$, we see $\mathord {\sim }^{2} C,\mathord {\sim }^{4}C\in \Delta$ implies $\mathord {\sim }^{2} B\in \Delta$, a contradiction. Hence $\lnot \forall {\Delta \ge \Sigma }(B\in \Delta \Rightarrow \exists {C}(\mathord {\sim }^{2}C,\mathord {\sim }^{4}C\in \Delta ))$. For the backward direction, if $\mathord {\sim }\mathord {\sim }B\in \Sigma$ and $B\in \Delta \supseteq \Sigma$, then $\mathord {\sim }^{2}B,\mathord {\sim }^{4}B\in \Delta$, as required.

Now if $\Gamma \nvdash _{h} A$, then there is (arguing like (Omori & Wansing, 2018, Lemma 3.7)) $\Gamma ' \supseteq \Gamma$ in the canonical model such that $A\notin \Gamma '$. Therefore $\Gamma '\nvDash A$. $\square$

3 Provable Contradictions in MP

As is mentioned in the introduction, (Omori & Wansing, 2018) observed that the systems CP and IP prove contradictions, and thus are negation inconsistent. We shall observe in this section that MP satisfies the same property. To be more precise, we shall say a formula A is a provable contradiction in a sequent calculus if the sequents $\Rightarrow A$ and $\Rightarrow \mathord {\sim }A$ are derivable. When it is a Hilbert-style system, then A being a provable contradiction will mean that both A and $\mathord {\sim }A$ are derivable.³

We will often appeal to the derivability of the sequents below, which correspond to well-known equivalences in minimal logic.

Proposition 8

The following sequents are derivable in MP.

• $\ \Rightarrow \mathord {\sim }^{4}(A\wedge B)\leftrightarrow (\mathord {\sim }^{4}A\wedge \mathord {\sim }^{4}B)$

• $\ \Rightarrow \mathord {\sim }^{4}(A\vee B)\leftrightarrow \mathord {\sim }^{4}(\mathord {\sim }^{4}A\vee \mathord {\sim }^{4}B)$

• $\ \Rightarrow \mathord {\sim }^{4}(A\rightarrow \mathord {\sim }^{4}B)\leftrightarrow (\mathord {\sim }^{4}A\rightarrow \mathord {\sim }^{4}B)$

In Omori and Wansing (2018), $\mathord {\sim }^{5} (A\wedge \mathord {\sim }\mathord {\sim }A)$ is given as an example of provable contradiction for IP. The same formula can be used to show the negation inconsistency of MP.

Proposition 9

$\mathord {\sim }^{5} (A\wedge \mathord {\sim }^{2} A)$ is a provable contradiction in MP.

Proof

We need to show that $\textbf{MP}\vdash \ \Rightarrow \mathord {\sim }^{5} (A\wedge \mathord {\sim }\mathord {\sim }A)$ and $\textbf{MP}\vdash \ \Rightarrow \mathord {\sim }^{6} (A\wedge \mathord {\sim }\mathord {\sim }A)$. For the former:

For the latter (where a double line indicates a repeated application of a rule):

$\square$

Hence the formula $\mathord {\sim }^{5} (A\wedge \mathord {\sim }^{2} A)$ is in a sense not a provable contradiction that is characteristic of IP. A natural question then is whether there is a contradiction that is provable in IP but not in MP.

Proposition 10

$\mathord {\sim }^{3}(\mathord {\sim }^{2}(A\rightarrow A)\rightarrow B)$ is a provable contradiction in IP.

Proof

It suffices to show that $\textbf{IP}\vdash \ \Rightarrow \mathord {\sim }^{3}(\mathord {\sim }^{2}(A\rightarrow A)\rightarrow B)$ and $\textbf{IP}\vdash \ \Rightarrow \mathord {\sim }^{4}(\mathord {\sim }^{2}(A\rightarrow A)\rightarrow B)$. For the former:

For the latter:

$\square$

Proposition 11

$\textbf{MP}\nvdash \ \Rightarrow \mathord {\sim }^{4}(\mathord {\sim }^{2}(A\rightarrow A)\rightarrow B)$.

Proof

By Theorem 3, if the sequent is provable then so is $\ \Rightarrow \lnot \lnot (\lnot (p\rightarrow p)\rightarrow q)$ in LM, which is known not to be the case.⁴$\square$

The observations above confirm that MP is strong enough to be a non-trivial negation inconsistent system. Where, however, does the contra-classicality⁵ come from? The relative weakness of minimal negation enables us to give the following explanation to this question. We may observe (in the manner of (Colacito, 2016, Proposition 1.2.5)) that we do not lose the strength of the system by replacing ($\mathord {\sim }\mathord {\sim }1$) with the rule:

It is straightforward to check that ($\mathord {\sim }\mathord {\sim }1$) is derivable from ($\mathord {\sim }\mathord {\sim }2$) and ($\mathord {\sim }\mathord {\sim }3$). One difference between ($\mathord {\sim }\mathord {\sim }1$) and ($\mathord {\sim }\mathord {\sim }3$) is that the latter rule is admissible in a classical sequent calculus when $\mathord {\sim }$ is identified with the classical negation. Thus in this alternative formulation, the cause of the contra-classicality is isolated to ($\mathord {\sim }\mathord {\sim }2$) alone.

4 Embedding Provable Contradictions

So far we have looked at provable contradictions in IP and MP on a more or less individual basis. Another, more general way to obtain provable contradictions in IP and MP is to appeal to negative translations extended to treat $\mathord {\sim }$. Using this method, we shall observe that MP proves, in a sense, as many contradictions as CP. We start with recalling CP and the Glivenko-like theorem in Kamide (2017), which embeds the theorems of CP into those of IP.

Definition 7

(CP) The system CP in $\mathcal {L}_{\mathord {\sim }}$ is defined by (Ax), (Ax$\mathord {\sim }$) and the following rules.

Glivenko’s theorem (Glivenko, 1998) states that if A is a classical theorem, then $\lnot \lnot A$ is an intuitionistic theorem. The Glivenko-like theorem (Kamide, 2017, Theorem 19) similarly states the following.

Theorem 12

$\textbf{CP}\vdash \ \Rightarrow A$ if and only if $\textbf{IP}\vdash \ \Rightarrow \mathord {\sim }^{4}A$.

This immediately implies that provable contradictions on CP can be embedded into IP.

Corollary 13

If A is a provable contradiction in CP, then $\mathord {\sim }^{4}A$ is a provable contradiction in IP.

The question is whether we can have a similar result with respect to MP. While the Glivenko-like theorem cannot be extended to MP, it is possible to extend the Gödel-Gentzen-like theorem, also considered by Kamide.

Definition 8

(Gödel-Gentzen-like translation) We define a translation h of formulas in $\mathcal {L}_{\mathord {\sim }}$ into itself by the following clauses.

where $\circ \in \{\wedge ,\rightarrow \}$.

Lemma 14

$\textbf{MP}\vdash \mathord {\sim }^{4}h(A)\Rightarrow h(A)$.

Proof

By induction on the complexity of A. For cases where h(A) has the form $\mathord {\sim }\mathord {\sim }B$, the statement follows from $\textbf{MP}\vdash \mathord {\sim }^{6}B\Rightarrow \mathord {\sim }^{2}B$. When $A\equiv B\rightarrow C$, use the derivability of $\mathord {\sim }^{4}(h(B)\rightarrow h(C))\Rightarrow h(B)\rightarrow \mathord {\sim }^{4}h(C)$ and (by I.H.) $\mathord {\sim }^{4}h(C)\Rightarrow h(C)$. For other cases, use the equivalence for conjunction in Proposition 8 via (Cut). $\square$

Given a finite set $\Gamma$ of formulas, we define $\mathord {\sim }\Gamma :=\{\mathord {\sim }A:A\in \Gamma \}$. Then we have the following lemma.

Lemma 15

If $\textbf{CP}\vdash \Gamma \Rightarrow \Delta$ then $\textbf{MP}\vdash h(\Gamma ),\mathord {\sim }^{2}h(\Delta )\Rightarrow \mathord {\sim }^{2}(p\rightarrow p)$.

Proof

By induction on the depth of derivation in CP. $\square$

Theorem 16

$\textbf{CP}\vdash \ \Rightarrow A$ if and only if $\textbf{MP}\vdash \ \Rightarrow h(A)$.

Proof

For the left-to-right direction, by Lemma 15 if $\textbf{CP}\vdash \ \Rightarrow A$ then $\textbf{MP}\vdash \mathord {\sim }\mathord {\sim }h(A)\Rightarrow \mathord {\sim }\mathord {\sim }(p\rightarrow p)$. Thus by ($\mathord {\sim }\mathord {\sim }1$), $\textbf{MP}\vdash \mathord {\sim }^{4}(p\rightarrow p)\Rightarrow \mathord {\sim }^{4}h(A)$. Apply (Cut) and Lemma 14 to conclude $\textbf{MP}\vdash \Rightarrow h(A)$. The right-to-left direction is obtained by showing $\textbf{CP}\vdash h(A)\Rightarrow A$; see also (Kamide, 2017, Lemma 10, Theorem 20). $\square$

The translation h is not sufficient to embed provable contradictions in CP into provable contradictions in MP. For instance, while $\mathord {\sim }(p\wedge \mathord {\sim }^{2} p)$ is known Omori and Wansing (2018) to be a provable contradiction in CP, the translations of the formulas do not preserve the form A and $\mathord {\sim }A$.

What would be desirable, in order to preserve the form of contradiction, is to have $h(\mathord {\sim }A)=\mathord {\sim }h(A)$ instead. However, this modification does not work for the Gödel-Gentzen-like translation, because $h(\mathord {\sim }(p\wedge \mathord {\sim }^{2} p))$ would then become $\mathord {\sim }(\mathord {\sim }^{4}p\wedge \mathord {\sim }^{6}p)$, which is not provable in MP.

What can be done instead is to use a different translation. We shall use a translation based on the minimal Kuroda-translation by Ferreira and Oliva (2011), which is a generalisation of Kuroda’s translation by Kuroda (1951) to minimal logic.

Definition 9

(minimal-Kuroda-like translation) We define a translation $A^{k}$ of formulas in $\mathcal {L}_{\mathord {\sim }}$ into itself by the following clauses.

where $\circ \in \{\wedge ,\vee \}$. Then we define $k(A)=\mathord {\sim }^{4}A^{k}$.

Lemma 17

$\textbf{MP}\vdash \ \Rightarrow h(A)\leftrightarrow k(A)$.

Proof

By induction on the complexity of A. The crucial case is when A has the form $\mathord {\sim }(B\rightarrow C)$. In this case,

By I.H., $\textbf{MP}\vdash \ \Rightarrow h(B)\leftrightarrow \mathord {\sim }^{4}B^{k}$ (since $k(B)\equiv \mathord {\sim }^{4}B^{k}$) and $\textbf{MP}\vdash \ \Rightarrow h(\mathord {\sim }C)\leftrightarrow \mathord {\sim }^{5}C^{k}$ (since $k(\mathord {\sim }C)\equiv \mathord {\sim }^{4}(\mathord {\sim }C)^{k}$). Then we can show the equivalence

$\square$

Theorem 18

$\textbf{CP}\vdash \ \Rightarrow A$ if and only if $\textbf{MP}\vdash \ \Rightarrow k(A)$.

Proof

Immediate from Theorem 16 and Lemma 17. $\square$

Corollary 19

If A is a provable contradiction in CP, then k(A) is a provable contradiction in MP.

Proof

If $\textbf{CP}\vdash \ \Rightarrow A$ and $\textbf{CP}\vdash \ \Rightarrow \mathord {\sim }A$, then by Theorem 18$\textbf{MP}\vdash \ \Rightarrow \mathord {\sim }^{4}A^{k}$ and $\textbf{MP}\vdash \ \Rightarrow \mathord {\sim }^{4}(\mathord {\sim }A)^{k}$, i.e. $\mathord {\sim }^{4}A^{k} (\equiv k(A))$ is a provable contradiction in MP. $\square$

Consequently, MP has, in a sense, no less advantage than CP in producing provable contradictions. This suggests that the properties classical/intuitionistic negation adds to minimal negation, such as the law of excluded middle or explosion, have only a limited effect for deriving provable contradictions.

5 Comparison with the Quarter Turn Operator

5.1 Classical Case

In CP, a triple negation $\mathord {\sim }^{3}$ gives the following equivalences:

• $\mathord {\sim }^{3}(A\wedge B)\leftrightarrow (\mathord {\sim }^{3}A\wedge \mathord {\sim }^{3}B)$

• $\mathord {\sim }^{3}(A\vee B)\leftrightarrow (\mathord {\sim }^{3}A\vee \mathord {\sim }^{3}B)$

• $\mathord {\sim }^{3}(A\rightarrow B)\leftrightarrow (A\rightarrow \mathord {\sim }^{3}B)$

It thus resembles the conflation operator of Fitting (1991) except that we do not have $\mathord {\sim }^{3}\mathord {\sim }^{3}A\leftrightarrow A$. In the semantics for CP given in Omori and Wansing (2018), the truth tables of Fig. 1 are given for $\mathord {\sim }$ and the quarter turn operator $\mathord {\circlearrowleft }$ Ruet (1996).⁶ It is observed in Omori and Wansing (2018) that $\mathord {\sim }$ rotates the values of FDE-style four-valued semantics in the opposite direction to $\mathord {\circlearrowleft }$. This immediately implies that $\mathord {\circlearrowleft }$ coincides with $\mathord {\sim }^{3}$ and $\mathord {\sim }$ coincides with $\mathord {\circlearrowleft }^{3}$. The correspondence can be to our advantage, because the equivalences above show that $\mathord {\circlearrowleft }$ makes a system more contra-classical than $\mathord {\sim }$ (when it is seen as a negation). One methodology to produce provable contradictions for $\mathord {\sim }$ then is to obtain it for $\mathord {\circlearrowleft }$ and then make a translation.

Fig. 1

Rotation of the values

The proof theory of Ruet’s operator has been investigated by Belikov et al. (2022) under the name of connegation. The history of this type of operator can be traced back to the cyclical negation of Post; see Karpenko (2017), Post (1921) for the details.

In what follows, we first define a classical system with $\mathord {\circlearrowleft }$ taken as primitive (i.e. in $\mathcal {L}_{\mathord {\circlearrowleft }}$). As we shall see, this system is only a slight variant to the system dCP in Belikov et al. (2022), and as such we adopt the same name. It will be established that we can embed the provable contradictions of each system (dCP, CP) into the other system. We then extend the idea to IP by introducing an intuitionistic system dIP and show an analogous result, this time with an additional help of the negative translations in the previous section.

Definition 10

(dCP) The system dCP in $\mathcal {L}_{\mathord {\circlearrowleft }}$ is defined by (Ax), (mCut)–(mR$\rightarrow$) and the following rules.

It is straightforward to check that $\textbf{dCP}\vdash A,\Gamma \Rightarrow \Delta , A$.

Remark 1

The difference between the current system and that of Belikov et al. (2022) is in the rules for $\mathord {\circlearrowleft }\rightarrow$, for which they have:

It is easy to see that the systems become equivalent by (mCut) and the derivability of $\mathord {\circlearrowleft }^{5}A\Rightarrow \mathord {\circlearrowleft }A$ and $\mathord {\circlearrowleft }A\Rightarrow \mathord {\circlearrowleft }^{5}A$ in both of the systems, if (Ax) and (Ax$\mathord {\circlearrowleft }$) in the formulation of Belikov et al. (2022) are replaced⁷ with $A\Rightarrow A$ and $\mathord {\circlearrowleft }A\Rightarrow \mathord {\circlearrowleft }A$.

Recall that a rule is said to be invertible (w.r.t. a premise) if the derivability of the conclusion of the rule implies that of the premise, i.e. its converse rule (w.r.t. the premise) is admissible. We need the next inversion lemma.

Lemma 20

(mL$\circ$),(mR$\circ$) for $\circ \in \{\wedge ,\vee \}$ and (mR$\rightarrow$) are invertible in both CP-(mCut) and dCP-(mCut); (mL$\mathord {\sim }{\circ }$) and (mR$\mathord {\sim }{\circ }$) for $\circ \in \{\wedge ,\vee ,\rightarrow ,\mathord {\sim }\}$ are invertible in CP-(mCut); and (mL$\mathord {\circlearrowleft }\circ$), (mR$\mathord {\circlearrowleft }\circ$) for $\circ \in \{\wedge ,\vee ,\mathord {\circlearrowleft }\}$ and ($mR\mathord {\circlearrowleft }{\rightarrow }$) are invertible in dCP-(mCut). Moreover, the following rules are admissible in CP-(mCut) and dCP-(mCut).

1. For both CP -(mCut) and dCP -(mCut)

• If $\vdash A\rightarrow B,\Gamma \Rightarrow \Delta$, then $\vdash \Gamma \Rightarrow \Delta , A$ and $\vdash B,\Gamma \Rightarrow \Delta$.

2. For dCP -(mCut):

• If $\vdash \mathord {\circlearrowleft }(A\rightarrow B),\Gamma \Rightarrow \Delta$, then $\vdash \Gamma \Rightarrow \Delta , A$ and $\vdash \mathord {\circlearrowleft }B,\Gamma \Rightarrow \Delta$.

Proof

By induction on the depth of derivation. $\square$

We now define a pair of translations between $\mathcal {L}_{\mathord {\sim }}$ and $\mathcal {L}_{\mathord {\circlearrowleft }}$.

Definition 11

We define translations $()^{t}:\mathcal {L}_{\mathord {\sim }}\longrightarrow \mathcal {L}_{\mathord {\circlearrowleft }}$ and $()^{s}:\mathcal {L}_{\mathord {\circlearrowleft }}\longrightarrow \mathcal {L}_{\mathord {\sim }}$ by the next clauses.

where $\circ \in \{\wedge ,\vee ,\rightarrow \}$.

Lemma 21

The following statements hold.

• 1. If $\textbf{CP}\text {-(mCut)}\vdash \Gamma \Rightarrow \Delta$, then $\textbf{dCP}\text {-(mCut)}\vdash \Gamma ^{t}\Rightarrow \Delta ^{t}$.

• 2. If $\textbf{dCP}\text {-(mCut)}\vdash \Gamma \Rightarrow \Delta$, then $\textbf{CP}\text {-(mCut)}\vdash \Gamma ^{s}\Rightarrow \Delta ^{s}$.

Proof

By induction on the depth of derivation. $\square$

Lemma 22

The following statements hold.

• 1. If $\textbf{CP}\text {-(mCut)}\vdash (A^{t})^s,\Gamma \Rightarrow \Delta$, then $\textbf{CP}\text {-(mCut)}\vdash A,\Gamma \Rightarrow \Delta$.

• 2. If $\textbf{CP}\text {-(mCut)}\vdash \Gamma \Rightarrow \Delta ,(A^{t})^s$, then $\textbf{CP}\text {-(mCut)}\vdash \Gamma \Rightarrow \Delta ,A$.

• 3. If $\textbf{dCP}\text {-(mCut)}\vdash (A^{s})^t,\Gamma \Rightarrow \Delta$, then $\textbf{dCP}\text {-(mCut)}\vdash A,\Gamma \Rightarrow \Delta$.

• 4. If $\textbf{dCP}\text {-(mCut)}\vdash \Gamma \Rightarrow \Delta ,(A^{s})^t$, then $\textbf{dCP}\text {-(mCut)}\vdash \Gamma \Rightarrow \Delta ,A$.

Proof

By induction on the complexity of A. For 1.–2., we must simultaneously show:

• 1’. If $\textbf{CP}\text {-(mCut)}\vdash \mathord {\sim }(A^{t})^s,\Gamma \Rightarrow \Delta$, then $\textbf{CP}\text {-(mCut)}\vdash \mathord {\sim }A,\Gamma \Rightarrow \Delta$.

• 2’. If $\textbf{CP}\text {-(mCut)}\vdash \Gamma \Rightarrow \Delta ,\mathord {\sim }(A^{t})^s$, then $\textbf{CP}\text {-(mCut)}\vdash \Gamma \Rightarrow \Delta ,\mathord {\sim }A$.

Here we consider the case for 1’. when A is $B\rightarrow C$. Since $((B\rightarrow C)^{t})^{s}\equiv (B^{t})^{s}\rightarrow (C^{t})^{s}$, assume $\textbf{CP}\text {-(mCut)}\vdash \mathord {\sim }((B^{t})^{s}\rightarrow (C^{t})^{s}),\Gamma \Rightarrow \Delta$. Then by Lemma 20, we have $\textbf{CP}\text {-(mCut)}\vdash (B^{t})^{s}, \mathord {\sim }(C^{t})^{s},\Gamma \Rightarrow \Delta$. Now by I.H. for 1. and 1’., $\textbf{CP}\text {-(mCut)}\vdash B, \mathord {\sim }C,\Gamma \Rightarrow \Delta$. Thus by (mL$\mathord {\sim }{\rightarrow }$) we conclude $\textbf{CP}\text {-(mCut)}\vdash \mathord {\sim }(B\rightarrow C),\Gamma \Rightarrow \Delta$. Other cases are similarly argued. For 3.–4., the induction must simultaneously show:

• 3’. If $\textbf{dCP}\text {-(mCut)}\vdash \mathord {\circlearrowleft }(A^{s})^t,\Gamma \Rightarrow \Delta$, then $\textbf{dCP}\text {-(mCut)}\vdash \mathord {\circlearrowleft }A,\Gamma \Rightarrow \Delta$.

• 4’. If $\textbf{dCP}\text {-(mCut)}\vdash \Gamma \Rightarrow \Delta ,\mathord {\circlearrowleft }(A^{s})^t$, then $\textbf{dCP}\text {-(mCut)}\vdash \Gamma \Rightarrow \Delta ,\mathord {\circlearrowleft }A$.

Otherwise the argument is analogous. $\square$

One consequence of the above lemmas is that (mCut) is eliminable in our formulation of dCP.

Corollary 23

(mCut) is admissible in dCP-(mCut).

Proof

Suppose $\textbf{dCP}\vdash \Gamma \Rightarrow \Delta$. Then it is easy to check that Lemma 21 2. holds even with the presence of (mCut), because it is admissible in CP-(mCut) (Kamide, 2017, Theorem 2). Then Lemma 21 1. implies $\textbf{dCP}\text {-(mCut)}\vdash (\Gamma ^{s})^{t}\Rightarrow (\Delta ^{s})^{t}$. Use Lemma 22 to conclude $\textbf{dCP}\text {-(mCut)}\vdash \Gamma \Rightarrow \Delta$. $\square$

We also obtain the desired correspondence between the two systems.

Theorem 24

The following statements hold.

• 1. $\textbf{CP}\vdash \Gamma \Rightarrow \Delta$ if and only if $\textbf{dCP}\vdash \Gamma ^{t}\Rightarrow \Delta ^{t}$.

• 2. $\textbf{dCP}\vdash \Gamma \Rightarrow \Delta$ if and only if $\textbf{CP}\vdash \Gamma ^{s}\Rightarrow \Delta ^{s}$.

Proof

For 1., by Lemma 21, it suffices to show that $\textbf{dCP}\vdash \Gamma ^{t}\Rightarrow \Delta ^{t}$ implies $\textbf{CP}\vdash \Gamma \Rightarrow \Delta$. This holds by Lemma 22. The argument for 2. is analogous. $\square$

We can now use the correspondence to obtain a characterisation of provable contradictions in the systems.

Corollary 25

The following statements hold.

• 1. $\textbf{CP}\vdash \ \Rightarrow A\wedge \mathord {\sim }A$ if and only if $\textbf{dCP}\vdash \ \Rightarrow \mathord {\circlearrowleft }^{3}A^{t}\wedge \mathord {\circlearrowleft }^{4} A^{t}$.

• 2. $\textbf{dCP}\vdash \ \Rightarrow A\wedge \mathord {\circlearrowleft }A$ if and only if $\textbf{CP}\vdash \ \Rightarrow \mathord {\sim }^{3}A^{s}\wedge \mathord {\sim }^{4} A^{s}$.

Proof

1. is an immediate consequence of Theorem 24 as well as $\textbf{dCP}\vdash C\Rightarrow \mathord {\circlearrowleft }^{4} C$ and $\textbf{dCP}\vdash \mathord {\circlearrowleft }^{4} C\Rightarrow C$. The case for 2. is analogous. $\square$

Corollary 25 allows us to obtain some provable contradictions in CP relatively simply. For instance, it is easy to note that $\textbf{dCP}\vdash \ \Rightarrow p\vee \mathord {\circlearrowleft }^{2} p$ and $\textbf{dCP}\vdash \ \Rightarrow \mathord {\circlearrowleft }(p\vee \mathord {\circlearrowleft }^{2} p)$. Then Corollary 25 tells that $\mathord {\sim }^{3}(p\vee \mathord {\sim }^{6}p)$ is a provable contradiction in CP. In addition, Corollary 25 clarifies that $\mathord {\circlearrowleft }$, which makes the system seem quite contra-classical if understood as a negation, does not produce more provable contradictions than $\mathord {\sim }$.

5.2 Intuitionistic Case

Let us turn our attention back to IP. The main questions here is to what extent it is possible to have a corresponding system like for CP. A natural starting point is to restrict dCP and move on to a single-conclusion system.

Definition 12

(dIP) The system dIP in $\mathcal {L}_{\mathord {\circlearrowleft }}$ is defined by (Ax), (Ax$\mathord {\circlearrowleft }$), (Cut)–(R$\rightarrow$) and the following rules.

where $i\in \{1,2\}$.

We shall establish some basic properties of dIP.

Definition 13

We define a translation g of formulas in $\mathcal {L}_{\mathord {\circlearrowleft }}$ into those of $\mathcal {L}_{\lnot }$ by the following clauses:

where $\circ \in \{\wedge ,\vee ,\rightarrow \}$.

Theorem 26

(Cut) is admissible in dIP.

Proof

The argument is analogous to Kamide (2017, Theorem 11,12) except that we need to use g instead of f in Definition 4. $\square$

Theorem 27

$\textbf{dCP}\vdash \ \Rightarrow A$ if and only if $\textbf{dIP}\vdash \ \Rightarrow \mathord {\circlearrowleft }^{4}A$.

Proof

Analogous to (Kamide, 2017, Theorem 19). $\square$

The translations t and s do not work for IP and dIP, because, for instance, (a) $\textbf{IP}\vdash \mathord {\sim }(p\wedge q)\Rightarrow \mathord {\sim }p\vee \mathord {\sim }q$ but $\textbf{dIP}\nvdash \mathord {\circlearrowleft }^{3}(p\wedge q)\Rightarrow \mathord {\circlearrowleft }^{3} p\vee \mathord {\circlearrowleft }^{3} q$; and (b) $\textbf{dIP}\vdash \mathord {\circlearrowleft }(p\vee q)\Rightarrow \mathord {\circlearrowleft }p\vee \mathord {\circlearrowleft }q$ but $\textbf{IP}\nvdash \mathord {\sim }^{3}(p\vee q)\Rightarrow \mathord {\sim }^{3} p\vee \mathord {\sim }^{3} q$, as can be checked easily by searching possible derivations. Nonetheless, it is still possible to give a restricted version of Corollary 25.

Corollary 28

The following statements hold.

• 1. $\textbf{IP}\vdash \ \Rightarrow \mathord {\sim }^{2}A\wedge \mathord {\sim }^{3} A$ if and only if $\textbf{dIP}\vdash \ \Rightarrow \mathord {\circlearrowleft }^{5}A^{t}\wedge \mathord {\circlearrowleft }^{6} A^{t}$.

• 2. $\textbf{dIP}\vdash \ \Rightarrow \mathord {\circlearrowleft }^{2}A\wedge \mathord {\circlearrowleft }^{3} A$ if and only if $\textbf{IP}\vdash \ \Rightarrow \mathord {\sim }^{5}A^{s}\wedge \mathord {\sim }^{6} A^{s}$.

Proof

(i) If $\textbf{IP}\vdash \ \Rightarrow \mathord {\sim }^{2}A\wedge \mathord {\sim }^{3} A$ then so is it derivable in CP. Hence by Theorem 24, $\textbf{dCP}\vdash \ \Rightarrow \mathord {\circlearrowleft }^{6}A^{t}\wedge \mathord {\circlearrowleft }^{9} A^{t}$. This is equivalent to $\textbf{dCP}\vdash \ \Rightarrow \mathord {\circlearrowleft }A^{t}\wedge \mathord {\circlearrowleft }^{2} A^{t}$. Then by Theorem 27 and the distributivity of $\mathord {\circlearrowleft }^{4}$ over conjunction, we obtain $\textbf{dIP}\vdash \ \Rightarrow \mathord {\circlearrowleft }^{5}A^{t}\wedge \mathord {\circlearrowleft }^{6} A^{t}$. The converse direction is argued along the same path, this time using the equivalence between $\mathord {\sim }^{6}$ and $\mathord {\sim }^{2}$. The argument for (ii) is analogous. $\square$

On the other hand, it is not possible to obtain Corollary 25 fully for IP and dIP. In order to see this, note that $\textbf{dIP}\vdash \ \Rightarrow \mathord {\circlearrowleft }^{6}(p\wedge \mathord {\circlearrowleft }^{6}p)\wedge \mathord {\circlearrowleft }^{7}(p\wedge \mathord {\circlearrowleft }^{6}p)$ and so we can show $\textbf{dIP}\vdash \ \Rightarrow \mathord {\circlearrowleft }^{3}(\mathord {\sim }(p\wedge \mathord {\sim }^{2}p))^{t}\wedge \mathord {\circlearrowleft }^{4}(\mathord {\sim }(p\wedge \mathord {\sim }^{2}p))^{t}$. However $\textbf{IP}\nvdash \ \Rightarrow \mathord {\sim }(p\wedge \mathord {\sim }^{2}p)$. Similarly, since it holds that $\textbf{IP}\vdash \ \Rightarrow \mathord {\sim }^{3}(p\vee \mathord {\sim }^{6}p)\wedge \mathord {\sim }^{4}(p\vee \mathord {\sim }^{6}p)$, we have $\textbf{IP}\vdash \ \Rightarrow \mathord {\sim }^{3}(p\vee \mathord {\circlearrowleft }^{2}p)^{s}\wedge \mathord {\sim }^{4}(p\vee \mathord {\circlearrowleft }^{2}p)^{s}$. However $\textbf{dIP}\nvdash \ \Rightarrow p\vee \mathord {\circlearrowleft }^{2}p$.

Remark 2

If we write both $\mathord {\sim }\mathord {\sim }$ and $\mathord {\circlearrowleft }\mathord {\circlearrowleft }$ as $\lnot$ (representing intuitionistic negation), then the above proof establishes that $\textbf{IP}\vdash \ \Rightarrow \lnot A$ iff $\textbf{dIP}\vdash \ \Rightarrow \lnot A^{t}$ as well as $\textbf{dIP}\vdash \ \Rightarrow \lnot A$ iff $\textbf{IP}\vdash \ \Rightarrow \lnot A^{s}$. Hence the intuition that $\mathord {\sim }$ and $\mathord {\circlearrowleft }$ represent rotations of values from opposite sides can be seen to be partially alive: for instance, in CP, applying $\mathord {\sim }$ to ($\mathord {\sim }$-free) A corresponds to applying $\mathord {\circlearrowleft }$ three times to it. In IP, applying $\mathord {\sim }$ to $\lnot A$ (i.e. $\mathord {\sim }^{3}A\equiv \lnot \mathord {\sim }A$) corresponds to applying $\mathord {\circlearrowleft }$ three times to it (i.e. $\mathord {\circlearrowleft }^{5}A\equiv \lnot \mathord {\circlearrowleft }^{3}A\equiv \lnot (\mathord {\sim }A)^{t}$).

Another possible restriction is to disallow applications of certain rules.

Proposition 29

The following statements hold.

• 1. If $\textbf{IP}\text {-(Cut)}\vdash \Gamma \Rightarrow A$ with no applications of (L$\mathord {\sim }\wedge$) or (L$\mathord {\sim }{\rightarrow }$1), then $\textbf{dIP}\vdash \Gamma ^{t}\Rightarrow A^{t}$.

• 2. If $\textbf{dIP}\text {-(Cut)}\vdash \Gamma \Rightarrow A$ with no applications of (L$\mathord {\circlearrowleft }\vee$), then $\textbf{IP}\vdash \Gamma ^{s}\Rightarrow A^{s}$.

Proof

For 1., by induction on the depth of derivation. For instance, when the last rule applied is an instance of (L$\mathord {\sim }{\rightarrow }$2),

then by I.H. we have a derivation on IP of $\mathord {\circlearrowleft }^{3} B^{t},\Gamma ^{t}\Rightarrow C^{t}$. Then since $\textbf{dIP}\text {-(Cut)}\vdash \mathord {\circlearrowleft }^{3}(A^{t}\rightarrow B^{t})\Rightarrow \mathord {\circlearrowleft }^{3}B^{t}$, by the admissibility of (Cut) we infer $\mathord {\circlearrowleft }^{3}(A^{t}\rightarrow B^{t}),\Gamma ^{t}\Rightarrow C^{t}$. 2. is argued likewise. $\square$

Corollary 30

If $\textbf{dIP}\vdash \ \Rightarrow A\wedge \mathord {\circlearrowleft }A$ and there is no occurrence of disjunction in A, then $\textbf{IP}\vdash \ \Rightarrow \mathord {\sim }^{3}A^{s}\wedge \mathord {\sim }^{4}A^{s}$.

Proof

From Proposition 29 and the fact that if a disjunction occurs in a derivation of dIP-(Cut), it must occur in the endsequent. $\square$

For example, we can show $\textbf{dIP}\vdash ((p\wedge \mathord {\circlearrowleft }p)\rightarrow p)\wedge \mathord {\circlearrowleft }((p\wedge \mathord {\circlearrowleft }p)\rightarrow p)$, and the corollary then tells that $\mathord {\sim }^{3}((p\wedge \mathord {\sim }^{3}p)\rightarrow p)$ is a provable contradiction in IP.

6 Some Subsystems of MP

In this section, we shall look at some examples of subsystems of MP, mainly ones which do not prove a contradiction, to point out certain limits for weakening the property of the double negation. We first give a general characterisation for a set of formulas to contain a contradictory pair, assuming that it satisfies N4-like conditions.

Theorem 31

Let L be a set of formulas in $\mathcal {L}_{\mathord {\sim }}$ such that:

Then $A,\mathord {\sim }A\in L$ for some A if and only if there is B such that

• $\mathord {\sim }B,\mathord {\sim }\mathord {\sim }B\in L$.

• for any C such that $\vert C\vert <\vert \mathord {\sim }B\vert$, either $C\notin L$ or $\mathord {\sim }C\notin L$.

Proof

The ‘if’ direction is immediate. For the ‘only if’ direction, we show the contrapositive. So suppose for all B, if $\mathord {\sim }B,\mathord {\sim }\mathord {\sim }B\in L$ then there is C such that $\vert C\vert <\vert \mathord {\sim }B\vert$ and $C,\mathord {\sim }C\in L$. We shall argue by induction on the complexity of A that $A,\mathord {\sim }A\in L$ leads to contradiction.

If A is p or $\mathord {\sim }p$, then $A,\mathord {\sim }A\in L$ implies $\mathord {\sim }p\in L$. By the condition 4. for L, we infer $\mathord {\sim }(D\rightarrow D)\in L$ and so $D\in L$ for all D by the conditions 2. and 8.. This contradicts the condition 1..

If A is $D\wedge E$, then $D\wedge E,\mathord {\sim }(D\wedge E)\in L$ and so $D,E\in L$ by the condition 2.. Also $\mathord {\sim }D\vee \mathord {\sim }E\in L$ and so either $\mathord {\sim }D\in L$ or $\mathord {\sim }E\in L$ by the conditions 5. and 6.. Consequently either $D,\mathord {\sim }D\in L$ or $E,\mathord {\sim }E\in L$, But by I.H. both lead to a contradiction. The case when A is $D\vee E$ is analogous.

If A is $D\rightarrow E$, then $D\rightarrow E, \mathord {\sim }(D\rightarrow E)\in L$ and so $D, \mathord {\sim }E\in L$ by the condition 8.. Also $D,D\rightarrow E\in L$ means $E\in L$ by the condition 3, so $E,\mathord {\sim }E\in L$ and by I.H. we obtain a contradiction.

If A is $\mathord {\sim }D$, then the case $\vert \mathord {\sim }D\vert =0$ is already treated. Otherwise, by our initial supposition there has to be a formula C of lower complexity such that $C,\mathord {\sim }C\in L$, to which we can apply I.H.. $\square$

6.1 Systems with Double Negation Rules

We will formulate our examples in this section axiomatically. For the first example, we keep the axiom schema $(A\rightarrow \mathord {\sim }\mathord {\sim }A)\rightarrow \mathord {\sim }\mathord {\sim }A$ in MP, but the other double negation axiom schema is weakened to a rule corresponding to $(A\leftrightarrow B)\rightarrow (\mathord {\sim }\mathord {\sim }A\leftrightarrow \mathord {\sim }\mathord {\sim }B)$⁸.

Definition 14

(H-WP) The system H-WP is defined from H-MP by replacing the axiom schema $(A\leftrightarrow B)\rightarrow (\mathord {\sim }\mathord {\sim }B\leftrightarrow \mathord {\sim }\mathord {\sim }A)$ by:

We check that H-WP satisfies the disjunction property, using the technique of the Aczel slash Aczel (1968).

Definition 15

(Aczel slash) We define the notion of $\vert A$ for formulas in $\mathcal {L}_{\mathord {\sim }}$ by the following clauses.

Lemma 32

$\vert A$ if and only if ${\textbf {H-WP}}\vdash A$.

Proof

The left-to-right direction is shown by induction on the complexity of formulas. The right-to-left direction is shown by induction on the depth of derivation. In particular, for the axiom schema $(A\rightarrow \mathord {\sim }\mathord {\sim }A)\rightarrow \mathord {\sim }\mathord {\sim }A$, it suffices to show that $\vert A\rightarrow \mathord {\sim }\mathord {\sim }A$ implies $\vert \mathord {\sim }\mathord {\sim }A$. The former implies ${\textbf {H-WP}}\vdash A\rightarrow \mathord {\sim }\mathord {\sim }A$, so ${\textbf {H-WP}}\vdash \mathord {\sim }\mathord {\sim }A$ and thus $\vert \mathord {\sim }\mathord {\sim }A$, as required. For the rule , if $\vert \mathord {\sim }\mathord {\sim }A$ then ${\textbf {H-WP}}\vdash \mathord {\sim }\mathord {\sim }A$ and so ${\textbf {H-WP}}\vdash \mathord {\sim }\mathord {\sim }B$. Thus $\vert \mathord {\sim }\mathord {\sim }B$ and consequently $\vert \mathord {\sim }\mathord {\sim }A\rightarrow \mathord {\sim }\mathord {\sim }B$. Similarly, $\vert \mathord {\sim }\mathord {\sim }B\rightarrow \mathord {\sim }\mathord {\sim }A$ and so $\vert \mathord {\sim }\mathord {\sim }A\leftrightarrow \mathord {\sim }\mathord {\sim }B$. $\square$

Proposition 33

If ${\textbf {H-WP}}\vdash A\vee B$ then either ${\textbf {H-WP}}\vdash A$ or ${\textbf {H-WP}}\vdash B$.

Proof

If ${\textbf {H-WP}}\vdash A\vee B$, then by Lemma 32$\vert A\vee B$ and so $\vert A$ or $\vert B$. By the same lemma, this implies either ${\textbf {H-WP}}\vdash A$ or ${\textbf {H-WP}}\vdash B$. $\square$

We now show that no formula of the form $\mathord {\sim }\mathord {\sim }A$ is derivable in the system, using a Gödel-Dummett style infinite-valued matrix (cf. e.g. Ono (2019)).

Definition 16

Let $T=\{2^{-i}:i\in {\mathbb {N}}\}\cup \{0\}$. Let v be an assignment of values $v^{+}(p),v^{-}(p)\in T$ to each propositional variable p. For compound formulas, we set:

A formula A is then said to be valid if $v^{+}(A)=1$ for any assignment v.

Proposition 34

${\textbf {H{-}WP}}\nvdash \mathord {\sim }\mathord {\sim }A$ for any A.

Proof

It is straightforward to check that H-WP is sound with respect to the above matrix. For instance, if $v^{+}(A)=0$ then $v^{+}(\mathord {\sim }\mathord {\sim }A)=v^{-}(\mathord {\sim }A)=1$. Otherwise, $v^{+}(A)=2^{-i}>2^{-(i+1)}=v^{+}(\mathord {\sim }\mathord {\sim }A)$ and so $v^{+}(A\rightarrow \mathord {\sim }\mathord {\sim }A)=v^{+}(\mathord {\sim }\mathord {\sim }A)$. So $v^{+}((A\rightarrow \mathord {\sim }\mathord {\sim }A)\rightarrow \mathord {\sim }\mathord {\sim }A)=1$ under any assignment v. Also, if $A\leftrightarrow B$ is valid, then for any v we have $v^{+}(A)=v^{+}(B)$, from which it also follows that $v^{+}(\mathord {\sim }\mathord {\sim }A\leftrightarrow \mathord {\sim }\mathord {\sim }B)=1$, and so the formula is valid.

Now, it is easy to see that if v is an assignment such that $v^{*}(p)>0$ for all p and $*\in \{+,-\}$, then $v^{*}(A)>0$ for all A. Hence under this assignment, for no A we have $v^{+}(\mathord {\sim }\mathord {\sim }A)=1$. The statement then follows by soundness. $\square$

Corollary 35

H-WP does not have a provable contradiction.

Proof

It readily from Proposition 33 that the set of theorems of H-WP satisfies the conditions of Theorem 31. Then the statement follows using Proposition 34. $\square$

This example in particular shows that $(A\rightarrow \mathord {\sim }\mathord {\sim }A)\rightarrow \mathord {\sim }\mathord {\sim }A$ is insufficient by itself to cause negation inconsistency.

At this point, one might wonder what happens for the other way of weakening MP, namely to retain $(A\leftrightarrow B)\rightarrow (\mathord {\sim }\mathord {\sim }A\leftrightarrow \mathord {\sim }\mathord {\sim }B)$ while $(A\rightarrow \mathord {\sim }\mathord {\sim }A)\rightarrow \mathord {\sim }\mathord {\sim }A$ is made into a rule . Let us call this system H-XP. We can confirm that this system is negation inconsistent.

Proposition 36

$\mathord {\sim }(\mathord {\sim }(A\wedge \mathord {\sim }^{2}A)\wedge \mathord {\sim }^{3}(A\wedge \mathord {\sim }^{2}A))$ is a provable contradiction in H-XP.

Proof

We first observe that $\mathbf{H\text {-}XP}\vdash \mathord {\sim }\mathord {\sim }(A\wedge \mathord {\sim }\mathord {\sim }A)$. This follows from $(A\wedge \mathord {\sim }\mathord {\sim }A)\rightarrow (A\leftrightarrow (A\wedge \mathord {\sim }\mathord {\sim }A))$ by first applying the double negation axiom schema of H-XP, giving $(A\wedge \mathord {\sim }\mathord {\sim }A)\rightarrow (\mathord {\sim }\mathord {\sim }A\rightarrow \mathord {\sim }\mathord {\sim }(A\wedge \mathord {\sim }\mathord {\sim }A))$. Hence $\mathbf{H\text {-}XP}\vdash (A\wedge \mathord {\sim }\mathord {\sim }A)\rightarrow \mathord {\sim }\mathord {\sim }(A\wedge \mathord {\sim }\mathord {\sim }A)$, to which we can apply the double negation rule. This implies then $\mathbf{H\text {-}XP}\vdash \mathord {\sim }(\mathord {\sim }(A\wedge \mathord {\sim }^{2}A)\wedge \mathord {\sim }^{3}(A\wedge \mathord {\sim }^{2}A))$. On the other hand, the negation of the formula is obtained by taking $\mathord {\sim }(A\wedge \mathord {\sim }\mathord {\sim }A)$ in place of A in $\mathord {\sim }\mathord {\sim }(A\wedge \mathord {\sim }\mathord {\sim }A)$. $\square$

Figure 2 summarises what happens to negation inconsistency when we weaken the axioms schemata of H-MP corresponding to ($\mathord {\sim }\mathord {\sim }2$) and ($\mathord {\sim }\mathord {\sim }3$) into the corresponding rules. Alternatively, we can also consider the weakening of the axiom schema corresponding to ($\mathord {\sim }\mathord {\sim }1$) as well. In that case, the negation inconsistency is kept even when both of the axiom schemata are weakened to rules: we have $\mathord {\sim }^{5}(A\wedge \mathord {\sim }^{2}A)$ as a provable contradiction, as can be checked by mimicking the derivations in Proposition 9.

Fig. 2

The effect of changing axioms to rules

7 Informational Interpretation of MP

The introduction by Kamide of the kind of negation we are considering seems to have been motivated more from a technical perspective. Hence it did not necessarily come with a (non-logical) philosophical project to which the formalisation of CP and IP is dedicated. Nonetheless, it will be of a considerable interest if these logics with unusual features get tied with a robust philosophical interpretation. At the same time, it may be unlikely to immediately reach a definite interpretation, so we shall aim at a more modest goal of enriching our understanding of the logics by suggesting an interpretation from a point of view alternative to the pre-existing one.

As mentioned in the introduction, the double negation in CP and IP are already explained in Omori and Wansing (2018) in terms of negative concord. This interpretation is however linguistic in character, and a more constructive interpretation is perhaps also beneficial for systems like IP and MP. A canonical example of such an interpretation is the BHK-interpretation for intuitionistic logic, which explains the meaning of a connective by the proof condition of a formula with the connective as the main connective (see e.g. Troelstra and van Dalen (1988)). For systems related to N4, an extended interpretation is often used, in which the explanation is given by the parallel notion of refutation/disproof condition as well (Nelson, 1949; López-Escobar, 1972).

If we allow ourselves to understand by a proof/disproof a construction that provides an evidence in favour of a statement’s truth/falsity, BHK-style interpretation can be connected to an interpretation based on the notion of information. The recent proposal of dimathematism by Wansing (2022) appears to be particularly suitable for IP and MP. As observed in that paper, IP (and also MP) satisfies the qualification of strong dimathematism:

Strong dimathematism is an informational view: some languages L and some contradictory L-formulas are such that their truth is supported by every state from every L-model. That is, where $\mathord {\sim }$ is negation, there are L-sentences A, such that for every L-model $\mathfrak {M}$ and every state w from $\mathfrak {M}$, in $\mathfrak {M}$ state w supports the truth of both A and $\mathord {\sim }A$. Given that a state supports the falsity of A iff it supports the truth of $\mathord {\sim }A$, this is to say that there are some L-formulas A, such that every L-model $\mathfrak {M}$ and state w from $\mathfrak {M}$ are such that in $\mathfrak {M}$ state w supports both the truth and the falsity of A. [Wansing (2022)]

The view thus liberates us from the perhaps constructively untenable notions of truth and falsity by replacing them with the more tangible notions of supports of truth and falsity. An interpretation of MP (or IP) from this viewpoint then has to answer how the falsity of $\mathord {\sim }A$ is supported.

7.1 Double Negation and Strong Support

Limiting our attention to MP, we have to explain the condition:

$$\begin{aligned} w \Vdash ^{-} \mathord {\sim }A\text { iff }\forall {w'\ge w}(w'{\Vdash ^{+}}A\Rightarrow w'\in Q). \end{aligned}$$

In minimal logic, Q is used to capture the absurdity constant $\bot$, and as a consequence Q is best understood as a set of worlds which disfavour the truth of A. Nonetheless, it is also possible to consider Q as a set of worlds which favour A. Although we in no way expect it to be a definitive interpretation, we tentatively suggest to deem Q as a set of worlds in which the supported formulas obtain a higher informational status or a strong support.

Once we understand Q in such a way, then the equivalence above seems less perplexing. One can perhaps defend it on the following ground: it is something unusual if any later state that supports the truth of A is one that is capable of giving a strong support. This regularity challenges the claim that A is false; so the falsity of $\mathord {\sim }A$ is supported,⁹. Then conversely the falsity of $\mathord {\sim }A$ can be taken to be supported only if the above situation holds.

Remark 3

To understand the naïve intuition behind the interpretation, it may help to see each world metaphorically as an agent (ordered by what they support), and Q as the set of ones who are trustworthy. Then consider as an example the case of an agent assessing the falsity of the statement ‘global warming is not a major issue.’. In order to evaluate the statement, the agent looks at other agents with whom he shares what to support (i.e. later worlds), and discovers that every agent who supports the truth of the statement ‘global warming is a major issue’ is trustworthy.¹⁰ Based on this evidence, the agent supports the falsity of the original statement. This method of evaluation seems rather natural, as we often refer to people making relevant claims and check their credibility, when we judge a claim.

It is hard to apply a similar kind of interpretation to IP, because in the intuitionistic setting, Q has to be empty. We can not, as a result, have a ‘positive’ reading of the support of falsity condition for negation, unlike in MP. This may be hinting that MP, which in a way liberates from the view that the double negation must resemble a demi-negation, is more preferable than IP from the informational point of view.

7.2 Extending the Interpretation

One possible objection to the support of falsity condition for negation in MP, when understood in the above manner, is that $w\Vdash ^{-}\mathord {\sim }A$ holds even when there is no $w'\ge w$ such that $w'\Vdash ^{+}A$. It may be suggested that the falsity of $\mathord {\sim }A$ should not be supported when the truth of A will not ever be supported. Accepting this criticism motivates one to make the following modification to the forcing conditions in the semantics for MP:

$$\begin{aligned} w \Vdash ^{-} \mathord {\sim }A\text { iff }\forall {w'\ge w}((w'{\Vdash ^{+}}A\Rightarrow w'\in Q)\text { and }\exists {x\ge w'}(x\Vdash ^{+} A)). \end{aligned}$$

This condition ensures that that the aforementioned situation does not occur, and also preserves the upward closure of the forcing relation. Let us denote the consequence for the modified semantics by $\vDash _{m}$.

We can show using a standard method (see e.g. van Dalen (2014)) that the modification does not affect the constructive character of the semantics.

Proposition 37

If $\vDash _{m} A\vee B$ then $\vDash _{m} A$ or $\vDash _{m} B$.

Proof

We show the contrapositive. So suppose $\nvDash _{m}A$ and $\nvDash _{m}B$. Then there are countermodels $\mathcal {M}_{i}=((W_{i},\le _{i},Q_{i}),\mathcal {V}_{i})$ for $i\in \{1,2\}$ such that there are $w_{i}\in W_{i}$ with $\mathcal {M}_{1},w_{1}\nVdash ^{+} A$ and $\mathcal {M}_{2},w_{2}\nVdash ^{+} B$. We may assume $W_{1}\cap W_{2}=\emptyset$. Define a new model $\mathcal {M}=((W,\le ,Q),\mathcal {V})$ where:

• $W=W_{1}\cup W_{2}\cup \{g\}$, where g is a new element.

• $w\le w'$ if $w,w'\in W_{i}$ and $w\le _{i}w'$, or $w=g$.

• $Q=Q_{1}\cup Q_{2}$.

• $\mathcal {V}^{*}(p)=\mathcal {V}^{*}_{1}(p)\cup \mathcal {V}^{*}_{2}(p)$ for $*\in \{+,-\}$.

Then for $i\in \{1,2\}$ and $*\in \{+,-\}$, it holds that for all $w\in W_{i}$, we have $\mathcal {M},w\Vdash ^{*} A$ iff $\mathcal {M}_{i},w\Vdash ^{*} A$. Consider as an example the case when A is $\mathord {\sim }B$, $w\in W_{1}$ and $*=-$. Then $\mathcal {M},w\Vdash ^{-}\mathord {\sim }B$ iff $\forall {w'\ge w}((\mathcal {M},w'\Vdash ^{+}B\Rightarrow w'\in Q)$ and $\exists {x\ge w'}(\mathcal {M},x\Vdash ^{+} B))$. By I.H., this is equivalent to $\forall {w'\ge w}((\mathcal {M}_{1},w'\Vdash ^{+}B\Rightarrow w'\in Q_{1})$ and $\exists {x\ge w'}(\mathcal {M}_{1},x\Vdash ^{+} B))$ and thus to $\mathcal {M}_{1},w\Vdash ^{-}\mathord {\sim }B$.

Now we have $\mathcal {M},w_{1}\nVdash ^{+} A$, $\mathcal {M},w_{2}\nVdash ^{+} B$ and so $\mathcal {M},g\nVdash ^{+} A\vee B$; thus $\nvDash _{m}A\vee B$. $\square$

On the other hand, if one is interested in a negation-inconsistent system, then the semantics is not adequate.

Proposition 38

$\nvDash _{m} \mathord {\sim }\mathord {\sim }A$ for any A.

Proof

Consider a model with $Q=\emptyset$. In the model, $\mathcal {M},w\Vdash ^{+}\mathord {\sim }\mathord {\sim }A$ iff $\forall {w'\ge w}(w'\nVdash ^{+}A$ and $\exists {x\ge w'}(x\Vdash ^{+} A))$. Hence $\mathord {\sim }\mathord {\sim }A$ is never forced in such a model. $\square$

Corollary 39

There is no formula A such that $\vDash _{m}A$ and $\vDash _{m}\mathord {\sim }A$.

Proof

Let $L=\{A:\vDash _{m}A\}$. Then the statement follows from Theorem 31 as well as Proposition 37 and 38. $\square$

Remark 4

It may be suggested that Proposition 38 can be avoided by putting an extra condition that $Q\ne \emptyset$. In that scenario, when $W=\{w\}$ we obtain the equivalence $w\Vdash ^{-}\mathord {\sim }A$ if and only if $w\Vdash ^{+} A$. In a model based on such a frame¹¹, if $w\Vdash ^{+}A$ and $w\Vdash ^{+}\mathord {\sim }A$, where $\vert A\vert \ge 1$, we can always find a strict subformula B of A such that $w\Vdash ^{+}B$ and $w\Vdash ^{+}\mathord {\sim }B$. It follows then that we do not have such A in a model where $\mathcal {V}^{+}(p)=\mathcal {V}^{-}(p)=\emptyset$. This gives a countermodel for $A\wedge \mathord {\sim }A$ in the suggested semantics, and so we again end up with a negation-consistent system.

The above observations suggest that it is essential for the negation inconsistency of MP that the falsity of negation can be ‘vacuously’ supported. Is it possible to make sense of such a support?

One reply to this question might be to note that a vacuous support does not mean it contains no information. Observing that the truth of A is never going to be supported provides enough information to rule out a counterexample to the support of falsity for $\mathord {\sim }A$, in the sense of a later world which supports the truth of A but not in Q. Hence a vacuous support is something more than a non-support. Nonetheless, one might argue that we cannot regard the observation as a support, because it gives less information than the non-vacuous cases. However, this should not be too much of a problem, as our interpretation presupposes that supports come in different degrees.

8 Concluding Remarks

This paper explored some subsystems of Kamide’s logics CP and IP, in order to analyse the cause of the non-trivial negation inconsistency of the systems. We formulated the system MP, whose double negation can be seen as the minimal negation. MP, as we found out, is not only negation inconsistent, but also is a system into which any provable contradiction in CP can be embedded, preserving the status of provable contradiction. This result was also used to show how provable contradictions in CP and IP correspond to those of the systems with quarter turn operator, dCP and dIP.

As the Hilbert-style system H-MP clarifies, $(A\rightarrow \mathord {\sim }\mathord {\sim }A)\rightarrow \mathord {\sim }\mathord {\sim }A$ is isolated as the sole axiom schema inducing the contra-classicality. Then to understand the role of the schema further, we looked at some subsystems of MP in which double negation axiom schemata are turned into rules. We observed the status of negation inconsistency depends on which axiom schema is weakened.

Lastly, we attempted to give an interpretation of MP from an informational, and more specifically dimathematic point of view. We suggested that the support of falsity for $\mathord {\sim }A$ can perhaps be understood as the regularity that the support of truth for A being always strong. We then observed that the negation consistency is lost if some stronger conditions are imposed.

MP may perhaps not rival N4 in terms of naturalness, but given the interpretation, the difference might be not as wide as it appears at first sight. The crucial question then is under which contexts it can work as a complementary system. This needs to be explored further in order to justify the importance of Kamide’s negation and the contradictions it creates.