Non-transitive Correspondence Analysis

Abstract

The paper’s novelty is in combining two comparatively new fields of research: non-transitive logic and the proof method of correspondence analysis. To be more detailed, in this paper the latter is adapted to Weir’s non-transitive trivalent logic ${\mathbf{NC}}_{\mathbf{3}}$. As a result, for each binary extension of ${\mathbf{NC}}_{\mathbf{3}}$, we present a sound and complete Lemmon-style natural deduction system. Last, but not least, we stress the fact that Avron and his co-authors’ general method of obtaining n-sequent proof systems for any n-valent logic with deterministic or non-deterministic matrices is not applicable to ${\mathbf{NC}}_{\mathbf{3}}$ and its binary extensions.

1 Introduction and Overview

1.1 Non-Transitive Logic

Non-transitive logic is a kind of substructural logic (Restall, 2000) which challenges transitivity, one of the basic properties of the entailment relation along with (various names might be found in the literature) reflexivity, monotonicity, contraction, and permutability. The properties of transitivity and cut (which should not be equated) are definable in different ways; we refer the reader to outlines in Ripley (2013, 2018), Barrio et al. (2019).¹ In particular, we are interested in the approach of Weir who presents three-valued, continuum-valued, and surreal-valued non-transitive logics within his analysis of the Curry paradox (Weir, 2013a; b).² We prefer the Weirian trivalent logic ${\mathbf{NC}}_{\mathbf{3}}$ because of its tabularity and functionally incompleteness that together make it a suitable choice for correspondence analysis (CA, hereafter).³

Let us briefly list and informally discuss the key features of ${\mathbf{NC}}_{\mathbf{3}}$ before getting into formal definitions. First, ${\mathbf{NC}}_{\mathbf{3}}$ is tabular trivalent; its negation, conjunction, disjunction, and implication are of the Łukasiewiczian trivalent logic Ł$_{\mathbf{3}}$ (Łukasiewicz et al., 1920) (which negation, conjunction, and disjunction are the same as in the Kleenian strong trivalent logic $\mathbf{K}_3$ Kleene 1938; 1952). The reason Weir uses the Łukasiewiczian implication is that, otherwise, ${\mathbf{NC}}_{\mathbf{3}}$ would lack theoremhood just like $\mathbf{K}_{\mathbf{3}}$ does. Theoremhood of ${\mathbf{NC}}_{\mathbf{3}}$ implies the second key feature that is about the transitivity property of its entailment relation. In his robust non-transitive logic ${\mathbf{NC}}_{\mathbf{3}}$, Weir clearly wants to reject generalized transitivity (if $\varGamma \vdash \varDelta , \phi$ and $\phi , \varGamma \vdash \varDelta$, then $\varGamma \vdash \varDelta$) and preserve, at least, simple transitivity (if $\psi \vdash \phi$ and $\phi \vdash \chi$, then $\psi \vdash \chi$).⁴

Third, in order to show that generalized transitivity fails in ${\mathbf{NC}}_{\mathbf{3}}$, Weir proposes an original definition of the entailment relation $\models _{{\mathbf{NC}}_3}$ such that it holds in two directions which coincide in classical logic: downwards truth-preservation and upwards falsity-preservation. Weir exemplifies a failure of generalized transitivity in the following way. Both $\phi \wedge \lnot \phi \models _{{\mathbf{NC}}_{\mathbf{3}}} \phi$ and $\phi \wedge \lnot \phi , \phi \models _{{\mathbf{NC}}_{\mathbf{3}}} \bot$, but $\phi \wedge \lnot \phi \not \models _{{\mathbf{NC}}_{\mathbf{3}}} \bot$ because upwards falsity-preservation fails: if $v(\phi ) = {1}/{2}$, then $v(\bot ) = 0$ and $v(\lnot \phi ) = v(\phi \wedge \lnot \phi ) = {1}/{2}$.

1.2 Correspondence Analysis

Segerberg who is the most likely candidate to be the pioneer of CA, proposed it for classical logic in the beginning of the eighties (Segerberg, 1983, 1982).⁵ Kooi and Tamminga (2012) are the first who applied CA to non-classical logic, viz., to Asenjo-Priest’s three-valued logic LP (Asenjo, 1966; Priest, 1979). Kooi and Tamminga’s motivations are explicitly traceable back to modal correspondence theory (Sahlqvist, 1975; van Benthem, 1976, 2001). The achievements of CA are outlined in Introduction of Petrukhin and Shangin (2021).

Following the Segerbergian motivation, CA, basically, takes some functionally incomplete k-valued (mostly but not limited to, trivalent or tetravalent ones)⁶ logic and outputs definitions of each n-ary (mostly but not limited to, unary or binary ones) extensions of the logic in question. Having been obtained thus, definitions are one-to-one correspondences (hence, correspondence in the name of CA) between each entry of the truth-table for a logical connective (that is, an extension of the logic being analysed) and a valid formula or an entailment. These correspondences (which we dub equivalences sometimes), moreover, allow setting up a sound and complete proof system (mostly but not limited to, a natural deduction system)⁷ for each extension of the logic under consideration. Lastly, CA might be equipped with an adequate proof searching procedure: it makes CA a powerful and flexible framework to study (fragments of) tabular logics.

CA is not the only general method for obtaining a proof system for some logic given its tabular semantics. For example, Anshakov-Rychkov’s method (Anshakov & Rychkov, 1994) allows one to formalize n-valued logics with Rosser and Turquette’s J-operators (Rosser & Turquette, 1952) via Hilbert systems. Another example of such a method is presented by Baaz et al. (1993) showing how n-sequent calculi as well as analytic tableaux can be presented for n-valued logics. In Baaz et al. (1993), these calculi are transformed into labelled natural deduction systems. Section 6 below is particularly addressed to the method for obtaining proof systems by Avron and his co-authors (Avron et al., 2007, 2013).

1.3 Lemmon-Style Natural Deduction

In choosing Lemmon-style natural deduction (Lemmon, 1998), we follow Weir who explains himself as follows: “Since the tree-form architecture tends to spread too much in all but the shortest proofs I will stick with the linear sequent format, in Lemmon-style” (Weir, 2013a, p. 101). The tree-like format or Gentzen-style natural deduction that Weir mentions above goes hand in hand with a linear format or Fitch-style natural deduction. However, Weir utilises Lemmon-style natural deduction, i. e. another (arguably, less popular) kind of the linear format.⁸

The crucial difference is that, basically, a line in a Lemmon-style derivation visually contains a set of the hypotheses (assumptions, premises, etc.) which a formula on this line follows from.⁹ In a Fitch-style derivation, a line contains a formula only and does not contain a set of the hypotheses which a formula on this line follows from. Moreover, it is sometimes very difficult to visually determine this set because some lines above might be discarded. Hence, the visualness in question might be obscure, and one needs much more (in the worst case) efforts to scrutinize the previous non-discarded lines in a derivation in order to detect this set. Let us refer the reader to the monograph by Indrzejczak (2010) which seems to be the most exhaustive up-to-date study of natural deduction. There she finds historical excursuses with a documented claim that the origin of natural deduction should be ascribed to Jaśkowski rather than Gentzen as well as a thorough discussion of the pros and cons of different formats of natural deduction that leads to a clear-cut decision pro hybrid systems.

The structure of this paper is as follows. Section 2 contains an application of CA to the trivalent non-transitive logic ${\mathbf{NC}}_{\mathbf{3}}$. Section 3 contains the Lemmon-style natural deduction system for ${\mathbf{NC}}_{\mathbf{3}}$. Examples of both ${\mathbf{NC}}_{\mathbf{3}}$-derivations and derivable rules are in Sect. 4. Section 5 contains Lemmon-style natural deduction systems for the binary extensions of ${\mathbf{NC}}_{\mathbf{3}}$ as well as proofs of their soundness and completeness. Section 6 discusses related works. Concluding remarks are in Sect. 7.

2 Correspondence Analysis for the Non-transitive Logic ${{\textbf {NC}}}_{\mathbf{3}}$

We start with the Weirian semantics for ${\mathbf{NC}}_3$ and then apply CA to it in order to obtain equivalences for each binary extension of ${\mathbf{NC}}_{\mathbf{3}}$.

2.1 The Weirian Semantics for ${{\textbf {NC}}}_{\mathbf{3}}$

${\mathbf{NC}}_{\mathbf{3}}$ is built over a propositional language ${\mathscr {L}}$ with an alphabet $\langle {\mathscr {P}},$ $\bot ,$ $\top ,$ $\lnot ,$ $\wedge ,$ $\vee ,$ $\rightarrow ,$ $(,$ $) \rangle$, where ${\mathscr {P}}$ is a denumerable set $\{p,q,r,s,p_1,\ldots \}$ of propositional variables. The set ${\mathscr {F}}$ of all ${\mathscr {L}}$-formulae is defined in a standard way. The letters $\phi$, $\psi$, $\chi$, $\rho$, $\varphi$ with subscripts run over ${\mathscr {L}}$-formulae. The letters $\varGamma$, $\varDelta$, X, Y, Z, $\varSigma$, $\varXi$ with subscripts run over finite sets of ${\mathscr {L}}$-formulae.

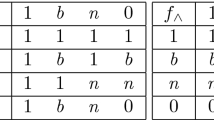
Let $\natural$ be a truth-functional operator (or connective) and $f_\natural$ be its truth table. Let us remind the reader that an interpretation v of all the connectives of ${\mathbf{NC}}_{\mathbf{3}}$, except $\bot$, $\top$ and $\rightarrow$, is as in the Kleenian strong logic $\mathbf{K}_3$: $1>{1}/{2}>0$, $v(\phi \wedge \psi ) = \mathrm{min} (v(\phi ), v(\psi ))$, $v(\phi \vee \psi ) = \mathrm{max} (v(\phi ), v(\psi ))$, and $v(\lnot \phi ) = 1-v(\phi )$, where 1, ${1}/{2}$, and 0 stand, respectively, for ‘true’, ‘indeterminate’, and ‘false’.¹⁰ Implication of ${\mathbf{NC}}_{\mathbf{3}}$, $\top$, and $\bot$ are the Łukasiewiczian ones: $v(\phi \rightarrow \psi )=\mathrm {min}(1, (1-v(\phi ))+ v(\psi ))$, $v(\top )=1$, and $v(\bot )=0$. The expression $\phi \leftrightarrow \psi$ is an abbreviation of $(\phi \rightarrow \psi ) \wedge (\psi \rightarrow \phi )$.

Definition 1

$\varGamma \models _{{\mathbf{NC}}_{\mathbf{3}}} \psi$ iff, for each valuation v and for every $\phi$ such that $\phi \in \varGamma$, it holds that if, for every $\chi$ such that $\chi \in \varGamma \setminus \left\{ \phi \right\}$, $v(\chi )=1$, then

a) if $v(\phi ) = 1$, then $v(\psi ) = 1$ and b) if $v(\psi ) = 0$, then $v(\phi ) = 0$.

The first effect of Definition 1, according to Weir, is that both conjunction and disjunction do not standardly interact with the entailment relation. For example, $\phi$, $\lnot \phi \models _{{\textbf {NC}}_{\mathbf{3}}} \bot$, but $\phi \wedge \lnot \phi \not \models _{{\textbf {NC}}_{\mathbf{3}}} \bot$. Note that such behaviour of conjunction is not specific to ${{\textbf {NC}}}_{\mathbf{3}}$. There might be conjunctions which behave alike in logics, where an entailment relation is standardly definable via one designated value, i. e. as in $\mathbf{K}_3$. It is easy to check that it holds in logics with one designated value, where conjunction takes a value “1” if both conjuncts take a value “${1}/{2}$”.¹¹ Examples of such conjunctions are conjunction of Sette’s logic $\mathbf{P}^1$ (Sette, 1973) and conjunction of Béziau-Franceschetto’s logic ${\textbf {L3B}}$ (Beziau & Franceschetto, 2015). However, in contrast to $\mathbf{K}_3$, both $\mathbf{P}^1$ and ${\textbf {L3B}}$ have two designated values.

Another effect of Definition 1 is that some classical entailments are neo-classically invalid (Weir, 2013a, p. 101):¹²

“My proposal for a restriction on classical logic focuses on ‘minimax unsound’ rules, where the rule is nonetheless sound (as a one-step natural deduction inference) with respect to $\models _3$. Examples of such rules are $\lnot E$, $\rightarrow E$, $\vee E$ and disjunctive syllogism, e.g. in the latter case with P false and Q gappy, the minimum value of $\{ (P \vee Q), \lnot Q \}$ is ${1}/{2}$ whilst the conclusion P takes the false value 0. The (sole) proposed restriction on classical propositional logic is that in such minimax unsound rules any assumption on which both major and minor premiss depends must be ‘determinate”’.

The rule of disjunctive syllogism is neo-classically problematic in case both its premisses depend on the same formula(e). Classically, $\phi \models \chi$ follows from both $\phi \models \psi \vee \chi$ and $\phi \models \lnot \psi$ whereas that is not the case neo-classically.¹³

In order to get neo-classically valid entailments from such entailments, Weir proposes so called Determinacy of a sentence $\phi$ and Indeterminacy of a sentence $\phi$ (abbreviated as $D(\phi )$ and $I(\phi )$, respectively). $I(\phi )$ is an abbreviation of $(\phi \rightarrow \lnot \phi ) \wedge (\lnot \phi \rightarrow \phi )$ and $D(\phi )$ is $\lnot I(\phi )$. Note that $D(\phi )\in {\mathscr {L}}$ and $I(\phi ) \in {\mathscr {L}}$. Weir himself prefers $\phi \leftrightarrow \lnot \phi$ rather than $(\phi \rightarrow \lnot \phi ) \wedge (\lnot \phi \rightarrow \phi )$. We follow him despite $\leftrightarrow$ $\notin {\mathscr {L}}$. $\lnot D(\phi )$ and $I(\phi )$ are used synonymously in this paper.¹⁴ Getting back to the entailment in the previous passage, $D(\phi ), \phi \models _{{\mathbf{NC}}_3} \chi$ follows from $\phi \models _{{\mathbf{NC}}_3} \psi \vee \chi$ and $\phi \models _{{\mathbf{NC}}_3} \lnot \psi$.

This trick illustrates the Weirian idea. To be sure, it is not the case that this trick makes neo-classically invalid entailments valid. The trick is that whenever one detects a weak problematic indeterminate point in reasoning one is able to effectively determine it in a special way. Hence, in checking out a classical proof one has an option to improve it. In the simplest cases, to be sure, the premise $D(\phi )$ is derivable from initial premisses. So, the proposed determination does not affect the entailment in question. However, in general, one has to pay the price of making a classically valid entailment neo-classically valid by adding the needed determinacy formulae.

Let us conclude with the important features of determinacy highlighted by Weir. First, $D(\phi )$ is a classical tautology. Therefore, $v(D(\phi )) = 0$ if $v(\phi )={1}/{2}$ only. This is the reason for reading $D(\phi )$ as the determinacy of $\phi$.¹⁵ Second, $\models _{{\mathbf{NC}}_{\mathbf{3}}} D(\phi ) \leftrightarrow D(\lnot \phi ) \leftrightarrow D(\lnot \lnot \phi ) \leftrightarrow \ldots \leftrightarrow D(\lnot \ldots \lnot \phi )$. Hence, in adding determinacy formulae to a problematic entailment one could skip negation(s), confine oneself to $D(\phi )$, and decrease the complexity of added formulae.¹⁶ Third, $v(D \ldots (D(\phi )) \ldots ) = 1$. Hence, higher-order determinacy is ruled out (this fact will be discussed on page 14 below).

2.2 Correspondence Analysis for ${{\textbf {NC}}}_{\mathbf{3}}$

Let ${\mathscr {L}}_{(\circ )_k}$ be an extension of ${\mathscr {L}}$ by binary truth-functional operators $\circ _1 ,$ $\ldots ,$ $\circ _k$. The set ${\mathscr {F}}_{(\circ )_k}$ of all ${\mathscr {L}}_{(\circ )_k}$-formulae is defined in a standard way. The common name of the corresponding logics is ${{\mathbf{NC}}}^{(\circ )_{ k }}_3$.

Definition 2

(Single  entry  correspondence (Kooi & Tamminga, 2012; Tamminga, 2014)) Let $\varGamma \subseteq {\mathscr {F}}_{(\circ )_k}$. Let $x,y,z \in \{1,{1}/{2},0\}$. Then the truth table entry $f_{\circ }(x,y)=z$ is characterized by an inference scheme $\varGamma /\phi$, if

$$\begin{aligned} f_{\circ }(x,y)=z \text {~if and only if~} \varGamma \models \phi . \end{aligned}$$

Definition 2 captures the key essence of CA: one-to-one correspondence between entries of the truth table for a binary connective and natural deduction rules for this connective. Below, in Sect. 5 there is a thorough explanation how this one-to-one correspondence works. In the further exposition, we use “$\models$” as an abbreviation for “$\models _{{\mathbf{NC}}_3^{(\circ )_{ k }}}$”.

Theorem 1

Let $\phi ,\varphi ,\chi \in {\mathscr {F}}_{(\circ )_k}$.¹⁷ Then:¹⁸

$$\begin{aligned} f_{\circ }(0,0)= & {} \left\{ \begin{array}{ccl} 0 &{} \;\;\text {iff}\;\; &{}\ \lnot \phi , \lnot \psi , D(\phi ), D(\psi ) \models D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi ) \\ {1}/{2}&{} \;\;\text {iff}\;\; &{} \lnot \phi , \lnot \psi , D(\phi ), D(\psi ) \models I(\phi \circ \psi )\\ 1 &{} \;\;\text {iff}\;\; &{}\ \lnot \phi , \lnot \psi , D(\phi ), D(\psi ) \models D(\phi \circ \psi )\wedge (\phi \circ \psi ) \\ \end{array} \right. \\ f_{\circ }(0,{1}/{2})= & {} \left\{ \begin{array}{ccl} 0 &{} \;\;\text {iff}\;\; &{}\ \lnot \phi , D(\phi ), I(\psi ) \models D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi ) \\ {1}/{2}&{} \;\;\text {iff}\;\; &{} \lnot \phi , D(\phi ), I(\psi ) \models I(\phi \circ \psi ) \\ 1 &{} \;\;\text {iff}\;\; &{}\ \lnot \phi , D(\phi ), I(\psi ) \models D(\phi \circ \psi )\wedge (\phi \circ \psi )\\ \end{array} \right. \\ f_{\circ }(0,1)= & {} \left\{ \begin{array}{ccl} 0 &{} \;\;\text {iff}\;\; &{}\ \lnot \phi , \psi , D(\phi ), D(\psi ) \models D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi ) \\ {1}/{2}&{} \;\;\text {iff}\;\; &{} \lnot \phi , \psi , D(\phi ), D(\psi ) \models I(\phi \circ \psi )\\ 1 &{} \;\;\text {iff}\;\; &{}\ \lnot \phi , \psi , D(\phi ), D(\psi ) \models D(\phi \circ \psi )\wedge (\phi \circ \psi ) \\ \end{array} \right. \\ f_{\circ }({1}/{2},0)= & {} \left\{ \begin{array}{ccl} 0 &{} \;\;\text {iff}\;\; &{}\ I(\phi ), \lnot \psi , D(\psi ) \models D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi )\\ {1}/{2}&{} \;\;\text {iff}\;\; &{} I(\phi ), \lnot \psi , D(\psi ) \models I(\phi \circ \psi ) \\ 1 &{} \;\;\text {iff}\;\; &{}\ I(\phi ), \lnot \psi , D(\psi ) \models D(\phi \circ \psi )\wedge (\phi \circ \psi ) \\ \end{array} \right. \\ f_{\circ }({1}/{2},{1}/{2})= & {} \left\{ \begin{array}{ccl} 0 &{} \;\;\text {iff}\;\; &{}\ I(\phi ), I(\psi ) \models D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi ) \\ {1}/{2}&{} \;\;\text {iff}\;\; &{}\ I(\phi ), I(\psi ) \models I(\phi \circ \psi ) \\ 1 &{} \;\;\text {iff}\;\; &{}\ I(\phi ), I(\psi ) \models D(\phi \circ \psi )\wedge (\phi \circ \psi ) \\ \end{array} \right. \\ f_{\circ }({1}/{2},1)= & {} \left\{ \begin{array}{ccl} 0 &{} \;\;\text {iff}\;\; &{}\ I(\phi ), \psi , D(\psi ), \models D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi )\\ {1}/{2}&{} \;\;\text {iff}\;\; &{} I(\phi ), \psi , D(\psi ), \models I(\phi \circ \psi ) \\ 1 &{} \;\;\text {iff}\;\; &{}\ I(\phi ), \psi , D(\psi ), \models D(\phi \circ \psi )\wedge (\phi \circ \psi ) \\ \end{array} \right. \\ f_{\circ }(1,0)= & {} \left\{ \begin{array}{ccl} 0 &{} \;\;\text {iff}\;\; &{}\ \phi , \lnot \psi , D(\phi ), D(\psi ) \models D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi ) \\ {1}/{2}&{} \;\;\text {iff}\;\; &{} \phi , \lnot \psi , D(\phi ), D(\psi ) \models I(\phi \circ \psi )\\ 1 &{} \;\;\text {iff}\;\; &{}\ \phi , \lnot \psi , D(\phi ), D(\psi ) \models D(\phi \circ \psi )\wedge (\phi \circ \psi ) \\ \end{array} \right. \\ f_{\circ }(1,{1}/{2})= & {} \left\{ \begin{array}{ccl} 0 &{} \;\;\text {iff}\;\; &{}\ \phi , D(\phi ), I(\psi ) \models D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi ) \\ {1}/{2}&{} \;\;\text {iff}\;\; &{} \phi , D(\phi ), I(\psi ) \models I(\phi \circ \psi ) \\ 1 &{} \;\;\text {iff}\;\; &{}\ \phi , D(\phi ), I(\psi ) \models D(\phi \circ \psi )\wedge (\phi \circ \psi ) \\ \end{array} \right. \\ f_{\circ }(1,1)= & {} \left\{ \begin{array}{ccl} 0 &{} \;\;\text {iff}\;\; &{}\ \phi , \psi , D(\phi ), D(\psi ) \models D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi ) \\ {1}/{2}&{} \;\;\text {iff}\;\; &{} \phi , \psi , D(\phi ), D(\psi ) \models I(\phi \circ \psi )\\ 1 &{} \;\;\text {iff}\;\; &{}\ \phi , \psi , D(\phi ), D(\psi ) \models D(\phi \circ \psi )\wedge (\phi \circ \psi ) \\ \end{array} \right. \\ \end{aligned}$$

Proof

We confine ourselves to the cases $f_{\circ }(0,0)=0$, $f_{\circ }(0,0)={1}/{2}$, and $f_{\circ }({1}/{2},{1}/{2})={1}/{2}$. The remaining ones are analogical.

Case $f_{\circ }(0,0)=0$. (From left to right)¹⁹ Suppose $\lnot \phi , \lnot \psi , D(\phi ), D(\psi ) \not \models D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi )$. Then there is a valuation v such that downwards truth-preservation fails or there is a valuation w such that upwards falsity-preservation fails. Let us start with the failure of downwards truth-preservation which implies $v(\lnot \phi )=v(\lnot \psi )=v(D(\phi ))=v(D(\psi )) = 1$ and ($v(D(\phi \circ \psi )) \ne 1$ or $v(\lnot (\phi \circ \psi ))\ne 1$). In the former case, $v(\phi )=v(\psi )= 0$ and $v(D(\phi \circ \psi )) =0$.²⁰ Hence, $v(\phi )=v(\psi )=0$ and $v(\phi \circ \psi ) ={1}/{2}$. Contradiction. In the latter case, contradiction is derived from $v(\phi )=v(\psi )= 0$ and $v(\phi \circ \psi ) \ne 0$.

With regard to upwards falsity-preservation, one must consider four cases depending on which formulae left of the double corkscrew are assumed to take a value distinct from 0: (1) $w(\lnot \phi )\ne 0$, $w(\lnot \psi )= w(D(\phi ))= w(D(\psi )) = 1$ and $w(D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi ))= 0$; (2) $w(\lnot \psi )\ne 0,$ $w(\lnot \phi )=w(D(\phi ))=w(D(\psi )) = 1$ and $w(D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi ))= 0$; (3) $w(D(\phi )) \ne 0,$ $w(\lnot \phi )=w(\lnot \psi )=w(D(\psi )) = 1$ and $w(D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi ))= 0$; (4) $w(D(\psi )) \ne 0,$ $w(\lnot \phi )=w(\lnot \psi )=w(D(\phi )) = 1$ and $w(D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi ))= 0$. Note that the assumption is that $f_{\circ }(0,0)=0$.

In the case (1), $w(\phi )\ne 1$ and $w(D(\phi )) = 1$ imply $w(\phi ) = 0$. On the other hand, $w(D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi ))= 0$ implies $w(\phi \circ \psi ) = {1}/{2}$ or $w (\phi \circ \psi )= 1$. Both alternatives contradict the assumption.

The case (2) is considered by analogy with the case (1).

The cases (3) and (4) are also considered by analogy with the case (1). However, arriving at contradiction is shorter due to $w(\phi )=w(\psi )=0$.

Case $f_{\circ }(0,0)=0$. (From right to left) By contraposition, showing that if $\lnot \phi , \lnot \psi , D(\phi ), D(\psi ) \models D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi )$, then $f_{\circ }(0,0)=0$ amounts to showing that if $f_{\circ }(0,0)\ne 0$, then $\lnot \phi , \lnot \psi , D(\phi ), D(\psi ) \not \models D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi )$. With regard to the latter, it is easy to see that if $w(\phi )=w(\psi )=0$ and $w(\phi \circ \psi )\ne 0$, then downwards truth-preservation fails.

Case $f_{\circ }(0,0)={1}/{2}$. (From left to right) Suppose $\lnot \phi , \lnot \psi , D(\phi ), D(\psi ) \not \models I(\phi \circ \psi )$. Then there is a valuation v such that downwards truth-preservation fails or there is a valuation w such that upwards falsity-preservation fails. Let us start with the failure of downwards truth-preservation which implies there is a valuation v such that $v(\lnot \phi )=v(\lnot \psi )=v(D(\phi ))=v(D(\psi ))= 1$ and $v(I(\phi \circ \psi )) \ne 1$. Then $v(\phi )=v(\psi )=0$ and $v(I(\phi \circ \psi )) =0$. Hence, $v(\phi \circ \psi ) \ne {1}/{2}$.²¹ Contradiction.

With regard to upwards falsity-preservation, one must consider four cases depending on which formulae left of the double corkscrew are assumed to take a value distinct from 0: (1) $w(\lnot \phi )\ne 0$, $w(\lnot \psi )=w(D(\phi ))=w(D(\psi )) = 1$ and $w(I(\phi \circ \psi )) = 0$; (2) $w(\lnot \psi ) \ne 0$, $w(\lnot \phi )=w(D(\phi ))=w(D(\psi )) = 1$ and $w(I(\phi \circ \psi )) = 0$; (3) $w(D(\phi ))\ne 0$, $w(\lnot \phi )=w(\lnot \psi )=w(D(\psi ))= 1$ and $w(I(\phi \circ \psi )) = 0$; (4) $w(D(\psi ))\ne 0$, $w(\lnot \phi )=w(\lnot \psi )=w(D(\phi ))= 1$ and $w(I(\phi \circ \psi )) = 0$. Note that the assumption is that $f_{\circ }(0,0)={1}/{2}$.

In the case (1), $w(\lnot \phi )\ne 0$ implies $w(\phi )\ne 1$. Together with $w(D(\phi )) = 1$, it implies $w(\phi )= 0$. On the other hand, $w(I(\phi \circ \psi )) = 0$ implies $w(\phi \circ \psi )\ne {1}/{2}$. Finally, $w(\lnot \psi )= 1$ implies $w(\psi )=0$. Contradiction.

The case (2) is considered by analogy with the case (1).

The cases (3–4) boil down to the subcase that $w(\phi )=w(\psi )=0$ and $w(I(\phi \circ \psi )) = 0$ which implies $w(\phi )=w(\psi )=0$ and $w(\phi \circ \psi ) \ne {1}/{2}$. Contradiction.

Case $f_{\circ }(0,0)={1}/{2}$. (From right to left) By contraposition, showing that if $\lnot \phi , \lnot \psi , D(\phi ), D(\psi ) \models I(\phi \circ \psi )$, then $f_{\circ }(0,0)={1}/{2}$ amounts to showing that if $f_{\circ }(0,0)\ne {1}/{2}$, then $\lnot \phi , \lnot \psi , D(\phi ), D(\psi ) \not \models I(\phi \circ \psi )$. With regard to the latter, it is easy to see that if $w(\phi )=w(\psi )=0$, and ($w(\phi \circ \psi ) =0$ or $w(\phi \circ \psi ) =1$), downwards truth-preservation fails.

Case $f_{\circ }({1}/{2},{1}/{2})={1}/{2}$. Suppose $I(\phi ), I(\psi ) \not \models I(\phi \circ \psi )$. Then there is a valuation v such that downwards truth-preservation fails or there is a valuation w such that upwards falsity-preservation fails. Let us start with the failure of downwards truth-preservation which implies there is a valuation v such that $v(I(\phi ))=v(I(\phi ))= 1$ and $v(I(\phi \circ \psi )) \ne 1$. Then $v(\phi )=v(\psi )={1}/{2}$ and $w(\phi \circ \psi ) \ne {1}/{2}$. Contradiction.

With regard to upwards falsity-preservation, one must consider two cases depending on which formulae left of the double corkscrew are assumed to take a value distinct from 0: (1) $w(I(\phi ))\ne 0$, $w(I(\psi )) = 1$ and $w(I(\phi \circ \psi )) = 0$ and (2) $w(I(\psi ))\ne 0$, $w(I(\phi )) = 1$ and $w(I(\phi \circ \psi )) = 0$. Note that the assumption is that $f_{\circ }({1}/{2},{1}/{2})={1}/{2}$.

In the case (1), $w(I(\phi ))\ne 0$ implies $w(I(\phi ))= 1$ which, in turn, implies $w(\phi )= {1}/{2}$. On the other hand, $w(I(\phi \circ \psi )) = 0$ implies $w(\phi \circ \psi )\ne {1}/{2}$. Finally, $w(I(\psi )) = 1$ implies $w(\psi )= {1}/{2}$. Contradiction.

The case (2) is considered by analogy with the case (1).

Case $f_{\circ }({1}/{2},{1}/{2})={1}/{2}$. (From right to left) By contraposition, showing that if $I(\phi ), I(\psi ) \models I(\phi \circ \psi )$, then $f_{\circ }({1}/{2},{1}/{2})={1}/{2}$ amounts to showing that if $f_{\circ }({1}/{2},{1}/{2})\ne {1}/{2}$, then $I(\phi ), I(\psi ) \not \models I(\phi \circ \psi )$. With regard to the latter, it is easy to see that if $w(\phi )=w(\psi )={1}/{2}$, and ($w(\phi \circ \psi ) =0$ or $w(\phi \circ \psi ) =1$), downwards truth-preservation fails. $\square$

We would like to stress that the equivalences above are, certainly, not unique.

This fact clearly indicates that obtaining CA, still, remains a creative and non-algorithmic task. Therefore, it is a future roadmap to make CA a routine and algorithmic task à la (Avron et al., 2007; Avron & Konikowska, 2005).

3 Natural Deduction System $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$

3.1 The Rules of Natural Deduction System for ${{\mathbf{NC}}}_3$

The rules of Weir’s natural deduction system for ${{\mathbf{NC}}}_3$ denoted here by $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$ operate on a line which is a quadruple $\langle hs , nl , fr , an\rangle$, where

• $hs$ stands for a (possibly, empty) set of hypotheses $fr$ depends on,

• $nl$ stands for a number of a line which $fr$ occurs on,

• $fr$ stands for a formula which is derivable on a line,

• an stands for an analysis of $fr$ and specifies whether $fr$ is a hypothesis, or an axiom, or is derived from the previous lines via some $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-rule.

For a line which has a standard structure of a sequent, then $hs$, $fr$, and $nl$ are referred to as the antecedent of, consequent of, and unary corkscrew of a sequent, respectively. For example, the line

is to mean the sequent $\psi \vdash \chi$. The letters $\alpha$ and $\beta$ with subscripts run over sequents.

The capital I or E stands for an ‘introduction’ and ‘elimination’, respectively.

Weir notes that the rule of Hypothesis includes thinning.²² The Weirian notation ‘(1)’ is not to mean that H is applicable to the first line only.²³

Let us kindly thank Alan Weir for the following explication of the notation (personal communication): “Here I indexes all the sentences in common to assumption sets X and $\varXi \cup Z$, and so (4.i) can be a large (finite, in the finitary systems) set of sub-proofs, collapsed to one line in this non tree-form format. I use square brackets as in [4.i] to indicate determinacy assumptions used to implement the restrictions which can block transitivity”. In derivations themselves, there are no i and the enumeration of lines is traditional.²⁴

Though Weir utilises the same name $\lnot I$ for the two previous rules, we would like to dub them differently: CL and INT stand for ‘classical’ and ‘intuitionistic’ versions of the Weirian $\lnot I$, respectively.

Note that Weir dubs it the ‘Mingle’ rule in Weir (2013b, p. 3) in order to stress the fact that it is derivable in Anderson and Belnap (1975) via the mingle axiom $\phi \rightarrow (\phi \rightarrow \phi )$. For the reason that such a name is not in line with the traditional usage of the term mingle rule (Kamide, 2002), we dub it M rather than Mingle.

DPC and DPD stand for distributivity principle for conjunction and disjunction, respectively.

LEM stands for the law of excluded middle restricted to determinacy.

Being a Lemmon-style (Suppes-style or a system with dependencies) natural deduction system,²⁵$\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$ has the distinctive feature of such systems, viz., a device of listing all the hypotheses which a formula follows from (depends on or rests on) in a special leftmost column. It allows for easily checking out the hypotheses on which premises of a rule are dependent on. Hence, an advantage of $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$ is the simplicity and clearness of the notion of a derivation for it (Lemmon, 1998; Suppes, 1957; Weir, 2013a, p. 31, pp. 8–9, p. 5).

Our definition is a slight modification of the one by Pavlović (2015, p. 79).

Definition 3

A derivation in $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$ ($\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-derivation) is a non-empty finite sequence of lines such that each line results from an application of some $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-rule to lines occurring earlier in the sequence.

A derivation in $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$ of a formula $\phi$ from a (possibly, empty) set of formulae $\varGamma$ is a derivation in $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$ such that the last line k of it is $\langle \varGamma , k, \phi , an\rangle$.

If $\varGamma = \varnothing$, then $\phi$ is said to be a theorem of $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$.

4 Examples of $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-derivations and the $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-derivability of some new $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-rules

This section is devoted to examples of $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-derivations. Some of them illustrate that the $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-derivability might be classical or neo-classical. The choice of examples is governed by metatheorems in Sect. 5.

Note that in the examples below, sets of hypotheses might contain a number of a formula instead of the formula itself or a mix of numbers and formulae. This feature, adopted for space-saving reasons, is characteristic of a Lemmon-style derivation (in contradistinction to, say, a sequent-style derivation) and is employed from the first pages of the textbooks (Lemmon, 1998; Suppes, 1957) and by Weir (2013b). Of course, any number is replaceable with the corresponding hypothesis because every hypothesis has its unique number in a derivation.

Example 1

$(p \rightarrow q) \rightarrow ((q \rightarrow r) \rightarrow ( p \rightarrow r))$ is a $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-theorem.

Example 2

$\lnot \lnot p \rightarrow p$ is a $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-theorem.

Examples 1–2 are used in showing the $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-derivability of the rule $\lnot \lnot E$:

Note that there are two ways to show its derivability. If $\lnot \phi \not \in X$, then the way is classical as in Example 3.1 below. Otherwise, it is neo-classical as in Example 3.2 below, where $X= \{X', \lnot \phi \}$.

Example 3.1

$\lnot \lnot E$ is $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-derivable if $\lnot \phi \not \in X$.

Example 3.2

$\lnot \lnot E$ is $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-derivable if $\lnot \phi \in X$.²⁶

In the same fashion, the $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-derivability of the rules $\lnot \lnot I$, ${\lnot \vee } E$, and ${\lnot \vee } I$ is shown.

Example 4

$D(p) \rightarrow D(\lnot p)$ is a $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-theorem.

Example 4 shows the $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-derivability of the rule $\lnot I_{D}$ which is to be read as “introduction of negation inside determinacy”.²⁷ In the same fashion, both $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-theoremhood of $D(\lnot p) \rightarrow D(p)$ and the $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-derivability of the rule $\lnot E_{D}$ (“elimination of negation inside determinacy”) are shown.

$\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$ enjoys a restricted version of the cut rule.

Its justification readily boils down to the one for $\rightarrow E$.

Let $D^{0}(\phi )$ be $\phi$ and $D^{n+1}$ be $D(D^{n}(\phi ))$. The case with $D^{m}I(\phi )$ is similar. Then higher-order determinacy, i. e. determinacy of determinacy or determinacy of indeterminacy, for instance, is ruled out by²⁸

Lemma 1

[Proposition 1 (Weir, 2013b)]. $\vdash D^{n}(\phi )$, for all $n \ge 2$, and $\vdash D^{m+1}I(\phi )$, for all $m \ge 0$.

Hence, two rules which we dub D(D) and D(I), respectively, are justified.²⁹

Let us remind the reader that in applying $\rightarrow E$, $\vee E$, and $\lnot E$ she has to check for an overlap between the premises of these rules and, if found, to determinate each formula from the overlap. However, derived classical, as Weir dubs it, variants of these rules are justified by³⁰

Lemma 4

[Proposition 2 (Weir, 2013b)]. Where we have proofs of the determinacy of the succedents of a premiss of $\lnot E$ and $\rightarrow E$ rules, and both disjuncts of the major premiss succedent of the $\vee E$ rule, then the full classical rule is neo-classically derivable, that is we do not need to establish the determinacy of the overlapping assumptions.

We denote them $\rightarrow E_{CL}$, $\vee E_{CL}$, and $\lnot E_{CL}$.

Another version of $\lnot E_{CL}$ is obtainable via replacing $D(\phi )$ with $D(\lnot \phi )$.

Another version of $\rightarrow E_{CL}$ is obtained via replacing $D(\phi )$ with $D(\phi \rightarrow \psi )$.

Cut, also, has a derived classical version $Cut_{CL}$ whose justification easily follows from the justification of $\rightarrow E_{CL}$. Another version of $Cut_{CL}$ is obtainable via replacing $D(\phi )$ with $D(\phi \rightarrow \psi )$.

The rule of disjunctive syllogism is justified in Weir (2013a, p. 101):

It is not difficult to justify rules of thinning³¹ and $I_E$:

At last, let us remind the reader of the entailments from footnote 16 above which proofs we do not present here due to space reasons only.

5 Natural Deduction Systems $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}^{(\circ )_{ k }}$ for the binary extensions of ${\mathbf{NC}}_{\mathbf{3}}$

Here we demonstrate the way CA allows one to obtain the rules of a natural deduction system for each binary extension of ${\mathbf{NC}}_{\mathbf{3}}$.

Suppose we are interested in the extension with exclusive disjunction $\veebar$ and take two entries as examples: $f_\circ ({1}/{2},{1}/{2}) = 0$ and $f_\circ (1, 1)=0$.

In the former entry, we need the equivalence $f_{\circ }({1}/{2},{1}/{2}) = 0$ iff $I(\phi ), I(\psi ) \models D(\phi \veebar \lnot \psi )\wedge \lnot (\phi \veebar \psi )$. So, $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}^{\veebar }$ contains the rule:

In the latter entry, we need the equivalence $f_{\circ }(1, 1)= 0$ iff $\phi , \psi , D(\phi ), D(\psi ) \models D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi )$. So, $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}^{\veebar }$ contains also the rule:

Thus, we obtain exactly nine rules for $\veebar$ (or any other connective) because its truth-table has nine entries and because each rule obtainable via CA is independent.³² We hope the reader easily manages to obtain the remaining rules for $\veebar$ herself. Sure, the rules look clumsy and dissimilar to the conventional ones. Arguably, this phenomenon is effected by the generality of CA. In practice, the number of rules for a connective is (considerably) fewer than the number of entries in its truth-table.³³ At present, the problem of finding the general (and algorithmically implemented) way to combine both conventional rules and the ones obtainable via CA, is still open.

We direct the reader’s attention to the difference between the Weirian rules and the rules obtained via CA with respect to introducing determinacy formulae into a derivation. In the former rules, one determines every hypothesis occurring in an overlap of sets in antecedents of premises of a rule. In the latter rules, one needs not check up the sets in question for overlapping. The needed determinacies have already occurred in the antecedents of the rules. To put it another way, the rules obtainable via CA are local rather than global in the Weirian sense (Weir, 2013a, p. 101). We believe this is another effect caused by the generality of CA, where $\circ$ might be any connective and, hence, has any truth-table. In a situation like this, there seems to be no alternative way to preserve soundness than guaranteeing it locally, at every line of a derivation.³⁴

6 Soundness and Completeness of $\mathfrak {ND}^{(\circ )_{ k }}_{{\mathbf{NC}}_{\mathbf{3}}}$

Let us remind the reader that ${\mathscr {L}}_{(\circ )_k}$ is an extension of ${\mathscr {L}}$ by binary truth-functional operators $\circ _1 ,$ $\ldots ,$ $\circ _k$, that ${\mathscr {F}}_{(\circ )_k}$ is the set of all ${\mathscr {L}}_{(\circ )_k}$-formulae defined in a standard way, and ${{\mathbf{NC}}}^{(\circ )_{ k }}_3$ is the common name of the corresponding logics.

Theorem 2

(Soundness) For each $\varGamma \subseteq {\mathscr {F}}_{(\circ )_k}$ and $\phi \in {\mathscr {F}}_{(\circ )_k}$, it holds that if $\varGamma \vdash _{{\mathbf{NC}}^{(\circ )_{ k }}_3} \phi$, then $\varGamma \models _{{\mathbf{NC}}^{(\circ )_{ k }}_3} \phi$.

Proof

is by induction on the depth of a derivation defined in the usual way. Note that each $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}$-rule is shown to be valid in Weir (2013a, p. 102) and Weir (2013b, pp. 5–7). The validity of $\mathfrak {ND}^{(\circ )_{ k }}_{{\mathbf{NC}}_{\mathbf{3}}}$-rules is shown in Theorem 1. $\square$

We would like to precede the completeness theorem with addressing the first referee’s point of view that “the method of prime theories simply cannot work for a logic without generalized transitivity, since this idea of ‘containing its own consequences’ seems strongly tied up with transitivity” and his (her) kind recommendation to look “at the work of Frankowski, particularly (Frankowski, 2004a), for ideas about related methods that might be more suitable”.

Let us start with acknowledging that the first referee’s point of view is fair, and the Henkinian method in the form suggested in the embryonic draft of this paper is not applicable to ${\mathbf{NC}}_{\mathbf{3}}$. Roughly, the standard condition of closure — $\varGamma \vdash \phi$ iff $\phi \in \varGamma$ — that holds of the Henkin-type sets used in Kooi and Tamminga’s completeness proofs (Kooi & Tamminga, 2012; Tamminga, 2014), fails for the equivalent sets in ${\mathbf{NC}}_{\mathbf{3}}$, as Weir notes (Weir, 2013b, pp. 8–9). As a result, below we employ the Henkinian method not in the standard form, but in the form that Weir tailors this method to the needs of ${\mathbf{NC}}_{\mathbf{3}}$ in Weir (2013b, pp. 9–18) following both Weir’s and the second referee’s amendments to this exposition.

Second, the need for modification of the Henkinian method to non-transitive approaches is not confined to the Weirian one only. For example, Wansing and Skurt wonder “if identity is deprived of transitivity, what does that mean for the Henkin-style completeness proof for classical first-order logic with the impoverished notion” and show how “the Henkin-style completeness proof for classical first-order logic with identity can thus be modified” (Wansing & Skurt, 2019, p. 536, 542).

Lastly, let us agree with the first referee’s kind recommendation that it is instructive to apply (see (Barrio et al., 2019) for one of applications) the method of Frankowski (2004a, 2004b) who underlines that his approach is closely related to the one of Malinowski (1990), to the logics discussed in this paper. With all due respect, both the first and the second points above together with the non-embryonic completeness proof below make applying the Frankowskian method a topic of a future paper.

The completeness theorem below is proved via the Henkinian paradigmatic method with $\mathfrak {ND}^{(\circ )_{ k }}_{{\mathbf{NC}}_{\mathbf{3}}}$-specific modifications and discriminations. We base our proof on the Weirian proof of the completeness theorem for ${\mathbf{NC}}_{\mathbf{3}}$ (Weir, 2013b, pp. 8–18). We start with auxiliary definitions and lemmata adapting the Weirian original terminology for $\vdash _{\mathfrak {ND}_{{\mathbf{NC}}_3}}$ to $\vdash _{\mathfrak {ND}_{{\mathbf{NC}}_3^{(\circ )_{ k }}}}$. In the remaining proofs and definitions from this Section, therefore, $\vdash$ stands for $\vdash _{\mathfrak {ND}_{{\mathbf{NC}}_3^{(\circ )_{ k }}}}$, and $\phi , \psi , \chi \in {\mathscr {F}}_{(\circ )_k}$.

Definition 4

Weir (2013b, p. 9) A set $\varGamma$ is

• 1. Weakly consistent iff $\varGamma \not \vdash \bot$;

• 2. Strongly consistent iff it is not the case that $\varGamma \vdash \phi$ and $\varGamma \vdash \lnot \phi$;

• 3. Negation-complete iff $\phi \in \varGamma$ or $\lnot \phi \in \varGamma$;

• 4. Negation-complete$_{1}$ iff $\varGamma \vdash \phi$ or $\varGamma \vdash \lnot \phi$.

Note that Weir employs special 1 and 4 rather than standard 2 and 3, respectively, employed in the Tammingian (in fact, standard) proof. The need for these discriminations is argued with the following

Lemma 5

(Weir 2013b, pp. 8–9). It is not the case that $\varGamma \vdash \phi$ iff $\phi \in \varGamma$.

Let us show how it works on the example of a weakly consistent $\varGamma = \{ \phi \wedge \lnot \phi \}$³⁵ suggested by the first referee. So, we start with the hypothesis $\phi \wedge \lnot \phi \ \vdash \phi \wedge \lnot \phi$. By $\wedge E_{1}$, we derive $\varGamma \vdash \phi$. (The case with $\wedge E_{2}$ is the same.) However, due to the failure of closure, this does not mean we should expand $\varGamma$ to a weakly inconsistent $\{ \phi \wedge \lnot \phi , \phi \}$.³⁶ On the other hand, we could continue and by $\wedge E_{2}$, derive $\varGamma \vdash \lnot \phi$. Again, this does not mean we should expand $\varGamma$ to a weakly inconsistent $\{ \phi \wedge \lnot \phi , \lnot \phi \}$. Moreover, $\phi \wedge \lnot \phi \vdash \phi$ and $\phi \wedge \lnot \phi \vdash \lnot \phi$ do not allow us to derive $\phi \wedge \lnot \phi \vdash \bot$, by $\lnot E$ because we lack determinacy of $\phi \wedge \lnot \phi$ that both $\phi$ and $\lnot \phi$ depend on. The failure of closure, nevertheless, does not prevent us from employing the Henkinian method. Instead of assigning truth-values of formulae in a maximally (weakly) consistent set standardly in terms of set-theoretic membership, we will do it in terms of the $\mathfrak {ND}^{(\circ )_{ k }}_{{\mathbf{NC}}_{\mathbf{3}}}$-derivability following Weir (2013b) (see the beginning of Lemma 11).

Now let us get back to the completeness proof and list all the preliminary definitions and lemmata that Weir employs (Weir, 2013b, pp. 8–18).

Lemma 6

Weir (2013b, pp. 8–9) Let $\varGamma$ be weakly consistent. Let $\varDelta$ be its expansion by the following Henkin-style construction, where $F_1,F_2,\ldots$ is an enumeration of all elements of ${\mathscr {F}}_{(\circ )_k}$:

$$\begin{aligned} \varDelta _1&= \varGamma ,\\ \varDelta _{j+1}&= \left\{ \begin{array}{cl} \varDelta _{j} \cup \{F_{j+1}\} , &{} if \varDelta _{j} \cup \lnot \{F_{j+1}\}\not \vdash \bot ,\\ \varDelta _{j} , &{} otherwise, \end{array}\right. \\ \varDelta&=\bigcup ^{\infty }_{j=1}\varDelta _{j}. \end{aligned}$$

Then $\varDelta$ is both weakly consistent and negation-complete$_{1}$.

In what follows, both $\varGamma$ and $\varDelta$ will be employed in the sense of Lemma 6.

Let us remind the reader that Weir’s Lemma 1, Proposition 1, Lemma 2, and Proposition 2 are Lemma 2 on page 14, Lemma 1 on page 14, Lemma 3 on page 14, and Lemma 4 on page 14, respectively.

Lemma 7

[Proposition 3 (Weir, 2013b)]. If $\varDelta \vdash _{\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}} \phi$ and $\varDelta \not \vdash _{\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}} \lnot \phi$, then $\varDelta \vdash _{\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}} D(\phi )$.

Another version of Lemma 7 is as follows: If $\varDelta \not \vdash _{\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}} \phi$ and $\varDelta \vdash _{\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}} \lnot \phi$, then $\varDelta \vdash _{\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}} D(\phi )$.

Lemma 7 justifies the following

Lemma 8

[Proposition 4 (Weir, 2013b) (primality)]. If $\varDelta \vdash _{\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}} \phi \vee \psi$, then $\varDelta \vdash _{\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}} \phi$ or $\varDelta \vdash _{\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}} \psi$.

Lemma 9

[Lemma 3 (Weir, 2013b)]. $I(\phi ), I(\psi ) \vdash _{\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}} \phi \rightarrow \psi$.

Lemma 10

[Lemma 4 (Weir, 2013b)]. If $\varDelta \vdash _{\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}} \lnot (\phi \rightarrow \psi )$, then $\varDelta \vdash _{\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}}} D(\phi ) \vee D(\psi )$.

Definition 5

A quasi-model or q-model for a set $\varGamma$ is a model such that $v(\phi ) \ne 0$, for each $\phi \in \varGamma$.

Lemmata  4, 7, 8, 9, and 10 justify the following

Lemma 11

[Proposition 5 (Weir, 2013b)] Let the canonical valuation v for the negation-complete$_{1}$ weakly consistent Henkin set $\varDelta$ be the function v generated from the semantic clauses for the connectives by extending the following assignment of truth values to propositional variables: $v(A) = 1$ iff $\varDelta \vdash A, \varDelta \not \vdash \lnot A$; $v(A) = 0$ iff $\varDelta \not \vdash A, \varDelta \vdash \lnot A$, and $v(A) = {1}/{2}$ iff $\varDelta \vdash A, \varDelta \vdash \lnot A$. For the canonical model valuation v for Henkin set $\varDelta$ the following holds:

• (1) $v(\varphi ) = 1$ iff $\varDelta \vdash \varphi , \varDelta \not \vdash \lnot \varphi$;

• (2) $v(\varphi ) = 0$ iff $\varDelta \not \vdash \varphi , \varDelta \vdash \lnot \varphi$;

• (3) $v(\varphi ) = {1}/{2}$ iff $\varDelta \vdash \varphi , \varDelta \vdash \lnot \varphi$

(negation-completeness$_{1}$ of $\varDelta$ rules out the possibility of neither $\phi$ nor its negation being provable).

Proof

The cases (1)–(3) for the other connectives than $\circ$ are proven by Weir. We are left to prove them for $\circ$.

Case (1) from left to right. Suppose $v(\phi \circ \psi ) = 1$. Let us consider $f_{\circ } (0,0)=1$ and $f_{\circ }({1}/{2},{1}/{2}) =1$. The 7 others are analogous.

$f_{\circ } (0,0)=1$. So, $v(\phi )=v(\psi )=0$. By IH, $\varDelta \not \vdash \phi , \varDelta \vdash \lnot \phi , \varDelta \not \vdash \psi , \varDelta \vdash \lnot \psi$. By Lemma 7, it follows that $\varDelta \vdash D(\lnot \phi )$ and $\varDelta \vdash D(\lnot \psi )$. Then $R_{\circ }(0,0,1)$ is a rule of $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ and the proof runs as follows, where $D(\phi \circ \psi ) \wedge (\phi \circ \psi )$ is denoted by $\omega$.

Now let us remind the reader footnote 18 caused by the second referee’s remark that both non-triviality of $\varDelta$ and the proof above that $\varDelta \vdash \phi \circ \psi$ do not imply that $\varDelta \not \vdash \lnot (\phi \circ \psi )$, i. e. the needed half of the condition for $v(\phi \circ \psi )= 1$.

In order to show that $\varDelta \not \vdash \lnot (\phi \circ \psi )$ we reason for the sake of contradiction, i. e. we assume that $\varDelta \vdash \lnot (\phi \circ \psi )$. This assumption, $\varDelta \vdash \phi \circ \psi$, and step 15 imply, by $\lnot E_{CL}$, that $\varDelta \vdash \bot$, i. e. triviality of $\varDelta$. And this fact contradicts the condition that $\varDelta$ is non-trivial.

$f_{\circ }({1}/{2},{1}/{2},1)$. So, $v(\phi )=v(\psi )={1}/{2}$. By IH, $\varDelta \vdash \phi , \varDelta \vdash \lnot \phi , \varDelta \vdash \psi , \varDelta \vdash \lnot \psi$. Then $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ has $R_{\circ }({1}/{2},{1}/{2},1)$. So, the proof runs as follows.

The justification that $\varDelta \not \vdash \lnot (\phi \circ \psi )$ is analogous to the above proof on page 19.

Case (1) from right to left. Suppose $\varDelta \vdash \phi \circ \psi$ and $\varDelta \not \vdash \lnot (\phi \circ \psi )$. Hence, by Lemma 7, $\varDelta \vdash D(\phi \circ \psi )$.

Because $\varDelta$ is negation-complete$_1$ by the Henkin construction, ($\varDelta \vdash \phi$ or $\varDelta \vdash \lnot \phi$) and ($\varDelta \vdash \psi$ or $\varDelta \vdash \lnot \psi$). Hence, out of the 16 combinations with regard to whether $\varDelta \vdash \phi$, or $\varDelta \vdash \lnot \phi$, or $\varDelta \vdash \psi$, or $\varDelta \vdash \lnot \psi$ we are left with nine.

Let us take the combination $\varDelta \not \vdash \phi$, $\varDelta \vdash \lnot \phi$, $\varDelta \vdash \psi$, and $\varDelta \vdash \lnot \psi$. The 8 others are analogous. By Lemma 7, $\varDelta \vdash D(\lnot \phi )$. By IH, $v(\phi )=0$, $v(\psi )={1}/{2}$. So, $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ has either the rule $R_{\circ }(0,{1}/{2},0)$, or the rule $R_{\circ }(0,{1}/{2},{1}/{2})$, or the rule $R_{\circ }(0,{1}/{2},1)$.

Suppose $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ has $R_{\circ }(0,{1}/{2},0)$. So, the proof runs as follows.

Hence, supposing that $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ has $R_{\circ }(0,{1}/{2},0)$ implies triviality of $\varDelta$. And this fact contradicts the condition that $\varDelta$ is non-trivial. Thus, $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ does not have the rule $R_{\circ }(0,{1}/{2},0)$.

Suppose $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ has $R_{\circ }(0,{1}/{2},{1}/{2})$. So, the proof runs as follows.

Hence, supposing that $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ has $R_{\circ }(0,{1}/{2},{1}/{2})$ implies triviality of $\varDelta$. And this fact contradicts the condition that $\varDelta$ is non-trivial. Therefore, $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ does not have the rule $R_{\circ }(0,{1}/{2},{1}/{2})$.

To conclude case (1), supposing that $\varDelta \vdash \phi \circ \psi$ and $\varDelta \not \vdash \lnot (\phi \circ \psi )$, leads to the fact that $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ does not have either the rule $R_{\circ }(0,{1}/{2},{1}/{2})$, or the rule $R_{\circ }(0,{1}/{2},{1}/{2})$. Therefore, it has the rule $R_{\circ }(0,{1}/{2},1)$. Therefore, $v(\phi \circ \psi ) = 1$.

Case (2) from left to right and from right to left is symmetrical to case (1).

Case (3) from left to right. Suppose $v(\phi \circ \psi ) = {1}/{2}$. Let us consider $f_{\circ } (0,0)={1}/{2}$ and $f_{\circ }({1}/{2},{1}/{2}) ={1}/{2}$. The 7 others are analogous.

$f_{\circ } (0,0)={1}/{2}$. So, $v(\phi )=v(\psi )=0$. By IH, $\varDelta \not \vdash \phi$, $\varDelta \vdash \lnot \phi$, $\varDelta \not \vdash \psi$, and $\varDelta \vdash \lnot \psi$. By Lemma 7, it follows that $\varDelta \vdash D(\lnot \phi )$ and $\varDelta \vdash D(\lnot \psi )$. Then $R_{\circ }(0,0,{1}/{2})$ is a rule of $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ and the proof runs as follows.

Now suppose that $\varDelta \vdash \phi \circ \psi$ and $\varDelta \not \vdash \lnot (\phi \circ \psi )$. (The case $\varDelta \not \vdash \phi \circ \psi$ and $\varDelta \vdash \lnot (\phi \circ \psi )$ is analogous.) By Lemma 7, it follows that $\varDelta \vdash D(\phi \circ \psi )$. So, the proof proceeds as follows.

Supposing that $\varDelta \not \vdash \phi \circ \psi$ or $\varDelta \not \vdash \lnot (\phi \circ \psi )$ leads to the fact that $\varDelta \vdash \bot$, i. e. triviality of $\varDelta$. And this fact contradicts the condition that $\varDelta$ is non-trivial. Hence, both $\varDelta \vdash \phi \circ \psi$ and $\varDelta \vdash \lnot (\phi \circ \psi )$.

$f_{\circ }({1}/{2},{1}/{2}) ={1}/{2}$. So, $v(\phi )=v(\psi )={1}/{2}$. By IH, $\varDelta \vdash \phi , \varDelta \vdash \lnot \phi , \varDelta \vdash \psi , \varDelta \vdash \lnot \psi$. Then $R_{\circ }({1}/{2},{1}/{2},{1}/{2})$ is a rule of $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ and the proof runs as follows.

The justification that steps (1)–(4) imply $\varDelta \vdash I(\phi )$ and $\varDelta \vdash I(\psi )$ is analogous to the one in the proof on page 19. Then the reader is referred to the previous proof in order to conclude this proof of triviality of $\varDelta$ if $\varDelta \not \vdash \phi \circ \psi$ or $\varDelta \not \vdash \lnot (\phi \circ \psi )$. Hence, both $\varDelta \vdash \phi \circ \psi$ and $\varDelta \vdash \lnot (\phi \circ \psi )$.

Case (3) from right to left. Suppose $\varDelta \vdash \phi \circ \psi$ and $\varDelta \vdash \lnot (\phi \circ \psi )$.

By the condition of this Lemma, we take $\varDelta \not \vdash \phi$, $\varDelta \vdash \lnot \phi$, $\varDelta \not \vdash \psi$, and $\varDelta \vdash \lnot \psi$ out of the 9 combinations specified in the beginning of the case (1). The 8 others are analogous. By Lemma 7, $\varDelta \vdash D(\lnot \phi )$ and $\varDelta \vdash D(\lnot \psi )$. By IH, $v(\phi )=v(\psi )=0$. So, $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ has either the rule $R_{\circ }(0,0,0)$, or the rule $R_{\circ }(0,0,{1}/{2})$, or the rule $R_{\circ }(0,0,1)$.

Suppose $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ has $R_{\circ }(0,0,0)$. So, the proof runs as follows.

The justification that steps 1–5 imply $\varDelta \vdash D(\phi \circ \psi )\wedge \lnot (\phi \circ \psi )$ is analogous to the one in the proof on page 19. The proof proceeds as follows.

Supposing that $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ has $R_{\circ }(0,0,0)$ contradicts the condition that $\varDelta$ is non-trivial. Therefore, $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ does not have the rule $R_{\circ }(0,0,0)$.

It is analogously to prove that supposing that $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ has $R_{\circ }(0,0,1)$ contradicts the condition that $\varDelta$ is non-trivial. Therefore, $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ does not have the rule $R_{\circ }(0,0,1)$.

To conclude the case (3), supposing that $\varDelta \vdash \phi \circ \psi$ and $\varDelta \vdash \lnot (\phi \circ \psi )$, leads to the fact that $\mathfrak {ND}_{{\mathbf{NC}}_{\mathbf{3}}^{(\circ )_{ k }}}$ does not have either the rule $R_{\circ }(0,0,0)$, or the rule $R_{\circ }(0,0,1)$. Therefore, it has the rule $R_{\circ }(0,0,{1}/{2})$. Therefore, $v(\phi \circ \psi ) = {1}/{2}$. $\square$

Lemma 11 justifies

Lemma 12

[Q-model Existence Theorem (Weir, 2013b)] If $\varGamma \not \vdash \bot$, then there is a model of $\varGamma$ such that $v(\phi ) \ne 0$, for each $\phi \in \varGamma$.

Theorem 3

(Completeness) [Completeness Theorem (Weir, 2013b)] If $\varGamma \models \phi$, then $\varGamma \vdash \phi$.

Proof

is by contraposition and by reductio.³⁷ Suppose that $\varGamma \not \vdash \phi$. Then we have $\varGamma , \lnot \phi \not \vdash \bot$. We expand it to a maximal weakly consistent negation-complete$_{1}$ set $\varDelta$ and use Lemma 12 to show that for all $\psi \in \varDelta$, $v(\psi ) \ne 0$. Since $\varDelta \not \vdash \bot$, there is at most one $\psi \in \varDelta$ such that $v(\psi )= {1}/{2}$ (Weir, 2013b, pp. 15–16).³⁸ If $v(\chi )=1$, for each $\chi \in \varGamma$, then $\varGamma \not \models \phi$ because $v(\lnot \phi ) \ge {1}/{2}$ and so downwards truth-preservation fails. If $v(\chi )= {1}/{2}$, for the only one $\chi \in \varGamma$, then $v(\lnot \phi ) = 1$ and so upwards falsity-preservation fails. $\square$

By Theorems 2 and 3, we obtain the following Corollary 1.

Corollary 1

For each $\varGamma \cup \{\phi \}\subseteq {\mathscr {F}}_{(\circ )_k}$, it holds that $\varGamma \models \phi$ iff $\varGamma \vdash \phi$.

7 Related Work

This section is an update to the comparative study of the CFOSC-method³⁹ and CA in Petrukhin and Shangin (2019), where footnote 4 contains the following hypothesis: “We don’t mean here we can provide an example of correspondence analysis being applied to a non-transitive logic. What we mean here is that transitivity property of the logical consequence relation (i. e. validity of cut-rule) is not a necessary part of correspondence analysis”. So, the present paper is a confirmation of this hypothesis, and CA is shown to be applicable to the logics which the CFOSC-method is not applicable to. We, again, underline that the CFOSC-method is more general than CA primarily due to the fact, that the former deals with both deterministic and non-deterministic matrices.⁴⁰ For non-deterministic matrices, we direct the reader to the lists of references in Avron and Zamansky (2011), Avron and Lev (2001), Avron and Konikowska (2005), Kearns (1981) and, especially, to the emeritus Lomonosov MSU professor Yuri Vasilyevich Ivlev’s contribution, who has been proposing non-deterministic matrices (he dubs them quasi-matrices) for propositional and modal logics since the year of 1972 (Ivlev, 1987, 1988, 1998, 2000, 2005, 2020).

Getting back to the CFOSC-method, we highlight that it sets up an n-sequent calculus for each n-valued logic that is characterizable by any finite-valued semantics based on the above-mentioned types of matrices. As a result, such a n-sequent calculus can be transformed into an ordinary sequent calculus and a natural deduction calculus. Proof systems of the latter type are usually (but dissimilar to the ones by the CFOSC-method) obtainable via CA, too. There are two crucial differences between the ways both methods set up proof systems. First, the ones by the CFOSC-method contain superficial, dependent rules, and special pruning procedures run in order to get rid of them. The ones by CA have independent rules only. Second, the CFOSC-method is designed to set up cut-free sequent calculi, and this type of proof system is well-known to be inefficient from the view of computational complexity theory (D’Agostino & Mondadori, 1994). On the other hand, natural deduction calculi are among the proof systems (in)efficiency of which is, still, unprovable (Cook & Reckhow, 1979; Urquhart, 1995).

The motivational reasons of the two methods are different, too. In the case of CFOSC, one of the reasons is to provide a general proof of the cut-elimination theorem, a corner stone of the modern automated proof theory. Such a general proof allows one to obtain cut-free sequent calculi, where a proof searching procedure becomes a routine and brute-force task [this procedure is highly inefficient, nevertheless: the complexity of a cut-free sequent calculus is shown to be factorial, i. e. it is worse than the exponential one of the truth-table method (Urquhart, 1995)].⁴¹ Hence, from the beginning CFOSC rests on the presupposition that the entailment relation of a treated logic is the Tarski-Scott one (Scott, 1974), that is, it enjoys the generalized transitivity (see, for instance, Avron and Lev (2001, p. 2) and Avron et al., (2007, 44). To be sure, we are claiming neither that it is a drawback of CFOSC (the general cut-elimination theorem is not expected to hold when the general transitivity fails), nor that CFOSC cannot be adapted to (the above-treated) non-transitive logics. On the other hand, Petrukhin (2018) shows flexibility of CA by generalizing different CAs.

8 Conclusion

We present CA for the Weirian non-transitive trivalent neo-classical logic ${\mathbf{NC}}_{\mathbf{3}}$ in order to obtain sound and complete Lemmon-style natural deduction systems for all the binary extensions of it. The future research will be about proof-searching for (the obtained extensions of) ${\mathbf{NC}}_{\mathbf{3}}$. An application of Frankowski’s method (Frankowski, 2004a, b) to the target logics is another future research.