Abstract
I compare the performance of solution methods in solving a standard real business cycle model with labor market search frictions. Under the conventional calibration, the model is solved by the projection method using the Chebyshev polynomials as its basis, and the perturbation methods up to third order in both levels and logs. Evaluated by two accuracy tests, the projection approximation achieves the highest degree of accuracy, closely followed by the third order perturbation in levels. Although different in accuracy, all the approximated solutions produce simulated moments similar in value.






Similar content being viewed by others
Notes
Instead of focusing on computing the Euler equation error, they make use of this observation to develop the projection methods on the realized (in simulation) state space only, for the purpose of mitigating the curse of dimensionality when solving models with a large number of state variables.
The notation, g and \({\tilde{g}}\), is adopted to track the source (through \(y_t\) or \(y_{t+1}\)) of derivatives of the policy function. This is necessary as (i) the \( {\tilde{s}}_{t+1}\) argument of \({\tilde{g}}\) is itself a function of g through its dependance on \(y_t\), and (ii) \({\upsigma }\) scales \(\upvarepsilon _{t+1}\) in the \( {\tilde{s}}_{t+1}\) argument of \({\tilde{g}}\), but not \(\upvarepsilon _{t}\) in the \(s_{t}\) argument of g. This follows from the conditional expectations in (22): \(\upvarepsilon _t\) realizes at time t and is in the time t information set—hence, it is not scaled by \({\upsigma }\); however, \(\upvarepsilon _{t+1}\) has not yet been realized and is the source of risk—hence, it is scaled by \({\upsigma }\). See also Anderson et al. (2006) and Michel (2011) for similar discussions.
See, Uhlig (1999) for example.
All the other endogenous variables can be recovered use model equations given the approximation of consumption and vacancy.
The projection solution is used to calibrate the model as it is the most accurate approximation of the policy function evaluated with Den Haan and Marcet’s (1994) accuracy test and the Euler equation error test. The detailed discussion of accuracy is presented in the next section.
Andofatto (1996) formulates this uncoordinated nature of the search process as \(M(v, (1-n))\le \min \left\{ v,(1-n) \right\} \), which implies \(M(v, (1-n))/(1-n)\equiv f(\uptheta )\le \min \left\{ \uptheta ,1 \right\} \) with the constant return to scale assumption on the matching function \(M(v, (1-n))\). Therefore, when \(\uptheta >1\), the search friction still exists and is nontrivial if \(f(\uptheta )<1\).
As noted by Judd (1992), the conditional expectation in the Euler equation involves an integral that cannot in general be evaluated explicitly and usually approximated with a finite sum.
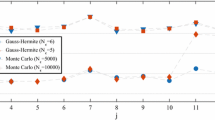
I am grateful to one of my referees for suggesting me to add this analysis of the size of shocks and the consequential accuracy of different approximations.
To produce the histogram, all the approximations are simulated in the environment described in Sect. 4.1.
I am grateful to one of my referees for suggesting me to include this comparison.
References
Adjemian, S., Bastani, H., Juillard, M., Mihoubi, F., Perendia, G. Ratto, M., & Villemot, S. (2011). Dynare: Reference Manual, Version 4. Dynare Working Papers 1, CEPREMAP.
Anderson, G. S., Levin, A., & Swanson, E. (2006). Higher-order pertubation solutions to dynamic discrete-time rational expectations models. Federal Reserve Bank of San Francisco Working Paper Series 2006-01.
Andofatto, D. (1996). Business cycles and labor-market search. American Economic Review, 86(1), 112–132.
Aruoba, S. B., Fernández-Villaverde, J., & Rubio-Ramírez, J. F. (2006). Comparing solution methods for dynamic equilibrium economies. Journal of Economic Dynamics and Control, 30(12), 2477–2508.
Atolia, M., Gibson, J., & Marquis, M. (2015). On using Hagedorn–Manovskii’s calibration to resolve the Shimer puzzle in a real business cycle search model.
Caldara, D., Fernández-Villaverde, J., Rubio-Ramírez, J., & Yao, W. (2012). Computing DSGE models with recursive preferences and stochastic volatility. Review of Economic Dynamics, 15(2), 188–206.
Den Haan, W. J., & De Wind, J. (2012). Nonlinear and stable perturbation-based approximations. Journal of Economic Dynamics and Control, 36(10), 1477–1497.
Den Haan, W. J., & Marcet, A. (1990). Solving the stochastic growth model by parameterizing expectations. Journal of Business & Economic Statistics, 8(1), 31–34.
Den Haan, W. J., & Marcet, A. (1994). Accuracy in simulations. The Review of Economic Studies, 61(1), 3–17.
Den Haan, W. J., Ramey, G., & Watson, J. (2000). Job destruction and propagation of shocks. American Economic Review, 90(3), 482–498.
Gaspar, J., & Judd, K. L. (1997). Solving large-scale rational-expectations models. Macroeconomic Dynamics, 1(01), 45–75.
Hagedorn, M., & Manovskii, I. (2008). The cyclical behavior of equilibrium unemployment and vacancies revisited. American Economic Review, 98(4), 1692–1706.
Jin, H.-H., & Judd, K. L. (2002). Pertubation methods for general dynamic stochastic models. Mimeo April.
Judd, K. L. (1992). Projection methods for solving aggregate growth models. Journal of Economic Theory, 58(2), 410–452.
Judd, K. L. (1998). Numerical methods in economics. Cambridge, MA: MIT Press.
Judd, K. L., & Guu, S.-M. (1997). Asymptotic methods for aggregate growth models. Journal of Economic Dynamics and Control, 21(6), 1025–1042.
Judd, K. L., Maliar, L., & Maliar, S. (2010). A cluster-grid projection method: Solving problems with high dimensionality. Working Paper 15965, National Bureau of Economic Research.
Judd, K. L., Maliar, L., & Maliar, S. (2011). Numerically stable and accurate stochastic simulation approaches for solving dynamic economic models. Quantitative Economics, 2(2), 173–210.
Judd, K. L., Maliar, L., & Maliar, S. (2012). Merging simulation and projection approaches to solve high-dimensional problems. NBER Working Papers 18501, National Bureau of Economic Research, Inc.
Maliar, L., & Maliar, S. (2014). Chapter 7—Numerical methods for large-scale dynamic economic models. In K. Schmedders & K. L. Judd (Eds.), Handbook of computational economics (Vol. 3, pp. 325–477). Amsterdam: Elsevier.
Merz, M. (1995). Search in the labor market and the real business cycle. Journal of Monetary Economics, 36(2), 269–300.
Michel, J. (2011). Local approximation of DSGE models around the risky steady state. WP.comunite 0087, Department of Communication, University of Teramo.
Mortensen, D. T., & Pissarides, C. A. (1994). Job creation and job destruction in the theory of unemployment. Review of Economic Studies, 61, 397–425.
Petrongolo, B., & Pissarides, C. A. (2001). Looking into the black box: A survey of the matching function. Journal of Economic Literature, 39(2), 390–431.
Petrosky-Nadeau, N., & Zhang, L. (2013). Solving the DMP model accurately. Working Paper 19208, National Bureau of Economic Research.
Pissarides, C. A. (1985). Short-run equilibrium dynamics of unemployment, vacancies, and real wages. American Economic Review, 75(4), 676–690.
Pissarides, C. A. (2000). Equilibrium unemployment theory (2nd ed.). Cambridge, MA: MIT Press.
Pissarides, C. A. (2009). The unemployment volatility puzzle: Is wage stickiness the answer? Econometrica, 77(5), 1339–1369.
Schmitt-Grohé, S., & Uribe, M. (2004). Solving dynamic general equilibrium models using a second-order approximation to the policy function. Journal of Economic Dynamics and Control, 28(4), 755–775.
Shimer, R. (2005). The cyclical behavior of equilibrium unemployment and vacancies. American Economic Review, 95(1), 25–49.
Uhlig, H. (1999). A toolkit for analysing nonlinear dynamic stochastic models easily. In R. Marimon & A. Scott (Eds.), Computational methods for the study of dynamic economies Chap. 3 (pp. 30–61). Oxford: Oxford University Press.
Author information
Authors and Affiliations
Corresponding author
Additional information
I am grateful to Michael Burda, Alexander Meyer-Gohde and Julien Albertini as well as participants of research seminars and workshops at HU Berlin for useful comments, suggestions, and discussions. I am indebted to the editor and two anonymous referees, whose comments and suggestions greatly improved my manuscript. This research was supported by the DFG through the SFB 649 “Economic Risk”. Any and all errors are entirely my own.
Appendix
Appendix
Starting with the capital grid, for any element of the set, \(k_t^i\in [k_{min}, k_{max}]\) with i being a positive integer for indexing purpose, the linear transformation
ensures that \(\upvarphi (k_t^i)\) is bounded to the set \([-1, 1]\). I choose \(n_k\) elements from the set, collected in the vector \(k_t = \begin{bmatrix} k_t^1&k_t^2&\ldots&k_t^{n_k} \end{bmatrix}'\), such that after applying the linear transformation (50) to \(k_t\), the elements of the resulting vector \(\upvarphi (k_t)=\begin{bmatrix} \upvarphi (k_t^1)&\upvarphi (k_t^2)&\ldots&\upvarphi (k_t^{n_k}) \end{bmatrix}' \) are the \(n_k\) roots of the following \(n_k\)th Chebyshev polynomial basis
where \(T_i(\cdot ) \equiv \cos (i\arccos (\cdot ))\) is the ith Chebyshev polynomial with \(T_0=1\) and \(T\left( \upvarphi (k_t)\right) \) is of dimension \((n_k+1)\times (n_k+1)\).
Analogous to my choice of elements from the capital set, I choose \(n_n\) and \(n_z\) elements from these two sets, \(n_t = \begin{bmatrix} n_t^1&n_t^2&\ldots&n_t^{n_n} \end{bmatrix}'\) and \(z = \begin{bmatrix} z_t^1&z_t^2&\ldots&z_t^{n_z} \end{bmatrix}'\), that after being transformed by \(\upvarphi (\cdot )\), are the \(n_n\) and \(n_z\) roots of the following \(n_n\)th and \(n_z\)th Chebyshev polynomial basis respectively
where \(T\left( \upvarphi (n_t)\right) \) and \(T\left( \upvarphi (z_t)\right) \) are of dimension \((n_n+1)\times (n_n+1)\) and \((n_z+1)\times (n_z+1)\) respectively.
As in Judd (1992), Aruoba et al. (2006) and Caldara et al. (2012), the multidimensional basis of the approximated policy function is the Kronecker product of the above three one-dimensional basis
with dimension \((n_g\times n_g)\) where \(n_g = (n_k+1)\times (n_n+1)\times (n_z+1)\) is the number of all triplets of the collocation points along three dimensions, i.e., the number of grid points in the three-dimensional state space \([k_{min}, k_{max}]\times [n_{min}, n_{max}]\times [z_{min}, z_{max}]\). With this multidimensional basis, the approximated policy function of consumption and vacancy writes
where \({\hat{}}\) indicates these are approximated policy functions, and \({\Theta }_c\) and \(\Theta _v\) are two vectors of coefficients to be determined. Both \({\hat{c}}_t\) and \({\hat{v}}_t\) are of dimension \((n_g\times 1)\).
I solve for the unknown coefficients \({\Theta }_c\) and \(\Theta _v\) from the two Euler equations (12) and (15) using Den Haan and Marcet’s (1990) functional iteration: at each grid point i
-
1.
use j-th iteration of the coefficients, \({\Theta }_c^j\) and \({\Theta }_v^j\), to compute
$$\begin{aligned} n_{t+1}^i&= (1-\mu )n_t^i + m_0 P_v\left( k_t^i,n_t^i,z_t^i;{\Theta }_v^j\right) ^{1-\upeta }(1-n_t^i)^{\upeta },\;\; i = 1,2,...,n_g \end{aligned}$$(57)$$\begin{aligned} k_{t+1}^i&= (1-{\updelta })k_t^i + e^{z_t^i} (k_t^i)^{{\upalpha }} (n_t^i)^{1-{\upalpha }} - P_c\left( k_t^i,n_t^i,z_t^i;{\uptheta }_c^j\right) \\&\quad - {\upkappa }_vP_c(k_t^i,n_t^i,z_t^i;{\Theta }_v^j) - m_0{\upkappa }_u(1-n_t^i)\nonumber \end{aligned}$$(58)$$\begin{aligned} c_{t+1}^i&= P_c\left( k_{t+1}^i, n_{t+1}^i, {\uprho }z_t^i+{\upvarepsilon }_t ;{\uptheta }_c^j\right) \end{aligned}$$(59)$$\begin{aligned} v_{t+1}^i&= P_v\left( k_{t+1}^i, n_{t+1}^i, {\uprho }z_t^i+{\upvarepsilon }_t ;{\uptheta }_v^j\right) \end{aligned}$$(60) -
2.
given (57)–(60) and approximating the conditional expectation with the Gauss–Hermite quadrature, the Euler equation for consumption (12) writes
$$\begin{aligned} \left( {\hat{c}}_t^i\right) ^{-1}&= {\upbeta }\sum _{r=1}^{m} \biggl [P_c\left( k_{t+1}^i, n_{t+1}^i, {\uprho }z_t^i+\sqrt{2}{\upsigma }\zeta _r ;{\Theta }_c^j\right) ^{-1}\\&\times \left( 1-{\updelta }+{\upalpha }\exp \left( {\uprho }z_t^i+\sqrt{2}{\upsigma }\zeta _r\right) (k_{t+1}^i)^{{\upalpha }-1} (n_{t+1}^i)^{1-{\upalpha }}\right) \frac{\omega _r}{\sqrt{\pi }}\nonumber \biggl ] \end{aligned}$$(61)where \(\zeta _r\) and \(\omega _r\) are Gauss–Hermite quadrature points and weights. From the foregoing solve for \({\hat{c}}_t^i\). Analogously, the Euler equation for employment (15) writes
$$\begin{aligned} \left( {\hat{v}}_t^i\right) ^{\upeta }&= \frac{(1-\upeta )m_0}{{\upkappa }_v} (1-n_t^i)^{\upeta }\left( {\hat{c}}_t^i\right) {\upbeta }\\&\quad \times \sum _{r=1}^{m} \biggl [ P_c\left( k_{t+1}^i, n_{t+1}^i, {\uprho }z_t^i+\sqrt{2}{\upsigma }\zeta _r ;{\Theta }_c^j\right) ^{-1}\nonumber \\&\quad \times \biggl (-\left( n_{t+1}^i\right) ^{-1/{\upgamma }}P_c\left( k_{t+1}^i, n_{t+1}^i, {\uprho }z_t^i+\sqrt{2}{\upsigma }\zeta _r ;{\Theta }_c^j\right) \nonumber \\&\quad + (1-{\upalpha })\exp \left( {\uprho }z_t^i+\sqrt{2}{\upsigma }\zeta _r\right) \left( k_{t+1}^i\right) ^{{\upalpha }}\left( n_{t+1}^i\right) ^{-{\upalpha }} +{\upkappa }_u\nonumber \\&\quad + \frac{{\upkappa }_v(1-\mu )P_v\left( k_{t+1}^i, n_{t+1}^i, {\uprho }z_t^i+\sqrt{2}{\upsigma }\zeta _r ;{\Theta }_v^j\right) ^{\upeta }}{(1-\upeta )m_0\left( 1-n_{t+1}^i\right) ^{\upeta }}\nonumber \\&\quad -\frac{\upeta {\upkappa }_v}{1-\upeta }\frac{P_v\left( k_{t+1}^i, n_{t+1}^i, {\uprho }z_t^i+\sqrt{2}{\upsigma }\zeta _r ;{\Theta }_v^j\right) }{1-n_{t+1}^i} \biggl )\frac{\omega _r}{\sqrt{\pi }} \biggl ]\nonumber \end{aligned}$$(62)from the foregoing solve for \({\hat{v}}_t^i\).
-
3.
repeat step 1–2 for all \(n_g\) grid points, get an estimation of the new coefficients with the following regression
$$\begin{aligned} {\hat{\Theta }}^{j+1} = \begin{bmatrix} {\uptheta }_c^{j+1}&{\Theta }_v^{j+1} \end{bmatrix} = \left[ X(k_t,n_t,z_t)'X(k_t,n_t,z_t)\right] ^{-1}X(k_t,n_t,z_t)' \begin{bmatrix} {\hat{c}}_t&{\hat{v}}_t \end{bmatrix} \end{aligned}$$(63)where \(X(k_t,n_t,z_t)\) is the multidimensional basis defined by (54). Then obtain the \((j+1)\)-th iteration of the coefficients with the following updating rule
$$\begin{aligned} \Theta ^{j+1} = \Lambda {\hat{\Theta }}^{j+1} + (1-\Lambda )\Theta ^j \end{aligned}$$(64)where \(\Lambda \in (0,1]\) is a parameter for stabilizing the iteration.
-
4.
repeat step 1–3 till \(\Vert \Theta ^{j+1} - \Theta ^j \Vert \) is smaller than a desired level of tolerance.
The choice of parameters for the iteration is summarized in Table 7.
Rights and permissions
About this article
Cite this article
Lan, H. Comparing Solution Methods for DSGE Models with Labor Market Search. Comput Econ 51, 1–34 (2018). https://doi.org/10.1007/s10614-017-9670-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10614-017-9670-z