Prediction of permeability of porous media using optimized convolutional neural networks

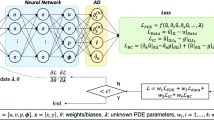
Abstract

Permeability is an important parameter to describe the behavior of a fluid flow in porous media. To perform realistic flow simulations, it is essential that the fine scale models include permeability variability. However, these models cannot be used directly in simulations because require high computational cost, which motivates the application of upscaling approaches. In this context, machine learning techniques can be used as an alternative to perform the upscaling of porous media properties with lower computational cost than traditional upscaling methods. Hence, in this work, an upscaling methodology is proposed to compute the equivalent permeability on the large grid through convolutional neural networks (CNN). This method achieves suitable precision, with less computational demand, when evaluated on 2D and 3D models, if compared with the local upscaling approach. We also present a genetic algorithm (GA) to automatically determine the optimal configuration of CNNs for the target problems. The GA procedure is applied to yield the optimal CNN architecture for upscaling of the permeability fields with outstanding results when compared with counterpart techniques.

Appendices

Appendix A: data generation

This section presents the equations that govern the single-phase for the calculation of the larger scale permeability fields through of local upscaling to train and validate the CNN (Section 3).

1.1 A.1 Governing equations

The mass conservation law for single-phase flow in porous media and in the absence of sources is given by:

$$ \frac{\partial (\rho \phi)} {\partial t}+\nabla \cdot (\rho \mathbf{v})=0, $$

(12)

where ρ is the density of the fluid, ϕ is the porosity of the medium and v is the Darcy velocity, and in the absence of gravitational effects, Darcy’s law is given by:

$$ \mathbf{v}=-\frac{\mathbf{k}}{\mu}\nabla p, $$

(13)

where k is the permeability of the medium, μ is the viscosity of the fluid, p is the pressure of the fluid and v is the Darcy velocity.

In terms of Darcy velocity, the mass conservation law can be expressed as:

$$ \frac{\partial (\rho \phi)} {\partial t}-\nabla \cdot \left( \rho \frac{\mathbf{\mathbf{k}}}{\mu}\nabla p\right)=0. $$

(14)

Considering the hypotheses that porosity does not vary with time and incompressible fluid, we have:

$$ \nabla \cdot \left( \frac{\mathbf{k}}{\mu}\nabla p\right)=0. $$

(15)

Assuming that the permeability varies on two different scales: a coarse x that describes a slow variation of this property and another fine y that describes a fast variation, and that the viscosity does not vary with pressure, then we can write (4) as:

$$ \nabla \cdot\left( \mathbf{k}\left( \mathbf{x}, \mathbf{y}\right) \nabla p\right)=0. $$

(16)

Applying the homogenization process [56] in (5), we obtain an equation characterized by a permeability, designated k^∗, which varies only in the coarse scale x, defined as:

$$ \nabla_{\mathbf{x}} \cdot\left( \mathbf{k}^{\ast}(\mathbf{x})\nabla_{\mathbf{x}} p\right)=0, $$

(17)

where the index x on the gradient operator indicates operation on the scale x.

To calculate k^∗, we need to solve the fine scale pressure equation subject to boundary conditions as follows:

$$ \left\{ \begin{array}{ll} \nabla_{\mathbf{y}} \cdot\left( \mathbf{k}(\mathbf{y})\nabla_{\mathbf{y}} p\right)=0, & \text{on}~ {\Omega}, \\ p(0,y_{2})=p_{1}, & \text{on}~ {\Gamma}_{D}, \\ p(y_{1},y_{2})=p_{2}, & \text{on}~ {\Gamma}_{D}, \\\mathbf{v}(y_{1},0)\cdot \mathbf{n}= \mathbf{v}(y_{1},y_{2}) \cdot \mathbf{n}=0, & \text{on}~ {\Gamma}_{N}, \end{array} \right. $$

(18)

where the index y on the gradient operator indicates operation on the y scale, p₁, p₂ are known pressures, Γ_D and Γ_N represent, respectively, Dirichlet and Neumann boundary and n is the normal vector.

There are different numerical methods that can be used to solve this problem (7). In this work, we use the finite difference method to obtain the numerical solution. The approximation of the fine scale pressure equation through centered differences is given by:

$$ \begin{array}{llllll} k_{y_{1},i+1/2,j}\left( p_{i+1,j}-p_{i,j} \right)-k_{y_{1},i-1/2,j}\left( p_{i,j}-p_{i-1,j}\right)+\\ k_{y_{2},i,j+1/2}\left( p_{i,j+1} - p_{i,j} \right) - k_{y_{2},i,j-1/2}\left( p_{i,j}-p_{i,j-1} \right)=0, \end{array} $$

(19)

where p_i,j represents the pressure in the cell centers, $k_{y_{1}, i + 1/2, j}$ and $k_{y_{2}, i, j + 1/2 }$ denote the permeability values at the cell boundaries, given by the harmonic mean as:

$$ k_{y_{1},i+1/2,j}= \frac{2 \left( {k_{y_{1},i,j}k_{y_{1},i+1,j}} \right)}{k_{y_{1},i,j}+k_{y_{1},i+1,j}}, $$

(20)

$$ k_{y_{2},i,j+1/2}= \frac{2 \left( {k_{y_{2},i,j}k_{y_{2},i,j+1}} \right)}{k_{y_{2},i,j}+k_{y_{2},i,j+1}}. $$

(21)

Upon resolution of (7), the average velocity 〈v〉 at the cell is determined as follows:

$$ \langle\mathbf{v}\rangle=-{\int}_{\Gamma}{\mathbf{v}\cdot \mathbf{n}}d{\Gamma}. $$

(22)

where Γ is the boundary, and n is the normal vector. Using the result of (11) in the coarse scale Darcy’s law, we obtain the upscaled permeability k^∗.

Fig. 30

Examples of images of the datasets. (a) MNIST, (b) CIFAR-10, and (c) Fashion-MNIST

1.2 A.2 Random fields

In this work, the random permeability is a scalar field with log-normal distribution, given by:

$$ \mathbf{k}(\mathbf{y})=\mathbf{k}_{0}e^{\rho\mathbf{Y(\mathbf{y})}}, $$

(23)

where $\mathbf {k} _{0}, \rho \in \mathbb {R}$ and $\vec {Y} \left (\mathbf {y}\right ) \sim \mathcal {N} \left (0,\mathcal {C}\right )$ is a Gaussian random field characterized by its mean $\langle \vec {Y} \left (\mathbf {y}\right )\rangle =0$ and covariance function $\mathcal {C}$. This field is generated by the Karhunen-Loève method (Appendix Appendix).

1.3 A.3 Karhunen-Loève expansion

This expansion represents the Gaussian random fields as follows:

$$ \mathbf{Y}\left( \mathbf{y}, \omega \right)=< \mathbf{Y}\left( \mathbf{y}\right)>+{\sum}_{n=1}^{\infty}\sqrt{\lambda_{n}}f_{n}(\mathbf{y})\xi_{n}(w), $$

(24)

where ξ_n(w) represents a set of Gaussian random variables, λ_n and f_n(y) denote, respectively, eigenvalues and eigenfunctions, that are obtained from the Fredholm integral:

$$ {\int}_{\Omega}\mathcal{C}(\mathbf{y},\mathbf{y^{\prime}})f_{n}(\mathbf{y})d\mathbf{y}=\lambda_{n} f_{n}(\mathbf{y^{\prime}}), $$

(25)

where $\mathcal {C}(\mathbf {y}, \mathbf {y^{\prime }})$ represents the covariance function, defined by:

$$ \mathcal{C}(\mathbf{y},\mathbf{y}^{\prime})=\sigma^{2}exp\left( -\frac{(y_{1}-y^{\prime}_{1})^{2}}{{\eta_{1}^{2}}}-\frac{(y_{2}-y^{\prime}_{2})^{2}}{{\eta_{2}^{2}}}\right), $$

(26)

where y = (y₁,y₂), $\mathbf {y '} = (y^{\prime } _{1}, y '_{2})$ represent spatial locations, σ² is the variance, η₁ and η₂ are the correlation lengths.

Appendix B: classification problem

In order to validate our GA methodology, we first apply it on classification tasks using the CIFAR-10 [57], CIFAR-100 [57], MNIST [9] and Fashion-MNIST [58] datasets. The MNIST contains 70,000 images of handwritten digits (0 to 9) in grayscale of size 28 × 28 pixels. This database contains 60,000 training images and 10,000 validation images. Examples of digits from the MNIST dataset are shown in Fig. 30(a). The CIFAR-10 dataset consists of 60,000 color images with the size of 32 × 32 pixels, divided into 10 different classes. This set contains 50,000 training images and 10,000 validation images. The CIFAR-100 contains the same number of images as CIFAR-10, but images are uniformly distributed over 100 classes. Figure 30(b) shows examples of images from the CIFAR-10 dataset. Similarly to the standard MNIST, the Fashion-MNIST is composed of 60,000 training images and 10,000 validation images of clothing as shown in Fig. 30(c).

Table 11 Structure of the best network for the CIFAR-10 dataset

We begin by analyzing the performance of the three best models on the CIFAR-10 dataset obtained with three independent executions of the GA methodology. Figure 31 depicts the fitness (accuracy) evolution of the best CNNs with the number of generations, as well as the average result. Note that there was no significant increase in the performance of the models after 20th generation. Among the accuracy results, we note that the best accuracy obtained on the experiments is 89.88% reported in the 95th generation (blue plot). Moreover, the best average accuracy in the dashed curve of Fig. 31 is 89.74%, as shown in the first line of Table 12. The best accuracy was achieved with a CNN that consists of 6 convolutional layers, and 2 fully connected layers, with filters and neurons, respectively, as specified in Table 11. The training is performed by Adam, with batch size of 20.

Table 12 Results obtained by CNNs constructed through GA on the CIFAR-10

After the hyperparameters optimization, the best CNN discovered by GA reaches with 400 epochs a higher accuracy of 90.16% over the validation set, and an average accuracy of 89.89% over the models obtained on five training of the best CNN architecture. These results are obtained using the weights and bias adjusted in the optimization phase as initialization, without data augmentation. Using the same CNN, we get on the best case an accuracy of 92.20% over the validation set, and an average accuracy of 91.93%, with data augmentation [47]. The mean results obtained after 400 epochs, on the validation set, by the three networks found are displayed on the boxplot in Fig. 32. Note that average and median accuracies of architecture 1 are superior to the results of architectures 2 and 3, whereas architecture 2 presents the performance with the smaller variability. Although the architectures present different results, they are statistically equal by the Anova statistical method.

Fig. 31

Evolution of the best fitness (accuracy) and average result of three executions of the GA

To evaluate the generalization ability of the best configuration of CNN found by GA on the CIFAR-10, we re-train five times the network on the MNIST dataset with 400 epochs. From the application of the five models over the MNIST, we get an average classification accuracy of 99.57% over the validation set. Similarly to the experiments on the MNIST, we obtain for the Fashion-MNIST an average classification accuracy of 94.23%. For the CIFAR-100, the network achieves an average accuracy of 63.47%. All the accuracy results are obtained without using any data argumentation technique. Using the same setup with data argumentation, we get for the MNIST, Fashion-MNIST and CIFAR-100 average accuracies of 99.63%, 94.86% and 69.10%, respectively.

Fig. 32

Boxplot of the accuracy of the three architectures discovered by GA, where the red line shows the median and the circle shows the mean

Table 13 Accuracy of different approaches for the classification problems

Table 13 presents the comparison between the classification accuracy of the CNNs generated by the proposed GA method and DENSER. Also, recognition rates of traditional architectures for classification tasks are reported to position our results in the state-of-the-art. Note that our outstanding model reaches average accuracy results for the MNIST, CIFAR-10 and CIFAR-100, which are 0.07%, 2.20% and 5.04% below, when compared to the DENSER, considered the state-of-the-art method to automatically design CNNs. For the Fashion-MNIST, the result obtained is 0.16% above in relation to the DENSER. These results indicate that the CNN found on the CIFAR-10 has good generalization ability and reaches competitive results with the methods for classification problems.