Optimization of sample size and order size in an inventory model with quality inspection and return of defective items

Abstract

To ensure all products as perfect, inspection is essential, even though it is not possible to inspect all products after producing them like some special type products as plastic joint for the water pipe. In this direction, this paper develops an inventory model with lot inspection policy. With the help of lot inspection, all products need not to be verified still the retailer can decide the quality of products during inspection. If retailer founds products as imperfect quality, the products are sent back to supplier. As it is lot inspection, mis-clarification errors (Type-I error and Type-II error) are introduced to model the problem. Two possible cases are discussed for sending back products as defective lots are immediately withdrawn from the system and send back to supplier with retailer’s payment and for second case, retailer sends defective products during receiving next lot from supplier with supplier’s investment, like in food industry or in hygiene product industry. The model is solved analytically and results indicate that optimal order size and sample size are intrinsically linked and maximize the total profit. Numerical examples, graphical representations, and sensitivity analysis are given to illustrate the model. The results suggest that sending defective products maintaining the first case is the more profitable than the second case.

Appendices

Appendix 1

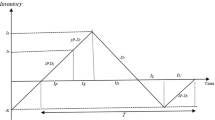
To determine holdings costs, we split the total area in two parts like in the Fig. 8 and express each area separately. The screening time could be expressed as ${ t}_{l}=\frac{yL}{X}$.

Fig. 8

Behavior of the inventory

The blue area is expressed as

$$\begin{aligned} (\uprho {\mathrm {L}}+n\left( \mathrm {1}-\uprho \right) \mathrm {)}\frac{ynL}{X}= \frac{y^{2}nL(\uprho \mathrm {L\,+\,}n\mathrm {(1}-\uprho ))}{X} \end{aligned}$$

The yellow area is expressed as a single triangle

$$\begin{aligned} \frac{\left( yL-(\uprho \mathrm {L\,+\,}n\mathrm {(1}-\uprho )) \right) ^{2}}{2D}=\frac{y^{2}{(1-{\uprho })}^{2}{(L-n)}^{2}}{2D} \end{aligned}$$

Appendix 2

Proof of $\left| \frac{\delta ^{2}{{\mathrm {TP}}}_{1}\left( y,n \right) }{{\delta n}^{2}} \right| >\left| \frac{\delta ^{2}{{\mathrm {TP}}}_{1}\left( y,n \right) }{\delta n\delta y} \right|$

To demonstrate the second condition, it is necessary to prove that

$$\begin{aligned}&\frac{2Dc_{U}}{\left( L-n \right) ^{3}}+\frac{2c_{l}DL}{\left( 1-{{\mathrm {E}}[\uprho }_{e}] \right) \left( L-n \right) ^{3}}+\frac{2\left( \mathrm {K+}{\mathrm {K}}_{d} \right) D}{y\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) \left( L-n \right) ^{3}}\nonumber \\&\quad +\frac{Dc_{a}E\left[ {\uprho } \right] {E\left[ m_{2} \right] }^{n}}{\left( \mathrm {1-E}\left[ {\uprho }_{e} \right] \right) \left( L-n \right) } \left[ \frac{2}{\left( L-n \right) ^{2}}+\frac{\ln \left( E\left[ m_{2} \right] \right) }{\left( L-n \right) }+\ln \left( E\left[ m_{2} \right] \right) ^{2} \right] \nonumber \\&\quad +\frac{Dc_{r}\left( 1-E\left[ {\uprho } \right] \right) {E\left[ m_{1} \right] }^{n}}{\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) (L-n)}\left[ \frac{2}{\left( L-n \right) ^{2}}+\frac{\ln \left( E\left[ m_{1} \right] \right) }{\left( L-n \right) }+\ln \left( E\left[ m_{1} \right] \right) ^{2} \right] \nonumber \\&\quad +h\frac{2DyL^{3}}{X\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) \left( L-n \right) ^{3}}\nonumber \\&\quad >\frac{\left( \mathrm {K+}{\mathrm {K}}_{d} \right) D}{y^{2}\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) \left( L-n \right) ^{2}}+h\frac{\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) }{\mathrm {2}}\nonumber \\&\quad -h\frac{DL\left( {\mathrm {L}}^{2}{\mathrm {E[\uprho }}_{e}\mathrm {]+2}Ln\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) -n^{2}\left( \mathrm {1-}{\mathrm {E[\uprho }}_{e}] \right) \right) }{X\left( \mathrm {1-E[}{\uprho }_{e}] \right) \left( L-n \right) ^{2}} \end{aligned}$$

(18)

In order to prove this step, some previous mathematical operations are required. Let’s first assume some obvious considerations and numerical range estimations as:

• 1. $0 \ll \left( L-n \right) \ll y$

• 2. ${\mathrm {E}}\left[ {\uprho } \right] \approx 0$ and ${\mathrm {E[\uprho }}_{e}] \approx 0$, but strictly positive and therefore $\left( {\mathrm {1-E}}\left[ {\uprho }_{e} \right] \right) \approx 1$

• 3. For $E\left[ m_{2} \right]$ and $E\left[ m_{1} \right]$ strictly positive tending to zero.

$$\begin{aligned}&\mathop {\lim }\limits _{\begin{array}{c} {0 \ll ({L - n}) \ll y}\\ {{\mathrm{E}}[{{\uprho }}_{e}] \rightarrow 0}\\ {{\mathrm{E}}[\uprho ] \rightarrow 0}\\ {{\mathrm{E}}[{{m_2}}] \rightarrow 0}\\ {{\mathrm{E}}[{{m_1}}] \rightarrow 0} \end{array}} {\frac{2Dc_{U}}{\left( L-n \right) ^{3}}}+\frac{2c_{l}DL}{\left( 1-{\mathrm {E}}[\uprho _{e}] \right) \left( L-n \right) ^{3}}+\frac{2\left( \mathrm {K+}{\mathrm {K}}_{d} \right) D}{y\left( \mathrm {1-}{\mathrm {E}}[\uprho _{e}] \right) \left( L-n \right) ^{3}}\nonumber \\&\qquad +\frac{Dc_{a}E\left[ {\uprho } \right] {E\left[ m_{2} \right] }^{n}}{\left( \mathrm {1-E}\left[ {\uprho }_{e} \right] \right) \left( L-n \right) } \left[ \frac{2}{\left( L-n \right) ^{2}}+\frac{\ln \left( E\left[ m_{2} \right] \right) }{\left( L-n \right) }+\ln \left( E\left[ m_{2} \right] \right) ^{2} \right] \nonumber \\&\qquad +\frac{Dc_{r}\left( 1-E\left[ {\uprho } \right] \right) {E\left[ m_{1} \right] }^{n}}{\left( \mathrm {1-}{\mathrm {E}}[\uprho _{e}] \right) (L-n)}\left[ \frac{2}{\left( L-n \right) ^{2}}+\frac{\ln \left( E\left[ m_{1} \right] \right) }{\left( L-n \right) }+\ln \left( E\left[ m_{1} \right] \right) ^{2} \right] \nonumber \\&\qquad +h\frac{2DyL^{3}}{X\left( \mathrm {1-}{\mathrm {E}}[\uprho _{e}] \right) \left( L-n \right) ^{3}}\nonumber \\&\quad >\mathop {\mathrm{{lim}}}\limits _{\begin{array}{c} {0 \ll \left( {L - n} \right) \ll y}\\ {{{\mathrm{E}}}[{{\uprho }}_{e}] \rightarrow 0}\\ {{\mathrm{E}}\left[ \uprho \right] \rightarrow 0}\\ {{\mathrm{E}}\left[ {{m_2}} \right] \rightarrow 0}\\ {{\mathrm{E}}\left[ {{m_1}} \right] \rightarrow 0} \end{array}} \frac{\left( \mathrm {K+}{\mathrm {K}}_{d} \right) D}{y^{2}\left( \mathrm {1-}{{\mathrm {E}}}[\uprho _{e}] \right) \left( L-n \right) ^{2}}+h\frac{\left( \mathrm {1-}{{\mathrm {E}}}[\uprho _{e}] \right) }{\mathrm {2}}\nonumber \\&\qquad -h\frac{DL\left( {\mathrm {L}}^{2}{{\mathrm {E}}}[\uprho _{e}]+2Ln\left( \mathrm {1-E}[\uprho _{e}] \right) -n^{2}\left( \mathrm {1-}{{\mathrm {E}}}[\uprho _{e}] \right) \right) }{X\left( \mathrm {1-}{{\mathrm {E}}}[\uprho _{e}] \right) \left( L-n \right) ^{2}} \end{aligned}$$

(19)

and with simplifications

$$\begin{aligned}&\mathop {\mathrm{{lim}}}\limits _{\begin{array}{c} {0 \ll \left( {L - n} \right) \ll y}\\ {\mathrm{{E}}[{{\uprho }}_{e}] \rightarrow 0}\\ {{\mathrm{E}}\left[ \uprho \right] \rightarrow 0}\\ {{\mathrm{E}}\left[ {{m_2}} \right] \rightarrow 0}\\ {{\mathrm{E}}\left[ {{m_1}} \right] \rightarrow 0} \end{array}} {\frac{2Dc_{U}}{\left( L-n \right) ^{3}}}\mathrm {+}\frac{2c_{l}DL}{\left( L-n \right) ^{3}}\mathrm {+}\frac{2\left( \mathrm {K+}{\mathrm {K}}_{d} \right) D}{y\left( L-n \right) ^{3}}+\frac{Dc_{a}E\left[ {\uprho } \right] {E\left[ m_{2} \right] }^{n}}{\left( L-n \right) } \left[ \frac{2}{\left( L-n \right) ^{2}} \right] \nonumber \\&\quad +\frac{Dc_{r}\left( 1-E\left[ {\uprho } \right] \right) {E\left[ m_{1} \right] }^{n}}{(L-n)}\left[ \frac{2}{\left( L-n \right) ^{2}} \right] \mathrm {+}h\frac{2DyL^{3}}{X\left( L-n \right) ^{3}}\nonumber \\&\quad >\mathop {\mathrm{{lim}}}\limits _{\begin{array}{c} {0 \ll \left( {L - n} \right) \ll y}\\ {\mathrm{{E}}[{{\uprho }}_{e}] \rightarrow 0}\\ {{\mathrm{E}}\left[ \uprho \right] \rightarrow 0}\\ {{\mathrm{E}}\left[ {{m_2}} \right] \rightarrow 0}\\ {{\mathrm{E}}\left[ {{m_1}} \right] \rightarrow 0} \end{array}} \frac{\left( \mathrm {K+}{\mathrm {K}}_{d} \right) D}{y^{2}\left( L-n\right) ^{2}}\mathrm {+}\frac{h}{\mathrm {2}}-h\frac{DL\left( \mathrm {2}Ln-n^{2} \right) }{X\left( L-n \right) ^{2}} \end{aligned}$$

(20)

As it can be stated that $\frac{2\left( \mathrm {K+}{\mathrm {K}}_{d} \right) D}{y\left( L-n \right) ^{3}}>\frac{\left( \mathrm {K+}{\mathrm {K}}_{d} \right) D}{y^{2}\left( L-n \right) ^{2}}$ for $\left( L-n \right) \ll y$, the inequality becomes

$$\begin{aligned}&\mathop {\mathrm{{lim}}}\limits _{\begin{array}{c} {0 \ll \left( {L - n} \right) \ll y}\\ {\mathrm{{E}}[{\mathrm{{\uprho }}_e}] \rightarrow 0}\\ {{\mathrm{E}}\left[ \uprho \right] \rightarrow 0}\\ {{\mathrm{E}}\left[ {{m_2}} \right] \rightarrow 0}\\ {{\mathrm{E}}\left[ {{m_1}} \right] \rightarrow 0} \end{array}}\frac{2Dc_{U}}{\left( L-n \right) ^{3}}\mathrm {+}\frac{2c_{l}DL}{\left( L-n \right) ^{3}}\mathrm {+}\frac{2Dc_{a}E\left[ {\uprho } \right] {E\left[ m_{2} \right] }^{n}}{\left( L-n \right) ^{3}}\mathrm {+}\frac{2Dc_{r}\left( 1-E\left[ {\uprho } \right] \right) {E\left[ m_{1} \right] }^{n}}{\left( L-n \right) ^{3}}\nonumber \\&\quad +h\frac{2DyL^{3}}{X\left( L-n \right) ^{3}}>\mathop {\mathrm{{lim}}}\limits _{\begin{array}{c} {0 \ll \left( {L - n} \right) \ll y}\\ {\mathrm{{E}}[{{\uprho }}_{e}] \rightarrow 0}\\ {{\mathrm{E}}\left[ \uprho \right] \rightarrow 0}\\ {{\mathrm{E}}\left[ {{m_2}} \right] \rightarrow 0}\\ {{\mathrm{E}}\left[ {{m_1}} \right] \rightarrow 0} \end{array}}\frac{h}{\mathrm {2}}-h\frac{DL\left( \mathrm {2}Ln-n^{2} \right) }{X\left( L-n \right) ^{2}} \end{aligned}$$

(21)

The first term of the inequality is always positive and the second term of the inequality is always negative as it is supposed that $\left( L-n \right) \ll y$ and therefore ${\mathrm {L}}\ll y$. The inequality is therefore true and the statement $\left| \frac{\delta {{\mathrm {TPU}}}_{1}(y,n)}{\delta n\delta n} \right| >\left| \frac{\delta {{\mathrm {TPU}}}_{1}(y,n)}{\delta n\delta y} \right|$ is verified. $\square$