The infinite-horizon investment–consumption problem for Epstein–Zin stochastic differential utility. II: Existence, uniqueness and verification for $\vartheta \in (0,1)$

Abstract

In this article, we consider the optimal investment–consumption problem for an agent with preferences governed by Epstein–Zin (EZ) stochastic differential utility (SDU) over an infinite horizon. In a companion paper Herdegen et al. (Finance Stoch. 27:127–158, 2023), we argued that it is best to work with an aggregator in discounted form and that the coefficients $R$ of relative risk aversion and $S$ of elasticity of intertemporal complementarity (the reciprocal of the coefficient of elasticity of intertemporal substitution) must lie on the same side of unity for the problem to be well founded. This can be equivalently expressed as $\vartheta := \frac{1-R}{1-S} >0$.

In this paper, we focus on the case $\vartheta \in (0,1)$. The paper has three main contributions: first, to prove existence of infinite-horizon EZ SDU for a wide class of consumption streams and then (by generalising the definition of SDU) to extend this existence result to any consumption stream; second, to prove uniqueness of infinite-horizon EZ SDU for all consumption streams; and third, to verify the optimality of an explicit candidate solution to the investment–consumption problem in the setting of a Black–Scholes–Merton financial market.

1 Introduction

This paper is the second of a trio of papers by the same authors; see also Herdegen et al. [4, 3]. The collective goal of these papers is to undertake a rigorous study of a Merton-style infinite-horizon investment–consumption problem in the setting of Epstein–Zin (EZ) stochastic differential utility (SDU). In particular, the aim is to study when the problem is mathematically well posed and economically well founded, and if so, to derive the candidate optimal strategy, the candidate value function and the candidate optimal utility process (see [4]). Once these issues have been resolved, the objective is to prove existence and uniqueness (where possible) of a utility process associated to an arbitrary consumption stream and to verify that the candidate optimal strategy is indeed optimal in a large class of admissible investment–consumption strategies (see the present paper and [3]).

EZ SDU has two key parameters: $R$, representing the coefficient of relative risk aversion, and $S$, representing the coefficient of elasticity of intertemporal complementarity (EIC), the reciprocal of the coefficient of the elasticity of intertemporal substitution. In [4], we argued that if $R$ and $S$ lie on opposite sides of unity, then EZ SDU is not well founded in the sense that even though it is possible to obtain (candidate) solutions to the backward stochastic differential equations (BSDEs) defining the utility process, these solutions have the characteristics of a utility bubble: the current value arises not from integrated consumption over time, but rather from a postulated ever larger value of the utility process at a future time. We must have $\vartheta := \frac{1-R}{1-S}>0$ for the utility process to have an interpretation which is economically sound.

One of the insights in [4] which led us to the above conclusion is that it is better to work with the discounted form of EZ SDU rather than the difference form. The advantage of the discounted form is that the aggregator takes values in either $[-\infty ,0]$ or $[0,\infty ]$ rather than in $[-\infty ,\infty ]$. Since the sign of the aggregator is unambiguous, it is always possible to assign a value to the integral of the aggregator against time (and also to the expected value of the integral of the aggregator).

In this paper, we focus on the case $\vartheta \in (0,1)$. The case $\vartheta >1$ is covered in [3]. Note that $\vartheta =1$ is the case of additive utility. This paper aims to answer three main questions under this parameter restriction:

1) To which consumption streams is it possible to assign a utility process?

2) For which consumption streams is the assigned utility process unique?

3) Can we verify that an explicit candidate optimal investment–consumption strategy in a Black–Scholes–Merton market is indeed optimal for the class of all admissible investment–consumption strategies?

The contributions of this paper are threefold, and each contribution addresses one of the three questions above.

First, we prove a set of existence results (covering $\vartheta \in (0,\infty )$) which show that there exists a well-defined utility process for a large class of consumption streams. Then, under the assumption $\vartheta <1$, we show how to extend the existence result further to give a well-defined (though not necessarily finite-valued) utility process for any consumption stream. Key to the proofs is the fact that under our formulation, the aggregator takes only one sign.

Second, we turn to uniqueness. Again assuming $\vartheta \in (0,1)$, we show that for EZ SDU preferences, the utility process associated to a consumption stream is unique. The main idea is to apply a comparison theorem for (sub- and super-)solutions to a representation of the utility process.

Third, we turn to the identification of the optimal investment–consumption strategy and the optimal utility process. At this point, we specialise to a constant-parameter Black–Scholes–Merton market. In this setting, the candidate optimal strategy and candidate optimal utility process are known (see Schroder and Skiadas [11], Melnyk et al. [8], Kraft et al. [6] as well as Herdegen et al. [4]), and the main techniques behind a verification argument are also well established in the literature. But what distinguishes our results is the fact that we optimise over all attainable consumption streams, i.e., all consumption streams which can be financed from an initial wealth $x > 0$. In the extant literature, optimisation typically only takes place over a sub-family of consumption streams for which the corresponding utility process possesses certain regularity and integrability conditions. Further, since there are very few existence results in the literature, it often happens that the only strategies for which it can be verified that the utility process indeed satisfies the required regularity conditions are the constant proportional investment–consumption strategies. Since we optimise over all attainable consumption streams, this is a significant advance.

The remainder of this paper is organised as follows. In Sect. 2, we introduce stochastic differential utility (SDU) and Epstein–Zin (EZ) SDU and summarise the results of [4]. Once this preliminary discussion has been completed, we are able in Sect. 3 to give a more thorough description of the issues which arise regarding existence and uniqueness of utility processes associated to general consumption streams, and of the strategy of our proofs. In Sect. 4, we prove existence of EZ SDU for a wide class of consumption streams, including all constant proportional consumption streams for which the problem is well posed, and any strategies which are ‘close’ to constant proportional streams in a sense to be made precise. Still, this does not cover all consumption streams; so in Sects. 5 and 6, we show how the utility process for an arbitrary consumption stream can be obtained by approximation and taking limits. Section 5 also proves uniqueness of the utility process. In Sect. 7, we introduce the Black–Scholes–Merton financial market and give expressions for the candidate optimal investment–consumption strategy and the candidate optimal utility process in this market. Finally, in Sect. 8, we prove optimality of the candidate optimal strategy (Theorem 8.1), where the optimisation is taken over all attainable consumption streams and not just those satisfying regularity and integrability conditions. Key results along the way include a comparison result (Theorem 5.8), existence and uniqueness results (Theorem 4.5, Theorem B.2) and an approximation result (Theorem 6.5).

2 Epstein–Zin stochastic differential utility

Throughout, we work on a filtered probability space $(\Omega , {\mathcal {F}}, (\mathcal {F}_{t})_{t \geq 0}, \mathbb{P})$ satisfying the usual conditions, where $\mathcal {F}_{0}$ is ℙ-trivial. Let $\mathscr{P}$ be the set of progressively measurable processes, and $\mathscr{P}_{+}$, $\mathscr{P}_{++}$ the restrictions of $\mathscr{P}$ to processes that take nonnegative and strictly positive values, respectively. Moreover, denote by $\mathscr{S}$ the set of all semimartingales. We identify processes in $\mathscr{P}$ or $\mathscr{S}$ that agree up to indistinguishability.

Stochastic differential utility (SDU) is a generalisation of time-additive discounted expected utility and is designed to allow a separation of risk preferences from time preferences. For a fuller discussion of the issues considered in this section, see Herdegen et al. [4, Sect. 4].

Under additive expected utility, the value or utility of a consumption stream, i.e., a process $C \in \mathscr{P}_{+}$, is given by $J_{U}(C) = \mathbb{E}^{} [ \int _{0}^{\infty }U(t,C_{t}) \,\mathrm {d}t ]$, and the value or utility process is given by $V_{t} = \mathbb{E}[\int _{t}^{\infty }U(s,C_{s}) \,\mathrm {d}s \,|\,{ \mathcal {F}}_{t}]$. Under SDU, the function $U=U(s,C_{s})$ is generalised to become an aggregator $g=g(s,C_{s},V_{s})$, and the stochastic differential utility process $V^{C}=(V^{C}_{t})_{t\geq 0}$ associated to a consumption stream $C$ solves

$$ V^{C}_{t} = \mathbb{E}\bigg[ \int _{t}^{\infty }g(s,C_{s},V^{C}_{s})\,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg]. $$

(2.1)

Note that if $g$ takes positive and negative values, the conditional expectation on the right-hand side of (2.1) need not be well defined. In the following definition, see also [4, Definition 3.1], $g$ takes values in $\mathbb{V}\subseteq \overline {\mathbb{R}}$. Throughout this paper, we assume that $g$ is one-signed so that $\mathbb{V}$ is a subset either of $[0,\infty ]$ or of $[-\infty ,0]$.

Definition 2.1

A one-signed aggregator is a function ${g:\mathbb{R}_{+}\times \mathbb{R}_{+} \times{ \mathbb{V}}\to \mathbb{V}}$. For $C\in \mathscr{P}_{+}$, define $\mathbb{I}(g,C):= \{V\in \mathscr{P}:~\mathbb{E}[\int _{0}^{\infty }| g(s,C_{s},V_{s})| \,\mathrm {d}s] < \infty \}$. Then $V \in \mathbb{I}(g,C)$ is a utility process associated to the pair $(g,C)$ if it has càdlàg paths and satisfies (2.1) for all $t \in [0,\infty )$. Further, let $\mathbb{U}\mathbb{I}(g,C)$ be the set of elements of $\mathbb{I}(g,C)$ which are uniformly integrable.

By [4, Remark 3.2], a utility process is a special semimartingale and lies in $\mathbb{U}\mathbb{I}(g,C)$.

Definition 2.2

A consumption stream $C \in \mathscr{P}_{+}$ is $g$-evaluable if there exists a utility process $V\in \mathbb{I}(g,C)$ associated to the pair $(g,C)$. The set of $g$-evaluable consumption streams $C$ is denoted by $\mathscr{E}(g)$. Furthermore, if the utility process is unique (up to indistinguishability), then $C$ is $g$-uniquely evaluable. The set of $g$-uniquely evaluable $C$ is denoted by $\mathscr{E}_{u}(g)$.

For a uniquely evaluable consumption stream $C$, we define the stochastic differential utility of $C$ and an aggregator $g$ by $J_{g}(C) := V^{C}_{0}$, where $V^{C}$ satisfies (2.1).

The Epstein–Zin (EZ) aggregator with parameters $(R,S)$ is defined as the function $g_{\mathrm{EZ}}:\mathbb{R}_{+} \times \mathbb{V}\to \mathbb{V}$ given by

$$ g_{\mathrm{EZ}}(c,v) := \frac{c^{1-S}}{{1-S}}\big( (1-R)v\big)^{ \frac{S-R}{1-R}}. $$

(2.2)

Here $\mathbb{V}= (1-R)\overline {\mathbb{R}}_{+}$ is the domain of the EZ utility process, and both parameters $R$ and $S$ lie in $(0,\infty ) \setminus \{1\}$. Note that some care is required when $\frac{c^{1-S}}{1-S},((1-R)v)^{\frac{S-R}{1-R}}$ are in $\{0,\infty \}$. This case is deferred to Sect. 4.

Remark 2.3

More generally, we can consider the aggregator

$$ g_{\mathrm{EZ}}(t,c,v) := b e^{-\delta t}\frac{c^{1-S}}{{1-S}}\big( (1-R)v \big)^{\frac{S-R}{1-R}}, $$

where $b>0$ and $\delta \in \mathbb{R}$. Here $b$ is a scaling parameter which can be factored out, and the discount factor $e^{-\delta t}$ can be eliminated by a change of numéraire; see [4, Remark 4.2, Sect. 5.2]. For this reason, and without loss of generality, we take $b=1$ and $\delta =0$ in this paper.

It is convenient to introduce the parameters $\vartheta := \frac{1-R}{1-S}$ and $\rho =\frac{S-R}{1-R} = \frac{\vartheta -1}{\vartheta }$, so that (2.2) becomes

$$ g_{\mathrm{EZ}}(c,v) = \frac{c^{1-S}}{{1-S}}\big( (1-R)v\big)^{\rho}. $$

(2.3)

When $S=R$, the aggregator reduces to the discounted CRRA utility function. This case corresponds to $\vartheta =1$ and $\rho =0$. We assume throughout that $R\neq S$ are both in $(0,\infty ) \setminus \{1\}$ so that $\vartheta \neq 1$ and $\delta \neq 0$.

If $g_{\mathrm{EZ}}$ is the EZ aggregator for (2.3), the utility process $V^{C} = V = (V_{t})_{t \geq 0}$ associated to consumption $C$ and aggregator $g_{\mathrm{EZ}}$ solves

$$ V_{t} = \mathbb{E}\bigg[\int _{t}^{\infty}\frac{C_{s}^{1-S}}{{1-S}}\big( (1-R)V_{s} \big)^{\rho }\,\mathrm {d}s\,\bigg| \,\mathcal {F}_{t} \bigg]. $$

(2.4)

One of the main results of [4] is the following theorem ([4, Theorem 4.4]).

Theorem 2.4

For EZ SDU over an infinite horizon with aggregator given by (2.3), we must have $\vartheta = \frac{1-R}{{1-S}} > 0$ for there to exist solutions to (2.4).

The condition $\vartheta > 0$, or equivalently $\rho \in (-\infty , 1)$, means that both $R$ and $S$ are either greater than unity or smaller than unity.

3 An overview of the arguments behind the existence and uniqueness proofs

Our first goal is to discuss existence and uniqueness of EZ SDU over an infinite horizon. (For general existence and uniqueness results for EZ SDU in a finite-horizon setting, we refer to Seiferling and Seifried [12].)

Our results and approach are as follows. The first major contribution is an existence result for all strictly positive consumption streams $C=(C_{t})_{t \geq 0}$ which satisfy $kC^{1-R}_{t} \leq \mathbb{E}[\int _{t}^{\infty }{C}_{s}^{1-R} \,\mathrm {d}s \,|\, \mathcal {F}_{t}]\leq K C_{t}^{1-R}$ for some constants $0 < k \leq K < \infty$. Note that it follows from the results of [4, Sect. 5.3] (see also Sect. 7 below) that in a constant-parameter Black–Scholes–Merton financial market, constant proportional investment–consumption strategies satisfy $\kappa C^{1-R}_{t} =\mathbb{E}[\int _{t}^{\infty }{C}_{s}^{1-R} \,\mathrm {d}s\,|\,\mathcal {F}_{t}]$ for some $\kappa \in (0, \infty )$, at least when $\mathbb{E}[\int _{0}^{\infty }C_{s}^{1-R} \,\mathrm {d}s] < \infty$. This means that our result can be interpreted as a statement about the evaluability of strategies that are, in a very precise sense, within a multiplicative constant of a constant proportional investment–consumption strategy. Moreover, for each such $C$, there is a unique utility process $V=(V^{C}_{t})_{t\geq 0}$ such that $k_{V} C_{t}^{1-R} \leq (1-R)V_{t} \leq K_{V} C^{1-R}_{t}$ for a different pair of constants $(k_{V},K_{V})$. (Note that this does not preclude the existence of other utility processes which do not satisfy such bounds.) The proof relies on the construction of a contraction mapping and a fixed point argument.

To make further progress, we assume that $\vartheta \in (0,1)$ (equivalently, $\rho < 0$). In this case, we can show that any utility process is unique (in fact, we show uniqueness for a wide class of aggregators, the main restriction being that they are nonincreasing in $v$). The key idea is to use concepts from the theory of BSDEs to extend the concept of a solution to (2.4) to include subsolutions and supersolutions, depending (roughly speaking) on whether the equality in (2.4) is replaced by ≤ or ≥. Then, again under the assumption that the aggregator is nonincreasing in $v$, we prove a comparison theorem which tells us that any subsolution always lies below any supersolution. Uniqueness of solutions then follows by a standard argument as any solution is simultaneously both a subsolution and a supersolution. So if $V^{1}$ and $V^{2}$ are solutions, then $V^{1} \leq V^{2}$ and $V^{2} \leq V^{1}$, and hence $V^{1} = V^{2}$.

For EZ SDU, when $\vartheta >1$, the comparison argument fails and the uniqueness argument does not hold. Note that it is not merely that we need to look for a different strategy of proof—instead, it is simple to give examples for which there are multiple solutions to (2.4). In this case, a different comparison theorem and a modification of the definition of the utility process are required. For these reasons, we defer the discussion of this case to Herdegen et al. [3].

Returning to the case $\vartheta \in (0,1)$, in order to remove the constraints $k>0$ and $K<\infty$, we again exploit the comparison theorem to obtain a monotonicity property for solutions. Provided we allow utility processes to take values in the extended real line, we can exploit the fact that the aggregator takes only one sign to show that it is possible to define a unique, possibly infinite-valued, utility process for any attainable consumption stream. Here we make use of the notion of generalised optional strong supermartingales.

Where proofs are not given in the main text, they are given in the appendices.

4 Existence of EZ SDU

For the EZ aggregator $g_{\mathrm{EZ}}$, it was shown in Herdegen et al. [4, Sect. 5.3] (see also Sect. 7 below) that the candidate optimal strategy—along with many other proportional consumption streams—is evaluable. The goal of this section is to prove existence for a much larger class of consumption streams. The authors are not aware of any results on the existence of infinite-horizon EZ stochastic differential utility; so this is an essential result that is currently missing from the literature.

A transformation of the coordinate system leads to a simplified problem. Define the $[0, \infty ]$-valued processes $W = (W_{t})_{t\geq 0}$ and $U = (U_{t})_{t\geq 0}$ by

$$ W_{t} = (1-R)V_{t}, \qquad U_{t} = u(C_{t}) = \vartheta C_{t}^{1-S}, $$

(4.1)

where we agree that $U_{t} := \infty$ if $C_{t} = 0$ and $S > 1$.

Let $h_{\mathrm{EZ}}(u,w): \overline {\mathbb{R}}_{+} \times \overline {\mathbb{R}}_{+} \to \overline {\mathbb{R}}_{+}$ be defined by

$$\begin{aligned} h_{\mathrm{EZ}}(u,w) := \textstyle\begin{cases} u w^{\rho}, &\quad (u,w) \in (0,\infty )\times (0,\infty ), \\w^{\rho}, &\quad (u,w) \in (0,\infty ) \times \{0, \infty \}, \\u, &\quad (u,w) \in \{0,\infty \} \times [0,\infty ], \end{cases}\displaystyle \end{aligned}$$

with the standard convention $0^{\rho }:= \infty$ and $\infty ^{\rho }= 0$ for $\rho < 0$. The motivation behind the definition on the boundary is to ensure the continuity in $w$ for fixed $u$. This also leads to a natural extension of the EZ aggregator in (2.2) to $(c, v) \in \overline {\mathbb{R}}_{+}\times (1-R)\overline {\mathbb{R}}_{+}$ by setting

$$\begin{aligned} g_{\mathrm{EZ}}(c,v) = \textstyle\begin{cases} \frac{1}{1-R}((1-R)v)^{\rho }&\quad \text{if } (c,v)\in \mathbb{R}_{++} \times \{0,(1-R)\infty \}, \\ \frac{1}{1-S}c^{1-S} &\quad \text{if } (c,v)\in \{0,(1-R)\infty \} \times (1-R)\overline {\mathbb{R}}_{+}. \end{cases}\displaystyle \end{aligned}$$

We use this definition of $g_{\mathrm{EZ}}$ for the remainder of the paper.

Note that $V \in \mathbb{I}(g_{\mathrm{EZ}},C)$ if and only if $W \in \mathbb{I}(h_{\mathrm{EZ}}, U)$. Consequently, $V^{C}$ is a utility process associated to a consumption stream $C$ with aggregator $g_{\mathrm{EZ}}$ if and only if $W^{U}$ is a utility process associated to the consumption stream $U$ with aggregator $h_{\mathrm{EZ}}$.

We next aim to define an operator $F_{U}$ from an appropriate subset of $\mathscr{P}_{++}$ to itself satisfying

$$ F_{U}(W)_{t} := \mathbb{E}\bigg[\int _{t}^{\infty }h_{\mathrm{EZ}}(U_{s},W_{s}) \,\mathrm {d}s\, \bigg| \,\mathcal {F}_{t} \bigg]. $$

(4.2)

Here, we always choose a càdlàg version for the right-hand side of (4.2). In particular, every fixed point of the operator $F_{U}$ has càdlàg paths. Note that $V$ is a solution to (2.1) with aggregator $g_{\mathrm{EZ}}$ and consumption $C$ if and only $W$ is a fixed point of the operator $F_{U}$ for the transformed consumption $U$.

Definition 4.1

Suppose that $U=(U_{t})_{t\geq 0} \in \mathscr{P}_{+}$ and $Y=(Y_{t})_{t\geq 0} \in \mathscr{P}_{+}$. We say that $U$ has the same order as $Y$ if there exist constants $k,K\in (0,\infty )$ such that $0\leq k Y \leq U \leq K Y$. Denote the set of processes with the same order as $Y$ by $\mathbb{O}(Y)$.

Definition 4.2

Define $L^{\vartheta }_{++}$ as the subset of all $\Lambda \in \mathscr{P}_{++}$ with $\mathbb{E}[\int _{0}^{\infty } \Lambda ^{\vartheta }_{s} \,\mathrm {d}s] <\infty$. For $\Lambda \in L^{\vartheta }_{++}$, define the càdlàg process $I^{\Lambda }= (I^{\Lambda}_{t})_{t\geq 0}$ by $I^{\Lambda}_{t} := \mathbb{E}[\int _{t}^{\infty }\Lambda _{s}^{\vartheta }\,\mathrm {d}s\,|\, \mathcal {F}_{t}]$. Further, define $\hat{L}^{\vartheta }_{++}\subseteq L^{\vartheta }_{++}$ by $\hat{L}^{\vartheta }_{++} = \{\Lambda \in L^{\vartheta }_{++}:~\Lambda ^{ \vartheta }\in \mathbb{O}(I^{\Lambda})\}$.

Example 4.3

Let $Z = (Z_{t})_{t\geq 0}$ be a geometric Brownian motion such that $Z^{\vartheta }$ has a negative drift. Then $Z\in \hat{L}^{\vartheta }_{++}$. Indeed, suppose that the drift is $-\gamma <0$. Then $Z^{\vartheta }= \frac{1}{\gamma}I^{Z}$.

Lemma 4.4

Let $\Lambda \in \hat{L}^{\vartheta }_{++}$ and $U\in \mathbb{O}(\Lambda )$. Then $F_{U}(\, \cdot \,)$ maps $\mathbb{O}(\Lambda ^{\vartheta })$ to itself.

Proof

This follows from the more general Lemma B.1 in Appendix B. □

We may now state a first existence result. While it is not the strongest existence result we prove in this paper (Theorem 4.5 is a special case of Theorem B.2), it forms the backbone of further existence arguments. The idea of the proof is to transform the problem to an alternative space where the transformed form of $F_{U}$ is a contraction mapping. The existence of a fixed point then follows from the Banach fixed point theorem.

Theorem 4.5

Let $\Lambda \in \hat{L}^{\vartheta }_{++}$ and $U\in \mathbb{O}(\Lambda )$. Then $F_{U}$ defined by (4.2) has a fixed point $W \in \mathbb{O}(\Lambda ^{\vartheta }) \subseteq \mathbb{I}(h_{\mathrm{EZ}}, U)$, which is unique in $\mathbb{O}(\Lambda ^{\vartheta })$ and has càdlàg paths.

Proof

This is a specific version of the more general Theorem B.2. For a stand-alone proof, one just needs to set $\varepsilon =0$ in the proof of Theorem B.2. □

The following result is a direct corollary to Theorem 4.5 and the definitions of $W$ and $U$ in terms of $V$ and $C$ given in (4.1).

Theorem 4.6

Suppose $C\in \mathscr{P}_{++}$ satisfies $\mathbb{E}[\int _{0}^{\infty }C_{s}^{1-R} \,\mathrm {d}s] < \infty$ and for some constants $0< k< K<\infty$ that

$$\begin{aligned} k\mathbb{E}\bigg[ \int _{t}^{\infty }C_{s}^{1-R} \,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg] \leq C_{t}^{1-R} \leq K\mathbb{E}\bigg[ \int _{t}^{\infty }C_{s}^{1-R} \,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg] \end{aligned}$$

for all $t\geq 0$. Then there exists a utility process $V=(V^{C}_{t})_{t \geq 0}$ associated with $g_{\mathrm{EZ}}$ and $C$. Moreover, this utility process is unique in the class of processes with the property that $(V_{t}/\mathbb{E}[\int _{t}^{\infty }\frac{C_{s}^{1-R}}{1-R} \,\mathrm {d}s \,|\,\mathcal {F}_{t}])$ is bounded above and below by strictly positive constants.

Proof

Take $U_{t}=\Lambda _{t}=C_{t}^{1-S}$. Then $U$ satisfies the conditions of Theorem 4.5 and so there exists a utility process $W$ associated to $(h_{\mathrm{EZ}},U)$ which is unique in $\mathbb{O}(\Lambda ^{\vartheta })$. Therefore, $V = \frac{W}{1-R}$ is a utility process associated to $(g_{\mathrm{EZ}},C)$; uniqueness in the appropriate class is also inherited. □

Relative to the extant literature, Theorem 4.6 massively expands the set of consumption streams which are known to be evaluable. However, it still does not allow us to assign a utility to every consumption stream. For example, the zero consumption stream is excluded. Note also that Theorem 4.6 does not exclude the possibility that there are other utility processes which do not satisfy the condition that $(V_{t}/\mathbb{E}[\int _{t}^{\infty }\frac{C_{s}^{1-R}}{1-R} \,\mathrm {d}s \,|\,\mathcal {F}_{t}])$ is bounded.

5 Subsolutions and supersolutions

The aim of this section is to introduce the notions of subsolutions and supersolutions and then prove a comparison theorem for aggregators that take only one sign and are nonincreasing in $v$. As a consequence, all evaluable consumption streams for such aggregators are uniquely evaluable.

Let $\mathbb{V}\subseteq [-\infty ,\infty ]$ denote the set in which $V$ may take values. Under our assumption that $g$ is one-signed, we have either $\mathbb{V}\subseteq \overline {\mathbb{R}}_{+}$ or $\mathbb{V}\subseteq \overline {\mathbb{R}} _{-}$. This one-sign property ensures that integrals are always well defined.

The following definition extends the notion of an aggregator, allowing it also to depend on the state $\omega \in \Omega$ of the world.

Definition 5.1

An aggregator random field $g:\mathbb{R}_{+}\times \Omega \times \mathbb{R}_{+} \times \mathbb{V}\to \mathbb{V}$ is a product-measurable mapping such that $g(\,\cdot \,,\omega ,\,\cdot \,,\,\cdot \,)$ is an aggregator for fixed $\omega \in \Omega$, and for progressively measurable processes $C=(C_{t})_{t\geq 0}$ and $V=(V_{t})_{t\geq 0}$, the process $(g(t,\omega ,C_{t}(\omega ),V_{t}(\omega )))_{t\geq 0}$ is progressively measurable.

Example 5.2

Let $G:\mathbb{R}_{+}\times \mathbb{V}\times \mathbb{R}\to \mathbb{V}$ be continuous and $Y:[0,\infty )\times \Omega \to \mathbb{R}$ a progressively measurable process. Then $g(t,\omega ,c,v) := G(c,v,Y(t,\omega ))$ is an aggregator random field.

Let $g$ be an aggregator random field. The definitions of $\mathbb{I}(g,C)$, $\mathbb{U}\mathbb{I}(g,C)$, the utility process associated to the pair $(g,C)$ and the sets of evaluable and uniquely evaluable consumption streams $\mathscr{E}(g)$ and $\mathscr{E}_{u}(g)$ follow verbatim from Definitions 2.1 and 2.2.

We now introduce the notion of subsolutions and supersolutions. To this end, recall that làd stands for “limites à droite”, i.e., for the process to admit right limits.

Definition 5.3

Let $C \in \mathscr{P}_{+}$ be a consumption stream and $g$ an aggregator random field. A $\mathbb{V}$-valued, làd, optional process $V$ is called

– a subsolution for the pair $(g,C)$ if $\limsup _{t\to \infty} \mathbb{E}^{} [ V_{t+} ] \leq 0$ and for all bounded stopping times ${\tau _{1}}\leq{\tau _{2}}$,

$$ V_{\tau _{1}} \leq \mathbb{E}\bigg[ V_{{\tau _{2}}{+}} + \int _{\tau _{1}}^{{\tau _{2}}} g(s,\omega , C_{s},V_{s})\,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{{\tau _{1}}} \bigg]. $$

(5.1)

– a supersolution for the pair $(g,C)$ if $\liminf _{t\to \infty}~ \mathbb{E}^{} [ V_{t+} ] \geq 0$ and for all bounded stopping times ${\tau _{1}}\leq{\tau _{2}}$,

$$ V_{\tau _{1}} \geq \mathbb{E}\bigg[ V_{{\tau _{2}}{+}} + \int _{\tau _{1}}^{{\tau _{2}}} g(s,\omega , C_{s},V_{s})\,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{{\tau _{1}}} \bigg]. $$

(5.2)

– a solution for the pair $(g,C)$ if it is both a subsolution and a supersolution and $V\in \mathbb{I}(g,C)$.

Remark 5.4

(a) $V$ is a supersolution associated to the pair $(g,C)$ if and only if $\tilde{V} := -V$ (which is valued in $\tilde {\mathbb{V}}:= -\mathbb{V}$) is a subsolution for the pair $(\tilde{g}, C)$, where $\tilde{g} (t,\omega , c, \tilde{v}) = - g (t,\omega , c, -\tilde{v})$.

(b) While we do not require sub- or supersolutions to be in $\mathbb{I}(g,C)$, we require this integrability for solutions.

(c) It might be expected that the definition would require subsolutions and supersolutions to be càdlàg. However, we construct the utility process for a general consumption stream by taking limits, and a monotone limit of càdlàg processes is not necessarily càdlàg. In contrast, optionality is preserved in the limit.

If $V$ is a utility process for the pair $(g,C)$, then $V\in \mathbb{I}(g,C)$ by definition. By [4, Remark 3.2], it then follows that $V$ is uniformly integrable. Similar results hold for sub- and supersolutions.

Lemma 5.5

Suppose that $\mathbb{V}\subseteq \overline {\mathbb{R}}_{+}$ and $V$ is a subsolution, or $\mathbb{V}\subseteq \overline {\mathbb{R}}_{-}$ and $V$ is a supersolution for the pair $(g, C)$. If $V\in \mathbb{I}(g,C)$, then $V\in \mathbb{U}\mathbb{I}(g,C)$.

Proof

By symmetry, we consider without loss of generality the case that $\mathbb{V}\subseteq \overline {\mathbb{R}}_{+}$ and $V \in \mathbb{I}(g,C)$ is a subsolution. Define the UI martingale $M = (M_{t})_{t \geq 0}$ by $M_{t} := \mathbb{E}[\int _{0}^{\infty }g(s, \omega , C_{s},V_{s})\,\mathrm {d}s\,|\,\mathcal {F}_{s}]$. Since $\mathbb{V}\subseteq \overline {\mathbb{R}}_{+}$, setting $\tau _{1} := t$ and $\tau _{2} := u$ in (5.1) and taking the limsup as $u \to \infty$ gives

$$ 0\leq V_{t} \leq \mathbb{E}\bigg[ \int _{t}^{\infty }g(s,\omega , C_{s},V_{s})\,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg] \leq M_{t}. $$

Hence $V$ is uniformly integrable. □

It is useful to introduce two monotonicity conditions on an aggregator random field.

Definition 5.6

Let $g:\mathbb{R}_{+}\times \Omega \times \mathbb{R}_{+} \times \mathbb{V}\to \mathbb{V}$ be an aggregator random field. Then $g$ is said to satisfy

– (c↑) if it is nondecreasing in $c$, its third argument $(\mathbb{P}\otimes \mathrm{d}t)$-a.e.

– (v↓) if it is nonincreasing in $v$, its fourth argument $(\mathbb{P}\otimes \mathrm{d}t)$-a.e.

Remark 5.7

For EZ SDU, (v↓) is satisfied if and only if $\vartheta \in (0, 1]$; if $\vartheta >1$, the aggregator is nondecreasing in its fourth argument.

The following result shows that under condition (v↓), a comparison result holds for sub- and supersolutions.

Theorem 5.8

Let $C \in \mathscr{P}_{+}$ and let $g$ be an aggregator random field satisfying (v↓). If $V^{1}$ is a subsolution and $V^{2}$ is a supersolution for the pair $(g,C)$, and $V^{1}$ or $V^{2}$ is in $\mathbb{U}\mathbb{I}(g,C)$, then $V^{1}_{\tau }\leq V^{2}_{\tau}$ $\mathbb{P}\textit{-a.s.}$ for all finite stopping times $\tau$.

We deduce two simple but important corollaries. The first one shows that under condition (v↓), all $g$-evaluable strategies are $g$-uniquely evaluable. The second shows that for aggregators $g$ satisfying (c↑) and (v↓), the utility associated to $(g,C)$ is nondecreasing in $g$ and $C$.

Corollary 5.9

Let $g$ be an aggregator random field satisfying (v↓). Then we have $\mathscr{E}(g) = \mathscr{E}_{u}(g)$.

Proof

Clearly, $\mathscr{E}(g) \supseteq \mathscr{E}_{u}(g)$. For the converse inclusion, fix $C\in \mathscr{E}(g)$. Suppose there are two utility processes $V^{1}$ and $V^{2}$ for the pair $(g,C)$. Since $V^{1}$ and $V^{2}$ are both solutions, they are in $\mathbb{U}\mathbb{I}(g,C)$ by Lemma 5.5. Since they are both sub- and supersolutions, we may apply Theorem 5.8 twice to show $V^{1}_{\tau }\geq V^{2}_{\tau}$ $\mathbb{P}\text{-a.s.}$ and $V^{2}_{\tau }\geq V^{1}_{\tau}$ $\mathbb{P}\text{-a.s.}$ for all finite stopping times $\tau \geq 0$. Thus $V^{1}_{\tau }= V^{2}_{\tau}$ $\mathbb{P}\text{-a.s.}$ for all finite stopping times $\tau$. Since $V^{1}$ and $V^{2}$ are both optional, this implies that they are indistinguishable (see e.g. Nikeghbali [10, Theorem 3.2]). □

Corollary 5.10

Let $C^{1}, C^{2} \in \mathscr{P}_{+}$ and $g^{1},g^{2}:\mathbb{R}_{+}\times \Omega \times \mathbb{R}_{+}\times \mathbb{V}\to \mathbb{V}$ be aggregator random fields satisfying (c↑) and (v↓). Suppose $C^{2} \geq C^{1}$ $(\mathbb{P}\otimes \mathrm{d}t)$-a.e. and $g^{2}(\,\cdot \,, \,\cdot \,, c, v) \geq g^{1}(\,\cdot \,, \,\cdot \,, c, v)$ $(\mathbb{P}\otimes \mathrm{d}t)$-a.e. for any $(c,v) \in \mathbb{R}_{+} \times \mathbb{V}$. Moreover, suppose there exists a utility process $V^{i}\in \mathbb{I}(g^{i},C^{i})$ for the pair $(g^{i},C^{i})$, $i \in \{1, 2\}$. Then $V^{1}_{\tau }\leq V^{2}_{\tau}$ for all finite stopping times $\tau$.

Remark 5.11

If $g_{1},g_{2}$ are both nonincreasing rather than nondecreasing in $c$ but otherwise the hypotheses of the corollary are unchanged, then $V^{1}_{\tau }\geq V^{2}_{\tau}$.

6 Removing the bounds on evaluable strategies when $\vartheta \in (0,1)$

The goal of this section is to show that if $\vartheta \in (0,1)$, we may first, extend the class of $U$ for which we can define a utility process by removing the lower bound restriction $k\Lambda \leq U$ from the hypotheses of Theorem 4.5, and second, generalise the notion of a utility process, allowing us to evaluate the EZ SDU of any consumption stream.

Standing Assumption 6.1

Henceforth we assume $\vartheta \in (0,1)$, or equivalently $\rho <0$.

Theorem 6.2

Let $\Lambda \in \hat{L}^{\vartheta }_{++}$ and suppose that $U\in \mathscr{P}_{+}$ is such that there exists $K\in \mathbb{R}_{+}$ with $0 \leq U \leq K \Lambda$. Then $F_{U}$ defined by (4.2) has a unique fixed point $W \in \mathbb{I}(h_{\mathrm{EZ}}, U)$.

Corollary 6.3

Suppose that $C\in \mathscr{P}_{+}$ is such that $C^{1-S}\leq K Z^{1-S}$, where $K\in \mathbb{R}_{+}$ and $Z$ is a geometric Brownian motion such that $Z^{1-R}$ has a negative drift. Then $C\in \mathscr{E}_{u}(g_{\mathrm{EZ}})$.

Proof

Setting $U := C^{1-S}$ and $\Lambda := Z^{1-S}$, it follows that $U \leq K \Lambda$. Furthermore, $\Lambda \in \hat{L}^{\vartheta }_{++}$ by Example 4.3 since $\Lambda ^{\vartheta }= Z^{1-R}$ has a negative drift. Finally, using Theorem 6.2, we may deduce that $U\in \mathscr{E}_{u}(h_{\mathrm{EZ}})$ and hence that $C\in \mathscr{E}_{u}(g_{\mathrm{EZ}})$. □

Corollary 6.3 gives us a large class of evaluable consumption streams. The rest of this section is dedicated to generalising the notion of a utility process. In particular, for any aggregator $g$ satisfying (c↑) and (v↓), the results of this section make it possible to assign a utility to any process $C\in \mathscr{P}_{+}$ that we can express as the monotone limit of processes $C^{n}\in \mathscr{E}_{u}(g)$. For the EZ aggregator, this includes all consumption streams.

Definition 6.4

For a general one-signed aggregator $g:\mathbb{R}_{+}\times \Omega \times \mathbb{R}_{+} \times \mathbb{V}\to \mathbb{V}$, let $\overline {\mathscr{E}}(g)$ denote the set of consumption streams $C\in \mathscr{P}_{+}$ that are monotone limits of a sequence $(C^{n})_{n\in \mathbb{N}}$ of processes in $\mathscr{E}(g)$ and either 1) $\mathbb{V}\subseteq \overline {\mathbb{R}}_{+}$ and $(C^{n})_{n\in \mathbb{N}}$ is nondecreasing, or 2) $\mathbb{V}\subseteq \overline {\mathbb{R}}_{-}$ and $(C^{n})_{n\in \mathbb{N}}$ is nonincreasing.

We now state the central result of this section—that we may extend the notion of a utility process and evaluate processes in $\overline{\mathscr{E}}(g)$.

Theorem 6.5

Let $g$ be a one-signed aggregator random field satisfying (c↑) and (v↓), and let $C\in \overline{\mathscr{E}}(g)$. Let $(C^{n})_{n\in \mathbb{N}}$ be a monotone approximating sequence. Let $V^{n}$ be the utility process associated to $C^{n}$ for each $n\in \mathbb{N}$. Then there exists an adapted càdlàg process $V^{\dagger }= \lim _{n\to \infty}V^{n}$ that is independent of the approximating sequence. Moreover, if $\mathbb{V}\subseteq \overline {\mathbb{R}}_{+}$, then $V^{\dagger}$ is the minimal supersolution and if $\mathbb{V}\subseteq \overline {\mathbb{R}}_{-}$, then $V^{\dagger}$ is the maximal subsolution.

Definition 6.6

We call the unique process $V^{\dagger }= (V^{\dagger}_{t})_{t\geq 0}$ constructed in Theorem 6.5 the generalised solution or the generalised utility process associated to $(g,C)$.

The following theorem tells us that the notion of a generalised solution extends the notion of a solution in the sense that if a solution exists, then it is equal to the generalised solution.

Theorem 6.7

Let $g$ be a one-signed aggregator random field satisfying (c↑) and (v↓). If there exists a solution $V$ associated to the pair $(g,C)$, then it agrees with the generalised solution $V^{\dagger}$.

Proof

We only prove the result in the case $\mathbb{V}\subseteq \overline {\mathbb{R}}_{+}$. The case $\mathbb{V}\subseteq \overline {\mathbb{R}}_{-}$ follows by a symmetric argument. By Theorem 6.5, $V^{\dagger}$ is the minimal supersolution. Let $\tau$ be an arbitrary finite stopping time. Since $V\in \mathbb{U}\mathbb{I}(g,C)$ is a subsolution and $V^{\dagger}$ is a supersolution, $V_{\tau}\leq V^{\dagger}_{\tau}$ by Theorem 5.8. Since $V$ is a supersolution and $V^{\dagger}$ is minimal in the class of supersolutions, $V^{\dagger}_{\tau}\leq V_{\tau}$. Hence $V^{\dagger}_{\tau}=V_{\tau}$. Since $V^{\dagger}$ and $V$ are both optional ($V^{\dagger}$ by Theorem 6.5, and $V$ by definition) and they agree for all bounded stopping times, $V^{\dagger}$ is equivalent to $V$ up to indistinguishability (see for example Nikeghbali [10, Theorem 3.2]). □

We henceforth drop the superscript ^† and denote the generalised utility process by $V$. The next proposition shows that the generalised solution is nondecreasing in $C$.

Proposition 6.8

Let $g$ be a one-signed aggregator random field satisfying (c↑) and (v↓) and $C^{1},C^{2}\in \overline{\mathscr{E}}(g)$. Suppose further that $C^{2}$ dominates $C^{1}$ $(\mathbb{P}\otimes \mathrm{d}t)$-a.e. For $i= 1,2$, let $V^{i}$ be the generalised solution associated to the pair $(g,C^{i})$. Then $V^{2}_{\tau }\geq V^{1}_{\tau}$ for all bounded stopping times $\tau$.

If we consider the EZ aggregator $g_{\mathrm{EZ}}$, we may assign a generalised utility process to any consumption stream.

Theorem 6.9

Let $C\in \mathscr{P}_{+}$. There exists a unique generalised utility process associated to the pair $(g_{\mathrm{EZ}},C)$.

Proof

First suppose $R<1$ so that $\mathbb{V}=\mathbb{R}_{+}$. We want to find a nondecreasing sequence of consumption streams $(C^{n})_{n\in \mathbb{N}}$ such that $C^{n} \in \mathscr{E}_{u}(g_{\mathrm{EZ}})$ for all $n\in \mathbb{N}$ and $C^{n}\nearrow C$. Let $Z$ be a geometric Brownian motion such that $Z^{1-R}$ has a negative drift. Let $C^{n} =C\wedge (n Z)$. Then it follows from Corollary 6.3 that $(C^{n})_{n\in \mathbb{N}}\in \mathscr{E}_{u}(g_{\mathrm{EZ}})$, and $C^{n} \nearrow C$. Therefore, by Theorem 6.5, there exists a unique generalised utility process for $C$.

Next, if $R > 1$ and $\mathbb{V}=\overline {\mathbb{R}}_{-}$, the proof goes through in exactly the same manner if we consider the sequence of processes $C^{n} = C \vee (\frac{1}{n} Z)$. □

We can now extend the definition of EZ utility to any consumption stream.

Definition 6.10

Let $C\in \mathscr{P}_{+}$. Define the EZ utility process associated to $C$ to be the generalised utility process $V^{C,g_{\mathrm{EZ}}}$ associated to the pair $(g_{\mathrm{EZ}},C)$. Define the EZ utility of the consumption stream to be $J_{g_{\mathrm{EZ}}}(C) := V^{C,g_{\mathrm{EZ}}}_{0}$.

7 The Black–Scholes–Merton financial market and the candidate optimal strategy

The Black–Scholes–Merton financial market consists of a risk-free asset with interest rate $r \in \mathbb{R}$, whose price process $S^{0}=(S^{0}_{t})_{t \geq 0}$ satisfies $S^{0}_{t} = \exp (r t)$, together with a risky asset whose price process $S^{1}= (S^{1}_{t})_{t \geq 0}$ follows a geometric Brownian motion with drift $\mu \in \mathbb{R}$ and volatility $\sigma > 0$, and whose initial value is $S^{1}_{0} = s^{1}_{0} > 0$. So $S^{1}_{t} = {s^{1}_{0}} \exp ( \sigma B_{t} + (\mu - \frac{1}{2} \sigma ^{2})t )$, where $B = (B_{t})_{t \geq 0}$ denotes a Brownian motion.

The agent optimises over the control variables given by the proportion of wealth invested in each asset and the rate of consumption. Let $\Pi _{t}$ represent the proportion of wealth invested in the risky asset at time $t$ and $\Pi ^{0}_{t}=1-\Pi _{t}$ the proportion of wealth held in the riskless asset at time $t$. Further, let $C_{t}$ denote the rate of consumption at time $t$. It then follows that the wealth process $X=(X_{t})_{t\geq 0}$ satisfies the SDE

$$ \,\mathrm {d}X_{t} = X_{t} \Pi _{t} \sigma \,\mathrm {d}B_{t} + \Big( X_{t} \big(r + \Pi _{t} (\mu - r)\big) - C_{t}\Big)\,\mathrm {d}t $$

(7.1)

with initial condition $X_{0}=x$, where $x$ is the initial wealth. Let $\lambda := \frac{\mu -r}{\sigma}$ be the Sharpe ratio of the risky asset.

Definition 7.1

(i) Given $x>0$, an admissible investment–consumption strategy is a pair $(\Pi ,C)= (\Pi _{t},C_{t})_{t \geq 0}$ of progressively measurable processes, where $\Pi$ is real-valued and $C$ is nonnegative, such that the SDE (7.1) has a unique strong solution $X^{x, \Pi , C}$ that is $\mathbb{P}\text{-a.s.}$ nonnegative. We denote the set of admissible investment–consumption strategies for $x > 0$ by $\mathscr{A}(x; r,\mu ,\sigma )$.

(ii) A consumption stream $C \in \mathscr{P}_{+}$ is called attainable for initial wealth $x > 0$ if there exists a progressively measurable process $\Pi = (\Pi _{t})_{t\geq 0}$ such that $(\Pi , C)$ is an admissible investment–consumption strategy. Denote the set of attainable consumption streams for $x > 0$ by $\mathscr{C}(x; r,\mu ,\sigma )$.

When it is clear which financial market we are considering, we simplify the notation and write $\mathscr{A}(x) = \mathscr{A}(x; r,\mu ,\sigma )$ and $\mathscr{C}(x) = \mathscr{C}(x; r,\mu ,\sigma )$.

The goal of an agent with EZ stochastic differential utility preferences is to maximise $J_{g_{\mathrm{EZ}}}(C)$ over attainable consumption streams, i.e., to find

$$\begin{aligned} V^{*}_{g_{\mathrm{EZ}}}(x) = \sup _{C \in \mathscr{C}(x)} V^{C,g_{\mathrm{EZ}}}_{0} = \sup _{C \in \mathscr{C}(x)}J_{g_{\mathrm{EZ}}}(C) . \end{aligned}$$

Remark 7.2

This definition of the stochastic control problem is different to that considered by Schroder and Skiadas [11], Xing [15], Matoussi and Xing [7], Melnyk et al. [8] and the rest of the literature on the Merton problem for EZ SDU in the fact that it optimises over all consumption streams and does not impose any regularity conditions beyond attainability.

We now turn to the candidate optimal strategy. Putting aside questions of existence and uniqueness (and allowing for the remainder of this section that we have $\vartheta \in (0, \infty )$), we seek an attainable consumption stream $C$ that maximises the value of $V^{C}_{0}$, where

$$\begin{aligned} V^{C}_{t} = \mathbb{E}\bigg[\int _{t}^{\infty }\frac{C_{s}^{1-S}}{{1-S}} \big( (1-R)V^{C}_{s}\big)^{\rho }\,\mathrm {d}s \,\bigg|\, \mathcal {F}_{t} \bigg]. \end{aligned}$$

As in the Merton problem with CRRA utility, it is reasonable to expect that the optimal strategy is to invest a constant proportion of wealth in the risky asset, and to consume a constant proportion of wealth. Consider the investment–consumption strategy $\Pi \equiv \pi \in \mathbb{R}$ and $C = \xi X$ for $\xi \in \mathbb{R}_{++}$. Let $X^{x,\pi ,\xi} = X = (X_{t})_{t \geq 0}$ be the corresponding wealth process, i.e., let $X^{x,\pi ,\xi}$ solve (7.1) for $\Pi \equiv \pi \in \mathbb{R}$ and $C = \xi X$. Note that $(\Pi , C) = (\pi , \xi X)$ is admissible.

Define $H: \mathbb{R}\times \mathbb{R}_{++} \to \mathbb{R}$ by

$$\begin{aligned} H(\pi , \xi ) = (R-1)\bigg({r} + \lambda \sigma \pi - \xi - \frac{\pi ^{2}\sigma ^{2}}{2}R\bigg), \end{aligned}$$

and define $\eta \in \mathbb{R}$ by

$$\begin{aligned} \eta = \frac{1}{S} \bigg( (S-1)r + (S-1) \frac{\lambda ^{2}}{2R} \bigg). \end{aligned}$$

For a proportional investment–consumption strategy $(\Pi = \pi ,~C=\xi X)$, it is easy to show (see Herdegen et al. [4, Remark 5.3]) that $(X^{x,\pi ,\xi})^{1-R}$ is a geometric Brownian motion with drift $-H(\pi ,\xi )$. Moreover, if $H(\pi ,\xi )$ is positive, $C = \xi X$ is evaluable and the associated utility process is given by

$$ V_{t} = \left ( \frac{\vartheta \xi ^{1-S} }{H(\pi ,\xi )} \right )^{ \vartheta }\frac{X_{t}^{1-R}}{1-R} . $$

(7.2)

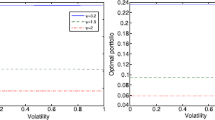
We can then maximise over $\pi$ and $\xi$ to find that the candidate optimal investment–consumption strategy is given by (see [4, Proposition 5.4, Equation (5.10)])

$$ \hat{\Pi} \equiv \hat{\pi} = \frac{\lambda}{\sigma R}, \qquad \hat{C} = \hat{\xi}X = \eta X. $$

(7.3)

Proposition 7.3

The candidate condition for a well-posed problem is $\eta >0$. In that case, the candidate optimal strategy is $(\hat{\Pi},\hat{C})$ from (7.3), the candidate utility process is $V = \eta ^{-\vartheta S} \tfrac{X^{1-R}}{1-R}$, and the candidate value function is

$$ \hat{V}(x) = \eta ^{-\vartheta S }\frac{x^{1-R}}{1-R}. $$

(7.4)

Remark 7.4

If $\eta >0$ and $(\hat{\Pi}, \hat{C})$ is the candidate optimal strategy from (7.3), then $\hat{U} = \vartheta \hat{C}^{1-S}$ is a geometric Brownian motion, and $(\hat{U})^{\vartheta }$ has drift $-\eta \vartheta <0$. Hence $\hat{U}\in \hat{L}^{\vartheta }_{++}$ by Example 4.3. Similarly, all the constant proportional investment–consumption strategies $(\pi ,\xi )$ with $H(\pi ,\xi )>0$ are such that $C = \xi X^{x,\pi ,\xi}$ lies in $\hat{L}^{\vartheta }_{++}$. Roughly speaking, the same holds true for any strategy which is close to a constant proportional strategy (for which $H(\pi ,\xi )>0$). Thus existence of a utility process for the candidate optimal consumption stream follows from Theorem 4.5 (whereas existence of a utility process for a general consumption stream follows from Theorem 6.9—at least for $\vartheta \in (0, 1)$).

8 The verification argument for the candidate optimal strategy

The goal of this final section is to verify that the candidate optimal strategy is indeed optimal. Our discussion of existence and uniqueness is valid in a general financial market, but in order to optimise over consumption streams, we need to specify the set of attainable consumption processes. We do this by specifying the financial market, which we take to be the Black–Scholes–Merton market of Sect. 7.

The general structure of a primal verification argument for recursive optimal investment problems is as follows: first, apply Itô’s lemma to $\hat{V}(X^{\Pi ,C})$ for a general strategy $(\Pi ,C)$; next, use the HJB equation to show that $\hat{V}(X^{\Pi ,C})$ is a supersolution associated to the pair $(g_{\mathrm{EZ}},C)$; finally, the comparison theorem (Theorem 5.8) for sub- and supersolutions implies $\hat{V}(x) \geq V^{C}_{0}$ for any admissible strategy $C\in \mathscr{C}(x)$. Optimality follows since we showed in Sect. 7 that $V^{\hat{C}}_{0} = \hat{V} (x)$.

Unfortunately, there are at least three difficulties with this approach. The first is that the candidate value function $\hat{V}(x)$ defined in (7.4) does not have a well-defined derivative at zero, meaning that we cannot apply Itô’s lemma to $\hat{V}(X^{\Pi ,C})$ for a general admissible wealth process $X^{\Pi ,C}$. The second is that for a general strategy $(\Pi ,C)$, the standard proof that $\hat{V}(X^{\Pi ,C})$ corresponds to a supersolution involves showing that the local martingale part of $\hat{V}(X^{\Pi ,C})$ is a supermartingale, and in the case $R>1$, this is not true in general. The third difficulty is that $V^{C}$ might fail to exist.

The first two issues arise also in the case of CRRA utility. In Herdegen et al. [2], the authors show how they may be overcome using a stochastic perturbation of the value function. We now extend the ideas in [2] to the setting of EZ SDU. The third issue has been dealt with in Sect. 6.

Theorem 8.1

Suppose that $\eta >0$ and $\vartheta \in (0,1)$. If $V^{C}$ is the (generalised) utility process associated to the pair $(g_{\mathrm{EZ}},C)$ and $\hat{V}(x)$ is the candidate optimal utility given in (7.4) then $\sup _{C \in \mathscr{C}(x)} V^{C}_{0} = V^{\hat{C}}_{0} = \hat{V}(x)$, and the optimal investment–consumption strategy is given by $(\hat{\Pi},\hat{C})$ from (7.3).

Proof

It follows from Sect. 7 that $V^{g_{\mathrm{EZ}},\hat{C}}_{0} = \hat{V}(x)$; so it only remains to prove that $\hat{V}(x) \geq \sup _{C\in \mathscr{C}(x)} V^{g_{\mathrm{EZ}},C}_{0}$.

Let $Y$ denote the candidate optimal wealth process started from unit wealth, i.e.,

$$ \frac{dY_{t}}{Y_{t} } = \frac{\lambda}{R} \,\mathrm {d}B_{t} + \bigg( r + \frac{\lambda ^{2}}{R} - \eta \bigg)\,\mathrm {d}t,\quad Y_{0} = 1. $$

Fix $\varepsilon > 0$ and let $g^{\varepsilon }_{\mathrm{EZ}}(c,y,v) = g_{\mathrm{EZ}}(c+\varepsilon y,v) = \frac{(c + \eta \varepsilon y)^{1-S}}{1-S}((1-R)v)^{\rho}$. Fix an arbitrary admissible strategy $(\Pi , C)\in \mathscr{C}(x)$. The dynamics of $X + \varepsilon Y := X^{\Pi , C} + \varepsilon Y$ are then given by

$$\begin{aligned} \mathrm {d}(X_{t} + \varepsilon Y_{t}) &= \bigg(\sigma \Pi _{t} X_{t} + \frac{\lambda \varepsilon }{R}Y_{t}\bigg) \,\mathrm {d}B_{t} \\ & \phantom{=:} + \bigg(X_{t}({r} + \Pi _{t}({\mu} - {r})) - C_{t} + \Big({r} + \frac{\lambda ^{2}}{R} - \eta \Big)\varepsilon Y_{t}\bigg) \,\mathrm {d}t. \end{aligned}$$

Let $\mathscr{L}^{c,\pi}$ denote the infinitesimal aggregator of the diffusion $X + \varepsilon Y$ when the instantaneous rates of investment and consumption are $\pi$ and $c$, respectively. Then for $h=h(x,y)$,

$$ \mathscr{L}^{c,\pi}h = \bigg(x ( {r} + \pi \sigma \lambda ) - c + \Big({r} + \frac{\lambda ^{2}}{R} - \eta \Big)\varepsilon y \bigg)h' + \frac{1}{2}\bigg(\sigma \pi x + \frac{\lambda}{R} \varepsilon y\bigg)^{2} h''. $$

The first aim is to show that $\hat{V}$ satisfies a perturbed HJB equation

$$ \sup _{c \in \mathbb{R}_{+},\pi \in \mathbb{R}}\Big(\mathscr{L}^{c,\pi} \hat{V}(x + \varepsilon y) + g^{\varepsilon }_{\mathrm{EZ}}\big(c,y, \hat{V}(x + \varepsilon y) \big)\Big) = 0. $$

(8.1)

This follows from the fact that for general $c \in \mathbb{R}_{+}$ and $\pi \in \mathbb{R}$,

$$ \mathscr{L}^{c,\pi} \hat{V}(x + \varepsilon y) + g^{\varepsilon }_{\mathrm{EZ}}\big(c,y, \hat{V}(x + \varepsilon y)\big) = A^{1}(c,x,y) + A^{2}(\pi ,x,y) + A^{3}(x,y), $$

where

$$\begin{aligned} A^{1}(c,x,y) &= \frac{(c + \eta \varepsilon y)^{1-S}}{1-S}\big((1-R) \hat{V}(x + \varepsilon y)\big)^{\rho } \\ & \phantom{=:} - \hat{V}'(x + \varepsilon y) \bigg(c + \eta \varepsilon y +\eta \frac{S}{1-S}(x + \varepsilon y)\bigg), \\ A^{2}(\pi ,x,y) &= \hat{V}'(x+\varepsilon y) \bigg(x \pi \sigma \lambda + \frac{\lambda ^{2}}{R} \varepsilon y \bigg) \\ & \phantom{=:} + \frac{1}{2}\hat{V}''(x+\varepsilon y) \bigg(\pi \sigma x + \frac{\lambda}{R} \varepsilon y \bigg)^{2} + \frac{\lambda ^{2}}{2} \frac{(\hat{V}'(x + \varepsilon y))^{2}}{\hat{V}''(x + \varepsilon y)}, \\ A^{3}(x,y) &= (x + \varepsilon y) \tilde{r}\hat{V}'(x + \varepsilon y) - \frac{\lambda ^{2}}{2} \frac{(\hat{V}'(x + \varepsilon y))^{2}}{\hat{V}''(x + \varepsilon y)} \\ & \phantom{=:} + \eta \frac{S}{1-S}(x + \varepsilon y)\hat{V}'(x + \varepsilon y), \end{aligned}$$

and the trio of inequalities $A^{1} \leq 0$, $A^{2} \leq 0$, $A^{3}=0$. Taking the derivative with respect to $c$, we find that the maximum of $A^{1}(c,x,y)$ is attained for

$$ c = \bigg( \frac{((1-R)\hat{V}(x + \varepsilon y))^{\rho}}{\hat{V}'(x + \varepsilon y)} \bigg)^{\frac{1}{S}} - \eta \varepsilon y, $$

and then using the explicit form of $\hat{V}$, we find that the maximising value of $c$ is $c=\eta x$ and that $A^{1}(\eta x, x, y) = 0$. Similarly, by taking the derivative with respect to $\pi$, the maximum of $A^{2}(\pi ,x,y)$ is attained when

$$ \pi = \frac{-\lambda}{\sigma x}\bigg(\frac{\varepsilon y}{R} + \frac{\hat{V}'(x + \varepsilon y)}{\hat{V}''(x + \varepsilon y)} \bigg) = \frac{\lambda}{\sigma R},$$

and then $A^{2}(\frac{\lambda}{\sigma R}, x, y) = 0$. Finally, by using the definition of $\hat{V}$ and $\eta$, we find that $A^{3}(x,y) = 0$. Consequently, (8.1) is satisfied and the supremum is attained. Note that since $\varepsilon Y$ is just a scaling of the wealth process under the optimal strategy, it follows that $(\hat{V}(\varepsilon Y_{t}))_{t\geq 0} \in \mathbb{U}\mathbb{I}(g_{\mathrm{EZ}}, \eta \varepsilon Y)$ is the utility process associated to the consumption stream $\eta \varepsilon Y$. Consequently, it follows by the form of $\hat{V}(x)$ given in (7.4) and by Remark 7.4 that $\lim _{t \to \infty} \mathbb{E}[\hat{V}(\varepsilon Y_{t+})] = 0$.

Next, fix arbitrary bounded stopping times $\tau _{1}\leq \tau _{2}$ and define the local martingale $N=(N_{t})_{t \geq 0}$ by

$$ N_{t} = \int _{0}^{t} \hat{V}'(X_{u} + \varepsilon Y_{u}) \left (\sigma \Pi _{u} X_{u} + \frac{\lambda}{R} \varepsilon Y_{u}\right ) d W_{u}.$$

Then for $n\in \mathbb{N}$, set $\zeta _{n}:= \inf \{s\geq \tau _{1}: \langle {N} \rangle _{s} - \langle {N} \rangle _{\tau _{1}} \geq n\}$. It follows from Itô’s lemma, (8.1) and the definition of $g^{\varepsilon }_{\mathrm{EZ}}$ that

$$\begin{aligned} &\hat{V}(X_{\tau _{1}} + \varepsilon Y_{\tau _{1}}) \\ & = \hat{V}(X_{{\tau _{2}}\wedge \zeta _{n}} + \varepsilon Y_{{\tau _{2}} \wedge \zeta _{n}}) - \int _{\tau _{1}}^{{\tau _{2}}\wedge \zeta _{n}} \mathscr{L}^{C_{s},\Pi _{s}} \hat{V}(X_{s} + \varepsilon Y_{s}) \,\mathrm {d}s \\ & \phantom{=:} + N_{\tau _{1}} - N_{{\tau _{2}}\wedge \zeta _{n}} \\ & \geq \hat{V}(X_{{\tau _{2}}\wedge \zeta _{n}} + \varepsilon Y_{{\tau _{2}} \wedge \zeta _{n}}) + \int _{\tau _{1}}^{{\tau _{2}}\wedge \zeta _{n}} f^{\varepsilon }_{\mathrm{EZ}}\big(C_{s}, Y_{s}, \hat{V}(X_{s} + \varepsilon Y_{s}) \big) \,\mathrm {d}s \\ & \phantom{=:} + N_{\tau _{1}} - N_{{\tau _{2}}\wedge \zeta _{n}} \\ & = \hat{V}(X_{{\tau _{2}}\wedge \zeta _{n}} + \varepsilon Y_{{\tau _{2}} \wedge \zeta _{n}}) + \int _{\tau _{1}}^{{\tau _{2}}\wedge \zeta _{n}} f_{\mathrm{EZ}}\big(C_{s}+\eta \varepsilon Y_{s},\hat{V}(X_{s} + \varepsilon Y_{s}) \big) \,\mathrm {d}s \\ & \phantom{=:} + N_{\tau _{1}} - N_{{\tau _{2}}\wedge \zeta _{n}}. \end{aligned}$$

Taking conditional expectations and using that $(N_{t \wedge \zeta _{n}} - N_{t \wedge \tau _{1}})_{t \geq 0}$ is an $L^{2}$-bounded martingale, the optional sampling theorem gives

$$\begin{aligned} \hat{V}(X_{\tau _{1}} + \varepsilon Y_{\tau _{1}}) &\geq \mathbb{E}[ \hat{V}(X_{{\tau _{2}}\wedge \zeta _{n}} + \varepsilon Y_{{\tau _{2}}\wedge \zeta _{n}}) \, \vert \,\mathcal {F}_{{\tau _{1}}} ] \\ & \phantom{=:} + \mathbb{E}\bigg[ \int _{\tau _{1}}^{{\tau _{2}}\wedge \zeta _{n}} f_{\mathrm{EZ}}\big(C_{s}+\eta \varepsilon Y_{s},\hat{V}(X_{s} + \varepsilon Y_{s})\big) \,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{{\tau _{1}}} \bigg]. \end{aligned}$$

Since $\hat{V}$ is nondecreasing, $\hat{V}(X_{{\tau _{2}}\wedge \zeta _{n}} + \varepsilon Y_{{\tau _{2}} \wedge \zeta _{n}}) \geq \hat{V}(\varepsilon Y_{{\tau _{2}}\wedge \zeta _{n}})$ $\mathbb{P}\text{-a.s.}$ Moreover, using that $(\hat{V}(\varepsilon Y_{t}))_{t \geq 0}$ is bounded below by a UI martingale by [4, Remark 3.2], taking the liminf as $n \to \infty$, the conditional version of Fatou’s lemma (with a UI martingale as lower bound) and the conditional monotone convergence theorem yields

$$\begin{aligned} \hat{V}(X_{\tau _{1}} + \varepsilon Y_{\tau _{1}}) &\geq \mathbb{E}[ \hat{V}(X_{\tau _{2}} + \varepsilon Y_{\tau _{2}}) \, \vert \,\mathcal {F}_{{\tau _{1}}} ] \\ & \phantom{=:} + \mathbb{E}\bigg[ \int _{\tau _{1}}^{\tau _{2}} f_{\mathrm{EZ}}\big(C_{s}+\eta \varepsilon Y_{s},\hat{V}(X_{s} + \varepsilon Y_{s})\big) \,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{{\tau _{1}}} \bigg]. \end{aligned}$$

(8.2)

Furthermore, $\liminf _{t\to \infty} \mathbb{E}[\hat{V}(X_{t+}+\varepsilon Y_{t+})]\geq \lim _{t\to \infty} \mathbb{E}[\hat{V}(\varepsilon Y_{t+})] = 0$. Consequently, $\hat{V}(X + \varepsilon Y)$ is a supersolution associated to the pair $(g_{\mathrm{EZ}},C+\eta \varepsilon Y)$.

In the penultimate step, we consider the cases $R < 1$ and $R > 1$ separately to conclude that $\hat{V}(X+\varepsilon Y)\geq V^{g_{\mathrm{EZ}},C}$. If $R < 1$, using that $C+\eta \varepsilon Y > C$ and $g_{\mathrm{EZ}}$ is nondecreasing in its first argument, it follows that $\hat{V}(X+\varepsilon Y)$ is a supersolution associated to the pair $(g_{\mathrm{EZ}}, C)$ by (8.2). Thus the (generalised) utility process $V^{g_{\mathrm{EZ}},C}$ associated to $(g_{\mathrm{EZ}},C)$ is the minimal supersolution by Theorem 6.5 and the claim follows.

If $R>1$, then also $S>1$ by our standing assumption that $\vartheta >0$. Then $(C+\eta \varepsilon Y)^{1-S} \leq (\eta \varepsilon )^{1-S} Y^{1-S}$, and so Corollary 6.3 gives $C+\eta \varepsilon Y\in \mathscr{E}_{u}(g_{\mathrm{EZ}})$. Hence there exists a utility process $V^{g_{\mathrm{EZ}},C+\eta \varepsilon Y}\in \mathbb{U}\mathbb{I}(g_{\mathrm{EZ}}, C+ \eta \varepsilon Y)$ associated to $C+\eta \varepsilon Y$. Since also $\hat{V}(X+\varepsilon Y)\leq 0$, the claim follows from Theorem 5.8 and Proposition 6.8.

Finally, in both cases, taking the supremum over attainable consumption streams at time zero gives $\hat{V} (x + \varepsilon ) \geq \sup _{C\in \mathscr{C}(x)} V_{0}^{g_{\mathrm{EZ}},C}$. Letting $\varepsilon \searrow 0$ gives the result. □

We conclude this section by showing that the correct wellposedness condition of the investment–consumption problem is indeed $\eta >0$.

Corollary 8.2

Suppose that $\vartheta \in (0,1)$. Then the infinite-horizon investment–consumption problem for EZ SDU is well posed if and only if $\eta > 0$.

Moreover, if $\eta \leq 0$ (recalling that $V^{C}$ denotes the (generalised) utility process for the pair $(g_{\mathrm{EZ}},C)$), then

$$\begin{aligned} \sup _{C \in \mathscr{C}(x)}V_{0}^{C} = \textstyle\begin{cases} \infty &\quad \textit{if } R < 1, \\ -\infty &\quad \textit{if } R > 1. \end{cases}\displaystyle \end{aligned}$$

Proof

If $\eta >0$, the investment–consumption problem is well posed by Theorem 8.1.

Suppose $\eta \leq 0$. As $\vartheta \in (0,1)$, the utility process is unique, and if $H(\pi ,\xi )>0$, then $V$ given by (7.2) is the utility process for a constant proportional strategy. We now consider the cases $R <1$ and $R > 1$ separately.

First, suppose $R<1$ so that then also $S<1$. Let $f(\pi , \xi ) = \frac{\xi ^{1-R}}{1-R}( \frac{\vartheta }{H(\pi ,\xi )} )^{ \vartheta }$ and $D=\{ (\pi , \xi ) \in \mathbb{R}\times (0,\infty ): H(\pi ,\xi ) > 0 \}$. Note that

$$ \vartheta \big(H(\hat{\pi}, \xi )\big)^{-1} = \big(\eta S + (1-S)\xi \big)^{-1}.$$

Letting $\xi \searrow -\eta \frac{S}{1-S}$ yields $\vartheta (H(\hat{\pi}=\frac{\mu -r}{\sigma R}, \xi ))^{-1}\nearrow \infty$. We may conclude that $f(\pi ,\xi )\nearrow \infty$ and the claim follows.

Next, suppose $R>1$. Fix an arbitrary $C\in \mathscr{C}(x; r,\mu ,\sigma )$ with associated wealth process $X$. Denote by $V$ the generalised utility process associated to the pair $(g_{\mathrm{EZ}},C)$. It suffices to show that $V_{0} = -\infty$. For $n\in \mathbb{N}$, let $\alpha _{n} := \frac{S}{S-1}(\frac{1}{n} - \eta ) > 0$, $r_{n}:= r+\alpha _{n}$ and $\mu _{n}:= \mu +\alpha _{n}$. Consider the modified consumption stream $C^{n}$ given by $C^{n}_{t}:= e^{\alpha _{n} t}C_{t}$. Then by calculating the dynamics of $X^{n}_{t}:= e^{\alpha _{n} t}X_{t}$, it can be shown that $C^{n}\in \mathscr{C}(x; r_{n},\mu _{n},\sigma )$. Furthermore, $\eta _{n} = \frac{(S-1)}{S}(r_{n} + \frac{\lambda ^{2}}{2R}) = \frac{1}{n} >0$. Then, considering the Black–Scholes–Merton financial market with parameters $(r_{n},\mu _{n},\sigma )$ and applying Theorem 8.1 gives $V^{n}_{0} \leq \hat{V}^{n}(x) = \eta _{n}^{-\vartheta S } \frac{x^{1-R}}{1-R}$. It follows from Proposition 6.8 that if $V^{n}$ is the (generalised) solution associated to the pair $(g_{\mathrm{EZ}},C^{n})$, then $C\leq C^{n}$ implies $V\leq V^{n}$. Combining the inequalities and taking limits yields $V_{0} \leq \lim _{n\to \infty} n^{\vartheta S } \tfrac{x^{1-R}}{1-R} = - \infty$. □

9 Summary

In [4], we argued that $\vartheta := \frac{1-R}{1-S}>0$ is a necessary condition for the EZ aggregator to lead to a well-founded problem. Moreover, it is convenient to use the aggregator in discounted form because it has the one-sign property, and hence integrals of the form $\int _{0}^{\infty }g(s,C_{s},V_{s}) \,\mathrm {d}s$ and their expectations are always well defined in $\overline{\mathbb{R}}$.

In this paper, we focussed mainly on the case $\vartheta \in (0,1)$ and showed that using the EZ aggregator in discounted form allows a utility process (possibly taking values in $\overline{\mathbb{R}}$ rather than ℝ) to be defined any consumption stream. Moreover, this utility process is unique. We also proved a verification lemma and showed (in cases where the problem is well posed) that the candidate optimal consumption stream is indeed optimal. This optimality is within the class of all attainable consumption streams for initial wealth $x> 0$ (and not just within some subclass with additional regularity and integrability properties). This is an important contribution since in the literature, solutions of the (additive) Merton optimal investment–consumption problem via stochastic control and the primal problem often restrict the class of allowed consumption streams to those with regularity properties, for example properties which guarantee that a certain local martingale is a martingale. (Instead, wild strategies should be ruled out because they are demonstrably sub-optimal, and not be excluded because the mathematical arguments cannot deal with them.)

Although some of the existence results cover $\vartheta \in (0,\infty )$, the focus of this paper is on Epstein–Zin stochastic differential utility with $\vartheta \in (0,1)$. The case $\vartheta >1$ is very interesting and is relegated to Herdegen et al. [3]. When $\vartheta >1$, uniqueness fails. It is not just that the mathematical arguments of the present paper are insufficient to deal with the technicalities of the problem, but rather that even in the case of proportional strategies (and a constant-parameter, Black–Scholes–Merton financial market), there are multiple utility processes which satisfy (4.1) for the aggregator $g_{\mathrm{EZ}}$. Given the non-uniqueness, the first task of [3] is to identify the (unique) utility process associated to $(g_{\mathrm{EZ}},C)$ with a certain extra property—properness—which has a clear economic as well as mathematical interpretation. Then the second goal of [3] is to solve the infinite-horizon investment–consumption problem (for the EZ aggregator in discounted form with $\vartheta >1$ and in a Black–Scholes–Merton financial market) where optimisation takes place over a large class of consumption streams, and utility processes are required to be proper. This brings new challenges, and requires further insights.

Appendices

Appendix A: Proof of the comparison theorem

Lemma A.1

Let $-\infty < a < b < \infty$. Every uncountable set $U\subseteq [a,b)$ contains at least one of its right accumulation points.

Proof

Seeking a contradiction, suppose $U$ contains none of its right accumulation points. Then for each $x\in U$, we may find $\varepsilon _{x}>0$ such that $[x,x+\varepsilon _{x})\cap U = \{x\}$. Let $U_{n} := \{x\in U:~\varepsilon _{x}>\frac{1}{n}\}$. Then each $U_{n}$ is finite since the pairwise disjoint union $\bigcup _{x\in U_{n}} [x,x+\frac{1}{n})$ is contained in the interval $[a,b+\frac{1}{n})$. Hence $U=\bigcup _{n\in \mathbb{N}}U_{n}$ is countable, and we arrive at a contradiction. □

Proof of Theorem 5.8

We prove the result when $\mathbb{V}\subseteq \overline {\mathbb{R}}_{+}$. The case $\mathbb{V}\subseteq \overline {\mathbb{R}}_{-}$ is symmetric.

Seeking a contradiction, suppose there exists a finite stopping time $\tau$ and a set $A \in \mathcal{F}_{\tau}$ of positive measure such that $V^{1}_{\tau}(\omega ) > V^{2}_{\tau}(\omega )$ for $\omega \in A$, which implies that $\mathbb{E}[\mathbf {1}_{A}(V^{1}_{\tau }- V^{2}_{\tau})] > 0$. Since $V^{1}$ and $V^{2}$ are làd, the processes $(V^{1}_{s+})_{s\geq 0}$ and $(V^{2}_{s+})_{s\geq 0}$ exist and are right-continuous. They are also adapted because the filtration is right-continuous. It follows that

$$ \sigma := \inf \{s\geq \tau : V^{1}_{s{+}} - V^{2}_{s{+}} \leq 0\}$$

is a stopping time. Moreover, the right-continuity of $(V^{1}_{s{+}})_{s\geq 0}$ and $(V^{2}_{s{+}})_{s\geq 0}$ gives $( V^{1}_{\sigma{+}} - V^{2}_{\sigma{+}} )\mathbf {1}_{\{\sigma < \infty \}} \leq 0$ $\mathbb{P}\text{-a.s.}$

For each $\omega \in A$, we have $V^{1}_{s}(\omega ) \geq V^{2}_{s}(\omega )$ for almost all $s\in [\tau (\omega ),\sigma (\omega ))$. Indeed, seeking a contradiction, suppose there are $\omega \in A$ and a set $U$ of positive Lebesgue measure such that $V^{1}_{s}(\omega ) < V^{2}_{s}(\omega )$ for $s\in U\subseteq [\tau (\omega ),\sigma (\omega ))$. Since $U$ is uncountable, it has a right accumulation point $q\in U$ by Lemma A.1. Then $q < \sigma (\omega )$ and $V^{1}_{q{+}}(\omega ) \leq V^{2}_{q{+}}(\omega )$, and we arrive at a contradiction.

Next, fix $n \in \mathbb{N}$. By subtracting (5.2) from (5.1) for the bounded stopping times $\tau _{1} := \tau \wedge n$ and $\tau _{2} := \sigma \wedge n$, noting that the expectations are well defined since $V^{1}$ or $V^{2}$ is in $\mathbb{U}\mathbb{I}(g,C)$, and using the fact that $g$ is a.s. decreasing in $v$ and $V^{1}_{s}(\omega ) \geq V^{2}_{s}(\omega )$ for almost all $s\in [\tau (\omega ),\sigma (\omega ))$ for $\omega \in A$, we obtain

$$\begin{aligned} &\mathbb{E}^{} [ \mathbf {1}_{A}\mathbf {1}_{\{\tau \leq n\}} (V^{1}_{\tau }- V^{2}_{\tau }) ] \\ & \leq \mathbb{E}^{}\big[ \mathbf {1}_{A}\mathbf {1}_{\{\tau \leq n\}} \big(V^{1}_{(\sigma \wedge n){+}} - V^{2}_{(\sigma \wedge n){+}} \big) \big] \\ & \phantom{=:} + \mathbb{E}^{}\bigg[ \mathbf {1}_{A}\mathbf {1}_{\{\tau \leq n\}}\bigg(\int _{ \tau \wedge n}^{\sigma \wedge n} \big(g(s,\omega ,C_{s},V^{1}_{s}) - g(s,\omega ,C_{s},V^{2}_{s})\big)\,\mathrm {d}s\bigg) \bigg] \\ & \leq \mathbb{E}^{}\big[ \mathbf {1}_{A}\mathbf {1}_{\{\tau \leq n\}} \big(V^{1}_{ (\sigma \wedge n){+}} - V^{2}_{(\sigma \wedge n){+}} \big) \big]. \end{aligned}$$

Finally, taking the limsup as $n \to \infty$, using monotone convergence, the fact that $(V^{1}_{s{+}})_{s\geq 0}$ and $(V^{2}_{s{+}})_{s\geq 0}$ are $\overline {\mathbb{R}}_{+}$-valued, the transversality condition for subsolutions and $( V^{1}_{\sigma{+}} - V^{2}_{\sigma{+}} )\mathbf {1}_{\{\sigma < \infty \}} \leq 0$ $\mathbb{P}\text{-a.s.}$, we arrive at the contradiction

$$\begin{aligned} \mathbb{E}^{} [ \mathbf {1}_{A}(V^{1}_{\tau }- V^{2}_{\tau}) ] &\leq \limsup _{n\to \infty} \mathbb{E}^{}\big[ \mathbf {1}_{A} \mathbf {1}_{\{\tau \leq n< \sigma \}}\big( V^{1}_{n{+}} - V^{2}_{n{+}}\big) \big] \\ & \phantom{=:} + \limsup _{n\to \infty} \mathbb{E}^{}\big[ \mathbf {1}_{A} \mathbf {1}_{\{\sigma \leq n\}}\big( V^{1}_{\sigma{+}} - V^{2}_{\sigma{+}}\big) \big] \\ &\leq \limsup _{n\to \infty} \mathbb{E}^{}\big[ V^{1}_{n{+}} \big]+ \mathbb{E}^{}\big[ \mathbf {1}_{A} \mathbf {1}_{\{\sigma < \infty \}} \big(V^{1}_{\sigma{+}} - V^{2}_{\sigma{+}}\big) \big] \leq 0. \end{aligned}$$

 □

Proof of Corollary 5.10

Suppose that $\mathbb{V}= \overline {\mathbb{R}}_{+}$; the proof for $\mathbb{V}\subseteq \overline {\mathbb{R}}_{-}$ is symmetric. As $g_{2}(\,\cdot \,, \,\cdot \,, c, v) \geq g_{1}(\,\cdot \,, \,\cdot \,, c, v)$ $(\mathbb{P}\otimes \,\mathrm {d}t)$-a.e. and $g_{1}$ and $g_{2}$ are nondecreasing in $c$, we have $g_{2}(s,\omega ,C^{2}_{s},V^{2}_{s}) \geq g_{1}(s,\omega ,C^{2}_{s},V^{2}_{s}) \geq g_{1}(s,\omega ,C^{1}_{s},V^{2}_{s})\geq 0$ for $(\mathbb{P}\otimes \,\mathrm {d}t)$-a.e. $(s, \omega )$. It then follows that for all bounded stopping times $\tau \leq \sigma$,

$$\begin{aligned} V^{2}_{\tau }&= \mathbb{E}\bigg[ V^{2}_{\sigma{+}} + \int _{\tau}^{\sigma }g_{2}(s,\omega ,C^{2}_{s},V^{2}_{s})\,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{\tau } \bigg] \\ &\geq \mathbb{E}\bigg[ V^{2}_{\sigma{+}} + \int _{\tau}^{\sigma }g_{1}(s,\omega ,C^{1}_{s},V^{2}_{s})\,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{\tau } \bigg]. \end{aligned}$$

Since $V^{2}$ is a utility process associated to $(g^{2},C^{2})$ it satisfies (2.1) (with $(g,C)$ replaced by $(g^{2},C^{2})$). Letting $t\to \infty$ then implies that ${\lim _{t\to \infty} \mathbb{E}^{} [ V^{2}_{t} ]=0}$. Therefore, $V^{2}$ satisfies the definition of a supersolution associated to the pair $(g_{1},C^{1})$. As $V^{2}\in \mathbb{U}\mathbb{I}(g_{2},C^{2})\subseteq \mathbb{U}\mathbb{I}(g_{1},C^{1})$ and $V^{1}$ is a (sub)solution associated to $(g_{1},C^{1})$, it follows that $V^{1}_{\tau }\leq V^{2}_{\tau}$ for all finite stopping times $\tau$ by Theorem 5.8. □

Appendix B: Proving existence and uniqueness of a utility process

For $\Lambda \in \hat{L}^{\vartheta }_{++}$, define the $\varepsilon$-perturbed operator $F^{\varepsilon }_{U,\Lambda}: \mathbb{I}(h_{\mathrm{EZ}},U)\to \mathscr{P}_{+}$ by

$$ F^{\varepsilon }_{U,\Lambda}(W)_{t} := \mathbb{E}\bigg[ \int _{t}^{\infty }(U_{s} W_{s}^{\rho }+ \varepsilon \Lambda _{s}^{\vartheta }) \,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg]. $$

(B.1)

Here, we always choose a càdlàg version for the right-hand side of (B.1). A key property of $F^{\varepsilon }_{U,\Lambda}$ is that when $\varepsilon >0$ and $\Lambda \in \hat{L}^{\vartheta }_{++}$, $F^{\varepsilon }_{0,\Lambda}$ is bounded away from zero. Another property is the following.

Lemma B.1

Let $\varepsilon \geq 0$, $\Lambda \in \hat{L}^{\vartheta }_{++}$ and $U\in \mathbb{O}(\Lambda )$. Then $F^{\varepsilon }_{U,\Lambda}(\, \cdot \,)$ maps $\mathbb{O}(\Lambda ^{\vartheta })$ to itself.

Proof

Fix arbitrary $W\in \mathbb{O}(\Lambda ^{\vartheta })$ and recall $I^{\Lambda}$ from Definition 4.2. It follows that there exist constants $k_{W},K_{W} \in (0,\infty )$ such that $k_{W} \Lambda ^{\vartheta }\leq W \leq K_{W} \Lambda ^{\vartheta }$. Similarly, since $U\in \mathbb{O}(\Lambda )$ and $\Lambda ^{\vartheta }\in \mathbb{O}(I^{\Lambda})$, there exist $k_{U},K_{U},k_{\Lambda},K_{\Lambda }\in (0,\infty )$ such that $k_{U} \Lambda \leq U \leq K_{U} \Lambda$ as well as $k_{\Lambda }I^{ \Lambda }\leq \Lambda ^{\vartheta }\leq K_{\Lambda }I^{\Lambda}$. We only prove that $F^{\varepsilon }_{U,\Lambda}(W) \geq \kappa \Lambda ^{ \vartheta }$ for $\rho <0$; the argument for $\rho >0$ involves $W^{\rho }\geq (k_{W} \Lambda )^{\vartheta \rho}$, and the argument for the upper bound is symmetric. By the definition of $F^{\varepsilon }_{U,\Lambda}(\, \cdot \,)$ in (B.1) and using that $U \geq k_{U} \Lambda$, $W \leq K_{W} \Lambda ^{\vartheta }$ and $\Lambda ^{\vartheta }\leq K_{\Lambda }I^{\Lambda}$ as well as $1+\vartheta \rho = \vartheta$, we obtain

$$\begin{aligned} F^{\varepsilon }_{U,\Lambda}(W)_{t} &\geq \mathbb{E}\bigg[ \int _{t}^{\infty }k_{U} \Lambda _{s} (K_{W} \Lambda ^{\vartheta })^{\rho }+ \varepsilon \Lambda _{s}^{\vartheta }\,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg] \\ &= (k_{U} K_{W}^{\rho }+ \varepsilon ) \mathbb{E}\bigg[ \int _{t}^{\infty }\Lambda _{s}^{\vartheta }\,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg] \\ &\geq \bigg(\frac{k_{U} K_{W}^{\rho }+ \varepsilon }{K_{\Lambda}}\bigg) \Lambda ^{\vartheta }. \end{aligned}$$

 □

The subsequent theorem is a preliminary existence result and includes Theorem 4.5 as a special case.

Theorem B.2

Let $\varepsilon \geq 0$, $\Lambda \in \hat{L}^{\vartheta }_{++}$ and $U\in \mathbb{O}(\Lambda )$. Then $F^{\varepsilon }_{U,\Lambda}$ defined by (B.1) has a fixed point $W \in \mathbb{O}(\Lambda ^{\vartheta }) \subseteq \mathbb{I}(h_{\mathrm{EZ}}, U)$, which is unique in $\mathbb{O}(\Lambda ^{\vartheta })$ and has càdlàg paths.

Set $\mathscr{B} := L^{\infty}(\Omega \times \mathbb{R}_{+}, \text{Prog}, \mathbb{P}\otimes \mathrm {d}t)$, where by $\text{Prog}$ we denote the progressive $\sigma \text{-algebra}$ on $\Omega \times \mathbb{R}_{+}$. For the proof of Theorem B.2, we use Blackwell’s sufficient conditions for an operator $T:\mathscr{B}\to \mathscr{B}$ to be a contraction mapping; see e.g. Stokey [14, Theorem 3.3] for a proof.

Lemma B.3

Let ℬ be a Banach space and $T: \mathscr{B} \to \mathscr{B}$ an operator that is nonincreasing. Suppose there exists $\beta \in (0,1)$ with

$$ T(X+a) \geq T(X) - \beta a \qquad \textit{for all }X \in \mathscr{B}, \ a > 0. $$

(B.2)

Then $T$ is a contraction mapping with constant $\beta$. Similarly, T is a contraction mapping if it is nondecreasing and there exists $\beta \in (0,1)$ with $T(X+a) \leq TX + \beta a$ for all $X \in \mathscr{B}$, $a > 0$.

Proof of Theorem B.2

Consider the change of variables

$$ P_{t} = \log U_{t} - \log \Lambda _{t} , \qquad Q_{t} = \log W_{t} - \vartheta \log \Lambda _{t} . $$

Then $U \in \mathbb{O}(\Lambda )$ if and only if $P \in \mathscr{B}$, and $W \in \mathbb{O}(\Lambda ^{\vartheta })$ if and only if $Q \in \mathscr{B}$. Moreover, the fixed point condition $W = F^{\varepsilon }_{U,\Lambda}(W)$ is equivalent to the fixed point condition $Q = G^{\varepsilon }_{P,\Lambda}(Q)$, where

$$ G^{\varepsilon }_{P,\Lambda}(Q)_{t} := \log \mathbb{E}\bigg[\int _{t}^{ \infty }\big(\Lambda _{s}^{\vartheta }\exp (P_{s} + \rho Q_{s}) + \varepsilon \Lambda _{s}^{\vartheta }\big)\,\mathrm {d}s\,\bigg|\,\mathcal {F}_{t} \bigg] - \vartheta \log \Lambda _{t} . $$

(B.3)

Note that since the first term on the right-hand side of (B.3) has càdlàg paths, every fixed point $Q$ to (B.3) corresponds to a $W$ with càdlàg paths. Since $G^{\varepsilon }_{P,\Lambda}(Q)$ is the difference of two continuous functions of progressive processes, it is progressive. Furthermore, as a consequence of Lemma B.1, $G^{\varepsilon }_{P,\Lambda}$ maps ℬ to itself.

Now suppose $\rho \in (-1,0)$ and let $a > 0$. Then the mapping $Q \mapsto G^{\varepsilon }_{P,\Lambda}(Q)$ is nonincreasing. Furthermore,

$$\begin{aligned} &G^{\varepsilon }_{P,\Lambda}(Q+a)_{t} \\ &= \log \bigg(\exp (\rho a) \mathbb{E}\bigg[ \int _{t}^{\infty }\bigg(\Lambda _{s}^{\vartheta }\exp (P_{s} + \rho Q_{s}) + \varepsilon \frac{\Lambda _{s}^{\vartheta }}{\exp (\rho a)} \bigg)\,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg] \bigg) - \vartheta \log \Lambda _{t} \\ &\geq \log \mathbb{E}\bigg[ \int _{t}^{\infty }\big(\Lambda _{s}^{\vartheta }\exp (P_{s} + \rho Q_{s}) + \varepsilon \Lambda _{s}^{\vartheta }\big) \,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg] - \vartheta \log \left (\Lambda _{t}\right ) + \rho a \\ &= G^{\varepsilon }_{P,\Lambda}(Q)_{t} + \rho a. \end{aligned}$$

By Lemma B.3, this implies that $G^{\varepsilon }_{P,\Lambda}$ is a contraction with constant $\rho$. Hence the contraction mapping theorem gives a unique $Q \in \mathscr{B}$ satisfying (B.3).

If $\rho \in (0,1)$, then the mapping $Q \mapsto G^{\varepsilon }_{P,\Lambda}(Q)$ is nondecreasing, and in this case one can show that $G^{\varepsilon }_{P,\Lambda}(Q+a)_{t} \leq G^{\varepsilon }_{P,\Lambda}(Q)_{t} + \rho a$. Again the result follows from Lemma B.3 and the contraction mapping theorem.

Finally, to extend the result to ${\rho \in (-\infty , -1]}$, we borrow an idea from Schroder and Skiadas [11] and show by induction that for each $k \in \mathbb{N}$, we have that

$$ \text{for $\rho \in (-k, 0)$ and $P\in \mathscr{B}$, $G^{\varepsilon }_{P,\Lambda}$ has a unique fixed point $Q \in \mathscr{B}$.} $$

(B.4)

The induction hypothesis ($k=1$) holds by the above. For the induction step, suppose that (B.4) holds for some $k \geq 1$. In order to show that (B.4) holds for $k+1$, it suffices to consider $\rho \in (-(k+1),k]$. So fix $\rho \in (-(k+1),k]$ and choose $\chi \in (0,1)$ small enough that $-k <\rho + \chi < 0$. Now define the map $\tilde{G}^{\varepsilon }_{P,\Lambda}: \mathscr{B}\times \mathscr{B}\to \mathscr{B}$ by

$$\begin{aligned} \tilde{G}^{\varepsilon }_{P,\Lambda}(Q, Z)_{t} &=\log \mathbb{E}\bigg[ \int _{t}^{\infty }\Big(\Lambda _{s}^{\vartheta }\exp \big(P_{s} - \chi Q_{s} + (\rho + \chi ) Z_{s}\big) + \varepsilon \Lambda _{s}^{\vartheta }\Big) \,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg] \\ & \phantom{=:} - \vartheta \log \Lambda _{t}. \end{aligned}$$

(B.5)

Here, we always choose a càdlàg version for the conditional expectation on the right-hand side of (B.5).

If suffices to show that there exists a unique $Q \in \mathscr{B}$ satisfying

$$ Q=\tilde{G}^{\varepsilon }_{P,\Lambda}(Q, Q). $$

(B.6)

Note that since the first term on the right-hand side of (B.5) has càdlàg paths, every $Q \in \mathscr{B}$ satisfying (B.6) corresponds to a $W$ with càdlàg paths. By the induction hypothesis, for each fixed $Q \in \mathscr{B}$ and since $P - \chi Q \in \mathscr{B}$, there exists a unique $Z \in \mathscr{B}$ such that $Z = \tilde{G}^{\varepsilon }_{P,\Lambda}(Q, Z)$. So we can define the operator $Z^{\varepsilon }_{P,\Lambda}: \mathscr{B}\to \mathscr{B}$ implicitly by

$$ Z^{\varepsilon }_{P,\Lambda}(Q) = \tilde{G}^{\varepsilon }_{P,\Lambda}\big(Q,Z^{ \varepsilon }_{P,\Lambda}(Q)\big). $$

(B.7)

If we can show that $Z^{\varepsilon }_{P,\Lambda}$ has a unique fixed point, we are done. To this end, arguing as above, it suffices to show that $Z^{\varepsilon }_{P,\Lambda}$ is a nonincreasing operator and satisfies (B.2) for $\beta := \chi$.

In order to show that $Z^{\varepsilon }_{P,\Lambda}$ is a nonincreasing operator, we take $Q^{1},Q^{2} \in \mathscr{B}$ with $Q^{1} \leq Q^{2}$ $(\mathbb{P}\otimes \mathrm {d}t)$-a.e. Moreover, for $i \in \{1, 2\}$, set $\tilde{C}^{i} := \Lambda ^{\vartheta }\exp (Q^{i})$ and $\tilde{V}^{i} := \Lambda ^{\vartheta }\exp (Z^{\varepsilon }_{P,\Lambda}(Q^{i}))$. Then (B.7) implies that

$$\begin{aligned} \tilde{V}_{t}^{i} &= \mathbb{E}\bigg[ \int _{t}^{\infty }\bigg( \Lambda _{s}^{\vartheta }\Big(\frac{U_{s}}{\Lambda _{s}} \Big) \Big(\frac{\tilde{C}_{s}^{i}}{\Lambda _{s}^{\vartheta }}\Big)^{-\chi}\Big(\frac{\tilde{V}_{s}^{i}}{\Lambda _{s}^{\vartheta }}\Big)^{\rho +\chi} + \varepsilon \Lambda _{s}^{\vartheta }\bigg) \,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg] \\ &= \mathbb{E}\bigg[ \int _{t}^{\infty }\big( U_{s} (\tilde{C}_{s}^{i} )^{-\chi} (\tilde{V}_{s}^{i} )^{\rho + \chi} + \varepsilon \Lambda _{s}^{\vartheta }\big) \,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg]. \end{aligned}$$

Since $\tilde{h}(t,\omega ,c,v) = U_{t}(\omega ) c^{-\chi} v ^{\rho + \chi} + \varepsilon (\Lambda _{t}(\omega ))^{\vartheta }$ is nonincreasing in $c$ and $v$, Remark 5.11 gives $\tilde{V}^{1} \geq \tilde{V}^{2}$, and consequently $Z^{\varepsilon }_{P,\Lambda}(Q^{1}) \geq Z^{\varepsilon }_{P,\Lambda}(Q^{2})$.

Finally, to show that $Z^{\varepsilon }_{P,\Lambda}$ satisfies (B.2) for $\beta := \chi$, let $a > 0$ and set

$$ \Psi = \big(Z^{\varepsilon }_{P,\Lambda}(Q+a) - Z^{\varepsilon }_{P,\Lambda}(Q) \big)/a \leq 0. $$

It suffices to show that $\Psi \geq -\chi$. Let $L := \Lambda ^{\vartheta }\exp (Z^{\varepsilon }_{P,\Lambda}(Q))$. Then

$$\begin{aligned} L_{t} \exp (\Psi _{t} a) &= \Lambda _{t}^{\vartheta }\exp \big(Z^{ \varepsilon }_{P,\Lambda}(Q)_{t}\big)\exp (\Psi _{t} a) \\ & = \Lambda _{t}^{\vartheta }\exp \big(Z^{\varepsilon }_{P,\Lambda}(Q+a)_{t} \big) \\ & = \mathbb{E}\bigg[ \int _{t}^{\infty }\big( \Lambda _{s}^{\vartheta }e^{P_{s} - \chi (Q_{s}+a) + (\rho + \chi ) Z^{\varepsilon }_{P,\Lambda}(Q+a)_{s}} + \varepsilon \Lambda _{s}^{\vartheta }\big) \,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg] \\ & = \mathbb{E}\bigg[ \int _{t}^{\infty }\big( \Lambda _{s}^{\vartheta }e^{-\chi a + (\rho + \chi )a \Psi _{s}} e^{P_{s} - \chi Q_{s} + (\rho + \chi ) Z^{\varepsilon }_{P,\Lambda}(Q)_{s}} + \varepsilon \Lambda _{s}^{\vartheta }\big) \,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg] \\ & \geq L_{t} \exp (-\chi a ), \end{aligned}$$

where we have used in the last line that $(\rho + \chi ) \Psi \geq 0$. Dividing by $L_{t}$, taking logarithms and dividing by $a$ gives $\Psi \geq -\chi$. □

We may now prove Theorem 6.2.

Proof of Theorem 6.2

The proof has two parts. The first part removes the lower bound on $U$ for $\varepsilon >0$; the second shows that we may remove the restriction $\varepsilon >0$.

Let $U^{n} = \max \{U,\frac{1}{n}\Lambda \}$. Then $U^{n}\in \mathbb{O}(\Lambda )$ for every $n\in \mathbb{N}$. Hence by Theorem B.2, for each $n\in \mathbb{N}$, there exists $W^{n}$ that satisfies

$$ W^{n}_{t} = \mathbb{E}\bigg[ \int _{t}^{\infty }\big(U^{n}_{s} (W^{n}_{s})^{\rho }+ \varepsilon \Lambda _{s}^{\vartheta }\big)\,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg]. $$

Since $\Lambda \in \hat{L}^{\vartheta }_{++}$, there exists $\kappa$ such that $\Lambda ^{\vartheta }\leq \kappa I^{\Lambda}$. Hence $W^{n} \geq \varepsilon I^{\Lambda }\geq \frac{\varepsilon }{\kappa} \Lambda ^{\vartheta }$ and

$$\begin{aligned} U^{n} (W^{n})^{\rho }\leq (K \Lambda ) (\varepsilon ^{\rho }\kappa ^{- \rho} \Lambda ^{\vartheta -1}) = K \kappa ^{-\rho} \varepsilon ^{\rho } \Lambda ^{\vartheta }. \end{aligned}$$

(B.8)

Since $\rho <0$, $g$ satisfies (v↓). Hence by Corollary 5.10, the sequence $(W^{n})_{n\in \mathbb{N}}$ is nonincreasing (and positive) so that it converges almost surely. Applying the dominated convergence theorem with the bound in (B.8) and the condition $\Lambda \in \hat{L}^{\vartheta }_{++}$, we find that ${W^{*} := \lim _{n\to \infty}W^{n}}$ satisfies

$$\begin{aligned} W^{*}_{t} &= \lim _{n\to \infty} \mathbb{E}\bigg[\int _{t}^{\infty }\big(U^{n}_{s} (W^{n}_{s})^{\rho }+ \varepsilon \Lambda ^{\vartheta }\big)\,\mathrm {d}s \, \bigg|\, \mathcal {F}_{t} \bigg] \\ &= \mathbb{E}\bigg[\int _{t}^{\infty }\big(U_{s} (W^{*}_{s})^{\rho }+ \varepsilon \Lambda _{s}^{\vartheta }\big) \,\mathrm {d}s \,\bigg|\, \mathcal {F}_{t} \bigg], \end{aligned}$$

so that $W^{*}$ is a fixed point of $F^{\varepsilon }_{U,\Lambda}(\, \cdot \,)$. Uniqueness follows from Corollary 5.9 since $h^{\varepsilon }(t,\omega ,u,v) = u v^{\rho }+ \varepsilon (\Lambda (t, \omega ))^{\vartheta }$ satisfies (v↓). This concludes the first part of the proof.

Let $U$ be a progressively measurable process with $0\leq U \leq K\Lambda$. Define the aggregator random field $h^{\varepsilon }$ by $h^{\varepsilon }(t,\omega ,u,v) := u v^{\rho }+ \varepsilon (\Lambda (t, \omega ))^{\vartheta }$. By the preceding argument, for each $\varepsilon >0$, there exists a utility process for the pair $(h^{\varepsilon },U)$. It follows from Corollary 5.10 that the fixed point $W^{\varepsilon }$ for the operator $F^{\varepsilon }$ given in (B.1) is nonincreasing as $\varepsilon \searrow 0$. Define $W_{t} = \lim _{\varepsilon \to 0}W^{\varepsilon }_{t}$. Then

$$\begin{aligned} W_{t} &= \lim _{\varepsilon \to 0} \mathbb{E}\bigg[ \int _{t}^{\infty }\big(U_{s} (W^{\varepsilon }_{s})^{\rho }+ \varepsilon \Lambda _{s}^{\vartheta }\big)\,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg] \\ &= \lim _{\varepsilon \to 0} \mathbb{E}\bigg[ \int _{t}^{\infty }h_{\mathrm{EZ}}(U_{s}, W^{\varepsilon }_{s}) \,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg] + \lim _{\varepsilon \to 0} \mathbb{E}\bigg[ \int _{t}^{\infty }\varepsilon \Lambda _{s}^{\vartheta }\,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg] \\ &= \mathbb{E}\bigg[ \int _{t}^{\infty }h_{\mathrm{EZ}}(U_{s}, W_{s}) \,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{t} \bigg], \end{aligned}$$

where the last line follows from monotone convergence and the fact that $h_{\mathrm{EZ}}$ was chosen so that we have $\lim _{w \rightarrow w_{0}} h_{\mathrm{EZ}}(u,w) = h_{\mathrm{EZ}}(w,w_{0})$ even for $(u,w_{0})=(0,0)$ and for $(u,w_{0})=(\infty ,\infty )$. Furthermore, we also have $W\in \mathbb{I}(h_{\mathrm{EZ}},U)$ because $\mathbb{E}^{} [ \int _{0}^{\infty }U_{s} W_{s}^{\rho }\,\mathrm {d}s ] = W_{0} \leq W^{\varepsilon }_{0} < \infty$. Uniqueness follows from Corollary 5.9 since $h_{\mathrm{EZ}}$ satisfies (v↓). □

Appendix C: Existence and uniqueness of a generalised utility process

To prove Theorem 6.5, we first introduce a generalisations of supermartingales (see Snell [13, Definition 1.2]). (We focus on the supermartingale case, but the submartingale case is symmetric.)

Definition C.1

A $(-\infty , \infty ]$-valued process $M = (M_{t})_{t\geq 0}$ is called a generalised supermartingale if $M^{-}_{t}\in L^{1}$ for all $t\geq 0$, $M$ is adapted and $M_{s} \geq \mathbb{E}\left [ M_{t} \,\middle \vert \,\mathcal{F}_{s} \right ]$ for all $t\geq s \geq 0$.

Remark C.2

Since $M^{-}_{t}\in L^{1}$ ($M_{t}$ is quasi-integrable), the conditional expectation $\mathbb{E}\left [ M_{t} \,\middle \vert \,\mathcal{F}_{s} \right ]$ exists and is unique, even if $M_{t} \notin L^{1}$.

Compared to an (ordinary) supermartingale, a generalised supermartingale need not have $M_{t} \in L^{1}$ for all $t \geq 0$. In particular, one can have $M_{s} = +\infty \geq \mathbb{E}\left [ M_{t} \, \middle \vert \,\mathcal{F}_{s} \right ]$. We next need to generalise this notion even further (Mertens [9] referred to the following processes simply as supermartingales).

Definition C.3

A generalised supermartingale is called a generalised optional strong supermartingale if it is optional and for all bounded pairs of stopping times $\tau _{1}\leq{\tau _{2}}$, we have $M_{\tau _{2}}^{-}\in L^{1}$ and $\mathbb{E}[ M_{\tau _{2}} \, \vert \,\mathcal {F}_{{\tau _{1}}} ] \leq M_{\tau _{1}}$.

Remark C.4

Note that every càdlàg supermartingale is an optional strong supermartingale by the optional sampling theorem.

Proposition C.5

A generalised optional strong supermartingale $M$ that is either bounded above or below is almost surely làdlàg and for a.e. $\omega$, the path $t \mapsto M_{t}(\omega )$ is right-continuous outside a countable set.

Proof

Suppose first that $M$ is bounded below by a constant $K$ and define the continuous bijection $f: [K,\infty ] \to [1-e^{-K},1]$ by $f(x) := 1-e^{-x}$ with the convention that $e^{-\infty} = 0$. It follows from Jensen’s inequality (note that $f^{-1}$ is convex) that

$$ M_{\tau _{1}} \geq \mathbb{E}[ M_{\tau _{2}} \, \vert \,\mathcal {F}_{{\tau _{1}}} ] = \mathbb{E}[ (f^{-1}\circ f)(M_{\tau _{2}}) \, \vert \,\mathcal {F}_{{\tau _{1}}} ] \geq f^{-1} \big(\mathbb{E}[ f(M_{\tau _{2}}) \, \vert \,\mathcal {F}_{{\tau _{1}}} ]\big). $$

Consequently, if $\tilde{M} = f(M)$, then for all bounded pairs of stopping times ${\tau _{1}} \leq {\tau _{2}}$,

$$ \tilde{M}_{\tau _{1}} = f(M_{\tau _{1}}) \geq \mathbb{E}[ f(M_{\tau _{2}}) \, \vert \,\mathcal {F}_{{\tau _{1}}} ] = \mathbb{E}[ \tilde{M}_{\tau _{2}} \, \vert \,\mathcal {F}_{{\tau _{1}}} ] $$

and $\tilde{M}$ is a bounded optional strong supermartingale. Hence it is làdlàg (see for example Dellacherie and Meyer [1, Theorem A1.4]). Moreover, it has a Mertens decomposition (see for example [1, Theorem A1.20]) given by $\tilde{M} = \tilde{N} - \tilde{A}$, where $\tilde{N} = (\tilde{N}_{t})_{t \geq 0}$ is a càdlàg local martingale and $\tilde{A} = (\tilde{A}_{t})_{t \geq 0}$ is a nondecreasing adapted làdlàg process. Since a nondecreasing làdlàg function is (right-)continuous up to a countable set, it follows that for a.e. $\omega$, the path $t \mapsto \tilde{M}_{t}(\omega )$ is right-continuous outside a countable set. Then, using that $f^{-1}$ is continuous, it follows that $M$ is làdlàg and for a.e. $\omega$, the path $t \mapsto M_{t}(\omega )$ is right-continuous outside a countable set.

When $M$ is bounded above, we use the concave function $g(x) = 1-e^{x}$. □

The following results are generalised versions of the backward martingale convergence theorem (BMCT) and Hunt’s lemma. Their proofs are straightforward extensions of classical results and may be found in Jerome [5, Proposition C.6 and Lemma C.7].

Proposition C.6

We suppose that $X$ is a $[0, \infty ]$-valued random variable and let

$$ \mathcal {F}\supseteq \mathcal {F}_{0} \supseteq \mathcal {F}_{-1} \supseteq \mathcal {F}_{-2} \supseteq \cdots $$

be a nonincreasing sequence of sub-$\sigma$-algebras and set $\mathcal {F}_{-\infty} := \bigcap _{k = 1}^{\infty }\mathcal {F}_{-k}$. Then $\lim _{n \to \infty} \mathbb{E}[ X \, \vert \,\mathcal {F}_{-n} ] = \mathbb{E}[ X \, \vert \,\mathcal {F}_{-\infty } ]$ $\mathbb{P}\textit{-a.s.}$

Lemma C.7

Let $(X_{n})_{n \in \mathbb{N}}$ be a nondecreasing sequence of $[0, \infty ]$-valued random variables with $\lim _{n \to \infty} X_{n} = X$ $\mathbb{P}\textit{-a.s.}$ Let $\mathcal {F}\supseteq \mathcal {F}_{0} \supseteq \mathcal {F}_{-1} \supseteq \mathcal {F}_{-2} \supseteq \cdots$ be a nonincreasing sequence of sub-$\sigma$-algebras and set $\mathcal {F}_{-\infty} := \bigcap _{k = 1}^{\infty }\mathcal {F}_{-k}$. Then we have $\lim _{n \to \infty} \mathbb{E}[ X_{n} \, \vert \,\mathcal {F}_{-n} ] = \mathbb{E}[ X \, \vert \,\mathcal {F}_{-\infty } ]$ $\mathbb{P}\textit{-a.s.}$

We may now prove Theorem 6.5, the central result of Sect. 6.

Proof of Theorem 6.5

We only prove the case that $(C^{n})_{n\in \mathbb{N}}$ is a nondecreasing sequence and $\mathbb{V}\subseteq \overline {\mathbb{R}}_{+}$. When $(C^{n})_{n\in \mathbb{N}}$ is a nonincreasing sequence and $\mathbb{V}\subseteq \overline {\mathbb{R}} _{-}$, the argument is symmetric. Since $(C^{n})_{n\in \mathbb{N}}$ is nondecreasing, so is $(V^{n})_{n\in \mathbb{N}}$ by Corollary 5.10. Then $V^{\dagger }=\lim _{n\to \infty}V^{n}$ exists and $V^{n} \leq V^{\dagger}$ for each $n\in \mathbb{N}$. Further, for any bounded stopping times ${\tau _{1}}$ and ${\tau _{2}}$ with ${\tau _{1}}\leq{\tau _{2}}$ $\mathbb{P}\text{-a.s.}$,

$$\begin{aligned} V^{\dagger}_{\tau _{1}} &= \lim _{n\to \infty} \mathbb{E}\bigg[ \int _{\tau _{1}}^{{\tau _{2}}} g(s,\omega ,C^{n}_{s} ,V^{n}_{s}) \,\mathrm {d}s + V^{n}_{{\tau _{2}}} \,\bigg\vert \,\mathcal {F}_{{\tau _{1}}} \bigg] \\ &\geq \lim _{n\to \infty} \mathbb{E}\bigg[ \int _{\tau _{1}}^{{\tau _{2}}} g(s,\omega ,C^{n}_{s} ,V^{\dagger}_{s}) \,\mathrm {d}s + V^{n}_{{\tau _{2}}} \,\bigg\vert \,\mathcal {F}_{{\tau _{1}}} \bigg] \\ &= \mathbb{E}\bigg[ \int _{\tau _{1}}^{{\tau _{2}}} g(s,\omega ,C_{s} ,V^{\dagger}_{s}) \,\mathrm {d}s + V^{\dagger}_{{\tau _{2}}} \,\bigg\vert \,\mathcal {F}_{{\tau _{1}}} \bigg]. \end{aligned}$$

(C.1)

It follows that $V^{\dagger}_{\tau _{1}} \geq \mathbb{E}[ V^{\dagger}_{\tau _{2}}\,|\, \mathcal {F}_{\tau _{1}}]$ so that $V^{\dagger}$ is a nonnegative generalised optional strong supermartingale. Hence by Proposition C.5, it is làdlàg. Combining the inequality $\mathbb{E}[V^{\dagger}_{\tau _{2}}\,|\,\mathcal {F}_{ \tau _{1}}] \geq \mathbb{E}[V^{\dagger}_{{\tau _{2}}{+}}\,|\,\mathcal {F}_{ \tau _{1}}]$ with (C.1), we obtain

$$ V^{\dagger}_{\tau _{1}} \geq \mathbb{E}\bigg[ \int _{\tau _{1}}^{{\tau _{2}}} g(s,\omega ,C_{s} ,V^{\dagger}_{s}) \,\mathrm {d}s + V^{\dagger}_{{\tau _{2}}{+}} \,\bigg\vert \,\mathcal {F}_{{\tau _{1}}} \bigg].$$

Furthermore, since $\mathbb{V}\subseteq \overline {\mathbb{R}}_{+}$, $\liminf _{t\to \infty}V^{\dagger}_{t+} \geq 0 \text{ a.s.}$ and $V^{\dagger}$ is a supersolution.

Now take any other nondecreasing sequence $(\tilde{C}^{n})_{n\in \mathbb{N}}$ whose limit equals $C$. Let $\tilde{V}^{n}$ be the utility process for $\tilde{C}^{n}$ and $\tilde{V}^{\dagger }= \lim _{n\to \infty}\tilde{V}^{n}$. Using that $\tilde{V}^{n}\in \mathbb{U}\mathbb{I}(g,C)$ is a subsolution for $(g,C)$ because $g$ satisfies (c↑), we may apply Theorem 5.8 and deduce that $V^{\dagger}_{\tau }\geq \tilde{V}^{n}_{\tau}$ for all finite stopping times $\tau$. Taking limits gives that $V^{\dagger}_{\tau } \geq \tilde{V}^{\dagger}_{\tau}$. Repeating the argument with the roles of $V^{\dagger}$ and $\tilde{V}^{\dagger}$ reversed, we find that $\tilde{V}^{\dagger}_{\tau }\geq V^{\dagger}_{\tau}$ for all finite stopping times $\tau$. Therefore $V^{\dagger}$ and $\tilde{V}^{\dagger}$ are optional processes that agree for all finite stopping times, and so they agree up to indistinguishability (see for example [10, Theorem 3.2]).

Next, we show that $V^{\dagger}$ is the minimal supersolution for $C$. Let $\overline{V}$ be any supersolution. Then, since $V^{n}\in \mathbb{U}\mathbb{I}(g,C)$ is a subsolution associated to $(g,C)$, we have $\overline{V}_{t} \geq V^{n}_{t}$ for all $t\geq 0$ by Theorem 5.8. Taking limits gives $\overline{V}_{t} \geq V^{\dagger}_{t}$.

Finally, we show that $V^{\dagger}$ is càdlàg. To this end, it suffices to show that the right-continuous process $(V^{\dagger}_{t+})_{t \geq 0}$ is also a supersolution because then the supermartingale property of $V^{\dagger}$ implies that

$$ V^{\dagger}_{\tau +} = \mathbb{E}[V^{\dagger}_{\tau +}|\mathcal {F}_{\tau}] \leq \mathbb{E}[V^{\dagger}_{\tau}|\mathcal {F}_{\tau}] = V^{\dagger}_{\tau}$$

for each bounded stopping time, and thus by the minimality of $V^{\dagger}$, we may conclude that $(V^{\dagger}_{t})_{t \geq 0} = (V^{\dagger}_{t+})_{t \geq 0}$ up to indistinguishability.

To show that $(V^{\dagger}_{t+})_{t \geq 0}$ is indeed a supersolution, fix bounded stopping times ${\tau _{1}}$ and ${\tau _{2}}$ with ${\tau _{1}}\leq{\tau _{2}}$. We first assume that there is $\delta > 0$ such that $\tau _{1} + \delta \leq \tau _{2}$. Then for each $\varepsilon < \delta$, by the fact that $V^{\dagger}$ is a supersolution and a generalised optional strong supermartingale,

$$ V^{\dagger}_{\tau _{1}+ \varepsilon } \geq \mathbb{E}\bigg[ \int _{\tau _{1}+\varepsilon }^{{\tau _{2}}} g(s,\omega ,C_{s} ,V^{\dagger}_{s}) \,\mathrm {d}s + V^{\dagger}_{{\tau _{2}}{+}} \,\bigg\vert \,\mathcal {F}_{{\tau _{1}+\varepsilon }} \bigg]. $$

Taking the limit as $\varepsilon \to 0$ and using the fact that for a.e. $\omega$, the path $t \mapsto V^{\dagger}_{t}(\omega )$ is right-continuous outside a countable set by Proposition C.5, we get by Hunt’s lemma in the form of Lemma C.7 that

$$\begin{aligned} V^{\dagger}_{\tau _{1}+} \geq \mathbb{E}\bigg[ \int _{\tau _{1}}^{{\tau _{2}}} g(s,\omega ,C_{s} ,V^{\dagger}_{s_{+}}) \,\mathrm {d}s + V^{\dagger}_{{\tau _{2}}{+}} \,\bigg\vert \,\mathcal {F}_{{\tau _{1}}} \bigg]. \end{aligned}$$

(C.2)

If $\tau _{2}$ is general, set $\tau _{2}^{\delta}:= \tau _{2} \vee (\tau _{1} + \delta )$ for $\delta > 0$. Then applying (C.2) for $\tau _{2}^{\delta}$ gives

$$\begin{aligned} V^{\dagger}_{\tau _{1}+} \mathbf {1}_{\{\tau _{2} \geq \tau _{1}+\delta \}} & \geq \mathbb{E}\bigg[ \int _{\tau _{1}}^{{\tau _{2}^{\delta}}} g(s,\omega ,C_{s} ,V^{\dagger}_{s_{+}}) \,\mathrm {d}s + V^{\dagger}_{{\tau ^{\delta}_{2}}{+}} \,\bigg\vert \,\mathcal {F}_{{\tau _{1}}} \bigg] \mathbf {1}_{\{\tau _{2} \geq \tau _{1}+\delta \}} \\ & = \mathbb{E}\bigg[ \int _{\tau _{1}}^{{\tau _{2}}} g(s,\omega ,C_{s} ,V^{\dagger}_{s_{+}}) \,\mathrm {d}s + V^{\dagger}_{{\tau _{2}}{+}} \,\bigg\vert \,\mathcal {F}_{{\tau _{1}}} \bigg] \mathbf {1}_{\{\tau _{2} \geq \tau _{1}+\delta \}}. \end{aligned}$$

Taking the limit as $\delta \to 0$, the monotone convergence theorem gives

$$\begin{aligned} V^{\dagger}_{\tau _{1}+} \mathbf {1}_{\{\tau _{2} > \tau _{1}\}} & \geq \mathbb{E}\bigg[ \int _{\tau _{1}}^{{\tau _{2}}} g(s,\omega ,C_{s} ,V^{\dagger}_{s_{+}}) \,\mathrm {d}s + V^{\dagger}_{{\tau _{2}}{+}} \,\bigg\vert \,\mathcal {F}_{{\tau _{1}}} \bigg] \mathbf {1}_{\{\tau _{2} > \tau _{1}\}}. \end{aligned}$$

Since trivially $V^{\dagger}_{\tau _{1}+} \mathbf {1}_{\{\tau _{2} = \tau _{1}\}} = \mathbb{E}[ \int _{\tau _{1}}^{{\tau _{2}}} g(s,\omega ,C_{s} ,V^{\dagger}_{s_{+}}) \,\mathrm {d}s + V^{\dagger}_{{\tau _{2}}{+}} \,|\,\mathcal {F}_{\tau _{1}}]\mathbf {1}_{ \{\tau _{2} = \tau _{1}\}}$, we conclude that

$$\begin{aligned} V^{\dagger}_{\tau _{1}+} & \geq \mathbb{E}\bigg[ \int _{\tau _{1}}^{{\tau _{2}}} g(s,\omega ,C_{s} ,V^{\dagger}_{s_{+}}) \,\mathrm {d}s + V^{\dagger}_{{\tau _{2}}{+}} \,\bigg\vert \,\mathcal {F}_{{\tau _{1}}} \bigg]. \end{aligned}$$

 □

Appendix D: Additional proofs omitted from the main text

Proof of Proposition 6.8

Suppose $V \subseteq \overline {\mathbb{R}}_{+}$; the case $V \subseteq \overline {\mathbb{R}}_{-}$ follows by a symmetric argument.

Let $(C^{2,n})$ be a nondecreasing sequence of processes in $\mathscr{E}(g)$ with limit $C^{2}$ and let $C^{1,n}:= C^{2,n}\wedge C^{1}$. Then $(C^{1,n})$ is a monotone sequence which approximates $C^{1}$. Furthermore, let $V^{1,n}\in \mathbb{U}\mathbb{I}(g,C^{1,n})\subseteq \mathbb{U}\mathbb{I}(g,C^{2,n})$ and $V^{2,n}\in \mathbb{U}\mathbb{I}(g,C^{2,n})$ be the utility processes for $C^{1,n}$ and $C^{2,n}$, respectively. Then if $V^{1,\dagger}$ and $V^{2,\dagger}$ are the generalised solutions associated to $C^{1}$ and $C^{2}$, it follows from Theorem 6.5 that $V^{1,\dagger} = \lim _{n\to \infty}V^{1,n}$ and $V^{2,\dagger} = \lim _{n\to \infty}V^{2,n}$.

As $C^{2,n}\geq C^{1,n}$ and $g$ satisfies $(c \uparrow )$, $g(t,\omega ,C^{2,n}_{t},V^{2,n}_{t}) \geq g(t,\omega ,C^{1,n}_{t},V^{2,n}_{t})$ for almost all $(t,\omega )$. Hence for all finite stopping times ${\tau _{1}} \leq {\tau _{2}}$,

$$\begin{aligned} V^{2,n}_{\tau _{1}} &= \mathbb{E}\bigg[ V^{2,n}_{{\tau _{2}}{+}} + \int _{\tau _{1}}^{{\tau _{2}}} g(s,\omega ,C^{2,n}_{s},V^{2,n}_{s}) \,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{{\tau _{1}}} \bigg] \\ &\geq \mathbb{E}\bigg[ V^{2,n}_{{\tau _{2}}{+}} + \int _{\tau _{1}}^{{\tau _{2}}} g(s,\omega ,C^{1,n}_{s},V^{2,n}_{s}) \,\mathrm {d}s \,\bigg\vert \,\mathcal {F}_{{\tau _{1}}} \bigg]. \end{aligned}$$

Since also $\liminf _{t \to \infty} V^{2,n}_{t{+}} \ge 0$ ℙ-a.s., $V^{2,n}$ satisfies the definition of a supersolution for the pair $(g,C^{1,n})$. Hence Theorem 5.8 gives $V^{2,n}_{\tau _{1}} \geq V^{1,n}_{\tau _{1}}$ ℙ-a.s. for all finite stopping times ${\tau _{1}}$. Letting $n\to \infty$ establishes the result. □