Duality in optimal consumption–investment problems with alternative data

Abstract

This study investigates an optimal consumption–investment problem in which the unobserved stock trend is modulated by a hidden Markov chain that represents different economic regimes. In the classic approach, the hidden state is estimated using historical asset prices, but recent technological advances now enable investors to consider alternative data in their decision-making. These data, such as social media commentary, expert opinions, COVID-19 pandemic data and GPS data, come from sources other than standard market data sources but are useful for predicting stock trends. We develop a novel duality theory for this problem and consider a jump-diffusion process for alternative data series. This theory helps investors identify “useful” alternative data for dynamic decision-making by providing conditions for the filter equation that enable the use of a control approach based on the dynamic programming principle. We apply our theory to provide a unique smooth solution for an agent with constant relative risk aversion once the distributions of the signals generated from alternative data satisfy a bounded likelihood ratio condition. In doing so, we obtain an explicit consumption–investment strategy that takes advantage of different types of alternative data that have not been addressed in the literature.

1 Introduction

The optimal consumption–investment problem is a classic problem of modern finance. An investor’s objective is to maximise the expected utility of consumption and terminal wealth over a finite horizon. By formulating the problem in a continuous-time framework, Merton’s pioneering work [35] became the cornerstone for the development of a stochastic optimal control theory to solve this type of problem. Many generalisations of the classic models have since been developed to more accurately model asset price dynamics. For example, Elliott and van der Hoek [20], Chen et al. [12], Sotomayor and Cadenillas [44], Yin and Zhou [50] and Zhou and Yin [52] study a regime-switching model in which the model coefficients are assumed to be modulated by a Markov chain. The different states of the chain are interpreted as different economic states or market modes. Bäuerle and Rieder [5, 6, 39], Honda [25] and Sass et al. [41] argue that the states of the Markov chain are not directly observable so that investors must learn and estimate them from observation, leading to partial information formulations. The literature refers to this model as a hidden Markov model.

In the past, investors have only been able to learn about the hidden state of the economy from easily accessible historical asset prices. However, investors are now actively acquiring alternative data, using modern technology to supplement their decision-making. Social media commentary, internet search results, COVID-19 pandemic data and GPS data are examples of such alternative data, that is, data that come from sources other than standard market data sources but are useful for predicting economic trends. Recent studies such as Frey et al. [24], Callegaro et al. [9], Fouque et al. [23] and Sass et al. [41] support the use of aggregate consumption and macroeconomic indicators and expert opinions as additional sources of observation. The effective use of alternative data can improve estimation accuracy and the performance of risk-sensitive benchmarked asset management; see Davis and Lleo [17, 18].

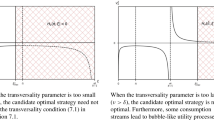
However, incorporating alternative data into dynamic decision-making creates new technical difficulties because of the additional randomness of these data. The aforementioned studies apply stochastic control techniques to an equivalent primal problem, the so-called separated problem, which is deduced from the original primal problem via filtering. This solution procedure is similar to that of a stochastic control problem with partial information, but the additional randomness complicates the mathematical analysis of the solvability of the problem and the eligibility of the solution procedure. Indeed, studies rarely discuss the conditions under which alternative data and their corresponding filters allow a stochastic control framework, such as the dynamic programming principle (DPP), to be applied to the underlying problem. One exception is the study of Frey et al. [24], which requires the density functions of the signals generated from alternative data to be continuously differentiable with common bounded support and to be uniformly bounded from below by a positive constant. This obviously excludes Gaussian signals and the most commonly used distributions. According to this criterion, [24] prove the DPP and show that there exists a unique value function for power utility. In other words, the relevance of different types of alternative data for dynamic decisions remains unclear. The lack of rigorous results in a general setting limits our understanding of optimal policies and the use of alternative data from various sources.

To fill this theoretical gap, we propose a new methodology based on duality theory that can be applied to general types of alternative data in the context of consumption–investment problems with a more general class of utility functions, in particular power utility functions with a negative exponent. We provide new and concrete results for specific problems that supplement those in the literature. For example, we identify in Condition 2.1 a bounded likelihood ratio (BLR) condition for alternative data signals in a bull–bear economy for an agent with power utility. That condition allows us to check the eligibility of signals from a wide range of distributions, such as Gaussian, exponential family and Gaussian mixture distributions. We provide three examples in Sect. 2.6.

Following the literature, we postulate the price of risky assets as a geometric Brownian motion in which the drift is modulated by a hidden economic state, which also affects alternative data. Inspired by Davis and Lleo [19], the alternative data are sampled from a regime-switching jump-diffusion process with parameters depending on the hidden state. This consideration aims to capture the realistic nature of alternative data sources, such as ecosystems, electricity prices, manufacturing and production forecasts; see for example Sethi and Zhang [42], Xi [46], Xi and Zhu [48], Yin and Zhu [51], Zhu et al. [53], Weron et al. [45] and the references therein. It also covers examples studied in the literature (including Callegaro et al. [9, Eq. (2.2) and Example 3.8] and Frey et al. [24, Sect. 2]). When alternative data are incorporated into hidden economic state estimations for dynamic decision-making, our problem formulation involves both a market and alternative data filtering scheme, so that appropriate regularity is required for the alternative data generation process to ensure the use of the DPP based on the adopted filter. Such use of alternative data is a clear difference from problems formulated using conventional jump-diffusion factor processes.

For the above general setup, our main theorem (Theorem 3.2) establishes an equivalence between the primal partial information problem and the dual problem, the latter simply involving a minimisation over a set of equivalent local martingale measures. To the best of our knowledge, our study is the first to extend the use of the duality approach from a partial information framework using a single observation process (such as Karatzas and Zhao [28], Lakner [33, 34], Pham and Quenez [37], Putschögl and Sass [38] and Sass and Haussmann [40]) to mixed-type observations using alternative data. The aforementioned studies characterise their dual formulation based on a single equivalent martingale measure, whereas we use non-unique equivalent martingale measures because of the additional randomness of alternative data. Once the dual problem is solved, the solution of the primal problem is obtained using convex duality. We find that the dual problem, which is a stochastic control problem but differs greatly from the primal problem, is more tractable. This enables us to use the DPP for the dual stochastic control problem under a general abstract condition for the filter equation. In terms of application, this condition describes the type of alternative data that can be considered “useful” for dynamic decision-making with the DPP. Specifically, the dual problem can be read at the analytical level of the Hamilton–Jacobi–Bellman (HJB) equation, thus providing a dual equation and improving our understanding of the optimal strategy. To demonstrate the entire solution procedure, we apply our general methodology to a concrete case study and explicitly derive a feedback optimal consumption–investment strategy by analysing the dual equation in Sect. 2. We prove a verification theorem (Theorem 2.7) which shows that the dual value function is the unique smooth solution of the dual equation. These results are obtained under a mild condition (Condition 2.1) for alternative data signals, including commonly seen examples that have not been addressed previously.

This study provides technical contributions to overcome the mathematical challenges to obtain these new results. In the framework of the aforementioned case study, the filter process is a jump-diffusion process with Lévy-type jumps, that is, the intensity of the jump measure depends on the filter process itself. This subtle feature creates analytical challenges in establishing the verification theorem. One may expect to derive the dual equation via the DPP first heuristically and then, based on the regularity of the solution to the dual equation (i.e., existence, uniqueness and smoothness), to verify the desired dual value function by formally applying Itô’s formula and a martingale argument. However, rigorously proving this regularity is difficult because the dual equation is a degenerate partial integro-differential equation (PIDE) with embedded optimisation. To overcome these difficulties, we first show that the dual value function is a bounded Lipschitz-continuous function and therefore a $C^{1}$-function of its arguments in Proposition 4.5. The result is technically innovative, as we introduce an auxiliary process and use Radon–Nikodým derivatives to address the Lévy-type jumps of the filter process. As an immediate consequence, the filter process turns out to be a Feller process (Proposition 2.6), indicating that the DPP is valid and the solution procedure is feasible. We then show that the dual equation has a unique smooth ($C^{1,2}$) solution. The method is based on the link between viscosity solutions and classical solutions for PIDEs, following Pham [36], Davis et al. [15] and Davis and Lleo [16]. However, our context differs from theirs in that ours contains an optimisation embedded in the nonlocal integro-differential operator of the PIDE. This distinct feature leads to both nonlinearity and degeneracy in the state space boundaries, so that we need to address both difficulties simultaneously. Finally, we obtain explicit formulas for the optimal strategies and wealth processes in terms of functions of the solution to the dual equation in Proposition 2.8.

We believe that an extensive analysis of such a well-known case study is a valuable contribution to the literature. Although some studies in the stochastic control literature examine a controlled jump-diffusion model (such as Barles and Imbert [4], Davis and Lleo [16], Pham [36] and Seydel [43]), most jump mechanisms are exogenous and do not depend on the state process. To the best of our knowledge, the only related result presented in Frey et al. [24, Sect. 4] proposes a distributional transformation and reconstruction of the filter process as an exogenous type of jump, so that the techniques used in the literature discussed above can be applied. Their approach imposes restrictive conditions on alternative data and a predominant constraint on trading strategies to obtain the necessary technical estimates. In contrast, we derive technical estimates to develop empirically testable conditions that are consistent with the abstract general condition of the duality approach, and then we solve the HJB equations for the dual problem in a more general setting.

The remainder of this paper is organised as follows. For simplicity and better illustration, Sect. 2 begins with a concrete optimal consumption–investment problem in a bull–bear stock market, where expert opinions are considered alternative data. We detail the solution procedure for solving such a stochastic optimisation problem and provide an explicit solution to the constant relative risk aversion (CRRA) utility function. This enables us to articulate the main mathematical challenges of the solution procedure and the advantage of the dual formulation. By considering a general regime-switching jump-diffusion model for alternative data series and a general set of utility functions, Sect. 3 develops the duality approach under partial information using alternative data. Specifically, we prove an equivalence between the primal and dual problems and present a condition for the filter process that ensures the validity of the DPP in the dual problem. Section 4 presents the proof of the verification theorem (Theorem 2.7) used in Sect. 2 to show that the dual value function is the unique classical solution of the HJB equation. Section 5 concludes the paper.

2 Expert opinions as alternative data

Before developing our duality theory with alternative data in a general setting, we specifically consider expert opinions and power utilities to present the solution procedure of our duality approach. This specification allows us to make the dual formulation and regularity of the approach transparent without an overwhelming notational burden. We also show that the solution procedure involves a stochastic optimal control problem in the dual problem and produces optimal solutions at the analytical level of the HJB equation in the dual problem. Section 3 then presents our analysis in a general setting.

2.1 A hidden Markov bull–bear financial market

For a fixed date $T>0$, which represents the fixed terminal time or investment horizon, we consider a filtered probability space $(\Omega ,\mathcal{F},\mathbb{F},\mathbb{P})$, where ℙ denotes the physical measure and $\mathbb{F}: = (\mathcal{F}_{t})_{t\in [0,T]}$ the full information filtration, satisfying the usual conditions, i.e., $\mathbb{F}$ is right-continuous and complete. For a generic process $G$, we denote by $\mathbb{F}^{G} = (\mathcal{F}_{t}^{G})_{t\in [0,T]}$ the natural filtration generated by $G$, made right-continuous and augmented with ℙ-nullsets.

We consider a two-regime hidden Markov financial market model in which the transitions of the “true” regime are described by a two-state continuous-time hidden Markov chain $\alpha =(\alpha _{t})_{t\in [0,T]}$ valued in $\mathcal{S}:=\{1,2\}$ on $(\Omega ,\mathcal{F},\mathbb{F},\mathbb{P})$. This model considers bull and bear markets, with $\alpha _{t}=1$ indicating the “bull market” and $\alpha _{t}=2$ the “bear market” state at time $t$. The Markov chain is characterised by a generator $\mathbf{A}$ of the form

$$\begin{aligned} \mathbf{A}= \begin{pmatrix} -a_{1} & a_{1} \\ a_{2} & -a_{2} \end{pmatrix},\qquad a_{1}, a_{2} >0. \end{aligned}$$

For times $t\in [0,T]$, we describe the financial market model as follows:

(i) The risk-free asset is given by $S^{0}_{t} = e^{rt}$ with a risk-free interest rate $r > 0$.

(ii) The risky asset $S=(S_{t})_{t\in [0,T]}$ satisfies the stochastic differential equation (SDE) given by

$$\begin{aligned} dS_{t} = \mu (\alpha _{t}) S_{t} dt +\sigma S_{t} dW_{t}, \end{aligned}$$

(2.1)

where $(W_{t})_{t\in [0,T]}$ is a standard $\mathbb{F}$-Brownian motion on $(\Omega ,\mathcal{F},\mathbb{P})$ independent of $\alpha$. The volatility of the risky asset $\sigma$ is a positive constant, and its drift function $\mu$ satisfies $\mu (\alpha _{t}) \in \{\mu _{1},\mu _{2}\}$, where $\mu _{1}>\mu _{2}$ are constant drifts under bull and bear markets, respectively.

Unlike the Markov-modulated regime-switching model, which treats $\alpha$ as observable, we assume that the representative agent does not observe $\alpha$ directly. The agent’s observation process has two components: the asset price process $S$ and an alternative data process in the form of expert opinions. Specifically, the agent receives noisy signals about the current state of $\alpha$ at discrete time points $T_{k}$. The aggregated alternative data process $\eta$ is a standard marked point process that depends on the Markov chain and is described by the double sequence $(T_{k}, Z_{k} )_{k\ge 0}$ representing the times at which the signal arrives and complemented by a sequence of random variables, one for each time, which denote the size of the signal; it satisfies

$$\begin{aligned} \eta _{t}: = \sum _{T_{k}\le t} Z_{k}. \end{aligned}$$

(2.2)

We assume that the intensity of the signal arrivals is given by a constant $\lambda$. In other words, the signal arrival time is independent of the hidden state. The signal $Z_{k}$ takes values in a set $\mathcal{Z} \subseteq \mathbb{R}$, and given $\alpha _{T_{k}} = i\in \{1,2\}$, the distribution of $Z_{k}$ is absolutely continuous with the Lebesgue density $f_{i}(z)$. Equivalently to (2.2), we have

(2.3)

where $\delta _{(T_{k}, \Delta \eta _{T_{k}})}(\,\cdot \,, \,\cdot \,)$ denotes the Dirac measure at the point $(T_{k}, \Delta \eta _{T_{k}}) \in [0,T]\times \mathcal{Z}$; so $N$ is an integer-valued random measure on $[0,T]\times \mathcal{Z}$, where $(\mathcal{Z}, \mathcal{B}(\mathcal{Z}))$ is a given Borel space. Specifically, the $\mathbb{F}$-dual predictable projection (see Definition D.2 in Appendix D) of the random measure $N$ is given by .

In other words, the information available to the agent is given by the observation filtration $\mathbb{H} = (\mathcal{H}_{t})_{t\in [0,T]}$ with $\mathbb{H}: = \mathbb{F}^{S} \vee \mathbb{F}^{\eta} \subseteq \mathbb{F}$. This is a partial information setting because (2.1)–(2.3) constitute a filtering system in which $\alpha$ and $(S, \eta )$ play the roles of state and observation, respectively.

2.2 The optimal consumption–investment problem

Let $\vartheta _{t}$ be the net amount of capital allocated to the risky asset and $c_{t}$ the rate at which capital is consumed at time $t$. The agent’s wealth process $V^{v,\vartheta ,c}$ corresponding to the choice $(\vartheta ,c)$ and initial wealth $v \in \mathbb{R}_{++}:=(0,\infty )$ follows

$$\begin{aligned} d V^{v,\vartheta ,c}_{t} = \big(\mu (\alpha _{t}) - r\big)\vartheta _{t} dt+ (r V^{v,\vartheta ,c}_{t} -c_{t} ) dt + \vartheta _{t} \sigma dW_{t}. \end{aligned}$$

(2.4)

Formally, we define the agent’s choices as follows:

(h1) $\vartheta =(\vartheta _{t})_{t \in [0, T]}$ is an investment process if it is a real-valued ℍ-predictable process with trajectories that are locally square-integrable on $[0,T)$.

(h2) $c=(c_{t})_{t \in [0, T]}$ is a consumption process if it is a real-valued nonnegative ℍ-predictable process with trajectories that are locally integrable on $[0,T)$.

As a class of admissible controls, we consider pairs of processes $(\vartheta ,c)$ satisfying (h1) and (h2) and such that the corresponding wealth process $V$ is nonnegative. The quantity to be maximised in our optimisation problem is

$$\begin{aligned} \mathbb{E}\bigg[U_{1}(V_{T})+\int _{0}^{T} U_{2}(c_{t}) dt\bigg], \end{aligned}$$

(2.5)

where $U_{i}:(0,\infty )\rightarrow \mathbb{R}$, $i=1,2$, is a utility function of the form

$$\begin{aligned} U_{1}(c) = U_{2}(c) = \frac{c^{\kappa}}{\kappa}, \qquad \kappa \neq 0 \text{ and } \kappa < 1. \end{aligned}$$

(2.6)

Note that the pair $(\vartheta ,c)$ must be predictable for the available information flow ℍ. Therefore, the stochastic control problem is under a partial information framework that contains more available information than that of classic partial information problems due to alternative data. These alternative data improve the estimation of the state $\alpha$ of the economy if they contain useful information. The estimation procedure is known as filtering, and we need to study the conditions that make expert opinions useful under a filtering scheme.

2.3 Filtering

Using standard notations in the filtering literature, the optional projection of a generic process $g=(g_{t})_{t\in [0,T]}$ onto the filtration ℍ is denoted by $\hat{g}_{t} = \mathbb{E}[g_{t}| \mathcal{H}_{t}]$. The filter of the hidden Markov chain $\alpha$ is $\pi =(\pi _{t})_{t\in [0,T]}$ with $\pi _{t} = \mathbb{P}[\alpha _{t}=1|\mathcal{H}_{t}]$. For a process of the form $g_{t} = G(\alpha _{t})$, its optional projection is given by

$$\begin{aligned} \hat{G}(\pi _{t}):=\hat{g}_{t} = \pi _{t} G(1) + (1-\pi _{t})G(2). \end{aligned}$$

We define the process $\widetilde{W}=(\widetilde{W}_{t})_{t\in [0,T]}$ such that for any $t\in [0, T]$,

$$\begin{aligned} \widetilde{W}_{t}: = \frac{1}{\sigma} \int _{0}^{t} \bigg( \frac{dS_{u}}{S_{u}} - rdu\bigg)-\int _{0}^{t}\hat{\theta}(\pi _{u})du = W_{t} - \int _{0}^{t} \big(\hat{\theta}(\pi _{u}) - \theta (\alpha _{u}) \big) du, \end{aligned}$$

(2.7)

where $\theta$ is the bounded function defined as

$$\begin{aligned} \theta (\alpha _{t}) : = \big(\mu (\alpha _{t}) - r\big)/\sigma \in \{ (\mu _{1}-r)/\sigma , (\mu _{2}-r)/\sigma \}. \end{aligned}$$

(2.8)

Then $\widetilde{W}$ is a $(\mathbb{P},\mathbb{H})$-Brownian motion (the so-called innovation process) according to classical results of filtering theory; see Bain and Crisan [3, Proposition 2.30]. We define the predictable random measure $\gamma ^{\mathbb{H}}$ and the function $\hat{f}:[0,1]\times \mathcal{Z}\rightarrow \mathbb{R}$ as

$$\begin{aligned} \gamma ^{\mathbb{H}}(dt,dz):=\lambda \hat{f}(\pi _{t-},z) dz dt, \qquad \hat{f}(x,z): = f_{1}(z)x+f_{2}(z)(1-x), \end{aligned}$$

(2.9)

and $\gamma ^{\mathbb{H}}$ is known as the ℍ-dual predictable projection of $N$ according to the standard results of filtering theory; see Ceci and Colaneri [11, Proposition 2.2]. We thus introduce the ℍ-compensated jump measure of $N$ given by

$$\begin{aligned} \overline{N}^{\pi}(dt,dz): = N(dt,dz) - \gamma ^{\mathbb{H}}(dt,dz)= N(dt,dz) -\lambda \hat{f}(\pi _{t-},z)dtdz. \end{aligned}$$

According to standard arguments from filtering theory (see Callegaro et al. [9, Theorem 3.6]), the filter $\pi$ is the unique strong solution of the Kushner–Stratonovich equation given by

$$\begin{aligned} d\pi _{t} &= \big(a_{2}-(a_{1}+a_{2})\pi _{t}\big) dt + \pi _{t}(1- \pi _{t})(\theta _{1} - \theta _{2}) d\widetilde{W}_{t} \\ & \hphantom{=:} + \int _{\mathcal{Z}} \big(\xi (\pi _{t-},z)-\pi _{t-}\big) { \overline{N}^{\pi}(dt,dz)}, \end{aligned}$$

(2.10)

with the initial value $\pi _{0}= x \in [0,1]$ and the function $\xi :[0,1]\times \mathcal{Z} \rightarrow \mathbb{R}$ defined as

$$\begin{aligned} \xi (x,z): = \frac{f_{1}(z)x}{f_{1}(z)x+f_{2}(z)(1-x)}. \end{aligned}$$

(2.11)

Note that the last term in (2.10) can be expressed as

$$\begin{aligned} &\int _{\mathcal{Z}} \big(\xi (\pi _{t-},z)-\pi _{t-}\big) \Big( N(dt,dz) -\lambda \big( f_{1}(z)\pi _{t-}+f_{2}(z)(1-\pi _{t-}) \big)dtdz \Big) \\ &= \int _{\mathcal{Z}} \big(\xi (\pi _{t-},z)-\pi _{t-}\big) N(dt,dz)- \lambda \int _{\mathcal{Z}} \big(f_{1}(z)\pi _{t-}-\pi _{t-}\hat{f}( \pi _{t-},z)\big)dz dt, \end{aligned}$$

where the last term in the above equation is equal to 0 because both $f_{1}$ and $f_{2}$ are density functions defined on $z\in \mathcal{Z}$. Therefore, this is equivalent to writing (2.10) as

$$\begin{aligned} d\pi _{t} &= \big(a_{2}-(a_{1}+a_{2})\pi _{t}\big) dt + \pi _{t}(1- \pi _{t})(\theta _{1} - \theta _{2}) d\widetilde{W}_{t} \\ & \hphantom{=:} + \int _{\mathcal{Z}} \big(\xi (\pi _{t-},z)-\pi _{t-}\big) {N(dt,dz)}. \end{aligned}$$

(2.12)

2.4 Primal and dual control problems

As we want to apply dynamic programming techniques, we start by embedding the optimisation problem into a family of problems indexed by generic time–space points $(t,x,v)\in [0, T]\times [0,1]\times \mathbb{R}_{++}$ which denote the starting time, the initial guess of the filter process and the initial wealth level. We denote the domain of $(t,x)$ by $\mathcal{U}_{T}:=[0,T)\times (0,1)$ and set $\overline{\mathcal{U}}_{T}:=[0,T]\times [0,1]$.

For any given and fixed $(t,x)\in \overline{\mathcal{U}}_{T}$, we define the filtration $\mathbb{H}^{t}:= (\mathcal{H}_{s}^{t})_{s\in [t,T]}$ by

$$\begin{aligned} \mathcal{H}_{s}^{t}=\sigma \Big(\big(\widetilde{W}(r)-\widetilde{W}(t), N(r,A)-N(t,A); A \in \mathcal{B}({\mathcal{Z}}), t \leq r \leq s \big)\cup \mathcal{N}_{\mathbb{P}}\Big), \end{aligned}$$

where $\mathcal{N}_{\mathbb{P}}$ is the family of all sets that are contained within a ℙ-nullset and $\widetilde{W}$ and $N$ are defined in (2.7) and (2.3). The solution of (2.12) on $[t,T]$ with the initial guess $\pi _{t}=x$ is denoted by $({\pi}_{s})_{s\in [t,T]}$. We introduce the measure $\mathbb{P}^{t,{x}}$ on $\mathcal{H}_{T}^{t}$ such that $\mathbb{P}^{t,{x}}[{\pi}_{t} = {x}]=1$, with $\mathbb{E}^{t,{x}}$ being the expectation operator under $\mathbb{P}^{t,{x}}$.

For $v\in \mathbb{R}_{++}$, consider all pairs $(\vartheta ,c)$ of $\mathbb{H}^{t}$-predictable processes that are defined analogously to (h1) and (h2), and $V^{t,x,v,\vartheta ,c}$ is the solution of (2.4) starting at time $t$ from $v$ under the control $(\vartheta ,c)$. The class $\mathcal{A}(t,x,v)$ of admissible controls, which depend on the initial value $(t,x,v)\in \overline{\mathcal{U}}_{T}\times \mathbb{R}_{++}$, is defined as the set of pairs $(\vartheta ,c)$ satisfying the above requirements and such that we have the no-bankruptcy constraint

$$\begin{aligned} V^{t,x,v,\vartheta ,c}_{s} \ge 0 \qquad \text{a.s., $t < s\le T$.} \end{aligned}$$

Clearly, the admissible set is not empty for all $v\in \mathbb{R}_{++}$ because for each initial value, the null strategy $(\vartheta ,c)\equiv (0,0)$ is always admissible. The agent’s objective function is postulated to be

$$\begin{aligned} \widetilde{J}(t, v,x;\vartheta ,c): = \mathbb{E}^{t,x}\bigg[ U_{1}(V^{t,x,v, \vartheta ,c}_{T}) + \int _{t}^{T} U_{2}(c_{t}) dt \bigg]. \end{aligned}$$

(2.13)

We define the primal problem as

$$\begin{aligned} J(t,x,v) : = \sup _{(\vartheta ,c) \in \mathcal{A}(t,x,v)} \widetilde{J}(t,x,v;\vartheta ,c), \qquad {(t,x,v)\in \overline{\mathcal{U}}_{T}\times \mathbb{R}_{++}}, \end{aligned}$$

(2.14)

with $J$ being its value function, which we call the primal value function. To apply the duality approach, we define the convex dual function $\widetilde{U}_{i}$ of the concave utility function $U_{i}$ as

$$\begin{aligned} \widetilde{U}_{i} (y) := \sup _{c>0} \big(U_{i}(c) -yc\big) = U_{i} \big(I_{i}(y)\big) - y I_{i}(y), \qquad y\in \mathbb{R}_{++}, \end{aligned}$$

(2.15)

where $I_{i}(\,\cdot \,)$ is the inverse function of $\partial _{c}U_{i}(\,\cdot \,)$. For the function $U_{i}$ in (2.6), we have $\widetilde{U}_{i}(y)=-y^{\beta}/\beta$ with $I_{i}(y) = y^{\beta -1}$ and $\beta :=-\kappa /(1-\kappa )$, $i=1,2$. We also introduce the process $(Z_{s}^{\nu})_{s\in [t,T]}$ with initial value $Z_{t}^{\nu}=1$ defined for an $\mathbb{H}^{t}$-predictable process $(\nu (s,z))_{s\in [t,T]}$ indexed by $\mathcal{Z}$ (see Definition D.1 in Appendix D) as

$$\begin{aligned} Z_{s}^{\nu} &:= \exp \bigg( -\frac{1}{2}\int _{t}^{s} \hat{\theta}( \pi _{u})^{2} du -\int _{t}^{s} \hat{\theta}(\pi _{u})d\widetilde{W}_{u} \bigg) \\ & \hphantom{=::} \times \exp \bigg( \int _{t}^{s}\int _{\mathcal{Z}} (1-e^{\nu (u,z)}) \hat{f}(\pi _{u-},z) dz du \\ & \hphantom{=:\times \exp \bigg(} + \int _{t}^{s}\int _{\mathcal{Z}} \nu (u,z) N(du,dz) \bigg), \end{aligned}$$

(2.16)

where $\hat{\theta}(\pi )$ is the optional projection of $\theta (\alpha )$ defined in (2.8) and $\hat{f}$ is defined in (2.9). We consider the admissible set of all $(\nu (s,z))_{s\in [t,T]}$ that satisfies the Lépingle–Mémin condition (see Ishikawa [26, Theorem 1.4]) given by

$$\begin{aligned} & \int _{t}^{T}\int _{\mathcal{Z}} \big(e^{2\nu (u,z)} + |\nu (u,z) |^{2} \big) \lambda f_{i}(z)dz du < \infty ,\qquad i=1,2; \end{aligned}$$

(2.17)

$$\begin{aligned} &\mathbb{E}^{t,x}\bigg[\exp \bigg(\int _{t}^{T}\int _{\mathbb{R}} \big(e^{\nu (u,z)}\nu (u,z) + 1-e^{\nu (u,z)}\big) \lambda \hat{f}( \pi _{u-},z) dz du \bigg)\bigg]< \infty . \end{aligned}$$

(2.18)

Let $\Theta ^{t}$ be the set of admissible $(\nu (s,z))_{s\in [t,T]}$. Specifically,

$$\begin{aligned} \Theta ^{t}: = \big\{ \nu =\big(\nu (s,z)\big)_{s\in [t,T]}: \,&\nu \text{ is }\mathbb{H}^{t}\text{-predictable and such that} \\ &\text{(2.17) and (2.18) hold} \big\} , \end{aligned}$$

which is not empty as $\nu \equiv 0$ is admissible. As $\hat{\theta}$ is bounded, the local martingale $Z^{\nu}$ is a martingale for all $\nu \in \Theta ^{t}$. We thus define a $\mathbb{P}^{t,x}$-equivalent probability measure $\mathbb{Q}^{\nu}$ on $(\Omega ,\mathcal{H}^{t}_{T})$ via ${d\mathbb{Q}^{\nu}}/{d\mathbb{P}^{t,x}}\vert _{\mathcal{H}^{t}_{T}} = Z^{\nu}_{T}$. We observe that

$$\begin{aligned} Z_{s}^{\nu} = \mathbb{E}^{t,{x}}\bigg[ \frac{d\mathbb{Q}^{\nu}}{d\mathbb{P}^{t,{x}}} \bigg\vert \mathcal{H}^{t}_{s} \bigg],\qquad s\in [t,T], \end{aligned}$$

and that $Z^{\nu}$ satisfies the SDE

$$\begin{aligned} d Z^{\nu}_{s}= -Z^{\nu}_{s}\hat{\theta}(\pi _{s})d\widetilde{W}_{s} + \int _{\mathcal{Z}}(1-e^{\nu (s,z)})Z^{\nu}_{s}\overline{N}^{\pi}(ds,dz), \end{aligned}$$

where $(\pi _{s})$ is the solution of (2.12) with $\pi _{t}= x$. In addition, for each $\nu \in \Theta ^{t}$,

$$\begin{aligned} \mathbb{Q}^{\nu} \in \mathcal{Q}: = \{\mathbb{Q}\approx \mathbb{P}^{t,x} : (e^{-r(s-t)}S_{s})_{s\in [t,T]} \text{ is a } \mathbb{Q} \text{-martingale} \}. \end{aligned}$$

(2.19)

Let $(t,x,v)\in \overline{\mathcal{U}}_{T}\times \mathbb{R}_{++}$, $(\vartheta ,c) \in \mathcal{A}(t,x,v)$, $\nu \in \Theta ^{t}$ and set $V=V^{t,x,v,\vartheta ,c}$. Itô’s lemma shows that $( e^{-rT}Z^{\nu}_{T}V_{T} + \int _{t}^{T} e^{-rs}Z^{\nu}_{s}c_{s} dt)$ is a $(\mathbb{P},\mathbb{H})$-supermartingale (as a positive local martingale), which implies that due to the arbitrariness of $\nu \in \Theta ^{t}$,

$$\begin{aligned} \sup _{\nu \in \Theta ^{t}} \mathbb{E}^{t,x}\bigg[ e^{-rT}Z^{\nu}_{T}V_{T} + \int _{t}^{T} e^{-rs}Z^{\nu}_{s}c_{s} ds \bigg] \le e^{-rt} v. \end{aligned}$$

With the definition of $\widetilde{U}_{i}$ in (2.15), for all $y\in \mathbb{R}_{++}$, $(\vartheta ,c) \in \mathcal{A}(t,x,v)$ and $\nu \in \Theta ^{t}$, the agent’s objective function $\widetilde{J}$ defined in (2.13) satisfies

$$\begin{aligned} \widetilde{J}(t, v,x; \vartheta ,c) &\le \mathbb{E}^{t,x}\bigg[ U_{1}(V_{T}) + \int _{t}^{T} U_{2}(c_{s}) ds\bigg] \\ & \hphantom{=:} - y\mathbb{E}^{t,x}\bigg[e^{-r(T-t)}Z_{T}^{\nu}V_{T} + \int _{t}^{T} e^{-r(s-t)}Z_{s}^{ \nu}c_{s} ds\bigg]+ vy \\ &\le \mathbb{E}^{t,x}\bigg[\widetilde{U}_{1}(y e^{-r(T-t)}Z_{T}^{\nu}) + \int _{t}^{T} \widetilde{U}_{2}(y e^{-r(s-t)}Z_{s}^{\nu}) ds\bigg] + vy. \end{aligned}$$

Taking the supremum of $\widetilde{J}$ over $(\vartheta ,c)\in \mathcal{A}(t, v,x)$, the primal value function $J$ defined in (2.14) satisfies for any $\nu \in \Theta ^{t}$ and $y\in \mathbb{R}_{++}$ that

$$\begin{aligned} J(t,x,v) \le \mathbb{E}^{t,x}\bigg[\widetilde{U}_{1}( y e^{-r(T-t)}Z_{T}^{ \nu}) + \int _{t}^{T} \widetilde{U}_{2}(y e^{-r(s-t)}Z_{s}^{\nu}) ds \bigg] + vy. \end{aligned}$$

(2.20)

Thus the right-hand side of (2.20) is an upper bound of $J$. Taking the infimum over $\nu \in \Theta ^{t}$ on the right-hand side of (2.20), we consider for $(t,x,y)\in \overline{\mathcal{U}}_{T}\times \mathbb{R}_{++}$ the dual optimisation problem

$$\begin{aligned} \inf _{\nu \in \Theta ^{t}} \widetilde{L}(t,x, y;\nu ), \end{aligned}$$

(2.21)

where $\widetilde{L}(t,x,y;\nu ) = \mathbb{E}^{t,x}[\widetilde{U}_{1}(y e^{-r(T-t)}Z_{T}^{ \nu}) + \int _{0}^{T} \widetilde{U}_{2}( y e^{-r(s-t)}Z_{s}^{\nu}) dt]$. Let $\hat{L}$ be the value function associated with this problem, called the dual value function, so that

$$\begin{aligned} \hat{L}(t,x, y):= \inf _{\nu \in \Theta ^{t}} \widetilde{L}(t, x, y; \nu ),\qquad (t,x,y)\in \overline{\mathcal{U}}_{T}\times \mathbb{R}_{++}. \end{aligned}$$

(2.22)

It then follows from (2.20) that

$$\begin{aligned} J(t,x,v) \le \inf _{y\in \mathbb{R}_{++}} \big( \hat{L}(t,x,y)+ vy \big),\qquad (t,x,v)\in \overline{\mathcal{U}}_{T}\times \mathbb{R}_{++}. \end{aligned}$$

(2.23)

There is no duality gap between the primal problem (2.14) and the dual problem (2.21) when we have equality in (2.23). The current formulation suggests that one can first work on the dual problem and then transform it back into the primal problem by closing the duality gap.

2.5 HJB in the dual problem

The dual problem reduces the original problem with two control variables to only one control process $\nu \in \Theta ^{t}$. The natural choice for solving this problem is a heuristic use of the DPP: for any $\mathbb{H}^{t}$-stopping time $\tau$ valued in $[t,T]$, we have

$$\begin{aligned} \hat{L}(t,x,y) = \inf _{\nu \in \Theta ^{t}} \mathbb{E}^{t,x}\bigg[ \hat{L}(\tau , {\pi}_{\tau}, ye^{-r(\tau -t)}Z_{\tau}^{\nu} ) + \int _{t}^{ \tau} \widetilde{U}_{2}(ye^{-r(s-t)}Z_{s}^{\nu}) ds\bigg]. \end{aligned}$$

(2.24)

Therefore, the HJB equation of the dual value function is derived as

$$\begin{aligned} \partial _{t} \hat{L}(t,x,y) + \inf _{\nu} \overline{\mathcal{L}}^{ \nu} \hat{L} + \widetilde{U}_{2}(y) = 0, \end{aligned}$$

(2.25)

where the dynamics of (2.16) for $Z^{\nu}$ and of (2.10) for $\pi$ generate the operator

$$\begin{aligned} \overline{\mathcal{L}}^{\nu}\hat{L}& := \lambda \int _{\mathcal{Z}} \Big(\hat{L}\big(t,\xi (x,z),e^{\nu}y\big) - \hat{L}(t,x,y) +(1-e^{ \nu})y\partial _{y} \hat{L}(t,x,y)\Big)\hat{f}(x,z) dz \\ & \hphantom{=::} + \bigg( \frac{1}{2}x^{2}(1-x)^{2}(\theta _{1} - \theta _{2}) \partial _{xx} + \hat{\theta}(x)\partial _{x} +\frac{1}{2}y^{2} \hat{\theta}(x)^{2} \partial _{yy} - ry\partial _{y}\!\bigg)\hat{L}(t,x,y). \end{aligned}$$

Intuitively, the dual optimiser $\nu ^{*}$ can be constructed in feedback form via the first-order conditions in the HJB equation (2.25) if the candidate process is admissible, i.e., fulfilling conditions (2.17) and (2.18). The remaining task is to determine regularity conditions under which the alternative data and corresponding filters enable the above prescription.

2.6 Regularity: bounded likelihood ratio

In Sect. 3, we study regularity much more generally, in terms of the choice of utility functions and alternative data processes, such that the above prescription is true. However, regularity turns out to be more abstract. Using the expert opinion setting in this section, we provide concrete technical conditions for the probability density functions of alternative data signals that validate (2.24) and the proposed solution procedure.

Condition 2.1

The probability density functions $f_{1}$ and $f_{2}$ of the signals in (2.2) have the same support $\mathcal{Z}$ and admit finite second moments such that

$$\begin{aligned} b_{\min} < \frac{f_{2}(z)}{f_{1}(z)} < b_{\max}, \qquad z\in \mathcal{Z}, \end{aligned}$$

for $0\le b_{\min}<1<b_{\max}$. We also want the dissimilarity between the two distributions to be reasonably bounded. Specifically, we use Amari’s alpha-divergence measure $D_{a}(f_{1} \| f_{2})$ (see Amari [2, Chap. 3.5]) with $a=3$ to characterise such dissimilarity and require that for some constant $C$, we have

$$\begin{aligned} D_{3}(f_{1} \| f_{2}): =\int _{\mathcal{Z}} \frac{1}{6}\big({f_{1}(z)^{3}}/{f_{2}(z)^{2}}-1 \big) dz \le C. \end{aligned}$$

The interpretation of Condition 2.1 is that it ensures a kind of bounded likelihood ratio — we should not expect the arriving signals to be particularly strong in terms of distinguishing between the two regimes. Otherwise, the situation becomes similar to direct observation of the state $\alpha$. Note that Condition 2.1 based on the dual problem covers a wider range of signals than those based on the primal problem in the literature. Indeed, it clearly covers examples in Frey et al. [24, Assumption 5.1 and Remark 5.2], i.e., continuously differentiable densities with common bounded support that are uniformly bounded from below by a strictly positive constant. Furthermore, Condition 2.1 covers more examples of discrete and continuous distributions defined in unbounded domains. We list a few examples below.

Example 2.2

Consider two exponential family distributions as

$$\begin{aligned} f_{1}(z)&= \exp \bigg(\sum _{j} g_{j}(z)v_{j}^{(1)}\bigg), \\ f_{2}(z) &= \exp \bigg(\sum _{j} g_{j}(z)v_{j}^{(2)}\bigg), \end{aligned}$$

where $v_{j}$ is a parameter of the distribution and $g_{j}$ is a fixed feature of the family, such as $(1,x,x^{2})$ in the Gaussian case. Condition 2.1 holds if there exists a constant $C$ such that $\sum _{j} (v_{j}^{(2)}-v_{j}^{(1)})g_{j}(z) \le C$ and $\sum _{j} (3v_{j}^{(1)}-2v_{j}^{(2)})g_{j}(z) \le C$ for all $z$. We provide an example that clearly satisfies these conditions as

$$\begin{aligned} f_{1}(z)& = \frac{\sqrt{1.6}}{\sqrt{2\pi}}e^{-0.8(z+1)^{2}}, \\ f_{2}(z) &= \frac{\sqrt{2}}{\sqrt{2\pi}}e^{-(z-1)^{2}}. \end{aligned}$$

Example 2.3

As a direct extension of Example 2.2, Condition 2.1 holds for a Gaussian density $f_{2}(z)$ and $f_{1}(z):=\sum _{j=1}^{n} a_{j} f_{1}^{(j)}(z)$ with $\sum _{j} a_{j} = 1$, which is a mixture of Gaussian distribution densities, when each pair $(f_{1}^{(j)}, f_{2})$ fulfils the conditions in Example 2.2.

Example 2.4

Consider a mixture distribution and a Gamma distribution defined on $\mathbb{R}_{++}$ given as

where $a_{1},a_{2}\in (0,1)$ and $\mathcal{G}(a):=\int _{\mathbb{R}_{++}} z^{a-1}e^{-z}dz$ is the Gamma function. Condition 2.1 holds when $b_{\min}=0$, $b_{\max}=\max \{ 1/a_{2}a_{1},1/(1-a_{2})e\} / \mathcal{G}(a_{1})$ and with $L_{F}=e^{3}\mathcal{G}(a_{1})^{2}\mathcal{G}(2-2a_{1})+2e^{2} \mathcal{G}(a_{1})^{2}a_{1}^{2}$.

Under Condition 2.1, we derive the following two useful properties of the filter process $\pi$. The proofs are provided in Appendix C.

Proposition 2.5

Under Condition 2.1, both 0 and 1 are unattainable boundaries for the filter process $\pi$, the solution of (2.12). In other words, they cannot be reached from inside the state space $(0,1)$.

Proposition 2.6

Under Condition 2.1, the Markov filter process $\pi ^{x_{0}}:=(\pi ^{x_{0}}_{t})_{t\ge 0}$, defined as the solution of (2.12) starting from time 0 and a given starting point $x_{0}\in (0,1)$, is a Feller process. For any bounded and continuous function $f$, it follows that $x \mapsto P_{t}f(x): = \mathbb{E}[f({\pi}^{x}_{t})]$ is continuous for all $t\ge 0$ and $\lim _{t\downarrow 0}P_{t}f(x) = f(x)$.

Proposition 2.5 implies that when characterising the dual value function $\hat{L}$ using the HJB method, no conditions should be imposed on the boundaries of the filter, neither on the value of the function nor on its partial derivatives (see Bayraktar et al. [7, Definition 2.5 and Remark 2.6]). Proposition 2.6 implies that a similar initial guess of the hidden state will lead to similar developments in filtering and that the filter itself changes in a reasonably continuous manner. The Feller property of the filter process further validates the DPP in (2.24) (see Theorem 3.1 in a general setting in Sect. 3). According to Propositions 2.5 and 2.6, we have the following verification theorem.

Theorem 2.7

Under Condition 2.1, the dual value function $\hat{L}$ is the unique classical solution in $C(\overline{\mathcal{U}}_{T}\times \mathbb{R}_{++})\cap C^{1,2,2}({ \mathcal{U}}_{T}\times \mathbb{R}_{++})$ of the HJB equation (2.25), subject to the boundary condition $\hat{L}(T,x,y) = \widetilde{U}_{2}(y)$ for $x \in [0,1]$ and $y \in \mathbb{R}_{++}$. In addition, $\hat{L}$ satisfies

$$\begin{aligned} \hat{L}(t,x,y)= -\frac{y^{\beta}}{\beta}\hat{\Lambda}(t,x), \qquad (t,x,y) \in \overline{\mathcal{U}}_{T}\times \mathbb{R}_{+}, \end{aligned}$$

(2.26)

where $\hat{\Lambda}\in C(\overline{\mathcal{U}}_{T})\cap C^{1,2}({ \mathcal{U}}_{T})$, $\beta =-\kappa /(1-\kappa )$ and $\kappa$ is the risk aversion parameter of the utility function defined in (2.6). For $y\in \mathbb{R}_{++}$, the dual problem (2.21) admits a dual optimiser $\nu ^{*}\in{\Theta}^{t}$ given by

$$\begin{aligned} {\nu}^{*}_{s}:=\hat{\nu}(s,\pi _{s-},z)=\frac{1}{1-\beta} \ln \frac{\hat{\Lambda} (s,\xi (\pi _{s-},z) )}{\hat{\Lambda}(s,\pi _{s-})} , \qquad s\in [t,T]. \end{aligned}$$

Proof

See Sect. 4. □

Given that there exists a dual optimiser in $\Theta ^{t}$ for the dual problem (2.21), we now turn to the proof that there is no duality gap. We have the following result (a special case of Theorem 3.2 below) that closes the duality gap and derives the optimal controls for the primal problem. The proof is provided in Appendix C.

Proposition 2.8

Under Condition 2.1, there is no duality gap between the primal and dual problems (2.14) and (2.21). For fixed $(t,x,v)\in \mathcal{U}_{T}\times \mathbb{R}_{++}$, the optimal wealth process is given by

$$\begin{aligned} {V}^{*}_{s} = v (e^{-r(s-t)}Z_{s}^{{\nu}^{*}})^{\beta -1} \frac{\hat{\Lambda}(s,\pi _{s})}{\hat{\Lambda}(t,x)}, \qquad s\in [t,T], \end{aligned}$$

where $\hat{\Lambda}$ and ${\nu}^{*}$ are given in Theorem 2.7and $(Z_{s}^{{\nu}^{*}})_{s\in [t,T]}$ satisfies

$$\begin{aligned} d Z^{{\nu}^{*}}_{s}:= -Z^{{\nu}^{*}}_{s}\hat{\theta}(\pi _{s})d \widetilde{W}_{s} + \int _{\mathcal{Z}}Z^{{\nu}^{*}}_{s}(1-e^{{\nu}^{*}_{s}}) \overline{N}^{\pi}(ds,dz),\qquad Z_{t}^{{\nu}^{*}} = 1. \end{aligned}$$

(2.27)

The optimal controls $({\vartheta}^{*},{c}^{*})$ of the primal problem take the feedback forms

$$\begin{aligned} &{\vartheta}^{*}_{s} = \hat{\vartheta}(s, \pi _{s},{V}^{*}_{s}) := \frac{1}{\sigma} {{V}^{*}_{s}}\bigg((1-\beta )\hat{\theta}(\pi _{s}) + \frac{\partial _{x} \hat{\Lambda}(s,\pi _{s})}{\hat{\Lambda}(s,\pi _{s})} \bigg), \qquad s\in [t,T], \\ &{c}^{*}_{s} = \hat{c}(s, \pi _{s},{V}^{*}_{s}) = \frac{{V}^{*}_{s}}{\hat{\Lambda}(s,\pi _{s})}, \qquad s\in [t,T]. \end{aligned}$$

3 Duality with alternative data: a general dynamic programming approach

In this section, we present a general dynamic programming approach to solve the optimal choice problem based on duality, under a broader class of time-dependent utility functions (Assumption A.1) and more general alternative data situations. We note that our results can be easily extended to cases with more than two economic states, which corresponds to a finite-state hidden Markov chain $\alpha$.

We start by describing the general alternative data model $\eta$ that serves as the setting for our (abstract) results. In numerous practical scenarios, systems have discontinuous trajectories and structural changes. Commonly used jump-diffusion models in financial asset pricing models (see Cont and Tankov [13, Chap. 1]) may fail to account for structural changes in alternative data from outside the standard financial market. Accordingly, we are interested in a regime-switching jump-diffusion model because it incorporates discontinuous changes with regime-switching jump sizes and intensities. Mathematically, we model $\eta$ by using

$$ d\eta _{t} = b_{1}(\eta _{t},\alpha _{t})dt + \sigma _{1}(\eta _{t-}) dW_{t} + \sigma _{2}(\eta _{t-}) dB_{t} + \int _{\mathcal{Z}} b_{2}(\eta _{t-},z) N_{\eta}(dt,dz), $$

(3.1)

where $B$ is a standard $\mathbb{F}$-Brownian motion, $N_{\eta}(dt,dz)$ is an $\mathbb{F}$-adapted integer-valued random measure on $[0,T] \times \mathcal{Z}$, both independent of the Brownian motion $W$ and the hidden Markov chain $\alpha$. In particular, the intensity measure of $N_{\eta}$ is given by $\gamma (\alpha _{t-},dz)dzdt$, which depends on the hidden state. To avoid unnecessary technical details, we simply assume what we need: (3.1) has a unique strong solution. Some sufficient conditions are summarised in Assumption D.3 in Appendix D.

To proceed, we need to know the structure of $\mathcal{Q}$ introduced in (2.19), i.e., the set of all ℙ-equivalent probability measures ℚ on $\mathcal{H}_{T}$ for which the discounted price of the risky asset is a ℚ-martingale. This requires us to define the innovation processes associated with the diffusion and jump parts of (3.1). Recalling the notations introduced at the beginning of Sect. 2.3 and using (2.7), we define a $(\mathbb{P},\mathbb{H})$-Brownian motion $\widetilde{B}$ and an ℍ-compensated jump measure $\overline{m}^{\pi}$ as

$$\begin{aligned} \widetilde{B}_{t} &: = B_{t} - \int _{0}^{t}\hat{\underline{\theta}}( \eta _{u},\pi _{u})-\underline{\theta}(\eta _{u},\alpha _{u}) du, \\ \underline{\theta}(\eta ,i) &: = \frac{b_{1}(\eta ,i) - {\theta (i)\sigma _{1}(\eta )}/{\sigma}}{\sigma _{2}(\eta )}, \\ \overline{m}^{\pi}(dt,dq) &:= m(dt,dq) - \hat{\lambda}(\pi _{t-}) \hat{\phi}_{t}(\pi _{t-},dq)dt, \end{aligned}$$

where $m(d t, d q):=\sum _{s: \Delta \eta _{s} \neq 0} \delta _{(s, \Delta \eta _{s})}(d t, d q)$ is the integer-valued random measure associated with the jumps of the process $\eta$, $\lambda _{t}(\alpha _{t-})\phi _{t}(\alpha _{t-}, dq)dt$ is the ℙ-dual predictable projection of $m$ (see Ceci [10, Proposition 3]) that satisfies

$$\begin{aligned} \lambda _{t}(\alpha _{t-})\phi _{t}(\alpha _{t-}, A)dt = \gamma \big( \alpha _{t-},\big\{ z\in \mathcal{Z}:b_{2}(\eta _{t-},z)\in A \setminus \{0\}\big\} \big), \qquad A\in \mathcal{B}(\mathbb{R}), \end{aligned}$$

and $\pi _{t} = \mathbb{P}[\alpha _{t}=1|\mathcal{H}_{t}]$ is the unique solution to the Kushner–Stratonovich equation

$$\begin{aligned} d \pi _{t} &= \pi _{t}(1-\pi _{t})(\theta _{1} - \theta _{2}) d \widetilde{W}_{t}+ \pi _{t}(1-\pi _{t})(\underline{\theta}_{1} - \underline{\theta}_{2})d\widetilde{B}_{t} \\ & \hphantom{=:} + \big(a_{2}-(a_{1}+a_{2})\pi _{t}\big) dt +\int _{\mathbb{R}} \big( \xi (t,q) -\pi _{t-} \big)\overline{m}^{\pi}(dt,dq), \\ \xi (s,q) &= \frac{d \pi _{s-}\lambda _{s}(1)\phi _{s}(1,dq)}{d(\hat{\lambda}(\pi _{s-})\hat{\phi}_{s}(\pi _{s-},dq))}. \end{aligned}$$

(3.2)

All $(\mathbb{P},\mathbb{H})$-local martingales can be constructed via the triplet $(\widetilde{W},\widetilde{B},\overline{m}^{\pi})$ (see Proposition D.4 in Appendix D). Hence for any given $t\in [0,T]$, ℚ belongs to $\mathcal{Q}$ if and only if its Radon–Nikodým derivative with respect to $\mathbb{P}^{t,x}$ on $\mathcal{H}^{t}_{T}$ is given by the Doléans-Dade exponential $Z^{\nu}$ (with a slight abuse of notation) defined for $s\in [t,T]$ as

$$\begin{aligned} Z^{\nu}_{s}&= \mathcal{E}\bigg( -\int _{t}^{\cdot} \hat{\theta}(\pi _{u})d \widetilde{W}_{u} - \int _{t}^{\cdot}\nu _{D}(u)d\widetilde{B}_{u} \\ & \hphantom{=: \mathcal{E}\bigg(} - \int _{t}^{\cdot}\int _{\mathbb{R}} (1-e^{\nu _{J}(u,q)}) \overline{m}^{\pi}(du,dq) \bigg)_{s} \end{aligned}$$

(3.3)

for a pair $\nu =(\nu _{D},\nu _{J})$ consisting of an $\mathbb{H}^{t}$-predictable process $(\nu _{D}(u))$ and an $\mathbb{H}^{t}$-predictable process $(\nu _{J}(u,q))$ indexed by ℝ, satisfying the Lépingle–Mémin condition

$$\begin{aligned} & \int _{t}^{T} \nu _{D}^{2}(s) ds + \int _{t}^{T}\int _{\mathbb{R}} e^{2 \nu _{J}(s,q)} + |\nu _{J}(s,q)|^{2} \lambda _{s}(i)\phi _{s}(i,dq)ds < \infty ,\qquad i=1,2, \\ &\mathbb{E}^{t,x}\bigg[\exp \bigg(\frac{1}{2}\int _{t}^{T} \nu _{D}^{2}(s) ds + \int _{t}^{T}\int _{\mathbb{R}}\big(e^{\nu _{J}(s,q)}\nu _{J}(s,q) + 1-e^{\nu _{J}(s,q)}\big) \\ & \hphantom{=:\bigg[\exp \bigg( + \int _{t}^{T}\int _{\mathbb{R}}\int _{t}^{T} \nu _{D}^{2}(sd \qquad } \times \hat{\lambda}(\pi _{s- })\hat{\phi}_{s}(\pi _{s-},dq)ds\bigg) \bigg]< \infty . \end{aligned}$$

Under the current general setting, the dual optimisation problem is formulated as

$$\begin{aligned} \hat{L}(t,x,y)= \inf _{\mathbb{Q}\in \mathcal{Q}}\mathbb{E}^{t,x} \bigg[\widetilde{U}_{1}(T, ye^{-r(T-t)}Z^{\nu}_{T} )+ \int _{t}^{T} \widetilde{U}_{2}(s, ye^{-r(s-t)} Z^{\nu}_{s}) ds \bigg]. \end{aligned}$$

(3.4)

A notable advantage of solving the dual problem in the context of general alternative data situations is the broad applicability of the DPP approach. We refer to Žitković [54, Theorem 3.17] which shows that the DPP is valid when the filter process is a Feller process. This condition provides important insight into the type of alternative data considered “useful” in terms of problem verification, that is, the solution procedure illustrated in Sect. 2.5. We cite [54, Theorem 3.17] as follows for completeness.

Theorem 3.1

Suppose that the filter process $({\pi}_{t})_{t\in [0,T]}$, the unique solution to the Kushner–Stratonovich system (3.2), is a Feller process. Then the DPP holds for the dual value function $\hat{L}$ defined in (3.4); specifically, we have:

• i) For any $\mathbb{H}^{t}$-stopping time $\tau$ valued in $[t,T]$ and each $(t,x,y)\in \overline{\mathcal{U}}_{T} \times \mathbb{R}_{++}$,

  $$\begin{aligned} \hat{L}(t,x,y) = \inf _{\mathbb{Q}\in \mathcal{Q}} \mathbb{E}^{t,x} \bigg[ \hat{L}(\tau , \pi _{\tau},ye^{r(t-\tau )}Z^{\nu}_{\tau}) + \int _{t}^{\tau} \widetilde{U}_{2}(s, ye^{r(t-s)}Z^{\nu}_{s}) ds \bigg]. \end{aligned}$$

• ii) For any $\epsilon >0$, an $\epsilon$-optimal $\mathbb{Q}^{*} \in \mathcal{Q}$ can be associated with any triple $(t,x,y)\in \overline{\mathcal{U}}_{T} \times \mathbb{R}_{++}$ in a universally measurable way.

We can now present the main result of this section, whose proof is provided in Appendix A. This establishes the equivalence between the primal and dual problems.

Theorem 3.2

For a class of time-dependent utility functions with suitable growth conditions (Assumption A.1), suppose that the dual optimiser $\mathbb{Q}^{y}\in \mathcal{Q}$ for (3.4) exists for all $y\in \mathbb{R}_{++}$. Then for any initial wealth level $v\in \mathbb{R}_{++}$, there exists a real number $y^{*}= y(v) >0$ such that

$$\begin{aligned} J(t,x,v) = \hat{L}(t,x,y^{*})+vy^{*} =\widetilde{L}(t,x,y^{*};\nu ^{y^{*}})+vy^{*} = \inf _{y\in \mathbb{R}_{++}} \!\big( \hat{L}(t,x,y)+vy \big), \end{aligned}$$

where $J$ is the primal value function and $\nu ^{y^{*}}$ is the dual optimiser of (3.4) for $y^{*}$. Specifically, there is no duality gap. There exists a pair $(\vartheta ^{*},c^{*})\in \mathcal{A}(t,x,v)$, with $c^{*}_{s} = I_{2}(s, e^{-r(s-t)}y^{*}\widetilde{Z}_{s}^{\mathbb{Q}^{y^{*}}})$ and $V_{T}^{t,x,v, \vartheta ^{*},c^{*}} = I_{1}( T, e^{-r(T-t)}y^{*} \widetilde{Z}_{T}^{\mathbb{Q}^{y^{*}}})$, that is optimal for the primal problem (2.14).

4 Dual value function as a classical solution of the HJB equation

4.1 Proof of Theorem 2.7

The main difficulties arise from the nonlinear integro-differential term and the degeneracy induced by the filter process, which cannot be addressed directly via the PDE theory of classical solutions. We first deduce the form of $\hat{L}$ given by (2.26). Recalling that $\widetilde{U}_{i}(y) = - y^{\beta}/\beta$, it is clear by the definition (2.22) that $\hat{L}$ is written as

$$\begin{aligned} \hat{L}(t,x,y) = y^{\beta}\inf _{\nu \in \Theta ^{t}} \bigg(- \frac{1}{\beta}\mathbb{E}^{t,x}\bigg[(e^{-r(T-t)} Z_{T}^{\nu})^{\beta} + \int _{t}^{T} (e^{-r(s-t)}Z_{s}^{\nu})^{\beta} ds\bigg] \bigg). \end{aligned}$$

For a fixed $y\in \mathbb{R}_{++}$, the dual optimisation in (2.21) is therefore reduced to the auxiliary dual problem defined as

$$\begin{aligned} \text{maximise [minimise] } \Lambda (t,x;\nu ):= \mathbb{E}^{t,x} \bigg[(e^{-r(T-t)}Z_{T}^{\nu})^{\beta} + \int _{t}^{T} (e^{-r(s-t)}Z_{s}^{ \nu})^{\beta} ds\bigg] \end{aligned}$$

over $\nu \in \Theta ^{t}$, where “maximise” or “minimise” depends on the sign of the utility parameter $\kappa$ in (2.6). With a change of measure, $\Lambda$ can be written as

$$\begin{aligned} \Lambda (t,x;\nu )= \widetilde{\mathbb{E}}^{t,x,\nu}\bigg[ e^{\int _{t}^{T} \Gamma ( \pi _{u},\nu )du} + \int _{t}^{T} e^{\int _{t}^{s}\Gamma ( \pi _{u},\nu )du} ds \bigg], \end{aligned}$$

(4.1)

where $\widetilde{\mathbb{E}}^{t,x,\nu}$ denotes the expectation associated with the measure $\widetilde{\mathbb{P}}^{t,x,\nu}$ which is defined via ${d\widetilde{\mathbb{P}}^{t,x,\nu}}/{d\mathbb{P}^{t,x}}\vert _{ \mathcal{H}^{t}_{T}} = \widetilde{Z}_{T}^{\nu}$ and

$$\begin{aligned} \widetilde{Z}_{T}^{\nu}&:= \exp \bigg( -\int _{t}^{T} \beta \hat{\theta}(\pi _{u}) d\widetilde{W}_{u} - \frac{1}{2}\int _{t}^{s} \beta ^{2} \hat{\theta}(\pi _{u})^{2} du \\ & \hphantom{=:\exp \big(:} + \int _{t}^{T}\int _{\mathcal{Z}}\beta \nu (u,z) N(du,dz) \\ & \hphantom{=:\exp \big(:} + \lambda \int _{t}^{T}\int _{\mathcal{Z}} (1-e^{\beta \nu (u,z)}) \hat{f}(\pi _{u-},z)dzdu \bigg), \\ \displaystyle \Gamma (x,\nu )&:= -\beta r-\frac{1}{2}\beta (1-\beta ) \hat{\theta}(x)^{2} \\ & \hphantom{=::} + \lambda \int _{\mathcal{Z}} \big(e^{\beta \nu (u,z)}-1+ \beta (1-e^{ \nu (u,z)})\big)\hat{f}(x,z)dz, \end{aligned}$$

recalling that $\hat{\theta}(x) = \theta (1)x+ \theta (2)(1-x)$ and $\hat{f}(x,z)= f_{1}(z)x+ f_{2}(z)(1-x)$ for $z \in \mathcal{Z}$. In addition, under $\widetilde{\mathbb{P}}^{t,x,\nu}$, the dynamics of the filter process $\pi$ evolve as

$$ d\pi _{s} = \overline{\mu}(\pi _{s}) ds + \overline{\sigma}(\pi _{s})dW^{ \beta}_{s}+\int _{\mathcal{Z}} \big(\xi (\pi _{s-},z)-\pi _{s-}\big) N(ds,dz), \qquad \pi _{t} = x, $$

(4.2)

with

$$ \overline{\mu}(x):= \big(a_{2}-(a_{1}+a_{2})x\big) -\beta \overline{\sigma}(x)\hat{\theta}(x), \qquad \overline{\sigma}(x):= x(1-x)( \theta _{1}-\theta _{2}). $$

By Girsanov’s theorem, $W^{\beta}: = \widetilde{W} + \beta \int _{t}^{\cdot} \hat{\theta}( \pi _{u}) du$ is a standard $(\mathbb{P}^{t,x,\nu},\mathbb{H})$-Brownian motion and $\widetilde{N}^{\beta}(ds,dz):= N(ds,dz)-e^{\beta \nu (s,z)}\lambda \hat{f}(\pi _{s-},z)dzds$ is the ℍ-compensated Poisson random measure under $\widetilde{\mathbb{P}}^{t,x,\nu}$. Depending on the sign of the utility parameter, $\kappa <0$ (resp. $0<\kappa <1$), the value function associated with the auxiliary dual problem is defined as

$$\begin{aligned} \hat{\Lambda}(t,x) : =\sup \ (\text{resp. inf})_{\nu \in \Theta ^{t}} \Lambda (t,x;\nu ),\qquad (t, x) \in \overline{\mathcal{U}}_{T}. \end{aligned}$$

(4.3)

We find that Theorem 2.7 is equivalent to the following result.

Theorem 4.1

Under Condition 2.1, the function $\hat{\Lambda}(t,x)\in C(\overline{\mathcal{U}}_{T})\cap C^{1,2}({ \mathcal{U}}_{T})$ is the unique classical solution of the HJB PIDE given as

$$ 0=\partial _{t} \hat{\Lambda}+ \overline{\mu}(x)\partial _{x} \hat{\Lambda}+ \frac{1}{2}\overline{\sigma}(x)^{2}\partial _{xx} \hat{\Lambda}- d_{0}(x)\hat{\Lambda} + \mathcal{I}_{\beta}( \hat{\Lambda}) +1 \qquad \textit{in } \mathcal{U}_{T}, $$

(4.4)

with

$$\begin{aligned} d_{0}(x) &= \beta r+ \frac{1}{2}\beta (1-\beta )\hat{\theta}(x), \end{aligned}$$

(4.5)

$$\begin{aligned} \mathcal{I}_{\beta}(\hat{\Lambda})(t,x)& = (1-\beta )\lambda \int _{ \mathcal{Z}} \Big( {\hat{\Lambda}(t,x)}^{\frac{\beta}{\beta -1}} { \hat{\Lambda}\big(t,\xi (x,z)\big)}^{\frac{1}{1-\beta}} \\ & \hphantom{=:(1-\beta )\lambda \int _{\mathcal{Z}} \Big(} - {\hat{\Lambda}(t,x)}\Big)\hat{f}(x,z)dz, \end{aligned}$$

(4.6)

with the boundary condition $\hat{\Lambda}(T,x)=1$ for $x\in [0,1]$. Furthermore, we have $\hat{\Lambda}(t,x) = \Lambda (t,x;{\nu}^{*})$, where ${\nu}^{*}\in \Theta ^{t}$ is the Markov policy given by

$$\begin{aligned} {\nu}^{*}_{s}:=\hat{\nu}(s,\pi _{s-},z)= \frac{1}{1-\beta} \ln \frac{\hat{\Lambda}(s,\xi (\pi _{s-},z))}{\hat{\Lambda}(s,\pi _{s-})}, \qquad s\in [t,T]. \end{aligned}$$

(4.7)

The proof is divided into several steps organised into three subsections. A preliminary step consists of showing that the control processes in the auxiliary dual problem (4.3) can be restricted to those $\nu$ in $\Theta ^{t}$ taking values in $[-M,M]$ for a sufficiently large fixed positive constant $M$. We call this set $\Theta ^{t,M}$ and the corresponding constrained auxiliary dual value function $\Lambda ^{M}(t,x)$. We first present lower and upper bounds for $\hat{\Lambda}$. These estimates are used to show that the restriction on $\nu$ can be removed.

Proposition 4.2

There exist positive constants $C_{\ell}$ and $C_{u}$ that only depend on the utility parameter $\kappa$ such that

$$\begin{aligned} C_{\ell} \le \hat{\Lambda}(t, x) \leq C_{u},\qquad (t, x) \in \overline{\mathcal{U}}_{T}. \end{aligned}$$

(4.8)

Proof

Consider the function $h(d): = e^{\beta d}-1+\beta (1-e^{d})$. For $\kappa <0$, note that $0<\beta <1$ and therefore $h$ satisfies $h(d)\le 0$ for $d \in \mathbb{R}$. Using (4.1), we have

$$\begin{aligned} &\widetilde{\mathbb{E}}^{t,x,\nu} \bigg[\exp \bigg( \int _{t}^{T} \Big( -\beta \Big(r+\frac{1}{2}(1-\beta )\theta _{1}^{2}\Big) + \lambda \int _{\mathcal{Z}} h\big(\nu (u,z)\big)\hat{f}(\pi _{u-},z)dz \Big) du \bigg) \\ & \hphantom{\widetilde{\mathbb{E}}^{t,x,\nu} \bigg[} + \int _{t}^{T} \exp \Big( \int _{t}^{s}\Big(-\beta \Big(r+ \frac{1}{2}(1-\beta )\theta _{1}^{2}\Big) \\ & \hphantom{:: \int _{t}^{T} \exp \bigg( \int _{t}^{s}} \qquad \quad \quad + \lambda \int _{\mathcal{Z}} h\big(\nu (u,z)\big) \hat{f}(\pi _{u-},z)dz d u \Big)\bigg) d s\bigg] \\ & \leq \Lambda (t,x;\nu ) \leq 1+T, \qquad (t, x) \in \overline{\mathcal{U}}_{T}, \end{aligned}$$

which implies that

$$\begin{aligned} 0< e^{-\beta (r+\frac{1}{2}(1-\beta )\theta _{1}^{2}) T}(1+T) \le \hat{\Lambda} (t, x) \le 1+T. \end{aligned}$$

For $0<\kappa <1$, note that $\beta <0$ and therefore $h$ satisfies $h(d)\ge 0$ for $d \in \mathbb{R}$. Similar arguments show that

$$\begin{aligned} 1 \le \hat{\Lambda} (t, x) \le e^{-\beta (r+\frac{1}{2}(1-\beta ) \theta _{1}^{2}) T}(1+T). \end{aligned}$$

As the above lower and upper bounds do not depend on the initial state of the filter process, $C_{\ell}$ and $C_{u}$ can be constructed for any given $\kappa <1$ with $\kappa \neq 0$. □

We propose the following auxiliary lemma.

Lemma 4.3

When $\kappa <0$, assume that the constrained auxiliary dual value function $\Lambda ^{M}(t,x)$ is the unique classical solution in $C(\overline{\mathcal{U}}_{T})\cap C^{1,2}({\mathcal{U}}_{T})$ of the HJB equation

$$ 0={\partial _{t}}\Lambda ^{M}(t, x)+\max _{\nu \in [-M,M]} \big( \Gamma (x,\nu ) \Lambda ^{M}(t, x)+\mathcal{L}^{\nu} \Lambda ^{M}(t, x) \big)+1 \qquad \textit{in }\mathcal{U}_{T}, $$

(4.9)

with

$$\begin{aligned} \mathcal{L}^{\nu} g(t, x)&= \overline{\mu}(x)\partial _{x}g(t,x)+ \frac{1}{2} \overline{\sigma}^{2}(x)\partial _{xx}g(t,x) \\ & \hphantom{=:} +\int _{\mathcal{Z}}\Big(g\big(t,\xi (x, z)\big)-g(t, x)\Big)\lambda e^{ \beta \nu (z)}\hat{f}(x,z) d z, \end{aligned}$$

(4.10)

subject to the boundary condition $\Lambda ^{M}(T,x) = 1$ for $x\in [0,1]$. When $0<\kappa <1$, assume instead the same, but with max in (4.9) replaced by min. Let $\Lambda ^{M}$ be the constrained auxiliary dual value function with

$$\begin{aligned} M > \frac{\ln (C_{u}/C_{\ell})}{1-\beta}. \end{aligned}$$

(4.11)

Then $\Lambda ^{M}(t,x) = \hat{\Lambda}(t,x)$, where $\hat{\Lambda}$ is the unconstrained value function in (4.3).

Proof

We provide a proof for the case where $\kappa <0$, but the case $0<\kappa <1$ follows the same logic. The maximum selector on the right-hand side of (4.9) induces a Markov policy $\hat{\nu}^{M}$, defined for $(s,x)\in \overline{\mathcal{U}}_{T}$ and indexed by $\mathcal{Z}$, as

$$\begin{aligned} \hat{\nu}^{M}(s,x,z) &:= \operatorname*{{\mathrm{arg\,max}}}_{\nu \in [-M,M]} \big(\Gamma (x, \nu ) \Lambda ^{M}(s, x)+\mathcal{L}^{\nu} \Lambda ^{M}(s, x) \big) \\ & \hphantom{:} = \textstyle\begin{cases} \frac{1}{1-\beta} \ln \frac{\Lambda ^{M}(s,\xi (x,z))}{\Lambda ^{M}(s,x)} , &\quad \text{if }\frac{1}{1-\beta} |\ln \frac{\Lambda ^{M}(s,\xi (x,z))}{\Lambda ^{M}(s,x)} | \le M, \\ M \mathrm{sgn} \ln \frac{\Lambda ^{M}(s,\xi (x,z))}{\Lambda ^{M}(s,x)} , &\quad \text{otherwise.} \end{cases}\displaystyle \end{aligned}$$

Using (4.8) (note that the estimates also hold for the constrained auxiliary dual value function $\Lambda ^{M}$), it follows that $\frac{1}{1-\beta}|\ln \frac{\Lambda ^{M}(s,\xi (x,z))}{\Lambda ^{M}(s,x)}| < M$ for $M$ satisfying (4.11) so that the constraints $\nu \in [-M,M]$ in (4.9) can be removed. For fixed $(t,x)\in \mathcal{U}_{T}$ and $(\pi _{s})_{s\ge t}$ defined as in (4.2), we have for $s\in [t,T]$ that

$$\begin{aligned} \big(\partial _{t}+\mathcal{L}^{\nu _{s}}+\Gamma (\pi _{s},\nu _{s}) \big) {\Lambda}^{M}(s,\pi _{s}) \le -1, \qquad \nu \in \Theta ^{t}. \end{aligned}$$

(4.12)

This inequality and the Feynman–Kac formula imply that for $\nu \in \Theta ^{t}$,

$$\begin{aligned} {\Lambda}^{M}(t,x) &= \widetilde{\mathbb{E}}^{t,x,\nu}\bigg[ e^{\int _{t}^{T} \Gamma ( \pi _{u},\nu _{u})du}{\Lambda}^{M}(T,\pi _{T}) \\ & \hphantom{=:\widetilde{\mathbb{E}}^{t,x,\nu}\bigg[} -\int _{t}^{T} e^{\int _{t}^{s}\Gamma ( \pi _{u},\nu _{u})du} \big( \partial _{t}+\mathcal{L}^{\nu _{s}}+\Gamma (\pi _{s},\nu _{s})\big){ \Lambda}^{M}(s,\pi _{s}) ds \bigg] \\ &\ge \Lambda (t,x;\nu ). \end{aligned}$$

(4.13)

Taking the supremum over $\nu \in \Theta ^{t}$, we have $\Lambda ^{M} \ge \hat{\Lambda}$ and therefore $\Lambda ^{M} = \hat{\Lambda}$ by definition. Given that ${\Lambda}^{M}$ is continuous and bounded, the Markov policy $\hat{\nu}$ defined in (4.7) is bounded, continuous and locally Lipschitz in $x$. Thus the Markov control process $\nu ^{*}$ in (4.7) belongs to $\Theta ^{t,M}\subseteq \Theta ^{t}$. From the definition of $\nu ^{*}$, the inequalities in (4.12) and (4.13) become equalities for $\nu ={\nu}^{*}$. Hence $\Lambda ^{M}(t,x) = \hat{\Lambda}(t,x) = \Lambda (t,x;{\nu}^{*})$. Finally, substituting the Markov policy $\nu ^{*}$ into the HJB equation (4.9), we obtain that $\Lambda ^{M}$ satisfies (4.4). □

In the rest of this section, we prove Theorem 4.1. It is convenient to restrict the control set to $\Theta ^{t,M}$ with a sufficiently large $M$ for now and remove this restriction later via Lemma 4.3. To help readers better understand the main idea of the proof, we provide an overview before discussing it in detail.

Step 1: $\Lambda ^{M}(t,x)$ is Lipschitz in $t$ and $x$ on the state space $\overline{\mathcal{U}}_{T}$. The analytical challenges come from the Lévy-type jumps of the filter process in (4.2), because the compensator of the jump measure $N(dt,dz)$ depends on the filter itself. To overcome this difficulty, we need to introduce an auxiliary process through the Radon–Nikodým derivatives and give the necessary estimates under Condition 2.1. The results are summarised in Sect. 4.2.

Step 2: $\Lambda ^{M}$ is a viscosity solution of the HJB PIDE (4.9). We adopt a classical definition (Definition 4.8) of a viscosity solution and show that ${\Lambda}^{M}$ is a viscosity solution of (4.9) in Theorem 4.9 in Sect. 4.3.

Step 3: From PIDE to PDE. Let $M$ be sufficiently large; we change the notation and rewrite the HJB PIDE (4.9) as a parabolic PDE given by

$$ \bigg(\partial _{t} + \overline{\mu}\partial _{x}+ \frac{1}{2} \overline{\sigma}^{2}\partial _{xx}-d_{0}\bigg)g+ \mathcal{I}_{\beta}({ \Lambda}^{M})+1= 0\qquad \text{in } {\mathcal{U}}_{T}, $$

(4.14)

where the functions $d_{0}(\,\cdot \,)$ and $\mathcal{I}_{\beta}(\,\cdot \,)$ are defined in (4.5) and (4.6).

Step 4: $\Lambda ^{M}$ is a viscosity solution of the PDE (4.14). We consider a viscosity solution $g$ of the PDE (4.14), which is interpreted as an equation for an “unknown” $g$, with the last term $\mathcal{I}_{\beta}({\Lambda}^{M})$ prespecified with ${\Lambda}^{M}$ characterised in Step 2. We demonstrate that ${\Lambda}^{M}$ also solves the PDE (4.14) in the viscosity sense. We need to show the equivalence of two definitions of viscosity solutions to the HJB PIDE (4.9) (i.e., Definitions 4.8 and 4.10; the first is the classical definition while the second has no replacement of the solution with a test function in the nonlocal integro-differential term). The results are presented in Proposition 4.11 and Corollary 4.12.

Step 5: Uniqueness of the viscosity solution to the PDE (4.14). It is clear that $g = {\Lambda}^{M}$ is a viscosity solution for both the PDE (4.14) and the PIDE (4.9), as the two equations are essentially the same. However, if a function $g$ solves the PDE (4.14), this does not mean that it also solves the PIDE (4.9), because the term $\mathcal{I}_{\beta}({\Lambda}^{M})$ in the PDE (4.14) depends on ${\Lambda}^{M}$, regardless of the choice of $g$. Thus we must show that the PDE (4.14) admits a unique viscosity solution. This requires applying a comparison result (see Amadori [1, Theorem 2]) for viscosity solutions to HJB equations with degenerate coefficients on the boundary.

Step 6: Existence of a classical solution to the PDE (4.14). The PDE (4.14) is parabolic when $\mathcal{I}_{\beta}({\Lambda}^{M})$ is considered an autonomous term. We refer to the literature on degenerate parabolic PDEs (see e.g. Fleming and Rishel [22, Appendix E] and Bayraktar et al. [7, Theorem 2.8]) to show the existence of a classical solution to the PDE (4.14). The result is presented in Theorem 4.16.

The results of Steps 3–6 are summarised in Sect. 4.4. Finally, we conclude that ${\Lambda}^{M}$ is a classical solution in $C(\overline{\mathcal{U}}_{T})\cap C^{1,2} (\mathcal{U}_{T})$ of (4.9), and with Lemma 4.3, the proof of Theorems 4.1 and 2.7 is complete.

4.2 Lipschitz-continuity of the auxiliary constrained dual value function ${\Lambda}^{M}$

We first show the Lipschitz-continuity of $\Lambda ^{M}(t,x)$ with respect to $x$, for each fixed $t\in [0,T]$. We initiate this analysis by establishing the Lipschitz property at $t=0$ using a specific Lipschitz constant. As this constant is independent of the choice of $t$, we extend this analysis to achieve uniform Lipschitz-continuity of $\Lambda ^{M}(t,x)$ with respect to $x$ for all $t\in [0,T]$. Unlike Frey et al. [24, Sect. 4] where the authors reformulate the dynamics of the filter process into an exogenous Poisson random measure while maintaining the law of the original filter process, we now establish other necessary estimates of the value function by introducing an auxiliary process via the Radon–Nikodým derivatives. This method effectively enables us to work under general alternative data signals satisfying Condition 2.1.

The path space of $(\pi _{t})_{t\in [0,T]}$ is denoted by $D_{T}:=D([0,T];[0,1])$, and $\mathcal{D}_{T}$ is the usual $\sigma$-field of $D_{T}$. Moreover, $P_{1}$ is the probability distribution on $(D_{T},\mathcal{D}_{T})$ induced by $(\pi _{t})_{t\in [0,T]}$ under $\widetilde{\mathbb{P}}^{0,x,\nu}$ for a given control process $\nu \in \Theta ^{0,M}$. Standard arguments show that with $\mathcal{L}^{\nu}$ defined in (4.10), the process

$$\begin{aligned} K_{g}(t): = g(\pi _{t}) - g(x) - \int _{0}^{t}\mathcal{L}^{\nu _{s}} g( \pi _{s}) ds, \qquad t \in [0,T], \end{aligned}$$

(4.15)

is a martingale under $P_{1}$ for each point $x\in [0,1]$ and each function $g\in C^{2}([0,1])$, and $P_{1}$ is the unique probability distribution with this property.

We introduce an auxiliary process $Y$ under a reference probability measure $\overline{\mathbb{P}}$ that satisfies

$$\begin{aligned} dY_{t} = \overline{\mu}(Y_{t})dt+\overline{\sigma}(Y_{t}) dW_{t}^{ \beta} + \int _{\mathcal{Z}} \big(\xi (Y_{t-},z)-Y_{t-}\big) N_{2}(dt,dz), \end{aligned}$$

(4.16)

where the functions $\overline{\mu}$ and $\overline{\sigma}$ are defined in (4.2), $W^{\beta}$ is a standard Brownian motion and $N_{2}$ is a Poisson random measure with intensity measure given by $\lambda f_{1}(z)dzdt$ under $\overline{\mathbb{P}}$. Note that $Y$ is a jump-diffusion process with an exogenous Poisson random measure. The process $Y$ with initial condition $x$ is denoted by $Y^{x}$. To ensure that (4.16) has a unique strong solution, the coefficients $\overline{\mu}$, $\overline{\sigma}$ and $\xi$ must satisfy certain Lipschitz and growth conditions; see Ceci and Colaneri [11, Appendix A]. We verify these conditions in the following result; its proof is presented in Appendix C.

Lemma 4.4

Under Condition 2.1, there exist a positive constant $C$ and a function $\rho :\mathcal{Z} \rightarrow \mathbb{R}_{++}$ with $\int _{\mathcal{Z}}\rho (z)^{2} f_{1}(z)dz <\infty$ such that for all $x$ and $y \in [0,1]$,

$$\begin{aligned} |\overline{\mu}(x)-\overline{\mu}(y)|+|\overline{\sigma}(x)- \overline{\sigma}(y)|& \leq C |x-y|, \\ |\overline{\mu}(x)|+|\overline{\sigma}(x)|& \leq C(1+|x|), \end{aligned}$$

(4.17)

$$\begin{aligned} |\xi (x, z)-\xi (y, z)| &\leq \rho (z)|x-y|, \\ |\xi (x, z)| &\leq (1+|x|). \end{aligned}$$

(4.18)

The probability distribution on $(D_{T},\mathcal{D}_{T})$ induced by $(Y_{t})_{t\in [0,T]}$ under $\overline{\mathbb{P}}$ is denoted by $P_{2}$. We show that $P_{1}$ is absolutely continuous with respect to $P_{2}$ and that the corresponding Radon–Nikodým derivative reads

$$\begin{aligned} \Xi _{T}(Y) :=& \frac{dP_{1}}{dP_{2}}(Y) \\ \hphantom{} =&\prod _{i=1}^{n(T)} \frac{e^{\beta \nu (\tau _{i},z_{i})}\hat{f}(Y_{\tau _{i}},z_{i})}{f_{1}(z_{i})} \\ & \hphantom{} \times \exp \bigg(\!\!- \!\sum _{i=0}^{n(T)}\int _{\tau _{i}}^{\tau _{i+1} \wedge T}\!\! \lambda \big(Y_{s}\mathbf{E}_{1}[e^{\beta \nu}]+(1-Y_{s}) \mathbf{E}_{2}[e^{\beta \nu}]-1 \big)ds \bigg), \end{aligned}$$

(4.19)

where $\mathbf{E}_{j}$ indicates the expectation over $z\in \mathcal{Z}$ under the density function $f_{j}$ with $j=1,2$, $(z_{i})$ is the sequence of jump sizes, and $(\tau _{i})$ and $n(T)$ are the sequence of jump times and the total number of jumps up to $T$, respectively, which are given by

$$\begin{aligned} \tau _{0} = 0, \quad \tau _{i+1}=\inf \{s>\tau _{i}: Y_{s} \neq Y_{s-} \}, \qquad n(T) = \max \{i:\tau _{i}\le T\}. \end{aligned}$$

Note that for $t>0$, when $T$ in (4.19) is replaced by $t$, we have

$$\begin{aligned} \Xi _{t}(Y) - 1 = \int _{0}^{t}\int _{\mathcal{Z}} \Xi _{s-}(Y)\bigg( \frac{e^{\beta \nu (s,z)}\hat{f}(Y_{s-},z)}{f_{1}(z)}-1\bigg) \widetilde{N}_{2}(ds,dz), \end{aligned}$$

where $\widetilde{N}_{2}(ds,dz)= N_{2}(ds,dz)-\lambda f_{1}(z)dzdt$ is the compensated random measure under $\overline{\mathbb{P}}$. The operator $\widetilde{\mathcal{L}}^{\nu}$ associated with $Y$ is given by

$$ \widetilde{\mathcal{L}}^{\nu} g(x):= \overline{\mu}(x) g'(x)+ \frac{1}{2} \overline{\sigma}^{2}(x) g''(x) +\int _{\mathcal{Z}}\Big(g \big(\xi (x, z)\big)-g(x)\Big)\lambda f_{1}(z) d z. $$

It follows that the process $\widetilde{K}_{g}(t): = g(Y_{t}) - g(x) - \int _{0}^{t} \widetilde{\mathcal{L}}^{\nu} g(Y_{s}) ds$, $t \in [0,T]$, is a martingale under $P_{2}$ for each point $x\in [0,1]$ and each function $g(x)\in C^{2}([0,1])$, and $P_{2}$ is the unique probability distribution with this property. Replacing $\pi$ by $Y$ in $K_{g}(t)$ defined in (4.15) and applying integration by parts, we have

$$\begin{aligned} &\Xi _{t} K_{g}(t) \\ &= \int _{0}^{t} K_{g}(s-)d\Xi _{s} + \int _{0}^{t}\Xi _{s-}d \widetilde{K}_{g}(s)+ \int _{0}^{t}\Xi _{s-}\big(dK_{g}(s)-d \widetilde{K}_{g}(s)\big) \\ & \hphantom{=:} +\sum _{0 < s \le t}(\Xi _{s} - \Xi _{s-})\big(K_{g}(s) - K_{g}(s-) \big) \\ &=\int _{0}^{t} K_{g}(s-)d\Xi _{s} + \int _{0}^{t}\Xi _{s-}d \widetilde{K}_{g}(s) \\ & \hphantom{=:} +\int _{0}^{t} \int _{\mathcal{Z}} \Xi _{s-}\bigg( \frac{e^{\beta \nu (s,z)}\hat{f}(Y_{s-},z)}{f_{1}(z)} -1 \bigg) \Big(g \big(\xi (Y_{s-},z)\big)-g(Y_{s-})\Big)\widetilde{N}_{2}(ds,dz). \end{aligned}$$

As both $\Xi$ and $\widetilde{K}_{g}$ are martingales under $P_{2}$, it follows that $\Xi K_{g}$ is a martingale under $P_{2}$. Now for any $A \in \mathcal{D}_{T}$, we set $\widetilde{P}_{1}[A] = \int _{A} \Xi _{T}(Y) dP_{2}$. We can clearly see that $K_{g}$ is a martingale under $\widetilde{P}_{1}$. We conclude that $\widetilde{P}_{1} = P_{1}$ by the uniqueness of $P_{1}$.

Having established the preparatory results above, we can now provide the main result of this subsection. For the sake of precision, the solutions to (4.2) and (4.16) starting from $x$ are denoted by $\pi ^{x}$ and $Y^{x}$, respectively.

Proposition 4.5

The value function ${\Lambda}^{M}(t,x)$ is Lipschitz-continuous in $x$.

Proof

For $x,y\in [0,1]$, we have

$$\begin{aligned} & \vert {\Lambda}^{M}(0,x)-\Lambda ^{M}(0,y) \vert \\ &\le \sup _{\nu \in \Theta ^{0,M}} \big\vert \widetilde{\mathbb{E}}^{0,x, \nu}\big[ e^{\int _{0}^{T}\Gamma ( \pi _{u}^{x},\nu )du }\big] - \widetilde{\mathbb{E}}^{0,y,\nu}\big[e^{\int _{0}^{T}\Gamma ( \pi _{u}^{y}, \nu )du } \big] \big\vert \\ & \hphantom{=:} + \bigg| \widetilde{\mathbb{E}}^{0,x,\nu}\bigg[\int _{0}^{T} e^{\int _{0}^{t} \Gamma ( \pi _{u}^{x},\nu )du} dt \bigg] - \widetilde{\mathbb{E}}^{0,y, \nu}\bigg[\int _{0}^{T} e^{\int _{0}^{t}\Gamma ( \pi _{u}^{y},\nu )du } dt \bigg]\bigg| \\ &\le \sup _{\nu \in \Theta ^{0,M}} \overline{\mathbb{E}} \bigg[ {A}_{T}+ {B}_{T} + \int _{0}^{T} {A}_{t} dt + \int _{0}^{T} {B}_{t} dt \bigg], \end{aligned}$$

where

$$\begin{aligned} {A}_{t} &: = \big\vert e^{\int _{0}^{t}\Gamma ( Y_{u}^{x},\nu )du} \big(\Xi _{t}(Y^{x})- \Xi _{t}(Y^{y})\big) \big\vert , \\ {B}_{t}&:= \Xi _{t}(Y^{y}) \big\vert e^{\int _{0}^{t}\Gamma ( Y_{u}^{x}, \nu )du} - e^{\int _{0}^{t}\Gamma ( Y_{u}^{y},\nu )du} \big\vert . \end{aligned}$$

We first focus on the term ${A}$. For ease of notation, we write

$$\begin{aligned} \varphi (x): = \exp \bigg(- \int _{0}^{T} \lambda \big(Y^{x}_{s} \mathbf{E}_{1}[e^{\beta \nu}]+(1-Y^{x}_{s})\mathbf{E}_{2}[e^{\beta \nu}]\big)ds \bigg). \end{aligned}$$

For $\nu \in [-M,M]$, as $\Gamma$ is bounded, we have $\overline{\mathbb{E}}[ {A}_{T}] \le C \overline{\mathbb{E}}[\vert \Xi _{T}(Y^{x})- \Xi _{T}(Y^{y})\vert ]$ for a positive constant $C$. Using the inequality

$$\begin{aligned} \bigg|\prod _{i=1}^{n} a_{i}-\prod _{i=1}^{n} b_{i}\bigg| \leq n\Big( \max _{i = 1, \dots , n} \max \{a_{i}, b_{i}\}\Big)^{n-1} \max _{i = 1, \dots , n}|a_{i}-b_{i}| \end{aligned}$$

for any two positive sequences $(a_{i})_{i=1, \dots , n}$ and $(b_{i})_{i=1, \dots , n}$, we obtain

with the constant $C_{1} = 2\max \{\lambda T,1+b_{\max}\}e^{\beta M}$. In the last inequality, we use the fact that $|\exp (-a)-\exp (-b)|\le |a-b|$ for any bounded $a$ and $b$. We find that the term in the last line is finite because $Y_{t}$ is always in the interval $[0,1]$. From the Cauchy–Schwarz inequality, we further obtain

Recall that $n(T)$ is the total number of jumps of a Poisson process with constant intensity rate $\lambda$ before $T$. It follows that for $C_{2}= (\lambda Te^{\beta M}(1+b_{\max})+1)$,

It remains to show that there exists a constant $C$ such that

$$\begin{aligned} \overline{\mathbb{E}} \Big[\sup _{0\le s \le T}\vert Y^{x}_{s} - Y^{y}_{s} \vert ^{2} \Big] \le C |x-y|^{2}. \end{aligned}$$

(4.20)

Note that

$$\begin{aligned} d(Y^{x}_{t} - Y^{y}_{t})&= \big(\overline{\mu}(Y^{x}_{t}) - \overline{\mu}(Y^{y}_{t}) \big) dt+ \big( \overline{\sigma}(Y^{x}_{t})- \overline{\sigma}(Y^{y}_{t})\big)dW_{t}^{\beta} \\ & \hphantom{=:} + \int _{\mathcal{Z}} \big( \xi (Y_{t-}^{x},z)-\xi (Y_{t-}^{y},z) - Y_{t-}^{x}+Y_{t-}^{y} \big)N_{2}(dt,dz). \end{aligned}$$

Applying Itô’s lemma to the function $|Y^{x}_{t} - Y^{y}_{t}|^{2}$ and using Kunita [31, Corollary 2.12], we obtain

$$\begin{aligned} &\overline{\mathbb{E}} \Big[\sup _{0\le s \le T}\vert Y^{x}_{s} - Y^{y}_{s} \vert ^{2} \Big] \\ &\le C\bigg( |x-y|^{2} + \overline{\mathbb{E}} \bigg[ \int _{0}^{T} | \overline{\mu}(Y^{x}_{t}) - \overline{\mu}(Y^{y}_{t})|^{2} dt \bigg] + \overline{\mathbb{E}} \bigg[ \int _{0}^{T} | \overline{\sigma}(Y^{x}_{t}) - \overline{\sigma}(Y^{y}_{t})|^{2} dt \bigg] \\ & \hphantom{= C\bigg( } + \overline{\mathbb{E}} \bigg[ \int _{0}^{T} \int _{\mathcal{Z}} \lambda | \xi (Y^{x}_{t},z) - \xi (Y^{y}_{t},z)|^{2} f_{1}(z) dz dt \bigg]\bigg). \end{aligned}$$

By the Lipschitz properties of $\overline{\mu}$, $\overline{\sigma}$ and $\xi$ given in Lemma 4.4, we obtain

$$\begin{aligned} \overline{\mathbb{E}} \Big[\sup _{0\le s \le T} \vert Y^{x}_{s} - Y^{y}_{s} \vert ^{2} \Big] \leq C\bigg(|x-y|^{2}+ \int _{0}^{T} \overline{\mathbb{E}} \Big[\sup _{0 \leq s \leq \tau}|Y_{s}^{x} -Y_{s}^{y} |^{2}\Big] d \tau \bigg), \end{aligned}$$

for a constant $C$. Thus by Gronwall’s inequality, we obtain (4.20).

We now consider the term $B$. From the Cauchy–Schwarz inequality, we obtain

$$\begin{aligned} \overline{\mathbb{E}}[ {B}_{T}] &\le \big(\overline{\mathbb{E}}[\Xi _{T}(Y^{x})^{2}] \overline{\mathbb{E}}\big[\big\vert e^{\int _{0}^{T}\Gamma ( Y_{u}^{x}, \nu )du} - e^{\int _{0}^{T}\Gamma ( Y_{u}^{y},\nu )du}\big\vert ^{2} \big] \big)^{\frac{1}{2}} \\ &\le C\overline{\mathbb{E}} [\Xi _{T}(Y^{x})^{2}]^{\frac{1}{2}} \overline{\mathbb{E}} \Big[ \sup _{0\le s\le T}| \Gamma ( Y_{s}^{x}, \nu ) - \Gamma ( Y_{s}^{y},\nu )|^{2} \Big]^{\frac{1}{2}} \\ & \le C\overline{\mathbb{E}}[\Xi _{T}(Y^{x})^{2}]^{\frac{1}{2}} \overline{\mathbb{E}}\Big[ \sup _{0\le s\le T}|Y^{x}_{s} - Y^{y}_{s} |^{2} \Big]^{\frac{1}{2}} \end{aligned}$$

for a constant $C$; in the second inequality, we use $|\exp (-a)-\exp (-b)|\le |a-b|$, and in the last inequality, we use the fact that $\Gamma (x,\nu )$ is Lipschitz-continuous in the state variable $x$ when $\nu \in [-M,M]$. Recalling (4.20), it remains to show that

$$\begin{aligned} \overline{\mathbb{E}}[\Xi _{T}(Y^{x})^{2}]& \le e^{2\lambda T} \overline{\mathbb{E}}\big[ \big(e^{2\beta M}(b_{\max}+1)^{2}\big)^{n(T)} \big] \\ &\le \exp \Big( \lambda T\big(e^{2\beta M}(b_{\max}+1)^{2}+1\big) \Big). \end{aligned}$$

The above analysis can be extended to the other two terms $\int _{0}^{T} {A}_{t} dt$ and $\int _{0}^{T} {B}_{t} dt$. Due to the arbitrariness of $\nu \in \Theta ^{0,M}$, the proof is complete. □

Next, we show the continuity of $\Lambda ^{M}(t,x)$ in the time variable $t$. The following estimates of the filter process $\pi$ are used; their proof is reported in Appendix C.

Proposition 4.6

For an arbitrary $\nu \in \Theta ^{t,M}$, $(\pi _{s}^{t,x,\nu})_{s\in [t,T]}$ is the solution of (4.2) starting from $(t,x)\in \overline{\mathcal{U}}_{T}$. For any $k\in [0,2]$, there exists a positive constant $C$ such that for all $0\le t \le s \le T$,

$$\begin{aligned} &\widetilde{\mathbb{E}}^{t,x,\nu}\Big[ \sup _{t \le u \le s}(1+|\pi _{u}^{t,x, \nu}|^{k}) \Big] \le C(1+|x|^{k}), \end{aligned}$$

(4.21)

$$\begin{aligned} &\widetilde{\mathbb{E}}^{t,x,\nu}\Big[ \sup _{t \le u \le s}|\pi _{u}^{t,x, \nu} - x|^{k} \Big] \le C(1+|x|^{k})(s-t)^{\frac{k}{2}}. \end{aligned}$$

(4.22)

Proposition 4.7

There exists a positive constant $C$ such that for all $t$, $s\in [0,T]$ and $x$, $y\in [0,1]$,

$$\begin{aligned} |\Lambda ^{M}(t,x) - \Lambda ^{M}(s,y)|\le C(|s-t|^{\frac{1}{2}} + |x-y|). \end{aligned}$$

Proof

Let $0\le t< s \le T$; by applying Theorem 3.1, we obtain

$$\begin{aligned} & |\Lambda ^{M}(t,x) - \Lambda ^{M}(s,x)| \\ &\le \sup _{\nu \in \Theta ^{t,M}} \widetilde{\mathbb{E}}^{t,x,\nu} \bigg[\bigg\vert e^{\int _{t}^{s}\Gamma (\pi _{u}^{t,x,\nu},\nu )du} \Lambda ^{M}(s,\pi ^{t,x,\nu}_{s}) + \int _{t}^{s} e^{\int _{t}^{\tau} \Gamma (\pi _{u}^{t,x,\nu},\nu )du} d\tau - \Lambda ^{M}(s,x) \bigg\vert \bigg] \\ &\le \sup _{\nu \in \Theta ^{t,M}} \widetilde{\mathbb{E}}^{t,x,\nu} \bigg[ e^{\int _{t}^{s}\Gamma (\pi _{u}^{t,x,\nu},\nu )du}|\Lambda ^{M}(s, \pi ^{t,x,\nu}_{s}) - \Lambda ^{M}(s,x) | \\ & \hphantom{=: \sup _{\nu \in \Theta ^{t,M}} \widetilde{\mathbb{E}}^{t,x,\nu}\bigg[} + \Lambda ^{M}(s,x) | e^{\int _{t}^{s}\Gamma (\pi _{u}^{t,x,\nu},\nu )du} - 1 | + \int _{t}^{s} e^{\int _{t}^{\tau}\Gamma (\pi _{u}^{t,x,\nu}, \nu )du} d\tau \bigg] \\ &=\text{(I)} + \text{(II)} + \text{(III)}. \end{aligned}$$

According to the boundedness of $\Gamma$ when $\nu \in [-M,M]$, the Lipschitz-continuity of $\Lambda ^{M}$ in $x$ due to Proposition 4.5, and (4.22), there exists a constant $C$ such that

$$\begin{aligned} \text{(I)} &\le C \sup _{\nu \in \Theta ^{t,M}} \widetilde{\mathbb{E}}^{t,x,\nu} [ |\pi _{s}^{t,x,\nu} - x| ] \le C(1+|x|)(s-t)^{ \frac{1}{2}}, \\ \text{(II)}& \le \Lambda ^{M}(s,x) | e^{C(s-t)}-1| \le C|s-t|, \\ \text{(III)}& \le C(s-t). \end{aligned}$$

Finally, we obtain $|\Lambda ^{M}(t,x) - \Lambda ^{M}(s,x)| \le (C+T^{\frac{1}{2}})|s-t|^{ \frac{1}{2}}$, and with Proposition 4.5, the proof is complete. □

4.3 The function $\Lambda ^{M}$ is a viscosity solution of the HJB PIDE (4.9)

We adapt the notion of viscosity solution introduced by Barles and Imbert [4, Definition 1] to the case of integro-differential equations; it is based on a test function and interprets (4.9) in a weaker sense. We focus on the case where $\kappa <0$, and we can follow a similar logic for $0<\kappa <1$.

Definition 4.8

A bounded function $g \in C(\overline{\mathcal{U}}_{T})$ is a viscosity supersolution (subsolution) of (4.9) if for any bounded test function $\psi \in C^{1,2}(\overline{\mathcal{U}}_{T})$ such that $(t_{0},x_{0})\in {\mathcal{U}}_{T}$ is a global minimum (maximum) point of $g-\psi$ with $g(t_{0},x_{0})=\psi (t_{0},x_{0})$, we have

$$\begin{aligned} \bigg(-{\partial _{t}}-\overline{\mu}(x_{0})\partial _{x}-\frac{1}{2} \overline{\sigma}(x_{0})^{2}\partial _{xx}\bigg)\psi (t_{0},x_{0}) - \max _{\nu \in [-M,M]} H_{\psi}(t_{0},x_{0},\nu ) \geq 1 \end{aligned}$$

(resp. $\leq 1$), where

$$\begin{aligned} H_{\psi}(t,x,\nu ): = \Gamma (x,\nu ) \psi (t, x)+\int _{\mathcal{Z}} \Big(\psi \big(t,\xi (x, z)\big)-\psi (t,x)\Big)\lambda e^{\beta \nu} \hat{f}(x,z) d z. \end{aligned}$$

A bounded function $g$ is a viscosity solution of (4.9) if it is both a viscosity subsolution and a viscosity supersolution of (4.9).

We obtain the following result.

Theorem 4.9

The function ${\Lambda}^{M}$ is a bounded Lipschitz-continuous viscosity solution of the HJB PIDE (4.9) in ${\mathcal{U}}_{T}$, subject to the terminal condition ${\Lambda}^{M}(T,x)=1$ for $x\in [0,1]$.

Proof

Step 1: Viscosity supersolution. Take $(t_{0},x_{0})\in {\mathcal{U}}_{T}$ and $\psi \in C^{1,2}(\overline{\mathcal{U}}_{T})$ with $0 = (\Lambda ^{M}-\psi )(t_{0},x_{0}) = \min _{(t,x)\in \mathcal{U}_{T}}( \Lambda ^{M}(t,x)-\psi (t,x))$ and therefore $\Lambda ^{M} \ge \psi$ on ${\mathcal{U}}_{T}$. Let $(t_{k},x_{k})$ be a sequence in ${\mathcal{U}}_{T}$ with $\lim _{k\rightarrow \infty} (t_{k},x_{k}) = (t_{0},x_{0})$ and define the sequence $( \varphi _{k} )$ as $\varphi _{k}: = \Lambda ^{M}(t_{k},x_{k}) - \psi (t_{k},x_{k})$. By the continuity of $\Lambda ^{M}$ (Proposition 4.7), we have $\lim _{k\rightarrow \infty} \Lambda ^{M}(t_{k},x_{k}) = \Lambda ^{M}(t_{0},x_{0})$; so $\lim _{k\rightarrow \infty} \varphi _{k} =0$.

Consider a given control ${\nu} \in \Theta ^{t,M}$, denote the filter process (the solution of (4.2)) with the initial state $\pi _{t_{k}}^{k} = x_{k}$ by $\pi ^{k}$ and define the stopping time $\tau _{k}$ as

$$\begin{aligned} \tau _{k}: = \inf \{s>t_{k}: (s, \pi ^{k}_{s})\notin [t_{k},t_{k}+ \beta _{k}) \times (x_{k}-\epsilon _{0}, x_{k}+\epsilon _{0} )\cap \mathcal{U}_{T} \} \end{aligned}$$

(4.23)

for a given constant $\epsilon _{0}\in (0,1/2)$ and ; then we have $\lim _{k \rightarrow \infty} \tau _{k} = 0$. Using Theorem 3.1, we obtain

$$\begin{aligned} \Lambda ^{M}(t_{k},x_{k}) &\ge \widetilde{\mathbb{E}}^{t_{k},x_{k}, \nu} \bigg[ e^{\int _{t_{k}}^{\tau _{k}}\Gamma (\pi _{u}^{k},\nu _{u})du} \psi (\tau _{k},\pi ^{k}_{\tau _{k}}) +\int _{t_{k}}^{\tau _{k}} e^{ \int _{t}^{s}\Gamma (\pi _{u}^{k},\nu _{u})du} ds \bigg]; \end{aligned}$$

thus by the definition of $\varphi _{k}$,

$$\begin{aligned} \varphi _{k}\ge \widetilde{\mathbb{E}}^{t_{k},x_{k},\nu} \bigg[ \zeta ^{k}(\tau _{k})\psi (\tau _{k},\pi ^{k}_{\tau _{k}}) - \psi (t_{k},x_{k}) +\int _{t_{k}}^{\tau _{k}} \zeta ^{k}(s) ds \bigg], \end{aligned}$$

(4.24)

where $\zeta ^{k}(s):= \exp (\int _{t_{k}}^{s}\Gamma (\pi _{u}^{k},\nu _{u})du)$. Applying Itô’s lemma to $\zeta ^{k}\psi$, we have

$$\begin{aligned} &\zeta ^{k}(\tau _{k})\psi (\tau _{k},\pi ^{k}_{\tau _{k}}) \\ & = \psi (t_{k},x_{k}) + \int _{t_{k}}^{\tau _{k}}\Big( \Gamma (\pi _{u}^{k}, \nu _{u})\zeta ^{k}(u) \psi (u,\pi ^{k}_{u})+ \zeta ^{k}(u)\big( ( \mathcal{L}^{\nu _{u}}+\partial _{t})\psi (u,\pi ^{k}_{u}) \big)\Big)du \\ & \hphantom{=:} +\int _{t_{k}}^{\tau _{k}} \zeta ^{k}(u)\overline{\sigma}(\pi _{u}^{k}) \partial _{x}\psi (u,\pi ^{k}_{u}) dW^{\beta}_{u} \\ & \hphantom{=:} +\int _{t_{k}}^{\tau _{k}} \zeta ^{k}(u) \int _{\mathcal{Z}} \Big( \psi \big(u,\xi (\pi _{u-}^{k},z)\big) - \psi (u, \pi _{u-}^{k}) \Big)\widetilde{N}^{\beta}(du,dz). \end{aligned}$$

By assumption, the last two terms are martingales under $\widetilde{\mathbb{P}}^{t_{k},x_{k},\nu}$. Thus

$$\begin{aligned} & \widetilde{\mathbb{E}}^{t_{k},x_{k},\nu} [ \zeta ^{k}(\tau _{k}) \psi (\tau _{k},\pi ^{k}_{\tau _{k}}) ] \\ &= \psi (t_{k},x_{k})+ \widetilde{\mathbb{E}}^{t_{k},x_{k},\nu} \bigg[\int _{t_{k}}^{\tau _{k}} \Big( \Gamma (\pi _{u}^{k},\nu _{u}) \zeta ^{k}(u) \psi (u,\pi ^{k}_{u}) \\ & \hphantom{=:+ \psi (t_{k},x_{k}) \widetilde{\mathbb{E}}^{t_{k},x_{k},\nu} \bigg[\int _{t_{k}}^{\tau _{k}} \Big(} + \zeta ^{k}(u)\big((\mathcal{L}^{\nu _{u}}+\partial _{t})\psi (u, \pi ^{k}_{u}) \big) \Big) du \bigg]. \end{aligned}$$

Recalling (4.24), we obtain

$$\begin{aligned} \varphi _{k} \ge \widetilde{\mathbb{E}}^{t_{k},x_{k},\nu} \bigg[\int _{t_{k}}^{ \tau _{k}} \zeta ^{k}(u)\big((\mathcal{L}^{\nu _{u}}+\partial _{t}) \psi (u,\pi ^{k}_{u}) +1+\Gamma (\pi _{u}^{k},\nu _{u}) \psi (u,\pi ^{k}_{u}) \big) du \bigg]. \end{aligned}$$

(4.25)

We now wish to let $k\rightarrow \infty$, but we cannot directly apply the mean value theorem because $u \mapsto g(u, \pi ^{k}_{u},\nu _{u})$ is not continuous for the function $g$ in general. We first show that the last term on the right-hand side of (4.25) satisfies

$$\begin{aligned} &\widetilde{\mathbb{E}}^{t_{k},x_{k},\nu} \bigg[\int _{t_{k}}^{\tau _{k}} \zeta ^{k}(u)\Gamma (\pi _{u}^{k},\nu _{u}) \psi (u,\pi ^{k}_{u})du \bigg] \\ & \ge \widetilde{\mathbb{E}}^{t_{k},x_{k},\nu} \bigg[\int _{t_{k}}^{ \tau _{k}} \Gamma (x_{k},\nu _{u}) \psi (t_{k},x_{k}) du \bigg] - \beta _{k} \epsilon (\beta _{k}) \end{aligned}$$

(4.26)

for $\epsilon (\beta _{k})\rightarrow 0$ as $\beta _{k} \rightarrow 0$, where $\beta _{k}$ is defined in (4.23). By choosing a sufficiently small $\epsilon _{0}$ and from the local Lipschitz-continuity of the bounded continuous function $\psi \in C^{1,2}(\overline{\mathcal{U}}_{T})$, we have

$$\begin{aligned} |\psi (u,\pi _{u}^{k}) - \psi (t_{k},x_{k})| \le C_{\epsilon _{0}}(|u-t_{k}|+| \pi _{u}^{k}-x_{k}| ),\qquad u\in [t_{k},\tau _{k}], \end{aligned}$$

for a constant $C_{\epsilon _{0}}$ depending on $\epsilon _{0}$. In addition, as $\Gamma (x,\nu )$ is bounded and Lipschitz-continuous in $x$ when $\nu \in \Theta ^{t,M}$, we find

$$\begin{aligned} |\Gamma (\pi ^{k}_{u},\nu _{u}) - \Gamma (x_{k},\nu _{u})|& \le C | \pi _{u}^{k} - x_{k}|, \\ |\zeta ^{k}(u) - 1| &\le C |u-t_{k}|\sup _{t_{k} \le s \le u}|\pi _{s}^{k} - x_{k}|. \end{aligned}$$

The uniform norm of the function $\psi$ is denoted by $\| \psi \|$, and we obtain

$$\begin{aligned} &\widetilde{\mathbb{E}}^{t_{k},x_{k},\nu}\bigg[\int _{t_{k}}^{\tau _{k}} \zeta ^{k}(u)\Gamma (\pi _{u}^{k},\nu _{u}) \psi (u,\pi ^{k}_{u}) du \bigg] \\ & \ge \widetilde{\mathbb{E}}^{t_{k},x_{k},\nu}\bigg[\int _{t_{k}}^{ \tau _{k}} \Gamma (\pi ^{k}_{u},\nu _{u}) \zeta ^{k}(u) \psi (t_{k},x_{k}) du \bigg] \\ & \hphantom{=:} -C_{\epsilon _{0}}\beta _{k}\Big( \beta _{k} + \widetilde{\mathbb{E}}^{t_{k},x_{k}, \nu}\Big[ \sup _{t_{k} \le u \le \tau _{k}}|\pi _{u}^{k} - x_{k}| \Big] \Big) \\ & \ge \widetilde{\mathbb{E}}^{t_{k},x_{k},\nu}\bigg[\int _{t_{k}}^{ \tau _{k}} \Gamma (x_{k},\nu _{u}) \psi (t_{k},x_{k}) du \bigg] \\ & \hphantom{=:} -C_{\epsilon _{0}}C \| \psi \|\beta _{k}\Big(\beta _{k} + C \| \psi \|\widetilde{\mathbb{E}}^{t_{k},x_{k},\nu}\Big[ \sup _{t_{k} \le u \le \tau _{k}}|\pi _{u}^{k} - x_{k}| \Big] \Big). \end{aligned}$$

Combined with (4.22) in Proposition 4.6, we obtain (4.26). Using the continuity of $\partial _{t} \psi$, $\partial _{x}\psi$ and $\partial _{xx}\psi$ and (4.17) in Lemma 4.4, similar arguments give

$$\begin{aligned} &\widetilde{\mathbb{E}}^{t_{k},x_{k},\nu} \bigg[\int _{t_{k}}^{\tau _{k}} \zeta ^{k}(u)\bigg(\partial _{t} + \overline{\mu}(\pi ^{k}_{u}) \partial _{x}+ \frac{1}{2}\overline{\sigma}^{2}(\pi ^{k}_{u}) \partial _{xx}\bigg)\psi (u,\pi ^{k}_{u}) du \bigg] \\ & \ge \widetilde{\mathbb{E}}^{t_{k},x_{k},\nu} \bigg[\int _{t_{k}}^{ \tau _{k}}\bigg(\partial _{t} + \overline{\mu}(x_{k})\partial _{x}+ \frac{1}{2}\overline{\sigma}^{2}(x_{k})\partial _{xx}\bigg)\psi (t_{k},x_{k}) du \bigg] -\beta _{k} \epsilon (\beta _{k}). \end{aligned}$$

Next, using (4.17), we have

$$\begin{aligned} &\big| \psi \big(u,\xi (\pi ^{k}_{u-},z)\big) - \psi \big(t_{k}, \xi (x_{k},z) \big) \big| \\ & \le C_{\epsilon _{0}}\big(|u-t_{k}| + | \xi (\pi ^{k}_{u-},z) - \xi (x_{k},z) | \big) \\ & \le C_{\epsilon _{0}}\Big(|u-t_{k}| + \big(\rho (z)+1\big)|\pi ^{k}_{u-} - x_{k}| \Big), \qquad u\in [t_{k},\tau _{k}]. \end{aligned}$$

As $\int _{\mathcal{Z}} \rho (z) (f_{1}(z) +f_{2}(z)) dz<\infty$ under Condition 2.1, we find

$$\begin{aligned} &\widetilde{\mathbb{E}}^{t_{k},x_{k},\nu} \bigg[ \int _{t_{k}}^{\tau _{k}} \zeta ^{k}(u)\lambda \int _{\mathcal{Z}} \Big(\psi \big(u,\xi (\pi ^{k}_{u-},z) \big) - \psi (u,\pi ^{k}_{u-})\Big) \hat{f}(\pi ^{k}_{u-},z)e^{\beta \nu _{u}} dz du \bigg] \\ & \ge \widetilde{\mathbb{E}}^{t_{k},x_{k},\nu} \bigg[ \int _{t_{k}}^{ \tau _{k}}\lambda \int _{\mathcal{Z}} \Big(\psi \big(t_{k},\xi (x_{k},z) \big) - \psi (t_{k},x_{k})\Big) \hat{f}(x_{k},z)e^{\beta \nu _{u}} dz du \bigg] \\ & \hphantom{=:} - \beta _{k}C\Big(\beta _{k} + \widetilde{\mathbb{E}}^{t_{k},x_{k}, \nu}\Big[ \sup _{t_{k} \le u \le \tau _{k}}|\pi _{u}^{k} - x_{k}| \Big] \Big). \end{aligned}$$

By substituting these estimates into (4.25), we obtain

$$\begin{aligned} \frac{\varphi _{k}}{\beta _{k}} &\ge \frac{1}{\beta _{k}} \widetilde{\mathbb{E}}^{t_{k},x_{k},\nu} \bigg[ \int _{t_{k}}^{\tau _{k}} \bigg(\Big({\partial _{t}}+\overline{\mu}(x_{k})\partial _{x} + \frac{1}{2} \overline{\sigma}(x_{k})^{2}\partial _{xx}\Big) \psi (t_{k},x_{k}) \\ & \hphantom{=: \frac{1}{\beta _{k}}\widetilde{\mathbb{E}}^{t_{k},x_{k},\nu} \bigg[ \int _{t_{k}}^{\tau _{k}} \bigg(} +1+H_{\psi}(t_{k},x_{k},\nu _{u}) \bigg)du \bigg]- \epsilon (\beta _{k}). \end{aligned}$$

Finally, using $k\rightarrow \infty$, $t_{k} \rightarrow t_{0}$, ${\varphi _{k}}/{\beta _{k}} \rightarrow 0$, $\epsilon (\beta _{k}) \rightarrow 0$, the mean value theorem, the bounded convergence theorem and replacing $\nu$ by a constant strategy, we obtain

$$\begin{aligned} \bigg(\partial _{t}+\overline{\mu}(x_{0})\partial _{x} +\frac{1}{2} \overline{\sigma}(x_{0})^{2}\partial _{xx}\bigg)\psi (t_{0},x_{0})+1 +H_{ \psi}(t_{0},x_{0},\nu ) \le 0. \end{aligned}$$

As $\nu \in [-M,M]$ is arbitrary, we obtain the supersolution viscosity inequality.

Step 2: Viscosity subsolution. Take some $(t_{0},x_{0})\in{\mathcal{U}}_{T}$ and $\psi \in C^{1,2}(\overline{\mathcal{U}}_{T})$ with $0 = ( \Lambda ^{M}-\psi )(t_{0},x_{0}) = \max _{(t,x)\in{\mathcal{U}}_{T}}( \Lambda ^{M}(t,x)-\psi (t,x) )$ and thus $\Lambda ^{M} \le \psi$ on ${\mathcal{U}}_{T}$. We aim to establish the subsolution viscosity inequality in $(t_{0},x_{0})$. We reason by contradiction and assume that there exists $\ell >0$ such that

$$\begin{aligned} \bigg(\partial _{t}+ \overline{\mu}(x_{0})\partial _{x} +\frac{1}{2} \overline{\sigma}(x_{0})^{2}\partial _{xx}\bigg) \psi (t_{0},x_{0})+1 + \max _{\nu \in [-M,M]} H_{\psi}(t_{0},x_{0},\nu ) < -\ell < 0. \end{aligned}$$

As $\mathcal{L}^{\nu} \psi$ is continuous, there exists an open set $\mathcal{N}_{\epsilon _{0}}$ around $(t_{0},x_{0})$ given by

$$\begin{aligned} \mathcal{N}_{\epsilon _{0}}:=\{ (t,x): (t,x)\in (t_{0}-\epsilon _{0},t_{0}+ \epsilon _{0})\times (x_{0} - \epsilon _{0},x_{0}+\epsilon _{0})\cap \mathcal{U}_{T} \} \end{aligned}$$

for $\epsilon _{0}\in (0,1/2)$ such that for $x\in \mathcal{N}_{\epsilon _{0}}$,

$$\begin{aligned} \bigg(\partial _{t}+ \overline{\mu}(x)\partial _{x} +\frac{1}{2} \overline{\sigma}(x)^{2}\partial _{xx}\bigg) \psi (t_{0},x_{0})+1 + \max _{\nu \in [-M,M]} H_{\psi}(t,x,\nu ) < -\frac{\ell}{2}. \end{aligned}$$

Take $\iota >0$ such that

$$\begin{aligned} \max _{(t,x)\in{\mathcal{U}}_{T}\backslash \mathcal{N}_{\epsilon _{0}}} (\Lambda ^{M} - \psi )(t,x) \le -\iota e^{-\epsilon _{0} C_{M}}< 0 \end{aligned}$$

for a constant $C_{M}=\max _{x\in [0,1], \nu \in [-M,M]} \max \{-\Gamma (x,\nu ),0\}$, which is finite. Let $(t_{k},x_{k})$ be a sequence in $\mathcal{N}_{\epsilon _{0}}$ with $\lim _{k\rightarrow \infty} (t_{k},x_{k}) = (t_{0},x_{0})$. We further define the sequence $( \varphi _{k} )$ as $\varphi _{k}: = \Lambda ^{M}(t_{k},x_{k}) - \psi (t_{k},x_{k})$. By continuity of $\Lambda ^{M}$ and $\psi$, we have $\lim _{k\rightarrow \infty} \varphi _{k} = 0$. For $k \ge 1$ and $\epsilon _{k} >0$ with $\lim _{k\rightarrow \infty} \epsilon _{k} = 0$, consider an $\epsilon _{k}$-optimal control $\nu ^{*,k}$ so that

$$\begin{aligned} \Lambda ^{M}(t_{k},x_{k}) \le \Lambda (t_{k},x_{k},\nu ^{*,k}) + \epsilon _{k}. \end{aligned}$$

(4.27)

We denote the filter process (the solution of (4.2)) with the initial state $\widetilde{\pi}_{t_{k}}^{k} = x_{k}$ and the control $\nu = \nu ^{*,k}$ by $\widetilde{\pi}^{k}$, and we define the stopping time

$$\begin{aligned} \tau _{k}: = \inf \{s>t_{k}: (s, \widetilde{\pi}^{k}_{s})\notin \mathcal{N}_{\epsilon _{0}} \}. \end{aligned}$$

By definition, we then have $\Lambda ^{M}(\tau _{k},\widetilde{\pi}^{k}_{ \tau _{k}}) -\psi ( \tau _{k},\widetilde{\pi}^{k}_{ \tau _{k}}) \le -\iota e^{-\epsilon _{0} C_{M}}$. If we now let $\widetilde{\zeta}^{k}(s):= \exp (\int _{t_{k}}^{s}\Gamma ( \widetilde{\pi}_{u}^{k},\nu ^{*,k}_{u})du)$, we get

$$\begin{aligned} &\widetilde{\zeta}^{k}(\tau _{k}) \Lambda ^{M}(\tau _{k}, \widetilde{\pi}^{k}_{ \tau _{k}}) + \int _{t_{k}}^{\tau _{k}} \widetilde{\zeta}^{k}(s)ds - \Lambda ^{M}(t_{k},x_{k}) \\ & \le \widetilde{\zeta}^{k}(\tau _{k}) \psi (\tau _{k}, \widetilde{\pi}^{k}_{ \tau _{k}}) + \int _{t_{k}}^{\tau _{k}} \widetilde{\zeta}^{k}(s)ds - \psi (t_{k},x_{k}) -\iota e^{-\epsilon _{0} C_{M}} \widetilde{\zeta}^{k}(\tau _{k}) - \varphi _{k} \\ & \le \int _{t_{k}}^{\tau _{k}} \widetilde{\zeta}^{k}(u)\big(( \partial _{t}+\mathcal{L}^{\nu ^{*,k}_{u}})\psi (u,\widetilde{\pi}^{k}_{u})+1 \big)du-\iota - \varphi _{k}. \end{aligned}$$

From the above calculations, we have

$$\begin{aligned} &\widetilde{\mathbb{E}}^{t_{k},x_{k},\nu ^{*,k}}\bigg[ \widetilde{\zeta}^{k}(\tau _{k}) \Lambda ^{M}(\tau _{k}, \widetilde{\pi}^{k}_{ \tau _{k}}) + \int _{t_{k}}^{\tau _{k}} \widetilde{\zeta}^{k}(s)ds \bigg] \\ & \le \Lambda ^{M}(t_{k},x_{k}) -\iota - \varphi _{k} - \frac{\ell}{2} \widetilde{\mathbb{E}}^{t_{k},x_{k},\nu ^{*,k}}[\tau _{k} - t_{k}]. \end{aligned}$$

However, from the optimality of $\Lambda ^{M}$ and (4.27), we have

$$\begin{aligned} \widetilde{\mathbb{E}}^{t_{k},x_{k},\nu ^{*,k}}\bigg[ \widetilde{\zeta}^{k}(\tau _{k}) \Lambda ^{M}(\tau _{k}, \widetilde{\pi}^{k}_{ \tau _{k}}) + \int _{t_{k}}^{\tau _{k}} \widetilde{\zeta}^{k}(s)ds \bigg] \ge \Lambda ^{M}(t_{k},x_{k})- \epsilon _{k}. \end{aligned}$$

By selecting $\epsilon _{k} = \varphi _{k}$, we have $\Lambda ^{M}(t_{k},x_{k})\le \Lambda ^{M}(t_{k},x_{k}) - \iota$, which is a contradiction, and therefore we have shown the subsolution inequality. □

4.4 The function $\Lambda ^{M}$ is a classical solution of the HJB equation (4.14)

We introduce an alternative definition of the viscosity solution first suggested by Pham [36, Lemma 2.1] and formalised in various contexts, as in Barles and Imbert [4], Davis et al. [15] and Seydel [43], and we show that this alternative definition is equivalent to Definition 4.8. In this definition, the integro-differential operator is evaluated using the actual solution.

Definition 4.10

A bounded function $g \in C(\overline{\mathcal{U}}_{T})$ is a viscosity supersolution (subsolution) of (4.9) if for any bounded test function $\psi \in C^{1,2}(\overline{\mathcal{U}}_{T})$ such that $(t_{0},x_{0})\in {\mathcal{U}}_{T}$ is a global minimum (maximum) point of $g-\psi$ with $g(t_{0},x_{0})=\psi (t_{0},x_{0})$, we have

$$ \bigg(-\partial _{t}-\overline{\mu}(x_{0})\partial _{x}-\frac{1}{2} \overline{\sigma}(x_{0})^{2}\partial _{xx}\bigg)\psi (t_{0},x_{0})- \max _{\nu \in [-M,M]} H_{g}(t_{0},x_{0},\nu ) \geq 1 $$

(resp. $\leq 1$), where

$$ H_{g}(t,x,\nu ): = \Gamma (x,\nu ) g(t, x)+\int _{\mathcal{Z}}\Big(g \big(t,\xi (x, z)\big)-g(t,x)\Big)\lambda e^{\beta \nu}\hat{f}(x,z) d z. $$

A bounded function $g$ is a viscosity solution of (4.9) if it is both a viscosity subsolution and a viscosity supersolution of (4.9).

Proposition 4.11

Definitions 4.8and 4.10of viscosity solutions are equivalent.

Proof

See Appendix C. □

With Theorem 4.9, we immediately obtain the following corollary corresponding to Step 4 in the proof of Theorem 4.1 in Sect. 4.1.

Corollary 4.12

The function ${\Lambda}^{M}$ is a viscosity solution of the PDE (4.14).

Given the results above, we formally define the functional $\mathcal{I}_{\beta}(g)$ as

$$\begin{aligned} \mathcal{I}_{\beta}(g)(t,x): = (1-\beta )\lambda \int _{\mathcal{Z}} {g(t,x)}^{ \frac{\beta}{\beta -1}} \Big({g\big(t,\xi (x,z)\big)}^{ \frac{1}{1-\beta}}-{g(t,x)^{\frac{1}{1-\beta}}}\Big)\hat{f}(x,z)dz. \end{aligned}$$

Under Condition 2.1, $\mathcal{I}_{\beta}(g)$ is well defined for any bounded function $g$. We observe that for a sufficiently large $M$ (given in (4.11) in Lemma 4.3), we have

$$\begin{aligned} \mathcal{I}_{\beta}(\Lambda ^{M})(t,x) = \max _{\nu \in [-M,M]} H_{ \Lambda ^{M}}(t,x,\nu ) + d_{0}(x). \end{aligned}$$

Thus we can rewrite the HJB PIDE (4.9) as the equivalent parabolic PDE (4.14), as stated in Step 3 of Sect. 4.1. We provide the following result on $\mathcal{I}_{\beta}$, which is used when we prove the uniqueness and existence of a classical solution of the PDE (4.14). Its proof is provided in Appendix C.

Lemma 4.13

The functional $\mathcal{I}_{\beta}({\Lambda}^{M})(t,x)$ is bounded and Lipschitz-continuous in $x$ on $\overline{\mathcal{U}}_{T}$; therefore, it is Hölder-continuous in $x$ with an exponent $0<\iota <1$.

As described in Step 5, we can use the comparison result in Amadori [1, Theorem 2] for the degenerate parabolic PDE to show the uniqueness of the solution of the PDE (4.14).

Theorem 4.14

We take $u$ and $v$ as a bounded continuous subsolution and a bounded lower continuous supersolution, respectively, to (4.14), subject to the terminal condition $u(T,x) = v(T,x) = 1$ for $x\in [0,1]$. Then $u \le v$ on ${\mathcal{U}}_{T}$.

By virtue of Proposition 2.5 (the boundaries of the filter process are unattainable), Proposition 4.2 (boundedness of $\Lambda ^{M}$) and Lemma 4.4 (Lipschitz and growth properties for the coefficients of the PDE), we easily check that the assumptions in [1, Assumptions 1 and 2] are satisfied in our case.

Corollary 4.15

The value function ${\Lambda}^{M}$ is the unique viscosity solution of the parabolic PDE (4.14) subject to the terminal condition ${\Lambda}^{M}(T,x)=1$ for $x\in [0,1]$.

Following Step 6, it remains to establish the existence of a classical solution to the PDE (4.14). We propose the following theorem, whose proof is provided in Appendix B.

Theorem 4.16

The PDE (4.14) admits a classical solution $g\in C^{1,2}(\mathcal{U}_{T})$ subject to the terminal condition $g(T,x) = 1$ for $x\in [0,1]$.

5 Conclusion

We have established the first duality approach to an optimal investment–consumption problem with partial information and mixed observations. Interestingly, the inclusion of alternative data places our problem in the family of incomplete markets, and our dual problem is an optimisation problem for a set of equivalent local martingale measures. We comprehensively demonstrate its application in a bull–bear economy by drawing on expert opinions as a complementary source of observation. The analytically tractable results for the power utility function show that the optimal investment and consumption policies are determined from the solution of a PIDE, which takes into account the effect of alternative observations.

Appendices

Appendix A: Proof of Theorem 3.2

Without loss of generality, we prove the result for starting time $t=0$ and arbitrary initial guess $x\in [0,1]$. For ease of notation, we remove the subscripts $t$ and $x$.

Assumption A.1

The time-dependent utility function $U_{i}(t,c)\in C^{2}([0,T]\times \mathbb{R}_{++})$ for $i=1,2$ has the following properties for any given $t\in [0,T]$:

• i) The function $U_{i}(t,c)$ is strictly concave with respect to $c$ and

  $$\begin{aligned} \lim _{c\rightarrow 0+} \partial _{c} U_{i}(t,c) = \infty ,\qquad \lim _{c\rightarrow \infty} \partial _{c} U_{i}(t,c) = 0. \end{aligned}$$

• ii) There exist $c_{0}>0$, $\zeta \in (0,1)$ and $\iota >1$ such that

  $$ \zeta \partial _{c}U_{i}(t,c) \ge \partial _{c} U_{i}(t, \iota c) \qquad \text{for }c>c_{0}. $$

• iii) There exist positive constants $K$ and $k_{0}$ such that

  $$\begin{aligned} \limsup _{c\rightarrow \infty} \max _{t \in [0,T]} \partial _{c} U_{i}(t,c) c^{k_{0}} \le K. \end{aligned}$$

Assumption A.1 i) is referred to as the Inada conditions, which are commonly applied in economic models. The two growth conditions in Assumption A.1 ii) and iii) are standard in duality approaches; see e.g. Karatzas et al. [27, Assumption 4.3], Cvitanić and Karatzas [14, Eq. (5.9)] and Yang and Koo [49, Assumption 1]. These conditions are used to easily obtain the regularity of various functions in the case of duality. Assumption A.1 is satisfied by most popular utility functions, such as CRRA and constant absolute risk aversion utility functions $U_{i}(t,c) = \frac{c^{\kappa ^{\prime}}}{\kappa ^{\prime}}$ with $0\neq \kappa ^{\prime} <1$, $U_{i}(t,c) = \ln c$ and $U_{i}(t,c) = 1 - e^{-\kappa ^{\prime \prime}c}$ with $\kappa ^{\prime \prime}>0$. It is also satisfied by a class of utility functions with time-varying risk aversion, such as $U_{i}(t,c) = c^{\kappa (t)}/\kappa (t)$ with a deterministic function $\kappa (t)$ satisfying $\underline{\kappa}_{\ell}\le \kappa (t) \le \underline{\kappa}_{u}$ for constants $\underline{\kappa}_{\ell}<\underline{\kappa}_{u}<1$ with $\underline{\kappa}_{\ell}>0$ or $\underline{\kappa}_{u}<0$. Some economists are interested in power utility functions, particularly with negative power, which is considered more realistic in terms of agent behaviour but needs to be treated differently and is therefore rarely discussed in the literature; see Federico et al. [21, Remark 2.1 (i)]. Assumption A.1 ii) covers the case of a power utility function with negative power, which is the case in the optimal control problem (2.5), (2.6) in Sect. 2.

In addition, if $U_{i}(t,\infty )>0$ for all $t\in [0,T]$, then Assumption A.1 ii) implies Assumption A.1 iii), and the asymptotic elasticity of the utility function is strictly less than 1, that is, $\mathrm{AE}(U_{i}(t,\,\cdot \,))= \limsup _{c\rightarrow \infty}{x \partial _{c}U_{i}(t,c)}/{U_{i}(t,c)}<1$; see Kramkov and Schachermayer [30, Lemmas 6.3 and 6.5].

For convenience of exposition, we list the properties of the convex dual functions $\widetilde{U}_{i}$ and $I_{i}$ (inverse function of $\partial _{c}U_{i}(t,\,\cdot \,)$) for the above general class of utility functions.

Lemma A.2

Under Assumption A.1, the convex dual functions $\widetilde{U}_{i}$ and $I_{i}$ for $i=1,2$ have the following properties: For any $t\in [0,T]$,

• i) The function $\widetilde{U}_{i}:[0,T]\times \mathbb{R}_{++} \rightarrow \mathbb{R}$ is strictly decreasing and strictly convex and satisfies

  $$\begin{aligned} &\partial _{y} \widetilde{U}_{i}(t,y) = - I_{i}(t,y), \quad y\in \mathbb{R}_{++}, \\ &U_{i}(t,c) = \inf _{y\in \mathbb{R}_{++}} \big(\widetilde{U}_{i}(t,y) + cy\big) = \widetilde{U}_{i}\big(t,\partial _{c}U_{i}(t, c)\big)+c \partial _{c}U_{i}(t, c),\quad c\in \mathbb{R}_{++}. \end{aligned}$$

• ii) $\lim _{y\rightarrow 0+} I_{i}(t,y)= \infty$ and $\lim _{y\rightarrow \infty} I_{i}(t,y) = 0$.

• iii) For the constant $k_{0}$ in Assumption A.1iii), there exists a constant $C$ such that

  $$\begin{aligned} I_{i}(t,y) \le C(1+y^{-\frac{1}{k_{0}}}),\qquad (t,y)\in [0,T]\times \mathbb{R}_{++}. \end{aligned}$$

• iv) There exists $y_{0}>0$ such that for any $\zeta \in (0,1)$, there exists a constant $\iota >1$ with

  $$\begin{aligned} I_{i}(t, \zeta y) \le \iota I_{i}(t,y),\qquad 0< y< y_{0}. \end{aligned}$$

  (A.1)

Recalling $Z^{\nu}$ defined in (3.3), we introduce the function $\chi :\mathbb{R}_{++}\times \Theta \rightarrow \mathbb{R}$ as

$$\begin{aligned} \chi (y;\nu ):= \mathbb{E}\bigg[e^{-rT}Z_{T}^{\nu} I_{1}(T, e^{-rT}yZ_{T}^{ \nu})+ \int _{0}^{T} e^{-rt}Z_{t}^{\nu}I_{2}(t, e^{-rt}yZ_{t}^{\nu})dt \bigg]. \end{aligned}$$

If the condition

$$\begin{aligned} \chi (y;\nu ) < \infty ,\qquad y\in \mathbb{R}_{++}, \end{aligned}$$

(A.2)

prevails, the monotone convergence theorem, the dominated convergence theorem and Lemma A.2 ii) imply that $\chi (\,\cdot \,;\nu )$ is continuous and

$$\begin{aligned} \lim _{y\rightarrow \infty} \chi (y;\nu ) = 0, \qquad \lim _{y \rightarrow 0+} \chi (y;\nu ) = \infty , \end{aligned}$$

(A.3)

and $\chi (\,\cdot \,;\nu )$ is strictly decreasing on $\mathbb{R}_{++}$ for any given $\nu \in \Theta$. We verify that condition (A.2) holds under Assumption A.1. By Lemma A.2 iii), for $y >0$, we find

$$\begin{aligned} \chi (y;\nu ) \le C +C y^{-\frac{1}{k_{0}}} \mathbb{E}\bigg[ e^{ \frac{rT}{k}}(Z_{T}^{\nu})^{-\frac{1}{k}}+ \int _{0}^{T} e^{ \frac{rt}{k}}(Z_{t}^{\nu})^{-\frac{1}{k}} dt\bigg],\qquad {k}: = \frac{k_{0}}{1-k_{0}}. \end{aligned}$$

Due to the boundedness of $\hat{\theta}$, i.e., the boundedness of $\theta$ in (2.8), and the fact that $\nu \in \Theta$ satisfies Conditions (2.17) and (2.18), we get $\chi (y;\nu )< \infty$.

We now prove Theorem 3.2. We first establish a useful fact for the dual optimiser $\nu ^{y}\in \Theta$ of (3.4), assuming its existence and writing

$$\begin{aligned} \hat{L}(y) = \inf _{\nu \in \Theta} \widetilde{L}(y;\nu ) = \widetilde{L}(y;\nu ^{y}) < \infty , \qquad y\in \mathbb{R}_{++}. \end{aligned}$$

Lemma A.3

For a given $y$, let $\nu ^{y}$ be the dual optimiser of (3.4) for $y$. Then we have

$$\begin{aligned} \sup _{\nu \in \Theta}\mathbb{E}\bigg[e^{-rT}Z_{T}^{\nu} I_{1}(T, e^{-rT}yZ_{T}^{ \nu ^{y}})+ \int _{0}^{T} \!\!\!e^{-rt}Z_{t}^{\nu}I_{2}(t, e^{-rt}yZ_{t}^{ \nu ^{y}})dt\bigg]\le \chi (y;\nu ^{y}). \end{aligned}$$

(A.4)

Proof

Fixing $\epsilon \in (0,1)$ and an arbitrary $\nu '=(\nu _{D}',\nu _{J}') \in \Theta$, we define

$$\begin{aligned} G_{\epsilon}(t)&= (1-\epsilon ) Z^{\nu ^{y}}_{t} + \epsilon Z^{\nu '}_{t}, \\ \nu ^{\epsilon}_{D}(t) &= G_{\epsilon}(t)^{-1} \big((1-\epsilon )Z_{t}^{ \nu ^{y}}\nu ^{y}_{D}(t) + \epsilon Z_{t}^{\nu '}\nu '_{D}(t)\big), \\ \nu ^{\epsilon}_{J}(t,q) &= \ln \Big( G_{\epsilon}(t)^{-1} \big((1- \epsilon )Z_{t}^{\nu ^{y}}e^{\nu ^{y}_{J}(t,q)} + \epsilon Z_{t}^{ \nu '}e^{\nu '_{J}(t,q)}\big)\Big) . \end{aligned}$$

Then $\nu ^{\epsilon}:=(\nu ^{\epsilon}_{D}, \nu ^{\epsilon}_{J}) \in \Theta$ and we have

$$ d G_{\epsilon}(t) = -\hat{\theta}(\pi _{t}) G_{\epsilon}(t) d \widetilde{W}_{t} -\nu ^{\epsilon}_{D}(t) G_{\epsilon}(t) d \widetilde{B}_{t} - \int _{\mathbb{R}} G_{\epsilon}(t)(1-e^{\nu ^{ \epsilon}_{J}(t,q)}) \overline{m}^{\pi}(dt,dq). $$

By comparing the solutions to the above SDE and (3.3), we find that $G_{\epsilon} = Z^{\nu ^{\epsilon}}$ by the uniqueness of the Doléans-Dade exponential. As $\nu ^{y}$ is optimal, we have

$$\begin{aligned} \epsilon ^{-1}\big(\widetilde{L}(y;\nu ^{y})-\widetilde{L}(y;\nu ^{ \epsilon})\big)\le 0 \end{aligned}$$

or equivalently

$$\begin{aligned} 0 &\geq \epsilon ^{-1} \mathbb{E}\bigg[ \widetilde{U}_{1}(T, y e^{-rT}Z_{T}^{ \nu ^{y}}) + \int _{0}^{T} \widetilde{U}_{2}(t, y e^{-rt}Z_{t}^{\nu ^{y}}) dt \\ & \hphantom{=:\epsilon ^{-1} \mathbb{E}\bigg[} -\widetilde{U}_{1}(T, y e^{-rT}Z_{T}^{\nu ^{\epsilon}}) - \int _{0}^{T} \widetilde{U}_{2}(t, y e^{-rt}Z_{t}^{\nu ^{\epsilon}}) dt\bigg] . \end{aligned}$$

(A.5)

Recalling that $\partial _{y}\widetilde{U}_{i}(t,y) = - I_{i}(t,y)$, we see that (A.4) can be obtained by taking the limit as $\epsilon \downarrow 0$ inside the expectation sign of (A.5). For a rigorous justification, we show that the random variable inside the expectation operator in (A.5) is bounded from below by uniformly integrable terms. For a given $t\in [0,T]$, we fix $\omega \in \Omega$ and omit writing its dependence. If $Z_{t}^{\nu ^{\prime}} > Z_{t}^{\nu ^{y}}$, the mean value theorem implies that

$$\begin{aligned} & \epsilon ^{-1} \big(\widetilde{U}_{i}(t, y e^{-rt}Z_{t}^{\nu ^{y}}) - \widetilde{U}_{i}(t, y e^{-rt}Z_{t}^{\nu ^{\epsilon}}) \big) \\ &=I_{i}(t,e^{-rt}y F)e^{-rt}y\epsilon ^{-1}\big(G_{\epsilon}(t) - Z_{t}^{ \nu ^{y}}\big) \\ &= I_{i}(t,e^{-rt}y F)e^{-rt}y(Z_{t}^{\nu ^{\prime}} - Z_{t}^{\nu ^{y}}), \end{aligned}$$

(A.6)

where $Z_{t}^{\nu ^{y}} \le F \le Z_{t}^{\nu ^{y}} + \epsilon ( Z_{t}^{ \nu ^{\prime}}- Z_{t}^{\nu ^{y}}) < Z_{t}^{\nu ^{\prime}}$; in the first equality, we use the fact that $G_{\epsilon}(t) = Z^{\nu ^{\epsilon}}_{t}$. As $I_{i}(t,y)$ decreases with $y$, we obtain

$$\begin{aligned} &I_{i}(t,e^{-rt}y F)e^{-rt}y(Z_{t}^{\nu ^{\prime}} - Z_{t}^{\nu ^{y}}) \ge -e^{-rt}yI_{i}(t,e^{-rt}y Z_{t}^{\nu ^{y}})Z_{t}^{\nu ^{y}}. \end{aligned}$$

Alternatively, if $Z_{t}^{\nu ^{\prime}} < Z_{t}^{\nu ^{y}}$, we have

where we use $(1-\epsilon )Z_{t}^{\nu ^{y}} \le (1-\epsilon )Z_{t}^{\nu ^{y}} + \epsilon Z_{t}^{\nu ^{\prime}}\le F \le Z_{t}^{\nu ^{y}}$ in the second line, and the last inequality holds for $\epsilon <1-\xi$, using the constants $y_{0}>0$, $\xi >0$ and $\iota >1$ defined in (A.1).

Repeating the proof of (A.2), we see that the random variable inside the expectation operator in (A.5) is bounded from below by uniformly integrable terms when $\epsilon$ is sufficiently small. As a result, Fatou’s lemma can be applied when taking the limit as $\epsilon \downarrow 0$ in (A.6), which implies (A.4) as the choice of $\nu '$ is arbitrary. □

Next, we show that $\nu ^{y}$ leads to an admissible strategy pair $(\vartheta ,c)\in \mathcal{A}(\chi (y;\nu ^{y}))$, as a corollary of the following theorem and Lemma A.3.

Theorem A.4

Let $X$ be a nonnegative $\mathcal{H}_{T}$-measurable random variable and $c$ a consumption rate process such that we have the budget constraint

$$\begin{aligned} \sup _{\nu \in \Theta} \mathbb{E}\bigg[e^{-rT}Z_{T}^{\nu}X + \int _{0}^{T} e^{-rt}Z_{t}^{\nu}c_{t} dt\bigg] \le v. \end{aligned}$$

(A.7)

Then there exists an investment process $\vartheta$ with $(\vartheta ,c)\in \mathcal{A}(v)$ and $V_{T}^{\vartheta ,c} \ge X$.

Proof

The techniques are similar to those in Pham and Quenez [37, Appendix A]. Specifically, we show that for a given candidate terminal wealth level $X$ and consumption plan $c$, the superhedging price (left-hand side of (A.7)) admits a dynamic characterisation so that the martingale representation theorem in Proposition D.4 can be applied. The differences arise from both the investment and consumption strategies considered, and the filtration ℍ includes both a Brownian filtration and a jump filtration in our analysis. We omit the details of the proof due to space constraints. □

Referring to (A.4) in Lemma A.3, $\nu ^{y}$ leads to a pair $X=I_{1}(T, e^{-rT}yZ_{T}^{\nu ^{y}})$ and $c_{t} = I_{2}(t, e^{-rt}yZ_{t}^{\nu ^{y}})$ that satisfies (A.7). Further, Theorem A.4 implies that there exists an investment process $\vartheta$ with $(\vartheta ,c)\in \mathcal{A}(\chi (y;\nu ^{y}))$ and $V_{T}^{\vartheta ,c} \ge X$. We conclude that $\nu ^{y}$ leads to an admissible strategy pair $(\vartheta ,c)\in \mathcal{A}(\chi (y;\nu ^{y}))$.

Finally, we show that for all $v\in \mathbb{R}_{++}$, there exists $y^{*}= y(v) \in \mathbb{R}_{++}$ such that $v = \chi (y^{*};\nu ^{y^{*}})$, where $\nu ^{y^{*}}$ is the dual optimiser in (3.4) for $y^{*}$. This statement is a corollary of the following result.

Lemma A.5

The dual value function $\hat{L}(y)$ defined in (3.4) is continuously differentiable with derivative $\partial _{y}\hat{L}(y) = - \chi (y;\nu ^{y})$ for $y\in \mathbb{R}_{++}$, with $\nu ^{y}$ being the dual optimiser for $y$. In addition,

$$\begin{aligned} \lim _{y\rightarrow 0+} \partial _{y}\hat{L}(y) = -\infty , \qquad \lim _{y\rightarrow \infty} \partial _{y}\hat{L}(y) = 0. \end{aligned}$$

(A.8)

Proof

By the properties of $\widetilde{U}_{i}$ in Lemma A.2 i), $\hat{L}$ is clearly decreasing and convex in $y$. First we show that $\hat{L}$ is differentiable with respect to $y$ and therefore continuously differentiable by its convexity. For a fixed $\bar{y}>0$, let $\nu ^{\bar{y}}$ be the corresponding minimiser so that $\hat{L}(\bar{y}) = \widetilde{L}(\bar{y};\nu ^{\bar{y}})$. We consider the function $\overline{L}(y) : = \widetilde{L}(y;\nu ^{\bar{y}})$ which is also convex and decreasing in $y$. We have $\overline{L}(y) \ge \hat{L}(y)$ for all $y\in \mathbb{R}_{++}$ and $\overline{L}(\bar{y}) = \hat{L}(\bar{y})$. It then follows that

$$ \partial _{-}\overline{L}(\bar{y})\le \partial _{-}\hat{L}(\bar{y}) \le \partial _{+}\hat{L}(\bar{y}) \le \partial _{+}\overline{L}( \bar{y}), $$

where $\partial _{\pm}$ denote the left and right derivatives, respectively, whose existence is guaranteed by the convexity of $\overline{L}$ and $\hat{L}$. By the monotone convergence theorem and the fact that $\partial _{y}\widetilde{U}_{i}(t,y)=-I_{i}(t,y)$, we have $\partial _{+}\overline{L}(\bar{y}) \le -\chi (\bar{y};\nu ^{\bar{y}})$. Moreover, by convexity,

$$\begin{aligned} \partial _{-} \overline{L}(\bar{y}) &\ge \limsup _{\epsilon \rightarrow 0+} \mathbb{E}\bigg[-e^{-rT}Z_{T}^{\nu ^{\bar{y}}} I_{1} \big(T, e^{-rT}(\bar{y}-\epsilon )Z_{T}^{\nu ^{\bar{y}}}\big) \\ & \hphantom{=: \limsup _{\epsilon \rightarrow 0+} \mathbb{E}\bigg[} - \int _{0}^{T} e^{-rt}Z_{t}^{\nu ^{\bar{y}}}I_{2}\big(t, e^{-rt}( \bar{y}-\epsilon )Z_{t}^{\nu ^{\bar{y}}}\big)dt\bigg], \end{aligned}$$

where the term inside the expectation operator is uniformly integrable when $\epsilon$ is sufficiently small following the same arguments as in the proof of Lemma A.3. We conclude that $\partial _{-} \overline{L}(\bar{y}) \ge -\chi (\bar{y};\nu ^{\bar{y}})$. Hence $\partial _{y}\hat{L}(\bar{y}) = - \chi (\bar{y};\nu ^{\bar{y}})$ for all $\bar{y}>0$.

Next we prove (A.8). For ease of notation, we write $\phi (0+): = \lim _{y\rightarrow 0+} \phi (y)$ for any function $\phi$. Note that $\hat{L}(0+) \ge \widetilde{U}_{1}(T,0+)+ \int _{0}^{T}\widetilde{U}_{2}(t,0+)dt$. Using Jensen’s inequality, the convexity and decreasing properties of $\widetilde{U}_{i}(t,\,\cdot \,)$ and the (super)martingale property of $Z^{\nu}$ for an arbitrary $\nu \in \Theta$, we have

$$\begin{aligned} \widetilde{L}(y;\nu ) &\ge \widetilde{U}_{1}(T,ye^{-rT}\mathbb{E}[Z_{T}^{ \nu}]) + \int _{0}^{T}\widetilde{U}_{2}(t,ye^{-rt}\mathbb{E}[Z_{t}^{ \nu}])dt \\ &\ge \widetilde{U}_{1}(T,ye^{-rT})+ \int _{0}^{T}\widetilde{U}_{2}(t,ye^{-rt})dt \\ &\longrightarrow \widetilde{U}_{1}(T,0+)+ \int _{0}^{T}\widetilde{U}_{2}(t,0+)dt \qquad \text{as $y\downarrow 0$,} \end{aligned}$$

taking the infimum over $\nu \in \Theta$ on both sides. If $\widetilde{U}_{1}(T,0+)+ \int _{0}^{T}\widetilde{U}_{2}(t,0+)dt = \infty$, then $\hat{L}(0+) = \infty$ and $\partial _{y}\hat{L}(0+)=-\infty$. If $\widetilde{U}_{1}(T,0+)+ \int _{0}^{T}\widetilde{U}_{2}(t,0+)dt < \infty$, we find that

$$\begin{aligned} \hat{L}(y) \le \mathbb{E}\bigg[ \widetilde{U}_{1}(T,ye^{-rT}Z^{0}_{T}) + \int _{0}^{T}\widetilde{U}_{2}(t,ye^{-rt}Z^{0}_{t})dt \bigg], \end{aligned}$$

(A.9)

where $Z_{t}^{0} := \exp ( -\int _{0}^{t}\hat{\theta}(\pi _{s})d \widetilde{W}_{s} -\frac{1}{2}\int _{0}^{t}\hat{\theta}(\pi _{s})^{2}ds )$, $t\in [0,T]$. Note that we have $\lim _{y\downarrow 0} yZ_{t}^{0} = 0$ a.s. for $t\in [0,T]$. The term inside the expectation operator in (A.9) is thus bounded from above by $\widetilde{U}_{1}(T,0+)+ \int _{0}^{T}\widetilde{U}_{2}(t,0+)dt < \infty$, and so the dominated convergence theorem implies that $\hat{L}(0+) = \widetilde{U}_{1}(T,0+)+ \int _{0}^{T}\widetilde{U}_{2}(t,0+)dt< \infty$. Therefore

$$\begin{aligned} -\partial _{y}\hat{L}(0+) \ge \frac{\hat{L}(0+) - \hat{L}(y)}{y}&\ge \frac{1}{y}\bigg( \widetilde{U}_{1}(T,0+)+ \int _{0}^{T}\widetilde{U}_{2}(t,0+)dt - \widetilde{L}(y;\nu ') \bigg), \end{aligned}$$

where the last term is greater than $\chi (y;\nu ')$ for all $y\in \mathbb{R}_{++}$ and $\nu '\in \Theta$. Using (A.3), we let $y\rightarrow 0$ and obtain $-\partial _{y}\hat{L}(0+)\ge \infty$, or $\partial _{y}\hat{L}(0+)= -\infty$.

In addition, $-\widetilde{U}_{i}(t,y)$ increases in $y$ and $\lim _{y\rightarrow \infty}-\partial _{y}\widetilde{U}_{i}(t,y) = 0$ for $t\in [0,T]$. Thus for any $\epsilon >0$, there exists a constant $K(\epsilon )$ depending on $\epsilon$ such that

$$\begin{aligned} -\widetilde{U}_{1}(T,y) \le K(\epsilon ) + \epsilon y, \quad \sup _{t \in [0,T]}\big(-\widetilde{U}_{2}(t,y)\big) \le K(\epsilon ) + \epsilon y, \qquad y\in \mathbb{R}_{++}. \end{aligned}$$

By L’Hospital’s rule, we have

$$\begin{aligned} 0&\le \lim _{y\rightarrow \infty}-\partial _{y}\hat{L}(y) = \lim _{y \rightarrow \infty}\frac{-\hat{L}(y)}{y} = \lim _{y\rightarrow \infty} \sup _{\nu \in \Theta} \frac{-\widetilde{L}(y;\nu )}{y} \\ &\le \lim _{y\rightarrow \infty} \sup _{\nu \in \Theta} \mathbb{E} \bigg[ \frac{K(\epsilon )(1+T)}{y} + \epsilon \bigg( e^{-rT}Z_{T}^{ \nu} + \int _{0}^{T}e^{-rt}Z_{t}^{\nu}dt \bigg) \bigg] \le 2\epsilon . \end{aligned}$$

Therefore we have $\lim _{y\rightarrow \infty}-\partial _{y}\hat{L}(y) = 0$. □

Proof of Theorem 3.2

Lemma A.5 implies that for all $v\in \mathbb{R}_{++}$, there exists $y^{*}\in \mathbb{R}_{++}$ such that $-\partial _{y}\hat{L}(y^{*}) = v$ or, equivalently, $\chi (y^{*},\nu ^{y^{*}})=v$. Theorem A.4 and Lemma A.3 imply the existence of $(\vartheta ^{*},c^{*})\in \mathcal{A}(v)$ with $c^{*}_{t}= I_{2}(t, e^{-rt}y^{*}Z_{t}^{\nu ^{y^{*}}})$ and $V_{T}^{\vartheta ^{*},c^{*}} \ge I_{1}(T, e^{-rT}y^{*}Z_{t}^{\nu ^{y^{*}}})$. To verify the optimality of $(\vartheta ^{*},c^{*})$ and that there is no duality gap, we show the inverse inequality in (2.23) by computing

$$\begin{aligned} &\widetilde{J}(v;\vartheta ^{*},c^{*}) \\ & \ge \mathbb{E}\bigg[U_{1}\big(T,I_{1}(T, e^{-rT}y^{*}Z_{t}^{\nu ^{y^{*}}}) \big)+ \int _{0}^{T}U_{2}(t,c^{*}_{t})dt\bigg] \\ &=\mathbb{E}\bigg[U_{1}\big(T,I_{1}(T, e^{-rT}y^{*}Z_{t}^{\nu ^{y^{*}}}) \big)+ \int _{0}^{T}U_{2}(t,c^{*}_{t})dt\bigg] -y^{*}\chi (y^{*};\nu ^{y^{*}})+ y^{*}v \\ & = \mathbb{E}\bigg[\widetilde{U}_{1}(T, y^{*} e^{-rT}Z_{T}^{\nu ^{y^{*}}}) + \int _{0}^{T} \widetilde{U}_{2}(t, y^{*} e^{-rt}Z_{t}^{\nu ^{y^{*}}}) dt\bigg] + y^{*}v \\ &= \hat{L}(y^{*}) + y^{*}v \\ &\ge \inf _{y^{\prime}>0} \big( \hat{L}(y^{\prime}) + y^{\prime}v \big). \end{aligned}$$

The calculations above show that $y^{*}$ attains $\inf _{y\in \mathbb{R}_{++}}(\hat{L}(y) + vy)$. □

Appendix B: Proof of Theorem 4.16

To streamline the presentation, we introduce the following notation. Consider a cylindrical domain $\mathcal{O}:=(t_{1},t_{2})\times O \subseteq (0,T) \times (0,1)$.

• Let $\partial ^{*}\mathcal{O}$ be the boundary of $\mathcal{O}$, i.e., $\partial ^{*}\mathcal{O}: = (\{t_{1},t_{2}\}\times O) \cup ((t_{1},t_{2}) \times \partial O)$.

• Let $\mathcal{L}^{p}(\mathcal{O})$ be the space of functions $g$ with $\| g\|_{p,\mathcal{O}} =(\int _{\mathcal{O}} |g|^{p} dxdt)^{1/p} < \infty$.

• Let $W_{p}^{1,2}(\mathcal{O})$, $1< p<\infty$, be the completion of $C^{\infty}(\mathcal{O})$ under the Sobolev-type norm $\| g\|_{W_{p}^{1,2}(\mathcal{O})}= ( \int _{\mathcal{O}} (|g|^{p}+| \partial _{t} g|^{p}+|\partial _{x} g|^{p}+|\partial _{xx} g|^{p})dtdx)^{1/p}$.

• Let $\overline{C}^{\iota}(\mathcal{O})$ and $\overline{C}^{2+\iota}(\mathcal{O})$, $0<\iota \le 1$, be the Hölder space of all functions $g$ such that $|g|_{C_{\iota ,\iota /2}(\mathcal{O})}<\infty$ and $|g|^{2}_{C_{\iota ,\iota /2}(\mathcal{O})}<\infty$, respectively, where

$$\begin{aligned} |g|_{C_{\iota ,\iota /2}(\mathcal{O})}&= \sup _{(t,x)\in \mathcal{O}} |g(t,x)| +\sup _{ \substack{(x, y) \in \overline{O}^{2} \\t_{1} \leq t \leq t_{2}}} \frac{|g(t, x)-g(t, y)|}{|x-y|^{\iota}} \\ & \hphantom{=: \sup _{(t,x)\in \mathcal{O}} |g(t,x)| } +\sup _{ \substack{x \in \overline{O}\\t_{1}\le s\le t_{2}\\t_{1}\le t\le t_{2} }} \frac{|g(s, x)-g(t, x)|}{|s-t|^{\iota / 2}}, \\ |g|^{1}_{C_{\iota ,\iota /2}(\mathcal{O})} &= |g|_{C_{\iota ,\iota /2}( \mathcal{O})} + |\partial _{x}g|_{C_{\iota ,\iota /2}(\mathcal{O})}, \\ |g|^{2}_{C_{\iota ,\iota /2}(\mathcal{O})}&= |g|^{1}_{C_{\iota , \iota /2}(\mathcal{O})} + |\partial _{xx}g|_{C_{\iota ,\iota /2}( \mathcal{O})}+|\partial _{t}g|_{C_{\iota ,\iota /2}(\mathcal{O})}. \end{aligned}$$

Step 1. The PDE (4.14) that we analyse has degenerate coefficients on the boundaries of the state space, i.e., in $x=0$ and $x=1$. Thus we start with an auxiliary problem. For a fixed $\ell > 2$, consider the bounded domain $\mathcal{O}_{\ell}: = (0,T) \times (1/\ell , 1-1/\ell )$. The PDE for this auxiliary problem is expressed as

$$\begin{aligned} 0&= \bigg(\partial _{t} + \overline{\mu}(x)\partial _{x}+ \frac{1}{2} \overline{\sigma}(x)^{2}\partial _{xx}-d_{0}(x)\bigg)g(t,x) \\ & \hphantom{=:} + \mathcal{I}_{\beta}({\Lambda}^{M})(t,x) +1 \qquad \text{in } \mathcal{O}_{\ell}, \end{aligned}$$

(B.1)

$$\begin{aligned} g(t,x) = \Psi (t,x), \qquad (t,x) \in \partial ^{*}\mathcal{O}_{\ell}& := \bigg( (0,T)\times \bigg\{ \frac{1}{\ell},1-\frac{1}{\ell}\bigg\} \bigg) \\ & \hphantom{=::} \cup \bigg(\{T\}\times \Big(\frac{1}{\ell}, 1-\frac{1}{\ell}\Big) \bigg), \end{aligned}$$

where $\Psi (t,x)\in C^{1,2}(\overline{\mathcal{O}}_{\ell})$ and $\Psi (T,x) = 1$ for $x=(1/\ell ,1-1/\ell )$. As $\overline{\mathcal{O}}_{\ell}$ avoids the boundaries $x=0$ and $x=1$, with the boundedness of $\overline{\mu}$, $\overline{\sigma}$ and $d_{0}$ and the autonomous term $\mathcal{I}_{\beta}(\Lambda ^{M})$, it follows from standard parabolic PDE results that the boundary value problem (B.1) has a unique solution in $W_{p}^{1,2}(\mathcal{O}_{\ell})$ for any $p>0$; see Fleming and Rishel [22, Appendix E]. By applying the estimate in [22, Eq. (E.8)], we obtain

$$\begin{aligned} \| g \|_{W_{p}^{1,2}(\mathcal{O}_{\ell})} \le C_{\ell}^{1}\big( \| \mathcal{I}_{\beta} (\Lambda ^{M})\|_{p,\mathcal{O}_{\ell}} + \| \Psi \|_{W_{p}^{1,2}(\mathcal{O}_{\ell})} \big) \end{aligned}$$

for some constant $C_{\ell}^{1}$ depending on $\ell$. For $p>3$, the finiteness of $\| g \|_{W_{p}^{1,2}(\mathcal{O}_{\ell})}$ implies the finiteness of $|g|_{C_{\iota ,\iota /2}(\mathcal{O}_{\ell})}$ for $\iota >0$. Moreover, the estimate of [22, Eq. (E.9)] yields

$$\begin{aligned} |g|^{1}_{C_{\iota ,\iota /2}(\mathcal{O}_{\ell})} \le C_{\ell}^{2}\| g \|_{W_{p}^{1,2}(\mathcal{O}_{\ell})} \end{aligned}$$

for some constant $C_{\ell}^{2}$ depending on $\ell$. We now consider an open subset $\mathcal{O}_{\ell}^{\prime}$ of $\mathcal{O}_{\ell}$ with $\overline{\mathcal{O}}_{\ell}^{\prime} \subseteq{\mathcal{O}}_{\ell}$. Recalling Lemma 4.13, $\mathcal{I}_{\beta}(\Lambda ^{M})(t,x)$ is Hölder-continuous in $x$ with an exponent $0<\iota <1$. According to the estimate of [22, Eq. (E.10)], we have

$$\begin{aligned} |g|^{2}_{C_{\iota ,\iota /2}(\mathcal{O}_{\ell}^{\prime})} \leq C_{3}^{ \ell}\Big(|\mathcal{I}_{\beta} (\Lambda ^{M})|_{C_{\iota ,\iota /2}( \mathcal{O}_{\ell})}+\sup _{(t,x)\in \mathcal{O}_{\ell}} |g(t,x)| \Big) \end{aligned}$$

(B.2)

for a constant $C_{3}^{\ell}$ depending solely on $\mathcal{O}_{\ell}^{\prime}$ and $\mathcal{O}_{\ell}$. The Hölder norm $|g|^{2}_{C_{\iota ,\iota /2}(\mathcal{O}_{\ell}^{\prime})}$ is finite, and thus we have $g\in \overline{C}^{2+\iota}(\mathcal{O}_{\ell}^{\prime})$ for any compact subset $\mathcal{O}_{\ell}^{\prime}$ of $\mathcal{O}_{\ell}$. From Ladyženskaja et al. [32, Theorem IV.10.1], we conclude that $g \in C^{1,2}(\mathcal{O}_{\ell})$.

Step 2. We construct a sequence of functions $\widetilde{g}_{\ell}$, $\ell \ge 3$, on the state space $\mathcal{U}_{T}$. We then show that these functions converge to a classical solution for the PDE (4.14). The $C^{1,2}$-property of the limit is derived from the convergence of the cylinder $\mathcal{O}_{\ell}$ to the state space $\mathcal{U}_{T}$. For $\ell = 3,4,\dots$, we construct a function $\psi _{\ell}$ satisfying

$$\begin{aligned} \psi _{\ell} \in C^{\infty}, \qquad 0 \le \psi _{\ell}(x) \le 1, \qquad |\psi _{\ell}'(x)| \le 2, \end{aligned}$$

with $\psi _{\ell}(x) = 1$ for $x\in \mathcal{O}_{\ell}$ and $\psi _{\ell}(x) = 0$ for $x\in \mathcal{U}_{T}\backslash \mathcal{O}_{\ell +1}$. Let $\widetilde{g}_{\ell}$ be a solution of the PDE given by

$$\begin{aligned} 0&= \partial _{t}\widetilde{g}_{\ell}+ \overline{\mu}\partial _{x} \widetilde{g}_{\ell}+ \frac{1}{2} (\overline{\sigma}+ 1-\psi _{\ell} )^{2}\partial _{xx} \widetilde{g}_{\ell}-d_{0}\widetilde{g}_{\ell} \\ & \hphantom{=:} + \mathcal{I}_{\beta}(\Lambda ^{M})+1 \qquad \text{in }\mathcal{U}_{T}, \end{aligned}$$

(B.3)

subject to the boundary condition $\widetilde{g}_{\ell}(T,x) = \psi _{\ell}(x)$. Note that the PDE (B.3) is uniformly parabolic with bounded inverse $(\overline{\sigma}+ 1- \psi _{\ell})^{-1}$. It then follows by a standard parabolic PDE result [22, Theorem VI.6.1] that (B.3) has a unique solution $\widetilde{g}_{\ell}$ which is in $C^{1,2}(\mathcal{U}_{T})$ and continuous in $\overline{\mathcal{U}}_{T}$.

Take any bounded $\mathcal{O}_{\ell _{0}}\subseteq \mathcal{U}_{T}$ for some $\ell _{0}>2$. For $\ell >\ell _{0}$, by applying the estimate in [22, Eq. (E.8)] to (B.3), we obtain that $\| \widetilde{g}_{\ell} \|_{W_{p}^{1,2}(\mathcal{O}_{\ell _{0}})}$ is bounded for $p>1$ and $\widetilde{g}_{\ell}$ satisfies a Hölder condition on $\mathcal{O}_{\ell _{0}}$. In particular, for $\ell > \ell _{0}$, $\widetilde{g}_{\ell}$ solves the PDE (4.4) in $\mathcal{O}_{\ell _{0}}$. That is,

$$\begin{aligned} \partial _{t} \widetilde{g}_{\ell}+ \overline{\mu}\partial _{x} \widetilde{g}_{\ell}+ \frac{1}{2}\overline{\sigma}^{2}\partial _{xx}\widetilde{g}_{\ell}-d_{0} \widetilde{g}_{\ell} + \mathcal{I}_{\beta}(\Lambda ^{M})+1= 0 \qquad \text{in }\mathcal{O}_{\ell _{0}}. \end{aligned}$$

Taking into account the estimates of (B.2) in Step 1, we see that $\partial _{t}\widetilde{g}_{\ell}$, $\partial _{x}\widetilde{g}_{\ell}$ and $\partial _{xx}\widetilde{g}_{\ell}$ also satisfy a uniform Hölder condition on $\mathcal{O}_{\ell _{0}}$. Note that the coefficients of these equations are the same for all $\ell$ and that the $\widetilde{g}_{\ell}$ are uniformly bounded from above on $\mathcal{O}_{\ell _{0}}$. According to [22, Theorem 15], it then follows that for any subsequence $( \widetilde{g}_{\ell '})$ of $(\widetilde{g}_{\ell})$, there exists a further subsequence $( \widetilde{g}_{\ell ''})$ (and its derivatives $( \partial _{t}\widetilde{g}_{\ell ''})$, $( \partial _{x}\widetilde{g}_{\ell ''})$ and $( \partial _{xx}\widetilde{g}_{\ell ''})$) that tends toward the limit $\widetilde{g}$ (and to $\partial _{t}\widetilde{g}$, $\partial _{x}\widetilde{g}$ and $\partial _{xx}\widetilde{g}$, respectively) uniformly on each compact subset of $\overline{\mathcal{O}}_{\ell _{0}}$ (resp. $\mathcal{O}_{\ell _{0}}$). From the continuity of $\widetilde{g}_{\ell ''}$ and the property of uniform convergence, it follows that $\widetilde{g}\in C^{1,2}(\mathcal{U}_{T})$ as $\mathcal{O}_{\ell _{0}}$ is arbitrarily chosen. In conclusion, $\widetilde{g}$ is a classical solution of the PDE (4.14) with the terminal condition $\widetilde{g}(T,x) = 1$.  □

Appendix C: Proofs omitted from the main text

Proof of Proposition 2.5

We introduce the infinitesimal generator ℒ associated with (2.12), which operates on $\phi \in C^{2}([0,1])$ by

$$\begin{aligned} \mathcal{L}\phi (x)&:= \big(a_{2}-(a_{1}+a_{2})x\big)\phi '(x)+ \frac{1}{2}x^{2}(1-x)^{2} (\theta _{1}-\theta _{2})^{2}\phi{''}(x) \\ & \hphantom{=::} + \lambda \int _{\mathcal{Z}} \Big(\phi \big(\xi (x,z)\big) - \phi (x) \Big)\hat{f}(x,z)dz. \end{aligned}$$

We show that the boundary 0 is unattainable from inside the state space; the arguments for the boundary 1 are similar. Without loss of generality, we prove this result for the process $\pi ^{x_{0}}:=(\pi ^{x_{0}}_{t})_{t \ge 0}$, which is defined as the solution of (2.12) starting from time 0 and a given starting point $x_{0}\in (0,1)$. For the function $\phi (x)=1/x$, we have $\phi '(x)= - 1/x^{2}$, $\phi ''(x) = 2/x^{3}$ and $\phi (x)\rightarrow \infty$ as $x\rightarrow 0$. Consequently,

$$\begin{aligned} \mathcal{L}\phi (x) &\le \frac{1}{x}\bigg( a_{1}+a_{2} + (1-x)^{2}( \theta _{1}-\theta _{2})^{2} \\ & \hphantom{= \frac{1}{x}\bigg(} +\lambda \int _{\mathcal{Z}} \frac{ (f_{2}(z)-f_{1}(z) )(1-x)\hat{f}(x,z)}{f_{1}(z)} dz \bigg) \\ &\le \frac{1}{x}\big( a_{1}+a_{2} + (\theta _{1}-\theta _{2})^{2} + \lambda (b_{\max}-1) \big) = L_{0} \phi (x), \end{aligned}$$

where $L_{0}: = a_{1}+a_{2} + (\theta _{1}-\theta _{2})^{2} +\lambda (b_{ \max}-1)>0$. Define $\tau _{n}:=\inf \{t>0:\pi _{t}^{x_{0}} \le n \}$ for $0\le n<1$. From the calculations above, we have

$$\begin{aligned} \mathbb{E}[ \phi (\pi ^{x_{0}}_{t \wedge \tau _{n} })] \le \phi (x_{0}) + L_{0}\int _{0}^{t}\mathbb{E}[ \phi (\pi ^{x_{0}}_{s \wedge \tau _{n} }) ]ds,\qquad t>0, n\in [0,1). \end{aligned}$$

By Gronwall’s lemma, we obtain

$$\begin{aligned} \mathbb{E}[ \phi (\pi ^{x_{0}}_{t \wedge \tau _{n} }) ] \le e^{C_{b}t} \phi (x_{0}), \qquad t>0. \end{aligned}$$

(C.1)

Assume that 0 is attainable, that is, $\mathbb{P}[\tau _{0} < \infty ] >0$. Then for a large $T_{0}>0$, we have $\mathbb{P}[\tau _{0} \le T_{0}] > 0$. Taking $t = T_{0}$ in (C.1), we get

(C.2)

As $\phi (\pi ^{x_{0}}_{\tau _{0}}) = \phi (0) = \infty$ on a subset $\{ \tau _{0} \le T_{0}\}$ of positive measure, the left-hand side of (C.2) is infinite while the right-hand side is finite, which is a contradiction. Therefore $\mathbb{P}[\tau _{0} < \infty ] = 0$. □

Proof of Proposition 2.6

This result is obtained by slightly modifying the proof of Proposition 4.5 in Sect. 4.2. Consider the case where $t=0$. From the definition of a Feller process, we only need to show that $|\mathbb{E}^{0,x}[f(\pi ^{x}_{s})]-\mathbb{E}^{0,y}[f(\pi _{s}^{y})]|$ tends to 0 when $|x-y|\rightarrow 0$ for any $s>0$ and any bounded continuous function $f$. The proof here is even simpler because we can use the uniform norm of the function $f$ to establish appropriate estimates as in the proof of Proposition 4.5. □

Proof of Proposition 2.8

For any given $(t,x,v) \in \mathcal{U}_{T}\times \mathbb{R}_{++}$, according to Theorems 2.7 and 3.2, there is no duality gap, that is,

$$\begin{aligned} J(t,x,v) = \inf _{y\in \mathbb{R}_{++}} \big(\hat{L}(t,x,y) +vy\big) = \frac{1}{\kappa} v^{\kappa} \Lambda ^{M}(t,x)^{1-\kappa}. \end{aligned}$$

We now derive the optimal controls for the primal problem. As $\hat{\Lambda}$ is smooth and due to the terminal condition $\hat{\Lambda}(T,x) = 1$ for $x \in [0,1]$, it is standard to verify that the process

$$\begin{aligned} \mathcal{M}_{s}: =( e^{-r(s-t)}Z_{s}^{\nu ^{*}})^{\beta} \hat{\Lambda}(s,\pi _{s}) + \int _{t}^{s} ( e^{-r(u-t)}Z_{u}^{\nu ^{*}})^{ \beta} du,\qquad s\in [t,T], \end{aligned}$$

is a $(\mathbb{P}^{t,x},\mathbb{H})$-martingale for $Z^{\nu ^{*}}$ defined as in (2.27). Thus $\mathbb{E}^{t,x}[\mathcal{M}_{T}|\mathcal{H}_{s}] = \mathcal{M}_{s}$. According to Theorem 3.2, the candidate optimal wealth process $V^{*}$ is defined as

$$\begin{aligned} {V}^{*}_{s} := \mathbb{E}^{t,x}\bigg[ e^{-r(T-s)}Z^{\nu ^{*}}_{T}X^{*} + \int _{s}^{T} e^{-r(u-s)}Z^{\nu ^{*}}_{u}{c}^{*}_{u} du \bigg\vert \mathcal{H}_{s} \bigg],\qquad s \in [t,T], \end{aligned}$$

and $X^{*}= {v}( e^{-r(T-t)}Z_{T}^{\nu ^{*}})^{\beta -1}/{\hat{\Lambda}(t,x)}$ and $c^{*}_{s} = {v}( e^{-r(s-t)}Z_{s}^{\nu ^{*}})^{\beta -1}/{ \hat{\Lambda}(t,x)}$. Hence

$$\begin{aligned} {V}^{*}_{s} &= \frac{ e^{r(s-t)}v}{\hat{\Lambda}(t,x) Z_{s}^{\nu ^{*}}}\mathbb{E}^{t,x} \bigg[ \mathcal{M}_{T} - \int _{t}^{s} ( e^{-r(u-t)}Z_{u}^{\nu ^{*}})^{ \beta} du \bigg\vert \mathcal{H}_{s} \bigg] \\ &= v (e^{-r(s-t)}Z_{s}^{t,{\nu}^{*}})^{\beta -1} \frac{\hat{\Lambda}(s,\pi _{s})}{\hat{\Lambda}(t,x)}. \end{aligned}$$

Applying Itô’s lemma to the discounted wealth process $(e^{-r(s-t)}V_{s}^{*})_{s \in [t,T]}$ and taking into account that $\hat{\Lambda}$ solves the PDE (4.4) by Theorem 4.1 and the form of $\nu ^{*}$ in (4.7), we have

$$ d(e^{-r(s-t)}V_{s}^{*}) = \frac{ve^{-\beta r(s-t)}(Z_{s}^{\nu ^{*}})^{\beta -1}}{\hat{\Lambda}(t,x) } \Big( -1ds + \big( \hat{\Lambda}(1-\beta )\hat{\theta} + \partial _{x} \hat{\Lambda}\big)(s,\pi _{s}) d\widetilde{W}^{\mathbb{Q}}_{s} \Big), $$

where $d\widetilde{W}^{\mathbb{Q}}_{s}: =\hat{\theta}(\pi _{s})ds+d \widetilde{W}_{s}$. Therefore

$$\begin{aligned} d(e^{-r(s-t)} V^{*}_{s}) + e^{-r(s-t)}c^{*}_{s}ds &= e^{-r(s-t)}{{ \vartheta}^{*}_{s}}\sigma d\widetilde{W}^{\mathbb{Q}}_{s}, \\ \vartheta ^{*}_{s} &=\hat{\vartheta}(s,\pi _{s},V_{s}^{*}) \\ &= \frac{{V}^{*}_{s}}{{\sigma}}\bigg((1-\beta )\hat{\theta}(\pi _{s}) + \frac{\partial _{x} \hat{\Lambda}(s,\pi _{s})}{\hat{\Lambda}(s,\pi _{s})} \bigg), \quad \,\,\, s\in [t,T]. \end{aligned}$$

The candidate optimal consumption process ${c}^{*}$ is written as

$$\begin{aligned} {c}^{*}_{s}= \hat{c}(s,\pi _{s}, {V}^{*}_{s}), \qquad \hat{c}(s,x,v): = \frac{v}{\hat{\Lambda}(s,x)},\qquad s\in [t,T]. \end{aligned}$$

From the boundedness and continuity of $\hat{\Lambda}$ (Proposition 4.2 and Theorem 4.1) and using the formula for ${V}^{*}$, we conclude that $({\vartheta}^{*},{c}^{*})$ is in $\mathcal{A}(t,x,v)$ and is therefore the optimal control pair for the primal problem (2.14). □

Proof of Lemma 4.4

According to the definitions in (4.2), $\overline{\mu}(\,\cdot \,)$ and $\overline{\sigma}(\,\cdot \,)$ are continuously differentiable functions of the state variable on the bounded interval $[0,1]$. Therefore, the Lipschitz and growth conditions (4.17) are met. Recall the definition of $\xi$ in (2.11); the second part of (4.18) holds because

$$\begin{aligned} 0\le \frac{xf_{1}(z)}{(xf_{1}(z)+(1-x)f_{2}(z))} \le 1,\qquad x\in [0,1]. \end{aligned}$$

Next, for the first part of (4.18), we have

$$\begin{aligned} |\xi (x, z)-\xi (y, z) | \le \max \bigg\{ \frac{f_{1}(z)}{f_{2}(z)}, \frac{f_{2}(z)}{f_{1}(z)}\bigg\} |x-y|. \end{aligned}$$

Let $\rho (z) = \max \{{f_{1}(z)}/{f_{2}(z)},{f_{2}(z)}/{f_{1}(z)}\}$. We have $\int _{\mathcal{Z}}\rho ^{2}(z)f_{1}(z)dz <\infty$ under Condition 2.1. □

Proof of Proposition 4.6

We provide the proof for $k=2$, and the assertions for $k\in [0,2]$ follow from the Hölder inequality. Using Kunita [31, Corollary 2.12] and $\nu \in \Theta ^{t,M}$, there exists a positive constant $C$ such that for all $t \geq s$,

$$\begin{aligned} &\widetilde{\mathbb{E}}^{t,x,\nu}\Big[ \sup _{t \le u \le s}|\pi _{u}^{t,x, \nu}|^{2} \Big] \\ &\le C \bigg( |x|^{2} + \widetilde{\mathbb{E}}^{t,x,\nu} \bigg[ \int _{t}^{s}| \overline{\mu}(\pi _{u}^{t,x,\nu})|^{2} du \bigg] + \widetilde{\mathbb{E}}^{t,x,\nu} \bigg[ \ \int _{t}^{s} | \overline{\sigma}(\pi _{u}^{t,x,\nu})|^{2} du \bigg] \\ & \hphantom{=:C \bigg(} + \widetilde{\mathbb{E}}^{t,x,\nu}\bigg[ \int _{t}^{s} \int _{ \mathcal{Z}} \lambda | \xi (\pi _{u-}^{t,x,\nu},z) - \pi _{u-}^{t,x, \nu}|^{2} \hat{f}(\pi _{u-}^{t,x,\nu},z) dz du \bigg]\bigg). \end{aligned}$$

We use the linear growth property of $\overline{\mu}$, $\overline{\sigma}$ and $\xi$ given in Lemma 4.4 to obtain

$$\begin{aligned} \widetilde{\mathbb{E}}^{t,x,\nu}\Big[ \sup _{t \le u \le s}|\pi _{u}^{t,x, \nu}|^{2} \Big] &\le C\bigg( |x|^{2} + \widetilde{\mathbb{E}}^{t,x, \nu} \bigg[ \int _{t}^{s} \Big(1+ \sup _{t \le u \le s}|(\pi _{u}^{t,x, \nu})|^{2} \Big)du \bigg] \bigg). \end{aligned}$$

Then (4.21) follows by Gronwall’s inequality. A similar argument applies to (4.22). □

Proof of Proposition 4.11

This proof is motivated by Barles and Imbert [4, Proposition 1.3] and Seydel [43, Proposition 5.4]. We extend their arguments to the current Lévy-type jump setting. We start by analysing the operator $H_{g}[t,x,\nu ]$. Let $\nu ^{(k)}\in [-M,M]$ with $\nu ^{(k)}\rightarrow \nu$, $x_{k}\in [0,1]$ with $x_{k} \rightarrow x$, and let $(g_{k})$ be a sequence of uniformly bounded functions such that $|g_{k}| \le \phi$ with bounded $\phi \in C(\overline{\mathcal{U}}_{T})$ and $\lim _{k \rightarrow \infty} g_{k} = g$. By dominated convergence, using the continuity of $\xi$ and $\hat{f}$ in $x$, we have

$$\begin{aligned} &\lim _{k\rightarrow \infty} \int _{\mathcal{Z}} \Big(g_{k}\big(t, \xi (x_{k},z)\big) - g_{k}(t, x_{k}) \Big) e^{\beta \nu ^{(k)}} \hat{f}(x_{k},z) dz \\ &= \int _{\mathcal{Z}} \Big(g\big(t,\xi (x,z)\big) - g(t, x) \Big)e^{ \beta \nu}\hat{f}(x,z) dz, \qquad t\in [0,T]. \end{aligned}$$

(C.3)

Let $g$ be a viscosity subsolution according to Definition 4.10. Take $(t_{0},x_{0})\in {\mathcal{U}}_{T}$ and $\psi \in C^{1,2}(\overline{\mathcal{U}}_{T})$ such that $v-\psi$ has a global maximum at $(t_{0},x_{0})$. By fixing $\nu \in [-M,M]$, we have $H_{g}(t_{0},x_{0},\nu ) \le H_{\psi}(t_{0},x_{0},\nu )$; therefore

$$\begin{aligned} \bigg(-{\partial _{t}}-\overline{\mu}(x_{0})\partial _{x}-\frac{1}{2} \overline{\sigma}(x_{0})^{2}\partial _{xx}\bigg)\psi (t_{0},x_{0})-1 - \max _{\nu \in [-M,M]} H_{\psi}(t_{0},x_{0},\nu )\leq 0, \end{aligned}$$

which implies that $g$ is also a viscosity subsolution according to Definition 4.8.

Conversely, let $g$ be a viscosity subsolution according to Definition 4.8. Take $(t_{0},x_{0})\in {\mathcal{U}}_{T}$ and $\psi \in C^{1,2}(\overline{\mathcal{U}}_{T})$ such that $g-\psi$ has a global maximum at $(t_{0},x_{0})$. Consider for a sufficiently small $\epsilon _{0}\in (0,1)$ the function

As $\varphi$ is clearly continuous, we can construct a bounded sequence $(\varphi _{k}) \subseteq C^{1,2}(\overline{\mathcal{U}}_{T})$ such that $|\varphi _{k}|\le \psi$ with $\lim _{k\rightarrow \infty}\varphi _{k} = g$. By construction, $g\le \varphi _{k}$ with equality at $(t_{0},x_{0})$. From Definition 4.8, we find that for all $k$,

$$\begin{aligned} \bigg(-{\partial _{t}}-\overline{\mu}(x_{0})\partial _{x}-\frac{1}{2} \overline{\sigma}(x_{0})^{2}\partial _{xx}\bigg)\psi (t_{0},x_{0})-1 - \max _{\nu \in [-M,M]} H_{\varphi _{k}}(t_{0},x_{0},\nu ) \leq 0. \end{aligned}$$

For each $k$, the maximum for the left-hand side of the above equation is attained by $\nu ^{(k)}$. By choosing a subsequence such that $\nu ^{(k)} \rightarrow \nu \in [-M,M]$ and using the limit in (C.3), we have

$$\begin{aligned} \bigg(-{\partial _{t}}-\overline{\mu}(x_{0})\partial _{x}-\frac{1}{2} \overline{\sigma}(x_{0})^{2}\partial _{xx}\bigg)\psi (t_{0},x_{0})-1 - \max _{\nu \in [-M,M]} H_{\varphi}(t_{0},x_{0},\nu ) \leq 0. \end{aligned}$$

Finally, sending $\epsilon _{0}$ to 0 completes the proof. □

Proof of Lemma 4.13

For $t\in [0,T)$ and $x,y\in [0,1]$, we have

$$\begin{aligned} &|\mathcal{I}_{\beta}(\Lambda ^{M})(t,x) - \mathcal{I}_{\beta}( \Lambda ^{M})(t,y)| \\ &\le (1-\beta )\lambda \int _{\mathcal{Z}} \big|{\Lambda ^{M}\big(t, \xi (x,z)\big)}^{\frac{1}{1-\beta}}-{\Lambda ^{M}(t,x)^{ \frac{1}{1-\beta}}}\big| \\ & \hphantom{=:(1-\beta )\lambda \int _{\mathcal{Z}}} \times \big| \Lambda ^{M}(t,x)^{\frac{\beta}{\beta -1}}\hat{f}(x,z) - \Lambda ^{M}(t,y)^{\frac{\beta}{\beta -1}}\hat{f}(y,z)\big| dz \\ & \hphantom{=:} + (1-\beta )\lambda \int _{\mathcal{Z}} \Lambda ^{M}(t,y)^{ \frac{\beta}{\beta -1}}\hat{f}(y,z) \Big( \big| \Lambda ^{M}\big(t, \xi (x,z)\big)^{\frac{1}{1-\beta}} -\Lambda ^{M}\big(t,\xi (y,z)\big)^{ \frac{1}{1-\beta}}\big| \\ & \hphantom{=:+ (1-\beta )\lambda \int _{\mathcal{Z}} \Lambda ^{M}(t,y)^{\frac{\beta}{\beta -1}}\hat{f}(y,z) \Big(} + \big|\Lambda ^{M}(t,x)^{\frac{1}{1-\beta}} -\Lambda ^{M}(t,y)^{ \frac{1}{1-\beta}}\big|\Big) dz. \end{aligned}$$

By repeatedly using the Lipschitz-continuity and boundedness of $\Lambda ^{M}$, the properties of $\xi$ given in Lemma 4.4 and Condition 2.1, we find that the above terms are bounded from above. □

Appendix D: Supplementary notations and conditions

Definition D.1

For any filtration $\mathbb{G}$, we denote the predictable $\sigma$-field on the product space $[0, T] \times \Omega$ by ${\mathcal{P}}(\mathbb{G})$ and the Borel $\sigma$-algebra on $\mathcal{Z}$ by $\mathcal{B}(\mathcal{Z})$. Then any $H:[0, T] \times \Omega \times \mathcal{Z} \rightarrow \mathbb{R}$ which is $({\mathcal{P}}(\mathbb{G}) \times \mathcal{B}(\mathcal{Z}))$-measurable is called a $\mathbb{G}$-pre- dictable process indexed by $\mathcal{Z}$.

Let $\mathcal{F}_{t}^{N}:=\sigma \{N((0, s] \times A): 0 \leq s \leq t, A \in \mathcal{B}(\mathcal{Z})\}$; then $\mathbb{F}^{N}=(\mathcal{F}_{t}^{N})_{0 \le t \le T}$ is the filtration generated by the random measure $N(d t, d z)$. It is right-continuous by Brémaud [8, Appendix A2, Theorem T25].

Definition D.2

Given any filtration $\mathbb{G}$ with $\mathbb{G} \subseteq \mathbb{F}^{N}$, the $\mathbb{G}$-dual predictable projection of $N$, denoted by $N^{\mathbb{P}, \mathbb{G}}(d s, d z)$, is the $\mathbb{G}$-predictable random measure such that for any nonnegative $\mathbb{G}$-predictable process $\Phi$ indexed by $\mathcal{Z}$, we have

$$\begin{aligned} \mathbb{E}\bigg[\int _{0}^{\infty} \int _{\mathcal{Z}} \Phi (s, z) N(d s, d z)\bigg]=\mathbb{E}\bigg[\int _{0}^{\infty} \int _{\mathcal{Z}} \Phi (s, z) N^{\mathbb{P}, \mathbb{G}}(d s, d z)\bigg]. \end{aligned}$$

Assumption D.3

For the model considered in (3.1), we make the following assumptions. For all $i\in \mathcal{S}:=\{1,2,\dots ,n_{0}\}$ with $n_{0} \ge 2$, the state space of the Markov chain $\alpha$, we assume that $\gamma$ is a Lévy kernel such that $\gamma (i,dz)$ is a nonnegative $\sigma$-finite measure on $\mathcal{B}(\mathcal{Z})$. There exists a constant $C$ such that $\sup _{i \in \mathcal{S}} \int _{\mathcal{Z}} \gamma (i,dz) \le C< \infty$. The functions $b_{1}(q,i)$ for $i\in \mathcal{S}$, $\sigma _{1}(q)$, $\sigma _{2}(q)$ and $b_{2}(q,z)$ for $z\in \mathcal{Z}$ are continuous in the variable $q$. In addition, we assume that the following two conditions hold:

• (i) For all $i \in \mathcal{S}$ and $q_{1}, q_{2}\in \mathbb{R}$, there is a constant $C$ such that

  $$\begin{aligned} &|b_{1}(q_{1}, i)-b_{1}(q_{2}, i)|^{2}+|\sigma _{1}(q_{1})-\sigma _{1}(q_{2})|^{2} +|\sigma _{2}(q_{1})-\sigma _{2}(q_{2})|^{2} \\ &+ \int _{\mathcal{Z}} |b_{2}(q_{1},z) -b_{2}(q_{2},z)|^{2} \gamma (i,dz) \\ &\leq C|q_{1}-q_{2}|^{2}. \end{aligned}$$

• (ii) For all $i \in \mathcal{S}$ and $q\in \mathbb{R}$, there is a constant $C$ such that

  $$\begin{aligned} |b_{1}(q, i)|^{2}+|\sigma _{1}(q)|^{2}+|\sigma _{2}(q)|^{2} +\int _{ \mathcal{Z}} |b_{2}(q,z)|^{2} \gamma (i,dz) \leq C(1+|q|^{2}). \end{aligned}$$

The above conditions ensure the existence and uniqueness of the solution to (3.1) (using the standard localisation technique in Xi and Zhu [47, Theorem 5.2] and Xi and Zhu [48, Theorem 3.6], then employing Komatsu [29, Theorem 5.2]).

Proposition D.4

Under Assumption D.3, let $Y$ be any $(\mathbb{P},\mathbb{H})$-local martingale with $Y_{0} = 0$. Then there exist ℍ-predictable processes $\psi$, $\Psi$ and $\varphi$ such that

$$\begin{aligned} Y_{t} = \int _{0}^{t} \psi _{u} d \widetilde{W}_{u} + \int _{0}^{t} \Psi _{u} \widetilde{B}_{u} + \int _{0}^{t}\int _{\mathbb{R}} \varphi (u,q) \overline{m}^{\pi}(du,dq), \qquad 0\le t \le T, \\ {\int _{0}^{T} (\psi _{u}^{2} + \Psi _{u}^{2}) du} + \int _{0}^{T} \int _{\mathbb{R}} |{\varphi}(u,q)| \hat{\lambda}(\pi _{u-}) \hat{\phi}_{u}(\pi _{u-},q)(du,dq) < \infty \qquad \mathbb{P} \textit{-a.s.} \end{aligned}$$

The proof follows by modifying the arguments in Callegaro et al. [9, Proposition 3.5] and Ceci and Colaneri [11, Proposition 2.4].