Machine learning with kernels for portfolio valuation and risk management

Abstract

We introduce a simulation method for dynamic portfolio valuation and risk management building on machine learning with kernels. We learn the dynamic value process of a portfolio from a finite sample of its cumulative cash flow. The learned value process is given in closed form thanks to a suitable choice of the kernel. We show asymptotic consistency and derive finite-sample error bounds under conditions that are suitable for finance applications. Numerical experiments show good results in large dimensions for a moderate training sample size.

Appendices

Appendix A: Some facts about Hilbert spaces

For the convenience of the reader, we collect here some basic definitions and facts about Hilbert spaces on which our framework builds. We first recall some basics, then introduce kernels and reproducing kernel Hilbert spaces, and finally review compact operators and random variables on separable Hilbert spaces. For more background, we refer to e.g. the textbooks by Kato [32, Chap. 5], Cucker and Zhou [16, Chap. 2], Steinwart and Christmann [62, Chaps. 4 and 6] and Paulsen and Raghupathi [43, Chap. 2].

1.1 A.1 Basics

We start with briefly recalling some elementary facts and conventions for Hilbert spaces. Let $H$ be a Hilbert space and ℐ some (not necessarily countable) index set. We call a set $\{\phi _{i}: i\in {\mathcal{I}}\}$ in $H$ an orthonormal system (ONS) in $H$ if $\langle \phi _{i},\phi _{j}\rangle _{H}=\delta _{ij}$ for the Kronecker delta $\delta _{ij}$. We call $\{\phi _{i}: i\in {\mathcal{I}}\}$ an orthonormal basis (ONB) of $H$ if it is an ONS whose linear span is dense in $H$. In this case, for every $h\in H$, we have $h=\sum _{i\in {\mathcal{I}}} \langle h,\phi _{i}\rangle _{H} \, \phi _{i}$ and the Parseval identity $\|h\|_{H}^{2} =\sum _{i\in {\mathcal{I}}} |\langle h,\phi _{i} \rangle _{H}|^{2}$ holds, where only a countable number of coefficients $\langle h,\phi _{i}\rangle _{H}$ are different from zero. Here we recall the elementary fact that the closure of a set $A$ in $H$ is equal to the set of all limit points of sequences in $A$; see Aliprantis and Border [1, Theorem 2.37].

1.2 A.2 Reproducing kernel Hilbert spaces

Let $k:E\times E\to {\mathbb{R}}$ be a kernel with RKHS ℋ, as introduced at the beginning of Sect. 2. We collect some basic facts that are used in the paper.

The following lemma gives some useful representations of $k$, see [43, Theorems 2.4 and 12.11], which hold for an arbitrary set $E$.

Lemma A.1

1) Let $\{\phi _{i}: i\in {\mathcal{I}}\}$ be an ONB of ℋ. Then $k(x,y)=\sum _{i\in {\mathcal{I}}}\phi _{i}(x)\phi _{i}(y)$, where the series converges pointwise.

2) There exists a stochastic process $\phi _{\omega }(x)$, indexed by $x\in E$, on some probability space $(\Omega ,{\mathcal{F}},{\mathbb{M}})$ such that $\omega \mapsto \phi _{\omega }(x):\Omega \to {\mathbb{R}}$ are square-integrable random variables and $k(x,y) = \int _{\Omega }\phi _{\omega }(x) \phi _{\omega }(y)\,d{\mathbb{M}}( \omega )$.

The next lemma provides sufficient conditions for continuity of the functions in ℋ and separability of ℋ.

Lemma A.2

Assume $(E,\tau )$ is a topological space. Then the following hold:

1) If $k$ is continuous at the diagonal in the sense that

$$ \lim _{y\to x} k(x,y) =\lim _{y\to x} k(y,y) = k(x,x)\qquad \textit{for all }x\in E, $$

(A.1)

then every $h\in {\mathcal{H}}$ is continuous.

2) If every $h\in {\mathcal{H}}$ is continuous and $(E,\tau )$ is separable, then ℋ is separable.

Proof

1) Let $h\in {\mathcal{H}}$. Then $|h(x)-h(y)| \le \| k(\cdot ,x)-k(\cdot ,y)\|_{{\mathcal{H}}}\|h\|_{{ \mathcal{H}}}$ by (2.2), where the term $\| k(\cdot ,x)-k(\cdot ,y)\|_{{\mathcal{H}}}= (k(x,x)-2 k(x,y)+k(y,y))^{1/2}$. By (A.1), we have that $h$ is continuous.

2) This follows from Berlinet and Thomas-Agnan [6, Theorem 15]. □

1.3 A.3 Compact operators on Hilbert spaces

Let $H,H'$ be separable Hilbert spaces. A linear operator (or simply an operator) $T:H\to H'$ is compact if the image $(Th_{n})_{n\ge 1}$ of any bounded sequence $(h_{n})_{n \ge 1}$ of $H$ contains a convergent subsequence.

An operator $T:H\to H'$ is called Hilbert–Schmidt if it satisfies

$$ \|T\|_{2}=\bigg(\sum _{i\in I} \|T \phi _{i}\|^{2}_{H'}\bigg)^{1/2} < \infty , $$

and trace-class if

$$ \|T\|_{1}=\sum _{i\in I} \big\langle (T^{\ast }T)^{1/2}\phi _{i}, \phi _{i} \big\rangle _{H} < \infty , $$

for some (and thus any) ONB $\{\phi _{i}: i\in I\}$ of $H$. We denote the usual operator norm by $\|T\|=\sup _{h\in H\setminus \{0\}} \|Th\|_{H'}/\|h\|_{H}$. We have $\|T\|\le \|T\|_{2}\le \|T\|_{1}$; thus trace-class implies Hilbert–Schmidt, and every Hilbert–Schmidt operator is compact.

A self-adjoint operator $T:H\to H$ is nonnegative if $\langle Th, h \rangle _{H} \ge 0$ for all $h \in H$. Let $T:H\to H$ be a nonnegative, self-adjoint, compact operator. Then there exist an ONS $\{\phi _{i}: i\in I\}$ for a countable index set $I$ and eigenvalues ${\mu }_{i}>0$ such that the spectral representation $T = \sum _{i\in I} {\mu }_{i}\langle \cdot ,\phi _{i}\rangle _{ \mathcal{H}}\, \phi _{i}$ holds.

1.4 A.4 Random variables in Hilbert spaces

Let $H$ be a separable Hilbert space and ℚ a probability measure on the Borel $\sigma$-field of $H$. The characteristic function $\widehat{{\mathbb{Q}}}:H\to {\mathbb{C}}$ of ℚ is then defined, for $h \in H$, by $\widehat{{\mathbb{Q}}}(h) = \int _{H} {\mathrm{e}}^{i \langle y,h \rangle _{H}} {\mathbb{Q}}[dy]$.

If $\int _{H} \|y\|_{H} {\mathbb{Q}}[dy] < \infty$, then the mean $m_{\mathbb{Q}}=\int _{H} y {\mathbb{Q}}[dy]$ of ℚ is well defined, where the integral is in the Bochner sense; see e.g. Da Prato and Zabczyk [17, Sect. 1.1]. If $\int _{H} \|y\|^{2}_{H} {\mathbb{Q}}[dy] < \infty$, then the covariance operator $Q_{\mathbb{Q}}$ of ℚ is defined by

$$ \langle Q_{\mathbb{Q}}h_{1}, h_{2} \rangle _{H} = \!\int _{H} \! \langle y, h_{1} \rangle _{H} \langle y, h_{2} \rangle _{H} { \mathbb{Q}}[dy] - \langle m_{\mathbb{Q}}, h_{1}\rangle _{H} \langle m_{ \mathbb{Q}},h_{2}\rangle _{H}, \qquad h_{1}, h_{2} \in H. $$

Hence $Q_{\mathbb{Q}}$ is a nonnegative, self-adjoint, trace-class operator. The measure ℚ is Gaussian, ${\mathbb{Q}}\sim {\mathcal{N}}(m_{\mathbb{Q}},Q_{\mathbb{Q}})$, if $\widehat{{\mathbb{Q}}}(h) = {\mathrm{e}}^{i \langle m_{\mathbb{Q}},h \rangle _{H} - \frac{1}{2} \langle Q_{\mathbb{Q}}h, h \rangle _{H}}$; see [17, Sect. 2.3].

Now let $(\Omega , {\mathcal{F}}, \mathbb{P})$ be a probability space and $(Y_{n})_{n \ge 1}$ a sequence of i.i.d. $H$-valued random variables with distribution $Y_{1} \sim {\mathbb{Q}}$. Assume that ${ \mathbb{E}}[Y_{1}]=0$. If we have $\mathbb{E}[\|Y_{1}\|^{2}_{H}] < \infty$, then $(Y_{n})_{n \ge 1}$ satisfies the law of large numbers (see Hoffmann-Jørgensen and Pisier [28, Theorem 2.1])

$$ \frac{1}{n} \sum _{i= 1}^{n} Y_{i} \xrightarrow{\ \ a.s.\ \ } 0 $$

(A.2)

and the central limit theorem (see [28, Theorem 3.6])

$$ \frac{1}{\sqrt{n}} \sum _{i = 1 }^{n} Y_{i} \xrightarrow{\ \ d\ \ } \mathcal{N}(0,Q_{\mathbb{Q}}). $$

(A.3)

If $\|Y_{1}\|_{H} \le 1$ a.s., then $(Y_{n})_{n \ge 1}$ satisfies the concentration inequality, called the Hoeffding inequality (see Pinelis [46, Theorem 3.5]), namely

$$ {\mathbb{P}}\bigg[\bigg\| \frac{1}{n} \sum _{i = 1}^{n} Y_{i} \bigg\| _{ \mathcal{H}}\ge \tau \bigg] \le 2 {\mathrm{e}}^{-\frac{\tau ^{2} n}{2}}, \qquad \tau >0. $$

(A.4)

Appendix B: Proofs

We collect here all proofs from the main text.

2.1 B.5 Properties of the embedding operator

For completeness, we first recall some basic properties of the operator $J$ defined in Sect. 2, which are used throughout the paper.

The operator $JJ^{\ast }$ is clearly nonnegative and self-adjoint, and trace-class since $J$ and $J^{\ast }$ are Hilbert–Schmidt. Therefore, there exist an ONS $\{v_{i}: i\in I\}$ in $L^{2}_{\mathbb{Q}}$ and eigenvalues ${\mu }_{i}>0$, $i\in I$, for a countable index set $I$ with $|I|=\dim (\operatorname{Im}J^{\ast })$ such that $\sum _{i\in I} {\mu }_{i}<\infty$ and the spectral representation

$$ J J^{\ast }= \sum _{i\in I} {\mu }_{i} \langle \cdot ,v_{i}\rangle _{ \mathbb{Q}}\, v_{i} $$

(B.1)

holds. The summability of the eigenvalues ${\mu }_{i}$ implies that the convergence in (B.1) holds in the Hilbert–Schmidt norm sense. By the open mapping theorem and since $\ker (J J^{\ast }) =\ker J^{\ast }$, we obtain that $JJ^{\ast }$ is invertible if and only if $\ker J^{\ast }=\{0\}$ and $\dim (L^{2}_{\mathbb{Q}})<\infty$. It follows by inspection that $u_{i} = {\mu }_{i}^{-1/2} J^{\ast }v_{i}$ form an ONS in ℋ and that $J^{\ast }J u_{i} = {\mu }_{i}^{-1/2} J^{\ast }J J^{\ast }v_{i} = {\mu }_{i} u_{i}$. Then, since we have ${\mathcal{H}}= \overline{\operatorname{Im}J^{\ast }} \oplus \ker J$ and $\overline{\operatorname{Im}J^{\ast }} = \overline{\operatorname{span}\{u_{i} : i \in I\}}$, $J^{\ast }J$ has the spectral representation

$$ J^{\ast }J = \sum _{i\in I} {\mu }_{i} \langle \cdot ,u_{i}\rangle _{ \mathcal{H}}\, u_{i}. $$

(B.2)

As in (B.1), the convergence in (B.2) holds in the Hilbert–Schmidt norm sense. Furthermore, by analogous arguments as for $JJ^{\ast }$, we obtain that $J^{\ast }J$ is invertible if and only if $\ker J =\{0\}$ and $\dim ({\mathcal{H}})<\infty$. As a straightforward consequence of ${\mathcal{H}}= \overline{\operatorname{Im}J^{\ast }} \oplus \ker J$ and $L^{2}_{\mathbb{Q}}= \overline{\operatorname{Im}J} \oplus \ker J^{\ast }$, we have the canonical expansions of $J^{\ast }$ and $J$ corresponding to (B.1) and (B.2), i.e.,

$$ J^{\ast }= \sum _{i\in I} {\mu }_{i}^{1/2}\langle \cdot ,v_{i}\rangle _{ \mathbb{Q}}\, u_{i} ,\qquad J = \sum _{i\in I} {\mu }_{i}^{1/2} \langle \cdot ,u_{i}\rangle _{\mathcal{H}}\, v_{i}. $$

(B.3)

Remark B.1

Note that (2.1) holds if and only if $J:{\mathcal{H}}\to L^{2}_{\mathbb{Q}}$ is Hilbert–Schmidt. Indeed, Steinwart and Scovel [64, Example 2.9] show a separable RKHS ℋ for which $J:{\mathcal{H}}\to L^{2}_{\mathbb{Q}}$ is compact, but not Hilbert–Schmidt, and $\|\kappa \|_{2,{\mathbb{Q}}}=\infty$. That example also shows that $\kappa \notin {\mathcal{H}}$ in general.

2.2 B.6 Proof of Lemma 2.3

Let $\{v_{i} : i \in I\}$ be the ONS in $L^{2}_{\mathbb{Q}}$ given in Sect. B.5. Then $f_{0} = \sum _{i \in I} \langle f_{0}, v_{i} \rangle _{2,{\mathbb{Q}}} \, v_{i}$. As $f_{\lambda }= J(J^{\ast }J +\lambda )^{-1} J^{\ast }f_{0}$, the spectral representation (B.2) of $J^{\ast }J$ and the canonical expansions (B.3) of $J^{\ast }$ and $J$ give $f_{\lambda }= \sum _{i \in I} \frac{{\mu }_{i}}{{\mu }_{i} + \lambda } \langle f_{0}, v_{i} \rangle _{2,{\mathbb{Q}}} \, v_{i}$. Hence

$$ \|f_{0} - f_{\lambda }\|^{2}_{2,{\mathbb{Q}}} = \bigg\| \sum _{i \in I} \frac{\lambda }{{\mu }_{i} + \lambda } \langle f_{0}, v_{i} \rangle _{2,{ \mathbb{Q}}} \, v_{i} \bigg\| ^{2}_{2,{\mathbb{Q}}} = \sum _{i \in I} \bigg(\frac{\lambda }{{\mu }_{i} + \lambda }\bigg)^{2} \langle f_{0}, v_{i} \rangle ^{2}_{2,{\mathbb{Q}}}. $$

The result follows from the dominated convergence theorem.  □

2.3 B.7 Proof of Theorem 3.1

For simplicity, we assume that the sampling measure $\widetilde{{\mathbb{Q}}}={\mathbb{Q}}$, that is, $w=1$, and omit the tildes. The extension to the general case is straightforward, using (3.3) and (3.4).

We write

$$\begin{aligned} f_{\boldsymbol{X}} - f_{\lambda }&= (J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}} + \lambda )^{-1}J_{ \boldsymbol{X}}^{\ast }f - (J^{\ast }J + \lambda )^{-1}J^{\ast }f \\ & = (J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}} + \lambda )^{-1} (J_{\boldsymbol{X}}^{\ast }f - J^{\ast }f) - \big( (J^{\ast }J + \lambda )^{-1}-(J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}} + \lambda )^{-1} \big)J^{\ast }f . \end{aligned}$$

Combining this with the elementary factorisation

$$ (J^{\ast }J + \lambda )^{-1} -(J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}} + \lambda )^{-1} = (J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}} + \lambda )^{-1}( J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}}-J^{\ast }J)(J^{\ast }J + \lambda )^{-1} , $$

(B.4)

we obtain

$$\begin{aligned} f_{\boldsymbol{X}} - f_{\lambda }&= (J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}} + \lambda )^{-1} \big(J_{\boldsymbol{X}}^{\ast }f - J^{\ast }f - ( J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}}-J^{\ast }J) f_{\lambda }\big) \\ &= (J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}} + \lambda )^{-1} \frac{1}{n} \sum _{i=1}^{n} \xi _{i}, \end{aligned}$$

(B.5)

where $\xi _{i}= (f(X^{(i)}) - f_{\lambda }(X^{(i)})) k_{X^{(i)}} - J^{\ast }(f - f_{\lambda })$ are i.i.d. ℋ-valued random variables with zero mean. Moreover, as

$$\begin{aligned} \|\xi _{i}\|^{2}_{{\mathcal{H}}} &= \big(f(X^{(i)}) - f_{\lambda }(X^{(i)}) \big)^{2} \kappa (X^{(i)})^{2} \\ &\phantom{=:} + \int _{E^{2}} \big(f(x) - f_{\lambda }(x)\big)\big(f(y) - f_{\lambda }(y) \big) k(x,y) {\mathbb{Q}}[dx] {\mathbb{Q}}[dy] \\ &\phantom{=:}-2 \int _{E} \big(f(X^{(i)})-f_{\lambda }(X^{(i)})\big)\big(f(y) - f_{\lambda }(y)\big) k(X^{(i)},y) {\mathbb{Q}}[dy], \end{aligned}$$

(B.6)

we infer that

$$\begin{aligned} {\mathbb{E}}[\|\xi _{i} \|^{2}_{\mathcal{H}}] &= \|(f-f_{\lambda }) \kappa \|_{2,{\mathbb{Q}}}^{2} - \|J^{\ast }(f-f_{\lambda })\|^{2}_{{ \mathcal{H}}} \\ & \le \|(f-f_{\lambda })\kappa \|_{2,{\mathbb{Q}}}^{2} \le 2\|f \kappa \|^{2}_{2,{\mathbb{Q}}} + 2\|f_{\lambda }\|_{\mathcal{H}}^{2}\| \kappa \|^{4}_{4,{ \mathbb{Q}}} < \infty , \end{aligned}$$

(B.7)

where the third inequality uses (2.2). Hence both the law of large numbers in (A.2) and the central limit theorem in (A.3) apply and we get

$$ \frac{1}{n} \sum _{i=1}^{n} \xi _{i} \xrightarrow{\,\,\,a.s.\,\,\,} 0, \qquad \frac{1}{\sqrt{n}} \sum _{i=1}^{n} \xi _{i} \xrightarrow{\ \ d\ \ } {\mathcal{N}}(0, C_{\xi }), $$

(B.8)

where $C_{\xi }$ is the covariance operator of $\xi$ which is given by

$$ \langle C_{\xi }h, h \rangle _{{\mathcal{H}}} = \| (f-f_{\lambda }) Jh\|^{2}_{2,{ \mathbb{Q}}} - \langle f-f_{\lambda }, Jh\rangle ^{2}_{2,{\mathbb{Q}}}, \qquad h \in {\mathcal{H}}. $$

(B.9)

From (B.5), (B.8) and Lemma B.2 below, the continuous mapping theorem gives $f_{\boldsymbol{X}} \xrightarrow{a.s.} f_{\lambda }$, and Slutsky’s lemma gives $\sqrt{n}(f_{\boldsymbol{X}} - f_{\lambda }) \xrightarrow{d} {\mathcal{N}}(0, Q)$ for the covariance operator $Q=(J^{\ast }J+\lambda )^{-1}C_{\xi }(J^{\ast }J+\lambda )^{-1}$. Using (B.9), we infer that

$$\begin{aligned} \langle Q h ,h\rangle _{\mathcal{H}}& = \| (f-f_{\lambda }) J(J^{\ast }J+ \lambda )^{-1}h\|^{2}_{2,{\mathbb{Q}}} - \langle f-f_{\lambda }, J(J^{\ast }J+\lambda )^{-1}h\rangle ^{2}_{2,{\mathbb{Q}}} \\ & = \mathbb{V}_{\mathbb{Q}}[(f - f_{\lambda } ) (J^{\ast }J+\lambda )^{-1} h] , \end{aligned}$$

as claimed.  □

Lemma B.2

We have $(J^{\ast }_{\boldsymbol{X} }J_{\boldsymbol{X} }+\lambda )^{-1} \xrightarrow{a.s.} (J^{\ast }J+\lambda )^{-1}$ as $n \to \infty$.

Proof of Lemma B.2

By (B.4), we have that

$$ \|(J^{\ast }J + \lambda )^{-1} -(J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}} + \lambda )^{-1} \| \le \lambda ^{-2}\| J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}}-J^{\ast }J\|. $$

Hence it is enough to prove that

$$ J^{\ast }_{\boldsymbol{X} }J_{\boldsymbol{X} } \xrightarrow{\ \ a.s. \ \ } J^{\ast }J . $$

(B.10)

To this end, we decompose

$$ J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}} - J^{\ast }J = \frac{1}{n} \sum _{i=1}^{n} \Xi _{i}, $$

(B.11)

where $\Xi _{i} = \langle \cdot , k_{X^{(i)}} \rangle _{\mathcal{H}}k_{X^{(i)}} - \int _{E} \langle \cdot , k_{x} \rangle _{\mathcal{H}}k_{x} { \mathbb{Q}}[dx]$ are i.i.d. random Hilbert–Schmidt operators with zero mean. Straightforward calculations show that

$$ \|\Xi _{i}\|^{2}_{2} = \kappa (X^{(i)})^{4} + \int _{E^{2}} k(x,y)^{2} {\mathbb{Q}}[dx] {\mathbb{Q}}[dy] - 2 \int _{E} k(x,X^{(i)})^{2} { \mathbb{Q}}[dx]. $$

(B.12)

It follows that

$$ {\mathbb{E}}_{\mathbb{Q}}[\|\Xi _{i}\|^{2}_{2}] = \|\kappa \|^{4}_{4,{ \mathbb{Q}}} - \int _{E^{2}} k(x,y)^{2} {\mathbb{Q}}[dx]{\mathbb{Q}}[dy]< \infty . $$

(B.13)

Hence the law of large numbers in (A.2) applies and (B.10) follows. □

2.4 B.8 Proof of Theorem 3.4

As in the proof of Theorem 3.1, we assume that the sampling measure $\widetilde{{\mathbb{Q}}}={\mathbb{Q}}$, that is, $w=1$, and omit the tildes. The extension to the general case is straightforward, using (3.3) and (3.4).

From (B.5), we infer the inequality $\|f_{\boldsymbol{X}} - f_{\lambda }\|_{\mathcal{H}}\le \frac{1}{\lambda } \| \frac{1}{n} \sum _{i=1}^{n} \xi _{i}\|_{\mathcal{H}}$, and hence $\boldsymbol{Q} [\|f_{\boldsymbol{X}} - f_{\lambda }\|_{\mathcal{H}}\ge \tau ] \le \boldsymbol{Q}[ \frac{1}{\lambda } \|\frac{1}{n} \sum _{i=1}^{n} \xi _{i}\|_{ \mathcal{H}}\ge \tau ]$. From (B.6), we infer that

$$ \|\xi _{i}\|_{\mathcal{H}}\le 2 \|(f-f_{\lambda })\kappa \|_{\infty , { \mathbb{Q}}} \le 2\|f \kappa \|_{\infty , {\mathbb{Q}}} + 2\|f_{\lambda }\|_{\mathcal{H}}\|\kappa \|^{2}_{\infty , {\mathbb{Q}}} < \infty , $$

where in the second inequality we used (2.2). Hence the Hoeffding inequality in (A.4) applies so that

$$ \boldsymbol{Q} \bigg[\bigg\| \frac{1}{n} \sum _{i=1}^{n} \xi _{i}\bigg\| _{ \mathcal{H}}\ge \tau \bigg] \le 2{\mathrm{e}}^{- \frac{\tau ^{2} n}{8 \|(f-f_{\lambda })\kappa \|^{2}_{\infty , {\mathbb{Q}}}}}, \qquad \tau >0, $$

(B.14)

which implies (3.6).  □

2.5 B.9 Proof of Lemma 3.6

By definition, we have $\widetilde{\kappa }=\kappa /\sqrt{w}$, and (3.3) gives $\|\widetilde{\kappa }\|_{\infty ,{ \mathbb{Q}}}\ge \|\widetilde{\kappa }\|_{2,\widetilde{{\mathbb{Q}}}}=\| \kappa \|_{2,{\mathbb{Q}}}$, with equality if and only if $\widetilde{\kappa }$ is constant ℚ-a.s. This proves the lemma.  □

2.6 B.10 Proof of Lemma 6.1

Denote by ${\mathcal{H}}_{G}$ the RKHS corresponding to the Gaussian kernel $k_{G}(x,y)={\mathrm{e}}^{-\alpha |x-y|^{2}}$. It is well known that ${\mathcal{H}}_{G}$ is densely embedded in $L^{2}_{\mathbb{Q}}$; see Sriperumbudur et al. [59, Proposition 8]. Denote by ${\mathcal{H}}_{E}$ the RKHS corresponding to the exponentiated kernel $k_{E}(x,y)={\mathrm{e}}^{\beta x^{\top }y}$. As $k(x,y)=k_{E}(x,y) k_{G}(x,y)$ and ${\mathcal{H}}_{E}$ contains the constant function $1=k_{E}(\cdot ,0)\in {\mathcal{H}}_{E}$, we conclude from Paulsen and Raghupathi [43, Theorem 5.16] that ${\mathcal{H}}_{G}\subseteq {\mathcal{H}}$. This proves the lemma.  □

Appendix C: Finite-dimensional target space

We discuss here the case where the target space $L^{2}_{\mathbb{Q}}$ from Sect. 2 is finite-dimensional. This is of independent interest and provides the basis for computing the sample estimator without sorting.

Assume that ${\mathbb{Q}}=\frac{1}{n}\sum _{i=1}^{n} \delta _{x_{i}}$, where $\delta _{x}$ denotes the Dirac point measure at $x$, for a sample of (not necessarily distinct) points $x_{1},\dots ,x_{n}\in E$, for some $n\in {\mathbb{N}}$. Then property (2.1) holds for any measurable kernel $k:E\times E\to {\mathbb{R}}$.

Note that $\bar{n}=\dim L^{2}_{\mathbb{Q}}\le n$, with equality if and only if $x_{i}\neq x_{j}$ for all $i\neq j$. We discuss this in more detail now. Let $\bar{x}_{1},\dots ,\bar{x}_{\bar{n}}$ be the distinct points in $E$ such that we have $\{\bar{x}_{1},\dots ,\bar{x}_{\bar{n}}\}=\{x_{1},\dots ,x_{n}\}$. Define the index sets $I_{j} =\{ i: x_{i}=\bar{x}_{j}\}$, $j=1,\dots ,\bar{n}$, so that

$$ {\mathbb{Q}}= \frac{1}{n}\sum _{j=1}^{\bar{n}} |I_{j}| \delta _{\bar{x}_{j}}. $$

(C.1)

Then (2.3) reads $J^{\ast }g = \frac{1}{n} \sum _{j=1}^{\bar{n}} k(\cdot ,\bar{x}_{j}) |I_{j}| g(\bar{x}_{j})$ so that

$$ JJ^{\ast }g (\bar{x}_{i}) = \frac{1}{n} \sum _{j=1}^{\bar{n}} k(\bar{x}_{i}, \bar{x}_{j}) |I_{j}| g(\bar{x}_{j}),\qquad i=1,\dots ,\bar{n}, g\in L^{2}_{ \mathbb{Q}}. $$

(C.2)

We denote by $V_{n}$ the space ${\mathbb{R}}^{n}$ endowed with the scaled Euclidean scalar product $\langle y,z\rangle _{n} =\frac{1}{n} y^{\top }z$. We define the linear operator $S:{\mathcal{H}}\to V_{n}$ by

$$ Sh = \big(h(x_{1}),\dots ,h(x_{n})\big)^{\top },\qquad h\in { \mathcal{H}}. $$

(C.3)

Its adjoint is given by $S^{\ast }y = \frac{1}{n}\sum _{j=1}^{n} k(\cdot ,x_{j}) y_{j}$ so that

$$ (SS^{\ast }y)_{i} = \frac{1}{n}\sum _{j=1}^{n} k(x_{i},x_{j}) y_{j}, \qquad i=1,\dots ,n, y\in V_{n}. $$

(C.4)

We define the linear operator $P:V_{n}\to L^{2}_{\mathbb{Q}}$ by $P y(\bar{x}_{j})=\frac{1}{|I_{j}|}\sum _{i\in I_{j}} y_{i}$, $j=1,\dots ,\bar{n}$, $y\in V_{n}$. Combining this with (C.1), we obtain

$$ \langle P y,g\rangle _{\mathbb{Q}}= \frac{1}{n}\sum _{j=1}^{\bar{n}} |I_{j}| P y(\bar{x}_{j}) g(\bar{x}_{j})=\frac{1}{n}\sum _{i=1}^{n} y_{i} g(x_{i}), \qquad g\in L^{2}_{\mathbb{Q}}. $$

It follows that the adjoint of $P$ is given by $P^{\ast }g = (g(x_{1}),\dots ,g(x_{n}))^{\top }$. In view of (C.3), we see that

$$ \operatorname{Im}S\subseteq \operatorname{Im}P^{\ast }, $$

(C.5)

and $PP^{\ast }$ equals the identity operator on $L^{2}_{\mathbb{Q}}$, i.e.,

$$\begin{aligned} P P^{\ast }g = g,\qquad g\in L^{2}_{\mathbb{Q}}. \end{aligned}$$

(C.6)

We claim that $J=PS$, that is, the following diagram commutes:

Indeed, for any $h\in {\mathcal{H}}$, we have $PSh (\bar{x}_{j}) = \frac{1}{|I_{j}|} \sum _{i\in I_{j}} h(x_{i}) = h( \bar{x}_{j})$, which proves (C.7).

Combining (C.5)–(C.7), we obtain

$$ \ker J = \ker S $$

(C.7)

and $P^{\ast }(J J^{\ast }+\lambda ) = (S S^{\ast }+\lambda )P^{\ast }$. This is a useful result for computing the sample estimators below. Indeed, as $\lambda >0$, we have that $g_{\lambda }$ in (2.7) is uniquely determined by the lifted equation

$$ (SS^{\ast }+\lambda ) P^{\ast }g_{\lambda }= P^{\ast }f. $$

(C.8)

In order to compute $f_{\lambda }=J^{\ast }g_{\lambda }= S^{\ast }P^{\ast }g_{\lambda }$, we can thus solve the $(n\times n)$-dimensional linear problem (C.9), with $P^{\ast }f\in V_{n}$ given, instead of the corresponding $(\bar{n}\times \bar{n})$-dimensional linear problem (4.3). This fact allows faster implementation of the sample estimation, as the test of whether $\bar{n}< n$ for a given sample $x_{1},\dots ,x_{n}$ is not needed; see Lemma C.1 below.

3.1 C.11 Computation without sorting

As an application of the above, we now discuss how to compute the sample estimator in (3.4) without sorting the sample $\boldsymbol{X}$. For this, we fix the orthogonal basis $\{e_{1},\dots ,e_{n}\}$ of $V_{n}$ given by $e_{i,j}= \delta _{ij}$, so that $\langle e_{i},e_{j}\rangle _{n}=\frac{1}{n}\delta _{ij}$ for $1\le i,j\le n$. We define the vector $\overline{\boldsymbol{f}}=(\widetilde{f}(X^{(1)}),\dots ,\widetilde{f}(X^{(n)}))^{\top }$ and the positive semidefinite $(n\times n)$-matrix $\overline{\boldsymbol{K}}$ by $\overline{\boldsymbol{K}}_{ij}=\widetilde{k}(X^{(i)},X^{(j)})$. From (C.4), we see that $\frac{1}{n}\overline{\boldsymbol{K}}$ is the matrix representation of $\widetilde{S} \widetilde{S}^{\ast }:V_{n}\to V_{n}$. Summarising, we arrive at the following alternative to Lemma 4.1.

Lemma C.1

The unique solution $\overline{\boldsymbol{g}}\in {\mathbb{R}}^{n}$ to

$$ \bigg(\frac{1}{n}\overline{\boldsymbol{K}}+\lambda \bigg) \overline{\boldsymbol{g}} = \overline{\boldsymbol{f}} $$

(C.9)

gives $f_{\boldsymbol{X}}=\frac{1}{n}\sum _{i=1}^{n} k(\cdot ,X^{(i)}) \frac{\overline{\boldsymbol{g}}_{i}}{\sqrt{w( X^{(i)})}}$. Moreover, the solutions of (4.3) and (C.10) are related by $\overline{\boldsymbol{g}}_{i}=|I_{j}|^{-1/2}{\boldsymbol{g}}_{j}$ for all $i\in I_{j}$, $j=1,\dots ,\bar{n}$.

Remark C.2

If $X^{(i)}\neq X^{(j)}$ for all $i\neq j$ (that is, if $\bar{n}=n$), then $\overline{\boldsymbol{K}}=\boldsymbol{K}$, $\overline{\boldsymbol{f}}=\boldsymbol{f}$ and Lemmas 4.1 and C.1 coincide. Otherwise they provide different computational schemes.

Appendix D: Finite-dimensional RKHS

We now discuss in more detail the case where the RKHS ℋ from Sect. 2 is finite-dimensional. In particular, we then extend some of our results to the case $\lambda =0$ without regularisation.

Let $\{\phi _{1},\dots ,\phi _{m}\}$ be a set of linearly independent measurable functions on $E$ with $\|\phi _{i}\|_{2,{\mathbb{Q}}}<\infty$, $i=1,\dots ,m$, for some $m\in {\mathbb{N}}$. Introduce the feature map $\phi =(\phi _{1},\dots ,\phi _{m})^{\top }:E \to {\mathbb{R}}^{m}$ and define the measurable kernel $k:E\times E\to {\mathbb{R}}$ by $k(x,y)=\phi (x)^{\top }\phi (y)$. It follows by inspection that (2.1) holds and $\{\phi _{1},\dots ,\phi _{m}\}$ is an ONB of ℋ, which echoes Lemma A.1, 1). Hence any function $h\in {\mathcal{H}}$ can be represented by the coordinate vector $\boldsymbol{h}=\langle h,\phi \rangle _{\mathcal{H}}\in {\mathbb{R}}^{m}$ as $h=\phi ^{\top }\boldsymbol{h}$. The operator $J^{\ast }:L^{2}_{\mathbb{Q}}\to {\mathcal{H}}$ is of the form $J^{\ast }g = \phi ^{\top }\langle \phi ,g\rangle _{\mathbb{Q}}$. Hence $J^{\ast }J:{\mathcal{H}}\to {\mathcal{H}}$ satisfies $J^{\ast }J \phi ^{\top }= \phi ^{\top }\langle \phi ,\phi ^{\top }\rangle _{ \mathbb{Q}}$ and can thus be represented by the $(m\times m)$-Gram matrix $\langle \phi ,\phi ^{\top }\rangle _{\mathbb{Q}}$. In other words, we have $J^{\ast }J h=J^{\ast }J\phi ^{\top }\boldsymbol{h} = \phi ^{\top }\langle \phi ,\phi ^{\top }\rangle _{\mathbb{Q}}\, \boldsymbol{h}$ for $h\in {\mathcal{H}}$.

We henceforth assume that $\ker J=\{0\}$ so that $J^{\ast }J:{\mathcal{H}}\to {\mathcal{H}}$ is invertible by Sect. B.5. This is equivalent to $\{ J\phi _{1},\dots ,J\phi _{m}\}$ being a linearly independent set in $L^{2}_{\mathbb{Q}}$. We transform it into an ONS. Consider the spectral decomposition $\langle \phi ,\phi ^{\top }\rangle _{\mathbb{Q}}= S D S^{\top }$ with an orthogonal matrix $S$ and a diagonal matrix $D$ with $D_{ii}>0$. Define the functions $\psi _{i}\in {\mathcal{H}}$ by $\psi ^{\top }=(\psi _{1} ,\dots ,\psi _{m} ) = \phi ^{\top }S D^{-1/2}$. Then $\langle \psi ,\psi ^{\top }\rangle _{\mathbb{Q}}=D^{-1/2} S^{\top }\langle \phi ,\phi ^{\top }\rangle _{\mathbb{Q}}S D^{-1/2} = I_{m}$ so that $\{J\psi _{1},\dots ,J\psi _{m}\}$ is an ONS in $L^{2}_{\mathbb{Q}}$. Moreover, we also have the identity

$$ J^{\ast }J\psi ^{\top }= J^{\ast }J\phi ^{\top }S D^{-1/2} = \phi ^{\top }\langle \phi ,\phi ^{\top }\rangle _{\mathbb{Q}}S D^{-1/2} = \psi ^{\top }D $$

so that $v_{i}=J\psi _{i}$ are the eigenvectors of $JJ^{\ast }$ with eigenvalues

$$ {\mu }_{i}=D_{ii}>0 ,\qquad i=1,\dots ,m, $$

(D.1)

and the spectral decomposition (B.1) holds with index set $I=\{1,\dots ,m\}$. The corresponding ONB of ℋ in the spectral decomposition (B.2) is given by

$$ (u_{1},\dots ,u_{m}) = J^{\ast }J\psi ^{\top }D^{-1/2} = \psi ^{\top }D^{1/2} =\phi ^{\top }S. $$

Note that we can express the kernel directly in terms of the rotated feature map $u$ via $k(x,y)= u(x)^{\top }u(y)$, echoing Lemma A.1, 1).

4.1 D.12 Approximation without regularisation

As $J^{\ast }J:{\mathcal{H}}\to {\mathcal{H}}$ is invertible, it follows that (2.4) always has a unique solution for $\lambda =0$, which obviously coincides with the projection $f_{0} = (J^{\ast }J)^{-1} J^{\ast }f$.

4.2 D.13 Sample estimation without regularisation

As in Sect. 3, we let $n\in {\mathbb{N}}$ and $\boldsymbol{X}=(X^{(1)},\dots ,X^{(n)})$ be a sample of i.i.d. $E$-valued random variables with $X^{(i)}\sim \widetilde{{\mathbb{Q}}}$. We henceforth assume that $\lambda =0$, and hence we have to address the case where $\widetilde{J}_{\boldsymbol{X}}^{\ast }\widetilde{J}_{\boldsymbol{X}}$ is not invertible on $\widetilde{{\mathcal{H}}}$. In this case, we denote by “$( \widetilde{J}_{\boldsymbol{X}}^{\ast }\widetilde{J}_{\boldsymbol{X}})^{-1}$” any linear operator on $\widetilde{{\mathcal{H}}}$ that coincides with the inverse of $\widetilde{J}_{\boldsymbol{X}}^{\ast }\widetilde{J}_{\boldsymbol{X}}$ restricted to $\operatorname{Im}\widetilde{J}_{\boldsymbol{X}}^{\ast }\subseteq \widetilde{{\mathcal{H}}}$. As a consequence, $\widetilde{f}_{\boldsymbol{X}} =(\widetilde{J}_{\boldsymbol{X}}^{\ast }\widetilde{J}_{\boldsymbol{X}})^{-1} \widetilde{J}_{\boldsymbol{X}}^{\ast }f$ is always well defined and solves (2.4) with $\lambda =0$ and ℚ replaced by $\widetilde{{\mathbb{Q}}}_{\boldsymbol{X}}$.

We first show that our limit theorems carry over. The proof is given in Sect. D.16.

Theorem D.1

Theorem 3.1literally applies for $\lambda =0$, and so does Remark 3.2 (but not Remark 3.3).

We denote by $\underline{\mu }=\min _{i\in I}\mu _{i} >0$ the minimal eigenvalue of $J^{\ast }J$; see (D.1). The finite-sample guarantee in Theorem 3.4 is modified as follows. The proof is given in Sect. D.17.

Theorem D.2

For any $\eta \in (0,1]$, we have for all $n>C(\eta )^{2}$ that

$$ \|f_{\boldsymbol{X}} - f_{0}\|_{\mathcal{H}}< \frac{2\sqrt{2 \log (4/\eta )}\|(1/w)(f-f_{0})\kappa \|_{\infty ,{\mathbb{Q}}}}{(1-C(\eta )/\sqrt{n})\underline{\mu }\sqrt{n}} $$

(D.2)

with sampling probability $\boldsymbol{Q}$ of at least $1-\eta$, where $C(\eta )= 2\sqrt{\log (4/\eta )} \underline{\mu }^{-1} \| \widetilde{\kappa }\|^{2}_{\infty , {\mathbb{Q}}}$.

Theorem D.2 is similar to Cohen and Migliorati [13, Theorem 2.1(iii)], but in contrast extends to unbounded $f$ under assumptions (3.1) and (3.2), and provides a learning rate $O((\frac{\log n}{n})^{1/2})$ for the sample error (set $\eta =n^{-r}$ for some $r>0$).

4.3 D.14 Computation

We now revisit Sect. 4 for the case of a finite-dimensional RKHS ℋ. Note that the vectors $\widetilde{\phi }_{j}= \phi _{j}/\sqrt{w}$ form an ONB of $\widetilde{{\mathcal{H}}}$. We define the $(\bar{n}\times m)$-matrix ${\boldsymbol{V}}$ by ${\boldsymbol{V}}_{ij} = |I_{i}|^{1/2} \widetilde{\phi }_{j}(\bar{X}^{(i)})$ so that ${\boldsymbol{K}}={\boldsymbol{V}} {\boldsymbol{V}}^{\top }$, which is given below (4.2). Then ${\boldsymbol{V}}$ is the matrix representation of $\widetilde{J}_{\boldsymbol{X}}:\widetilde{{\mathcal{H}}}\to L^{2}_{ \widetilde{{\mathbb{Q}}}_{\boldsymbol{X}}}$, also called the design matrix, and $\frac{1}{n}{\boldsymbol{V}}^{\top }$ is the matrix representation of $\widetilde{J}_{\boldsymbol{X}}^{\ast }:L^{2}_{\widetilde{{\mathbb{Q}}}_{\boldsymbol{X}}} \to \widetilde{{\mathcal{H}}}$; note that the matrix transpose ${\boldsymbol{V}}^{\top }$ is scaled by $\frac{1}{n}$ because the orthogonal basis $\{\psi _{1},\dots ,\psi _{\bar{n}}\}$ of $L^{2}_{\widetilde{{\mathbb{Q}}}_{\boldsymbol{X}}}$ is not normalised. Note that $k$ is tractable if and only if ${\mathbb{E}}_{\mathbb{Q}}[ \phi (X)\mid {\mathcal{F}}_{t}]$ is given in closed form for all $t$. We arrive at the following result, which corresponds to Lemma 4.1 and which holds for any $\lambda \ge 0$. If $\lambda =0$, we assume that $\ker \widetilde{J}_{\boldsymbol{X}}=\{0\}$ so that $\widetilde{J}_{\boldsymbol{X}}^{\ast }\widetilde{J}_{\boldsymbol{X}}$ is invertible.

Lemma D.3

The unique solution $\boldsymbol{h}\in {\mathbb{R}}^{m}$ to

$$ \bigg(\frac{1}{n} {\boldsymbol{V}}^{\top }{\boldsymbol{V}} +\lambda \bigg) \boldsymbol{h} = \frac{1}{n} {\boldsymbol{V}}^{\top }{\boldsymbol{f}} $$

(D.3)

gives $f_{\boldsymbol{X}} = \phi ^{\top }\boldsymbol{h}$. The sample version of problem (2.4),

$$ \min _{\boldsymbol{h}\in {\mathbb{R}}^{m}} \bigg( \frac{1}{n} |{\boldsymbol{V}} \boldsymbol{h} - { \boldsymbol{f}}|^{2} + \lambda |\boldsymbol{h}|^{2}\bigg), $$

(D.4)

has a unique solution $\boldsymbol{h}\in {\mathbb{R}}^{m}$, which coincides with the solution to (D.3). If, moreover, the kernel $k$ is tractable, then

$$V_{\boldsymbol{X},t}={\mathbb{E}}_{\mathbb{Q}}[ \phi (X) | {\mathcal{F}}_{t}]^{\top }\boldsymbol{h},\qquad t=0,\dots ,T, $$

is given in closed form.

The least-squares problem (D.4) can be efficiently solved using stochastic gradient methods such as the randomised extended Kaczmarz algorithm in Zouzias and Freris [71] and Filipović et al. [24].

4.4 D.15 Computation without sorting

Following up on Appendix C.11, we define the $(n\times m)$-matrix $\overline{\boldsymbol{V}}$ by $\overline{\boldsymbol{V}}_{ij} = \widetilde{\phi }_{j}(X^{(i)})$ so that $\overline{\boldsymbol{K}}=\overline{\boldsymbol{V}} \overline{\boldsymbol{V}}^{\top }$. Note that $\overline{\boldsymbol{V}}$ is the matrix representation of $\widetilde{S}:\widetilde{{\mathcal{H}}}\to V_{n}$ in (C.3), and $\frac{1}{n}\overline{\boldsymbol{V}}^{\top }$ is the matrix representation of $\widetilde{S}^{\ast }:V_{n}\to \widetilde{{\mathcal{H}}}$; note that the matrix transpose $\overline{\boldsymbol{V}}^{\top }$ is scaled by $\frac{1}{n}$ because the orthogonal basis $\{e_{1},\dots ,e_{n}\}$ of $V_{n}$ is not normalised. From (C.8), we thus infer that $\ker \overline{\boldsymbol{V}} = \ker \widetilde{J}_{\boldsymbol{X}}$. As a consequence, or by direct verification, we further obtain $\overline{\boldsymbol{V}}^{\top }\overline{\boldsymbol{V}}=\boldsymbol{V}^{\top }\boldsymbol{V}$, $\overline{\boldsymbol{V}}^{\top }\overline{\boldsymbol{f}} = \boldsymbol{V}^{\top }\boldsymbol{f}$ and $|\overline{\boldsymbol{V}} \boldsymbol{h} - \overline{\boldsymbol{f}}| = |\boldsymbol{V} \boldsymbol{h} - \boldsymbol{f}|$. Summarising, we thus infer that Lemma D.3 literally applies to $\overline{\boldsymbol{V}}$ and $\overline{\boldsymbol{f}}$ in lieu of $\boldsymbol{V}$ and $\boldsymbol{f}$.

4.5 D.16 Proof of Theorem D.1

As in the proof of Theorem 3.1, we assume for simplicity that the sampling measure $\widetilde{{\mathbb{Q}}}={\mathbb{Q}}$, that is, $w=1$, so that we can omit the tildes.

We fix $\delta \in [0,1)$ and define the sampling event

$$ {\mathcal{S}}_{\delta }=\{ \|J^{\ast }_{\boldsymbol{X}} J_{\boldsymbol{X}} - J^{\ast }J\|_{2} \le \delta / \| (J^{\ast }J)^{-1}\|\}\subseteq \boldsymbol{E} . $$

The following lemma collects some properties of ${\mathcal{S}}_{\delta }$.

Lemma D.4

1) On ${\mathcal{S}}_{\delta }$, the operator $J_{\boldsymbol{X}}^{\ast }J_{\boldsymbol{X}} :{\mathcal{H}}\to {\mathcal{H}}$ is invertible and

$$ \|(J^{\ast }_{\boldsymbol{X} }J_{\boldsymbol{X} })^{-1}\| \le \frac{\|(J^{\ast }J )^{-1}\|}{1-\delta }. $$

(D.5)

2) The sampling probability of ${\mathcal{S}}_{\delta }$ is bounded below by

$$ {\boldsymbol{Q}}[ {\mathcal{S}}_{\delta }]\ge 1 -2{\mathrm{e}}^{- \frac{\delta ^{2} n}{4 \|\kappa \|_{\infty ,{\mathbb{Q}}}^{4} \|(J^{\ast }J )^{-1}\|^{2}}}. $$

(D.6)

Proof

1) We write $J^{\ast }_{\boldsymbol{X}} J_{\boldsymbol{X}} = J^{\ast }J(J^{\ast }J )^{-1} J^{\ast }_{\boldsymbol{X}} J_{ \boldsymbol{X}}$ so that $J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}}$ is invertible if and only if $(J^{\ast }J )^{-1}J^{\ast }_{\boldsymbol{X}} J_{\boldsymbol{X}}$ is. If $\| (J^{\ast }J )^{-1}\|\| J^{\ast }J{-}J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}}\|_{2}\le \delta$, then $\|1 {-} (J^{\ast }J )^{-1}J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}} \| \le \delta$, which proves the invertibility of $(J^{\ast }J )^{-1}J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}}$ and hence of $J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}}$. Furthermore, using the Neumann series of $1 - (J^{\ast }J)^{-1} J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}}$, we obtain (D.5).

2) We decompose $J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}} - J^{\ast }J$ as in (B.11). From (B.12), we infer that we have $\|\Xi _{i}\| \le \sqrt{2} \|\kappa \|^{2}_{\infty , {\mathbb{Q}}} <\infty$. Consequently, the Hoeffding inequality (A.4) applies and we obtain

$$ \boldsymbol{Q}[\|J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}}-J^{\ast }J\|_{2} \ge \tau ] \le 2 { \mathrm{e}}^{-\frac{\tau ^{2} n}{4\|\kappa \|^{4}_{\infty , {\mathbb{Q}}}}}, $$

(D.7)

which is equivalent to (D.6). □

In view of Lemma D.4, 1), it now follows by inspection that (B.4) and (B.5) hold on ${\mathcal{S}}_{\delta }$ for $\lambda =0$. We thus obtain the global identity

$$ f_{\boldsymbol{X}} - f_{0} = \Delta _{\boldsymbol{X}} + (J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}})^{-1} \frac{1}{n} \sum _{i=1}^{n} \xi _{i}, $$

(D.8)

where the ℋ-valued random variable $\Delta _{\boldsymbol{X}} = f_{\boldsymbol{X}} - f_{0} - (J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}})^{-1} \frac{1}{n} \sum _{i=1}^{n} \xi _{i}$ satisfies $\Delta _{\boldsymbol{X}}=0$ on ${\mathcal{S}}_{\delta }$. In view of (D.6) and the Borel–Cantelli lemma, we thus have $\sqrt{n}\Delta _{\boldsymbol{X}} \xrightarrow{a.s.} 0$ as $n \to \infty$.

Note that (B.6)–(B.9) clearly hold with $\lambda =0$. Theorem D.1 now follows as in the proof of Theorem 3.1 with $\lambda =0$, with (B.5) replaced by (D.8) and with Lemma B.2 replaced by the following lemma.

Lemma D.5

We have $(J^{\ast }_{\boldsymbol{X} }J_{\boldsymbol{X} })^{-1} \xrightarrow{a.s.} (J^{\ast }J)^{-1}$ as $n \to \infty$.

Proof

Let $\tau >0$. We have

$$\begin{aligned} \boldsymbol{Q}[\|(J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}} )^{-1} - (J^{\ast }J )^{-1}\| \ge \tau ] &= \boldsymbol{Q}[ \{ \|(J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}} )^{-1} - (J^{\ast }J )^{-1} \| \ge \tau \} \cap {\mathcal{S}}_{\delta }] \\ &\phantom{=:}+ \boldsymbol{Q}[ \boldsymbol{E} \setminus {\mathcal{S}}_{\delta }]. \end{aligned}$$

(D.9)

Using (B.4) and (D.5), we obtain on ${\mathcal{S}}_{\delta }$ that

$$ \|(J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}} )^{-1} - (J^{\ast }J )^{-1}\| \le \frac{\|(J^{\ast }J )^{-1}\|^{2}}{1-\delta }\|J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}} -J^{\ast }J \|_{2}. $$

Combining this with (D.7), we obtain

$$\begin{aligned} \boldsymbol{Q}[\{\|(J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}} )^{-1} - (J^{\ast }J )^{-1}\| \ge \tau \} \cap {\mathcal{S}}_{\delta }] &\le \boldsymbol{Q}\bigg[ \frac{\|(J^{\ast }J )^{-1}\|^{2}}{1-\delta }\|J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}}-J^{\ast }J\|_{2} \ge \tau \bigg] \\ &\le 2{\mathrm{e}}^{ \frac{-\tau ^{2}(1-\delta )^{2} n}{4 \|\kappa \|_{\infty , {\mathbb{Q}}}^{4} \|(J^{\ast }J )^{-1}\|^{4}}}. \end{aligned}$$

Combining this with (D.6) and (D.9), we infer that

$$ \boldsymbol{Q}[\|(J^{\ast }_{\boldsymbol{X}}J_{\boldsymbol{X}} )^{-1} - (J^{\ast }J )^{-1}\| \ge \tau ] \le 2 {\mathrm{e}}^{ \frac{-\tau ^{2}(1-\delta )^{2} n}{4 \|\kappa \|_{\infty , {\mathbb{Q}}}^{4} \|(J^{\ast }J )^{-1}\|^{4}}} + 2 {\mathrm{e}}^{ \frac{-\delta ^{2} n}{4 \|\kappa \|_{\infty ,{\mathbb{Q}}}^{4} \|(J^{\ast }J )^{-1}\|^{2}}}. $$

As the right-hand side is summable over $n\ge 1$ for any $\tau >0$, the result follows from the Borel–Cantelli lemma. □

4.6 D.17 Proof of Theorem D.2

As in the proof of Theorem 3.4, we assume that the sampling measure $\widetilde{{\mathbb{Q}}}={\mathbb{Q}}$, that is, $w=1$. The extension to the general case is straightforward, using (3.3) and (3.4).

We let the sampling event ${\mathcal{S}}_{\delta }$ be as in Lemma D.4 and let $\tau >0$. We have

$$ {\boldsymbol{Q}} [ \| f_{\boldsymbol{X}} - f_{0}\|_{\mathcal{H}}\ge \tau ] \le {\boldsymbol{Q}} [ \{\| f_{\boldsymbol{X}} - f_{0}\|_{\mathcal{H}}\ge \tau \} \cap {\mathcal{S}}_{\delta }] + {\boldsymbol{Q}} [\boldsymbol{E}\setminus {\mathcal{S}}_{\delta }]. $$

(D.10)

Using (B.5) and (D.5), we obtain on ${\mathcal{S}}_{\delta }$ that

$$ \| f_{\boldsymbol{X}} - f_{0}\|_{\mathcal{H}}\le \frac{\|(J^{\ast }J )^{-1}\|}{1-\delta }\bigg\| \frac{1}{n}\sum _{i=1}^{n} \xi _{i}\bigg\| _{{\mathcal{H}}}. $$

Combining this with (B.14), we obtain

$$ \begin{aligned} {\boldsymbol{Q}} [\{ \| f_{\boldsymbol{X}} - f_{0}\|_{\mathcal{H}}\ge \tau \} \cap {\mathcal{S}}_{\delta }] &\le \boldsymbol{Q}\bigg[ \frac{\|(J^{\ast }J )^{-1}\|}{1-\delta }\bigg\| \frac{1}{n}\sum _{i=1}^{n} \xi _{i}\bigg\| _{{\mathcal{H}}}\ge \tau \bigg] \\ &\le 2{\mathrm{e}}^{- \frac{\tau ^{2} (1-\delta )^{2} n}{8 \|(f-f_{0})\kappa \|^{2}_{\infty , {\mathbb{Q}}}\|(J^{\ast }J )^{-1}\|^{2}}}. \end{aligned} $$

Combining this with (D.6) and (D.10), we infer that

$$ {\boldsymbol{Q}} [ \| f_{\boldsymbol{X}} - f_{0}\|_{\mathcal{H}}\ge \tau ] \le 2{\mathrm{e}}^{- \frac{\tau ^{2} (1-\delta )^{2} n}{8 \|(f-f_{0})\kappa \|^{2}_{\infty , {\mathbb{Q}}}\|(J^{\ast }J )^{-1}\|^{2}}} + 2 {\mathrm{e}}^{ \frac{-\delta ^{2} n}{4 \|\kappa \|_{\infty ,{\mathbb{Q}}}^{4} \|(J^{\ast }J )^{-1}\|^{2}}}. $$

Now we choose $\delta = \frac{\|\kappa \|_{\infty , {\mathbb{Q}}}^{2} \tau }{\sqrt{2} \|(f-f_{0})\kappa \|_{\infty , {\mathbb{Q}}}+\|\kappa \|_{\infty , {\mathbb{Q}}}^{2} \tau }$ so that the two exponents on the right-hand side match. Therefore, we obtain

$$ {\boldsymbol{Q}} [ \| f_{\boldsymbol{X}} - f_{0}\|_{\mathcal{H}}\ge \tau ] \le 4{\mathrm{e}}^{- \frac{\delta ^{2} n}{4\|\kappa \|^{4}_{\infty , {\mathbb{Q}}}\|(J^{\ast }J )^{-1}\|^{2}}} = 4{\mathrm{e}}^{- \frac{\tau ^{2}n}{4\|(J^{\ast }J )^{-1}\|^{2}(\sqrt{2}\|(f-f_{0})\kappa \|_{\infty , {\mathbb{Q}}} + \|\kappa \|_{\infty ,{\mathbb{Q}}}^{2} \tau )^{2}}}. $$

Using that $\| (J^{\ast }J)^{-1}\|= \underline{\mu }^{-1}$, see (B.2), straightforward rewriting gives (D.2).  □

Appendix E: Comparison with regress-now

The method we have developed in this paper gives an estimation of the entire value process $V$. In practice, one could be interested in the estimation of the portfolio value $V_{t}$ only at some fixed time $t$, e.g. $t=1$. In Glasserman and Yu [26], two least-squares Monte Carlo approaches are described to deal with this problem in the context of American options pricing. The first approach, called “regress-later”, consists in approximating the payoff function $f$ by means of a projection on a finite number of basis functions. The basis functions are chosen in such a way that their conditional expectation at time $t=1$ is in closed form. Our method can be seen as a double extension of this approach because it also covers the case where the number of basis functions could potentially be infinite and gives closed-form estimation of the portfolio value $V_{t}$ at any time $t$. The second approach, called “regress-now”, consists in approximating $V_{1}$ by means of a projection on a finite number of basis functions that depend solely on the variable $x_{1} \in E_{1}$ of interest.

We compare our approach, which corresponds to “regress-later” and gives the estimator $V_{\boldsymbol{X}, 1}$ in (4.4), to its regress-now variant, whose estimator we denote by $V_{\boldsymbol{X}, 1}^{\text{now}}$. To this end, we briefly discuss how to construct $V_{\boldsymbol{X}, 1}^{\text{now}}$ and implement it in the context of the three examples studied in Sect. 6.

To construct $V_{\boldsymbol{X}, 1}^{\text{now}}$, only a few changes need to be carried out to the previous construction of $V_{\boldsymbol{X}, 1}$. We sample directly from ℚ which gives $\boldsymbol{X} = (X^{(1)}, \dots , X^{(n)})$ and the vector $\boldsymbol{f} = (f(X^{(1)}), \dots , f(X^{(n)}))^{\top }$. The expression of $V_{\boldsymbol{X}, 1}^{\text{now}}$ is given by (4.4) for $t=1$, where the kernel $k$ is of the form (5.1) with $T$ replaced by 1 so that its domain is $E_{1}\times E_{1}$. Instead of using the whole sample $\boldsymbol{X}$ to construct the matrix $\boldsymbol{K}$ in (4.3), only the $(t=1)$-cross-section $\boldsymbol{X}_{1} = (X^{(1)}_{1},\dots , X^{(n)}_{1})$ is needed.¹⁰ Since the sampling measure ℚ is Gaussian, property (4.1) holds for the sample $\boldsymbol{X}_{1}$ so that $\bar{n}=n$, $\bar{X}_{1}^{(j)}=X_{1}^{(j)}$ and $|I_{j}|=1$ for all $j=1,\dots ,n$. The conditional kernel embeddings in (4.4) boil down to $M_{1}( X^{(j)})=k( X_{1}, X^{(j)}_{1})$.

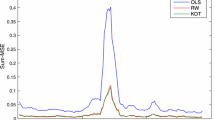
Table 5 shows the normalised $L^{2}_{{\mathbb{Q}}}$-errors of $V_{\boldsymbol{X}, 1}^{\text{now}}$ and compares them to the respective values of $V_{\boldsymbol{X}, 1}$ which are taken from Table 2. We observe that for all three examples, our regress-later estimator performs better than the regress-now estimator. This finding is confirmed by Fig. 4, which corresponds to Figs. 1, 2 and 3.

Fig. 4

Comparison of $V_{\boldsymbol{X}, 1}$ and $V_{\boldsymbol{X}, 1}^{\text{now}}$ with $\gamma = 0$. In the detrended Q–Q plots, the blue, cyan and lawngreen (red, orange and pink) dots are built using the regress-later (regress-now) estimator and the test data. $[0\%, 0.01\%)$ refers to the quantiles of levels $\{0.001\%,0.002\%, \dots , 0.009\%\}$, $[0.01\%, 1\%)$ to the quantiles of levels $\{0.01\%,0.02\%, \dots , 0.99\%\}$, $[1\%, 99\%]$ to the quantiles of levels $\{1\%,2\%, \dots , 99\%\}$, $(99\%, 99.99\%]$ to the quantiles of levels $\{99.01\%,99.02\%, \dots , 99.99\%\}$ and $(99.99\%, 100\%]$ to the quantiles of levels $\{99.991\%,99.992\%, \dots , 100\%\}$

Table 5 Normalised $L^{2}_{\mathbb{Q}}$-error $\|V_{1}- \widehat{V}_{1}\|_{2,{\mathbb{Q}}}/V_{0}$ in % for $\widehat{V}_{1} = V_{\boldsymbol{X}, 1}^{\text{now}}, V_{\boldsymbol{X}, 1}$ with $\gamma = 0$

Table 6 shows the computing times for the full estimation of $V_{\boldsymbol{X}, 1}^{\text{now}}$ and $V_{\boldsymbol{X}, 1}$. Computation is performed on Skylake processors running at 2.3 GHz, using 14 cores and 100 GB of RAM. We see that our estimator requires less computing time than the regress-now estimator. Indeed, note that the dimension of the regression problem, which equals the training sample size $n=20\text{'}000$, is the same for both methods.

Table 6 Computing times (in seconds) for estimating $V_{\boldsymbol{X}, 1}^{\text{now}}$ and $V_{\boldsymbol{X}, 1}$ with $\gamma = 0$, for sample size $n= 20\text{'}000$

Thus both in terms of accuracy in the estimation of $V_{1}$, measured by the normalised $L^{2}_{\mathbb{Q}}$-error, and of computing time, our regress-later estimator outperforms the regress-now estimator and is thus better suited for portfolio valuation tasks. This is surprising since the estimation of the entire value process $V$ by regress-later is a high-dimensional problem (path-space dimension 12 for the min-put and max-call, and 36 for the barrier reverse convertible), whereas the direct estimation of $V_{1}$ by regress-now is a problem of much smaller dimension (state-space dimension 6 for the min-put and max-call, and 3 for the barrier reverse convertible). A reason for the inferior performance of regress-now could be that the training data $\boldsymbol{f}$ represents noisy observations of the true values $V_{1}(X^{(1)}_{1}), \dots , V_{1}(X^{(n)}_{1})$ which we cannot directly observe. This is in contrast to our regress-later approach where $\boldsymbol{f}$ are the true values of the target function $f$. Our findings suggest that for portfolio valuation, it is more efficient to first estimate the payoff function $f$ on a high-dimensional domain and with non-noisy observations, rather than directly estimate the time $(t=1)$-value function $V_{1}$ on a low-dimensional domain but with noisy observations.

How about the risk measures? Tables 7 and 8 show normalised value-at-risk and expected shortfall of $\mathrm{L}_{\boldsymbol{X}} = \widehat{V}_{0}-\widehat{V}_{1}$ and $-\mathrm{L}_{\boldsymbol{X}}$, where $\widehat{V}_{t}$ stands for either $V_{\boldsymbol{X}, t}$ or $V_{\boldsymbol{X}, t}^{\text{now}}$, for $t=0, 1$. We observe that regress-later outperforms regress-now in all risk-measure estimates of long positions, whereas for risk-measure estimates of short positions, regress-now is best in 4 cases out of 6.¹¹ This mixed outcome is somewhat at odds with the above observed superiority of regress-later over regress-now. On the other hand, it serves as an illustration of the no-free-lunch theorem in Wolpert and Macready [67], which states that there exists no single best method for portfolio valuation and risk management that outperforms all other methods in all situations.

Table 7 Normalised true and estimated values for value-at-risk $\mathrm{VaR}_{99.5\%}(\mathrm{L})/V_{0}$, $\mathrm{VaR}_{99.5\%}(\mathrm{L}_{\boldsymbol{X}})/V_{0}$, $\mathrm{VaR}_{99.5\%}(-\mathrm{L})/V_{0}$ and $\mathrm{VaR}_{99.5\%}(-\mathrm{L}_{\boldsymbol{X}})/V_{0}$ with $\gamma = 0$. All values are expressed in basis points

Table 8 Normalised true and estimated values for expected shortfall $\mathrm{ES}_{99\%}(\mathrm{L})/V_{0}$, $\mathrm{ES}_{99\%}(\mathrm{L}_{\boldsymbol{X}})/V_{0}$, $\mathrm{ES}_{99\%}(-\mathrm{L})/V_{0}$ and $\mathrm{ES}_{99\%}(-\mathrm{L}_{\boldsymbol{X}})/V_{0}$ with $\gamma = 0$. All values are expressed in basis points

We note that finite-sample guarantees similar to that in Theorem 3.4 can be derived for the regress-now estimator, but only under boundedness assumptions on $f$ and $\kappa$. In fact, the boundedness assumptions (3.1) and (3.2) are not enough because they do not guarantee the boundedness of the noise; $f(X)-V_{1}$. In the literature, the boundedness assumption on $f$ is relaxed by making assumptions on the noise; see e.g. Rastogi and Sampath [49].