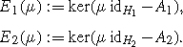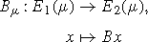Mercer’s Theorem on General Domains: On the Interaction between Measures, Kernels, and RKHSs

Abstract

Given a compact metric space X and a strictly positive Borel measure ν on X, Mercer’s classical theorem states that the spectral decomposition of a positive self-adjoint integral operator T _k :L ₂(ν)→L ₂(ν) of a continuous k yields a series representation of k in terms of the eigenvalues and -functions of T _k . An immediate consequence of this representation is that k is a (reproducing) kernel and that its reproducing kernel Hilbert space can also be described by these eigenvalues and -functions. It is well known that Mercer’s theorem has found important applications in various branches of mathematics, including probability theory and statistics. In particular, for some applications in the latter areas, however, it would be highly convenient to have a form of Mercer’s theorem for more general spaces X and kernels k. Unfortunately, all extensions of Mercer’s theorem in this direction either stick too closely to the original topological structure of X and k, or replace the absolute and uniform convergence by weaker notions of convergence that are not strong enough for many statistical applications. In this work, we fill this gap by establishing several Mercer type series representations for k that, on the one hand, make only very mild assumptions on X and k, and, on the other hand, provide convergence results that are strong enough for interesting applications in, e.g., statistical learning theory. To illustrate the latter, we first use these series representations to describe ranges of fractional powers of T _k in terms of interpolation spaces and investigate under which conditions these interpolation spaces are contained in L _∞(ν). For these two results, we then discuss applications related to the analysis of so-called least squares support vector machines, which are a state-of-the-art learning algorithm. Besides these results, we further use the obtained Mercer representations to show that every self-adjoint nuclear operator L ₂(ν)→L ₂(ν) is an integral operator whose representing function k is the difference of two (reproducing) kernels.

Appendices

Appendix A: Related Operators and the Spectral Theorem

This appendix recalls some facts from the spectral theory of compact, self-adjoint operators acting between Hilbert spaces. We begin with the classical spectral theorem, see, e.g., [18, Theorem V.2.10 on p. 260] or [45, Theorem VI.3.2].

Theorem A.1

(Spectral Theorem)

Let H be a Hilbert space and A:H→H be a compact, positive, and self-adjoint operator. Then there exist an at most countable ONS (e _i ) _i∈I of H and a family (μ _i ) _i∈I converging to 0 such that μ ₁≥μ ₂≥…>0 and

(53)

(54)

Moreover, (μ _i ) _i∈I is the family of nonzero eigenvalues of A (including geometric multiplicities), and, for all i∈I, e _i is an eigenvector for μ _i . Finally, both (53) and (54) actually hold for all ONSs $(\tilde{e}_{i})_{i\in I}$ of H for which, for all i∈I, the vector $\tilde{e}_{i}$ is an eigenvector of μ _i .

The next well known theorem, see, e.g., [27, Theorem 12.10], relates the image of an operator B to the null-space of its adjoint B ^∗.

Theorem A.2

Let H ₁ and H ₂ be Hilbert spaces and B:H ₁→H ₂ be a bounded linear operator. Then we have

$$\overline{ \operatorname {ran}B} = \bigl(\ker B^*\bigr)^\perp.$$

In particular, B ^∗ is injective if and only if B has a dense image.

The following theorem lists other well-known facts about the eigenvalues and the spectral representations of certain operators. These facts are widely known, but since we are unaware of a reference for the particular formulation we need, we decided to include its relatively straightforward proof for the sake of completeness. The name for this theorem was borrowed from [23, Sect. 3.3.4].

Theorem A.3

(Principle of Related Operators)

Let H ₁ and H ₂ be Hilbert spaces and B:H ₁→H ₂ be a bounded linear operator. We define the self-adjoint and positive operators A ₁:H ₁→H ₁ and A ₂:H ₂→H ₂ by A ₁:=B ^∗ B and A ₂:=BB ^∗, respectively. Then the following statements are true:

• (i) Given a μ>0, we denote the eigenspaces of A ₁ and A ₂ that correspond to μ by

  

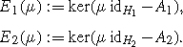
  Then the map

  

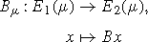
  is well defined, bijective, and, in addition, we have $B^{*}_{\mu}B_{\mu}=\mu \operatorname {id}_{E_{1}(\mu)}$.

• (ii) We have kerA ₁=kerB and kerA ₂=kerB ^∗.

• (iii) Assume that A ₁ is compact, and let (e _i ) _i∈I be an at most countable ONS of H ₁ and (μ _i ) _i∈I be a family converging to 0 such that μ ₁≥μ ₂≥…>0 and

  $$A_1x = \sum_{i \in I} \mu_i\langle x,e_i\rangle_{H_1} e_i,\quad x\in H_1,$$

  where we note that there exist such (e _i ) _i∈I and (μ _i ) _i∈I by Theorem A.1. For i∈I, we define $f_{i} := \mu_{i}^{-1/2} B e_{i}$. Then (f _i ) _i∈I is an ONS of H ₂, and A ₂ has the spectral representation

  $$ A_2 y = \sum_{i \in I}\mu_i \langle y,f_i\rangle_{H_2}f_i, \quad y\in H_2.$$

  (55)

  Finally, we have $e_{i} = \mu_{i}^{-1/2} B^{*} f_{i}$ for all i∈I.

• (iv) A ₁ is compact if and only if A ₂ is compact.

• (v) If A ₁ is compact, we have $\overline{\operatorname {ran}B} = \overline {\operatorname {span}\{f_{i}:i\in I \}} = \overline{\operatorname {ran}A_{2}}$ and $\overline{\operatorname {ran}B^{*}} = \overline{\operatorname {span}\{e_{i}:i\in I \}} =\overline{\operatorname {ran}A_{1}}$.

Proof

(i) It is easy to check that A ₁ and A ₂ are indeed self-adjoint and positive. Let us first show that B _μ is well defined, that is, that Bx∈E ₂(μ) for all x∈E ₁(μ). To this end, we pick an x∈E ₁(μ); i.e., we have A ₁ x=μx. From this we conclude A ₂ Bx=BB ^∗ Bx=BA ₁ x=μBx, and thus we have Bx∈E ₂(μ). Similarly, for x∈E ₁(μ) with Bx=0, we obtain μx=Ax=B ^∗ Bx=0, and since μ>0, we conclude x=0; i.e., B _μ is injective. By interchanging the role of B and B ^∗, we analogously see that

is well defined and injective. To show that B _μ is surjective, we now pick an y∈E ₂(μ) and define x:=μ ⁻¹ B ^∗ y. Our previous consideration then gives x∈E ₁(μ), and since we further have Bx=μ ⁻¹ BB ^∗ y=μ ⁻¹ A ₂ y=y, we obtain the surjectivity of B _μ . The last assertion is a consequence of B ^∗ B=A ₁.

(ii) By symmetry, it suffices to show kerA ₁=kerB. Moreover, the inclusion kerA ₁⊃kerB immediately follows from A ₁=B ^∗ B. To show the converse inclusion, we fix an x∈kerA ₁. Then the definition of A ₁ yields $0 = \langle A_{1}x,x\rangle_{H_{1}} =\langle Bx,Bx\rangle_{H_{2}}$, which implies x∈kerB.

(iii) Let us show that (f _i ) _i∈I is an ONS of H ₂. To this end, we fix i,j∈I and find

$$\langle f_i, f_j\rangle_{H_2} = \frac{1}{\sqrt{ \mu_i \mu_j}} \langle Be_i,Be_j\rangle_{H_2} = \frac{1}{\sqrt{ \mu_i\mu_j}}\langle e_i, A_1 e_j\rangle_{H_1} = \sqrt{\frac{\mu_j}{\mu_i}} \langle e_i,e_j\rangle_{H_1},$$

and since (e _i ) _i∈I is an ONS, we then conclude that (f _i ) _i∈I is an ONS. Moreover, by (i) we have

$$ A_2f_i = BB^* f_i= \mu_i^{-1/2}BB^*B e_i = \mu^{1/2}_iBe_i = \mu_i f_i, \quad i\in I.$$

(56)

By Theorem A.1 and (ii), the compactness of A ₁ further implies

Using Theorem A.2 and (ii), we then find

$$H_2 = \ker B^* \oplus\overline{ \operatorname {ran}B} = \ker A_2\oplus\overline{{\operatorname {span}\{f_i:i\in I\}}},$$

and combining this with (56), we obtain (55) by Theorem A.1. The last assertion follows from $\mu_{i}^{-1/2} B^{*} f_{i} = \mu_{i}^{-1} B^{*}B e_{i} = e_{i}$, where in the last step we used (i).

(iv) If A ₁ is compact, we obtain the spectral representation (55) for A ₂, and hence A ₂ is compact. The inverse implication follows by symmetry.

(v) The proof of (iii) has already shown $\overline {\operatorname {ran}B} = \overline{\operatorname {span}\{f_{i}:i\in I \}}= \overline{\operatorname {ran}A_{2}}$, and the second equality follows by symmetry and (iv). □

Appendix B: Liftings

In this appendix, we briefly recall some results related to liftings on the space of bounded measurable functions. To this end, we assume that $(X,\mathcal {A})$ is a measurable space. We denote by

$$\mathcal {L}_{\infty}(X) := \{f:X\to \mathbb {R}\, | \, f \mbox{ bounded and measurable} \}$$

the space of all bounded measurable functions on X and equip this space with the usual supremum norm ∥⋅∥_∞. Furthermore, if ν is a σ-finite measure² on $(X,\mathcal {A})$, we define, for a measurable f:X→ℝ,

$$\Vert f \Vert _{\mathcal {L}_{\infty}(\nu)} := \inf\bigl\{ a\geq0 : \bigl\{x\in X:\bigl|f(x)\bigr| > a\bigr \} \mbox{ is a $\nu$-zero set} \bigr\}.$$

This leads to the space

$$\mathcal {L}_{\infty}(\nu):= \bigl\{ f:X\to \mathbb {R}\, | \, f \mbox{ measurable and }\Vert f \Vert _{\mathcal {L}_{\infty}(\nu)} < \infty\bigr\}$$

of essentially bounded, measurable functions on X. By considering a sequence $\alpha_{n}\searrow \Vert f \Vert _{\mathcal {L}_{\infty}(\nu)}$, it is straightforward to show that the infimum in the definition of $\Vert \cdot \Vert _{\mathcal {L}_{\infty}(\nu)}$ is actually attained; that is,

$$ \nu\bigl( \bigl\{|f|> \Vert f \Vert _{\mathcal {L}_{\infty}(\nu)} \bigr\} \bigr )=0,\quad f\in \mathcal {L}_{\infty}(\nu).$$

(57)

Furthermore, we write ${L}_{\infty}(\nu):= \mathcal {L}_{\infty}(\nu)_{/\sim}$ for the quotient space with respect to the usual equivalence relation f∼g:⇔ν({f≠g})=0 on $\mathcal {L}_{\infty}(\nu)$. From (57), we can then conclude that the linear map

is a metric surjection, and hence its quotient map $\bar{I}_{\nu}:\mathcal {L}_{\infty}(X)_{/\sim} \to {L}_{\infty}(\nu)$, which is given by $\bar{I}([f]_{\sim}) = [f]_{\sim}$, is an isometric isomorphism. Here we note that, given an $f\in \mathcal {L}_{\infty}(X)$, the equivalence class [f]_∼ in L _∞(ν) consists, in general, of more functions than the corresponding equivalence class [f]_∼ in $\mathcal {L}_{\infty}(X)_{/\sim}$. Nevertheless, $\bar{I}_{\nu}$ gives us a canonical tool to identify the spaces $\mathcal {L}_{\infty}(X)_{/\sim}$ and L _∞(ν). Our next goal is to find a continuous and linear right-inverse of I _ν . To this end, we recall the definition of a lifting on $\mathcal {L}_{\infty}(X)$.

Definition B.1

Let $(X,\mathcal {A})$ be a measurable space and ν be a σ-finite measure on $(X,\mathcal {A})$. We say that a map $\rho:\mathcal {L}_{\infty}(X)\to \mathcal {L}_{\infty}(X)$ is a ν-lifting if the following conditions are satisfied:

• (i) ρ is an algebra homeomorphism; that is, ρ is linear and ρ(fg)=ρ(f)ρ(g) for all $f,g\in \mathcal {L}_{\infty}(X)$.

• (ii) ρ(1 _X )=1 _X .

• (iii) [ρ(f)]_∼=[f]_∼ for all $f\in \mathcal {L}_{\infty}(X)$.

• (iv) ρ(f)=ρ(g) for all $f,g\in \mathcal {L}_{\infty}(X)$ with [f]_∼=[g]_∼.

If $\rho:\mathcal {L}_{\infty}(X)\to \mathcal {L}_{\infty}(X)$ is a ν-lifting and $f\in \mathcal {L}_{\infty}(X)$ satisfies f(x)≥0, then $h:=\sqrt{f} \in \mathcal {L}_{\infty}(X)$, and hence we obtain

$$\rho(f) = \rho\bigl(h^2\bigr) = \rho^2(h) \geq0.$$

Consequently, ρ also respects the ordering on $\mathcal {L}_{\infty}(X)$. From this we can conclude that ρ is also continuous with respect to ∥⋅∥_∞. Indeed, if we have an $f\in \mathcal {L}_{\infty}(X)$ with ∥f∥_∞≤1, we find −1 _X ≤f≤1 _X , and since ρ is linear and respects the ordering, we obtain

$$-\boldsymbol {1}_X = \rho(-\boldsymbol {1}_X ) \leq\rho(f)\leq\rho(\boldsymbol {1}_X) = \boldsymbol {1}_X;$$

that is, ∥ρ(f)∥_∞≤1. In other words, we have shown ∥ρ∥≤1. Moreover, from conditions (iii) and (iv), we can conclude that

$$\ker\rho= \bigl\{ f\in \mathcal {L}_{\infty}(X): \nu\bigl(\{f\neq0\}\bigr) =0 \bigr\} =[0]_\sim,$$

where the equivalence class [0]_∼ is the one in $\mathcal {L}_{\infty}(X)$. Consequently, the quotient map $\bar{\rho}:\mathcal {L}_{\infty}(X)_{/\sim} \to \mathcal {L}_{\infty}(X)$, defined by [f]_∼↦f, is a well-defined, bounded, linear, and injective operator with $\Vert \bar{\rho}\Vert \leq1$. Moreover, from condition (ii), we obtain

$$\bigl[\bar{\rho}\bigl([f]_\sim\bigr)\bigr]_\sim= \bigl[\rho(f)\bigr]_\sim= [f]_\sim, \quad f\in \mathcal {L}_{\infty}(X);$$

that is, $[\,\cdot \,]_{\sim}\circ\bar{\rho}= \operatorname {id}_{\mathcal {L}_{\infty}(X)_{/\sim}}$. Considering the isometric isomorphism $\bar{I}_{\nu}^{-1}: {L}_{\infty}(\nu)\to \mathcal {L}_{\infty}(X)_{/\sim}$, we can now define the bounded, linear, and injective operator

$$ \varphi:=\bar{\rho}\circ\bar{I}_\nu^{-1}:{L}_{\infty}(\nu)\to \mathcal {L}_{\infty}(X),$$

(58)

which, by construction and our previous considerations, satisfies ∥φ∥≤1 and

$$ \bigl[\varphi\bigl([f]_\sim\bigr)\bigr]_\sim=[f]_\sim, \quad f\in \mathcal {L}_{\infty}(\nu),$$

(59)

where the outer [ ⋅ ]_∼ on the left-hand side and [ ⋅ ]_∼ on the right-hand side both refer to equivalence classes in $\mathcal {L}_{\infty}(X)_{/\sim}$. Applying $\bar{I}_{\nu}$ to both sides, we conclude that $I_{\nu}\circ\varphi= \operatorname {id}_{{L}_{\infty}(\nu)}$; i.e., φ is the desired right-inverse of I _ν . In other words, φ picks from each equivalence class of L _∞(ν) a bounded representative in a linear and continuous way. Moreover, it is not hard to check that φ is actually an algebra homeomorphism with φ([1 _X ]_∼)=1 _X , and, in addition, it also respects the ordering of L _∞(ν) and $\mathcal {L}_{\infty}(X)$. Consequently, the map φ has highly desirable properties. So far, however, we have not shown that there actually exists a ν-lifting, and hence we do not know whether a map φ with the above properties exists. This gap is filled by the following theorem:

Theorem B.2

(Existence of liftings)

Let $(X,\mathcal {A})$ be a measurable space and ν be a σ-finite measure on $(X,\mathcal {A})$ such that $\mathcal {A}$ is ν-complete. Then there exists a ν-lifting $\rho:\mathcal {L}_{\infty}(X)\to \mathcal {L}_{\infty}(X)$.

Proof

See [39, Theorem 3.2], where we note that σ-finite measures are strictly localizable and Carathéodory completeness of $\mathcal {A}$ equals ν-completeness. □

As [39, Theorem 3.2] shows, the σ-finiteness of the measure is not necessary if one assumes, instead, some other, technically more involved conditions on ν. Finally, further information on liftings and their applications can be found in, e.g., [24, 42].