Abstract
It is well known that over the eighteenth century the calculus moved away from its geometric origins; Euler, and later Lagrange, aspired to transform it into a “purely analytical” discipline. In the 1780 s, the Portuguese mathematician José Anastácio da Cunha developed an original version of the calculus whose interpretation in view of that process presents challenges. Cunha was a strong admirer of Newton (who famously favoured geometry over algebra) and criticized Euler’s faith in analysis. However, the fundamental propositions of his calculus follow the analytical trend. This appears to have been possible due to a nominalistic conception of variable that allowed him to deal with expressions as names, rather than abstract quantities. Still, Cunha tried to keep the definition of fluxion directly applicable to geometrical magnitudes. According to a friend of Cunha’s, his calculus had an algebraic (analytical) branch and a geometrical branch, and it was because of this that his definition of fluxion appeared too complex to some contemporaries.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Geometry and analysis in eighteenth-century calculus
When the calculus appeared at the end of the seventeenth century, it concerned variable geometrical quantities associated with curves: abscissa, ordinate, arc-length, and son on (Bos 1974, 5).
As the eighteenth century progressed, algebraic, or analytical, expressions, which at first were tools for studying geometrical objects, gained ascendance.Footnote 1 Between 1748 and 1770, Leonhard Euler published a set of treatises on the calculus where, for the first time, this was presented as being primarily about functions – “function of a variable quantity” being defined as an “analytical expression composed in any way from that variable quantity and numbers or constant quantities”; as examples, “\(a+3z\); \(az-4zz\); \(az+b\surd (aa-zz)\); \(c^z\); &c. are functions of z”.Footnote 2 In the preface to his treatise on differential calculus Euler states that in it “all is contained within the boundaries of pure Analysis, so that no figure is necessary to explain all the rules of this calculus”.Footnote 3
This move away from geometry and towards analysis was not immediately followed by every author. In particular, most textbook authors resisted or ignored it. A clear example of survival of a geometrical version of the calculus can be found in the section on the calculus in (Bézout 1767). This was an extremely successful text, reprinted several times up to the end of the eighteenth century; it is quite relevant to us that this section on the calculus was translated into Portuguese (Bézout 1774) and adopted as a textbook in the newly founded Faculty of Mathematics of the University of Coimbra.Footnote 4 In that textbook, the word “function” is first defined nearly 70 pages after “differential”, as a mere detail in a section on multiple points of curvesFootnote 5 and for a second time at the beginning of the integral calculus: “We will call function of a quantity, any expression for calculation where that quantity enters, whatever way it enters”Footnote 6. Geometrical applications occupy a major portion of Bézout’s calculus (about two thirds of the differential calculus); and several results are based on geometrical reasonings—for instance, the determination of maxima and minima comes from the study of tangents that are parallel to the axis of abscissas (Bézout 1774, 51, 55), while in (Euler 1755, 580–581) the condition \(\frac{dy}{dx}=0\) comes from the Taylor series expansion of y as function of x.
What has been said above applies directly to the Leibnizian calculus, which was dominant in continental Europe. In Britain, Newton’s method of fluxions prevailed. Although equivalent for many purposes, these two calculi were conceptually distinct and followed different paths. Overall, it may be said that the method of fluxions was more consistently geometric, lacking an analytic version such as Euler’s. It is true that formal manipulation of series was a fundamental component—so much so that Newton called it “method of fluxions and of series”; however, after an analytical youth, Newton came to see geometry as epistemologically superior to analysis. The objects of the method were geometrical quantities generated by motion (fluents), a fluxion being the velocity of a fluent’s generation, or flow. Moreover, after the famous attack by Berkeley on the use of infinitely small quantities in 1734, most British mathematicians adopted the stance that the method of fluxions was a generalization of the ancient Greek geometers’ method of exhaustion (Guicciardini 1989, 47–51).Footnote 7 The analytic perspective only gained ground in Britain in the 19th century.
It is a well-known fact that the word “analysis” has multiple meanings. It should be made explicit that the important distinction in this text is that between analysis and geometry, rather than that between analysis and synthesis. It is, in a sense, an ontological distinction, rather than a methodological distinction: we are interested in the nature of the fundamental objects of the calculus, not in how the presentation of this subject is organized. We will see arguments that are ontologically analytical, because they consist of manipulations of analytical expressions and do not appeal to geometrical properties, but are methodologically synthetical, because they do not show how a result can be obtained, only that it is true.
However, we should keep in mind that since the seventeenth century there was a traditional association between the synthetic method and classical geometry, as the paradigm of the synthetic method was Euclid’s Elements; while the word “analysis” was often given as synonymous of “algebra”.
2 José Anastácio da Cunha, a heterodox mathematician
José Anastácio da Cunha (1744–1787) was certainly the most original Portuguese mathematician of the 18th century.Footnote 8
Cunha was initially educated at the Oratorian college of his hometown, Lisbon, where he studied elementary mathematics reading works by Andreas Tacquet, Tomás Vicente Tosca, and Alexis Claude Clairaut (Rodrigues et al. 2013, 55–56). In 1764, he joined the army and was stationed in the northern border town of Valença. There he befriended several foreign officers who worked for the Portuguese army. Among these were captain Richard Muller, son of John Muller, the first director of the Royal Military Academy at Woolwich, and colonel James Ferrier, a Scotsman. These two gave Cunha access to British scientific books, including Simpson’s Algebra and Newton’s Arithmetica Universalis and Principia Mathematica (Rodrigues et al. 2013, 56–57).
In 1773, Cunha was appointed professor at the newly founded Faculty of Mathematics of the University of Coimbra—part of a major reformation of the university ordered by the Marquis of Pombal, the all-powerful prime minister who was a reformer aligned with the European enlightenment, but also a ruthless autocrat. In Coimbra Cunha had access to advanced works of continental European mathematics; his friend and biographer José Maria de Sousa told a story of how Cunha borrowed Euler’s Integral Calculus from his colleague José Monteiro da Rocha (1734–1819) to study it, and later had to explain a particular passage in it to Monteiro da Rocha (Rodrigues et al. 2013, 62–63). There is an inventory of Cunha’s personal library in 1778, when it was confiscated by the Inquisition, and it is possible to say that its mathematical section was modest, when compared with the literary section: apart from some elementary books, we find several works by Newton (eight volumes in total), d’Alembert’s Traité de l’équilibre, Bossut’s Traité de hydrodynamique, and three unidentified works by Euler bound in one volume (Giusti 1990, 35–37). But of course his readings were not limited to the books he owned: besides borrowing books from Monteiro da Rocha, he could use the University’s library.
Cunha’s position in the university only lasted 5 years, because a political turn in the country (including the dismissal of Pombal) led to a persecution of free thinkers by the Inquisition (which, although much weakened, still existed). Since Valença, Cunha had had opinions and behaviours that were not in keeping with Roman Catholic orthodoxy of the time. He read, and translated, authors such as Alexander Pope and Voltaire (besides writing his own poetry, which was often also heterodox), and at least neglected religious observance. He was arrested in July 1778 and found guilty of heresy and apostasy.Footnote 9
Cunha was detained in Lisbon, at the Oratorian house of Necessidades. This was in the same building where the new Science Academy of Lisbon (Academia Real das Sciencias de Lisboa, founded in 1779) was based. Although he was never admitted into the Academy, the Oratorian priest Teodoro de Almeida, his friend and spiritual director, was a founding member; thus, Cunha had close, albeit indirect contact with the Academy in its early years (Estrada et al. 2006). During this time, he kept working in mathematics: he wrote a text entitled “Principios do Calculo Fluxionario” (“Principles of fluxionary calculus”), which survives only in a fragmentary state, with the date March 1780 (Cunha 2006b; Domingues et al. 2006).
Cunha was released in 1781, but forbidden from returning to Coimbra. He was appointed director of studies of a school for poor boys in Lisbon, but apparently by 1785 he had lost that position too. In his final 2 or 3 years, he depended on friends, as he was jobless and his health was frail (Rodrigues et al. 2013, 71–72). He died on the 1st January 1787.
In 1785–86, he was involved in two polemics with other mathematicians. The most important one was with his former university colleague José Monteiro da Rocha. What is left of it are three letters, two by Cunha and one by Monteiro da Rocha, which were published in the 1890s in the journal O Instituto and reprinted in (Ferraz et al. 1990). In particular, the first one (Cunha 1785), addressed to his friend João Manuel de Abreu, but which appears to have circulated in manuscript copies, is an important source for Cunha’s opinions on several issues in his final years. He was highly critical of how mathematics was usually taught in Portugal and of the scientific level of the Science Academy of Lisbon (where Monteiro da Rocha was the foremost mathematician). He repeatedly praised Newton and d’Alembert,Footnote 10 while presenting Monteiro da Rocha as as an ardent follower of Euler,Footnote 11 as if projecting d’Alembert’s rivalry with Euler on to his own disagreements with Monteiro da Rocha.
Around 1782, a book by Cunha, entitled Principios Mathematicos (Mathematical Principles), began being printed; according to João Manuel de Abreu, who later translated the book into French, as each section of the book was printed, it was used in the college where he worked at the time (Cunha 1790, French transl., iii). But the printing of the book was interrupted when Cunha lost his position. Only 3 years after his death was it published (Cunha 1790).
(Cunha 1790) is a relatively short book (little over 300 pages) that tries to present in a logical order the main branches of pure mathematics, from elementary geometry to some calculus of variations. To cover so much ground, it is naturally an extremely concise text. It also has a few peculiarities, both in the organization of the subjects and in several definitions. As Grattan-Guinness (1990, 59) put it: “Impressive but odd, powerful but cryptic, this book [...] ‘interesting’, but too off-beat to gain the attention that he deserved”.
A French translation of (Cunha 1790), by his friend João Manuel de Abreu, was published in 1811 (and reissued in 1816) but it did not have much impact (Duarte and Silva 1990; Domingues 2014).
In the late twentieth century Cunha’s book received some attention from historians of mathematics, particularly for three originalities:
-
in book 9 he defined “convergent series” as one that satisfies what would later be called the Cauchy criterion, proceeding to actually prove the convergence of some series using this definitionFootnote 12;
-
also in book 9 he defined the power \(a^b\) as \( 1+bc+\frac{bbcc}{2}+\frac{bbbccc}{2\times 3}+ \& \text {c}.\), where c is such that \( a=1+c+\frac{cc}{2}+\frac{ccc}{2\times 3}+ \& \text {c}.\) (i. e., \(a^b\) is defined via the power series for \(\text {e}^{b\log (a)}\)) covering rational, real and even complex exponents in the definition;
-
in book 15 he defined “fluxion” in a way that has been described as corresponding to the modern definition of differential.
Only the third will be directly relevant here. Although Cunha, naturally, used power series in his calculus, he did not address their convergence in that context. As far as I can tell, the word “convergent” does not appear after book 9.
Notice that all these originalities are related to the issue of how to (properly) define particular concepts. Notice also that they are not merely descriptive definitions (as often happened in the eighteenth century): they are actually used in proofs and in the development of theories (albeit short theories, because of the concise nature of the book).
Another posthumous publication (Cunha 1807), about the principles of mechanics, should be mentioned. According to Cunha, the first principles of mechanics cannot be proven mathematically (unlike what many authors tried to do in the eighteenth century). There are then two possibilities: in a physico-mathematical work these first principles must be proven experimentally or come from observation of nature; in a purely mathematical work they must be taken as axioms. In the latter case, the author is, in theory, free to assume the laws of mechanics at will, even that light propagates in a circular, rather than straight, line: “mathematical truth consists solely in the legitimacy with which theorems and solutions of problems are derived from definitions, postulates, and axioms”Footnote 13. It is true that, to avoid being criticized for lack of usefulness, the mathematician should take as axioms factual truths taught by nature. But that theoretical freedom was very unusual, to say the least, in the eighteenth century.
3 Cunha’s fluxionary calculus: geometry or analysis?
It is possible to glimpse the evolution of José Anastácio da Cunha’s personal views on the foundations of the calculus, but it is not possible to have a full picture.
In his essay on the principles of mechanics, whose date of composition is not known, he spoke of ultimate ratios (Cunha 1807, 344–345) and used the dot notation for fluxions.Footnote 14 Thus, it seems that at some point Cunha was a canonical follower of the Newtonian calculus of fluxions.Footnote 15
A manuscript discovered in 2005 and published in (Ralha et al. 2006, II) bears the title “Principles of the fluxionary calculus” and the date March 1780 (Cunha 2006b). But it is only a copy, by someone else, of very incomplete fragments from at least two different versions of Cunha’s work (Domingues et al. 2006, 265–266). In the first part (the one actually dated 1780), Cunha gives a definition of fluxion very close to the one that later appeared in (Cunha 1790),Footnote 16 and uses the d notation; in another part, on higher-order fluxions, he uses the dot notation; near the end, he refers to a definition of limit (which is not extant) and says that “A is the limit of \( A+By+Cy^2+Dy^3+ \& c.\) in regard to infinitesimal y”.Footnote 17 The word “infinitesimal” should be understood in the non-Leibnizian sense of a variable (not a magnitude) capable of assuming arbitrarily small (but finite) values; this is the sense in which Cunha defined it in the first part of the manuscript and later in (1790).Footnote 18
Finally, it must be mentioned that João Manuel de Abreu reported that among the manuscripts that Cunha had left, one had the title “Against the doctrine of prime and ultimate ratios of nascent and evanescent quantities”Footnote 19. Neither the date nor the content of this text are known. But in (Cunha 2006b, 50–51) he distanced himself from the idea, used by Newton, of quantities being generated by motion, which would entail the consideration of time in geometry.
All this suggests that Cunha’s opinions moved from a canonical Newtonian calculus to a somewhat original take on d’Alembert’s proposal of using limits (not surprising, given that d’Alembert, according to himself, was following Newton), and later developed into a more original version of the calculus, using a peculiar definition of infinitesimal. The last one, the version that appeared in (Cunha 1790), is the only one that survives in a form that we may call complete, and the only that will be considered henceforth.
We will see that Cunha used the Leibnizian notation \(dx,d\Gamma x\) (and also \(\int dx\,\Gamma x\)) in (1790), but he kept the Newtonian word “fluxion” (as well as “fluent”). In (2006b, 52–53), he had commented that those names might appear improper, but added that “it matters little: in the definitions lies everything”Footnote 20.
Cunha’s definition of fluxion is the following:
“Some magnitude having been chosen, homogeneous to an argument x, to be called fluxion of that argument, and denoted by dx; we will call fluxion of \(\Gamma x\), and will denote by \(d\Gamma x\), the magnitude that would make \(\frac{d\Gamma x}{dx}\)
constant and \(\frac{\Gamma \left( x+dx\right) -\Gamma x}{dx}-\frac{ d\Gamma x}{dx}\) infinitesimal or zero, if dx were infinitesimal and all that does not depend on dx constant.”Footnote 21
Speaking of this definition, Youschkevitch (1973, 19) said that “it was Cunha who, for the first time, formulated a rigorous analytical definition of the differential, taken up again and used later by the mathematicians of the nineteenth century”Footnote 22. Mawhin (1990, 100) was more specific, saying that it “corresponds to the modern definition of differential of f at x as a linear function \(h\rightarrow Ah\) such that \(f(x+h)-f(x)-Ah=hB(h)\) where \(B(h)\rightarrow 0\) when \(h\rightarrow 0\)”Footnote 23; that is, \(d\Gamma x\) is a linear function of dx (since \(\frac{d\Gamma x}{dx}\) is constant) such that \(\lim _{dx\rightarrow 0}\frac{\Gamma \left( x+dx\right) -\Gamma \left( x\right) -d\Gamma x }{dx}=0\). Of course, this “correspondence” must be taken with a grain of salt. Even apart from some linguistic or conceptual differences (for instance, Cunha does not explicitly say that \(d\Gamma x\) is a function of dx, even though he spoke of functions), his definition is not strictly equivalent, in the mathematical sense, to the modern one, nor could it be without a modern theory of real functions; among other details, and like all his contemporaries, he assumed that all functions were differentiable, or considered only differentiable functions.
A question that naturally arises is whether Cunha’s version of the calculus was more geometrical or followed the analytical trend of the late eighteenth century. Historians or mathematicians who have studied Cunha’s calculus have focused mostly on how rigourous it was, and have not really addressed this question. We will take a brief look at a couple of passing remarks, by Youschkevitch and Gomes Teixeira, that apparently point in opposite directions, simply to show that the classification of Cunha’s calculus as geometrical or analytical is not immediate.
On one hand, Youschkevitch, as quoted above, explicitly stated that “Cunha [...] formulated a rigorous analytical definition of the differential”. It is far from straightforward that in this sentence the word “analytical” is particularly meaningful or used in a sense similar to the one described in section 1; however, it should be remarked that Youschkevitch immediately pointed out that “a precise definition of the differential had already been given, under a geometrical form, by Leibniz”Footnote 24 (but also that this precise geometrical definition by Leibniz, dependent on subtangents, was useless for calculations).
On the other hand, Gomes TeixeiraFootnote 25, although praising the rigour of Cunha’s fluxionary calculus, included too large a role for geometrical intuition as one of its few flaws:
“It would suffice to introduce in the exposition the word limit, which Anastácio da Cunha, bound to the Greek tradition, did not want to employ, to make explicit some conditions included in proofs, and to give a less intense role to geometrical intuition, in order to reduce our geometer’s doctrine to the modern form.”Footnote 26
Cunha’s personal opinions about Newton and Euler seem to suggest that he favoured geometry over analysis (speaking of general approaches to mathematics, not limited to the calculus). Cunha repeatedly expressed his admiration for Newton, while he disliked Euler, and in particular Euler’s faith in analysis. In a letter included in the polemic against Monteiro da Rocha (see page 5 above), he wrote, right after praising d’Alembert:
“But in Coimbra c’est tout une autre chose [it is completely different] Newton, d’Alembert, ne sont que de petits génies [are only little geniuses]. Euler is the only god of mathematics, and Monteiro [da Rocha] his prophet. And which author could our masters, nos sages maîtres [our wise masters], find more suitable to the characters and interests but the one who established implicit faith in matters of mathematics? I do not know if I have ever told you that this author, when perplexed between manifest truths and Algebra, which contradicts them, would close his eyes and cry out as a faithful algebraist: Quidquid sit, calculo potius, quam judicio nostro, est fidendum! [Whatever the question, we should rely on calculation, better than on our judgement!]”Footnote 27
Some of Cunha’s philosophical opinions, which will be the subject of the next section, also suggest, at first sight, a preference for geometry.
But, as we will see in later sections, things are not so simple. In a sense, both Youschkevitch and Gomes Teixeira were right: Cunha’s calculus had an analytical part and a geometrical part. And Euler was probably a bigger influence than Cunha himself would like to admit.Footnote 28
4 Cunha’s mathematical ontology
One of the most marked characteristics in José Anastácio da Cunha’s Principios Mathematicos is the near absence of commentaries or explanatory notes. A consequence is that no motivation is presented there for the frequently unusual and sometimes truly original paths that the text follows.
However, Cunha also left several shorter manuscripts on particular mathematical topics, and in those texts he did include several methodological and philosophical reflexions, often very critical of the ways in which several mathematical topics were usually developed in the eighteenth century.
Based on one of the few of those texts then known (his essay on the principles of mechanics, already mentioned), Norberto Ferreira da Cunha noted in (2001) Anastácio da Cunha’s nominalistic, or anti-essentialist, stance: he rejected the real existence of universals (abstract ideas).Footnote 29 But one of the most clear passages in this respect can be found in another text, discovered only in 2005, a prologue for a presentation of the principles of geometryFootnote 30:
“[there is no reason to] seriously consider, analyse and combine beings of reason, mere Aristotelian substantial forms, such as would be, in the literal sense of almost every author, point, line, surface, angle, ratio between two magnitudes, incomparable indivisibles, infinitely large and infinitely small [quantities], fluxions, prime and ultimate ratios, velocity, momentum, force, action, reaction, collision, attraction, repulsion. It is not usually noticed that such words are but descriptions of phenomena, abbreviations of phrases, of arguments, sometimes intricate and even unfeasible; and this negligence together with the unprofitable mistake or imprudence of taking them for names of substances, such as are e. g. the words man, tree, flower, Sun, stars, etc. has been an extremely plentiful source of logomachies and relevant errors”.Footnote 31
Cunha’s concern with proper definitions (pages 6-7 above) was, at least in part, a consequence of his nominalism. For most mathematicians of the 18th century, definitions were merely descriptions of mathematical objects that were assumed to exist a priori; they were intended to convey the general meaning of a word, but did not need to exhaust that meaning [Ferraro 1999, 103–104; Petrie 2012, 282–285]. Not so for the nominalist Cunha: for instance, in a manuscript (in English) on logarithms and powers, he complained of authors who
“employ sophistry to prove what the narrowness of their definition renders not only incapable of demonstration, but even unintelligible. They define the power of a number to be what is form’d by its continual multiplication. Admit this, and then I will ask you what does \(a^\frac{1}{2}\) or \(a^\frac{1}{3}\) signify?” (Cunha 1778, 58).Footnote 32
For Cunha, the word “power”, or the symbol \(a^b\), could mean only what its definition said it meant; hence he sought to define power, in (Cunha 1778) and in (Cunha 1790, 108–109), in ways not limited to integer exponents.Footnote 33 We have seen in page 9 that when discussing the appropriateness of the names “fluent and fluxion”, he concluded that “it matters little: in the definitions lies everything”.
Another, but related, aspect of Cunha’s ontology is his physicalism. In the same prologue to the principles of geometry, following a quotation from Newton, Cunha concludes that “thus, in the opinion of Sir Isaac, geometry is properly a part of physics. And in truth I do not know what else it might be”Footnote 34. Accordingly, Cunha defined the simpler objects of geometry (points, lines, surfaces) as “bodies”: for instance, the first definition in Cunha (1790) reads
“The Body, whose length is such that no remarkable error comes from disregarding it, is called Point”Footnote 35.
More complex objects (for instance, fluxion or velocity) are just names, words that abbreviate more intricate phrases.Footnote 36
Anti-essentialism, nominalism, or physicalism are not, of course, originalities of Cunha (although we will see that he drew some original consequences from his nominalism). David Sepkoski (2005) identified nominalist and physicalist conceptions in Barrow and Newton (and, as had been said, Newton was one of Cunha’s mathematical heroes).
It is important to notice that the anti-essentialism of Barrow and Newton is associated to their preference for geometry over algebra. Analytic/algebraic methods and concepts, being more abstract, would be more palatable to mathematicians with essentialist stances. Giovanni Ferraro, in a paper on “analytical symbols and geometrical figures in eighteenth-century calculus” (2001), used Aristotelian references to interpret the analytical definitions of variable, in particular those of Euler and Lagrange. While for authors of geometrical versions of the calculus, a variable was literally a (geometrical) quantity that varied, increasing or decreasing, for the great analysts Euler and Lagrange, a variable was “an indeterminate or universal quantity” (Euler) or an “abstract quantity” (Lagrange); being “generated from particular geometrical quantities by means of a process of abstraction [...] the notion of a variable concerned the essence of quantity” (Ferraro 2001, 541) (emphasis in the original).
Actually, Cunha’s definition of variable may have have been inspired by Euler’s, but with a crucial nominalistic twist: for Euler, to quote in full, “a variable quantity is an indeterminate or universal quantity, which comprises in itself absolutely all determinate values”Footnote 37; for Cunha, “if an expression can assume more than one value, while another can assume only one, the latter will be called constant, and the former variable”Footnote 38 — that is, Cunha’s variable is an expression (rather than a quantity) that can assume, if not all values like Euler’s, at least several.
Cunha’s definition seems more distant from the traditional geometrically-inspired definitions (quantities that vary), of which he was very critical (notice the opposition between the explanation by “common authors”, which allegedly results in a contradiction, and the understanding of “the geometer”, i. e. a proper mathematician):
“Common authors [say] that, e. g. in a given circle, the diameter is constant and the chord is variable; and [the reader] understands that the same magnitude is now the chord of 10° then of 11° etc.; that is, one magnitude is and is not the same. — The geometer understands by variability only what consists in the possibility of denoting several magnitudes by a single expression.”Footnote 39
5 The algebraic and the geometrical branches in Cunha’s calculus
The question of whether Cunha’s calculus was more geometrical or more analytical received an answer over 200 years ago, from João Manuel de Abreu, a friend of Cunha’s and the translator of (Cunha 1790) into French. He was not trying to answer this question. A review of the French edition of (Cunha 1790) had appeared in the Edinburgh Review (anonymously but almost certainly by the Scottish mathematician John Playfair) (Domingues 2014, 37–38). This review was globally positive, but criticised several aspects of Cunha’s book. Abreu published a reply (but in Portuguese, in a Portuguese periodical published in London) (Abreu 1813–1814).Footnote 40 In that reply, addressing Playfair’s criticism that Cunha’s definition of fluxion was “very difficult to be understood”, Abreu stated that
“[Anastácio da Cunha] divided his theory of fluxions into two branches, an algebraic one, composed of proposition 1 of book 15, and of all propositions that depend on it; and a geometrical one, whose first proposition is Archimedes’ axiom, and which is composed of propositions 13, 14, 15, 17, and 18, of book 15, and 39, 40, 41, of book 16, &c. In the first, algebraic, branch he followed his ordinary method, always resorting to the fundamental definition, or to theorems deduced from it; in the second, geometrical, branch, he adopted the ancients’ method of proof, commonly called of exhaustion. Now, definition 4 of book 15 is common to both; thus, it must be more complex, and consequently less intelligible than any definition of fluxion that comprehends but one of the two branches.”Footnote 41
These “branches” do not reflect the formal organization of (Cunha 1790), nor are they ever mentioned in Cunha’s known writings. Rather, they reflect Abreu’s classification of those propositions, a classification made about 25 years after Cunha’s death. But it is a classification that makes sense: as we will see, the “algebraic” branch is composed of purely analytical propositions (and will often be called in the following “analytical”, rather than “algebraic”), while geometrical objects and arguments appear in the geometrical branch. This classification even seems to reflect, if we restrict ourselves to book 15, a subtle difference in language, namely in some verb moods (see Sect. 5.4).
5.1 The algebraic/analytical branch in book 15
(Cunha 1790) is organized in chapters called “books”, following the Euclidean model. Book 15 is dedicated to the calculus, starting with fundamental definitions. We have seen that, according to João Manuel de Abreu, definition 4, of fluxion, is common to both the algebraic (analytical) and the geometrical branches. How can we classify the other definitions in book 15?
We have already seen definition 1, of constant and variable (pages 14–15 above). Its classification is not straightforward. It is not a typical analytical definition (variable as an universal or abstract quantity), but it is even more distant from traditional geometrical traditions (quantities that vary). It may be a nominalistic adaptation of Euler’s analytical definition.Footnote 42
A similar difficulty occurs with definition 2:
“A variable always capable of assuming a value greater than any proposed magnitude will be called infinite; and a variable always capable of assuming a value smaller than any proposed magnitude will be called infinitesimal.”Footnote 43
Throughout the eighteenth century there were plenty of discussions about the nature of infinite and infinitesimal quantities, and whether they actually existed or instead something like limits was more advisable. This definition by Cunha, which must be read in conjunction with his definition 1, does not correspond to any of the common solutions of the period: it introduces infinitesimals, but as variables and hence expressions, not quantities.Footnote 44
Like definition 1, definition 2 may best be classified as nominalistic. Notice that neither of them introduces new ontological categories, but only names for certain types of expressions. However, being about expressions, they are in a sense (albeit not the traditional one) in an analytical domain.
Definition 3 reinforces the analytical course: “If the value of an expression A depends on another expression B, A will be called function of B”Footnote 45. It is significant that “function” is defined so early in Cunha’s calculus, suggesting that this is a central object here, as it was in Euler’s; and indeed it is.
This is followed by definition 4, of fluxion, two definitions (of fluent as antiderivative, and of higher order fluxions) that are not important for our purpose, some remarks on notation, and then propositions.
According to Abreu, propositions 1 to 12 are part of the algebraic branch. Indeed, in these propositions, Cunha presents fundamental results of the differential calculus in a purely analytical context, without any geometrical concepts or arguments. A simple example of the typical format of these propositions is proposition 2, to the effect that \(d(x^n)=nx^{n-1}dx\). Proposition 1 had established that a polynomial in an infinitesimal variable is itself infinitesimal; this is now used to verify that \(nx^{n-1}dx\) satisfies the conditions in the definition of fluxion (page 9 above):
“dx infinitesimal and what does not depend on dx constant make \(\frac{nx^{n-1}dx}{dx}\left( =nx^{n-1}\right) \) constant and \(\frac{(x+dx)^n-x^n}{dx}-\frac{nx^{n-1}dx}{dx}\)
infinitesimal.”Footnote 46
Another example, whose analytical character is very obvious, is proposition 8, where the fluxion of the logarithm is obtained differentiating term by term the series of the exponential:
“Let x stand for any number and l indicate hyperbolic logarithms: then \(dx=xdlx\).
For
.”Footnote 47
In this case Bézout (1774, 23–26) is not explicitly geometrical, but neither really analytical: the result equivalent to this is obtained going back to the definition of logarithms as terms in an arithmetical progression in a correspondence with a geometrical progression, establishing the relation \(\frac{ma(y'-y)}{y}=x'-x\) between consecutive terms in these progressionsFootnote 48 and then imagining the differences \(y'-y\) and \(x'-x\) infinitely small. Other authors from this period are more directly geometrical: (Cousin 1777, 29–30) uses the logarithmic curve (defined by the property that, if the abscissas are in arithmetical progression, then the ordinates are in geometrical progression); while (Saladini 1775, II, 44–47) uses the characterization of the logarithm as the area under a hyperbola.
5.2 The geometrical branch in book 15
According to João Manuel de Abreu, the geometric branch starts in proposition 13, whose enunciation reads:
“Let AB stand for the abscissa and BC for the ordinate corresponding to an arbitrary arc AC of a regular curve AD (that is, of a curve whose ordinate is a function of the abscissa); let any other ordinate DE be drawn and the parallelogram BF be completed: if BE is fluxion of AB, BF will be fluxion of the area ACB.”Footnote 49
Diagram for propositions 13 and 14 of book 15 of (Cunha 1790)
There is here a surprisingly analytical detail: the explicit condition that the ordinate be a function of the abscissa. However, the proof is geometrical: Cunha assumes that the ordinate function is monotonicFootnote 50 and trusts the diagram (Fig. 1; notice oblique coordinates) to convince the reader that area CDF is contained in the parallelogram with diagonal CD (not drawn):
“ \(\frac{BF}{BE}\) will be the perpendicular drawn from point C to line BE, produced if need be; let \(\frac{BF}{BE}+\pi \) be the perpendicular drawn from point D to the same line AE; then \(\frac{CDF}{BE}<\pi \). AB constant and BE infinitesimal would make BC constant, \(\frac{BF}{BE}\) constant, \(\pi \) infinitesimal and the area CDF infinitesimal; and therefore \(\frac{BF}{BE}\) constant and \(\frac{ADE-ACB}{BE}-\frac{BF}{BE}\) ( \(=\frac{BCDE}{BE}-\frac{BF}{BE}=\frac{CDF}{BE}<\pi \)) infinitesimal. Therefore if BE is fluxion of AB, BF will be fluxion of the area ACB.”Footnote 51
( \(\frac{BF}{BE}\), that is, the area of parallelogram BF divided by the length of base BE, is the height of parallelogram BF; Cunha assumes that the curved region CDF is contained in the parallelogram CD, so that the area of that region divided by the length of base \(BE=CF\) is less than the height \(\pi \) of parallelogram CD; it remains only to verify the conditions of the definition of fluxion — page 9 above)
A modern reader might be tempted to see in this proposition a version of the (first) fundamental theorem of the calculus.Footnote 52 However, as was usual in the eighteenth century, for Cunha the definite integral was not a central concept: it has already been observed that “fluent” is defined as an antiderivative (“every magnitude is called fluent of its fluxion”Footnote 53). Therefore, proposition 13 is only the first geometrical application of the fluxionary calculus, equivalent to deriving the area under the graph of a function.
The remaining propositions in the geometrical branch of book 15 are yet geometrical applications of the calculus: the characteristic triangle, with the tangent to the curve and the fluxion of the arc; and the fluxion of the volume of a solid.
5.3 The following books of Principios Mathematicos
Book 16 is dedicated to trigonometry. The initial approach is geometrical, sine, tangent, etc. being defined as lines. Cunha even waits thirteen pages (and 28 propositions) until he assumes the radius of the circle to be 1; thus, his versions of the basic trigonometric formulas must take the radius in account (for instance, \(\sin (\zeta +z)=\frac{\sin \zeta \cos z+\cos \zeta \sin z}{r}\)). This is partly due to some peculiarities in the organization of the subject. Euler had given in [1748, I, 93–107; 1755, 164–177] a purely analytical calculus of trigonometric functions, but he had done so assuming the reader to already know the basic formulas of trigonometry (for example, \(sin.(y+z)=sin.y.cos.z+cos.y.sin.z\) (Eul er 1748, I, 94)), presumably from more elementary books, that certainly used geometrical arguments. Cunha could have done something similar, presenting a geometrical version of elementary trigonometry in an earlier book of (1790) and then, after book 15, developing the fluxionary calculus of trigonometric functions in an analytical way. Instead, in his very economical style, he concentrated all of trigonometry in book 16, organizing it in a peculiar order: it practically starts with the fluxion of the sine ( \(r\,d{{\,\textrm{sen}\,}}z=dz\cos z\)), demonstrated with a geometrical argument and invoking proposition 14 of book 15 (part of the geometrical branch); from there, he derives the power series for the sine and cosine, and it is from these that comes the formula for the sine of the sum of two arcs. In spite of frequent use of analytical arguments such as this, book 16 must be classified as geometrical, because the basic definitions and some fundamental arguments are geometrical.
In book 17, we find topics of elementary differential geometry of curves: multiple points, asymptotes, radius of curvature. Naturally, it is geometrical.
The next three books, however, are purely analytical. In book 18, we find several techniques of integration (such as partial fraction decomposition), and L’Hôpital’s rule, which is proven using Taylor series expansions of the numerator and of the denominator. Book 19 deals with differential equations, in a purely analytical way, including Euler’s solution for linear differential equations with constant coefficients (Baroni 2001, 34–35). Book 20 deals with the calculus of finite differences.
Book 21, the last one, is a case apart. It is a miscellany, probably compiled from several short manuscripts left by Cunha on diverse topics, by whoever arranged for the final publication of (Cunha 1790). It was almost certainly not revised by Cunha. It is here that we see what is possibly the only case in (Cunha 1790) of a fundamental proposition of the calculus that, not being about a geometrical object, resorts to a geometrical reasoning; but the argument is so vague that it is not clear whether it is geometrical. The proposition in question is proposition 12: “To find the maximum value of a given function \(\Gamma x\)”Footnote 54. Cunha just: 1 - states that “the fluxions of any two values of \(\Gamma x\) that are each on each side of the maximum, will be opposite [i. e., will have opposite signs]”,Footnote 55, but does not explain why (the relationship between the sign of the fluxion and the increasing or decreasing property of the function is not explained before), and 2 - invokes a scholium from book 17 according to which “experience has shown geometers that any variable whose values have infinitesimal differences, when passing from positive to negative becomes equal either to 0 or to \(\frac{1}{0}\)”Footnote 56—a version of the intermediate value property, grounded on experience, for lack of a proof.
5.4 A linguistic distinction between the two branches
Let us recall Cunha’s definition of fluxion:
“Some magnitude having been chosen, homogeneous to an argument x, to be called fluxion of that argument, and denoted by dx; we will call fluxion of \(\Gamma x\), and will denote by \(d\Gamma x\), the magnitude that would make \(\frac{d\Gamma x}{dx}\)
constant and \(\frac{\Gamma \left( x+dx\right) -\Gamma x}{dx}-\frac{ d\Gamma x}{dx}\) infinitesimal or zero, if dx were infinitesimal and all that does not depend on dx constant.”
Are Cunha’s fluxions infinitesimal, using this word in the sense of definition 2 (p. 17 above)? The counterfactual clause “if dx were infinitesimal” suggests that dx is not. Furthemore, if fluxions were infinitesimal, according to definition 2 they would be variables, that is, expressions that can assume multiple values; while the definition of fluxion says explicitly that a fluxion is a magnitude—thus, presumably, having only one value. See the quotation in pages 14–15 above, which shows his reservations about talking of variable geometrical magnitudes.
Yet, going beyond the definition and looking at the language used in propositions of book 15, we see a clear distinction in this respect between the analytical branch and the geometrical branch, and in the former fluxions seem to actually be infinitesimal.
In fact, in the analytical branch, Cunha systematically uses phrases like “dx infinitesimal and what does not depend on dx constant make [...] \(nx^{n-1}\) constant and \(\frac{(x+dx)^n-x^n}{dx}-\frac{nx^{n-1}dx}{dx}\) [...] infinitesimal” (prop. 2, quoted above; my emphasis), using the indicative mood, which indicates that fluxions are infinitesimal.
On the other hand, in the geometrical branch, at least in book 15, we find phrases such as “AB constant and BE infinitesimal would make [...] area CDF infinitesimal” (prop. 13, quoted above; my emphasis).Footnote 57 In the geometrical branch of book 15, fluxions are never said to actually be infinitesimal.
At first hand, this may seem inconsistent. However, in the analytical branch x, dx, \(\Gamma x\), \(d\Gamma x\),...are expressions that stand for multiple magnitudes, so that they can be infinitesimal in Cunha’s sense; apparently, this did not happen in the geometrical branch, perhaps because he did not see the phrase “line BE” as representing several segments.
An actual inconsistency in (Cunha 1790) is that from book 16 onwards these subtleties of language disappear, and we find phrases stating that geometrical magnitudes are infinitesimal. For instance, in book 16: “let AD be constant and DF infinitesimal; \(\frac{BEm}{DF}\) will be infinitesimal”Footnote 58. Maybe all this concern with language might be difficult to maintain, and it was enforced only in book 15. Or, perhaps, Cunha’s death in 1787 prevented him from revising the text from book 16 onwards in order to introduce subjunctives when speaking of magnitudes.
Still, it seems clear that in book 15 Cunha made an effort to use language consistent with the following scheme:
-
Speaking of geometrical magnitudes, their fluxions are magnitudes, homogeneous to them, therefore not infinitesimal (although, in calculating them, one operates as if they were infinitesimal);
-
Speaking of expressions that may represent several magnitudes (that is, variables), their fluxions are naturally also variables, and are indeed infinitesimal.
In practical terms, this linguistic distinction is inconsequential, but it suggests that Cunha actually distinguished in his mind between the two branches, and indicates that, at a theoretical level, the geometrical branch took precedence—the definition of fluxion is worded in the manner of the geometrical branch.
6 Final remarks
José Anastácio da Cunha’s personal and philosophical ideas, such as his dislike of Euler and of Euler’s faith in algebra, his admiration for Newton, his preference for a geometry grounded on physical bodies, his anti-essentialism, all suggest at first sight that his version of the calculus should be geometrical, not in line with the analytical trend of the late eighteenth century.
Also, an attentive reading of Cunha’s definition of fluxion brings out geometrically inclined characteristics: fluxions are defined as magnitudes, and dx must be homogeneous to x (concern with homogeneity is a hallmark of geometrical thinking).
And yet, we see that he developed the fundamental propositions of his version of the calculus in an analytical way, thanks to an original, nominalistic, conception of variable that allowed him to talk of functions and infinitesimals as mere expressions, not, as he would put it, “beings of reason”. What Abreu called the “geometrical branch” and what has been classified as geometrical in Sect. 5.3 are really geometrical applications, not results that might instead be derived analytically.Footnote 59
It is significant that Cunha felt that his definition of fluxion had to speak of magnitudes and conform with homogeneity to accommodate geometrical objects. Unlike Euler, he did not see variables as a more general kind of magnitude. But in practice, apart from a convoluted definition, his calculus was mainly analytical; certainly more analytical than the one adopted in the University of Coimbra (Bézout 1774).
Actually, the conclusion must be drawn (or reinforced) that, despite his dislike of Euler, Cunha was heavily influenced by him. He was always very critical, but he managed to reconcile his anti-essentialism with the analytical ways that were gaining ground in his time.
Notes
(Bos 1974), already cited, covers this process from Leibniz to Euler; (Fraser 1987) addresses Lagrange’s later, more radically algebraic, version of the calculus; (Fraser 1989) identifies the common algebraic characteristics of Euler’s and Lagrange’s versions (which were different in other aspects). (Jahnke 2003) gives a general view of the calculus in the eighteenth century; (Domingues 2008, 53–59) presents a picture of the question of the foundations of the calculus at about the same period as Cunha’s work.
“Functio quantitatis variabilis, est expressio analytica quomodocunque composita ex illa quantitate variabili, & numeris seu quantitatibus constantibus. [...] Sic \(a+3z\); \(az-4zz\); \(az+b\surd (aa-zz)\); \(c^z\); &c. sunt Functiones ipsius z.” (Euler 1748, 4).
“Hic autem omnia ita intra Analyseos purae limites continentur, ut ne ulla quidem figura opus fuerit, ad omnia huius calculi praecepta explicanda.” (Euler 1755, xx).
“[...] F, \(F'\), &c., T denoting quantities composed as one may wish of x, y and constants, which, to abbreviate, are usually called functions of x, y and constants” (“[...] F, \(F'\), &c., T marquant des quantités composées, comme on le voudra, de x, y & de constantes, ce que, pour abréger, on appelle des fonctions de x, y & de constantes” (Bézout 1767, 78); cf. (Bézout 1774, 74)); that is, the word “function” appeared only as an “abbreviation”, it did not correspond to a fundamental concept.
Guicciardini addresses the rare exceptions to this in a chapter called “The analytic art (1755–85)” (1989, 82–91).
(Queiró 1988) is a very good introduction to José Anastácio da Cunha in English, but it is outdated in some aspects, particularly because several manuscripts by or about Cunha have since been discovered. In English, see also (Oliveira 1988) and (Domingues 2014). (Ferraz et al. 1990) and (Ralha et al. 2006, I) contain important studies about Cunha, mostly in Portuguese but also, in the former case, a few in French or English.
His file at the Inquisition has been published as (Ferro 1987).
By the end of his life, Monteiro da Rocha owned most of Euler’s books, and drew on his work about the orbits of comets; but there is no evidence, apart from Cunha’s “accusation”, that Monteiro da Rocha was more Eulerian than the average mathematician of his time (Domingues 2007, 97–100).
“A verdade mathematica não consiste senão na legitimidade com que os theoremas, e as soluções dos problemas se derivam das definições, postulados e axiomas” (Ferraz et al. 1990, 340).
The editor of the 1807 edition added footnotes with the Leibnizian d notation, and the editor of the 1856 edition used only the d notation; the editors of the 1990 edition copied the 1856 edition, but acknowledged this issue (Ferraz et al. 1990, 315).
But with all verbs in the indicative, rather than subjunctive mood (see Sect. 5.4).
“A he o limite de \( A+By+Cy^2+Dy^3+ \& c.\) a respeito de y infinitessimo” (Cunha 2006b, 54–55).
On Cunha’s non-Leibnizian concept of infinitesimal, see (Domingues 2004, 23–26) and page 17 below.
“isso pouco importa: nas definições está tudo”.
“Escolhida qualquer grandeza, homogénea a uma raiz x, para se chamar fluxão dessa raiz e denotada assim dx; chamar-se-á fluxão de \(\Gamma x\), e se denotará assim \(d\Gamma x\), a grandeza que faria \(\frac{d\Gamma x}{dx}\) constante e \(\frac{\Gamma \left( x+dx\right) -\Gamma x}{dx}-\frac{ d\Gamma x}{dx}\) infinitésimo ou cifra, se dx fosse infinitésimo e constante tudo o que não depende de dx” (Cunha 1790, 194).
“C’est da Cunha qui a, pour la première fois, formulé une définition analytique rigoureuse de la différentielle, reprise et utilisée plus tard par les mathématiciens du XIXe siécle.”
“correspond [...] á la définition moderne de différentielle de f en x comme fonction linéaire \(h\rightarrow Ah\) telle que \(f(x+h)-f(x)-Ah=hB(h)\) oú \(B(h)\rightarrow 0\) lorsque \(h\rightarrow 0\)”.
“une définition exacte de la différentielle avait déjá été donnée, sous une forme géométrique, par Leibniz” (Youschkevitch 1973, 19).
Francisco Gomes Teixeira (1851–1933) was, by far, the foremost Portuguese mathematician of his time. An analyst at first, he then turned his attention to geometry and, in his later years, to the history of mathematics in Portugal. His History of Mathematics in Portugal (1934) is, regrettably, still the most recent general account of the subject; it is, naturally, quite dated.
“Bastaria introduzir na exposição a palavra limite, que Anastácio da Cunha, prêso á tradição grega, não quis empregar, tornar explícitas algumas condições incluídas nas demonstrações e dar á intuïção geométrica um papel menos intenso, para reduzir a doutrina do nosso geómetra á forma moderna.” (Teixeira 1934, 257).
“Mas em Coimbra c’est tout une autre chose Newton, d’Alembert, ne sont que de petits génies. Euler é o único Deus da Mathematica, e Monteiro o seu propheta. E que auctor podiam os nossos mestres, nos sages maîtres, achar mais acommodado aos characteres e interesses senão o que instituiu a fé implícita em pontos de Mathematica? Não sei se algum dia lhe contei, que este auctor, quando se via perplexo entre verdades manifestas, e a Algebra, que as contradiz, fechava os olhos, e exclamava como fiel algebrista: Quidquid sit, calculo potius, quam judicio nostro, est fidendum!” (Cunha 1785, 367) A sentence very close to the last one (“Quicquid autem sit hic calculo potius, quam nostro iudicio est fidendum”) occurs in (Euler 1736, I, 108), in a discussion of a body under a force of attraction inversely proportional to the distance: this body reaches the centre of attraction with infinite speed but, contrary to what common judgement would imagine, does not go beyond it, because if it did its speed would become imaginary. However, the possibility should not be excluded that Cunha knew this sentence from a satyrical pamphlet by Voltaire, part of a polemic against Maupertuis, who was supported by Euler: a supposed “peace treatise” where Euler begged forgiveness to all logicians for having written such a sentence (Voltaire 1877–1885, XXIII, 578).
The word “essentialism” was proposed by Popper (1944, 94) to refer to the belief in the actual existence of universals (or essences); the traditional term is “realism”, but “essentialism” has gained some ground in the last decades. “Nominalism” is the traditional name for the view that universals are merely names. Popper’s example is the following: “The universal term ‘white’, for instance, seemed to [the nominalists] to be nothing but a label attached to a set of many different things, snowflakes, table-cloths, and swans, for instance. [...] Essentialists deny that we first collect a group of single things and then label them ‘white’; rather, they say, we call each single white thing ‘white’ on account of a certain intrinsic property that they have in common—their ‘whiteness’” (Popper 1944, 94).
Those principles of geometry were probably an early version of the first few “books” of (Cunha 1790).
“[Não há razão para] seriamente contemplar, analysar e combinar entes de razão, meras formas substanciaes, aristotelicas, quaes seriam no sentido literal de quasi todos os Autores o ponto, a linha, a superficie, o angulo, a razão de duas grandezas, os indivisiveis incomparaveis, infinitamente grandes, e infinitamente pequenos, fluxões, razões, primeiras e ultimas, velocidade, quantidade de movimento, força, acção, reacção, percussão, attracção, repulsão. Geralmente n[ão] se custuma reparar que semelhantes palavras não são senão [des]cripções de phenomenos, abreviaçoens de frases, de discursos, as vezes, entrincados, e athe impraticaveis: e esta incuria junta com a mal succedida equivocação ou temeridade de as tomar por nomes de substancias, como o são v. g. as palavras homem, arvore, flor, Sol, Estrellas, &c. tem sido um manancial copiosissimo he Logomachias, e de relevantes erros” (Cunha 2006a, II, 6–7)
Although not using the word “definition”, Euler opens the chapter on powers of his Elements of Algebra stating that “When a number is multiplied several times by itself, the product is called a power” (“Wann eine Zahl mehrmalen mit sich selbsten multiplicirt wird, so wird das Product eine [...] Potenz [...] genennet” (Euler 1770, I, 99)). Later, he concludes that \(a^0=1\), \(a^{-1}=\frac{1}{a}\), \(a^\frac{1}{2}=\sqrt{a}\), and so on (Euler 1770, I, 104–105, 116–117).
There is more to these attempts than a philosophical standpoint on definitions: Cunha also wished to present a proper proof of the binomial theorem.
“Hé pois propriamente a geometria na opinião de Sir Isaac huma parte da physica. E na verdade, não sei que outra cousa possa ser [...]” (Cunha 2006a, 6–7).
“O Corpo, cujo comprimento he tal, que de se naõ attender a elle, naõ resulta erro notavel, chama-se Ponto” (Cunha 1790, 1).
This distinction made here between simpler and more complex objects is somewhat artificial: “point” is also an abbreviation, for the more intricate phrase “body whose length is such, that no remarkable error comes from disregarding it”.
“Quantitas variabilis est quantitas indeterminata seu universalis, quae omnes omnino valores determinatos in se complectitur” (Euler 1748, I, 4).
“Se huma expressaõ admittir mais de hum valor, quando outra expressaõ admitte hum só, chamarse-ha esta constante, e aquella variavel” (Cunha 1790, 193).
“Os autores vulgares [dizem] que, v. g. em hum circulo dado, o diametro hé constante e a corda variavel; e fica entendendo que huma mesma grandeza hé ora corda de 10° ora de 11° &c.a; isto hé, que huma mesma grandeza hé e não hé a mesma. — O geometra não entende por variabilidade se não o que consiste na possibilidade de notar com huma so expressão grandezas diversas.” (Cunha 2006b, 54–55).
Playfair’s review and Abreu’s reply were reprinted as appendices in (Ferraz et al. 1990).
“[Anastácio da Cunha] dividio a sua theorica das fluxoens em dous ramos, hum algebraico, que se compoem da proposiçaõ 1 do livro 15, e de todas as que della dependem; outro geometrico, cuja proposiçaõ primeira he o axioma de Archimedes, e que se compoem das proposiçoens 13, 14, 15, 17, e 18, liv. 15, e 39, 40, 41, liv. 16, &c. No primeiro ramo algebraico seguio o seu methodo ordinario, recorrendo sempre á definiçaõ fundamental, ou á theoremas deduzidos della; no segundo ramo Geometrico adoptou o methodo de demonstraçaõ dos antigos, chamado vulgarmente d’exhaustaõ. Ora a definiçaõ 4, liv. 15, he comum a ambos; logo deve ser mais complicada, e por consequencia menos intelligivel que qualquer definiçaõ de fluxaõ, que naõ comprehenda senaõ hum dos dous ramos.” (Abreu 1813–1814, 451–452)
On definitions 1 and 2, in their eighteenth-century context, see also (Domingues 2004).
“A variavel que podér sempre admittir valor maior que qualquer grandeza que se proponha chamarse-ha infinita; e a variavel que podér sempre admittir valor menor que qualquer grandeza que se proponha, chamarse-ha infinitessima.” (Cunha 1790, 193).
It is obvious that Cunha’s infinites and infinitesimals are potential, rather than actual. This is consistent with all that we know about Cunha (“the attitude of considering only potential infinites and infinitesimals permeates all the Principios” (Queiró 1988, 41)). But there is more here than the classical opposition between potential and actual infinities: in Cunha’s time, the usual route for those who rejected the actual infinite was to follow the method of limits, as proposed by d’Alembert in the Encyclopédie (Domingues 2008, 57–59); Cunha apparently at some point used limits (see page 8), but later changed paths.
“Se o valor de huma expressaõ A depender de outra expressaõ B, chamarse-ha A funcçaõ de B” (Cunha 1790, 193).
“dx infinitessimo, e o que de dx naõ depende, constante, fazem \(\frac{nx^{n-1}dx}{dx}\left[ =nx^{n-1}\right] \) constante e
 infinitessimo.” (Cunha 1790, 195).
infinitessimo.” (Cunha 1790, 195).“Represente x qualquer numero e indique l logarithmos hyperbolicos: será \(dx=xdlx\). Pois he
 .” (Cunha 1790, 196).
.” (Cunha 1790, 196).a is the first term in the geometrical progression and m is the quotient between the difference between the two first terms in the arithmetical progression and the difference between the two first terms in the geometrical progression.
“Represente AB a abscissa, e BC a ordenada correspondentes ao arco qualquer AC de huma curva regular AD [isto he, de huma curva, cuja ordenada he funcçaõ da abscissa]; tire-se outra qualquer ordenada DE e complete-se o parallelogramo BF: se BE for fluxaõ de AB, será BF fluxaõ da area ACB.” (Cunha 1790, 200).
Or, at least, piecewise monotonic. In a proof included in a letter to João Manuel de Abreu, Cunha wrote: “Let the ordinates always increase or always decrease from \(\Gamma 0\) to \(\Gamma x\) (for all cases may be reduced to this one) [...]” (“Cresçam sempre ou diminuam sempre as ordenadas desde \(\Gamma 0\) até \(\Gamma x\) (pois a este caso de podem reduzir todos) [...]” (Ferraz et al. 1990, 363)).
“ \(\frac{BF}{BE}\) será a perpendicular conduzida do ponto C á recta BE, produzida se necessario for; seja \(\frac{BF}{BE}+\pi \) a perpendicular conduzida do ponto D á mesma recta AE; será \(\frac{CDF}{BE}<\pi \). AB constante e BE infinitessima fariam BC constante, \(\frac{BF}{BE}\) constante, \(\pi \) infinitessima e a área CDF infinitessima; e logo \(\frac{BF}{BE}\) constante, e \(\frac{ADE-ACB}{BE}-\frac{BF}{BE}\) [ \(=\frac{BCDE}{BE}-\frac{BF}{BE}=\frac{CDF}{BE}<\pi \)] infinitessimo. Logo se for BE fluxaõ de AB, será BF fluxaõ da area ACB.” (Cunha 1790, 200–201).
This theorem was fundamental in the creation of the calculus, but by the middle of the eighteenth century, with the integral seen almost always as an antiderivative, it had become only a geometrical application of the calculus—for instance, in (Bézout 1767, 111–113). It is absent from (Euler 1768–1770), because this treatise does not include geometrical applications. It became fundamental again in the 19th century, when the definite integral became a fundamental concept.
“Toda a grandeza se chama fluente da sua fluxaõ [...]” (Cunha 1790, 194).
“Achar o maximo valor de huma funcçaõ proposta \(\Gamma x\)” (Cunha 1790, 294).
“As fluxoens de quaesquer dois valores de \(\Gamma x\), que estaõ hum de huma parte, outro de outra do maximo, seraõ contrarias”.
“A experiencia tem mostrado aos Geometras, que toda a variavel, entre cujos valores ha differenças infinitessimas, ao passar de positiva para negativa, se acha igual, ou a 0, ou a \(\frac{1}{0}\).” (Cunha 1790, 247).
The French translation appears to be faithful in this respect. The passages quoted in these two paragraphs are rendered as “dx infinitiéme, et ce qui ne dépend pas de dx constant, rendent [...] \(nx^{n-1}\) constante et \(\frac{(x+dx)^n-x^n}{dx}-\frac{nx^{n-1}dx}{dx}\) [...] infinitiéme” and “AB constante et BE infinitiéme rendroient [...] l’aire CDF infinitiéme” (Cunha 1790, Fr. tr., 198, 203), my emphases. Of course, the translator was the same João Manuel de Abreu who wrote about the two branches.
“Seja AD constante, e DF infinitessima; será \(\frac{BEm}{DF}\) [...] infinitessimo” (Cunha 1790, 222).
With the possible exception of the determination of the maximum of a funcion, in book 21.
References
Abreu, João Manuel de. (1813–1814). “Notas de Joaõ Manuel de Abreu sobre varios lugares da censura dos Redactores do Edinburgo Review aos Principios Mathematicos de Joze Anastacio da Cunha”, O Investigador Portuguez em Inglaterra. (8:235–249, 442–455, 612–623; reprinted, (Ferraz et al. 1990, 449–476)).
Alfonsi, Liliane. 2011. Étienne Bézout (1730–1783): Mathématicien des Lumières. Paris: L’Harmattan.
Baroni, Rosa Lúcia Sverzut. 2001. Aspects of differential equations in José Anastácio da Cunha’s Mathematical Principles. Revista Brasileira de História da Matemática. 1 (2): 27–36.
Bézout, Étienne. 1767. Cours de Mathématiques á l’usage des gardes du Pavillon et de la Marine, 4th part, Paris: J. B. G. Musier.
Bézout, Étienne .1774. Elementos de Analisi Mathematica, vol. II, Coimbra. (Portuguese translation of (Bézout 1767, 1–226)).
Blanco, Mónica. 2013. The mathematical courses of Pedro Padilla and Étienne Bézout: teaching calculus in Eighteenth-Century Spain and France. Science & Education 22: 769–788. https://doi.org/10.1007/s11191-012-9537-6.
Bos, Henk J. M. 1974. Differentials, higher-order differentials and the derivative in the Leibnizian calculus. Archive for History of Exact Sciences 14: 1–90.
Cousin, Jacques-Antoine-Joseph .1777. Leçons de Calcul Différentiel et de Calcul Intégral, Paris: Jombert.
Cunha, José Anastácio da .1778. “Logarithms and powers”, ms. dated 6th May , (Ralha et al. 2006, II, 58–85).
Cunha, José Anastácio da. 1785. “Cópia de uma carta de José Anastácio da Cunha datada de 3 de Junho de 1785”. (Ferraz et al. 1990, 359-370).
Cunha, José Anastácio da, Principios Mathematicos, Lisbon, 1790; online: https://purl.pt/13843 (accessed 17 October 2021). Translated into French by João Manuel d’Abreu, Principes Mathématiques, Bordeaux: Racle, 1811; online: https://gallica.bnf.fr/ark:/12148/bpt6k96341421 (accessed 22 October 2021). Reissued, Principes de Mathématiques, Paris: Courcier, 1816; online: https://www.digitale-sammlungen.de/en/view/bsb10593778 (Accessed 22 October 2021).
Cunha, José Anastácio da . 1807. Ensayo sobre os Principios de Mechanica, London: J. Bud. 2nd ed. in O Instituto, 4 (1856), 212-214, 222-223, 236-238. 3rd ed. (Ferraz et al. 1990, 339–351).
Cunha, José Anastácio da. 2006a. “Principios de Geometria tirados dos de Euclides; Prologo”. (Ralha et al. II, 2–25).
Cunha, José Anastácio da.2006b. “Principios do Calculo Fluxionario”. (Ralha et al. 2006, II, 44–55).
Cunha, Norberto Ferreira da. 2001. “As ideias filosóficas e religiosas de José Anastácio da Cunha”, Elites e Académicos na Cultura Portuguesa Setecentista, Imprensa Nacional—Casa da Moeda, 191–217.
Domingues, João Caramalho, Maria Elfrida Ralha, José Francisco Rodrigues, Jaime Carvalho e Silva. 2006.“Notas ao manuscrito Principios do Calculo Fluxionario. Março de 1780 de José Anastácio da Cunha”. (Ralha et al. 2006, I, 265–275).
Domingues, João Caramalho. 2004. Variables, limits, and infinitesimals in Portugal in the late 18th century. Historia Mathematica 31: 15–33. https://doi.org/10.1016/S0315-0860(03)00004-1.
Domingues, João Caramalho. 2007.“A recepção dos trabalhos de Euler em Portugal”, Boletim da Sociedade Portuguesa de Matemática, special issue on Euler. 87–111.
Domingues, João Caramalho. 2008. Lacroix and the Calculus. Basel: Birkhäuser. https://doi.org/10.1007/978-3-7643-8638-2.
Domingues, João Caramalho. 2014. The repercussion of José Anastácio da Cunha in Britain and USA in the nineteenth century. BSHM Bulletin 29: 32–50. https://doi.org/10.1080/17498430.2013.802111.
Duarte, António Leal, Jaime Carvalho e Silva. 2006.“Sobre a influência da obra matemática de José Anastácio da Cunha”. (Ferraz et al. 1990, 133–145)
Estrada, Maria Fernanda, Maria Elfrida Ralha, Jaime Carvalho e Silva. 2006.“José Anastácio da Cunha: o militar-‘académico”’. (Ralha et al. 2006, I 297–318).
Euler, Leonhard. 1736.Mechanica sive Motus Scientia Analytice Exposita, 2 vols., St. Petersburg: Academia Imperialis Scientiarum.
Euler, Leonhard. 1748.Introductio in Analysin Infinitorum, vol 2. Marcus-Michael Bousquet, Lausanne.
Euler, Leonhard. 1755. Institutiones Calculi Differentialis. Academia Imperialis Scientiarum, Saint Petersburg.
Euler, Leonhard. 1768–1770. Institutionum Calculi Integralis volumen primum, [...] secundum, [...] tertium. Academia Imperialis Scientiarum, Saint Petersburg.
Euler, Leonhard. 1770. Vollständige Anleitung zur Algebra, 2 vols. Kayserlich Academie der Wissenschaften, Saint Petersburg.
Ferraro, Giovanni. 1999. The first modern definition of the sum of a divergent series: an aspect of the rise of 20th Century Mathematics. Archive for History of Exact Sciences 54: 101–135.
Ferraro, Giovanni. 2001. Analytical symbols and geometrical figures in Eighteenth-Century calculus. Studies in History and Philosophy of Science Part A 32: 535–555. https://doi.org/10.1016/S0039-3681(01)00009-7.
Ferro, João Pedro., ed. 1987. O Processo de José Anastácio da Cunha na Inquisição de Coimbra (1778). Lisbon: Palas Editores.
Ferraz, Maria de Lurdes, José Francisco Rodrigues, Luís Saraiva (eds.) 1990. Anastácio da Cunha 1744/1787, o matemático e o poeta, Imprensa Nacional - Casa da Moeda, (proceedings of a colloquium held in 1987, with several documental appendices).
Fraser, Craig G. 1987. Joseph Louis Lagrange’s algebraic vision of the calculus. Historia Mathematica 14: 38–53.
Fraser, Craig G. 1989. The calculus as algebraic analysis: some observations on mathematical analysis in the 18th century. Archive for History of Exact Sciences 39 (1988–1989): 317–335.
Giusti, Enrico. 2006. “Quelques réflexions sur les “Principios” de da Cunha”, (Ferraz et al. 1990, 33–52).
Grattan-Guinness, Ivor. 2006. “Da Cunha’s calculus in its time”. ( Ferraz et al. 1990, 53–62).
Guicciardini, Niccolò. 1989. The development of Newtonian calculus in Britain, 1700–1800. Cambridge: Cambridge University Press.
Guicciardini, Niccolò. 2003. “Newton’s Method and Leibniz’s Calculus”, in Hans Niels Jahnke (ed.), A History of Analysis, American Mathematical Society / London Mathematical Society. pp 73–103.
Jahnke, Hans Niels. 2003. “Algebraic Analysis in the 18th Century”, in Hans Niels Jahnke (ed.), A History of Analysis, American Mathematical Society / London Mathematical Society. pp 105–136.
Lamandé, Pierre. 1988. Deux manuels mathématiques rivaux : le Bézout et le Lacroix. Ancien contre nouveau régime en calcul infinitésimal. Wissenschaftliche Zeitschrift der Wilhelm-Pieck-Universität Rostock, G-Reihe 37: 16–25.
Mawhin, Jean. 2006. “Le concept de différentielle chez da Cunha et ses successeurs”. (Ferraz et al. 1990, 97–105).
Oliveira, A.J. 1988. Franco de, “Anastácio da Cunha and the concept of convergent series.” Archive for History of Exact Sciences. 39: 1–12.
Petrie, Bruce J. 2012. Leonhard Euler’s use and understanding of mathematical transcendence. Historia Mathematica 39: 280–291. https://doi.org/10.1016/j.hm.2012.06.003.
Popper, Karl. 1944. The poverty of historicism, I. Economica, New Series 11: 86–103.
Queiró, João Filipe. 1988. José Anastácio da Cunha: a forgotten forerunner. The Mathematical Intelligencer 10: 38–43.
Ralha, Maria Elfrida, Maria Fernanda Estrada, Maria do Céu Silva, Abel Rodrigues (eds.), José Anastácio da Cunha: o tempo, as ideias, a obra e... os inéditos, 2 vols., Braga: Arquivo Distrital de Braga / Universidade do Minho, Centro de Matemática da Universidade do Minho, Centro de Matemática da Universidade do Porto, 2006 (vol. I contains studies about Cunha and his time, vol. II contains several works by Cunha discovered in 2005).
Rodrigues, Abel, António Leal Duarte, Maria Elfrida Ralha, and Maria Luísa Malato (eds.) 2013. Anecdotas de J. A. d. C. - Reminiscências de D. José Maria de Sousa, Morgado de Mateus, sobre o Mestre e Amigo José Anastácio da Cunha, V. N. Famalicão: Húmus.
Saladini, Girolamo. 1775. Compendio d’Analisi, 2 vols., Bologna: S. Tommaso d’Aquino.
Saraiva, Luís Manuel. 2015. Étienne Bézout in Portugal: the reform of the Portuguese University and beyond (1772–1838). Historia Mathematica. 42: 14–46. https://doi.org/10.1016/j.hm.2014.05.002.
Sepkoski, David. 2005. Nominalism and constructivism in seventeenth-century mathematical philosophy. Historia Mathematica 32: 33–59. https://doi.org/10.1016/j.hm.2003.09.002.
Teixeira, Francisco Gomes. 1934. História das Matemáticas em Portugal. Lisbon: Academia das Ciências.
Voltaire. 1877–1885. Œuvres Complètes de Voltaire, 52 vols. Garnier, Paris.
Youschkevitch, A.P. 1973. J. A. da Cunha et les fondements de l’analyse infinitésimale. Revue d’histoire des sciences 26: 3–22.
Acknowledgements
The author would like to thank Antoni Malet and an anonymous reviewer for their comments on an earlier version of this paper that helped to clarify several of its passages.
Funding
Open access funding provided by FCT|FCCN (b-on). This research was partially financed by Portuguese Funds through FCT (Fundação para a Ciência e a Tecnologia) within the Projects UIDB/00013/2020 and UIDP/00013/2020.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author has no competing interests to declare that are relevant to the content of this article.
Additional information
Communicated by Craig Fraser.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Domingues, J.C. Geometry and analysis in Anastácio da Cunha’s calculus. Arch. Hist. Exact Sci. 77, 579–600 (2023). https://doi.org/10.1007/s00407-023-00313-1
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00407-023-00313-1


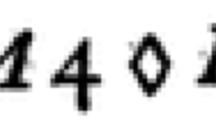


 infinitesimal.”
infinitesimal.” .”
.”
 infinitessimo.” (Cunha
infinitessimo.” (Cunha  .” (Cunha
.” (Cunha