Analysis of the expected density of internal equilibria in random evolutionary multi-player multi-strategy games

Abstract

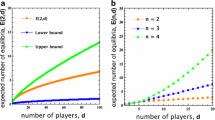
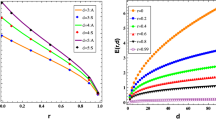
In this paper, we study the distribution and behaviour of internal equilibria in a d-player n-strategy random evolutionary game where the game payoff matrix is generated from normal distributions. The study of this paper reveals and exploits interesting connections between evolutionary game theory and random polynomial theory. The main contributions of the paper are some qualitative and quantitative results on the expected density, $f_{n,d}$, and the expected number, E(n, d), of (stable) internal equilibria. Firstly, we show that in multi-player two-strategy games, they behave asymptotically as $\sqrt{d-1}$ as d is sufficiently large. Secondly, we prove that they are monotone functions of d. We also make a conjecture for games with more than two strategies. Thirdly, we provide numerical simulations for our analytical results and to support the conjecture. As consequences of our analysis, some qualitative and quantitative results on the distribution of zeros of a random Bernstein polynomial are also obtained.

Appendix

Detailed proofs of some lemmas and theorems in the previous sections are presented in this appendix.

1.1 Proof of Lemma 3

This relation has appeared in (Graham et al. 1994, Exercise 101,Chapter 5). For the readers’ convenience, we provide a proof here.

Proof of Lemma 3

Let $x=\frac{1+q}{1-q}$, from (28) we have

$$\begin{aligned} P_d\left( \frac{1+q}{1-q}\right)&=\frac{1}{2^d}\sum _{i=0}^d\begin{pmatrix} d\\ i \end{pmatrix}^2\left( \frac{1+q}{1-q}-1\right) ^{d-i}\left( \frac{1+q}{1-q}+1\right) ^i \\ {}&=\frac{1}{2^d}\sum _{i=0}^d\begin{pmatrix} d\\ i \end{pmatrix}^2\left( \frac{2q}{1-q}\right) ^{d-i}\left( \frac{2}{1-q}\right) ^i \\ {}&=\frac{1}{(1-q)^d}\sum _{i=0}^d\begin{pmatrix} d\\ i \end{pmatrix}^2q^{d-i} \\ {}&=\frac{1}{(1-q)^d}\sum _{i=0}^d\begin{pmatrix} d\\ i \end{pmatrix}^2q^{i}. \end{aligned}$$

Therefore,

$$\begin{aligned} \sum _{i=0}^d\begin{pmatrix} d\\ i \end{pmatrix}^2q^{i}=(1-q)^d P_d\left( \frac{1+q}{1-q}\right) . \end{aligned}$$

By taking $q=t^2$, we obtain (31). $\square$

1.2 Proof of Theorem 3

Proof of Theorem 3

By taking the derivative of both sides in (31), we obtain

$$\begin{aligned} M_{d+1}'(t)&=-2\,t\,d\,(1-t^2)^{d-1}P_d\left( \frac{1+t^2}{1-t^2}\right) +4t(1-t^2)^{d-2}P_d'\left( \frac{1+t^2}{1-t^2}\right) \\&=-2\,t\,d\,\frac{M_{d+1}(t)}{1-t^2}+4t(1-t^2)^{d-2}P_d'\left( \frac{1+t^2}{1-t^2}\right) . \end{aligned}$$

It follows that

$$\begin{aligned} \frac{M_{d+1}'(t)}{M_{d+1}(t)}=\frac{-2\,t\,d}{1-t^2}+\frac{4t}{(1-t^2)^2}\frac{P_d'}{P_d}\left( \frac{1+t^2}{1-t^2}\right) . \end{aligned}$$

Now we compute the expression inside the square-root of the right-hand side of (32). We have

$$\begin{aligned} t\frac{M_{d+1}'(t)}{M_{d+1}(t)}=\frac{-2\,t^2\,d}{1-t^2}+\frac{4t^2}{(1-t^2)^2}\frac{P_d'}{P_d}\left( \frac{1+t^2}{1-t^2}\right) , \end{aligned}$$

and

$$\begin{aligned} \left( t\frac{M_{d+1}'(t)}{M_{d+1}(t)}\right) '= & {} -\frac{4\,t\,d}{(1-t^2)^2}+\frac{8t(1+t^2)}{(1-t^2)^3}\frac{P_d'}{P_d}\left( \frac{1+t^2}{1-t^2}\right) \\&+\frac{16t^3}{(1-t^2)^4}\frac{P_d''\,P_d-(P'_d)^2}{P_d^2}\left( \frac{1+t^2}{1-t^2}\right) . \end{aligned}$$

Substituting this expression into (33), we get

$$\begin{aligned} (2\pi f_{d+1}(t))^2= & {} -\frac{4\,d}{(1-t^2)^2}+\frac{8(1+t^2)}{(1-t^2)^3}\frac{P_d'}{P_d}\left( \frac{1+t^2}{1-t^2}\right) \nonumber \\&+\frac{16t^2}{(1-t^2)^4}\frac{P_d''\,P_d-(P'_d)^2}{P_d^2}\left( \frac{1+t^2}{1-t^2}\right) . \end{aligned}$$

(48)

According to (27), the Legendre polynomial $P_d$ satisfies the following equation for all $x\in \mathbf { R}$

$$\begin{aligned} -2x P_d'(x)+(1-x^2)P''_d(x)=-d(d+1)P_d(x). \end{aligned}$$

As a consequence, we obtain

$$\begin{aligned} \frac{P''_d(x)}{P_d(x)}=\frac{1}{1-x^2}\left( 2x\frac{P_d'(x)}{P_d(x)}-d(d+1)\right) . \end{aligned}$$

Substituting this expression into (48) with $x=\frac{1+t^2}{1-t^2}$, we get

which is the claimed relation (33). $\square$

1.3 Proof of Theorem 4

Proof of Theorem 4

Using the following relation of the Legendre polynomials for all $x\in \mathbf { R}$

$$\begin{aligned} P_d'(x)=\frac{d}{x^2-1}\left( xP_d(x)-P_{d-1}(x)\right) , \end{aligned}$$

we get

$$\begin{aligned} \frac{P_d'(x)}{P_d(x)}=\frac{d}{x^2-1}\left( x-\frac{P_{d-1}(x)}{P_d(x)}\right) . \end{aligned}$$

(49)

In particular, taking $x=\frac{1+t^2}{1-t^2}$, we obtain

$$\begin{aligned} \frac{P'_d}{P_d}\left( \frac{1+t^2}{1-t^2}\right)&=\frac{d}{\left( \frac{1+t^2}{1-t^2}\right) ^2-1}\left[ \frac{1+t^2}{1-t^2}-\frac{P_{d-1}}{P_d}\left( \frac{1+t^2}{1-t^2}\right) \right] \\&=\frac{d(1-t^2)^2}{4t^2}\left[ \frac{1+t^2}{1-t^2}-\frac{P_{d-1}}{P_d}\left( \frac{1+t^2}{1-t^2}\right) \right] . \end{aligned}$$

Substituting this expression into (33), we achieve

$$\begin{aligned} (2\pi f_{d+1}(t))^2=\frac{4d^2}{(1-t^2)^2}-\frac{d^2}{t^2}\left[ \frac{1+t^2}{1-t^2}-\frac{P_{d-1}}{P_d}\left( \frac{1+t^2}{1-t^2}\right) \right] ^2, \end{aligned}$$

which is (35). $\square$

1.4 Proof of Lemma 4

Proof of Lemma 4

This lemma follows directly from Constantinescu 2005 (Theorem 2.1) where the authors proved that

$$\begin{aligned} P_d(x)^2 - P_{d+1}(x)P_{d-1}(x) = \frac{1-x^2}{d (d+1)} \left( \sum _{i=1}^d \frac{1}{i} + \sum _{i=1}^{d-1} \frac{1}{i+1} \sum _{j=1}^i (2j+1) P_j^2(x)\right) , \end{aligned}$$

which is negative for all $|x| \ge 1$. $\square$

1.5 Proof of Proposition 2

Proof of Proposition 2

We will prove that

$$\begin{aligned} f^2_{d+2}(t)-f^2_{d+1}(t)\ge 0 \quad \Longleftrightarrow \quad (38). \end{aligned}$$

(50)

From (35), we have

$$\begin{aligned}&4\pi ^2(f^2_{d+2}(t)-f^2_{d+1}(t))\\&\quad =\frac{4(d+1)^2}{(1-t^2)^2}-\frac{(d+1)^2}{t^2}\left[ \frac{1+t^2}{1-t^2}-\frac{P_{d}}{P_{d+1}}\left( \frac{1+t^2}{1-t^2}\right) \right] ^2\\&\qquad -\frac{4d^2}{(1-t^2)^2}+\frac{d^2}{t^2}\left[ \frac{1+t^2}{1-t^2}-\frac{P_{d-1}}{P_d}\left( \frac{1+t^2}{1-t^2}\right) \right] ^2\\&\quad =\frac{4(2d+1)}{(1-t^2)^2}-\frac{1}{t^2}\left[ \frac{1+t^2}{1-t^2}-\frac{(d+1)P_d^2-dP_{d-1}P_{d+1}}{P_dP_{d+1}}\left( \frac{1+t^2}{1-t^2}\right) \right] \\&\qquad \times \left[ (2d+1)\frac{1+t^2}{1-t^2}-\frac{(d+1)P_d^2+dP_{d-1}P_{d+1}}{P_dP_{d+1}}\left( \frac{1+t^2}{1-t^2}\right) \right] . \end{aligned}$$

Therefore $f_d(t)$ is increasing as a function of d if and only if

$$\begin{aligned}&\left[ \frac{1+t^2}{1-t^2}-\frac{(d+1)P_d^2-dP_{d-1}P_{d+1}}{P_dP_{d+1}}\left( \frac{1+t^2}{1-t^2}\right) \right] \\&\quad \times \left[ (2d+1)\frac{1+t^2}{1-t^2}-\frac{(d+1)P_d^2+dP_{d-1}P_{d+1}}{P_dP_{d+1}}\left( \frac{1+t^2}{1-t^2}\right) \right] \\&\qquad \le \frac{4(2d+1)t^2}{(1-t^2)^2}. \end{aligned}$$

We re-write the expression above using the variable x, using the relation $x^2-1=\frac{4t^2}{(1-t^2)^2}$, as follows

$$\begin{aligned}&\left[ x-\frac{(d+1)P_d^2-dP_{d-1}P_{d+1}}{P_dP_{d+1}}(x)\right] \times \left[ (2d+1)x-\frac{(d+1)P_d^2+dP_{d-1}P_{d+1}}{P_dP_{d+1}}(x)\right] \nonumber \\&\quad \le (2d+1)(x^2-1). \end{aligned}$$

(51)

We now simplify this expression using the recursion relation of the Legendre polynomials, i.e. $dP_{d-1}=(2d+1)xP_d-(d+1)P_{d+1}$. Namely, we have

$$\begin{aligned}&xP_dP_{d+1}-(d+1)P_d^2+dP_{d-1}P_{d+1}=xP_dP_{d+1}-(d+1)P_d^2\\&+[(2d+1)xP_d-(d+1)P_{d+1}]P_{d+1}\\&\quad =(d+1)[-P_d^2-P_{d+1}^2+2xP_dP_{d+1}] \end{aligned}$$

and

$$\begin{aligned}&(2d+1)xP_dP_{d+1}-(d+1)P_d^2-dP_{d-1}P_{d+1}\\&\qquad =(2d+1)xP_dP_{d+1}-(d+1)P_d^2-[(2d+1)xP_d-(d+1)P_{d+1}]P_{d+1}\\&\qquad =(d+1)(P^2_{d+1}-P_d^2). \end{aligned}$$

Substituting these calculations into (51) we obtain (38).

To prove the second assertion of Proposition 2, we proceed as follows. Let

$$\begin{aligned} H_{d+1}&= (d+1)^2\left[ P^2_{d+1}(x)+P^2_{d}(x)-2x P_{d+1}(x)P_d(x)\right] \\&= \left[ (2d+1)x P_{d}(x)- d P_{d-1}(x)\right] ^2 + (d+1)^2 P^2_{d}(x)\\&\qquad -2x (d+1) \left[ (2d+1)x P_{d}(x)- d P_{d-1}(x)\right] P_d(x) \\&=\left[ (2d+1)^2 x^2 + (d+1)^2 - 2(d+1)(2d+1) x^2 \right] P^2_{d}(x)\\&\qquad -\left[ 2d(2d+1)x - 2d(d+1) x \right] P_{d}(x) P_{d-1}(x) + d^2 P^2_{d-1}(x) \\&= \left[ d^2 + (2d+1)(1-x^2) \right] P^2_{d}(x)+d^2 P^2_{d-1}(x)-2x d^2 P_{d}(x)P_{d-1}(x) \\&= d^2 \left[ P^2_{d}(x)+P^2_{d-1}(x)-2x P_{d}(x)P_{d-1}(x)\right] + (2d+1)(1-x^2) P^2_{d}(x) \\&= H_d + (2d+1)(1-x^2) P^2_{d}(x). \end{aligned}$$

Hence, the expression in (38) can be simplified as follows

$$\begin{aligned}&H_{d+1} [P^2_{d+1}(x)-P^2_{d}(x)] +(2d+1)(x^2-1)P^2_d(x)P^2_{d+1}(x) \\&\quad = [H_d + (2d+1)(1-x^2) P^2_{d}(x)][P^2_{d+1}(x)-P^2_{d}(x)] \\&\qquad +(2d+1)(x^2-1)P^2_d(x)P^2_{d+1}(x) \\&\quad = H_d [P^2_{d+1}(x)-P^2_{d}(x)] +(2d+1)(x^2-1)P^4_d(x) \\&\quad = \frac{P^2_{d+1}(x)-P^2_{d}(x)}{P^2_{d}(x)-P^2_{d-1}(x)}\\&\qquad \times \left[ H_d \left( P^2_{d}(x)-P^2_{d-1}(x)\right) +(2d-1)(x^2-1)P^2_d(x)P^2_{d-1}(x) \cdot Q \right] , \end{aligned}$$

where $Q = \frac{(2d+1)P^2_{d}(P^2_{d}-P^2_{d-1})}{(2d-1)P^2_{d-1}(P^2_{d+1}-P^2_{d})}$. Suppose that (39) is true, i.e.,

$$\begin{aligned} (2d+1)P_d^4 \ge P_{d-1}^2 \left[ (2d-1) P_{d+1}^2 + 2 P_d^2 \right] . \end{aligned}$$

This implies that $Q\ge 1$ for all x and d. Then it follows that

$$\begin{aligned}&H_{d+1} [P^2_{d+1}(x)-P^2_{d}(x)] +(2d+1)(x^2-1)P^2_d(x)P^2_{d+1}(x)\nonumber \\&\qquad \ge \frac{P^2_{d+1}(x)-P^2_{d}(x)}{P^2_{d}(x)-P^2_{d-1}(x)}\left[ H_d \left( P^2_{d}(x)-P^2_{d-1}(x)\right) +(2d-1)(x^2-1)P^2_d(x)P^2_{d-1}(x)\right] \nonumber \\&\qquad \ge \frac{P^2_{d+1}(x)-P^2_{d}(x)}{P^2_{d}(x)-P^2_{d-1}(x)}\times \frac{P^2_{d}(x)-P^2_{d-1}(x)}{P^2_{d-1}(x)-P^2_{d-2}(x)}\nonumber \\&\qquad \qquad \times \left[ H_{d-1} \left( P^2_{d-1}(x)-P^2_{d-2}(x)\right) +(2d-3)(x^2-1)P^2_{d-1}(x)P^2_{d-2}(x)\right] \nonumber \\&\qquad \ge \cdots \nonumber \\&\qquad \ge \prod \limits _{i=1}^{d}\frac{P^2_{i+1}(x)-P^2_{i}(x)}{P^2_{i}(x)-P^2_{i-1}(x)}\times \left[ H_1 \left( P^2_{1}(x)-P^2_{0}(x)\right) +(x^2-1)P^2_{1}(x)P^2_{0}(x)\right] . \end{aligned}$$

(52)

By definition of $H_d$, we have

$$\begin{aligned} H_1=P_1^2(x)+P^2_0(x)-2x P_{1}(x)P_0(x)=x^2+1-2x^2=1-x^2. \end{aligned}$$

Substituting this into (52), we obtain

$$\begin{aligned}&H_{d+1} [P^2_{d+1}(x)-P^2_{d}(x)] +(2d+1)(x^2-1)P^2_d(x)P^2_{d+1}(x) \\&\quad \ge (x^2-1)\prod \limits _{i=1}^{d}\frac{P^2_{i+1}(x)-P^2_{i}(x)}{P^2_{i}(x)-P^2_{i-1}(x)} \\&\quad = P^2_{d+1}(x)-P_d^2(x)\ge 0, \end{aligned}$$

i.e., the condition (38) is satisfied. $\square$