Skip to main content
SpringerLink
Log in

The Early Exercise Boundary Under the Jump to Default Extended CEV Model

  • Published:
Applied Mathematics & Optimization Submit manuscript

Abstract

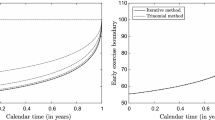
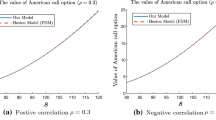
This paper proves the existence, uniqueness, monotonicity and continuity of the early exercise boundary attached to American-style standard options under the jump to default extended constant elasticity of variance model of Carr and Linetsky (Financ Stoch 10(3):303–330, 2006).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Notes

  1. The valuation of American-style contingent claims has a long history and a complete literature review on the topic is outside the scope of the present paper. A general overview of this literature may be found, for example, in the survey papers of Myneni [1], Broadie and Detemple [2] and Barone-Adesi [3], as well as in the monographs of Shreve [4, Chapter 8] and Detemple [5, Chapters 3, 4 and 8].

  2. A comparison of the different methods is available, for instance, in Broadie and Detemple [6], Huang et al. [7], Ju [8], Nunes [9] and Ruas et al. [10].

  3. See, for instance, Cox [16], Emanuel and MacBeth [17], Schroder [18], Davydov and Linetsky [19, 20], Linetsky [21] and Larguinho et al. [22] for background on the CEV process.

  4. See, for example, Borodin and Salminen [33], Göing-Jaeschke and Yor [34], Jeanblanc et al. [35, Chapter 6] and Katori [36] for background on Bessel processes.

  5. For any two real numbers x and y, we denote by \(x\vee y\) and \(x\wedge y\) , respectively, their maximum and minimum.

  6. The default intensity specification as the negative power of the stock price has become also popular for pricing convertible bonds and other hybrid securities. See, for example, Das and Sundaram [55].

  7. Intuitively, at time \(\tilde{\zeta }\), \(\mathcal {D}\) jumps from 0 to 1, \( dS_{t}^{\Delta }=-S_{t^{-}}^{\Delta }\), and the stock price falls to 0 where it remains forever.

  8. See, for instance, Katori [36, p. 28].

  9. A strict inequality is not obtained because it is possible that \(\theta ^{*}=T\wedge \zeta \).

  10. See, for instance, Protter [60, p. 220].

  11. Note that, in both cases, the stock price is initialized at the same level—i.e. \(S_{t}^{\Delta }=x\) and \(S_{t_{0}}^{\Delta }=x\)—and, therefore, the monotonicity of function (5.37) is a sufficient condition to yield the inequality (5.38).

  12. Again, please note that the partial integro-differential inequality (5.49) should be interpreted in a distributional—e.g. Jaillet et al. [66]—or in a viscosity sense—see, for instance, Pham [65].

  13. Left-continuity has only been proved for strictly positive interest rates because Eq. (5.51) would be trivially satisfied if \(r\left( u\right) =q\left( u\right) =0\).

References

  1. Myneni, R.: The pricing of the American option. Ann. Appl. Probab. 2(1), 1–23 (1992)

    MathSciNet  MATH  Google Scholar 

  2. Broadie, M., Detemple, J.: Option pricing: valuation models and applications. Manag. Sci. 50(9), 1145–1177 (2004)

    Google Scholar 

  3. Barone-Adesi, G.: The saga of the American put. J. Bank. Financ. 29(11), 2909–2918 (2005)

    Google Scholar 

  4. Shreve, S.: Stochastic Calculus for Finance II: Continuous-Time Models. Springer, New York (2004)

    MATH  Google Scholar 

  5. Detemple, J.: American-Style Derivatives: Valuation and Computation. Chapman & Hall/CRC, Boca Raton (2006)

    MATH  Google Scholar 

  6. Broadie, M., Detemple, J.: American option valuation: new bounds, approximations, and a comparison of existing methods. Rev. Financ. Stud. 9(4), 1211–1250 (1996)

    Google Scholar 

  7. Huang, J.-Z., Subrahmanyam, M., Yu, G.: Pricing and hedging American options: a recursive integration method. Rev. Financ. Stud. 9(1), 277–300 (1996)

    Google Scholar 

  8. Ju, N.: Pricing an American option by approximating its early exercise boundary as a multipiece exponential function. Rev. Financ. Stud. 11(3), 627–646 (1998)

    Google Scholar 

  9. Nunes, J.: Pricing American options under the constant elasticity of variance model and subject to bankruptcy. J. Financ. Quant. Anal. 44(5), 1231–1263 (2009)

    Google Scholar 

  10. Ruas, J., Dias, J., Nunes, J.: Pricing and static hedging of American options under the jump to default extended CEV model. J. Bank. Financ. 37(11), 4059–4072 (2013)

    Google Scholar 

  11. Merton, R.: Option pricing when underlying stock returns are discontinuous. J. Financ. Econ. 3(1–2), 125–144 (1976)

    MATH  Google Scholar 

  12. Linetsky, V.: Pricing equity derivatives subject to bankruptcy. Math. Financ. 16(2), 255–282 (2006)

    MathSciNet  MATH  Google Scholar 

  13. Black, F., Scholes, M.: The pricing of options and corporate liabilities. J. Polit. Econ. 81(3), 637–654 (1973)

    MathSciNet  MATH  Google Scholar 

  14. Merton, R.: Theory of rational option pricing. Bell J. Econ. Manag. Sci. 4(1), 141–183 (1973)

    MathSciNet  MATH  Google Scholar 

  15. Carr, P., Linetsky, V.: A jump to default extended CEV model: an application of Bessel processes. Financ. Stoch. 10(3), 303–330 (2006)

    MathSciNet  MATH  Google Scholar 

  16. Cox, J.: Notes on option pricing I: constant elasticity of variance diffusions. In: Working Paper, Stanford University. Reprinted in Journal of Portfolio Management, 23 (1996), pp. 15–17 (1975)

  17. Emanuel, D., MacBeth, J.: Further results on the constant elasticity of variance call option pricing model. J. Financ. Quant. Anal. 17(4), 533–554 (1982)

    Google Scholar 

  18. Schroder, M.: Computing the constant elasticity of variance option pricing formula. J. Financ. 44(1), 211–219 (1989)

    Google Scholar 

  19. Davydov, D., Linetsky, V.: Pricing and hedging path-dependent options under the CEV process. Manag. Sci. 47(7), 949–965 (2001)

    MATH  Google Scholar 

  20. Davydov, D., Linetsky, V.: Pricing options on scalar diffusions: an eigenfunction expansion approach. Oper. Res. 51(2), 185–209 (2003)

    MathSciNet  MATH  Google Scholar 

  21. Linetsky, V.: Lookback options and diffusion hitting times: a spectral expansion approach. Financ. Stoch. 8(3), 373–398 (2004)

    MathSciNet  MATH  Google Scholar 

  22. Larguinho, M., Dias, J., Braumann, C.: On the computation of option prices and greeks under the CEV model. Quant. Financ. 13(6), 907–917 (2013)

    MathSciNet  MATH  Google Scholar 

  23. Black, F.: Studies of stock price volatility changes. In: Proceedings of the Meetings of the American Statistical Association, Business and Economics Statistics Division, pp. 177–181 (1976)

  24. Christie, A.: The stochastic behavior of common stock variances: value, leverage and interest rate effects. J. Financ. Econom. 10(4), 407–432 (1982)

    Google Scholar 

  25. Bekaert, G., Wu, G.: Asymmetric volatility and risk in equity markets. Rev. Financ. Stud. 13(1), 1–42 (2000)

    Google Scholar 

  26. Dennis, P., Mayhew, S.: Risk-neutral skewness: evidence from stock options. J. Financ. Quant. Anal. 37(3), 471–493 (2002)

    Google Scholar 

  27. Bakshi, G., Kapadia, N., Madan, D.: Stock return characteristics, skew laws, and the differential pricing of invididual equity options. Rev. Financ. Stud. 16(1), 101–143 (2003)

    Google Scholar 

  28. Campbell, J., Taksler, G.: Equity volatility and corporate bond yields. J. Financ. 58(6), 2321–2349 (2003)

    Google Scholar 

  29. Bakshi, G., Madan, D., Zhang, F.: Investigating the role of systematic and firm-specific factors in default risk: lessons from empirically evaluating credit risk models. J. Bus. 79(4), 1955–1987 (2006)

    Google Scholar 

  30. Cremers, M., Driessen, J., Maenhout, P., Weinbaum, D.: Individual stock-option prices and credit spreads. J. Bank. Financ. 32(12), 2706–2715 (2008)

    Google Scholar 

  31. Zhang, B., Zhou, H., Zhu, H.: Explaining credit default swap spreads with the equity volatility and jump risks of individual firms. Rev. Financ. Stud. 22(12), 5099–5131 (2009)

    Google Scholar 

  32. Carr, P., Wu, L.: Stock options and credit default swaps: a joint framework for valuation and estimation. J. Financ. Econom. 8(4), 409–449 (2010)

    Google Scholar 

  33. Borodin, A .N., Salminen, P.: Handbook of Brownian Motion—Facts and Formulae, 2nd edn. Birkhauser, Basel (2002)

    MATH  Google Scholar 

  34. Göing-Jaeschke, A., Yor, M.: A survey and some generalizations of Bessel processes. Bernoulli 9(2), 313–349 (2003)

    MathSciNet  MATH  Google Scholar 

  35. Jeanblanc, M., Yor, M., Chesney, M.: Mathematical Methods for Financial Markets. Springer, New York (2009)

    MATH  Google Scholar 

  36. Katori, M.: Bessel Processes, Schramm-Loewner Evolution, and the Dyson Model (SpringerBriefs in Mathematical Physics). Springer, Tokyo (2016)

    Google Scholar 

  37. Mendoza-Arriaga, R., Linetsky, V.: Pricing equity default swaps under the jump-to-default extended CEV Model. Financ. Stoch. 15(3), 513–540 (2011)

    MathSciNet  MATH  Google Scholar 

  38. Dias, J., Nunes, J., Ruas, J.: Pricing and static hedging of European-style double barrier options under the jump to default extended CEV model. Quant. Financ. 15(12), 1995–2010 (2015)

    MathSciNet  MATH  Google Scholar 

  39. Nunes, J., Ruas, J., Dias, J.: Pricing and static hedging of American-style knock-in options on defaultable stocks. J. Bank. Financ. 58, 343–360 (2015)

    Google Scholar 

  40. Kolodner, I.: Free boundary problem for the heat equation with applications to problems of change of phase. Commun. Pure Appl. Math. 9(1), 1–31 (1956)

    MathSciNet  MATH  Google Scholar 

  41. Samuelson, P.: Rational theory of warrant pricing. Ind. Manag. Rev. 6(2), 13–32 (1965)

    Google Scholar 

  42. McKean Jr., H.: Appendix: a free boundary problem for the heat equation arising from a problem of mathematical economics. Ind. Manag. Rev. 6(2), 32–39 (1965)

    Google Scholar 

  43. Van Moerbeke, P.: On optimal stopping and free boundary problems. Arch. Ration. Mech. Anal. 60(2), 101–148 (1976)

    MathSciNet  MATH  Google Scholar 

  44. Bensoussan, A.: On the theory of option pricing. Acta Appl. Math. 2(2), 139–158 (1984)

    MathSciNet  MATH  Google Scholar 

  45. Karatzas, I.: On the pricing of American options. Appl. Math. Optim. 17(1), 37–60 (1988)

    MathSciNet  MATH  Google Scholar 

  46. Kim, I.: The analytic valuation of American options. Rev. Financ. Stud. 3(4), 547–572 (1990)

    MathSciNet  Google Scholar 

  47. Jacka, S.: Optimal stopping and the American put. Math. Financ. 1(2), 1–14 (1991)

    MATH  Google Scholar 

  48. Carr, P., Jarrow, R., Myneni, R.: Alternative characterizations of American put options. Math. Financ. 2(2), 87–106 (1992)

    MATH  Google Scholar 

  49. Jamshidian, F.: An analysis of American options. Rev. Futur. Mark. 11(1), 72–80 (1993)

    Google Scholar 

  50. Detemple, J., Tian, W.: The valuation of American options for a class of diffusion processes. Manag. Sci. 48(7), 917–937 (2002)

    MATH  Google Scholar 

  51. Lamberton, D., Mikou, M.: The critical price for the American put in an exponential Lévy model. Financ. Stoch. 12(4), 561–581 (2008)

    MATH  Google Scholar 

  52. Monoyios, M., Ng, A.: Optimal exercise of an executive stock option by an insider. Int. J. Theoret. Appl. Financ. 14(1), 83–106 (2011)

    MathSciNet  MATH  Google Scholar 

  53. Karlin, S., Taylor, H.M.: A Second Course in Stochastic Processes. Academic Press, San Diego (1981)

    MATH  Google Scholar 

  54. Linetsky, V., Mendoza-Arriaga, R.: Unified credit-equity modeling. In: Bielecki, T.R., Brigo, D., Patras, F. (eds.) Credit Risk Frontiers: Subprime Crises, Pricing and Hedging, CVA, MBS, Ratings, and Liquidity, chap. 18, pp. 553–583. Bloomberg Press, New Jersey (2011)

  55. Das, S., Sundaram, R.: An integrated model for hybrid securities. Manag. Sci. 53(9), 1439–1451 (2007)

    MATH  Google Scholar 

  56. Andersen, L., Buffum, D.: Calibration and implementation of convertible bond models. J. Comput. Financ. 7(2), 1–34 (2003)

    Google Scholar 

  57. Zhang, X.: Analyse Numérique des Options Américaines dans un Modèle de Diffusion avec Sauts, Ph.D. thesis, Ecole des Ponts ParisTech (1994)

  58. Pham, H.: Optimal stopping, free boundary, and American option in a jump-diffusion model. Appl. Math. Optim. 35(2), 145–164 (1997)

    MathSciNet  MATH  Google Scholar 

  59. Detemple, J., Kitapbayev, Y.: On American VIX options under the generalized 3/2 and 1/2 Models. Math. Financ. 28(2), 550–581 (2018)

    MathSciNet  MATH  Google Scholar 

  60. Protter, P.: Stochastic Integration and Differential Equations, 2nd edn. Springer, New York (2005)

    Google Scholar 

  61. Peskir, G.: A change-of-variable formula with local time on curves. J. Theor. Probab. 18(3), 499–535 (2005)

    MathSciNet  MATH  Google Scholar 

  62. Øksendal, B.: Stochastic Differential Equations: An Introduction with Applications, 4th edn. Springer, Berlin (1995)

    MATH  Google Scholar 

  63. Karatzas, I., Shreve, S.: Methods of Mathematical Finance. Springer, New York (1998)

    MATH  Google Scholar 

  64. Bielecki, T.R., Rutkowski, M.: Credit Risk: Modeling Valuation and Hedging. Springer, Berlin (2002)

    MATH  Google Scholar 

  65. Pham, H.: Optimal stopping of controlled jump diffusion processes: a viscosity solution approach. J. Math. Syst. Estim. Control 8(1), 1–27 (1998)

    MathSciNet  Google Scholar 

  66. Jaillet, P., Lamberton, D., Lapeyre, B.: Variational inequalities and the pricing of American options. Acta Appl. Math. 21(3), 263–289 (1990)

    MathSciNet  MATH  Google Scholar 

  67. Chung, S.-L., Shih, P.-T.: Static hedging and pricing American options. J. Bank. Financ. 33(11), 2140–2149 (2009)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Business Research Unit (BRU-IUL), Instituto Universitário de Lisboa (ISCTE-IUL), Lisbon, Portugal

    João Pedro Vidal Nunes, José Carlos Dias & João Pedro Ruas

  2. Sociedade Gestora dos Fundos de Pensões do Banco de Portugal, Lisbon, Portugal

    João Pedro Ruas

Authors
  1. João Pedro Vidal Nunes
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. José Carlos Dias
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. João Pedro Ruas
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to João Pedro Vidal Nunes.

Additional information

The authors thank the editor (Professor Huyên Pham) and an anonymous referee, whose suggestions and corrections have significantly improved this article. We also thank the participants in the 9th World Congress of the Bachelier Finance Society (New York) and in the Nova SBE 16/17 Economics Seminars (Lisbon) for useful comments on an earlier draft of this paper as well as Yerkin Kitapbayev for very helpful discussions. Financial support from Fundação para a Ciência e Tecnologia (FCT), grant number UID/GES/00315/2013, is also gratefully acknowledged. Of course, all the remaining errors are the exclusive responsibility of the authors. João Pedro Ruas: The analysis, opinions, and findings of this paper represent the views of the authors, and they are not necessarily those of the Sociedade Gestora dos Fundos de Pensões do Banco de Portugal, the Banco de Portugal, or the Eurosystem.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nunes, J.P.V., Dias, J.C. & Ruas, J.P. The Early Exercise Boundary Under the Jump to Default Extended CEV Model. Appl Math Optim 82, 151–181 (2020). https://doi.org/10.1007/s00245-018-9496-7

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00245-018-9496-7

Keywords

Mathematics Subject Classification

Search

Navigation