Computational optimization of gas compressor stations: MINLP models versus continuous reformulations

Abstract

When considering cost-optimal operation of gas transport networks, compressor stations play the most important role. Proper modeling of these stations leads to nonconvex mixed-integer nonlinear optimization problems. In this article, we give an isothermal and stationary description of compressor stations, state MINLP and GDP models for operating a single station, and discuss several continuous reformulations of the problem. The applicability and relevance of different model formulations, especially of those without discrete variables, is demonstrated by a computational study on both academic examples and real-world instances. In addition, we provide preliminary computational results for an entire network.

1 Introduction

Natural gas is one of the most important energy sources. In 2013, it accounted for 25 % of the fossil energy used in Europe (Eurostat 2013). It is used in industrial processes, for heating, and, more recently, for natural gas vehicles. Especially in Germany, its low price leads to its role as a “bridging energy” during the transition to a future energy mix based primarily on regenerative energy. In Europe, natural gas is transported through pipeline networks with a total length of 100,000 km. Gas transport in pipeline networks is pressure-driven, i.e., the gas flows from higher to lower pressure. Thus, pipeline-based gas transport requires compressor stations. The power required to compress the gas is delivered by drives that use either electrical power or gas from the network itself. The energy consumption of compressors is responsible for a large fraction of the variable operating costs of a gas network.

In this article we focus on the stationary optimization of a single compressor station. More specifically, we consider fixed boundary conditions, i.e., fixed inflow and outflow pressures together with a fixed throughput, and ask the following questions:

• Can the station be operated in a way that satisfies the given boundary conditions? In other words: are those boundary conditions feasible?

• If the boundary conditions are feasible: What is a minimum cost operation that satisfies the boundary condition?

Transport of natural gas has been a rich source of mathematical optimization problems for roughly half a century. The first publications on optimization in gas networks address tree-like or gun-barrel topologies with dynamic programming as a solution technique (Wong and Larson 1968a, b); see Carter (1998) for a later survey. In the following, we give a brief overview on mathematical optimization in this field. More extensive reviews can be found in Koch et al. (2015).

One main branch of research investigates the problems of minimum cost operation and feasibility testing for the stationary as well as the transient case. These problems require models of complete gas networks comprising various types of elements like pipes, compressors, (control) valves, etc. The combination of nonlinear gas physics with the switching of controllable network elements typically leads to mixed-integer nonlinear optimization models (MINLPs); see, e.g., Cobos-Zaleta et al. (2002) and Domschke et al. (2011). One standard approach for tackling these MINLPs is the application of (piecewise) linearizations of the nonlinearities in order to reduce the problems to mixed-integer linear models (MILPs) (Geißler 2011; Geißler et al. 2013; Martin et al. 2006, 2007; Martin and Möller 2005). Other investigations focus on the nonlinear aspects under fixed discrete controls (Ehrhardt and Steinbach 2004, 2005; Schmidt et al. 2015a, c; Steinbach 2007), or attempt to approximate discrete aspects by continuous reformulations (Schmidt 2013; Schmidt et al. 2013, 2015b). For more references and reviews in the areas of cost minimization and feasibility testing we refer to Koch et al. (2015) and, especially, the chapter Schewe et al. (2015) therein.

The second major research branch that we want to highlight considers selected types of network elements and studies them in more detail. For pipes, theoretical studies include the controllability and stabilization of the governing system of partial differential equations, the Euler equations (cf. Banda and Herty 2008; Banda et al. 2006; Brouwer et al. 2011; Gugat et al. 2015). The best-investigated problem for compressor stations is the one considered in this paper, which is of nonconvex MINLP type: minimum cost operation under given boundary conditions (Carter 1996; Carter et al. 1994; Jeníček and Králik 1993; Osiadacz 1980; Wright et al. 1998). See also Králik (1993) for a simulation based model of compressor stations and Odom and Muster (2009) for a recent survey on modeling centrifugal gas compressors. As already mentioned, the compressor stations are the dominant variable cost factor in gas network operation.

In this article we study discrete-continuous models for the problem of minimum cost compressor station operation. We give an almost complete isothermal description of all relevant devices and their interplay. This description is comparable in accuracy with isothermal simulation models. However, we neglect some minor model aspects that would only complicate the presentation without influencing the solutions significantly. We explicitly mention these simplifications later in the description of the considered problem. The specific structure of the resulting MINLP allows for a large variety of continuous reformulations that will be discussed in detail and that are applied to the problem under consideration. The approach of continuous reformulation is in line with recent publications that develop techniques based on mathematical programs with equilibrium constraints (MPECs) for reformulating other discrete aspects of network optimization models (Pfetsch et al. 2015; Schmidt 2013; Schmidt et al. 2013, 2015b). Thus, by combining the MPEC techniques from the cited publications with the reformulation schemes discussed in this paper, it is possible to state purely continuous NLP type models of the genuinely discrete-continuous problems of minimum cost operation or feasibility testing. The outcome of this achievement is twofold. First, it allows us to state highly detailed models of gas networks. This in particular is not viable with approaches based on linearizations since the resulting MILP models tend to be very hard for state-of-the-art MILP solvers. Second, it allows us to solve the resulting models with local NLP solvers, which are typically faster than global MI(N)LP solvers. Obviously, this comes at the price of finding only locally optimal solutions. For further applications of continuous reformulations of discrete-continuous optimization problems, especially in the field of process engineering, see Baumrucker et al. (2008), Kraemer et al. (2007), Kraemer and Marquardt (2010), and Stein et al. (2004). We remark that, despite the fact that continuous reformulations are being used in practice, an extensive numerical study like ours is yet missing in the literature.

The paper is organized as follows. The problem of optimizing a gas compressor station under steady-state boundary conditions is presented in Sect. 2. Afterwards, Sect. 3 introduces a mixed-integer nonlinear formulation of the problem and briefly discusses an equivalent general disjunctive programming formulation. Then, in Sect. 4, the concept of pseudo NCP (nonlinear complementarity problem) functions is introduced and a collection of continuous reformulation techniques is discussed that can be applied to the MINLP model of Sect. 3. These reformulations are applied to artificial and real-world compressor stations in Sect. 5 and the solutions are compared. In addition, this section also provides preliminary results for an entire large-scale network that is fully reformulated using continuous variables and smooth constraints. Finally, Sect. 6 gives some remarks on further work and open questions.

2 Problem description

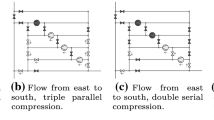
A compressor station hosts a fixed number of compressor machines called units. It can operate in finitely many discrete states that arise from the three operation modes (closed, bypass mode, and active) and a certain number of configurations in the active mode. Every configuration consists of a serial combination of parallel arrangements of compressor units, see Fig. 2. Every compressor unit has an associated drive that provides the power for compressing the gas. For ease of exposition we assume that every drive powers just a single compressor unit. We also neglect the frictional pressure loss caused by station piping, measurement devices, etc., which is usually modeled by fictitious elements called resistors.

In this section we present the required models of all types of compressor machines and drives and then describe their interplay. Full details can be found in Schmidt et al. (2015c) where models of all network elements have been developed. For later reference, the models are presented in constraint form, with constraint functions being denoted by $c$ and super-indexed with an abbreviated name indicating the semantics of the constraint.

2.1 Physical quantities

The dynamics of natural gas is modeled in terms of the mass flow $q$, pressure $p$, temperature $T$, and density $\rho$, where $p, T, \rho$ are coupled by an equation of state. In specific, we use the thermodynamical standard equation,

$$\begin{aligned} \rho (p, T, z) = \frac{p}{R_{\text {s}}zT}. \end{aligned}$$

Here the compressibility factor $z$ models the deviation between real and ideal gas, for which we use an empirical formula of the American Gas Association (AGA),

$$\begin{aligned} z(p, T) = 1 + 0.257 p/ p_{\text {c}} - 0.533\frac{p/ p_{\text {c}}}{T/ T_{\text {c}}} . \end{aligned}$$

We will later formulate certain constraints using $\rho (p, T, z)$ and $z(p, T)$ with fixed $T$.

Table 1 Principal physical quantities and constants

Finally we need the volumetric flow $Q$, given by the constraint

$$\begin{aligned} 0 = c_{}^{\text {flow-conv}}(q, \rho , Q) = q- \rho Q. \end{aligned}$$

See Table 1 (or Schmidt et al. 2015c) for explanations of the physical quantities and constants.

2.2 Boundary conditions

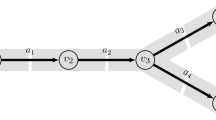
We are interested in feasibility testing and in computing cost optimal controls of a compressor station for given boundary values. In accordance with our general network models (Schmidt et al. 2015c), a compressor station is seen as an arc $a= (u, v)$ of a directed network graph $G =(\mathbb {V}, \mathbb {A})$. The boundary conditions at which the compressor station $a$ has to operate consist of a mass flow range,

$$\begin{aligned} q_a\in [q_a^{-},q_a^{+}], \end{aligned}$$

and of inlet and outlet pressure ranges,

$$\begin{aligned} p_u\in [p_u^{-},p_u^{+}], \quad p_v\in [p_v^{-},p_v^{+}]. \end{aligned}$$

Each of the values $q_a, p_u, p_v$ can be fixed by setting its bounds to identical values.

Table 2 Compressor quantities

2.3 Compressor machines

We distinguish turbo compressors and piston compressors and start with the common parts of their models. For an overview of relevant compressor quantities see Table 2.

The compression of a gas stream from $p_\text {in}$ to $p_\text {out}$ results in a specific change in adiabatic enthalpy, $H_{\text {ad}}$:

$$\begin{aligned} 0 = c_{}^{\text {ad-head}}(H_{\text {ad}}, p_\text {in}, p_\text {out}, z_\text {in}) = H_{\text {ad}}- z_\text {in}T_\text {in}R_{\text {s}}\frac{\kappa }{\kappa - 1} \left( \left( \frac{p_\text {out}}{p_\text {in}} \right) ^{\frac{\kappa - 1}{\kappa }} - 1 \right) . \end{aligned}$$

Here $z_\text {in}= z(p_\text {in}, T_\text {in})$, and we assume that the isentropic exponent $\kappa$ is constant. The power $P$ required for compressing the mass flow $q$ is given by

$$\begin{aligned} 0 = c_{}^{\text {power}}(P, q, H_{\text {ad}}, \eta _{\text {ad}}) = P- \frac{qH_{\text {ad}}}{\eta _{\text {ad}}}. \end{aligned}$$

Its upper limit is the maximal power $P^{+}$ that the associated drive can deliver:

$$\begin{aligned} 0 \le c_{}^{\text {power-limit}}(P, P^{+}) = P^{+}- P. \end{aligned}$$

(1)

Fig. 1

Characteristic diagrams of a turbo compressor (left) and a piston compressor (right)

2.4 Turbo compressors

Turbo compressors are modeled by characteristic diagrams in $(Q, H_{\text {ad}})$-space, see Fig. 1 (left). The curves are defined using biquadratic and quadratic polynomials $F_2(x, y; A)$ and $F_1(z; b)$ whose coefficients A and b are obtained from least-squares fits for given measurements of the compressor:

and

The isolines of speed $n$ (solid) and adiabatic efficiency $\eta _{\text {ad}}$ (dashed) are given by

The compressor’s operating range (gray area) is bounded by the isolines of minimal and maximal speeds $n^\pm$, by the surgeline (left), and by the chokeline (right),

2.5 Piston compressors

Piston compressors are modeled by characteristic diagrams in $(Q, M)$-space, see Fig. 1 (right). The volumetric flow $Q$ satisfies

and the shaft torque $M$ (with constant efficiency $\eta _{\text {ad}}$) is given by

The speed bounds $n\in [n^{-},n^{+}]$ induce left and right bounds of the operating range, $Q\in [V_{\text{ op }}n^{-}, V_{\text{ op }}n^{+}]$. The upper limit can be given in one of three forms depending on the specific compressor: either by a maximum compression ratio $\varepsilon ^{+}$,

by a maximum pressure increase $\varDelta p^{+}$,

or by a maximum shaft torque $M^{+}$,

2.6 Drives

The four most frequently used drive types are gas turbines, gas driven motors, electric motors, and steam turbines. Here we focus on the common model aspects and consider a generic “catchall” drive model that incorporates the two main aspects: the maximal power $P^{+}$ that the drive can deliver (cf. (1)),

$$\begin{aligned} 0 = c_{}^{\text {max-power}}(P^{+}, n) = P^{+}- F_2(n, T_{\text {amb}}; A_{P^{+}}) , \end{aligned}$$

(2)

and its specific energy consumption $b$,

$$\begin{aligned} 0 = c_{}^{\text {spec-ener-cons}}(b, P) = b- F_1(P; a_{b}) . \end{aligned}$$

(3)

Here, $T_{\text {amb}}$ denotes the ambient temperature at the compressor station and $A_{P^{+}}$ as well as $a_{b}$ are the coefficients of the fitted (bi)quadratic polynomials. For specific drive types, (2) or (3) may simplify or vanish completely. The fuel consumption of a gas-powered drive is the mass flow $q^{\text{ fc }}$,

$$\begin{aligned} 0 = c_{}^{\text {fuel-cons}}(q^{\text{ fc }}, b) = q^{\text{ fc }}- \frac{bm}{H_{\text {u}}}. \end{aligned}$$

The fuel consumption of an electric drive is zero, $0 = c_{}^{\text {fuel-cons}}(q^{\text{ fc }}, b) = q^{\text{ fc }}$.

Fig. 2

Complete set of possible configurations of a compressor station with two machines (a real station may offer only a subset)

2.7 Configurations

Recall that a compressor station can be closed, in bypass mode, or active. We denote the set of configurations of an active compressor station by $\mathscr {C}= \{1, \dots , n_\mathscr {C}\}$, the set of serial stages of configuration $i\in \mathscr {C}$ by $\mathscr {S}_i= \{1, \dots , n_{\mathscr {S}_i}\}$, and the set of parallel units of stage $j\in \mathscr {S}_i$ by $\mathscr {P}_{ij} = \{1, \dots , n_{\mathscr {P}_{ij}}\}$. For instance, in Fig. 2 we have $\mathscr {C}= \{1, \dots , 4\}$ and

$$\begin{aligned}&n_{\mathscr {S}_1} = n_{\mathscr {S}_3} = n_{\mathscr {S}_4} = 1, \quad n_{\mathscr {S}_2} = 2, \\&n_{\mathscr {P}_{11}} = 2, \quad n_{\mathscr {P}_{21}} = n_{\mathscr {P}_{22}} = n_{\mathscr {P}_{31}} = n_{\mathscr {P}_{41}} = 1. \end{aligned}$$

In what follows, we refer to individual compressor units by the index triple $ijk$.

Given a triple $(q_a, p_u, p_v)$ of boundary values, the selected configuration $i$ must satisfy the following: the flow $q_j$ of every serial stage $j\in \mathscr {S}_i$ equals $q_a$ and is distributed over the $n_{\mathscr {P}_{ij}}$ parallel units:

$$\begin{aligned} q_a= q_j= \sum _{k\in \mathscr {P}_{ij}} q_{ijk} \quad \text {for all}\quad j\in \mathscr {S}_i. \end{aligned}$$

Moreover, all parallel units in stage $j\in \mathscr {S}_i$ have to increase the gas pressure to a common outflow value $p_{i, j+1}$, which becomes the inflow pressure of stage $j+1$. The first and last stages must satisfy $p_{i1} = p_u$ and $p_{i, n_{\mathscr {S}_i} + 1} = p_v$, respectively.

2.8 Objective function

There are various reasonable objective functions in our context, which can mainly be categorized as feasibility or optimization goals. If one merely wishes to know whether given boundary conditions are feasible, it suffices to use a zero objective, $f\equiv 0$. If the boundary conditions are infeasible, it may be useful to add slack variables to a certain set of constraints and minimize the total infeasibility, measured by a suitable norm of the vector of slack variables. The reader interested in problem-specific slack variable formulations for gas network planning is referred to Schmidt et al. (2015a).

If one is convinced of having feasible boundary conditions, it is straightforward to minimize operating costs, power, or fuel consumption. Specific objective functions will be formulated after stating the optimization models in the following section.

3 Mixed-integer and general disjunctive programming models

One generic way to model the problem described in the previous section is presented in Sect. 3.1: a mixed-integer nonlinear program (MINLP) that incorporates binary variables for the discrete states of the compressor station. An equivalent general disjunctive programming (GDP) formulation of the problem is given in Sect. 3.2. Continuous reformulations of the MINLP and GDP models are discussed later in Sect. 4.

One further possibility of tackling the problem is to enumerate all states of the compressor station and solve all the resulting (continuous) problems by a local or global method. However, this is only suitable when single compressor stations are considered, whereas continuous reformulations can also be used for models of the entire transport network; cf. Sect. 5.5. Another way is to apply suitable heuristics, see, e.g., Schmidt et al. (2015b).

We denote individual continuous variables by $x$ and discrete ones by $s$. Variable vectors are written with bold letters, like $\mathbf {x}$ or $\mathbf {s}$. Sub-indices refer to corresponding elements of the compressor station or to sets of elements. In the constraint notation of Sect. 2, we now also use sub-indices with the same meaning as for variables. Additional sub-indices $\mathscr {E}$ or $\mathscr {I}$ distinguish equality and inequality constraints.

3.1 MINLP formulation

With $\mathbf {x}\in \mathbb {R}^n$ and $\mathbf {s}\in \{0,1\}^m$, the optimization problem under consideration takes the general MINLP form

The boundary conditions correspond to the variable sub-vector $\mathbf {x}_\mathscr {B}= (q_a, p_u, p_v)$.

For a suitable formulation of the discrete decisions and their implications on other parts of the model, we review the concept of indicator constraints.

3.1.1 Indicator constraints

Indicator constraints use a binary indicator variable to control whether a certain constraint is enabled or disabled. If $c(\mathbf {x})$ is any equality or inequality constraint with indicator variable $s$, we denote the associated indicator constraints generically by

$$\begin{aligned} c_{\mathscr {E}}^{\text {ind}}(c(\mathbf {x}), s) = 0, \quad c_{\mathscr {I}}^{\text {ind}}(c(\mathbf {x}), s) \ge 0. \end{aligned}$$

(4)

The formulation (4) is chosen in such a way that the original constraint $c(\mathbf {x}) = 0$ or $c(\mathbf {x}) \ge 0$ must hold if $s= 1$ whereas it becomes irrelevant if $s= 0$. In this article we use two specific types: big-M and bilinear indicator constraints. The big-M indicator constraints of the equality constraint $c(\mathbf {x}) = 0$ take the form

$$\begin{aligned} {-}M_c^- (1-s) \le c(\mathbf {x}) \le M_c^+ (1-s) . \end{aligned}$$

(5)

For the inequality constraint $c(\mathbf {x}) \ge 0$ we obtain the single inequality

$$\begin{aligned} {-}M_c^- (1-s) \le c(\mathbf {x}). \end{aligned}$$

(6)

Bilinear indicator constraints for equality and inequality constraints, respectively, are given by

$$\begin{aligned} 0 = sc(\mathbf {x}) \quad \text {and}\quad 0 \le sc(\mathbf {x}) . \end{aligned}$$

(7)

The big-$M$ formulation offers the advantage that convex constraints yield convex indicator constraints. However, the big-M constants must be chosen sufficiently large to ensure that the constraint is properly enabled or disabled: $M_c^- \ge |\min _\mathbf {x}c(\mathbf {x})|$ and $M_c^+ \ge |\max _\mathbf {x}c(\mathbf {x})|$ in (5), and $M_c^- \ge |\min _\mathbf {x}c(\mathbf {x})|$ in (6). Numerical difficulties are to be expected if $M_c^\pm$ are very large. The bilinear formulation avoids this but has the disadvantage that even convex constraints yield nonconvex indicator constraints. We later review these issues when discussing the numerical results of different problem formulations in Sect. 5.

Finally we need two more notions: an indicator expression y is a term whose value is $y \ge 1$ if the associated state is enabled and zero otherwise, like $s$ in (7). Conversely, a negation expression is a term whose value is $y \ge 1$ if the associated state is disabled and zero otherwise, like $1 - s$ in (5), (6).

3.1.2 Discrete states

To represent the set of states of a compressor station, we introduce the binary variable vector

$$\begin{aligned} \mathbf {s}= ( (s_i)_{i\in \mathscr {C}}, s_\text {bp}, s_\text {cl}) \in \{0,1\}^m, \quad m = {|\mathscr {C}| + 2}, \end{aligned}$$

with the following interpretation:

• the station is active in configuration $i\in \mathscr {C}$ if and only if $s_i= 1$;

• the station is in bypass mode if and only if $s_\text {bp}= 1$;

• the station is closed if and only if $s_\text {cl}= 1$.

Since precisely one state must be selected, we add the special-ordered-set-1 (SOS-1) constraint

In bypass mode, the inflow and outflow pressures have to be identical,

yielding indicator constraints

Note that only equality constraints are required if bilinear indicator constraints (7) are used, whereas only inequality constraints are needed in the case of big-$M$ constraints; cf. (5). That is, in the former case the vector $c_{\mathscr {I}}^{\text {bypass-ind}}$ is empty and in the latter case the vector $c_{\mathscr {E}}^{\text {bypass-ind}}$ is empty. Likewise, if the compressor station is closed, we have

$$\begin{aligned} 0 = c_{}^{\text {closed}}(q_a) = q_a, \end{aligned}$$

yielding

$$\begin{aligned} 0 = c_{\mathscr {E}}^{\text {closed-ind}} (c_{}^{\text {closed}}(q_a),s_\text {cl}), \quad 0 \le c_{\mathscr {I}}^{\text {closed-ind}} (c_{}^{\text {closed}}(q_a),s_\text {cl}). \end{aligned}$$

3.1.3 Configurations

Now we turn to the details of individual configurations. The continuous variable vector of configuration $i\in \mathscr {C}$ reads

Here $q^{\text{ fc }}_{i}$ is the total fuel consumption, $p_{ij}$ and $p_{i,n_{\mathscr {S}_i}+1}$ denote the inflow pressure of stage $j$ and the outflow pressure of the last stage, respectively, and $z_{ij}$, $\rho _{ij}$ represent the inflow compressibility factor and inflow gas density of stage $j$. Finally, $\mathbf {x}_{ijk}$ is the variable vector of compressor unit $ijk$ and its associated drive, see Sect. 3.1.4.

The inflow quantities $z_{ij}$ and $\rho _{ij}$ are coupled to the physical inflow conditions by the constraints

The total fuel consumption $q^{\text{ fc }}_{i}$ is the sum over all compressor units:

$$\begin{aligned} 0 = c_{i}^{\text {fuel-1}} (q^{\text{ fc }}_{i}, (q^{\text{ fc }}_{ijk})_ {j\in \mathscr {S}_i, k\in \mathscr {P}_{ij}}) = q^{\text{ fc }}_{i} - \sum _{j\in \mathscr {S}_i} \sum _{k\in \mathscr {P}_{ij}} q^{\text{ fc }}_{ijk} . \end{aligned}$$

This constraint must be enabled if and only if configuration $i$ is active:

$$\begin{aligned} 0&= c_{\mathscr {E},i}^{\text {ind-fuel-1}} (c_{i}^{\text {fuel-1}}(q^{\text{ fc }}_{i}, (q^{\text{ fc }}_{ijk})_ {j\in \mathscr {S}_i, k\in \mathscr {P}_{ij}}), s_i) , \\ 0&\le c_{\mathscr {I},i}^{\text {ind-fuel-1}} (c_{i}^{\text {fuel-1}}(q^{\text{ fc }}_{i}, (q^{\text{ fc }}_{ijk})_ {j\in \mathscr {S}_i, k\in \mathscr {P}_{ij}}), s_i) . \end{aligned}$$

Otherwise configuration $i$ is inactive,

$$\begin{aligned} 0 \le c_{i}^{\text {fuel-0}}(q^{\text{ fc }}_{i}, s_i) = s_i (q^{\text{ fc }}_{i})^+ - q^{\text{ fc }}_{i}, \end{aligned}$$

where $(q^{\text{ fc }}_{i})^+$ is a suitable upper bound of $q^{\text{ fc }}_{i}$. Next, the inflow and outflow pressures of the active configuration must equal the inflow and outflow pressures of the station:

$$\begin{aligned} 0&= c_{\mathscr {E}, i}^{\text {ind-p-in}} (c_{i}^{\text {p-in}}(p_{i1}, p_u), s_i), \\ 0&\le c_{\mathscr {I}, i}^{\text {ind-p-in}} (c_{i}^{\text {p-in}}(p_{i1}, p_u), s_i),\\ 0&= c_{\mathscr {E}, i}^{\text {ind-p-out}} (c_{i}^{\text {p-out}} (p_{i, n_{\mathscr {S}_i}+1}, p_v), s_i), \\ 0&\le c_{\mathscr {I}, i}^{\text {ind-p-out}} (c_{i}^{\text {p-out}} (p_{i, n_{\mathscr {S}_i}+1}, p_v), s_i), \end{aligned}$$

where

$$\begin{aligned} 0&= c_{i}^{\text {p-in}}(p_{i1}, p_u) = p_{i1} - p_u, \\ 0&= c_{i}^{\text {p-out}} (p_{i, n_{\mathscr {S}_i}+1}, p_v) = p_{i, n_{\mathscr {S}_i}+1} - p_v. \end{aligned}$$

The flow distribution over the parallel units of every stage $j$ finally completes the configuration model:

In summary, the equality constraints of configuration $i$ read

and the inequality constraints are given by

3.1.4 Compressor units and drives

Lastly, we formulate MINLP models of turbo and piston compressors within a configuration. The continuous variable vector of a turbo compressor $\nu = ijk$ with its associated drive reads

and for a piston compressor $\nu$ with associated drive it reads

The equality constraints of a turbo compressor are then given by

and its inequality constraints read

Here we introduce indicator constraints to disable the associated limits of physical and technical quantities of inactive configurations: otherwise irrelevant infeasible values of those inactive configurations would render the entire compressor model infeasible.

The equality constraints of a piston compressor are given by

and the inequality constraints read

Here the indicator constraints are introduced for the same reason as for turbo compressors.

3.1.5 Model summary

As already mentioned, we may choose the objective $f\equiv 0$ if we are only interested in feasibility testing. If we aim at minimum cost operation, a suitable objective is

$$\begin{aligned} f(\mathbf{x,s}) = \sum _{i\in \mathscr {C}}s_i\sum _{j\in \mathscr {S}_i} \sum _{k\in \mathscr {P}_{ij} \cap \mathscr {U}^\text {fuel}} \omega ^\text {fuel} q^{\text{ fc }}_{ijk} + \sum _{i\in \mathscr {C}} s_i\sum _{j\in \mathscr {S}_i} \sum _{k\in \mathscr {P}_{ij} \cap \mathscr {U}^\text {el}} \omega ^\text {el} P_{ijk} , \end{aligned}$$

(8)

where $\mathscr {U}^\text {fuel}$ and $\mathscr {U}^\text {el}$ are the sets of fuel gas and electricity driven compressor units, respectively, and $\omega ^\text {fuel}$ and $\omega ^\text {el}$ represent fuel gas and electricity costs. The complete MINLP model is then obtained with the variable vector

$$\begin{aligned} \mathbf {x}= (\mathbf {x}_\mathscr {B}, (\mathbf {x}_i)_{i\in \mathscr {C}}) \end{aligned}$$

and the constraints

3.2 General disjunctive programming formulation

The shortest and possibly most natural way to model the cost minimization problem presented in Sect. 2 is a general disjunctive programming (GDP) formulation (Grossmann 2002; Raman and Grossmann 1994). Since it is a convenient form that is often used in engineering, we also state this model here for completeness. Using the notation from the preceding section, the GDP model reads

(9a)

(9b)

(9c)

(9d)

GDP models like this are generally built from separate sets of “local” constraints and objective terms that are combined in a logical disjunction. Every part of the disjunction is controlled by a decision variable (here $s_\text {bp}$, $s_\text {cl}$, or $s_i$, $i\in \mathscr {C}$): the local constraints are enabled if and only if the associated decision variable is true ($s_i= 1$), and the local objective terms $\gamma _i$ are set to zero otherwise. The SOS-1 constraint (9d) ensures that precisely one decision variable is true. In a general GDP, any set of feasible combinations of decision variables could be defined by a suitable logical expression. Moreover, “global” constraints and objective terms might be added.

4 Continuous reformulations

As discussed in Sect. 1, it is reasonable to study continuous reformulations of the MINLP and GDP models of Sects. 3.1 and 3.2 in order to tackle optimization problems for compressor stations or entire gas networks with continuous (local) optimization methods, which tend to be faster than global methods for mixed-integer nonlinear and nonconvex problems.

This section discusses five model reformulation schemes from the literature that can be applied to any model with binary variables that exhibit the structure of a logical disjunction, such as the problem under consideration.

First we introduce the concepts of NCP and pseudo NCP functions in Sect. 4.1. Then we present all reformulation schemes and discuss their feasible sets and regularity properties with a view towards solving them by local algorithms.

4.1 Pseudo NCP functions

NCP functions are bivariate functions: $\varphi :\, \mathbb {R}^2 \rightarrow \mathbb {R}$ with the property that

$$\begin{aligned} \varphi (a, b) = 0 \iff a, b \ge 0, \quad a b = 0. \end{aligned}$$

(10)

Classical NCP functions include, e.g., the minimum function $\varphi _{\min }(a, b) = \min (a, b)$ and the Fischer–Burmeister function (Fischer 1992),

$$\begin{aligned} \varphi _{\text {FB}}(a,b) = \sqrt{a^2 + b^2} - (a + b). \end{aligned}$$

See Sun and Qi (1999) and the references therein for an overview of NCP functions. NCP functions can be used to replace binary variables with continuous variables. However, the right-hand side of (10) introduces some difficulties if it is considered from an NLP perspective. The constraints $a, b \ge 0$, $a b = 0$ lead to mathematical programs with equilibrium constraints (MPECs). The problem is that standard NLP regularity concepts like the linear independence constraint qualification (LICQ) or the Mangasarian–Fromovitz constraint qualification (MFCQ) are violated at every feasible point of an MPEC (Ye and Zhu 1995); see Luo et al. (1996) for an overview of the theory and applications of MPECs. However, the nonnegativity constraints in (10) are not needed for the reformulations discussed below. This leads us to extend the class of NCP functions: We call a function $\phi :\, \mathbb {R}^2 \rightarrow \mathbb {R}$ a pseudo NCP function if

$$\begin{aligned} \phi (a, b) = 0 \implies a = 0 \quad \text {or}\quad b = 0. \end{aligned}$$

In the remainder of this article we use the following two pseudo NCP functions:

$$\begin{aligned} \phi _{\text {prod}}(a,b) \mathrel {{\mathop :}{=}}ab, \quad \phi _{\text {FB}}(a,b) \mathrel {{\mathop :}{=}}\varphi _{\text {FB}}(a,b). \end{aligned}$$

Note that the Fischer–Burmeister $\phi _{\text {FB}}$ function has a lack of regularity, whereas the product formulation $\phi _{\text {prod}}$ is favorable since we do not have to impose nonnegativity constraints here as in the classical NCP setting.

4.2 Reformulation schemes

It is well-known that local solvers tend to be very sensitive to the specific formulation of a nonlinear model. This is the reason why it is often useful in practice to have different equivalent formulations to evaluate which formulation is best suited for the used solver. In this section we discuss five schemes that allow to reformulate the MINLP and GDP models of Sects. 3.1 and 3.2 with continuous variables and additional smooth constraints. Since the geometry of the feasible regions of the resulting continuous models and their regularity properties also have a strong influence on the solution process, we analyze these aspects for every reformulation.

To be applicable in the context of the model of Sect. 3.1, the reformulations have to possess the following properties:

• 1. Every feasible solution of the reformulation has to be uniquely translatable into a feasible solution of the original MINLP (or GDP). This means that there exists a mapping (a left-total right-unique relation) from the feasible set of the reformulation to the feasible set of the original model.

• 2. For every binary variable $s\in \{0,1\}$, the reformulation has variables from which indicator and negation expressions can be constructed (cf. Sect. 3.1.1).

• 3. The reformulation has variables from which the SOS-1 constraint can be constructed.

In what follows, we only present the representations of a set of binary variables $s_1, \dots , s_m \in \{0,1\}$ together with the SOS-1 constraint $\sum _{i = 1}^m s_i = 1$, rather than stating complete reformulated models. The latter can easily be reproduced from Sect. 3.1. We frequently use the sets $\mathscr {M}\mathrel {{\mathop :}{=}}\{1, \dots , m\}$ and $\mathscr {M}_i \mathrel {{\mathop :}{=}}\mathscr {M}\setminus \{i\}$.

As already stated in Sect. 1, all reformulation schemes below can be found in the existing literature—in particular, see Baumrucker et al. (2008), Kraemer and Marquardt (2010), and Stein et al. (2004)—except that we use pseudo NCP functions rather than NCP functions.

4.2.1 Exact bivariate reformulation

The first reformulation requires two continuous variables $(\sigma _i, \tau _i) \in \mathbb {R}^2$ per binary variable $s_i$ together with the constraints

$$\begin{aligned} \phi (\sigma _i, \tau _i)&= 0 \quad \text {for all}\quad i \in \mathscr {M}, \end{aligned}$$

(11a)

$$\begin{aligned} \sigma _i + \tau _i&= 1 \quad \text {for all}\quad i \in \mathscr {M}, \end{aligned}$$

(11b)

$$\begin{aligned} \sum _{i \in \mathscr {M}} \sigma _i&= 1, \end{aligned}$$

(11c)

where $\phi$ is an arbitrary pseudo NCP function. Clearly, the constraints (11) imply $(\sigma _i, \tau _i) \in \{(1,0), (0,1)\}$, giving the required mapping:

$$\begin{aligned} (\sigma _i, \tau _i) = (1,0) \mapsto s_i = 1, \quad (\sigma _i, \tau _i) = (0,1) \mapsto s_i = 0. \end{aligned}$$

An indicator expression is $\sigma _i$ and valid negation expressions are $\tau _i$ or $(1 - \sigma _i)$. The feasible region of (11) is illustrated in Fig. 3 (left).

Since this scheme adds 2 m continuous variables and $2 m + 1$ equality constraints, it introduces a lack of regularity (in the LICQ and MFCQ sense) in the $(\sigma _i, \tau _i)$-space. However, (11) can be equivalently reformulated by replacing (11a) with

$$\begin{aligned} \phi (\sigma _i, \tau _i) = 0 \quad \text {for all}\quad i \in \mathscr {M}_1, \quad \sigma _1 \ge 0. \end{aligned}$$

For $\phi \in \{\phi _\text {prod}, \phi _\text {FB}\}$, it can be shown that the latter formulation satisfies the LICQ if and only if $\sigma _1 \ne 0$. Of course, $\mathscr {M}_1$ can be replaced with every other $\mathscr {M}_j$.

Fig. 3

Left: Feasible set of the exact bivariate reformulation. The axes are the feasible sets of (11a). Together with (11b) the feasible set $\{(1,0),(0,1)\}$ (bullets) remains. Right: Feasible set of the approximate bivariate reformulation. The axes are the feasible sets of (12a) and the shaded area is the feasible region of (12b). The intersection consists of the two disjoint bold lines

4.2.2 Approximate bivariate reformulation

The second reformulation works like the first one but relaxes (11b):

$$\begin{aligned} \phi (\sigma _i, \tau _i)&= 0 \quad \text {for all}\quad i \in \mathscr {M}, \end{aligned}$$

(12a)

$$\begin{aligned} \sigma _i + \tau _i&\ge 1 \quad \text {for all}\quad i \in \mathscr {M}, \end{aligned}$$

(12b)

$$\begin{aligned} \sum _{i \in \mathscr {M}} \sigma _i&= 1. \end{aligned}$$

(12c)

The feasible set is illustrated in Fig. 3 (right): it is readily seen that $(\sigma _i, \tau _i) \in (\{0\} \times [1, \infty )) \cup ([1, \infty ) \times \{0\})$, and that exactly one $i \in \mathscr {M}$ exists with $\sigma _i = 1$ and $\sigma _j = 0$ for all $j \ne i$. Here we have added 2 m variables with $m + 1$ equality and m inequality constraints. Depending on the activity status of inequalities, the LICQ might be satisfied or again be violated. An indicator expression is $\sigma _i$ and a valid negation expression is given by $\tau _i$. This scheme cannot be reformulated again like the exact bivariate reformulation since one would lose the property of being able to formulate indicator and negation expressions.

4.2.3 Exact univariate reformulation

This scheme requires only one continuous variable $\sigma _i$ per binary variable $s_i$ and adds the following constraints:

$$\begin{aligned} \phi (\sigma _i, 1-\sigma _i)&= 0 \quad \text {for all}\quad i \in \mathscr {M}, \end{aligned}$$

(13a)

$$\begin{aligned} \sum _{i \in \mathscr {M}} \sigma _i&= 1. \end{aligned}$$

(13b)

The feasible set is shown in Fig. 4 (left). Clearly we have $\sigma _i \in \{0,1\}$ for all $i \in \mathscr {M}$. An indicator expression is $\sigma _i$ and a negation expression is $(1 - \sigma _i)$. The number of equality constraints exceeds the number of variables again by one ($m + 1$ vs.  m), but (13) can be equivalently replaced with

$$\begin{aligned} \phi (\sigma _i, 1-\sigma _i) = 0 \quad \text {for all}\quad i \in \mathscr {M}_1, \quad \sigma _1 \ge 0, \quad \sum _{i \in \mathscr {M}} \sigma _i = 1 , \end{aligned}$$

satisfying the LICQ for $\phi \in \{\phi _\text {prod}, \phi _\text {FB}\}$ if and only if $\sigma _1 \ne 0$.

Fig. 4

Left: Feasible set $\{0, 1\}$ of the exact univariate reformulation (13) and the alternative exact univariate reformulation (14). Right: Feasible set $\{0\} \cup [1, \infty )$ of the alternative univariate reformulation (15)

4.2.4 Alternative exact univariate reformulation

Here, the set of constraints reads

$$\begin{aligned} \phi \left( \sigma _i, \textstyle \sum \limits _{j \in \mathscr {M}_i} \sigma _j\right)&= 0 \quad \text {for all}\quad i \in \mathscr {M}, \end{aligned}$$

(14a)

$$\begin{aligned} \sum \limits _{i \in \mathscr {M}} \sigma _i&= 1. \end{aligned}$$

(14b)

These constraints imply $\phi (\sigma _i, 1 - \sigma _i) = 0$, yielding $\sigma _i \in \{0,1\}$ for all i. As before, there is one more equality constraint than variables ($m + 1$ vs.  m), and we have the equivalent reformulation

$$\begin{aligned} \phi \left( \sigma _i, \textstyle \sum \limits _{j \in \mathscr {M}_i} \sigma _j\right) = 0 \quad \text {for all}\quad i \in \mathscr {M}_1, \quad \sigma _1 \ge 0, \quad \sum \limits _{i \in \mathscr {M}} \sigma _i = 1 . \end{aligned}$$

In both cases, an indicator expression is $\sigma _i$ and a negation expression is $(1 - \sigma _i)$ or, equivalently, $\sum _{j \in \mathscr {M}_i} \sigma _j$. The feasible set is the same as before, see Fig. 4 (left). Again, the LICQ is satisfied for $\phi \in \{\phi _\text {prod}, \phi _\text {FB}\}$ if and only if $\sigma _1 \ne 0$.

4.2.5 Approximate univariate reformulation

The set of constraints for the final scheme is given by

$$\begin{aligned} \phi \left( \sigma _i, \textstyle \sum \limits _{j \in \mathscr {M}_i} \sigma _j\right)&= 0 \quad \text {for all}\quad i \in \mathscr {M}, \end{aligned}$$

(15a)

$$\begin{aligned} \sum _{i \in \mathscr {M}} \sigma _i&\ge 1. \end{aligned}$$

(15b)

The feasible set is illustrated in Fig. 4 (right). Clearly we have $\sigma _i \in \{0\} \cup [1, \infty )$ for all i. An indicator expression is $\sigma _i$, and a negation expression is $\sum _{j \in \mathscr {M}_i} \sigma _j$. This reformulation has the disadvantage that it always violates the LICQ for both $\phi _{\text {prod}}$ and $\phi _{\text {FB}}$, even if the inequality constraint (15b) is not active. Again, (15) can be equivalently reformulated by replacing (15a) with

$$\begin{aligned} \phi \left( \sigma _i, \textstyle \sum \limits _{j \in \mathscr {M}_i} \sigma _j\right) = 0 \quad \text {for all}\quad i \in \mathscr {M}_1, \quad \sigma _1 \ge 0. \end{aligned}$$

This formulation satisfies the LICQ for $\phi \in \{\phi _\text {prod}, \phi _\text {FB}\}$ if and only if $\sigma _1 \ne 0$.

Table 3 lists the main properties of the five reformulation schemes.

Table 3 Summary of all reformulation schemes. Index 1 denotes the first version and index 2 denotes the second version of the reformulation

5 Computational study

In the preceding sections we have discussed the problem of compressor station optimization and we have presented several model formulations. With these formulations at hand, the question arises whether all models are comparably well suited for numerical computations, or whether there are benefits or disadvantages for any of them. In this section we present an extensive computational study and compare the results of local and global solvers applied to different model formulations. We will see that the continuous reformulations work quite well in comparison to MINLP approaches.

As mentioned in the introduction, one main contribution of this paper is that—in combination with techniques presented in Pfetsch et al. (2015), Schmidt (2013), Schmidt et al. (2013) and Schmidt et al. (2015b)—our approach allows the purely continuous reformulation of genuinely discrete-continuous models of entire gas networks. In order to demonstrate that this is also viable in practice, in the sense that one can compute locally optimal values of the corresponding MINLPs, we present some promising first results.

Section 5.1 introduces two compressor stations with boundary conditions as test instances and describes the hardware and software used in the study. Section 5.2 then discusses performance profiles for measuring performance and robustness of different model formulations and solvers. Next, Sects. 5.3 and 5.4 present the numerical results for single compressor stations while Sect. 5.5 presents a preliminary computational study on entire gas networks. Finally, Sect. 5.6 gives a summary of the results.

5.1 Test instances and computational setup

We consider minimum cost problems using the objective (8) with cost coefficients and , and feasibility testing using the objective $f\equiv 0$. These objectives are combined with all presented models for two different compressor stations. The first station, called GasLib-582 station in the following, is compressorStation_5 from the network GasLib-582 (Humpola et al. 2015). It contains one turbo compressor and one piston compressor and can be operated in three configurations. This station is comparatively small and serves as a proof of concept for the applicability of the continuous reformulations. Moreover, the data of this test set are publicly available, so that other researchers can compare their models or algorithms on the same data. The second station, called HG station in the following, is a real-world compressor station of our former industry partner Open Grid Europe¹ (OGE). It is one of OGE’s largest compressor stations, containing five turbo compressors that can be operated in 14 configurations in our model. The results on this station illustrate the applicability of the presented models on real-world data.

The boundary values for our test instances are constructed as follows. We always prescribe the in- and outflow pressures as well as the flow through the station. For both stations, the set of inflow pressures (in bar) is $\mathscr {P}_\text {in}= \{20,50,80\}$. For every inflow pressure $p_\text {in}\in \mathscr {P}_\text {in}$, we then construct a set of outflow pressures $\mathscr {P}_{\text {out},i}(p_\text {in}) = \{p_\text {in}+ k \varDelta p_i:k = 0, \dots , 3\}$, $i = 1, 2$, where $\varDelta p_1 = 13.3 \hbox { bar}$ (GasLib-582 station) and $\varDelta p_2 = 20\hbox { bar}$ (HG station). The sets of flows (in $10^3\hbox { Nm}^{3}\hbox {h}^{-1}$) are $\mathscr {Q}_1 = \{0, 375, 750, \dots , 2250\}$ (GasLib-582 station) and $\mathscr {Q}_2 = \{0, 800, 1600, \dots , 4800\}$ (HG station). Thus, the complete set of boundary conditions for the GasLib-582 station is

$$\begin{aligned} \mathscr {T}_1 = \{(p_\text {in},p_\text {out},Q_{0}):p_\text {in}\in \mathscr {P}_\text {in}, p_\text {out}\in \mathscr {P}_{\text {out},1}(p_\text {in}), Q_{0}\in \mathscr {Q}_1\} , \end{aligned}$$

and the corresponding set for the HG station is

$$\begin{aligned} \mathscr {T}_2 = \{(p_\text {in},p_\text {out},Q_{0}):p_\text {in}\in \mathscr {P}_\text {in}, p_\text {out}\in \mathscr {P}_{\text {out},2}(p_\text {in}), Q_{0}\in \mathscr {Q}_2\} . \end{aligned}$$

All values are chosen based on our experience with the technical capabilities of the stations and with typical values in gas networks. Note that the flow values for the test sets are given as volumetric flow under normal conditions, $Q_{0}$, measured in 1000 normal cubic meters per hour, as this is the standard technical unit in gas transportation. It can easily be converted to mass flow via $q= c Q_{0}\rho _0$, where $c = 1000/3600$, and $\rho _0$ is the gas density under normal conditions. The sizes of the test sets are $|\mathscr {T}_1| = |\mathscr {T}_2| = 84$.

All models are implemented using the modeling language GAMS  (McCarl 2009) and the C software framework LaMaTTO  (LaMaTTO++ 2015). As global solvers for the MINLP model and its continuous (NLP type) reformulations we use BARON 12.3.3 (Tawarmalani and Sahinidis 2002, 2004, 2005) and SCIP 3.0  (SCIP 2015; Vigerske 2012). Additionally, we use the convex MINLP solver KNITRO 8.1.1 (Byrd et al. 2006) as a heuristic for the nonconvex MINLPs and as NLP solver for the continuous reformulations. As local solvers for the continuous reformulations we use the interior-point code Ipopt 3.11 (Wächter and Biegler 2006) and the reduced-gradient code CONOPT4 (Drud 1994, 1995, 1996) as well as the three MINLP solvers. The solvers are run with default settings throughout, even for solution tolerances, as it is virtually impossible to find settings that make the results comparable in a strict mathematical sense.

All computations are executed on a six-core AMD Opteron Processor 2435 with 2600 MHz and 64 GB RAM. The operating system is Debian 7.5.

5.2 Measuring performance and robustness

To compare the computing times of different combinations of model formulations and solvers, we use standard performance profiles (Dolan and Moré 2002). To this end, let us define the performance measure

$$\begin{aligned} t_{p,s} \mathrel {{\mathop :}{=}}\text {computing time required to solve problem } p \in \mathscr {T}_i \text { by } s \in \mathscr {S}, \end{aligned}$$

where the set $\mathscr {S}$ contains all 106 combinations of model formulations and solvers: the MINLP model in big-$M$ and bilinear product formulation combined with BARON, SCIP, and KNITRO ($1 \times 2 \times 3 = 6$), and each of the five continuous reformulations in four variants (big-$M$ and bilinear product with both pseudo NCP functions each) combined with all five solvers ($5 \times 4 \times 5 = 100$). We consider only the subsets of feasible boundary values, $\mathscr {F}_i \subset \mathscr {T}_i$, defined to contain those instances for which at least one combination $s\in \mathscr {S}$ produces a feasible solution. Now the performance ratio $r_{p,s}$ associated with $t_{p,s}$ is

$$\begin{aligned} r_{p,s} \mathrel {{\mathop :}{=}}\frac{t_{p,s}}{\min \{t_{p,s'}:s' \in \mathscr {S}\}} \in [1, \infty ) . \end{aligned}$$

Moreover, we set $r_{p,s} = r_M \mathrel {{\mathop :}{=}}\max \{r_{p',s'}:p' \in \mathscr {F}_i, \, s' \in \mathscr {S}_i\}$ for those instances p that cannot be solved by s. The logarithmically scaled performance profile is finally given by

$$\begin{aligned} \rho _s(\tau ) \mathrel {{\mathop :}{=}}\frac{1}{|\mathscr {F}_i|}|\{p \in \mathscr {F}_i:\log _2(r_{p,s}) \le \tau \}| \in [0, 1] . \end{aligned}$$

Finally, we remark that we use two different objective functions depending on the goal of our analysis: If we consider the performance of the solution process, we minimize costs using objective (8). For this case we also discuss the different solution qualities obtained by the local solvers. If we consider the robustness of the solution process, we use the empty objective $f\equiv 0$ since we are only interested in whether a feasible point can be found or not. In the latter case, the time used for the performance profiles thus equals the time required to find the first feasible point.

5.3 The GasLib-582 test set

The set $\mathscr {F}_1$ contains 48 instances of $\mathscr {T}_1$, hence 36 of the 84 instances are infeasible. The computing times are up to 62 s in cases where solutions are found and up to 59 s in cases where a solver detects infeasibility. Some of the instances are solved in fractions of a second. This can happen, for instance, in the preprocessing of BARON due to bound strengthening. As one would expect, the largest differences of computing times are observed for the global solvers.

First we discuss the objective values that are obtained by the different formulations and solvers. In theory, the global solvers BARON and SCIP should produce identical objective values whereas the local optima found by the local solvers can be larger by arbitrary amounts. However, our results show that the values of BARON and SCIP slightly differ in some cases and that all model formulations and solvers produce almost identical values on the current test set.

Table 4 GasLib-582 test set: numbers of false infeasibility reports and solver failures. Top: solver does not find a feasible solution with any model, bottom: no solver finds a feasible solution with any variant of given model

For every problem $p \in \mathscr {F}_1$, we compute the minimum and maximum objective values $f^*_{p,\min }$ and $f^*_{p,\max }$ as well as the maximal absolute gap $g^*_p = f^*_{p,\max } - f^*_{p,\min }$. The minimal values $f^*_{p,\min }$ range from 0 to 0.008735 (operating cost in €/s), with maximal gaps ranging from 0 to 0.008765. The average maximal gap over $p \in \mathscr {F}_1$ is approximately 0.0012, but most of the individual gaps are actually zero. We assume that differing objective values are mainly caused by different numerical properties of the solvers. We also compared the discrete states of the compressor stations in the optimal solutions for every instance. Different active states are found for 9 of the 48 feasible instances, 3 of which have boundary values of the form $Q_{0}= 0$ and $p_u= p_v$, where the bypass mode and the closed mode are both feasible and globally optimal with zero cost. The remaining 6 instances have different active configurations. Thus, we have the surprising observation that on the current test set the local solvers always yield optimal values close to the global minima. A possible reason could be that many instances admit just one feasible discrete configuration. Unfortunately we cannot find out whether this is true since it would require the huge effort of testing feasibility for all discrete configurations.

Next, we turn to the issue of infeasibility detection. A substantial fraction of the boundary values of our test set are infeasible: 36 out of 84. In theory, if a global solver detects infeasibility of an instance, this is considered as an infeasibility proof. However, due to numerical inaccuracy, this is not always true in practice. To give a more detailed overview, we also list the numbers of feasible instances that are not solved (i.e., infeasibility is reported or the solver simply fails) in Table 4. Among the solvers, BARON clearly shows the most reliable results: for every feasible instance there is at least one model formulation for which BARON produces a solution. All other solvers report false infeasible results or fail in 7 or 8 cases. Surprisingly, this is also true for the global solver SCIP. Regarding the different continuous reformulations, the approximate bivariate and exact univariate reformulations are solved for every feasible instance (at least by one solver). The worst result is obtained for the MINLP model (7 failures). However, this result has to be carefully interpreted because the MINLP is handled by only 3 solvers whereas all 5 solvers can handle the continuous reformulations. Within the set of reformulations, the approximate univariate reformulation has by far the largest number of false infeasibility reports and solver failures.

Let us now investigate the performance (measured in computing time) of all combinations $s \in \mathscr {S}$. We define the fastest combination to be the one that has the largest number of instances that it solves at least as fast as all other combinations, i.e., the combination s with the largest value $\rho _s(0)$ in the corresponding logarithmically scaled performance profile. We use this value because it is a generally accepted quality measure. Of course, one might also be interested in other measures such as the total runtime of a model/solver combination s on all instances. To give a visual illustration, we need some aggregation and compare the 106 combinations in two stages: in the first stage we determine the best combination of a solver with indicator constraint type and pseudo NCP function for each of the 6 basic models: MINLP and 5 reformulations. In the second stage, only the 6 best combinations of the first stage are compared. Table 5 lists the fastest solvers for the MINLP model and the 5 reformulations. The solver printed in bold is the fastest solver of the entire row, i.e., over all combinations of indicator constraint types and pseudo NCP functions. Note that the MINLP model does not involve any pseudo NCP functions, hence the first row has only two entries (big-$M$ and BP).

Table 5 GasLib-582 test set: fastest solvers for every combination of MINLP model or continuous reformulation with indicator constraint type and pseudo NCP function (BP: bilinear product)

First, it can be seen that the global solver BARON is the fastest solver for 18 of the 22 model formulations. The local solvers Ipopt or CONOPT4 are faster in only three cases. CONOPT4 is the overall fastest solver for the alternative exact and approximate univariate reformulations. Second, it is apparent that the bilinear product used as pseudo NCP function yields clearly faster runs than the Fischer–Burmeister function: all the bold model/solver combinations use the bilinear product. Third, a best choice of the type of indicator constraints (big-$M$ vs. bilinear product) is not apparent by this criterion. The full data set actually shows that the choice does not have a significant impact here.

Figure 5 shows the 6 performance profiles of the fastest model/solver combinations (bold) for each row of Table 5. Although BARON is faster than all other solvers on the largest number of model formulations, it turns out that the preferable model/solver combination does not use BARON. In order to determine the overall fastest combination, we again compare the values $\rho _s(0)$. It can be seen that the local solver CONOPT4 (applied to the alternative exact and approximate univariate reformulations) produces the shortest solution times for approximately 40 % of all feasible instances. Notice that both formulations solved with CONOPT4 are faster than all other combinations if an instance can be solved by CONOPT4 at all (the “horizontal” lines of the performance profiles of AEUR and AUR in Fig. 5 extend almost to the left boundary). This is to be expected since local solvers typically tend to be faster than global solvers. The global solver BARON applied to the other continuous reformulations yields significantly slower solution times and is the fastest combination for 15 to 25 % of the feasible instances. Finally, BARON applied to the original MINLP model is distinctly the slowest combination of solver and model formulation.

Fig. 5

GasLib-582 test set: comparison of fastest combinations of indicator constraint type, pseudo NCP function, and solver for MINLP and continuous reformulations; cf. Table 5

We now turn to robustness. The most robust combination is defined as the one that solves the largest fraction of instances to optimality, i.e., the combination s with the largest value

$$\begin{aligned} \rho ^*_s \mathrel {{\mathop :}{=}}\lim _{\tau \nearrow r_M} \rho _s(\tau ). \end{aligned}$$

As in the performance comparison, we list the most robust solver for every combination of model reformulation, indicator constraint type, and pseudo NCP function in Table 6.

Table 6 GasLib-582 test set: most robust solvers for every combination of MINLP model or continuous reformulation with indicator constraint type and pseudo NCP function (BP: bilinear product)

Here BARON appears even more often than in the case of computing times: It is always the most robust solver, except for the single case where SCIP is applied to the MINLP model with bilinear products as indicator constraints. In contrast to the case of computing times, the choice of pseudo NCP functions does not seem to have a significant impact here.

Again we compare the 6 performance profiles of the best combinations (bold) for each row of Table 6, see Fig. 6.

Fig. 6

GasLib-582 test set: comparison of most robust combinations of indicator constraint type, pseudo NCP function, and solver for MINLP and continuous reformulations; cf. Table 6

Overall, the results look more “homogeneous” than in Fig. 5. All combinations produce comparatively good values $\rho _s^*$ from 85 to 98 % of solved instances. The two bivariate reformulations produce the best values (significantly above 90 %). Note further that these model formulations use big-$M$ indicator constraints. The good robustness is probably caused by the convexity conserving property of the big-$M$ formulation, which contrasts with the inherently nonconvex bilinear products.

5.4 The HG test set

The set $\mathscr {F}_2$ contains 41 instances of $\mathscr {T}_2$, hence 43 of the 84 instances are infeasible. The computing times are up to 67 s in cases where solutions are found and up to 45 s in cases where a solver detects infeasibility.

The minimal objective values (in €/s) now range from 0 to 0.069505 and the maximal gaps from 0 to 0.022102. The average maximal gap over all $p \in \mathscr {F}_2$ is significantly smaller than for $\mathscr {F}_1$ at approximately 0.0006778 and most of the individual gaps are again zero. Except for one case, the active states in the optimal solutions for a given set of boundary values are identical for all $s \in \mathscr {S}$ or consist of different sets of identical compressor units yielding the same objective value.² The exceptional case is exactly the one leading to the maximal gap. Excluding this case reduces the maximal gap over all instances by one order of magnitude.

In Table 7 we list the numbers of feasible instances for which a model could not be solved to optimality (i.e., infeasibility is reported or the solver fails). As it was the case for the GasLib-582 station, BARON yields the smallest number of false infeasibility reports (just one). Moreover, the choice of the class of solver (global vs. local) seems to be more crucial than the choice of the specific model formulation: the MINLP solvers report false infeasibility in 1 to 3 cases whereas the local solvers have significantly larger numbers of failure of 5 and 8.

Table 7 HG test set: numbers of false infeasibility reports and solver failures. Top: solver does not find a feasible solution with any model, bottom: no solver finds a feasible solution with any variant of given model

Turning to the performance investigation, we follow the same two-stage approach as before. Table 8 lists the fastest solvers for the MINLP model and all tested continuous reformulations. It can be seen that BARON is the fastest solver for the MINLP model (to which only global solvers can be applied) and that local solvers (CONOPT4 and Ipopt) are the fastest for all continuous reformulations, where both global and local solvers are applied. This is in line with our expectations since local solvers typically tend to be faster than global solvers. Moreover, it is noticeable that the pseudo NCP function $\phi _\text {prod}$ yields better results than the Fischer–Burmeister function $\phi _\text {FB}$, and that global solvers outperform local solvers when applied to big-$M$ indicator constraints while the converse behavior is observed for bilinear indicator constraints (except for the case of BARON applied to the exact bivariate reformulation using bilinear indicator constraints and $\phi = \phi _\text {prod}$).

Table 8 HG test set: fastest solvers for every combination of MINLP model or continuous reformulation with indicator constraint type and pseudo NCP function (BP: bilinear product)

Fig. 7

HG test set: comparison of fastest combinations of indicator constraint type, pseudo NCP function, and solver for MINLP and continuous reformulations; cf. Table 8

Figure 7 shows the performance profiles for every bold combination of Table 8. The approximate bivariate reformulation (ABR) solved with CONOPT4 is the overall fastest combination, performing best on more than 30 % of all instances. The approximate univariate (AUR), exact bivariate (EBR), and alternative exact univariate (AEUR) reformulations combined with CONOPT4 come next, each performing best on roughly 20 % of all instances. Since the approximate univariate formulation shows better results than EBR and AEUR for small values $\tau > 0$, we may summarize that the approximate reformulations (combined with $\phi = \phi _\text {prod}$) tend to be the fastest combinations. A possible reason might be that for local solvers the enlarged feasible set is preferable to the feasible sets of lower dimension of the exact reformulations. In addition, the overall preferable approximate bivariate scheme is also the “most regular” formulation with respect to the LICQ (cf. Sect. 4.2). Finally we note that in terms of solution times both the exact univariate reformulation and the MINLP model cannot compete with the other reformulations.

Regarding robustness, the situation changes completely. We list the most robust solver (the one with largest $\rho _s^*$) for every combination of model reformulation, indicator constraint type, and pseudo NCP function in Table 9. For the original MINLP model, KNITRO (with big-$M$ indicator constraints) and SCIP (with bilinear indicator constraints) are equally robust. BARON is the most robust solver in 80 % of all continuous reformulations. The bilinear product indicator constraints always yield better results than the big-$M$ ones. Except for KNITRO applied to the approximate univariate reformulation using bilinear indicator constraints and $\phi = \phi _\text {FB}$, no local solver is more robust than one of the global solvers.

Table 9 HG test set: most robust solvers for every combination of MINLP model or continuous reformulation with indicator constraint type and pseudo NCP function (BP: bilinear product)

The performance profiles of the most robust combinations of Table 9 are given in Fig. 8. All models yield comparable results, solving 85 to 93 % of all instances. The highest percentages are obtained by the original MINLP and the exact bivariate reformulation (EBR). The fastest continuous reformulations, i.e., the approximate bivariate and the alternative approximate univariate reformulation, yield the smallest values at approximately 85 %. Thus, we have exactly the opposite situation as for the performance comparison.

Fig. 8

HG test set: comparison of most robust combinations of indicator constraint type, pseudo NCP function, and solver for MINLP and continuous reformulations; cf. Table 9

5.5 Continuous reformulations of entire networks

Let us now extend our approach of continuous reformulations to MINLP models of entire gas networks. To this end, we combine the reformulations presented in this paper with suitable MPEC based reformulations of all controllable network devices (except compressor stations) (Pfetsch et al. 2015; Schmidt 2013; Schmidt et al. 2013, 2015b). In our computational study, we combine the MPEC based model of the network with all combinations of pseudo NCP functions, indicator constraints, continuous reformulations, and local solvers discussed in the previous sections. Each of these combinations is applied to 50 randomly chosen instances of the GasLib-582 network.³ All instances are solved with the goal of feasibility testing, i.e., with objective function $f \equiv 0$; cf. Sect. 5.2. The time limit of all computations is set to 2 min, and we use the same hardware and software as in the preceding sections.

The results for embedding continuous reformulations of compressor stations in entire network models are of interest for, at least, two reasons. First, they give insight into the situation where boundary values are restricted to nontrivial ranges, rather than being fixed as in the study presented so far. Second, they provide a first impression on the robustness of solving purely continuous network models.

Table 10 Number of solved instances (k) for every combination of pseudo NCP function (pNCP), indicator constraint type ($c^{\text {ind}}$), continuous reformulation, and local solver. All combinations for which no feasible solution could be found are not listed

Table 10 lists the number of feasible solutions found by the individual reformulations. It turns out that the choice of the pseudo NCP function (Fischer–Burmeister vs. product) is not crucial here: 51 combinations using $\phi _\text {FB}$ and 57 combinations using $\phi _\text {prod}$ are solved to feasibility. Similarly, the choice of the specific indicator constraint type does not appear to be of great importance for entire networks (61 feasible solutions for big-$M$ constraints and 47 for bilinear product constraints).

In contrast, the choices of reformulation scheme and local solver have a strong influence. All univariate reformulation schemes (EUR, AEUR, and AAUR) yield feasible solutions significantly less often (9, 13, and 8 times) than the exact bivariate (EBR; 45 feasible solutions) and the approximate bivariate reformulation scheme (ABR; 33 feasible solutions). Concerning the tested local solvers, Ipopt (70 feasible solutions) clearly outperforms both CONOPT4 (37) and KNITRO (1).

In total, 38 instances (76 %) are solved to feasibility. The most successful combination (printed bold in Table 10) combines the Fischer–Burmeister pseudo NCP function with big-$M$ indicator constraints, the exact bivariate reformulation scheme, and the local solver CONOPT4.

The analysis of the results shows that feasibility testing for entire gas networks is possible with purely continuous models in principle. However, the used combinations of MPEC models and continuous compressor station reformulations have to be tested in more detail in order to increase the robustness of the formulations. This is a subject of future research.

5.6 Summary

A major result of our study is that local solvers applied to continuous reformulations tend be faster than global solvers applied to the mixed-integer model and its continuous reformulations. This was to be expected. Moreover, our numerical results suggest that this tendency becomes more evident for larger instances. When comparing only the continuous reformulations, the results for the larger compressor station HG indicate that reformulations with larger feasible sets are preferable and that the regularity of the formulation has a strong impact on the performance of the solution process. (Recall that the “most regular” approximate bivariate reformulation yields the best solution times on the large test set.) Finally, global solvers (especially BARON) produce more robust results, independent of the choice of model formulation.

Our results also indicate which types of indicator constraints work well with a given solver. Especially for larger instances, global solvers tend to be faster on big-$M$ formulations while local solvers perform better with bilinear products. A probable reason for this is that the behavior of global solvers is stronger influenced by nonconvexity than it is the case for local solvers. The situation changes with regard to robustness of the solution process, where the bilinear indicator constraint is clearly preferable to the big-$M$ formulation.

A second observation concerns the preferable type of pseudo NCP functions: The product formulation $\phi _\text {prod}$ distinctly outperforms Fischer–Burmeister functions. Although the latter are quite prominent in the literature, the simple formulation using products usually produces faster and more robust formulations in practice.

Finally we can state that, for the models considered in this paper, there are no significant drawbacks concerning the quality of solutions when local solvers are used. These results are perhaps not entirely surprising for the considered class of real-world problems. However, no systematic study exists in the literature up to now.

The tendencies observed above might change when fixed boundary values are replaced with nontrivial feasible ranges. This happens, e.g., when the tested continuous reformulations of compressor stations are used in continuous models of entire networks. As expected, the resulting instances are hard, but we have seen in Sect. 5.5 that in principle they can be solved by local solvers. Nevertheless, more extensive testing of model combinations and possibly the development of further model variants are required in order to obtain more robust formulations. Both issues are subjects of future research.

6 Conclusion

In this article we have presented MINLP and GDP models for cost optimization and feasibility testing of gas compressor stations. Moreover, we have considered different types of continuous reformulation techniques from the literature and applied them to the application problem. Our computational study shows that local solvers applied to continuous reformulations can be used to replace MINLP formulations that can only be tackled by global solvers. The continuous reformulations yield comparably robust results, optimal values of almost the same quality on our test set, and tend to be solvable within shorter solution times. Together with the techniques developed in Pfetsch et al. (2015), Schmidt (2013), Schmidt et al. (2013), and Schmidt et al. (2015b), this article provides a complete continuous reformulation of the discrete-continuous problem of stationary gas transport optimization. Additionally, first promising numerical results on a large-scale network underpin the practical usability of continuous reformulations for entire networks.

However, some questions remain open. We have considered a stationary and isothermal variant of the problem of compressor station optimization. Since including gas temperature as a dynamic variable mainly leads to increased nonlinearity and nonconvexity in the model, we expect that continuous reformulations tend to be even more favorable for these models. In contrast, the consideration of the transient case will also increase the amount of discrete aspects so that it is unclear which formulation will be favorable in this case. Finally, more extensive testing of suitable continuous models for entire networks is a subject of future research.