Properties of Non-symmetric Macdonald Polynomials at $q=1$ and $q=0$

Abstract

We examine the non-symmetric Macdonald polynomials $\mathrm {E}_\lambda$ at $q=1$, as well as the more general permuted-basement Macdonald polynomials. When $q=1$, we show that $\mathrm {E}_\lambda (\mathbf {x};1,t)$ is symmetric and independent of t whenever $\lambda$ is a partition. Furthermore, we show that, in general $\lambda$, this expression factors into a symmetric and a non-symmetric part, where the symmetric part is independent of t, and the non-symmetric part only depends on $\mathbf {x}$, t, and the relative order of the entries in $\lambda$. We also examine the case $q=0$, which gives rise to the so-called permuted-basement t-atoms. We prove expansion properties of these t-atoms, and, as a corollary, prove that Demazure characters (key polynomials) expand positively into permuted-basement atoms. This complements the result that permuted-basement atoms are atom-positive. Finally, we show that the product of a permuted-basement atom and a Schur polynomial is again positive in the same permuted-basement atom basis. Haglund, Luoto, Mason, and van Willigenburg previously proved this property for the identity basement and the reverse identity basement, so our result can be seen as an interpolation (in the Bruhat order) between these two results. The common theme in this project is the application of basement-permuting operators as well as combinatorics on fillings, by applying results in a previous article by Per Alexandersson.

1 Introduction

The non-symmetric Macdonald polynomials $\mathrm {E}_\lambda (\mathbf {x};q,t)$ were introduced by Macdonald and Opdam in [19, 22]. They can be defined for arbitrary root systems. We only consider the type A for which there is a combinatorial rule, discovered by Haglund et al. [11]. These non-symmetric Macdonald polynomials specialize to the Demazure characters, $\mathcal {K}_\lambda$, (or key polynomials) at $q=t=0$ (or at $t=0$), they are affine Demazure characters, see [14]. Furthermore, at $q=t=\infty$, $\mathrm {E}_\lambda (\mathbf {x};\infty ,\infty )$ reduces to the so-called Demazure atoms, $\mathcal {A}_\lambda$ (also known as standard bases), see [16, 21]. The stable limit of $\mathrm {E}_\lambda (\mathbf {x};q,t)$ gives the classical symmetric Macdonald polynomials (up to a rational function in q and t, depending on $\lambda$), denoted $P_\lambda (\mathbf {x};q,t)$, see [18]. For a quick overview, see the diagram (1.1) below, where $*$ denotes this stable limit:

The topic of this paper is a generalization that arises naturally from the Haglund–Haiman–Loehr (HHL) combinatorial formula, namely the permuted-basement Macdonald polynomials, see [1, 9]. Recently, an alcove walk model was given for these, as well, see [7, 8]. This generalizes the alcove walk model by Ram and Yip [24] for general type non-symmetric Macdonald polynomials.

The permuted-basement Macdonald polynomials are indexed with an extra parameter, $\sigma$, which is a permutation. For each fixed $\sigma \in S_n$, the set $\{ \mathrm {E}^\sigma _\lambda (\mathbf {x};q,t)\}_\lambda$ is a basis for the polynomial ring $\mathbb {C}[x_1,\cdots ,x_n]$, as $\lambda$ ranges over weak compositions of length n.

The current paper is the only one (to our knowledge) that studies this property in the permuted-basement setting. There has been previous research regarding various factorization properties of Macdonald polynomials; for example, [5, 6] concern symmetric Macdonald polynomials and the modified Macdonald polynomials when t is taken to be a root of unity. In [4], various factorization properties of non-symmetric Macdonald polynomials are observed experimentally (in particular, the specialization $q=u^{-2}$, $t=u$) in the last section of the article.

1.1 Main Results

The first part of the paper concerns properties of the specialization $\mathrm {E}^\sigma _\lambda (\mathbf {x};1,t)$. We show that, for any fixed basement $\sigma$ and composition $\lambda$:

$$\begin{aligned} \mathrm {E}^\sigma _\lambda (\mathbf {x};1,t) = \left( \mathrm {e}_{\lambda '}(\mathbf {x}) / \mathrm {e}_{\mu '}(\mathbf {x}) \right) \mathrm {E}^\sigma _{\mu }(\mathbf {x};1,t), \end{aligned}$$

where $\mu$ is the weak standardization (defined below) of $\lambda$. Observe that $\mathrm {e}_{\lambda '}(\mathbf {x}) / \mathrm {e}_{\mu '}(\mathbf {x})$ is an elementary symmetric polynomial independent of t. We also show that, in the case, $\lambda$ is a partition, we have the following:

$$\begin{aligned} \mathrm {E}^\sigma _\lambda (\mathbf {x};1,t) = \mathrm {e}_{\lambda '}(\mathbf {x}), \end{aligned}$$

which is independent of $\sigma$ and t. This property is rather surprising and not evident from the HHL combinatorial formula [10]. Our proofs mainly use properties of Demazure–Lusztig operators, see (2.5) below for the definition.

In the second half of the paper, we study properties of the specialization $\mathrm {E}^\sigma _\lambda (\mathbf {x};0,t)$. At $\sigma = {{\,\mathrm{id}\,}}$, these are t-deformations of the so-called Demazure atoms, so it is natural to introduce the notation $\mathcal {A}^{\sigma }_\lambda (\mathbf {x};t) {:}{=}\mathrm {E}^\sigma _\lambda (\mathbf {x};0,t)$, which are referred to as t-atoms. The t-atoms for $\sigma ={{\,\mathrm{id}\,}}$ were initially considered in [12], where they proved a close connection with Hall–Littlewood polynomials. The Hall–Littlewood polynomials $\mathrm {P}_\lambda (\mathbf {x};t)$ are obtained as the specialization $q=0$ of the classical Macdonald polynomial $\mathrm {P}_\lambda (\mathbf {x};q,t)$. In fact, it was proven in [12] that the ordinary Hall–Littlewood polynomials $\mathrm {P}_\mu (\mathbf {x};t)$ can be expressed as follows:

$$\begin{aligned} \mathrm {P}_\mu (\mathbf {x};t) = \sum _{\gamma :\mathrm {par}(\gamma )=\mu } \mathcal {A}_\gamma (\mathbf {x};t), \end{aligned}$$

whenever $\mu$ is a partition, and $\mathrm {par}(\gamma )$ denotes the unique partition with the parts of $\gamma$ rearranged in decreasing order.

Our main result regarding the t-atoms is as follows: If $\tau \ge \sigma$ in Bruhat order, then $\mathcal {A}^{\tau }_\gamma (\mathbf {x};t)$ admits the expansion:

$$\begin{aligned} \mathcal {A}^{\tau }_\gamma (\mathbf {x};t) = \sum _{\lambda :\mathrm {par}(\lambda ) = \mathrm {par}(\gamma ) } c^{\tau \sigma }_{\gamma \lambda }(t) \mathcal {A}^{\sigma }_\lambda (\mathbf {x};t), \end{aligned}$$

(1.2)

with the sum being over all compositions $\lambda$ whose parts rearrange to the parts of $\gamma$ and the $c^{\tau \sigma }_{\gamma \lambda }(t)$ are polynomials in t with the property that $c^{\tau \sigma }_{\gamma \lambda }(t) \ge 0$ whenever $0\le t \le 1$.

Equation (1.2) is a generalization of the fact that key polynomials and permuted-basement atoms expand positively into Demazure atoms, see e.g. [20, 23]. Letting $t=0$, we obtain the general result that whenever $\tau \ge \sigma$ in Bruhat order:

$$\begin{aligned} \mathcal {A}^\tau _\gamma (\mathbf {x}) = \sum _{\lambda : \mathrm {par}(\lambda ) = \mathrm {par}(\gamma ) } c^{\tau \sigma }_{\gamma \lambda } \mathcal {A}^{\sigma }_\lambda (\mathbf {x}),\qquad \text {where}\qquad c^{\tau \sigma }_{\gamma \lambda }\in \{0,1\}. \end{aligned}$$

(1.3)

Figure 1 illustrates how various bases of polynomials are related under expansion. We prove the dashed relations (1.2) and (1.3) in this paper. In the figure, we have the permuted-basement atoms, $\mathcal {A}^{\tau }_\gamma (\mathbf {x}) {:}{=}\mathcal {A}^{\tau }_\gamma (\mathbf {x};0)$, the key polynomials $\mathcal {K}_\gamma (\mathbf {x}) {:}{=}\mathcal {A}^{\omega _0}_\gamma (\mathbf {x})$, and the Demazure atoms $\mathcal {A}_\gamma (\mathbf {x}) {:}{=}\mathcal {A}^{{{\,\mathrm{id}\,}}}_\gamma (\mathbf {x})$. Finally, $\omega _0$ denotes the longest permutation (in $S_n$).

Fig. 1

This graph shows various families of polynomials. The arrows indicate “expands positively in” which means that the coefficients are either non-negative numbers or polynomials in t with non-negative coefficients. Here, $\tau \ge \sigma$ in Bruhat order, and Schur polynomials should be interpreted as polynomials in n variables or symmetric functions depending on context

As a final corollary, by taking $\tau =\omega _0$, we see that key polynomials expand positively into permuted-basement Demazure atoms:

$$\begin{aligned} \mathcal {K}_\gamma (\mathbf {x}) = \sum _{\alpha :\mathrm {par}(\alpha ) = \mathrm {par}(\gamma ) } c^{\sigma }_{\gamma \alpha } \mathcal {A}^{\sigma }_\alpha (\mathbf {x}),\qquad \text {where}\qquad c^{\sigma }_{\gamma \alpha }\in \{0,1\}. \end{aligned}$$

2 Preliminaries

We now give the necessary background on the combinatorial model for the permuted-basement Macdonald polynomials. The notation and some of the preliminaries is taken from [1].

Let $\sigma = (\sigma _1,\dots ,\sigma _n)$ be a list of n different positive integers and let $\lambda =(\lambda _1,\dots ,\lambda _n)$ be a weak integer composition, that is, a vector with non-negative integer entries. An augmented filling of shape $\lambda$ and basement$\sigma$ is a filling of a Young diagram of shape $(\lambda _1,\cdots ,\lambda _n)$ with positive integers, augmented with a zeroth column filled from top to bottom with $\sigma _1,\cdots ,\sigma _n$. Note that we use English notation rather than the skyline fillings used in [10, 21]. We motivate this choice with the fact that row operations are easier to work with compared with column operations.

Definition 2.1

Let F be an augmented filling. Two boxes a and b are attacking if $F(a)=F(b)$ and the boxes are either in the same column, or they are in adjacent columns with the rightmost box in a row strictly below the other box:

A filling is non-attacking if there are no attacking pairs of boxes.

Definition 2.2

A triple of type A is an arrangement of boxes, a, b, c, located, such that a is immediately to the left of b, and c is somewhere below b, and the row containing a and b is at least as long as the row containing c.

Similarly, a triple of type B is an arrangement of boxes, a, b, c, located, such that a is immediately to the left of b, and c is somewhere above a, and the row containing a and b is strictly longer than the row containing c.

A type A triple is an inversion triple if the entries ordered increasingly form a counter-clockwise orientation. Similarly, a type B triple is an inversion triple if the entries ordered increasingly form a clockwise orientation. If two entries are equal, the one with the largest subscript in Eq. (2.1) is considered to be largest:

If $u = (i,j)$ let d(u) denote $(i,j-1)$, i.e., the box to the left of u. A descent in F is a non-basement box u, such that $F(d(u)) < F(u)$. The set of descents in F is denoted by ${{\,\mathrm{\mathrm {Des}}\,}}(F)$.

Example 2.3

Below is a non-attacking filling of shape (4, 1, 3, 0, 1) with basement (4, 5, 3, 2, 1). The bold entries are descents and the underlined entries form a type A inversion triple. There are 7 inversion triples (of type A and B) in total:

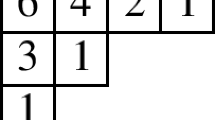
The leg of a box, denoted by ${{\,\mathrm{leg}\,}}(u)$, in an augmented diagram is the number of boxes to the right of u in the diagram. The arm of a box $u = (r,c)$, denoted by ${{\,\mathrm{arm}\,}}(u)$, in an augmented diagram $\lambda$ is defined as the cardinality of the union of the sets:

$$\begin{aligned} \{ (r', c) \in \lambda :r< r' \text { and } \lambda _{r'} \le \lambda _r \} \text { and } \{ (r', c-1) \in \lambda :r'< r \text { and } \lambda _{r'} < \lambda _r \}. \end{aligned}$$

We illustrate the boxes x and y (in the first and second set in the union, respectively) contributing to ${{\,\mathrm{arm}\,}}(u)$ below. The boxes marked l contribute to ${{\,\mathrm{leg}\,}}(u)$. The ${{\,\mathrm{arm}\,}}$ values for all boxes in the diagram are shown in the diagram on the right.

The major index, ${{\,\mathrm{maj}\,}}(F)$, of an augmented filling F is given by the following:

$$\begin{aligned} {{\,\mathrm{maj}\,}}(F) = \sum _{ u \in {{\,\mathrm{\mathrm {Des}}\,}}(F) } {{\,\mathrm{leg}\,}}(u)+1. \end{aligned}$$

The number of inversions, denoted by ${{\,\mathrm{inv}\,}}(F)$, of a filling is the number of inversion triples of either type. The number of coinversions, ${{\,\mathrm{coinv}\,}}(F)$, is the number of type A and type B triples which are not inversion triples.

Let $\mathrm {NAF}_\sigma (\lambda )$ denote all non-attacking fillings of shape $\lambda$ with basement $\sigma \in S_n$ and entries in $\{1,\cdots ,n\}$.

Example 2.4

The set $\mathrm {NAF}_{3124}(1,1,0,2)$ consists of the following augmented fillings:

Recall that the length of a permutation, ${{\,\mathrm{\ell }\,}}(\sigma )$, is the number of inversions in $\sigma$. We let $\omega _0$ denote the unique longest permutation in $S_n$. Furthermore, given an augmented filling F, the weight of F is the composition $\mu _1,\mu _2,\dots ,$ such that $\mu _i$ is the number of non-basement entries in F that are equal to i. We then let $\mathbf {x}^F$ be a shorthand for the product $\prod _i x_i^{\mu _i}$.

Definition 2.5

(Combinatorial formula) Let $\sigma \in S_n$ and let $\lambda$ be a weak composition with n parts. The non-symmetric permuted-basement Macdonald polynomial$\mathrm {E}^\sigma _\lambda (\mathbf {x};q,t)$ is defined as follows:

$$\begin{aligned} \mathrm {E}^\sigma _\lambda (\mathbf {x}; q,t) {:}{=}\sum _{ F \in \mathrm {NAF}_\sigma (\lambda )} \mathbf {x}^F q^{{{\,\mathrm{maj}\,}}F} t^{{{\,\mathrm{coinv}\,}}F} \!\!\! \prod _{ \begin{array}{c} u \in F \\ u \text { is in the basement or} \\ F(d(u))\ne F(u) \end{array}} \!\!\! \frac{1-t}{1-q^{1+{{\,\mathrm{leg}\,}}u} t^{1+{{\,\mathrm{arm}\,}}u}}.\nonumber \\ \end{aligned}$$

(2.2)

The product is over all boxes u in F, such that either u is in the basement or $F(d(u))\ne F(u)$.

When $\sigma = \omega _0$, we recover the non-symmetric Macdonald polynomials $\mathrm {E}_\lambda (\mathbf {x};q,t)$ defined in [10].

Note that the number of variables which we work over is always finite and implicit from the context. For example, if $\sigma \in S_n$, then $\mathbf {x}{:}{=}(x_1,\cdots ,x_n)$ in $\mathrm {E}^\sigma _\lambda (\mathbf {x}; q,t)$, and it is understood that $\lambda$ has n parts.

2.1 Bruhat Order, Compositions, and Operators

If $\omega \in S_n$ is a permutation, we can decompose $\omega$ as a product $\omega = s_{i_1}s_{i_2}\cdots s_{i_k}$ of elementary transpositions, $s_i = (i,i+1)$. When k is minimized, $s_{i_1}s_{i_2}\cdots s_{i_k}$ is a reduced word of $\omega$, and k is the length of $\omega$, which we denote by ${{\,\mathrm{\ell }\,}}(\omega )$.

The strong order on permutations in $S_n$ is a partial order defined via the cover relations that u covers v if $(a,b) u = v$ and ${{\,\mathrm{\ell }\,}}(u) + 1 = {{\,\mathrm{\ell }\,}}(v)$ for some transposition (a, b). The Bruhat order is defined in a similar fashion, where only elementary transpositions are allowed in the covering relations. We illustrate these partial orders in Fig. 2.

Fig. 2

The Bruhat order and strong order on $S_4$. Permutations expressed in one-line notation and solid lines correspond to elementary transposition

Given a composition $\alpha$, let $\mathrm {par}(\alpha )$ be the unique integer partition where the parts of $\alpha$ have been rearranged in decreasing order. For example, $\mathrm {par}(2,0,1,4,9)$ is equal to (9, 4, 2, 1, 0). We can act with permutations on compositions (and partitions) by permutation of the entries:

$$\begin{aligned} \omega (\lambda ) = (3,0,1,5) \text { if } \omega =(2,4,3,1) \text { and } \lambda = (5,3,1,0), \end{aligned}$$

where $\omega$ is given in one-line notation.

To prove the main result of this paper, we rely heavily on the Knop–Sahi recurrence, basement-permuting operators, and shape-permuting operators. The Knop–Sahi recurrence relation for Macdonald polynomials [15, 25] is given by the relation:

$$\begin{aligned} \mathrm {E}_{{\hat{\lambda }}}(\mathbf {x};q,t) = q^{\lambda _1} x_1 \mathrm {E}_{\lambda }(x_2,\cdots ,x_n,q^{-1}x_1;q,t), \end{aligned}$$

(2.3)

where ${\hat{\lambda }} = (\lambda _2,\cdots ,\lambda _n, \lambda _1 +1)$. Furthermore, note that the combinatorial formula implies that

$$\begin{aligned} \mathrm {E}^\sigma _{(\lambda _1+1,\cdots ,\lambda _n+1)}(\mathbf {x};q,t) = (x_1\cdots x_n) \mathrm {E}^\sigma _{(\lambda _1,\cdots ,\lambda _n)}(\mathbf {x};q,t). \end{aligned}$$

(2.4)

We need some brief background on certain t-deformations of divided difference operators. Let $s_i$ be a simple transposition on indices of variables and define

$$\begin{aligned} \partial _i = \frac{1-s_i}{x_i-x_{i+1}}, \quad \pi _i = \partial _i x_i, \quad \theta _i = \pi _i - 1. \end{aligned}$$

The operators $\pi _i$ and $\theta _i$ are used to define the key polynomials and Demazure atoms, respectively. Now, define the following t-deformations of the above operators:

$$\begin{aligned} {\tilde{\pi }}_i(f) = (1-t)\pi _i(f) + t s_i(f), \qquad {\tilde{\theta }}_i(f) = (1-t)\theta _i(f) + t s_i(f). \end{aligned}$$

(2.5)

The ${\tilde{\theta }}_i$ are called the Demazure–Lusztig operators. They generate the affine Hecke algebra, see e.g. [10] (where ${\tilde{\theta }}_i$ correspond to $T_i$). Note that these operators satisfy the braid relations, and that ${\tilde{\theta }}_i {\tilde{\pi }}_i = {\tilde{\pi }}_i {\tilde{\theta }}_i = t$.

Example 2.6

As an example, ${\tilde{\theta }}_1( x_1^2 x_2 ) = (1 - t) x_1 x_2^2 + t x_1 x_2^2$.

With these definitions, we can now state the following two propositions which were proved in [1]:

Proposition 2.7

(Basement-permuting operators). Let $\lambda$ be a composition and let $\sigma$ be a permutation. Furthermore, let $\gamma _i$ be the length of the row with basement label i, that is, $\gamma _i = \lambda _{\sigma ^{-1}_i}$.

If ${{\,\mathrm{\ell }\,}}(\sigma s_i) < {{\,\mathrm{\ell }\,}}(\sigma )$, then

$$\begin{aligned} {\tilde{\theta }}_i \mathrm {E}_\lambda ^{\sigma }(\mathbf {x};q,t) = \mathrm {E}_\lambda ^{\sigma s_i}(\mathbf {x};q,t) \times {\left\{ \begin{array}{ll} t, \text { if } \gamma _i \le \gamma _{i+1}, \\ 1, \text { otherwise.} \end{array}\right. } \end{aligned}$$

Similarly, if ${{\,\mathrm{\ell }\,}}(\sigma s_i) > {{\,\mathrm{\ell }\,}}(\sigma )$, then

$$\begin{aligned} {\tilde{\pi }}_i \mathrm {E}_\lambda ^{\sigma }(\mathbf {x};q,t) = \mathrm {E}_\lambda ^{\sigma s_i}(\mathbf {x};q,t) \times {\left\{ \begin{array}{ll} t, \text { if } \gamma _i < \gamma _{i+1}, \\ 1, \text { otherwise.} \end{array}\right. } \end{aligned}$$

Consequently, we see that ${\tilde{\pi }}_i$ and ${\tilde{\theta }}_i$ move the basement up and down, respectively, in the Bruhat order.

Proposition 2.8

(Shape-permuting operators). If $\lambda _j < \lambda _{j+1}$, $\sigma _j = i+1$ and $\sigma _{j+1} =i$ for some i and j, then

$$\begin{aligned} \mathrm {E}^\sigma _{s_j \lambda }(\mathbf {x}; q, t) = \left( {\tilde{\theta }}_i + \frac{1-t}{1-q^{1+{{\,\mathrm{leg}\,}}u}t^{{{\,\mathrm{arm}\,}}u}} \right) \mathrm {E}^\sigma _{\lambda }(\mathbf {x}; q, t), \end{aligned}$$

where $u = (j+1, \lambda _{j}+1)$ in the diagram of shape $\lambda$.

Note that these formulas together with the Knop–Sahi recurrence uniquely define the Macdonald polynomials recursively, with the initial condition that for the empty composition: $\mathrm {E}_{(0,\ldots , 0)}(\mathbf {x};q,t)=1$.

Finally, we will need the following result from [1]:

Theorem 2.9

(Partial symmetry). Suppose $\lambda _j = \lambda _{j+1}$ and $\{\sigma _j, \sigma _{j+1} \}$ take the values $\{i, i+1\}$ for some j, i, then $\mathrm {E}^\sigma _\lambda (\mathbf {x};q,t)$ is symmetric in $x_i, x_{i+1}$.

3 A Basement Invariance

Recall that the elementary symmetric function $\mathrm {e}_\mu (\mathbf {x})$ with the partition $\mu$ having $\ell$ parts is defined as follows:

$$\begin{aligned} \mathrm {e}_\mu (\mathbf {x}){:}{=}\mathrm {e}_{\mu _1}(\mathbf {x}) \cdots \mathrm {e}_{\mu _\ell }(\mathbf {x}), \text { where } \mathrm {e}_{k}(\mathbf {x}) {:}{=}\sum _{i_1<i_2<\cdots < i_k} x_{i_1}x_{i_2}\cdots x_{i_k}. \end{aligned}$$

In this section, we use a bijective construction to prove that whenever $\lambda$ is a partition, we have $\mathrm {E}_\lambda ^\sigma (\mathbf {x};1,0) = \mathrm {e}_{\lambda '}(\mathbf {x})$. Note that this is independent of the basement $\sigma$, which, at a first glance, might be surprising.

Lemma 3.1

Let D be a diagram of shape $2^m 1^n$, where the first column has fixed distinct entries in $\mathbb {N}$. If $S\subseteq \mathbb {N}$ is a set of m integers, then there is a unique way of placing the entries in S into the second column of D, such that the resulting non-attacking filling has no coinversions.

Proof

We provide an algorithm for filling in the second column of the diagram. Begin by letting C be the topmost box in the second column and let L(C) be the box to the left of C. To pick an entry for C, we do the following:

If there is an element in S which is less than or equal to L(C), remove it from S and let it be the value of C.

Otherwise, remove the maximal element in S and let this be the value of C.

Iterate this procedure for the remaining entries in the second column while moving C downwards. It is straightforward to verify that the result is coinversion-free and that every choice for the element in the second column is forced.$\square$

Corollary 3.2

If $\lambda$ is a partition with at most n parts and $\sigma \in S_n$, then

$$\begin{aligned} \mathrm {E}_\lambda ^\sigma (\mathbf {x};1,0) = \mathrm {e}_{\lambda '}(\mathbf {x}). \end{aligned}$$

Proof

Fix a basement $\sigma$ and choose sets of elements for each of the remaining columns. Note that all such choices are in natural correspondence with the monomials whose sum is $\mathrm {e}_{\lambda '}(\mathbf {x})$. By applying the previous lemma inductively column by column, it follows that there is a unique filling with the specified column sets. The combinatorial formula now implies that $\mathrm {E}_\lambda ^\sigma (\mathbf {x};1,0) = \mathrm {e}_{\lambda '}(\mathbf {x})$ as desired.$\square$

We use a similar approach to give bijections among families of coinversion-free fillings of general composition shapes in [2].

Example 3.3

Here are the nine fillings associated with $\mathrm {E}_{210}^{132}(\mathbf {x};1,0)$. In other words, it is the set of non-attacking, coinversion-free fillings of shape (2, 1, 0) and basement 132:

The sum of the weights is $x_1^2x_2 + x_1^2x_3 + \cdots + x_2x_3^2 = \mathrm {e}_{210}(\mathbf {x})$.

4 The Factorization Property

Let $\lambda$ be a composition. The weak standardization of $\lambda$, denoted by ${\tilde{\lambda }}$, is the lex-smallest composition, such that, for all i, j, we have the following:

$$\begin{aligned} \lambda _i \le \lambda _j \Rightarrow {\tilde{\lambda }}_i \le {\tilde{\lambda }}_j. \end{aligned}$$

For example, $\lambda = (6,2,5,2,3,3)$ gives ${\tilde{\lambda }} = (3,0,2,0,1,1)$.

Lemma 4.1

If $\lambda = 1^m0^n$, then $\mathrm {E}^{\sigma }_{\lambda }(\mathbf {x};1,t) = \mathrm {e}_m(\mathbf {x}).$

Proof

We begin by showing this statement for $\sigma = \text {id}$.

Using Theorem 2.9, we have that $\mathrm {E}^{\text {id}}_{\lambda }(\mathbf {x};1,t)$ is symmetric in $x_1$, ..., $x_m$ and symmetric in $x_{m+1}$, ..., $x_{m+n}$. Furthermore, using the combinatorial formula, we can easily see that there is exactly one non-attacking filling of weight $\lambda$. This filling has major index 0. In other words:

$$\begin{aligned} \left[ \mathbf {x}^\lambda \right] \mathrm {E}^{\text {id}}_{\lambda }(\mathbf {x};1,t) = 1. \end{aligned}$$

It is, therefore, enough to show that the polynomial is symmetric in $x_m$ and $x_{m+1}$. A result in [10] implies that a polynomial f is symmetric in $x_m,x_{m+1}$ if and only if ${\tilde{\pi }}_m(f)=f$. Hence, it suffices to show that

$$\begin{aligned} {\tilde{\pi }}_m \mathrm {E}^{\text {id}}_{\lambda }(\mathbf {x};1,t) = \mathrm {E}^{\text {id}}_{\lambda }(\mathbf {x};1,t). \end{aligned}$$

Proposition 2.7 gives that

$$\begin{aligned} {\tilde{\pi }}_m \mathrm {E}^{\text {id}}_{\lambda }(\mathbf {x};1,t) = \mathrm {E}^{s_m}_{\lambda }(\mathbf {x};1,t). \end{aligned}$$

Hence, it remains to show that $\mathrm {E}^{\text {id}}_{\lambda }(\mathbf {x};1,t) = \mathrm {E}^{s_m}_{\lambda }(\mathbf {x};1,t)$. We do this by exhibiting a weight-preserving bijection between fillings of shape $\lambda$ with identity basement, and those with $s_m$ as basement. The bijection is given by simply permuting the basement labels in row m and $m+1$, since both coinversions and the non-attacking condition are preserved, so the result is a valid filling. Finally, since ${{\,\mathrm{arm}\,}}(u)=0$ for the box in position (m, 1), it is straightforward to verify that the weight is preserved under this map.

The statement for general $\sigma$ now follows by applying the basement-permuting operators ${\tilde{\pi }}_i$ repeatedly on both sides of the identity $\mathrm {E}^{\sigma }_{\lambda }(\mathbf {x};1,t) = \mathrm {e}_m(\mathbf {x})$. The right-hand side is unchanged, since these operators preserve symmetric functions. $\square$

We say that $\lambda \le \mu$ in the Bruhat order if there is a sequence of transpositions, $s_{i_1}\cdots s_{i_k}$, such that $s_{i_1}\cdots s_{i_k} \lambda = \mu$ and where each application of a transposition increases the number of inversions.

Lemma 4.2

If $\lambda$ and $\mu$ are compositions, such that $\lambda \le \mu$ in the Bruhat order, then the following implication holds:

$$\begin{aligned} \frac{ \mathrm {E}^{w_0}_{\lambda }(\mathbf {x};1, t) }{ \mathrm {E}^{w_0}_{{\tilde{\lambda }}}(\mathbf {x};1,t) } = F_\lambda (\mathbf {x}) \qquad \Longrightarrow \qquad \frac{ \mathrm {E}^{w_0}_{\mu }(\mathbf {x};1, t) }{ \mathrm {E}^{w_0}_{{\tilde{\mu }}}(\mathbf {x};1,t) } = F_\lambda (\mathbf {x}), \end{aligned}$$

where $F_\lambda (\mathbf {x})$ is any function symmetric in $x_1,\cdots ,x_n$.

Proof

It suffices to show the implication for any simple transposition, $s_i \lambda = \mu$ that increases the number of inversions. Suppose that

$$\begin{aligned} \mathrm {E}^{w_0}_{\lambda }(\mathbf {x};1, t) = F_\lambda (\mathbf {x}) \mathrm {E}^{w_0}_{{\tilde{\lambda }}}(\mathbf {x};1,t) \end{aligned}$$

for some composition $\lambda$. By Proposition 2.8, we note that the shape-permuting operator is the same on both sides for $q=1$. That is, for any composition $\lambda$ with $\lambda _i < \lambda _{i+1}$, we have the following:

$$\begin{aligned} \left( {\tilde{\theta }}_i + \frac{1-t}{1-t^{{{\,\mathrm{arm}\,}}u}} \right) \mathrm {E}^{w_0}_{\lambda }(\mathbf {x};1, t) = \mathrm {E}^{w_0}_{s_i\lambda }(\mathbf {x};1,t) \end{aligned}$$

and

$$\begin{aligned} \left( {\tilde{\theta }}_i + \frac{1-t}{1-t^{{{\,\mathrm{arm}\,}}u}} \right) F_\lambda (\mathbf {x}) \mathrm {E}^{w_0}_{{\tilde{\lambda }}}(\mathbf {x};1, t) = F_\lambda (\mathbf {x})\mathrm {E}^{w_0}_{s_i{\tilde{\lambda }}}(\mathbf {x};1, t), \end{aligned}$$

where ${{\,\mathrm{arm}\,}}(u)\ge 1$ has the same value in both diagrams $\lambda$ and ${\tilde{\lambda }}$. $\square$

To simplify typesetting of the upcoming proofs, we will sometimes use the notation:

$$\begin{aligned} \mathrm {E}\left[ (a_1)^{b_1}, \cdots , (a_k)^{b_k} \right] {:}{=}\mathrm {E}^{w_0}_\lambda (\mathbf {x};1,t), \end{aligned}$$

where $\lambda$ is the composition:

$$\begin{aligned} (\underbrace{a_1,\cdots ,a_1}_{b_1},\underbrace{a_2,\cdots ,a_2}_{b_2},\cdots , \underbrace{a_k,\cdots ,a_k}_{b_k}). \end{aligned}$$

Lemma 4.3

We have the identity:

$$\begin{aligned} \frac{ \mathrm {E}\left[ (1)^{b_1},(2)^{b_2}, \cdots , (k)^{b_k},(0)^{b_0} \right] }{ \mathrm {E}\left[ (0)^{b_1},(1)^{b_2}, \cdots , (k-1)^{b_k},(0)^{b_0}\right] } =\mathrm {e}_{b_1+\cdots +b_k}(\mathbf {x}). \end{aligned}$$

Proof

We prove this lemma by induction on k, where the base case $k=1$ is given by Lemma 4.1. For $k >1$, by Proposition 2.8 and a similar reasoning as in Lemma 4.2, it is enough to prove that

$$\begin{aligned} \frac{ \mathrm {E}\left[ (1)^{b_1},(0)^{b_0},(2)^{b_2}, \cdots , (k)^{b_k} \right] }{ \mathrm {E}\left[ (0)^{b_0+b_1},(1)^{b_2}, \cdots , (k-1)^{b_k}\right] } =\mathrm {e}_{b_1+\cdots +b_k}(\mathbf {x}). \end{aligned}$$

Furthermore, through repeated application of the Knop–Sahi recurrence [Eq. (2.3)], it suffices to prove that

$$\begin{aligned} \frac{ \mathrm {E}\left[ (1)^{b_2}, \cdots , (k-1)^{b_k},(1)^{b_1},(0)^{b_0}\right] }{ \mathrm {E}\left[ (0)^{b_2}, \cdots , (k-2)^{b_k},(0)^{b_0+b_1}\right] } =\mathrm {e}_{b_1+\cdots +b_k}(\mathbf {x}). \end{aligned}$$

Again using Proposition 2.8, we reduce the above to the $k-1$ case:

$$\begin{aligned} \frac{ \mathrm {E}\left[ (1)^{b_1+b_2}, \cdots , (k-1)^{b_k},(0)^{b_0}\right] }{ \mathrm {E}\left[ (0)^{b_1+b_2}, \cdots , (k-2)^{b_k},(0)^{b_0}\right] } =\mathrm {e}_{b_1+\cdots +b_k}(\mathbf {x}), \end{aligned}$$

which is true by induction. $\square$

Proposition 4.4

If $\lambda$ is a composition, then

$$\begin{aligned} \frac{ \mathrm {E}^{w_0}_{\lambda }(\mathbf {x};1, t) }{ \mathrm {E}^{w_0}_{{\tilde{\lambda }}}(\mathbf {x};1,t) } = F_\lambda (\mathbf {x}), \end{aligned}$$

where $F_\lambda (\mathbf {x})$ is an elementary symmetric polynomial.

Proof

We prove the proposition by induction on $|\lambda |$ and the number of inversions of $\lambda$. Note that the result is trivial if $|\lambda | \le 1$.

Given $\lambda$, there are several cases to consider:

Case 1: $\min _i\lambda _i \ge 1$. The result follows by inductive hypothesis on the size of the composition using Eq. (2.4) in the numerator.

Case 2: $\lambda$ is not weakly increasing. We can reduce this case to a composition with fewer inversions using Lemma 4.2.

Case 3: $\lambda$ is weakly increasing. It is enough to prove that

$$\begin{aligned} \frac{ \mathrm {E}\left[ (a_0)^{b_0}, \cdots , (a_k)^{b_k} \right] }{ \mathrm {E}\left[ (0)^{b_0}, \cdots , (k)^{b_k} \right] } \end{aligned}$$

is an elementary symmetric polynomial where $0=a_0<a_1<a_2<\cdots$. Using the cyclic shift relation (2.3) in the numerator and denominator, it suffices to show that

$$\begin{aligned} \frac{ \mathrm {E}\left[ (a_1-1)^{b_1},(a_2-1)^{b_2}, \cdots , (a_k-1)^{b_k}, (0)^{b_0} \right] }{ \mathrm {E}\left[ (0)^{b_1},(1)^{b_2}, \cdots , (k-1)^{b_k}, (0)^{b_0}\right] } \end{aligned}$$

(4.1)

is an elementary symmetric polynomial. If $a_1=1$, the result follows by the inductive hypothesis on the size of the composition. Otherwise, by rewriting Eq. (4.1), it is enough to prove that

$$\begin{aligned} \frac{ \mathrm {E}\left[ (a_1-1)^{b_1}, \cdots , (a_k-1)^{b_k}, (0)^{b_0} \right] }{ \mathrm {E}\left[ (1)^{b_1},(2)^{b_2}, \cdots , (k)^{b_k}, (0)^{b_0}\right] }\cdot \frac{ \mathrm {E}\left[ (1)^{b_1},(2)^{b_2}, \cdots , (k)^{b_k}, (0)^{b_0} \right] }{ \mathrm {E}\left[ (0)^{b_1},(1)^{b_2}, \cdots , (k-1)^{b_k}, (0)^{b_0}\right] } \end{aligned}$$

is an elementary symmetric polynomial. The first fraction is an elementary symmetric polynomial by induction, since it is of the right form with a smaller size. According to Lemma 4.2, the second fraction is also an elementary symmetric polynomial. $\square$

Theorem 4.5

If $\lambda$ is a composition and $\sigma \in S_n$, then

$$\begin{aligned} \frac{ \mathrm {E}^{\sigma }_\lambda (\mathbf {x};1,t) }{ \mathrm {E}^{\sigma }_{{\tilde{\lambda }}}(\mathbf {x};1,t) } = F_\lambda (\mathbf {x}), \end{aligned}$$

where $F_\lambda (\mathbf {x})$ is an elementary symmetric polynomial independent of t.

Proof

From Proposition 4.4, we have that

$$\begin{aligned} \mathrm {E}^{w_0}_\lambda (\mathbf {x};1,t) = F_\lambda (\mathbf {x}) \mathrm {E}^{w_0}_{{\tilde{\lambda }}}(\mathbf {x};1,t), \end{aligned}$$

where $F_\lambda$ is an elementary symmetric polynomial. Applying basement-permuting operators from Proposition 2.7 on both sides, then gives

$$\begin{aligned} \mathrm {E}^\sigma _\lambda (\mathbf {x};1,t) = F_\lambda (\mathbf {x}) \mathrm {E}^\sigma _{{\tilde{\lambda }}}(\mathbf {x};1,t). \end{aligned}$$

Note that applying a basement-permuting operator might give an extra factor of t, but, since $\lambda _{i} \le \lambda _{j}$ if and only if $\tilde{\lambda _{i}}\le \tilde{\lambda _{j}}$, these extra factors cancel. $\square$

We are now ready to prove the following surprising identity, which was first observed through computational evidence by J. Haglund and the first author.

Theorem 4.6

If $\lambda$ is a partition and $\sigma \in S_n$, then

$$\begin{aligned} \mathrm {E}^\sigma _\lambda (\mathbf {x};1,t) = \mathrm {E}^\sigma _{{\lambda }}(\mathbf {x};1,0)=\mathrm {e}_{\lambda '}(\mathbf {x}). \end{aligned}$$

Proof

It is enough to prove that $\mathrm {E}^{w_0}_\lambda (\mathbf {x};1,t)=\mathrm {e}_{\lambda '}(\mathbf {x})$ as the more general statement follows from using Proposition 2.7.

Using the previous theorem, it is enough to prove that

$$\begin{aligned} \frac{ \mathrm {E}\left[ (k)^{b_0},\cdots , (0)^{b_k} \right] }{ \mathrm {E}\left[ (k-1)^{b_0}, \cdots , (0)^{b_{k-1}+b_k}\right] }=\mathrm {E}\left[ (1)^{b_0+\cdots +b_{k-1}},(0)^{b_k}\right] . \end{aligned}$$

We show this via induction on k. The base case $k=1$ is trivial, so assume $k>1$ and note that repeated use of Proposition 2.8 implies that it is enough to prove that

$$\begin{aligned} \frac{ \mathrm {E}\left[ (k-1)^{b_1},\cdots , (0)^{b_k},(k)^{b_0} \right] }{ \mathrm {E}\left[ (k-2)^{b_1}, \cdots , (0)^{b_{k-1}+b_k},(k-1)^{b_0}\right] }=\mathrm {E}\left[ (1)^{b_0+\cdots +b_{k-1}},(0)^{b_k}\right] . \end{aligned}$$

Using the Knop–Sahi recurrence (2.3), it suffices to show that

$$\begin{aligned} \frac{ \mathrm {E}\left[ (k-1)^{b_0+b_1},\cdots , (0)^{b_k} \right] }{ \mathrm {E}\left[ (k-2)^{b_0+b_1}, \cdots , (0)^{b_{k-1}+b_k}\right] }=\mathrm {E}\left[ (1)^{b_0+\cdots +b_{k-1}},(0)^{b_k}\right] , \end{aligned}$$

which now follows from induction.$\square$

Corollary 4.7

The previous proof can be extended to show that

$$\begin{aligned} F_{\lambda }(\mathbf {x})=\frac{\mathrm {e}_{\lambda '}(\mathbf {x})}{\mathrm {e}_{({\tilde{\lambda }})'}(\mathbf {x})} \end{aligned}$$

for partition $\lambda$.

Note that the parts of $\lambda '$ are a superset of the parts of $({\tilde{\lambda }})'$, so the above expression is, indeed, some elementary symmetric polynomials.

Our results are in some sense optimal: for general compositions $\lambda$, it happens that $\mathrm {E}^\sigma _{{\tilde{\lambda }}}(\mathbf {x};1,t)$ cannot be factorized further. For example, Mathematica computations suggest that

$$\begin{aligned} \mathrm {E}^{(3,1,5,2,4)}_{(0,2,3,1,0)}(\mathbf {x};1,t) \text { and } \mathrm {E}^{(3,1,5,2,4)}_{(0,1,1,1,0)}(\mathbf {x};1,0) \end{aligned}$$

are irreducible.

4.1 Discussion

It is natural to ask whether or not there are bijective proofs of the identities which we consider.

Question 4.8

Is there a bijective proof of the case $\sigma =\omega _0$ of Theorem 4.5 that establishes

$$\begin{aligned} \mathrm {E}_{\lambda }(\mathbf {x};1, t)= \frac{\mathrm {e}_{\lambda '}(\mathbf {x})}{\mathrm {e}_{({\tilde{\lambda }})'}(\mathbf {x})} \mathrm {E}_{{\tilde{\lambda }}}(\mathbf {x};1,t)? \end{aligned}$$

Since a priori $\mathrm {E}^\sigma _{{\lambda }}(\mathbf {x};1,t)$ is only a rational function in t, this seems like a difficult challenge. We, therefore, pose a more conservative question:

Question 4.9

Is there a combinatorial explanation of the identity $\mathrm {E}^\sigma _\lambda (\mathbf {x};1,t) = \mathrm {e}_{\lambda '}(\mathbf {x})$ whenever $\lambda$ is a partition?

We finish this section by discussing properties of the family $\{\mathrm {E}_\lambda (\mathbf {x};1,0)\}$ as $\lambda$ ranges over compositions with n parts. It is a basis for $\mathbb {C}[x_1,\cdots ,x_n]$ and is a natural generalization of the elementary symmetric functions in the same manner the key polynomials extend the family of Schur polynomials. For example, in a recent paper [3], it is proved that $\mathrm {E}_\lambda (\mathbf {x};1,0)$ expands positively into key polynomials, where the coefficients are given by the classical Kostka coefficients. This generalizes the classical result that elementary symmetric functions expand positively into Schur polynomials. Furthermore, $\{\mathrm {E}_\lambda (\mathbf {x};q,0)\}$ exhibit properties very similar to those of modified Hall–Littlewood polynomials. In particular, these expand positively into key polynomials with Kostka–Foulkes polynomials (in q) as coefficients. There are representation–theoretical explanations for these expansions, as well, see [2, 3] and references therein for details.

It is known that the product of a Schur polynomial and a key polynomial is key-positive (see e.g. Proposition 5.8 below), and thus, the product of an elementary symmetric polynomial and a key polynomial is key-positive. It is, therefore, natural to ask if this extends to the non-symmetric elementary polynomials. However, a quick computer search reveals that

$$\begin{aligned} \mathrm {E}_{030}(\mathbf {x};1,0) \mathcal {K}_{201}(\mathbf {x}) \end{aligned}$$

does not expand positively into key polynomials.

5 Positive Expansions at $q=0$

By specializing the combinatorial formula [Eq. (2.2)] with $q=0$, we obtain a combinatorial formula for the permuted-basement Demazure t-atoms.

Example 5.1

As an example, $\mathcal {A}^{1423}_{2301}(x_1,x_2,x_3,x_4;t)$ is equal to

$$\begin{aligned}&(1-t) t \cdot x_1^2 x_2^3 x_3 + (1-t)\cdot x_1^2 x_2^2 x_3 x_4 + (1-t)^2 \cdot x_1^2 x_2 x_3^2 x_4 + (1-t) \cdot x_1^2 x_3^3 x_4\\&\quad + (1-t)\cdot x_1^2 x_2 x_3 x_4^2 + (1-t)\cdot x_1^2 x_3^2 x_4^2 + x_1^2 x_3 x_4^3, \end{aligned}$$

where the corresponding fillings are as follows:

In this section, we show how to construct permuted-basement Demazure t-atoms via Demazure–Lusztig operators. First, consider Proposition 2.7 and Proposition 2.8 at $q=0$. Note that Proposition 2.8 simplifies, where we use the fact that ${\tilde{\theta }}_i +(1-t) = {\tilde{\pi }}_i$. Hence, the shape-permuting operator reduces to a basement-permuting operator. This “duality” between shape and basement was first observed at $t=0$ in [21], where S. Mason gave an alternative combinatorial description of key polynomials which is not immediate from the combinatorial formula for the non-symmetric Macdonald polynomials. A similar duality holds for general values of t, see [1].

To get a better overview of Propositions 2.7 and 2.8, we present the statements as actions on the basement and shape as follows:

Example 5.2

The operators ${\tilde{\pi }}_i$ and ${\tilde{\theta }}_i$ act as follows on diagram shapes and basements. Note that we only care about the relative order of row lengths. A box with a dot might either be present or not, indicating weak or strict difference between row lengths:

The operators acting on the shape can be described pictorially as follows:

which are easily obtained from Proposition 2.8 at $q=0$, together with the fact that ${\tilde{\theta }}_i {\tilde{\pi }}_i = t$.

The following proposition also appeared in [1]; however, the proof that we present here is different and more constructive.

Proposition 5.3

Given a composition $\lambda$ with n parts and a permutation $\sigma \in S_n$, there is a sequence of operators ${\tilde{\rho }}_{i_1}, \cdots ,{\tilde{\rho }}_{i_\ell }$, such that

$$\begin{aligned} \mathcal {A}_\lambda ^\sigma (\mathbf {x};t) = {\tilde{\rho }}_{i_1}\cdots {\tilde{\rho }}_{i_\ell } \mathbf {x}^{\mathrm {par}(\lambda )}, \end{aligned}$$

(5.4)

where $\mathrm {par}(\lambda )$ is the partition with the parts of $\lambda$ in decreasing order and each operator ${\tilde{\rho }}_{i_j}$ is in the set $\big \{ {\tilde{\theta }}_1,\cdots , {\tilde{\theta }}_{n-1}, {\tilde{\pi }}_1,\cdots , {\tilde{\pi }}_{n-1} \big \}$.

Proof

Given $(\sigma ,\lambda )$, let the number of monotone pairs be the number of pairs (i, j), such that

$$\begin{aligned} \sigma _i< \sigma _j \text { and } \lambda _i < \lambda _j \qquad \text { or } \qquad \sigma _i > \sigma _j \text { and } \lambda _i \ge \lambda _j. \end{aligned}$$

We do induction over the number of monotone pairs. First note that if there are no monotone pairs in $(\sigma ,\lambda )$, then the longest row has basement label 1, the second longest row has basement label 2 and so on. It then follows that every row in a filling with basement $\sigma$ and shape $\lambda$ has to be constant, implying that $\mathcal {A}_\lambda ^\sigma (\mathbf {x};t) = \mathbf {x}^\lambda$.

Assume that there are some monotone pairs determined by $(\sigma ,\lambda )$. A permutation with at least one inversion must have a descent, and for a similar reason, there is at least one monotone pair of the form:

These match the right-hand sides of (5.2) and (5.1). By induction, $\mathcal {A}_\lambda ^\sigma (\mathbf {x};t)$ can, therefore, be obtained from some $\mathcal {A}_\lambda ^{\sigma s_i}(\mathbf {x};t)$ by applying either ${\tilde{\pi }}_i$ or ${\tilde{\theta }}_i$. $\square$

Example 5.4

We illustrate the above proposition by expressing $\mathcal {A}^{3142}_{3102}(\mathbf {x};t)$ in terms of operators. The shape and basement associated with this atom is given in the first augmented diagram in (5.5):

The rows with labels 2 and 3 constitute a monotone pair and can be obtained using (5.2), which explains the ${\tilde{\pi }}_2$-arrow. Continuing on with ${\tilde{\pi }}_1$ followed by ${\tilde{\theta }}_2$ leads to an augmented diagram without any monotone pairs, so $\mathcal {A}^{1342}_{3102}(\mathbf {x};t) = \mathbf {x}^{(3,2,1,0)}$. Finally, following the arrows yields the operator expression:

$$\begin{aligned} \mathcal {A}^{3142}_{3102}(\mathbf {x};t) = {\tilde{\pi }}_2 {\tilde{\pi }}_1 {\tilde{\theta }}_2 \mathbf {x}^{(3,2,1,0)}. \end{aligned}$$

Proposition 5.5

If $\sigma = s_i \tau$ with ${{\,\mathrm{\ell }\,}}(\sigma )>{{\,\mathrm{\ell }\,}}(\tau )$, then

$$\begin{aligned} \mathcal {A}^{\sigma }_\lambda (\mathbf {x};t) = {\left\{ \begin{array}{ll} \mathcal {A}^{\tau }_{s_i\lambda }(\mathbf {x};t) + t^{{{\,\mathrm{stat}\,}}(\lambda ,\sigma ,i)}(1-t)\mathcal {A}^{\tau }_\lambda (\mathbf {x};t), &{}\text { if } \lambda _{i} > \lambda _{i+1}, \\ \mathcal {A}^{\tau }_{s_i\lambda }(\mathbf {x};t), &{}\text { otherwise}, \end{array}\right. } \end{aligned}$$

(5.6)

where ${{\,\mathrm{stat}\,}}(\lambda ,\sigma ,i)$ is a non-negative integer depending on $\lambda$, $\sigma$, and i.

Proof

We prove this statement via induction over ${{\,\mathrm{\ell }\,}}(\tau )$.

Case $\tau = {{\,\mathrm{id}\,}}$ and $\lambda _{i} \le \lambda _{i+1}$: We need to show that $\mathcal {A}^{s_i}_\lambda (\mathbf {x};t) = \mathcal {A}^{{{\,\mathrm{id}\,}}}_{s_i\lambda }(\mathbf {x};t)$. Since ${\tilde{\pi }}_i$ is invertible, it suffices to show that

$$\begin{aligned} {\tilde{\pi }}_i \mathcal {A}^{s_i}_\lambda (\mathbf {x};t) = {\tilde{\pi }}_i \mathcal {A}^{{{\,\mathrm{id}\,}}}_{s_i\lambda }(\mathbf {x};t). \end{aligned}$$

This equality now follows from using (5.3) on the left-hand side and (5.2) on the right-hand side.

Case $\tau = {{\,\mathrm{id}\,}}$ and $\lambda _{i} > \lambda _{i+1}$: It suffices to prove that

$$\begin{aligned} \mathcal {A}^{s_i}_\lambda (\mathbf {x};t) = \mathcal {A}^{{{\,\mathrm{id}\,}}}_{s_i\lambda }(\mathbf {x};t) + (1-t)\mathcal {A}^{{{\,\mathrm{id}\,}}}_\lambda (\mathbf {x};t). \end{aligned}$$

Note that the left-hand side is equal to ${\tilde{\pi }}_i \mathcal {A}^{{{\,\mathrm{id}\,}}}_\lambda (\mathbf {x};t)$ using (5.2), while the left-hand side is equal to $[{\tilde{\theta }}_i + (1-t)] \mathcal {A}^{{{\,\mathrm{id}\,}}}_\lambda (\mathbf {x};t)$ where we use (5.3). Since ${\tilde{\pi }}_i = [{\tilde{\theta }}_i + (1-t)]$, this proves the identity.

This proves the base case. The general case now follows from applying ${\tilde{\pi }}_j$ on both sides, thus, increasing the lengths of the basements. We examine the details in the following two cases.

Case $\tau \in S_n$ and $\lambda _{i} \le \lambda _{i+1}$: suppose $\mathcal {A}^{\sigma }_\lambda (\mathbf {x};t) = \mathcal {A}^{\tau }_{s_i\lambda }(\mathbf {x};t)$. As diagrams, we have the equality:

for rows i and $i+1$, $b>a$, while the remaining rows are identical. If ${{\,\mathrm{\ell }\,}}(\sigma s_j) > {{\,\mathrm{\ell }\,}}(\sigma )$, we can conclude that if $a=j$, then $b \ne j+1$. We now compare the row lengths of the rows with basement label j and $j+1$ and apply the basement-permuting ${\tilde{\pi }}_j$ from (5.2) on both sides. Note that the row lengths that are compared are the same on both sides, meaning that if we need (5.2) to increase the basement on the left-hand side, the same relation acts the same way on the right-hand side. In other words, we have the implication:

$$\begin{aligned} \mathcal {A}^{\sigma }_\lambda (\mathbf {x};t) = \mathcal {A}^{\tau }_{s_i\lambda }(\mathbf {x};t) \quad \Longrightarrow \quad \mathcal {A}^{\sigma s_j}_\lambda (\mathbf {x};t) = \mathcal {A}^{\tau s_j}_{s_i\lambda }(\mathbf {x};t), \end{aligned}$$

whenever ${{\,\mathrm{\ell }\,}}(\sigma s_j) > {{\,\mathrm{\ell }\,}}(\sigma )$ and $\lambda _{i} \le \lambda _{i+1}$.

Case $\tau \in S_n$ and $\lambda _{i} > \lambda _{i+1}$: Again, suppose that we have the diagram identity:

for some $\lambda$, $\sigma$, and that ${{\,\mathrm{\ell }\,}}(\sigma s_j) > {{\,\mathrm{\ell }\,}}(\sigma )$. As in the previous case, if $a=j$, then $b \ne j+1$. If $j \notin \{a-1,a,b-1,b\}$, applying ${\tilde{\pi }}_j$ on both sides yields the implication:

$$\begin{aligned} \mathcal {A}^{\sigma }_\lambda (\mathbf {x};t)&= \mathcal {A}^{\tau }_{s_i\lambda }(\mathbf {x};t) + t^{{{\,\mathrm{stat}\,}}(\lambda ,\sigma ,i)}(1-t)\mathcal {A}^{\tau }_\lambda (\mathbf {x};t) \\&\Longrightarrow \\ \mathcal {A}^{\sigma s_j}_\lambda (\mathbf {x};t)&= \mathcal {A}^{\tau s_j}_{s_i\lambda }(\mathbf {x};t) + t^{{{\,\mathrm{stat}\,}}(\lambda ,\sigma ,i)}(1-t)\mathcal {A}^{\tau s_j}_\lambda (\mathbf {x};t), \end{aligned}$$

because—depending on the relative row lengths of the rows with basement labels j, $j+1$—we either multiply each of the three terms by t or not at all.

It remains to verify the cases $j \in \{a-1,a,b-1,b\}$. Case-by-case study after applying ${\tilde{\pi }}_j$ on both sides shows that

$$\begin{aligned} \mathcal {A}^{\sigma s_j}_\lambda (\mathbf {x};t) = \mathcal {A}^{\tau s_j}_{s_i\lambda }(\mathbf {x};t) + t^{\epsilon +{{\,\mathrm{stat}\,}}(\lambda ,\sigma ,i)}(1-t)\mathcal {A}^{\tau s_j}_\lambda (\mathbf {x};t), \end{aligned}$$

where (using the same notation as in Proposition 2.7, $\gamma _i$ being the length of the row with basement label i):

• $\epsilon = -1$ if $j=a-1$ and $\gamma _a > \gamma _{a-1} \ge \gamma _b$,

• $\epsilon = 1$ if $j=a$ and $\gamma _a \ge \gamma _{a+1} > \gamma _b$,

• $\epsilon = 1$ if $j=b-1$ and $\gamma _a > \gamma _{b-1} \ge \gamma _b$,

• $\epsilon = -1$ if $j=b$ and $\gamma _a \ge \gamma _{b+1} > \gamma _b$,

and $\epsilon =0$ otherwise. Thus, we have that

$$\begin{aligned} \mathcal {A}^{\sigma s_j}_\lambda (\mathbf {x};t) - \mathcal {A}^{\tau s_j}_{s_i\lambda }(\mathbf {x};t) = t^{\epsilon +{{\,\mathrm{stat}\,}}(\lambda ,\sigma ,i)}(1-t)\mathcal {A}^{\tau s_j}_\lambda (\mathbf {x};t), \end{aligned}$$

where the left-hand side is a polynomial. Furthermore, $\mathcal {A}^{\tau s_j}_\lambda (\mathbf {x};t)$ is not a multiple of t—this follows from the combinatorial formula (2.2). Hence, $\epsilon +{{\,\mathrm{stat}\,}}(\lambda ,\sigma ,i)$ must be non-negative.$\square$

Corollary 5.6

If $\tau \ge \sigma$ in Bruhat order, then $\mathcal {A}^{\tau }_\gamma (\mathbf {x};t)$ admits the expansion:

$$\begin{aligned} \mathcal {A}^{\tau }_\gamma (\mathbf {x};t) = \sum _{\lambda :\mathrm {par}(\lambda ) = \mathrm {par}(\gamma ) } c^{\tau \sigma }_{\gamma \lambda }(t) \mathcal {A}^{\sigma }_\lambda (\mathbf {x};t), \end{aligned}$$

where the $c^{\tau \sigma }_{\gamma \lambda }(t)$ are polynomials in t, with the property that $c^{\tau \sigma }_{\gamma \lambda }(t) \ge 0$ whenever $0\le t \le 1$.

Corollary 5.7

If $\tau \ge \sigma$ in Bruhat order, then $\mathcal {A}^{\tau }_\gamma (\mathbf {x})$ admits the expansion:

$$\begin{aligned} \mathcal {A}^{\tau }_\gamma (\mathbf {x}) = \sum _{\lambda :\mathrm {par}(\lambda ) = \mathrm {par}(\gamma ) } c^{\tau \sigma }_{\lambda \gamma } \mathcal {A}^{\sigma }_\lambda (\mathbf {x}), \quad \text { where }\quad c^\sigma _{\lambda \gamma } \in \{0,1\}. \end{aligned}$$

Proof

Let $t=0$ in (5.6). It is then clear that all coefficients are non-negative integers. Furthermore, since key polynomials $(\tau = \omega _0)$ expand into Demazure atoms $(\sigma = {{\,\mathrm{id}\,}})$ with coefficients in $\{0,1\}$ (see e.g., [16, 21]), the statement follows. $\square$

In [13], the cases $\sigma = {{\,\mathrm{id}\,}}$ and $\sigma =\omega _0$ of the following proposition were proved. We give an interpolation (in the Bruhat order) between these results. Recall that $\mathbf {x}= (x_1,\cdots ,x_n)$, so we evaluate $\mathrm {s}_\mu (\mathbf {x})$ in a finite alphabet.

Proposition 5.8

The coefficients $d^{\mu \sigma }_{\lambda \gamma }$ in the expansion

$$\begin{aligned} \mathrm {s}_\mu (\mathbf {x}) \times \mathcal {A}^\sigma _\lambda (\mathbf {x}) = \sum _{\gamma } d^{\mu \sigma }_{\lambda \gamma } \mathcal {A}^\sigma _\gamma (\mathbf {x}) \end{aligned}$$

are non-negative integers.

Proof

With the case $\sigma ={{\,\mathrm{id}\,}}$ as a starting point (proved in [13]), we can apply $\pi _i$ on both sides, ($\pi _i$ commutes with any symmetric function, in particular $\mathrm {s}_\lambda (\mathbf {x})$), and thus, we may walk upwards in the Bruhat order and obtain the statement for any basement $\sigma$. Note that Proposition 2.7 implies that $\pi _i$ applied to $\mathcal {A}^\sigma _\gamma (\mathbf {x})$ either increases $\sigma$ in Bruhat order, or kills that term. $\square$

Note that the above result implies that the products $\mathrm {e}_\mu \times \mathcal {A}^\sigma _\lambda (\mathbf {x})$ and $h_\mu \times \mathcal {A}^\sigma _\lambda (\mathbf {x})$ also expand non-negatively into $\sigma$-atoms. It would be interesting to give a precise rule for this expansion, as well as a Murnaghan–Nakayama rule for the permuted-basement Demazure atoms.

Remark 5.9

We need to mention the paper [17], which also concerns a different type of general Demazure atoms. These objects are also studied in [13], but are, in general, different from ours when $\sigma \ne {{\,\mathrm{id}\,}}$. In particular, the polynomial families which they study are not bases for $\mathbb {C}[x_1,\cdots ,x_n]$, and they are not compatible with the Demazure operators. The authors of [13, 17] construct these families by imposing an additional restriction¹ on Haglund’s combinatorial model, which enables them to perform a type of RSK.

The introductions of both the papers [13, 17] mention the permuted-basement Macdonald polynomials $\mathrm {E}^\sigma _\mu (\mathbf {x};q,t)$. However, the additional restriction imposed further on breaks this connection whenever $\sigma \ne {{\,\mathrm{id}\,}}$. This fact is unfortunately hidden, since the same notation, ${\hat{E}}_\gamma$, is used for two different families of polynomials.