Introduction

Active suspension systems have become an integral part of modern-day automobiles for providing passengers better ride comfort and minimizing vehicle tires’ wear and tear. Designing controller strategies for active suspension systems to improve ride quality under road disturbance conditions is a major challenging task for the automobile industry and academicians. Many researchers have proposed conventional and artificial intelligence-based techniques for the last few decades.

Gordon [1] proposed a non-quadratic cost function-based optimum control technique for semi-active vehicle suspension systems for minimizing suspension deflection and body acceleration during bumpy and random road conditions. Hrovat [2] presented a detailed survey of active suspension's advanced developments and control techniques from quarter car vehicle models to full car models. Baumal et al. [3] developed a genetic algorithm-based approach for designing active suspension system parameters to minimize the vehicle body acceleration. Kuo and Li [4] proposed a genetic algorithm-based optimum fuzzy PI/PD controller design for a four-wheeler’s active suspension system to improve the passengers' ride quality. Lin and Lian [5] developed a hybrid fuzzy and neural networks-based intelligent controller to improve the ride comfort of the car and service life of the active suspension system. Prabhakar et al. [6] proposed non dominated sorting genetic algorithm (NSGA II)-based multiobjective approach for improving the active suspension system of a car considering a half-car vehicle model with a magnetorheological damper. Du and Zhang [7] proposed the H infinity control technique for active suspension systems with an actuator time delay to minimize sprung mass acceleration, suspension deflection and tyre deflection. Gao et al. [8] proposed robust sample data-based H-infinity control technique for uncertain active vehicle suspension systems. Lu and DePoyster [9] developed a control technique based on H-two and H-infinity norms for minimizing vehicle body acceleration and tyre deflection derivatives. Koch and Kloiber [10] proposed an adaptive vehicle suspension system to adjust the controller parameters dynamically to enhance ride comfort and maintain the suspension deflection within safety limits. Vaijayanti et al. [11] designed a disturbance observer-based sliding mode controller to improve the vehicle’s active suspension system performance in terms of sprung mass displacement and acceleration. Li et al. [12] designed a reliable fuzzy H-infinity controller for active suspension systems with actuator delay and fault. Deshpande et al. [13] developed a nonlinear control law for an active suspension system to improve passenger ride comfort and minimize the suspension deflection of a four-wheeler vehicle. Gampa and Das [14] proposed a PSO-based optimum P–I–D controller design methodology considering the objective of minimizing sprung mass acceleration to improve the dynamics of the active suspension system. They developed MATLAB Simulink-based models for the active suspension system and bump road disturbances in their methodology. Pan et al. [15] developed an adaptive tracking control strategy for active suspension systems to improve the vehicle's dynamic performance in the presence of external disturbances. Na et al. [16] proposed an adaptive control technique for active suspension systems with unknown nonlinear sprung mass and damper dynamics.

Utkarsh et al. [17] proposed a sliding mode control technique based on linear disturbance observer for active suspension systems with nonideal actuators. Cao et al. [18] proposed a multiobjective H-infinity parameterized controller using Lyapunov and symbolic computation for vehicle active suspension systems. Na et al. [19] developed a novel control technique for active suspension systems with unknown nonlinearities using suspension error for full-car active suspension systems with unknown nonlinearities without function approximation. Li et al. [20] proposed a Pareto optimality-based particle swarm optimization approach for the active suspension system of electric vehicles for compensating electromechanical coupling effects. Reza and Mortaza [21] have developed an interval type 2 fractional order fuzzy controller for a tractor active suspension system to minimize the fluctuations due to uneven road surfaces. Zhao et al.[22] developed an adaptive radial basis function neural network for an active suspension system with actuator saturation to deal with the parametric uncertainties and road disturbances. Moradi and Fekih [23] designed an adaptive PID sliding mode-based fault-tolerant controller to handle the uncertainties and actuator faults for an active suspension system. Liu et al.[24] proposed adaptive neural network controller for active suspension systems considering time-varying constraints. Chen and Huang [25] proposed an adaptive sliding mode controller for active suspension systems with time-varying loads. Guimin et al. [26] developed a new regenerative active suspension system with dual actuators Based on the advanced-dynamic-damper mechanism for in-wheel motor-driven electric vehicles, Sun et al. [27] proposed a multiobjective-based adaptive backstepping control strategy for vehicle active suspension systems considering time-domain constraints. Min et al. [28] developed an adaptive fuzzy inverse optimal output feedback control strategy for vehicular active suspension systems with unknown nonlinearities. Min et al. [29] developed an adaptive fuzzy optimal controller for active suspension systems with nonlinearities and dynamic characteristics. Taghavifar et al. [30] designed a state observer-based sliding mode interval fuzzy type 2 neural network controller to mitigate the vibrations of a nonlinear suspension system. Ghazally et al. [31] proposed particle swarm optimization-based model free fuzzy intelligent PID controller. Hurel et al. [32] proposed a fuzzy PSO-based algorithm to improve the dynamics of the active suspension system.

So far, many researchers have used a conventional weighted multiobjective approach for solving the active suspension system problem considering the objectives of minimizing suspension deflection, tyre deflection and sprung mass acceleration minimization. In the present work, in addition to the above objectives, eigenvalue-based stability objective is also considered for improving the active suspension system stability. In the multiobjective approach, when some of the objectives are decreasing and others are increasing in nature, the weighted objective function approach is not suitable. Therefore, in such a case, Pareto multiobjective is very effective. In the present work, the objectives of suspension deflection, tyre deflections and acceleration are decreasing nature and the eigenvalue stability-based objective function is increasing in nature. Hence, grasshopper optimization and Pareto multiobjective approach is considered for improving the vehicle's active suspension system dynamics.

The following assumptions and constraints have been considered [33]

  • The vehicle body is considered to be rigid.

  • The suspension system is modeled with spring and damper system, and their behavior is assumed to be linear.

  • Single point contact has been assumed between the wheel and rail of the vehicle.

  • In this work, quarter vehicle model for the active suspension system is considered for state space modeling.

State space modeling of active suspension system for quarter vehicle model

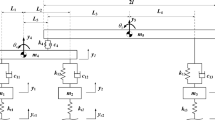
An active suspension system can be modeled considering the quarter-vehicle car model, as shown in Fig. 1. The active suspension system model consists of a mass spring damper system with an actuator which provides the required control force to the suspension system. The actuator is modeled as an ideal force generator neglecting the dynamics.

Fig. 1
figure 1

Quarter vehicle active suspension system

Full size image

The dynamics of the sprung and unsprung masses of the quarter-vehicle suspension system can be derived from Newton’s second law and expressed by the following equations

$$M_{{{\text{SM}}}} \ddot{Z}_{{{\text{SM}}}} + K_{{\text{s}}} \left( {Z_{{{\text{SM}}}} - Z_{{{\text{UM}}}} } \right) + C_{{\text{d}}} \left( {\dot{Z}_{{{\text{SM}}}} - \dot{Z}_{{{\text{UM}}}} } \right) - F_{{\text{a}}} = 0$$
(1)
$$M_{{{\text{UM}}}} \ddot{Z}_{{{\text{UM}}}} + K_{{\text{s}}} \left( {Z_{{{\text{UM}}}} - Z_{{{\text{SM}}}} } \right) + C_{{\text{d}}} \left( {\dot{Z}_{{{\text{UM}}}} - \dot{Z}_{{{\text{SM}}}} } \right) + K_{{\text{t}}} \left( {Z_{{{\text{UM}}}} - Z_{{\text{r}}} } \right) + F_{{\text{a}}} = 0$$
(2)

where MSM and MUM are sprung mass and unsprung mass, representing mass of car chassis and wheel assembly, respectively. Ks is the suspension spring stiffness constant, and Cd is the damping coefficient of the suspension system. Kt is the stiffness of the pneumatic tyre. ZSM and ZUM are the vertical displacements of sprung mass and unsprung mass, respectively. Zr is the displacement of the tyre from the base-level position.

In the present work, grasshopper optimization-based PID controller is designed to improve the performance of the active suspension system. The state space model of the active suspension system with the PID controller can be developed with the help of vertical dynamic equations described by Eqs. (1) and (2), and the block diagram is shown in Fig. 2.

Fig. 2
figure 2

State space modeling of active suspension system

Full size image

The actuator force Fa is generated from the output of the PID controller and can be written as follows

$$F_{{\text{a}}} = K_{{\text{p}}} e(t) + K_{{\text{i}}} \int {e(t){\text{d}}t} + K_{{\text{d}}} \frac{{{\text{d}}(e(t))}}{{{\text{d}}t}}$$
(3)

where Kp, Ki and Kd are the proportional, integral and derivative gains of the PID controller and the e(t) is the error function.

The state variables for the quarter vehicle model with PID controller-based active suspension system, including the road inputs, are chosen as follows:

$$X_{1} = Z_{{{\text{SM}}}} \;{\text{is}}\;{\text{the}}\;{\text{sprung}}\;{\text{mass}}\;{\text{of}}\;{\text{the}}\;{\text{vehicle}}$$
(4)
$$X_{2} = Z_{{{\text{UM}}}} \;{\text{is}}\;{\text{the}}\;{\text{displacement}}\;{\text{of}}\;{\text{unsprung}}\;{\text{mass}}$$
(5)
$$X_{3} = \dot{Z}_{{{\text{SM}}}} \;{\text{is}}\;{\text{the}}\;{\text{sprung}}\;{\text{mass}}\;{\text{vertical}}\;{\text{velocity}}$$
(6)
$$X_{4} = \dot{Z}_{{{\text{UM}}}} \;{\text{is}}\;{\text{the}}\;{\text{unsprung}}\;{\text{mass}}\;{\text{vertical}}\;{\text{velocity}}$$
(7)
$$X_{5} = K_{{\text{i}}} \int {e(t){\text{d}}t} .$$
(8)

The input to the P–I–D controller law can be written as an error function by the following equation.

$$e(t) = R_{{{\text{ref}}}} - \left( {X_{1} - X_{2} } \right)$$
(9)

The state space model can be described by the following state equation,

$$\dot{X} = AX + BR$$
(10)

where X and R are state and input vectors, respectively, and P and \(\Gamma\) are constant matrices of an active suspension system with the P–I–D controller.

$$X^{\prime } = {[}X_{1} ,X_{2} ,X_{3} ,X_{4} ,X_{5} {]}$$
(11)
$$R^{\prime } = \left[ {R_{{{\text{ref}}}} \;R_{{\text{d}}} } \right]$$
(12)

\(R_{{{\text{ref}}}}\) and \(R_{{\text{d}}}\) are reference input and road disturbance of the active suspension system. The \(X^{\prime }\) and \(R^{\prime }\) are transpose matrices of X and R.

$$A = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ {\frac{{ - (K_{{\text{p}}} + K_{{\text{s}}} )}}{{M_{{{\text{SM}}}} }}} & {\frac{{(K_{{\text{p}}} + K_{{\text{s}}} )}}{{M_{{{\text{SM}}}} }}} & {\frac{{ - (K_{{\text{d}}} + C_{{\text{d}}} )}}{{M_{{{\text{SM}}}} }}} & {\frac{{(K_{{\text{d}}} + C_{{\text{d}}} )}}{{M_{{{\text{SM}}}} }}} & {\frac{1}{{M_{{{\text{SM}}}} }}} \\ {\frac{{(K_{{\text{p}}} + K_{{\text{s}}} )}}{{M_{{{\text{UM}}}} }}} & {\frac{{ - (K_{{\text{p}}} + K_{{\text{s}}} + K_{{\text{t}}} )}}{{M_{{{\text{UM}}}} }}} & {\frac{{(C_{{\text{d}}} - K_{{\text{d}}} )}}{{M_{{{\text{UM}}}} }}} & {\frac{{( - C_{{\text{d}}} + K_{{\text{d}}} )}}{{M_{{{\text{UM}}}} }}} & {\frac{ - 1}{{M_{{{\text{UM}}}} }}} \\ { - K_{{\text{i}}} } & {K_{{\text{i}}} } & 0 & 0 & 0 \\ \end{array} } \right]$$
(13)
$$B = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ {\frac{{K_{{\text{p}}} }}{{M_{{{\text{SM}}}} }}} & 0 \\ {\frac{{ - K_{{\text{p}}} }}{{M_{{{\text{UM}}}} }}} & {\frac{{K_{{\text{t}}} }}{{M_{{{\text{UM}}}} }}} \\ {K_{{\text{i}}} } & 0 \\ \end{array} } \right]$$
(14)

The constant matrices A and B of the active suspension system are derived from the block diagram shown in Fig. 2 and are represented with Eqs. (13) and (14).

The discrete form of state equation can be written for the continuous form state equation by the following equation [34].

$$X\;[(k + 1)T] = \Phi \;X\;[(k)T] + \Psi \;R\;[(k)T]$$
(15)

where

$$\Phi \, = \, e^{AT}$$
(16)
$$\Psi = \left( {e^{AT} - I} \right) \, A^{ - 1} B.$$
(17)

In general, many road disturbances are due to bumpy roads. The bumpy road disturbances that appear with high intensity will cause severe distress to the passengers and may also lead to loss of holding of the road surface. The road disturbances are modeled with simple sinusoidal functions for studying the dynamic performance of the vehicle suspension system on a rough road.

The road disturbance with one bump (Rd1) can be modeled by the following equation.

$$R_{{{\text{d}}1}} (t) = \left\{ {\begin{array}{*{20}l} {\frac{H}{2}\left( {1 - \cos \left( {2\pi \left( {\frac{t}{{T_{b} }}} \right)} \right)} \right),} \hfill & {{\text{for}}\;t_{{{\text{st}}}} \le t \le t_{{{\text{end}}}} } \hfill \\ 0 \hfill & {{\text{Otherwise}}} \hfill \\ \end{array} } \right.$$
(18)

where Rd1(t) is the bump road disturbance with a single bump. Tb is the bump duration. The starting and ending times of the bumps are tst and tend. H is the height of the bump.

The road disturbance with two bumps (Rd2) of different magnitudes is modeled using sinusoidal functions, and the expression is shown in Eq. (19).

$$R_{{{\text{d}}2}} (t) = \left\{ {\begin{array}{*{20}l} {\frac{{H_{1} }}{2}\left( {1 - \cos \left( {2\pi \left( {\frac{t}{{T_{1} }}} \right)} \right) } \right),} \hfill & {{\text{for}}\;t_{{{\text{st}}1}} \le t \le t_{{{\text{end}}1}} } \hfill \\ {\frac{{H_{2} }}{2}\left( {1 - \cos \left( {2\pi \left( {\frac{t}{{T_{2} }}} \right)} \right) } \right),} \hfill & {{\text{for}}\;t_{{{\text{st}}2}} \le t \le t_{{{\text{end}}2}} } \hfill \\ 0 \hfill & {{\text{Otherwise}}} \hfill \\ \end{array} } \right.$$
(19)

Rd2 is the bump road disturbance with two bumps. H1 and H2 are the heights of the first bump and second bump. T1 and T2 are the durations of first bump and second bump. The starting and ending times of first bump are tst1 and tend1. The starting and ending times of the second bump are tst2 and tend2.

Multiobective function formulation

In the present work, Pareto multiobjective approach-based PID controller design methodology is proposed for improving the vehicle active suspension system dynamics. The PID controller gains are tuned using the grasshopper optimization technique. Furthermore, the Pareto multiobjective-based methodology is compared with the genetic algorithm-based conventional weighted multiobjective function.

The following equations define the objectives functions suspension deflection, tyre deflection, sprung mass acceleration, and eigenvalue stability. The role of the active suspension system is to improve ride comfort by minimizing the acceleration and the tyre and suspension deflections.

The suspension deflection (ZSD) is defined as the difference between the vertical displacement of the sprung mass and the unsprung mass.

$$Z_{{{\text{SD}}}} (k) = \left( {X_{1} (k) - X_{2} (k)} \right)$$
(20)

The excessive vertical movement of the vehicle wheel results in hard impact with body of the vehicle. To maintain quality ride and conformability, the suspension deflections of the vehicle during the bump road disturbance period should be minimized as little as possible. The performance index for minimizing suspension deflection JSD can be expressed by the following equation.

$$J_{{{\text{SD}}}} = \sum\limits_{k = 1}^{N} {\left( {Z_{{{\text{SD}}}} (k)} \right)^{2} }$$
(21)

JSD is the performance index of the suspension deflection and can be calculated by the sum of N samples considered during the period crossing the bump road disturbance.

Excessive tyre deflections lead to poor contact between the tyre and the road surface (for the tyre extended) and hence a reduced ability to control the vehicle, for example, during braking. The tyre deflection (ZTD) is the difference between the vertical displacement of unsprung mass and road input.

$$Z_{{{\text{TD}}}} (k) = \left( {X_{2} (k) - R_{{\text{d}}} (k)} \right)$$
(22)

The following equation shows the performance index for minimizing the tyre deflection.

$$J_{{{\text{TD}}}} = \sum\limits_{k = 1}^{N} {\left( {Z_{{{\text{TD}}}} (k)} \right)^{2} }$$
(23)

JTD is the performance index of the tyre deflection calculated from the N samples considering road disturbance input.

The sprung mass acceleration can be calculated from the following expression.

$$\ddot{Z}_{{{\text{SM}}}} (k) = \frac{{(X_{3} (k) - X_{3} (k - 1))}}{T}$$
(24)

The performance objective for minimizing the vertical acceleration of the sprung mass can be expressed by the following equation.

$$J_{{{\text{VA}}}} = \sum\limits_{k = 1}^{N} {\left( {\ddot{Z}_{{{\text{SM}}}} (k)} \right)^{2} }$$
(25)

JVA is the sum of the acceleration samples calculated over N samples.

Conventional weighted multiobjective function

For formulating a multiobjective function, all the above objectives are normalized with respect to passive suspension system performance. The normalized conventional weighted multiobjective [35] function (JC) can be formulated as follows:

$$J_{{\text{C}}} = W_{1} \, \frac{{J_{{{\text{SD}}}}^{A} }}{{J_{{{\text{SD}}}}^{P} }} + W_{2} \, \frac{{J_{{{\text{TD}}}}^{A} }}{{J_{{{\text{TD}}}}^{P} }} + W_{3} \, \frac{{J_{{{\text{VA}}}}^{A} }}{{J_{{{\text{VA}}}}^{P} }}.$$
(26)

In the above expression, W1, W2 and W3 are weighting factors for the three objective functions considered and can be selected based on the importance given to the objective functions. In the present case, equal importance is considered for all the objectives. The \(J_{{{\text{VA}}}}^{A}\) is the objective function for acceleration in the case of an active suspension system, and \(J_{{{\text{VA}}}}^{P}\) is the objective function for vehicle acceleration in the case of a passive suspension system.

Pareto-based multiobjective function formation

An active suspension system is a multiobjective problem where suspension deflection and ride quality are equally important. In addition, the system's stability with a controller should also be satisfactory for the successful function of the active suspension system. In the present case, the objectives are suspension deflection, vehicle acceleration and tyre deflection. In addition to the three objectives mentioned, it is also essential to consider the stability of the system. The system is said to be stable if all the eigenvalues lie on the s plane’s left half. Furthermore, the real values of the eigenvalues must be far from the origin. Hence the following objective function is considered to improve the stability of the vehicle’s active suspension system with a PID controller.

$$\zeta = \max ({\text{real}}(\lambda_{i} );\;i = 1,2, \ldots n$$
(27)
$$J_{{{\text{EV}}}} = \left\{ {\begin{array}{*{20}l} {\left| \zeta \right|} \hfill & {{\text{if}}\;\zeta < 0} \hfill \\ 0 \hfill & {{\text{if}}\;\zeta > 0} \hfill \\ \end{array} } \right.$$
(28)

where \(\lambda_{i}\) is the ith eigenvalue of the system. JEV is the eigenvalue-based objective function to improve the stability of the system. A solution is said to be Pareto optimal if and only if all the objectives are improved compared to the solution obtained in the previous iteration [36].

The Pareto objective set can be defined as

$$J_{{\text{P}}}^{m} = \, \left[ {J_{{{\text{SD}}}}^{m} ,\;J_{{{\text{TD}}}}^{m} ,\;J_{{{\text{VA}}}}^{m} ,\;J_{{{\text{EV}}}}^{m} } \right].$$
(29)

According to Pareto optimality, the (m + 1)th solution vector \(J_{{\text{P}}}^{m + 1}\) is a better solution than the mth solution vector if and only if at least one of the Pareto objectives related to (m + 1)th solution vector must be improved over the mth solution vector \(J_{{\text{P}}}^{m}\) while the others retain their advantage. The Pareto optimality conditions on four objectives considered are shown by the following equations.

If m is the iteration number, the solution \(J_{{\text{P}}}^{m + 1}\) is Pareto optimal only when all the following conditions are satisfied.

$$J_{{{\text{SD}}}}^{m + 1} \le J_{{{\text{SD}}}}^{m}$$
(30)
$$J_{{{\text{TD}}}}^{m + 1} \le J_{{{\text{TD}}}}^{m}$$
(31)
$$J_{{{\text{VA}}}}^{m + 1} \le J_{{{\text{VA}}}}^{m}$$
(32)
$$J_{{{\text{EV}}}}^{m + 1} \ge J_{{{\text{EV}}}}^{m}$$
(33)

The Pareto objectives for suspension deflection, tyre deflection and vehicle acceleration must be less than the previous generation's best values before moving to next generation while the eigenvalue-based objective must be greater than the previous generation's best value to improve the system's stability.

Tuning of PID controller using the grasshopper optimization algorithm

The grasshopper optimization algorithm [37, 38] is a bioinspired evolutionary optimization technique [39] developed by imitating the swarming behavior of grasshoppers hunting for food. The positions of the grasshopper are dependent on the social behavior, gravitational impact and wind advection. The position of the grasshopper, influenced by the three factors, i.e., social, gravitational and wind forces, can be modeled mathematically by the following equation.

$$X_{m} = S_{m} + G_{m} + W_{m}$$
(34)

where Xm is the mth grasshopper position in the search domain. Sm is the influence factor of social behavior. Gm and Wm are the gravitational force and wind force effects on the mth grasshopper.

$$S_{m} = \sum\limits_{\begin{subarray}{l} n = 1 \\ n \ne m \end{subarray} }^{NG} {s\left( {D_{mn} } \right)} \frac{{\left( {x_{n} - x_{m} } \right)}}{{D_{mn} }}$$
(35)
$$s(t) = fe^{ - t/\tau } - e^{ - t}$$
(36)

In the above Eqs. (35) and (36), Dmn is the distance between mth and nth grasshopper, and the ‘s’ function represents the social forces. In the present work, the values of f and τ are taken 0.5 and 1.5 in the algorithm. The gravitational force factor Gm is negligible as the mass of the grasshoppers are not significant, and the wind advection factor Wm is considered as the global best of the swarm.

In this work, the PID controller parameters are required to be tuned to satisfy the Pareto objectives for improving the performance quality of the active suspension system. The minimum and maximum limits the PID controller gains KP, KI and KD are considered separately for improving the flexibility in tuning the parameters using GOA optimization algorithm. Hence the equations for updating the gain parameters in the GOA algorithm are considered separately for proportional, integral and derivative gains.

$$x_{m}^{k} = C\left( {\sum\limits_{\begin{subarray}{l} n = 1 \\ n \ne m \end{subarray} }^{NG} {C\frac{{(x_{\max }^{k} - x_{\min }^{k} )}}{2}s\left( {D_{mn}^{P} } \right)\frac{{\left( {x_{n}^{k} - x_{m}^{k} } \right)}}{{D_{mn}^{P} }}} } \right) + x_{{{\text{gbest}}}}^{k} \,$$
(37)
$$C = C_{\max } - {\text{itr}}\frac{{C_{\max } - C_{\min } }}{{{\text{itr}}_{\max } }}$$
(38)

In the above Eq. (37), \(x_{m}^{k}\) is the mth position of the kth variable in the swarm population where the variables k = 1, 2,3 corresponding to the proportional, integral and derivative gains. \(D_{mn}^{k}\) is Euclidean distance between mth and nth position of the kth variable, and \(x_{{{\text{gbest}}}}^{k}\) is the global best value of kth variable population upto the current iteration. The constants Cmax and Cmin are taken as 1 and 0.00001.

Step-by-step algorithm for P–I–D controller tuning using GOA

The proposed Pareto optimality-based PID controller design using GOA is explained by the following step-by-step algorithm.

Step-1: Read vehicle active suspension system data.

Step-2: Initialize the population vector for P–I–D controller gains for Kp, KI and Kd.

Step-3: Set generation count gen = 1.

Step-4: Evaluate the objectives JSD, JTD, JVA and JEV for each member of the population.

Step-5: Apply Pareto optimality conditions among the first generation population and identify the Global best.

Step-6: Set generation count gen = gen + 1.

Step-7: Update the population vector.

Step-8: Evaluate the objectives JSD, JTD, JVA and JEV for each member of the population of current generation.

Step-9: Apply Pareto optimality conditions for the current population comparing with the global best solution of the previous generation.

Step-10: Update the global best value.

Step-11: If gen < MaxGen, go to step-6 otherwise go to Step-12.

Step-12: Store the Results.

The procedure for optimum P–I–D controller design for vehicle active suspension system using Pareto-based multiobjective function and grasshopper optimization algorithm is given in the flowchart shown in Fig. 3.

Fig. 3
figure 3

Flowchart for tuning of PID controller using GOA

Full size image

Results and discussions

This work proposes optimum P–I–D controller tuning using the grasshopper optimization technique for improving vehicle active suspension system dynamics considering the Pareto optimality-based multiobjective approach. The objectives considered are suspension deflection, tyre deflection, vertical acceleration of sprung mass and eigenvalue stability of the state space model. The optimization is performed with bump road disturbance, and the performance is analyzed for both single bump and double bump disturbances. In this work, a quarter vehicle active suspension system model is considered and the parameters [32] are shown in Table 1.

Table 1 Parameters of active suspension system [32]
Full size table

For the present analysis of the vehicle dynamics, a bump road disturbance of height (H) 0.04 m and length (L) 5 m is chosen and the vehicle velocity (V) is considered as 18 km/h. The duration of the bump Tb1 is (L/V) and is 1 s in the present case. The time interval for vehicle crossing the bump road is taken for 2–3 s. The bump road disturbance with a single bump is shown in Fig. 4.

Fig. 4
figure 4

Road disturbance with a single bump

Full size image

The optimum P–I–D controller gains for improving the dynamics of the active suspension system are obtained using grasshopper optimization algorithm using the Pareto multuobjective function described by Eqs. (27) to (32). The performance is compared with GA-based conventional multiobjective function described by Eq. (26). The PID controller gains obtained with Pareto-based GOA algorithm are Kp = 25,897, Ki = 1500 and Kd = 1000. The PID controller gains obtained with GA-based conventional objective function are Kp = 1765.70, Ki = 189.14 and Kd = 884.97.

The convergence of the Pareto objectives using GOA while obtaining optimum PID controller gains for the active suspension system is shown in Fig. 5.

Fig. 5
figure 5

Pareto objectives using GOA

Full size image
Fig. 6
figure 6

Conventional objective function using GA

Full size image

The convergence of the conventional objective function with GA is shown in Fig. 6.

Fig. 7
figure 7

Comparison of results for suspension deflection

Full size image

The simulation results for suspension deflection dynamics with proposed Pareto objective-based GOA and conventional GA-based approach are compared in Fig. 7. From Fig. 7, it can be observed that with the proposed GOA-based approach the suspension deflection of the active suspension system significantly reduced compared to GA-based approach and passive suspension system. In the present work, the state space modeling is developed for the total active suspension system with the P–I–D controller incorporated. The P–I–D controller gains Kp, Ki and Kd are part of the developed state space modeling matrices A and B represented by Eqs. (13) and (14). The controller gains Kp, Ki and Kd are obtained by the proposed Pareto GOA approach considering the objectives of minimizing suspension deflection, tyre deflection and suspension acceleration and improving eigenvalue stability when the bump road input (Rd) is given as disturbance. The bump road disturbance (Rd) mentioned by the state space modeling represented in Eqs. (10) and (11) is modeled by the sinusoidal equations given by Eqs. (18) and (19). The performance improvement shown in Figs. 7, 8 and 9, and the stability improvement shown in Table 2 is obtained by the optimum P–I–D controller gains obtained using proposed Pareto GOA-based multiobjective approach for the bump road input shown in Fig. 4.

Fig. 8
figure 8

Comparison of results for tyre deflection

Full size image
Fig. 9
figure 9

Comparison of results for sprung mass acceleration

Full size image
Table 2 Eigenvalues of the suspension system
Full size table

The dynamics for tyre deflection and sprung mass acceleration are shown in Figs. 8 and 9. From Figs. 8 and 9, it can be observed that the with PID-based active suspension system tyre deflection and sprung mass acceleration are improved compared to passive suspension system. From Figs. 8 and 9, it can also be observed that the active suspension system’s performance in tyre deflection and acceleration is almost similar to the proposed GOA- and GA-based optimum PID controllers.

The eigenvalues of the passive and active suspension system with GOA- and GA-based methods are shown in Table 2.

From Table 2, it can be observed that the stability of the active suspension system is much better since the real eigenvalue is much farther with the proposed Pareto-based methodology compared to other methods considered for comparison.

In the conventional weighted objective approach, the overall sum of all the normalized objectives improvement only considered. Hence, there may be chance of some of the objectives may be even less better than the previous iteration even though overall multiobjective function may be improved compared to the previous iteration. In the case of Pareto optimality multiobjective approach, the optimum parameters are updated if and only if all the objectives considered independently are improved compared to the previous iteration. From Fig. 7, it can be observed that the suspension deflection reduction is much better with the proposed Pareto multiobjective-based GOA approach. From Figs. 8 and 9, it can be observed that the tyre deflection and suspension acceleration are almost similar to conventional approach. From Table 2, it can be observed that the stability of the system with proposed Pareto-based GOA approach is much better compared to conventional-based approach. Out of the four objectives considered, the main objectives suspension deflection reduction and stability of the system are improved to much better extent with the proposed Pareto-based GOA while slightly better performance in the case of tyre deflection and sprung mass acceleration. Hence, the proposed Pareto GOA multiobjective technique is much better compared to GA-based conventional approach.

The optimum P–I–D controller gains are obtained for single sinusoidal bump road disturbance shown in Fig. 4 using proposed GOA-based Pareto multiobjective approach for minimizing the suspension and tyre deflections and improving stability. For the same P–I–D controller gains, the robustness of the controller is tested for two bumps of different heights as shown in Fig. 10.

Fig. 10
figure 10

Road disturbance with two bumps

Full size image

In this case, a second bump with height 0.06 m during the between 6 and 7 s is considered in addition to the first bump. The performance comparisons of the active suspension system for road disturbance with two bumps are shown in Fig. 11.

Fig. 11
figure 11

Comparison of results with two bumps for suspension deflection

Full size image

From Fig. 11, it can be observed that the performance of the Pareto objectives-based optimum PID controller obtained using GOA is much better even in the case of road disturbance with two bumps for the same controller gains compared to conventional GA methodology.

Conclusions

In this work, Pareto optimality conditions and grasshopper optimization algorithm-based methodology are proposed for optimum P–I–D controller design for improving the performance of the active suspension system. For improving the vehicle ride comfort and minimizing wear and tear of tyres under road disturbance conditions, the objectives of minimization of suspension deflection, tyre deflection and sprung mass acceleration are considered. For improving the stability of the system under different bump road disturbance conditions, the Eigenvalue-based objective function is included in the Pareto optimality. The Pareto optimality has the advantage of simultaneously handling the objectives of increasing and decreasing nature. The simulation results show that the dynamic performance of the active suspension system is much better with the proposed approach in the case of suspension deflection and stability compared to the GA-based conventional objective technique. The dynamics of tyre deflection and sprung mass acceleration are almost similar with conventional and Pareto objective-based approaches. It can also be observed that the suspension deflection, tyre deflection and sprung mass acceleration successfully converged with the proposed GOA and Pareto optimality technique while improving the eigenvalue-based objective which increases to improve the stability. The proposed P–I–D controller's robustness is successfully verified for the road disturbances with two bumps for the same gains obtained with a single road bump disturbance.