Abstract
Stability of nominal frequency and voltage level in an electric power system is the primary control issue of practicing engineers. Any deterioration in these two parameters will affect the performance and life expectancy of the associated machinery to the power system. Hence, controllers are installed and set for a specific working situation and deal with small variations in load demand to keep the frequency and terminal voltage magnitude within the permissible limits. As the system performance can be improved with selecting suitable controller, an attempt has been made to design fractional-order PID (FOPID) controller for combined frequency and voltage control problems. This paper presents plan and execution examination of FOPID controller for simultaneous load frequency and voltage control of power system using recently developed nature-motivated powerful optimization technique, i.e., moth flame optimization algorithm. The first part of the present work demonstrates the implementation of the proposed technique on frequency stabilization of isolated power system with AVR for excitation voltage control. The superiority and effectiveness of the proposed approach are tested by comparing the dynamic response of the system with PID controllers optimized by other intelligent techniques. Then the present work is extended to multi-unit two-area power system. The tuning ability of the algorithm is extensively and comparatively investigated.
Similar content being viewed by others
Introduction
Stability of nominal frequency and voltage level in an electric power system is the primary control issue of practicing engineers. Any deterioration in these two parameters will affect the performance and life expectancy of the associated machinery to the power system. In power system, controllers are installed and set for a specific working situation and deal with small variations in load demand to keep the frequency and terminal voltage magnitude within the permissible limits. Therefore, two numbers of loops are provided for each generator. The load frequency control (LFC) loop regulates the real power and frequency, whereas the automatic voltage regulator (AVR) loop takes care of the reactive power and voltage magnitude [1, 2]. Earlier, researchers have done a study on LFC [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23] and AVR loop [24,25,26,27,28,29,30,31,32,33,34,35,36,37] independently. Because the prime mover time constant is much higher than the excitation system time constant, the transients in the excitation system settle down quickly and never influence the LFC dynamics. However, the two loops are not in the most genuine sense non-communicating [2]. When the end consumer’s demands vary, both frequency and voltage change. The control action in AVR loop influences the magnitude of the generator voltage, and the voltage magnitude decides the value of real power. Recently, researchers have started focusing on combined LFC-AVR control problem [38, 39].
Various controllers such as classical, optimal, adaptive and robust controller are proposed for LFC study [3,4,5,6,7,8,9]. Similarly, adaptive optimal control design for AVR is proposed in Ref. [24]. PID controllers have wide application in industries on account of its simple concept and robustness. The only limitation is the tuning of controller parameters. But, this problem is solved by recent development of intelligent techniques. The authors have reported intelligent techniques, for example, GA, particle swarm optimization (PSO), firefly algorithm (FA) and grey wolf optimization (GWO) algorithm for improvement of system performance [15,16,17,18,19, 30,31,32,33,34,35,36]. A few authors suggested hybrid technique and achieved excellent dynamic performance of the framework [20, 21]. On the way of development of new techniques, few researchers have reported different structures of PID controllers such as variable structure controller, integral–double derivative controller, two-degree-of-freedom PID controller, PID plus second-order derivative controller with filter, fractional-order controller and FP + FI + FD controller for LFC and AVR for improvement of dynamic performance of the system [22, 23, 25,26,27,28,29]. Also, the progress in soft computing technique such as artificial neural network (ANN) and fuzzy logic has solved many problems in LFC and AVR [10,11,12,13,14]. A few among the previous works listed have been based on independent control of LFC and AVR loop for system performance improvement. The combined control of frequency and excitation voltage has been proposed for single-area power system in [38]. The LFC loop is equipped with fuzzy-based secondary PID controller. A comparison is made between power system stabilizer (PSS)-controlled AVR and PID-controlled AVR. The examination sets up that the PSS-controlled AVR system is significantly heartier in stabilizing the effect of disturbances in the system over an extensive range of system configuration. The joint LFC-AVR of multi-unit multi-area system applying simulated annealing (SA) technique is proposed in [39]. The system performance is judged by comparing the results with Zeigler Nichol’s (ZN) optimized PID controller and without secondary controller. The restriction of the work is that the tuning of the AVR controller parameters is finished by ZN technique and LFC secondary controller parameters’ tuning is performed by SA algorithm.
In perspective of the above literature review, the present work proposes combined LFC and AVR strategy for the development of the dynamic response of the system. Both the LFC and AVR controller parameters are optimized by recently developed nature-inspired powerful optimization technique, i.e., moth flame optimization (MFO) algorithm [40]. The motivation behind preferring the MFO algorithm is that it requires least number of controlling parameters (i.e., number of search agents and number of iterations), which make it simple, effective, faster convergence mobility for optimum global solutions. The convergence of the MFO algorithm for finding the solution of the problem is ensured in light of the fact that the moths constantly refresh their positions with respect to flames that are the most encouraging solutions obtained so far finished the course of emphases. The MFO algorithm is successfully used for designing of LFC for multi-unit multi-region power systems, and also its superiority is proven [41, 42]. As the system performance can also be improved with selecting suitable controller, an attempt has been made to design fractional-order PID (FOPID) controller for combined LFC and AVR study. In FOPID controllers the order of derivative and integral is not an integer. These controllers have been successfully applied by researchers in different fields of engineering, such as designing aerospace control systems [43], hypersonic flight vehicle [44], AVR system [45, 46] and LFC study [47,48,49,50]. The FO controller provides greater control flexibility for system dynamics and has good disturbance rejection capability than PID controller.
Methods
The details of contributions of the present works are as follows:
- (a)
An intelligent application of moth flame optimization algorithm is done for combined LFC and AVR of power systems.
- (b)
The significance of different objective functions such as integral of absolute error (IAE), integral of time-multiplied absolute error (ITAE), integral of squared error (ISE) and integral of time-multiplied squared error (ITSE) is studied in combined LFC and AVR control perspectives.
- (c)
The first part of the present work demonstrates the implementation of the proposed technique on frequency stabilization of isolated power system with AVR for excitation voltage control.
- (d)
The superiority and effectiveness of the proposed approach are tested by comparing the dynamic response of the system with PID/FOPID controllers optimized by other intelligent techniques.
- (e)
Then the present work is extended to multi-unit two-area power system. The tuning ability of the algorithm is extensively and comparatively investigated.
Thus, the first part of the present work demonstrates the implementation of the proposed MFO-tuned FOPID control technique on frequency stabilization of isolated power system with AVR for excitation voltage control. The prevalence and adequacy of the proposed methodology are tested by looking at the system dynamic response with PSO, differential evolution (DE) and GWO-tuned PID controllers. Then the present work is extended to multi-source multi-area power system with combined LFC and AVR loop. The analysis results on performance of the proposed MFO-tuned controller are accounted with the results of latest publications such as ZN- and SA-tuned controllers for the same power system. Followed by the introduction in “Introduction” section and methods in “Methods” section, “Modeling of the system” section discusses the modeling of power system with LFC and AVR loop. Then, “Controller structure and objective function” section discusses the formulation of the present optimization work. The overview of optimization technique is presented in “Overview of MFO algorithm” section. Results and discussion are given in “Results and discussion” section. At the end, conclusion is being drawn in “Conclusions” section.
Modeling of the system
Load frequency control model
This section details the dynamic model of LFC loop [2]. The power system mainly comprises generator, turbine and speed-governing framework. The two inputs are the controller input \(\Delta P_{\text{ref}}\) and load disturbance \(\Delta P_{\text{D}}\). The outputs are variations of the generator frequency \(\Delta \omega\) and area control error (ACE).
The transfer function of the turbine and governor is given in Eqs. (1) and (2), respectively.
where \(T_{\text{T}}\) is the turbine time constant, \(\Delta P_{\text{T}}\) is the change in turbine power output and \(\Delta P_{\text{V}}\) is the change in input power to the turbine.
where \(T_{\text{G}}\) is the governor time constant and \(\Delta P_{\text{G}}\) is the change in governor power output.The rotating mass is sensitive to the frequency change and can be analyzed by speed load characteristic as given below,
where \(\Delta \omega\) is change in frequency and \(H\) is inertia constant.The \(\Delta P_{\text{G}}\), the reference input \(\Delta P_{\text{ref}}\) and \(\Delta \omega\) can be correlated by Eq. (4).
where \(R\) is the speed regulation of governor.The frequency biased factor \(\left( B \right)\) is sum of frequency-sensitive load change (D) and speed regulation as given below,
AVR system model
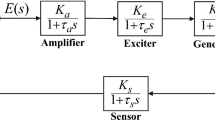
An AVR holds the terminal voltage of a synchronous generator at a predetermined level. A basic AVR system incorporates four fundamental components, such as sensor, amplifier, exciter and generator. The input and output relationship of an amplifier, exciter, generator and sensor models is provided in Eqs. (6), (7), (8) and (9), respectively.
Amplifier model
The values of gain \(K_{\text{a}}\) are in the range of 10–400, and the amplifier time constant \(T_{\text{a}}\) is ranging from 0.02 to 0.1 s.
Exciter model
The values of gain \(K_{\text{e}}\) are in the limit between 10 and 400, and the exciter time constant \(T_{\text{e}}\) is ranging from 0.5 to 1.0 s.
Generator model
The values of gain \(K_{\text{field}}\) may vary between 0.7 and 1.0, and the time constant \(T_{\text{field}}\) ranges from 1.0 to 2.0 s.
Sensor model
The value of gain \(K_{\text{S}}\) is around 1.0, and the time constant \(T_{\text{S}}\) is ranging from 0.001 to 0.06 s.
Relation of LFC and AVR model
If AVR model is taken into consideration by including the small effect of voltage upon real power, then the generator load system has one more input \(\Delta P_{\text{Real}} (s)\) along with \(\Delta P_{\text{T}} (s)\) and \(\Delta P_{\text{D}} (s)\), with one output \(\Delta \omega\) given by,
where
Additionally, including the small effect of rotor angle upon the generator terminal voltage, the equation can be written as follows:
The modification of the generator field transfer function to include the effect of rotor angle and the stator emf can be expressed as follows:
where \(K_{1} ,\,K_{2} ,\,K_{3} \,{\text{and}}\,K_{4}\) are constants. A linearized transfer function model for the combined LFC and AVR system is shown in Figs. 1 and 2.
Controller structure and objective function
One of the most well-known controllers available commercially is PID controller which is used to improve the dynamic response as well as to minimize steady-state error.
The transfer function of PID controller is expressed as follows in Eq. (14):
where \(K_{\text{P}}\), \(K_{\text{I}}\) and \(K_{\text{D}}\) are the proportional, integral and derivative gains of the controller, respectively.For FOPID controller, the above equation is written as follows:
where \(\lambda\) and \(\mu\) indicate order of integration and differentiation, respectively, and its values lie in the range [0, 1]. Also, the additional FO controller parameters \(\lambda\) and \(\mu\) approach better flexibility and system dynamics than integer-order PID controller. If \(\lambda = 1\) and \(\mu = 1\), the equation may be reduced to integer-order PID controller. The structure of FOPID controller is shown in Fig. 3. The MATLAB/Simulink block of FOPID controller is shown in Fig. 4.
The FO differ-integers are basically infinite number of poles and zeroes. From the practical point of view, band-limited realizations of FO controllers are necessary. However, an approximation with a finite number of poles and zeroes can be obtained using the CRONE approximation proposed by Oustaloup [42, 43]. The higher-order filter having an order of \(\left( {2N + 1} \right)\), which approximates the FO elements \(s^{\alpha }\) within a selected frequency band \(\left[ {\omega_{\text{L}} ,\,\omega_{\text{H}} } \right]\), can be written as follows Eq. (16):
where \(\alpha\) is the order of differentiation–integration and \(\left( {2N + 1} \right)\) is the order of the approximation filter. \(K\) is the gain, and \(\omega_{\text{k}}^{{\prime }}\) and \(\omega_{\text{k}}\) define the zeros and poles of the analog filter, respectively, and can be recursively found as follows:
The present work considers a fifth-order Oustaloup’s approximation for all the FO elements within the frequency range of \(\omega \in \left\{ {10^{ - 3} ,\,10^{3} } \right\}\) rad/s.
In the design of the controller parameters, the objective function is initially characterized in view of the desired specifications and constraints. Common yield determinations in time domain are maximum overshoot, rise time, settling time and steady-state errors. The execution criteria normally fixed in control configuration are the IAE, ITAE, ISE and ITSE. These criteria in the frequency domain have their own specific purposes of interest and impediments. These criteria are formulated as follows:
where \(e(t)\) is the error function.The objective function \(J\) for controller parameters optimization of the power system is depicted below:
In the above equation, \(\Delta \omega\) is the system frequency deviation and \(\Delta V_{\text{t}}\) is the change in terminal voltage.The objective function \(J\) for controller parameters optimization of the interconnected power system is depicted below.
In the above equation, \(\Delta F_{1}\) and \(\Delta F_{2}\) are the system frequency deviations in respective area 1 and 2; \(\Delta P_{\text{tie}}\) is the incremental variation in tie-line power. \(t_{\text{sim}}\) is the simulation time. Thus, the optimization problem can be formulated as follows:
Overview of MFO algorithm
The MFO algorithm depends on the route strategy of moths in nature [40]. Those fly in night by keeping up an adjusted edge with respect to the moon, a particularly convincing instrument for going in a straight line for long separations. The moths fly in spiral route and follow the light, when the light source is very near. The moth in the long run centers toward the light. If moths are to be considered as search agents and flames to be the solution, then the solution can be reached very quickly through this algorithm. The details of the algorithm are given in [40, 41]. The controller parameters to be tuned by proposed algorithm are the search agents. Keeping in view minimum objective function in Eq. (26), the initial solution matrix for controller parameters is formed. The objective function is minimized by MFO algorithm by optimizing the controller parameters. The inputs to the MFO program are the errors (\(\left| {\Delta \omega } \right|\,\,{\text{and}}\,\,\left| {\Delta V_{\text{t}} } \right|\) or \(\left| {\Delta F_{1} } \right|,\left| {\Delta F_{2} } \right|,\left| {\Delta P_{\text{tie}} } \right|,\left| {\Delta V_{{{\text{t}}1}} } \right|\,\,\,{\text{and}}\,\,\,\left| {\Delta V_{{{\text{t}}2}} } \right|\)), and outputs are the controller parameters values (KP, KI, KD, λ and µ). The objective value is calculated in the Simulink model file and transferred to .mfile through workspace. The objective function values are used to access the populations. The best agent is chosen in each iteration with minimum objective function value, and over the course of iterations the best position is evaluated and ranking of agents are done. The optimal variables (gains) of the controller are found from the best agents at the end of the iterations.
The following steps are involved in the proposed algorithm:
The arrangement of moths spoke to in a lattice frame is as given below:
where the number of moths and the number of variables (dimensions) are denoted by \(n\) and \(d\), respectively.
For all the moths, the corresponding fitness values can be sorted in an array form as follows:
A framework like the moth matrix and flame matrix is considered as:
The dimensions of \(M\) and \(F\) arrays are equal. For the flames, the corresponding fitness values can be sorted in an array form as follows:
It ought to be noted here that moths and flames are both potential solutions. The moths are real pursuit operators that navigate around the search space, whereas flames are the best position for moths that gets so far. In this way, every moth seeks around a flag (flame) and updates it if there should arise an occurrence of finding a superior solution.
The MFO algorithm has three fundamental parts that gauge the arrangement and might be expressed as follows:
The \(I\) generates a random population of moths and corresponding fitness value. It may be expressed as follows:
The \(P\) function is the function that decides the movement of the moths around the search space. This function eventually returns to its updated form of the matrix of \(M\) after receiving it.
The \(T\) function returns true if the termination criterion is satisfied and otherwise false.
Then, the function \(I\) has to compute the objective function values after generating initial solutions.
There are two other arrays that define the upper and the lower bounds of the variables (\({\text{ub}}\) and \({\text{lb}}\)). The matrixes may be stated as follows:
where \({\text{ub}}_{i}\) represents the upper bound of the \(i{\text{th}}\) variable.
where \({\text{lb}}_{i}\) represents the lower bound of the \(i{\text{th}}\) variable.
The position of each of the moths is updated with respect to a flame using the equation stated below:
where \(M_{i}\) indicates the \(i{\text{th}}\) moth, \(F_{j}\) indicates the \(j{\text{th}}\) flame and \(S\) is the spiral function.
Keeping in mind the starting point, end point and boundary condition, a logarithmic spiral is defined for the MFO algorithm as presented in Eq. (19). It defines the next position of a moth with respect to a flame:
where \(D_{i}\) shows the distance of the \(i{\text{th}}\) moth for the \(j{\text{th}}\) flame, \(b\) is a constant for representing the shape of the logarithmic spiral and \(t\) is a random number in \(\left[ { - 1,\,\,1} \right]\). The variable \(D_{i}\) may be calculated as follows:
The best solutions acquired so far are considered as the flames and stored in \(F\) matrix. The number of flames is diminished adaptively over the course of iterations as follows:
where \(l\) is the current number of iteration, \(N\) is the maximum number of flames and \(T\) indicates the maximum number of iterations. In the initial steps of iterations, there is \(N\) number of flames. The moths update their positions just as for the best flame in the last steps of iterations.
The variables named \(K_{\text{P}}\), \(K_{\text{I}}\) and \(K_{\text{D}}\) in PID controller and \(K_{\text{P}}\), \(K_{\text{I}}\), \(K_{\text{D}}\),\(\lambda\) and \(\mu\) in FOPID controller are tuned by proposed algorithm, keeping in view minimum objective function in Eq. (24). The best agent is selected in each iteration with minimum objective function, and over the course of iterations, the best position is evaluated and ranking of agents are done. The optimal variables (gains) of the controller are found from the best agents at the end of the iterations.
Results and discussion
Implementation of proposed control strategy to isolated power system
The system under consideration as appeared in Figs. 1 and 2 is created in MATLAB/Simulink environment. The model is a coordinated LFC and AVR loop of an isolated power system subjected to a step load perturbation (SLP) of 0.01 per unit. The model of AVR subsystem is shown in Fig. 2. Both the LFC and AVR loops’ controller gains are optimized using PSO, DE, GWO and MFO algorithm. The mentioned algorithm programs are written in (.mfile). The selected parameters of controllers are within the range [0, 2]. In this work, the parameters of MFO are taken as: population size = 20, maximum iteration = 100. For deciding the ideal values of the weights of the controller, IAE, ITAE, ISE and ITSE are considered as objective function. Since intelligent techniques are stochastic in nature, the optimization procedure is run for 30 times. The best controller gains owing to the least objective function as fitness score among 30 independent simulations are presented in Table 1. Simulation studies are done keeping in mind the best performance of the PID controller optimized using different cost functions. The performance criteria of the framework in terms of peak overshoot, undershoot and settling time are given in Table 2. Figure 5a, b shows frequency and terminal voltage response of the system, respectively. The results show that minimum settling time is found when ITAE is taken as objective function. However, when ISE is considered as a fitness function peak overshoot reduced, but the obtained values are very near when ITAE is used as target function. Hence, ITAE is selected as targeted index for further analysis.
The execution of MFO technique for optimizing controller parameters can be analyzed from dynamic response of the system. The corresponding controller parameters obtained from different techniques and performance indices in terms of peak overshoot, minimum undershoot, settling time (2% tolerance band) and ITAE objective values are presented in Table 2. For comparison, the responses of the system with PSO, DE, GWO and MFO algorithms are shown in Fig. 6a, b. It is clear from Fig. 6a, b and validated from Table 2 that the adopted fractional-order control mechanism outperforms the others in terms of performance indices mentioned above. The frequency oscillation of the system neutralizes in faster rate and settles very quickly with SLP. The voltage profile also improves. Comparison of simulation results for different techniques for ITAE value is presented in Table 3. The minimum and maximum values of ITAE obtained in 30 independent runs are listed in Table 4. Also, the mean as well as standard deviations is calculated as reported. The least mean value along with standard deviation of the obtained results proves the superiority and reliability of MFO algorithm. Table 4 gives the quantitative analysis of the different methods in terms of minimum, maximum, average and standard deviations. The details of convergence of different algorithms are depicted in Fig. 7, and it indicates the widely acceptability of the MFO algorithm.
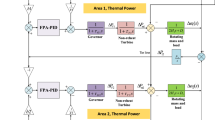
Expansion to multi-area multi-unit power system
The system under consideration is a two-area multi-generation hydrothermal system as shown in Fig. 8. The operating capacity of area 1 is 1250 MW and of area 2 is 750 MW. The transfer function model of boiler system is depicted in Fig. 9. The pertinent data of the system are presented in “Appendix B”. The nonlinearities such as governor dead band (GDB) as well as boiler dynamics are included in the thermal power plant. The developed model is simulated considering 0.01 p.u. SLP in the first area. The parameters of the PID/FOPID controllers for LFC loops are chosen in the range [0, 10] and for AVR loops in the range [0, 1]. Corresponding controller parameters obtained from different techniques are given in Table 5. The variation of frequencies and tie-line power is appeared in Fig. 10a–c. Similarly, the improvements of terminal voltage profiles of each area are appeared in Fig. 11a, b. The execution of the MFO-tuned PID/FOPID controller is compared with results of latest publications such as ZN- and SA-tuned controllers for the same power system [39]. The performance indices in terms of peak overshoot, minimum undershoot, settling time (2% tolerance band) and ITAE objective values are presented in Table 6. It is clear from Figs. 10 and 11 and proven from Table 6 that MFO-optimized FOPID controller performs better as compared to others.
Conclusions
This paper presents outline and execution investigation of PID- and FOPID-controlled power system for simultaneous load frequency as well as automatic voltage control. The study investigates the application of MFO algorithm as the recent nature-inspired powerful optimization technique keeping in mind the end goal to take care of the control issue. It may be noted that the MFO algorithm requires minimum numbers of controlling parameter, which make it simple, effective, faster convergence mobility for optimum global solutions. The first part of the present work demonstrates the implementation of the proposed technique on frequency stabilization of isolated power system with AVR for excitation voltage control. The predominance and viability of the proposed strategy are verified by looking the dynamic response of the framework with PID controllers optimized by other intelligent techniques. The performance indices regarding peak overshoot, minimum undershoot, settling time (2% tolerance band) and ITAE objective values are compared with other techniques. The simulation results infer that the frequency oscillation of the system stabilizes in faster rate and settles very quickly with step load perturbation. Then the present work is extended to multi-unit multi-area power network. The execution of the proposed MFO-tuned PID/FOPID controller is accounted with the results of latest publications such as ZN- and SA-tuned PID controllers for the similar power system. The findings of the simulations work confirm the acceptability of the MFO-tuned FOPID control technique.
Availability of data and materials
Not applicable.
Abbreviations
- ANN:
-
Artificial neural network
- AVR:
-
Automatic voltage regulator
- DE:
-
Differential evolution
- FA:
-
Firefly algorithm
- FOPID:
-
Fractional-order proportional–integral–derivative
- GA:
-
Genetic algorithm
- GWO:
-
Grey wolf optimization
- IAE:
-
Integral of absolute error
- ISE:
-
Integral of squared error
- ITAE:
-
Integral of time-multiplied absolute error
- ITSE:
-
Integral of time-multiplied squared error
- LFC:
-
Load frequency control
- MFO:
-
Moth flame optimization
- SA:
-
Simulated annealing
- PSS:
-
Power system stabilizer
- ZN:
-
Zeigler Nichol’s
References
Saadat H (2002) Power system analysis. McGraw-Hill, New York
Elgerd OI (2008) Electric energy system theory: an introduction, 2nd edn. McGraw-Hill, New York
Kumar P, Kothari DP (2005) Recent philosophies of automatic generation control strategies in power systems. IEEE Trans Power Syst 20(1):346–357
Fosha CE, Elgerd OI (1970) The megawatt frequency control problem: a new approach via optimal control theory. IEEE Trans Power Appar Syst PAS-89(4):563–577
Elgerd OI, Fosha C (1970) Optimum megawatt frequency control of multi-area electric energy systems. IEEE Trans Power Appar Syst PAS-89(4):556–563
Yamashita K, Taniguchi T (1986) Optimal observer design for load frequency control. Int Electr Power Energy Syst 8(2):93–100
Ismail A (1992) Robust load frequency control. In: Proceedings IEEE conference on control applications, vol 2. New York, Dayton, pp 634–5
Wang Y, Zhou R, Wen C (1993) Robust load-frequency controller design for power systems. Proc Inst Electr Eng C 140(1):111–116
Pan CT, Liaw CM (1989) An adaptive controller for power system load-frequency control. IEEE Trans Power Syst 4(1):122–128
Beaufays F, Abdel-Magid Y, Widrow B (1994) Application of neural networks to load-frequency control in power systems. Neural Netw 7(1):183–194
Chaturvedi DK, Satsangi PS, Kalra PK (1999) Load frequency control: a generalized neural network approach. Int Electr Power Energy Syst 21(6):405–415
Demiroren A, Neslihan S, Sengor H, Lale Zeynelgil A (2001) Automatic generation control by using ANN technique. Electr Power Compon Syst 29(10):883–896
Indulkar CS, Raj B (1995) Application of fuzzy controller to automatic generation control. Electr Mach Power Syst 23(2):209–220
Yeşil E, Güzelkaya M, Eksin I (2004) Self tuning fuzzy PID type load and frequency controller. Energy Convers Manag 45(3):377–390
Aditya SK, Das D (2003) Design of load frequency controllers using genetic algorithm for two areas interconnected hydro power system. Electr Power Compon Syst 31(1):81–94
Ali ES, Abd-Elazim SM (2011) Bacteria foraging optimization algorithm based load frequency controller for interconnected power system. Int J Electr Power Energy Syst 33:633–638
Rout UK, Sahu RK, Panda S (2013) Design and analysis of differential evolution algorithm based automatic generation control for interconnected power system. Ain Shams Eng J 4(3):409–421
Padhan S, Sahu RK, Panda S (2014) Application of firefly algorithm for load frequency control of multi-area interconnected power system. Electr Power Compon Syst 42(13):1419–1430
Guha D, Roy PK, Banerjee S (2016) Load frequency control of interconnected power system using grey wolf optimization. Swarm Evolut Comput 27:97–115
Sahu RK, Panda S, Padhan S (2015) A hybrid firefly algorithm and pattern search technique for automatic generation control of multi area power systems. Int J Electr Power Energy Syst 64:9–23
Sahu RK, Panda S, Chandrasekhar GTC (2015) A novel hybrid PSO-PS optimized fuzzy PI controller for AGC in multi area interconnected power systems. Int J Electr Power Energy Syst 64:880–893
Chandrakala KRMV, Balamurugan S, Sankaranarayanan K (2013) Variable structure fuzzy gain scheduling based load frequency controller for multi source multi area hydro thermal system. Int J Electr Power Energy Syst 53:375–381
Raju M, Saikia LC, Sinha N (2016) Automatic generation control of a multi-area system using ant lion optimizer algorithm based PID plus second order derivative controller. Int J Electr Power Energy Syst 80:52–63
Prasad LB, Gupta HO, Tyagi B (2014) Application of policy iteration technique based adaptive optimal control design for automatic voltage regulator of power system. Int J Electr Power Energy Sys 63:940–949
Aguila-Camacho N, Duarte-Mermoud MA (2013) Fractional adaptive control for an automatic voltage regulator. ISA Trans 52(6):807–815
Zamani M, Karimi-Ghartemani M, Sadati N, Parniani M (2009) Design of a fractional order PID controller for an AVR using particle swarm optimization. Control Eng Pract 17(12):1380–1387
Tang Y, Cui M, Hua C, Li L, Yang Y (2012) Optimum design of fractional order PI λ D μ controller for AVR system using chaotic ant swarm. Expert Syst Appl 39(8):6887–6896
Zeng GQ, Chen J, Dai YX, Li LM, Zheng CW, Chen MR (2015) Design of fractional order PID controller for automatic regulator voltage system based on multi-objective extremal optimization. Neurocomputing 160:173–184
Chern TL, Chang GK (1998) Automatic voltage regulator design by modified discrete integral variable structure model following control. Automatica 34(12):1575–1582
Chatterjee S, Mukherjee V (2016) PID controller for automatic voltage regulator using teaching-learning based optimization technique. Int J Electr Power Energy Syst 77:418–429
Zhangh DL, Ying-Gan T, Xin-Ping G (2014) Optimum design of fractional order PID controller for an AVR system using an improved artificial bee colony algorithm. Acta Automatica Sin 40(5):973–979
Li C, Li H, Kou P (2014) Piecewise function based gravitational search algorithm and its application on parameter identification of AVR system. Neurocomputing 124:139–148
Hasanien HM (2013) Design optimization of PID controller in automatic voltage regulator system using Taguchi combined genetic algorithm method. IEEE Syst J 7(4):825–831
Gaing ZL (2004) A particle swarm optimization approach for optimum design of PID controller in AVR system. IEEE Trans Energy Convers 19(2):384–391
Gozde H, Taplamacioglu MC (2011) Comparative performance analysis of artificial bee colony algorithm for automatic voltage regulator (AVR) system. J Frankl Inst 348(8):1927–1946
Panda S, Sahu BK, Mohanty PK (2012) Design and performance analysis of PID controller for an automatic voltage regulator system using simplified particle swarm optimization. J Frankl Inst 349(8):2609–2625
Shayeghi H, Younesi A, Hashemi Y (2015) Optimal design of a robust discrete parallel FP + FI + FD controller for the automatic voltage regulator system. Int J Electr Power Energy Syst 67:66–75
Mukherjee V, Ghoshal SP (2007) Comparison of intelligent fuzzy based AGC coordinated PID controlled and PSS controlled AVR system. Int J Electr Power Energy Syst 29(9):679–689
Chandrakala KRMV, Balamurugan S (2016) Simulated annealing based optimal frequency and terminal voltage control of multi source multi area system. Int J Electr Power Energy Syst 78:823–829
Mirjalili S (2015) Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm. Knowl Based Syst 89:228–249
Barisal AK, Lal DK (2018) Application of moth flame optimization algorithm for AGC of multi-area interconnected power systems. Int J Energy Optim Eng 7(1):22–49
Lal DK, Bhoi KK, Barisal AK (2016) Performance evaluation of MFO algorithm for AGC of a multi area power system. In: 2016 IEEE international conference on signal processing, communication, power and embedded system (SCOPES), pp 903–908
Aboelela MA, Ahmed MF, Dorrah HT (2012) Design of aerospace control systems using fractional PID controller. J Adv Res 3:225–232
Changmao Q, Naiming Q, Zhiguo S (2010) Fractional PID controller design of hypersonic flight vehicle, computer, mechatronics. Int Conf Control Electron Eng (CMCE) 3:466–469
Zamani M, Karimi-Ghartemani M, Sadati N, Parniani M (2009) Design of fractional order PID controller for an AVR using particle swarm optimization. Control Eng Pract 17:1380–1387
Aguila-Camacho N, Duarte-Mermoud MA (2013) Fractional adaptive control for an automatic voltage regulator. ISA Trans 52:807–815
Taher SA, Fini MH, Aliabadi SF (2014) Fractional order PID controller design for LFC in electric power systems using imperialist competitive algorithm. Ain Shams Eng J 5:121–135
Dahiya P, Sharma V, Naresh R (2015) Solution approach to automatic generation control problem using hybridized gravitational search algorithm optimized PID and FOPID controllers. Adv Electr Comput Eng 15:23–34
Lal DK, Barisal AK, Madasu SD (2019) AGC of a two area nonlinear power system using BOA optimized FOPID + PI multistage controller. In: 2019 second IEEE international conference on advanced computational and communication paradigms (ICACCP), pp 1–6
Guha D, Roy PK, Banerjee S (2019) Grasshopper optimization algorithm-scaled fractional-order PI-D controller applied to reduced-order model of load frequency control system. Int J Model Simul. https://doi.org/10.1080/02286203.2019.1596727
Acknowledgements
Not applicable.
Funding
This work was partially supported by TEQIP Cell, Veer Surendra Sai University of Technology, Burla, Odisha, India, and AICTE, New Delhi, India, MODROB Project (Ref. No. 9-44/RIFD/MODROB/Policy-1/2016-17). The necessary equipments have been procured, and infrastructure has been developed for the research using this.
Author information
Authors and Affiliations
Contributions
The details of contributions of the authors in the present works are as follows: (a) DKL proposed an intelligent application of moth flame optimization algorithm for combined load frequency control and automatic voltage regulator of power systems using PID controller. The first part of the present work demonstrates the implementation of the proposed technique on frequency stabilization of isolated power system with AVR for excitation voltage control. (b) AKB proposed the usefulness of fractional-order PID (FOPID) controller. The superiority and effectiveness of the proposed approach are tested by comparing the dynamic response of the system with PID/FOPID controllers optimized by other intelligent techniques. Then the present work is extended to multi-unit two-area power systems. The tuning ability of the algorithm is extensively and comparatively investigated. (c) The results are analyzed and discussed by all the authors. Finally, all authors read and approved the final manuscript. All the authors have read and approved the manuscript.
Authors’ information
Deepak Kumar Lal, born in 1984 and received the B. Tech. degree from the BPUT, Rourkela, Odisha, in 2008 and M. Tech. degree in Power System Engineering in Electrical Engineering Department, National Institute of Technology, Jamshedpur, India, in 2010. He completed his PhD from Veer Surendra Sai University of Technology, Burla, Odisha, India. Since 2011, he is working as an Assistant Professor in the Department of Electrical Engineering, Veer Surendra Sai University of Technology, Burla, Odisha, India. His research interests include automatic generation control, economic load dispatch, renewable energy integration and power quality.
Ajit Kumar Barisal, is a Professor in the Department of Electrical Engineering, College of Engineering and Technology, Bhubaneswar, Odisha, India, since 2018. He was an Associate Professor in the Department of Electrical Engineering, Veer Surendra Sai University of Technology, Burla, Odisha, India, from 2015 to 2018 and was an Assistant Professor since 2006. He received the “Odisha Young Scientist Award 2010”, IEI Young Engineers Award 2010” and “Union Ministry of Power, Department of Power Prize 2010” for his outstanding contribution to engineering and technology research. His research interests include economic load dispatch, hydrothermal scheduling and soft computing applications to power system.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
The nominal data of system 1 [38]:
Thermal power plant
\(R =\) 2.4 Hz/p.u. MW, \(T_{\text{G}} =\) 0.08 s, \(T_{\text{T}} =\) 0.3 s, \(c =\) steam turbine reheats constant
\(T_{\text{r}} =\) steam turbine reheats time constant, \(H =\) inertia constant = 3.5 s, \(D =\) 1.0 MW/Hz
\(\Delta P_{\text{D}} =\) 0.01 p.u.
Exciter
\(\Delta \delta =\) rotor angle deviation of the generator,
\(\Delta V_{\text{ref}} =\) reference terminal voltage deviation = 0.0
\(P_{\text{S}} =\) 0.145 p.u.MW/radian, \(K_{\text{e}} =\) 1.0, \(T_{\text{e}} =\) 0.4 s, \(K_{\text{a}} =\) 10, \(T_{\text{a}} =\) 0.1 s, \(K_{\text{field}} =\) 0.8, \(T_{\text{field}} =\) 1.4
\(K_{\text{S}} =\) 1.0, \(T_{\text{S}} =\) 0.05 s, \(K_{1} =\) 1.0, \(K_{2} =\) − 0.1, \(K_{3} =\) 0.5, \(K_{4} =\) 1.4
Appendix B
The nominal data of system 2 [38, 39]:
Thermal power plant
\(R_{1} =\) 2 Hz/p.u. MW, \(T_{\text{H}} =\) 0.08 s, \(T_{\text{T}} =\) 0.3 s, \(K_{{{\text{P}}1}} =\) 80, \(K_{{{\text{P}}2}} =\) 133.33, \(T_{{{\text{P}}1}} =\) 16 s, \(T_{{{\text{P}}2}} =\) 26.67 s
\(\Delta P_{{{\text{D}}1}} = \Delta P_{{{\text{D}}2}} =\) 0.01 p.u, \(B_{1} = B_{2} =\) 0.425 p.u.MW/Hz
Hydropower plant
\(R_{2} =\) 2 Hz/p.u. MW, \(K_{1} =\) Hydro governor gain = 1.0, \(T_{1} =\) 48.7 s, \(T_{\text{R}} =\) 5 s, \(T_{2} =\) 0.513 s, \(T_{\text{W}} =\) 1.0 s
Exciter
\(\Delta \delta = \Delta \delta_{1} = \Delta \delta_{2} =\) rotor angle variation of the generator in both areas
The remaining data for exciter are same as given in “Appendix A.”
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lal, D.K., Barisal, A.K. Combined load frequency and terminal voltage control of power systems using moth flame optimization algorithm. Journal of Electrical Systems and Inf Technol 6, 8 (2019). https://doi.org/10.1186/s43067-019-0010-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s43067-019-0010-3