Abstract
The primary objective of a power system is to provide safe and reliable electrical energy to consumers. This objective is achieved by maintaining the stability of the power system, a multifaceted concept that can be divided into three distinct classes. The focus of this study is on one of these classes, voltage stability. A critical component in maintaining voltage stability is the automatic voltage regulator (AVR) system of synchronous generators. In this paper, a novel control method, the sigmoid-based fractional-order PID (SFOPID), is introduced with the aim of improving the dynamic response and the robustness of the AVR system. The dandelion optimizer (DO), a successful optimization algorithm, is used to optimize the parameters of the proposed SFOPID control strategy. The optimization process for the DO-SFOPID control strategy includes a variety of objective functions, including error-based metrics such as integral of absolute error, integral of squared error, integral of time absolute error, and integral of time squared error, in addition to the user-defined Zwee Lee Gaing’s metric. The effectiveness of the DO-SFOPID control technique on the AVR system has been rigorously investigated through a series of tests and analyses, including aspects such as time domain, robustness, frequency domain, and evaluation of nonlinearity effects. The simulation results are compared between the proposed DO-SFOPID control technique and the fractional-order PID (FOPID) and sigmoid-based PID (SPID) control techniques, both of which have been tuned using different metaheuristic algorithms that have gained significant recognition in recent years. As a result of these comparative analyses, the superiority of the DO-SFOPID control technique is confirmed as it shows an improved performance with respect to the other control techniques. Furthermore, the performance of the proposed DO-SFOPID control technique is validated within an experimental setup for the AVR system. The simulation results show that the proposed DO-SFOPID control technique is highly successful in terms of stability and robustness. In summary, this study provides comprehensive evidence supporting the effectiveness and superiority of the DO-SFOPID control technique on the AVR system through both simulation and experimental results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Background
The main objective of a power system is to provide safe and reliable electrical energy to consumers [1]. Therefore, the stability of the power system plays a crucial role in ensuring its functionality. Power system stability can be divided into three main aspects: frequency, voltage, and rotor angle [2]. This paper discusses the automatic voltage regulator (AVR) system of synchronous generators, which plays an essential role in the voltage stability of a power system.
The voltage level in a power system is subject to fluctuations due to various factors, including changes in load, generation, transmission, and distribution losses. Such voltage variations can potentially cause problems for electrical equipment connected to the system. For example, excessively low voltage levels can lead to poor performance or even malfunction of equipment, while high voltage levels can damage equipment. To address these concerns, an automatic voltage regulator (AVR) plays a crucial role. The AVR automatically regulates the current flow in response to fluctuations in the voltage level. This helps to maintain a constant and stable voltage level, ensuring the smooth operation of electrical equipment. In addition, the AVR system can help reduce energy losses and improve the overall efficiency of the power system [3].
There are several types of controllers that have been used in AVR systems to improve their transient response, robustness, and stability: proportional–integral–derivative (PID) controller [4,5,6], PID plus second-order derivative (PIDD\(^2\)) controller [7, 8], sigmoid-based PID (SPID) controller [9], PID-accelerated (PIDA) controller [10], two-degree-of-freedom (2DOF) PID controller [11], fractional-order PID (FOPID) controller [12,13,14], fractional-order PID with double derivative (FOPIDD) controller [15], fractional-order PID with double integrator and double derivative (FOPIIDD) controller [16], multi-term fractional-order PID (MFOPID) controller [17], fuzzy PID controller [18], fuzzy logic-based controller (FP + FI + FD) controller [19], sliding mode controller [20], neural network predictive controller [21], reinforcement learning-based controller [22], high-order differential feedback controller (HODFC), and fractional HODFC [23] are some of the reported control approaches.
While PID controllers are widely used to control AVRs because of their effective operation and ease of installation, FOPID controllers are often preferred. This preference is due to the fact that the fractional-order derivative operator and fractional-order integral operator in FOPID controllers can better represent the dynamics of the AVR system. Published studies have shown that FOPID controllers outperform conventional PID controllers in terms of transient response, robustness, and stability [12, 24, 25]. The tuning of the PID and FOPID controller parameters is crucial to ensure the stability of the AVR system. Improper tuning can lead to slow responses to load changes and disturbances, resulting in instability. The researchers therefore used evolutionary algorithms to design the controller in the AVR system. This approach optimizes the controller parameters, enhancing the system’s response and overall performance. Genetic algorithm (GA) [26], particle swarm optimization (PSO) [26], differential evolution (DE) [27], artificial bee colony (ABC) [27], chaotic ant swarm (CAS) algorithm [28], multi-objective extremal optimization (MOEO) [29], simulated annealing optimization (SAO) [30], cuckoo search (CS) algorithm [31], improved kidney inspired algorithm (IKA) [32], chaotic yellow saddle goatfish algorithm (C-YSGA) [33], Rao optimization [17], enhanced Aquila optimizer (enAO) [34], and improved slime mould algorithm [35] are among the optimization algorithms used in the controller techniques for the AVR system to achieve the desired results.
A recent study conducted by Suid and Ahmad [9] highlights that there are still several problems in achieving improved AVR system response through the controller design process using evolutionary algorithms. Two specific problems are identified:
-
1.
The imbalance between the exploration and exploitation phases, which can lead to local optimum stagnation and premature convergence, affects many current approaches [36].
-
2.
The use of traditional controllers or their variants with fixed off-line parameters [37].
The first problem can be effectively overcome by selecting the optimization algorithm based on its performance on various test and engineering problems with known results. The second problem is overcome by using a sigmoid-based PID (SPID) controller, as introduced by Suid and Ahmad [9], which has demonstrated superior AVR system response compared to the state-of-the-art studies in the literature.
1.2 Motivation and contributions
Although it has been shown that the SPID controller [9] improves the response of the AVR system and provides higher stability margins under a variety of circumstances, it is hypothesized that further improvements are possible. This assertion is based on comparisons of FOPID and PID controllers, which suggest that a more complex controller design may provide better results in AVR systems. The motivation behind this research is the belief that a sigmoid-based fractional-order PID (SFOPID) controller has the potential to significantly improve the system response and stability margins compared to the SPID controller.
The objective of this study is to make the AVR system more stable and reliable by using the dandelion optimizer (DO) algorithm to find the best values for the 11 parameters of the proposed SFOPID controller. The study uses different performance metrics to identify the best parameter values for the SFOPID controller approach. Error-based metrics such as integral of absolute error (IAE), integral of squared error (ISE), integral of time absolute error (ITAE), and integral of time squared error (ITSE) and Zwee Lee Gaing’s (ZLG) metric [26] are used as objective functions in this study.
In this study, finding the optimal parameters of the SFOPID controller approach with the ZLG performance metric is particularly advantageous. The ZLG metric shows superior transient response for the AVR and outperforms other objective functions such as the error-based IAE, ISE, ITAE, and ITSE metrics.
To demonstrate the superior performance of the proposed SFOPID controller, a comparison is made with the SPID controller and different metaheuristic algorithm-based FOPID controllers recently published in the literature. These publications in the literature are listed in Table 1.
Time-domain (TD), frequency-domain (FD), and robustness (R) analyses are used to compare with studies in the literature, and their results are presented. In addition, an investigation is carried out to evaluate the performance of the proposed SFOPID controller when faced with a nonlinearity (N) generator input. As a final analysis, the AVR system with the SFOPID control mechanism is verified as a good performer through its testing on an experimental setup (ES).
The motivation for the research and the approach taken in line with this motivation have been mentioned above. In this way, the contribution to the literature is also mentioned. As a result, the main contributions of this research to the literature can be summarized as follows:
-
1.
The SFOPID control technique is introduced to the literature for the first time, with a pioneering application in the AVR system.
-
2.
The superiority and effectiveness of the proposed adaptive fractional control technique are demonstrated by comparison with existing SPID and FOPID control techniques.
-
3.
The proposed control technique has been extensively analysed using various methods, and its superior performance has been demonstrated.
-
4.
The optimum parameter values of the proposed SFOPID control technique are determined using the DO algorithm.
The rest of the paper is organized as follows: Sect. 2 deals with the AVR system and its modelling. Section 3 presents the design process of the proposed SFOPID control scheme. Section 4 gives a detailed description of the DO algorithm. The modelling of the experimental benchmark system is described in Sect. 5. Finally, conclusions are given.
2 Modelling of automatic voltage regulator system
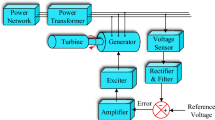
Achieving precise control of the terminal voltage of a synchronous generator is made possible by the use of the AVR system model, which consists of integral components, namely the controller, amplifier, exciter, generator, and sensor. The purpose of these components can be defined as follows:
-
Sensor: By detecting the voltage level at the synchronous generator terminals, the sensor generates a feedback signal which is sent to the system to regulate the generator output.
-
Controller: The aim of the controller is to minimize the error between the synchronous generator reference voltage and the feedback signal from the sensor.
-
Amplifier: The signal at the controller output is amplified by the amplifier.
-
Exciter: The exciter plays a critical role in regulating the output voltage of the generator by controlling the amount of excitation applied to the field winding and providing the necessary voltage and current.
-
Generator: Together with the excitation signal applied to the field winding of the generator, the terminal voltage is produced.
The block diagram in Fig. 1 shows how each component of an AVR system without a controller is modelled using a first-order transfer function that includes both a gain and a time constant. \(V_{{\rm{ref}}}(s)\) and \(V_s(s)\) denote the reference and measured terminal voltages, respectively, in the Laplace domain and are used to generate the error signal E(s). \(V_g(s)\) is the terminal voltage signal of the generator expressed in the Laplace domain.
The parameters of the AVR system components have different gain and time constant values. Therefore, the upper and lower limits of the AVR system components are given in Table 2 [12, 33].
Although Table 2 gives the range values for AVR system components, researchers prefer to use the values in Table 3 to ensure a fair comparison in the literature [13, 14, 38, 39]. Figure 2 shows the transient response of the AVR system when it is not under control, and this response has been generated using the parameter values in Table 3. In the absence of a controller in the AVR system, it has a settling time (%2) of 6.9865 s, a rise time of 0.2607 s, a peak time of 0.7526 s, and a steady-state error of 0.0909 p.u. for a reference value of 1 p.u. These results indicate that a controller is required to operate the AVR system. Therefore, when designing controllers for the AVR system, researchers aim to achieve the optimum transient response.
3 The proposed sigmoid-based FOPID controller
The FOPID controller is an advanced control technique that uses the principles of fractional calculus to achieve better performance in the control of complex processes. The FOPID controller differs from the traditional PID controller in that it incorporates a fractional-order integrator operator and a fractional-order differentiator operator. This feature of the FOPID controller excels in systems with non-integer dynamics, such as those with time delays or fractional-order transfer functions, providing improved performance and stability. Compared to conventional PID controllers, the FOPID controller is able to provide faster response time and superior disturbance rejection, which can improve the overall performance of the control system.
The transfer function of the FOPID controller in the Laplace domain is represented by (1).
The variables \(K_p\), \(K_i\), and \(K_d\) correspond to the proportional, integral, and derivative gains, while \(\lambda \) and \(\mu \) denote the fractional integrator and fractional derivative orders, respectively. As can be seen in (1), the parameters \(K_p\), \(K_i\), and \(K_d\) of the FOPID controller are fixed values and therefore not affected by changes in the input error variable. Therefore, the FOPID controller cannot fully demonstrate the improvement in control accuracy. Considering the above situation, a controller has been designed that combines elements of both the sigmoid function and the FOPID controller.
The sigmoid function, characterized by an S-shaped curve, allows the error variable to change between predefined lower and upper limits in the controller parameters. This allows the controller parameters to be adaptively tuned in response to changes in the error, resulting in a more appropriate control signal. In addition, controllers combined with the sigmoid function can achieve a faster response with less overshoot in the dynamic behaviour [9, 40].
The general form of the proposed SFOPID controller is written in conjunction with both s and t as in (2), where s and t denote the complex frequency variable and the physical time variable, respectively.
As expressed in (3)–(5), the lower bounds of the proportional, integral, and derivative parameters are given by the coefficients \(K_{plb}\), \(K_{ilb}\), and \(K_{dlb}\), while the upper bounds are given by \(K_{pub}\), \(K_{iub}\), and \(K_{dub}\), respectively. The error function \(\Delta e(t)\) is defined as the difference between the reference voltage and the sensor voltage. In addition, \(\Delta p = |K_{pub}-K_{plb} |\), \(\Delta i = |K_{iub}-K_{ilb} |\), and \(\Delta d = |K_{dub}-K_{dlb} |\) are defined to simplify the parameter tuning process. Figure 3 shows how the parameters \(K_{pv}(t)\), \(K_{iv}(t)\), and \(K_{dv}(t)\) change with respect to the \(\Delta e(t)\) for different values of \(\sigma _{p}\), \(\sigma _{i}\), and \(\sigma _{d}\). The figures effectively show the adaptability of the proposed SFOPID controller, demonstrating its ability to continuously tune the parameters \(K_{pv}(t)\), \(K_{iv}(t)\), and \(K_{dv}(t)\) in response to changing errors. Moreover, higher values of \(\sigma _{p}\), \(\sigma _{i}\), and \(\sigma _{d}\) result in sharper transitions between the lower and upper bounds, leading to faster controller response with reduced overshoot [9].
The aforementioned 9 coefficients, i.e. \(K_{plb}\), \(K_{ilb}\), \(K_{dlb}\), \(\Delta p\), \(\Delta i\), \(\Delta d\), \(\sigma _{p}\), \(\sigma _{i}\), \(\sigma _{d}\), and 2 fractional orders, i.e. \(\lambda \) and \(\mu \), of the proposed SFOPID controller must be optimally tuned to achieve satisfactory performance in the AVR system. Therefore, the 11 coefficients are optimally determined using the DO algorithm, the method of which is explained in detail in the following section. Furthermore, to ensure the proper design of the fractional-order operators in the proposed SFOPID controller, the fifth-order Oustaloup approximation method is used in the frequency range \(w \in [10^{-5}, 10^5]\) rad/s.
4 Dandelion optimizer
The main determinants of dandelion seed dispersal are wind speed and weather conditions. Wind speed plays a role in seed dispersal over long or short distances [41]. Weather conditions not only determine whether dandelion seeds will fly or not, but also affect their growth in nearby or distant places. The journey of dandelion seeds is divided into three stages, as described below.
-
Rising Stage: In weather conditions with sun and wind, the dandelion seed is lifted by a vortex and rises due to the dragging force. In contrast, in rainy weather, there is only local search, as no vortex will form.
-
Descending Stage: After reaching a certain height, the dandelion seeds fall steadily at this stage.
-
Landing Stage: The landing stage culminates in the dandelion seeds landing at a random location. Here, new dandelions are formed with the help of wind and weather factors.
Considering the three stages mentioned above, Zhao et al. proposed a dandelion optimizer algorithm in 2022 [42].
4.1 Initialization of the algorithm
In the dandelion optimizer, each dandelion seed symbolizes a potential solution. The population of these seeds is given in (6).
The Pop and Dim in (6) refer to the population and dimension of the variable, respectively. (7) shows how each potential solution lies within the upper (\(U_{B}\)) and lower (\(L_{B}\)) bounds of the problem.
The variable i in (7) takes on integer values from 1 to Pop, while the variable rand is a randomly generated number in the range [0, 1].
\(L_{B}\) and \(U_{B}\) can be expressed as in (8).
When initialized, DO considers the candidate with the best fitness to be the initial elite. The initial elite is also recognized as the optimal position for the growth of dandelion seeds.
Given the minimum value, the mathematical expression for \(X_{elite}\), also known as the initial elite, is given in (9).
where find() refers to two indices that have the same value.
4.2 First stage: rising stage
When they reach a certain height, the dandelion seeds separate from their parents. Several factors, such as humidity and wind speed, are influential in determining the height achieved by dandelion seeds. Depending on the weather, there are two different cases.
4.2.1 Case 1
On a clear day, the wind speed is represented by a lognormal distribution. In this case, the algorithm focuses mainly on exploration. Here, dandelion seeds are randomly positioned in the search space due to the effect of the wind. The height of the seed changes depending on the variability of the wind speed. The strength of the wind determines how high and how far the dandelion seeds can fly. Furthermore, the speed of the wind creates vortexes on the dandelion seeds.
The mathematical expression for this case is as in (10).
The mathematical formula for the randomly generated dandelion position is shown in (11). This position is denoted as X(t) while iterating through the tth step in the search space.
\(\ln Y\) represents a lognormal distribution, where \(\mu ^2 = 0\) and \(\sigma ^2 = 1\). The mathematical formula for this distribution is as follows:
where a is an adaptive variable used to adjust the search step size, while y is a standard normal distribution corresponding to N(0, 1).
The separated eddy motion on a dandelion is represented by the variables \(v_x\) and \(v_y\). The mathematical formula for \(v_x\) and \(v_y\) is given in (14).
4.2.2 Case 2
Dandelion seeds face obstacles such as air resistance and humidity in rainy weather. This prevents the dandelion seeds from rising properly in the wind. The mathematical expression in (15) shows the exploitation of dandelion seeds in their local search.
where the size of the local search domain for dandelion is set by the variable k.
q represented by the domain is calculated as follows:
As a result, the rising stage of dandelion seeds can be described mathematically as in (17).
where the standard normal distribution is associated with the random number generated by randn().
4.3 Second stage: descending stage
In the descending stage, exploration is also a key focus of the DO algorithm. Once the dandelion seeds have risen to a certain distance, they begin to fall steadily. To mimic the movement of the dandelion, the DO algorithm uses the Brownian motion expressed in (18).
where the variable \(\beta _t\) is used to describe the Brownian motion. The mean population position of the ith iteration is denoted by \(X_{\textit{mean}_{-}t}\).
4.4 Third stage: landing stage
In the final stage, exploitation is a key focus of the DO algorithm. The DO algorithm aims to approach the optimal solution over time by randomly selecting the landing position of the dandelion seed based on the results of previous stages. As the algorithm progresses through iterations, it attempts to converge on the best possible solution.
The mathematical formula for this behaviour is given in (20).
The mathematical expression of the Levy function is shown in (21).
In (21), the parameter \(\beta \) is a random number in the range [0, 2]. The value of s is constant and is set to 0.01. On the other hand, both w and t are random numbers in the interval [0, 1].
The mathematical expression for \(\sigma \) is given in (22).
\(\delta \) is a linear function, and its mathematical formula is given in (23).
Finally, the pseudo-code for the DO algorithm is shown in Algorithm 1 [42]. In addition, Zhao et al. [42] demonstrated the efficiency and effectiveness of the DO algorithm using the CEC2017 unconstrained benchmark functions. They performed a comprehensive performance comparison with nine well-known metaheuristic algorithms to demonstrate the excellence of the algorithm.
4.5 Objective function
The choice of the appropriate objective function is crucial to achieve the desired result in the optimization process. This choice directly affects the result, so it may be necessary to test different objective functions to achieve a good result [43]. For this reason, many objective functions are tested in the study of the proposed SFOPID controller. In the literature, IAE, ISE, ITAE, and ITSE metrics are often used as performance criteria when selecting objective functions for the optimization process [44]. All of these objective functions attempt to minimize error. In addition, the ZLG objective function is used as an alternative to the error-based objective functions in the study [26].
In the literature, comparisons for the AVR transient response are made over \(t_s\), \(t_r\), and OS. While IAE and ISE objective functions are effective on OS, they may not give effective results for \(t_s\) [45]. These objective functions do not include time. These objective functions are given below.
In (24)–(25), the variables t and e(t) correspond to time and error, respectively.
When time is added to the IAE and ISE objective functions, the ITAE and ITSE objective functions are obtained. This allows \(t_s\) to be reduced in the transient response of the system. Among the error-based objective functions, ITAE is usually the most prominent [46, 47]. ITAE and ITSE objective functions are given below.
The ZLG objective function proposed by Gaing [26] takes into account the transient response characteristics of the system, namely overshoot (OS), steady-state error (\(E_{ss}\)), settling time (\(t_s\)), and rise time (\(t_r\)). The ZLG objective function is given below.
where \(\beta \) (\(\beta \) is 1.) is the weight coefficient and e is the Euler number.
5 Simulation results
This section provides a comprehensive overview of the design and evaluation of the DO-SFOPID controller for the AVR system, including a detailed analysis of its performance, stability, and robustness. Firstly, in order to assess how the choice of objective function affects the optimization process, a number of objective functions, i.e. IAE, ISE, ITAE, ITSE, and ZLG, are used, and the 11 different parameters of the proposed DO-SFOPID controller are optimized. The comparison includes a comprehensive analysis of the controllers’ performance, covering both their transient and steady-state responses, as well as their robustness to parameter uncertainties, reference changes, and external disturbances. Furthermore, to ensure a fair comparison of the proposed DO-SFOPID and NSCA-SPID controllers in the frequency domain (using Bode analysis), the adaptive nature of both controllers is also taken into account. Finally, the effectiveness of the proposed DO-SFOPID control strategy for the AVR system is tested on a benchmark system. The modelling of the studies is carried out in the MATLAB/Simulink environment with a sampling period of 10 ms. Note that the bold type indicates the best results in the comparative analysis tables.
5.1 Time-domain analysis
5.1.1 The influence of the choice of the objective function on the optimization process
The parameter ranges \(K_{pv}\), \(K_{iv}\), and \(K_{dv}\) for the SPID controller are discussed in [9]. In the design of the proposed SFOPID controller, the parameter ranges used in the previous study on the AVR system that are relevant to its fractional part (\(\lambda \) and \(\mu \)) have been considered [37]. Considering these parameter ranges in the literature, the parameter ranges given in Table 4 are used in the optimization process of the study.
The optimization processes are performed ten times for each of the objective functions IAE, ISE, ITAE, ITSE, and ZLG. The statistical analysis for the results obtained is given in Table 5. The objective functions of the ISE and the ITSE have quite low standard deviation values, as can be seen from the results. This means that the same result is found almost every time for the ISE and ITSE objective functions during the optimization process. Although the standard deviation of the IAE objective function is lower than that of the ISE and ITSE objective functions, a similar situation applies to the IAE. The standard deviation values of the ITAE and ZLG objective functions are high, but the optimization results obtained are quite satisfactory (Figs. 4, 5).
The optimal parameter values obtained for all the objective functions are given in Table 6. The effect of the IAE, ISE, ITAE, ITSE, and ZLG objective functions on the step response of the AVR system is analysed, and the best results obtained are shown in Fig. 6. The results obtained from the ITAE and ZLG objective functions are successful for the control, as shown in Fig. 6. As the two results obtained are quite close, the transient response characteristics are examined in order to see the difference. The results of the time-domain analysis, consisting of the settling time (\(t_s\)), rise time (\(t_r\)), and overshoot (OS) values obtained for all the objective functions, are given in Table 7. Table 7 clearly shows that the ZLG objective function produced the most successful result.
5.1.2 Comparison with literature
In the previous subsection, the parameters of the proposed SFOPID controller are optimally determined for different objective functions. This subsection presents a comparison of the step response of the AVR system using parameter values generated from the ZLG objective function, which gave the best results, with state-of-the-art FOPID and SPID controllers from the literature. The optimal parameters obtained in this study and in the literature are listed in Tables 8 and 9.
Both the proposed study and the results of the time-domain analysis of the state-of-the-art studies are given in Table 10. Based on the analysis results presented in Table 10, it is evident that the proposed SFOPID controller demonstrates superior performance compared to other controllers. The transient responses of some of the recent studies and the proposed SFOPID controller are shown in Fig. 6.
5.2 Frequency-domain analysis
The stability of the proposed DO-SFOPID controller in the frequency domain is illustrated by the Bode diagram. In Sect. 3, it is stated that the parameter values \(K_{pv}(t)\), \(K_{iv}(t)\), and \(K_{dv}(t)\) change with time and error. Figure 7 shows how the parameters \(K_{pv}(t)\), \(K_{iv}(t)\), and \(K_{dv}(t)\) change over time. In this analysis, to ensure a fair comparison with the NSCA-SPID study, the \(K_{pv}\), \(K_{iv}\), and \(K_{dv}\) parameter values of the DO-SFOPID controller are taken at the same time intervals. That is, the parameter values \(K_{pv}\), \(K_{iv}\), and \(K_{dv}\) are taken at \(t=0.2\) s, \(t=0.6\) s, and \(t=8\) s, as shown in Fig. 7a–c, respectively. The comparative Bode plots of the proposed DO-SFOPID and NSCA-SPID controllers at \(t=0.2\) s, \(t=0.6\) s, and \(t=8\) s are also shown in Figs. 8, 9 and 10, respectively. Bode analysis results, i.e. peak gain, phase margin, delay margin, and bandwidth, are obtained at three different time intervals (\(t=0.2\) s, \(t=0.6\) s, and \(t=8\) s ) and are shown in Tables 11, 12 and 13, respectively. The results in Table 11 show that the DO-SFOPID controller outperforms the NSCA-SPID controller in terms of phase margin and bandwidth. Tables 12 and 13 clearly show that the DO-SFOPID controller has better performance than the NSCA-SPID controller in terms of peak gain, phase margin, and bandwidth.
Bode plots of proposed DO-SFOPID and NSCA-SPID [9] controllers at \(t=0.2\) s
Bode plots of DO-SFOPID and NSCA-SPID [9] controllers at \(t=0.6\) s
Bode plots of the proposed DO-SFOPID and NSCA-SPID [9] controllers at \(t=8\) s
5.3 Robustness analysis
5.3.1 Robustness against reference change
In this subsection, the performance of the proposed DO-SFOPID controller in tracking the reference signal is evaluated. The reference signal used is a novel mixture of both soft and aggressive signals. The generated reference signal is shown in Fig. 11. The reference change responses obtained by DO-SFOPID, NSCA-SPID, and state-of-the-art FOPID controllers are shown in Fig. 12. At the same time, the error metrics IAE, ISE, ITAE, and ITSE are used to show the numerical performance of the controllers. As given in Table 14, the proposed DO-SFOPID controller outperforms the other controllers in all metrics.
5.3.2 Robustness against parameter changes
AVR system parameters can change as a result of internal or external causes. The controller ought to be able to keep the system stable in such exceptional circumstances. In this context, the robustness of the proposed DO-SFOPID controller against parameter changes in the AVR system should be analysed.
The effect of changes in time constants on stability is greater than the gain constants. For this reason, this subsection focuses on the effects of changes in AVR system parameters on the time constants. The AVR system parameters are changed between + 50% and − 50%. The changes in the AVR system parameters and their effect on the transient response of the system are shown in Fig. 13, where the nominal condition is also given for comparison.
The transient response characteristics of the AVR system are given in Table 15. The results of the analysis are summarized below:
-
It is determined that as the amplifier time constant (\(\tau _a\)) increases, the rise time increases. When the peak values are examined, a situation similar to the rise time emerges. As for the settling time, there are both an increase and a decrease in the settling time as the amplifier time constant (\(\tau _a\)) increases.
-
It is concluded that as the exciter time constant (\(\tau _e\)) increases, the rise time increases. A decrease in the exciter time constant (\(\tau _e\)) leads to a significant increase in the peak value. As for the settling time, there are both an increase and a decrease in the settling time as the exciter time constant (\(\tau _e\)) increases.
-
The effect of changing the generator time constant (\(\tau _g\)) is very similar to the effect of changing the exciter time constant (\(\tau _e\)).
-
It is determined that as the sensor time constant (\(\tau _s\)) increases, the rise time decreases, and the peak value increases. Increasing the sensor time constant (\(\tau _s\)) has a negative effect on the settling time.
5.3.3 Robustness against load disturbance
The effect of a load disturbance is often analysed in the AVR system to test how robust the AVR system is to a load change. It is desired that the AVR system returns quickly to the reference voltage and is stable against the changing load. The analysis in this subsection consists of two steps. In the first step, a unit step signal is applied to the reference voltage value of the AVR system. In the second step, the system is subjected to a disturbance load to assess its ability to maintain voltage stability. The way in which the load disturbance is applied to the AVR system is shown in Fig. 14. Figure 15 shows that the transient response of the proposed DO-SFOPID controlled AVR system does not have a very high overshoot, and the system stabilizes quickly. The capability of the proposed DO-SFOPID controller under load disturbance is further evaluated by comparing it with different state-of-the-art controllers. The performance superiority of the proposed DO-SFOPID controller over state-of-the-art controllers is verified by the error-based IAE, ISE, and ITSE metrics given in Table 16.
5.4 Generator input nonlinearity analysis
This subsection examines the ability of the DO-SFOPID control technique to cope with the nonlinearity of the AVR system. In order to add the effect of nonlinearity, a saturation block is inserted between the exciter and the generator, as shown in Fig. 16 [43]. The saturation block, inserted between the exciter and the generator, has a lower limit of \(-6\) and an upper limit of \(+9\) [43].
Figure 17 shows graphically how the AVR system using the DO-SFOPID control technique behaves under both linearity and nonlinearity effects. The numerical results in Table 17 clearly confirm that the proposed DO-SFOPID control technique performs well even when there is no linear effect in the AVR system.
5.5 Experimental setup analysis
In this subsection, the functionality of the DO-SFOPID controller that is integrated with the AVR is evaluated in the an experimental setup. The experimental setup modelled by Modabbernia et al. [51] comprises a 13.8 kV synchronous generator of 200 MVA linked to a 230 kV electric power network of 10,000 MVA through a 210 MVA \(\Delta \)-Y transformer. As shown in Fig. 18, the experimental system has been modelled in MATLAB/Simulink. The components of this experimental system, the synchronous generator and hydraulic turbine governor, are connected to the 230 kV network via DO-SFOPID controlled AVR system. The active power of the synchronous generator is 150 MV in a steady-state condition at \(t=0\) s. The system experiences a three-phase-to-ground fault at \(t=0.1\) s, but within 6 cycles, it is cleared at \(t=0.2\) s [17, 51]. In order to prove the functionality of the proposed DO-SFOPID control technique, three different cases are created by taking the gain and time constant values of the amplifier and exciter at minimum, nominal, and maximum values. The parameter values for each case are given in Table 18. The results presented in Fig. 19 show that the proposed DO-SFOPID control technique exhibits excellent performance in all three different scenarios of the experimental setup.
6 Conclusion
This study focuses on the SFOPID control technique, an adaptive control method that aims to achieve better system response in an AVR system. The 11 different parameters of this control technique are optimally determined by the DO algorithm, which uses different objective functions such as error-based IAE, ISE, ITAE, ITSE, and ZLG metrics. As a result of the optimization process, the best parameters are obtained with the ZLG objective function. Time-domain analysis, frequency-domain analysis, robustness analysis, generator input nonlinearity analysis, and experimental setup analysis are performed on using the proposed DO-SFOPID controller in order to show its performance in terms of stability and robustness. The obtained results of the analyses are summarized as follows:
-
The time-domain analysis shows that the proposed DO-SFOPID controller outperforms the works in the literature listed in Table 10, especially the NSCA-SPID controller [9], which has a rise time of 0.1038 s, a settling time of 0.1369 s, and an overshoot time of 0%.
-
Frequency-domain analysis is carried out for different time values (\(t=0.2\) s, \(t=0.6\) s, and \(t=8\) s) due to the adaptive nature of the DO-SFOPID controller. From the Bode plots obtained for \(t=0.2\) s, \(t=0.6\) s, and \(t=8\) s, respectively, the peak gain is 7.66 dB, 8.01 dB, and 8.66 dB; the phase margin is 55.7 deg, 54.6 deg, and 52.8 deg; the delay margin is 0.0129 s, 0.0123 s, and 0.0114 s; and the bandwidth is 85.60 Hz, 87.53 Hz, and 91.82 Hz. The obtained results for different time values are close to each other and indicate that the AVR system is stably controlled by the proposed DO-SFOPID controller.
-
Three different analyses, i.e. load disturbance, parameter, and reference signal changes, are discussed in the robustness analysis. The results of the robustness analysis show that the controller is able to maintain stability and operate with high efficiency.
-
By incorporating a saturation block into the AVR system, it becomes possible to evaluate the effectiveness of the proposed SFOPID controller in dealing with nonlinear effects that may be present in the system. Under the nonlinear effect, a transient response close to that of normal conditions is obtained. The rise time is 0.1146 s, the settling time is 0.1495 s, the peak time is 1.0845 s, and the peak value is 1.0008 under the nonlinearity effect.
-
Finally, the AVR system with the proposed SFOPID controller is evaluated by simulating it on an experimental setup. The results verify that the DO-SFOPID controller also shows also good performance in the amplifier and exciter of the AVR system in three different scenario conditions.
In general, the performance of the proposed DO-SFOPID controller is quite high in time-domain analysis, robustness analysis, nonlinear effect analysis, and experimental setup analysis. The results are also satisfactory in the frequency-domain analysis.
Data availability
All data generated or analysed during this study are included in this published article [and its supplementary information files].
References
Dudgeon GJ, Leithead WE, Dysko A, o’Reilly J, McDonald JR (2007) The effective role of AVR and PSS in power systems: frequency response analysis. IEEE Trans Power Syst 22(4):1986–1994
Kundur P, Paserba J, Ajjarapu V, Andersson G, Bose A, Canizares C et al (2004) Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions. IEEE Trans Power Syst 19(3):1387–1401
Dogruer T, Can MS (2022) Design and robustness analysis of fuzzy PID controller for automatic voltage regulator system using genetic algorithm. Trans Inst Meas Control 44(9):1862–1873
Köse E (2020) Optimal control of AVR system with tree seed algorithm-based PID controller. IEEE Access 8:89457–89467
Çelik E (2018) Incorporation of stochastic fractal search algorithm into efficient design of PID controller for an automatic voltage regulator system. Neural Comput Appl 30(6):1991–2002
Ekinci S, Izci D, Abu Zitar R, Alsoud AR, Abualigah L (2022) Development of Lévy flight-based reptile search algorithm with local search ability for power systems engineering design problems. Neural Comput Appl 34(22):20263–20283
Izci D, Ekinci S, Mirjalili S (2022) Optimal PID plus second-order derivative controller design for AVR system using a modified Runge Kutta optimizer and Bode’s ideal reference model. Int J Dyn Control 66:1–18
Izci D, Ekinci S, Mirjalili S, Abualigah L (2023) An intelligent tuning scheme with a master/slave approach for efficient control of the automatic voltage regulator. Neural Comput Appl 66:1–17
Suid M, Ahmad M (2022) Optimal tuning of sigmoid PID controller using nonlinear sine cosine algorithm for the automatic voltage regulator system. ISA Trans 128:265–286
Mosaad AM, Attia MA, Abdelaziz AY (2019) Whale optimization algorithm to tune PID and PIDA controllers on AVR system. Ain Shams Eng J 10(4):755–767
Rajinikanth V, Satapathy SC (2015) Design of controller for automatic voltage regulator using teaching learning based optimization. Procedia Technol 21:295–302
Ayas MS, Sahin E (2021) FOPID controller with fractional filter for an automatic voltage regulator. Comput Electr Eng 90:106895
Mok R, Ahmad MA (2022) Fast and optimal tuning of fractional order PID controller for AVR system based on memorizable-smoothed functional algorithm. Int J Eng Sci Technol 35:101264
Bakir H, Guvenc U, Kahraman HT, Duman S (2022) Improved Lévy flight distribution algorithm with FDB-based guiding mechanism for AVR system optimal design. Comput Ind Eng 168:108032
Tabak A (2021) Maiden application of fractional order PID plus second order derivative controller in automatic voltage regulator. Int Trans Electr Energy Syst 31(12):e13211
Çavdar B, Şahin E, Akyazı Ö, Nuroğlu FM (2023) A novel optimal PI \(\lambda \) 1 I \(\lambda \) 2 D \(\mu \) 1 D \(\mu \) 2 controller using mayfly optimization algorithm for automatic voltage regulator system. Neural Comput Appl 66:1–20
Paliwal N, Srivastava L, Pandit M (2022) Rao algorithm based optimal Multi-term FOPID controller for automatic voltage regulator system. Opt Control Appl Methods 43(6):1707–1734
Al Gizi AJ (2019) A particle swarm optimization, fuzzy PID controller with generator automatic voltage regulator. Soft Comput 23(18):8839–8853
Shayeghi H, Younesi A, Hashemi Y (2015) Optimal design of a robust discrete parallel FP + FI + FD controller for the automatic voltage regulator system. Int J Electr Power Energy Syst 67:66–75
Furat M, Cücü GG (2022) Design, implementation, and optimization of sliding mode controller for automatic voltage regulator system. IEEE Access 10:55650–55674
Elsisi M (2019) Design of neural network predictive controller based on imperialist competitive algorithm for automatic voltage regulator. Neural Comput Appl 31(9):5017–5027
Ayas MS, Sahin AK (2023) A reinforcement learning approach to automatic voltage regulator system. Eng Appl Artif Intell 121:106050
Ayas MS (2019) Design of an optimized fractional high-order differential feedback controller for an AVR system. Electr Eng 101(4):1221–1233
Bhookya J, Jatoth RK (2019) Optimal FOPID/PID controller parameters tuning for the AVR system based on sine-cosine-algorithm. Evol Intell 12:725–733
Izci D, Ekinci S, Zeynelgil HL, Hedley J (2021) Fractional order PID design based on novel improved slime Mould algorithm. Electr Power Compon Syst 49(9–10):901–918
Gaing ZL (2004) A particle swarm optimization approach for optimum design of PID controller in AVR system. IEEE Trans Energy Convers 19(2):384–391
Gozde H, Taplamacioglu MC (2011) Comparative performance analysis of artificial bee colony algorithm for automatic voltage regulator (AVR) system. J Frankl Inst 348(8):1927–1946
Tang Y, Cui M, Hua C, Li L, Yang Y (2012) Optimum design of fractional order PI\(\lambda \)D\(\mu \) controller for AVR system using chaotic ant swarm. Expert Syst Appl 39(8):6887–6896
Zeng GQ, Chen J, Dai YX, Li LM, Zheng CW, Chen MR (2015) Design of fractional order PID controller for automatic regulator voltage system based on multi-objective extremal optimization. Neurocomputing 160:173–184
Lahcene R, Abdeldjalil S, Aissa K (2017) Optimal tuning of fractional order PID controller for AVR system using simulated annealing optimization algorithm. In: 2017 5th International conference on electrical engineering-Boumerdes (ICEE-B), pp. 1–6. IEEE (2017)
Bingul Z, Karahan O (2018) A novel performance criterion approach to optimum design of PID controller using cuckoo search algorithm for AVR system. J Frankl Inst 355(13):5534–5559
Ekinci S, Hekimoğlu B (2019) Improved kidney-inspired algorithm approach for tuning of PID controller in AVR system. IEEE Access 7:39935–39947
Micev M, Ćalasan M, Oliva D (2020) Fractional order PID controller design for an AVR system using chaotic yellow saddle goatfish algorithm. Mathematics 8(7):1182
Ekinci S, Izci D, Eker E, Abualigah L (2022) An effective control design approach based on novel enhanced aquila optimizer for automatic voltage regulator. Artif Intell Rev 66:1–32
Izci D, Ekinci S, Zeynelgil HL, Hedley J (2022) Performance evaluation of a novel improved slime Mould algorithm for direct current motor and automatic voltage regulator systems. Trans Inst Meas Control 44(2):435–456
Gupta S, Deep K, Mirjalili S, Kim JH (2020) A modified sine cosine algorithm with novel transition parameter and mutation operator for global optimization. Expert Syst Appl 154:113395
Jumani TA, Mustafa MW, Hussain Z, Rasid MM, Saeed MS, Memon MM et al (2020) Jaya optimization algorithm for transient response and stability enhancement of a fractional-order PID based automatic voltage regulator system. Alex Eng J 59(4):2429–2440
Altbawi SMA, Mokhtar ASB, Jumani TA, Khan I, Hamadneh NN, Khan A (2021) Optimal design of Fractional order PID controller based automatic voltage regulator system using gradient-based optimization algorithm. J King Saud Univ Eng Sci 6:66
Micev M, Ćalasan M, Ali ZM, Hasanien HM, Aleem SHA (2021) Optimal design of automatic voltage regulation controller using hybrid simulated annealing-Manta ray foraging optimization algorithm. Ain Shams Eng J 12(1):641–657
Ateş A, Alagöz BB, Yeroğlu C, Alisoy H (2015) Sigmoid based PID controller implementation for rotor control. In: 2015 European control conference (ECC). IEEE, pp 458–463
Soons MB, Heil GW, Nathan R, Katul GG (2004) Determinants of long-distance seed dispersal by wind in grasslands. Ecology 85(11):3056–3068
Zhao S, Zhang T, Ma S, Chen M (2022) Dandelion optimizer: a nature-inspired metaheuristic algorithm for engineering applications. Eng Appl Artif Intell 114:105075
Paliwal N, Srivastava L, Pandit M (2021) Equilibrium optimizer tuned novel FOPID-DN controller for automatic voltage regulator system. Int Trans Electr Energy Syst 31(8):e12930
Mohanty PK, Sahu BK, Panda S (2014) Tuning and assessment of proportional-integral-derivative controller for an automatic voltage regulator system employing local unimodal sampling algorithm. Electr Power Compon Syst 42(9):959–969
Sikander A, Thakur P, Bansal RC, Rajasekar S (2018) A novel technique to design cuckoo search based FOPID controller for AVR in power systems. Comput Electr Eng 70:261–274
Jumani TA, Mustafa MW, Rasid MM, Memon ZA (2020) Dynamic response enhancement of grid-tied ac microgrid using salp swarm optimization algorithm. Int Trans Electr Energy Syst 30(5):e12321
Sahu RK, Panda S, Rout UK, Sahoo DK (2016) Teaching learning based optimization algorithm for automatic generation control of power system using 2-DOF PID controller. Int J Electr Power Energy Syst 77:287–301
Tabak A (2021) A novel fractional order PID plus derivative (PI\(\lambda \)D\(\mu \)D\(\mu \)2) controller for AVR system using equilibrium optimizer. COMPEL Int J Comput Math Electr Electron Eng 6:66
Munagala VK, Jatoth RK (2022) Improved fractional PI\(\lambda \)D\(\mu \) controller for AVR system using chaotic black widow algorithm. Comput Electr Eng 97:107600
Khan IA, Alghamdi AS, Jumani TA, Alamgir A, Awan AB, Khidrani A (2019) Salp swarm optimization algorithm-based fractional order PID controller for dynamic response and stability enhancement of an automatic voltage regulator system. Electronics 8(12):1472
Modabbernia M, Alizadeh B, Sahab A, Moghaddam MM (2020) Robust control of automatic voltage regulator (AVR) with real structured parametric uncertainties based on H\(\infty \) and \(\mu \)-analysis. ISA Trans 100:46–62
Funding
Open access funding provided by the Scientific and Technological Research Council of Türkiye (TÜBİTAK).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
We wish to indicate that we do not have any conflict of interest to declare.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sahin, A.K., Cavdar, B. & Ayas, M.S. An adaptive fractional controller design for automatic voltage regulator system: sigmoid-based fractional-order PID controller. Neural Comput & Applic (2024). https://doi.org/10.1007/s00521-024-09816-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00521-024-09816-6