Introduction

With the development of Global Positioning System (GPS), GLObal NAvigation Satellite System (GLONASS), Galileo satellite navigation system (Galileo), and BeiDou Navigation Satellite System (BDS), Global Navigation Satellite System (GNSS) plays an important role in the Positioning, Navigation, and Timing (PNT) nowadays, especially for the high-precision applications (Teunissen and Montenbruck 2017). Due to its advantages of cost-efficiency, flexibility, and global coverage, the Precise Point Positioning (PPP) proposed by Zumberge et al. (1997) has been one of the most promising techniques in both science and engineering. e.g., earthquake and tsunami early warning, GNSS-based weather forecasting navigation, etc. (Kouba and Héroux 2001; Guerova et al. 2016; Yigit and Gurlek 2017). However, compared with the traditional Real-Time Kinematic (RTK) technique, the PPP in Real-Time (RT) applications is hindered by its long convergence time, typically 30 min.

To overcome this problem, Gabor and Nerem (1999) first presented the work on integer Ambiguity Resolution (AR) in PPP with Single Differenced (SD) observations. The key point is that the fractional-cycle part of the carrier phase ambiguity that destroys its integer property should be estimated from a network for each satellite, and then applied for the users to enable its AR (Geng et al. 2019). Based on this principle, different models, e.g., Uncalibrated Phase Delay (UPD), integer clock and decoupled clock, etc., have been developed since then (Ge et al. 2008; Laurichesse et al. 2009; Collins et al. 2010). In addition, the recent advances in multi-frequency multi-GNSS data processing have provided the ways for a more reliable and efficient AR in PPP (Gu et al. 2015a, b). These studies are classified into the optimal combination of multi-GNSS multi-frequency observations, and the signal bias modeling and correction for pseudo range and carrier phase. The former includes the studies to find the basic observation as the alternatives to the traditional Ionosphere Free (IF) combination that originally formulated for dual-frequency observations. Notably there is an undifferenced and uncombined GNSS model in which the individual signals from the various frequencies of multi-GNSS are incorporated in a single parameter estimation system directly, giving its flexibility in a multi-frequency multi-GNSS environment (Sch \(\ddot{\mathrm{o}}\) nemann et al. 2011; Gu et al., 2015a, b). The latter mainly focuses on the bias calibration to align the signals generated from different channels, which removes the inconsistencies in multi-frequency multi-GNSS data processing due to hardware delay (Hauschild and Montenbruck 2016; Lou et al. 2017). Among other benefits with increasing number of signals, Partial Ambiguity Resolution (PAR) can be significantly improved in which a sufficiently large subset of ambiguities is selected instead of resolving the complete vector of integer ambiguities (Teunissen et al. 1999). Psychas et al. (2021) further argued that the contribution of multi-frequency observations in PPP AR is significant and largely driven by frequency separation. However, with multi-frequency multi-GNSS the PPP with PAR still needs about 5 min to get a position precision better than 10 cm (Psychas et al. 2020).

Aside from multi-frequency multi-GNSS PAR, the constraint of the priori ionospheric information presents another way to speed up PPP convergence, especially by considering the undifferenced and uncombined PPP model, in which the ionospheric delay cannot be eliminated as the IF model (Zhao et al. 2018). Obviously, the performance of the ionospheric delay model plays an important role in the ionosphere constrained undifferenced uncombined PPP (e.g. Olivares-Pulido et al. 2021).

The worldwide distributed GNSS Continuously Operating Reference Station (CORS) can measure the Total Electron Content (TEC) with an unprecedented temporal and spatial resolution. Thus, GNSS is regarded as an excellent ionospheric sounding system nowadays. Attribute to the continued efforts of the Ionosphere Working Group (Iono-WG) within the International GNSS Service (IGS) community, the Global Ionosphere Maps (GIM) have been independently generated on a regular basis by Different Ionospheric Associate Analysis Centers (IAACs) since 1998 with a typical latency of several days (Schaer 1999; Li et al. 2012; Li et al. 2019; Liu et al. 2018). To cope with the requirements of real-time (RT) GNSS data processing, IGS further issued a call for participation in IGS RT Pilot Project (IGS-RTPP) in 2007 (Caissy et al. 2012), and over 200 IGS stations now provide real-time observations with a sampling rate of 1 Hz (Romero et al. 2018). More recently, several IAACs, including Centre National dÉtudes Spatiales (CNES), Chinese Academy of Sciences (CAS), Technical University of Catalonia (UPC-IonSAT), and Wuhan University (WHU) started to provide RT GIM products publicly by Networked Transport of Radio Technical Commission for Maritime (RTCM) via Internet Protocol (NTRIP) (Liu et al. 2021). Since then, a wide range of valuable literature has been published concerning the precision evaluation of the GIM products (Hernández-Pajares et al. 2009), as well as its performance in the applications of space weather monitoring and high precision positioning augmentation (Hernández-Pajares et al. 2017). Depending on the stations involved, solar activity, and data processing models (post or real time), the results suggested that the precision of GIM usually varies from 0.32–1.28 m on GPS L1 (Wielgosz et al. 2021). Though these studies illustrated the efficiency of GIM in the ionospheric constrained PPP, especially for the single-frequency, the improvement is rather limited in the real time centimeter (cm) level positioning, i.e., PPP-RTK (Rovira-Garcia et al. 2015).

An efficient way to improve the precision of ionospheric delay correction is to interpolate the Slant Ionospheric Delay (SID) along Line of Sight (LOS) from a regional network for each satellite. As demonstrated by Teunissen et al. (2010), this network-based PPP has the comparable performance with that of Network-RTK (NRTK). It should be noted that the receiver biases are absorbed by the ionospheric delay to remove the rank deficiency, thus special attention should be given to the SID modeling for inconsistent receiver networks. Shi et al. (2012b) and Zhao et al. (2018) presented a sophisticated ionospheric parameter constrain model, i.e., DEterministic plus Stochastic Ionosphere models for GNSS (DESIGN), and it was demonstrated that the ionospheric delay can be separated from the receiver biases in this case (Gu et al. 2020; Zhang et al. 2021). Typically, the SID modeling performs much better than that of GIM since it uses the LOS ionospheric delay in modelling directly, thus avoiding the errors induced by the elevation mapping function and the constant-height thin-layer model (Li et al. 2017). Though the LOS ionospheric delays are highly correlated with each other for a small network, it can be hardly extended to wide-area ionospheric delay modeling. As a result, the networks involved in the above-mentioned study are rather small with a typical baseline length of around 15 km and 50 km, respectively (Teunissen et al. 2010).

In summary, both GIM and SID models are widely used nowadays, respectively, for wide-area coverage and high precision. In this study, we proposed a novel approach, the Quasi-4-Dimension Ionospheric Modeling (Q4DIM), which takes the advantages of both models. Besides the latitude and longitude factors in GIM modeling, the elevation and azimuth are further optionally considered in Q4DIM, thus both GIM and SID models can be regarded as the special cases of Q4DIM with specified grid division approach along latitude, longitude, elevation, and azimuth. In addition, it is demonstrated that Q4DIM is sparse as a 4-dimension (optional) grid matrix, and the sparse storage technique is suggested to improve the efficiency. This paper is organized as follows: Q4DIM is first introduced; then its property is analyzed by a comparison with the GIM and SID models; finally, the performance of Q4DIM is assessed in both Single-Frequency (SF) and Dual-Frequency PPP (DF-PPP) with the one month’s data in 2014 and 2020.

Q4DIM

As the estimation of the LOS ionospheric delay from a GNSS satellite has been discussed in many publications, we start the Q4DIM with a set of LOS ionospheric delays directly. Concerning the details of GNSS ionospheric delay estimation of this work, we refer to the study in Shi et al. (2012b); Zhao et al. (2018), in which the undifferenced and uncombined model constrained with DESIGN is utilized. Suppose that we generated a set of LOS ionospheric delays with \(j\) satellites and \(k\) receivers as:

$$\begin{array}{*{20}c} {I = \left\{ {I_{r}^{s} } \right\}} & {\text{s.t.}\left( {\begin{array}{*{20}c} {\text{subject}} & {\text{to}} \\ \end{array} } \right)} & {s \in \left( {1 \cdots {\kern 1pt} j} \right),r \in \left( {1 \cdots k} \right)} \\ \end{array}$$
(1)

Our purpose is to divide the whole set \(I\) into n pre-defined clusters \(C = \left\{ {C_{i} } \right\} \left( {i \in \left( {1 \cdots n} \right)} \right)\), and the ionospheric delay samples in each cluster are highly correlated with each other.

Algorithm

For a given network, we can select the grids in latitude, longitude, elevation, and azimuth as

$$\left\{ \begin{gathered} {\varvec{b}} = \left( {b_{1} \cdots b_{n(b)} } \right) \hfill \\ {\varvec{l}} = \left( {l_{1} \cdots l_{n(l)} } \right) \hfill \\ {\varvec{e}} = \left( {e_{1} \cdots e_{n(e)} } \right) \hfill \\ {\varvec{a}} = \left( {a_{1} \cdots a_{n(a)} } \right) \hfill \\ \end{gathered} \right.$$
(2)

where \(n\left( b \right)\), \(n\left( l \right)\), \(n\left( e \right)\), and \(n\left( a \right)\) are the number of grids in latitude, longitude, elevation, and azimuth, respectively, which are selected to balance data volume and model precision according to the demand. Then \({\varvec{b}}\), \({\varvec{l}}\), \({\varvec{e}}\), and \({\varvec{a}}\) can be determined by uniform spatial subdivision for a given region and the selected number \(n\left( b \right)\), \(n\left( l \right)\), \(n\left( e \right)\), and \(n\left( a \right)\) directly. The total number of clusters is

$$n = n\left( b \right) \cdot n\left( l \right) \cdot n\left( e \right) \cdot n\left( a \right)$$
(3)

For the i-th cluster \(C_{i}\), it is defined with its center point \({\varvec{o}}_{{\varvec{i}}}\) as

$$\begin{array}{*{20}c} {C_{i} ({\varvec{o}}_{{\varvec{i}}} ){\kern 1pt} } & {\text{s.t.}{\kern 1pt} } & {{\varvec{o}}_{{\varvec{i}}} = \left( {\begin{array}{*{20}c} {b_{i(b)} } & {l_{i(l)} } & {e_{i(e)} } & {a_{i(a)} } \\ \end{array} } \right)^{\text{T}} ,{\varvec{i}} = \left( {\begin{array}{*{20}c} {i_{b} } & {i_{l} } & {i_{e} } & {i_{a} } \\ \end{array} } \right) \cdot {\varvec{d}}_{{{\mathbf{ldm}}}} } \\ \end{array}$$
(4)

with \(b_{i(b)} \in {\varvec{b}},l_{i(l)} \in {\varvec{l}},e_{i(e)} \in {\varvec{e}},a_{i(b)} \in {\varvec{a}}\); \({\varvec{d}}_{{{\mathbf{ldm}}}} = \left( {\begin{array}{*{20}c} {l_{b} } & {l_{l} } & {l_{e} } & {l_{a} } \\ \end{array} } \right)^{\text{T}}\) being the leading dimension for latitude, longitude, elevation, and azimuth, respectively,

$$\left\{ \begin{gathered} l_{b} = n_{l} \cdot n_{e} \cdot n_{a} \hfill \\ l_{l} = n_{e} \cdot n_{a} \hfill \\ l_{e} = n_{a} \hfill \\ l_{a} = 1 \hfill \\ \end{gathered} \right.$$
(5)

For the slant ionospheric delay \(I_{r}^{s}\) in Eq. (1), the corresponding LOS vector \({\varvec{L}}_{{{\text{LOS}}}} = \left( {\begin{array}{*{20}c} b & l & e & a \\ \end{array} } \right)^{\text{T}}\) can be uniquely determined for specific satellites and receivers. For a specific LOS, \(b\) and \(l\) are the latitude and longitude of Ionospheric Pierce Point (IPP), and \(e\) and \(a\) are the elevation and azimuth that can be derived from the coordinates of the receiver and satellite, thus the set of slant ionospheric delays in Eq. (1) can be rewritten as \(I = \left\{ {I_{L}^{{\text{LOS}}} } \right\}\). Then with the clusters defined by Eq. (2–5), each \(I_{L}^{{\text{LOS}}}\) can be grouped into cluster \(C_{i}\) by iterating over the set \(I\)

$$\begin{array}{*{20}c} {C_{i} = \left\{ {I_{L}^{{\text{LOS}}} } \right\}} & {\text{st.}} & {\forall j \in \left( {1 \cdots n} \right)} & {\begin{array}{*{20}c} \to & {\left\| {{\varvec{L}}_{{\text{LOS}}} - {\varvec{o}}_{{\varvec{i}}} } \right\|} \\ \end{array} } \\ \end{array} \le \left\| {{\varvec{L}}_{{\text{LOS}}} - {\varvec{o}}_{{\varvec{j}}} } \right\|$$
(6)

where \(\left\| \cdot \right\|\) denotes the 1-norm of the corresponding vector. Thus, for the cluster \(C_{i}\), its averaged LOS ionospheric delay \(\mu_{i}\) and STandard Deviation (STD) \(\sigma_{i}\) are derived as:

$$\left\{ \begin{gathered} \mu_{i} = \frac{1}{{\left| {C_{i} } \right|}}\sum\limits_{m = 1}^{n} {I_{L}^{{\text{LOS}}} (m)} \hfill \\ \sigma_{i} = \sqrt {\frac{1}{{\left| {C_{i} } \right|}}\sum\limits_{m = 1}^{n} {\left( {I_{L}^{{\text{LOS}}} (m) - \mu_{i} } \right)^{2} } } \hfill \\ \end{gathered} \right.$$
(7)

in which \(I_{L}^{{\text{LOS}}} (m)\) and \(C_{i}\) denote the samples and the number of samples, respectively.

Having derived the numerical characteristics, i.e., \(\mu_{i}\), \(\sigma_{i}\), for each cluster \(C_{i} ({\varvec{o}}_{{\varvec{i}}} )\), a straightforward way to represent the whole clusters is in a large matrix. However, the direct processing of the whole matrix is costly and usually not applicable due to a large number of clusters. Moreover, it is also not necessary as the matrix is rather sparse, i.e., in most cases the number of samples in a cluster \(\left| {C_{i} } \right| = 0\), due to a limited distribution of both satellites and receivers. Thus, only those clusters with sufficient samples, e.g., \(\left| {C_{i} } \right| \ge 2\), are retained in Q4DIM in a key-value form

$$\begin{array}{*{20}c} {C_{{\text{map}}} } & : & {\begin{array}{*{20}c} i & - & {\left( {\begin{array}{*{20}c} {\mu_{i} } & {\sigma_{i} } \\ \end{array} } \right)} \\ \end{array} } \\ \end{array}$$
(8)

Obviously, for the Q4DIM users, its cluster index \(i_{u}\) of a given LOS vector \({\varvec{L}}_{u}^{{{\text{LOS}}}}\) can be obtained with Eqs. (2) and (4), then the corresponding ionospheric delay corrections can be obtained by looking up the key-value map defined by Eq. (8). In addition, \(\sigma_{i}\) is the precision indicator for each cluster and can also be used for weighting in the user ionospheric delay correction with Q4DIM. We also define the STD \(\sigma\) in Q4DIM as the averaged value of the STD for all cluster \(\sigma_{i}\) in Eq. (7)

$$\sigma = \frac{{\sum\limits_{i = 1}^{n} {\sigma_{i} } }}{n}$$
(9)

Discussion

Recall the grids in Eq. (2), the popular GIM model can be regarded as a special case of Q4DIM once the empty set is selected for both elevation and azimuth, i.e., \({\varvec{e}} = \user2{\emptyset },{\varvec{a}} = \user2{\emptyset }\). However, since the sparse representation and processing technique is promoted in Q4DIM to improve its efficiency, the ionospheric delay corrections are not available for all the grids as that of GIM. To overcome this dilemma, the LOS ionospheric delay is further divided into deterministic and stochastic parts, i.e., \(I_{L}^{{{\text{LOS}}(0)}}\), \(r_{L}^{{{\text{LOS}}}}\), as that of DESIGN (Shi et al., 2012b; Zhao et al., 2018)

$$I_{L}^{{{\text{LOS}}}} = I_{L}^{{{\text{LOS}}(0)}} + r_{L}^{{{\text{LOS}}}}$$
(10)

while \(I_{L}^{{{\text{LOS}}(0)}}\) can be either interpolated from grids or calculated with the Spherical Harmonic Function (SHF) of GIM with a mapping function. Then the set of ionospheric delay residuals \(r = \left\{ {r_{L}^{{{\text{LOS}}}} } \right\}\) can be grouped into different clusters and represented with a key-value map following the procedure in the algorithm section.

For the Q4DIM users, the ionospheric delay corrections of any LOS \({\varvec{L}}_{u}^{{{\text{LOS}}}}\) are obtained as:

$$I_{L}^{{{\text{LOS(}}u)}} = I_{L}^{{{\text{LOS(}}u,0)}} + \left\{ \begin{gathered} r_{L}^{{{\text{LOS(}}u)}} , \, C_{{\text{map}}} \left( {i_{u} } \right) \ne \emptyset \hfill \\ 0, \, C_{{\text{map}}} \left( {i_{u} } \right) = \emptyset \hfill \\ \end{gathered} \right.$$
(11)

Here again \(I_{L}^{{{\text{LOS(}}u,0)}}\) is either interpolated from grids or calculated with the SHF of GIM. Concerning the stochastic part \(r_{L}^{{{\text{LOS(}}u)}}\), the key \(i_{u}\) may exist in the Q4DIM map, then the ionospheric delay correction is further refined with the residual. Otherwise, the model is equivalent to GIM.

In addition to its compatibility with GIM model, we further argue that the SID model, which is widely accepted in the regional network augmentation, is also a special case of Q4DIM model

$$\begin{array}{*{20}c} {\exists C = \left\{ {C_{i} } \right\}} & {\text{s.t.}} & {\max \left( {\left| {C_{i} } \right|} \right) = 1} & {\forall i \in \left( {\begin{array}{*{20}c} 1 & \cdots & n \\ \end{array} } \right)} \\ \end{array}$$
(12)

In the selection of clusters there exists the case that each cluster contains only one sample \(I_{L}^{{{\text{LOS}}}} = r_{L}^{{{\text{LOS}}}}\) at most. Then the key-value map consists of individual LOS ionospheric delays, i.e., SID model.

As a result, according to the grid definition in Eq. (2), Q4DIM presents a resilient model that is usable for both wide-area coverage and high precision.

$$\underbrace {{{\varvec{o}}_{{\varvec{i}}} = \left( {\begin{array}{*{20}c} {b_{i(b)} } & {l_{i(l)} } \\ \end{array} } \right)^{\text{T}} }}_{{\begin{array}{*{20}c} {\text{GIM}} & {\text{case}} \\ \end{array} }}\xleftarrow{{{\varvec{e}} = \emptyset ,{\varvec{a}} = \emptyset }}C = \left\{ {C_{i} ({\varvec{o}}_{{\varvec{i}}} )} \right\}\mathop{\longrightarrow}\limits_{{\begin{array}{*{20}c} {\text{defined}} & {\text{sufficiently}} & {\text{fine}} \\ \end{array} }}^{{{\varvec{b}},{\varvec{l}},{\varvec{e}},{\varvec{a}}}}\underbrace {{\max (\left| {C_{i} } \right|) = 1}}_{{\begin{array}{*{20}c} {\text{SID}} & {\text{case}} \\ \end{array} }}$$

Several statements should be emphasized here. First, though the LOS ionospheric delay is used in the algorithm derivation, we can also convert it to the vertical in Q4DIM without considering the mapping function error, as this error is elevation angle dependent and can be much compensated with a similar elevation angle for each cluster in modeling and positioning. Secondly, we can use GIM/RT-GIM from IGS, or even the broadcast ionospheric models, e.g., KLOBUCHAR, as the deterministic ionospheric delay \(I_{L}^{{{\text{LOS}}(0)}}\) directly. In this sense Q4DIM is compatible with the existing model. Thirdly, the stochastic part \(r_{L}^{{{\text{LOS}}(u)}}\) stands for the irregular spatial and temporal variations, and is the key to improve the ionospheric delay precision. It typically requires a much higher spatial–temporal resolution. Thus, by separating \(r_{L}^{{{\text{LOS}}(u)}}\) from the large deterministic part, it can be represented with fewer data and consequently has the advantage to compress the data volume, which is of special importance for real-time service. Finally, we denote the model as quasi-4-dimension since it is not a direct extension of the widely acknowledged 3-dimensional model, i.e., the tomography ionospheric model. In addition, it may also be a 2-dimensional model like that of GIM as we pointed out.

Experimental validation

To assess the performance of Q4DIM, the above algorithm is realized with the FUSing IN Gnss (FUSING) software and validated with both SF-PPP and DF-PPP in the following experiment. Up to now, FUSING is capable for real-time multi-GNSS precise orbit determination (Gong et al. 2018; Lou et al. 2022), satellite clock and bias estimation (Guo et al. 2022; Lou et al. 2017; Shi et al. 2016, 2019; Zhang et al. 2020), atmosphere modeling (Zheng et al. 2017; Luo et al. 2020; Luo et al. 2021), and multi-sensor navigation (Gu et al. 2021; Gu et al. 2022).

Data and processing strategy

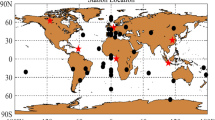
The experiment was carried out with the data of EUREF Permanent Network (EPN). As shown in Fig. 1, the 200 stations in red were used for Q4DIM, and the 30 stations in blue were used for PPP. The observations were collected over the period of Day Of Year (DOY) 001 to 030 in high solar activity year 2014 and low solar activity year 2020, with an interval of 30 s. The detail of the experiment is illustrated in Table 1. In addition, as presented in Table 2, four solutions for Q4DIM denoted as A, B, C, and D with different grid definitions were first compared. Then, the performance of Q4DIM in PPP was assessed in terms of convergence time and precision.

Fig. 1
figure 1

Distribution of 230 tracking stations over Europe, in which the red denoted 200 stations are used for Q4DIM, while the blue denoted 30 stations are used for PPP

Full size image
Table 1 Details of the experiment
Full size table
Table 2 Q4DIM strategy
Full size table

Comparison of Q4DIM

To get an intuitive impression on Q4DIM, we presented the LOS for the original SID, as well as LOS of each cluster, i.e., \({\varvec{o}}_{{\varvec{i}}}\) in Eq. (4) for different solutions in Fig. 2. As we can see, by defining different clusters with Table 2, Q4DIM presents a rather flexible algorithm with resilient resolution and precision that satisfies different requirements on modeling precision, coverage, and data volume (Yang 2019). As we pointed out, Q4DIM is a GIM-like 2-dimensional map once we ignore the residual part \(r_{L}^{{{\text{LOS}}}}\) in Eq. (10), denoted as Q4DIM-2D, and this is also the case that an empty set is selected for both elevation and azimuth, \({\varvec{e}} = \user2{\emptyset },{\varvec{a}} = \user2{\emptyset }\). While the corresponding results are presented in Fig. 3 for different solutions. Recall Table 2, the number of grids over latitude and longitude is 12 × 8, 24 × 16, 36 × 24 and 48 × 32 for solutions A, B, C, and D, respectively. As expected, more detailed ionospheric delay structure can be revealed with a higher spatial resolution as illustrated in Fig. 3. Concerning the precision of different Q4DIM solutions in Fig. 4, we presented the series of \(\sigma\) defined by Eq. (9) on DOY 001, 2020 as an example. As we can see, the precision can be hardly improved with the higher spatial resolution over latitude and longitude. This is reasonable since the error in this case is most likely due to the mapping function and anisotropy. This result is in line with the previous studies on GIM, in which it is suggested that the precision of 2-dimensional modeling can be hardly improved by increasing the degrees of SH function (Yunbin et al. 2017; Zhao et al. 2018).

Fig. 2
figure 2

The LOS map for the original SID, and each cluster, i.e., \({\varvec{o}}_{{\varvec{i}}}\) in Eq. (4) for solution A (12 × 8 × 6 × 25), solution B (24 × 16 × 12 × 50), solution C (36 × 24 × 18 × 75), and solution D (48 × 32 × 24 × 100)

Full size image
Fig. 3
figure 3

Distribution of the 2-dimensional TEC map with the resolution of \(12\times 8\), \(24\times 16\), \(36\times 24\), and \(48\times 32\) in latitude and longitude for Q4DIM-2D on DOY 001, 2020

Full size image
Fig. 4
figure 4

Series of \({\sigma }_{i}\) in Eq. (9) for Q4DIM-2D TEC map of solution A (black) \(12\times 8\), solution B (red) \(24\times 16\), solution C (green) \(36\times 24\) and solution D (blue) \(48\times 32\) on DOY 001, 2020

Full size image

To solve the above dilemma, Q4DIM introduces the residual ionospheric delay correction as Eq. (10) for each 2-dimensional grid, and the residual is further divided according to its elevation and azimuth angle. Selecting a latitude and longitude grid arbitrarily for each solution, Figs. 5, 6, 7, 8 present the distribution of the statistics defined by Eq. (7), i.e., number of samples \(\left| {C_{i} } \right|\), averaged LOS ionospheric delay \(\mu_{i}\), and standard deviation \(\sigma_{i}\) for each cluster. While the top two sub-plots present \(\left| {C_{i} } \right|\), the left-bottom sub-plot presents \(\mu_{i}\), and the right-bottom sub-plot presents \(\sigma_{i}\). Taking Fig. 5 of solution A as an example, for each 2-dimensional grid, it is further divided into 6 × 25 grids according to the elevation and azimuth angle. As indicated by the left-top sub-plot, the Q4DIM clusters are sparse as a 4-dimensional grid matrix since only a few grids have enough samples, i.e., \(\left| {C_{i} } \right| \ge 2\). Thus, the left three sub-plots are enlarged for those grids with enough samples. From the left-bottom sub-plot, it is noted that the residuals \(\mu_{i}\) for different grids vary from around -1.9 to 3.6 Total Electron Content Units (TECU), and they are exactly the errors in 2-dimensional TEC map in Fig. 5. By correcting these residuals, the precision can be improved significantly as implied by the right-bottom sub-plot with less than 0.5 TECU. While, for solution B to solution D, a similar conclusion can be derived from Figs. 5, 6, 7, 8, the latitude and longitude are different since the grids of each solution are different as derived with Eq. (2). Thus, for comparison purpose, we selected the grid points of different solutions relatively close to each other in these figures.

Fig. 5
figure 5

Distribution of \(\left| {C_{i} } \right|\) (the top two sub-plots), μi (the left-bottom sub-plot), σi (the right-bottom sub-plot) in Eq. (7) against elevation angle and azimuth angle for latitude 64.6° and longitude 40.7° of solution A (\(12\times 8\times 6\times 25\)) on DOY 001, 2020

Full size image
Fig. 6
figure 6

Distribution of \(\left| {C_{i} } \right|\) (the top two sub-plots), μi (the left-bottom sub-plot), σi (the right-bottom sub-plot) in Eq. (7) against elevation angle and azimuth angle for latitude 65.6° and longitude 41.7° of solution B (\(24\times 16\times 12\times 50\)) on DOY 001, 2020

Full size image
Fig. 7
figure 7

Distribution of \(\left| {C_{i} } \right|\) (the top two sub-plots), μi (the left-bottom sub-plot), σi (the right-bottom sub-plot) in Eq. (7) against elevation angle and azimuth angle for latitude 65.9° and longitude 42.0° of solution C (\(36\times 24\times 18\times 75\)) on DOY 001, 2020

Full size image
Fig. 8
figure 8

Distribution of \(\left| {C_{i} } \right|\) (the top two sub-plots), μi (the left-bottom sub-plot), σi (the right-bottom sub-plot) in Eq. (7) against elevation angle and azimuth angle for latitude 71.3° and longitude 32.4° of solution D (\(48\times 32\times 24\times 100\)) on DOY 001, 2020

Full size image

In Fig. 9 we further present the series of averaged STD σ in Eq. (9) for different solutions. As expected, with a higher resolution in the latitude, longitude, elevation, and azimuth, the precision of Q4DIM is improved from 0.46 TECU to 0.22 TECU, the number of valid clusters increased from 0.6 to 6.5 K, the sparsity rate dropped from 4.4 to 0.2%, and correspondingly the number of LOS per cluster dropped from 9.7 to 3.3. By a comparison with the result in Fig. 4, it is argued that the ionospheric delay modeling precision can be improved significantly by taking elevation and azimuth into consideration. Besides the precision, the data volume is also a critical issue for the bandwidth-sensitive applications, e.g., satellite-based PPP-RTK service (Zhang et al. 2020). Figures 5, 6, 7, 8 already demonstrate that the 4-dimensional matrix is sparse. Thus, the two middle sub-plots of Fig. 9 show the series of the number of valid clusters, i.e., the clusters with, and the sparsity rate that defines as the ratio of the number of valid clusters to the total number of clusters n in Eq. (3). Taking solution B as an example, though there are 230 400 clusters in total, the number of valid clusters is around 2 100, and the sparsity rate is 0.9%. The results are promising and implies that the Q4DIM has the potential to be used for wide-area satellite-based augmentation service with a precision of better than 0.5 TECU. Finally, the bottom sub-plot gives the series of the LOS number for each valid cluster.

Fig. 9
figure 9

Time series of \(\sigma\), number of valid clusters, sparsity rate and number of LOS per cluster for different Q4DIM solutions on DOY 001, 2020

Full size image

PPP

Based on the discussion in Sect. 3.2, Q4DIM with solution B is selected and further validated in both SF-PPP and DF-PPP. The rover stations are denoted in blue as shown in Fig. 1. Four solutions with different ionospheric delay elimination strategies as presented in Table 3, i.e., IF, CODG, Q4DIM-2D, and Q4DIM are compared for both SF-PPP and DF-PPP. Concerning the IF strategy, we used the GRoup And PHase Ionosphere Calibration (GRAPHIC) approach for SF-PPP (Shi et al. 2012b), and the widely acknowledged IF combination for DF-PPP (Lou et al. 2015). Though the stations are static, they are all processed in kinematic model with a forward square root information filter, and the filters restarted every hour. Then the convergence serial in 68% confidence level and the Root Mean Square (RMS) with the last 20 min series of all the one-hour samples were derived.

Table 3 PPP strategy
Full size table

As we can see from the SF-PPP series in Figs. 10 and 11, the solution with undifferenced and uncombined observations constrained with DESIGN performs much better than that of the traditional IF-PPP. In addition, though CODG and Q4DIM-2D are both 2-dimensional GIM-like ionospheric models, Q4DIM-2D performs better since more local stations participated in the ionospheric delay modeling. While Q4DIM performs the best among all the ionospheric augmentation SF-PPP solutions in both vertical and horizontal directions. Its better performance over Q4DIM-2D demonstrates the advantage of elevation and azimuth angle division.

Fig. 10
figure 10

Single frequency PPP convergence serial for DOY 001–030, 2014, respectively. While for different ionospheric delay processing mode with IF, CODG, Q4DIM-2D and Q4DIM, the results are denoted in black, red, green, and blue, respectively

Full size image
Fig. 11
figure 11

Single frequency PPP convergence serial for DOY 001–030, 2020, respectively. While for different ionospheric delay processing mode with IF, CODG, Q4DIM-2D and Q4DIM, the results are denoted in black, red, green, and blue, respectively

Full size image

The DF-PPP series are further presented in Figs. 12 and 13 for 2014 and 2020, respectively. Different from SF-PPP, the 2D GIM-like ionospheric model augmented PPP, i.e., CODG and Q4DIM-2D, is only slightly better than that of IF-PPP, and the result is in line with our previous studies (Lou et al. 2015). While the performance of CODG and Q4DIM-2D in DF-PPP are almost the same. This is reasonable since that the DF-PPP is less sensitive to ionospheric delay, and the accuracy of CODG and Q4DIM-2D, typically has the value of a few TECU, is limited for high-precision positioning, thus the effect is not significant. While by comparing Figs. 4 and 9, since the accuracy is improved from about 1.5 TECU of Q4DIM-2D to 0.5 TECU of Q4DIM, the convergence of DF-PPP augmented with Q4DIM is much faster. The result further confirms the advantage of the proposed model.

Fig. 12
figure 12

Double frequency PPP convergence serial for DOY 001–030, 2014, respectively. While for different ionospheric delay processing mode with IF, CODG, Q4DIM-2D and Q4DIM, the results are denoted in black, red, green, and blue, respectively

Full size image
Fig. 13
figure 13

Double frequency PPP convergence serial for DOY 001–030, 2020, respectively. While for different ionospheric delay processing mode with IF, CODG, Q4DIM-2D and Q4DIM, the results are denoted in black, red, green, and blue, respectively

Full size image

In addition, we calculated the RMSs for different solutions based on the last 20 min series of all the one-hour samples, and the results are in Tables 4 and 5. As we can see, compared with IF combination, PPP benefits from the undifferenced and uncombined model constrained with ionospheric delay models, especially with Q4DIM. And the accuracy of PPP for 2020 is much better than that of 2014.

Table 4 SF-PPP positioning error of RMS in Up(U) / North(N) / East (E) in 2014 and 2020
Full size table
Table 5 DF-PPP positioning error of RMS in Up(U) / North(N) / East (E) in 2014 and 2020
Full size table

Conclusions

As the development of multi-frequency multi-GNSS, the ionospheric delay becomes one of the critical issues in the high precision data processing with the undifferenced and uncombined model. Moreover, ionospheric delay augmentation is an efficient approach to speed up PPP convergence. Thus, high precision ionospheric delay modeling receives increasing attention nowadays.

GIM and SID are the most popular ionospheric models in GNSS community, while each has its merits and demerits. In this study, we proposed a novel ionospheric delay model, i.e., Q4DIM, that takes full advantages of GIM and SID. In Q4DIM, the LOS ionospheric delay is divided into different clusters according to their latitude, longitude, elevation, and azimuth. While both GIM and SID can be regarded as the special cases of Q4DIM by defining the clusters properly. The properties of Q4DIM are discussed for four sets of clusters with different spatial resolution based on 200 EPN stations. The results suggest that by inducting the elevation and azimuth angle dependent residuals, the precision of the 2-dimensional GIM like model, i.e., Q4DIM-2D, is improved from around 1.5 TECU to better than 0.5 TECU. In addition, treating Q4DIM as a 4-dimensional matrix in latitude, longitude, elevation, and azimuth, which is sparse, can guarantee its feasibility in a bandwidth-sensitive applications, e.g., satellite-based PPP-RTK service. Finally, with two months' data from 30 EPN stations, the performance of Q4DIM and its advantages in SF-PPP and DF-PPP over the 2-dimensional models are demonstrated for both high solar activity year 2014 and low solar activity year 2020.