Abstract
Mantle control on planetary dynamos is often studied by imposing heterogeneous core-mantle boundary (CMB) heat flux patterns on the outer boundary of numerical dynamo simulations. These patterns typically enter two main categories: Either they are proportional to seismic tomography models of Earth’s lowermost mantle to simulate realistic conditions, or they are represented by single spherical harmonics for fundamental physical understanding. However, in reality the dynamics in the lower mantle is much more complicated and these CMB heat flux models are most likely oversimplified. Here we term alternative any CMB heat flux pattern imposed on numerical dynamos that does not fall into these two categories, and instead attempts to account for additional complexity in the lower mantle. We review papers that attempted to explain various dynamo-related observations by imposing alternative CMB heat flux patterns on their dynamo models. For present-day Earth, the alternative patterns reflect non-thermal contributions to seismic anomalies or sharp features not resolved by global tomography models. Time-dependent mantle convection is invoked for capturing past conditions on Earth’s CMB. For Mars, alternative patterns account for localized heating by a giant impact or a mantle plume. Recovered geodynamo-related observations include persistent morphological features of present-day core convection and the geomagnetic field as well as the variability in the geomagnetic reversal frequency over the past several hundred Myr. On Mars the models aim at explaining the demise of the paleodynamo or the hemispheric crustal magnetic dichotomy. We report the main results of these studies, discuss their geophysical implications, and speculate on some future prospects.
Similar content being viewed by others
Introduction
General
Various geophysical observations have been recovered by imposing heterogeneous heat flux patterns on the outer boundary of numerical dynamo simulations. For the Earth, the most popular prescribed heat flux patterns are either proportional to seismic velocity anomalies obtained from tomography models of the lowermost mantle to mimic realistic conditions, or spherical harmonic degree and order 2 which is the dominant term in these tomography models (Aubert et al. 2007, 2008; Bloxham 2002; Christensen and Olson 2003; Davies et al. 2008; Glatzmaier et al. 1999; Gubbins et al. 2007, 2011; Heimpel and Evans 2013; Kutzner and Christensen 2004; Olson and Amit 2014; Olson and Christensen 2002; Olson et al. 2010; Sreenivasan 2009; Sreenivasan and Gubbins 2011; Takahashi et al. 2008). For other planets, various single harmonics are often used, for example degree-1 for Mars (Amit et al. 2011a; Dietrich and Wicht 2013; Stanley et al. 2008) and degree-2 for Mercury and Saturn (Cao et al. 2014; Stanley 2010, respectively), reflecting the low-resolution information on planetary deep interiors. Various single harmonics were imposed for the geodynamo as well in order to obtain fundamental physical understanding of the complex dynamo simulations (e.g., Glatzmaier et al. 1999).
Inferring core-mantle boundary (CMB) heat flux from tomography models relies on the assumption that seismic and thermal anomalies in the lowermost mantle are highly correlated. However, this idealized linear relation may not hold in reality. Observational and numerical studies of the lower mantle suggest that the structures and dynamics there are far more complex. First, non-thermal contributions (e.g., compositional, phase changes) perturb the idealized linear seismic-thermal mapping (Bull et al. 2009; Deschamps et al. 2012; Lay et al. 2008; Nakagawa and Tackley 2008; Tackley 2011; Trampert et al. 2004). Second, while the spatial resolution inherent to tomographic models in the lowermost mantle (e.g., Lekic et al. 2012) exceeds the resolution of the observed core field, strong lateral gradients of shear wave velocities are not captured. As revealed by detailed waveform analyses at several locations, boundaries of large low shear-wave velocity provinces (LLSVPs) might however be very sharp (e.g., Ni et al. 2005; To et al. 2005). Similarly, synthetic single harmonic patterns for planetary mantle heterogeneity, for example for the CMB conditions that prevailed during the paleo dynamo of Mars, are oversimplified. Even if the Martian anomaly was indeed large-scale (Elkins-Tanton et al. 2005; Harder and Christensen 1996; Ke and Solomatov 2006; Roberts and Zhong 2006; Roberts et al. 2009), it was likely more complex than a single harmonic pattern. Note finally that simulating the geodynamo at earlier times requires information about the time-dependent mantle convection pattern, which is not witnessed by present-day tomography (Yoshida and Santosh 2011; Zhang and Zhong 2011; Zhang et al. 2010; Zhong et al. 2007).
Here we term any CMB heat flux pattern that is neither tomographic nor single harmonic as alternative. For the Earth, the alternative patterns include those that account for non-thermal effects or non-resolved small scales in various ways (Amit and Choblet 2009, 2012; Amit et al. in press) and those that model the mantle heterogeneity in the past hundreds of Myr in various ways (Amit and Olson 2015; Olson et al. 2013). For Mars, the alternative patterns are obtained by modeling localized mantle heating induced by a mantle plume (Sreenivasan and Jellinek 2012) or a giant impact (Kuang et al. 2014; Monteux et al. 2015).
Figure 1 a illustrates some proposed dynamical scenarios of Earth’s lower mantle that result in alternative CMB heat flux patterns (see also, e.g., Lay et al. 2008). Subducting slabs bring cold material to the CMB and locally increase the heat flux. Time-dependent plate motions therefore change the location of these large CMB heat flux regions. Further complications arise from the presence of post-perovskite phase transition (or even its double crossing) in the slab reservoirs of the lowermost mantle. LLSVPs may represent thermochemical piles of a not only hot but also compositionally different material (e.g., Trampert et al. 2004). Growth and collapse of these thermochemical piles, as observed in analog experiments (Davaille 1999), may yield temporal changes in the total heat loss through the CMB and the amplitude of the lateral heterogeneity. Ultra low velocity zones (ULVZs) at the edges of LLSVPs (McNamara et al. 2010) form hot regions that are too narrow to be captured by global large-scale tomography models.
Figure 1 b illustrates the effects of localized mantle heating on Mars’ CMB heat flux. Giant impacts heat the mantle and reduce the CMB heat flux right below the impact site. Likewise, mantle plumes that originate at the lowermost mantle and may have produced extensive volcanism such as Tharsis are also potential zones of reduced CMB heat flux. It may also be naively expected that core heating by impacts would yield a CMB heat flux increase. However, core impact heating leads to the formation of a hot layer at the top of the core (within 10 kyr) which prevents the core from cooling (Arkani-Hamed 2012; Arkani-Hamed and Olson 2010; Roberts and Arkani-Hamed 2014). Thus, core impact heating could inhibit the dynamo generation during a timescale that is governed by the efficiency of the surrounding mantle to extract the impact induced core thermal anomaly (from several kyr up to 100 Myr).
Numerical simulations of mantle convection may shed light on the relation between the observed seismic anomalies and the CMB heat flux heterogeneity. Nakagawa and Tackley (2008) assumed a linear equation of state to relate their models’ thermal, mineral, and chemical anomalies with seismic anomalies. Their purely thermal case gives nearly perfect linear relation between seismic and thermal anomalies, whereas adding post-perovskite effects breaks the linearity but maintains a unique relation (Fig. 2 a). The situation is more complicated when chemical anomalies are accounted for; when the density contrast is large enough, a parallel branch appears and the thermal-seismic relation becomes non-unique (Fig. 2 b). Implementation of the results of Nakagawa and Tackley (2008) might be problematic because due to limited vertical resolution global tomographic models do not sample precisely the CMB but rather a vertically averaged region above it.
Scatter plots of CMB heat flux anomalies vs. seismic shear velocity anomalies at the lowermost mantle based on mantle convection simulations. a Isochemical cases without (red) and with (green) post-perovskite. b Thermochemical cases with various density contrasts δ ρ m at the CMB. From Nakagawa and Tackley (2008)
The outline of this review paper is as follows. In the “Alternative models of core-mantle boundary heat flux” subsection, we introduce motivations for alternative CMB heat flux models. Related dynamo properties inferred from observations are listed in subsection “Relevant observed planetary dynamo properties”. In the section “Methods”, we recall the governing equations and control parameters of numerical dynamo simulations. We describe the incorporation of mantle control effects by imposing an outer thermal boundary condition. In the section “Review”, we describe the results of papers that imposed alternative outer boundary conditions on numerical dynamos. For each of these papers, we specify the procedure used to construct the alternative CMB heat flux model and we report how the perturbation from the conventional reference pattern affected the resulting planetary dynamo features. We discuss the results in the subsection “Discussion”, and we propose some future prospects in subsection “Future prospects”.
Alternative models of core-mantle boundary heat flux
The existence of the post-perovskite phase transition (Murakami et al. 2004; Oganov and Ono 2004) was invoked to explain the seismic heterogeneity of the lowermost mantle (Lay et al. 2006). Post-perovskite is needed to explain core-reflected (Hernlund et al. 2005) and diffracted (Cobden et al. 2012) waves. It may also be a good candidate for the D” discontinuity, at least in regions where P- and S-waves have opposite signs (Cobden and Thomas 2013). In contrast, in probabilistic tomography models the thermal distribution is similar with and without post-perovskite (Mosca et al. 2012). Mantle convection simulations that incorporate post-perovskite effects indicate that its presence affects mantle dynamics (Cizkova et al. 2010; Nakagawa and Tackley 2011) and distorts the thermal-seismic relation from its linearity (Nakagawa and Tackley 2008).
Sharp margins of LLSVPs were suggested by local studies of the lowermost mantle (Ni et al. 2002; To et al. 2005; Wang and Wen 2007). Dynamical models indicate that ULVZs likely correspond to the hottest regions of LLSVPs (McNamara et al. 2010). Thin hot narrow regions on the edges of the LLSVPs were identified in two end-member models of lower mantle dynamics (Bull et al. 2009). The low spatial resolution of global tomography models excludes such short wavelength features (e.g., Ritsema et al. 2007).
LLSVPs are better explained if a compositional component is also present (Deschamps et al. 2012; Mosca et al. 2012; Trampert et al. 2004). These structures could be primitive or may consist of recycled crustal material, although the seismic sensitivity of mantle material indicates that the latter is less likely (Deschamps et al. 2012). By taking into account seismic normal modes, Ishii and Tromp (1999) provided an independent constraint on mantle density distributions, which can be used to resolve thermal and compositional contributions to seismic anomalies, as done by probabilistic tomography studies (Mosca et al. 2012; Trampert et al. 2004).
One obvious motivation to consider alternative CMB heat flux patterns is the time-dependence of mantle dynamics. Global plate motion models indicate that the distribution of continents has evolved from a spherical harmonic degree-1 heterogeneity before the breakup of supercontinent Pangea to its present-day degree-2 structure (Seton et al. 2012). Some mantle convection models constrained by reconstructed time-dependent plate motions suggest that the supercontinent formation and breakup was accompanied by substantial change in mantle convection pattern (Zhang and Zhong 2011; Zhang et al. 2010; Zhong et al. 2007). According to these dynamical models, the low seismic velocity structures below the Pacific and Africa predate and postdate, respectively, the Pangea breakup (McNamara and Zhong 2005; Zhang et al. 2010). These time-dependent mantle convection patterns would inevitably correspond to time-dependent CMB heat flux with patterns distinctively different from that inferred from present-day tomography models.
In contrast, the pattern of LLSVPs has been interpreted as a root mantle structure that prevailed for several hundreds of Myr (Burke 2011; Burke et al. 2008; Dziewonski et al. 2010). Evidence for long-lived mantle structure comes from hotspot reconstructions (Torsvik et al. 2006) and paleomagnetic pole locations that indicate substantial true polar wander in the Mesozoic (Courtillot and Besse 1987). The dynamical origin of this (stationary) degree-2 pattern may be two mantle superplumes (Romanowicz and Gung 2002; Torsvik et al. 2010), plume clusters (Schubert et al. 2004) or dense chemical piles above the CMB (McNamara and Zhong 2005; Tackley 2002; Tan and Gurnis 2007). Permanent or not, the thermochemical piles are clearly dynamic and respond to changes in the global mantle circulation, through variations in their footprints above the CMB and their height in the lower mantle. Variations in either or both of these would affect the mean CMB heat flux and the amplitude of its heterogeneity.
Alternative CMB heat flux models were also constructed for planets other than the Earth. It has been argued that the emergence of the Tharsis volcanic complex coincided with the termination of the Martian dynamo (Jellinek et al. 2008; Johnson and Phillips 2005; Lillis et al. 2008). Mars’ mantle may contain a single huge plume (Harder and Christensen 1996; Srámek and Zhong 2010). If Tharsis emerged from such a deep mantle plume, then it may indeed have affected the thermal heterogeneity on Mars’ CMB.
Another possible scenario is localized mantle heating by giant impacts. This process enhances the iron/silicate separation and modifies the heat repartition between the mantle and the core. Thus, large impacts potentially affected the efficiency of core cooling and dynamo activity during (Monteux et al. 2011, 2012) or after terrestrial core formation (Glenn Sterenborg and Crowley 2013; Ke and Solomatov 2009; Monteux and Arkani-Hamed 2014; Monteux et al. 2013; Reese and Solomatov 2010). This large-scale heating also strongly influences mantle dynamics (Reese et al. 2002; Roberts and Arkani-Hamed 2012; Roberts and Barnouin 2012; Watters et al. 2009) and hence the heat repartition in the deepest part of terrestrial bodies. The onset or demise of terrestrial dynamos were modeled by giant impacts (Arkani-Hamed and Olson 2010; Kuang et al. 2014; Monteux and Arkani-Hamed 2014; Monteux et al. 2013; Roberts et al. 2009). Large impacts heated Mars’ mantle below the impact site, with the heated volume depending mostly on the impactor’s size and velocity (Pierazzo et al. 1997; Tonks and Melosh 1993). The impact-driven heating may be modeled by a uniform spherical temperature increase with rapid temperature decrease away from the isothermal sphere (Monteux et al. 2007, 2013; Senshu et al. 2002). Hence, for large impacts, the CMB heat flux may be affected.
Giant impacts may also have affected the morphology of the Martian paleomagnetic field. These events were invoked to explain the Martian and lunar topographic hemispheric dichotomies (Jutzi and Asphaug 2011; Marinova et al. 2008; Nimmo et al. 2008). Numerical dynamos with a synthetic \({Y_{1}^{0}}\) heat flux pattern lead to magnetic fields concentrated at the large heat flux hemisphere (Amit et al. 2011a; Dietrich and Wicht 2013; Stanley et al. 2008). Giant impacts may produce a similar effect with a more realistic CMB heat flux pattern (Monteux et al. 2015).
Relevant observed planetary dynamo properties
Alternative (or any) heterogeneous CMB heat flux is expected to influence the dynamo on very long timescales (Olson and Christensen 2002), but some statistical preference can already be detected on shorter timescales (Amit et al. 2010a; Bloxham 2002). Stronger heat flux heterogeneity amplitudes increase the probability of a high correlation between a dynamo property and its mantle-driven long-term average (Aubert et al. 2007). If the heterogeneity amplitude is very large compared to the mean superadiabatic CMB heat flux, locking may occur and a mantle signature may appear in a snapshot (Willis et al. 2007).
Because neither the dynamo equations nor the geometry of planetary outer cores contain any special longitude, any persistent deviation of a dynamo property from axisymmetry can only be explained by boundary heterogeneity. In contrast there are special latitudes, obviously the geographic equator and poles, but also the latitude of the tangent cylinder (Aurnou et al. 2003). However, there is no preferred hemisphere (neither in the dynamo equations nor in the geometry of planetary outer cores), so any persistent deviation of a dynamo property from equatorial symmetry may also require boundary heterogeneity. Below we list the main dynamo-related observations that motivated imposing heterogeneous CMB heat flux, in particular alternative patterns.
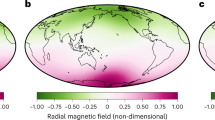
The primary dynamo observation is the observed magnetic field at the surface, from which a truncated (or large-scale) part can be downward continued to model the radial magnetic field on the CMB. Many studies attempted to reproduce the locations of high-latitude intense geomagnetic flux patches. The existence of two of these prominent geomagnetic field features at each hemisphere (Jackson et al. 2000) is consistent with the \({Y_{2}^{2}}\) dominance of the lowermost mantle seismic heterogeneity (e.g., Masters et al. 2000). The longitudes of the flux patches and the large seismic shear velocity structures seem to be correlated (Gubbins 2003), although some patches exhibit significant mobility (Amit et al. 2011b; Korte and Holme 2010). The time-average radial field of the dynamo model of Aubert et al. (2008) decently reproduces the longitudes of the flux patches in the paleomagnetic field (Kelly and Gubbins 1997). However, a shift between the locations of the large heat flux structures and the patches was observed, with the shift value depending on the dynamo internal parameters (Aubert et al. 2007; Olson and Christensen 2002; Takahashi et al. 2008). Alternatively, some geomagnetic (or paleomagnetic) spectral information, e.g., the number of patches at each hemisphere (corresponding to the dominant order), may be used as an observational constraint (Amit and Choblet 2009).
While high-latitude intense flux patches near the edge of the tangent cylinder (Aurnou et al. 2003) are a robust feature of dipole-dominated numerical dynamos (Christensen et al. 1998), the observed intense geomagnetic flux patches at low-latitude (Jackson 2003) are less characteristic of these models. The morphological criteria for Earth-like dynamos proposed by Christensen et al. (2010) identify well magnetic field models that resemble the geomagnetic field, but these criteria contain no information about the latitudinal distribution of magnetic flux. Alternative CMB heat flux heterogeneity offers a ready explanation for localized low-latitude intense flux patches (Amit and Choblet 2012; Amit et al. in press). However, such flux patches are not necessarily connected to boundary heterogeneity. Mobile low-latitude flux patches are seen in numerical dynamos without boundary heterogeneity when a strong enough influence of rotation on outer core convection is present (Wicht et al. 2011).
Other geodynamo properties apart from the magnetic field may also be used as observational constraints to dynamo models with heterogeneous CMB heat flux. For example, core flow models inverted from the geomagnetic secular variation (Holme 2007) show active Atlantic vs. quiet Pacific hemispheres (Amit and Olson 2006; Aubert et al. 2013; Gillet et al. 2009; Holme and Olsen 2006; Hulot et al. 2002). In addition, the seismic velocity, anisotropy, and attenuation of the inner core exhibit an east-west hemispheric dichotomy (Tanaka and Hamaguchi 1997), although these three seismic properties may sample different parts of the inner core (Deuss 2014; Irving and Deuss 2011). Aubert et al. (2008) recovered the observed patterns of the paleomagnetic field and the inner core hemispheric dichotomy in the corresponding time-average quantities of their dynamo model. The inner core hemispheric dichotomy may indeed be mantle-driven (Aubert et al. 2008; Gubbins et al. 2011), or alternatively independent inner core dynamics (Alboussiére et al. 2010; Monnereau et al. 2010) may produce anomalous bouyancy flux that would affect the outer core dynamics and the properties of the CMB (Aubert et al. 2013; Olson and Deguen 2012).
On much longer timescales of hundreds of Myr, the enigmatic variability of the geomagnetic reversal frequency may constrain changes in mantle conditions. In particular, the existence of long superchrons of tens of Myr in which no reversal was found in the paleomagnetic record in contrast to periods of hyper-reversing behavior (Gradstein et al. 2012; Merrill et al. 1998) is difficult to reconcile without time-dependent CMB conditions (Amit and Olson 2015; Biggin et al. 2012; Olson et al. 2013). In mantle convection simulations constrained by reconstructed plate motions the timing of the Kiaman Reversed Superchron (KRS) at around 270–315 Ma coincides with the low mean and equatorial CMB heat flux (Zhang and Zhong 2011). However, fast plate motions during the most recent Cretaceous Normal Superchron (CNS) may result in large CMB heat flux and frequent reversals (Olson et al. 2013).
Strong crustal magnetic field measured by Mars Global Surveyor is suggestive of a core dynamo that ceased at some time during the Noachian (Acuña et al. 2001; Langlais and Purucker 2007; Lillis et al. 2008; Milbury et al. 2012). Localized mantle heating may have affected the efficiency of the dynamo generation on Mars. A strong mantle plume rooted at the CMB could have terminated the Martian dynamo (Sreenivasan and Jellinek 2012). Alternatively, if the Martian dynamo was subcritical (Kuang et al. 2008), a moderate CMB heat flux anomaly induced by a giant impact could have stopped the dynamo (Kuang et al. 2014).
It has been proposed that the hemispheric dichotomy in Mars’ crustal magnetic field was caused by heterogeneous CMB heat flux when the Martian paleo dynamo operated (Stanley et al. 2008). The magnitude of this dichotomy (Amit et al. 2011a) is recovered only with strongly convecting reversing dynamo models (Dietrich and Wicht 2013). Thus, in order to record hemispheric magnetization, the Martian crust should have cooled over a shorter period than the typical chron time (Lebrun et al. 2013), which poses a constraint on the feasibility of the hemispherical dynamo scenario for explaining the hemispheric dichotomy in Mars’ crustal magnetic field (Dietrich and Wicht 2013; Monteux et al. 2015).
Methods
The following set of self-consistent non-dimensional Boussinesq (i.e., incompressible) magnetohydrodynamics equations for dynamo action due to thermochemical convection of an electrically conducting fluid in a rotating spherical shell were solved (e.g., Olson et al. 1999):
where \({\vec u}\) is the velocity, \({\vec B}\) is the magnetic field, T is co-density (Braginsky and Roberts 1995), t is time, \(\hat {z}\) is a unit vector in the direction of the rotation axis, P is modified pressure which contains centrifugal effects, \({\vec r}\) is the position vector, r o is the core radius, and ε is co-density source or sink. Four internal non-dimensional parameters in (1)–(5) control the dynamo action. The Ekman number represents the ratio of viscous and Coriolis forces
where ν is kinematic viscosity. The Prandtl number is the ratio of kinematic viscosity to thermal diffusivity κ
and the magnetic Prandtl number is the ratio of kinematic viscosity to magnetic diffusivity λ
The strength of buoyancy force driving the convection relative to retarding forces is represented by the Rayleigh number. When the CMB heat flux is strongly superadiabatic, Ra can be defined based on the mean CMB heat flux q 0 as (Olson and Christensen 2002)
where α is thermal expansivity, g 0 is gravitational acceleration on the outer boundary at radius r o , D is shell thickness, and k is thermal conductivity. The heat flux based Ra (9) was used with either generic thermochemical convection (Amit and Choblet 2009; Amit et al. in press; Amit and Choblet 2012) or purely thermal convection (Monteux et al. 2015). Alternatively, when convection is dominantly chemical, Ra can be defined based on the rate of light elements release into the outer core due to inner core freezing as (Olson 2007a)
where \(\dot {\chi }\) is the time rate of change of the light element concentration (mixing ratio) in the outer core due to inner core growth. The mixing ratio based Ra (10) was invoked with dominantly (or purely) chemical convection (Amit and Olson 2015; Olson et al. 2013). The final internal control parameter is ε, the sink (or source) term that appears in the co-density equation (Christensen and Wicht 2007), which parameterizes the effects of mixing of light elements in the outer core due to inner core freezing, secular cooling of the outer core, and radioactivel heat sources.
Various alternative CMB heat flux models were imposed on the outer boundary of the dynamo models. In the “Review” section below, we describe in details the procedures for their constructions. The non-dimensional heat flux anomaly amplitude is classically defined in numerous studies by the peak-to-peak difference normalized by twice the mean value (e.g., Olson and Christensen 2002) as
When the CMB heat flux is localized (11) appears to be inappropriate, hence various alternative measures were proposed. Sreenivasan and Jellinek (2012) proposed their control parameter f as the peak-to-background difference normalized by the background heat flux H B
They also defined the ratio of the average heat flux, either over the plume footprint or over the entire CMB, to the background heat flux, i.e. \(\bar {q}_{\text {plume}}/q_{B}\) or \(\bar {q}_{\textit {CMB}}/q_{B}\), respectively (Sreenivasan and Jellinek 2012). Kuang et al. (2014) defined their control parameter ε l as the relative post-impact heterogeneity amplitude, as in (12). In contrast, according to the model of mantle heating by impact of Monteux et al. (2015), in the vicinity of the impact, the lower mantle is heated to the core temperature and the CMB heat flux becomes zero, whereas away from it the lower mantle temperature is unchanged. Therefore, the control parameter \({q_{0}^{r}}\) of Monteux et al. (2015) is based on the portion of the CMB heated by the impact
where \({q_{0}^{h}}\) and q 0 are the pre- and post-impact mean CMB heat flux values, respectively.
To dimensionalize the dynamo models output, D, D 2/ν, and \(\sqrt {\rho \mu _{0} \lambda \Omega }\) were used to scale length, time, and magnetic field, respectively, where ρ is the fluid density and μ 0 the permeability of free space. Co-density is scaled either by D q 0/k when (9) is used or by \(\rho \beta D^{2}\dot {\chi }/\nu \) when Ra is defined by (10). For studying the present-day geodynamo an Earth-like inner-outer core radii ratio of r i /r o =0.35 was applied (Amit and Choblet 2009, 2012; Amit et al. in press). A smaller ratio of r i /r o =0.2 was applied for Mars (Monteux et al. 2015) to approach no inner core conditions while avoiding numerical instability. The past geodynamo was modeled with a variable aspect ratio based on thermal history modeling (Olson et al. 2013). Numerical dynamos with rigid insulating boundary conditions were analyzed. Overall, the models differ in the imposed outer boundary heat flux pattern, the amplitude of its variation and the convection vigor and style—all of these choices depend on the particular geophysical application.
Parametric studies of numerical dynamos found two main types of solutions: non-reversing dipole-dominated and reversing multipolar (Christensen and Aubert 2006; Kutzner and Christensen 2002; Olson and Christensen 2006). Careful choice of control parameters may yield some “Earth-like” overlap of dipole-dominated reversing dynamos (Olson 2007a; Wicht et al. 2009). In this review, studies that focus on morphological features of the present-day field had dipole-dominated non-reversing models as a reference state, whereas in studies of reversal frequency either reversing dynamos or models of both types were analyzed. Both types of solutions were examined in the context of the paleo dynamo of Mars. Table 1 summarizes the control parameters, convection styles, inner to outer core ratios, and dynamo types in the papers reviewed here.
Review
To our best knowledge, only eight papers have examined the effects of alternative (i.e., neither tomographic nor single harmonic) CMB heat flux on planetary dynamos (Amit and Choblet 2009, 2012; Amit and Olson 2015; Amit et al. in press; Kuang et al. 2014; Monteux et al. 2015; Olson et al. 2013; Sreenivasan and Jellinek 2012). Here we describe for each of these papers the CMB heat flux models that were imposed as outer boundary conditions on the dynamo simulations. Then, for each paper, we compare the results with those obtained with a reference heat flux model (Table 2) and we report the consequences for the resulting dynamo properties.
Lower mantle thermal-chemical-phase heterogeneity and geodynamo morphological features
Here we review the papers by Amit and Choblet (2009), Amit and Choblet (2012), and Amit et al. (in press). As in previous studies, a reference CMB heat flux anomaly of purely thermal origin δ q T was assumed to be linearly proportional to the lowermost mantle seismic shear velocity anomaly δ v s :
Figure 3 a shows the CMB heat flux based on the tomography model of Masters et al. (2000) and (14). Nakagawa and Tackley (2008) found that when incorporating post-perovskite phase transition in their mantle convection models, the δ q to δ v s relation becomes an inclined step function (Fig. 2 a), with the spreading effect well approximated by a tanh function. Following equation (B8) of Nakagawa and Tackley (2008), Amit and Choblet (2009) attempted to parameterize the thermal-phase interpretation δ q Tp as
Non-dimensional CMB heat flux patterns based on the mantle tomography model of Masters et al. (2000): a Thermal linear interpretation T and b interpretation including a post-perovskite effect Tp1. From Amit and Choblet (2009)
The non-dimensional parameters in (15) are the amplitude A, the tanh spreading factor B, and the offset D. For a given amplitude A, the spreading factor B is constrained by reaching the tanh asymptote while maintaining an inclined step function (rather than Z-like curve).
Figure 3 b shows a heat flux anomaly map that accounts for post-perovskite according to (15). The patterns in Fig. 3 a, b are similar, but the relative magnitudes of the positive/negative heat flux structures vary. When the post-perovskite effect is included, the positive structures weaken and spread over larger areas, whereas the negative structures remain strong and more localized (Fig. 3 b). This is due to the particular pattern of the tomographic model that contains larger amplitude narrower regions of negative seismic velocity anomalies (δ v s ,δ q T <0) as opposed to broader regions of weaker positive anomalies (Fig. 3 a). The tanh function strongly reduces intermediate δ v s while it reduces extreme δ v s more mildly, resulting in a spreading effect acting stronger on the positive δ q T .
Following Aubert et al. (2008), Amit and Choblet (2009) compared three long-term time-average properties of their dynamo models with relevant observations: the radial magnetic field on the outer boundary with the time-average paleomagnetic field over the past 5 Myr (Kelly and Gubbins 1997), the flow at the top of the shell with the core flow model of Amit and Christensen (2008) obtained from inversions of the historical geomagnetic secular variation (Jackson et al. 2000) and averaged over the period 1840–1990, and the inner boundary buoyancy flux with seismic anomalies of the upper inner core (Tanaka and Hamaguchi 1997). As an example, we highlight here the latter comparison (Fig. 4). The inner boundary buoyancy flux is characterized by two isolated positive low-latitude structures both in the thermal case (Fig. 4 a, denoted as T) as well as when accounting for post-perovskite (Fig. 4 b, denoted as Tp1). In addition, however, the ICB buoyancy fluxes contain other orders. More vigorous convection leads to stronger filtering of the CMB order 2 content and the ICB pattern remains dominantly order 1 (Aubert et al. 2008), whereas slightly supercritical convection leaves the ICB pattern with nearly non-distorted order 2 (Gubbins et al. 2011). Amit and Choblet (2009) found that the ratio of order 1 to order 2 in Fig. 4 b is significantly larger than that in 4 a. This suggests that accounting for post-perovskite improves the agreement of the dynamo models with the order 1 dominance in seismic properties of the upper inner core (Tanaka and Hamaguchi 1997), although the phase may vary substantially from one dynamo model to another. Amit and Choblet (2009) argued that accounting for post-perovskite also improves the recovery of the Atlantic/Pacific hemispheric dichotomy in core flow activity (Amit and Christensen 2008; Gillet et al. 2009) and the single intense paleomagnetic flux patch in the southern hemisphere (Kelly and Gubbins 1997).
Time-average inner-core boundary buoyancy flux anomalies normalized by the mean buoyancy flux: a Model T and b Model Tp1. From Amit and Choblet (2009)
Next, narrow features that are not captured by global tomography models were considered. Lower mantle tomography models are dominated by a \({Y_{2}^{2}}\) component (e.g., Masters et al. 2000), which is classically interpreted as the largest scale temperature anomaly. Such a pattern was imposed by many authors as heat flux on the outer boundary of their numerical dynamo models (e.g., Aubert et al. 2007; Bloxham 2002; Olson and Christensen 2002; Sreenivasan 2009). Amit and Choblet (2012) used the \({Y_{2}^{2}}\) pattern as a reference case and superimposed on it low heat flux ridges at the four margins of hot and cold large-scale structures (Table 2). The ridges were modeled using a Gaussian geometry with an amplitude equal to that of the hot large-scale features (Fig. 5).
Non-dimensional CMB heat flux based on a \({Y_{2}^{2}}\) pattern with narrow hot ridges superimposed on the boundaries between large-scale hot and cold structures. From Amit and Choblet (2012)
Figure 6 presents two close-ups of the time-average dynamo model velocity and magnetic field, one on the center of Fig. 5 (i.e., center of a ridge with a positive heat flux anomaly to its east), the other centered on a ridge with a positive heat flux anomaly to its west. In places where a positive heat flux anomaly appears east of the ridge (Fig. 6 left), the poloidal flow dominates and the fluid diverges from the hot ridge. Stronger field appears east of the ridge where cold fluid downwelling concentrates magnetic flux. In contrast, in places where a positive heat flux anomaly appears west of the ridge (Fig. 6 right), the upwelling associated with this ridge is broken at the equator, westward toroidal flow dominates, and the magnetic field exhibits patches of comparable intensity on both sides of the ridge. Note that the fluid upwellings appear very close to the longitudes of the hot CMB heat flux ridges, in contrast to previous studies of numerical dynamos with a \({Y_{2}^{2}}\) CMB heat flux pattern in which a phase shift was found between the heat flux and the flow structures (Aubert et al. 2007; Olson and Christensen 2002; Takahashi et al. 2008).
Zoom into two ridges at low-latitude of the time-average of a dynamo case with imposed CMB heat flux as in Fig. 5, with a positive heat flux anomaly to the east (left, where Fig. 5 is centered) and with a positive heat flux anomaly to the west (right). Non-dimensional velocity at the top of the free stream is shown in the top panel, non-dimensional magnetic field in the bottom panel. Radial components are in colors, tangential components in arrows. From Amit and Choblet (2012)
Amit and Choblet (2012) interpreted the low-latitude dynamics around the ridge locations by a combined effect of westward drift in the time-average homogeneous dynamo (Aubert 2005) and the steady boundary-driven flow that roughly goes from hot to cold regions (Gubbins 2003). When cold material is east of the ridge the two flows counteract and the ridge acts as a flow barrier, whereas when cold material is west of the ridge both flows are westward and the barrier effect is diminished. Applying these inferences to the tomography model of Masters et al. (2000), Amit and Choblet (2012) predicted (in a statistical sense) fluid upwelling at the top of the core and a barrier for azimuthal flow below central Asia and the Indian Ocean and below the American Pacific coast. Below east Asia and Oceania and below the Americas they predicted persistent intense low-latitude geomagnetic flux patches. These predictions are in agreement with preferred longitudes of virtual geomagnetic poles during reversals both in paleomagnetic data (Hoffman 1996; Love 1998; Merrill and McFadden 1999) and in tomographic reversing dynamo models (Coe et al. 2000; Kutzner and Christensen 2004). It also resonates with the persistent production of low-latitude geomagnetic flux patches below Indonesia during the historical era (Jackson et al. 2000).
Finally, probabilistic tomography may be used to isolate the thermal component of the observed seismic anomalies. A limitation of the probabilistic tomography models published so far is that only even spherical harmonic degrees are included (Mosca et al. 2012; Trampert et al. 2004). To overcome this problem, Amit et al. (in press) mapped the ratio between shear-wave velocity \(\delta ln {V_{s}^{e}}\) (even degrees) and thermal anomalies δ T e (even degrees) in probabilistic tomography and applied this mapping to a conventional lower mantle seismic tomography model \(\delta ln {V_{s}^{C}}\) (even and odd degrees) to obtain a rescaled thermal anomaly distribution δ T P with both even and odd degrees. Mathematically they wrote
To avoid numerical instabilities at regions where \(\delta ln {V_{s}^{e}}\) is low, at each node of the probabilistic tomography model δ T e and \(\delta ln {V_{s}^{e}}\) were sampled according to their full probability distribution functions (PDFs) rather than their mean values, resulting in a full PDF of the ratio \(\delta T^{e} / \delta ln {V_{s}^{e}}\). Amit et al. (in press) applied the above procedure on the conventional seismic tomography model of Masters et al. (2000) and the probabilistic tomography model of Mosca et al. (2012) for the seismic and thermal anomalies. The resulting CMB heat flux pattern inferred from probabilistic tomography (Fig. 7) exhibits positive structures mostly concentrated at low latitude.
Non-dimensional normalized CMB heat flux pattern inferred from probabilistic tomography. The same pattern was used for different q ∗ values (see Table 1), hence the absence of a color bar. Red/blue denotes positive/negative heat flux anomalies, respectively. From Amit et al. (in press)
The dynamo models with an imposed probabilistic tomography heat flux pattern are characterized by stronger magnetic and convective activity at low-latitude than the dynamo models with conventional tomography heat flux. The timeseries of the ratio of RMS low-latitude magnetic flux to RMS high-latitude magnetic flux as well as the ratio of maximum low-latitude magnetic flux to maximum high-latitude magnetic flux (Fig. 8) show larger mean values and much larger temporal fluctuations in the probabilistic dynamo models (Fig. 8 b) than those obtained with conventional tomography (Fig. 8 a). For comparison, Amit et al. (in press) found that the historical geomagnetic field model gufm1 (Jackson et al. 2000) exhibits for the period 1840–1990 average RMS and maxima ratios of 0.675 and 0.725, respectively. The higher resolution model CHAOS-4 (Olsen et al. 2014) for the period 2000–2010 is characterized by somewhat larger average ratios of 0.797 and 0.882, and the average ratios in the lower resolution archeomagnetic field model Cals3k.3 (Korte et al. 2009) for the past three millennia are 0.470 and 0.648. Accounting for the temporal fluctuations in the dynamo models with the CMB heat flux pattern inferred from probabilistic tomography, any of these models may occasionally recover the observed low- to high-latitude geomagnetic flux ratios.
Timeseries of low/high-latitude magnetic flux ratios for dynamo models with the same control parameters but different outer boundary heat flux patterns, one with a pattern from conventional tomography (a, case C2 of Amit et al. in press) and the other with a pattern inferred from probabilistic tomography (b, case P2 of Amit et al. in press). Black/red curves are RMS/maxima ratios, respectively. From Amit et al. (in press)
Lower mantle history and geomagnetic reversal frequency
Here we review the papers by Olson et al. (2013) and Amit and Olson (2015). Zhang and Zhong (2011) imposed a reconstructed plate tectonics model for the period 0–120 Ma (Lithgow-Bertelloni and Richards 1998) and Atlantic hemisphere continent reconstructions for older periods (Scotese 2001) as a time-dependent mechanical upper boundary condition on their mantle thermochemical convection model to infer the time-dependent CMB heat flux. According to one of the CMB heat flux models of Zhang and Zhong (2011), termed HF1, relatively large/low mean CMB heat flux corresponds to fast/slow plate reconstructions (Lithgow-Bertelloni and Richards 1998; Scotese 2001), respectively. In addition, HF1 includes temporal changes in the heat flux pattern (Fig. 9) and amplitude (Table 1), most notably a transition from degree-1 dominance during Pangea to degree-2 dominance at present.
Snapshots of CMB heat flux (colors) and plate boundaries (solid black lines) from the mantle history model HF1 of Zhang and Zhong (2011). From Olson et al. (2013)
Olson et al. (2013) imposed snapshots of HF1 (Fig. 9) on chemical convection dominated numerical dynamos. In addition, they accounted for the time-dependent core evolution that is controlled by the mean CMB heat flux. Using thermal history modeling (Labrosse 2003), Olson et al. (2013) determined the time-dependent CMB heat flux and consequently the time-dependent inner core size and inner core boundary buoyancy flux. According to these models, a few tens of Myrs after inner core nucleation outer core convection indeed becomes dominantly chemical. Very high core thermal conductivity (e.g., Pozzo et al. 2012) implies that higher CMB heat flux, radiogenic heating, or some presently unknown form of chemical differentiation in the core would be needed to power the geodynamo prior to inner core nucleation. However, the debate on core thermal conductivity is still ongoing (Zhang et al. 2015). Finally, Olson et al. (2013) also accounted for the observed nearly linear increase in length of day (Williams 2000) to derive a time-dependent rotation rate. Overall, they established the relative temporal evolution of the Rayleigh and Ekman numbers for the period corresponding to the HF1 model.
Olson et al. (2013) compared the time-dependent reversal frequency of two types of dynamo models, one with time-dependent and another with fixed present-day CMB heat flux (both cases include time-dependent core evolution). This comparison allows distinguishing between the direct effects of the CMB heterogeneity and the effects of the core evolution. Figure 10 shows comparison of the reversal frequency of the dynamo models of Olson et al. (2013) with the observed paleomagnetic reversal frequency record (Gradstein et al. 2012). The dynamo model with fixed CMB heat flux is characterized by weaker temporal variability in reversal frequency. In contrast, the dynamo model with time-dependent CMB heat flux shows larger reversal frequency fluctuations including superchrons and rather hyper-reversing periods. In particular, at 275 Ma when Pangea was at its height and prior to it, the dynamo model with time-dependent CMB heat flux recovers the low reversal frequency, whereas that is not the case for the dynamo model with fixed CMB heat flux. Olson et al. (2013) argued that the transition from low to high reversal frequency is driven by the supercontinent cycle. Both dynamo models fail to reproduce the robust Cretaceous Normal Superchron at 120 Ma. However, Olson et al. (2013) demonstrated that the reversal frequency is strongly sensitive to mild changes in the CMB heat flux (mean, pattern, and its amplitude).
Top: Geomagnetic reversal frequency (yellow and barcode below) based on the Geomagnetic Polarity Time Scale (GPTS) database of Gradstein et al. (2012) vs. reversal frequency in dynamo models with time-dependent CMB heat flux (black pluses) and fixed present-day tomographic pattern (red crosses). The Cretaceous Normal Superchron (CNS), Kiaman Reversed Superchron (KRS), and Moyero Normal Superchron (MNS) are grey shaded. Bottom: Polarity bias, i.e., the difference between time spent in normal and reversed polarities normalized by their sum. From Olson et al. (2013)
In contrast, the lower mantle may exhibit a quasi-stationary pattern. Amit and Olson (2015) proposed that the extreme variability in the recorded geomagnetic reversal frequency, from hyper-reversing periods to superchrons, may be explained by lower mantle piles with a fixed lateral pattern but time-dependent height. Amit and Olson (2015) proposed a simple model of the D” layer with fixed temperature difference, conserved volume with time, and a conductive equilibrium. Based on these assumptions, they derived analytically the dependence of the mean CMB heat flux and the amplitude of its lateral heterogeneity on the pile height. They showed that superplume growth increases both the mean CMB heat flux and the amplitude of its lateral heterogeneity, whereas pile collapse decreases these two quantities.
Figure 11 shows the rotated \({Y_{2}^{0}}\) CMB heat flux pattern based on the model of lower mantle seismic heterogeneity by Dziewonski et al. (2010). The mean heat flux was assumed to be close to the core adiabat, i.e., the dynamo models are dominated by chemical convection. The heterogeneity pattern was generated using spherical harmonics \({Y_{2}^{0}}\), \({Y_{2}^{2}}\), and \({Y_{1}^{1}}\), with relative amplitudes of 10:10:1, respectively. Amit and Olson (2015) determined the amplitudes of mean heat flux and heterogeneity in their dynamo models based on their analytical piles model as functions of pile height. In addition, they set the Rayleigh number based on the mean heat flux from their analytical piles model.
CMB heat flux pattern in the dual superplume configuration. The mean heat flux is 100 m W/m 2 and the peak-to-peak variation is 60 m W/m 2. From Amit and Olson (2015)
Figure 12 shows the non-dimensional reversal frequency as functions of pile height and mean outer boundary heat flux for the rotated \({Y_{2}^{0}}\) (Fig. 11) dynamos. The error bars correspond to \(\sqrt {N}/\tau _{d}\) (where N is the reversal frequency and τ d is the dipole free decay time), consistent with a Poisson distribution (Lhuillier et al. 2013). The reversal frequency increases approximately linearly beyond onset. There is a fairly small window separating the pile height that would produce magnetic superchrons and the pile height that would produce hyper-reversing dynamos. A relatively moderate increase of ∼35 % in CMB heat flux corresponds to a transition from dynamo models exhibiting superchrons to those in a hyper-reversing state. Amit and Olson (2015) concluded that pile growth may stimulate polarity reversals, whereas pile collapse may inhibit reversals.
Non-dimensional reversal frequency vs. non-dimensional pile height a and vs. non-dimensional mean CMB heat flux b in the set of dual pile (rotated \({Y_{2}^{0}}\)) dynamo models. From Amit and Olson (2015)
Localized mantle heating and the paleo dynamo of Mars
Here we review the papers by Sreenivasan and Jellinek (2012), Kuang et al. (2014), and Monteux et al. (2015). Sreenivasan and Jellinek (2012) simulated the localized CMB anomaly induced by the mantle plume that produced Tharsis by
where θ and ϕ are latitude and longitude, θ p and ϕ p are the corresponding coordinates of the plume center, and \(\delta _{\theta }^{2}\) and \(\delta _{\phi }^{2}\) are the corresponding exponential decay coefficients, set to be 15° at the equator. The localized CMB plume-induced heat flux heterogeneity is visualized in the inlet of Fig. 13 a.
a Critical heat flux heterogeneity amplitudes required for dynamo failure vs. plume latitude for a mantle plume centered at 15°S (see CMB heat flux pattern in inlet). The three curves are based on three definitions of the heterogeneity amplitude: f (blue, Eq. (12)), \(\bar {H}_{\textit {CMB}}/H_{B}\) (solid black), and \(\bar {H}_{\text{plume}}/H_{B}\) (dashed black). b Timeseries of normalized magnetic energy for a mantle plume centered at 45°S with f=0 (blue), f=4 (red), f=10 (black), f=25 (magenta), and f=29 (green). From Sreenivasan and Jellinek (2012)
The dynamo models of Sreenivasan and Jellinek (2012) are strongly supercritical (Table 1), requiring large heterogeneity amplitudes to terminate the dynamo (Fig. 13 a). Increasing heterogeneity amplitude attenuates the field and eventually leads to the dynamo failure (Fig. 13 b). In addition, it is easier to kill the dynamo if the mantle plume is centered at low-latitude (Fig. 13 a).
The underlying mechanism for the demise of the dynamo due to the localized CMB heating is visualized in Fig. 14. The boundary heterogeneity weakens the axial flow and reverses its direction. As a result, the kinetic helicity also weakens significantly. The weakening of helicity reduces the field generation efficiency (Moffatt 1978) and leads to the demise of the dynamo (Sreenivasan and Jellinek 2012).
Zonal profiles of non-dimensional axial velocity a and non-dimensional axial kinetic helicity b in dynamo models without (left) and with (right) a plume. The minimum and maximum axial velocity values are [ −40.4, 34.4] (left) and [ −19.3, 18.3] (right); the minimum and maximum axial kinetic helicity values are [ −174.6, 137.8] (left) and [ −23.6, 24.8] (right). From Sreenivasan and Jellinek (2012)
Kuang et al. (2014) also studied the possibility of Martian dynamo cessation due to localized CMB heating, but by a giant impact. The impact-induced thermal heterogeneity is modeled by shock wave heating emanating from the impact site (Pierazzo et al. 1997; Watters et al. 2009). The temperature rapidly decays from the impact center. In contrast to Sreenivasan and Jellinek (2012), the dynamo models of Kuang et al. (2014) are subcritical with moderate heterogeneity amplitudes of ε l ≤0.3 (see Table 1). These subcritical dynamos were found to be hemispheric (Kuang et al. 2008), in contrast to other studies that argued that under subcritical conditions helicity generation is more efficient when the field is dipole-dominated (Hori and Wicht 2013; Sreenivasan and Jones 2011).
Kuang et al. (2014) also found that a giant impact at low-latitude and with a large heterogeneity amplitude is more likely to terminate the dynamo. Figure 15 shows that when the impacts where placed at latitude 60°N and higher the dynamos survived. The dynamos failed if the CMB heat flux heterogeneity amplitude was larger than a critical value. This critical value decreases with increasing latitude of the impact site. The dynamo failure occurs when the helicity is reduced in the hemisphere where most of the field is expected to be induced.
Survivability of dynamos as a function of CMB heat flux heterogeneity amplitude ε l (radial distance) and the co-latitude of the impact θ l (angle from vertical axis). From Kuang et al. (2014)
Localized mantle shock heating by a giant impact could have also altered the morphology of the Martian paleo dynamo. Monteux et al. (2015) uniquely determined the CMB heat flux lateral variations as well as the reduction in the mean CMB heat flux by the size and geographic location of the impactor. Figure 16 shows the CMB heat flux patterns resulting from an impactor of 800 km radius falling on the north pole (left) or the equator (right) of Mars’ surface. Because it is thought that there is no inner core in Mars (Breuer et al. 2010; Schubert and Spohn 1990), purely thermal convection was modeled, with a volumetric homogeneous heat source ε that compensated for the loss of heat through the outer boundary (Amit et al. 2011a; Dietrich and Wicht 2013). A small inner core corresponding to r i /r o =0.2 was retained to avoid numerical instabilities, but the inner boundary was set to be convectively passive (Table 1). Both non-reversing and reversing dynamos were examined.
Non-dimensional CMB heat flux resulting from an impactor of radius 800 km falling on the north pole (left) or the equator (right). The same pattern was used for different q ∗ values (see Table 1), hence the absence of a color bar. Red/blue denotes positive/negative heat flux anomalies, respectively. From Monteux et al. (2015)
Figure 17 shows the time-average RMS radial field at the CMB and the time-average field intensity at the surface of Mars for a dynamo model with an impactor of radius 800 km falling on the north geographic pole (Fig. 16 left). The impactor yields an hemispheric field similar to those obtained with synthetic \({Y_{1}^{0}}\) CMB heat flux patterns (Amit et al. 2011a; Dietrich and Wicht 2013; Stanley et al. 2008). Monteux et al. (2015) found that a polar impactor leads to a north-south hemispheric magnetic dichotomy that is stronger than an east-west dichotomy created by an equatorial impactor (in agreement with Amit et al. 2011a, Dietrich and Wicht 2013).
Time-average magnetic field properties on the CMB (left) and on the surface of Mars (right) in a dynamo model with imposed outer boundary heat flux due to a polar impactor as in Fig. 16. From Monteux et al. (2015)
Monteux et al. (2015) found that an impactor radius of about 1000 km could have recovered the magnetic dichotomy observed in the Martian crustal field. However, strong enough magnetic dichotomies were obtained only for frequently reversing dynamos (as in Dietrich and Wicht 2013). Therefore, such dynamos may account for the observed field dichotomy only if very rapid post-impact magma cooling took place (Lebrun et al. 2013).
Conclusions
Discussion
The study of mantle control on planetary dynamos may be classified into three categories. In the first category, numerical dynamos with homogeneous boundary conditions have already reproduced successfully the most fundamental observed geodynamo properties, in particular the dipole dominance of the field (Glatzmaier and Roberts 1997) and its reversibility (Glatzmaier and Roberts 1995). Parametric studies of numerical dynamos show that increasing convection vigor (which is controlled by the mean CMB heat flux) causes a transition from dipole dominated non-reversing to multipolar reversing dynamos (Aubert et al. 2009; Christensen and Aubert 2006; Kutzner and Christensen 2002). The very different magnetic field geometries and amplitudes observed for the various planets and moons (Stevenson 1983) may represent different locations of their dynamos in parameter space with respect to this transition (Olson and Christensen 2006). In the second category, heterogeneous but simplified (i.e., not alternative) boundary conditions may help explain more refined dynamo properties, in particular for the Earth where detailed observations are available. In a third category, numerical dynamos with imposed alternative CMB heat flux can be considered as the next step to approach the recovery of more refined observations using more realistic CMB conditions.
Persistent morphological features of the present-day geodynamo were explained using alternative CMB heat flux models (Amit and Choblet 2009, 2012; Amit et al. in press). The modifications of the CMB heat flux patterns due to post-perovskite and thermal ridges are mild, and therefore their impact on the dynamo properties are also mild. Thus, in order to detect the differences between the reference dynamo models and those modified by the post-perovskite and thermal ridges effects (Table 2), long-term time-averaging is required (Amit and Choblet 2009, 2012). In contrast, the CMB heat flux pattern inferred from probabilistic tomography is dramatically distinctive from its reference (Amit et al. in press), and therefore provides a genuinely new insight into the possible control of the mantle heterogeneity on the geodynamo.
Dynamo models with imposed CMB heat flux inferred from both thermal ridges and probabilistic tomography were invoked to explain the presence of intense geomagnetic flux patches at low latitude (Amit and Choblet 2012; Amit et al. in press). In the latter models, enhanced low-latitude convective and magnetic activity is found, in particular during some occasional bursts during which the models exceed the observed relative low-latitude geomagnetic flux (Amit et al. in press). These robust low-latitude geomagnetic features (Jackson 2003) are more difficult to reproduce in dynamo models than high-latitude flux patches (Christensen et al. 1998), possibly due to flux dispersion by upwelling (Wicht et al. 2009) that reconnects with the downwellings near the tangent cylinder in the dynamo’s meridional circulation (Aubert 2005). Intense low-latitude geomagnetic flux patches, which are indeed easier to recover with alternative CMB heat flux, have so far not been included explicitly as a morphological constraint for Earth-like dynamo models (Christensen et al. 2010).
Due to the very low viscosity and very large scale of planetary outer cores, dynamo models operate in a parametric regime very far from realistic conditions (e.g., Christensen and Wicht 2007; Glatzmaier 2002). The situation is more severe if long-term time-averaging is required to detect the impact of alternative or any heterogeneous mantle control, because long simulations are needed for adequate statistical convergence of the time-average dynamo properties. An especially extreme case concerns the study of reversal frequency which requires very long simulations to obtain significant statistics of rare events. Indeed the Ekman and magnetic Prandtl numbers in the studies by Olson et al. (2013) and Amit and Olson (2015) are very large (Table 1); the Ekman number is more than 10 orders of magnitude larger than its geophysical estimate (e.g., Olson 2007b). Amit and Olson (2015) explored some simulations with a lower Ekman number. They found qualitative agreement with their larger Ekman number results, but computational limitations prevented them from providing a confident quantitative analysis, in this case of the reversal frequency vs. pile height.
The variability in the paleomagnetic reversal frequency was explained by alternative time-dependent CMB heat flux models (Amit and Olson 2015; Olson et al. 2013). The larger temporal variability in reversal frequency in the dynamo models with time-dependent CMB heat flux compared to those with a fixed tomographic pattern, in particular the presence of superchrons in the former, supports a time-dependent mantle convection structure over the past ∼500 Myr (Olson et al. 2013). It also shows that core evolution by its own cannot account for the large variability in the paleomagnetic reversal frequency. The HF1 model (Zhang and Zhong 2011) exhibits temporal variations in the mean CMB heat flux, its pattern and the amplitude of lateral heterogeneity (Fig. 9 and Table 1), all of which may affect reversal frequency (see Olson and Amit 2014, and references therein).
According to the HF1 model, the CMB heat flux pattern evolved from degree-1 dominance during Pangea to degree-2 at present. This transition is reflected in the time-average magnetic field of the dynamo models with prescribed heat flux pattern inferred from HF1. Olson et al. (2013) showed that at present, the dipole is very axial, whereas with increasing age the dipole axis substantially deviated from the geographic pole. The symmetry of the early time-average magnetic field highly correlates with the symmetry of the CMB heat flux heterogeneity, exhibiting magnetic field concentrations aligned with the axis of the large CMB heat flux.
Dziewonski et al. (2010) proposed that the CMB heat flux is quasi-stationary with two stable states that may each persist for hundreds of Myr. When the plates are organized in one supercontinent at Earth’s surface, the CMB heat flux may be characterized by a rotated \({Y_{1}^{0}}\) pattern; when two continents are present, the CMB heat flux is expressed by a rotated \({Y_{2}^{0}}\) pattern. Amit and Olson (2015) showed that in both scenarios increasing pile height increases the mean CMB heat flux, the amplitude of its heterogeneity, and the resulting reversal frequency. For a given pile height, the rotated \({Y_{1}^{0}}\) pattern yields larger mean heat flux, heterogeneity amplitude and reversal frequency than the rotated \({Y_{2}^{0}}\) pattern (Amit and Olson 2015), suggesting higher sensitivity of the paleomagnetic reversal frequency to changing mantle conditions prior to the KRS.
The dependence of the reversal frequency on the heterogeneity amplitude is not trivial. In particular, the rotated \({Y_{2}^{0}}\) case contains polar cooling that according to most studies may suppress reversals (Glatzmaier et al. 1999; Kutzner and Christensen 2004). Polar cooling results in axial-dipole dominance due to flux concentration at high-latitudes (Amit et al. 2010b) and therefore indeed suppresses reversals (a state termed geographic control by Olson and Amit 2014). However, when the dynamo is far from the onset of reversals, Olson and Amit (2014) found that the opposite occurs and polar cooling increases reversal frequency by producing more turbulent conditions (which they termed inertial control). In the piles model of Amit and Olson (2015), the effects of variable mean CMB heat flux and heterogeneity amplitude are non-separable. However, if indeed the rotated \({Y_{2}^{0}}\) pattern works in unison with the mean CMB heat flux to trigger reversals, it is suggestive of inertial rather than geographic control (Olson and Amit 2014).
The demise of the Martian dynamo was explained by a localized CMB heating (Kuang et al. 2014; Sreenivasan and Jellinek 2012). Sreenivasan and Jellinek (2012) imposed plume-induced thermal anomalies with large heterogeneity amplitudes on highly supercritical numerical dynamos, whereas Kuang et al. (2014) imposed impact-induced thermal anomalies with moderate heterogeneity amplitudes on subcritical dynamos. Under supercritical conditions, the CMB anomaly causes the dynamo to decay relatively slow—the field drops by one order of magnitude in ∼1.7 magnetic diffusion times (Sreenivasan and Jellinek 2012), whereas under subcritical conditions the termination is more sudden—the field decays ∼4 times faster (Kuang et al. 2014). The large heterogeneity amplitudes in the dynamo models of Sreenivasan and Jellinek (2012) imply that below the mantle plume the heat is flowing unrealistically into the core. Another problem is that under vigorous convection the dynamo is expected to restart once the mantle anomaly vanishes. Note that reducing dynamo efficiency by heterogeneous CMB heat flux is not trivial; another pattern may have the opposite effect, as was shown for \({Y_{2}^{2}}\) heterogeneity which enhances helical core flow and hence improves dynamo efficiency (Sreenivasan 2009).
In both cases (Kuang et al. 2014; Sreenivasan and Jellinek 2012) it was found that low-latitude localized heating is favorable for terminating the dynamo, despite the distinctive role of convection in these two types of dynamo models. Sreenivasan and Jellinek (2012) argued that the critical latitude for plume location in order to kill the dynamo depends on the lowest latitude where axial columns driven by rapid rotation (Busse 1970) impinge the CMB (see Fig. 14 a). Overall, these results may pose upper bounds on the amount of possible planet reorientation in the history of the Martian paleodynamo (Kuang et al. 2014; Sreenivasan and Jellinek 2012). The possibility of a major true polar wander (TPW) event on Mars is under debate. Significant TPW has been advocated for Early Noachian from studies of the crustal geoid associated to dynamical models for the formation of the crustal dichotomy (Roberts and Zhong 2007). TPW was also proposed for the subsequent 4 Gyr from studies of paleomagnetic poles (Hood et al. 2005) and paleoshorelines (Perron et al. 2007) or from theoretical models (Matsuyama et al. 2006). However, to our best knowledge, observed geological evidence for such processes (e.g., Grimm and Solomon 1986) are still lacking. Furthermore, models of lithospheric shell rotation associated with the apparent migration of Tharsis (e.g., Srámek and Zhong 2012) could lead to tectonic observations identical to that caused by TPW, although the two underlying physical processes are very different.
Some of the results obtained by Kuang et al. (2014) seem somewhat counter-intuitive, in particular the field morphology (see their Fig. 3). Their homogeneous CMB heat flux subcritical dynamo model indeed produces a hemispheric magnetic field (as previously reported by Kuang et al. 2008), with a peak at a specific latitude (∼ 30°S). However, the field may reverse and this peak can migrate to different latitudes with time. It is therefore not clear why would the peak magnetic field of the heterogeneous dynamos almost coincide with that of the homogeneous case. It is also not intuitive that the field becomes spatially less heterogeneous with increasing heterogeneity amplitude. In addition, there is no suggestion for a depleted field at the location of the impact, as may be expected. Overall, it seems that the effects of mantle control on subcritical dynamos are distinctive from those in supercritical dynamos.
Finally, Monteux et al. (2015) imposed a localized impact-induced CMB heat flux pattern on numerical dynamos to explain the observed hemispheric dichotomy in the Martian crustal field (Acuña et al. 1998; Langlais et al. 2004). The amplitude of the hemispheric magnetic dichotomy is mostly controlled by the horizontal Rayleigh number which represents the vigor of the convection driven by the lateral variations of the CMB heat flux. Monteux et al. 2015 showed that, for a given horizontal Rayleigh number, an impact-induced CMB heat flux heterogeneity is more efficient than a synthetic degree-1 heterogeneity in generating strong hemispheric magnetic dichotomies. However, even with the more efficient impact-induced CMB heat flux pattern, several important conditions should be met in order to accept the impact-induced hemispheric dynamo scenario as the origin of the crustal field dichotomy, in particular the need for a very rapid crustal cooling rate (Dietrich and Wicht 2013). Dynamo models that recover the observed magnetic hemisphericity have a short average chron time of about 18 kyr (Monteux et al. 2015). However, in the case of molten material induced by a giant impact a major part of the atmosphere can be eroded and crustal formation may occur within only 1000 years (Lebrun et al. 2013; Solomatov 2007), possibly enabling the recording of the magnetic hemisphericity in the crust.
Future prospects
Because the CMB heat flux is an input to the dynamo models, understanding the dynamics of the lower mantle is a fundamental key to improve core dynamics models. In addition, progress in dynamo modeling is obviously relevant for all core-related problems, including the influence of heterogeneous (alternative or not) boundary conditions. Improved observations, in particular higher quality planetary magnetic field models, may provide tighter constraints on the dynamo models. Here we list some future prospects concerning alternative CMB heat flux and its influence on planetary dynamos. We also mention alternative scenarios that may also explain the non-trivial dynamo-related observations.
Knowledge of planetary magnetic fields will continue to grow in the coming years thanks to several new satellite missions that are currently flying or will soon be launched. Geomagnetic field and secular variation models will benefit from the successful Swarm ESA mission (Olsen et al. 2013). Three identical and magnetically dedicated satellites were launched simultaneously during the end of 2013 at two different altitudes to monitor with unprecedented quality the Earth’s magnetic field and its secular variation. Measurements of the NASA MESSENGER mission around Mercury revealed a weak, dipole-dominated, and hemispheric magnetic field (Anderson et al. 2012). However, these measurements have not yet been fully exploited, and it is anticipated that alternative modeling techniques (Oliveira et al. 2015) and/or the very low-altitude measurements at the end of the mission will bring new insights on the field morphology of Mercury. The ESA/JAXA BepiColombo mission that will be launched in 2017 will complete the geographical coverage of low altitudes of the planet and will lead to the first global view of the magnetic field of Mercury (Benkhoff et al. 2010). The description of the past Martian magnetic field and its interpretation in terms of past dynamo processes will be improved by the recently inserted-into-orbit MAVEN mission. These measurements will be completed by the upcoming InSight mission, which will study the internal structure of Mars and bring constraints on the size of the liquid core. The CASSINI mission to Saturn (Dougherty et al. 2004) is extended until 2016, and the forthcoming Juno (around Jupiter) and later JUICE (around Jupiter moons) missions (Grasset et al. 2013) will also bring new measurements around the giant gas planets and their moons. These new planetary magnetic field models will provide more reliable observational constraints on the processes generating the fields in the interior of the planets and moons.
The identification of the post-perovskite phase transition (Murakami et al. 2004) provided better constraints on the Earth’s deepest mantle. Seismic observations with improved tomographic images as well as sophisticated analyses of seismic waves were obtained. A better description of lower mantle materials with laboratory experiments reaching the appropriate high pressure range as well as time-consuming ab initio quantum chemistry computations became possible. As can be expected, the emerging picture bears a much greater complexity which includes the probable role of compositional variations and possible contributions of mantle melting and spin transitions of iron. While the last decade opened new questions such as the complex effect of composition on the post-perovskite phase transition, the precise nature of the melting curve and the points of dissent that remain between laboratory experiments and computational mineralogy, the establishment over the coming decade of an integrative framework (Shim and Lay 2014) would offer a much clearer interpretation of seismic observations and allow to better extract the purely thermal contribution from tomographic models.
Progress in understanding the dynamics of the Earth mantle in the last hundreds of Myr ultimately requires a better description of plate motions in the framework of mantle convection. Promising research paths include conceptual developments such as the understanding of lithospheric damage (Bercovici and Ricard 2014) as well as an improved treatment of plate-like behavior in spherical simulations of mantle dynamics (Bello et al. 2014; Rolf et al. 2012, 2014). In the meantime, improved reconstructions of plate velocities (Seton et al. 2012) can be prescribed to mantle convection models to investigate the role of specific ingredients such as mantle rheology, phase transitions and the nature of a possible dense basal layer. A more thorough investigation of mantle convection models than the pioneering attempt of Zhang and Zhong (2011) may establish more robust CMB heat flux evolution models than HF1.
One direct consequence of the results of the reversal frequency studies is the possibility to invert the record of paleomagnetic reversal frequency (Gradstein et al. 2012) for time-dependent core energetics. If the relation between pile height and CMB heat flux (mean and heterogeneity amplitude) is indeed approximately linear (Amit and Olson 2015; Olson and Amit 2014), the observed reversal frequency may be transformed into a relative CMB heat flux. This may provide a glimpse into the history of core convection.
As for the distant past of the Earth, prospects for other planetary objects mostly rely on modeling progress. Specific planetary scenarios that involve large impacts will most probably remain attractive in the next decade, concerning the ancient Martian magnetic field as well as other planets. Better descriptions of such events than the simplified approaches mentioned above can be simulated (Marinova et al. 2008, 2011). In terms of CMB heat flux, the geometry of impact heating with both a mantle contribution and a possible core contribution (Roberts and Arkani-Hamed 2014) could be described by such numerical tools. As mentioned in Monteux et al. (2015), the presence of impact-induced molten material is key in recording the impact-influenced magnetic field, and the interplay between the cooling time of this material and the transient dynamo properties will ultimately dictate the nature of remnant magnetism. In this regard, impact simulations could also supply patterns and volumes of ejecta deposits on the planetary surface. Describing the dynamics of the bulk molten material could involve on longer timescale phenomena such as isostatic adjustment of the retained melt region and lateral spreading as a gravity current (Reese et al. 2011).
Applications to other planets (apart from the Earth and Mars) may also be considered by invoking alternative CMB heat flux models. A \({Y_{2}^{0}}\) CMB heat flux pattern combined with internal heating may trigger an unstable odd convective mode which may explain the hemispheric field of Mercury (Cao et al. 2014; Wicht and Heyner 2014) as observed by MESSENGER (Anderson et al. 2012). While their dynamical scenario is convincing, the justification for a \({Y_{2}^{0}}\) thermal heterogeneity at the mantle of Mercury is somewhat vague. Examination of gravity and topographic heterogeneities in Mercury may provide a more realistic (alternative) model for the CMB heat flux which can be invoked to recover MESSENGER’s magnetic observations.
Due to computational limitations, dynamo models operate in a parametric regime very far from that of planetary core conditions (Glatzmaier 2002). This is especially restrictive for long simulations, as is the case when the long-term impact of an heterogeneous mantle is investigated. One of the most challenging problems in terms of computer power is that of modeling strongly time-variable magnetic reversal frequency, because adequate statistics require extremely long simulations. For example, the Ekman numbers used by Olson et al. (2013) and Amit and Olson (2015) are about four orders of magnitudes off the lowest values that were reported for numerical dynamos (Sakuraba and Roberts 2009). Improved numerical techniques which will allow running simulations with more challenging parameters, in particular lower Ekman and magnetic Prandtl numbers, are therefore of great interest for studies of mantle control on planetary dynamos. More efficient, massively parallelized dynamo codes are currently under development (http://geodynamics.org/cig/working-groups/geodynamo/).
More accurate incorporation of physical phenomena in dynamo models will also improve their predictions. In particular, correct implementation of thermochemical convection is necessary. Currently, most studies use the co-density formulation (Braginsky and Roberts 1995). Apart from neglecting double-diffusive convection, this approach fails to accurately prescribe the inner boundary condition. Some models have already incorporated thermal and chemical convection with appropriate boundary conditions in numerical dynamos (Manglik et al. 2010; Takahashi 2014; Trümper et al. 2012). Tracer methods which are commonly used in mantle convection simulations (e.g., Tackley and King 2003) may be applied to chemical convection in dynamo codes for more accurate numerical schemes. Other physical complications such as stable stratification in some regions of the outer core (Gubbins and Davies 2013) and compressibility may also be incorporated into dynamo models.
Observed dynamo properties that require boundary heterogeneity may alternatively be explained by lateral anomalies at the inner core boundary. Olson and Deguen (2012) showed that the dipole eccentricity in archeomagnetic field models can be reproduced by dynamo simulations with heterogeneous \({Y_{1}^{1}}\) inner boundary bouyancy flux pattern, corresponding to the east-west seismic anomalies at the upper inner core (Tanaka and Hamaguchi 1997). Aubert et al. (2013) showed that the localization of the westward drift of the geomagnetic field at the Atlantic hemisphere is controlled by the same heterogeneous inner boundary buoyancy flux. In these studies, the inner boundary heterogeneity amplitude was set to be significantly larger than that of the outer boundary, therefore the role of the CMB heterogeneity becomes secondary. It would be interesting to explore dynamo models with comparable amplitude heterogeneities on both boundaries to investigate competing effects.
Progress in understanding mantle dynamics will lead to better description of boundary conditions for the dynamo and thus improved knowledge of core dynamics. On the other hand, magnetic observations may be used to constrain mantle convection scenarios. Overall, a multidisciplinary approach with interactive exchange of information among the different envelopes may advance the study of planetary deep interiors.
Abbreviations
- CMB:
-
core-mantle boundary
- LLSVPs:
-
large low shear-wave velocity provinces
- ULVZs:
-
ultra low velocity zones
- KRS:
-
Kiaman reversed superchron
- CNS:
-
cretaceous normal superchron
- ESA:
-
European Space Agency
- NASA:
-
National Aeronautics and Space Administration
- MESSENGER:
-
MErcury surface: Space ENvironment: GEochemistry: and ranging
- JAXA:
-
Japan Aerospace eXploration Agency
- MAVEN:
-
Mars atmosphere and volatile evolution
- InSight:
-
Interior exploration using seismic investigations: Geodesy and Heat Transport
- JUICE:
-
JUpiter ICy moon explorer
References
Acuña, M, Connerney J, Wasilewski P, Lin R, Mitchell D, Anderson K, Carlson C, McFadden J, Remè H, Mazelle C, Vignes D, Bauer S, Cloutier P, Ness N (2001) Magnetic field of mars: Summary of results from the aerobraking and mapping orbits. J Gephys Res 106: 23403–23417.
Acuña, MH, Connerney JEP, Wasilewski P, Lin RP, Anderson KA, Carlson CW, McFadden J, Curtis DW, Mitchell D, Reme H, Mazelle C, Sauvaud JA, d’Uston C, Cros A, Medale JL, Bauer SJ, Cloutier P, Mayhew M, Winterhalter D, Ness NF (1998) Magnetic field and plasma observations at Mars: Initial results of the Mars global surveyor mission. Science 279: 1676–1680.
Alboussiére, T, Deguen R, Melzani M (2010) Melting-induced stratification above the Earth’s inner core due to convective translation. Nature 466: 744–747.
Amit, H, Aubert J, Hulot G (2010a) Stationary, oscillating or drifting mantle-driven geomagnetic flux patchesJ Geophys Res B07108. doi:10.1029/2009JB006542.
Amit, H, Choblet G (2009) Mantle-driven geodynamo features - effects of post-perovskite phase transition. Earth Planets Space 61: 1255–1268.
Amit, H, Choblet G (2012) Mantle-driven geodynamo features - effects of compositional and narrow d” anomalies. Phys Earth Planet Inter190-191: 34–43.
Amit, H, Christensen U (2008) Accounting for magnetic diffusion in core flow inversions from geomagnetic secular variation. Geophys J Int 175: 913–924.
Amit, H, Christensen U, Langlais B (2011a) The influence of degree-1 mantle heterogeneity on the past dynamo of Mars. Phys Earth Planet Inter 189: 63–79.
Amit, H, Deschamps F, Choblet G (in press) Numerical dynamos with outer boundary heat flux inferred from probabilistic tomography – consequences for latitudinal distribution of magnetic flux. Geophys J Int. doi:10.1093/gji/ggv332.
Amit, H, Korte M, Aubert J, Constable C, Hulot G (2011b) The time-dependence of intense archeomagnetic flux patches. J Geophys Res 116: B12106. doi:10.1029/2011JB008538.
Amit, H, Leonhardt R, Wicht J (2010b) Polarity reversals from paleomagnetic observations and numerical dynamo simulations. Space Sci Rev 155: 293–335.
Amit, H, Olson P (2006) Time-average and time-dependent parts of core flow. Phys Earth Planet Inter 155: 120–139.
Amit, H, Olson P (2015) Lower mantle superplume growth excites geomagnetic reversals. Earth Planet Sci Lett 414: 68–76.
Anderson, BJ, Johnson CL, Korth H, Purucker ME, Winslow RM, Slavin JA, Solomon SC, McNutt RL, Raines JM, Zurbuchen TH (2012) The global magnetic field of Mercury from MESSENGER orbital observations. Science 333: 1859–1862.
Arkani-Hamed, J (2012) Life of the Martian dynamo. Phys Earth Planet Inter 196: 83–96.
Arkani-Hamed, J, Olson P (2010) Giant impact stratification of the Martian core. Geophys Res Lett 37: L02201. doi:10.1029/2009GL041417.
Aubert, J (2005) Steady zonal flows in spherical shell fluid dynamos. J Fluid Mech 542: 53–67.
Aubert, J, Amit H, Hulot G (2007) Detecting thermal boundary control in surface flows from numerical dynamos. Phys Earth Planet Inter 160: 143–156.
Aubert, J, Amit H, Hulot G, Olson P (2008) Thermo-chemical wind flows couple Earth’s inner core growth to mantle heterogeneity. Nature 454: 758–761.
Aubert, J, Finlay CC, Fournier A (2013) Bottom-up control of geomagnetic secular variation by the Earth’s inner core. Nature 502: 219–223.
Aubert, J, Labrosse S, Poitou C (2009) Modelling the paleo-evolution of the geodynamo. Geophys J Int 179: 1414–1428.
Aurnou, J, Andreadis S, Zhu L, Olson P (2003) Experiments on convection in Earth’s core tangent cylinder. Earth Planet Sci Lett 212: 119–134.
Bello, L, Coltice N, Rolf T, Tackley PJ (2014) On the predictability limit of convection models of the Earth’s mantle. Geochem Geophys Geosys 15. doi:10.1002/2014GC005254.
Benkhoff, J, van Casteren J, Hayakawa H, Fujimoto M, Laakso H, Novara M, Ferri P, Middleton HR, Ziethe R (2010) BepiColombo - Comprehensive exploration of Mercury: Mission overview and science goals. Planet Space Sci58. doi:10.1016/j.pss.2009.09.020.
Bercovici, D, Ricard Y (2014) Plate tectonics, damage and inheritance. Nature 508: 513–516.
Biggin, AJ, Steinberger B, Aubert J, Suttie N, Holme R, Torsvik TH, van der Meer DG, van Hinsbergen DJJ (2012) Possible links between long-term geomagnetic variations and whole-mantle convection processes. Nature Geosci 5: 526–533.
Bloxham, J (2002) Time-independent and time-dependent behaviour of high-latitude flux bundles at the core-mantle boundary. Geophys Res Lett 29. doi:10.1029/2001gl014543.
Braginsky, SI, Roberts PH (1995) Equations governing convection in Earth’s core and the geodynamo. Geophys Astrophys Fluid Dyn 79: 1–97.
Breuer, D, Labrosse S, Spohn T (2010) Thermal evolution and magnetic field generation in terrestrial planets and satellites. Space Sci Rev 152: 449–500.
Bull, AL, McNamara AK, Ritsema J (2009) Synthetic tomography of plume clusters and thermochemical piles. Earth Planet Sci Lett 278: 152–162.
Burke, K (2011) Plate tectonics, the Wilson cycle, and mantle plumes: geodynamics from the top. Annu Rev Earth Planet Sci 39: 1–29.
Burke, K, Steinberger B, Torsvik TH, Smethhurst MA (2008) Plume generation zones at the margins of large low shear velocity provinces on the core-mantle boundary. Earth Planet Sci Lett 265: 49–60.
Busse, FH (1970) Thermal instabilities in rapidly rotating systems. J Fluid Mech 44: 441–460.
Cao, H, Aurnou JM, Wicht J, Dietrich W, Soderlund KM, Russell CT (2014) A dynamo explanation for Mercury’s anomalous magnetic field. Geophys Res Lett 41. doi:10.1002/2014GL060196.
Christensen, U, Aubert J (2006) Scaling properties of convection-driven dynamos in rotating spherical shells and application to planetary magnetic fields. Geophys J Int 166: 97–114.
Christensen, U, Aubert J, Hulot G (2010) Conditions for Earth-like geodynamo models. Earth Planet Sci Lett 296: 487–496.
Christensen, U, Olson P (2003) Secular variation in numerical geodynamo models with lateral variations of boundary heat flow. Phys Earth Planet Inter 138: 39–54.
Christensen, U, Olson P, Glatzmaier G (1998) A dynamo model interpretation of geomagnetic field structures. Geophys Res Lett 25: 1565–1568.
Christensen, U, Wicht J (2007) Numerical dynamo simulations. In: Olson P (ed)Treatise on Geophysics Vol 8.. Elsevier Science, Amsterdam.
Cizkova, H, Cadek O, Matyska C, Yuen D (2010) Implications of post-perovskite properties for core-mantle dynamics. Phys Earth Planet Inter 180: 235–243.
Cobden, L, Mosca I, Trampert JJR (2012) On the likelihood of post-perovskite near the core-mantle boundary: a statistical interpretation of seismic observations. Phys Earth Planet Inter210-211: 21–35.
Cobden, L, Thomas C (2013) The origin of d” reflections a systematic study of seismic array data sets. Geophys J Int 194: 1091–1118.
Coe, RS, Hongre L, Glatzmaier GA (2000) An examination of simulated geomagnetic reversals from a palaeomagnetic perspective. Phil Trans R Soc Lond 358: 1141–1170.
Courtillot, V, Besse J (1987) Magnetic field reversals, polar wander, and core-mantle coupling. Science 237: 1140–1147.
Davaille, A (1999) Simultaneous generation of hotspots and superswells by convection in a heterogeneous planetary mantle. Nature 402: 756–760.
Davies, CJ, Gubbins D, Willis AP, Jimack PK (2008) Time-averaged paleomagnetic field and secular variation: Predictions from dynamo solutions based on lower mantle seismic tomography. Phys Earth Planet Inter 169: 194–203.
Deschamps, F, Cobden L, Tackley PJ (2012) The primitive nature of large low shear-wave velocity provinces. Earth Planet Sci Lett349-350: 198–208.
Deuss, A (2014) Heterogeneity and anisotropy of Earth’s inner core. Ann Rev Earth Planet Sci 42: 103–126.
Dietrich, W, Wicht J (2013) A hemispherical dynamo model: Implications for the Martian crustal magnetization. Phys Earth Planet Inter 217: 10–21.
Dougherty, MK, Kellock S, Southwood DJ, Balogh A, Smith EJ, Tsurutani BT, Gerlach B, Glassmeier K-H, Gleim F, Russell CT, Erdos G, Neubauer FM, Cowley SWH (2004) The Cassini magnetic field investigation. Space Sc Rev 114. doi:10.1007/s11214--004--1432--2.
Dziewonski, AM, Lekic V, Romanowicz BA (2010) Mantle anchor structure: an argument for bottom up tectonics. Earth Planet Sci Lett 299: 69–79.
Elkins-Tanton, LT, Zaranek SE, Parmentier EM, Hess PC (2005) Early magnetic field and magmatic activity on Mars from magma ocean cumulate overturn. Earth Planet Sci Lett 236: 1–12.
Gillet, N, Pais MA, Jault D (2009) Ensemble inversion of time-dependent core flow models. Geochem Geophys Geosyst 10. doi:10.1029/2008GC002290.
Glatzmaier, GA (2002) Geodynamo simulations: how realistic are theyAnnu Rev Earth Planet Sci Lett 30: 237–257.
Glatzmaier, GA, Coe R, Hongre L, Roberts PH (1999) The role of the earth’s mantle in controlling the frequency of geomagnetic reversals. Nature 401: 885–890.
Glatzmaier, GA, Roberts PH (1995) A three-dimensional self-consistent computer simulation of a geomagnetic field reversal. Nature 377: 203–209.
Glatzmaier, GA, Roberts PH (1997) Simulating the geodynamo. Contemp Phys 38: 269–288.
Glenn Sterenborg, M, Crowley JW (2013) Thermal evolution of early solar system planetesimals and the possibility of sustained dynamos. Phys Earth Planet Inter 214: 53–73.
Gradstein, F, Ogg J, Schmitz M, Ogg G (2012) The Geologic Time Scale 2012. Elsevier Science, Amsterdam.
Grasset, O, Dougherty MK, Coustenis A, Bunce EJ, Erd C, Titov D, Blanc M, Coates A, Drossart P, Fletcher LN, Hussmann H, Jaumann R, Krupp N, Lebreton J-P, Prieto-Ballesteros O, Tortora P, Tosi F, Van Hoolst T (2013) JUpiter ICy moons Explorer (JUICE): An ESA mission to orbit Ganymede and to characterise the Jupiter system. Planet Space Sci 78. doi:10.1016/j.pss.2012.12.002.
Grimm, RE, Solomon SC (1986) Tectonic tests of proposed polar wander paths for Mars and the Moon. Icarus 65: 110–121.
Gubbins, D (2003) Thermal core-mantle interactions: theory and observations. In: Dehant V, Creager K, Karato S, Zatman S (eds)Earth’s Core: dynamics, structure and rotation. AGU Geodynamics Series American Geophysical Union, Washington DC.
Gubbins, D, Davies CJ (2013) The stratified layer at the core-mantle boundary caused by barodiffusion of oxygen, sulphur and silicon. Phys Earth Planet Inter 215: 21–28.
Gubbins, D, Sreenivasan B, Mound J, Rost S (2011) Melting of the Earth’s inner core. Nature 473: 361–363.
Gubbins, D, Willis PW, Sreenivasan B (2007) Correlation of Earth’s magnetic field with lower mantle thermal and seismic structure. Phys Earth Planet Inter 162: 256–260.
Harder, H, Christensen UR (1996) A one-plume model of Martian mantle convection. Nature 380: 507–509.
Heimpel, MH, Evans ME (2013) Testing the geomagnetic dipole and reversing dynamo models over Earth’s cooling history. Phys Earth Planet Inter 224: 124–131.
Hernlund, J, Thomas C, Tackley PJ (2005) A doubling of the post-perovskite phase boundary and structure of the Earth’s lowermost mantle. Nature 434: 882–886.
Hoffman, KA (1996) Transitional paleomagnetic field behavior: Preferred paths or patches?Surv Geophys 17: 207–211.
Holme, R (2007) Large-scale flow in the core. In: Olson P (ed)Treatise on Geophysics, Vol 8.. Elsevier Science, Amsterdam.
Holme, R, Olsen N (2006) Core surface ow modelling from high-resolution secular variation. Geophys J Int 166: 518–528.
Hood, LL, Young CN, Richmond NC, Harrison KP (2005) Modeling of major Martian magnetic anomalies: Further evidence for polar reorientations during the Noachian. Icarus 177. doi:10.1016/j.icarus.2005.02.008.
Hori, K, Wicht J (2013) Subcritical dynamos in the early Mars’ core: Implications for cessation of the past Martian dynamo. Phys Earth Planet Inter 219: 21–33.
Hulot, G, Eymin C, Langlais B, Mandea M, Olsen N (2002) Small-scale structure of the geodynamo inferred from Oersted and Magsat satellite data. Nature 416: 620–623.
Irving, JCE, Deuss A (2011) Hemispherical structure in inner core velocity anisotropy. J Geophys Res 116. doi:10.1029/2010JB007942.
Ishii, M, Tromp J (1999) Normal-mode and free-air gravity constraints on lateral variations in velocity and density of Earth’s mantle. Science 285: 1231–1236.
Jackson, A (2003) Intense equatorial flux spots on the surface of the Earth’s core. Nature 424: 760–763.
Jackson, A, Jonkers ART, Walker MR (2000) Four centuries of geomagnetic secular variation from historical records. Phil Trans R Soc Lond A 358: 957–990.
Jellinek, AM, Johnson CL, Schubert G (2008) Constraints on the elastic thickness, heat flow, and melt production at early Tharsis from topography and magnetic field observations. J Geophys Res 113: E09004.
Johnson, CL, Phillips RJ (2005) Evolution of the tharsis region of Mars: insights from magnetic field observations. Earth Planet Sci Lett 230: 241–254.
Jutzi, M, Asphaug E (2011) Forming the lunar farside highlands by accretion of a companion moon. Nature 476: 69–72.
Ke, Y, Solomatov VS (2006) Early transient superplumes and the origin of the Martian crustal dichotomy. J Geophys Res 111: 10001.
Ke, Y, Solomatov VS (2009) Coupled core-mantle thermal evolution of early Mars. J Geophys Res 114: 1–12.
Kelly, P, Gubbins D (1997) The geomagnetic field over the past 5 million years. Geophys J Int 128: 315–330.
Korte, M, Donadini F, Constable C (2009) The geomagnetic field for 0-3ka: 2. a new series of time-varying global models. J Geophys Res 10: Q06008. doi:10.1029/2008GC002297.
Korte, M, Holme R (2010) On the persistence of geomagnetic flux lobes in global Holocene field models. Phys Earth Planet Inter 182: 179–186.
Kuang, W, Jiang W, Roberts J, Frey HV (2014) Could giant basin-forming impacts have killed martian dynamoGeophys Res Lett 41: 8006–8012.
Kuang, W, Jiang W, Wang T (2008) Sudden termination of Martian dynamo? implications from subcritical dynamo simulations. Geophys Res Lett 35: L14204.
Kutzner, C, Christensen UR (2002) From stable dipolar towards reversing numerical dynamos. Phys Earth Planet Inter 131: 29–45.
Kutzner, C, Christensen UR (2004) Simulated geomagnetic reversals and preferred virtual geomagnetic pole paths. Geophys J Int 157: 1105–1118.
Labrosse, S (2003) Thermal and magnetic evolution of the earth’s core. Phys Earth Planet Inter 140: 127–143.
Langlais, B, Purucker M (2007) A polar magnetic paleopole associated with Apoolinaris Patera Mars. Planet Space Sci 55: 270–279.
Langlais, B, Purucker M, Mandea M (2004) Crustal magnetic field of Mars. J Geophys Res 109: E02008.
Lay, T, Herlund J, Buffett B (2008) Core-mantle boundary heat flow. Nature Geosci 1: 25–32.
Lay, T, Hernlund J, Garnero EJ, Thorne MS (2006) A post-perovskite lens and D” heat flux beneath the central Pacific. Science 314: 1272–1276.
Lebrun, T, Massol H, Chassefiére E, Davaille A, Marcq E, Sarda P, Leblanc F, Branedeis G (2013) Thermal evolution of an early magma ocean in interaction with the atmosphere. J Geophys Res 118: 1155–1176.
Lekic, V, Cottaar S, Dziewonski A, Romanowicz B (2012) Cluster analysis of global lower mantle tomography: A new class of structure and implications for chemical heterogeneity. Earth Planet Sci Lett357-358: 68–77.
Lhuillier, F, Hulot G, Gallet Y (2013) Statistical properties of reversals and chrons in numerical dynamos and implications for the geodynamo. Phys Earth Planet Inter 220: 19–36.
Lillis, RJ, Frey HV, Manga M (2008) Rapid decrease in Martian crustal magnetisation in the Noachian era: implications for the dynamo and climate of early mars. Geophys Res Lett 35: L14203.
Lithgow-Bertelloni, C, Richards MA (1998) Dynamics of cenozoic and mesozoic plate motion. Rev Geophys 36: 27–78.
Love, JJ (1998). Paleomagnetic volcanic data and geometric regularity of reversals and excursions 103: 12435–12452.
Manglik, A, Wicht J, Christensen UR (2010) A dynamo model with double diffusive convection for Mercury’s core. Earth Planet Sci Lett 289: 619–628.
Marinova, MM, Aharonson O, Asphaug E (2008) Mega-impact formation of the Mars hemispheric dichotomy. Nature 453: 1216–219.
Marinova, MM, Aharonson O, Asphaug E (2011) Geophysical consequences of planetary-scale impacts into a Mars-like planet. Icarus 211: 960–985.
Masters, G, Laske G, Bolton H, Dziewonski A (2000) The relative behavior of shear velocity, bulk sound velocity, and compressional velocity in the mantle: Implications for chemical and thermal structure. In: Karato S, Forte A, Liebermann R, Masters G, Stixrude L (eds)Earths deep interior, Vol 117.. AGU Monograph, Washington D.C.
Matsuyama, I, Mitrovica JX, Manga M, Perron JT, Richards MA (2006) Rotational stability of dynamic planets with elastic lithospheres. J Geophys Res 111. doi:10.1029/2005JE002447.
McNamara, A, Garnero E, Rost S (2010) Tracking deep mantle reservoirs with ultra-low velocity zones. Earth Planet Sci Lett 299: 1–9.
McNamara, A, Zhong S (2005) Thermochemical structures beneath Africa and the Pacific Ocean. Nature 437: 1136–1139.
Merrill, RT, McElhinny MW, McFadden PL (1998) The Magnetic Field of the Earth: Paleomagnetism, the Core, and the Deep Mantle. Academic Press, San Diego, California, USA.
Merrill, RT, McFadden PL (1999) Geomagnetic polarity transitions37: 201–226.
Milbury, C, Schubert G, Raymond CA, Smrekar SE, Langlais B (2012) The history of Mars’ dynamo as revealed by modeling magnetic anomalies near Tyrrhenus Mons and Syrtis Major. J Geophys Res 117. doi:10.1029/2012JE004099
Moffatt, HK (1978) Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press, Cambridge, UK.
Monnereau, M, Calvet M, Margerin L, Souriau A (2010) Lopsided growth of Earth’s inner core. Science 238: 1014–1017.
Monteux, J, Amit H, Choblet G, Langlais B, Tobie G (2015) Giant impacts, heterogeneous mantle heating and a past hemispheric dynamo on Mars. Phys Earth Planet Inter 240: 114–124.
Monteux, J, Arkani-Hamed J (2014) Consequences of giant impacts in early Mars: Core merging and Martian dynamo evolution. J Geophys Res 119: 480–505.
Monteux, J, Coltice N, Dubuffet F, Ricard Y (2007) Thermo-mechanical adjustment after impacts during planetary growth. Geophys Res Lett 34: 24201–24205.
Monteux, J, Jellinek AM, Johnson CL (2011) Why might planets and moons have early dynamosEarth Planet Sci Lett 310: 349–359.
Monteux, J, Jellinek AM, Johnson CL (2013) Dynamics of core merging after a mega-impact with applications to Mars’ early dynamo. Icarus 226: 20–32.
Monteux, J, Schaeffer N, Amit H, Cardin P (2012) Can a sinking metallic diapir generate a dynamoJ Geophys Res 117: E10005. doi:10.1029/2012JE004075.
Mosca, I, Cobden L, Deuss A, Ritsema J, Trampert J (2012) Seismic and mineralogical structures of the lower mantle from probabilistic tomography. J Geophys Res 117. doi:10.1029/2011JB008851.
Murakami, M, Hirose K, Sata N, Ohishi Y, Kawamura K (2004) Post-perovskite phase transition in MgSio3. Science 304: 855–858.
Nakagawa, T, Tackley PJ (2008) Lateral variations in cmb heat flux and deep mantle seismic velocity caused by a thermal-chemical-phase boundary layer in 3d spherical convection. Earth Planet Sci Lett 271: 348–358.
Nakagawa, T, Tackley PJ (2011) Effects of low-viscosity post-perovskite on thermo-chemical mantle convection in a 3-D spherical shell. Geophys Res Lett 38: L04309.
Ni, S, Helmberger DV, Tromp J (2005) Three-dimensional structure of the African superplume from waveform modelling. Geophys J Int 161: 283–294.
Ni, S, Tan E, Gurnis M, Helmberger D (2002) Sharp sides to the African superplume. Science 296: 1850–1852.
Nimmo, F, Hart SD, Horycansky DG, Agnor CB (2008) Implications of an impact origin for the Martian hemispheric dichotomy. Nature 453: 1220–1223.
Oganov, A, Ono S (2004) Theoretical and experimental evidence for a post-perovskite phase of MgSio3 in Earth’s D” layer. Nature 430: 445–448.
Oliveira, JS, Langlais B, Pais MA, Amit H (2015) A new method to model partially distributed magnetic field measurements, with application to Mercury. J Geophys Res. 120. doi:10.1002/2014JE004734.
Olsen, N, Luehr H, Finlay CC, Sabaka TJ, Michaelis I, Rauberg J, Tøffner-Clausen L (2014) The CHAOS-4 geomagnetic field model. Geophys J Int 197: 815–827.
Olson, P (2007a) Gravitational dynamos and the low frequency geomagnetic secular variation. Proc Nat Acad Sci 104: 20159–20166.
Olson, P (2007b) Overview. In: Olson P (ed)Treatise on Geophysics, Vol 8.. Elsevier Science, Amsterdam.
Olsen, N, Friis-Christensen E, Floberghagen R, Alken P, Beggan CD, Chulliat A, Doornbos E, da Encarnação JT, Hamilton B, Hulot G, van den IJssel J, Kuvshinov A, Lesur V, Lühr H, Macmillan S, Maus S, Noja M, Olsen PEH, Park J, Plank G, Püthe C, Rauberg J, Ritter P, Rother M, Sabaka TJ, Schachtschneider R, Sirol O, Stolle C, Thébault E, Thomson AWP, et al (2013) The Swarm Satellite Constellation Application and Research Facility (SCARF) and Swarm data products. Earth, Planets and Space 65(11): 1189–1200. doi:10.5047/eps.2013.07.001.
Olson, P, Amit H (2014) Magnetic reversal frequency scaling in dynamos with thermochemical convection. Phys Earth Planet Inter 229: 122–133.
Olson, P, Christensen U (2002) The time averaged magnetic field in numerical dynamos with nonuniform boundary heat flow. Geophys J Int 151: 809–823.
Olson, P, Christensen U (2006) Dipole moment scaling for convection-driven planetary dynamos. Earth Planet Sci Lett 250: 561–571.
Olson, P, Christensen UR, Glatzmaier GA (1999) Numerical modeling of the geodynamo: Mechanisms of field generation and equilibration. J Geophys Res 104: 10383–110404.
Olson, P, Coe RS, Driscoll PE, Glatzmaier GA, Roberts PH (2010) Geodynamo reversal frequency and heterogeneous core-mantle boundary heat flow. Phys Earth Planet Inter 180: 66–79.
Olson, P, Deguen R (2012) Lopsided inner core growth and eccentricity of the geomagnetic dipole. Nat Geosci 5(8): 565–569.
Olson, P, Deguen R, Hinnov LA, Zhong S (2013) Controls on geomagnetic reversals and core evolution by mantle convection in the Phanerozoic. Phys Earth Planet Inter 214: 87–103.
Perron, JT, Mitrovica JX, Manga M, Matsuyama I, Richards MA (2007) Evidence for an ancient Martian ocean in the topography of deformed shorelines. Nature 447: 840–843.
Pierazzo, E, Vickery AM, Melosh HJ (1997) A reevaluation of impact melt production. Icarus 127: 408–423.
Pozzo, M, Davies C, Gubbins D, Alfè D (2012) Thermal and electrical conductivity of iron at Earth’s core conditions. Nature 485: 355–358.
Reese, CC, Orth CP, Solomatov VS (2011) Impact megadomes and the origin of the martian crustal dichotomy. Icarus 213: 433–442.
Reese, CC, Solomatov VS (2010) Early martian dynamo generation due to giant impacts. Icarus 207: 82–97.
Reese, CC, Solomatov VS, Baumgardner JR (2002) Survival of impact-induced thermal anomalies in the Martian mantle. J Geophys Res 107: 1–12.
Ritsema, J, McNamara A, Bull A (2007) Tomographic filtering of geodynamic models: Implications for model interpretation and large-scale mantle structure. J Geophys Res 112: B01303.
Roberts, JH, Arkani-Hamed J (2012) Impact-induced mantle dynamics on Mars. Icarus 218: 278–289.
Roberts, JH, Arkani-Hamed J (2014) Impact heating and coupled core cooling and mantle dynamics on Mars. J Geophys Res 119: 729–744.
Roberts, JH, Barnouin OS (2012) The effect of the Caloris impact on the mantle dynamics and volcanism of Mercury. J Geophys Res 117: E02007.
Roberts, JH, Lillis RJ, Manga M (2009) Giant impacts on early Mars and the cessation of the Martian dynamo. J Geophys Res 114: E04009. doi:10.1029/2008JE003287.
Roberts, JH, Zhong S (2006) Degree-1 convection in the Martian mantle and the origin of the hemispheric dichotomy. J Geophys Res 111: E06013.
Roberts, JH, Zhong S (2007) The cause for the north-south orientation of the crustal dichotomy and the equatorial location of Tharsis on Mars. Icarus 190(1): 24–31.
Rolf, T, Coltice N, Tackley PJ (2012) Linking continental drift, plate tectonics and the thermal state of the Earth’s mantle. Earth Planet Sci Lett. 351–352: 134–146.
Rolf T, Coltice N, Tackley PJ (2014) Statistical cyclicity of the supercontinent cycle. Geophys Res Lett 41. doi:10.1002/2014GL059595.
Romanowicz, B, Gung Y (2002) Superplumes from the core-mantle boundary to the lithosphere: Implications for heat flux. Science 296: 513–516.
Sakuraba, A, Roberts PH (2009) Generation of a strong magnetic field using uniform heat flux at the surface of the core. Nat Geosci 2: 802–805.
Schubert, G, Masters G, Olson P, Tackley P (2004) Superplumes or plume clustersPhys Earth Planet Inter 146: 147–162.
Schubert, G, Spohn T (1990) Thermal history of Mars and the sulfur content of its core. J Geophys Res 95: 14095–14104.
Scotese, CR (2001) Atlas of Earth history In: PALEOMAP Progress Rep. 90-0497. Dep. of Geol, Univ. of Tex. at Arlington.
Senshu, H, Kuramoto K, Matsui T (2002) Thermal evolution of a growing mars. J Geophys Res 107: 1–13.
Seton, M, Müller RD, Zahirovic S, Gaina C, Torsvik T, Shephard G, Talsma A, Gurnis M, Turner M, Maus S, Chandler M (2012) Global continental and ocean basin reconstructions since 200 Ma. Earth-Sci Rev 113: 212–270.
Shim, S-H, Lay T (2014) Post-perovskite at ten. Nat Geosci 7: 621–623.
Solomatov, VS (2007) Magma oceans and primordial mantle differentiation. In: Schubert G (ed)Treatise on Geophysics, Vol 9.. Elsevier Science, Amsterdam.
Srámek, O, Zhong S (2010) Long-wavelength stagnant lid convection with hemispheric variation in lithospheric thickness: link between Martian crustal dichotomy and TharsisJ Geophys Res 115: E09010.
Srámek, O, Zhong S (2012) Martian crustal dichotomy and Tharsis formation by partial melting coupled to early plume migration. J Geophys Res 117: E01005.
Sreenivasan, B (2009) On dynamo action produced by boundary thermal coupling. Phys Earth Planet Inter 177: 130–138.
Sreenivasan, B, Gubbins D (2011) On mantle-induced heat flow variations at the inner core boundary. Phys Earth Planet Inter 187: 336–341.
Sreenivasan, B, Jellinek AM (2012) Did the tharsis plume terminate the Martian dynamo?Earth Planet Sci Lett 209–217.
Sreenivasan, B, Jones CA (2011) Helicity generation and subcritical behaviour in rapidly rotating dynamos. J Fluid Mech 688: 5–30.
Stanley, S (2010) A dynamo model for axisymmetrizing Saturn’s magnetic field. Geophys Res Lett 37: 5201.
Stanley, S, Elkins-Tanton L, Zuber MT, Parmentier EM (2008) Mars’ paleomagnetic field as the result of a single-hemisphere dynamo. Science 321: 1822–1825.
Stevenson, D (1983) Planetary magnetic fields. Rep Prog Phys 46: 555–620.
Tackley, P (2002) The strong heterogeneity caused by deep mantle layering. Geophys Geochem Geosyst 3. doi:10.1029/2001GC000167.
Tackley, PJ (2011) Living dead slabs in 3-D: The dynamics of compositionally-stratified slabs entering a ’slab graveyard’ above the core-mantle boundary. Phys Earth Planet Inter 188: 150–162.
Tackley, PJ, King SD (2003) Testing the tracer ratio method for modeling active compositional fields in mantle convection simulations. Geochem Geophys Geosyst 4. doi:10.1029/2001GC000214.
Takahashi, F (2014) Double diffusive convection in the Earth’s core and the morphology of the geomagnetic field. Phys Earth Planet Inter 226: 83–87.
Takahashi, F, Tsunakawa H, Matsushima M, Mochizuki N, Honkura Y (2008) Effects of thermally heterogeneous structure in the lowermost mantle on the geomagnetic field strength. Earth Planet Sci Lett 272: 738–746.
Tan, E, Gurnis M (2007) Compressible thermochemical convection and application to lower mantle structures. J Geophys Res 112. doi:10.1029/2006JB004505.
Tanaka, S, Hamaguchi H (1997) Degree one heterogeneity and hemispherical variation of anisotropy in the inner core from PKP(BC)-PKP(DF) times. J Geophys Res 102: 2925–2938.
To, A, Romanowicz B, Capdeville Y, Takeuchi N (2005) 3D effects of sharp boundaries at the borders of the African and Pacific superplumes: Observation and modeling. Earth Planet Sci Lett 233: 137–153.
Tonks, WB, Melosh HJ (1993) Magma ocean formation due to giant impacts. J Geophys Res 98: 5319–5333.
Torsvik, TH, Burke K, Steinberger B, Webb SJ, Ashwel LD (2010) Diamonds sampled by plumes from the core-mantle boundary. Nature 466: 352–355.
Torsvik, TH, Smethhurst MA, Burke K, Steinberger B (2006) Large igneous provinces generated from the margins of the large low-velocity provinces in the deep mantle. Geophys J Int 167: 1447–1460.
Trampert, J, Deschamps F, Resovsky J, Yuen D (2004) Probabilistic tomography maps chemical heterogeneities throughout the lower mantle. Science 306: 853–856.
Trümper, T, Breuer M, Hansen U (2012) Numerical study on double-diffusive convection in the Earth’s core. Phys Earth Planet Inter 194–195: 55–63.
Wang, Y, Wen L (2007) Geometry and P and S velocity structure of the “African Anomaly”. J Geophys Res 112: B05313.
Watters, WA, Zuber MT, Hager BH (2009) Thermal perturbations caused by large impacts and consequences for mantle convection. J Geophys Res 114: E02001.
Wicht, J, Heyner D (2014) Mercury’s magnetic field in the messenger era. In: Shuanggen J (ed)Planetray Geodesy and Remote Sensing.. CRC Press, London.
Wicht, J, Stellmach S, Harder H (2009) Numerical models of the geodynamo: From fundamental Cartesian models to 3D simulations of field reversals. In: Glassmeier H, Soffel H, Negendank J (eds)Geomagnetic Field Variations - Space-time structure, processes, and effects on system Earth.. Springer, Berlin.
Wicht, J, Stellmach S, Harder H (2011) Numerical dynamo simulations: From basic concepts to realistic models. In: Freeden W, Nashed M, Sonar T (eds)Handbook of Geomathematics.. Springer, Berlin - Heidelberg - New York.
Williams, GE (2000) Geological constraints on the Precambrian history of Earth’s rotation and the Moon’s orbit. Rev Geophys 38: 37–59.
Willis, PW, Sreenivasan B, Gubbins D (2007) Thermal core-mantle interaction: Exploring regimes for ’locked’ dynamo action. Phys Earth Planet Inter 165: 83–92.
Yoshida, M, Santosh M (2011) Supercontinents, mantle dynamics and plate tectonics: A perspective based on conceptual vs. numerical models. Earth Sci Rev 105: 1–24.
Zhang, N, Zhong S (2011) Heat fluxes at the Earth’s surface and core-mantle boundary since Pangea formation and their implications for the geomagnetic superchrons. Earth Planet Sci Lett 306: 205–2016.
Zhang, N, Zhong SJ, Leng W, Li ZX (2010) A model for the evolution of the Earth’s mantle structure since the early Paleozoic. J Geophys Res 115: B06401.
Zhang, P, Cohen RE, Haule K (2015) Effects of electron correlations on transport properties of iron at Earth’s core conditions. Nature 517: 605–607.
Zhong, S, Zhang N, Li Z-X, Roberts JH (2007) Supercontinent cycles, true polar wander, and very long-wavelength mantle convection. Earth Planet Sci Lett 261: 551–564.
Acknowledgements
We thank Takashi Nakagawa, Binod Sreenivasan, and Weijia Kuang for providing material from their papers and for helpful discussions. H. Amit, G. Choblet, J. Monteux, and B. Langlais were partly supported by ANR project MARMITE (ANR-13-BS05-0012). J. Monteux was partly funded by ANR project Oxydeep (ANR-13-BS06-0008). F. Deschamps was supported by Academia Sinica grant 102-CDA-M02. We are grateful to James Roberts and Johannes Wicht for detailed reviews that significantly improved this review paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The idea to this paper was in fact conceived following an invitation of HA by Takashi Nakagawa to give a talk on the topic of this paper in SEDI 2014. HA and GC wrote the first draft. GC, FD, and JM designed the illustrative Fig. 1. All authors discussed and improved the draft. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Amit, H., Choblet, G., Olson, P. et al. Towards more realistic core-mantle boundary heat flux patterns: a source of diversity in planetary dynamos. Prog. in Earth and Planet. Sci. 2, 26 (2015). https://doi.org/10.1186/s40645-015-0056-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40645-015-0056-3