Numerical study of the square-root conformation tensor formulation for confined and free-surface viscoelastic fluid flows

Abstract

We present a numerical study of a stabilization method for computing confined and free-surface flows of highly elastic viscoelastic fluids. In this approach, the constitutive equation based on the conformation tensor, which is used to define the viscoelastic model, is modified introducing an evolution equation for the square-root conformation tensor. Both confined and free-surface flows are considered, using two different numerical codes. A finite volume method is used for confined flows and a finite difference code developed in the context of the marker-and-cell method is used for confined and free-surface flows. The implementation of the square-root formulation was performed in both numerical schemes and discussed in terms of its ability and efficiency to compute steady and transient viscoelastic fluid flows. The numerical results show that the square-root formulation performs efficiently in the tested benchmark problems at high-Weissenberg number flows, such as the lid-driven cavity flow, the flow around a confined cylinder, the cross-slot flow and the impacting drop free surface problem.

Background

Many engineering applications deal with viscoelastic (or non-Newtonian) fluids, characterizing soft materials such as polymer solutions (fluids containing polymer molecules which typically have thousands to millions of atoms per macromolecule), colloidal suspensions, gels, emulsions, or surfactants. These viscoelastic fluids can be represented by appropriate constitutive equations, that describe the rheological behavior of the material as a relation between the stress (force per unit area) and strain (a measure of deformation history) or rate of strain. Such constitutive equations depend on the structure of the fluid, and can be represented in the form of algebraic, differential, integral, or integro-differential equations [1, 2]. Two dimensionless numbers are frequently used to represent ratios of relevant forces or ratios of time scales in viscoelastic fluid flows, namely, the Weissenberg (Wi) and Deborah (De) numbers. The Deborah number, $De=\lambda U/H$, is the ratio between the fluid relaxation time $\lambda$ and a flow time scale [3]. The Weissenberg number [4] is a dimensionless parameter that measures the degree of anisotropy or orientation generated by the deformation, and is defined as the ratio between elastic and viscous forces [5].

When numerical methods are applied to flows of viscoelastic fluids, the momentum and mass conservation equations are inherently coupled to the constitutive equation for the extra-stress, $\varvec{\tau }$ (or conformation tensor, $\mathbf {A}$). The inclusion of the constitutive equation does not only increase the total number of degrees of freedom of the problem but also modifies the type of the resulting system of governing equations [6]. Moreover, the evolutionary character of the constitutive models and the hyperbolic nature of the equations require preserving the positive definiteness of the conformation tensor [6, 7], and numerical discretization errors could, eventually, lead to the loss of such positive definiteness, resulting in a loss of topological evolutionary that can trigger Hadamard instabilities [6]. This numerical breakdown, which occurs when Wi increases, is known as the High Weissenberg Number Problem (HWNP), and has been a great challenge for those working on numerical simulations of viscoelastic fluid flows. The HWNP was first identified by the breakdown of the numerical schemes for macroscopic continuum mechanics constitutive equations. This numerical failure at moderate/low Weissenberg/Deborah numbers, was accompanied by numerical inaccuracies and lack of mesh-convergent solutions, particularly when geometrical corners or stagnation points are present, due to the exponential growth of the normal stresses at such locations characterized by large deformation rates and low velocities. Therefore, in order to perform numerical simulations at high elasticity, the constitutive equation needs to be solved using an appropriate, stable, convergent and positivity preserving numerical method.

Although a definite solution to the HWNP is still an open problem in Computational Rheology, several effective stabilization methods have been developed during the past years. For direct numerical simulations in turbulent flow, Sureshkumar and Beris [8] introduced an artificial stress diffusion term into the evolution equation of the conformation tensor, leading to successful results when used with spectral methods. Vaithianathan et al. [9] developed another method that also guarantees positive eigenvalues of the conformation tensor, while preventing over-extension for dumbbell-based models, such as the Oldroyd-B, FENE-P and Giesekus models. Their finite difference method (FDM) was coupled with a pseudo-spectral scheme for homogeneous turbulent shear flow.

In the framework of laminar flow computational rheology, and specifically for the inertialess ($Re \sim 0$) HWNP case, Lozinski and Owens [10] presented theoretical nonlinear (energy) estimates for the stress and velocity components in a general setting, for an Oldroyd-B fluid. The authors worked with the configuration tensor, and derived a method that guarantees a well-posed evolutionary Hadamard problem.

Fattal and Kuperfman [11, 12] proposed a reformulation of the constitutive laws which describe viscoelastic fluids, using a formulation based on a tensorial transformation of the conformation tensor, a method known as log-conformation, which reformulates the constitutive equation using the natural logarithm of the positive-definite conformation tensor, thus linearizing the exponential stress growth in regions near singularities. Lee and Xu [13] presented a class of positivity preserving discretization schemes applied for rate-type viscoelastic constitutive equations, using a semi-Lagrangian approach and a finite element method (FEM), based on the observation that the rate-type constitutive equations can be cast into the general form of the Riccati differential equations, and demonstrated that their method is second-order accurate in both time and space. Cho [14] proposed a vector decomposition of the Maxwell-type evolution equations of the conformation tensor. In his transformation, the vectorized equations were considered as the sum of dyadics of the conformation tensor. This vector decomposition preserved the positive definiteness of the conformation tensor and avoided the solution of the eigenvalue problem at every calculation step, decreasing the computation cost. Nevertheless, in a generic 3D simulation, the vector decomposition requires the calculation of nine components instead of the six independent components as in the log-conformation tensor approach, thus limiting its efficiency in 3D numerical calculations, when compared with the log-conformation transformation approach. Balci et al. [15] proposed a method in which the square root of the conformation tensor is used for Oldroyd-B and FENE-P models. They derive an evolution equation for the square root of the conformation tensor, by taking advantage of the fact that the positive definite symmetric polymer conformation tensor possesses a unique symmetric square-root tensor that satisfies a closed-form evolution equation. Balci et al. [15] claimed that their method can be easily implemented in numerical simulations, because it does not require the determination of eigenvectors and eigenvalues of the conformation tensor at every time step, resulting in a significant reduction of the computational time. Afonso et al. [16] proposed a generic framework with applications to a wide range of matrix transformations of the conformation tensor evolution equation. In order to present a robust algorithm for solving steady solutions at high Weissenberg number flows, Saramito [17] used a non-singular log-conformation formulation based on the resolution by a Newton method. Another modification in the original log-conformation formulation was proposed in [18] where a fully-implicit method is used to solve a new constitutive equation. The application of all these stabilization methods invariably has showed good stability properties for solving challenging problems in viscoelastic flows [19–26].

In the present study, we employ the stabilization method proposed by Balci et al. [15] for confined and free-surface flows, using two different numerical codes and methods. A finite volume method [23, 27–29] (FVM) is used for confined flows and a finite difference code developed in the context of the Marker-And-Cell (MAC) method [30, 31] is used for confined and free-surface flows. The square-root formulation is implemented in both numerical schemes and the results obtained are discussed in terms of stability and efficiency to compute transient viscoelastic fluid flows.

The remainder of the paper is organized as follows. The governing equations are discussed in Sect. “Governing equations”. Section “Square-root conformation tensor methodology” describes the mathematical formulation of the symmetric square root representation of the conformation tensor and its application to the constitutive models used in the present study. The numerical implementation of the algorithm is presented in Sect. “Numerical method”, for both the finite difference and the finite volume methods used. The validations of the numerical formulations are presented in Sect. “Validation: laminar lid-driven cavity flow”. Results and discussion of the numerical simulations of flow problems at high-Weissenberg number flows, such as the confined lid-driven cavity flow, the flow around a confined cylinder, the cross-slot flow and the impacting drop problem, are presented in Sect. “Applications”. Finally, the main conclusions from the study are summarized in Sect. “Conclusions”.

Governing equations

The governing equations for transient, incompressible and isothermal flow of viscoelastic fluids can be written in a compact and dimensionless form as follows

$$\begin{aligned}&\dfrac{\partial \mathbf u }{\partial t} + \nabla \cdot \left( \mathbf u {} \mathbf u \right) = -\nabla p + \dfrac{\beta }{Re}\nabla ^{2}{} \mathbf u + \nabla \cdot \varvec{\tau } +\frac{1}{Fr^{2}}{} \mathbf g , \end{aligned}$$

(1)

$$\begin{aligned}&\nabla \cdot \mathbf u = 0, \end{aligned}$$

(2)

$$\begin{aligned}&\dfrac{\partial \mathbf A }{\partial t} + \nabla \cdot \left( \mathbf u \mathbf A \right) = \nabla \mathbf u {} \mathbf A + \mathbf A \nabla \mathbf u ^{T} + \dfrac{1}{Wi}\,\, f(\mathbf A )\mathbf P ( \mathbf A ), \end{aligned}$$

(3)

$$\begin{aligned}&\varvec{\tau } = \xi \left( \mathbf A - \mathbf I \right) . \end{aligned}$$

(4)

In these equations, t is the time, $\mathbf u$ is the velocity vector, p is the pressure, $\mathbf g$ is the gravitational field, and $\varvec{\tau }$ and $\mathbf A$ are the extra-stress and conformation tensors, respectively. The dimensionless parameters $Re=\frac{\rho LU}{\eta _0}$ and $Fr=U/\sqrt{gL}$ are the Reynolds and Froude numbers, respectively, where L and U are appropriate length and velocity scales, g is the magnitude of the gravity field and $\rho$ is the fluid density. The amount of Newtonian solvent is controlled by the dimensionless solvent viscosity coefficient, $\beta = \frac{\eta _S}{\eta _0}$, where $\eta _0 = \eta _S + \eta _P$ denotes the total shear viscosity, while $\eta _S$ and $\eta _P$ represent the Newtonian solvent and polymeric viscosities, respectively. The Weissenberg number in Eq. (3) is defined as $Wi=\lambda U{/}L$ where $\lambda$ is the relaxation time of the fluid. The variable $\xi$ and functions $f\left( \mathbf A \right)$ and $\mathbf P \left( \mathbf A \right)$ in Eqs. (3) and (4) are, respectively, scalar-valued and tensor-valued functions constructed according to the viscoelastic model which take the following forms for the Oldroyd-B model used in the simulations of this work: $f\left( \mathbf A \right) =1$, $\mathbf P \left( \mathbf A \right) = \mathbf I - \mathbf A$ and $\xi = \frac{1-\beta }{ReWi}$. We note that in the dimensionless governing equations the stress tensor is normalized as $\varvec{\tau } = \varvec{\tau }' / (\rho U^2)$ where $\varvec{\tau }'$ is the dimensional extra-stress tensor. For pressure, a similar normalization is used, $p= p' / (\rho U^2)$.

The initial conditions used for solving numerically the system (1)–(4) are $\mathbf u =\mathbf 0$ and $\mathbf A =\mathbf I$. In addition, boundary conditions are required at inlets, outlets, walls and free surfaces. These conditions can be summarized as:

• Inlets: The normal velocity component is specified while the tangential velocity component is set to zero. Moreover, the extra-stress tensor $\varvec{\tau }$ is computed assuming fully-developed flow conditions. Once the value of $\varvec{\tau }$ is imposed, the conformation tensor can be obtained from Eq. (4).

• Outlets: The homogeneous Neumann conditions are employed for the velocity field and the extra-stress tensor.

• Walls: The no-slip condition is used ($\mathbf {u}=\mathbf {u}_{wall}$) for the velocity field.

• Moving free surfaces: In the absence of surface tension effects, the normal and tangential components of the total stress must be continuous across any free surface, i.e.,

  $$\begin{aligned}&\mathbf n \cdot \varvec{\sigma }\cdot \mathbf n ^{\mathrm{T}}=0, \end{aligned}$$

  (5)
  $$\begin{aligned}&\mathbf m \cdot \varvec{\sigma }\cdot \mathbf n ^{\mathrm{T}}=0, \end{aligned}$$

  (6)

  where $\varvec{\sigma }$ is the total stress tensor, given by

  $$\begin{aligned} \varvec{\sigma }=-p\mathbf I +\beta \frac{2}{Re}{} \mathbf D +\varvec{\tau }, \end{aligned}$$

  (7)

  and $\mathbf D$ is the rate of deformation tensor defined by $\mathbf D = \frac{1}{2}(\nabla \mathbf u + \nabla \mathbf u ^{T} )$, with $\left( \nabla \mathbf u \right) _{i,j} = {\partial u_{i}} / {\partial x_{j}}$.

  In Eqs. (5) and (6), $\mathbf n$ represents a unit vector normal to the free surface and pointing outwards, and $\mathbf m$ is a unit vector tangent to the free surface. Equation (3) is enforced at free surface cells for computing the conformation tensor, and after this, $\varvec{\tau }$ is directly obtained from Eq. (4).

Square-root conformation tensor methodology

In the square-root conformation tensor formulation proposed by Balci et al. [15], the conformation tensor is decomposed in the form:

$$\begin{aligned} \mathbf A = \mathbf Q ^{T}{} \mathbf Q , \end{aligned}$$

(8)

where $\mathbf Q$ is a symmetric positive definite matrix.

The key of this method is the construction of an evolution equation for the (unique) symmetric square root of the conformation tensor, denoted here as $\mathbf Q$. Substituting Eq. (8) into Eq. (3), and taking into acount that $\mathbf Q =\mathbf Q ^{T}$, leads to

$$\begin{aligned} \mathbf Q \dfrac{ D \mathbf Q }{Dt} = - \dfrac{D \mathbf Q }{Dt} \mathbf Q + \nabla \mathbf u \mathbf Q ^{2} + \mathbf Q ^{2}\nabla \mathbf u ^{T} + \dfrac{f\left( \mathbf Q ^{2} \right) }{Wi}{} \mathbf P \left( \mathbf Q ^{2} \right) . \end{aligned}$$

(9)

Pre-multiplying Eq. (9) by $\mathbf Q ^{-1}$, one arrives at the equivalent equation

$$\begin{aligned} \dfrac{D \mathbf Q }{Dt} = -\mathbf Q ^{-1}\dfrac{D \mathbf Q }{Dt}{} \mathbf Q + \mathbf Q ^{-1}\nabla \mathbf u \mathbf Q ^{2} + \mathbf Q \nabla \mathbf u ^{T} + \dfrac{f\left( \mathbf Q ^{2}\right) }{Wi}{} \mathbf Q ^{-1}{} \mathbf P \left( \mathbf Q ^{2} \right) , \end{aligned}$$

(10)

which can be rewritten as

$$\begin{aligned} \dfrac{D \mathbf Q }{Dt} - \mathbf Q \nabla \mathbf u ^{T} - \dfrac{f\left( \mathbf Q ^{2}\right) }{2Wi}{} \mathbf Q ^{-1}{} \mathbf P \left( \mathbf Q ^{2} \right)&= \mathbf Q ^{-1}\left( -\dfrac{D \mathbf Q }{Dt} + \nabla \mathbf u \mathbf Q + \dfrac{f\left( \mathbf Q ^{2}\right) }{2Wi}{} \mathbf P \left( \mathbf Q ^{2} \right) \mathbf Q ^{-1} \right) \mathbf Q . \nonumber \\ \end{aligned}$$

(11)

By defining [26]:

$$\begin{aligned} \mathbf V \equiv \dfrac{D \mathbf Q }{Dt} - \mathbf Q \nabla \mathbf u ^{T} - \dfrac{f\left( \mathbf Q ^{2}\right) }{2Wi}{} \mathbf Q ^{-1}{} \mathbf P \left( \mathbf Q ^{2} \right) , \end{aligned}$$

(12)

Eq. (11) can be rewritten as:

$$\begin{aligned} \mathbf V = \mathbf Q ^{-1}\left( - \mathbf V ^{T} \right) \mathbf Q , \end{aligned}$$

(13)

or equivalently

$$\begin{aligned} \mathbf V {} \mathbf Q ^{-1} = -\left( \mathbf V {} \mathbf Q ^{-1} \right) ^{T}. \end{aligned}$$

(14)

Finally, introducing this anti-symmetric matrix,

$$\begin{aligned} \mathbf G = \mathbf V {} \mathbf Q ^{-1} = -\mathbf Q ^{-1} \mathbf V ^{T}, \end{aligned}$$

(15)

into Eq. (11), leads to the following evolution equation

$$\begin{aligned} \dfrac{D \mathbf Q }{Dt} = \mathbf G {} \mathbf Q + \mathbf Q \nabla \mathbf u ^{T} + \dfrac{f\left( \mathbf Q ^{2} \right) }{2Wi} \mathbf Q ^{-1} \mathbf P \left( \mathbf Q ^{2} \right) . \end{aligned}$$

(16)

We need to write the form of matrix $\mathbf G$ for solving Eq. (16). The procedure used in this work to define this anti-symmetric matrix is the same that is described in [15, 26]. First, a matrix $\mathbf K$ is defined as

$$\begin{aligned} \mathbf K =\mathbf G {} \mathbf Q + \mathbf Q \nabla \mathbf u ^{T}, \end{aligned}$$

(17)

and after this, the matrix $\mathbf G$ is constructed imposing that $\mathbf K$ is symmetric

$$\begin{aligned} \mathbf K ^{T} = \mathbf K \Leftrightarrow \nabla \mathbf u \mathbf Q - \mathbf Q \nabla \mathbf u ^{T} = \mathbf G {} \mathbf Q + \mathbf Q {} \mathbf G . \end{aligned}$$

(18)

For instance, considering the two-dimensional case in Cartesian coordinates, Eq. (18) can be used to obtain

$$\begin{aligned} G_{12} = \dfrac{\left( Q_{12}\dfrac{\partial u}{\partial x} + Q_{22}\dfrac{\partial u}{\partial y} \right) - \left( Q_{11}\dfrac{\partial v}{\partial x} + Q_{12}\dfrac{\partial v}{\partial y} \right) }{Q_{11} + Q_{22}}, \end{aligned}$$

(19)

while for the three-dimensional case, we can calculate the components of $\mathbf G$ from the following system [15]:

$$\begin{aligned} \begin{pmatrix} Q_{11}+Q_{22} &{}\quad Q_{23} &{}\quad -Q_{13}\\ Q_{23} &{}\quad Q_{11}+Q_{33} &{}\quad Q_{12}\\ -Q_{13} &{}\quad Q_{12} &{}\quad Q_{22}+Q_{33}\\ \end{pmatrix} \begin{pmatrix} G_{12}\\ G_{13}\\ G_{23} \end{pmatrix}= \begin{pmatrix} a\\ b\\ c \end{pmatrix} \end{aligned}$$

(20)

where

$$\begin{aligned} a= & {} \left( \dfrac{\partial u}{\partial x}Q_{12} - \dfrac{\partial v}{\partial x}Q_{11} \right) + \left( \dfrac{\partial u}{\partial y}Q_{22} - \dfrac{\partial v}{\partial y}Q_{12} \right) + \left( \dfrac{\partial u}{\partial z}Q_{23} - \dfrac{\partial v}{\partial z}Q_{13} \right) \end{aligned}$$

(21)

$$\begin{aligned} b= & {} \left( \dfrac{\partial u}{\partial x}Q_{13} - \dfrac{\partial w}{\partial x}Q_{11} \right) + \left( \dfrac{\partial u}{\partial y}Q_{23} - \dfrac{\partial w}{\partial y}Q_{12} \right) + \left( \dfrac{\partial u}{\partial z}Q_{33} - \dfrac{\partial w}{\partial z}Q_{13} \right) \end{aligned}$$

(22)

$$\begin{aligned} c= & {} \left( \dfrac{\partial v}{\partial x}Q_{13} - \dfrac{\partial w}{\partial x}Q_{12} \right) + \left( \dfrac{\partial v}{\partial y}Q_{23} - \dfrac{\partial w}{\partial y}Q_{22} \right) + \left( \dfrac{\partial v}{\partial z}Q_{33} - \dfrac{\partial w}{\partial z}Q_{23} \right) \end{aligned}$$

(23)

More details can be found in [15, 26].

Numerical method

Overview of the finite difference code

The MAC-type scheme used in the present paper was firstly introduced in [30] (see also [31]). In this section, we describe the corresponding modifications to introduce the square-root conformation tensor in the context of the finite difference methodology.

Initially, a pressure-segregation method is applied in order to uncouple the velocity and pressure fields. This projection method is widely used for solving the Navier-Stokes Eqs. (1) and (2) [32].

The main modification introduced in the method of Oishi et al. [30] to incorporate the square-root formulation regards the solution of Eq. (16) for the square-root conformation tensor, from which the extra-stress is then calculated from Eq. (4) instead of the direct solution of the constitutive equation for the extra-stress tensor $\varvec{\tau }$. For this purpose, note that Eq. (16) can be re-written as

$$\begin{aligned} \frac{\partial \mathbf Q }{\partial t}=\mathbf z \left( \mathbf u ,\mathbf Q ,\mathbf G \right) , \end{aligned}$$

(24)

where

$$\begin{aligned} \mathbf z \left( \mathbf u ,\mathbf Q ,\mathbf G \right) = - \nabla \cdot \left( \mathbf u \mathbf Q \right) + \mathbf G {} \mathbf Q + \mathbf Q \nabla \mathbf u ^{T} + \dfrac{f\left( \mathbf Q ^{2} \right) }{2Wi} \mathbf Q ^{-1} \mathbf P \left( \mathbf Q ^{2} \right) . \end{aligned}$$

(25)

Considering the second order accurate Runge-Kutta scheme for the temporal discretization of Eq. (24), we obtain:

$$\begin{aligned} \frac{\mathbf{Q }^{(n+1)}-{\overline{\mathbf{Q }}}^{(n+1)}}{\delta t}=\frac{1}{2}\left[ \mathbf z \left( \mathbf{u }^{(n)},\mathbf{Q }^{(n)},\mathbf{G }^{(n)}\right) +\mathbf z \left( \mathbf{u }^{(n+1)},{\overline{\mathbf{Q }}}^{(n+1)},{\overline{\mathbf{G }}}^{(n+1)}\right) \right] , \end{aligned}$$

(26)

where the intermediate value of $\overline{\mathbf{Q }}^{(n+1)}$ is computed with the explicit forward Euler discretization:

$$\begin{aligned} \frac{\overline{\mathbf{Q }}^{(n+1)}-\mathbf{Q }^{(n)}}{\delta t}=\mathbf z \left( \mathbf{u }^{(n)},\mathbf{Q }^{(n)},\mathbf{G }^{(n)}\right) . \end{aligned}$$

(27)

The anti-symmetric matrix is calculated in an intermediate stage $\overline{\mathbf{G }}^{(n+1)}$ which for 2D flows simplifies to

$$\begin{aligned} {\overline{G}_{12}^{(n+1)}} = \dfrac{\left( {\overline{Q}_{12}^{\left( n+1 \right) }}\dfrac{\partial u^{(n+1)}}{\partial x} + {\overline{Q}_{22}^{\left( n+1 \right) }} \dfrac{\partial u^{(n+1)}}{\partial y} \right) - \left( {\overline{Q}_{11}^{\left( n+1 \right) }} \dfrac{\partial v^{(n+1)}}{\partial x} + {\overline{Q}_{12}^{\left( n+1 \right) }} \dfrac{\partial v^{(n+1)}}{\partial y} \right) }{{\overline{Q}_{11}^{\left( n+1 \right) }} + {\overline{Q}_{22}^{\left( n+1 \right) }}}. \nonumber \\ \end{aligned}$$

(28)

Similarly, ${G}_{12}^{(n)}$ is constructed with all terms discretized in the time level n.

Therefore, the new algorithm incorporating the square-root method to compute the conformation tensor contains the following steps:

• 1. Given $\mathbf{Q }^{(n)}$, $\mathbf{u }^{(n)}$ and $\mathbf{G }^{(n)}$, solve the evolution Eq. (27) to obtain the intermediate value ${\overline{\mathbf{Q }}}^{(n+1)}$;

• 2. From ${\overline{\mathbf{Q }}}^{(n+1)}$, compute the intermediate value of the conformation tensor ${\overline{\mathbf{A }}}^{(n+1)}$ using Eq. (8). Then, Eq. (4) is directly applied to determine the extra-stress tensor ${\overline{\varvec{\tau }}}^{(n+1)}$ which is used to obtain an intermediate velocity from the momentum equation (sub-step of the projection method).

• 3. Apply the projection method to obtain the final velocity $\mathbf{u }^{(n+1)}$ and pressure $p^{(n+1)}$ fields (more details can be found in [30]).

• 4. Construct the matrix ${\overline{\mathbf{G }}}^{(n+1)}$ (see Eq. 28).

• 5. Calculate the final value of the square-root matrix $\mathbf{Q }^{(n+1)}$ using Eq. (26). At this stage, the final conformation and extra-stress tensors are computed using Eqs. (8) and (4), respectively.

Remark 1

To start the algorithm, homogeneous isotropic initial data are imposed, i.e., $\mathbf{Q }^{2}_{t=t_0} = \mathbf I$.

Remark 2

For free surface flows, the last step of the algorithm is the advection of the free surface interface. Each particle is convected by the velocity field, from their position $\mathbf {x}^{(n)}$ at $t=t_{n}$ to the position $\mathbf {x}^{(n+1)}$ at $t=t_{n+1}$ as

$$\begin{aligned} \frac{d\mathbf {x}}{dt}=\mathbf {u}. \end{aligned}$$

(29)

This equation is solved using the second-order RK21 scheme as described in [30].

Overview of the finite volume code

The square-root formulation was also implemented in a Finite Volume Method (see [23, 27–29], for more details). This FVM uses collocated non-orthogonal meshes, central differences for the discretization of diffusive terms, a first or second order backward implicit time discretization, and the SIMPLEC [33] algorithm to ensure simultaneously the momentum balance and mass conservation.

The transport equations for mass conservation and momentum are not modified by the change of variable in the constitutive Eq. (16); only the conformation tensor equation needs to be changed. The FVM code works with general non-orthogonal coordinates, therefore the equation of the evolution of the square-root formulation is written first in an orthogonal coordinate system ($x_{1}$, $x_{2}$, $x_{3}$) as (considering the Oldroyd-B model, $f\left( \mathbf{Q }^{2} \right) =1$ and $\mathbf P \left( \mathbf{Q }^{2} \right) =\mathbf I - \mathbf{Q }^{2}$)

$$\begin{aligned} \frac{\partial Q_{ij}}{\partial t}+u_{k}\frac{\partial Q_{ij}}{\partial x_{k}}=K_{ij} - \dfrac{1}{2Wi}(Q_{ij}-R_{ij}) \end{aligned}$$

(30)

and subsequently transformed into a general non-orthogonal coordinate system ($\zeta _{1}$, $\zeta _{2}$, $\zeta _{3}$) before being discretized. The evolution equation written in non-orthogonal coordinates reads

$$\begin{aligned} \frac{\partial JQ_{ij}}{\partial t}+\frac{\partial }{\partial \zeta _{l}}(u_{k}\beta _{lk}Q_{ij}) = JK_{ij} + \dfrac{J}{2Wi}\left( R_{ij}-Q_{ij}\right) \end{aligned}$$

(31)

where J is the Jacobian of the transformation $x_i = x_i (\zeta _{i})$ and $\beta _{lk}$ are metric coefficients (see [27] for more details) and $R_{ij}$ is the ij component of $\mathbf R =\mathbf Q ^{-1}$. Note that Eqs. (30) and (31) use Einstein’s convention for summation over repeated indices.

These transformations are a necessary step towards using a general FVM based on the collocated mesh arrangement, as described in Oliveira et al. [27] and Alves et al. [28, 29]. In the discretization of Eq. (31), the $\beta _{lk}$ coefficients are replaced by area components of the surface whose normal vector points towards direction l, the Jacobian J is replaced by the cell volume V, and the derivatives $\partial$/$\partial \zeta _{l}$ become differences between values along direction l [27].

The discretized constitutive equation based on the square-root formulation results from the integration of Eq. (31) and can be written in the form

$$\begin{aligned} a_{P}^{Q}Q^{(n+1)}_{ij,P}-\sum _{F}a_{F}^{Q}Q^{(n+1)}_{ij,F}=S_{Q_{ij}}+\frac{\lambda _{P}V_{P}}{\delta t}Q^{(n)}_{ij,P} \end{aligned}$$

(32)

where $Q^{(n)}_{ij,P}$ refers to the ij component of the square-root tensor at the previous time level $\left( n \right)$, $a_{P}^{Q}$ represents the central coefficient, $a_{F}^{Q}$ represents the coefficients of the neighbouring cells (with F spanning the near-neighbouring cells of cell P) and $S_{Q_{ij}}$ is the source term.

The numerical procedure [27–29] was modified to incorporate the new Eq. (32) to compute tensor $Q_{ij}$ and consists in the following steps:

• 1. First, the square-root tensor components $Q_{ij}$ are initialized;

• 2. The components of the anti-symmetric tensor $G_{ij}$ are calculated with the information of the known velocity gradient using Eq. (19);

• 3. The components of the symmetric tensor $K_{ij}$ are calculated using Eq. (17) with the information of the velocity gradient $G_{ij}$ and $Q_{ij}$;

• 4. The evolution equation for $\mathbf {Q}$ is solved implicitly (Eq. 32);

• 5. The conformation tensor matrix $\mathbf {A}$ is recovered using Eq. (8);

• 6. The new extra-stress components $\tau _{ij}$ are now calculated from the conformation tensor using Eq. (4);

• 7. The momentum equations are solved for each velocity component, $u_{i}$ to determine the new velocity field;

• 8. As generally the velocity components do not satisfy the continuity equation, this step of the algorithm involves a correction to $u_{i}$ and to the pressure field p, so that the updated velocity field $u_{i}$ and the corrected pressure field p satisfy simultaneously the continuity and the momentum equations. This part of the algorithm remains unchanged and is described in detail in Oliveira et al. [27];

• 9. Steps 2–8 are repeated until convergence is reached (steady-state calculations), or until the desired final time is reached (unsteady calculations)

Remark 3

The CUBISTA high-resolution scheme [29] is used to discretize the advection terms of the governing equations in the FDM and FVM.

Validation: laminar lid-driven cavity flow

In this section, we present the validation of both numerical implementations, using the lid-driven cavity benchmark flow problem [34]. This flow is generated by the motion of one or more walls of a closed cavity. There are several experimental and numerical studies involving lid-driven cavity flows, mainly with Newtonian fluids [35], whereas for viscoelastic fluids, the interest is fairly recent, and mainly used to assess numerical methods for highly elastic flows [12, 36–40] which requires a regularization on the lid motion due to the singular behavior near the corners.

The standard problem relies on the following regularized parabolic profile for the top lid, $u(x,t)=8[1+\tanh (8t-4)]x^{2}(1-x)^{2}$. The remaining cavity walls are stationary and the no-slip boundary condition is imposed in the four walls. We have fixed the Reynolds number, $Re=0.01$, and the solvent viscosity ratio, $\beta =0.5$. To assess the mesh convergence of both the finite difference and finite volume methods, the cavity flow was simulated using two uniform meshes: M1 ($h=\min (\Delta x,\Delta y)=\frac{1}{128},\,128\times 128$ cells) and M2 ($h=\min (\Delta x,\Delta y)=\frac{1}{256},\,256\times 256$ cells).

For all figures in this section, the profiles of u-velocity and of the non-Newtonian $\tau _{xx}$ component are plotted along the vertical line $x=0.5$ while the v-velocity component is reported at the horizontal line $y=0.75$. The origin of the Cartesian coordinate system is placed at the lower left corner of the square cavity, and the moving wall is located at $y=1$, from $x=0$ to $x=1$.

In order to assess the implementation of the codes, we compare our results of the lid-driven cavity flow with those of Fattal and Kupferman [12] and Pan et al. [36]. The results are presented in Figs. 1 and 2 for $Wi=1$ and $Wi=2$, respectively, and confirm that the results are independent of the numerical method when the meshes are sufficiently fine, as expected.

In Fig. 1, we plot the velocity components u and v for $Wi=1$ at the dimensionless time $t=40$, showing that the square-root formulation converges to the literature results. For $Wi=2$, we have simulated until $t=80$, and according to Fig. 2 the results are again in good agreement with the literature.

In order to provide additional data for this benchmark problem, we have plotted in Fig. 3 the $\tau _{xx}$ component profile along the vertical line $x=0.5$, illustrating the convergence with mesh refinement of the square-root formulation for $Wi=1$ and $Wi=2$. Note that in Fig. 3, the extra-stress is normalized as $\tau _{xx}' / (\frac{\eta _{0}U}{L})$, where U is the maximum velocity of the lid.

In addition, we plot in Fig. 4, for mesh M2, the time evolution of the kinetic energy, $E = \int \int ||\mathbf u ||^2 dxdy$, for this benchmark problem showing again that the square-root formulation produces similar results compared to the literature. In this figure, we have also included results obtained with the log-conformation formulation using both finite difference and finite volume methods. In the context of finite differences, the version of the log-conformation used in this simulation was recently presented in [19] while the finite volume code was described in [23].

Fig. 1

Numerical simulation of the lid-driven cavity flow using the Oldroyd-B model for $Re=0.01$, $Wi=1$ and $\beta =0.5$. Results at $t=40$, corresponding to steady-state flow conditions

Fig. 2

Numerical simulation of the lid-driven cavity flow using the Oldroyd-B model for $Re=0.01$, $Wi=2$ and $\beta =0.5$. Results at $t=80$, corresponding to steady-state flow conditions

Fig. 3

Numerical simulation of the lid-driven cavity flow using the Oldroyd-B model for $Re=0.01$ and $\beta =0.5$. The non-Newtonian component of the dimensionless normal stress $\frac{\tau _{xx}^{'}}{\eta _{0}U/L}$ is plotted along the vertical line $x=0.5$ for a $Wi=1$ and b $Wi=2$

Fig. 4

Time evolution of the kinetic energy for the square-root and log-conformation (Log) formulations and comparison with results obtained from the literature: Oldroyd-B model at $Re=0.01$ and $\beta =0.5$, for a $Wi=1$ and b $Wi=2$

Applications

Confined flow: 2D flow around a cylinder

The two-dimensional (2D) flow around a confined cylinder in a channel is an important benchmark test in computational rheology [41]. It is representative of fundamental flow dynamics of viscoelastic fluids around submerged solid bodies and it can be encountered in many engineering processes, namely in the food industry, in composite and textile coating operations and flows through porous media. From a numerical point of view, this flow is considered a smooth flow, due to the absence of geometrical singularities, such as a re-entrant or salient corners found in entry flows. However, it also introduces important challenges associated with the development of thin stress layers on the cylinder wall and large normal stresses along the centerline in the cylinder rear wake, imposing a limiting Weissenberg number for which steady-state solutions can be obtained. For all these reasons this flow was selected as a benchmark problem in computational rheology in the VIIIth international workshop on numerical methods for non-Newtonian flows [41].

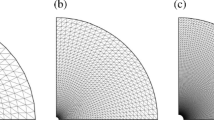
In this problem, the ratio of channel half-width h to cylinder radius R is set equal to 2, which corresponds to the benchmark 50 % blockage ratio case [41]. The Weissenberg number based on the fluid relaxation time, $\lambda$, the average inlet velocity, U, and the cylinder radius, R, is here defined as $Wi=\lambda U/R$. The computational domain is 200R long, with 99R upstream and 99R downstream of the forward and rear stagnation points of the cylinder, respectively. The downstream length is large enough for the flow to become fully-developed and to avoid any effect of the Neumann outflow boundary condition upon the flow in the vicinity of the cylinder. Zero axial gradients are applied to all variables, including the pressure gradient, at the outlet plane. No-slip boundary conditions are imposed at both the cylinder surface ($r=R$: $u=0$, $v=0$) and the channel walls ($y'=\pm h$: $u=0$, $v=0$).

In this confined flow problem, the simulations were restricted to the square-root formulation using the FVM. Simulations were performed in two meshes MC1 and MC2, mapping the complete flow domain, i.e., no symmetry boundary condition was imposed along the centerline. Mesh MC1 is composed of 30 cells placed radially and non-uniformly from the cylinder to the channel wall, leading to a minimum cell spacing normalized with the cylinder radius along the radial ($\Delta r$) and the azimuthal ($\Delta s = \Delta \theta$) directions, of 0.008 and 0.0012, respectively. In mesh MC2, those dimensions are reduced to 0.004 and 0.0006, respectively. Mesh MC2 is the same as $M60_{WR}$ used in previous works [16, 23, 42] and corresponds to highly refined meshes along the wake.

All the calculations were carried out at a low Reynolds number, $Re=\rho UR/\eta =0.01$. The viscosity ratio was fixed at $\beta =0.59$, a value that characterizes the MIT Boger fluid used in previous experiments [41]. All simulations started from a quiescent state velocity field ($u=v=0$), meaning that $\mathbf {A}\left( \mathbf {x},t=0 \right) =\mathbf {I}$ and for the square-root tensor, $\mathbf {Q}\left( \mathbf {x},t=0 \right) =\mathbf {I}$.

The simulations for the square-root formulation were performed at moderate elasticity, $Wi=0.6$, and compared with the solution obtained in previous works using different methods, namely the results of Alves et al. [42] obtained using the extra-stress tensor formulation or those results obtained with the log-conformation formulation. For all the simulations, the numerical solutions were consistent with previous benchmark results found in the literature, such as those obtained by Fan et al. [43] and Kim et al. [44], as observed in the normal stress profiles along the cylinder surface and the rear wake presented in Fig. 5 and in the values for the dimensionless drag coefficient, K, listed in Table 1. The dimensionless drag coefficient is calculated as

$$\begin{aligned} K=\frac{1}{\eta _{0}U}\int _{S}^{}\left( \varvec{\tau }^{'} _{tot}-p'\mathbf {I}\right) \cdot \mathbf {n}\cdot \mathbf {i}\begin{array}{cc} {\mathrm{d}S^{'}}&{}\end{array} \end{aligned}$$

(33)

where n is the unit vector normal to the cylinder surface and $\mathbf {i}$ is the unitary vector aligned with the streamwise direction.

Fig. 5

Normal stress profiles along the cylinder surface ($0 \le x \le 1$) and along the downstream centerline for the Oldroyd-B model, $\beta =0.59$ at a $Wi=0.6$ and b $Wi=1$ ($t'=200\lambda$) and mesh MC2

Table 1 Dimensionless drag coefficient, K, computed using different meshes MC1 and MC2

In order to assess the stability of the square-root method for high Wi, we carried out additional simulations at a higher value of elasticity, $Wi=1$. For this Wi number, the non-stabilized version of the conformation tensor formulation diverges, while the use of the square-root formulation allowed the simulation of unsteady flows.

Figure 5b presents the profiles of longitudinal normal stress ($\frac{\tau _{xx}^{'}}{\eta _0 U/R}$) along the cylinder wall and wake centerline obtained with the square-root formulation and compared with the data obtained using the log-conformation by Afonso et al. [23]. The normal stress profiles were obtained at a fixed time for both simulations, $t'=200\lambda$. The normal stress profiles show a sharp maximum in the wake, some distance downstream from the rear stagnation point. The normal stress peaks obtained for both simulations at $t'=200\lambda$ are different due to time-dependent flow characteristics. Simulations at higher Wi numbers will require the use of a high order time discretization scheme and more refined meshes, in order to improve the accuracy and will be pursued in future work because these calculations are very time consuming. The simulations using the square-root formulation showed no signs of violation of the positive definitiveness since $\left| \mathbf {A}\right|$ is always positive by design. Note that according to Hulsen [45], for an Oldroyd-B fluid, $\left| \mathbf {A}\right| =\left| \mathbf {Q}^{T}\mathbf {Q}\right| \ge 1$, a condition that is shown in Fig. 6 to hold for the simulations using the square-root conformation tensor.

Fig. 6

Contour map of the determinant of the conformation tensor, $\left| \mathbf {Q}^{T}\mathbf {Q}\right|$ computed with the square-root formulation, for the Oldroyd-B model, $\beta =0.59$ at $Wi=1$, mesh MC2 and $t'=200\lambda$

Confined flow: 2D flow in a cross-slot

The cross-slot flow, illustrated in Fig. 7a), and other strong extensional flows, such as the four roll mill and opposed jet apparatus, have been extensively investigated because of the need to develop methods for measuring the extensional viscosity of polymer solutions [46].

It is now well established that viscoelastic flows often generate purely-elastic flow instabilities, which lead to unsteady flows, even under creeping flow conditions. Of particular relevance to the study of elastic instabilities is the experimental observation of flow instabilities in a cross-slot microchannel by Arratia et al. [47], which motivated the numerical work of Poole et al. [48] on the two-dimensional cross-slot flow of an upper-convected Maxwell (UCM) fluid under low Reynolds number flow conditions. Poole et al. [48] were able to predict the first type of flow instability (steady and asymmetric flow) in a two-dimensional cross-slot channel flow of an UCM fluid, which led to a reduction of pressure loss, and reported also the stabilizing effect of inertia. This flow was proposed recently as a benchmark problem by Cruz et al. [49], due to its conceptually simple geometry and well defined steady asymmetric flow instability. The benchmark results were presented for a wide range of differential constitutive equations, namely the UCM, Oldroyd-B and Phan-Thien and Tanner models, showing that, in the limit of negligible inertia, i.e. when Re approaches zero, the flow exhibits two types of purely-elastic instabilities for fluids with high extensional viscosity. Above a first critical value of the Deborah number, $De_{crit}$, the steady flow becomes spatially asymmetric, even though the geometry is perfectly symmetric; at higher De a second instability occurs and the flow becomes time-dependent. Recently, Cruz and Pinho [50] presented a general analytical solution for the two-dimensional steady planar extensional flow with wall-free stagnation point for the UCM model.

In this work, we performed simulations using both the FVM and FDM together with the square-root and log-conformation formulations for the Oldroyd-B model, with $\beta =1/9$ and $Re=0.01$. The mesh used in the numerical simulations has 51 cells in the central square region (see partial view of the mesh in Fig. 7b) of the cross-slot along x and y directions, leading to minimum cell sizes of $\Delta x_{min}=\Delta y_{min} \approx 0.02$. For the Oldroyd-B model, the local Weissenberg number, $Wi=\lambda \dot{\varepsilon }$, at the stagnation point can exceed the theoretical critical value of 1/2 (this occurs for $De = \lambda U/D \ge 0.2$ [49]). Therefore, the normal stresses at the stagnation point can become unbounded, since the residence time is infinitely large. This fact can be used to verify the accuracy of the numerical method on the predictions of the normal stresses at the stagnation point. Figure 8 presents the results obtained for the dimensionless polymeric first normal stress difference, $N_{1} = \left( \tau ^{'}_{yy}-\tau ^{'}_{xx}\right) /\left( \eta _{o}U/D\right)$, along the axial direction in the centerline $y=0$, with both the log-conformation and the square-root formulations for $De=0.1, 0.2, 0.3$ and 0.35. In this figure, we have also included the analytic solution at the stagnation point for $De=0.1$ [50]. We can observe that for simulations where the extensional stresses become unbounded, i.e., when $De \ge 0.2$, the first normal stress difference predicted by both methods presents very small differences, in spite of the large gradients observed in the vicinity of the stagnation point.

Fig. 7

Cross-slot problem: a geometry and boundary conditions; b view of the mesh at the central square of the cross-slot

Fig. 8

Dimensionless polymeric first normal stress difference, $N_{1} = \left( \tau ^{'}_{yy}-\tau ^{'}_{xx}\right) /\left( \eta _{o}U/D\right)$, as function of x at $y=0$ for the log-conformation and square-root formulations: $De=0.1, 0.2, 0.3, 0.35$

Table 2 Oldroyd-B model data (DQ and Wi), with $\beta =1/9$, for a cross-slot with sharp corners

In order to compare our data with the benchmark results of Cruz et al. [49], we also use the following parameter to quantify the flow asymmetry [48]:

$$\begin{aligned} DQ=\frac{Q_{2}-Q_{1}}{Q_{2}+Q_{1}} \end{aligned}$$

The total flow rate per unit depth supplied to each inlet channel, $Q=Q_1+Q_2$, divides into two outlet streams, $Q_1$ and $Q_2$, as illustrated in Fig. 7a). For a symmetric flow $Q_1 = Q_2$ and $DQ=0$, while for a completely asymmetric flow $|DQ|=1$, i.e. flow from one inlet channel going completely to a single outlet channel. The results obtained for DQ and Wi evaluated at the stagnation point using both the log-conformation and the square-root formulations are presented in Table 2. We can observe that above the first critical value of the Deborah number, $De_{crit}=0.37$, the flow exhibits a purely-elastic instability in which the flow becomes steady and spatially asymmetric, leading to non-zero values of DQ. For both conformation tensor reformulations and both discretization methods (FVM and FDM) the values of DQ and Wi are close to those obtained by Cruz et al. [49] using similar mesh refinement. When compared with the extrapolated values of Cruz et al. [49], our results are slightly different, due to the use of a coarse mesh.

Fig. 9

Numerical simulation of the impacting drop problem using the Oldroyd-B model ($Re=5.0$; $Wi=1.0$; $\beta =0.1$; $Fr=2.26$). Illustration of the drop shape and contour plot of u-velocity component for different dimensionless times: a $t=0$, b $t=2.0$, c $t=4.0$ and d $t=6.0$

Free surface flow: the impacting drop problem

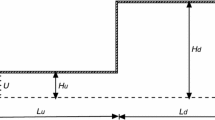
In this problem, we compute the time evolution of the shape of a 2D drop that falls under the action of gravity from a distance H above a rigid plate. Figure 9 illustrates the drop shape and u-velocity field for different phases of the transient motions for $Wi= \lambda U/D = 1$, where U is the initial velocity of the drop at height H, and D is the initial diameter of the drop.

Typical difficulties in this simulation are the numerical instability for highly elastic flows in following the large deformation of the interface between liquid and air making the time-dependent impacting drop problem a popular benchmark for free surface flows of viscoelastic fluids [51–54]. However, the literature is scarce for high-Weissenberg number flows due to the inherent numerical difficulties. Therefore, in order to obtain more insight into the physics of this free surface flow, we have used the square-root formulation in the context of FDM for solving this problem at high Wi flows.

The parameters used in this study were: $D = 0.02\,\mathrm {m}$, $U = 1\,\mathrm {m/s}$ and $|g| =9.81\,\mathrm {m/s^2}$. We consider a drop with an initial velocity of $|v_0|=1\,\mathrm {m/s}$ at a distance $H = 0.04\,\mathrm {m}$ measured from the center of the drop to the impacting rigid plate.

First, to verify the implementation of the code, we simulate the problem with the Oldroyd-B model considering $Re=5.0$, $Fr=2.26$, $Wi=1.0$ and $\beta =0.1$. Three meshes were adopted for the computations: M1 with $h= 0.025$, M2 with $h= 0.0125$ and M3 with $h = 0.00625$, where h is the mesh cell size of the uniform square cells. Figure 10 shows the comparison between our results and values from the literature for the dimensionless drop width. The results obtained with the square-root formulation for three meshes show a good convergence with mesh refinement, and in comparison with the other methods, the FDM code produces similar results.

Fig. 10

Numerical prediction of the time variation of the normalized width (W / D) of an Oldroyd-B fluid drop at $Re=5.0$, $Wi=1.0$, $\beta =0.1$, and $Fr=2.26$

Fig. 11

Influence of Wi on the numerical prediction of the dimensionless drop width for Oldroyd-B fluid at $Re=5.0$, $\beta =0.1$, and $Fr=2.26$. Results for the Newtonian fluid ($Wi=0$) are also included ($Re=5$ and $Re=50$ )

To assess the influence of fluid viscoelasticity on the impacting drop problem, Fig. 11 presents, for mesh M2, the time evolution of the drop width for different values of Wi. In this figure, we have also included the results for the Newtonian fluid ($Wi=0$) considering $Re=5$ and $Re=50$. We can observe that increasing Wi leads to an increase of the drop width with a more efficient spreading, as also observed when comparing in Fig. 9. In order to compare the square-root stabilization results with the log-conformation method in this free surface benchmark, we have also plotted in Fig. 11 the drop width obtained by the log-conformation formulation at $Wi=1$ and 200. From this figure, we can conclude that the square-root formulation produces similar results as the log-conformation method.

It might seem counter-intuitive, but for smaller Wi the normal stress growth after the impact is faster (due to the smaller relaxation time compared with the deformation time) and this leads to some recoil effect observed due to the viscoelasticity. Increasing Wi leads to larger normal stresses, but occurring only for larger times and this reduces the resistance due to normal stress in the initial times after the impact. As a consequence, for $Wi \ge 50$ the drop diameter does not suffer a significant overshoot as observed for lower Wi. In particular, for the largest Wi the polymer stresses do not have time to grow during the fast deformation process after the drop impact and in practice the fluid response is identical to the Newtonian solvent with viscosity $\beta \eta _0$, thus the curve for $Wi=500$ approaches the Newtonian case ($Wi=0$) with an effective Reynolds number of $Re= 5/ \beta = 50$, as shown in Fig. 11.

Conclusions

This work presented the application of the square-root conformation tensor stabilization method for computation of confined and free-surface flows of viscoelastic fluids. The results showed the ability of this methodology for efficient and stable computations of high-Weissenberg number flows using the Oldroyd-B model. The numerical studies include the lid-driven cavity, the flow around a confined cylinder, the flow in a cross-slot and the impacting drop problem.

Both the FDM and FVM implementations of the square-root formulation presented stable and efficient results for all the 2D confined and free surface benchmark flows studied in this work. When compared with the non-stabilized conformation tensor version, the square-root formulation allowed calculations at higher Weissenberg numbers. When both methods converge to a steady solution, the use of the square-root formulation provides similar results as those of the non-stabilized conformation tensor version. When compared to other stabilized methodologies, the accuracy and stability of the square-root formulation is found to be similar to the log-conformation approach or with the kernel-conformation with the equivalent transformation functions. From the numerical performance point of view, and by design, the square-root formulation can introduce some reduction of the computational time since it does not require the computation of eigenvectors and eigenvalues of the conformation tensor at every time step needed in both the log-conformation or kernel-conformation approaches, thus offering an alternative methodology for addressing the High-Weissenberg Number Problem. Nevertheless, this CPU time reduction can be compensated in the log-conformation and kernel-conformation methodologies using efficient techniques to compute the conformation tensor diagonalization.