A hybrid inertial algorithm for approximating solution of convex feasibility problems with applications

Abstract

An inertial iterative algorithm for approximating a point in the set of zeros of a maximal monotone operator which is also a common fixed point of a countable family of relatively nonexpansive operators is studied. Strong convergence theorem is proved in a uniformly convex and uniformly smooth real Banach space. This theorem extends, generalizes and complements several recent important results. Furthermore, the theorem is applied to convex optimization problems and to J-fixed point problems. Finally, some numerical examples are presented to show the effect of the inertial term in the convergence of the sequence of the algorithm.

1 Introduction

An inertial-type algorithm was first introduced and studied by Polyak [35], as a method of speeding up the convergence of the sequence of an algorithm. This algorithm is a two step iterative procedure in which the successive iterates are obtained by using two previous iterates. Numerical experiments have shown that an algorithm with an inertial extrapolation term converges faster than an algorithm without it. Thus, one can see an increasing interest in the class of inertial-type algorithms (see, for example, the following papers [12, 26, 44] and the references therein).

Let X be a real normed space with dual space $X^{*}$. Let $T:X\to 2^{X^{*}}$, be a set-valued operator with domain $D(T):=\{p\in X :Tp \neq\emptyset\}$, range $R(T):=\bigcup_{p\in D(T)}\{ Tp\}$ and graph $G(T):=\{(p,p^{*}) : p^{*}\in Tp\}$. Then T is called monotone if

$$ \bigl\langle p-q, p^{*} -q^{*} \bigr\rangle \geq0,\quad \forall p^{*}\in Tp, q^{*}\in Tq. $$

(1.1)

T is said to be maximal monotone if $G(T)$ is not properly contained in the graph of any other monotone operator. Monotone maps were first introduced by Minty [29] to aid in the abstract study of electrical networks and later studied by Browder [4] in the setting of partial differential equations. Later, Kačurovskii [19], Minty [30], Zarantonello [48] and many other authors studied this class of operators in Hilbert spaces. Interest in monotone operators stems mainly from their various applications (see e.g., the following monographs [2, 5, 17] and the references therein).

A fundamental problem of interest in the study of monotone operators in Banach spaces is the following:

$$ \text{Find}\quad p\in X \quad\text{such that}\quad 0\in Tp. $$

(1.2)

For the prove of existence of solutions of (1.2) see, for example, Browder [3], and Martin [27]. Many problems in applications can be transformed into the form of the inclusion (1.2). For example, problems arising from convex minimization, variational inequality, Hammerstein equations, and evolution equations can be transformed into the form of the inclusion (1.2) (see, e.g., Chidume et al. [8, 14], Rockafellar [37]).

Iterative methods for approximating solutions of the inclusion (1.2) have been studied extensively by various authors in Hilbert spaces and in more general Banach spaces. One of the classical methods for approximating solution(s) of (1.2) in Hilbert spaces is the celebrated proximal point algorithm (PPA) introduced by Martinet [28] and studied extensively by Rockafellar [37] and a host of other authors. Concerning the iterative approximation of solution(s) of (1.2) in more general Banach space, see, e.g., [6, 11, 14, 20, 32].

Let $S: X \to X$ be a map and let $p\in X$, p be called an asymptotic fixed point of S if X contains a sequence $\{ p_{n}\}$ which converges weakly to p and $\lim_{n \to \infty} \|p_{n}-Sp_{n}\|=0$. We denote the set of asymptotic fixed points of S by $\widehat{F}(S)$. The map S is said to be relatively nonexpansive if $\widehat{F}(S)=F(S)\neq\emptyset$ and $\psi(p,Sq)\leq\psi(p,q)$, for all $p\in F(S)$ and $q\in X$, where $F(S)=\{p\in X : Sp=p\}$ and ψ is the Lyapunov function (see, e.g., Alber [1]).

One of the motivations for the study of relatively nonexpansive self or nonself mappings in Banach spaces is the fact that they are an extension of nonexpansive mappings with nonempty fixed point sets in Hilbert spaces. In 2018, Chidume et al. [12] introduced and studied an inertial-type algorithm in a uniformly convex and uniformly smooth real Banach space. They proved the following theorem.

Theorem 1.1

LetBbe a uniformly convex and uniformly smooth real Banach space. Let$T_{i} :B\rightarrow B$, $i=1,2,3,\ldots$be a countable family of relatively nonexpansive maps such that$\bigcap_{i=1}^{\infty}F(T_{i})\neq \emptyset$. Suppose${\lbrace\eta_{i} \rbrace} \subset(0,1)$and${\lbrace\beta_{i} \rbrace} \subset(0,1)$are sequences such that$\sum_{i=1}^{\infty}\eta_{i}=1$and$T :B \rightarrow B$is defined by$Tp=J^{-1} (\sum_{i=1}^{\infty}\eta_{i}(\beta_{i}Jp+(1-\beta _{i})JT_{i}p) )$for each$p\in B$. Let$\lbrace x_{n}\rbrace$be generated by the following algorithm:

$$ \textstyle\begin{cases} C_{0}=B,\\ w_{n}=x_{n}+\alpha_{n}(x_{n}-x_{n-1}),\\ y_{n}=J^{-1} ( (1-\beta)Jw_{n}+\beta JTw_{n} ),\\ C_{n+1}=\{z\in C_{n}: \psi(z,y_{n})\leq\psi(z,w_{n}) \},\\ x_{n+1}=\varPi_{C_{n+1}}x_{0}, \end{cases} $$

(1.3)

$n\geq0$, where$\alpha_{n}\in[0,1)$, $\beta\in(0,1)$. Then$\{x_{n}\}$converges strongly to$p=\varPi_{F(T)}x_{0}$.

Several iterative algorithms for approximating fixed points of self maps satisfying certain contractive conditions and zeros of monotone and monotone type operators has recently been studied extensively by various authors; see e.g., [24, 33, 34, 39–42]. In 2009, Inoue et al. [18] introduced and studied a hybrid algorithm in a uniformly convex and uniformly smooth Banach space. They proved the following theorem.

Theorem 1.2

LetBbe a uniformly convex and uniformly smooth Banach space and letCbe a nonempty closed and convex subset ofB. Let$A: B\to 2^{B^{*}}$be a maximal monotone operator satisfying$D(A) \subset C$and let$J_{r}=(J+rA)^{-1}J$for all$r>0$. Let$S: C \to C$be a relatively nonexpansive mapping such that$F(S)\cap A^{-1}0 \neq\emptyset$. Let$\{x_{n}\}$be a sequence generated by$x_{0}=x\in C$and

$$ \textstyle\begin{cases} u_{n}=J^{-1} ( \beta_{n} Jx_{n}+(1-\beta_{n})JSJ_{r_{n}}x_{n} ), & \\ C_{n}=\{ z\in C: \psi(z, u_{n})\leq\psi(z,x_{n}) \}, &\\ Q_{n}=\{ z\in C : \langle x_{n}-z,Jx_{0}-Jx_{n} \rangle\geq0 \}, & \\ x_{n+1}=\varPi_{C_{n}\cap Q_{n}}x, \end{cases} $$

(1.4)

for all$n\in \Bbb {N}\cup\{0\}$, whereJis the duality mapping onB, $\{\beta_{n}\}\subset[0,1]$, and$\{r_{n}\}\subset[a,\infty)$for some$a>0$. If$\liminf_{n\to\infty}(1-\beta_{n})>0$, then$\{x_{n}\}$converges strongly to$\varPi_{F(S)\cap A^{-1}0}x_{0}$.

In 2009, Klin et al. [21] extended the results of Inoue et al. [18]. They proved the following theorem.

Theorem 1.3

LetBbe a uniformly convex and uniformly smooth Banach space and letCbe a nonempty closed and convex subset ofB. Let$A: B\to 2^{B^{*}}$be a maximal monotone operator satisfying$D(A) \subset C$and let$J_{r}=(J+rA)^{-1}J$for all$r>0$. LetSandTbe relatively nonexpansive mappings fromCinto itself such that$\varOmega =F(S)\cap F(T)\cap A^{-1}0 \neq\emptyset$. Let$\{x_{n}\}$be a sequence generated by$x_{0}\in C$and

$$ \textstyle\begin{cases} u_{n}=J^{-1} ( \alpha_{n} Jx_{n}+(1-\alpha_{n})JTz_{n} ), & \\ z_{n}=J^{-1} ( \beta_{n} Jx_{n}+(1-\beta_{n})JSJ_{r_{n}}x_{n} ), & \\ C_{n}=\{ z\in C: \psi(z, u_{n})\leq\psi(z,x_{n}) \}, &\\ Q_{n}=\{ z\in C : \langle x_{n}-z,Jx_{0}-Jx_{n} \rangle\geq0 \}, & \\ x_{n+1}=\varPi_{C_{n}\cap Q_{n}}x_{0}, \end{cases} $$

(1.5)

for all$n\in \Bbb {N}\cup\{0\}$, whereJis the duality mapping onB, $\{\alpha_{n}\},\{\beta_{n}\}\subset[0,1]$, and$\{r_{n}\}\subset [a,\infty)$for some$a>0$. If$\liminf_{n\to\infty}(1-\alpha _{n})>0$and$\liminf_{n\to\infty}(1-\beta_{n})>0$, then$\{x_{n}\}$converges strongly to$\varPi_{\varOmega}x_{0}$.

Motivated by the results of Chidume et al. [12] and Klin et al. [21], in this paper we introduce and study an inertial iterative algorithm in a uniformly convex and uniformly smooth real Banach space and prove a strong convergence theorem for approximating a common element in the set of zeros of a maximal monotone operator and the sets of fixed points of countable family of relatively nonexpansive mappings. Furthermore, we give applications of our theorem to convex optimization and J-fixed point. Finally, we present numerical examples to demonstrate the effect of the inertial term on the convergence of the sequence of our algorithm.

2 Preliminaries

The following definitions and lemmas will be needed in the sequel.

Definition 2.1

Let X be a real normed space. The normalized duality map J from X to $2^{X^{*}}$ is defined by $Jp := \lbrace p^{*}\in X^{*} :\langle p,p^{*} \rangle=\|p\|^{2}=\|p^{*}\| ^{2}, \forall p\in X \rbrace$, where $\langle\cdot, \cdot \rangle$ denotes the value of $p^{*}$ at p and $X^{*}$ is the dual space of X. It is well known that if X is smooth then J is single-valued and if X is uniformly smooth, then J is uniformly continuous on bounded subsets of X.

Definition 2.2

Let B be a smooth real Banach space; the Lyapunov functional $\psi: B\times B \to \Bbb {R}$ is defined by

$$ \psi(p,y)= \Vert p \Vert ^{2}-2\langle p, Jy \rangle+ \Vert y \Vert ^{2}. $$

(2.1)

The mapping ψ was introduced by Alber [1]. Since its introduction, one can notice an increasing interest in the functional see e.g., [7, 10, 38, 43, 45, 46, 49]. Observe that, in a real Hilbert space H, Eq. (2.1) reduces to $\psi(p,y)=\|p-y\|^{2}$, $\forall p,y\in H$. Furthermore, the following properties of ψ can be verified easily from its definition:

• (P1) $(\|p\|-\|q\|)^{2}\leq\psi(p,q) \leq(\|p\|+\|q\|)^{2}$,

• (P2) $\psi(p,q)= \psi(p,z)+\psi(z,q)+2\langle p-z, Jz-Jq \rangle$,

• (P3) $\psi(p,q) \leq\|p\|\|Jp-Jq\|+\|q-p\|\|q\|$,

for all $p,q,z \in B$.

Definition 2.3

Let B be a strictly convex, smooth and reflexive real Banach space and let C be a nonempty, closed and convex subset of B. The map $\varPi_{C}:B\rightarrow C$ defined by $\tilde{t}:=\varPi_{C} (t)$ such that $\psi(\tilde{t},t)= \inf_{y\in C}\psi(y,t)$ is called the generalized projection of t onto C. Observe that in a real Hilbert space, the generalized projection $\varPi_{C}$ and the metric projection $P_{C}$ are equivalent.

Lemma 2.4

(Rockafellar, [36])

LetBbe a smooth, strictly convex and reflexive real Banach space and$A: B\to2^{B^{*}}$be a monotone mapping. ThenAis maximal if and only if$R(J+rA)=B^{*}$, $\forall r>0$.

Lemma 2.5

(Alber, [1])

LetCbe a nonempty closed and convex subset of a smooth, strictly convex and reflexive real Banach spaceB. Then:

• (1) given$t\in B$and$y \in C$, $\tilde{t} =\varPi_{C}t$if and only if$\langle\tilde{t}-y, Jt-J\tilde{t} \rangle\geq0$, for all$y\in C$,

• (2) $\psi(y,\tilde{t})+\psi(\tilde{t},t)\leq\psi(y,t)$, for all$t\in B, y \in C$.

Lemma 2.6

(Nilsrakoo and Saejung, [31])

Let B be a smooth Banach space. Then

$$\begin{aligned} \psi \bigl(u,J^{-1}\bigl[\beta Jt + (1-\beta)Jy\bigr] \bigr)\le\beta \psi (u,t)+(1-\beta)\psi(u,y),\quad \forall \beta\in[0, 1], u, t,y \in B. \end{aligned}$$

Remark 1

Let B be a smooth, strictly convex and reflexive real Banach space, let C be a nonempty closed and convex subset of B and let $A: B\to 2^{B^{*}}$ be a monotone operator satisfying

$$ D(A)\subset C\subset J^{-1} \biggl( \bigcap _{r>0}R(J+rA) \biggr). $$

(2.2)

Then we can define the resolvent $J_{r}: C\to D(A)$ of A by

$$J_{r}t=\bigl\{ y\in D(A) : Jt\in(Jy+rAy) \bigr\} , \quad\forall t\in C. $$

It is well known that $J_{r}t$ is single-valued. For $r>0$, the Yosida approximation $A_{r}:C\to B^{*}$ is defined by $A_{r}t=(Jt-JJ_{r}t)/r$ for all $t\in C$.

Lemma 2.7

(Kohsaka and Takahashi, [22])

LetBbe a smooth, strictly convex and reflexive real Banach space, letCbe a nonempty closed convex subset ofBand let$A: B\to 2^{B^{*}}$be a monotone operator satisfying (2.2). Let$r>0$and let$J_{r}$and$A_{r}$be the resolvent and the Yosida approximation ofA, respectively. Then the following hold:

• (i) $\psi(u,J_{r}t)+\psi(J_{r}t,t)\leq\psi(u,t)$, $\forall t\in C$, $u\in A^{-1}0$;

• (ii) $(J_{r}t, A_{r}t)\in A$, $\forall t\in C$, where$(t,t^{*})\in A$denotes the value of$t^{*}$att ($t^{*}\in At$).

• (iii) $F(J_{r})=A^{-1}0$.

Lemma 2.8

(Xu, [47])

LetBbe a uniformly convex Banach space and let$r>0$. Then there exists a strictly increasing, continuous, and convex function$g:[0,\infty) \to[0,\infty)$such that$g(0)=0$and

$$\bigl\Vert \tau t+(1-\tau)y \bigr\Vert ^{2}\leq\tau \Vert t \Vert ^{2}+(1-\tau) \Vert y \Vert ^{2}-\tau(1-\tau )g\bigl( \Vert t-y \Vert \bigr), $$

for all$t,y\in B_{r}(0)$and$\tau\in[0,1]$.

Lemma 2.9

(Kamimura and Takahashi, [20])

LetBbe a uniformly convex and smooth real Banach space, and let$\{ x_{n}\}$and$\{y_{n}\}$be two sequences ofB. If either$\{x_{n}\}$or$\{y_{n}\}$is bounded and$\psi(x_{n},y_{n} )\to0$, then$\Vert x_{n}-y_{n}\Vert\to0$.

Lemma 2.10

(Kohsaka and Takahash, [23])

LetCbe a closed convex subset of a uniformly smooth and uniformly convex Banach spaceBand let$(S_{i})_{i=1}^{\infty}$, $S_{i}: C \to B$, for each$i \ge1$, be a family of relatively nonexpansive maps such that$\bigcap_{i=1}^{\infty}F(S_{i}) \neq\emptyset$. Let$(\eta_{i})_{i=1}^{\infty}\subset(0,1)$and$(\mu_{i})_{i=1}^{\infty}\subset(0,1)$be sequences such that$\sum_{i=1}^{\infty}\eta_{i} =1$. Consider the map$T:C \to B$defined by

$$ Tt=J^{-1} \Biggl(\sum_{i=1}^{\infty}\eta_{i}\bigl(\mu_{i}Jt+(1-\mu_{i})JS_{i}t \bigr)\Biggr) \quad\textit{for each } t \in C. $$

(2.3)

ThenTis relatively nonexpansive and$F(T)=\bigcap_{i=1}^{\infty}F(S_{i})$.

3 Main result

Theorem 3.1

LetBbe a uniformly convex and uniformly smooth real Banach space. Let$A: B\to2^{B^{*}}$be a maximal monotone operator and let$J_{r}=(J+rA)^{-1}J$, for all$r>0$. Let$S:B\to B$and$T:B \to B$be relatively nonexpansive mappings such that$\varOmega =F(S)\cap F(T)\cap A^{-1} 0 \neq\emptyset$. Define inductively the sequence$\{x_{n}\}$by: $x_{0},x_{1} \in B$

$$ \textstyle\begin{cases} C_{0}=B, & \\ w_{n}=x_{n}+\alpha_{n}(x_{n}-x_{n-1}), & \\ z_{n}=J^{-1} ((1-\beta) Jw_{n}+\beta JSJ_{r_{n}}w_{n} ), & \\ u_{n}= J^{-1} ((1-\gamma)Jw_{n}+\gamma JTz_{n} ),&\\ C_{n+1}=\{z\in C_{n} : \psi(z,u_{n})\leq\psi(z,w_{n}) \}, & \\ x_{n+1}= \varPi_{C_{n+1}}x_{0}, & \end{cases} $$

(3.1)

for all$n\in \Bbb {N}\cup\{0\}$, $\{\alpha_{n}\} \subset[0,1)$, $\beta, \gamma\in(0,1)$and$\{r_{n}\} \subset[a,\infty)$, for some$a>0$. Then$\{x_{n}\}$converges strongly to$\varPi_{\varOmega}x_{0}$.

Proof

We divide the proof into four steps.

Step 1. We show that $\{x_{n}\}$ is well defined and $\varOmega \subset C_{n}$, $\forall n\geq0$. Observe that by definition, $C_{n+1}$ is closed and convex, $\forall n\geq0$. We now show that $\varOmega \subset C_{n}$. Let $y_{n}=J_{r_{n}}w_{n}$ and $u\in\varOmega$. Using Lemma 2.6, the fact that S is relatively nonexpansive and Lemma 2.7(i), we obtain

$$\begin{aligned} \psi(u,z_{n}) &=\psi \bigl(u,J^{-1} \bigl((1- \beta)Jw_{n}+\beta JSy_{n} \bigr) \bigr) \\ &\leq(1-\beta)\psi(u,w_{n})+\beta\psi(u,Sy_{n}) \\ &\leq(1-\beta)\psi(u,w_{n})+\beta\psi(u,y_{n}) \end{aligned}$$

(3.2)

$$\begin{aligned} &=(1-\beta)\psi(u,w_{n})+\beta\psi(u,J_{r_{n}}w_{n}) \\ &\leq(1-\beta)\psi(u,w_{n})+\beta\psi(u,w_{n}) \\ &=\psi(u,w_{n}). \end{aligned}$$

(3.3)

Similarly, using Lemma 2.6, the fact that T is relatively nonexpansive and inequality (3.3), we have

$$\begin{aligned} \psi(u,u_{n})&=\psi \bigl(u,J^{-1} \bigl( (1- \gamma)Jw_{n}+\gamma JTz_{n} \bigr) \bigr) \\ &\leq(1-\gamma)\psi(u,w_{n})+\gamma\psi(u, Tz_{n}) \\ &\leq(1-\gamma)\psi(u,w_{n})+\gamma\psi(u,z_{n}) \\ &\leq(1-\gamma)\psi(u,w_{n})+\gamma\psi(u,w_{n})= \psi(u,w_{n}) , \end{aligned}$$

(3.4)

which implies $u\in C_{n+1}$. So, by induction, $\varOmega\subset C_{n}$, $\forall n\geq 0$. Thus, $\{x_{n}\}$ is well defined.

Step 2. We show that $\{x_{n}\}$, $\{w_{n}\}$, $\{z_{n}\}$, $\{u_{n}\}$ are bounded and $\{x_{n}\}$ is Cauchy. We observe that $x_{n}=\varPi_{C_{n}}x_{0}$ and $C_{n+1}\subset C_{n}$, $\forall n\geq0$. So, by Lemma 2.5(2)

$$\psi(x_{n},x_{0})\leq\psi(x_{n+1},x_{0}). $$

Thus, $\{\psi(x_{n},x_{0})\}$ is nondecreasing. Furthermore, we have

$$\psi(x_{n},x_{0})=\psi(\varPi_{C_{n}}x_{0},x_{0}) \leq\psi(u,x_{0})-\psi (u,x_{n})\leq \psi(u,x_{0}), $$

which implies that $\{\psi(x_{n},x_{0})\}$ is bounded and by (P1), $\{x_{n}\}$ is also bounded. Since $\{\psi(x_{n},x_{0})\}$ is nondecreasing, $\{\psi (x_{n},x_{0})\}$ is convergent. Furthermore, $\{x_{n}\}$ bounded implies $\{ w_{n}\}$ is bounded which also imply that $\{z_{n}\}$ and $\{u_{n}\}$ are bounded (by using inequalities (3.3) and (3.4), respectively and (P1)).

Next we show that $\{x_{n}\}$ is Cauchy. Using Lemma 2.5(2)

$$\psi(x_{m},x_{n})=\psi(x_{m}, \varPi_{C_{n}}x_{0})\leq\psi(x_{m},x_{0})- \psi (x_{n},x_{0})\to0, \quad\text{as }n,m\to\infty. $$

Hence, $\{x_{n}\}$ is Cauchy and this implies that $\|x_{n+1}-x_{n}\|\to 0$, as $n\to\infty$.

Step 3. We show the following:

• $\lim_{n\to\infty} \|x_{n}-w_{n}\|=0$, $\lim_{n\to\infty} \| x_{n}-u_{n}\|=0$,

• $\lim_{n\to\infty} \|z_{n}-Tz_{n}\|=0$, $\lim_{n\to\infty} \| y_{n}-Sy_{n}\|=0$.

Using the definition of $w_{n}$, we have

$$\Vert x_{n}-w_{n} \Vert = \bigl\Vert \alpha_{n}(x_{n}-x_{n-1}) \bigr\Vert \leq \Vert x_{n}-x_{n-1} \Vert \to0, \quad\text{as }n\to\infty. $$

Now, using the fact that $\{w_{n}\}$ is bounded, we have $\psi (x_{n},w_{n})\to0$, as $n\to\infty$. Since $x_{n+1}\in C_{n}$, it follows that

$$0\leq\psi(x_{n+1},u_{n})\leq\psi(x_{n+1},w_{n}) \to0. $$

Thus, $\lim_{n\to\infty}\psi(x_{n+1},u_{n})=0$, which implies that $\lim_{n\to\infty}\|x_{n+1}-u_{n}\|=0$. Hence, $\lim_{n\to\infty}\| x_{n}-u_{n}\|=0$. By the uniform continuity of J on bounded sets, we have

$$\lim_{n\to\infty} \Vert Jx_{n+1}-Jx_{n} \Vert =\lim_{n \to\infty} \Vert Jx_{n+1}-Ju_{n} \Vert =\lim_{n\to\infty} \Vert Jx_{n}-Ju_{n} \Vert =0. $$

Observe that

$$\begin{aligned} \Vert Jx_{n+1}-Ju_{n} \Vert &= \bigl\Vert Jx_{n+1}-(1-\gamma)Jw_{n}-\gamma JTz_{n} \bigr\Vert \\ &= \bigl\Vert (1-\gamma) (Jx_{n+1}-Jw_{n})+ \gamma(Jx_{n+1}-JTz_{n}) \bigr\Vert \\ &= \bigl\Vert \gamma(Jx_{n+1}-JTz_{n})-(1-\gamma) (Jw_{n}-Jx_{n+1}) \bigr\Vert \\ &\geq\gamma \Vert Jx_{n+1}-JTz_{n} \Vert -(1-\gamma) \Vert Jw_{n}-Jx_{n+1} \Vert , \end{aligned}$$

(3.5)

which implies

$$\Vert Jx_{n+1}-JTz_{n} \Vert \leq \frac{1}{\gamma} \bigl( \Vert Jx_{n+1}-Ju_{n} \Vert +(1-\gamma) \Vert Jw_{n}-Jx_{n+1} \Vert \bigr). $$

Thus, $\lim_{n\to\infty}\|Jx_{n+1}-JTz_{n}\|=0$. By the uniform continuity of $J^{-1}$ on bounded sets, we have $\lim_{n\to\infty} \|x_{n+1}-Tz_{n}\|=0$. Furthermore,

$$\Vert w_{n}- Tz_{n} \Vert \leq \Vert w_{n}-x_{n+1} \Vert + \Vert x_{n+1}-Tz_{n} \Vert \quad\Rightarrow\quad \lim_{n\to\infty} \Vert w_{n}-Tz_{n} \Vert =0. $$

Next we show that $\lim_{n\to\infty} \|z_{n}-Tz_{n}\|= \lim_{n\to\infty} \|y_{n}-Sy_{n}\|=0$. Using Lemma 2.8 we have

$$\begin{aligned} \begin{aligned} \psi(u,z_{n})&=\psi \bigl(u,J^{-1} \bigl((1- \beta)Jw_{n}+\beta JSy_{n} \bigr) \bigr) \\ &= \Vert u \Vert ^{2}-2\bigl\langle u, (1-\beta)Jw_{n}+ \beta JSy_{n}\bigr\rangle + \bigl\Vert (1-\beta )Jw_{n}+ \beta JSy_{n} \bigr\Vert ^{2} \\ &\leq \Vert u \Vert ^{2}-2\bigl\langle u, (1- \beta)Jw_{n}\bigr\rangle -2\langle u, \beta JSy_{n} \rangle+(1-\beta) \Vert w_{n} \Vert ^{2}+\beta \Vert Sy_{n} \Vert ^{2} \\ &\quad -\beta(1-\beta)g\bigl( \Vert Jw_{n}-JSy_{n} \Vert \bigr) \\ &=(1-\beta)\psi(u,w_{n})+\beta\psi(u, Sy_{n})-\beta(1- \beta)g\bigl( \Vert Jw_{n}-JSy_{n} \Vert \bigr) \\ &\leq\psi(u,w_{n})-\beta(1-\beta)g\bigl( \Vert Jw_{n}-JSy_{n} \Vert \bigr).\end{aligned} \end{aligned}$$

This implies that

$$ \beta(1-\beta)g\bigl( \Vert Jw_{n}-JSy_{n} \Vert \bigr)\leq\psi(u,w_{n})-\psi(u,z_{n}). $$

(3.6)

Let $\{\|w_{n_{k}}-Sy_{n_{k}}\|\}$ be an arbitrary subsequence of $\{\| w_{n}-Sy_{n}\|\}$. Since $\{w_{n_{k}}\}$ is bounded, there exists a subsequence $\{w_{n_{k_{j}}}\}$ of $\{w_{n_{k}}\}$ such that

$$\lim_{j\to\infty} \psi(u,w_{n_{k_{j}}})=\limsup _{k\to\infty}\psi (u, w_{n_{k}})=a. $$

Using (P2), (P3) and the fact that T is relatively nonexpansive, we obtain

$$\begin{aligned} \psi(u,w_{n_{k_{j}}})&= \psi(u, Tz_{n_{k_{j}}})+\psi (Tz_{n_{k_{j}}},w_{n_{k_{j}}})+2\langle u-Tz_{n_{k_{j}}}, JTz_{n_{k_{j}}}-Jw_{n_{k_{j}}}\rangle \\ &\leq\psi(u,z_{n_{k_{j}}})+ \Vert Tz_{n_{k_{j}}} \Vert \Vert JTz_{n_{k_{j}}}-Jw_{n_{k_{j}}} \Vert + \Vert Tz_{n_{k_{j}}}-w_{n_{k_{j}}} \Vert \Vert w_{n_{k_{j}}} \Vert \\ &\quad +2 \Vert u-Tz_{n_{k_{j}}} \Vert \Vert JTz_{n_{k_{j}}}-Jw_{n_{k_{j}}} \Vert . \end{aligned}$$

(3.7)

Since $\lim_{n\to\infty}\|w_{n}-Tz_{n}\|=0$ and hence $\lim_{n\to \infty}\|Jx_{n}-JTz_{n}\|=0$ we obtain

$$a= \lim_{j\to\infty}\psi(u,w_{n_{k_{j}}})\leq\liminf _{j\to\infty} \psi(u,z_{n_{k_{j}}}). $$

We also have from inequality (3.3)

$$\limsup_{j \to\infty}\psi(u,z_{n_{k_{j}}})\leq\limsup _{j\to\infty } \psi(u,w_{n_{k_{j}}})=a, $$

and hence

$$\lim_{j\to\infty} \psi(u,w_{n_{k_{j}}})= \lim _{j \to\infty}\psi (u,z_{n_{k_{j}}})=a. $$

Thus, it follows from inequality (3.6) that $\lim_{j\to \infty}g(\|Jw_{n_{k_{j}}}-JSy_{n_{k_{j}}}\|)=0$. By the properties of g, we have $\lim_{j \to\infty}\|Jw_{n_{k_{j}}}-JSy_{n_{k_{j}}}\|=0$. By the uniform continuity of $J^{-1}$ on bounded sets, we obtain $\lim_{j\to\infty} \|w_{n_{k_{j}}}-Sy_{n_{k_{j}}}\|=0$. Hence, $\lim_{n \to\infty}\|w_{n}-Sy_{n}\|=0$. So, we have $\lim_{n \to\infty} \| Jw_{n}-JSy_{n}\|=0$. Observe that

$$\begin{aligned} \begin{aligned} \Vert Jz_{n}-Jw_{n} \Vert &= \bigl\Vert (1- \beta)Jw_{n}+\beta JSy_{n}-Jw_{n} \bigr\Vert \\ &=\beta \Vert JSy_{n}-Jw_{n} \Vert \\ &\leq \Vert JSy_{n}-Jw_{n} \Vert .\end{aligned} \end{aligned}$$

This implies that $\lim_{n\to\infty}\|Jz_{n}-Jw_{n}\|=0$, and hence $\lim_{n\to\infty}\|w_{n}-z_{n}\|=0$. Furthermore, from inequality (3.2), we have

$$ \frac{1}{\beta} \bigl( \psi(u,z_{n})-(1- \beta)\psi(u,w_{n}) \bigr)\leq \psi(u,y_{n}). $$

(3.8)

Using $y_{n}=J_{r_{n}}w_{n}$ and Lemma 2.7(i), we have

$$\psi(y_{n},w_{n})=\psi(J_{r_{n}}w_{n},w_{n}) \leq\psi(u,w_{n})-\psi (u,J_{r_{n}}w_{n})= \psi(u,w_{n})-\psi(u,y_{n}). $$

Thus, using inequality (3.8), we have

$$\begin{aligned} \psi(y_{n},w_{n})&\leq\psi(u,w_{n})- \psi(u,y_{n}) \\ &\leq\psi(u,w_{n})-\frac{1}{\beta} \bigl( \psi(u,z_{n})-(1-\beta)\psi (u,w_{n}) \bigr) \\ &=\frac{1}{\beta} \bigl(\psi(u,w_{n})-\psi(u,z_{n}) \bigr) \\ &=\frac{1}{\beta} \bigl( \Vert w_{n} \Vert ^{2}- \Vert z_{n} \Vert ^{2}-2\langle u, Jw_{n}-Jz_{n}\rangle \bigr) \\ &\leq\frac{1}{\beta} \bigl( \bigl\vert \Vert w_{n} \Vert - \Vert z_{n} \Vert \bigr\vert \bigl( \Vert w_{n} \Vert + \Vert z_{n} \Vert \bigr)+2 \Vert u \Vert \Vert Jw_{n}-Jz_{n} \Vert \bigr) \\ &\leq\frac{1}{\beta} \bigl( \Vert w_{n}-z_{n} \Vert \bigl( \Vert w_{n} \Vert + \Vert z_{n} \Vert \bigr)+2 \Vert u \Vert \Vert Jw_{n}-Jz_{n} \Vert \bigr). \end{aligned}$$

This implies that $\lim_{n\to\infty} \psi(y_{n},w_{n})=0$. It follows from Lemma 2.9 that

$$ \lim_{n \to\infty} \Vert y_{n}-w_{n} \Vert =0. $$

(3.9)

Observe that

$$\begin{aligned}& \Vert z_{n}-Tz_{n} \Vert \leq \Vert z_{n}-w_{n} \Vert + \Vert w_{n}-Tz_{n} \Vert \quad \text{and} \\& \Vert y_{n}-Sy_{n} \Vert \leq \Vert y_{n}-w_{n} \Vert + \Vert w_{n}-Sy_{n} \Vert , \end{aligned}$$

imply

$$\lim_{n \to\infty} \Vert z_{n}-Tz_{n} \Vert =\lim_{n\to\infty} \Vert y_{n}-Sy_{n} \Vert =0. $$

Step 4. Finally, we show that $\{x_{n}\}$ converges strongly to a point in Ω. Since $\{w_{n}\}$ is bounded, there exists a subsequence $\{w_{n_{k}}\}$ of $\{w_{n}\}$ such that $w_{n_{k}} \rightharpoonup p$. Furthermore, since $\lim_{n\to\infty} \|w_{n}-y_{n}\|=0$ and $\lim_{n \to\infty} \|w_{n}-z_{n}\|=0$, we have $y_{n_{k}}\rightharpoonup p$ and $z_{n_{k}}\rightharpoonup p$. Moreover, since S and T are relatively nonexpansive, we have $p\in\widehat{F}(S)\cap\widehat {F}(T)=F(S)\cap F(T)$. Next, we show that $p\in A^{-1} 0$. By the uniform continuity of J on bounded sets, it follows from inequality (3.9) that

$$\lim_{n\to\infty} \Vert Jw_{n}-Jy_{n} \Vert =0. $$

Since $r_{n}\geq a$, we have $\lim_{n\to\infty}\frac{1}{r_{n}} \|Jw_{n}-Jy_{n}\|=0$. Therefore,

$$\lim_{n \to\infty} \Vert A_{r_{n}}w_{n} \Vert =\lim_{n\to\infty} \frac {1}{r_{n}} \Vert Jx_{n}-Jy_{n} \Vert =0. $$

Using the fact that A is monotone and Lemma 2.7 (ii), we have

$$\bigl\langle v-y_{n},v^{*}-A_{r_{n}}w_{n} \bigr\rangle \geq0, \quad\forall n \geq0. $$

This implies that $\lim_{k \to\infty}\langle v-y_{n_{k}},v^{*}-A_{r_{n_{k}}}w_{n_{k}} \rangle=\langle v-p, v^{*}\rangle\geq 0$. Thus, $p\in A^{-1}0$, since A is maximal monotone. Therefore, $p\in\varOmega$. From Step 3, there exists $\{x_{n_{k}}\}$ a subsequence of $\{x_{n}\}$, such that $x_{n_{k}}\rightharpoonup p$, as $k \to\infty$. We now show that $p=\varPi_{\varOmega}x_{0}$. Set $q=\varPi _{\varOmega}x_{0}$. Using the fact that $x_{n}=\varPi_{C_{n}} x_{0}$ and $\varOmega\subset C_{n}$, $\forall n\geq0$, we have $\psi(x_{n},x_{0})\leq \psi(q,x_{0})$. Using the fact that the norm is weakly lower semi-continuous, we obtain

$$\begin{aligned} \psi(p,x_{0})&= \Vert p \Vert ^{2}-2\langle p,Jx_{0}\rangle+ \Vert x_{0} \Vert ^{2} \\ &\leq\liminf_{k \to\infty} \bigl( \Vert x_{n_{k}} \Vert ^{2}-2\langle x_{n_{k}},Jx_{0}\rangle+ \Vert x_{0} \Vert ^{2} \bigr) \\ &\leq\liminf_{k \to\infty}\psi(x_{n_{k}},x_{0}) \leq\limsup_{k\to \infty}\psi(x_{n_{k}},x_{0}) \leq \psi(q,x_{0}) . \end{aligned}$$

(3.10)

But

$$ \psi(q,x_{0})\leq\psi(z,x_{0}), \quad\forall z\in\varOmega. $$

(3.11)

Thus, $\psi(p,x_{0})=\psi(q,x_{0})$. By uniqueness of $\varPi_{\varOmega}x_{0}$, $p=q$. Next, we show that $x_{n_{k}}\to p$, as $k\to\infty$. Using inequalities (3.10) and (3.11), we obtain $\psi(x_{n_{k}},x_{0})\to\psi(p,x_{0})$, as $k\to\infty$. Thus, $\| x_{n_{k}}\|\to\|p\|$, as $k \to\infty$. By the Kadec–Klee property of B, we conclude that $x_{n_{k}}\to p$ as $k \to\infty$. Therefore, $x_{n} \to\varPi_{\varOmega}x_{0}$. This completes the proof. □

Theorem 3.2

LetBbe a uniformly convex and uniformly smooth real Banach space. Let$A: B\to2^{B^{*}}$be a maximal monotone operator and let$J_{r}=(J+rA)^{-1}J$, for all$r>0$. Let$T: B \to B$be a relatively nonexpansive and let$\{ S_{i} \}_{i=1}^{\infty}$be a countable family of relatively nonexpansive maps such that$\bigcap_{i=1} ^{\infty}F(S_{i}) \neq\emptyset$, where$S_{i}: B \to B$, ∀i. Let$\{ \zeta_{i}\}_{i=1}^{\infty}\subset(0,1)$and$\{\tau_{i}\}_{i=1}^{\infty}\subset(0,1)$be sequences such that$\sum_{i=1}^{\infty}\zeta_{i} =1$. Assume$\varOmega= (\bigcap_{i=1} ^{\infty}F(S_{i}) ) \cap F(T) \cap {A^{-1} 0 \neq\emptyset}$. Define inductively the sequence$\{x_{n}\}$by: $x_{0},x_{1} \in B$

$$ \textstyle\begin{cases} C_{0}=B, & \\ w_{n}=x_{n}+\alpha_{n}(x_{n}-x_{n-1}), & \\ z_{n}=J^{-1} ((1-\beta) Jw_{n}+\beta JSJ_{r_{n}}w_{n} ), & \\ u_{n}= J^{-1} ((1-\gamma)Jw_{n}+\gamma JTz_{n} ), &\\ C_{n+1}=\{z\in C_{n} : \psi(z,u_{n})\leq\psi(z,w_{n}) \}, & \\ x_{n+1}= \varPi_{C_{n+1}}x_{0}, & \end{cases} $$

(3.12)

for all$n\in \Bbb {N}\cup\{0\}$, where$St=J^{-1} (\sum_{i=1}^{\infty}\zeta_{i}(\tau_{i}Jt+(1-\tau_{i})JS_{i}t) )$for each$t \in B$, $\{\alpha_{n}\} \subset[0,1)$, $\beta, \gamma\in(0,1)$and$\{r_{n}\} \subset[a,\infty)$, for some$a>0$. Then$\{x_{n}\}$converges strongly to$\varPi_{\varOmega}x_{0}$.

Proof

By Lemma 2.10, S is relatively nonexpansive and $F(S)=\bigcap_{i=1} ^{\infty}F(S_{i})$. The conclusion follows from Theorem 3.1. □

4 Applications

4.1 Application to a convex optimization problem

Let X be a normed space and let $f : X\to(-\infty, \infty]$ be a convex, proper and lower semi-continuous function. The subdifferential of f is defined by

$$\partial f(t):=\bigl\{ t^{*} \in X^{*} : f(y)-f(t) \geq\bigl\langle y-t, t^{*}\bigr\rangle , \forall y \in X\bigr\} . $$

Observe that $0\in\partial f(u)$ if and only if u is a minimizer of f. Furthermore, it is well known that the subdifferential of f, ∂f is maximal monotone (see, e.g., Rockafellar [37]). Set $A=\partial f$ in Theorem 3.2.

4.2 Application to J-fixed point

The notion of J-fixed point (which has also been called semi-fixed point, Zegeye [49], duality fixed point, Liu [25]) has been defined and studied by Chidume and Idu [11], for maps from a space, say X, to its dual space $X^{*}$.

Definition 4.1

Let $T:X\to2^{X^{*}}$ be any map. A point $u\in X$ is called a J-fixed point of T if $Ju \in Tu$, where $J:X\to X^{*}$ is the single-valued normalized duality map on X.

Consider, for example, the evolution inclusion

$$ \frac{du}{dt}+Au \ni0, $$

(4.1)

where $A : B \to2^{B^{*}}$ is monotone. At equilibrium, we have

$$ 0\in Au, $$

(4.2)

and the solutions of Eq. (4.2) correspond to equilibrium states of (4.1). Define $T:B\to2^{B^{*}}$ by $T:=J-A$. Then u is a J-fixed point of T if and only if u is a solution of (4.2). Consequently, approximating solutions of (4.2) is equivalent to approximating J-fixed points of maps $T:X\to2^{X^{*}}$ defined by $T:=J-A$. This connection is now generating considerable research interest in the study of J-fixed points (see, e.g., Chidume and Idu [11], Chidume and Monday [13], Chidume et al. [15, 16], and the references contained in them). This notion turns out to be very useful and applicable in approximating solutions of Eq. (4.2). For example, Chidume and Idu [11], introduced the concept of J-pseudocontractive maps and proved a strong convergence theorem for approximating J-fixed points of a J-pseudocontractive map. As an application of their theorem, they proved a strong convergence theorem for approximating a zero of a maximal monotone operator.

Recently, Chidume et al. [9] introduced the concept of relativelyJ-nonexpansive maps in a uniformly smooth and uniformly convex real Banach spaces. They gave the following definitions.

Definition 4.2

Let $T:B\to B^{*}$ be a map. A point $x^{*}\in B$ is called an asymptoticJ-fixed point ofT if there exists a sequence $\{x_{n}\}\subset B$ such that $x_{n}\rightharpoonup x^{*}$ and $\|Jx_{n}-Tx_{n}\| \to0$, as $n \to\infty$. We shall denote the set of asymptotic J-fixed points of T by $\widehat{F}_{J}(T)$.

Definition 4.3

A map $T:B\to B^{*}$ is said to be relativelyJ-nonexpansive if

• (i) $\widehat{F}_{J}(T)=F_{J}(T) \neq\emptyset$,

• (ii) $\psi(p,J^{-1}Tx)\leq\psi(p,x)$, $\forall x\in B$, $p\in F_{J}(T)$; where $F_{J}(T)=\{x\in B: Tx=Jx \}$.

Chidume et al. [9] used these new definitions in approximating a common J-fixed point of a countable family of relatively J-nonexpansive mappings in a uniformly convex and uniformly smooth real Banach space. We now use these definitions to prove a similar result. The following remark is key in the proof of the theorem below.

Remark 2

Observe that in the definition above, a mapping T is relatively J-nonexpansive if and only if $J^{-1}T$ is relatively nonexpansive in the usual sense. Furthermore, $x^{*}\in F_{J} (T ) \Leftrightarrow x^{*}\in F (J^{-1} T )$.

Theorem 4.4

LetBbe a uniformly convex and uniformly smooth real Banach space. Let$A: B\to2^{B^{*}}$be a maximal monotone operator and let$J_{r}=(J+rA)^{-1}J$, for all$r>0$. Let$T: B \to B^{*}$be a relatively nonexpansive and let$\{ S_{i} \}_{i=1}^{\infty}$be a countable family of relatively nonexpansive maps such that$\bigcap_{i=1} ^{\infty}F(S_{i}) \neq\emptyset$, where$S_{i}: B \to B^{*}$, ∀i. Let$\{\zeta_{i}\}_{i=1}^{\infty}\subset(0,1)$and$\{\tau_{i}\} _{i=1}^{\infty}\subset(0,1)$be sequences such that$\sum_{i=1}^{\infty}\zeta_{i} =1$. Assume$\varOmega= (\bigcap_{i=1} ^{\infty}F(S_{i}) ) \cap F(T) \cap {A^{-1} 0 \neq\emptyset}$. Define inductively the sequence$\{x_{n}\}$by: $x_{0},x_{1} \in B$

$$ \textstyle\begin{cases} C_{0}=B, & \\ w_{n}=x_{n}+\alpha_{n}(x_{n}-x_{n-1}), & \\ z_{n}=J^{-1} ((1-\beta) Jw_{n}+\beta SJ_{r_{n}}w_{n} ), & \\ u_{n}= J^{-1} ((1-\gamma)Jw_{n}+\gamma Tz_{n} ), &\\ C_{n+1}=\{z\in C_{n} : \psi(z,u_{n})\leq\psi(z,w_{n}) \}, & \\ x_{n+1}= \varPi_{C_{n+1}}x_{0}, & \end{cases} $$

(4.3)

for all$n\in \Bbb {N}\cup\{0\}$, where$Sx=J^{-1} (\sum_{i=1}^{\infty}\zeta_{i}(\tau_{i}Jx+(1-\tau_{i})JS_{i}x) )$for each$t \in B$, $\{\alpha_{n}\} \subset[0,1)$, $\beta, \gamma\in(0,1)$and$\{r_{n}\} \subset[a,\infty)$, for some$a>0$. Then$\{x_{n}\}$converges strongly to$\varPi_{\varOmega}x_{0}$.

Proof

By Remark 2, $J^{-1}T$ is relatively nonexpansive and $J^{-1}S_{i}$ is relatively nonexpansive for each i. The conclusion follows from Theorem 3.2. □

5 Numerical illustrations

In this section, we give some examples to illustrate the effect of the inertial term in the fast convergence of the sequence of our algorithm. For simplicity, we consider an example in $\Bbb {R}$ and choose A such that the resolvent can be easily computed.

Example 1

In Theorems 1.3 and 3.1, set $B=C_{0}=\Bbb {R}$,

$$Ax=\frac{x}{3},\qquad Tx=\sin x,\qquad Sx=\frac{1}{2}(x-\sin x). $$

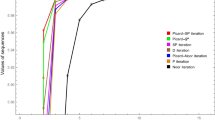
Clearly, A is maximal monotone and, T and S are relatively nonexpansive. Furthermore, $\varOmega=\{0\}$. We choose $\alpha _{n}=\beta_{n}=\frac{4n}{4n+5}$, $r_{n}=\frac{2n+1}{n}$, $\beta=\frac {1}{2}$, $\gamma=\frac{1}{4}$ as the parameters. Obviously, these parameters satisfy the hypothesis of Theorems 1.3 and 3.1. We choose $x_{0}=x_{1}=0.5$ and use a tolerance of 10⁻¹⁴ and set maximum number of iteration to be 2000 (see Tables 1 and 2 and Figs. 1 and 2).

Figure 1

Graph of the first 85 iterates of Algorithms (1.5) and (3.1) choosing $x_{0}=x_{1}=0.5$

Figure 2

Graph of the first 85 iterates of Algorithms (1.5) and (3.1) choosing $x_{0}=-2$, $x_{1}=3$

Table 1 Table of values choosing $x_{0}=x_{1}=0.5$

Table 2 Table of values choosing $x_{0}=-2$, $x_{1}=3$

Next, we give an example to show that Algorithm (3.12) is implementable.

Example 2

In Theorem 3.2, set $C_{0}=\Bbb {R}$

$$Ax=x,\qquad Tx=\frac{x}{3},\qquad S_{i}x =-\frac{\sin x}{2^{i}}. $$

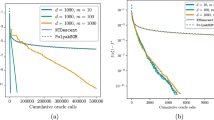
Clearly, A is maximal monotone, T is relatively nonexpansive and $S_{i}$ is relatively nonexpansive for each i. Furthermore, $\varOmega = (\bigcap_{i=1} ^{\infty}F(S_{i}) ) \cap F(T) \cap A^{-1} 0 =\{0\}$. We choose $\zeta_{i}=\tau_{i}=\frac{1}{2^{i}}$, $i\geq1$, and $\alpha_{n}=\beta_{n}=\frac{4n}{4n+5}$, $r_{n}=\frac{2n+1}{n}$, $\beta =\frac{1}{2}$, $\gamma=\frac{1}{4}$ as the parameters. Clearly, these parameters satisfy the hypothesis of Theorem 3.2. Observe that $Sx=J^{-1} (\sum_{i=1}^{\infty}\eta_{i}(\mu_{i}Jx+{(1-\mu_{i})S_{i}x}) )=\frac{7x-4\sin x}{21}$. We choose $x_{0}=1$, $x_{1}= 2.5$ and use a tolerance of 10⁻¹⁴ and set the maximum number of iterations to be 2000 (see Table 3 and Fig. 3).

Figure 3

Graph of the first 55 iterates of Algorithm (3.12) choosing $x_{0}=1$, $x_{1}=2.5$

Table 3 Table of values choosing $x_{0}=1$, $x_{1}=2.5$

Conclusion. From the numerical experiments above, we observe that indeed incorporating the inertial term in our algorithm speeds up the convergence of the sequence generated by our algorithm to the desired solution.