Abstract
This paper investigates the problem of finite-/fixed-time synchronization for Clifford-valued recurrent neural networks with time-varying delays. The considered Clifford-valued drive and response system models are firstly decomposed into real-valued drive and response system models in order to overcome the difficulty of the noncommutativity of the multiplication of Clifford numbers. Then, suitable time-delayed feedback controllers are devised to investigate the synchronization problem in finite-/fixed-time of error system. On the basis of new Lyapunov–Krasovskii functional and new computational techniques, finite-/fixed-time synchronization criteria are formulated for the corresponding real-valued drive and response system models. Two numerical examples demonstrate the effectiveness of the theoretical results.
Similar content being viewed by others
1 Introduction
Recurrent neural network (RNN) models have been used effectively to address optimization, associative memory, signal and image processing, as well as other complex problems. Recently, the dynamic analysis of RNN models has attracted immense interest from various researchers, and useful methods with respect to the stability theory of RNN models have been published [1–4]. In this respect, time delays are frequently observed in neural network (NN) models, owing to the slow speed of signal spread. Time delays are the main source of various dynamics such as chaos, poor functionality, divergence, and instability [5–9]. As such, studies on NN dynamics involving constant or time-varying delays are essential. On the other hand, quaternion-valued and complex-valued NN models are useful in many fields, including night vision color, radar images, polarized signals classification, 3D wind forecasts, and others [10–14]. Recently, many important results concerning different dynamics of the complex-valued and quaternion-valued NN models have been published [6–8, 15–18]. For example, stability analysis [8, 9, 16, 17], finite-time stability [6], stabilizability and instabilizability [7], optimization [19, 20], controllability and observability [21], multistability [18], and so on.
Clifford algebra provides a solid principle to solve geometry problems. It has been implemented in many diverse areas, e.g., neural systems, computers, robot and control problems [22–26]. Clifford-valued NN models represent a generalization of real-, complex-, and quaternion-valued NN models. To address the challenges associated with high-dimensional data and spatial geometric transformation, Clifford-valued NN models are superior to real-, complex-, and quaternion-valued NN models [24–27]. Recently, theoretical and applied studies on Clifford-valued NN models have become a new research subject. However, the dynamic properties of Clifford-valued NN models are usually more complex than those of real-, complex-, and quaternion-valued NN models. Due to the noncommutativity of multiplication with respect to Clifford numbers [28–36], studies on Clifford-valued NN dynamics are still limited. By using the linear matrix inequality approach, the authors in [28] derived the global exponential stability criteria for delayed Clifford RNN models. By using the decomposition process, the issue of global asymptotic stability in Clifford-valued NN models was explored in [29]. In [31], the authors studied the presence of globally asymptotic almost automorphic synchronization to the problem of Clifford-valued RNN models by using suitable feedback controllers. Utilizing the Banach fixed point theorem and Lyapunov functional, the global asymptotic almost periodic synchronization problems for Clifford-valued NN models were examined in [33]. Recently, the effects of neutral delay and discrete delays have been considered in a class of Clifford-valued NNs [37], and the associated existence, uniqueness, and global stability criteria have been obtained. By considering impulsive effects, the problem of global exponential stability of Clifford-valued NN models with time-varying delays has been investigated in [38].
On the other hand, synchronization is an important dynamical behavior in network systems, which has been applied in many different areas, including image processing, neural computing, traffic systems, and secure communication. As such, various kinds of synchronization have already been suggested in the previous literature [39–46]. Different from the classical synchronization analysis, finite-time synchronization means that the dynamical behaviors of coupled systems achieve the same time spatial state in finite settling time. Therefore, the concept of finite-time synchronization occurs naturally. In recent decades, literature for the finite-time synchronization of NNs has been widely published [47–52]. The use of the feedback controller technique to achieve finite-time synchronization of complex dynamical networks with time delay has been investigated [47]. In [48], the authors showed a detailed study of the finite-time synchronization of stochastic coupled NNs subject to Markovian switching and input saturation. In [49], the authors explored synchronization issues in finite-time complex-valued RNN models with time-varying delays and discontinuous activation functions. With respect to finite-time distributed delays, the synchronization issue of finite-time complex-valued NN models was examined in the work [50].
However, in practical networks, it is difficult to obtain initial values in advance. Therefore, finite-time synchronization of such networks is impossible. Fixed-time synchronization would be a reasonable choice for scientists and engineers in this case as well. The settling time for fixed-time synchronization is calculated using known parameters and does not depend on the initial values, so it is widely accepted when compared to classical finite-time synchronization [53–56]. Furthermore, in realistic engineering problems, it is desirable that the systems can be synchronized for any initial conditions within a fixed-time period. The definition of fixed-time stability was suggested in [53]. Thereafter, the principle of fixed-time stability in various areas, including rigid spacecraft, secure communication, and power systems, was successfully utilized [57–59]. In the papers [54, 55], during fixed-time synchronization of the NNs being addressed, the controllers were designed so as to achieve synchronization criteria within a fixed settling time interval. In [56], a unified control framework was designed for finite-time and fixed-time synchronization of discontinuous complex networks. In [57], fixed-time synchronization of quaternion-valued NNs was obtained by the feedback control principle and the Lyapunov functional method.
However, to the best of authors’ knowledge, the problem of finite-/fixed-time synchronization of Clifford-valued RNN with time-varying delays has not yet been considered by any researcher. Indeed, this interesting topic is still an open challenge. Therefore, we attempt to derive sufficient conditions pertaining to finite-/fixed-time synchronization of Clifford-valued RNN models in this paper. The main contributions of this paper are as follows:
-
(1)
The finite-time and fixed-time synchronization of Clifford-valued RNNs with time-varying delays is investigated for the first time.
-
(2)
By considering appropriate feedback controllers, Lyapunov functional, and new computational methods, some sufficient conditions that ascertain the finite-/fixed-time synchronization of Clifford-valued RNN models are derived by decomposing the Clifford-valued RNN model into real-valued models.
-
(3)
When Clifford-valued NN model is reduced to real-, complex-, and quaternion-valued ones, the results obtained in this paper are valid as special cases.
-
(4)
Two numerical examples with simulations are given to support the effectiveness and merits of the theoretical results.
We organize this paper as follows. The proposed Clifford-valued RNN model is formally defined in Sect. 2. The finite-/fixed-time synchronization criteria are presented in Sect. 3, while two numerical examples are given in Sect. 4. The conclusion of this paper is given in Sect. 5.
2 Mathematical fundamentals and problem formulation
2.1 Notations
The superscripts T and ∗ indicate the matrix transposition and matrix involution transposition, respectively. Any matrix  (<0) denotes a positive (negative) definite matrix, while \(\mathbb{A}\) is defined as the Clifford algebra which has m generators over real number \(\mathbb{R}\). In addition, \(\mathbb{R}^{n}\) and \(\mathbb{A}^{n}\) denote the n-dimensional real vector space and n-dimensional real Clifford vector space, respectively; while \(\mathbb{R}^{n \times n}\) and \(\mathbb{A}^{n \times n}\) denote the set of all \(n \times n\) real matrices and the set of all \(n \times n\) real Clifford matrices, respectively. We define the norm of \(\mathbb{R}^{n}\) as \(\|r\|=\sum_{i=1}^{n}|r_{i}|\), and for \(A=(a_{ij})_{n\times n}\in \mathbb{R}^{n\times n}\), denote \(\|A\|=\max_{1\leq i\leq n} \{\sum_{j=1}^{n}|a_{ij}| \}\). While \(r=\sum_{A}r^{A}e_{A}\in \mathbb{A}\), denote \(|r|_{\mathbb{A}}=\sum_{A}|r^{A}|\), and for \(A=(a_{ij})_{n\times n}\in \mathbb{A}^{n\times n}\), denote \(\|A\|_{\mathbb{A}}=\max_{1\leq i\leq n} \{\sum_{j=1}^{n}|a_{ij}|_{ \mathbb{A}} \}\). For \(\varphi \in \mathcal{C}([-\tau , 0], \mathbb{A}^{n})\), \(\|\varphi \|_{\tau }\leq \sup_{-\tau \leq s\leq 0}\|\varphi (t+s) \|\).
(<0) denotes a positive (negative) definite matrix, while \(\mathbb{A}\) is defined as the Clifford algebra which has m generators over real number \(\mathbb{R}\). In addition, \(\mathbb{R}^{n}\) and \(\mathbb{A}^{n}\) denote the n-dimensional real vector space and n-dimensional real Clifford vector space, respectively; while \(\mathbb{R}^{n \times n}\) and \(\mathbb{A}^{n \times n}\) denote the set of all \(n \times n\) real matrices and the set of all \(n \times n\) real Clifford matrices, respectively. We define the norm of \(\mathbb{R}^{n}\) as \(\|r\|=\sum_{i=1}^{n}|r_{i}|\), and for \(A=(a_{ij})_{n\times n}\in \mathbb{R}^{n\times n}\), denote \(\|A\|=\max_{1\leq i\leq n} \{\sum_{j=1}^{n}|a_{ij}| \}\). While \(r=\sum_{A}r^{A}e_{A}\in \mathbb{A}\), denote \(|r|_{\mathbb{A}}=\sum_{A}|r^{A}|\), and for \(A=(a_{ij})_{n\times n}\in \mathbb{A}^{n\times n}\), denote \(\|A\|_{\mathbb{A}}=\max_{1\leq i\leq n} \{\sum_{j=1}^{n}|a_{ij}|_{ \mathbb{A}} \}\). For \(\varphi \in \mathcal{C}([-\tau , 0], \mathbb{A}^{n})\), \(\|\varphi \|_{\tau }\leq \sup_{-\tau \leq s\leq 0}\|\varphi (t+s) \|\).
2.2 Clifford algebra
In this subsection, we recall some definitions, notations, and basic results of Clifford algebra. The Clifford real algebra over \(\mathbb{R}^{m}\) is defined as
where \(e_{A}=e_{l_{1}}e_{l_{2}},\ldots, e_{l_{\nu }}\) with \(A=\{l_{1},l_{2},\ldots ,l_{\nu }\}\), \(1 \leq l_{1} < l_{2} <\cdots < l_{\nu }\leq m\). Moreover, \(e_{\emptyset }=e_{0}=1\) and \(e_{l}=e_{\{l\}}\), \(l=1,2,\ldots ,m\), are denoted as the Clifford generators, and they satisfy \(e_{i}e_{j} + e_{j}e_{i} = 0\), \(i \neq j\), \(i,j={1,2,\ldots ,m}\), \(e_{i}^{2} =-1\), \(i = 1,2,\ldots ,m\).
Remark 2.1
When one element is the product of multiple Clifford generators, we will write its subscripts together: \(e_{4}e_{5}e_{6}e_{7}=e_{4567}\).
Let \(\Lambda =\{\emptyset ,1,2,\ldots , A,\ldots , 12,\dots, m\}\), and we have
where \(\sum_{A}\) denotes \(\sum_{A\in \Lambda }\) and \(\dim \mathbb{A}=\sum_{k=0}^{m}\binom{m}{k}=2^{m}\). For \(r=\sum_{A}r^{A}e_{A}:\mathbb{R}\rightarrow \mathbb{A}\), where \(r^{A}:\mathbb{R}\rightarrow \mathbb{R}\), \(A\in \Lambda \), its derivative is represented by \(\frac{dr(t)}{dt}=\sum_{A}\frac{dr^{A}(t)}{dt}e_{A}\). For more knowledge about Clifford algebra, we refer the reader to [28–30].
2.3 Problem definition
Consider the following Clifford-valued RNN model with time-varying delays:
where \(i\in N\), \(j\in N\) (\(N=1,2,\ldots,n\)), and n corresponds to the number of neurons; \(r_{i}(t)\in \mathbb{A}\) represents the state vector of the ith unit; \(d_{i}\in \mathbb{R}^{+}\) indicates the rate with which the ith unit will reset its potential to the resting state in isolation when it is disconnected from the network and external inputs; \(a_{ij}, b_{ij}\in \mathbb{A}\) indicate the strengths of connection weights without and with time-varying delays between cells i and j, respectively; \(k_{i}\in \mathbb{A}\) is an external input on the ith unit; \(h_{j}(\cdot ):\mathbb{A}^{n} \rightarrow \mathbb{A}^{n}\) is the activation function of signal transmission; \(\tau _{j}(t)\) corresponds to the transmission delay which satisfies \(0\leq \tau _{j}(t)\leq \tau \), where τ is a positive constant, and \(\tau =\max_{1\leq j\leq n}\{\tau _{j}(t)\}\). Furthermore, \(\varphi _{i}\in \mathcal{C}([-\tau , 0],\mathbb{A}^{n})\) is the initial condition with respect to model (1).
Remark 2.2
It is clear that NN model (1) includes real-valued, complex-valued, and quaternion-valued NN models. These mean that the proposed NN model is more general than the corresponding one in the existing articles. For example, when we consider \(m=0\) in NN model (1), then the model can be reduced to the real-valued NN model proposed in [5]. If we take \(m=1\) in NN model (1), then the model can be reduced to the complex-valued NN model proposed in [9]. If we choose \(m=2\) in NN model (1), then the model can be reduced to the quaternion-valued NN model proposed in [17].
The corresponding response system is defined by
where \(i\in N\), \(j\in N\) (\(N=1,2,\ldots,n\)), and n corresponds to the number of neurons; \(s_{i}(t)\in \mathbb{A}\) represents the state vector of the ith unit; \(\phi _{i}\in \mathcal{C}([-\tau , 0],\mathbb{A}^{n})\) is the initial condition for model (3). In addition, \(u_{i}(t)\) is state-feedback controller, while other notations associated with (3) and (4) are the same as those in (1) and (2).
-
(A1)
Function \(h_{j}(\cdot )\) fulfills the Lipschitz continuity condition with respect to the n-dimensional Clifford vector. For each \(j\in N\), there exists a positive constant \(l_{j}\) such that, for any \(x, y\in \mathbb{A}\),
$$\begin{aligned} \bigl\vert h_{j}(x)-h_{j}(y) \bigr\vert _{\mathbb{A}}\leq l_{j} \vert x-y \vert _{\mathbb{A}}, \quad j \in N, \end{aligned}$$(5)where \(l_{j}\) (\(j\in N\)) is known as the Lipschitz constant and \(h_{j}(0)=0\). In addition, there exists a positive constant \(l_{j}\) such that \(|h_{j}(x)|_{\mathbb{A}}\leq l_{j}\) for any \(x\in \mathbb{A}\).
3 Main results
To address the issue of noncommutativity of multiplication of Clifford numbers, we transform the original Clifford-valued models into multidimensional real-valued models. This can be achieved with the help of \(e_{A}\bar{e}_{A}=\bar{e}_{A}e_{A}=1\) and \(e_{B}\bar{e}_{A}e_{A}=e_{B}\). Given any \(\mathscr{G}\in \mathbb{A}\), unique \(\mathscr{G}^{C}\) that is able to satisfy \(\mathscr{G}^{C}e_{C}h^{A}e_{A}=(-1)^{\sigma [B.\bar{A}]}\mathscr{G}^{C}h^{A}e_{B}= \mathscr{G}^{B.\bar{A}}h^{A}e_{B}\) can be identified. By decomposing (1) and (2) into \(\dot{r}=\sum_{A}\dot{r}^{A}e_{A}\), we have the following real-valued models:
where
Remark 3.1
If \(r=(r_{1}^{0}, r_{1}^{1}, r_{1}^{2}, \ldots , r_{1}^{1,2, \ldots,m}, r_{2}^{0}, r_{2}^{1}, r_{2}^{2}, \ldots , r_{2}^{1,2, \ldots,m}, \ldots , r_{n}^{0}, r_{n}^{0}, r_{n}^{2}, \ldots , r_{n}^{1,2, \ldots,m})^{T}=\{r_{i}^{A}\}\) is a solution to system (6), then \(r=(r_{1}, r_{2}, \ldots , r_{n})^{T}\) must be a solution to system (1), where \(r_{i}=\sum_{A}r_{i}^{A}e^{A}\), \(i=1,2,\ldots,n\), \(A\in \Lambda \).
Also, we can use the same method to transform (3) and (4) into the following real-valued models:
where
Note that the remaining notations of (8) and (9) are the same as those in (6) and (7).
Define the error vector between the real-valued drive models (6), (7) and the real-valued response models (8), (9) as  and \(\psi _{i}^{A}(t)=\phi _{i}^{A}(t)-\varphi _{i}^{A}(t)\); then, from (6)–(9), the following error models are produced:
and \(\psi _{i}^{A}(t)=\phi _{i}^{A}(t)-\varphi _{i}^{A}(t)\); then, from (6)–(9), the following error models are produced:


Remark 3.2
As we all know, the multiplication of Clifford numbers does not satisfy the commutative law, which complicates the investigation of Clifford-valued NNs dynamics. Therefore, the known results on Clifford-valued neural networks are limited. On the other hand, the decomposition approach is very effective to overcome the difficulty of the noncommutativity of the multiplication of Clifford numbers. Therefore, it is highly meaningful to use the decomposition method to study Clifford-valued NNs. Recently, most existing results have been derived by decomposing Clifford valued NNs into real-valued NNs [28, 29, 33, 37, 38].
The following lemmas, definitions are used as the main techniques in the paper.
Definition 3.3
([58])
The origin of a nonlinear dynamical model is said to be globally finite-time stable if, for any solution \(r(t, r_{0})\), the following are true:
-
(1)
Lyapunov stability: For any \(\epsilon >0\), there is \(\delta =\delta (\epsilon )>0\) such that \(\|r(t, r_{0})\|<\epsilon \) for any \(\|r_{0}\|<\delta \) and \(t\geq t_{0}\).
-
(2)
Finite-time convergence: There exists a function \(T: \mathbb{R}^{n}\setminus \{0\}\rightarrow (0, +\infty )\), denoted as the settling time function, such that \(\lim_{t\rightarrow T(r_{0})}=0\) and \(r(t, r_{0})=0\) for all \(t\geq T(r_{0})\).
Definition 3.4
([59])
The origin of the nonlinear dynamical model is said to be fixed-time stable if it is globally finite-time stable and the settling time function \(T(r_{0})\) is bounded for any \(r_{0}\in \mathbb{R}^{n}\), i.e., there exists \(T_{\max }>0\) such that \(T(r_{0})\leq T_{\max }\) for all \(r_{0}\in \mathbb{R}^{n}\).
Definition 3.5
([60])
Consider drive-response models (6) and (7) as well as (8) and (9). If, for a suitable controller \(u_{i}(t)=\sum_{A}u^{A}_{i}(t)e_{A}\), there exists a function \(T=T(\psi _{i})>0\), depending on the initial value \(\psi _{i}\), such that

and  for \(t>T\), \(i\in N\), \(A\in \Lambda \), then drive models (6) and (7) and response models (8) and (9) achieve synchronization in finite-time.
for \(t>T\), \(i\in N\), \(A\in \Lambda \), then drive models (6) and (7) and response models (8) and (9) achieve synchronization in finite-time.
Definition 3.6
([61])
A function  is C-regular if it is
is C-regular if it is
-
(1)
regular in \(\mathbb{R}^{n}\),
-
(2)
positive definite, i.e.,
 for \(r\neq 0\) and
for \(r\neq 0\) and  ,
, -
(3)
radially unbounded, i.e.,
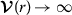 as \(\|r\|\rightarrow \infty \).
as \(\|r\|\rightarrow \infty \).
Definition 3.7
([57])
Drive-response models (6) and (7) as well as (8) and (9) are said to achieve fixed-time synchronization if, for any initial condition, there exist time \(T_{\max }\) and a settling time function  such that
such that

and  , where
, where  ,
,  , \(i\in N\), \(A\in \Lambda \).
, \(i\in N\), \(A\in \Lambda \).
Lemma 3.8
([62])
Suppose that  is continuous, differentiable, positive definite, and it satisfies the following differential inequality:
is continuous, differentiable, positive definite, and it satisfies the following differential inequality:

where  and \(0<\upsilon <1\) are constants. Then, for any given \(t_{0}\),
and \(0<\upsilon <1\) are constants. Then, for any given \(t_{0}\),  satisfies the following inequality:
satisfies the following inequality:

and

and the settling time \(T^{+}\) is given by

Lemma 3.9
([59])
If there exists a continuous radically unbounded function  such that
such that
-
(1)
 ,
, -
(2)
If there exist
 ,
, 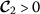 ,
,  , and
, and  such that
such that  (12)
(12)
where V̇ denotes the derivative of  .
.
Then  , \(\forall t\geq T_{\max }^{+}\) with the settling time \(T_{\max }^{+}\) given by
, \(\forall t\geq T_{\max }^{+}\) with the settling time \(T_{\max }^{+}\) given by

Lemma 3.10
([63])
If \(\xi _{1}, \xi _{2},\ldots, \xi _{n}\) are the positive constants and \(0<\alpha _{1}<\alpha _{2}\), then
3.1 Finite-time synchronization
In this subsection, the finite-time synchronization criterion for the error system models (10) and (11) is derived. The state-feedback controllers for models (10) and (11) are chosen as follows:

where \(i\in N\), \(j\in N\), \(A\in \Lambda \), and \(0<\alpha <1\) and \(\lambda _{1i}\), \(\lambda _{2i}\), \(\lambda _{3i}\) are the parameters that will be determined.
Theorem 3.11
Based on Assumption (A1) and a proper selection of the parameters to satisfy the following conditions:
Then the error system models (10) and (11) can achieve the finite-time synchronization with controller (14). Moreover, the settling time of synchronization \(T^{+}\) satisfies

Proof
Consider the following Lyapunov function which is positive definite and radially unbounded:

The Dini derivative  is computed with model (10). We derive
is computed with model (10). We derive

By combining similar terms, we have

From Lemma (3.10), we obtain

Replacing (22) in (21), we have

According to Lemma (3.8), response model (8) with controller (14) can be synchronized in finite-time with drive model (6). Furthermore, the settling time of synchronization \(T^{+}\) is given by (18). Thus, Theorem 3.11 is proved. □
3.2 Fixed-time synchronization
The fixed-time synchronization criterion for drive-response models (10) and (11) is derived. The time-delay feedback controller for model (10) is chosen as follows:

where \(i\in N\), \(j\in N\), \(A\in \Lambda \), and \(0<\alpha <1\), \(\beta >1\) and \(\lambda _{1i}\), \(\lambda _{2i}\), \(\lambda _{3i}\) \(\lambda _{4i}\) are the parameters that will be determined.
Theorem 3.12
Based on Assumption (A1) and a proper selection of the parameters to satisfy the following conditions:
The error system models (10) and (11) can achieve the fixed-time synchronization with controller (24). Moreover, the settling time of synchronization \(T^{+}\) satisfies
Proof
Consider the same Lyapunov function defined in Theorem 3.11:

The Dini derivative  is computed with model (10). We derive
is computed with model (10). We derive

By combining similar terms, we have

From Lemma (3.10), we obtain


Replacing (32) and (33) in (31), we have

According to Lemma (3.9), response model (8) can be synchronized in fixed time with drive model (6) under controller (24). The settling time of synchronization \(T_{\max }^{+}\) max is given by (28) with \(\Pi _{1}=[\min_{i\in N}(\lambda _{3i})]^{\beta }\), \(\Pi _{2}=[\min_{i\in N}(\lambda _{2i})]^{\alpha }\). Thus, Theorem 3.12 is proved. □
Remark 3.13
In Theorem 3.11 and Theorem 3.12, by decomposing the original n-dimensional Clifford-valued system into a multidimensional real-valued system, several sufficient conditions are derived to show that the considered system model is finite-time and fixed-time synchronized, but the result we get is really about Clifford-valued systems themselves.
Remark 3.14
As everyone knows, Clifford-valued neural networks aim to investigate new capabilities and better accuracy in order to solve problems that cannot be solved with real-valued, complex-valued, quaternion-valued counterparts. For example, the results of finite-time and fixed-time synchronization of complex-valued NNs [49], fixed-time synchronization of quaternion-valued NNs [57] can then be summarized as a special case of the results of this paper.
Remark 3.15
In [30], fuzzy operations are incorporated into the Clifford-valued cellular NN model to investigate its \(S^{p}\)-almost periodic solutions. The effects of discrete delays in Clifford-valued recurrent NNs are considered in [31], and the associated globally asymptotic almost automorphic synchronization criteria are obtained. The leakage delay is introduced into Clifford-valued high-order Hopfield NN models in [32] to explore its existence and global exponential stability of almost automorphic solutions. However, any work on the topic of finite-/fixed-time synchronization of Clifford-valued RNN with time-varying delays has not yet been reported. Therefore, trying to fill such gaps, we for the first time derived new sufficient conditions to ensure the finite/fixed-time synchronization of Clifford-valued RNN models with time delays. Therefore, the main results of this paper are new and different compared with those in the existing literature.
Remark 3.16
The computational complexity depends primarily on the maximum number of LMI decision variables. As everyone knows, the number of decision variables increases when using the augmented Lyapunov–Krasovskii functionals and the free-weighting-matrix method; while when the delay subintervals number becomes higher, it might prompt the complexity and the computational burden of the main results. In order to handle this issue easily, we utilized standard Lyapunov functional and estimated its time derivative without any integral inequalities and delay-decomposition approach. Hence, the proposed results in this paper may provide a smaller computational burden.
Remark 3.17
Compared with many controllers derived by early works [45, 46], the feedback controller methods are economic and easy to implement, they possess high value in real industry processes and applications.
4 Numerical examples
In this section, we present two numerical examples to demonstrate the feasibility and effectiveness of the results established in Sect. 3.
Example 1
For \(m=2\) and \(n=2\), the following two-neuron drive model (1) is considered:
The corresponding response model (3) is
The multiplication generators are: \(e_{1}^{2}=e_{2}^{2}=e_{12}^{2}=e_{1}e_{2}e_{12}=-1\), \(e_{1}e_{2}=-e_{2}e_{1}=e_{12}\), \(e_{1}e_{12}=-e_{12}e_{1}=-e_{2}\), \(e_{2}e_{12}=-e_{12}e_{2}=e_{1}\), \(r_{1}=r^{0}_{1}e_{0}+r^{1}_{1}e_{1}+r^{2}_{1}e_{2}+r^{12}_{1}e_{12}\), \(r_{2}=r^{0}_{2}e_{0}+r^{1}_{2}e_{1}+r^{2}_{2}e_{2}+r^{12}_{2}e_{12}\), \(s_{1}=s^{0}_{1}e_{0}+s^{1}_{1}e_{1}+s^{2}_{1}e_{2}+s^{12}_{1}e_{12}\), \(s_{2}=s^{0}_{2}e_{0}+s^{1}_{2}e_{1}+s^{2}_{2}e_{2}+s^{12}_{2}e_{12}\).
Furthermore, we take

in which  and
and  , \(i=1,2\). The time-varying delays are considered as \(\tau _{1}(t)=\tau _{2}(t)=0.4|\cos (t)|+0.03\) with \(\tau _{1}=\tau _{2}=0.43\). Furthermore, the activation function satisfies Assumption (A1) with \(l_{1}=l_{2}=0.5\). By selecting \(\lambda _{11}=2.5\), \(\lambda _{12}=2.6\), \(\lambda _{21}=3.5\), \(\lambda _{22}=3.8\), \(\lambda _{31}=1.95\), \(\lambda _{32}=2\), and \(\alpha =0.5\).
, \(i=1,2\). The time-varying delays are considered as \(\tau _{1}(t)=\tau _{2}(t)=0.4|\cos (t)|+0.03\) with \(\tau _{1}=\tau _{2}=0.43\). Furthermore, the activation function satisfies Assumption (A1) with \(l_{1}=l_{2}=0.5\). By selecting \(\lambda _{11}=2.5\), \(\lambda _{12}=2.6\), \(\lambda _{21}=3.5\), \(\lambda _{22}=3.8\), \(\lambda _{31}=1.95\), \(\lambda _{32}=2\), and \(\alpha =0.5\).
Besides it is easy to obtain \(d_{1}=2.2\), \(d_{2}=2.4\), \(a^{A.\bar{B}}_{11}= 0.6\), \(a^{A.\bar{B}}_{12}= 0.9\), \(a^{A.\bar{B}}_{21}= 0.7\), \(a^{A.\bar{B}}_{22}= 0.9\), \(b^{A.\bar{B}}_{11}= 0.8\), \(b^{A.\bar{B}}_{12}=0.8\), \(b^{A.\bar{B}}_{21}= 0.7\), \(b^{A.\bar{B}}_{22}= 0.5\). The initial conditions of drive-response systems (1) and (3) are taken as \(\varphi _{1}(t)=1.5e_{0}-1.2e_{1}-0.9e_{2}+2e_{12}\) for \(t\in [-0.43, 0]\), \(\varphi _{2}(t)=-1.6e_{0}+2.5e_{1}+2.2e_{2}-1.4e_{12}\) for \(t\in [-0.43, 0]\), \(\phi _{1}(t)=-2.5e_{0}+1.1e_{1}+2.2e_{2}-1.5e_{12}\) for \(t\in [-0.43, 0]\), and \(\phi _{2}(t)=2.6e_{0}-2.1e_{1}-2.2e_{2}+e_{12}\) for \(t\in [-0.43, 0]\). By simple calculation, we have
Moreover, the settling time of synchronization \(T^{+}\) satisfies

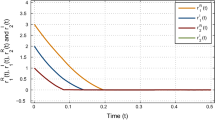
Clearly, all conditions of Theorem 3.11 are satisfied. Drive-response models (1) and (3) can achieve synchronization in finite-time with controller (14). Figures 1, 2, 4, 5, 7, 8, 10, and 11, respectively, show the time responses of the states of drive-response models (1) and (3). Besides, Figures 3, 6, 9, and 12 disclose the time responses of the states of error systems (10). From Figures 3, 6, 9, and 12, it can be seen that model (6) synchronizes with model (8) in finite-time through the controller (14) with the given initial values.
Example 2
For \(m=2\) and \(n=2\), the following two-neuron drive model (1) is considered:
The corresponding response model (3) is
The multiplication generators are: \(e_{1}^{2}=e_{2}^{2}=e_{12}^{2}=e_{1}e_{2}e_{12}=-1\), \(e_{1}e_{2}=-e_{2}e_{1}=e_{12}\), \(e_{1}e_{12}=-e_{12}e_{1}=-e_{2}\), \(e_{2}e_{12}=-e_{12}e_{2}=e_{1}\), \(r_{1}=r^{0}_{1}e_{0}+r^{1}_{1}e_{1}+r^{2}_{1}e_{2}+r^{12}_{1}e_{12}\), \(r_{2}=r^{0}_{2}e_{0}+r^{1}_{2}e_{1}+r^{2}_{2}e_{2}+r^{12}_{2}e_{12}\), \(s_{1}=s^{0}_{1}e_{0}+s^{1}_{1}e_{1}+s^{2}_{1}e_{2}+s^{12}_{1}e_{12}\), \(s_{2}=s^{0}_{2}e_{0}+s^{1}_{2}e_{1}+s^{2}_{2}e_{2}+s^{12}_{2}e_{12}\).
Furthermore, we take

in which  and
and  , \(i=1,2\). By selecting \(\lambda _{11}=2.5\), \(\lambda _{12}=2.6\), \(\lambda _{21}=3.5\), \(\lambda _{22}=3.8\), \(\lambda _{31}=4.2\), \(\lambda _{32}=4.4\), \(\lambda _{41}=1.95\), \(\lambda _{42}=2\), \(\alpha =0.5\), and \(\beta =1.5\)
, \(i=1,2\). By selecting \(\lambda _{11}=2.5\), \(\lambda _{12}=2.6\), \(\lambda _{21}=3.5\), \(\lambda _{22}=3.8\), \(\lambda _{31}=4.2\), \(\lambda _{32}=4.4\), \(\lambda _{41}=1.95\), \(\lambda _{42}=2\), \(\alpha =0.5\), and \(\beta =1.5\)
The time-varying delays are considered as \(\tau _{1}(t)=\tau _{2}(t)=0.5|\cos (t)|+0.02\) with \(\tau _{1}=\tau _{2}=0.52\). Furthermore, the activation function satisfies Assumption (A1) with \(l_{1}=l_{2}=0.5\). Besides it is easy to obtain \(d_{1}=2.6\), \(d_{2}=2.8\), \(a^{A.\bar{B}}_{11}= 0.7\), \(a^{A.\bar{B}}_{12}= 0.8\), \(a^{A.\bar{B}}_{21}= 0.5\), \(a^{A.\bar{B}}_{22}= 0.8\), \(b^{A.\bar{B}}_{11}= 0.5\), \(b^{A.\bar{B}}_{12}=0.6\), \(b^{A.\bar{B}}_{21}= 0.5\), \(b^{A.\bar{B}}_{22}= 0.8\). The initial conditions of drive-response models (1) and (3) are taken as \(\varphi _{1}(t)=-1.5e_{0}+1.8e_{1}-0.9e_{2}+2e_{12}\) for \(t\in [-0.52, 0]\), \(\varphi _{2}(t)=1.6e_{0}-2e_{1}+2.2e_{2}-1.4e_{12}\) for \(t\in [-0.52, 0]\), \(\phi _{1}(t)=-2.5e_{0}+1.7e_{1}+2.2e_{2}-1.5e_{12}\) for \(t\in [-0.52, 0]\), and \(\phi _{2}(t)=2.6e_{0}+1.2e_{1}-2.2e_{2}+e_{12}\) for \(t\in [-0.52, 0]\). By simple computation, we have
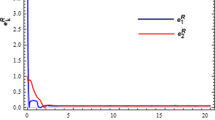
Clearly, all conditions of Theorem 3.12 are satisfied. Therefore, drive-response models (6) and (8) achieve fixed-time synchronization with controller (24). Moreover, the settling time of synchronization \(T_{\max }^{+}\) satisfies
5 Conclusion
In this article, we have studied the finite-/fixed-time synchronization for Clifford-valued RNN models with time-varying delays. In order to overcome the difficulty of the noncommutativity of the multiplication of Clifford numbers, we first decomposed the considered Clifford-valued drive and response models into real-valued drive and response models. Besides, suitable time-delayed feedback controllers have been constructed to examine the synchronization problem associated with the finite-/fixed-time error models. By utilizing the finite-/fixed-time stability concepts, some computational techniques, new synchronization criteria have been derived through appropriate Lyapunov functions to guarantee that the drive-response models achieve synchronization in finite-/fixed-time. Finally, we have also presented numerical examples to illustrate the effectiveness of the results. The results obtained in this paper can be further extended to other complex systems. We would like to extend our results to more general Clifford-valued NN models, such as Cohen–Grossberg Clifford-valued NNs, Clifford-valued inertial NNs, Clifford-valued high-order Hopfield NNs, and fuzzy Clifford-valued NNs. Moreover, we will focus on the problem of global stabilization analysis of Clifford-valued NN models with the help of various control systems. The corresponding results will be carried out in the near future.
Availability of data and materials
Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.
References
Cao, J., Wang, J.: Global asymptotic stability of a general class of recurrent neural networks with time-varying delays. IEEE Trans. Circuits Syst. I 50, 34–44 (2003)
Cao, J., Wang, J.: Global asymptotic and robust stability of recurrent neural networks with time delays. IEEE Trans. Circuits Syst. I 52, 417–426 (2005)
Cao, J., Yuan, K., Li, H.: Global asymptotical stability of recurrent neural networks with multiple discrete delays and distributed delays. IEEE Trans. Neural Netw. 17, 1646–1651 (2006)
Zhang, Z., Liu, X., Chen, J., Guo, R., Zhou, S.: Further stability analysis for delayed complex-valued recurrent neural networks. Neurocomputing 251, 81–89 (2017)
Yang, B., Hao, M., Cao, J., Zhao, X.: Delay-dependent global exponential stability for neural networks with time-varying delay. Neurocomputing 338, 172–180 (2019)
Zhang, Z., Liu, X., Guo, R., Lin, C.: Finite-time stability for delayed complex-valued BAM neural networks. Neural Process. Lett. 48, 179–193 (2018)
Zhang, Z., Liu, X., Zhou, D., Lin, C., Chen, J., Wang, H.: Finite-time stabilizability and instabilizability for complex-valued memristive neural networks with time delays. IEEE Trans. Syst. Man Cybern. Syst. 48, 2371–2382 (2018)
Samidurai, R., Sriraman, R., Zhu, S.: Leakage delay-dependent stability analysis for complex-valued neural networks with discrete and distributed time-varying delays. Neurocomputing 338, 262–273 (2019)
Pan, J., Liu, X., Xie, W.: Exponential stability of a class of complex-valued neural networks with time-varying delays. Neurocomputing 164, 293–299 (2015)
Hirose, A.: Complex-Valued Neural Networks: Theories and Applications. World Scientific, Singapore (2003)
Nitta, T.: Solving the XOR problem and the detection of symmetry using a single complex-valued neuron. Neural Netw. 16, 1101–1105 (2003)
Isokawa, T., Nishimura, H., Kamiura, N., Matsui, N.: Associative memory in quaternionic Hopfield neural network. Int. J. Neural Syst. 18, 135–145 (2008)
Matsui, N., Isokawa, T., Kusamichi, H., Peper, F., Nishimura, H.: Quaternion neural network with geometrical operators. J. Intell. Fuzzy Syst. 15, 149–164 (2004)
Mandic, D.P., Jahanchahi, C., Took, C.C.: A quaternion gradient operator and its applications. IEEE Signal Process. Lett. 18, 47–50 (2011)
Li, Y., Meng, X.: Almost automorphic solutions for quaternion-valued Hopfield neural networks with mixed time-varying delays and leakage delays. J. Syst. Sci. Complex. 33, 100–121 (2020)
Tu, Z., Zhao, Y., Ding, N., Feng, Y., Zhang, W.: Stability analysis of quaternion-valued neural networks with both discrete and distributed delays. Appl. Math. Comput. 343, 342–353 (2019)
Shu, H., Song, Q., Liu, Y., Zhao, Z., Alsaadi, F.E.: Global μ-stability of quaternion-valued neural networks with non-differentiable time-varying delays. Neurocomputing 247, 202–212 (2017)
Tan, M., Liu, Y., Xu, D.: Multistability analysis of delayed quaternion-valued neural networks with nonmonotonic piecewise nonlinear activation functions. Appl. Math. Comput. 341, 229–255 (2019)
Xia, Z., Liu, Y., Lu, J., Cao, J., Rutkowski, L.: Penalty method for constrained distributed quaternion-variable optimization. IEEE Trans. Cybern. (2020). https://doi.org/10.1109/TCYB.2020.3031687
Liu, Y., Zheng, Y., Lu, J., Cao, J., Rutkowski, L.: Constrained quaternion-variable convex optimization: a quaternion-valued recurrent neural network approach. IEEE Trans. Neural Netw. Learn. Syst. 31, 1022–1035 (2020)
Jiang, B.X., Liu, Y., Kou, K.I., Wang, Z.: Controllability and observability of linear quaternion-valued systems. Acta Math. Sin. Engl. Ser. 36, 1299–1314 (2020)
Pearson, J.K., Bisset, D.L.: Neural networks in the Clifford domain. In: Proc. IEEE ICNN, Orlando (1994)
Pearson, J.K., Bisset, D.L.: Back Propagation in a Clifford Algebra. ICANN, Brighton (1992)
Buchholz, S., Sommer, G.: On Clifford neurons and Clifford multi-layer perceptrons. Neural Netw. 21, 925–935 (2008)
Kuroe, Y.: Models of Clifford recurrent neural networks and their dynamics. In: IJCNN-2011, pp. 1035–1041. IEEE, San Jose (2011)
Hitzer, E., Nitta, T., Kuroe, Y.: Applications of Clifford’s geometric algebra. Adv. Appl. Clifford Algebras 23, 377–404 (2013)
Buchholz, S.: A theory of neural computation with Clifford algebras. PhD thesis, University of Kiel (2005)
Zhu, J., Sun, J.: Global exponential stability of Clifford-valued recurrent neural networks. Neurocomputing 173, 685–689 (2016)
Liu, Y., Xu, P., Lu, J., Liang, J.: Global stability of Clifford-valued recurrent neural networks with time delays. Nonlinear Dyn. 332, 259–269 (2019)
Shen, S., Li, Y.: \(S^{p}\)-Almost periodic solutions of Clifford-valued fuzzy cellular neural networks with time-varying delays. Neural Process. Lett. 51, 1749–1769 (2020)
Li, Y., Xiang, J., Li, B.: Globally asymptotic almost automorphic synchronization of Clifford-valued recurrent neural netwirks with delays. IEEE Access 7, 54946–54957 (2019)
Li, B., Li, Y.: Existence and global exponential stability of pseudo almost periodic solution for Clifford-valued neutral high-order Hopfield neural networks with leakage delays. IEEE Access 7, 150213–150225 (2019)
Li, Y., Xiang, J.: Global asymptotic almost periodic synchronization of Clifford-valued CNNs with discrete delays. Complexity 2019, Article ID 6982109 (2019)
Li, B., Li, Y.: Existence and global exponential stability of almost automorphic solution for Clifford-valued high-order Hopfield neural networks with leakage delays. Complexity 2019, Article ID 6751806 (2019)
Li, Y., Xiang, J., Li, B.: Globally asymptotic almost automorphic synchronization of Clifford-valued RNNs with delays. IEEE Access 7, 54946–54957 (2019)
Aouiti, C., Gharbia, I.B.: Dynamics behavior for second-order neutral Clifford differential equations: inertial neural networks with mixed delays. Comput. Appl. Math. 39, 120 (2020)
Rajchakit, G., Sriraman, R., Lim, C.P., Unyong, B.: Existence, uniqueness and global stability of Clifford-valued neutral-type neural networks with time delays. Math. Comput. Simul. (2021). https://doi.org/10.1016/j.matcom.2021.02.023
Rajchakit, G., Sriraman, R., Boonsatit, N., Hammachukiattikul, P., Lim, C.P., Agarwal, P.: Global exponential stability of Clifford-valued neural networks with time-varying delays and impulsive effects. Adv. Differ. Equ. 2021, 208 (2021). https://doi.org/10.1186/s13662-021-03367-z
Tong, D., Zhang, L., Zhou, W., Zhou, J., Xu, Y.: Asymptotical synchronization for delayed stochastic neural networks with uncertainty via adaptive control. Int. J. Control. Autom. Syst. 14, 706–712 (2016)
Selvaraj, P., Sakthivel, R., Kwon, O.M.: Finite-time synchronization of stochastic coupled neural networks subject to Markovian switching and input saturation. Neural Netw. 105, 54–165 (2018)
Lee, S.H., Park, M.J., Kwon, O.M., Selvaraj, P.: Improved synchronization criteria for chaotic neural networks with sampled-data control subject to actuator saturation. Int. J. Control. Autom. Syst. 17, 2430–2440 (2019)
Karthick, S.A., Sakthivel, R., Wang, C., Ma, Y.-K.: Synchronization of coupled memristive neural networks with actuator saturation and switching topology. Neurocomputing 383, 138–150 (2020)
Karthick, S.A., Sakthivel, R., Alzahrani, F., Leelamani, A.: Synchronization of semi-Markov coupled neural networks with impulse effects and leakage delay. Neurocomputing 386, 221–231 (2020)
Guo, Z., Gong, S., Yang, S., Huang, T.: Global exponential synchronization of multiple coupled inertial memristive neural networks with time-varying delay via nonlinear coupling. Neural Netw. 108, 260–271 (2018)
Zheng, C., Cao, J.: Robust synchronization of coupled neural networks with mixed delays and uncertain parameters by intermittent pinning control. Neurocomputing 141, 153–159 (2014)
Hu, C., Jiang, H., Teng, Z.: Impulsive control and synchronization for delayed neural networks with reaction–diffusion terms. IEEE Trans. Neural Netw. 21, 67–81 (2010)
Mei, J., Jiang, M., Xu, W.: Finite-time synchronization control of complex dynamical networks with time delay. Commun. Nonlinear Sci. Numer. Simul. 18, 2462–2478 (2013)
Selvaraj, P., Sakthivel, R., Kwon, O.M.: Finite-time synchronization of stochastic coupled neural networks subject to Markovian switching and input saturation. Neural Netw. 105, 154–165 (2018)
Aouiti, C., Bessifi, M., Li, X.: Finite-time and fixed-time synchronization of complex-valued recurrent neural networks with discontinuous activations and time-varying delays. Circuits Syst. Signal Process. 39, 5406–5428 (2020)
Liu, Y.J., Huang, J., Qin, Y., Yang, X.: Finite-time synchronization of complex-valued neural networks with finite-time distributed delays. Neurocomputing 416, 152–157 (2020)
Yang, X., Song, Q., Liang, J., He, B.: Finite-time synchronization of coupled discontinuous neural networks with mixed delays and nonidentical perturbations. J. Franklin Inst. 352, 4382–4406 (2015)
Zhang, Z., Liu, X., Lin, C., Chen, B.: Finite-time synchronization for complex-valued recurrent neural networks with time delays. Complexity 2018, Article ID 8456737 (2018)
Polyakov, A.: Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 57, 2106–2110 (2012)
Hu, C., Yu, J., Chen, Z., Jiang, H., Huang, T.: Fixed-time stability of dynamical systems and fixed-time synchronization of coupled discontinuous neural networks. Neural Netw. 89, 74–83 (2017)
Wang, L., Zeng, Z., Hu, J., Wang, X.: Controller design for global fixed-time synchronization of delayed neural networks with discontinuous activations. Neural Netw. 87, 122–131 (2017)
Ji, G., Hu, C., Yu, J., Jiang, H.: Finite-time and fixed-time synchronization of discontinuous complex networks: a unified control framework design. J. Franklin Inst. 355, 4665–4685 (2018)
Deng, H., Bao, H.: Fixed-time synchronization of quaternion-valued neural networks. Physica A 527, Article ID 121351 (2019)
Bhat, S.P., Bernstein, D.S.: Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 38, 751–766 (2000)
Du, H., Li, S., Qian, C.: Finite-time attitude tracking control of spacecraft with application to attitude synchronization. IEEE Trans. Autom. Control 56, 2711–2717 (2011)
Abdurahman, A., Jiang, H., Teng, Z.: Finite-time synchronization for fuzzy cellular neural networks with time-varying delays. Fuzzy Sets Syst. 297, 96–111 (2016)
Forti, M., Grazzini, M., Nistri, P., Pancioni, L.: Generalized Lyapunov approach for convergence of neural networks with discontinuous or non-Lipschitz activations. Physica D 214, 88–99 (2006)
Yang, X., Cao, J.: Finite-time stochastic synchronization of complex networks. Appl. Math. Model. 34, 3631–3641 (2010)
Kanter, I., Kinzel, W., Kanter, E.: Secure exchange of information by synchronization of neural networks. Europhys. Lett. 57, 141–147 (2002)
Acknowledgements
This research is made possible through financial support from the Rajamangala University of Technology Suvarnabhumi, Thailand. The authors are grateful to the Rajamangala University of Technology Suvarnabhumi, Thailand for supporting this research.
Funding
The research is supported by the Rajamangala University of Technology Suvarnabhumi, Thailand.
Author information
Authors and Affiliations
Contributions
Funding acquisition, NB; Conceptualization, GR; Software, GR and NB; Formal analysis, GR and NB; Methodology, GR and NB; Supervision, RS, PA, GR and CPL; Writing–original draft, GR; Validation, GR; Writing–review and editing, GR and NB. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Boonsatit, N., Rajchakit, G., Sriraman, R. et al. Finite-/fixed-time synchronization of delayed Clifford-valued recurrent neural networks. Adv Differ Equ 2021, 276 (2021). https://doi.org/10.1186/s13662-021-03438-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03438-1



 for
for  ,
,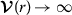 as
as  ,
, ,
, 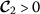 ,
,  , and
, and  such that
such that 



 ,
,  of NN model (
of NN model (


 ,
,  of NN model (
of NN model (


 ,
,  of NN model (
of NN model (


 ,
,  of NN model (
of NN model (