1 Introduction

The study of the infectious diseases dynamics is one of the most important and essential tasks to be done in order to have a good understanding of the emergence of diseases in a population. If until now, there are diseases that continue to ravage populations in low- and middle-income countries, such as the Democratic Republic of the Congo (DRC), it is largely due to the lack of understanding of the dynamics of these diseases. Despite government efforts and extensive research to control tuberculosis (TB) transmission in Congo, the disease continues to spread and settle in various parts of the country. The study of the spread of diseases allows decision-makers to try to eradicate them in the population based, for example, on the results of simulations or any other experiments. This way can also help to make predictions and thus to make a good decision at the right time. Efforts are made each year and funds are used to reduce the burden of TB, for its control through the TB stop strategy from 2015 for its elimination in 2035 in line with the Sustainable Development Goals (SDG) of the United Nations (UN) which focus on the global tuberculosis epidemic elimination. The global report 2018 [1] recently confirms that this UN Sustainable Development Goals and End TB Strategy targets for 2035 cannot be met without intensified scientific research. The DRC has also entered this program line [2], despite the low resources in its possession.

Tuberculosis is a global public health problem. The 2018 World Health Organization report [1] shows that nearly a third of the world’s population is infected with tuberculosis, with millions of deaths as well as millions of new cases of infection each year. That report confirms that tuberculosis is one of the top 10 causes of death worldwide. For example in 2015, 10.4 million people contracted TB and more than 1.5 million died from the disease, including 0.4 million among people with HIV (Human Immunodeficiency Virus). Over 95% of TB deaths occur in low- and middle-income countries. Recently, the WHO reports confirm that DRC is one of 22 countries the most infected by TB and is one of 27 states which support 85% of estimated number of multi-resistant TB in the world. The report indicates that more than 130,000 infected new cases are reported each year in DRC. This situation is due to a misunderstanding of the dynamics of the disease. It is therefore crucial to put in place strategies and methods to easily understand the transmission of this disease in order to anticipate its evolution. This disease is caused by Mycobacterium tuberculosis [3]. It should be noted that the TB usually spreads by coughing, sneezing, kissing, spitting of people with active pulmonary TB. The infection also spreads through the use of non-sterilized utensils (dishes, drinking glasses) of an infected person. It mainly attacks the lungs for pulmonary tuberculosis, but can also affect other organs of the human body, including the central nervous system, the circulatory system, the genital urinary system, bones, joints and even the skin [4, 5]. In some cases, an infectious pregnant woman may infect the fetus [6]. Only people with active TB can transmit the disease. The latent infected cases do not transmit it. Transmission from one individual to another depends on the number of infected and expelled drops, the activity of environmental ventilation, the duration of exposure to the risk of contamination, and the virulence of the Mycobacterium tuberculosis [4, 7, 8].

In order to identify ways to control diseases in the population, several studies have been conducted in mathematics [9–14]. Mathematical models are developed and applied in ecology, and also are used to understand epidemiological phenomena [15, 16]. One of the main objectives of these mathematical models is to try to understand how a given disease spreads in the population, in order to try to eradicate it in the future [17]. In other words, mathematical models attempt to answer the question of how to control a disease (prevention and surveillance) in the population.

Several mathematical models of tuberculosis have been developed [18]. These models have a significant role to play in the process of controlling TB worldwide that is ongoing. In the literature, these mathematical models are compartment one. Compartmental models are used since years. The Kermack and Mac Kendrick model is one of those models on which current models are based [19]. Most of TB models we find in the literature are of the SIR [20] or SEIR type [21–26]. Basically, there are groups or class of individuals, each group has a status that characterize it as susceptible (S), latent (E), infectious (I) or recovered (R). The transition of individuals from a group to another is generally defined by a proportion and/or a rate.

In this article, we model, analyze and simulate a mathematical model of the dynamics of pulmonary tuberculosis with eight compartments that include groups of individuals lost to follow-up and transferred. The basic reproduction number is obtained and used to propose ways to control TB in the population. Being a general and adaptable model for different contexts and scenarios, the objective here is to contribute to the understanding of TB dynamics in the population and provide materials that can be used to strengthen TB control strategies. So, this article is structured as follows. First, we present the description of the proposed model, then we present its mathematical analysis. Here we show the positivity of the solution, its existence and uniqueness, the computation of equilibrium points (DFE and EE), the basic reproduction number \(\mathcal{R}_{0}\) and the stability of equilibrium points. Some simulations are presented before to discuss the results obtained. The concluding remarks finalize this research paper.

2 Model description

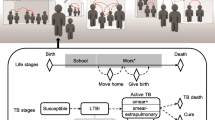
We consider a compartmental model with 8 compartments (groups). In the model we consider a population S that is susceptible to contract TB infection. This population can be infected according to a contact rate α and a transmission rate λ. For this, there is a proportion \(1-p\) of this population that will be infected and therefore will be part of compartment I, this is a fast progression to the active TB. We note that a susceptible individual can become latent \(L_{e}\) (latent early) following a contact rate α and a transmission rate λ. In this model a latent individual (\(L_{e}\) and \(L_{f}\)) is not yet able to transmit the disease. A latent individual \(L_{e}\) can become \(L_{f}\) (latent late) following a given rate h. A latent \(L_{e}\) can also directly become infectious (able to infect other people) at a rate q, an individual \(L_{f}\) can also become infectious I at a rate w, this is the low progression to the active TB.

In this model, infected and infectious individuals, who are in the I, \(L_{e}\) and \(L_{f}\) compartments can heal spontaneously and move in the compartment \(R_{2}\) according, respectively, to the rates σ, \(g_{2}\) and \(k_{2}\). They can also heal after treatment process and move in the compartment \(R_{1}\) according, respectively, to the rates γ, \(g_{1}\) and \(k_{1}\). These healed individuals can be re-infected according to a rate of transmission λ, a contact rate α and a re-infection rate r. Infectious people I, under treatment can also became \(L_{e}\) according to a rate \(r_{1}\). During the treatment process, there are people who are lost to follow-up, so people who stop treatment (K). These individuals can be re-infected according to a rate \(r_{3}\). In the model, we consider other people who are transferred to other hospitals for lack of capacity or medication (T). These people can be re-infected at a rate \(r_{2}\).

Demography is considered in the TB proposed model. We note Λ the rate of recruitment of susceptible individuals S. In the model people can die, for that we consider \(\mu _{1}\) as the rate of natural mortality (not related to TB infection) and \(\mu _{2}\) the rate of mortality linked to TB infection. Figure 1 below presents the TB transmission dynamics between the different compartments of the model.

Figure 1
figure 1

Diagram describing the dynamics between compartments for TB transmission

Full size image

Based on presented information, we obtain the Ordinary Differential Eq. System below:

$$ \textstyle\begin{cases} \dot{S} = \Lambda -\alpha \lambda p SI-\alpha \lambda (1-p)SI-\mu _{1} S , \\ \dot{L_{e}} = \alpha \lambda p S I+ \alpha \lambda r I(R_{1}+R_{2})+r_{1} I + r_{2} T + r_{3} K - \widetilde{B} L_{e} , \\ \dot{L_{f}} = hL_{e}-(\mu _{1}+w+ k_{1} + k_{2})L_{f} , \\ \dot{I} = w L_{f}+qL_{e}- \widetilde{A} I+\alpha \lambda R_{1} I + \alpha \lambda R_{2} I +\alpha \lambda (1-p)SI , \\ \dot{R_{1}} = g_{1} L_{e} + k_{1} L_{f} + \gamma I- \alpha \lambda r R_{1} I - \mu _{1} R_{1} - \alpha \lambda R_{1} I , \\ \dot{R_{2}} = \sigma I + k_{2} L_{f} + g_{2} L_{e} - \alpha \lambda R_{2} I - \alpha \lambda r R_{2} I - \mu _{1} R_{2} , \\ \dot{T} = \beta I-(\mu _{1}+\mu _{2} + r_{2})T , \\ \dot{K} = v I-(\mu _{1}+\mu _{2} + r_{3})K , \\ N = S+L_{e}+L_{f}+I+R_{1}+R_{2}+T+K. \end{cases} $$
(1)

Here \(\widetilde{A}= (r_{1} +\gamma +\beta +\sigma + v +\mu _{1}+\mu _{2})\) and \(\widetilde{B}=(\mu _{1}+h+q+g_{1} + g_{2})\).

3 Mathematical analysis

In this section, the proposed model is analyzed in order to show the positivity of the solution, the existence and uniqueness of the solution, the calculation of equilibrium points (DFE and EE), the basic reproduction number \(\mathcal{R}_{0}\) and the stability of the equilibrium points.

3.1 Positivity of the solution

By adding all the equations of system (1), we have

$$\begin{aligned}& N = \Lambda -\alpha \lambda p SI-\alpha \lambda (1-p)SI-\mu _{1} S + \alpha \lambda p S I+ \alpha \lambda r I(R_{1}+R_{2})+r_{1} I + r_{2} T \\& \hphantom{N ={}}{} + r_{3} K -(\mu _{1}+h+q+g_{1} + g_{2})L_{e} + hL_{e}-(\mu _{1}+w+ k_{1} + k_{2})L_{f} + w L_{f} \\& \hphantom{N ={}}{} +qL_{e}- (r_{1} +\gamma +\beta +\sigma + v +\mu _{1}+\mu _{2}) I+ \alpha \lambda R_{1} I + \alpha \lambda R_{2} I - \alpha \lambda r R_{1} I \\& \hphantom{N ={}}{} +\alpha \lambda (1-p)SI + g_{1} L_{e} + k_{1} L_{f} + \gamma I - \mu _{1} R_{1} - \alpha \lambda R_{1} I + \sigma I + k_{2} L_{f} + g_{2} L_{e} \\& \hphantom{N ={}}{} - \alpha \lambda R_{2} I - \alpha \lambda r R_{2} I \\& \hphantom{N ={}}{} - \mu _{1} R_{2} + \beta I-(\mu _{1}+\mu _{2} + r_{2})T + v I-(\mu _{1}+ \mu _{2} + r_{3})K, \\& N =\Lambda -\mu _{1} S -\mu _{1} L_{e} -\mu _{1} L_{f} -\mu _{1} I - \mu _{1} R_{1} - \mu _{1} R_{2} - \mu _{1} T -\mu _{1} K -\mu _{2} I - \mu _{2} T -\mu _{2} K. \end{aligned}$$

By simplifying the obtained expression of N, we have \(\dot{N} =\Lambda -\mu _{1} N-\mu _{2}(I+T+K)\) with \(N = S + L_{e} + L_{f} + I + R_{1} + R_{2} + T + K\). If we assume that there is no disease in the population, we have \(N=S\), this implies that \(L_{e} = L_{f} = I = T = K = R_{1} = R_{2} = 0\).

By setting \(\dot{N}=0\), we have \(\Lambda -\mu _{1} N-\mu _{2}(I+T+K)= 0\), considering \(I = T = K =0\), we obtain

$$ N=\frac{\Lambda }{\mu _{1}}. $$
(2)

The obtained result (2) means that when there is no disease in the population, it is naturally expected that the spread of Tuberculosis in the population will reduce N (that is, \(N> \frac{\Lambda }{\mu _{1}}\)). The feasible region of the model system (1) is

$$ \Omega _{\epsilon }=\biggl\lbrace (S, L_{e}, L_{f}, I, R_{1}, R_{2}, T, K) \in \mathbb{R}^{8}_{+}, 0\leq N \leq \frac{\Lambda }{\mu _{1}}+ \epsilon \biggr\rbrace , $$

where ϵ is a positive constant. With regard to the model system (1) that describes the TB dynamics in the population, we have the following results.

Theorem 3.1

The compact whole \(\Omega _{\epsilon }\) is an absorptive and invariant whole which attracts all existing solutions of the model system (1) in \(\mathbb{R}^{8}_{+}\).

Proof

A Lyapounov–LaSalle function \(W(t)\) can be defined as \(W(t)=N(t)\) with \(N(t)=S(t)+L_{e}(t)+L_{f}(t)+I(t)+R_{1}(t)+R_{2}(t)+T(t)+K(t)\) satisfies

$$ \frac{dW}{dt}=\Lambda -\mu _{1} W-\mu _{2}(I+T+K)\leq \Lambda -\mu _{1} W . $$
(3)

Therefore, \(\frac{dW}{dt}\leq 0\) for \(W>\frac{\Lambda }{\mu _{1}}\). This implies that \(\Omega _{\epsilon }\) is a positively invariant whole. By solving (3), we obtain \(0< W(t)<\frac{\Lambda }{\mu _{1}}+W(0)e^{\mu _{1} t}\), in which case \(W(t)\) has as initial condition \(W(0)\). Consequently, as \(t \longrightarrow +\infty \), we have \(0 \leq W(t)\leq \frac{\Lambda }{\mu _{1}}\). Then we can conclude that \(\Omega _{\epsilon }\) is an attractive whole (set) and this achieves the proof. □

3.2 Existence and uniqueness of the solution

The system (1) is described by a system of autonomous non-linear first order ordinary differential equations. It can be rewritten in the following matrix form:

$$ \dot{X}(t)=F\bigl(X(t)\bigr), \quad \mbox{where } X(t)= \begin{pmatrix} S(t) \\ L_{e}(t) \\ L_{f}(t) \\ I(t) \\ R_{1}(t) \\ R_{2}(t) \\ T(t) \\ K(t) \end{pmatrix} = \begin{pmatrix} x_{1}(t) \\ x_{2}(t) \\ x_{3}(t) \\ x_{4}(t) \\ x_{5}(t) \\ x_{6}(t) \\ x_{7}(t) \\ x_{8}(t) \end{pmatrix}. $$

F is the function \(C^{\infty }\) on \(\mathbb{R}^{8}_{+}\) described by

$$\begin{aligned}& F\bigl(X(t)\bigr)= \begin{pmatrix} f_{1}(x_{1},\ldots ,x_{8}) \\ f_{2}(x_{1},\ldots ,x_{8}) \\ f_{3}(x_{1},\ldots ,x_{8}) \\ f_{4}(x_{1},\ldots ,x_{8}) \\ f_{5}(x_{1},\ldots ,x_{8}) \\ f_{6}(x_{1},\ldots ,x_{8}) \\ f_{7}(x_{1},\ldots ,x_{8}) \\ f_{8}(x_{1},\ldots ,x_{8}) \end{pmatrix}, \\& F\bigl(X(t)\bigr)= \begin{pmatrix} \Lambda -\alpha \lambda x_{1}x_{4}-\alpha \lambda (1-p)x_{1}x_{4}- \mu _{1}x_{1} \\ \alpha \lambda x_{1}x_{4}+\alpha \lambda rx_{4}(x_{5}+x_{6})+r_{1}x_{4}+r_{2}x_{7}+r_{3}x_{8}- \mathcal{A} \\ hx_{2}-\mathcal{B}x_{3} \\ \omega x_{3}+q x_{2}-\mathcal{C}x_{4}+\alpha \lambda x_{5} x_{4}+\alpha \lambda x_{6} x_{4}+\alpha \lambda (1-p)x_{1}x_{4} \\ g_{1}x_{2}+k_{1}x_{3}+\gamma x_{4}-\alpha \lambda rx_{5} x_{4}-\mu _{1} x_{5}-\alpha \lambda x_{5} x_{4} \\ \sigma x_{4}+k_{2} x_{3}+g_{2} x_{2}-\alpha \lambda x_{6} x_{4}- \alpha \lambda r x_{6} x_{4}-\mu _{1} x_{6} \\ \beta x_{4}-\mathcal{D}x_{7} \\ \upsilon x_{4}-\mathcal{E} x_{8} \end{pmatrix}. \end{aligned}$$

Here \(\mathcal{A}=\mu _{1}+h+q+g_{1}+g_{2}\), \(\mathcal{B}=\mu _{1}+w+k_{1}+k_{2}\), \(\mathcal{C}= r_{1}+\gamma +\beta +\sigma +v+\mu _{1}+\mu _{2}\), \(\mathcal{D}= \mu _{1}+\mu _{2}+r_{2} \) and \(\mathcal{E}=\mu _{1}+\mu _{2}+r_{3}\).

Also, \(X(t)=(x_{1}(t),x_{2}(t),x_{3}(t),\ldots ,x_{8}(t))\), as F is of class \(C^{1}\), therefore locally Lipschitzian on \(\mathbb{R}^{8}_{+}\), we deduce the existence and uniqueness of the maximum solution to the problem of Cauchy associated to the differential equation (1), with the initial condition \((t_{0}, X_{0}) \in \mathbb{R} \times \mathbb{R}^{8}_{+}\).

Moreover, F being of class \(C^{\infty }\), we deduce that this solution is also of class \(C^{\infty }\).

3.3 Calculation of equilibrium points

To find equilibria of the system (1), we set \(\dot{S} = \dot{L_{e}}= \dot{L_{f}}= \dot{I}=\dot{R_{1}}=\dot{R_{2}} = \dot{T} =\dot{K} = 0\). Considering that \(X^{\ast }= ( S^{\ast }, L_{e}^{\ast }, L_{f}^{\ast }, I^{\ast }, R_{1}^{\ast }, R_{2}^{\ast }, T^{\ast }, K^{\ast })\) is the endemic equilibrium, we have

$$ \textstyle\begin{cases} \Lambda -\alpha \lambda p S^{\ast }I^{\ast }-\alpha \lambda (1-p)S^{\ast }I^{\ast }-\mu _{1} S^{\ast }= 0, \\ \alpha \lambda p S^{\ast }I^{\ast }+ \alpha \lambda r I^{\ast }(R_{1}^{\ast }+R_{2}^{\ast })+r_{1} I^{\ast }+ r_{2} T^{\ast }+ r_{3} K^{\ast }- \widetilde{B} L_{e}^{\ast }= 0, \\ hL_{e}^{\ast }-(\mu _{1}+w+ k_{1} + k_{2})L_{f}^{\ast }= 0, \\ w L_{f}^{\ast }+qL_{e}^{\ast }- \widetilde{A} I^{\ast }+\alpha \lambda R_{1}^{\ast }I^{\ast }+\alpha \lambda R_{2}^{\ast }I^{\ast }+\alpha \lambda (1-p)S^{\ast }I^{\ast }= 0, \\ g_{1} L_{e}^{\ast }+ k_{1} L_{f}^{\ast }+ \gamma I^{\ast }- \alpha \lambda r R_{1}^{\ast }I^{\ast }- \mu _{1} R_{1}^{\ast }- \alpha \lambda R_{1}^{\ast }I^{\ast }= 0, \\ \sigma I^{\ast }+ k_{2} L_{f}^{\ast }+ g_{2} L_{e}^{\ast }- \alpha \lambda R_{2}^{\ast }I^{\ast }- \alpha \lambda r R_{2}^{\ast }I^{\ast }- \mu _{1} R_{2}^{\ast }= 0, \\ \beta I^{\ast }-(\mu _{1}+\mu _{2} + r_{2})T^{\ast }= 0, \\ v I^{\ast }-(\mu _{1}+\mu _{2} + r_{3})K^{\ast }= 0. \end{cases} $$
(4)

Here \(\widetilde{A}= (r_{1} +\gamma +\beta +\sigma + v +\mu _{1}+\mu _{2})\) and \(\widetilde{B}=(\mu _{1}+h+q+g_{1} + g_{2})\).

By solving the system (4), we obtain two possible equilibria. The first one is \(X_{0}=(S_{0},0,0,0,0,0,0,0)\), which represents the disease-free equilibrium (DFE) with \(S_{0}=\frac{\Lambda }{\mu _{1}}\), and the second one is \(X^{\ast }= ( S^{\ast }, L_{e}^{\ast }, L_{f}^{\ast }, I^{\ast }, R_{1}^{\ast },R_{2}^{\ast }, T^{\ast }, K^{\ast })\), which represents the endemic equilibrium (EE). For that, we extract \(S^{\ast }\), \(L_{e}^{\ast }\), \(L_{f}^{\ast }\), \(R_{1}^{\ast }\), \(R_{2}^{\ast }\), \(T^{\ast }\) and \(K^{\ast }\) from the system (4) in function of \(I^{\ast }\) as follows:

By extracting \(S^{\ast }\), \(L_{f}^{\ast }\), \(T^{\ast }\) and \(K^{\ast }\) from the system (4) we obtain

$$\begin{aligned}& S^{\ast }= \frac{\Lambda }{\alpha \lambda I^{\ast }+ \mu _{1}} , \end{aligned}$$
(5)
$$\begin{aligned}& L_{f}^{\ast }= \frac{h L_{e}^{\ast }}{\mathcal{B}} , \end{aligned}$$
(6)
$$\begin{aligned}& T^{\ast }= \frac{\beta I^{\ast }}{\mathcal{D}} , \end{aligned}$$
(7)
$$\begin{aligned}& K^{\ast }= \frac{v I^{\ast }}{\mathcal{E}} . \end{aligned}$$
(8)

The substitution of Eqs. (5) and (6) in the second equation of the system (4) yields

$$\begin{aligned}& \alpha \lambda p \biggl( \frac{\Lambda }{\alpha \lambda I^{\ast }+ \mu _{1}} \biggr)I^{\ast }+ \alpha \lambda r I^{\ast }\bigl(R_{1}^{\ast }+ R_{2}^{\ast }\bigr) + r_{1} I^{\ast }+ r_{2} \biggl(\frac{\beta I^{\ast }}{\mathcal{D}} \biggr) + r_{3} \biggl( \frac{v I^{\ast }}{\mathcal{E}} \biggr) - \mathcal{A} L_{e}^{\ast }= 0 , \end{aligned}$$
(9)
$$\begin{aligned}& L_{e}^{\ast }= \frac{1}{\mathcal{A}} I^{\ast } \biggl[\biggl( \frac{\Lambda \alpha p \lambda }{\alpha \lambda I^{\ast }+ \mu _{1}} \biggr)+ \alpha \lambda r\bigl(R_{1}^{\ast }+ R_{2}^{\ast }\bigr) + r_{1} + r_{2} \frac{\beta }{\mathcal{D}} + r_{3} \frac{v}{\mathcal{E}} \biggr]. \end{aligned}$$
(10)

By inserting (6) and (5) in the fourth equation of (4) we have

$$\begin{aligned}& w \biggl(\frac{h L_{e}^{\ast }}{\mathcal{B}} \biggr) + q L_{e}^{\ast }- \widetilde{A} I^{\ast }+ \alpha \lambda R_{1}^{\ast }I^{\ast }+ \alpha \lambda R_{2}^{\ast }I^{\ast }+ \alpha \lambda (1 - p) \biggl( \frac{\Lambda }{\alpha \lambda I^{\ast }+ \mu } \biggr) I^{\ast }= 0 , \end{aligned}$$
(11)
$$\begin{aligned}& L_{e}^{\ast }= \biggl( \frac{\mathcal{B}}{w h + q \mathcal{B}} \biggr) \biggl[ \widetilde{A} - \alpha \lambda R_{1}^{\ast }- \alpha \lambda R_{2}^{\ast }- \alpha \lambda (1 - p) \biggl( \frac{\Lambda }{\alpha \lambda I^{\ast }+ \mu }\biggr) \biggr]I^{\ast }. \end{aligned}$$
(12)

We equate (10) and (12) and we obtain

$$\begin{aligned}& \begin{aligned} & \frac{1}{\mathcal{A}} I^{\ast } \biggl[ \biggl( \frac{\Lambda \alpha p \lambda }{\alpha \lambda I^{\ast }+ \mu _{1}} \biggr)+ \alpha \lambda r\bigl(R_{1}^{\ast }+ R_{2}^{\ast }\bigr) + r_{1} + r_{2} \frac{\beta }{\mathcal{D}} + r_{3} \frac{v}{\mathcal{E}} \biggr] \\ &\quad = \frac{\mathcal{B}}{w h + q \mathcal{B} } \biggl[\widetilde{A} - \alpha \lambda R_{1}^{\ast }- \alpha \lambda R_{2}^{\ast }- \alpha \lambda (1 - p) \biggl(\frac{\Lambda }{\alpha \lambda I^{\ast }+ \mu }\biggr) \biggr]I^{\ast }, \end{aligned} \end{aligned}$$
(13)
$$\begin{aligned}& \begin{aligned} \frac{\alpha \lambda r}{\mathcal{A}} \bigl(R_{1}^{\ast }+ R_{2}^{\ast }\bigr) + \frac{\mathcal{B} \alpha \lambda R_{1}^{\ast }}{w h + q \mathcal{B}} + \frac{\mathcal{B} \alpha \lambda R_{2}^{\ast }}{w h + q \mathcal{B}} = {}& \frac{-1}{\mathcal{A}} \biggl[ \biggl( \frac{\Lambda \alpha p \lambda }{\alpha \lambda I^{\ast }+ \mu _{1}} \biggr) + r_{1} + r_{2} \frac{\beta }{\mathcal{D}} + r_{3} \frac{v}{\mathcal{E}} \biggr] \\ &{} + \frac{\mathcal{B}}{w h + q \mathcal{B}} \biggl[\widetilde{A} - \frac{\alpha \lambda \Lambda (1 - p)}{\alpha \lambda I^{\ast }+ \mu _{1}} \biggr], \end{aligned} \end{aligned}$$
(14)
$$\begin{aligned}& \begin{aligned} R_{1}^{\ast } \biggl( \frac{\alpha \lambda r}{\mathcal{A}} + \frac{\alpha \lambda \mathcal{B}}{w h + q \mathcal{B}} \biggr) ={} & \frac{-1}{\mathcal{A}} \biggl[ \biggl( \frac{\Lambda \alpha p \lambda }{\alpha \lambda I^{\ast }+ \mu _{1}} \biggr) + r_{1} + r_{2} \frac{\beta }{\mathcal{D}} + r_{3} \frac{v}{\mathcal{E}} \biggr] \\ &{} + \frac{\mathcal{B}}{w h + q \mathcal{B}} \biggl[\widetilde{A} - \frac{\alpha \lambda \Lambda (1 - p)}{\alpha \lambda I^{\ast }+ \mu _{1}} \biggr] \\ &{} - \alpha \lambda R_{2}^{\ast } \biggl( \frac{r}{\mathcal{A}} + \frac{\mathcal{B}}{w h + q \mathcal{B}} \biggr), \end{aligned} \end{aligned}$$
(15)
$$\begin{aligned}& \begin{aligned} R_{1}^{\ast }={} & \frac{\mathcal{A} (w h + q \mathcal{B})}{\alpha \lambda \mathcal{A} \mathcal{B} + \alpha \lambda r (w h + q \mathcal{B})} \\ & {}\times\biggl[ \frac{-1}{\mathcal{A}} \biggl[ \biggl( \frac{\Lambda \alpha p \lambda }{\alpha \lambda I^{\ast }+ \mu _{1}} \biggr) + r_{1} + r_{2} \frac{\beta }{\mathcal{D}} + r_{3} \frac{v}{\mathcal{E}} \biggr] + \frac{\mathcal{B}}{w h + q \mathcal{B}} \biggl[\widetilde{A} - \frac{\alpha \lambda \Lambda (1 - p)}{\alpha \lambda I^{\ast }+ \mu _{1}} \biggr] \biggr] \\ &{} - \alpha \lambda R_{2}^{\ast } \biggl( \frac{r}{\mathcal{A}} + \frac{\mathcal{B}}{w h + q \mathcal{B}} \biggr). \end{aligned} \end{aligned}$$
(16)

By inserting (6) in the fifth equation of (4) we have

$$\begin{aligned}& g_{1} L_{e}^{\ast }+ \frac{k_{1} h L_{e}^{\ast }}{\mathcal{B}} + \gamma I^{\ast }- \alpha \lambda R_{1}^{\ast }I^{\ast }(r + 1) - \mu _{1} R_{1}^{\ast }= 0, \end{aligned}$$
(17)
$$\begin{aligned}& L_{e}^{\ast }= \frac{\mathcal{B} (\alpha \lambda R_{1}^{\ast }I^{\ast }(r + 1) - \gamma I^{\ast }+ \mu _{1} R_{1}^{\ast } )}{g_{1} \mathcal{B} + k_{1} h}. \end{aligned}$$
(18)

By inserting (6) into the sixth equation of (4) we have

$$\begin{aligned}& \sigma I^{\ast }+ \frac{k_{2} h L_{e}^{\ast }}{\mathcal{B}} + g_{2} L_{e}^{\ast }- \alpha \lambda R_{2}^{\ast }I^{\ast }(r + 1) - \mu _{1} R_{2}^{\ast }= 0 , \end{aligned}$$
(19)
$$\begin{aligned}& L_{e}^{\ast } \biggl( \frac{k_{2} h}{\mathcal{B}} + g_{2} \biggr) = \alpha \lambda R_{2}^{\ast }I^{\ast }(r + 1) + \mu _{2} R_{2}^{\ast }- \sigma I^{\ast}, \end{aligned}$$
(20)
$$\begin{aligned}& L_{e}^{\ast }= \frac{\mathcal{B} (\alpha \lambda R_{2}^{\ast }I^{\ast }(r + 1) + \mu _{2} R_{2}^{\ast }- \sigma I^{\ast } )}{k_{2} h + \mathcal{B} g_{2}}. \end{aligned}$$
(21)

Equating (18) and (21) we obtain

$$\begin{aligned}& \biggl(\frac{\mathcal{B}}{g_{1} \mathcal{B} + k_{1} h} \biggr) \bigl[ \alpha \lambda R_{1}^{\ast }I^{\ast }(r + 1) - \gamma I^{\ast }+ \mu _{1} R_{1}^{\ast } \bigr] = \frac{\mathcal{B} (\alpha \lambda R_{2}^{\ast }I^{\ast }(r + 1) + \mu _{2} R_{2}^{\ast }- \sigma I^{\ast } )}{k_{2} h + \mathcal{B} g_{2}} , \end{aligned}$$
(22)
$$\begin{aligned}& R_{1}^{\ast }= \frac{(g_{1} \mathcal{B} + h k_{1}) (\alpha \lambda R_{2}^{\ast }I^{\ast }(r + 1) + \mu _{2} R_{2}^{\ast }- \sigma I^{\ast }) + \gamma I^{\ast }}{(k_{2} h + \mathcal{B} g_{2})(\alpha \lambda I^{\ast }(r + 1) + \mu _{1} )}. \end{aligned}$$
(23)

Equating (16) and (23) we obtain

$$ \begin{aligned} &\frac{\mathcal{A} (w h + q \mathcal{B})}{\alpha \lambda \mathcal{A} \mathcal{B} + \alpha \lambda r (w h + q \mathcal{B})} \\ &\qquad{}\times \biggl[ \frac{-1}{\mathcal{A}} \biggl[ \biggl( \frac{\Lambda \alpha p \lambda }{\alpha \lambda I^{\ast }+ \mu _{1}} \biggr) + \widetilde{Z_{1}} \biggr] + \frac{\mathcal{B}}{w h + q \mathcal{B}} \biggl[\widetilde{A} - \frac{\alpha \lambda \Lambda (1 - p)}{\alpha \lambda I^{\ast }+ \mu _{1}} \biggr] \biggr] \\ &\qquad {} - \alpha \lambda R_{2}^{\ast } \biggl( \frac{r}{\mathcal{A}} + \frac{\mathcal{B}}{w h + q \mathcal{B}} \biggr) \\ &\quad = \frac{(g_{1} \mathcal{B} + h k_{1}) (\alpha \lambda R_{2}^{\ast }I^{\ast }(r + 1) + \mu _{2} R_{2}^{\ast }- \sigma I^{\ast }) + \gamma I^{\ast }}{(k_{2} h + \mathcal{B} g_{2})(\alpha \lambda I^{\ast }(r + 1) + \mu _{1} )}. \end{aligned} $$
(24)

Here \(\widetilde{Z_{1}}= r_{1} + r_{2} \frac{\beta }{\mathcal{D}} + r_{3} \frac{v}{\mathcal{E}}\).

From (24) we can extract \(R_{2}^{\ast }\) and then we obtain

$$\begin{aligned}& \begin{aligned} &\frac{\mathcal{A} (w h + q \mathcal{B})}{\alpha \lambda \mathcal{A} \mathcal{B} + \alpha \lambda r (w h + q \mathcal{B})} \\ &\qquad {}\times \biggl[ \frac{-1}{\mathcal{A}} \biggl[ \biggl( \frac{\Lambda \alpha p \lambda }{\alpha \lambda I^{\ast }+ \mu _{1}} \biggr) + \widetilde{Z_{1}} \biggr] + \frac{\mathcal{B}}{w h + q \mathcal{B}} \biggl[\widetilde{A} - \frac{\alpha \lambda \Lambda (1 - p)}{\alpha \lambda I^{\ast }+ \mu _{1}} \biggr] \biggr] \\ &\qquad {} - \frac{I^{\ast }(g_{1} \mathcal{B} \sigma + hk_{1} \sigma + \gamma )}{I^{\ast }\widetilde{Z_{3}} + k_{2} h u_{1} + \mathcal{B} g_{2} u_{1}} \\ &\quad = R_{2}^{\ast } \biggl( \frac{I^{\ast }\widetilde{Z_{2}} + g_{1} \mathcal{B} u_{2} + hk_{1}u_{2}}{I^{\ast }\widetilde{Z_{3}} + k_{2} h u_{1} + \mathcal{B} g_{2} u_{1}} \biggr) + \alpha \lambda R_{2}^{\ast } \biggl(\frac{r}{\mathcal{A}} + \frac{\mathcal{B}}{w h + q \mathcal{B}} \biggr), \end{aligned} \end{aligned}$$
(25)
$$\begin{aligned}& \begin{aligned} &\frac{\mathcal{A} (w h + q \mathcal{B})}{\alpha \lambda \mathcal{A} \mathcal{B} + \alpha \lambda r (w h + q \mathcal{B})} \\ &\qquad {}\times \biggl[ \frac{-1}{\mathcal{A}}\biggl[ \biggl( \frac{\Lambda \alpha p \lambda }{\alpha \lambda I^{\ast }+ \mu _{1}} \biggr) + \widetilde{Z} \biggr] + \frac{\mathcal{B}}{w h + q \mathcal{B}} \biggl[\widetilde{A} - \frac{\alpha \lambda \Lambda (1 - p)}{\alpha \lambda I^{\ast }+ \mu _{1}} \biggr] \biggr] \\ &\qquad {} - \frac{I^{\ast }(g_{1} \mathcal{B} \sigma + hk_{1} \sigma + \gamma )}{I^{\ast } \widetilde{Z_{3}} + k_{2} h u_{1} + \mathcal{B} g_{2} u_{1}} \\ &\quad = R_{2}^{\ast } \biggl( \frac{I^{\ast }\widetilde{Z_{2}} + g_{1} \mathcal{B} u_{2} + hk_{1}u_{2}}{I^{\ast } \widetilde{Z_{3}} + k_{2} h u_{1} + \mathcal{B} g_{2} u_{1}} \biggr) + R_{2}^{\ast } \biggl( \frac{r \alpha \lambda }{\mathcal{A}} + \frac{\alpha \lambda \mathcal{B}}{w h + q \mathcal{B}} \biggr). \end{aligned} \end{aligned}$$
(26)

Here \(\widetilde{Z_{2}} = (g_{1} \mathcal{B} \alpha \lambda + g_{1} \mathcal{B} \alpha \lambda + hk_{1} \alpha \lambda r + hk_{1} \alpha \lambda )\) and \(\widetilde{Z_{3}}= (k_{2} h \alpha \lambda r + k_{2} h \alpha \lambda + \mathcal{B} g_{2} \alpha \lambda r + \mathcal{B} g_{2} \alpha \lambda )\).

Addressing \(R_{2}^{\ast }\) we obtain

$$ \begin{aligned} &\frac{\mathcal{A} (w h + q \mathcal{B})}{\alpha \lambda \mathcal{A} \mathcal{B} + \alpha \lambda r (w h + q \mathcal{B})} \\ &\qquad {}\times \biggl[ \frac{-1}{\mathcal{A}}\biggl[ \biggl( \frac{\Lambda \alpha p \lambda }{\alpha \lambda I^{\ast }+ \mu _{1}} \biggr) + \widetilde{Z_{1}} \biggr] + \frac{\mathcal{B}}{w h + q \mathcal{B}} \biggl[\widetilde{A} - \frac{\alpha \lambda \Lambda (1 - p)}{\alpha \lambda I^{\ast }+ \mu _{1}} \biggr] \biggr] \\ &\qquad {} - \frac{I^{\ast }(g_{1} \mathcal{B} \sigma + hk_{1} \sigma + \gamma )}{I^{\ast } \widetilde{Z_{3}} + k_{2} h u_{1} + \mathcal{B} g_{2} u_{1}} \\ &\quad = R_{2}^{\ast } \biggl( \frac{I^{\ast }\widetilde{Z_{2}} + g_{1} \mathcal{B} u_{2} + hk_{1}u_{2}}{I^{\ast }\widetilde{Z_{3}} + k_{2} h u_{1} + \mathcal{B} g_{2} u_{1}} + \frac{r \alpha \lambda }{\mathcal{A}} + \frac{\alpha \lambda \mathcal{B}}{w h + q \mathcal{B}} \biggr). \end{aligned} $$
(27)

Then \(R_{2}^{\ast }\) is given by

$$ R_{2}^{\ast }= \frac{\widetilde{Z_{4}} [ \frac{-1}{\mathcal{A}} [ (\frac{\Lambda \alpha p \lambda }{\alpha \lambda I^{\ast }+ \mu _{1}} ) + \widetilde{Z_{1}} ] + \frac{\mathcal{B}}{w h + q \mathcal{B}} [\widetilde{A} - \frac{\alpha \lambda \Lambda (1 - p)}{\alpha \lambda I^{\ast }+ \mu _{1}} ] ] - \frac{I^{\ast }(g_{1} \mathcal{B} \sigma + hk_{1} \sigma + \gamma )}{I^{\ast }\widetilde{Z_{3}} + k_{2} h u_{1} + \mathcal{B} g_{2} u_{1}}}{ (\frac{I^{\ast }\widetilde{Z_{2}} + g_{1} \mathcal{B} u_{2} + hk_{1}u_{2}}{I^{\ast }\widetilde{Z_{3}} + k_{2} h u_{1} + \mathcal{B} g_{2} u_{1}} + \frac{r \alpha \lambda }{\mathcal{A}} + \frac{\alpha \lambda \mathcal{B}}{w h + q \mathcal{B}} )}. $$
(28)

Here \(\widetilde{Z_{4}}= \frac{\mathcal{A} (w h + q \mathcal{B})}{\alpha \lambda \mathcal{A} \mathcal{B} + \alpha \lambda r (w h + q \mathcal{B})}\).

In (23) we insert (28) and we obtain

$$ R_{1}^{\ast }= \frac{(g_{1} \mathcal{B} + h k_{1}) (\alpha \lambda \widetilde{Z_{5}} I^{\ast }(r + 1) + \mu _{2} \widetilde{Z_{5}} - \sigma I^{\ast }) + \gamma I^{\ast }}{(k_{2} h + \mathcal{B} g_{2})(\alpha \lambda I^{\ast }(r + 1) + \mu _{1} )} .$$
(29)

Here

$$ \widetilde{Z_{5}} = \frac{\widetilde{Z_{4}} [ \frac{-1}{\mathcal{A}} [ (\frac{\Lambda \alpha p \lambda }{\alpha \lambda I^{\ast }+ \mu _{1}} ) + \widetilde{Z_{1}} ] + \frac{\mathcal{B}}{w h + q \mathcal{B}} [\widetilde{A} - \frac{\alpha \lambda \Lambda (1 - p)}{\alpha \lambda I^{\ast }+ \mu _{1}} ] ] - \frac{I^{\ast }(g_{1} \mathcal{B} \sigma + hk_{1} \sigma + \gamma )}{I^{\ast }\widetilde{Z_{3}} + k_{2} h u_{1} + \mathcal{B} g_{2} u_{1}}}{ (\frac{I^{\ast }\widetilde{Z_{2}} + g_{1} \mathcal{B} u_{2} + hk_{1}u_{2}}{I^{\ast }\widetilde{Z_{3}} + k_{2} h u_{1} + \mathcal{B} g_{2} u_{1}} + \frac{r \alpha \lambda }{\mathcal{A}} + \frac{\alpha \lambda \mathcal{B}}{w h + q \mathcal{B}} )}. $$
(30)

By inserting (29) in (18) we obtain

$$ L_{e}^{\ast }= \frac{\mathcal{B} (\alpha \lambda \widetilde{Z_{6}} I^{\ast }(r + 1) - \gamma I^{\ast }+ \mu _{1} \widetilde{Z_{6}} )}{g_{1} \mathcal{B} + k_{1} h} . $$
(31)

Here

$$ \widetilde{Z_{6}} = \frac{(g_{1} \mathcal{B} + h k_{1}) (\alpha \lambda \widetilde{Z_{5}} I^{\ast }(r + 1) + \mu _{2} \widetilde{Z_{5}} - \sigma I^{\ast }) + \gamma I^{\ast }}{(k_{2} h + \mathcal{B} g_{2})(\alpha \lambda I^{\ast }(r + 1) + \mu _{1} )} . $$
(32)

By inserting (31) in (6) we obtain

$$ L_{f}^{\ast }= \frac{h (\alpha \lambda \widetilde{Z_{6}} I^{\ast }(r + 1) - \gamma I^{\ast }+ \mu _{1} \widetilde{Z_{6}} )}{g_{1} \mathcal{B} + k_{1} h} .$$
(33)

We obtain the expressions of \(S^{\ast }\), \(L_{e}^{\ast }\), \(L_{f}^{\ast }\), \(R_{1}^{\ast }\), \(R_{2}^{\ast }\), \(T^{\ast }\) and \(K^{\ast }\) as a function of \(I^{\ast }\). Actually, the expression of \(I^{\ast }\) can be extracted from obtained expressions. Hence, disease-free equilibrium (DFE) and the endemic equilibrium (EE) are found.

3.4 Basic reproduction number

The DFE of the system (1) is \(X_{0}=(S_{0},0,0,0,0,0,0,0)\), with \(S_{0}=\frac{\Lambda }{\mu _{1}}\). The Jacobian matrix of the system (1) at \(X_{0}\) is

$$ J= \begin{pmatrix} -\mu _{1} & 0 & 0 & -\frac{\alpha \lambda \Lambda }{\mu _{1}} & 0 & 0 & 0 & 0 \\ 0 & -\mathcal{Y} & 0 & \frac{\alpha \lambda p \Lambda }{\mu _{1}} & 0 & 0 & r_{2} & r_{3} \\ 0 & h & - \mathcal{Z} & 0 & 0 & 0 & 0 & 0 \\ 0 & q & w & -\mathcal{A} & 0 & 0 & 0 & 0 \\ 0 & g_{1} & k_{1} & \gamma & -\mu _{1} & 0 & 0 & 0 \\ 0 & g_{2} & k_{2} & \sigma & 0 & -\mu _{1} & 0 & 0 \\ 0 & 0 & 0 & \beta & 0 & 0 & -\mathcal{B} & 0 \\ 0 & 0 & 0 & v & 0 & 0 & 0 & -\mathcal{C} \end{pmatrix} . $$

Here \(\mathcal{Y}=(\mu _{1} + h + g_{1} + g_{2} + q ) \), \(\mathcal{Z}=(\mu _{1} + w + k_{1} + k_{2}) \), \(\mathcal{A}=((r_{1}+ \beta + v + \mu _{1}+ \mu _{2}+ \sigma + \gamma ) - (\alpha \lambda (1-p) \frac{\Lambda }{\mu _{1}}))\), \(\mathcal{B}=(\mu _{1} + \mu _{2} + r_{2})\) and \(\mathcal{C}= (\mu _{1} + \mu _{2} + r_{3}) \).

Considering just the infected compartments as noted in [27], the resulting Jacobian matrix is given by

$$ J= \begin{pmatrix} -\mathcal{Y} & 0 & \frac{\alpha \lambda p \Lambda }{\mu _{1}} & r_{2} & r_{3} \\ h & - \mathcal{Z} & 0 & 0 & 0 \\ q & w & -\mathcal{A} & 0 & 0 \\ 0 & 0 & \beta & -\mathcal{B} & 0 \\ 0 & 0 & v & 0 & -\mathcal{C} \end{pmatrix} . $$
(34)

Writing \(J=F-V\) where F contains the new infections in the compartment of infectious individuals. In order to determine F and V we write the system (1) as follows:

$$ \textstyle\begin{cases} \dot{L_{e}} = \alpha \lambda p S I+ \alpha \lambda r I(R_{1}+R_{2})+r_{1}I+r_{2}T+r_{3}K- \widetilde{B}L_{e} , \\ \dot{L_{f}} = hL_{e}-(\mu _{1}+w+k_{1}+k_{2})L_{f} , \\ \dot{I} = w L_{f}+qL_{e}- \widetilde{A}I+\alpha \lambda R_{1} I+ \alpha \lambda R_{2} I+\alpha \lambda (1-p)SI , \\ \dot{T} = \beta I-(\mu _{1}+\mu _{2}+r_{2})T , \\ \dot{K} = v I-(\mu _{1}+\mu _{2}+r_{3})K , \\ \dot{S} = \Lambda -\alpha \lambda p SI-\alpha \lambda (1-p)SI-\mu _{1} S , \\ \dot{R_{1}} = g_{1}L_{e}+k_{1}L_{f}+\gamma I-\alpha \lambda r R_{1} I- \mu _{1} R_{1}-\alpha \lambda R_{1} I , \\ \dot{R_{2}} = \sigma I+k_{2}L_{f}+g_{2}L_{e}- \alpha \lambda r R_{2} I- \mu _{1} R_{2}-\alpha \lambda R_{2} I , \\ N = S+L_{e}+L_{f}+I+R_{1}+R_{2}+T+K. \end{cases} $$
(35)

Here \(\widetilde{A}=(r_{1}+\gamma +\beta +\sigma +v+\mu _{1}+\mu _{2})\) and \(\widetilde{B}=(\mu _{1}+h+q+g_{1} + g_{2})\).

We note \(\mathcal{F}_{i}(x)\) the rates of new individuals in the compartment i, \(\mathcal{V}^{+}_{i}(x)\) represents the rates that individuals come in the compartment i for any others reasons; \(\mathcal{V}^{-}_{i}(x)\), represents the rates that individual go out from the compartment i.

We set \(\mathcal{V}_{i}(x)=\mathcal{V}^{-}_{i}(x)+\mathcal{V}^{+}_{i}(x)\). Considering the system (35) we obtain the values of \(\mathcal{F}\), \(\mathcal{V}^{+}(x)\) and \(\mathcal{V}^{-}(x)\) as follows.

\(\mathcal{F}\) is given by

$$ \mathcal{F}= \begin{pmatrix} \alpha \lambda p S I+ \alpha \lambda r I(R_{1}+R_{2}) \\ 0 \\ \alpha \lambda R_{1} I+\alpha \lambda R_{2} I+\alpha \lambda (1-p)SI \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{pmatrix} . $$

\(\mathcal{V}^{+}(x)\) is given by

$$ \mathcal{V}^{+}(x)= \begin{pmatrix} r_{1}I+r_{2}T+r_{3}K \\ hL_{e} \\ w L_{f}+qL_{e} \\ \beta I \\ v I \\ \Lambda \\ g_{1}L_{e}+k_{1}L_{f}+\gamma I \\ \sigma I+k_{2}L_{f}+g_{2}L_{e} \end{pmatrix} , $$

and \(\mathcal{V}^{-}(x)\) is given by

$$ \mathcal{V}^{-}(x)= \begin{pmatrix} (\mu _{1}+h+q+g_{1}+g_{2})L_{e} \\ (\mu _{1}+w+k_{1}+k_{2})L_{f} \\ (r_{1}+\gamma +\beta +\sigma +v+\mu _{1}+\mu _{2})I \\ (\mu _{1}+\mu _{2}+r_{2})T \\ (\mu _{1}+\mu _{2}+r_{3})K \\ \alpha \lambda p SI+\alpha \lambda (1-p)SI+\mu _{1} S \\ \alpha \lambda r R_{1} I+\mu _{1} R_{1}+\alpha \lambda R_{1} I \\ \alpha \lambda r R_{2} I+\mu _{1} R_{2}+\alpha \lambda R_{2} I \end{pmatrix} . $$

Considering that \(\mathcal{V}(x)=\mathcal{V}^{-}(x)-\mathcal{V}^{+}(x)\) we obtain

$$ \mathcal{V}= \begin{pmatrix} (\mu _{1}+h+q+g_{1}+g_{2})L_{e}- r_{1}I-r_{2}T-r_{3}K \\ (\mu _{1}+w+k_{1}+k_{2})L_{f}-hL_{e} \\ \alpha \lambda R_{1} I+\alpha \lambda R_{2} I+\alpha \lambda (1-p)SI \\ (r_{1}+\gamma +\beta +\sigma +v+\mu _{1}+\mu _{2})I- w L_{f}-qL_{e} \\ (\mu _{1}+\mu _{2}+r_{2})T-\beta I \\ (\mu _{1}+\mu _{2}+r_{3})K-v I \\ \alpha \lambda p SI+\alpha \lambda (1-p)SI+\mu _{1} S-\Lambda \\ \alpha \lambda r R_{1} I+\mu _{1} R_{1}+\alpha \lambda R_{1} I -g_{1}L_{e}-k_{1}L_{f}- \gamma I \\ \alpha \lambda r R_{2} I+\mu _{1} R_{2}+\alpha \lambda R_{2} I- \sigma I-k_{2}L_{f}-g_{2}L_{e} \end{pmatrix} . $$

Considering only the compartment which contains infected individuals (\(L_{e}\), \(L_{f}\), I, T, K) and calculation of the first partial derivative on the DFE at \(X_{0}=(0,0,0,0,0,S_{0},0,0)\) with \(S_{0}=\frac{\Lambda }{\mu _{1}}\) we obtain

$$ F= \begin{pmatrix} 0 & 0 & \mathcal{Q} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & \mathcal{G} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{pmatrix}. $$

Here \(\mathcal{Q}=\frac{\alpha \lambda p \Lambda }{\mu _{1}}\) and \(\mathcal{G}=\frac{\alpha \lambda (1-p) \Lambda }{\mu _{1}}\).

For \(\mathcal{V}(x)\) we obtain the following result:

$$ V= \begin{pmatrix} \mathcal{A} & 0 & -r_{1} & -r_{2} & -r_{3} \\ -h & \mathcal{B} & 0 & 0 & 0 \\ -q & -w & \mathcal{C} & 0 & 0 \\ 0 & 0 & -\beta & \mathcal{D} & 0 \\ 0 & 0 & -v & 0 & \mathcal{E} \end{pmatrix} . $$

Here \(\mathcal{A}=\mu _{1}+h+q+g_{1}+g_{2}\), \(\mathcal{B}=\mu _{1}+w+k_{1}+k_{2}\), \(\mathcal{C}= r_{1}+\gamma +\beta +\sigma +v+\mu _{1}+\mu _{2}\), \(\mathcal{D}= \mu _{1}+\mu _{2}+r_{2} \) and \(\mathcal{E}=\mu _{1}+\mu _{2}+r_{3}\).

By definition, the basic reproduction number \(\mathcal{R}_{0}\) is the spectral radius of the next generation matrix, as follows: \(\mathcal{R}_{0} = \rho (FV^{-}{}^{1})\).

The eigenvalues of the matrix \(\rho (FV^{-}{}^{1})\) is given by

$$ \biggl[- \frac{\mathcal{A} \mathcal{B} \mathcal{D} \mathcal{E} \mathcal{G} + \mathcal{B} \mathcal{D} \mathcal{E} \mathcal{Q} q + \mathcal{D} \mathcal{E} \mathcal{Q} h w }{\widetilde{Y}}, 0, 0, 0, 0 \biggr].$$
(36)

The value of \(\mathcal{R}_{0}\) is the maximum eigenvalue:

$$ \begin{aligned} \mathcal{R}_{0}&= \biggl\vert - \frac{\mathcal{A} \mathcal{B} \mathcal{D} \mathcal{E} \mathcal{G} + \mathcal{B} \mathcal{D} \mathcal{E} \mathcal{Q} q + \mathcal{D} \mathcal{E} \mathcal{Q} h w }{{\widetilde{Y}}} \biggr\vert \\ &= \frac{\mathcal{A} \mathcal{B} \mathcal{D} \mathcal{E} \mathcal{G} + \mathcal{B} \mathcal{D} \mathcal{E} \mathcal{Q} q + \mathcal{D} \mathcal{E} \mathcal{Q} h w }{\widetilde{Y}}. \end{aligned} $$
(37)

Here

$$ \begin{aligned} \widetilde{Y} = {}& \mathcal{A} \mathcal{B} \mathcal{C} \mathcal{D} \mathcal{E} - \mathcal{B} \mathcal{D} \mathcal{E} q r_{1} - \mathcal{B} \mathcal{E} \beta q r_{2} - \mathcal{B} \mathcal{D} q r_{3} v \\ &{} - \mathcal{D} \mathcal{E} w h r_{1} - \mathcal{E} \beta w h r_{2} - \mathcal{D} w h r_{3} v. \end{aligned} $$

3.5 Stability of equilibrium points

By Theorem 2 in [27], if \(\mathcal{R}_{0} < 1\), then the DFE given by \(X_{0}\) is locally asymptotically stable, but if \(\mathcal{R}_{0} > 1\), it is unstable. This leads to the following theorem.

Theorem 3.2

If \(R_{0} < 1\) the disease-free equilibrium \(X_{0}\) of the system (1) is locally asymptotically stable. If \(R_{0} > 1\), then \(X_{0}\) is unstable.

The proof of Theorem 3.2 follows the same steps as Theorem 2 in [27].

We note that the global stability of DFE and EE were observed from simulations and that the mathematical proof was not realized here.

4 Numerical simulations

In this section, numerical simulations of the proposed TB model are presented. The total population is set at 1000 susceptible individuals. The performed simulations aim to show the stability of the DFE and EE of the system (1). The impact of some parameters and groups/compartments of individuals on the dynamics of the TB infection is also presented through numerical simulations.

4.1 Parameters used in the model

Table 1 presents the parameters used for simulations. Most of them was taken from the literature and other was fitted based on data at our disposal. The meanings of all parameters are also presented in the Table 1.

Table 1 Parameter values and their meanings
Full size table

4.2 The EE of the model, \(\mathcal{R}_{0} >1\)

In the first simulation we present the actual situation of TB in the DRC that is endemic. The stability of the endemic equilibrium (EE), \(X^{\ast }\), of the model system (1) is presented in Fig. 2. Here we simulated the model with \(\mathcal{R}_{0}>1\). The simulation is carried out over several years and attests to the persistence of TB disease in the population.

Figure 2
figure 2

Evolution of the model for several years and endemic equilibrium stability using parameters presented in Table 1 with \(\mathcal{R}_{0}>1\). Simulation of the model for \(\mathcal{R}_{0}=3.99347\) and \(S=1000\), respectively

Full size image

4.3 The DFE of the model, \(\mathcal{R}_{0} <1\)

In the second simulation we present the stability of the DFE, \(X_{0}\), of the system (1). Figure 3 shows the disease-free equilibrium of the full model. We reduce the rapid progression rate q from \(L_{e}\) (early latent) to I (infectious compartment) with the aim of reducing the incidence rate of TB in the population.

Figure 3
figure 3

Evolution of the model for several years and disease-free equilibrium stability of the model system (1) with \(\mathcal{R}_{0}=0.68873\) (\(\mathcal{R}_{0}<1\)). The values of I, \(L_{e}\) and \(L_{f}\) reach zero between the 50th and 60th year

Full size image

4.4 Impact of lost to follow-up and transferred individuals

The third simulation presents the impact of individuals lost to follow-up (K) and transferred (T) on the dynamics of the TB in the DRC population. Figures 4(a) and 4(b) show, respectively, the evolution of the number of infectious individuals over time for several different values of K and T. Figure 4(c) shows the result of simulation when T and K are considered simultaneously. Figure 4(d) presents results of simulation with several values of the rate of lost to follow-up.

Figure 4
figure 4

Evolution of the model with \(\mathcal{R}_{0}>1\). (a) and (b) present the evolution of the compartment \(I(t)\) for several values of K and T for \(v=0.030\) and \(\beta = 0.010\). With the same parameters (c) shows the evolution of the compartment \(I(t)\) when T and K are considered simultaneously. In (d) there are several values of v considered to see the evolution of I over time

Full size image

4.5 Impact of transmission and contact rates on the disease dynamics

The fourth simulation presents the impact of α and λ on the dynamics of the TB proposed model. By maintaining the value of the rate of transmission \(\lambda =0.100\) as in [30], the simulation will try several values of the rates of contact and we will see its impact on the proposed TB model. Figure 5 shows the results obtained.

Figure 5
figure 5

Evolution of the model by maintaining the transmission rate of TB \(\lambda =0.100\), we show the result of simulation when \(\alpha = 0.0010,0.0015,0.0020,0.0025,0.0030\) and 0.0035

Full size image

5 Discussion of results

5.1 General discussion

By considering parameters used (Table 1), the actual situation of TB in the Democratic Republic of the Congo is endemic. Results obtained show that there is at least an endemic equilibrium point because \(\mathcal{R}_{0}>1\). Figure 2 with \(\mathcal{R}_{0}=3.99347\) shows that the simulation was performed for several years in order to confirm the stability of the endemic equilibrium which implies that the TB will persist in the DRC population according to this condition.

To reach the DFE, the DRC health system is called to find mechanism that can help to reduce contamination. The simulation of our mathematical model shows that with certain value of parameters (\(\mathcal{R}_{0}<1\)), the DFE is globally stable. It means that the tuberculosis will die out in the DRC population. As shown in Fig. 3 we simulate the model for several years to be sure that there is stability of the DFE. To confirm the asymptotically stability of the DFE, we also simulate the model with different several values of infectious people I. We note that the values of I, \(L_{e}\) and \(L_{f}\) reach zero between the 50th and 60th year, while the model is simulated for several years (300 years). Based on the results obtained here, it is clear that if the Congolese public health authorities focus on setting up mechanisms that can help to reduce \(\mathcal{R}_{0}\) to a value below 1, pulmonary tuberculosis will be totally eradicated from the Congolese population in the future.

Results obtained show that lost to follow-up and transferred individuals constitute a risk, but less than the cases carrying germs. Rapidly evolving latent/exposures are responsible for the incidence increase in the short and medium term, while slower evolving exposures will be responsible for the persistent long-term incidence and maintenance of TB and delay elimination in the DRC population. Results obtained in Fig. 4 show that if some people are lost to follow-up and/or transferred (not followed), the number of these individuals who are untreated has an impact on the incidence of the disease but negligible compared to people with latent tuberculosis. Indeed, if the number of these individuals is high, the results show that the number of new cases of TB increases. By setting the rate of infectious individuals who are lost to follow-up equal to zero, \(v=0\), this means that these people are not followed by health care personnel and therefore remain infectious. The results obtained in Fig. 4(d) show that the number of new infected cases is increasing and spreading over several years. This situation means that the individuals lost to follow-up (3% in the DRC [2]) who remain untreated, infect susceptible individuals in the population and then the disease continue to spread in uncontrolled areas. Once the rate of lost to follow-up v is increased, the results show that the number of new cases of infected individuals decreases significantly. In this case, individuals who are lost to follow-up can become Le according to the rate of re-infection \(r_{3}\). It means that these individuals can be treated and cure according to the rate of recovered. It is consequently important that Congolese public health authorities set up patient monitoring teams in order to reduce the rate of lost to follow-up and transferred (no followed), because these individuals are a permanent danger and constitute the source of TB emergence in the DRC population.

The value of the contact rate has a significant impact on the dynamics of TB disease in the population. Figure 5 shows that, as the contact rate is high, there are more new cases each year and therefore the severity of infection increases while the recovery rate decreases. These results imply that if the contact rate of infectious people is significantly reduced, this will significantly reduce the incidence of TB in the population. To reduce contamination (parameters α and λ), it will be necessary to strengthen preventive measures, i.e. against contamination. This is where early detection of patient and treatment measures have their major role, because they reduce the number of potential unknown infected individuals. In addition to these measures, tuberculosis infection control measures include all measures to reduce contact between healthy and infectious people (ventilation of buildings, avoid confinement of patients and wearing masks for caregivers and visitors in the pavilions of tuberculosis patients).

5.2 Concluding remarks

We have presented in this paper the analysis and simulation of a compartmental mathematical model of the dynamics of tuberculosis in Democratic Republic of the Congo for a population that incorporates various factors like the lost to follow-up and transferred individuals. The results obtained demonstrate that control lost to follow-up and transferred individuals, monitoring contact, detection of latent individuals and their treatment are actions to be taken to reduce the incidence of the disease and thus effectively control it in the DRC population. This will enable the Congolese authorities in charge of public health to significantly reduce the value of \(\mathcal{R}_{0}\) and move towards a possible elimination of TB in the future. This is the first instance where such analysis is performed in the DRC popultion and therefore improves the preceding ones. It contributes to our knowledge of the spread of this disease, which remains one of the priorities of the DRC’s public health policy agenda. In order to maintain the validity of the proposed model, most of parameters used in this paper was taken from literature, some parameters was estimated based on TB data from DRC. The compartmental model proposed in this paper is well adapted to the reality of the DRC, in the sense that it takes into account groups of individuals who are not generally considered in existing compartmental models. This research provides to the DRC government another way of understanding TB dynamics in the population, which allows it to improve its unsuccessful TB control. It also gives it necessary materials for fruitful Sustainable Development Goals (SDG) of the United Nations which focus on the global tuberculosis epidemic elimination in 2035.

As part of the perspectives, we intend to integrate the consideration of antibiotic resistance into this model. Obtained model should provide solutions in the fight against multi-resistant TB, which nowadays presents one of the challenges in the fight against TB worldwide [34] and more particularly in the Democratic Republic of the Congo.