1 Introduction

The study of nonlinearity in physical phenomena is a well-established field of interest and its imperativeness is thought of through a sweer-amplitude wave oscillation investigated in various areas including plasma, chemical reactions, fluids, biological and solid states, to mention a few. In this manner, the enthralling perspective in nonlinear physical phenomena are solitons. The accessibility of solitonic ideas is due to the philosophical equalization of dispersion and nonlinearity [1]. A great deal of looks into solitons and related parts of solitary wave solutions, for instance mono-pulse water wave which delineates the main soliton, can be found in Miller and Ross [2], Podlubny [3], Oldham [4], Kiryakova [5], El-Sayed and Gaber [6]. Also, different scientific understanding and modeling can be deciphered through optical solitons for their numerical and analytical structures of various mechanisms. These stimulated numerous specialists and researchers to concentrate on the establishments of solitons with optical structures with the assistance of different integration schemes [7, 8].

Over the previous few years, different powerful strategies have been introduced for extracting the exact solutions of the NLDEs in scientific material science. For example, the symmetry method [9], tanh-coth function method [10], sine-cosine technique [11], new extended direct algebraic method [12, 13], extended trial equation method [14], and the exp-function method [15] are utilized to examine nonlinear dispersive and dissipative problems.

Besides, fractional calculus (FC) has started to be incredibly known in a few fields of science and engineering. It has been applied to breakdown numerous dynamical processes and complex nonlinear physical phenomena in physics, electromagnetic, engineering, anomalous diffusion, chemistry, visco-elasticity, and electro-chemistry. This subject has attained a valuable importance over the last decades due to its widespread application in the above mentioned fields. Recently, many efforts have been devoted to this subject, a few of them are reported in [16–18]. It does provide potent tools for computing solutions of differential equations. Also, it helps us to solve the problems arising in mathematical physics as well as their extensions in more than one variable. Many recent developments in analytical and numerical techniques for finding the solutions of fractional differential equations are suggested in [19–22].

The nonlinear fractional differential equations (NFDEs) assume an imperative job in numerous fields including control theory, biology, designing, signal processing, acoustic waves, hydro magnetic waves, fractal dynamics, and many more. The concept of fractional derivative with real order has been known throughout the previous few decades. The investigation of finding fractional derivative operators is always a hot topic of research. A lot of efforts have been devoted in recent times, and many discoveries have been made in this direction, some of them are listed in [23–27]. In this paper, we consider some of the masterpiece definitions for derivatives known as conformable [25], beta [26], and M-truncated [27].

The complex Ginzburg–Landau (CGL) equation of the form

$$ iu_{t} +au_{xx}+c\mathcal{F}\bigl( \vert u \vert ^{2}\bigr)u=\frac{1}{ \vert u \vert ^{2} u^{*}} \bigl\{ \delta \bigl( \vert u \vert ^{2}\bigr)_{xx} \vert u \vert ^{2} -N \bigl(\bigl( \vert u \vert ^{2}\bigr)_{x} \bigr)^{2} \bigr\} +Pu $$
(1)

is one of well-known nonlinear PDEs in physics. It represents a lot of various phenomena in physics like nonlinear waves, superfluidity, second-order phase transitions, superconductivity, Bose–Einstein condensation, strings and liquid crystals in field theory. The CGL equation was generalized into its fractional form by Weitzner and Zaslavsky [28]. The computation of optical solitons of Eq. (1) has been done by many researchers (see [29–31] and the references therein). The purpose of this article is not only to find out new families of optical solitons of fractional CGL equation but also to have a comparative analysis between different definitions of derivatives on the obtained soliton structures. According to the authors’ knowledge, such type of investigation has not been done before for the considered model and thus it is interesting to report here.

The format of the paper in hand is as follows: Section (2) is devoted to some basic definitions from the literature. In Section (3), the analysis of the governing model with different definitions is presented. The general algorithm of the algebraic extended expansion method and its application are given in Section (4). A detailed comparative analysis is practiced in Section (5). Conclusion is stated at the end.

2 Preliminaries

2.1 Conformable derivative and its properties

Here [32–35] is some important work on the conformable derivative in recent times.

Definition 2.1

Suppose that

$$ g:[0,\infty )\rightarrow R $$

is a function. Then conformable derivative of g of \(\alpha 's\) order is defined by [25]

$$ D^{\alpha }_{t} \bigl(g(t)\bigr)=\lim_{\varepsilon \rightarrow 0} \frac{g(t+\varepsilon t^{1-\alpha })-g(t)}{\varepsilon }, $$
(2)

in which \(t >0\) and \(\alpha \in (0,1]\).

Some properties for conformable derivative [25, 36] are reported as follows.

Theorem 2.1

Suppose that if \(0 < \alpha \leq 1 \) and assuming \(g(t)\) and \(h(t)\) are differentiable of \(\alpha 's\) order at \(t > 0\), then

  1. 1.

    \(D^{\alpha }_{t} (t^{\beta })=\beta t^{\beta -\alpha }\) for all \(\beta \in R\);

  2. 2.

    \(D^{\alpha }_{t} (c)=0\) for all constants;

  3. 3.

    \(D^{\alpha }_{t} (\mu g(t))=\mu D^{\alpha }_{t} (g(t))\), where μ is a constant;

  4. 4.

    \(D^{\alpha }_{t} (\mu g(t)+\nu h(t))=\mu D^{\alpha }_{t}(g(t))+\nu D^{\alpha }_{t}(h(t))\) for all \(\mu ,\nu \in R\);

  5. 5.

    \(D^{\alpha }_{t}(g(t)\times h(t))=h(t)\times D^{\alpha }_{t}(g(t))+g(t) \times D^{\alpha }_{t}(h(t))\);

  6. 6.

    \(D^{\alpha }_{t} (\frac{g(t)}{h(t)} )= \frac{h(t)D^{\alpha }_{t} (g(t))-g(t)D^{\alpha }_{t} (h(t))}{h^{2}(t)}\);

  7. 7.

    \(D^{\alpha }_{t} g(t)=t^{1-\alpha }\frac{dg}{dt}\);

  8. 8.

    \(D^{\alpha }_{t}(g(t)\circ h(t))=t^{1-\alpha }h^{\prime }(t)g^{\prime }(h(t))\).

2.2 Beta derivative

Definition 2.2

Beta derivative [26] is defined as follows:

$$ {}^{A}_{0}T^{\alpha }_{x}\bigl(G(x)\bigr)= \lim_{\varepsilon \rightarrow 0} \frac{G (x+ \varepsilon (x+\frac{1}{\Gamma (\alpha )}) )-G(x)}{\varepsilon }, $$
(3)

along with the properties as follows.

Theorem 2.2

If \(0 < \alpha \leq 1\), \(a, b \in R\), \(F, G\) and differentiable of α order at a point \(t > 0\), then:

  1. 1.

    \({}^{A}_{0}T^{\alpha }_{x}(aF(x)+bG(x))=a{}^{A}_{0} T^{\alpha }_{x}F(x)+b{}^{A}_{0} T^{\alpha }_{x}G(x)\);

  2. 2.

    \(T^{\alpha }_{x}(k)=0\), here k is a constant;

  3. 3.

    \({}^{A}_{0}T^{\alpha }_{x}(F(x)*G(x))=G(x){}^{A}_{0}T^{\alpha }_{x}F(x)+F(x){}^{A}_{0}T^{\alpha }_{x}G(x)\);

  4. 4.

    \({}^{A}_{0}T^{\alpha }_{x} (\frac{F(x)}{G(x)} )= \frac{G(x){}^{A}_{0}T^{\alpha }_{x}F(x)-F(x){}^{A}_{0} T^{\alpha }_{x}G(x)}{G^{2}(x)}\),taking \(\varepsilon = (x+\frac{1}{\Gamma (\alpha )} )^{1-\alpha }h,h \rightarrow 0\) when \(\varepsilon \rightarrow 0\), therefore, we have \({}^{A}_{0}T^{\alpha }_{x}F(x)= (x+\frac{1}{\Gamma (\alpha )} )^{1-\alpha }\frac{dF(x)}{dx}\) with \(\xi =\frac{\mu }{\alpha } (x+\frac{1}{\Gamma (\alpha )} )^{ \alpha }\), where μ is a constant;

  5. 5.

    \({}^{A}_{0}T^{\alpha }_{x} (\frac{F(t)}{G(x)} )=t \frac{dF(t)}{dt}\).

2.3 M-truncated derivative

Definition 2.3

The truncated Mittag-Leffler function [27] with one parameter is defined as follows:

$$ {}_{i}E_{\beta }(z)=\sum _{k=0}^{i}\frac{z^{k}}{\Gamma (\beta k+1)}, $$
(4)

in which \(\beta > 0\) and \(z \in C\). It is defined in the sense of non-fuzzy concept as given below.

Definition 2.4

Suppose that

$$ g : [0,\infty )\rightarrow R $$

and \(\alpha \in (0,1)\), the M-truncated derivative of g of order α is defined by

$$ {}_{i}T^{\alpha ,\beta }_{M}g(t)=\lim_{\varepsilon \rightarrow 0 } \frac{g(t+{}_{i}E_{\beta }(\varepsilon t^{-\alpha }))-g(t)}{\varepsilon } $$
(5)

for \(t>0\) and \({}_{i}E_{\beta }(\cdot)\), \(\beta > 0\).

Theorem 2.3

Suppose that f is a differentiable function of α order at \(t_{0} > 0\) with \(\alpha \in (0, 1]\) and \(\beta > 0\). Then f is continuous at \(t_{0}\).

Theorem 2.4

If \(\alpha \in (0,1]\), \(\beta > 0\), g, h are differentiable up to α order at \(t > 0\), then:

  1. 1.

    \({}_{i}T^{\alpha ,\beta }_{M}(pg+qh)=p{}_{i} T^{\alpha ,\beta }_{M}(g) +q{}_{i}T^{ \alpha ,\beta } _{M}(h)\), where \(p,q\) are real constants;

  2. 2.

    \({}_{i}T^{\alpha ,\beta }_{M}(t^{\nu })=\nu t^{\nu -\alpha }, \nu \in R\);

  3. 3.

    \({}_{i}T^{\alpha ,\beta }_{M}(gh)=g{}_{i}T^{\alpha ,\beta }_{M}(h)+h{}_{i} T^{\alpha ,\beta } _{M}(g)\);

  4. 4.

    \({}_{i}T^{\alpha ,\beta }_{M}(\frac{g}{h})= \frac{g{}_{i}T^{\alpha ,\beta }_{M}(h)- h{}_{i}T^{\alpha , \beta }_{M}(g)}{h^{2}}\);

  5. 5.

    \({}_{i}T^{\alpha ,\beta }_{M}(g)(t)= \frac{t^{1-\alpha }}{\Gamma (\beta +1)}\frac{dg}{dt}\);

  6. 6.

    \({}_{i}T^{\alpha ,\beta }_{M}(g\circ h)(t)=f^{\prime }(h(t)){}_{i}T^{ \alpha ,\beta }_{M}h(t)\).

3 Governing equation

In this section, we present the fractional CGL equation [28] with respect to different definitions of derivatives.

(1): In conformable derivative, the equation can be defined as follows:

$$ i D_{t}^{\alpha }u+au_{xx}+c\mathcal{F} \bigl( \vert u \vert ^{2}\bigr)u= \frac{1}{ \vert u \vert ^{2} u^{*}} \bigl\{ \delta \bigl( \vert u \vert ^{2}\bigr)_{xx} \vert u \vert ^{2} -N \bigl(\bigl( \vert u \vert ^{2} \bigr)_{x}\bigr)^{2} \bigr\} +Pu, $$
(6)

where \(D^{\alpha }_{t}u\) is the conformable derivative of u with respect to t, \(0 <\alpha \leq 1\), a, c, δ, N and P are real constants.

(2): By taking beta derivative into account, the considered equation can be written as follows:

$$ i{}^{A}_{0}D^{\alpha }_{t}u+a{}^{A}_{0}D^{2\alpha }_{x}u+c \mathcal{F}\bigl( \vert u \vert ^{2}\bigr)u= \frac{1}{ \vert u \vert ^{2} u^{*}} \bigl\{ \delta {}^{A}_{0} D^{2\alpha }_{x}\bigl( \vert u \vert ^{2}\bigr) \vert u \vert ^{2} -N \bigl({}^{A}_{0}D^{\alpha }_{x}\bigl( \vert u \vert ^{2}\bigr)\bigr)^{2} \bigr\} +Pu, $$
(7)

where \({}^{A}_{0}D^{\alpha }_{t}\) and \({}^{A}_{0}D^{\alpha }_{x}\) are beta derivatives with t and x respectively.

(3): Whereas by considering M-truncated derivative definition, the equation under study takes the form

$$\begin{aligned} & i{}^{A}_{0}D^{\alpha ,\beta }_{M,t}u+a{}^{A}_{0}D^{2\alpha ,\beta }_{M,x}u+c \mathcal{F}\bigl( \vert u \vert ^{2}\bigr)u \\ &\quad =\frac{1}{ \vert u \vert ^{2} u^{*}} \bigl\{ \delta {}^{A}_{0}D^{2 \alpha ,\beta }_{M,x}\bigl( \vert u \vert ^{2}\bigr) \vert u \vert ^{2} -N \bigl({}^{A}_{0}D^{\alpha ,\beta }_{M,x}\bigl( \vert u \vert ^{2}\bigr)\bigr)^{2} \bigr\} +Pu, \end{aligned}$$
(8)

where \({}^{A}_{0}D^{\alpha ,\beta }_{M,t}\) and \({}^{A}_{0}D^{\alpha ,\beta }_{M,x}\) are beta derivatives with t and x respectively.

In Eq. (1), Eq. (7), and Eq. (8), \(\mathcal{F}\) is a real-valued function, and its smoothness is possessed by a complex function \(\mathcal{F}(|u|^{2})u:C \rightarrow C\). Now, taking C as a complex plane to be a two-dimensional linear space \(R^{2}\), the \(\mathcal{F}(|u|^{2})u\) is k times continuously differentiable, so that

$$ \mathcal{F}\bigl( \vert u \vert ^{2}\bigr)u \in \bigcup _{p,q=1}^{\infty } C^{k} \bigl((-q, q) \times (-p,p); R^{2} \bigr). $$
(9)

3.1 Mathematical analysis

To solve Eq. (1), Eq. (7), and Eq. (8), we will take the following transformation:

$$ u(x,t)=U(\zeta )e^{i\Phi (x,t)}, $$
(10)

where \(u(x,t)\) represents the pulse shape of soliton, while ζ and Φ are defined with respect to different definitions:

(i): For conformable derivative, we take

$$\begin{aligned} & \zeta =x- \biggl(\frac{v}{\alpha } \biggr)t^{\alpha }, \end{aligned}$$
(11)
$$\begin{aligned} &\Phi (x,t)=-kx+ \biggl(\frac{\omega }{\alpha } \biggr)t^{\alpha }+ \theta . \end{aligned}$$
(12)

(ii): In the sense of beta derivative, we have

$$ \zeta =\frac{1}{\alpha } \biggl(x+\frac{1}{\Gamma (\alpha )} \biggr)^{\alpha }-\frac{v}{\alpha } \biggl(t+\frac{1}{\Gamma (\alpha )} \biggr)^{\alpha } $$
(13)

and

$$ \Phi (x,t)=-\frac{k}{\alpha } \biggl(x+\frac{1}{\Gamma (\alpha )} \biggr)^{\alpha }+\frac{w}{\alpha } \biggl(t+\frac{1}{\Gamma (\alpha )} \biggr)^{\alpha }+\theta _{0}(\zeta ). $$
(14)

(iii): By means of M-truncated derivative, we get

$$\begin{aligned} &\zeta =\frac{\Gamma (\beta +1)}{\alpha }\bigl(x^{\alpha }-vt^{\alpha } \bigr), \end{aligned}$$
(15)
$$\begin{aligned} &\Phi (x,t)=-\frac{\Gamma (\beta +1)}{\alpha }\bigl(kx^{\alpha }-vwt^{\alpha } \bigr)+ \theta _{0}(\zeta ), \end{aligned}$$
(16)

where w, k, v, \(\Phi (x,t)\), and \(\theta _{0}(\zeta )\) represent the wave number, frequency, speed, phase component, and phase function of solitons respectively.

Substituting (10) in Eqs. (1)–(8) one by one and separating the resulting equation into real and imaginary parts, we end up with the following equations:

$$ -wU+a\bigl(U^{\prime \prime }-k^{2}U\bigr)+c\mathcal{F} \bigl(U^{2}\bigr)U=2(\delta -2N) \frac{U^{\prime ^{2}}}{U}+2\delta U^{\prime \prime }+PU $$
(17)

and

$$ v=-2ak, $$
(18)

putting \(\delta =2N\) into Eq. (17), we have

$$ (a-4N)U^{\prime \prime }-\bigl(w+ak^{2}+P\bigr)U+c \mathcal{F}\bigl(U^{2}\bigr)U=0. $$
(19)

3.2 Kerr law nonlinearity

The main fact of the origin of this law is due to non-harmonic motion of electrons bounded in molecules, light wave during its propagation faces nonlinear responses under application of electric field. Although these effects are negligible, for long range distances these responses are measured by light wavelength parameter. The Kerr law takes the value of \(\mathcal{F}(U)=U\). Thus, Eq. (19) takes the following form:

$$ (a-4N)U^{\prime \prime }-\bigl(w+ak^{2}+P \bigr)U+cU^{3}=0. $$
(20)

4 Optical solitons

In this section, we use a new extended direct algebraic method to find optical solitons for the fractional CGL equation with conformable, beta, and M-truncated derivative.

4.1 Description of method

In this section, we present the description of the new extended direct algebraic method [31, 37]. This technique is a more remarkable and effective approach in evaluating solitary wave solutions for a number of classes of nonlinear problems and can be applied to numerous other nonlinear partial differential equations arising in scientific development area. When parameters including this technique are taken to be specific values, we can get the solitary wave solutions from different techniques, for example, the \((G^{\prime }/G)\)-expansion technique, the modified Kudryashov technique, the extended tanh-function technique, etc. It is indicated that the new extended algebraic method technique, with the assistance of symbolic calculation, gives a more impressive mathematical tool for all other nonlinear partial differential equations.

Suppose a nonlinear ordinary differential equation of the form

$$ J\bigl(U,U^{\prime },U^{\prime \prime },U^{\prime \prime \prime }\cdots \bigr)=0. $$
(21)

We suppose the solution of ODE (21) of the type

$$ U(\zeta )=\sum_{i=0}^{m}a_{i}Q^{i}( \zeta ), $$
(22)

where \(a_{i}\) \((0 < i \leq n)\) are the coefficients which can be found later and \(Q(\zeta )\) satisfies ODE of the form

$$ Q^{\prime }(\zeta )=\ln (\rho ) \bigl(\nu +\kappa Q(\zeta )+ \lambda Q^{2}( \zeta ) \bigr), \quad\rho \neq 0,1, $$
(23)

where ν, κ, and λ are constants. The solutions of Eq. (23) can be written as follows:

1: When \(\Theta < 0\) and \(\lambda \neq 0\),

$$\begin{aligned} &Q_{1}(\zeta )=-\frac{\kappa }{2\lambda }+ \frac{\sqrt{-\Theta }}{2\lambda }\tan _{\rho } \biggl( \frac{\sqrt{-\Theta }}{2} \zeta \ \biggr),\\ &Q_{2}(\zeta )=-\frac{\kappa }{2\lambda }- \frac{\sqrt{-\Theta }}{2\lambda }\cot _{\rho } \biggl( \frac{\sqrt{-\Theta }}{2}\zeta \ \biggr),\\ &Q_{3}(\zeta )=-\frac{\kappa }{2\lambda }+ \frac{\sqrt{-\Theta }}{2\lambda } \bigl(\tan _{\rho } (\sqrt{-\Theta } \zeta \ )\pm \sqrt{mn}\sec _{\rho } ( \sqrt{-\Theta } \zeta \ ) \bigr),\\ &Q_{4}(\zeta )=-\frac{\kappa }{2\lambda }- \frac{\sqrt{-\Theta }}{2\lambda } \bigl(\cot _{\rho } (\sqrt{-\Theta } \zeta \ )\pm \sqrt{mn}\csc _{\rho } ( \sqrt{-\Theta } \zeta \ ) \bigr),\\ &Q_{5}(\zeta )=-\frac{\kappa }{2\lambda }+ \frac{\sqrt{-\Theta }}{4\lambda } \biggl(\tan _{\rho } \biggl( \frac{\sqrt{-\Theta }}{4} \zeta \ \biggr)- \cot _{\rho } \biggl(\frac{\sqrt{-\Theta }}{4} \zeta \ \biggr) \biggr). \end{aligned}$$

2: When \(\Theta > 0\) and \(\lambda \neq 0\),

$$\begin{aligned} &Q_{6}(\zeta )=-\frac{\kappa }{2\lambda }- \frac{\sqrt{\Theta }}{2\lambda }\tanh _{\rho } \biggl( \frac{\sqrt{\Theta }}{2} \zeta \ \biggr),\\ &Q_{7}(\zeta )=-\frac{\kappa }{2\lambda }- \frac{\sqrt{\Theta }}{2\lambda }\coth _{\rho } \biggl( \frac{\sqrt{\Theta }}{2}\zeta \ \biggr),\\ &Q_{8}(\zeta )=-\frac{\kappa }{2\lambda }- \frac{\sqrt{\Theta }}{2\lambda } \bigl(\tanh _{\rho } (\sqrt{\Theta } \zeta \ )\pm i \sqrt{mn} \operatorname {sech}_{\rho } ( \sqrt{\Theta } \zeta \ ) \bigr),\\ &Q_{9}(\zeta )=-\frac{\kappa }{2\lambda }- \frac{\sqrt{\Theta }}{2\lambda } \bigl(\coth _{\rho } (\sqrt{\Theta } \zeta \ )\pm \sqrt{mn} \operatorname {csch}_{\rho } ( \sqrt{\Theta } \zeta \ ) \bigr),\\ &Q_{10}(\zeta )=-\frac{\kappa }{2\lambda }- \frac{\sqrt{\Theta }}{4\lambda } \biggl(\tanh _{\rho } \biggl( \frac{\sqrt{\Theta }}{4} \zeta \ \biggr)+\coth _{\rho } \biggl( \frac{\sqrt{\Theta }}{4} \zeta \ \biggr) \biggr). \end{aligned}$$

3: When \(\nu \lambda > 0\) and \(\kappa =0\),

$$\begin{aligned} &Q_{11}(\zeta )=\sqrt{\frac{\nu }{\lambda }} \tan _{\rho }(\sqrt{ \nu \lambda } \zeta ),\\ &Q_{12}(\zeta )=-\sqrt{\frac{\nu }{\lambda }} \cot _{\rho }(\sqrt{ \nu \lambda } \zeta ),\\ &Q_{13}(\zeta )=\sqrt{\frac{\nu }{\lambda }}\bigl(\tan _{\rho }(2 \sqrt{\nu \lambda } \zeta ) \pm \sqrt{mn}\sec _{\rho }(2\sqrt{\nu \lambda } \zeta )\bigr),\\ &Q_{14}(\zeta )=- (\sqrt{\frac{\nu }{\lambda }}\bigl(\cot _{\rho }(2\sqrt{ \nu \lambda } \zeta ) \pm \sqrt{mn}\csc _{\rho }(2 \sqrt{\nu \lambda } \zeta ) \bigr),\\ &Q_{15}(\zeta )=\frac{1}{2}\sqrt{\frac{\nu }{\lambda }} \biggl(\tan _{ \rho } \biggl(\frac{\sqrt{\nu \lambda }}{2} \zeta \biggr)- \cot _{\rho } \biggl(\frac{\sqrt{\nu \lambda }}{2} \zeta \biggr) \biggr). \end{aligned}$$

4: When \(\nu \lambda < 0\) and \(\kappa =0\),

$$\begin{aligned} &Q_{16}(\zeta )=-\sqrt{-\frac{\nu }{\lambda }} \tanh _{\rho }( \sqrt{- \nu \lambda } \zeta ),\\ &Q_{17}(\zeta )=-\sqrt{-\frac{\nu }{\lambda }} \coth _{\rho }(- \sqrt{ \nu \lambda } \zeta ),\\ &Q_{18}(\zeta )=-\sqrt{\frac{-\nu }{\lambda }} \bigl(\tanh _{\rho }(2 \sqrt{-\nu \lambda } \zeta ) \pm i \sqrt{mn} \operatorname {sech}_{\rho }(2\sqrt{-\nu \lambda } \zeta ) \bigr),\\ &Q_{19}(\zeta )=-\sqrt{-\frac{\nu }{\lambda }} \bigl(\coth _{\rho }(2 \sqrt{-\nu \lambda } \zeta ) \pm \sqrt{mn} \operatorname {csch}_{\rho }(2\sqrt{-\nu \lambda } \zeta ) \bigr),\\ &Q_{20}(\zeta )=-\frac{1}{2}\sqrt{\frac{-\nu }{\lambda }} \biggl( \tanh _{ \rho } \biggl(\frac{\sqrt{-\nu \lambda }}{2} \zeta \biggr)+\coth _{\rho } \biggl(\frac{\sqrt{-\nu \lambda }}{2} \zeta \biggr) \biggr). \end{aligned}$$

5: When \(\kappa =0\) and \(\lambda =\nu \),

$$\begin{aligned} &Q_{21}(\zeta )= \tan _{\rho }(\nu \zeta ),\\ &Q_{22}(\zeta )= -\cot _{\rho }(\nu \zeta ),\\ &Q_{23}(\zeta )= \tan _{\rho }(2\nu \zeta ) \pm \sqrt{mn}\sec _{\rho }(2 \nu \zeta ),\\ &Q_{24}(\zeta )= -\cot _{\rho }(2\nu \zeta ) \pm \sqrt{mn}\csc _{\rho }(2 \nu \zeta ),\\ &Q_{25}(\zeta )= \frac{1}{2} \biggl(\tan _{\rho } \biggl( \frac{\nu }{2} \zeta \biggr)- \cot _{\rho } \biggl(\frac{\nu }{2} \zeta \biggr) \biggr). \end{aligned}$$

6: When \(\kappa =0\) and \(\lambda =-\nu \),

$$\begin{aligned} &Q_{26}(\zeta )= -\tanh _{\rho }(\nu \zeta ),\\ &Q_{27}(\zeta )= -\coth _{\rho }(\nu \zeta ),\\ &Q_{28}(\zeta )= -\tanh _{\rho }(2\nu \zeta ) \pm i \sqrt{mn} \operatorname {sech}_{ \rho }(2\nu \zeta ),\\ &Q_{29}(\zeta )= -\coth _{\rho }(2\nu \zeta ) \pm \sqrt{mn} \operatorname {csch}_{ \rho }(2\nu \zeta ),\\ &Q_{30}(\zeta )= -\frac{1}{2} \biggl(\tanh _{\rho } \biggl(\frac{\nu }{2} \zeta \biggr)+ \coth _{\rho } \biggl( \frac{\nu }{2} \zeta \biggr) \biggr). \end{aligned}$$

7: When \(\kappa ^{2}=4\nu \lambda \),

$$\begin{aligned} Q_{31}(\zeta )= \frac{-2\nu (\kappa \zeta \ln (\rho )+2)}{\kappa ^{2}\zeta \ln (\rho )}. \end{aligned}$$

8: When \(\kappa =\Lambda \), \(\nu =q\Lambda (q\neq 0)\), and \(\lambda =0\),

$$\begin{aligned} Q_{32}(\zeta )=\rho ^{\Lambda \zeta }-q. \end{aligned}$$

9: When \(\kappa =\lambda =0\),

$$\begin{aligned} Q_{33}(\zeta )=\nu \zeta \ln (\rho ). \end{aligned}$$

10: When \(\kappa =\nu =0\),

$$\begin{aligned} Q_{34}(\zeta )=\frac{-1}{\lambda \zeta \ln (\rho )}. \end{aligned}$$

11: When \(\nu =0\) and \(\kappa \neq 0\),

$$\begin{aligned} &Q_{35}(\zeta )=- \frac{s\kappa }{\lambda (\cosh _{\rho }(\kappa \zeta )-\sinh _{\rho }(\kappa \zeta )+s)},\\ &Q_{36}(\zeta )=- \frac{\kappa (\sinh _{\rho }(\kappa \zeta )+\cosh _{\rho }(\kappa \zeta ))}{\lambda (\sinh _{\rho }(\kappa \zeta )+\cosh _{\rho }(\kappa \zeta )+r)}. \end{aligned}$$

12: When \(\kappa =\Lambda \), \(\lambda =q\lambda (q\neq 0)\), and \(\nu =0\),

$$\begin{aligned} Q_{37}(\zeta )= \frac{s\rho ^{\Lambda \zeta }}{r-qs\rho ^{\Lambda \zeta }}. \end{aligned}$$

Here, we define the hyperbolic and trigonometric functions as follows:

$$\begin{aligned} &\sinh _{\rho }(\zeta )=\frac{q\rho ^{\zeta }-s\rho ^{-\zeta }}{2},\qquad \cosh _{\rho }(\zeta ) =\frac{r\rho ^{\zeta }+s\rho ^{-\zeta }}{2},\\ &\tanh _{\rho }(\zeta )= \frac{r\rho ^{\zeta }-s\rho ^{-\zeta }}{r\rho ^{\zeta } +s\rho ^{-\zeta }}, \qquad\coth _{\rho }(\zeta )= \frac{r\rho ^{\zeta }+s\rho ^{-\zeta }}{r\rho ^{\zeta }-s\rho ^{-\zeta }},\\ &\operatorname {csch}_{\rho }(\zeta )=\frac{2}{r\rho ^{\zeta }-s\rho ^{-\zeta }}, \qquad \operatorname {sech}_{\rho }(\zeta ) =\frac{2}{r\rho ^{\zeta }+s\rho ^{-\zeta }},\\ &\sin _{\rho }(\zeta )= \frac{r\rho ^{\iota \zeta }-s\rho ^{-\iota \zeta }}{2\iota },\qquad \cos _{ \rho }(\zeta )= \frac{r\rho ^{\iota \zeta }+s\rho ^{-\iota \zeta }}{2},\\ &\tan _{\rho }(\zeta )=-i \frac{r\rho ^{\iota \zeta }- s\rho ^{-\iota \zeta }}{r\rho ^{\iota \zeta }+s\rho ^{-\iota \zeta }},\qquad \cot _{\rho }(\zeta )=i \frac{r\rho ^{\iota \zeta }+s\rho ^{-\iota \zeta }}{r\rho ^{\iota \zeta }-s\rho ^{-\iota \zeta }},\\ &\csc _{\rho }(\zeta )= \frac{2\iota }{r\rho ^{\iota \zeta }- s\rho ^{-\iota \zeta }}, \qquad \operatorname {sech}_{ \rho }(\zeta )= \frac{2}{r\rho ^{\iota \zeta }+s\rho ^{-\iota \zeta }}, \end{aligned}$$

where r and s are constants also called deformation parameters, while \(\Theta =\kappa ^{2}-4\nu \lambda \).

4.2 Application of the new extended direct algebraic method

In this section, our aim is to obtain the optical solitons of Eqs. (1)–(8). For this, one needs to solve only Eq. (20) first. After balancing the highest-order derivative terms with the nonlinear terms appearing in Eq. (20), one can take the solution of the form

$$ U(\zeta )=a_{0}+a_{1}Q(\zeta ). $$
(24)

After plugging (24) into (20) and equating coefficients of various powers of \(Q(\zeta )\), we get the following system of algebraic equations:

$$\begin{aligned} \begin{aligned} &Q^{3}(\zeta ) : 2aa_{1}\lambda ^{2}\ln (\rho )^{2}-8Na_{1} \lambda ^{2}\ln (\rho )^{2}+ca_{1}^{3}=0, \\ &Q^{2}(\zeta ) : 3aa_{1}\kappa \ln (\rho )^{2} \lambda -12Na_{1} \kappa \ln (\rho )^{2}\lambda +3ca_{0}a_{1}^{2} =0, \\ &Q^{1}(\zeta ) : aa_{1}\kappa ^{2}\ln (\rho )^{2}+2aa_{1}\lambda \ln ( \rho )^{2}\nu -4Na_{1} \kappa ^{2} \ln (\rho )^{2}-8Na_{1} \lambda \ln (\rho )^{2}\nu \\ &\phantom{Q^{1}(\zeta ) :}{} \quad -aa_{1}k^{2}-a_{1}P-a_{1}w+3ca_{0}^{2}a_{1}=0, \\ &Q^{0}(\zeta ) :aa_{1}\kappa \ln (\rho )^{2}\nu -4Na_{1}\kappa \ln ( \rho )^{2} \nu -a_{0}ak^{2}-a_{0}P-a_{0}w+ca_{0}^{3}=0. \end{aligned} \end{aligned}$$
(25)

Solving the above system of (25) with the help of Maple for \(a_{0}\), \(a_{1}\), and w, we get the following solution:

$$\begin{aligned} \begin{aligned}& a_{0}=\pm \Pi \kappa ,\qquad a_{1}=\pm 2\lambda \Pi ,\\ & w= \biggl(-\kappa ^{2}a-P+ \ln (\rho )^{2} \biggl( \frac{1}{2}a-2N \biggr) \bigl(4\nu \lambda -\kappa ^{2}\bigr) \biggr), \end{aligned} \end{aligned}$$
(26)

where

$$ \Pi =\frac{\ln (\rho ) \sqrt{-2c(a-4N)}}{2c}. $$

After substituting (26) into (24) and using transformation (10), we get the solutions as follows.

Case 1. When \(\Theta < 0\) and \(\lambda \neq 0\),

$$\begin{aligned} &u_{1}(x,t)=\pm \Pi \sqrt{-\Theta } \tan _{\rho }\biggl( \frac{\sqrt{-\Theta }}{2} \zeta \biggr) e^{i\Phi (x,t)},\\ &u_{2}(x,t)=\pm \Pi \sqrt{-\Theta } \cot _{\rho }\biggl( \frac{\sqrt{-\Theta }}{2} \zeta \biggr) e^{i\Phi (x,t)},\\ &u_{3}(x,t)=\pm \Pi \sqrt{-\Theta } \bigl(\tan _{\rho }(\sqrt{- \Theta } \zeta ) \pm \sqrt{mn}\sec _{\rho }(\sqrt{-\Theta }\zeta ) \bigr)e^{i \Phi (x,t)},\\ &u_{4}(x,t)=\pm \Pi \sqrt{-\Theta } \bigl(-\cot _{\rho }( \sqrt{-\Theta } \zeta ) \pm \sqrt{mn}\csc _{\rho }(\sqrt{-\Theta }\zeta ) \bigr)e^{i \Phi (x,t)},\\ &u_{5}(x,t)=\pm \frac{1}{2}\Pi \sqrt{-\Theta } \biggl(\tan _{\rho } \biggl(\frac{\sqrt{-\Theta }}{4}\zeta \biggr) \pm \cot _{\rho } \biggl( \frac{\sqrt{-\Theta }}{4}\zeta \biggr) \biggr)e^{i\Phi (x,t)}. \end{aligned}$$

Case 2. When \(\Theta > 0\) and \(\lambda \neq 0\),

$$\begin{aligned} &u_{6}(x,t)=\pm \Pi \sqrt{\Theta } \tanh _{\rho }\biggl( \frac{\sqrt{\Theta }}{2} \zeta \biggr) e^{i\Phi (x,t)},\\ &u_{7}(x,t)=\pm \Pi \sqrt{\Theta } \coth _{\rho }\biggl( \frac{\sqrt{\Theta }}{2} \zeta \biggr) e^{i\Phi (x,t)},\\ &u_{8}(x,t)=\pm \Pi \sqrt{\Theta } \bigl(-\tanh _{\rho }(\sqrt{ \Theta } \zeta ) \pm i \sqrt{mn} \operatorname {sech}_{\rho }(\sqrt{\Theta }\zeta ) \bigr)e^{i \Phi (x,t)},\\ &u_{9}(x,t)=\pm \Pi \sqrt{\Theta } \bigl(-\coth _{\rho }(\sqrt{ \Theta } \zeta ) \pm \sqrt{mn} \operatorname {csch}_{\rho }(\sqrt{\Theta }\zeta ) \bigr)e^{i \Phi (x,t)},\\ &u_{10}(x,t)=\pm \frac{1}{2}\Pi \sqrt{\Theta } \biggl(-\tanh _{\rho } \biggl(\frac{\sqrt{\Theta }}{4}\zeta \biggr) \pm \coth _{\rho } \biggl( \frac{\sqrt{\Theta }}{4}\zeta \biggr) \biggr)e^{i\Phi (x,t)}. \end{aligned}$$

Case 3. When \(\lambda \nu > 0\) and \(\kappa =0\),

$$\begin{aligned} &u_{11}(x,t)=\pm 2 \Pi \sqrt{\nu \lambda }\tan _{\rho }(\sqrt{ \nu \lambda }\zeta ) e^{i\Phi (x,t)},\\ &u_{12}(x,t)=\pm 2 \Pi \sqrt{\nu \lambda }\cot _{\rho }(\sqrt{ \nu \lambda }\zeta ) e^{i\Phi (x,t)},\\ &u_{13}(x,t)=\pm 2 \Pi \sqrt{\nu \lambda } \bigl(\tan _{\rho } (2\sqrt{ \nu \lambda } \zeta ) \pm \sqrt{mn}\sec _{\rho }(2\sqrt{\nu \lambda } \zeta ) \bigr)e^{i\Phi (x,t)},\\ &u_{14}(x,t)=\pm 2 \Pi \sqrt{\nu \lambda } \bigl(-\cot _{\rho } (2\sqrt{ \nu \lambda } \zeta ) \pm \sqrt{mn}\csc _{\rho }(2\sqrt{\nu \lambda } \zeta ) \bigr)e^{i\Phi (x,t)},\\ &u_{15}(x,t)=\pm \Pi \sqrt{\nu \lambda } \biggl(\tan _{\rho } \biggl( \frac{\sqrt{\nu \lambda }}{2} \zeta \biggr)\pm \cot _{\rho } \biggl( \frac{\sqrt{\nu \lambda }}{2}\zeta \biggr) \biggr)e^{i\Phi (x,t)}. \end{aligned}$$

Case 4. When \(\lambda \nu < 0\) and \(\kappa =0\),

$$\begin{aligned} &u_{16}(x,t)=\pm 2 \Pi \sqrt{-\nu \lambda }\tanh _{\rho }( \sqrt{-\nu \lambda }\zeta ) e^{i\Phi (x,t)},\\ &u_{17}(x,t)=\pm 2 \Pi \sqrt{-\nu \lambda }\coth _{\rho }( \sqrt{-\nu \lambda } \zeta ) e^{i\Phi (x,t)},\\ &u_{18}(x,t)=\pm 2 \Pi \sqrt{-\nu \lambda } \bigl(-\tanh _{\rho } (2 \sqrt{-\nu \lambda } \zeta ) \pm i\sqrt{mn} \operatorname {sech}_{\rho }(2\sqrt{-\nu \lambda }\zeta ) \bigr)e^{i\Phi (x,t)},\\ &u_{19}(x,t)=\pm 2 \Pi \sqrt{\nu \lambda } \bigl(-\coth _{\rho } (2\sqrt{- \nu \lambda } \zeta ) \pm \sqrt{mn} \operatorname {csch}_{\rho }(2\sqrt{-\nu \lambda } \zeta ) \bigr)e^{i\Phi (x,t)},\\ &u_{20}(x,t)=\pm \Pi \sqrt{2\nu \lambda } \biggl(-\tanh _{\rho } \biggl( \frac{\sqrt{-\nu \lambda }}{2} \zeta \biggr)\pm \coth _{\rho } \biggl( \frac{\sqrt{-\nu \lambda }}{2}\zeta \biggr) \biggr)e^{i\Phi (x,t)}. \end{aligned}$$

Case 5. When \(\kappa =0\) and \(\lambda =\nu \),

$$\begin{aligned} &u_{21}(x,t)=\pm 2 \Pi \nu \tan _{\rho }(\nu \zeta )e^{i\Phi (x,t)},\\ &u_{21}(x,t)=\pm 2 \Pi \nu \cot _{\rho }(\nu \zeta )e^{i\Phi (x,t)},\\ &u_{23}(x,t)=\pm 2 \Pi \nu (\tan _{\rho }(2\nu \zeta ) \pm \sqrt{mn} \sec _{\rho }(2\nu \zeta ) e^{i\Phi (x,t)},\\ &u_{24}(x,t)=\pm 2 \Pi \nu (-\cot _{\rho }(2\nu \zeta ) \pm \sqrt{mn} \csc _{\rho }(2\nu \zeta ) e^{i\Phi (x,t)},\\ &u_{25}(x,t)=\pm \Pi \nu \biggl(\tan _{\rho }\biggl( \frac{\nu }{2} \zeta \biggr) \pm \cot _{\rho }\biggl(\frac{\nu }{2} \zeta \biggr) \biggr) e^{i\Phi (x,t)}. \end{aligned}$$

Case 6. When \(\kappa =0\) and \(\lambda =-\nu \),

$$\begin{aligned} &u_{26}(x,t)=\pm 2 \Pi \nu \tanh _{\rho }(\nu \zeta )e^{i\Phi (x,t)},\\ &u_{27}(x,t)=\pm 2 \Pi \nu \coth _{\rho }(\nu \zeta )e^{i\Phi (x,t)},\\ &u_{28}(x,t)=\pm 2 \Pi \nu (-\tanh _{\rho }(2\nu \zeta ) \pm i \sqrt{mn} \operatorname {sech}_{\rho }(2\nu \zeta ) e^{i\Phi (x,t)},\\ &u_{29}(x,t)=\pm 2 \Pi \nu (-\coth _{\rho }(2\nu \zeta ) \pm \sqrt{mn} \operatorname {csch}_{\rho }(2\nu \zeta ) e^{i\Phi (x,t)},\\ &u_{30}(x,t)=\pm \Pi \nu \biggl(-\tan _{\rho }\biggl( \frac{\nu }{2} \zeta \biggr) \pm \coth _{\rho }\biggl( \frac{\nu }{2} \zeta \biggr) \biggr) e^{i\Phi (x,t)}. \end{aligned}$$

Case 7. When \(\kappa ^{2}=4\nu \lambda \),

$$\begin{aligned} u_{31}(x,t)=\pm \Pi \biggl(\kappa + \frac{(\kappa \zeta \ln (\rho )+2)}{\zeta \ln {\rho }} \biggr)e^{i\Phi (x,t)} , \end{aligned}$$

Case 8. When \(\kappa =\nu =0 \),

$$\begin{aligned} u_{32}(x,t)= \pm \Pi \biggl(\frac{-2}{\ln (\rho )\zeta }\biggr)e^{i\Phi (x,t)}. \end{aligned}$$

Case 9. When \(\kappa =0\), \(\lambda =0\),

$$\begin{aligned} u_{33}(x,t)=0. \end{aligned}$$

Case 10. When \(\kappa =\lambda =0\),

$$\begin{aligned} u_{34}(x,t)=0 . \end{aligned}$$

Case 11. When \(\nu =0\) and \(\kappa \neq 0\),

$$\begin{aligned} &u_{35}(x,t)=\pm \kappa \Pi \biggl(1- \frac{2q}{[\cosh _{\rho }(\kappa \zeta )-\sinh _{\rho }(\kappa \zeta )+s]} \biggr)e^{i\Phi (x,t)},\\ &u_{36}(x,t)=\pm \kappa \Pi \biggl( \frac{2[\cosh _{\rho }(\kappa \zeta )+\sinh _{\rho }(\kappa \zeta )]}{[\cosh _{\rho }(\kappa \zeta )+\sinh _{\rho }(\kappa \zeta )+r]} \biggr)e^{i\Phi (x,t)}. \end{aligned}$$

Case 12. When \(\kappa =\Lambda \), \(\lambda =m\Lambda (m \neq 0)\), and \(\nu =0\),

$$\begin{aligned} u_{37}(x,t)=\pm \Lambda \Pi \frac{2rm\rho ^{\Lambda \zeta }}{r-mq\rho ^{\Lambda \zeta }}e^{i\Phi (x,t)}, \end{aligned}$$

where ζ and Φ are defined by Eq. (11) and Eq. (12) for conformable derivative, Eq. (13) and Eq. (14) for beta derivative, and Eq. (15) and Eq. (16) for M-truncated derivative.

Remark

Sufficient conditions for the existence of the obtained solutions are presented in the form of the following proposition.

Proposition 1

If \(u(x,t)\) represents the solitary wave solution of Eq. (1), then necessary and sufficient conditions for its existence are \(c>0\) and \(a-4N< 0\).

It is important to note here that the obtained solutions of Eq. (1) represent different types of soliton solutions. As \(u_{6}\), \(u_{16}\), and \(u_{26}\) represent dark soliton solutions, \(u_{8}\), \(u_{18}\), and \(u_{28}\) are the dark-bright soliton solutions, \(u_{10}\), \(u_{20}\), and \(u_{30}\) show the dark-singular solutions, \(u_{9}\), \(u_{19}\), and \(u_{29}\) belong to a family of singular solutions of Type 1 and 2, while \(u_{7}\), \(u_{17}\), and \(u_{27}\) are labeled as singular solution of Type 2.

5 Comparative analysis of solutions with different fractional derivatives

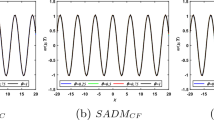
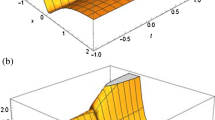
In this section, two solutions \(u_{1}(x,t)\) and \(u_{8}(x,t)\) are taken into consideration in the sense of different derivatives and shown in Figs. 1–10 for different values of fractional parameter α.

Figure 1
figure 1

(a) 3D-plot of \(u_{1}\) with conformable, (b) 3D-plot of \(u_{1}\) for beta with \(\alpha =0.5\). (c) 3D-plot of \(u_{1}\) for M-truncated with \(\alpha =0.5\), (d) 2D-plot of \(u_{1}\) with \(t=1\)

Full size image

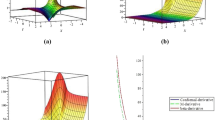
Figure 1: In this figure, we took \(a=1\), \(\rho =2\), \(c=1\), \(\alpha =0.5\), \(\kappa =1\), \(\lambda =1\), \(\nu =1\), \(v=1\), \(k=1\), \(P=1\), \(\theta =1\) in \(u_{1}(x,t)\) where 1(a) represents its 3D shape with conformable derivative definition, 1(b) shows its behavior with beta derivative, while 1(c) presents its graphs with M-truncated derivative with \(\beta =0.9\). Figure 1(d) represents a 2D-graph of \(u_{1}(x,t)\) at \(t=1\) by using different definitions of derivatives. It is observed that at \(t=1\) all definitions lead to different structures. The amplitude of soliton is much higher as compared to other two definitions with the same value of fractional parameter α.

Figure 2: In this figure, we take \(a=1\), \(\rho =2\), \(c=1\), \(\alpha =0.7\), \(\kappa =1\), \(\lambda =1\), \(\nu =1\), \(v=1\), \(k=1\), \(P=1\), \(\theta =1\) in \(u_{1}(x,t)\) where 2(a) shows its 3D structure for conformable derivative, 2(b) presents its graphs with beta derivative, 2(c) shows a 3D graph at \(\beta =0.9\) with M-truncated derivative, and 2(d) is for the 2D-graph of \(u_{1}(x,t)\) at \(t=1\) by using different definitions of derivatives. No overlapping exists by changing the definitions for solution \(u_{1}(x,t)\) with \(\alpha =0.7\), but it is very interesting to note that this time curves have very similar behavior, which was not the case for \(\alpha =0.5\) given in Fig. 1(d).

Figure 2
figure 2

(a) 3D-plot of \(u_{1}\) for conformable, (b) 3D-plot of \(u_{1}\) for beta with \(\alpha =0.7\). (c) 3D-plot of \(u_{1}\) for M-truncated with \(\alpha =0.7\), (d) 2D-plot of \(u_{1}\) with \(t=1\)

Full size image

Figure 3: In this graph, we assume \(a=1\), \(\rho =2\), \(c=1\), \(\alpha =0.9\), \(\kappa =1\), \(\lambda =1\), \(\nu =1\), \(v=1\), \(k=1\), \(P=1\), \(\theta =1\) in \(u_{1}(x,t)\) where 3(a) shows its 3D structure for conformable derivative, 3(b) presents its graphs with beta derivative, in 3(d) at \(t=1\) 2D behavior is observed by using different definitions of derivative. It is important to mention that at \(\alpha =0.9\) conformable and M-truncated derivatives come very close to each other but beta derivative shows different behavior. In Fig. 4, a change within the same definition of derivative for different values of α is presented for \(t=1\). Here, it is very important to note that the amplitude of the soliton’s profile decreases by increasing the value of α in case of three different definitions of derivatives.

Figure 3
figure 3

(a) 3D-plot of \(u_{1}\) for conformable, (b) 3D-plot of \(u_{1}\) for beta with \(\alpha =0.9\). (c) 3D-plot of \(u_{1}\) for M-truncated with \(\alpha =0.9\), (d) 2D-plot of \(u_{1}\) with \(t=1\)

Full size image
Figure 4
figure 4

2D-plot of \(u_{1}\) for different derivatives at \(t=1\) for different values of α

Full size image

Here, it is important to mention that for \(u_{1}(x,t)\) no overlapping is seen between the curves by testing different fractional values of α, but in Fig. 5 the same curves are obtained for conformable and M-truncated derivative with \(\alpha =1\), while the same solution shows different behavior for the same values of physical parameters for beta derivative.

Figure 5
figure 5

2D-plot with \(\alpha =1, \beta =0\) of \(u_{1}(x,t)\) for different derivatives

Full size image

Remark

In Figs. 6–10, the same comparison is done for the solution \(u_{8}(x,t)\) by taking the same parametric values as taken for \(u_{8}(x,t)\). Surprisingly, it is observed that for \(\alpha =1\) and \(t=1\) all definitions have different structures, which was not the case for \(u_{1}(x,t)\).

Figure 6
figure 6

(a) 3D-plot of \(u_{8}\) for conformable, (b) 3D-plot of \(u_{8}\) for beta with \(\alpha =0.5\). (c) 3D-plot of \(u_{8}\) for conformable, (d) 2D-plot of \(u_{8}\) with \(t=1\)

Full size image
Figure 7
figure 7

(a) 3D-plot of \(u_{8}\) for conformable, (b) 3D-plot of \(u_{8}\) for beta with \(\alpha =0.7\). (c) 3D-plot of \(u_{8}\) for M-truncated with \(\alpha =0.7\), (d) 2D-plot of \(u_{8}\) with \(t=1\)

Full size image
Figure 8
figure 8

(a) 3D-plot of \(u_{8}\) for conformable, (b) 3D-plot of \(u_{8}\) for beta with \(\alpha =0.9\). (c) 3D-plot of \(u_{8}\) for M-truncated, (d) 2D-plot of \(u_{8}\) with \(t=1\)

Full size image
Figure 9
figure 9

2D-plot of \(u_{8}\) for different derivatives at \(t=1\) for different values of α

Full size image
Figure 10
figure 10

2D-plot with \(\alpha =1, \beta =0\) of \(u_{8}(x,t)\) for different derivatives

Full size image

6 Conclusion

In this study, we have used conformable, beta, and M-truncated derivatives to find the optical solitons of the fractional CGL equation with Kerr law. The new extended algebraic method is used to obtain these solutions in detail. The physical features of the obtained solutions have been accounted for in this equation. Here, we have acquired the optical solitons with three different definitions. We have seen the different classes of soliton solutions in both discussed models in terms of dark soliton solutions, dark-bright soliton, dark singular soliton, singular soliton of Type 1 and 2, and sufficient conditions for the existence of these structures are presented. The optical solitons with beta definition are found to have different behavior for different values of α as compared to other two definitions which were found very close in shape and structure. An overlapping was found for \(\alpha =1, \beta =0\) when using conformable and M-truncated derivatives for solution \(u_{1}(x,t)\), but that was not true for \(u_{8}(x,t)\). These discussions have been presented in Figures 1–10 by taking appropriate values of parameters. The applied technique is simple, concise, direct, and clear to apply as contrasted to other existing techniques in the literature. Likewise, it is very skilled and practically well developed for obtaining new exact solutions of nonlinear dispersive equations arising in science and engineering.