1 Introduction

Recently, many scientists have applied fractional derivatives with different types of definitions, such as Atangana–Baleanu fractional integral [1], Caputo fractional derivative [2], and Caputo–Fabrizio fractional derivative [3], to many real-world problems and pointed out the powerfulness of using such noninteger-order and nonlocal kernels to numerically solve different types of integral equations and to describe the dynamics and properties of these problems; see, for example, [4–37].

One of these problems is studying numerical solution of the nonlinear Volterra–Fredholm integral equations by involving the well-known Atangana–Baleanu fractional derivative. Note that nonlinear Volterra–Fredholm integral equations appear in many applications in different disciplines such as neural networks [38], the pulses of sound reflections [39], and mathematical physics such as Lane–Emden-type equations [40], and many more can be found, for example, in [41] and references therein. On the other hand, finding exact solutions of such equations is usually difficult and sometimes even impossible. Therefore developing numerical algorithms to simulate exact solutions with this new involvement of noninteger order is crucial.

There are many numerical methods for solving Fredholm and Voltera integral equations, such as the Galerkin method, collocation method, Taylor series, Legendre wavelets, Taylor and recently Chebyshev polynomials, homotopy perturbation method, power series method, and expansion method [42–48]. Besides these contributions, other authors have also applied wavelet bases and gained much attention during the last decade. However, these bases are typically nonredundant, and thus corruption or loss of transform coefficients can be serious. Motivated by the above, our main goal in this work is to propose a new efficient method based on framelet systems to numerically solve fractional nonlinear Volterra and Fredholm integral equations by involving the Atangana–Baleanu fractional order derivative. Framelet theory is a relatively emerging area in mathematical analysis and known as redundant systems. The redundancy of the framelet system requires that a given function would be represented by a different structure as a convergent sum. These expansions have recently emerged as another effective tool and popular through the use in numerous applications. One of the major advantages of a redundant system is that it is implemented by a frame fast transform, which provides us with better recovery and higher accuracy order. Indeed, one of our main contributions in this work is simulation of the solution of a given fractional nonlinear Volterra and Fredholm integral equation based on these framelet expansions (redundant setting). This means that the right representation is critical if we intend to effectively perform our solution.

A framelet system contains a set of functions called generators. We construct them using some known and effective principles such as the unitary and oblique extension principles (of course, including their generalizations) and based on nonnegative functions called B-splines. This provides us with simple and better reconstruction of the coefficients to obtain the corresponding unknown elements of the space \(L^{2}(\mathbb{R})\) and also gives us better accuracy order and relatively small errors. In practice, framelet-based methods have been applied to provide accurate and efficient numerical schemes for solving several types of integral and differential equations; see, for example, [49–59].

We consider the following form of fractional nonlinear Volterra–Fredholm integral equation (FV-FIE):

$$\begin{aligned} \begin{aligned} \mathcal{D}^{\lambda }u(x)={}&g(x)+a \int _{0}^{x}{\mathcal{K}_{1}(x,t) \mathcal{P}_{1}\bigl(u(t)\bigr)\,dt} \\ &{}+b \int _{0}^{1}{\mathcal{K}_{1}(x,t) \mathcal{P}_{2}\bigl(u(t)\bigr)\,dt}, \quad x\in [0,1], \lambda >0, \end{aligned} \end{aligned}$$
(1.1)

with initial conditions (ICs)

$$\begin{aligned} u^{(p)}(0)=d_{p}, \quad p=0,1,2,\ldots,m-1, \text{and } \lambda \in (n,n+1], n\in \mathbb{N}, \end{aligned}$$
(1.2)

where \(\mathcal{D}^{\lambda }u\) is the Atangana–Baleanu fractional-order derivative given by

$$ \mathcal{D}^{\lambda }u(x)=\frac{M(\lambda )}{1-\lambda } \int _{0}^{x}{ \frac{du(t)}{dt}E_{\lambda } \biggl( \frac{-\lambda (x-t)^{\lambda }}{1-\lambda } \biggr) \,dt}, $$

where \(M(\lambda )\) is a normalization function satisfying \(M(0)=M(1)=1\), and \(E_{\lambda }\) is the Mittag-Leffler function. The integral operator corresponding to this definition is given by

$$ \mathcal{I}^{\lambda }u(x)=\frac{(1-\lambda )u(x)}{M(\lambda )}+ \frac{\lambda }{M(\lambda )\Gamma (\lambda )} \int _{0}^{x}{ \frac{u(t)}{(x-t)^{1-\lambda }}}. $$
(1.3)

We refer the reader to [1, 13, 60, 61] for more details and properties of the fractional derivative.

The paper is organized as follows. In Sect. 2, we provide some preliminaries and basics of frames with necessary theory needed for the construction of the framelet systems. In Sect. 3, we establish a matrix formulation of the proposed method based on the constructed framelet systems and using the collocation technique. Numerical examples with numerical comparison and graphical illustration are presented in Sect. 4 to validate our main expansion technique.

2 Framelet expansion method

The purpose in this section is providing an approximate solution of the FV-FIE given in Equations (1.1)–(1.2) in the form of truncated expansions of a given framelet system.

A set of functions

$$ \{ u_{j}, j=1,\ldots,\infty \} $$

is called a frame for \(L^{2}(\mathbb{R})\) if there exists positive numbers A, B such that

$$ A \Vert v \Vert ^{2}\leq \sum_{j=1}^{\infty } \bigl\vert \langle v,u_{j} \rangle \bigr\vert ^{2}\leq B \Vert v \Vert ^{2} $$
(2.1)

for all functions \(v\in L^{2}(\mathbb{R})\). The set is called tight frame (or framelet) if it is possible to have \(A=B\).

Note that, according to inequality (2.1), for a function \(g\in L^{2}(\mathbb{R})\), we obviously obtain the following associated framelet representation:

$$ g=\sum_{j\in \mathbb{Z}} \langle g,u_{j} \rangle u_{j}. $$
(2.2)

The framelets are constructed using B-spline functions. The B-splines \(B_{M}\) of order M, where \(M\in \mathbb{N}\), are recursively defined by the equation

$$ B_{M} ( x )= \int _{0}^{1}B_{M-1} ( x-t ) \,dt, \quad M=1,2, \ldots, $$

where \(B_{1}(x)\) is the indicator function over the interval \([0,1)\).

The Fourier transform of an integrable function f, denoted by f̂, is defined by

$$ \hat{f}(\omega )= \int _{\mathbb{R}}{f(t)e^{-2\pi i\omega t}\,d\omega }, $$

and the discrete Fourier series of a sequence \(a(k)\), denoted by â, is given by

$$ \hat{a}(\omega )=\sum_{k=0}^{M-1}{a(k)e^{2\pi ik\omega /M}}. $$

B-splines are nonnegative refinable functions in the sense that

$$ \widehat{B}_{M}(\omega )=\hat{a}(\omega /2)\hat{\phi }(\omega /2), $$

with

$$ \hat{a}(\omega )=2^{-n}\bigl(1+\mathbf{e}^{-i\omega } \bigr)^{n}p(\omega ), $$
(2.3)

where \(p(\omega )\) is a polynomial of trigonometric functions with \(p(0)=1\), and â is a 2π-periodic function in the frequency domain, called the low mask of \(B_{M}\).

The framelet system \(X(\Omega )\) is constructed via the oblique extension principle (OEP) [49] and it has the form

$$ X(\Omega )= \bigl\{ u _{\ell ,j,k}=2^{j/2}u\bigl(2^{j}x-k \bigr): \ell =1,\ldots,r; j,k\in \mathbb{Z} \bigr\} $$
(2.4)

and satisfies the following equations:

$$ \sum_{\ell =0}^{r} \bigl\vert \hat{a}_{\ell }(\omega ) \bigr\vert ^{2}=1\quad \text{and} \quad \sum_{\ell =0}^{r}\hat{a}_{\ell }( \omega ) \hat{a}_{\ell }(\omega + \pi )=0, $$
(2.5)

where \(\hat{a}_{0}\), \(\hat{a}_{\ell }\), \(\ell =1,\ldots,r\), are the low and high masks of \(u=B_{M}\), respectively. The OEP deals with the notion of constructing a framelet system using a refinable function ϕ where for some trigonometric function \(\hat{\Omega }(\omega )\),

  • \(\hat{\Omega }(\omega ) \vert \hat{\phi }(0) \vert ^{2}=1\), and

  • \(\hat{\Omega }(\omega )\hat{a}(\omega /2+\pi i) \overline{\hat{{a}}(\omega /2)}+\sum_{\ell \in E}{\hat{a}_{\ell }( \omega /2+\pi i)\overline{\hat{{a}}_{\ell }(\xi /2)}}=\Omega (\cdot /2) \delta _{i}\), \(\{ i:i= 0,1 \} \).

Then the system \(X(\Omega )\) defined in Equation (2.4) forms a framelet system for \(L_{2}({\mathbb{R}})\). The representation in Equation (2.2) is truncated by the series \(\mathcal{W}_{n}\) such that

$$ \mathcal{W}_{n}g=\sum_{\ell =1}^{r} \sum_{j=-n}^{n}\sum _{k\in \mathbb{Z}}c_{\ell ,j,k} u _{\ell ,j,k}, $$
(2.6)

where \(c_{\ell ,j,k}= \langle g,u _{\ell ,j,k} \rangle \).

Let us present some examples of framelet systems via the OEP setting.

Example 2.1

Consider the refinable function \(B_{2}(x)\). Then, based on the OEP presented in [49], we are able to explicitly construct the following framelets:

$$\begin{aligned}& \hat{\psi }_{1}(\omega ) = - \frac{16 e^{-\frac{1}{2} (i \omega )}}{\omega ^{2}}- \frac{16 e^{-\frac{1}{2} (3 i \omega )}}{\omega ^{2}}+ \frac{24 e^{-i \omega }}{\omega ^{2}}+ \frac{4 e^{-2 i \omega }}{\omega ^{2}}+\frac{4}{\omega ^{2}}+ \frac{1}{\sqrt{2 \pi }}, \\& \begin{aligned} \hat{\psi }_{2}(\omega )&= \frac{2 \sqrt{\frac{2}{\pi }} e^{\frac{i \omega }{2}}}{\omega ^{2}}+ \frac{30 \sqrt{\frac{2}{\pi }} e^{-\frac{1}{2} (i \omega )}}{\omega ^{2}}+ \frac{30 \sqrt{\frac{2}{\pi }} e^{-\frac{1}{2} (3 i \omega )}}{\omega ^{2}}+ \frac{2 \sqrt{\frac{2}{\pi }} e^{-\frac{1}{2} (5 i \omega )}}{\omega ^{2}}- \frac{40 \sqrt{\frac{2}{\pi }} e^{-i \omega }}{\omega ^{2}} \\ &\quad {} -\frac{12 \sqrt{\frac{2}{\pi }} e^{-2 i \omega }}{\omega ^{2}}- \frac{12 \sqrt{\frac{2}{\pi }}}{\omega ^{2}}. \end{aligned} \end{aligned}$$

Then according to the OEP, the set \(X(\Omega _{1})\) where \(\Omega _{1}= \{ \psi _{1},\psi _{2} \} \) forms a framelet system for \(L^{2}(\mathbb{R})\). The graph of the generators of the corresponding framelet system is given in Fig. 1 (the left subfigure).

Figure 1
figure 1

The graphs of the functions in \(X(\Omega _{1})\) for Examples 2.1 and 2.2, respectively

Full size image

Example 2.2

Consider the refinable function \(B_{4}(x)\). Then, again based on the OEP, we have

$$\begin{aligned}& \begin{aligned} \hat{\psi }_{1}(\omega )&=\frac{e^{-i \omega }}{1920\omega ^{2}} \biggl(4720 \cos \biggl( \frac{\omega }{2} \biggr)-880 \cos \biggl( \frac{3 \omega }{2} \biggr) \\ &\quad {}-10{,}178 \cos (\omega )-1352 \cos (2 \omega )+ 3337 \cos (3 \omega ) \\ &\quad {}-742 \cos (4 \omega )-71 \cos (5 \omega )+5166\biggr) , \end{aligned} \\& \begin{aligned} \hat{\psi }_{2}(\omega )&= \frac{1}{960 \sqrt{2 \pi } \omega ^{2}}\bigl(-1+e^{- \frac{1}{2} (i \omega )} \bigr)^{4} \\ &\quad {}\times \bigl(-726 e^{-\frac{1}{2} (i \omega )} \bigl(1+e^{i \omega } \bigr)+85 \bigl(e^{-i \omega }+e^{i \omega } \bigr)+458 \bigl(e^{-2 i \omega }+e^{2 i \omega } \bigr) \\ &\quad {}+412 e^{-\frac{1}{2} (3 i \omega )} \bigl(1+e^{3 i \omega } \bigr)+71 \bigl(e^{-3 i \omega }+e^{3 i \omega } \bigr)+284 e^{- \frac{1}{2} (5 i \omega )} \bigl(1+e^{5 i \omega } \bigr)-1228\bigr). \end{aligned} \end{aligned}$$

Therefore the set \(X(\Omega _{2})\) where \(\Omega _{2}= \{ \psi _{1},\psi _{2} \} \) forms a framelet system for \(\in L^{2}(\mathbb{R})\). The graph of the generators of the corresponding framelet system is plotted in Fig. 1 (the right subfigure).

3 Matrix formulation using framelets

In this section, we provide a general framework of the proposed algorithm based on the collocation division of the domain.

Consider the FV-FIE defined in Equation (1.1). Based on the truncated expansion obtained in Equation (2.6), we have

$$\begin{aligned} \frac{M(\lambda )}{1-\lambda } \int _{0}^{x}{ \frac{d\mathcal{W}(u_{m}(t))}{dt}E_{\lambda } \biggl( \frac{-\lambda (x-t)^{\lambda }}{1-\lambda } \biggr) \,dt} =&g(x)+a \int _{0}^{x}{\mathcal{K}_{1}(x,t) \mathcal{I}^{\lambda }\mathcal{P}_{1}\bigl( \mathcal{W}_{m}u(t) \bigr)\,dt} \\ & {}+b \int _{0}^{1}{\mathcal{K}_{1}(x,t) \mathcal{I}^{\lambda } \mathcal{P}_{2}\bigl(\mathcal{W}_{m}u(t) \bigr)\,dt}, \end{aligned}$$
(3.1)

where \(\mathcal{I}^{\lambda }\) is the Riemann–Liouville fractional-integral operator defined by Equation (1.3).

With a few algebra, Equation (3.1) can be simplified to

$$\begin{aligned} &\frac{M(\lambda )}{1-\lambda } \int _{0}^{x}{ \frac{d\mathcal{W}(u_{m}(t))}{dt}E_{\lambda } \biggl( \frac{-\lambda (x-t)^{\lambda }}{1-\lambda } \biggr) \,dt} \\ &\quad = g(x)+a \int _{0}^{x}{\mathcal{K}_{1}(x,t) \frac{(1-\lambda )\mathcal{P}_{1}(\mathcal{W}_{m}u(x))}{M(\lambda )}}\,dt \\ &\quad \quad {} +\frac{\lambda }{M(\lambda )\Gamma (\lambda )} \int _{0}^{x} \int _{0}^{t}{ \frac{\mathcal{P}_{1}(\mathcal{W}_{m}u(s))}{(x-s)^{1-\lambda }}}\,ds\,dt + b \int _{0}^{1}{\mathcal{K}_{2}(x,t) \frac{(1-\lambda )\mathcal{P}_{2}(\mathcal{W}_{m}u(x))}{M(\lambda )}}\,dt \\ &\quad \quad {} +\frac{\lambda }{M(\lambda )\Gamma (\lambda )} \int _{0}^{1} \int _{0}^{x}{ \frac{\mathcal{P}_{2}(\mathcal{W}_{m}u(t))}{(x-t)^{1-\lambda }}}\,ds. \end{aligned}$$

Hence,

$$\begin{aligned} &\frac{M(\lambda )}{1-\lambda } \int _{0}^{x}{ \frac{d\mathcal{W}(u_{m}(t))}{dt}E_{\lambda } \biggl( \frac{-\lambda (x-t)^{\lambda }}{1-\lambda } \biggr) \,dt}-a \int _{0}^{x}{ \mathcal{K}_{1}(x,t) \frac{(1-\lambda )\mathcal{P}_{1}(\mathcal{W}_{m}u(x))}{M(\lambda )}}\,dt \\ &\quad {} +\frac{\lambda }{M(\lambda )\Gamma (\lambda )} \int _{0}^{x} \int _{0}^{t}{ \frac{\mathcal{P}_{1}(\mathcal{W}_{m}u(s))}{(x-s)^{1-\lambda }}}\,ds\,dt - b \int _{0}^{1}{\mathcal{K}_{2}(x,t) \frac{(1-\lambda )\mathcal{P}_{2}(\mathcal{W}_{m}u(x))}{M(\lambda )}}\,dt \\ &\quad {} - \frac{\lambda }{M(\lambda )\Gamma (\lambda )} \int _{0}^{1} \int _{0}^{x}{ \frac{\mathcal{P}_{2}(\mathcal{W}_{m}u(t))}{(x-t)^{1-\lambda }}}\,ds=g(x). \end{aligned}$$

Now, based on a dyadic division points of the domain of the framelet system used, say \(\{ \xi _{q},q\in \Delta \} \), plugging these points into this equation, we have

$$\begin{aligned} &\frac{M(\lambda )}{1-\lambda } \int _{0}^{\xi _{q}}{ \frac{d\mathcal{W}(u_{m}(t))}{dt}E_{\lambda } \biggl( \frac{-\lambda (\xi _{q}-t)^{\lambda }}{1-\lambda } \biggr) \,dt}-a \int _{0}^{\xi _{q}}{\mathcal{K}_{1}(x,t) \frac{(1-\lambda )\mathcal{P}_{1}(\mathcal{W}_{m}u(x))}{M(\lambda )}}\,dt \\ &\quad {} -\frac{\lambda }{M(\lambda )\Gamma (\lambda )} \int _{0}^{\xi _{q}} \int _{0}^{t}{ \frac{\mathcal{P}_{1}(\mathcal{W}_{m}u(s))}{(\xi _{q}-s)^{1-\lambda }}}\,ds\,dt \\ &\quad {} - b \int _{0}^{1}{\mathcal{K}_{2}(\xi _{q},t) \frac{(1-\lambda )\mathcal{P}_{2}(\mathcal{W}_{m}u(\xi _{q}))}{M(\lambda )}}\,dt \\ &\quad {} -\frac{\lambda }{M(\lambda )\Gamma (\lambda )} \int _{0}^{1} \int _{0}^{\xi _{q}}{ \frac{\mathcal{P}_{2}(\mathcal{W}_{m}u(t))}{(\xi _{q}-t)^{1-\lambda }}}\,ds=g( \xi _{q}). \end{aligned}$$

By approximating the integrals in this equation based on the composite trapezoidal rule, we get a generated system of equations, which can be solved to obtain the unknown coefficients \(c_{\ell ,j,k}\), as in Equation (2.6), in order to have an approximated solution of order m.

4 Numerical applications

In this section, we consider some examples to test the proposed algorithm. The absolute errors are given by

$$ \mathcal{E}_{m}u={ \bigl\vert u-\mathcal{I}^{n}( \mathcal{P}_{m}u) \bigr\vert }, \quad \lambda \leq n. $$

For comparison, we provide some numerical results for Example 4.1 based on Cos and Sin (CAS) wavelets defined by

$$ \tau _{a,b}(x)=2^{a/2}\operatorname{SAC}_{p} \bigl(2^{a}x-(b-1)\bigr), \quad 2^{-a}(b-1)\leq x \leq 2^{-a}b, $$

and based on the collocation method, where the translation parameter is given by

$$ \operatorname{SAC}_{p}(x)=\cos (2p\pi x)+\sin (2p \pi x), \quad b=1, \ldots, 2^{a}. $$

The truncated expansion using such bases is given by

$$ \mathcal{M}u(x)=\sum_{n=0}^{2^{k}-1}\sum _{p=-p^{*}}^{p^{*}}{d_{np^{*}} \tau _{np^{*}}(x)}. $$

Example 4.1

Consider the FVIE

$$ \textstyle\begin{cases} \frac{M(\lambda )}{1-\lambda }\int _{0}^{x}{ \frac{d\mathcal{P}u_{m}(t)}{dt}E_{\lambda } ( \frac{-\lambda (x-t)^{\lambda }}{1-\lambda } ) \,dt}-\int ^{x}_{0}{e^{-t}( \mathcal{I}^{n}(\mathcal{P}_{m}u)^{2}(t)\,dt}=1, \\ u(0)=1, \\ u'(0)=1, \\ u''(0)=1, \\ u'''(0)=1, \end{cases} $$
(4.1)

where

$$ M(\lambda )= \frac{\Gamma (\lambda )(1-\lambda )+\lambda }{\Gamma (\lambda )}. $$

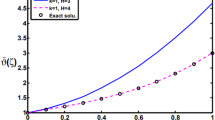
The exact solution solution is \(u(x)=e^{x}\), where \(\lambda =4\). Applying the above algorithm yields the numerical results presented in Tables 1, 2, and 3. Graphical illustrations using different values of λ to compare the results between the exact and approximate solutions are also given in Figs. 2, 3, 4, and 5.

Figure 2
figure 2

Comparison of the exact and approximate solutions of Example 4.1 for \(m=3\) and \(\lambda =3.25\)

Full size image
Figure 3
figure 3

Comparison of the exact and approximate solutions of Example 4.1 for \(m=3\) and \(\lambda =3.25\) using the framelet systems \(X(\Omega _{1})\) and \(X(\Omega _{2})\)

Full size image
Figure 4
figure 4

Comparison of the exact and approximate solutions of Example 4.1 for \(m=3\) and \(\lambda =3.5\)

Full size image
Figure 5
figure 5

Comparison of the exact and approximate solutions of Example 4.1 for \(m=3\) and \(\lambda =3.75\)

Full size image
Table 1 Numerical results of Example 4.1 using the framelet systems \({{X(\Omega _{1})}}\) and \({{X(\Omega _{2})}}\) for \(m=3\) and \(\lambda =3.25\)
Full size table
Table 2 Numerical results of Example 4.1 using the framelet systems \({{X(\Omega _{1})}}\) and \({{X(\Omega _{2})}}\) for \(m=3\) and \(\lambda =3.5\)
Full size table
Table 3 Numerical results of Example 4.1 using the framelet systems \({{X(\Omega _{1})}}\) and \({{X(\Omega _{2})}}\) for \(m=3\) and \(\lambda =3.75\)
Full size table

Example 4.2

Let us consider the following nonlinear equation, which appears in some applications of Newtonian gravity:

$$ u''(x)+2x^{-1}u'(x)+u^{5}(x)=0 $$

with ICs \(u(0)=1\) and \(u'(0)=0\). The equation can be transferred to the Volterra integral equation form

$$ \textstyle\begin{cases} u(x)-\frac{1}{x}\int ^{x}_{0}{(t^{2}-tx)u^{5}(t)\,dt}=1, \\ u(0)=1, \\ u'(0)=0. \end{cases} $$
(4.2)

The exact solution is

$$ u(x)=\frac{\sqrt{3}}{\sqrt{x^{2}+3}}. $$

In Figs. 6 and 7, we present some graphical illustrations to compare the exact and approximate solutions and error bounds.

Figure 6
figure 6

Comparison of the exact and approximate solutions of Example 4.2 for \(m=3\)

Full size image
Figure 7
figure 7

Comparison of the exact and approximate solutions of Example 4.2 for \(m=3\)

Full size image

Example 4.3

We consider the following nonlinear fractional differential equation with mixed boundary conditions:

$$ \textstyle\begin{cases} D^{\lambda +1}u(x)-\int ^{1}_{0}{xtu^{6}(t)\,dt}-\int ^{x}_{0}{(e^{t}-1)u^{2}(t)\,dt} \\ \quad =- \frac{1}{3} (e^{x}-x-1)^{3}- (-2 e+\frac{e^{2}}{4}+\frac{11}{3} ) x+e^{x}, \\ u(0)=-u'(0), \\ u(1)=u'(1)+2e-3, \end{cases} $$
(4.3)

where

$$ D^{\lambda +1}u(x)=\frac{M(\lambda +1)}{2-\lambda } \int _{0}^{x}{ \frac{d\mathcal{P}u_{m}(t)}{dt}E_{\lambda +1} \biggl( \frac{-\lambda -1 (x-t)^{\lambda +1}}{2-\lambda } \biggr) \,dt}. $$

The exact solution is \(u(x)=e^{x}-x-1\). The graphical illustrations are given in Figs. 8 and 9.

Figure 8
figure 8

Comparison of the exact and approximate solutions of Example 4.3 for \(m=3\) and \(\lambda =0.9\)

Full size image
Figure 9
figure 9

Comparison of the exact and approximate solutions of Example 4.3 for \(m=3\) and \(\lambda =0.95\)

Full size image

Example 4.4

Now, we consider the FVIE

$$ \textstyle\begin{cases} \frac{M(\lambda )}{1-\lambda }\int _{0}^{x}{ \frac{d\mathcal{P}u_{m}(t)}{dt}E_{\lambda } ( \frac{-\lambda (x-t)^{\lambda }}{1-\lambda } ) \,dt}-\int ^{x}_{0}{(x-t)^{2}u^{3}(t)\,dt}=-(x^{9}/252) + \frac{5 x^{4/5}}{2 \Gamma [4/5]}, \\ u(0)=0, \\ u(1)=1. \end{cases} $$

The exact solution for this equation when \(\lambda =6/5\) is \(u(x)=x^{2}\). The numerical results of this example are presented in Table 4, and the graphical illustrations of the exact, approximate, and error results are depicted in Figs. 10 and 11.

Figure 10
figure 10

Comparison of the exact and approximate solutions of Example 4.4 for \(m=3\) and \(\lambda =1.2\)

Full size image
Figure 11
figure 11

Error graphs of Example 4.4 for \(m=3\) and \(\lambda =1.2\) using framelet systems \({{X(\Omega _{1})}}\) and \({{X(\Omega _{2})}}\), respectively

Full size image
Table 4 Numerical results of Example 4.4 using the framelet systems \({{X(\Omega _{1})}}\) and \({{X(\Omega _{2})}}\) for \(m=3\) and \(\lambda =6/5\)
Full size table

5 Conclusion

In this work, we presented an efficient method based on framelet systems to solve nonlinear Volterra–Fredholm integral and integro-differential equations by involving the Atangana–Baleanu fractional derivative. We used some constructed framelet systems generated using the B-spline functions with high vanishing moments to numerically solve the related equations. We converted the considered problem given in Equation (1.1) to a matrix system after employing the Atangana–Baleanu fractional derivative definition, where the resulted integrals are approximated using the composite trapezoidal rule. The obtained results indicate that the method produces high accuracy order and reliable results with only a few terms of the truncated framelet partial sums with a proper discretization. We have also supported our results by some graphical illustrations of the exact and approximate solutions and provided error bounds of the solved examples.