1 Introduction

From the past three decades, optical solitons emerge as a fast growing area of research due to their use in transmission technology, through different forms of wave-guides. Solitons are utilized to represent the particle-like properties of nonlinear pulses. The importance of solitons is due to their presence in a variety of nonlinear differential equations portraying many complex nonlinear phenomena, including acoustics, nonlinear optics, telecommunication industry, convictive fluids, plasma physics, condensed matter, and solid-state physics. Nonlinear Schrödinger’s equation and its variant forms are used in dispersive mediums in different fields of mathematical physics and have been studied mathematically in recent years [1–15].

Solitons exist due to an accurate balance among nonlinearity and group velocity dispersion (GVD) in the area. If the value of GVD is small, this balance may be at risk. Therefore, to keep the balance among the two, expression terms with dispersive effects need to be investigated. One of the known models which is relevant is the Fokas–Lenells (FL) equation [16–18]. FL equation is one of the known forms of nonlinear Schrödinger’s equation, introduced about a decade ago. Due to its vast applications in fiber-optics communication, this sort of equation is crucial in research and thus the search for different forms of wave solutions is very significant. Many computational methodologies have been developed for constructing wave solutions for such equations, including the improved \(\tan (\phi (\eta )/2)\)-expansion method, the trial equation method, improved Bernoulli subequation function method, the extended Fan subequation method, extended and the modified simple equation methods, Riccati–Bernoulli’s sub-ODE method, the Lie group analysis, extended Jacobi’s elliptic function approach, and many others [19–35].

Nowadays, fractional science is a flourishing area of mathematical analysis along with fractional operators, such as Caputo, Grunwald–Letnikov, and Riemann–Liouville [36–44]. In 1695, in a letter to Leibniz, l’Hospital asked him about the detection of expanding the sense of an integer-order derivative \(\frac{d^{\lambda }y}{dx^{\lambda }}\) to the case of a fraction of the order. This problem started the development of a modern calculus that was named the calculus of arbitrary order and is now commonly called the calculus of fractions. Many forms of fractional derivatives, including Riemann–Liouville, Caputo, Hadamard, Caputo–Hadamard, and Riesz [40, 41, 43], have been developed to date. Almost all of these derivatives are described in the Riemann–Liouville sense based on the corresponding fractional integral.

In 2017, Sousa introduced a new fractional derivative that generalizes the so-called alternative fractional derivative [45]. This new differential operator is denoted by \(D^{\lambda , \mu }_{M}\), where λ is the order, such that \(0<\lambda \leq 1\), \(\mu >0\), and M denotes that the derived function includes a Mittag-Leffler function along with one parameter. This new type of derivative is known as a local M-derivative, it fulfills certain characteristics of integer-order calculus, e.g., linearity, quotient rule, product rule, chain rule, and function composition. Furthermore, the local M-derivative of a constant is zero. Since the Mittag-Leffler function is the generalization of the exponential function, some of the classical outcomes of calculus of the integer-order can be extended, namely the mean value theorem, Rolle’s theorem, and its extensions. Moreover, when the derivative order is \(\lambda =1\) and the Mittag-Leffler function parameter is also unitary, our specification is analogous to that of the ordinary derivative of order one.

This work aims to build specific fractional spatio-temporal optical solitons of FL equation by using two versatile integration gadgets, namely improved \(\tan (\frac{\phi (\eta )}{2})\)-expansion method [46–48] and generalized projective Riccati equation method (GPREM) [49, 50].

2 Governing model

Using the definition of the local M-derivative and its properties, the space-time fractional FL equation is introduced as follows:

$$\begin{aligned} &i D_{M,t}^{\alpha ; \delta _{1}}\Psi +a_{1} D_{M,x}^{2\alpha ; \delta _{1}}\Psi +a_{2}D_{M,t}^{\alpha ; \delta _{1}}D_{M,x}^{\alpha ; \delta _{1}} \Psi + \vert \Psi \vert ^{2}\bigl(\beta \Psi +i \sigma D_{M,x}^{\alpha ; \delta _{1}}\Psi \bigr) \\ &\quad {}-i\delta D_{M,x}^{\alpha ; \delta _{1}}-i\rho D_{M,x}^{\alpha ; \delta _{1}} \bigl( \vert \Psi \vert ^{2n}\Psi \bigr)-i \gamma \Psi D_{M,x}^{\alpha ; \delta _{1}}\bigl( \vert \Psi \vert ^{2n}\bigr)=0, \quad 0< \alpha \leq 1, n>0, \end{aligned}$$
(1)

where \(i=\sqrt{-1}\), \(\Psi =\Psi (x,t)\) is a complex-valued wave function. The first term of Eq. (1) gives the fractional temporal evolution of the pulse; \(a_{1}\), \(a_{2}\) are the spatio-temporal dispersion (STD), group velocity dispersion (GVD) coefficients, while ρ, δ, and γ represent the self-steepening, inter-modal dispersion (IMD), and nonlinear dispersion (ND) coefficients respectively [16–18].

When \(\alpha =1\), Eq. (1) is converted to the original FL equation [16–18]. The FL equation emerges as a model equation that defines the nonlinear pulse propagation in optical fibers by maintaining terms up to the next leading asymptotic order (the nonlinear Schrödinger equation (NLSE) results in the leading asymptotic order). In the context of nonlinear optics, this equation sculpts the promulgation of nonlinear light pulses in monomode optical fibers as assumed nonlinear higher-order effects are captured in the elaboration [51]. It is worth noticing that the FL equation is a fully integrable equation in nonlinear PDEs which has been developed as an integrable generalization of the NLSE using bi-Hamiltonian techniques [52].

2.1 Local M-derivative

Consider the function \(f:[0,\infty )\rightarrow R \) where \(t>0\). For \(0<\mu <1\), let us define the local M-derivative of order μ for the function f, denoted by \(D^{\mu ;\delta }_{M}\) [53–56], by

$$ D^{\mu ;\delta }_{M}\bigl\{ f(t)\bigr\} :=\lim _{\epsilon \rightarrow 0}\frac{f(t{E}_{\delta }(\epsilon t^{-\mu }))-f(t)}{\epsilon },\quad \forall t>0, $$
(2)

where \({E}_{\delta }(\cdot )\) is the Mittag-Leffler function with one parameter. Here \(f(t)\) is a p-differentiable function in some interval \((0,p), p>0\), and if \(\lim_{t\rightarrow 0^{+}}D^{\mu ;\delta }_{M}\) exists, then we have

$$ D^{\mu ;\delta }_{M}\bigl\{ f(0)\bigr\} =\lim _{t\rightarrow 0^{+}}D^{\mu ;\delta }_{M}\bigl\{ f(t)\bigr\} . $$
(3)

The local M-derivative possess the following properties:

$$ D^{\mu ;\delta }_{M}\bigl\{ f(t)\bigr\} =\frac{t^{1-\mu }}{\Gamma (\delta +1)} \frac{df(t)}{dt}, $$
(4)

therefore

$$ D^{\mu ;\delta }_{M}\biggl(\frac{t^{\mu }\Gamma (\delta +1)}{\alpha }\biggr)=1. $$
(5)

This local fractional-order M-derivative also has the following chain rule property:

$$ D^{\mu ;\delta }_{M}(f.g) (a)=f'\bigl(g(a) \bigr)D^{\mu ;\delta }_{M}. $$
(6)

Using Eqs. (4)–(6), we obtain the following expression:

$$ D^{\mu ;\delta }_{M}F\biggl(\frac{\Gamma (\delta +1)t^{\mu }}{\mu } \biggr)=F'\biggl(\frac{\Gamma (\delta +1)t^{\mu }}{\mu }\biggr) D^{\mu ;\delta }_{M} \biggl(\frac{\Gamma (\delta +1)t^{\mu }}{\mu }\biggr)=F'\biggl(\frac{\Gamma (\delta +1)t^{\mu }}{\mu }\biggr), $$
(7)

with

$$ \eta =\frac{m}{\mu }\Gamma (\delta +1)t^{\mu } , $$
(8)

where m is a constant. The last property is given as

$$ D^{\mu ;\delta }_{M}F(\eta )=mF'(\eta ). $$
(9)

3 Traveling wave hypothesis

Consider the following complex traveling wave transformation:

$$\begin{aligned} &\Psi (x,t)=U(\eta )e^{i\Theta },\qquad \eta =\nu \biggl( \Gamma (\delta _{1}+1) \biggl(\frac{x^{\alpha }}{\alpha }-v\frac{t^{\alpha }}{\alpha } \biggr) \biggr), \\ & \Theta =\Gamma (\delta _{1}+1) \biggl(-k \frac{x^{\alpha }}{\alpha }+\omega \frac{t^{\alpha }}{\alpha } \biggr)+\theta . \end{aligned}$$
(10)

Substituting Eq. (10) into Eq. (1) yields

$$ \nu ^{2}(a_{1}-a_{2}v)U''+ \bigl(a_{2}k\omega -\omega -a_{1}k^{2}-\delta k \bigr)U+(\beta +k\sigma )U^{3}-k\rho U^{1+2n}=0, $$
(11)

from the real part, and

$$ \bigl(\bigl(v+\delta +2a_{1}k-a_{2}(vk+\omega )\bigr)-\sigma U^{2}+(\rho +2n\rho +2n\gamma )U^{2n} \bigr)U'=0, $$
(12)

from the imaginary part.

Considering \(n=1\), Eqs. (1), (11), and (12) become

$$\begin{aligned} &iD^{\alpha ;\delta _{1}}_{M, t}\Psi +a_{1}D^{2\alpha ;\delta _{1}}_{M, x}+a_{2}D^{\alpha ;\delta _{1}}_{M, t}D^{\alpha ;\delta _{1}}_{M, x} \Psi + \vert \Psi \vert ^{2}\bigl(\beta \Psi +i\sigma D^{\alpha ;\delta _{1}}_{M, x}\Psi \bigr) \end{aligned}$$
(13)
$$\begin{aligned} &\quad {}-i\delta D^{\alpha ;\delta _{1}}_{M, x}\Psi -i\rho D^{\alpha ;\delta _{1}}_{M, x}\bigl( \vert \Psi \vert ^{2}\Psi \bigr)-i\gamma \Psi D^{\alpha ;\delta _{1}}_{M, x}\bigl( \vert \Psi \vert ^{2}\bigr)=0,\quad 0\leq \alpha \leq 1, \\ &\nu ^{2}(a_{1}-a_{2}v)U''+ \bigl(a_{2}k\omega -\omega -a_{1}k^{2}-\delta k \bigr)U+\bigl(\beta -k(\rho -\sigma )\bigr)U^{3}=0, \end{aligned}$$
(14)

and

$$ \bigl(\bigl(v+\delta +2a_{1}k-a_{2}(vk+\omega )\bigr)+(3\rho +2\gamma -\sigma )U^{2}\bigr)U'=0, $$
(15)

respectively.

Setting \((3\rho +2\gamma -\sigma )=0\) into Eq. (15), we get the following relations:

$$ \sigma =3\rho +2\gamma , \qquad v=\frac{\delta +2a_{1}k-a_{2}\omega }{a_{2}k-1}, $$
(16)

where v in Eq. (16) represents the velocity of solitons.

4 Soliton solutions

In this section soliton solutions are extracted for Eq. (13) with the help of two different integration schemes, namely the improved \(\tan (\frac{\phi (\eta )}{2})\)-expansion method and generalized projective Riccati equation method. In order to obtain these solutions, it is enough to solve the real part of Eq. (13), which is given in Eq. (14).

4.1 Improved \(\tan (\frac{\phi (\eta )}{2})\)-expansion method

Consider the initial hypothesis in the following form [46–48]:

$$ U(\eta )=S(\Phi )=\sum^{m}_{l=0}A_{k} \biggl[p+\tan \biggl(\frac{\Phi (\eta )}{2} \biggr) \biggr]^{k}+ \sum ^{m}_{l=1}B_{k} \biggl[p+\tan \biggl(\frac{\Phi (\eta )}{2} \biggr) \biggr]^{-k}, $$
(17)

where \(A_{k}(0\leq l\leq m)\) and \(B_{k}(1\leq l\leq m)\) are constants to be determined, such that \(A_{m}\neq 0\), \(B_{m}\neq 0\) and \(\Phi =\Phi (\eta )\) satisfies the following ordinary differential equation:

$$ \Phi '(\eta )=a\sin \bigl(\Phi (\eta )\bigr)+b\cos \bigl(\Phi (\eta )\bigr)+c. $$
(18)

By using the homogeneous balance principle between the terms \(U''\) and \(U^{3}\) of Eq. (14) lead us to the value \(l=1\). For \(p=0\), Eq. (17) takes the following form:

$$\begin{aligned} U(\eta )=A_{0}+A_{1} \biggl[\tan \biggl( \frac{\Phi (\eta )}{2} \biggr) \biggr]+B_{1} \biggl[\tan \biggl( \frac{\Phi (\eta )}{2} \biggr) \biggr]^{-1}. \end{aligned}$$
(19)

Herein the objective is to find the values of \(A_{0}\), \(A_{1}\), and \(B_{1}\). In order to find these values, substitute Eq. (19) into Eq. (14), and comparing all the coefficients of \((\tan (\frac{\Phi (\eta )}{2} ) )^{n}\), where \(n=-3,-2,-1,0,1,2,3\), with zero provides the following set of algebraic equations:

$$ \begin{aligned} &\omega =\frac{1}{(a_{2} k-1)a^{2}} (A_{0}^{2}(k \rho -k\sigma -\beta ) \bigl(a^{2}+b^{2}-c^{2} \bigr)+k a^{2}(\delta +a_{1} v ), \\ &A_{0}=A_{0},\qquad A_{1}=-\frac{A_{0}(b-c)}{a},\qquad B_{1}=0,\\ & v=\frac{2A_{0}^{2}k(\sigma -\rho )+2\beta A_{0}^{2}+\nu ^{2}a_{1}a^{2}}{\nu ^{2} a_{2} a^{2}}.\end{aligned} $$
(20)

Now equating the values of velocities in Eqs. (16) and (20), we will get subsequent value of \(a_{1}\):

$$ a_{1}=\frac{\nu ^{2}a_{2}a^{2}(a_{2}\omega -\delta )+2A_{0}^{2}(ka_{2}-1)(k\sigma -k\rho +\beta )}{\nu ^{2}a^{2}(a_{2}k+1)}. $$
(21)

Substituting the above value of \(a_{1}\) in ω, we get

$$ \omega =\frac{A_{0}^{2}(k\sigma -k\rho +\beta )(\nu ^{2}(a^{2}+b^{2}-c^{2})(ka_{2}+1)+2k^{2}(1-ka_{2}))}{\nu ^{2}a^{2}}. $$
(22)

Substituting these values in Eq. (19) and using the relation in Eq. (18) yields the following soliton solutions for Eq. (13).

When \(a^{2}+b^{2}-c^{2}<0\), the subsequent periodic soliton solution is obtained as

$$\begin{aligned} \Psi _{1}(x,t)=\frac{A_{0} \sqrt{c^{2}-b^{2}-a^{2}}}{a}\tan \biggl(\frac{\sqrt{c^{2}-b^{2}-a^{2}}}{2}(\eta +C) \biggr)e^{i\Theta }. \end{aligned}$$
(23)

If \(a^{2}+b^{2}-c^{2}>0\), then the following dark soliton solution is obtained:

$$\begin{aligned} \Psi _{2}(x,t)=-\frac{A_{0} \sqrt{b^{2}+a^{2}-c^{2}}}{a}\tanh \biggl(\frac{\sqrt{b^{2}+a^{2}-c^{2}}}{2}(\eta +C) \biggr)e^{i\Theta }. \end{aligned}$$
(24)

If \(a^{2}+b^{2}-c^{2}>0\), \(b\neq 0\), and \(c=0\), then

$$\begin{aligned} \Psi _{3}(x,t)=-\frac{A_{0} \sqrt{b^{2}+a^{2}}}{a}\tanh \biggl(\frac{\sqrt{b^{2}+a^{2}}}{2}( \eta +C) \biggr)e^{i\Theta }. \end{aligned}$$
(25)

If \(a^{2}+b^{2}-c^{2}<0\), \(c\neq 0\), and \(b=0\), then

$$\begin{aligned} \Psi _{4}(x,t)=-\frac{A_{0} \sqrt{c^{2}-a^{2}}}{a}\tan \biggl(\frac{\sqrt{c^{2}-a^{2}}}{2}(\eta +C) \biggr)e^{i\Theta }. \end{aligned}$$
(26)

If \(a^{2}+b^{2}=c^{2}\), then

$$\begin{aligned} \Psi _{5}(x,t)= A_{0} \biggl(1+\frac{(b^{2}-c^{2})(a(\eta +C)+2)}{a^{3}(\eta +C)} \biggr)e^{i\Theta }. \end{aligned}$$
(27)

If \(a=c=la\) and \(b=-l a\), then

$$\begin{aligned} \Psi _{6}(x,t)= A_{0} \biggl(1+\frac{2le^{la(\eta +C)}}{1-e^{la(\eta +C)}} \biggr)e^{i\Theta }. \end{aligned}$$
(28)

If \(c=a\), then

$$\begin{aligned} \Psi _{7}(x,t)= A_{0} \biggl(1+\frac{b-a}{a} \biggl[ \frac{(a+b)e^{b(\eta +C)}-1}{(a-b)e^{b(\eta +C)}-1} \biggr] \biggr)e^{i\Theta }. \end{aligned}$$
(29)

If \(a=c\), then

$$\begin{aligned} \Psi _{8}(x,t)= A_{0} \biggl(1-\frac{b-c}{c} \biggl[ \frac{(b+c)e^{b(\eta +C)}+1}{(b-c)e^{b(\eta +C)}-1} \biggr] \biggr)e^{i\Theta }. \end{aligned}$$
(30)

If \(c=-a\), then

$$\begin{aligned} \Psi _{9}(x,t)= A_{0} \biggl(1-\frac{b+a}{a} \biggl[ \frac{e^{b(\eta +C)}+b-a}{e^{b(\eta +C)}-b-a} \biggr] \biggr)e^{i\Theta }. \end{aligned}$$
(31)

If \(b=-c\), then

$$\begin{aligned} \Psi _{10}(x,t)= A_{0} \biggl(1+\frac{2ce^{a(\eta +C)}}{ce^{a(\eta +C)}-1} \biggr)e^{i\Theta }. \end{aligned}$$
(32)

If \(b=0\) and \(a=c\), then

$$\begin{aligned} \Psi _{11}(x,t)= A_{0} \biggl(1- \biggl[\frac{c(\eta +C)+2}{c(\eta +C)} \biggr] \biggr)e^{i\Theta }. \end{aligned}$$
(33)

In Eqs. (23)–(33), \(\eta =\nu (\Gamma (\delta _{1}+1) (\frac{x^{\alpha }}{\alpha }-v\frac{t^{\alpha }}{\alpha } ) )\) and \(\Theta =\Gamma (\delta _{1}+1) (-k\frac{x^{\alpha }}{\alpha }+\omega \frac{t^{\alpha }}{\alpha } )+\theta \).

4.2 Generalized projective Riccati equation method

Consider the following initial solution in order to solve Eq. (14) to find soliton solution of Eq. (13) with the aid of generalized projective Riccati equation method [49, 50]:

$$\begin{aligned} U(\eta )= A_{0}+ \sum_{j=0}^{N} \bigl(A_{j} \varrho (\eta )+ B_{j} \tau (\eta )\bigr). \end{aligned}$$
(34)

In Eq. (14), the homogeneous balance principle gives \(N=1\). Equation (34) becomes

$$\begin{aligned} U(\eta )= A_{0}+ A_{1} \varrho (\eta )+ B_{1}\tau (\eta ), \end{aligned}$$
(35)

where \(\varrho (\eta )\) and \(\tau (\eta )\) satisfy the projective Riccati system (PRS)

$$\begin{aligned}& \varrho '(\eta )= \epsilon \varrho (\eta ) \tau (\eta ), \end{aligned}$$
(36)
$$\begin{aligned}& \tau '(\eta )= \epsilon \tau ^{2}(\eta )- m \varrho (\eta )+ R, \end{aligned}$$
(37)

and PRS first integral is expressed as

$$\begin{aligned} \tau ^{2}(\eta )= -\epsilon \biggl(R- 2 \mu \varrho ( \eta )+ \frac{\mu ^{2}-1}{R}\varrho ^{2}(\eta ) \biggr). \end{aligned}$$
(38)

Substituting Eqs. (35), (36), and (38) into Eq. (14) provides a polynomial in \((\varrho ^{i}(\eta ), \tau ^{j}(\eta ))\), setting whose coefficients to zero yields a set of algebraic equations. When solving this system of equation with the aid of Maple, we will get

Set 1.

$$\begin{aligned} &R=\frac{2(-a_{2}k\omega +a_{1}k^{2}+\omega +\delta k)}{(a_{1}-a_{2}v)\nu ^{2}\epsilon },\quad \lambda =\lambda , \mu =1, A_{0}=0, A_{1}=0, \\ &B_{1}=\sqrt{-\frac{4a_{2}v\epsilon ^{2}+3a_{1}-3a_{2}v-4a_{1}\epsilon ^{2}}{2k\rho -2k\sigma -2\beta }}\nu . \end{aligned}$$
(39)

Set 2.

$$\begin{aligned} &R=\frac{(-a_{2}k\omega +a_{1}k^{2}+\omega +\delta k)}{2(a_{1}-a_{2}v)\nu ^{2}\epsilon },\quad \lambda =\lambda , \mu =0, A_{0}=0, A_{1}=0, \\ &B_{1}=\sqrt{\frac{-2a_{1}+2a_{2}v}{k\rho -k\sigma -\beta }}\nu \epsilon . \end{aligned}$$
(40)

Case 1. When \(\epsilon =-1\) and \(R\neq 0\), the PRS system has the following solutions:

$$\begin{aligned} &\sigma _{1}(\eta )=\frac{R\operatorname{sech}(\sqrt{R}\eta )}{\mu \operatorname{sech}(\sqrt{R}\eta )+1}, \qquad \tau _{1}(\eta )=\frac{\sqrt{R}\tanh (\sqrt{R}\eta )}{\mu \tanh (\sqrt{R}\eta )+1}, \\ & \sigma _{2}(\eta )=\frac{R \operatorname{csch}(\sqrt{R}\eta )}{\mu \operatorname{csch}(\sqrt{R}\eta )+1}, \qquad \tau _{2}(\eta )=\frac{\sqrt{R}\coth (\sqrt{R}\eta )}{\mu \coth (\sqrt{R}\eta )+1}. \end{aligned}$$
(41)

Case 2. When \(\epsilon =1\) and \(R\neq 0\), the PRS system has the subsequent solutions:

$$\begin{aligned} &\sigma _{3}(\eta )=\frac{R \sec (\sqrt{R}\eta )}{\mu \sec (\sqrt{R}\eta )+1}, \qquad \tau _{3}(\eta )=\frac{\sqrt{R}\tan (\sqrt{R}\eta )}{\mu \tan (\sqrt{R}\eta )+1}, \\ &\sigma _{4}(\eta )=\frac{R\csc (\sqrt{R}\eta )}{\mu \csc (\sqrt{R}\eta )+1}, \qquad \tau _{4}(\eta )=\frac{\sqrt{R}\cot (\sqrt{R}\eta )}{\mu \cot (\sqrt{R}\eta )+1}. \end{aligned}$$
(42)

Case 3. If \(R=\mu =0\), then

$$\begin{aligned} \sigma _{5}(\eta )=\frac{C}{\xi }=C\epsilon \tau _{5}( \xi ), \qquad \tau _{5}(\xi )=\frac{1}{\epsilon \xi }, \end{aligned}$$
(43)

where C is a constant.

Substituting the values of Set 1 along with equations (35), (41), and (42) into Eq. (10) provides the following solutions:

$$\begin{aligned}& \Psi _{12}(x,t)=\sqrt{\frac{k(a_{1}k+\delta )+\omega (1-a_{2}k)}{\beta -k\rho +k\sigma }} \biggl(\frac{\tanh (\sqrt{\frac{2(a_{2}k\omega -a_{1}k^{2}-\omega -\delta k)}{(a_{1}-a_{2}v)\nu ^{2}}}\eta )}{ \tanh (\sqrt{\frac{2(a_{2}k\omega -a_{1}k^{2}-\omega -\delta k)}{(a_{1}-a_{2}v)\nu ^{2}}}\eta )+1} \biggr)e^{i\Theta }, \end{aligned}$$
(44)
$$\begin{aligned}& \Psi _{13}(x,t)=\sqrt{\frac{k(a_{1}k+\delta )+\omega (1-a_{2}k)}{\beta -k\rho +k\sigma }} \biggl(\frac{\coth (\sqrt{\frac{2(a_{2}k\omega -a_{1}k^{2}-\omega -\delta k)}{(a_{1}-a_{2}v)\nu ^{2}}}\eta )}{ \coth (\sqrt{\frac{2(a_{2}k\omega -a_{1}k^{2}-\omega -\delta k)}{(a_{1}-a_{2}v)\nu ^{2}}}\eta )+1} \biggr)e^{i\Theta }, \end{aligned}$$
(45)
$$\begin{aligned}& \Psi _{14}(x,t)=\sqrt{\frac{k(a_{1}k+\delta )+\omega (1-a_{2}k)}{k\rho -k\sigma -\beta }} \biggl(\frac{ \tan (\sqrt{\frac{2(-a_{2}k\omega +a_{1}k^{2}+\omega +\delta k)}{(a_{1}-a_{2}v)\nu ^{2}}}\eta )}{ \tan (\sqrt{\frac{2(-a_{2}k\omega +a_{1}k^{2}+\omega +\delta k)}{(a_{1}-a_{2}v)\nu ^{2}}}\eta )+1} \biggr)e^{i\Theta }, \end{aligned}$$
(46)
$$\begin{aligned}& \Psi _{15}(x,t)=\sqrt{\frac{k(a_{1}k+\delta )+\omega (1-a_{2}k)}{k\rho -k\sigma -\beta }} \biggl(\frac{\cot (\sqrt{\frac{2(-a_{2}k\omega +a_{1}k^{2}+\omega +\delta k)}{(a_{1}-a_{2}v)\nu ^{2}}}\eta )}{ \cot (\sqrt{\frac{2(-a_{2}k\omega +a_{1}k^{2}+\omega +\delta k)}{(a_{1}-a_{2}v)\nu ^{2}}}\eta )+1} \biggr)e^{i\Theta }, \end{aligned}$$
(47)

where \(\eta =\nu (\Gamma (\delta _{1}+1) (\frac{x^{\alpha }}{\alpha }-v\frac{t^{\alpha }}{\alpha } ) ) \) and \(\Theta =\Gamma (\delta _{1}+1) (-k\frac{x^{\alpha }}{\alpha }+\omega \frac{t^{\alpha }}{\alpha } )+\theta \).

Using the values of Set 2 along with equations (35), (41), and (42) in Eq. (10) yields the subsequent solutions:

$$\begin{aligned}& \Psi _{16}(x,t)=\sqrt{\frac{k(a_{1}k+\delta )+\omega (1-a_{2}k)}{k\rho -k\sigma -\beta }} \biggl(\tanh \biggl(\sqrt{ \frac{(a_{2}k\omega -a_{1}k^{2}-\omega -\delta k)}{2(a_{1}-a_{2}v)\nu ^{2}}}\eta \biggr) \biggr)e^{i\Theta }, \end{aligned}$$
(48)
$$\begin{aligned}& \Psi _{17}(x,t)=\sqrt{\frac{k(a_{1}k+\delta )+\omega (1-a_{2}k)}{k\rho -k\sigma -\beta }} \biggl(\coth \biggl(\sqrt{ \frac{(a_{2}k\omega -a_{1}k^{2}-\omega -\delta k)}{2(a_{1}-a_{2}v)\nu ^{2}}}\eta \biggr) \biggr)e^{i\Theta }, \end{aligned}$$
(49)
$$\begin{aligned}& \Psi _{18}(x,t)=\sqrt{\frac{k(a_{1}k+\delta )+\omega (1-a_{2}k)}{\beta -k\rho +k\sigma }} \biggl( \tan \biggl(\sqrt{ \frac{(-a_{2}k\omega +a_{1}k^{2}+\omega +\delta k)}{2(a_{1}-a_{2}v)\nu ^{2}}}\eta \biggr) \biggr)e^{i\Theta }, \end{aligned}$$
(50)
$$\begin{aligned}& \Psi _{19}(x,t)=\sqrt{\frac{k(a_{1}k+\delta )+\omega (1-a_{2}k)}{\beta -k\rho +k\sigma }} \biggl(\cot \biggl(\sqrt{ \frac{(-a_{2}k\omega +a_{1}k^{2}+\omega +\delta k)}{2(a_{1}-a_{2}v)\nu ^{2}}}\eta \biggr) \biggr)e^{i\Theta }, \end{aligned}$$
(51)

where \(\eta =\nu (\Gamma (\delta _{1}+1) (\frac{x^{\alpha }}{\alpha }-v\frac{t^{\alpha }}{\alpha } ) ) \) and \(\Theta =\Gamma (\delta _{1}+1) (-k\frac{x^{\alpha }}{\alpha }+\omega \frac{t^{\alpha }}{\alpha } )+\theta \).

5 Results and discussion

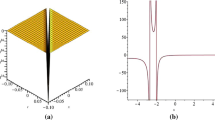
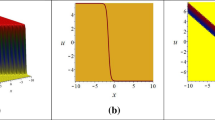
This section deals with graphical demonstration of the obtained results and provides a brief discussion on the effect of fractional parameter α. Figure 1(a) depicts the physical appearance of the periodic soliton solution \(|\Psi _{1}(x,t)|\), and Fig. 1(b) demonstrates the effect of fractional parameter \(\alpha =0.8,0.9,1.0\), along the time domain with fixed space parameter. A graphical illustration of the dark soliton solution \(|\Psi _{2}(x,t)|\) can be viewed in Fig. 2(a), and its 2D fractional parameter effects are depicted in Fig. 2(b). Figures 3(a), 4(a), 5(a), and 6(a) highlight the physical appearance of the traveling wave solution \(|\Psi _{10}(x,t)|\), dark soliton solution \(|\Psi _{16}(x,t)|\), singular soliton solution \(|\Psi _{17}(x,t)|\), and periodic soliton solution \(|\Psi _{10}(x,t)|\), respectively, and their respective 2D fractional parameter effects are given in Figs. 3(b), 4(b), 5(b), and 6(b).

Figure 1
figure 1

Graphical representation of periodic soliton obtained by the \(\tan (\frac{\phi (\eta )}{2})\)-expansion method

Full size image
Figure 2
figure 2

Dark soliton solution profile retrieved by the \(\tan (\frac{\phi (\eta )}{2})\)-expansion method

Full size image
Figure 3
figure 3

Graphical depiction of a traveling wave solution obtained by the \(\tan (\frac{\phi (\eta )}{2})\)-expansion method

Full size image
Figure 4
figure 4

Physical appearance of the dark soliton solution retrieved by GPREM

Full size image
Figure 5
figure 5

Graphical demonstration of a singular soliton solution obtained by GPREM

Full size image
Figure 6
figure 6

Physical illustration of a periodic soliton solution gained by GPREM

Full size image

6 Conclusion

An M-fractional FL equation representing the propagation of short light pulses in the monomode optical fibers is investigated using the improved \(\tan (\frac{\phi (\eta )}{2})\)-expansion method and GPREM. The FL model is a higher-order nonlinear Schrödinger shape equation that gives bright soliton solutions with internal freedom. Furthermore, the dark soliton solutions for the equation with the M-fractional effect, which have no internal freedom and exist for both focusing and lake of focusing equations, are investigated. The improved \(\tan (\frac{\phi (\eta )}{2})\)-expansion method is used to extract dark, singular, and rational soliton solutions, and GPREM provides dark, singular, periodic, and some forms of combo soliton solutions. These solutions are also demonstrated graphically. The fractional parameter effect on the dispersion is also highlighted through 2D graphical representation. The reported outcomes are useful in the empirical application of fiber optics. The essential advantages of the proposed schemes over all the other methods are that these methods provide new explicit analytic wave solutions including many real free parameters. The closed-form wave solutions of the nonlinear PDEs have their significant meaning to reveal the interior device of the complex physical phenomena. More problems in applied mathematics, mathematical physics, and engineering might be solved through the presented methods. In the future work, we will find the multisoliton solutions for the FL equation by the aid of the Hirota method.