An explicit fourth-order compact difference scheme for solving the 2D wave equation

Abstract

In this paper, an explicit fourth-order compact (EFOC) difference scheme is proposed for solving the two-dimensional(2D) wave equation. The truncation error of the EFOC scheme is $O({\tau ^{4}} + {\tau ^{2}}{h^{2}} + {h^{4}})$, i.e., the scheme has an overall fourth-order accuracy in both time and space. Because the scheme is explicit, it does not need any iterative processes. Afterwards, the stability condition of the scheme is obtained by using the Fourier analysis method, which has a wider stability range than other explicit or alternation direction implicit (ADI) schemes. Finally, some numerical experiments are carried out to verify the accuracy and stability of the present scheme.

1 Introduction

In this paper, we consider the 2D wave equation as follows:

$$\begin{aligned} &\frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} = {a^{2}} \biggl( \frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} + \frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}} \biggr) + f(x,y,t),\quad (x,y,t) \in \varOmega \times [0,T], \end{aligned}$$

(1)

with the initial conditions

$$\begin{aligned} &u(x,y,0) = \varphi (x,y),\quad (x,y)\in \varOmega , \end{aligned}$$

(2)

$$\begin{aligned} &\frac{{\partial u(x,y,0)}}{{\partial t}} = \psi (x,y),\quad (x,y)\in \varOmega , \end{aligned}$$

(3)

and the boundary conditions

$$\begin{aligned} &u(0,y,t) = {\alpha _{0}}(y,t),\quad\quad u(l,y,t) = {\alpha _{l}}(y,t), \end{aligned}$$

(4)

$$\begin{aligned} &u(x,0,t) = {\beta _{0}}(x,t),\quad\quad u(x,l,t) = {\beta _{l}}(x,t), \quad (x,y,t) \in \partial \varOmega \times [0,T], \end{aligned}$$

(5)

where $\varOmega ={(x,y):0\leq x,y\leq l}$ and ∂Ω is the boundary of Ω. Unknown function $u(x,y,t)$ is displacement, a is the wave velocity, $f(x,y,t)$ is the source term, $\varphi (x,y)$ and $\psi (x,y)$ are initial displacement and speed, respectively, ${\alpha _{0}}(y,t)$, ${\alpha _{l}}(y,t)$, ${\beta _{0}}(x,t)$, and ${\beta _{l}}(x,t)$ are displacements on the boundaries. We assume that all the functions are sufficiently smooth for achieving the accuracy order of the difference scheme.

Solution to wave propagation problems has received considerable attention for many years [1–17, 19–32, 34]. Numerical methods are particularly attractive for structurally complex subsurface geometries because of the great difficulties encountered in obtaining analytical solutions. Among the numerical techniques available in the literature, the method of finite differences is particularly versatile [1–15, 19–23, 25–28, 31, 32, 34]. The most commonly used for solving this equation is the second-order central difference scheme. Since it is lower accuracy and lower resolution, at least 20 grid points is necessary to be input into each propagating wavelength. In other words, if fewer grid points are used, dispersion errors would make numerical solution oscillating. In order to cut down dispersion error and get dependable results, people usually have to use fine grids for computation, which inevitably increases computational costs and storage requirements significantly. An alternate approach for overcoming this difficulty is pseudospectral (PS) method [17]. In theory of the PS method, only two grid points are required for each wavelength (although four or more are required in practice), and discrete Fourier transforms on each time step are quite expensive. The space operators of the PS method fit the Nyquist frequency, but it needs Fourier transform that is time-consuming and the use of a global basis, resulting in inaccuracies in wave fields for models with strong heterogeneity or sharp boundaries [16]. To effectively eliminate numerical dispersion error when coarse grids are used to discretize the wave equation, Yang et al. [30] proposed the nearly-analytic discrete (NAD) approach. Later, they [29, 31] further developed several NAD-type approaches to restrain numerical dispersion. Recently, many research works [15, 18–32] have been done to develop higher-order finite difference methods for the above mentioned wave equations. Furthermore, it has been demonstrated that high accuracy numerical approaches and techniques are very effective in restraining the dispersion errors [5, 8, 21, 31].

On the other hand, for multi-dimensional problems, operator splitting methods, such as the alternating direction implicit (ADI) [5, 6, 13, 19–23, 25] methods and local one-dimensional (LOD) approaches [15, 34], are studied extensively. The advantage of the operator splitting methods is the solution of a multi-dimensional problem reduced into a series of 1D problems, and thus the efficient algorithms for 1D such as tri-diagonal matrix algorithm can be employed, which is more efficient than full implicit schemes. Unconditionally stable high-order compact ADI schemes with spatially fourth-order and temporally second-order are investigated in [6, 13, 22, 23, 25]. Liao and Sun [19, 20] used Richardson extrapolation technique to promote the temporally second-order to fourth-order accuracy, but the second-order accuracy solutions on finer grid are needed to get the fourth-order solution on coarser grid. So, computed results on fine grid still show second-order accuracy. Das et al. [23] proposed some ADI schemes for solving the 2D wave equation, which are fourth-order accuracy in both time and space. However, they are conditionally stable and suffer from the stability conditions which only allow Courant–Friedrichs–Lewy (CFL) numbers from 0.7321 to 0.8186. Liao and Sun [19] extended this method to the 3D wave equation. It is also fourth-order accuracy in both time and space and the stability condition allows CFL number to be about 0.6079. For the study of LOD methods, the readers are referred to [15, 34], which still suffers from a strict stability condition for the fourth-order scheme in both time and space.

In this paper, we shall introduce an explicit high-order compact difference scheme for solving the 2D wave equation. Our basic strategy is to perform a modified equation technique for temporal derivative, but we use the fourth mixed derivative of temporal and spatial variables instead of pure fourth derivative of spatial variables, thus only three grid points are used for spatial dimension. And spatial derivatives are computed by directly using the classical fourth-order Padé schemes [18] at known time steps. This allows us to obtain an explicit difference scheme that is formally fourth-order accurate in both space and time. An outline of the article is as follows. In the next section, a new three-level explicit high-order compact difference scheme for solving Eq. (1) is introduced. Section 3 gives the Fourier analysis about the scheme, and the range of stability condition is obtained. In Sect. 4, we give some numerical experiments to show numerical stability and accuracy of the present new scheme. The last section draws conclusions.

2 EFOC difference scheme

Mesh point is marked as $({x_{i}},{y_{j}},{t_{n}})$, in which ${x_{i}} = ih$, ${y_{j}} = jh$, ${t_{n}} = n\tau$, $i,j = 0,1,2,\ldots,N$, and $n>0$. Let $u_{ij}^{n}$ be an approximation to $u_{(}{x_{i}},{y_{j}},{t_{n}})$. τ is temporal mesh step length and h is spatial mesh step length.

2.1 Computation of the first time step

Using Taylor’s expansions, we have

$$\begin{aligned} u_{ij}^{1} = u_{ij}^{0} + \tau \biggl( \frac{{\partial u}}{{\partial t}} \biggr)_{ij}^{0} + \frac{{{\tau ^{2}}}}{2} \biggl( \frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{ij}^{0} + \frac{{{\tau ^{3}}}}{6} \biggl( \frac{{{\partial ^{3}}u}}{{\partial {t^{3}}}} \biggr)_{ij}^{0} + \frac{{{\tau ^{4}}}}{{24}} \biggl( \frac{{{\partial ^{4}}u}}{{\partial {t^{4}}}} \biggr)_{ij}^{0} + {\mathrm{O}} \bigl({ \tau ^{5}} \bigr). \end{aligned}$$

(6)

Employing Eq. (1) and initial conditions (2) and (3), we have

$$\begin{aligned}& \biggl(\frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{ij}^{0} = {a^{2}} \biggl[ \biggl( \frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} \biggr)_{ij}^{0} + \biggl( \frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}} \biggr)_{ij}^{0} \biggr] + f_{ij}^{0} = {a^{2}} \biggl[ \biggl( \frac{{{\partial ^{2}}\varphi }}{{\partial {x^{2}}}} \biggr)_{ij} + \biggl( \frac{{{\partial ^{2}}\varphi }}{{\partial {y^{2}}}} \biggr)_{ij} \biggr] + f_{ij}^{0}, \end{aligned}$$

(7)

$$\begin{aligned}& \begin{aligned}[b] \biggl(\frac{{{\partial ^{3}}u}}{{\partial {t^{3}}}} \biggr)_{ij}^{0} &= \frac{\partial }{{\partial t}} \biggl( \frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{ij}^{0} = \frac{\partial }{{\partial t}} \biggl[{a^{2}} \biggl( \frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} \biggr)_{ij}^{0} + {a^{2}} \biggl( \frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}} \biggr)_{ij}^{0} + f_{ij}^{0} \biggr] \\ &= {a^{2}} \biggl[ \frac{{{\partial ^{2}}}}{{\partial {x^{2}}}} \biggl( \frac{{\partial u}}{{\partial t}} \biggr)_{ij}^{0} + \frac{{{\partial ^{2}}}}{{\partial {y^{2}}}} \biggl( \frac{{\partial u}}{{\partial t}} \biggr)_{ij}^{0} \biggr] + \biggl( \frac{{\partial f}}{{\partial t}} \biggr)_{ij}^{0} \\ &= {a^{2}} \biggl[ \biggl( \frac{{{\partial ^{2}}\psi }}{{\partial {x^{2}}}} \biggr)_{ij} + \biggl( \frac{{{\partial ^{2}}\psi }}{{\partial {y^{2}}}} \biggr)_{ij} \biggr] + \biggl( \frac{{\partial f}}{{\partial t}} \biggr)_{ij}^{0}, \end{aligned} \end{aligned}$$

(8)

$$\begin{aligned}& \begin{aligned}[b] \biggl(\frac{{{\partial ^{4}}u}}{{\partial {t^{4}}}} \biggr)_{ij}^{0} &= \frac{{{\partial ^{2}}}}{{\partial {t^{2}}}} \biggl( \frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{ij}^{0} = \frac{{{\partial ^{2}}}}{{\partial {t^{2}}}} \biggl[{a^{2}} \biggl( \frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} \biggr)_{ij}^{0} + {a^{2}} \biggl( \frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}} \biggr)_{ij}^{0} + f_{ij}^{0} \biggr] \\ &= {a^{2}} \biggl[ \frac{{{\partial ^{2}}}}{{\partial {x^{2}}}} \biggl( \frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{ij}^{0} + \frac{{{\partial ^{2}}}}{{\partial {y^{2}}}} \biggl( \frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{ij}^{0} \biggr]+ \biggl( \frac{{{\partial ^{2}}f}}{{\partial {t^{2}}}} \biggr)_{ij}^{0} \\ &= {a^{4}} \biggl[ \biggl( \frac{{{\partial ^{4}}\varphi }}{{\partial {x^{4}}}} \biggr)_{ij} + \biggl( \frac{{{\partial ^{4}}\varphi }}{{\partial {y^{4}}}} \biggr)_{ij} + 2 \biggl( \frac{{{\partial ^{4}}\varphi }}{{\partial {x^{2}}\partial {y^{2}}}} \biggr)_{ij} \biggr] \\ &\quad{} + {a^{2}} \biggl[ \biggl(\frac{{{\partial ^{2}}f}}{{\partial {x^{2}}}} \biggr)_{ij}^{0} + \biggl( \frac{{{\partial ^{2}}f}}{{\partial {y^{2}}}} \biggr)_{ij}^{0} \biggr] + \biggl( \frac{{{\partial ^{2}}f}}{{\partial {t^{2}}}} \biggr)_{ij}^{0}. \end{aligned} \end{aligned}$$

(9)

Substituting (7)–(9) into (6) and throwing away the truncation error term $O(\tau ^{5})$, we obtain the fourth-order compact difference scheme for the first time step as follows:

$$\begin{aligned} u_{ij}^{1} &= {\varphi _{ij}} + \tau {\psi _{ij}} + \frac{{{{a^{2}}\tau ^{2}}}}{2} \biggl[{ \biggl( \frac{{{\partial ^{2}}\varphi }}{{\partial {x^{2}}}} \biggr)_{ij}} + { \biggl( \frac{{{\partial ^{2}}\varphi }}{{\partial {y^{2}}}} \biggr)_{ij}} \biggr] + \frac{\tau ^{2}}{2}f_{ij}^{0} \\ &\quad {} + \frac{{{a^{2}\tau ^{3}}}}{6} \biggl[{ \biggl( \frac{{{\partial ^{2}}\psi }}{{\partial {x^{2}}}} \biggr)_{ij}} + { \biggl( \frac{{{\partial ^{2}}\psi }}{{\partial {y^{2}}}} \biggr)_{ij}} \biggr] + \frac{\tau ^{3}}{6} \biggl( \frac{{\partial f}}{{\partial t}} \biggr)_{ij}^{0} \\ &\quad {} + \frac{{{a^{4}}{\tau ^{4}}}}{{24}} \biggl[{ \biggl( \frac{{{\partial ^{4}}\varphi }}{{\partial {x^{4}}}} \biggr)_{ij}} + { \biggl( \frac{{{\partial ^{4}}\varphi }}{{\partial {y^{4}}}} \biggr)_{ij}} + 2{ \biggl( \frac{{{\partial ^{4}}\varphi }}{{\partial {x^{2}}\partial {y^{2}}}} \biggr)_{ij}} \biggr] \\ &\quad {} + \frac{{{a^{2}}{\tau ^{4}}}}{{24}} \biggl[ \biggl( \frac{{{\partial ^{2}}f}}{{\partial {x^{2}}}} \biggr)_{ij}^{0} + \biggl( \frac{{{\partial ^{2}}f}}{{\partial {y^{2}}}} \biggr)_{ij}^{0} \biggr] + \frac{{{\tau ^{4}}}}{{24}} \biggl( \frac{{{\partial ^{2}}f}}{{\partial {t^{2}}}} \biggr)_{ij}^{0}. \end{aligned}$$

(10)

For interior grid points at the $(n)$th time moment, we use the following fourth-order Padé approximation schemes [18]:

$$\begin{aligned}& \begin{aligned}[b] & \biggl(\frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} \biggr)_{i + 1j}^{n} + 10 \biggl( \frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} \biggr)_{ij}^{n} + \biggl( \frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} \biggr)_{i - 1j}^{n} \\ &\quad = 12 \frac{{u_{i + 1j}^{n} - 2u_{ij}^{n} + u_{i - 1j}^{n}}}{{{h^{2}}}} + O \bigl({h^{4}} \bigr), \quad i = 1,2,\ldots,N - 1, j = 0,1,2,\ldots,N, \end{aligned} \end{aligned}$$

(11)

$$\begin{aligned}& \begin{aligned}[b] & \biggl(\frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}} \biggr)_{ij + 1}^{n} + 10 \biggl( \frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}} \biggr)_{ij}^{n} + \biggl( \frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}} \biggr)_{ij - 1}^{n} \\ &\quad = 12 \frac{{u_{ij + 1}^{n} - 2u_{ij}^{n} + u_{ij - 1}^{n}}}{{{h^{2}}}} + O \bigl({h^{4}} \bigr), \quad i = 0,1,2,\ldots,N, j = 1,2,\ldots,N - 1, \end{aligned} \end{aligned}$$

(12)

and for grid points on the boundaries, we use Eqs. (1), (4), and (5) to give out directly

$$\begin{aligned}& \begin{aligned}[b] \biggl(\frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} \biggr)_{0j}^{n} &= \frac{1}{{{a^{2}}}} \biggl(\frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} - f \biggr)_{0j}^{n} - \biggl(\frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}} \biggr)_{0j}^{n}\\ & = \frac{1}{{{a^{2}}}} \biggl( \frac{{{\partial ^{2}}\alpha _{0}}}{{\partial {t^{2}}}} - f \biggr)_{0j}^{n} - \biggl(\frac{{{\partial ^{2}}{\alpha _{0}}}}{{\partial {y^{2}}}} \biggr)_{0j}^{n}, \quad j = 0,1,2,\ldots,N, \end{aligned} \end{aligned}$$

(13)

$$\begin{aligned}& \begin{aligned}[b] \biggl(\frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} \biggr)_{Nj}^{n} &= \frac{1}{{{a^{2}}}} \biggl(\frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} - f \biggr)_{Nj}^{n} - \biggl(\frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}} \biggr)_{Nj}^{n} \\ & = \frac{1}{{{a^{2}}}} \biggl( \frac{{{\partial ^{2}}\alpha _{l}}}{{\partial {t^{2}}}} - f \biggr)_{Nj}^{n} - \biggl(\frac{{{\partial ^{2}}{\alpha _{l}}}}{{\partial {y^{2}}}} \biggr)_{Nj}^{n}, \quad j = 0,1,2,\ldots,N, \end{aligned} \end{aligned}$$

(14)

$$\begin{aligned}& \begin{aligned}[b] \biggl(\frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}} \biggr)_{i0}^{n} &= \frac{1}{{{a^{2}}}} \biggl(\frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} - f \biggr)_{i0}^{n} - \biggl(\frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} \biggr)_{i0}^{n} \\ & = \frac{1}{{{a^{2}}}} \biggl( \frac{{{\partial ^{2}}\beta _{0}}}{{\partial {t^{2}}}} - f \biggr)_{i0}^{n} - \biggl(\frac{{{\partial ^{2}}{\beta _{0}}}}{{\partial {x^{2}}}} \biggr)_{i0}^{n}, \quad i = 0,1,2,\ldots,N, \end{aligned} \end{aligned}$$

(15)

$$\begin{aligned}& \begin{aligned}[b] \biggl(\frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}} \biggr)_{iN}^{n} &= \frac{1}{{{a^{2}}}} \biggl(\frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} - f \biggr)_{iN}^{n} - \biggl(\frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} \biggr)_{iN}^{n} \\ & = \frac{1}{{{a^{2}}}} \biggl( \frac{{{\partial ^{2}}\beta _{l}}}{{\partial {t^{2}}}} - f \biggr)_{iN}^{n} - \biggl(\frac{{{\partial ^{2}}{\beta _{l}}}}{{\partial {x^{2}}}} \biggr)_{iN}^{n}, \quad i = 0,1,2,\ldots,N. \end{aligned} \end{aligned}$$

(16)

We notice that the coefficient matrixes of Eqs. (11) and (12), with boundary conditions (13)–(16), are tri-diagonal, so they can be solved by the efficient tri-diagonal matrix algorithm.

2.2 Total time marching scheme

For the temporal derivative $(\frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}})_{ij}^{n}$, we use the second-order central difference and keep the leading term of the truncation errors to get

$$\begin{aligned} \biggl(\frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{ij}^{n} = \delta _{t}^{2}u_{ij}^{n} - \frac{{{\tau ^{2}}}}{{12}} \biggl( \frac{{{\partial ^{4}}u}}{{\partial {t^{4}}}} \biggr)_{ij}^{n} + O \bigl({\tau ^{4}} \bigr), \end{aligned}$$

(17)

in which $\delta _{t}^{2}u_{ij}^{n}= \frac{u_{ij}^{n+1}-2u_{ij}^{n}+u_{ij}^{n-1}}{\tau ^{2}}$, and by using Eq. (1), we get

$$\begin{aligned} \frac{{{\partial ^{4}}u}}{{\partial {t^{4}}}} = {a^{2}} \biggl( \frac{{{\partial ^{4}}u}}{{\partial {x^{2}}\partial {t^{2}}}} + \frac{{{\partial ^{4}}u}}{{\partial {y^{2}}\partial {t^{2}}}} \biggr) + \frac{{{\partial ^{2}}f}}{{\partial {t^{2}}}}. \end{aligned}$$

(18)

Substituting (18) into (17), we have

$$\begin{aligned} \biggl(\frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{ij}^{n} &= \delta _{t}^{2}u_{ij}^{n} - \frac{{{a^{2}\tau ^{2}}}}{{12}} \biggl[ \frac{{{\partial ^{2}}}}{{\partial {x^{2}}}} \biggl( \frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{ij}^{n} + \frac{{{\partial ^{2}}}}{{\partial {y^{2}}}} \biggl( \frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{ij}^{n} \biggr]- \frac{\tau ^{2}}{12} \biggl(\frac{{{\partial ^{2}}f}}{{\partial {t^{2}}}} \biggr)_{ij}^{n} + O \bigl({\tau ^{4}} \bigr) \\ &= \delta _{t}^{2}u_{ij}^{n} - \frac{{{a^{2}\tau ^{2}}}}{{12}} \biggl[\delta _{x}^{2} \biggl( \frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{ij}^{n} + \delta _{y}^{2} \biggl( \frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{ij}^{n} \biggr]- \frac{\tau ^{2}}{12} \biggl(\frac{{{\partial ^{2}}f}}{{\partial {t^{2}}}} \biggr)_{ij}^{n} \\ &\quad{} + O \bigl({\tau ^{4}} + {\tau ^{2}} {h^{2}} \bigr), \end{aligned}$$

(19)

in which $\delta _{x}^{2}(\frac{\partial ^{2}u}{\partial t^{2}})_{ij}^{n}= \frac{(\frac{\partial ^{2}u}{\partial t^{2}})_{i+1j}^{n}-2(\frac{\partial ^{2}u}{\partial t^{2}})_{ij}^{n}+(\frac{\partial ^{2}u}{\partial t^{2}})_{i-1j}^{n}}{h^{2}}$, $\delta _{y}^{2}(\frac{\partial ^{2}u}{\partial t^{2}})_{ij}^{n}= \frac{(\frac{\partial ^{2}u}{\partial t^{2}})_{ij+1}^{n}-2(\frac{\partial ^{2}u}{\partial t^{2}})_{ij}^{n}+(\frac{\partial ^{2}u}{\partial t^{2}})_{ij-1}^{n}}{h^{2}}$. Rearranging (19) and neglecting the truncation error, we have

$$\begin{aligned} u_{ij}^{n + 1} &= 2u_{ij}^{n} - u_{ij}^{n - 1} \\ &\quad{} + \frac{{{a^{2}}{\tau ^{4}}}}{{12{h^{2}}}} \biggl[ \biggl( \frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{i + 1j}^{n} + \biggl( \frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{ij + 1}^{n}- 4 \biggl( \frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{ij}^{n} + \biggl( \frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{i - 1j}^{n}+ \biggl( \frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{ij - 1}^{n} \biggr] \\ &\quad{} + {\tau ^{2}} \biggl(\frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} \biggr)_{ij}^{n}+ \frac{{{\tau ^{4}}}}{{12}} \biggl( \frac{{{\partial ^{2}}f}}{{\partial {t^{2}}}} \biggr)_{ij}^{n}. \end{aligned}$$

(20)

Using Eq. (1) again, (20) becomes

$$\begin{aligned} u_{ij}^{n + 1} &= 2u_{ij}^{n} - u_{ij}^{n - 1}+ \biggl({a^{2}} {\tau ^{2}} - \frac{{{a^{4}}{\tau ^{4}}}}{{3{h^{2}}}} \biggr) \biggl[ \biggl( \frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} \biggr)_{ij}^{n}+ \biggl( \frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}} \biggr)_{ij}^{n} \biggr] \\ &\quad{} + \frac{{{a^{4}}{\tau ^{4}}}}{{12{h^{2}}}} \biggl[ \biggl( \frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} \biggr)_{i - 1j}^{n} + \biggl( \frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} \biggr)_{i + 1j}^{n} + \biggl(\frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} \biggr)_{ij - 1}^{n} + \biggl( \frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} \biggr)_{ij + 1}^{n} \\ &\quad{} + \biggl( \frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}} \biggr)_{i - 1j}^{n} + \biggl( \frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}} \biggr)_{i + 1j}^{n} + \biggl( \frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}} \biggr)_{ij - 1}^{n} + \biggl( \frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}} \biggr)_{ij + 1}^{n} \biggr] \\ &\quad{} + \frac{{{\tau ^{4}}}}{{12}} \biggl( \frac{{{\partial ^{2}}f}}{{\partial {t^{2}}}} \biggr)_{ij}^{n} + \biggl({\tau ^{2}} - \frac{{{a^{2}}{\tau ^{4}}}}{{3{h^{2}}}} \biggr)f_{ij}^{n}+ \frac{{{a^{2}}{\tau ^{4}}}}{{12{h^{2}}}} \bigl(f_{i - 1j}^{n} + f_{i + 1j}^{n} + f_{ij - 1}^{n} + f_{ij + 1}^{n} \bigr). \end{aligned}$$

(21)

Equation (21) is an explicit high-order compact difference scheme for solving Eq. (1). Through the derivation process, it is easy to know that the truncation error of the scheme is $O({\tau ^{4}} + {\tau ^{2}}{h^{2}} + {h^{4}})$, i.e., it has the fourth-order accuracy for both time and space. We mark it as EFOC scheme (explicit fourth-order compact scheme). It should be pointed out that $(\frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}})_{ij}^{n}$ and $(\frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}})_{ij}^{n}$ must be computed by Eqs. (11)–(16) in advance. Now, we can get an algorithm for solving wave equation (1) with initial and boundary conditions (2)–(5) as follows.

Algorithm 1

• Step 1: Let $n = 1$, use Eq. (10) to compute the values of $u(x,y,t)$ at first time step, i.e., $u_{ij}^{1}$;

• Step 2: Use Eq. (11) and Eq. (12) to compute the values of the second derivatives of $u(x,y,t)$ about x and y at the $(n)$th time step, i.e., $(\frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}})_{ij}^{n}$ and $(\frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}})_{ij}^{n}$, in which the boundary values of them are computed by Eqs. (13)–(16);

• Step 3: Use Eq. (21) to compute the values of $u(x,y,t)$ at the $(n+1)$th time step, i.e., $u_{ij}^{n + 1}$;

• Step 4: Let $n \leftarrow n + 1$, repeat Step 2 and Step 3, till the final time step is reached.

2.3 Stability analysis

In this part, von Neumann linear stability analysis method is used to get the stability condition of the present EFOC scheme(21).

Lemma 1

([33])

If b and c are real, then both roots of the quadratic equation ${x^{2}} - bx + c = 0$are less than or equal to one in modulus if and only if $\vert c \vert \le 1$and $\vert b \vert \le 1 + c$.

We suppose that u is a periodic function, $v_{ij}^{n + 1} = u_{ij}^{n}$, and the source function $f \equiv 0$. Letting $u_{ij}^{n} = {\xi ^{n}}{e^{I({\sigma _{1}}{x_{i}} + {\sigma _{2}}{y_{j}})}}$, $({u_{xx}})_{ij}^{n} = {\eta ^{n}}{e^{I({\sigma _{1}}{x_{i}} + { \sigma _{2}}{y_{j}})}}$, $({u_{yy}})_{ij}^{n} = {\gamma ^{n}}{e^{I({\sigma _{1}}{x_{i}} + { \sigma _{2}}{y_{j}})}}$, in which ξ, η, and γ are amplitudes, ${\sigma _{1}}$ and ${\sigma _{2}}$ are wave numbers in x and y direction, respectively. $I = \sqrt{ - 1}$ is an imaginary unit.

Substituting the expressions of $({u_{xx}})_{ij}^{n}$ and $({u_{yy}})_{ij}^{n}$ into Eq. (11) and Eq. (12), we have

$$\begin{aligned}& {\eta ^{n}} {e^{I({\sigma _{1}}{x_{i}} + {\sigma _{2}}{y_{j}})}} \bigl({e^{I{ \sigma _{1}}h}} + 10 + {e^{ - I{\sigma _{1}}h}} \bigr) = \frac{{12}}{{{h^{2}}}}{\xi ^{n}} {e^{I({\sigma _{1}}{x_{i}} + {\sigma _{2}}{y_{j}})}} \bigl({e^{I{ \sigma _{1}}h}} - 2 + {e^{ - I{\sigma _{1}}h}} \bigr), \end{aligned}$$

(22)

$$\begin{aligned}& {\gamma ^{n}} {e^{I({\sigma _{1}}{x_{i}} + {\sigma _{2}}{y_{j}})}} \bigl({e^{I{ \sigma _{2}}h}} + 10 + {e^{ - I{\sigma _{2}}h}} \bigr) = \frac{{12}}{{{h^{2}}}}{\xi ^{n}} {e^{I({\sigma _{1}}{x_{i}} + {\sigma _{2}}{y_{j}})}} \bigl({e^{I{ \sigma _{2}}h}} - 2 + {e^{ - I{\sigma _{2}}h}} \bigr). \end{aligned}$$

(23)

Using Euler’s formula ${e^{I\sigma h}} + {e^{ - I\sigma h}} = 2\cos (\sigma h)$, after rearranging them, we get

$$\begin{aligned}& {\eta ^{n}} = \frac{{12[\cos ({\sigma _{1}}h) - 1]}}{{{h^{2}}[\cos ({\sigma _{1}}h) + 5]}}{ \xi ^{n}}, \end{aligned}$$

(24)

$$\begin{aligned}& {\gamma ^{n}} = \frac{{12[\cos ({\sigma _{2}}h) - 1]}}{{{h^{2}}[\cos ({\sigma _{2}}h) + 5]}}{ \xi ^{n}}. \end{aligned}$$

(25)

Equation (21) is rewritten as follows:

$$\begin{array}{rl}\left(\begin{array}{c}{u}_{ij}^{n+1}\\ v_{ij}^{n+1}\end{array}\right)& =\left(\begin{array}{cc}2& -1\\ 1& 0\end{array}\right)\left(\begin{array}{c}{u}_{ij}^n\\ v_{ij}^n\end{array}\right)+\left(\begin{array}{cc}{a}^2{\tau }^2-\frac{a^2{\tau }^2{r}^2}{3}& 0\\ 0& 0\end{array}\right)\left(\begin{array}{c}{(u_{xx})}_{ij}^n+{(u_{yy})}_{ij}^n\\ {(v_{xx})}_{ij}^n+{(v_{yy})}_{ij}^n\end{array}\right)\\ & +\left(\begin{array}{cc}\frac{a^2{\tau }^2{r}^2}{12}& 0\\ 0& 0\end{array}\right)\left(\begin{array}{c}{(u_{xx})}_{ij+1}^n+{(u_{yy})}_{ij+1}^n\\ {(v_{xx})}_{ij+1}^n+{(v_{yy})}_{ij+1}^n\end{array}\right)\\ & +\left(\begin{array}{cc}\frac{a^2{\tau }^2{r}^2}{12}& 0\\ 0& 0\end{array}\right)\left(\begin{array}{c}{(u_{xx})}_{ij-1}^n+{(u_{yy})}_{ij-1}^n\\ {(v_{xx})}_{ij-1}^n+{(v_{yy})}_{ij-1}^n\end{array}\right)\\ & +\left(\begin{array}{cc}\frac{a^2{\tau }^2{r}^2}{12}& 0\\ 0& 0\end{array}\right)\left(\begin{array}{c}{(u_{xx})}_{i-1j}^n+{(u_{yy})}_{i-1j}^n\\ {(v_{xx})}_{i-1j}^n+{(v_{yy})}_{i-1j}^n\end{array}\right)\\ & +\left(\begin{array}{cc}\frac{a^2{\tau }^2{r}^2}{12}& 0\\ 0& 0\end{array}\right)\left(\begin{array}{c}{(u_{xx})}_{i+1j}^n+{(u_{yy})}_{i+1j}^n\\ {(v_{xx})}_{i+1j}^n+{(v_{yy})}_{i+1j}^n\end{array}\right).\end{array}$$

(26)

Letting $U_{ij}^{n} = {(u_{ij}^{n},v_{ij}^{n})^{T}}$, $U_{ij}^{n} = {\zeta ^{n}}{e^{I({\sigma _{1}}h + {\sigma _{2}}h)}}$, then substituting them into Eq. (26), we get

$$\begin{array}{rl}{\xi }^{n+1}& =\left(\begin{array}{cc}2& -1\\ 1& 0\end{array}\right){\xi }^n+\left(\begin{array}{cc}{a}^2{\tau }^2-\frac{a^2{\tau }^2{r}^2}{3}& 0\\ 0& 0\end{array}\right)({\eta }^n+{\gamma }^n)\\ & +\left(\begin{array}{cc}\frac{a^2{\tau }^2{r}^2}{12}{e}^{I{\sigma }_{2}h}& 0\\ 0& 0\end{array}\right)({\eta }^n+{\gamma }^n)+\left(\begin{array}{cc}\frac{a^2{\tau }^2{r}^2}{12}{e}^{-I{\sigma }_{2}h}& 0\\ 0& 0\end{array}\right)({\eta }^n+{\gamma }^n)\\ & +\left(\begin{array}{cc}\frac{a^2{\tau }^2{r}^2}{12}{e}^{-I{\sigma }_{1}h}& 0\\ 0& 0\end{array}\right)({\eta }^n+{\gamma }^n)+\left(\begin{array}{cc}\frac{a^2{\tau }^2{r}^2}{12}{e}^{I{\sigma }_{1}h}& 0\\ 0& 0\end{array}\right)({\eta }^n+{\gamma }^n),\end{array}$$

(27)

in which $\lambda = \tau /h$, $r = a\lambda$. Substituting Eq. (24) and Eq. (25) into Eq. (27), we get the propagation matrix of error of the EFOC difference scheme (21) as follows:

$$G(\tau ,{\sigma }_1,{\sigma }_2)=\left(\begin{array}{cc}C& -1\\ 1& 0\end{array}\right),$$

(28)

in which

$$\begin{aligned} C &= 2 + 2{r^{4}} \bigl[\cos ({\sigma _{1}}h) + \cos ({ \sigma _{2}}h) - 2 \bigr] \biggl[ \frac{{\cos ({\sigma _{1}}h) - 1}}{{\cos ({\sigma _{1}}h) + 5}} + \frac{{\cos ({\sigma _{2}}h) - 1}}{{\cos ({\sigma _{2}}h) + 5}} \biggr] \\ &\quad{} + 12{r^{2}} \biggl[ \frac{{\cos ({\sigma _{1}}h) - 1}}{{\cos ({\sigma _{1}}h) + 5}} + \frac{{\cos ({\sigma _{2}}h) - 1}}{{\cos ({\sigma _{2}}h) + 5}} \biggr], \end{aligned}$$

(29)

the eightvalues μ of $G(\tau ,{\sigma _{1}},{\sigma _{2}})$ satisfy the following equation:

$$\begin{aligned} {\mu ^{2}} - b\mu + 1 = 0, \end{aligned}$$

(30)

where

$$\begin{aligned} b &= 2 + 2{r^{4}} \bigl[\cos ({\sigma _{1}}h) + \cos ({ \sigma _{2}}h) - 2 \bigr] \biggl[ \frac{{\cos ({\sigma _{1}}h) - 1}}{{\cos ({\sigma _{1}}h) + 5}} + \frac{{\cos ({\sigma _{2}}h) - 1}}{{\cos ({\sigma _{2}}h) + 5}} \biggr] \\ &\quad {} + 12{r^{2}} \biggl[ \frac{{\cos ({\sigma _{1}}h) - 1}}{{\cos ({\sigma _{1}}h) + 5}} + \frac{{\cos ({\sigma _{2}}h) - 1}}{{\cos ({\sigma _{2}}h) + 5}} \biggr]. \end{aligned}$$

(31)

From Lemma 1, we know that the necessary and sufficient condition for $\vert \mu \vert \le 1$ is $\vert b \vert \le 2$, i.e.,

$$\begin{aligned} \begin{aligned}[b] & \biggl\vert 2 + 2{r^{4}} \bigl[\cos ({\sigma _{1}}h) + \cos ({\sigma _{2}}h) - 2 \bigr] \biggl[ \frac{{\cos ({\sigma _{1}}h) - 1}}{{\cos ({\sigma _{1}}h) + 5}} + \frac{{\cos ({\sigma _{2}}h) - 1}}{{\cos ({\sigma _{2}}h) + 5}} \biggr] \\ &\quad {} + 12{r^{2}} \biggl[ \frac{{\cos ({\sigma _{1}}h) - 1}}{{\cos ({\sigma _{1}}h) + 5}} + \frac{{\cos ({\sigma _{2}}h) - 1}}{{\cos ({\sigma _{2}}h) + 5}} \biggr] \biggr\vert \le 2. \end{aligned} \end{aligned}$$

(32)

Inequality (32) is equivalent to two inequalities as follows:

$$\begin{aligned}& \begin{aligned}[b] &2{r^{4}} \bigl[\cos ({\sigma _{1}}h) + \cos ({\sigma _{2}}h) - 2 \bigr] \biggl[ \frac{{\cos ({\sigma _{1}}h) - 1}}{{\cos ({\sigma _{1}}h) + 5}} + \frac{{\cos ({\sigma _{2}}h) - 1}}{{\cos ({\sigma _{2}}h) + 5}} \biggr] \\ &\quad{} + 12{r^{2}} \biggl[ \frac{{\cos ({\sigma _{1}}h) - 1}}{{\cos ({\sigma _{1}}h) + 5}} + \frac{{\cos ({\sigma _{2}}h) - 1}}{{\cos ({\sigma _{2}}h) + 5}} \biggr] \le 0, \end{aligned} \end{aligned}$$

(33)

$$\begin{aligned}& \begin{aligned}[b] &2{r^{4}} \bigl[\cos ({\sigma _{1}}h) + \cos ({\sigma _{2}}h) - 2 \bigr] \biggl[ \frac{{\cos ({\sigma _{1}}h) - 1}}{{\cos ({\sigma _{1}}h) + 5}} + \frac{{\cos ({\sigma _{2}}h) - 1}}{{\cos ({\sigma _{2}}h) + 5}} \biggr] \\ &\quad {}+ 12{r^{2}} \biggl[ \frac{{\cos ({\sigma _{1}}h) - 1}}{{\cos ({\sigma _{1}}h) + 5}} + \frac{{\cos ({\sigma _{2}}h) - 1}}{{\cos ({\sigma _{2}}h) + 5}} \biggr] + 4 \ge 0. \end{aligned} \end{aligned}$$

(34)

For inequality (33), it can be easily solved

$$\begin{aligned} 0 \le {r^{2}} \le \frac{6}{{2 - \cos ({\sigma _{1}}h) - \cos ({\sigma _{2}}h)}}, \end{aligned}$$

(35)

because inequality (35) must hold for arbitrary ${\sigma _{1}}$ and ${\sigma _{2}}$, we have

$$\begin{aligned} 0 \le {r^{2}} \le \frac{6}{{2 - ( - 1) - ( - 1)}} = \frac{3}{2},\quad \text{or}\quad \vert a \vert \lambda \le \sqrt{6} /2. \end{aligned}$$

(36)

For inequality (34), we can easily get the two roots of its equality form

$$\begin{aligned} \begin{aligned}[b] r_{1,2}^{2} = {}&\frac{3}{{2 - \cos ({\sigma _{1}}h) - \cos ({\sigma _{2}}h)}} \\ &{}\pm \sqrt{ \frac{9}{{{{[2 - \cos ({\sigma _{1}}h) - \cos ({\sigma _{2}}h)]}^{2}}}} - \frac{2}{{[2 - \cos ({\sigma _{1}}h) - \cos ({\sigma _{2}}h)]A}}}, \end{aligned} \end{aligned}$$

(37)

where $A = \frac{{1 - \cos ({\sigma _{1}}h)}}{{\cos ({\sigma _{1}}h) + 5}} + \frac{{1 - \cos ({\sigma _{2}}h)}}{{\cos ({\sigma _{2}}h) + 5}}$. Letting $\alpha = 1 - \cos ({\sigma _{1}}h)$, $\beta = 1 - \cos ({\sigma _{2}}h)$, we have

$$\begin{aligned} S(\alpha ,\beta ) = \frac{3}{{\alpha + \beta }} + \sqrt{ \frac{9}{{{{(\alpha + \beta )}^{2}}}} - \frac{2}{{(\alpha + \beta )(\frac{\alpha }{{6 - \alpha }} + \frac{\beta }{{6 - \beta }})}}}, \end{aligned}$$

(38)

since $\alpha \in [0,2]$, $\beta \in [0,2]$, we notice that when $\alpha = \beta = 2$, $S{(\alpha ,\beta )_{\min }} = S(2,2) = 1$, i.e., $r_{1}^{2} = 1$. On the other hand, we notice that $r_{1}^{2}$ and $r_{2}^{2}$ are symmetric about $\frac{3}{{\alpha + \beta }}$, so we can get that the other root of Eq. (38) is $1/2$. Thus, we get that the solution of inequality (34) is

$$\begin{aligned} \vert r \vert \in [0,\sqrt{2} /2] \cup [1, + \infty ),\quad \text{or}\quad \vert a \vert \lambda \in [0,\sqrt{2} /2] \cup [1, + \infty ). \end{aligned}$$

(39)

Combining inequalities (36) and (39), we get that the stability condition of the EFOC difference scheme (21) is

$$\begin{aligned} \vert a \vert \lambda \in [0,\sqrt{2} /2] \cup [1,\sqrt{6} /2]. \end{aligned}$$

(40)

Remark 1

Table 1 gives the stability regions of the EFOC difference scheme and several ADI and LOD schemes proposed in Ref. [5]. We find that a critical value for the stability condition is 0.7321 for the THOC-ADI scheme and the HOC-LOD scheme, 0.7657 for the CPD-ADI scheme, and 0.8186 for the NCPD-ADI scheme, while just 0.7071 for the present EFOC scheme. But the EFOC scheme has another stability region $[1, 1.2247]$, i.e., we can use comparably bigger temporal step length to decrease computational cost only if we choose appreciate values of mesh ratio between 1 and 1.2247. In other words, the EFOC scheme has a wider range of stability conditions than the ADI and LOD schemes in the literature.

Table 1 CFL conditions for various finite difference schemes

3 Numerical experiments

To validate the accuracy and stability of the present EFOC scheme, two test problems are solved by the present EFOC scheme with different temporal step length, spatial step length, and final time. Numerical results for ${L_{\infty }}$ and ${L_{2} }$ norm errors and convergence rate are given, in which ${L_{\infty }}$ and ${L_{2}}$ norm errors and convergence rate are defined as follows:

$$\begin{aligned}& {L_{\infty }} \textit{-error} = \max_{ij} \bigl\vert {u_{ij}^{n} - u({x_{i}},{y_{j}},{t_{n}})} \bigr\vert , \\& {L_{2}}\textit{-error} = \sqrt{{h^{2}}\sum _{ij} {{{ \bigl[u_{ij}^{n} - u({x_{i}},{y_{j}},{t_{n}}) \bigr]}^{2}}} }, \\& \mathit{Rate} = \frac{{\log (\frac{{{L_{\infty }} \textit{-error}({h_{1}})}}{{{L_{\infty }} \textit{-error}({h_{2}})}})}}{{\log (\frac{{{h_{1}}}}{{{h_{2}}}})}}. \end{aligned}$$

Problem 1

([5])

$$\begin{aligned} &\frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} = \frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} + \frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}}, \quad 0 < x,y < 1 ,t > 0, \\ &u(x,y,0) = \cos ( - x - y),\quad\quad \frac{{\partial u(x,y,0)}}{{\partial t}} = - \sqrt{2} \sin ( - x - y), \\ &u(0,y,t) = \cos (\sqrt{2} t - y),\quad\quad u(1,y,t) = \cos (\sqrt{2} t - 1 - y), \\ &u(x,0,t) = \cos (\sqrt{2} t - x),\quad\quad u(x,1,t) = \cos (\sqrt{2} t - x - 1), \end{aligned}$$

the exact solution is

$$\begin{aligned} u(x,t) = \cos (\sqrt{2} t - x - y). \end{aligned}$$

Table 2 and Table 3 give $L_{\infty }$ and $L_{2}$ norm errors for $t=1$ with $\tau =0.0025$ and different spatial grid sizes for Problem 1 with the EFOC scheme, respectively. For comparison, we also list the computed results in Ref. [5], in which the THOC-ADI scheme, the HOC-LOD scheme, the CPD-ADI scheme, and the IPD-ADI schemes were given. We find that all of these schemes reach fourth-order accuracy. The EFOC scheme yields a bit more accurate solution than the THOC-ADI scheme, the HOC-LOD scheme, and the CPD-ADI scheme, but a bit less accurate than the IPD-ADI scheme. But we notice that the IPD-ADI scheme, with five grid points along one direction, is non-compact, so the computation process is more complicated and the computational cost is higher than that of the present EFOC scheme.

Table 2 The $L_{\infty }$ norm error with $\tau = 0.0025$ at $t = 1$ for different h for Problem 1

Table 3 The $L_{2}$ norm error with $\tau = 0.0025$ at $t = 1$ for Problem 1

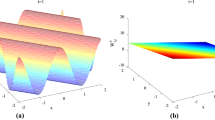
Figure 1 shows the numerical solution (a), the exact solution (b), the absolute error (c), and the contour plots of the numerical solution and exact solution (d) by the EFOC scheme in this article when $\tau =0.0025$, $t=1$, $N=40$, respectively, for Problem 1. It can be seen from Fig. 1 that the numerical solution in this article agrees well with the exact solution.

Figure 1

(a) The numerical solution, (b) the exact solution, (c) the absolute error, and (d) the contour plots of the numerical solution and exact solution with $\tau =0.0025$, $t=1$, $N=40$, respectively, for Problem 1

Problem 2

([34])

$$\begin{aligned} &\frac{{{\partial ^{2}}u}}{{\partial {t^{2}}}} = \frac{{{\partial ^{2}}u}}{{\partial {x^{2}}}} + \frac{{{\partial ^{2}}u}}{{\partial {y^{2}}}}, \quad 0 < x,y < 1 ,t > 0, \\ &u(x,y,0) = \sin (\pi x)\sin (\pi y),\quad\quad \frac{{\partial u(x,y,0)}}{{\partial t}} = 0, \\ &u(0,y,t) = u(1,y,t) = u(x,0,t) = u(x,1,t) = 0, \end{aligned}$$

the exact solution is

$$\begin{aligned} u(x,y,t) = \sin (\pi x)\sin (\pi y)\cos (\sqrt{2} \pi t). \end{aligned}$$

We computed this problem with the present EFOC scheme and compared the results with Ref. [34], in which a local one-dimensional scheme (New LOD scheme) and a typical fourth-order scheme are developed. Table 4 gives the numerical results with $\tau =0.0002$, $h = 1/10,1/20,\ldots,1/320$, and $t=0.02$. It shows that the $L_{\infty }$ and $L_{2}$ norm errors of the three schemes decrease on behalf of the spatial grid size and fourth-order accuracy is obtained. We notice that the present EFOC scheme produces more accurate solution than the new LOD scheme and the typical fourth-order scheme [34].

Table 4 The $L_{\infty }$ and $L_{2}$ norm errors with $\tau =0.0002$ at $t=0.02$ for different h for Problem 2

Figure 2 shows the numerical solution (a), the exact solution (b), the absolute error (c), and the contour plots of the numerical solution and exact solution (d) for the EFOC scheme of Problem 2 when $\tau =0.0002$, $t=0.02$, $N=40$, respectively. In Fig. 2(d) the solid line is exact solution and the dotted line is numerical solution. It is not difficult to find that the numerical solution obtained from the EFOC scheme in this article agrees well with the exact solution, and the dispersion error is very small.

Figure 2

(a) The numerical solution, (b) the exact solution, (c) the absolute error, and (d) the contour plots of the numerical solution and exact solution with $\tau =0.0002$, $t=0.02$, $N=40$, respectively, for Problem 2

4 Conclusion

In this paper, an explicit fourth-order compact difference scheme is proposed for solving the 2D wave equation. It is constructed by applying the fourth-order accurate Padé scheme in space and the remainder of the truncation error correction of the second-order central difference method is employed to discrete temporal derivative. The truncation error of the schemes is $O({\tau ^{4}} + {\tau ^{2}}{h^{2}} + {h^{4}})$, which means the scheme has an overall fourth-order accuracy. Afterwards, the stability condition of the scheme, which is $\vert a \vert \lambda \in [0,\sqrt{2} /2] \cup [1,\sqrt{6} /2]$, is obtained by the Fourier analysis method. Since the EFOC scheme has another stability region $[1,\sqrt{6} /2]$, it allows us to use relatively bigger temporal step length to decrease computational cost. Finally, the accuracy and reliability of the present scheme are verified by some numerical experiments.

Recently, some authors have considered high-order compact difference schemes for the wave equation with a variable coefficient [2, 12] or with a nonlinear source term [6]. An implicit difference scheme is constructed and an iterative method is employed to resolve the arising linear system [2, 12], or the ADI method and Newton’s iterative method are used [6]. To generalize the present explicit high-order compact difference method to these two kinds of problems is our research interest in the near future.