1 Introduction

Deterministic Nicholson’s blowflies models (including their various generalized forms) have been extensively studied, see e.g. [1–6]. In [7], Wang studied a class of impulsive stochastic Nicholson’s blowflies models with patch structure and nonlinear harvesting terms on time scales and obtained the existence and exponential stability of piecewise mean-square almost periodic solutions for the model by using the contraction mapping principle and the Gronwall–Bellman inequality technique. The authors [8] considered a class of impulsive stochastic Nicholson’s blowflies models. By applying Cauchy matrix, they obtained the existence and exponential stability of square-mean almost periodic solutions for the model with multiple nonlinear harvesting terms and delays. In recent years, the research for stochastic Nicholson’s blowflies models has gradually become a hot topic. In 2019, Wang et al. [9] studied a stochastic Nicholson’s blowflies delayed differential equation. After that, Zhu et al. [10] generalized the equation in [9] to the stochastic Nicholson’s blowflies delay differential equation with regime switching.

Furthermore, behaviors of population model are influenced and determined by incorporating migration [11]. Hence, adding patch structure term in the Nicholson’s blowflies models appears to be necessary. In 2001, Berezansky et al. [12] investigated a deterministic Nicholson’s blowflies system with patch structure as follows:

$$ \textstyle\begin{cases} x_{1}'(t)=-(a_{1}+b_{2})x_{1}(t)+b_{1}x_{2}(t)+p_{1}x_{1}(t-\tau )e^{- \gamma _{1}x_{1}(t)}, \\ x_{2}'(t)=-(a_{2}+b_{1})x_{2}(t)+b_{2}x_{1}(t)+p_{2}x_{2}(t-\tau )e^{- \gamma _{2}x_{2}(t)}. \end{cases} $$
(1.1)

Then, in 2019, Wang, Shi, and Chen [13], Yi and Liu [14] generalized Nicholson’s blowflies system in [12] to the following two-dimensional stochastic system:

$$ \textstyle\begin{cases} dx_{1}(t)=[-(a_{1}+b_{2})x_{1}(t)+b_{1}x_{2}(t)+p_{1}x_{1}(t-\tau )e^{- \gamma _{1}x_{1}(t)}]\,dt +\sigma _{1}x_{1}(t)\,dB_{1}(t), \\ dx_{2}(t)=[-(a_{2}+b_{1})x_{2}(t)+b_{2}x_{1}(t)+p_{2}x_{2}(t-\tau )e^{- \gamma _{2}x_{2}(t)}]\,dt +\sigma _{2}x_{2}(t)\,dB_{2}(t). \end{cases} $$
(1.2)

For more results about Nicholson’s blowflies system, see e.g. [15–17].

Motivated by the above discussions, this paper is devoted to studying a stochastic Nicholson’s blowflies system involving mixed delays and patch structure as follows:

$$ \textstyle\begin{cases} dx_{1}(t)= [-a_{11}(t)+b_{11}(t)e^{-x_{1}(t)}+a_{12}(t)-b_{12}(t)e^{-x_{2}(t)} \\ \hphantom{dx_{1}(t)=}{} +\alpha _{11}(t)x_{1}(t-\tau _{11}(t))e^{-\beta _{11}(t)x_{1}(t- \gamma _{11}(t))} \\ \hphantom{dx_{1}(t)=} {} +\alpha _{12}(t)x_{1}(t-\tau _{12}(t))e^{-\beta _{12}(t)x_{1}(t- \gamma _{12}(t))} ]\,dt+\sigma _{1}(t)x_{1}(t)\,dB_{1}(t), \\ dx_{2}(t)= [-a_{22}(t)+b_{22}(t)e^{-x_{2}(t)}+a_{21}(t)-b_{21}(t)e^{-x_{1}(t)} \\ \hphantom{dx_{2}(t)=} {} +\alpha _{21}(t)x_{2}(t-\tau _{21}(t))e^{-\beta _{21}(t)x_{2}(t- \gamma _{21}(t))} \\ \hphantom{dx_{2}(t)=}{} +\alpha _{22}(t)x_{2}(t-\tau _{22}(t))e^{-\beta _{22}(t)x_{2}(t- \gamma _{22}(t))} ]+\sigma _{2}(t)x_{2}(t)\,dB_{1}(t), \end{cases} $$
(1.3)

with the initial condition

$$ x_{i}(t)=\phi _{i}(t)\in C\bigl([-\tau ,0], \mathbb{R}^{+}\bigr),\quad t\in [-\tau ,0], i=1,2, $$
(1.4)

which has the maximum norm \(\Vert \cdot \Vert \), where \(\mathbb{R}^{+}=(0,\infty )\), \(\tau =\max_{t\geq 0}\{\tau _{ij}(t),\gamma _{ij}(t),i,j=1,2\}\). For \(i,j=1,2\), \(a_{ij}\), \(b_{ij}\), \(\alpha _{ij}\), \(\beta _{ij}\), \(\sigma _{i}(t)\), \(\tau _{ij}(t)\), and \(\gamma _{ij}(t)\), are all positive continuous functions. When the case \(\tau _{ij}=\gamma _{ij}\) (\(i,j=1,2\)), there exist lots of results, see [9–12]. For \(i,j=1,2\), \(a_{ii}(t)-b_{ii}(t)e^{-x_{i}(t)}\) is a density-dependent mortality term in ith patch; \(\alpha _{ij}(t)x_{i}(t-\tau _{ij}(t))e^{-\beta _{ij}(t)x_{i}(t- \gamma _{ij}(t))}\) is a birth function with maturation delay \(\tau _{ij}\) and feedback delay \(\gamma _{ij}\); \(B_{i}(t)\) is the standard Brownian motion defined on a complete probability space \((\varOmega ,\mathcal{F}, \mathbb{P})\) with a filtration \(\{\mathcal{F}_{t}\}_{t\geq 0}\). Throughout this paper, denote \(f^{+}=\sup_{t\geq 0}f(t)\), \(f^{-}=\inf_{t\geq 0}f(t)\).

The main highlights list as follows:

  1. (1)

    We study a new stochastic model which is a generalization of the classic Nicholson’s blowflies system;

  2. (2)

    We develop a stochastic analysis technique for studying dynamic properties of the stochastic Nicholson’s blowflies system.

The following sections are organized as follows: In Sect. 2, we obtain some sufficient conditions for global existence and uniqueness to a positive solution of system (1.3). In Sect. 3, we obtain stochastically ultimate boundedness positive solution of system (1.3). Section 4 gives global asymptotic stability of system (1.3). In Sect. 5, a numerical example verifies the accuracy of the results in the present paper. Section 6 contains some conclusions of this paper and further research for the topic of this paper.

2 Existence and uniqueness of global positive solution

Theorem 2.1

For any given initial data (1.4), there is a unique positive solution\((x_{1}(t), x_{2}(t))^{\top }\)on\([-\tau ,\infty )\)and the solution will remain in\(\mathbb{R}^{+}\times \mathbb{R}^{+}\)with probability one.

Proof

The proof method of this theorem comes from Theorem 2.1 in Sect. 11.2 of [18]. Since the coefficients of (1.3) satisfy the local Lipschitz condition, then for any given initial condition (1.4), there exists a unique local solution \(x_{1}(t)\) and \(x_{2}(t)\) on \([\tau ,\tau _{b})\), where \(\tau _{b}\) is explosion time. For showing this solution is global, we shall prove \(\tau _{b}=\infty \) a.s. Let \(k_{0}>0\) be sufficiently large for initial values (1.4) in \((\frac{1}{k_{0}},k_{0})\). For each \(k>k_{0}\), define the stopping time

$$ \tau _{n}=\inf \biggl\{ t\in [0,\tau _{b}), x_{i}(t)\notin \biggl(\frac{1}{k_{0}},k_{0}\biggr), i=1,2 \biggr\} . $$

Obviously, \(\tau _{n}\) is increasing as \(n\rightarrow \infty \) and \(\tau _{\infty }\leq \tau _{b}\) a.s. Set \(\inf \emptyset =\infty \), where ∅ is an empty set. We claim that if \(\tau _{\infty }=\infty \), then \(\tau _{b}=\infty \) and \(x_{i}(t)\in \mathbb{R}^{+}\) for \(i=1,2\), \(t\geq 0\). If not, there exist constants \(T>0\) and \(\varepsilon \in (0,1)\) such that \(\mathbb{P}(\tau _{\infty }\leq T)>\varepsilon \). Thus, there exists a number \(n_{1}>n_{0}\) such that \(\mathbb{P}(\tau _{\infty }\leq T)>\varepsilon \) for \(n>n_{1}\). Define a \(C^{2}\)-function \(V:\mathbb{R}^{+}\times \mathbb{R}^{+}\rightarrow \mathbb{R}^{+}\) by \(V(x_{1},x_{2})=\sum_{i=1}^{2}(x_{i}-1-\ln x_{i})\). Itô’s formula shows that

$$ \begin{aligned}[b] dV(x_{1},x_{2})&= \biggl[ \biggl(1-\frac{1}{x_{1}}\biggr)F(x_{1},x_{2})+ \frac{\sigma _{1}^{2}}{2} \biggr]\,dt+\sigma _{1}(x_{1}-1) \,dB_{1}(t) \\ & {} + \biggl[\biggl(1-\frac{1}{x_{2}}\biggr)G(x_{1},x_{2})+ \frac{\sigma _{2}^{2}}{2} \biggr]\,dt+\sigma _{2}(x_{2}-1) \,dB_{2}(t), \end{aligned} $$
(2.1)

where

$$ \begin{gathered} \begin{aligned} F(x_{1},x_{2})&=-a_{11}(t)+b_{11}(t)e^{-x_{1}(t)}+a_{12}(t)-b_{12}(t)e^{-x_{2}(t)} \\ &\quad {} +\alpha _{11}(t)x_{1}\bigl(t-\tau _{11}(t) \bigr)e^{-\beta _{11}(t)x_{1}(t- \gamma _{11}(t))} \\ &\quad {} +\alpha _{12}(t)x_{1}\bigl(t-\tau _{12}(t) \bigr)e^{-\beta _{12}(t)x_{1}(t- \gamma _{12}(t))}, \end{aligned} \\ \begin{aligned} G(x_{1},x_{2})&=-a_{22}(t)+b_{22}(t)e^{-x_{2}(t)}+a_{21}(t)-b_{21}(t)e^{-x_{1}(t)} \\ &\quad {} +\alpha _{21}(t)x_{2}\bigl(t-\tau _{21}(t) \bigr)e^{-\beta _{21}(t)x_{2}(t- \gamma _{21}(t))} \\ &\quad {} +\alpha _{22}(t)x_{2}\bigl(t-\tau _{22}(t) \bigr)e^{-\beta _{22}(t)x_{2}(t- \gamma _{22}(t))}. \end{aligned} \end{gathered} $$
(2.2)

Compute the term in (2.1):

$$ \begin{aligned}[b] &\biggl(1-\frac{1}{x_{1}}\biggr)F(x_{1},x_{2}) \\ &\quad = \biggl(1-\frac{1}{x_{1}}\biggr) \bigl[-a_{11}(t)+b_{11}(t)e^{-x_{1}(t)}+a_{12}(t)-b_{12}(t)e^{-x_{2}(t)} \\ &\quad\quad {} +\alpha _{11}(t)x_{1}\bigl(t-\tau _{11}(t) \bigr)e^{-\beta _{11}(t)x_{1}(t- \gamma _{11}(t))} +\alpha _{12}(t)x_{1}\bigl(t-\tau _{12}(t)\bigr)e^{-\beta _{12}(t)x_{1}(t- \gamma _{12}(t))} \bigr] \\ &\quad \leq \biggl(1-\frac{1}{x_{1}}\biggr) \bigl[-a_{11}+a_{12}+b_{11}e^{-x_{1}}-b_{12}e^{-x_{2}} \\ &\quad\quad {} +\alpha _{11}\bigl( \Vert \phi _{1} \Vert +x_{1}\bigr)e^{-\beta _{11}(t)x_{1}}+\alpha _{12}\bigl( \Vert \phi _{1} \Vert +x_{1}\bigr)e^{-\beta _{12}(t)x_{1}} \bigr] \\ &\quad \leq a_{12}^{+}+b_{11}^{+}+\alpha _{11}^{+} \Vert \phi _{1} \Vert + \frac{\alpha _{11}^{+}}{\beta _{11}^{-}e} +\alpha _{12}^{+} \Vert \phi _{1} \Vert + \frac{\alpha _{12}^{+}}{\beta _{12}^{-}e}:=K_{1}, \end{aligned} $$
(2.3)

where we use \(\sup_{x\in \mathbb{R}^{+}}xe^{-x}=\frac{1}{e}\). Similar to the above proof, we gain

$$ \biggl(1-\frac{1}{x_{2}}\biggr)G(x_{1},x_{2})\leq a_{21}^{+}+b_{22}^{+}+\alpha _{21}^{+} \Vert \phi _{2} \Vert + \frac{\alpha _{21}^{+}}{\beta _{21}^{-}e} +\alpha _{22}^{+} \Vert \phi _{2} \Vert +\frac{\alpha _{22}^{+}}{\beta _{22}^{-}e}:=K_{2}. $$
(2.4)

Let

$$ \operatorname{LV}(x_{1},x_{2})=\biggl(1-\frac{1}{x_{1}} \biggr)F(x_{1},x_{2})+ \frac{\sigma _{1}^{2}}{2} +\biggl(1- \frac{1}{x_{2}}\biggr)G(x_{1},x_{2})+ \frac{\sigma _{2}^{2}}{2}. $$

By (2.3) and (2.4), there is a constant \(K>0\) such that

$$ \operatorname{LV}(x_{1},x_{2})\leq K. $$
(2.5)

Integrating both sides of (2.5) from −τ to \(\tau _{n}\wedge T\) and taking the expectation \(\mathbb{E}\), it follows by (2.1) that

$$ \mathbb{E}V\bigl(x_{1}(\tau _{n}\wedge T),x_{2}(\tau _{n}\wedge T)\bigr)\leq V \bigl(x_{1}(- \tau ),x_{2}(-\tau )\bigr)+K(t+\tau ). $$

Let \(\varTheta _{n}=\{\tau _{n}\leq T\}\), then \(\mathbb{P}(\varTheta _{n})\geq \varepsilon \). Then, for each \(\vartheta \in \varTheta _{n}\), \(x_{1}(\tau _{n},\vartheta )\) or \(x_{2}(\tau _{n},\vartheta )\) equals n or \(\frac{1}{n}\) Thus, \(V(x_{1}(\tau _{n}\wedge T),x_{2}(\tau _{n}\wedge T))\) is no less than \((n-1-\ln n)\wedge (\frac{1}{n}-\ln n)\). Thus,

$$ \begin{aligned} V\bigl(x_{1}(-\tau ),x_{2}(- \tau )\bigr)+K(t+\tau )&\geq \mathbb{E} \bigl[1_{ \varTheta _{n}}V \bigl(x_{1}(\tau _{n} ),x_{2}(\tau _{n})\bigr) \bigr] \\ &\geq \mathbb{P}(\varTheta _{n}) \biggl[(n-1-\ln n)\wedge \biggl(\frac{1}{n}-\ln n\biggr) \biggr] \\ &\geq \varepsilon \biggl[(n-1-\ln n)\wedge \biggl(\frac{1}{n}-\ln n \biggr) \biggr], \end{aligned}$$

where \(1_{\varTheta _{n}}\) is the indicator function of \(\varTheta _{n}\). Letting \(n\rightarrow \infty \) leads to \(\infty >V(x_{1}(-\tau ),x_{2}(-\tau ))+KT=\infty \), which is a contradiction. So we gain \(\tau _{\infty }=\infty \) a.s. The proof is finished. □

3 Stochastically ultimate boundedness

Definition 3.1

System (1.3) is said to be stochastically ultimately bounded if, for \(\varepsilon \in (0,1)\), there exists a constant \(L(\varepsilon )\) such that, for any initial data (1.4), the solution \(x=(x_{1},x_{2})^{\top }\) of (1.3) satisfies

$$ \lim_{t\rightarrow \infty }\sup \mathbb{P}\bigl\{ \bigl\vert x(t) \bigr\vert \leq L\bigr\} \geq 1- \varepsilon . $$

Lemma 3.1

Let\(\gamma \in (0,1)\). There is a constant\(M(\gamma )>0\)which is independent initial data (1.4) such that the solution\(x=(x_{1},x_{2})^{\top }\)of (1.3) satisfies\(\lim_{t\rightarrow \infty }\sup \mathbb{E} \vert x(t) \vert ^{\gamma }\leq M\).

Proof

Let \(V(x_{1},x_{2})=x_{1}^{\gamma }+x_{2}^{\gamma }\) for \(\gamma \in (0,1)\), \(x_{1},x_{2}>0\). Itô’s formula shows that

$$ \begin{aligned} dV(x_{1},x_{2})&= \mathcal{L}V(x_{1},x_{2})\,dt+\sigma _{1}\gamma x_{1}^{\gamma }\,dB_{1}(t)+\sigma _{2} \gamma x_{2}^{\gamma }\,dB_{2}(t), \end{aligned} $$
(3.1)

where

$$ \begin{aligned}[b] \mathcal{L}V(x_{1},x_{2})&= \gamma x_{1}^{\gamma -1}F(x_{1},x_{2})+0.5 \gamma (\gamma -1)\sigma _{1}^{2}x_{1}^{\gamma } \\ & \quad {} +\gamma x_{2}^{\gamma -1}G(x_{1},x_{2})+0.5 \gamma (\gamma -1)\sigma _{2}^{2}x_{2}^{\gamma }, \end{aligned} $$
(3.2)

\(F(x_{1},x_{2})\) and \(G(x_{1},x_{2})\) are defined by (2.2). Compute the term in (3.2):

$$ \begin{aligned}[b] \gamma x_{1}^{\gamma -1}F(x_{1},x_{2})&= \gamma x_{1}^{\gamma -1} \bigl[ -a_{11}(t)+b_{11}(t)e^{-x_{1}(t)}+a_{12}(t)-b_{12}(t)e^{-x_{2}(t)} \\ &\quad {} +\alpha _{11}(t)x_{1}\bigl(t-\tau _{11}(t) \bigr)e^{-\beta _{11}(t)x_{1}(t- \gamma _{11}(t))} \\ & \quad {} +\alpha _{12}(t)x_{1}\bigl(t-\tau _{12}(t) \bigr)e^{-\beta _{12}(t)x_{1}(t- \gamma _{12}(t))} \bigr] \\ &\leq \gamma b_{11}^{+}+\gamma a_{12}^{+}+ \gamma \alpha _{11}^{+} \Vert \phi _{1} \Vert +\frac{\gamma \alpha _{11}^{+}}{\beta _{11}^{-}e} +\gamma \alpha _{12}^{+} \Vert \phi _{1} \Vert + \frac{\gamma \alpha _{12}^{+}}{\beta _{12}^{-}e} :=M_{1}, \end{aligned} $$
(3.3)

where we use \(\sup_{x\in \mathbb{R}^{+}}xe^{-x}=\frac{1}{e}\). Similar to the above proof, we have

$$ \gamma x_{1}^{\gamma -1}G(x_{1},x_{2})\leq \gamma b_{22}^{+}+\gamma a_{21}^{+}+ \gamma \alpha _{21}^{+} \Vert \phi _{1} \Vert + \frac{\gamma \alpha _{21}^{+}}{\beta _{21}^{-}e} +\gamma \alpha _{22}^{+} \Vert \phi _{1} \Vert +\frac{\gamma \alpha _{22}^{+}}{\beta _{22}^{-}e} :=M_{2}. $$
(3.4)

In view of (3.1)–(3.4), we have

$$ \begin{aligned} dV(x_{1},x_{2})&=(M_{1}+M_{2}) \,dt+\sigma _{1}\gamma x_{1}^{\gamma } \,dB_{1}(t)+ \sigma _{2}\gamma x_{2}^{\gamma } \,dB_{2}(t). \end{aligned} $$
(3.5)

By (3.5) we gain

$$ \begin{aligned} d \bigl[e^{t}V(x_{1},x_{2}) \bigr]&=e^{t} \bigl[V(x_{1},x_{2}) \,dt+dV(x_{1},x_{2}) \bigr] \\ &\leq e^{t}(M_{1}+M_{2})\,dt+e^{t} \sigma _{1}\gamma x_{1}^{\gamma }\,dB_{1}(t)+e^{t} \sigma _{2}\gamma x_{2}^{\gamma }\,dB_{2}(t), \end{aligned}$$

and \(e^{t}\mathbb{E}V(x_{1},x_{2})\leq V(x_{1}(0),x_{2}(0))+(M_{1}+M_{2})e^{t}-M_{1}-M_{2}\), which implies \(\lim_{t\rightarrow \infty }\sup \mathbb{E}V(x_{1},x_{2})\leq M_{1}+M_{2}\). Furthermore, \(\vert x \vert ^{2}\leq 2 (\max \{x_{1},x_{2}\} )^{2}\), which implies

$$ \vert x \vert ^{\gamma }\leq 2^{\frac{\gamma }{2}} \bigl(\max \{x_{1},x_{2}\} \bigr)^{\gamma }\leq 2^{\frac{\gamma }{2}}V(x_{1},x_{2}). $$

Thus,

$$ \lim_{t\rightarrow \infty }\sup \mathbb{E} \vert x \vert ^{\gamma } \leq 2^{ \frac{\gamma }{2}}(M_{1}+M_{2}):=M. $$

 □

Theorem 3.1

System (1.3) is stochastically ultimately bounded.

Proof

By Lemma 3.1, there exists a positive constant \(K>0\) such that

$$ \lim_{t\rightarrow \infty }\sup \mathbb{E} \vert x \vert ^{\frac{1}{2}} \leq K. $$

Let \(H=\frac{K^{2}}{\varepsilon ^{2}}\). Then, for any \(\varepsilon >0\), by Chebyshev’s inequality, we have

$$ \mathbb{P}\bigl\{ \bigl\vert x(t) \bigr\vert > H\bigr\} \leq \frac{\mathbb{E} \vert x \vert ^{\frac{1}{2}}}{H^{\frac{1}{2}}}=\varepsilon . $$

Thus,

$$ \lim_{t\rightarrow \infty }\sup \mathbb{P}\bigl\{ \bigl\vert x(t) \bigr\vert \leq H\bigr\} \geq 1- \varepsilon . $$

 □

4 Global asymptotic stability

Definition 4.1

For any two positive solutions \((x_{1}(t),x_{2}(t))^{\top }\) and \((y_{1}(t),y_{2}(t))^{\top }\) of system (1.3), system (1.3) is said to be globally asymptotically stable if

$$ \lim_{t\rightarrow \infty } \bigl\vert x_{1}(t)-x_{2}(t) \bigr\vert =\lim_{t\rightarrow \infty } \bigl\vert y_{1}(t)-y_{2}(t) \bigr\vert =0 \quad \textit{a.s.} $$

Lemma 4.1

Let\((x_{1}(t),x_{2}(t))^{\top }\)be a solution of (1.3) with initial data (1.4). Then there exist constants\(L(p), G(p)>0\)such that

$$ \mathbb{E}\bigl[x_{1}^{p}(t)\bigr]\leq L(p) \quad \textit{and} \quad \mathbb{E}\bigl[x_{2}^{p}(t)\bigr] \leq G(p) \quad \textit{for all } p>1, t\geq -\tau . $$
(4.1)

Furthermore, each solution\((x_{1}(t),x_{2}(t))^{\top }\)of system (1.3) is uniformly continuous on\(t\geq 0\).

Proof

Define \(V(u)=u^{p}\) for \(u>0\) and \(p>1\). Itô’s formula shows that

$$ \begin{aligned} dV(x_{1})&=\bigl[px_{1}^{p-1}F(x_{1},x_{2})+0.5 \sigma _{1}^{2}p(p-1)x_{1}^{p}\bigr] \,dt+ \sigma _{1}px_{1}^{p} \,dB_{1}(t), \end{aligned} $$
(4.2)

where \(F(x_{1},x_{2})\) is defined by (2.2). Use Itô’s formula again to \(e^{t}V(x_{1})\) and (4.2), then

$$ \begin{aligned}[b] d\bigl[e^{t}V(x_{1}) \bigr]&=e^{t}V(x_{1})\,dt+e^{t} \,dV(x_{1}) \\ &=\bigl[e^{t}x_{1}^{p}+e^{t}px_{1}^{p-1}F(x_{1},x_{2})+0.5e^{t} \sigma _{1}^{2}p(p-1)x_{1}^{p}\bigr] \,dt+e^{t} \sigma _{1}px_{1}^{p} \,dB_{1}(t). \end{aligned} $$
(4.3)

Integrate both sides of (4.3) from −τ to t and and take expectations, then

$$ \begin{aligned} \mathbb{E}\bigl[e^{t}x_{1}^{p} \bigr]&\leq \phi _{1}^{p}(-\tau )+\mathbb{E} \int _{- \tau }^{t}e^{s}x_{1}^{p}(s) \bigl[1+ pb_{11}e^{-x_{1}}+pa_{12}+p\alpha _{11}\bigl( \Vert \phi _{1} \Vert +x_{1} \bigr)e^{-\beta _{11}x_{1}} \\ & \quad {} +p\alpha _{12}\bigl( \Vert \phi _{1} \Vert +x_{1}\bigr)e^{-\beta _{12}x_{1}}+0.5p(p-1) \sigma _{1}^{2} \bigr]\,ds \\ &\leq \phi _{1}^{p}(-\tau )+\mathbb{E} \int _{-\tau }^{t}e^{s}x_{1}^{p}(s) \biggl[1+ pb_{11}^{+}+pa_{12}^{+}+p \alpha _{11}^{+} \Vert \phi _{1} \Vert + \frac{p\alpha _{11}^{+}}{\beta _{11}^{-}e} \\ &\quad {} +p\alpha _{12}^{+} \Vert \phi _{1} \Vert + \frac{p\alpha _{12}^{+}}{\beta _{12}^{-}e}+0.5p(p-1) \bigl(\sigma _{1}^{2} \bigr)^{+} \biggr]\,ds. \end{aligned}$$

Thus,

$$ \mathbb{E}\bigl[e^{t}x_{1}^{p}\bigr]\leq \phi _{1}^{p}(-\tau )+ \int _{-\tau }^{t}L_{1}(p) \mathbb{E} \bigl[e^{s}x_{1}^{p}\bigr]\,ds, $$

where

$$ L_{1}(p)=1+ pb_{11}^{+}+pa_{12}^{+}+p \alpha _{11}^{+} \Vert \phi _{1} \Vert + \frac{p\alpha _{11}^{+}}{\beta _{11}^{-}e} +p\alpha _{12}^{+} \Vert \phi _{1} \Vert + \frac{p\alpha _{12}^{+}}{\beta _{12}^{-}e}+0.5p(p-1) \bigl(\sigma _{1}^{2}\bigr)^{+}. $$

By Gronwall’s inequality, we have \(\mathbb{E}[e^{t}x_{1}^{p}]\leq \phi _{1}^{p}(-\tau )e^{L_{1}(p)(t+ \tau )}\). Hence, there exists a constant \(T>0\) such that \(\mathbb{E}[x_{1}^{p}(t)]\leq 2e^{L_{1}(p)}\) for all \(t\geq T\). Due to \(\mathbb{E}[x_{1}^{p}(t)]\) is continuous, there exists a constant \(L_{2}>0\) such that \(\mathbb{E}[x_{1}^{p}(t)]\leq L_{2}\) for all \(t\in [-\tau ,T]\). Let \(L(p)=\max \{2e^{L_{1}(p)}, L_{2}, \Vert \phi _{1} \Vert \}\), then \(\mathbb{E}[x_{1}^{p}(t)]\leq L(p)\) for all \(t\geq -\tau \). Similar to the above proof, there exists a constant \(G(p)>0\) such that \(\mathbb{E}[x_{2}^{p}(t)]\leq G(p)\) for all \(t\geq -\tau \). □

Lemma 4.2

([19])

Assume that ann-dimensional stochastic process\(\mathcal{X}\)on\(t\geq 0\)satisfies the condition

$$ \mathbb{E} \bigl\vert \mathcal{X}(t)-\mathcal{X}(s) \bigr\vert ^{k_{1}}\leq c \vert t-s \vert ^{1+k_{2}} \quad \textit{for } t,s \geq 0, $$

where\(k_{1}\), \(k_{2}\), andcare positive constants. Then there is a continuous modification\(\overline{\mathcal{X}}(t)\)of\(\mathcal{X}(t)\)such that

$$ \mathbb{P} \biggl\{ \omega :\sup_{0< \vert t-s \vert < h(\omega )} \frac{\overline{\mathcal{X}}(t)-\mathcal{X}(t)}{ \vert t-s \vert ^{\theta }}\leq \frac{2}{1-2^{-\theta }} \biggr\} =1, $$

where\(h(\omega )\)is a positive random variable, \(\theta \in (0,\frac{k_{2}}{k_{1}})\). In other words, almost every sample path of\(\overline{\mathcal{X}}(t)\)is locally but uniformly Hölder continuous with exponent θ.

Lemma 4.3

Let\((x_{1}(t),x_{2}(t))^{\top }\)be a solution of (1.3) with initial data (1.4). Then almost every sample path of\((x_{1}(t),x_{2}(t))^{\top }\)is uniformly continuous on\(t\geq 0\).

Proof

The first equation of system (1.3) is equivalent to the following stochastic integer equation:

$$ \begin{aligned}[b] x_{1}(t)&=\phi _{1}(0)+ \int _{0}^{t} \bigl[-a_{11}(s)+b_{11}(s)e^{-x_{1}(s)}+a_{12}(s)-b_{12}(s)e^{-x_{2}(s)} \\ &\quad {} +\alpha _{11}(s)x_{1}\bigl(s-\tau _{11}(s) \bigr)e^{-\beta _{11}(s)x_{1}(s- \gamma _{11}(s))} \\ & \quad {} +\alpha _{12}(s)x_{1}\bigl(s-\tau _{12}(s) \bigr)e^{-\beta _{12}(s)x_{1}(s- \gamma _{12}(s))} \bigr]\,ds + \int _{0}^{t}\sigma _{1}(s)x_{1}(s) \,dB_{1}(s). \end{aligned} $$
(4.4)

By (4.1), computing the term in (4.4), we gain

$$\begin{aligned} \begin{aligned}[b] \mathbb{E} \bigl\vert F(x_{1},x_{2}) \bigr\vert ^{p}&\leq \mathbb{E} \bigl\vert a_{11}^{+}+b_{11}^{+}+a_{12}^{+}+b_{12}^{+}+ \alpha _{11}^{+} \Vert \phi _{1} \Vert + \alpha _{11}^{+}x_{1}+\alpha _{12}^{+} \Vert \phi _{1} \Vert +\alpha _{12}^{+}x_{1} \bigr\vert ^{p} \\ &\leq 2^{p-1} \bigl[\bigl(a_{11}^{+}+b_{11}^{+}+a_{12}^{+}+b_{12}^{+}+ \alpha _{11}^{+} \Vert \phi _{1} \Vert + \alpha _{12}^{+} \Vert \phi _{1} \Vert \bigr)^{p}+\bigl( \alpha _{11}^{+}+\alpha _{12}^{+}\bigr)\mathbb{E}x_{1}^{p} \bigr] \\ &\leq \mathbb{E} \bigl\vert a_{11}^{+}+b_{11}^{+}+a_{12}^{+}+b_{12}^{+}+ \alpha _{11}^{+} \Vert \phi _{1} \Vert + \alpha _{11}^{+}x_{1}+\alpha _{12}^{+} \Vert \phi _{1} \Vert +\alpha _{12}^{+}x_{1} \bigr\vert ^{p} \\ &\leq 2^{p-1} \bigl[\bigl(a_{11}^{+}+b_{11}^{+}+a_{12}^{+}+b_{12}^{+}+ \alpha _{11}^{+} \Vert \phi _{1} \Vert + \alpha _{12}^{+} \Vert \phi _{1} \Vert \bigr)^{p}+\bigl( \alpha _{11}^{+}+\alpha _{12}^{+}\bigr)L(p) \bigr] \\ &:=L_{1}(p). \end{aligned} \end{aligned}$$
(4.5)

Furthermore, by moment inequality for stochastic integrals, for \(0\leq t_{1}\leq t_{2}\) and \(p>2\), we gain

$$ \begin{aligned}[b] &\mathbb{E} \biggl\vert \int _{t_{1}}^{t_{2}}\sigma _{1}(t)x_{1}(t) \,dB_{1}(t) \biggr\vert ^{p} \\ &\quad \leq \bigl[\bigl(\sigma _{1}^{2}\bigr)^{+} \bigr]^{p}\bigl[0.5p(p-1)\bigr]^{\frac{p}{2}}(t_{2}-t_{1})^{ \frac{p}{2}-1} \int _{t_{1}}^{t_{2}} \mathbb{E} \bigl\vert x_{1}(t) \bigr\vert ^{p}\,dt \\ &\quad \leq \bigl[\bigl(\sigma _{1}^{2}\bigr)^{+} \bigr]^{p}\bigl[0.5p(p-1)\bigr]^{\frac{p}{2}}(t_{2}-t_{1})^{ \frac{p}{2}}L(p). \end{aligned} $$
(4.6)

 □

In view of (4.4)–(4.6), for \(0\leq t_{1}\leq t_{2}\), \(t_{2}-t_{1}\leq 1\), and \(p>2\), we have

$$ \begin{aligned} \mathbb{E} \bigl\vert x_{1}(t_{2})-x_{1}(t_{1}) \bigr\vert ^{p}&=\mathbb{E} \biggl\vert \int _{t_{1}}^{t_{2}}F\bigl(x_{1}(t),x_{2}(t) \bigr)\,dt+ \int _{t_{1}}^{t_{2}}\sigma _{1}(t)x_{1}(t) \,dB_{1}(t) \biggr\vert ^{p} \\ &\leq 2^{p-1}\mathbb{E} \biggl\vert \int _{t_{1}}^{t_{2}}F\bigl(x_{1}(t),x_{2}(t) \bigr)\,dt \biggr\vert ^{p} +2^{p-1}\mathbb{E} \biggl\vert \int _{t_{1}}^{t_{2}}\sigma _{1}(t)x_{1}(t) \,dB_{1}(t) \biggr\vert ^{p} \\ &\leq 2^{p-1}L_{1}(p)^{p}(t_{2}-t_{1})^{p}+2^{p-1} \bigl[\bigl(\sigma _{1}^{2}\bigr)^{+} \bigr]^{p}\bigl[0.5p(p-1)\bigr]^{ \frac{p}{2}}(t_{2}-t_{1})^{\frac{p}{2}}L(p) \\ &\leq \bigl(2^{p-1}L_{1}(p)^{p} +2^{p-1} \bigl[\bigl(\sigma _{1}^{2}\bigr)^{+} \bigr]^{p}\bigl[0.5p(p-1)\bigr]^{ \frac{p}{2}}L(p) \bigr) (t_{2}-t_{1})^{\frac{p}{2}}. \end{aligned} $$

By Lemma 4.2, almost every path of \(x_{1}(t)\) is locally but uniformly Hölder continuous with exponent \(\theta \in (0,\frac{p-2}{2p})\). Similar to the above proof, almost every path of \(x_{2}(t)\) is locally but uniformly Hölder continuous.

Lemma 4.4

([20])

Letfbe a nonnegative function defined on\([0,\infty )\)which is integrable and is uniformly continuous. Then\(\lim_{t\rightarrow \infty }f(t)=0\).

Theorem 4.1

If\((a_{11}-a_{12})^{-}-b_{11}^{+}-\alpha _{11}^{+} \Vert \phi _{1} \Vert -\alpha _{11}^{+} >0\)and\((a_{22}-a_{21})^{-}-b_{22}^{+}-\alpha _{21}^{+} \Vert \phi _{2} \Vert -\alpha _{21}^{+}>0\), then system (1.3) is globally asymptotically stable.

Proof

For any two positive solutions \((x_{1}(t),x_{2}(t))^{\top }\) and \((y_{1}(t),y_{2}(t))^{\top }\) of (1.3), define \(\mathcal{V}(t)\) on \(t\geq 0\) by \(\mathcal{V}(t)= \vert \ln x_{1}(t)-\ln x_{2}(t) \vert + \vert \ln y_{1}(t)-\ln y_{2}(t) \vert \). Compute the right differential of \(\mathcal{V}(t)\)

$$ \begin{aligned}[b] d^{+}\mathcal{V}(t)&=\operatorname{sgn}(x_{1}-x_{2}) \biggl[\biggl(\frac{1}{x_{1}}- \frac{1}{x_{2}}\biggr) F(x_{1},x_{2})+0.5 \sigma _{1}^{2}\bigl(x_{1}^{2}-x_{2}^{2} \bigr) \biggr] \\ & \quad {} +\operatorname{sgn}(y_{1}-y_{2}) \biggl[\biggl( \frac{1}{y_{1}}-\frac{1}{y_{2}}\biggr) G(y_{1},y_{2})+0.5 \sigma _{2}^{2}\bigl(y_{1}^{2}-y_{2}^{2} \bigr) \biggr] \\ &\leq - \bigl[(a_{11}-a_{12})^{-}-b_{11}^{+}- \alpha _{11}^{+} \Vert \phi _{1} \Vert - \alpha _{11}^{+} \bigr] \vert x_{1}-x_{2} \vert \,dt \\ & {} - \bigl[(a_{22}-a_{21})^{-}-b_{22}^{+}- \alpha _{21}^{+} \Vert \phi _{2} \Vert - \alpha _{21}^{+} \bigr] \vert y_{1}-y_{2} \vert \,dt. \end{aligned} $$
(4.7)

In view of assumptions of Theorem 4.1, integrating both sides of (4.7) leads to

$$ \begin{aligned} &V(t) + \int _{0}^{t} \bigl[(a_{11}-a_{12})^{-}-b_{11}^{+}- \alpha _{11}^{+} \Vert \phi _{1} \Vert -\alpha _{11}^{+} \bigr] \bigl\vert x_{1}(s)-x_{2}(s) \bigr\vert \,ds \\ &\quad\quad {} + \int _{0}^{t} \bigl[(a_{22}-a_{21})^{-}-b_{22}^{+}- \alpha _{21}^{+} \Vert \phi _{2} \Vert -\alpha _{21}^{+} \bigr] \bigl\vert y_{1}(s)-y_{2}(s) \bigr\vert \,ds \\ &\quad \leq V(0)< \infty . \end{aligned} $$

Thus, \(\vert x_{1}(t)-x_{2}(t) \vert , \vert y_{1}(t)-y_{2}(t) \vert \in L^{1}[0,\infty )\) and the desired assertion follows from Lemmas 4.3 and 4.4 immediately. □

5 Numerical examples

Consider the following example:

$$ \textstyle\begin{cases} dx_{1}(t)= [-(12+\sin t)+(2+\sin t)e^{-x_{1}(t)}+2-\sin t-(2- \sin t)e^{-x_{2}(t)} \\\hphantom{dx_{1}(t)=} {} +(2-\sin ^{2}t)x_{1}(t-1)e^{-(2+\sin ^{2}t)x_{1}(t-1.5)} \\ \hphantom{dx_{1}(t)=}{} +(2-\cos ^{2}t)x_{1}(t-1)e^{-(2+\cos ^{2}t)x_{1}(t-1.2)} ]\,dt+0.2x_{1}(t)\,dB_{1}(t), \\ dx_{2}(t)= [-(12-\cos ^{2} t)+(2-\cos t)e^{-x_{2}(t)}+{2-\cos ^{2}t}-(2- \cos ^{2}t)e^{-x_{1}(t)} \\\hphantom{dx_{2}(t)=} {} +(2-\cos ^{2}t)x_{2}(t-1.5)e^{-(3+\sin ^{2}t)x_{2}(t-1.2)} \\ \hphantom{dx_{2}(t)=}{} +(2+\cos ^{2}t)x_{2}(t-0.5)e^{-(3+\cos ^{2}t)x_{2}(t-1.2)} ]\,dt+0.1x_{2}(t)\,dB_{2}(t), \end{cases} $$
(5.1)

where

$$\begin{aligned}& a_{11}(t)=12+\sin t, \quad\quad b_{11}(t)=2+\sin t, \quad \quad a_{12}(t)=2-\sin t, \quad\quad b_{12}(t)=2- \sin t, \\& \alpha _{11}(t)=2-\sin ^{2}t, \quad\quad \tau _{11}(t)=1, \quad\quad \beta _{11}(t)=2+ \sin ^{2}t, \quad\quad \gamma _{11}(t)=1.5, \\& \alpha _{12}(t)=2-\cos ^{2}t, \quad\quad \tau _{12}(t)=0.5, \quad\quad \beta _{12}(t)=2+ \cos ^{2}t, \quad\quad \gamma _{12}(t)=\cos ^{2} \frac{\pi t}{2}, \\& \sigma _{1}=0.2, \\& a_{22}(t)=12-\cos ^{2} t, \quad\quad b_{22}(t)=2- \cos t, \quad\quad a_{21}(t)={2-\cos ^{2}t}, \\& b_{21}(t)={2- \cos ^{2}t}, \\& \alpha _{21}(t)=2-\cos ^{2}t, \quad\quad \tau _{21}(t)=1.5, \quad\quad \beta _{21}(t)=3+ \sin ^{2}t, \quad\quad \gamma _{21}(t)=1.2, \\& \alpha _{22}(t)=2+\cos ^{2}t, \quad\quad \tau _{22}(t)=0.5, \quad\quad \beta _{22}(t)=3+ \cos ^{2}t, \quad\quad \gamma _{21}(t)=1.2, \\& \sigma _{2}=0.1. \end{aligned}$$

Obviously, \(\tau =\max \{\tau _{ij},\gamma _{ij},i,j=1,2\}=1.5\), then the initial value of system (4.2) takes \(x_{i}(t)=\phi _{i}(t)=\sin ^{2}t\), \(i=1\), 2, \(t\in [-1.5,0]\). After simple calculation, we have

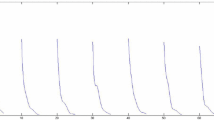
$$\begin{aligned}& (a_{11}-a_{12})^{-}=10, \quad\quad b_{11}^{+}=3, \quad\quad \alpha _{11}^{+}=2,\quad\quad \Vert \phi _{1} \Vert =1, \\& (a_{11}-a_{12})^{-}-b_{11}^{+}- \alpha _{11}^{+} \Vert \phi _{1} \Vert -\alpha _{11}^{+} =3>0, \\& (a_{22}-a_{21})^{-}=8, \quad\quad b_{22}^{+}=3, \quad\quad \alpha _{21}^{+}=2, \quad\quad \Vert \phi _{2} \Vert =1, \\& (a_{22}-a_{21})^{-}-b_{22}^{+}- \alpha _{21}^{+} \Vert \phi _{2} \Vert -\alpha _{21}^{+}=1>0. \end{aligned}$$

Then the conditions of Theorem 4.1 hold and system (5.1) is globally asymptotically stable. The numerical solutions with proper initial values are shown in Fig. 1.

Figure 1
figure 1

State trajectories of system (5.1) for \(x(t)\)

Full size image

6 Conclusions

In this paper, we study a patch structure stochastic Nicholson’s blowflies system with mixed delay and obtain some very simple conditions for guaranteeing the existence and global asymptotic stability of the considered system. It is interesting that the delays of system (1.3) are not the same, which is different from the corresponding ones of the past work. The methods in this paper can be extended to study other types of differential dynamic systems such as stochastic differential impulsive equations, stochastic fractional differential equations, etc. We hope other researchers can use the method provided in this article to do more in-depth research on various types of stochastic differential dynamic systems.