Abstract
In this article, a finite volume element method with the second-order weighted and shifted Grünwald difference (WSGD) formula is proposed and studied for nonlinear time fractional mobile/immobile transport equations on triangular grids. By using the WSGD formula of approximating the Riemann–Liouville fractional derivative and an interpolation operator \(I_{h}^{*}\), a second-order fully discrete finite volume element (FVE) scheme is formulated. The existence, uniqueness, and unconditional stability for the fully discrete FVE scheme are derived, the optimal a priori error estimates in \(L^{\infty }(L^{2}(\varOmega))\) and \(L^{2}(H^{1}(\varOmega))\) norms are obtained, in which the convergence orders are independent of the fractional parameters. At the end of this article, two numerical examples with different nonlinear terms are given to verify the feasibility and effectiveness.
Similar content being viewed by others
1 Introduction
The theories and numerical methods of fractional differential equations (FDEs) have become hot topics, which attract more and more scholars in science and engineering. This is because the FDEs are widely used in many fields, such as physics, chemistry, biology, and ecology [1–7]. Many practical problems with some properties such as memory, heterogeneity, or heredity can be described well by the corresponding FDEs, including fractional cable equations, fractional diffusion equations, fractional Allen–Cahn equations, and so on. However, due to the existence and complexity of fractional derivative, it is difficult to obtain the analytical solutions for most of the FDEs. Thus, many numerical methods [8–19] have been proposed and studied to solve different types of the FDEs.
In this article, we focus on the following nonlinear time fractional mobile/immobile transport equations
for \((\boldsymbol{x},t)\in\varOmega\times J\), with boundary and initial conditions
where \(\varOmega\subset\mathbb{R}^{2}\) is a bounded convex polygonal domain with boundary ∂Ω, \(J=(0,T]\) with \(0< T<\infty\), \(\beta_{1}>0\) and \(\beta_{2}\geq0\) are two given nonnegative constants. The source function \(f(\boldsymbol{x},t)\) and initial data \(u_{0}(\boldsymbol{x})\) are smooth enough. Moreover, we assume that the coefficient \(\mathcal{A}(\boldsymbol {x})=\{ a_{i,j}(\boldsymbol{x})\}_{2\times2}\) is a sufficiently smooth matrix function, which is symmetric and uniformly positive definite, that is, there exists a constant \(\beta_{0}>0\) such that
The nonlinear term \(g(u)\) satisfies \(|g'(u)|\leq C\), where \(C>0\) is a constant. Also \(\frac{\partial^{\alpha}u(\boldsymbol{x},t)}{\partial t^{\alpha}}\) is the Riemann–Liouville time fractional derivative defined by
The mobile/immobile transport equations have been widely used in unsaturated transport through homogeneous media [20–24]. Due to some partitioning between the phases [25], mobile/immobile formulations equate the divergence of advective and dispersive flux of a mobile phase to the change in concentration in both the mobile and immobile zones. Fractional mobile/immobile transport equations, as described in [26] by Schumer et al., are equivalent to the mobile/immobile model with power law memory function, and are considered to be the limiting equation which governs continuous time random walks with heavy tailed random waiting times. Recently, some numerical methods have been designed to solve the fractional mobile/immobile models. Liu et al. [27] proposed an implicit finite difference (FD) method for the fractional mobile/immobile advection–dispersion equation, in which the Caputo time fractional derivative is discretized by L1 formula [12, 13] and the Riemann–Liouville space fractional derivative is discretized by shifted Grünwald–Letnikov formula [1, 28]. Zhang et al. [29] provided a stable implicit Euler approximation scheme to solve the fractional mobile/immobile advection–dispersion equation with the Coimbra variable-order derivative. Liu et al. [30] proposed a meshless method to treat the two-dimensional fractional mobile/immobile transport equation based on radial basis functions for the spatial discretization. Wang [31] constructed a high-order compact FD scheme to solve the fractional mobile/immobile convection–diffusion equations, and gave a Richardson extrapolation algorithm to improve the temporal convergence accuracy. Yin et al. [32] constructed a generalized BDF2-θ scheme for the fractional mobile/immobile transport equations with the initial singularity of the time fractional derivative. However, we find that there is no report about the finite volume element method with the weighted and shifted Grünwald–Letnikov difference (WSGD) formula to solve the nonlinear time fractional mobile/immobile transport equations.
The finite volume element (FVE) method, as an important numerical method, has been widely used to solve various differential equations [33–39] in the field of science and engineering. This method can preserve the local conservation laws for some physical quantities, which is very important in scientific computing. Recently, the FVE method has been used to solve some FDEs by some scholars. Sayevand and Arjang [40] designed an FVE scheme to solve the time fractional subdiffusion equation on a rectangular partition, where the Caputo fractional derivative was approximated by using L1 formula. Karaa et al. [41] constructed an FVE scheme for the time fractional subdiffusion equation with the Riemann–Liouville fractional derivative, and applied a piecewise linear discontinuous Galerkin method in time, where the convergence rate in time was \(k^{1+\alpha}\) (\(0<\alpha<1\)). In order to improve the results in [41], Karaa and Pani [42] considered smooth and nonsmooth initial data, and gave two fully discrete numerical schemes by using convolution quadrature in time generated by the backward Euler difference method and the second-order backward difference method. Recently, numerical methods based on the WSGD formula have attracted more and more scholars, and have been studied to solve many FDEs [43–49]. Compared with the L1 formula, the WSGD formula can obtain the second-order convergence rate, which is independent of the fractional parameters. This motivates us to find a way to combine the FVE methods with the WSGD formula so that we can use their advantages to solve more FDEs.
In this article, our purpose is to construct an FVE scheme for the nonlinear time fractional mobile/immobile transport equations on triangular girds by using the WSGD formula. In spatial discretization, we construct the primal and dual partitions, select the piecewise linear polynomial space and the piecewise constant function space as the trial and test function spaces, respectively, then construct the FVE scheme by using the interpolation operator. In temporal discretization, we adopt the second-order WSGD formula to approximate the Riemann–Liouville fractional derivative \(\partial ^{\alpha}u / \partial t^{\alpha}\), apply a second-order three-level difference scheme to approximate the time derivative \(\partial u / \partial t\), and give a second-order approximation formula for the nonlinear term \(g(u)\). We give the existence, uniqueness, and unconditional stability analyses for the FVE scheme in detail, and obtain the optimal a priori error estimates in \(L^{\infty }(L^{2}(\varOmega))\) and \(L^{2}(H^{1}(\varOmega))\) norms. Compared with the discrete schemes in [27, 29, 30], our scheme can achieve second-order temporal convergence rate.
This article is organized as follows. In Sect. 2, a fully discrete FVE scheme for the nonlinear time fractional mobile/immobile transport equation (1)–(2) is proposed. In Sect. 3, the existence, uniqueness, and unconditional stability analyses are derived. In Sect. 4, the optimal a prioir error estimates are obtained. Finally, in Sect. 5, two examples with different nonlinear terms are given to illustrate the feasibility and effectiveness. Furthermore, we use general definitions and notations of the Sobolev spaces as in [50], and adopt the symbol C to represent a generic positive constant, which is independent of temporal and spatial mesh.
2 Fully discrete finite volume element scheme
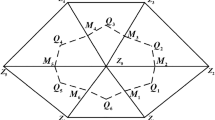
In order to construct the FVE scheme, we first give primal and dual partitions. Let \(\mathcal{T}_{h}=\{K\}\) be a set of quasiuniform triangulation mesh of the domain Ω with \(h=\max\{h_{K}\}\), referring to Fig. 1, where \(h_{K}\) denote the diameter of the triangle \(K\in\mathcal{T}_{h}\). Then we have \(\overline{\varOmega}=\bigcup_{K\in\mathcal{T}_{h}}K\). Moreover, let \(\mathcal{Z}_{h}=\{Z:Z \text{ is a vertex of element } K, K\in\mathcal{T}_{h}\}\) represent all vertices, and \(\mathcal{Z}_{h}^{0}\subset\mathcal{Z}_{h}\) represent the set of interior vertices in \(\mathcal{T}_{h}\).
Next, let \(\mathcal{T}_{h}^{*}\) be the dual mesh based on the primary mesh \(\mathcal{T}_{h}\). With \(Z_{0}\in\mathcal{Z}_{h}^{0}\) as an interior node, let \(Z_{i}\) (\(i=1,2,\ldots,m\)) be the corresponding adjacent nodes (as shown in Fig. 1, \(m=6\)). We denote the midpoints of \(\overline{Z_{0}Z_{i}}\) by \(M_{i}\) (\(i=1,2,\ldots,m\)), and denote the barycenters of the triangle \(\triangle Z_{0}Z_{i}Z_{i+1}\) by \(Q_{i}\) (\(i=1,2,\ldots,m\)), where \(Z_{m+1}=Z_{1}\). Thus, we define the control volume\(K_{Z_{0}}^{*}\) by joining successively \(M_{1},Q_{1},\ldots,M_{m},Q_{m},M_{1}\). Then, we denote the union of the control volumes \(K_{Z_{i}}^{*}\) as the dual mesh \(\mathcal{T}_{h}^{*}\). With \(Q_{i}\), \(i=1,2,\ldots,m\) as the nodes of control volume \(K_{Z_{0}}^{*}\), we denote \(\mathcal{Z}_{h}^{*}\) be the set of all dual nodes \(Q_{i}\).
Then, we define the following piecewise linear function space \(V_{h}\) as the trial function space:
and define the piecewise constant function space \(V_{h}^{*}\) as the test function space, that is,
Let \(\varPhi_{Z}\) be the general nodal linear basis function associated with the node \(Z\in\mathcal{Z}_{h}^{0}\), and \(\varPsi_{z}\) be the characteristic function of the control volume \(K_{Z}^{*}\). We have \(V_{h}=\operatorname{span}\{\varPhi_{Z}(\boldsymbol{x}) : Z\in \mathcal{Z}_{h}^{0}\}\) and \(V_{h}^{*}=\operatorname{span}\{\varPsi_{Z}(\boldsymbol{x}) : Z\in \mathcal{Z}_{h}^{*}\}\). Let \(I_{h} : C(\varOmega)\rightarrow V_{h}\) be the classical piecewise linear interpolation operator and \(I_{h}^{*} : C(\varOmega)\rightarrow V_{h}^{*}\) be the piece constant interpolation operator, that is,
Now, integrating (1) on the relevant control volume \(K_{Z}^{*}\) with a vertex \(Z\in Z_{h}\), and applying the Green formula, we have
where n denotes the outer-normal direction on \(\partial K_{Z}^{*}\). We apply the operator \(I_{h}^{*}\) to rewrite (5) as the following formulation:
where the bilinear form \(a(\cdot,\cdot)\), following [33, 34], can be taken as follows:
In our theoretical analysis, we also need to give the variational formulation of the problem (1)–(2) to find \(u(t)\in H_{0}^{1}(\varOmega)\) such that
where \(a(u,v)=\int_{\varOmega}\mathcal{A}\nabla u\cdot\nabla v\,\mathrm{d} \boldsymbol{x}\), \(\forall u,v\in H_{0}^{1}(\varOmega)\).
Now, we introduce the mesh of the temporal interval \(\bar{J}=[0,T]\) given by \(0=t_{0}< t_{1}<\cdots<t_{N}=T\) for some positive integer N, where \(t_{n}=n\tau\) and \(\tau=T/N\), \(n=0,1,\dots,N\). We denote \(\varphi^{n} =\varphi(t_{n})\) for a function φ and
Next, following [43, 44], we apply the WSGD formula to approximate the Riemann–Liouville fractional derivative \(\frac{\partial^{\alpha}u(\boldsymbol{x},t)}{\partial t^{\alpha}}\) at time \(t=t_{n+1}\) as follows:
where the truncation error \(E_{u,\alpha}^{n+1}=O(\tau^{2})\), and
For approximating the nonlinear term \(g(u)\) at \(t=t_{n+1}\), as in [51], we use the linearized formulation denoted by \(G[u^{n+1}]\) as follows:
Then, we can obtain the equivalent formulation of variational formulation (8) at \(t=t_{n+1}\) which is to find \(u^{n+1}=u(t_{n+1})\in H_{0}^{1}(\varOmega )\) such that
where
and
Now, we denote by \(U^{n}\) the approximate solution of u at \(t=t_{n}\), make use of (9), (10), and (13), and obtain the fully discrete FVE scheme to find \(U^{n+1}\in V_{h}\) (\(n=0,1,\ldots,N-1\)) such that
We can also split the FVE scheme (17) into the following equivalent iterative formulation:
Case \(n=0\):
Case \(n\geq1\):
Then we will prove the existence and uniqueness of the fully discrete solutions for the FVE scheme (17) (or (18)–(19)) in the next section.
Remark 2.1
For the fully discrete FVE scheme (17) or equivalent formulations (18)–(19), in the practical calculations, we can obtain \(U^{1}\) by using \(U^{0}\) and solving (18), where \(U^{0}=P_{h} u_{0}\) defined in Sect. 4. Thus, when \(U^{n}\) and \(U^{n-1}\) (\(n\geq1\)) have been obtained, we can solve (19) to obtain \(U^{n+1}\).
3 Existence, uniqueness, and stability analyses
In this section, we will derive the results of the existence, uniqueness, and stability for the fully discrete FVE scheme (17). First, we give some properties of the coefficients in WSGD formula and the interpolation operator \(I_{h}^{*}\) in Sect. 3.1.
3.1 Some lemmas
Lemma 3.1
For the sequence\(\{g_{k}^{\alpha}\}\)defined by (12), we have
Lemma 3.2
([33])
The interpolation operators\(I_{h}\)and\(I_{h}^{*}\)satisfy the following properties:
Lemma 3.3
([33])
The bilinear form\((\cdot,I_{h}^{*}\cdot)\)satisfies the following property:
and there exist two positive constants\(\mu_{1}\)and\(\mu_{2}\)independent ofhsuch that
Lemma 3.4
There exist positive constants\(h_{0}\), \(\mu_{3}\), and\(\mu_{4}\)such that, for\(0< h\leq h_{0}\),
Making use of Lemma 3.3, similar to the proof in [43, 44], we can also obtain the following property of the sequence \(\{q_{\alpha }(k)\}_{k=1}^{\infty}\).
Lemma 3.5
For the sequence\(\{q_{\alpha}(k)\}_{k=1}^{\infty}\)defined by (11), and any real vector\((u^{0},u^{1}, \ldots,u^{P})\in\mathbb{R}^{P+1}\), wherePis an arbitrary positive integer, the following inequality holds:
Lemma 3.6
Let\(\{\phi^{n}\}\)be a function sequence on\(V_{h}\). Then the following inequalities hold:
where
Proof
When \(n=0\), making use of Lemma 3.3 and the definition of \(\partial_{t}^{2}\phi^{n}\), we obtain the following result:
For the case of \(n\geq1\), we have
Noting that
we substitute (33) into (32), and obtain the desired result. □
3.2 Existence and uniqueness
Theorem 3.1
There exists a unique discrete solution for the fully discrete FVE scheme (17).
Proof
Let \(M_{Z}^{0}\) be the number of the vertices in \(Z_{h}^{0}\), and \(\{\varPhi_{i} : i=1,2,\dots,M_{Z}^{0}\}\) be the basis functions of the space \(V_{h}\), then \(U^{n}\in V_{h}\) can be expressed as follows:
We substitute (34) into the formulations (18) and (19) equivalent to the FVE scheme (17), take \(v_{h}=\varPhi_{j}\) (\(j=1,2,\dots,M_{Z}^{0}\)), then rewrite (18) and (19) in the matrix form, and search for \(\tilde {\boldsymbol {u}}^{n}\) such that
where
It is easy to see that \(A_{1}\) is a symmetric positive definite matrix. Let \(B_{1}=\beta_{1}A_{1}+\beta_{2}\tau^{1-\alpha}q_{\alpha}(0)A_{1}+\tau A_{2}\) and \(B_{2}=\frac{3}{2}\beta_{1}A_{1}+\beta_{2}\tau^{1-\alpha}q_{\alpha }(0)A_{1}+\tau A_{2}\). Next, we will prove \(B_{1}\) and \(B_{2}\) are invertible. Applying Lemma 3.4, for \(\forall Y=(y_{1},y_{2},\dots ,y_{M_{Z}^{0}})^{T}\in R^{M_{Z}^{0}}\setminus\{\boldsymbol{0}\}\), we have \(Y^{T}A_{2}Y=a(z_{h},I_{h}^{*}z_{h})\geq\mu_{3}\|z_{h}\|_{1}^{2}>0\), where \(z_{h}=\sum_{i=1}^{M_{Z}^{0}} y_{i}\varPhi_{i}\neq0\). This means that \(Y^{T}A_{2}Y\) (for \(Y\in R^{M_{Z}^{0}}\)) is a positive definite quadratic form generated by the asymmetric matrix \(A_{2}\). Therefore, \(Y^{T} B_{1} Y\) and \(Y^{T} B_{2} Y\) (for \(Y\in R^{M_{Z}^{0}}\)) are positive definite quadratic forms generated by asymmetric matrices \(B_{1}\) and \(B_{2}\), respectively. Then we have that \(B_{1}\) and \(B_{2}\) are invertible. Hence, the linear equations (35) have a unique solution, and so the FVE scheme (17) has a unique solution. Thus, we complete the proof of Theorem 3.1. □
3.3 Stability
The fully discrete FVE scheme (17) satisfies the following unconditional stability results.
Theorem 3.2
Let\(\{U^{n}\}_{n=1}^{N}\)be the solutions of the fully discrete FVE scheme (17), then there exists a constant\(C>0\)independent ofhandτsuch that
Proof
Taking \(v_{h}=U^{n+1}\) in (17) yields the following result:
Making use of Lemma 3.4, and applying the Cauchy–Schwarz and Young inequalities, we have
For the term \(\|G[U^{n+1}]\|^{2}\) in (37), when \(n \geq1\), we have
When \(n=0\), we have
Next, for the case of \(n \geq1\) in (37), we apply Lemma 3.6 to obtain
Multiplying (40) by 4τ, and summing over n from 1 to m, we have
For the case of \(n=0\) in (37), taking \(v_{h}=U^{1}\) in the FVE system (17), we have
Multiplying (42) by 2τ, and applying Lemma 3.4, we obtain
Substitute (39) into (43) to obtain
We rewrite (44) as follows:
Use Lemma 3.5 to obtain
Now, making use of (41) and (45), we have
Applying Lemma 3.6, we obtain
Substituting (48) into (47), and making use of (46), we rewrite (47) as follows:
Applying Lemma 3.5 and the discrete Gronwall lemma yields
Thus, we apply Lemma 3.3 to complete the proof. □
Remark 3.1
From the results (50), we can also see that the fully discrete solution is unconditional stable in the discrete \(L^{2}(H^{1}(\varOmega))\) norm, that is,
In the next section, we also give the optimal a priori error estimate in this discrete \(L^{2}(H^{1}(\varOmega))\) norm.
4 A priori error analysis
In order to give the error analysis for the fully discrete FVE scheme (17), we need to introduce an elliptic projection operator \(P_{h}: H_{0}^{1}(\varOmega)\cap H^{2}(\varOmega)\rightarrow V_{h}\), which is defined by
Following [33], the above projection operator \(P_{h}\) satisfies the following estimates.
Lemma 4.1
There exists a positive constant C such that
Next, we give the main results in this paper about the error estimates.
Theorem 4.1
Let\(u(t_{n})\)and\(U^{n}\)be the solutions of system (8) and the FVE scheme (17), respectively. Suppose that\(U^{0}=P_{h}u_{0}\). Then there exists a positive constantCindependent ofhandτsuch that
Moreover, we can also obtain the following error estimate:
Proof
We split the error \(u(t_{n})-U^{n}=(u(t_{n})-P_{h}u(t_{n}))+(P_{h}u(t_{n})-U^{n})=\xi ^{n}+\eta^{n}\). Applying Lemma 4.1, we only need to estimate \(\|\eta^{n}\|\). It is easy to see that \(\|\eta^{n}\|\) satisfies the following error equation:
Choose \(v_{h}=\eta^{n+1}\) in (54) to obtain
Making use of Lemma 3.4, we can obtain
Next, we estimate some terms on the right-hand side of the inequality (56). Applying Lemma 4.1 and the triangle inequality, for the case of \(n \geq1\), we have
For the case of \(n=0\), we have
We discuss the term \(\|G[u^{n+1}]-G[U^{n+1}]\|^{2}\) separately. For the case of \(n \geq1\), we have
and for the case of \(n=0\), we have
From the definitions of \(E_{u,t}^{n+1}\), \(E_{u,\alpha}^{n+1}\), and \(E_{g}^{n+1}\), we easily get
Now, for the case of \(n \geq1\), making use of (57)–(61) in (56), and applying Lemma 3.6, we obtain
Multiplying (62) by 4τ, and summing over n from 1 to m, we have
For the case of \(n=0\), taking \(v_{h}=\eta^{1}\) in (54), and applying Lemma 3.6, we obtain
Multiplying (64) by 2τ, we have
Making use of (58), (60), and (61) in (65), we can obtain
Thus, we rewrite (66) as follows:
Noting that \(\eta^{0}=0\), and applying Lemma 3.5, we have
Next, adding (63) and (67), we have
Making use of (30) and (68), we have
Substituting (70) into (69), we rewrite (69) as follows:
Noting that \(\eta^{0}=0\), and applying Lemma 3.5 and the discrete Gronwall lemma, we obtain
Finally, we apply Lemma 4.1 and the triangle inequality to complete the proof. □
5 Numerical examples
In order to illustrate the feasibility and effectiveness for the proposed FVE scheme, we give two numerical examples with different nonlinear terms \(g(u)=\sin(u)\) and \(g(u)=u^{3}-u\) and different exact solutions.
Example 1
We consider the following nonlinear time fractional mobile/immobile transport equation:
for \((\boldsymbol{x},t)\in\varOmega\times J\), with boundary and initial conditions
where \(\varOmega=(0,1)\times(0,1)\), \(J=(0,1]\), the coefficient \(\mathcal{A}(\boldsymbol{x})\) defined as follows:
We choose the exact solution
Then we can get the corresponding source function \(f(\boldsymbol{x},t)\).
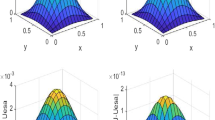
In this example, we choose some different mesh sizes and parameters α to conduct numerical experiments, and give the error results in \(L^{\infty}(L^{2}(\varOmega))\) and \(L^{2}(H^{1}(\varOmega))\) norms for \(u(\boldsymbol{x},t)\), in which we use the Gauss integral formula with fifth-order algebraic accuracy to calculate the space norms of the errors. In Table 1, we give the corresponding error results with different parameters \(\alpha=0.01, 0.5, 0.99\) and mesh sizes \((h,\tau)=(\frac{\sqrt{2}}{10},\frac{1}{10})\), \((\frac{\sqrt {2}}{20},\frac{1}{20})\), \((\frac{\sqrt{2}}{40},\frac{1}{40})\), \((\frac{\sqrt{2}}{80},\frac {1}{80})\). We point out here that error behaviors with other different parameters α such as \(\alpha=0.1, 0.3, 0.7, 0.9\) are similar, so we will not repeat them. From the error results, we can easily see that the convergence order for u in \(L^{\infty}(L^{2}(\varOmega))\) norm is approximately equal to 2, and the convergence order for \(u(\boldsymbol{x},t)\) in \(L^{2}(H^{1}(\varOmega))\) norm is approximately equal to 1. In order to observe the approximation effect intuitively, we choose the fractional parameter \(\alpha=0.5\) in (73), and give the graphs of the exact solution and the numerical solution at time \(t=1\) in Fig. 2(a) (with mesh \(h=\frac{\sqrt{2}}{40}\)) and Fig. 2(b) (with mesh \((h,\tau)=(\frac{\sqrt {2}}{20},\frac{1}{20})\)), respectively. It is easy to see that the graph of the numerical solution is also consistent with that of the exact solution.
Example 2
We consider the space domain Ω̄, time domain J̄, initial data \(u_{0}(\boldsymbol{x})\) and coefficient \(\mathcal {A}(\boldsymbol{x})\) as in Example 1. In this example, we choose the nonlinear term \(g(u)=u^{3}-u\) and the exact solution is then
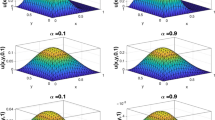
In this example, we also take some different mesh sizes and parameters α to conduct numerical experiments, and give the corresponding error results in \(L^{\infty}(L^{2}(\varOmega ))\) and \(L^{2}(H^{1}(\varOmega))\) norms for \(u(\boldsymbol{x},t)\) in Table 2 with parameters \(\alpha=0.01, 0.5, 0.99\) and mesh sizes \((h,\tau)=(\frac{\sqrt{2}}{10},\frac{1}{10})\), \((\frac{\sqrt {2}}{20},\frac{1}{20})\), \((\frac{\sqrt{2}}{40},\frac{1}{40})\), \((\frac{\sqrt{2}}{80},\frac {1}{80})\). We can see that the error behaviors are consistent with those in Example 1. In Figs. 3(a) and 3(b), we describe the graphs of the exact and numerical solutions with parameter \(\alpha=0.5\) for \(u(\boldsymbol{x},t)\) at time \(t=1\), respectively, where the mesh sizes are same as in Example 1. We also find that the exact solution u is approximated well by the fully discrete FVE solution U. The numerical behaviors and figures show that the constructed FVE scheme with second order WSGD formula for the nonlinear time fractional mobile/immobile transport equations in two-dimensional spatial regions is feasible and effective.
6 Conclusions
We apply the FVE methods based on the second-order WSGD formula to treat the nonlinear time fractional mobile/immobile equations with the Riemann–Liouville time fractional derivative. We construct the second-order fully discrete FVE scheme, give the existence, uniqueness, and unconditional stability results, derive the optimal a priori error estimates in \(L^{\infty }(L^{2}(\varOmega))\) and \(L^{2}(H^{1}(\varOmega))\) norms, and give two numerical examples with different nonlinear terms to verify the theoretical results. The proposed method by combining the FVE method with the WSGD formula can not only make use of the advantages of the FVE method, but also obtain the second-order convergence accuracy in time direction independent of the fractional parameters. In the future, we will extend and apply the proposed method to solve more fractional differential equations.
References
Podlubny, I.: Fractional Differential Equations. Mathematics in Science and Engineering. Academic Press, San Diego (1999)
Hilfer, R.: Applications of Fractional Calculus in Physics. Word Scientific, Singapore (2000)
Magin, R.L.: Fractional Calculus in Bioengineering. Begell House, Redding (2006)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Application of Fractional Differential Equations. Elsevier, Amsterdam (2006)
Baleanu, D., Machado, J.A.T., Luo, A.: Fractional Dynamics and Control. Springer, New York (2012)
Atangana, A.: Non validity of index law in fractional calculus: a fractional differential operator with Markovian and non-Markovian properties. Physica A 505, 688–706 (2018)
Atangana, A., Qureshi, S.: Modeling attractors of chaotic dynamical systems with fractal-fractional operators. Chaos Solitons Fractals 123, 320–337 (2019)
Li, C.P., Zeng, F.H.: Numerical Methods for Fractional Calculus. Chapman & Hall/CRC, Boca Raton (2015)
Li, C.P., Cai, M.: Theory and Numerical Approximations of Fractional Integrals and Derivatives. SIAM, Philadelphia (2019)
Liu, F.W., Zhuang, P.H., Liu, Q.X.: Numerical Methods of Fractional Partial Differential Equations and Applications. Chinese Science Press, Beijing (2015)
Sun, Z.Z., Gao, G.H.: Finite Difference Methods for Fractional Differential Equations. Chinese Science Press, Beijing (2015)
Sun, Z.Z., Wu, X.N.: A fully discrete scheme for a diffusion–wave system. Appl. Numer. Math. 56, 193–209 (2006)
Lin, Y.M., Xu, C.J.: Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 225, 1533–1552 (2007)
Kumar, S., Pandey, P., Das, S.: Operational matrix method for solving nonlinear space-time fractional order reaction–diffusion equation based on Genocchi polynomial. Spec. Top. Rev. Porous Media 11, 33–47 (2020)
Kumar, S., Pandey, P., Das, S., Craciun, E.M.: Numerical solution of two dimensional reaction–diffusion equation using operational matrix method based on Genocchi polynomial—part I: Genocchi polynomial and opperatorial matrix. Proc. Rom. Acad., Ser. A: Math. Phys. Tech. Sci. Inf. Sci. 20, 393–399 (2019)
Kumar, S., Pandey, P., Das, S.: Gegenbauer wavelet operational matrix method for solving variable-order non-linear reaction–diffusion and Galilei invariant advection–diffusion equations. Comput. Appl. Math. 38, Article ID 162 (2019)
Kumar, S., Pandey, P.: A Legendre spectral finite difference method for the solution of non-linear space-time fractional Burger’s–Huxley and reaction–diffusion equation with Atangana–Baleanu derivative. Chaos Solitons Fractals 130, Article ID 109402 (2020)
Kumar, S., Pandey, P.: Quasi wavelet numerical approach of non-linear reaction diffusion and integro reaction–diffusion equation with Atangana–Baleanu time fractional derivative. Chaos Solitons Fractals 130, Article ID 109456 (2020)
Zhao, J., Li, H., Fang, Z.C., Liu, Y.: A mixed finite volume element method for time-fractional reaction–diffusion equations on triangular grids. Mathematics 7, Article ID 600 (2019)
Van Genuchten, M.T., Wierenga, P.J.: Mass transfer studies in sorbing porous media I. Analytical solutions. Soil Sci. Soc. Am. J. 40, 473–480 (1976)
Gaudet, J.P., Jegat, H., Vachaud, G., Wierenga, P.: Solute transfer, with exchange between mobile and stagnant water, through unsaturated sand. Soil Sci. Soc. Am. J. 41, 665–671 (1977)
De Smedt, F., Wierenga, P.J.: Solute transfer through columns of glass beads. Water Resour. Res. 20, 225–232 (1984)
Padilla, I.Y., Yeh, T.C.J., Conklin, M.H.: The effect of water content on solute transport in unsaturated porous media. Water Resour. Res. 35, 3303–3313 (1999)
Bromly, M., Hinz, C.: Non-Fickian transport in homogeneous unsaturated repacked sand. Water Resour. Res. 40, Article ID W07402 (2004)
Coats, K.H., Smith, B.D.: Dead-end pore volume and dispersion in porous media. Soc. Pet. Eng. J. 4, 73–84 (1964)
Schumer, R., Benson, D.A., Meerschaert, M.M., Baeumer, B.: Fractal mobile/immobile solute transport. Water Resour. Res. 39, Article ID 1296 (2003)
Liu, F.W., Zhuang, P.H., Burrage, K.: Numerical methods and analysis for a class of fractional advection–dispersion models. Comput. Math. Appl. 64, 2990–3007 (2012)
Meerschaert, M.M., Tadjeran, C.: Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 56, 80–90 (2006)
Zhang, H., Liu, F., Phanikumar, M.S., Meerschaert, M.M.: A novel numerical method for the time variable fractional order mobile–immobile advection–dispersion model. Comput. Math. Appl. 66, 693–701 (2013)
Liu, Q., Liu, F., Turner, I., Anh, V., Gu, Y.T.: A RBF meshless approach for modeling a fractal mobile/immobile transport model. Appl. Math. Comput. 226, 336–347 (2014)
Wang, Y.M.: A high-order compact finite difference method and its extrapolation for fractional mobile/immobile convection–diffusion equations. Calcolo 54, 733–768 (2017)
Yin, B.L., Liu, Y., Li, H.: A class of shifted high-order numerical methods for the fractional mobile/immobile transport equations. Appl. Math. Comput. 368, Article ID 124799 (2020)
Li, R.H., Chen, Z.Y., Wu, W.: Generalized Difference Methods for Differential Equations: Numerical Analysis of Finite Volume Methods. Marcel Dekker, New York (2000)
Ewing, R., Lazarov, R., Lin, Y.: Finite volume element aproximations of nonlocal reactive flows in porous media. Numer. Methods Partial Differ. Equ. 16, 285–311 (2000)
Chatzipantelidis, P., Lazarov, R.D., Thomée, V.: Error estimates for a finite volume element method for parabolic equations in convex polygonal domains. Numer. Methods Partial Differ. Equ. 20, 650–674 (2004)
Zhang, Z.Y.: Error estimates of finite volume element method for the pollution in groundwater flow. Numer. Methods Partial Differ. Equ. 25, 259–274 (2009)
Carstensen, C., Dond, A.K., Nataraj, N., Pani, A.K.: Three first-order finite volume element methods for Stokes equations under minimal regularity assumptions. SIAM J. Numer. Anal. 56, 2648–2671 (2018)
Zhang, T., Li, Z.: An analysis of finite volume element method for solving the Signorini problem. Appl. Math. Comput. 270, 830–841 (2015)
Luo, Z.D., Xie, Z., Shang, Y., Chen, J.: A reduced finite volume element formulation and numerical simulations based on POD for parabolic problems. J. Comput. Appl. Math. 235, 2098–2111 (2011)
Sayevand, K., Arjang, F.: Finite volume element method and its stability analysis for analyzing the behavior of sub-diffusion problems. Appl. Math. Comput. 290, 224–239 (2016)
Karaa, S., Mustapha, K., Pani, A.K.: Finite volume element method for two-dimensional fractional subdiffusion problems. IMA J. Numer. Anal. 37, 945–964 (2017)
Karaa, S., Pani, A.K.: Error analysis of a FVEM for fractional order evolution equations with nonsmooth initial data. ESAIM: M2AN 52, 773–801 (2018)
Wang, Z.B., Vong, S.W.: Compact difference schemes for the modified anomalous fractional sub-diffusion equation and the fractional diffusion–wave equation. J. Comput. Phys. 277, 1–15 (2014)
Tian, W.Y., Zhou, H., Deng, W.H.: A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput. 84, 1703–1727 (2015)
Liu, Y., Du, Y.W., Li, H., Wang, J.F.: A two-grid finite element approximation for a nonlinear time-fractional Cable equation. Nonlinear Dyn. 85, 2535–2548 (2016)
Liu, Y., Zhang, M., Li, H., Li, J.C.: High-order local discontinuous Galerkin method combined with WSGD-approximation for a fractional sub-diffusion equation. Comput. Math. Appl. 73, 1298–1314 (2017)
Du, Y.W., Liu, Y., Li, H., Fang, Z.C., He, S.: Local discontinuous Galerkin method for a nonlinear time-fractional fourth-order partial differential equation. J. Comput. Phys. 344, 108–126 (2017)
Liu, Y., Du, Y.W., Li, H., Liu, F., Wang, Y.J.: Some second-order θ schemes combined with finite element method for nonlinear fractional cable equation. Numer. Algorithms 80, 533–555 (2019)
Feng, R.H., Liu, Y., Hou, Y.X., Li, H., Fang, Z.C.: Mixed element algorithm based on a second-order time approximation scheme for a two-dimensional nonlinear time fractional coupled sub-diffusion model. Eng. Comput. (2020). https://doi.org/10.1007/s00366-020-01032-9
Adams, R.: Sobolev Spaces. Academic Press, New York (1975)
Wang, J.F., Liu, T.Q., Li, H., Liu, Y., He, S.: Secoond-order approximation scheme combined with \(H^{1}\)-Galerkin MFE method for nonlinear time fractional convection–diffusion equation. Comput. Math. Appl. 73, 1182–1196 (2017)
Liu, Y., Du, Y.W., Li, H., Li, J.C., He, S.: A two-grid mixed finite element method for a nonlinear fourth-order reaction diffusion problem with time-fractional derivative. Comput. Math. Appl. 70, 2474–2492 (2015)
Meerschaert, M.M., Tadjeran, C.: Finite difference approximations for fractional advection–dispersion flow equations. J. Comput. Appl. Math. 172, 65–77 (2004)
Acknowledgements
The authors thank the editors and reviewers for their helpful comments and suggestions to improve the paper.
Availability of data and materials
The authors declare that all data and material in the paper are available and veritable.
Funding
This work was supported by the National Natural Science Foundation of China (11701299, 11761053, 11661058), the Natural Science Foundation of Inner Mongolia Autonomous Region (2017MS0107), the Program for Young Talents of Science and Technology in Universities of Inner Mongolia Autonomous Region (NJYT-17-A07), and the Prairie Talent Project of Inner Mongolia Autonomous Region.
Author information
Authors and Affiliations
Contributions
All authors worked together and contributed to the draft of the manuscript, all authors wrote, read, and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhao, J., Fang, Z., Li, H. et al. Finite volume element method with the WSGD formula for nonlinear fractional mobile/immobile transport equations. Adv Differ Equ 2020, 360 (2020). https://doi.org/10.1186/s13662-020-02786-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-02786-8