1 Introduction

Nonlinear evolution equations have a significant job in applied sciences, especially in physics. Obtaining traveling wave solutions of these equations has been of major benefit primarily within the context of mathematical physics. Such examinations have prompted many intriguing sorts of solutions in the past, for example, the soliton solutions, the periodic solutions, the cnoidal solutions, the peakon solutions. In any case, searching these solutions has not been simple at all as is showed in the literature. So, many powerful manners have been introduced, such as the homogeneous balance manner [1], the first integral manner [2], the tanh-coth manner [3], the modified tanh-coth manner [4], the inverse scattering manner [5], Hirota’s bilinear manner [6], the RB sub-Ode manner [7, 8], the sine-Gordon manner [9], the \((G'/G)\)-expansion manner [10], the \((G'/G,1/G)\)-expansion manner [11], the Exp-function manner [12], F-expansion manner [13, 14], and so on.

There are abundant and full treatises related to the fractional and conformable derivatives. Conformable fractional formulation of the fractional calculus was introduced in [15]. The conformable calculus of time-scale was evidenced in [16]. In [17], the fractional traditional mechanics was discussed by some conformable-type derivatives. Lately, the conformable-type differential equations have become a significant object in physics and mathematics. So, abundant experts focus their attention on the analytical and the approximate integrals to these equations [18, 19]. Existence and uniqueness results for some conformable-type partial differential equations (PDEs) have been proved by Gokdogan et al. [20] and by Sania et al. [21]. In [22], a conformable sub-equation manner was suggested to create exact solutions to the space and time fractional nonlinear resonant Schrödinger equation. Also, fractional modulation to the Nipah virus was given by Markovian process and some local time differential maps [23]. Overall, many studies have been done about the solutions and properties of fractional and conformable-type PDEs [24–29].

Many researchers have been interested in the subject of random traveling wave, it is a very important topic in the field of stochastic partial differential equations (SPDEs). The stochastic KdV equation was proposed by Wadati [30] in 1983. He studied the diffusion of soliton of the equation due to KdV under the Gaussian noise effect. The stochastic traveling wave solutions for the local fractal KdV equation have been obtained by the Exp-function technique in [31] and [32], respectively. Moreover, on account of [14, 33–39], many kinds of Wick-type stochastic and fractional evolution equations have been studied by utilizing diverse expansion techniques and white noise analysis.

Consider a nonlinear PDE (NPDE)

$$ \mathcal{F}(\chi,\alpha,u_{\alpha},u_{\chi},u_{\chi \chi},u_{\chi\chi\chi}, \ldots)=0, $$
(1)

where \((\chi,\alpha)\in\mathbb{R}\times\mathbb{R}_{+}\) is the freelance variable and \(u(\chi,\alpha)\) is its follower variable. Applying the one-variable transformation

$$ u(\chi,\alpha)=u(\varkappa), \quad \varkappa=\chi-\epsilon \alpha, $$
(2)

we change (1) to an ordinary and nonlinear differential equation (NODE)

$$ \mathcal{G}\bigl(\varkappa,u,u',u'',u''', \ldots\bigr)=0, $$
(3)

where \(':=\frac{d}{d\varkappa}\). In [40], Kudryashov proposed his manner to find analytical solutions to Eq. (1). He researched for the exact solutions taking into account the expression \(u(\varkappa)=\sum_{i=0}^{x} \mu_{i} \mathfrak{X}^{i}\), where \(\mathfrak{X}=\frac{1}{1+e^{\varkappa}}\), which is the integral to the equation \(\frac{d\mathfrak{X}}{d\varkappa}=\mathfrak{X}^{2}-\mathfrak{X}\). A modified Kudryashov manner was presented by exchanging the ordinary exponential function \(e^{\varkappa}\) by means of the general sort of the exponential function \(a^{\varkappa}\) in [41–44]. In these contributions, experts got the exact solutions to the NPDE (1) by using the expansion \(u(\varkappa)=\sum_{i=0}^{x} \mu_{i} \mathfrak{X}^{i}\), where \(\mathfrak{X}=\frac{1}{1\pm a^{\varkappa}}\), which is the integral to the equation \(\frac{d\mathfrak{X}}{d\varkappa }=\ln a(\mathfrak{X}^{2}-\mathfrak{X})\). Thereafter, some authors [45–48] applied a general sort of the Kudryashov manner to rummage exact solutions of the NPDE (1). They have selected a rational expansion \(u(\varkappa)=\sum_{i=0}^{x}\mu_{i}\mathfrak{X}^{i}/\sum _{j=0}^{y}\nu_{j}\mathfrak{X}^{j} \), where \(\mathfrak{X}=\frac{1}{1+C e^{\varkappa}}\), which is the integral to the equation \(\frac {d\mathfrak{X}}{d\varkappa}=\mathfrak{X}^{2}-\mathfrak{X}\). Lately, Abdus Salam and Habiba [49] improved the general Kudryashov manner given in [45] by electing the auxiliary equation \(\frac{d\mathfrak {X}}{d\varkappa}=\sigma \mathfrak{X}^{3}-\mathfrak{X}\), \(0\neq\sigma\in\mathbb{R}\). This helpful equation has the comprehensive solution \(\mathfrak{X}=\frac{\pm1}{\sqrt{\sigma+Ce^{2\varkappa}}}\).

In this work, the general Kudryashov method [45] is improved by the novel auxiliary equation

$$ \mathfrak{X}'(\varkappa)=\sigma \mathfrak{X}^{n}(\varkappa)-\mathfrak{X}(\varkappa), \quad 1< n\in \mathbb{N}, 0\neq\sigma\in\mathbb{R}, $$
(4)

which has numerous general solutions depending on the natural number n (see Eq. (25)). Thus, a novel technique to build exact solutions for nonlinear evolution equations is obtained. This technique is called the GIKM. The major feature of the GIKM over the others lies in the way that it utilizes an especially clear and powerful algorithm to obtain exact solutions for large families of nonlinear evolution equations. Also, a large set of exact solutions can be determined effectively on picking the parameters that showed up. Besides, the proposed GIKM generalizes some previous techniques. It depends on improving the general Kudryashov technique by the general auxiliary equation (4), which has various general solutions. Moreover, we apply the GIKM and white noise topics to construct exact solutions for the Wick-type stochastic combined KdV–mKdV equation with conformable derivatives. Also, numerical simulations with 3D profiles are provided to the obtained exact solutions.

The remnant of this work is structured as follows: Sect. 2 contains the needed topics about the conformable calculus and the Gaussian analysis of white noise. In Sect. 3, the GIKM is demonstrated. In Sect. 4, we apply the GIKM, jointly with the Gaussian analysis of white noise, to investigate the Wick-type stochastic combined KdV–mKdV equation with conformable derivatives. Section 5 gives discussions and numerical simulations for the obtained results. Section 6 presents a conclusion.

2 Preliminaries

2.1 The conformable derivative and integral

In this division, we recollect the paramount aspects of the conformable-type derivative and its integral.

Definition 2.1

([50, 51])

Assume that ξ is a function from \((0,\infty )\) into \(\mathbb{R}\). For \(\varpi\in(0,1]\), we define the conformable-type derivative of ξ of order ϖ as follows:

$$ D_{\alpha}^{\varpi}\xi(\alpha)=\lim_{h\rightarrow0} \frac{\xi(\alpha+h \alpha^{1-\varpi})-\xi(\alpha)}{h},\quad \alpha>0. $$
(5)

Definition 2.2

([50, 51])

Assume that ξ is a ϖ-conformable differentiable function for \(\alpha\in(0,a)\), \(a>0\) and \(\lim_{\alpha\rightarrow 0^{+}}D_{\alpha}^{\varpi}\xi(\alpha)\) exists. Then \(D_{\alpha }^{\varpi}\xi(0)=\lim_{\alpha\rightarrow0^{+}}D_{\alpha}^{\varpi }\xi(\alpha)\) and the conformable-type integral of the function ξ beginning from \(\alpha_{0}\in [0,\alpha)\) is given by

$$ I^{\varpi,\alpha_{0}}\xi(\alpha)= \int_{\alpha_{0}}^{\alpha}\frac{\xi(\eta)}{\eta^{1-\varpi}}\, d\eta, $$
(6)

where the integral is the classical improper Riemann integral and \(\varpi\in(0,1]\).

The coming theorems give some precious properties for the conformable-type derivative.

Theorem 2.1

([50, 51])

Assume that\(\varpi\in(0,1]\), ξandζareϖ-order conformable differentiable functions at\(\alpha\in(0,\infty)\), andξis differentiable (in the usual sense) with respect to α. Then:

  1. (i)

    \(D_{\alpha}^{\varpi} (a \xi+b \zeta )=a D_{\alpha}^{\varpi }\xi+b D_{\alpha}^{\varpi }\zeta\)for all\(a, b\in\mathbb{R}\);

  2. (ii)

    \(D_{\alpha}^{\varpi} (\alpha^{a} )=a \alpha^{a-\varpi}\)for all\(a\in\mathbb{R}\);

  3. (iii)

    \(D_{\alpha}^{\varpi} (\xi\zeta )=\xi D_{\alpha}^{\varpi }\zeta+\zeta D_{\alpha}^{\varpi}\xi\);

  4. (iv)

    \(D_{\alpha}^{\varpi} (\frac{\xi}{\zeta} )=\frac{\zeta D_{\alpha}^{\varpi}\xi-\xi D_{\alpha}^{\varpi}\zeta}{\zeta^{2}}\);

  5. (v)

    \(D_{\alpha}^{\varpi}(\xi(\alpha))=\alpha^{1-\varpi}\xi '(\alpha)\),

where ′ denotes the usual derivative with regard toα.

Theorem 2.2

([44])

Assume that the functionξis a differentiable andϖ-order conformable differentiable function on\((0,\infty)\). Also, assume thatζis a differentiable function defined on the range ofξ. Then

$$ D_{\alpha}^{\varpi}(\xi\circ\zeta) (\alpha)=\alpha ^{1-\varpi}\bigl[\zeta(\alpha)\bigr]^{\varpi-1}\zeta '(\alpha) \bigl(D_{\alpha}^{\varpi}\xi(\alpha) \bigr)_{\alpha=\zeta}. $$
(7)

2.2 Basilar topics of white noise discipline

The Gaussian white noise discipline begins with the rigging \(\mathcal{D}(\mathbb{R}^{N})\subset L^{2}(\mathbb{R}^{N})\subset \mathcal{D}^{*}(\mathbb{R}^{N})\) where \(\mathcal{D}(\mathbb{R}^{N})\) is the Schwartz space of quickly decreasing, unlimited differentiable functions on \(\mathbb{R}^{N}\) and \(\mathcal{D}^{*}(\mathbb{R}^{N})\) is the tempered space of distributions. Depending on the Bochner–Minlos theorem [52], we have a lonesome white noise measure \(\mu_{w}\) on \((\mathcal {D}^{*}(\mathbb{R}^{N}),\beta (\mathcal{D}^{*}(\mathbb{R}^{N}) ) )\). Presume that \(\zeta_{n}(x)=\pi^{-1/4}((n-1)!)^{-1/2}e^{-x^{2}/2}\)\(h_{n-1}(\sqrt{2x})\), \(n\in\geq1\) are the Hermite functions, where \(h_{n}(x)\) denotes the Hermite polynomials. It is well known that the gathering \((\zeta_{n})_{n\in \mathbb{N}}\) fabricates an orthonormal basis for \(L^{2}(\mathbb{R})\). Let \(m=(m_{1},\ldots,m_{N})\) be N-dimensional multi-indices with \(m_{1},\ldots,m_{N}\in\mathbb{N}\), then the tensor multiplications \(\zeta_{m}:=\zeta_{(m_{1},\ldots,m_{N})} =\chi _{m_{1}}\otimes\cdots\otimes\chi_{m_{N}}\), \(m\in\mathbb{N}^{N}\) fabricate an orthonormal basis to \(L^{2}(\mathbb{R}^{N})\). Introduce an ordering in \(\mathbb{N}^{N}\) by

$$ i< j\Rightarrow\sum_{k=1}^{N} m_{k}^{(i)}\leq\sum_{k=1}^{N} m_{k}^{(j)}, \quad \text{where } m^{(i)}= \bigl(m^{(i)}_{k} \bigr)_{k=1}^{N},\ m^{(j)}= \bigl(m^{(j)}_{k} \bigr)_{k=1}^{N}\in\mathbb{N}^{N}. $$
(8)

Using the above ordering, we define \(\varrho_{i}:=\zeta _{m^{(i)}}=\zeta_{m^{(i)}_{1}}\otimes\cdots\otimes\zeta _{m^{(i)}_{N}}\), \(i\in\mathbb{N}\). Let \(\mathbb{J}= (\mathbb {N}_{0}^{\mathbb{N}} )_{c}\) be the aggregate of sequences \(m=(m_{i})_{i\in\mathbb{N}}\) with compact support and \(m_{i}\geq1\). For \(m\in\mathbb{J}\), we set

$$ \mathbb{H}_{m}(\vartheta)=\prod _{i=1}^{\infty}h_{m_{i}}\bigl(\langle \vartheta,\varrho_{i}\rangle\bigr),\quad \vartheta\in \mathcal{D}^{*}\bigl(\mathbb{R}^{N}\bigr). $$
(9)

Let \(n\in\mathbb{N}\), the Kondrative space of test stochastic functions \((\mathcal{D})_{1}^{n}\) is defined by

$$\begin{aligned} (\mathcal{D})_{1}^{n} =& \Biggl\{ f= \sum_{m}c_{m}\mathbb{H}_{m} \in\bigoplus_{k=1}^{n} L^{2}(\mu_{w}): c_{m}\in \mathbb{R}^{n} \text{ and} \\ &{}\Vert f \Vert ^{2}_{1,k}:=\sum_{m} c_{m}^{2}(m!)^{2}(2 \mathbb{N})^{km}< \infty\ \forall k\in\mathbb{N} \Biggr\} , \end{aligned}$$
(10)

and the Kondrative space of distribution stochastic functions \((\mathcal {D})_{-1}^{n}\) is defined by

$$\begin{aligned} (\mathcal{D})_{-1}^{n} =& \biggl\{ F= \sum_{m}b_{m}\mathbb{H}_{m}: b_{m}\in\mathbb{R}^{n} \text{ and} \\ &{}\Vert F \Vert ^{2}_{-1,k}:=\sum_{m} b_{m}^{2}(2 \mathbb{N})^{-qm}< \infty\text{ for some } q\in\mathbb{N} \biggr\} . \end{aligned}$$
(11)

The Wick product of two stochastic distributions \(F=\sum_{m}a_{m} \mathbb{H}_{m}\), \(G=\sum_{\bar{m}}b_{\bar{m}}\mathbb{H}_{\bar{m}} \in (\mathcal{D})_{-1}^{n}\) with \(a_{m}, b_{\bar{m}} \in\mathbb{R}^{n}\) is known as

$$ F\diamond G=\sum_{m,\bar{m}}(a_{m}, b_{\bar{m}}) \mathbb{H}_{m+\bar{m}}. $$
(12)

Let \(F=\sum_{m}a_{m} \mathbb{H}_{m}\in(\mathcal{D})_{-1}^{n}\) with \(a_{m}\in\mathbb{R}^{n}\). The Hermite transform of F is defined by

$$ \mathcal{H}F(z)=\widetilde{F}(z)=\sum _{m}a_{m} z^{m}\in \mathbb{C}^{n} \quad \text{(when convergent)}, $$
(13)

where \(z=(z_{1},z_{2},\ldots)\in\mathbb{C}^{\mathbb{N}}\) and \(z^{m}=\prod_{i=1}^{\infty }z_{i}^{m_{i}}\), with \(m=(m_{1},m_{2},\ldots)\in\mathbb{J}\) and \(z_{i}^{0}=1\).

For \(F,G\in(\mathcal{D})^{n}_{-1}\), via the shape of Hermite transformation, we have

$$ \widetilde{F\diamond G}(z)=\widetilde{F}(z)\bullet \widetilde{G}(z) $$
(14)

for all z such that \(\widetilde{F}(z)\) and \(\widetilde{G}(z)\) exist. The relation “•” indicates the bilinear multiplication in \(\mathbb {C}^{n}\), which is known as \((z_{1}^{1},\ldots, z_{n}^{1})\bullet (z_{1}^{2},\ldots,z_{n}^{2})=\sum_{i=1}^{n} z_{i}^{1}z_{i}^{2}\), where \(z_{i}^{k}\in\mathbb{C}\). Thus, the Hermite transform changes the Wick multiplication into the classical multiplication and convergence in \((\mathcal{D})_{-1}^{n}\) into bounded and pointwise convergence in a certain neighborhood of the origin in \(\mathbb{C}^{n}\). For more specifics about Kondrative spaces, Hermite transformation, and Wick multiplication, we refer to [52].

In the following, the distribution stochastic process (or \((\mathcal {D})^{n}_{-1}\)-process) is a measurable map u from \(\mathbb {R}^{N}\) into \((\mathcal{D})^{n}_{-1}\). Furthermore, if the \((\mathcal{D})^{n}_{-1}\)-valued function u is continuous, differentiable, \(C^{k}\), etc., then the \((\mathcal {D})^{n}_{-1}\)-process u has the same features, respectively. Now, for \(\pi<\infty\), \(\rho>0\), deem the infinite dimensional neighborhoods \(\mathcal{O}_{\pi}(\rho)=\{ (z_{1},z_{2},\ldots)\in\mathbb{C}^{\mathbb{N}}:\sum_{m\neq 0}|z^{m}|^{2}(2\mathbb{N})^{\pi m}<\rho^{2}\}\) of the origin in \(\mathbb{C}^{\mathbb{N}}\) [52]. To study the stochastic conformable PDEs, we require the following facts.

Lemma 2.1

([52, 53])

Suppose that\(X(\alpha,\vartheta)\)and\(Y(\alpha,\vartheta)\)are\((\mathcal{D})_{-1}\)-processes such that

  1. (i)

    \(D_{\alpha}^{\varpi}\widetilde{X}(\alpha,z)=\widetilde {Y}(\alpha,z)\)\(\forall (\alpha,z)\in(s,t)\times\mathcal{O}_{\pi }(\rho)\)and that

  2. (ii)

    \(\widetilde{Y}(\alpha,z)\)is a bounded function for\((\alpha,z)\in(s,t)\times\mathcal{O}_{\pi}(\rho)\)and continuous for\(\alpha\in(s,t)\)\(\forall z\in\mathcal{O}_{\pi}(\rho)\).

Then\(X(\alpha,\vartheta)\)has aϖ-order conformable derivative for each\(\alpha\in(s,t)\)and

$$ D_{\alpha}^{\varpi}X(\alpha,\vartheta)=Y(\alpha,\vartheta)\quad \textit{in } (\mathcal{D})_{-1}. $$
(15)

Lemma 2.2

([52, 53])

Let\(X(\alpha,\vartheta)\)be a\((\mathcal{D})_{-1}\)-process. Suppose that there exist\(\pi<\infty\), \(\rho>0\)such that

$$ \sup\bigl\{ \widetilde{X}(\alpha,z):\alpha\in[s,t], z\in \mathcal{O}_{\pi}(\rho)\bigr\} < \infty $$
(16)

and\(\widetilde{X}(\alpha,z)\)is a continuous function for\(\alpha\in[s,t]\)\(\forall z\in\mathcal{O}_{\pi}(\rho)\). Then theϖ-order conformable integral operator of\(X(\alpha)\)exists and

$$ \widetilde{I^{\varpi,s}X(\alpha)}(z)=I^{\varpi,s}\widetilde{X}( \alpha,z)\quad \textit{for } \varpi, s\geq0, \ \alpha\in[s,t],\ z\in \mathcal{O}_{\pi}(\rho). $$
(17)

Theorem 2.3

([52])

Suppose that\(u(\chi,\alpha,z)\)is a solution (in the usual strong and pointwise sense) of the equation

$$ \widetilde{\varOmega}\bigl(u,\chi,\alpha, z, D_{\alpha}^{\varpi},D_{\chi_{1}}^{\varpi}, \ldots,D_{\chi_{N}}^{\varpi}\bigr)=0 $$
(18)

for\((\chi,\alpha)\)in some bounded open set\(\mathbf{D}\subset \mathbb{R}^{N}\times\mathbb{R}_{+}\), \(\forall z\in\mathcal{O}_{\pi}(\rho)\)and for\(\pi<\infty\)\(\rho>0\). Moreover, suppose that\(u(\chi,\alpha,z)\)and all its conformable derivatives, which are implicated in Eq. (18), are bounded for\((\chi,\alpha,z)\in\mathbf{D}\times\mathcal{O}_{\pi}(\rho)\), continuous for\((\chi,\alpha)\in\mathbf{D}\)\(\forall z\in\mathcal {O}_{\pi}(\rho)\), and analytic\(\forall z\in\mathcal{O}_{\pi }(\rho)\)for all\((\chi,\alpha)\in\mathbf{D}\). Then ∃ \(U(\chi,\alpha)\in(\mathcal{D})_{-1}\)such that\(u(\chi,\alpha,z)=\tilde{U}(\chi,\alpha)(z)\)for all\((\chi ,\alpha,z)\in\mathbf{D}\times \mathcal{O}_{\pi}(\rho)\)and\(U(\chi,\alpha)\)solves (in the strong sense) the equation

$$ \varOmega^{\diamond}\bigl(U,\chi,\alpha, \vartheta, D_{\alpha }^{\varpi},D_{\chi_{1}}^{\varpi}, \ldots,D_{\chi_{N}}^{\varpi}\bigr)=0 \quad \textit{in } ( \mathcal{D})_{-1}. $$
(19)

3 Demonstration of the GIKM

Consider a conformable NPDE in the form

$$ \mathcal{P}\bigl(u,\chi,\alpha, D_{\alpha}^{\varpi}u, D_{\chi}^{\varpi}u, D_{\chi}^{2\varpi} u, D_{\chi}^{3\varpi} u, \ldots\bigr)= 0, $$
(20)

where \(u=u(\chi,\alpha)\) is the unknown function and \(\mathcal{P}\) is a polynomial function in u and its conformable derivatives. To obtain wave solution for Eq. (20), we use the wave transformation

$$ u=u(\varkappa),\qquad \varkappa(\chi,\alpha)= \frac{\chi^{\varpi}}{\varpi}+\omega \int_{a}^{\alpha}\frac{\theta(\eta)}{\eta^{1-\varpi}}\, d\eta, $$
(21)

where \(a\geq0\), ω are constants and θ is a nonzero function to be determined later. Hence, Eq. (21) converts Eq. (20) to a NODE

$$ \mathcal{Q} \biggl(u,\varkappa,\frac{du}{d\varkappa },\frac{d^{2}u}{d\varkappa^{2}},\frac {d^{3}u}{d\varkappa^{3}},\ldots \biggr)=0. $$
(22)

For easiness, we integrate Eq. (22) as long as all terms involve derivatives. Then, we equalize the integration constants to zero. Thereafter, the solution of Eq. (22) can be expanding as the form

$$ u(\varkappa)=\frac{ \sum_{i=0}^{x}\mu_{i}(\alpha)\mathfrak {X}^{i}(\varkappa)}{ \sum_{j=0}^{y}\nu_{j}(\alpha)\mathfrak {X}^{j}(\varkappa)}, $$
(23)

where \(\mu_{i}\), \(\nu_{j}\) (\(i=0,1,\ldots,x\), \(j=0,1,\ldots,y\)) are functions to be determined and \(\mathfrak{X}\) solves the common auxiliary equation

$$ \mathfrak{X}'(\varkappa)=\sigma \mathfrak{X}^{n}(\varkappa)-\mathfrak{X}(\varkappa),\quad 1< n\in \mathbb{N}, 0\neq\sigma\in\mathbb{R}. $$
(24)

Solving Eq. (24) gives a general family of solutions

$$ \mathfrak{X}(\varkappa)= \textstyle\begin{cases} \frac{1}{\sqrt[n-1]{\sigma+C\exp[(n-1)\varkappa]}},& n= 2,4,6,8,\ldots, \\ \frac{\pm1}{\sqrt[n-1]{\sigma+C\exp[(n-1)\varkappa]}},& n= 3,7,11,15,\ldots, \\ \frac{\pm1}{\sqrt[n-1]{\sigma+C\exp[(n-1)\varkappa]}},\qquad \frac{\pm i}{\sqrt[n-1]{\sigma+C\exp[(n-1)\varkappa]}},& n= 5,9,13,17,\ldots. \end{cases} $$
(25)

The integer numbers x and y can be appointed by balancing the highest order linear and nonlinear terms in Eq. (22). By inserting Eqs. (23) and (24) into Eq. (22), we get an algebraic-form equation in \(\mathfrak{X}\) and its powers. Placing the coefficients of all terms that include the similar power for \(\mathfrak{X}\) to be zero, gives a system of algebraic-form equations in \(\mu_{i}\), \(\nu_{j}\), and θ. By employing the symbolic system Mathematica, we can determine \(\mu_{i}\), \(\nu_{j}\), and θ. Lastly, by utilizing these values and Eq. (25), we can construct some exact and traveling wave solutions to Eq. (20).

4 Application to Wick-type stochastic combined KdV–mKdV equation with conformable derivatives

In this section, GIKM for \(n=5\), white noise theory, Hermite transform, and computerized symbolic computation are applied to find exact traveling wave solutions of Wick-type stochastic combined KdV–mKdV with conformable derivatives. The KdV and mKdV equations are solitary equations, which have been widely researched. For these equations, the nonlinear terms usually arise in abundant physical issues, like flow mechanics, quantum fields, and plasma physics. This section is devoted to constructing exact traveling wave solutions of Wick-type stochastic combined KdV–mKdV equation with conformable derivatives

$$ D_{\alpha}^{\varpi}U+\Delta(\alpha)\diamond U \diamond D_{\chi}^{\varpi}U+\varLambda(\alpha) \diamond U^{\diamond2} \diamond D_{\chi}^{\varpi}U+D_{\chi}^{3\varpi}U=0, $$
(26)

where \((\chi,\alpha) \in\mathbb{R}\times\mathbb{R}_{+}\) and \(0<\varpi\leq1\), while Δ and Λ are real and integrable nonzero functions with values in \((\mathcal{D})_{-1}\). Equation (26) is the perturbation of the variable coefficients combined KdV–mKdV equation with conformable derivatives

$$ D_{\alpha}^{\varpi}u+\delta(\alpha)u D_{\chi}^{\varpi}u+\lambda(\alpha) u^{2} D_{\chi}^{\varpi}u+D_{\chi}^{3\varpi}u=0, $$
(27)

where δ, λ are nonzero integrable functions on \(\mathbb {R}_{+}\). Moreover, if Eq. (27) is considered in some random ambience, we have a random combined KdV–mKdV equation. To construct exact solutions of the random combined KdV–mKdV equation, we only examine it in a white noise ambience, thus, we will investigate the Wick-type stochastic combined KdV–mKdV equation (26).

By using Hermite transform and Eq. (26), we get a conformable deterministic equation

$$\begin{aligned}& D_{\alpha}^{\varpi}\widetilde{U}(\chi,\alpha ,z) +\widetilde{\Delta}(\alpha,z)\widetilde{U}(\chi,\alpha,z) D_{\chi}^{\varpi}\widetilde{U}(\chi,\alpha,z) \\& \quad {} +\widetilde{\varLambda}(\alpha,z) \widetilde{U}^{2} D_{\chi}^{\varpi}\widetilde{U}(\chi,\alpha,z) +D_{\chi}^{3\varpi}\widetilde{U}(\chi,\alpha,z)=0, \end{aligned}$$
(28)

where \(z=(z_{1},z_{2},\ldots)\in(\mathbb{C}^{\mathbb{N}})_{c}\). To construct traveling wave solutions to Eq. (28), we employ the transformations \(\widetilde{\Delta}(\alpha,z)=\delta(\alpha,z)\), \(\widetilde{\varLambda}(\alpha,z)=\lambda(\alpha,z)\), \(\widetilde {U}(\chi,\alpha,z)=u(\chi,\alpha,z)=u(\varkappa(\chi,\alpha,z))\) with

$$ \varkappa(\chi,\alpha,z)=\frac{\chi^{\varpi}}{\varpi }+\omega \int_{a}^{\alpha}\frac{\theta(\eta,z)}{\eta^{1-\varpi}}\, d\eta, $$
(29)

where ω is a free constant and θ is a nonzero function to be specified. Hence, Eq. (28) can be transformed to the following NODE

$$ \omega\theta\frac{du}{d\varkappa}+\delta u \frac{du}{d\varkappa}+\lambda u^{2} \frac{du}{d\varkappa}+ \frac{d^{3}u}{d\varkappa^{3}}=0. $$
(30)

Integrating the NODE (30) and placing the integration constants to be zero give

$$ \omega\theta u+\frac{\delta}{2} u^{2}+ \frac{\lambda}{3} u^{3} +\frac{d^{2}u}{d\varkappa^{2}}=0. $$
(31)

Considering the homogeneous balance for \(\frac{d^{2}u}{d\varkappa ^{2}}\) and \(u^{3}\), we get \(x-y-4=0\). Let \(y=1\), then \(x=5\). So, we can set the wave solution of Eq. (31) as the form

$$ u\bigl(\varkappa(\chi,\alpha,z)\bigr)=\frac{ \sum _{i=0}^{5}\mu_{i}(\alpha,z)\mathfrak{X}^{i}(\varkappa(\chi,\alpha ,z))}{ \sum_{j=0}^{1}\nu_{j}(\alpha,z)\mathfrak{X}^{j}(\varkappa (\chi,\alpha,z))}. $$
(32)

Substituting Eqs. (32) and (24) for \(n=5\) into Eq. (31) gives an algebraic-form equation in \(\mathfrak{X}\) and its powers. Equating the coefficients of the terms that contain the same power for \(\mathfrak{X}\) to zero gives a system of algebraic-form equations in \(\mu_{i}\), \(\nu_{j}\) (\(i=0,\ldots,5\), \(j=0,1\)) and θ (see the Appendix). By treating this system via Mathematica, we obtain the following sets of values.

Case I.

$$ \textstyle\begin{cases} \mu_{0}=\mu_{0},\qquad \mu_{1}=\frac{36\mu_{0}\nu_{0}^{2}\nu_{1}-180\mu _{0}^{2}\nu_{0}\nu_{1}\delta+12\mu_{0}^{2}\nu_{1}(3\nu_{0}\delta +2\mu_{0}\lambda)}{6(\mu_{0}^{2}\lambda+\nu_{0}^{2}+\mu_{0}\nu _{0}\delta)-\mu_{0}(3\nu_{0}\delta+2\mu_{0}\lambda)}, \\ \mu_{2}=\pm\frac{155\nu_{0}^{3}}{102\nu_{1}^{2}\sqrt{6\lambda}},\qquad \mu_{3}=\pm \frac{10\nu_{0}^{2}}{\nu_{1}\sqrt{96\lambda}},\qquad \mu_{4}=0,\qquad \mu _{5}=\pm \frac{\sqrt{96}\nu_{1}\sigma}{\sqrt{\lambda}}, \\ \nu_{0}=\nu_{0},\qquad \nu_{1}=\nu_{1},\qquad \theta=\frac{\mu_{0}(3\nu _{0}\delta+2\mu_{0}\lambda)}{6\omega\nu_{0}^{2}}, \end{cases} $$
(33)

where \(\mu_{0}\), \(\nu_{0}\), and \(\nu_{1}\) are free integrable functions on \(\mathbb{R}_{+}\). Substituting the values (33) into (32) and using (25) produce traveling wave solutions to Eq. (28) as follows:

$$\begin{aligned}& u_{1}(\chi,\alpha,z) = \frac{\sqrt[4]{\sigma+C\exp [4\varkappa(\chi,\alpha,z)]}}{\nu_{1}(\alpha,z)\pm\nu_{0}(\alpha ,z)\sqrt[4]{\sigma+C\exp[4\varkappa(\chi,\alpha,z)]}} \biggl[\frac{\mu_{0}(\alpha,z)+A(\alpha,z)}{102\nu_{1}^{2}(\alpha ,z)\sqrt{6\lambda(\alpha,z)}} \\& \hphantom{u_{1}(\chi,\alpha,z) ={}}{} \pm {\frac{155\nu_{0}^{3}(\alpha,z)}{ (\sigma+C\exp[4\varkappa (\chi,\alpha,z)] )^{\frac{1}{2}}}}+ {\frac{255\nu_{1}^{3}(\alpha ,z)}{ (\sigma+C\exp[4\varkappa(\chi,\alpha,z)] )^{\frac{3}{4}}}} \\& \hphantom{u_{1}(\chi,\alpha,z) ={}}{} + {\frac{2448\sigma\nu_{1}^{3}(\alpha,z)}{ (\sigma+C\exp [4\varkappa(\chi,\alpha,z)] )^{\frac{5}{4}}}} \biggr], \end{aligned}$$
(34)
$$\begin{aligned}& u_{2}(\chi,\alpha,z) = \frac{\sqrt[4]{\sigma+C\exp [4\varkappa(\chi,\alpha,z)]}}{\nu_{1}(\alpha,z)\pm i \nu _{0}(\alpha,z)\sqrt[4]{\sigma+C\exp[4\varkappa(\chi,\alpha,z)]}} \biggl[\frac{\mu_{0}(\alpha,z)+A(\alpha,z)}{102\nu_{1}^{2}(\alpha ,z)\sqrt{6\lambda(\alpha,z)}} \\& \hphantom{u_{2}(\chi,\alpha,z) ={}}{} \pm i {\frac{155\nu_{0}^{3}(\alpha,z)}{ (\sigma+C\exp[4\varkappa (\chi,\alpha,z)] )^{\frac{1}{2}}}}\pm i {\frac{255\nu_{1}^{3}(\alpha ,z)}{ (\sigma+C\exp[4\varkappa(\chi,\alpha,z)] )^{\frac{3}{4}}}} \\& \hphantom{u_{2}(\chi,\alpha,z) ={}}{} \pm i {\frac{2448\sigma\nu_{1}^{3}(\alpha,z)}{ (\sigma+C\exp [4\varkappa(\chi,\alpha,z)] )^{\frac{5}{4}}}} \biggr], \end{aligned}$$
(35)

where

$$ A(\alpha,z)=\frac{ \biggl(\textstyle\begin{array}{l} 36\mu_{0}(\alpha,z)\nu_{0}^{2}(\alpha,z)\nu_{1}(\alpha,z)-180\mu _{0}^{2}(\alpha,z)\nu_{0}(\alpha,z)\nu_{1}(\alpha,z)\delta(\alpha ,z) \\ \quad {}+12\mu_{0}^{2}(\alpha,z)\nu_{1}(\alpha,z)(3\nu_{0}(\alpha ,z)\delta(\alpha,z)+2\mu_{0}(\alpha,z)\lambda(\alpha,z)) \end{array}\displaystyle \biggr) }{ \biggl(\textstyle\begin{array}{l} 6(\mu_{0}^{2}(\alpha,z)\lambda(\alpha,z)+\nu_{0}^{2}(\alpha ,z)+\mu_{0}(\alpha,z)\nu_{0}(\alpha,z)\delta(\alpha,z))\\ \quad {}-\mu_{0}(\alpha,z)(3\nu_{0}(\alpha,z)\delta(\alpha,z)+2\mu _{0}(\alpha,z)\lambda(\alpha,z)) \end{array}\displaystyle \biggr) } $$
(36)

and

$$ \varkappa(\chi,\alpha,z)=\frac{\chi^{\varpi}}{\varpi }+ \int_{a}^{\alpha}\frac{\mu_{0}(\eta,z)(3\nu_{0}(\eta,z)\delta (\eta,z)+2\mu_{0}(\eta,z)\lambda(\eta,z))}{6\eta^{1-\varpi}\nu _{0}^{2}(\eta,z)}\, d\eta, $$
(37)

provided that \(\lambda>0\) and \(\nu_{0}\neq0\).

Case II.

$$ \textstyle\begin{cases} \mu_{0}=\frac{\nu_{0}\sqrt{9\delta^{2}-384\lambda}-3\nu_{0}\delta }{8\lambda},\qquad \mu_{1}=\frac{\nu_{1}\sqrt{3\delta^{2}-128\lambda }-3\nu_{1}\delta}{8\lambda}, \\ \mu_{2}=\frac{\mu_{4}(813\nu_{0}^{2}\sigma^{2}-8\mu _{4}^{2}\lambda)}{120\nu_{1}^{2}\sigma^{2}}, \qquad \mu_{3}=\frac{-306\mu _{4}\nu_{0}}{72\nu_{1}},\qquad \mu_{4}=\mu_{4},\qquad \mu_{5}=0, \\ \nu _{0}=\nu_{0},\qquad \nu_{1}=\nu_{1},\qquad \theta=\frac{\delta (3\delta-\sqrt {9\delta^{2}-384\lambda} )-64\lambda}{32\omega\lambda}, \end{cases} $$
(38)

where \(\mu_{4}\), \(\nu_{0}\), and \(\nu_{1}\) are free integrable functions on \(\mathbb{R}_{+}\). Substituting the values (38) into (32) and using (25) produce traveling wave solutions to Eq. (28) as follows:

$$\begin{aligned}& u_{3}(\chi,\alpha,z) = \frac{\sqrt[4]{\sigma+C\exp [4\varkappa(\chi,\alpha,z)]}}{\nu_{1}(\alpha,z)\pm\nu_{0}(\alpha ,z)\sqrt[4]{\sigma+C\exp[4\varkappa(\chi,\alpha,z)]}} \\& \hphantom{u_{3}(\chi,\alpha,z) ={}}{} \times \biggl[\frac{ ( \nu_{0}(\alpha,z)\sqrt{9\delta^{2}(\alpha,z)-384\lambda(\alpha ,z)}-3\nu_{0}(\alpha,z)\delta(\alpha,z) ) }{8\lambda(\alpha,z)} \\& \hphantom{u_{3}(\chi,\alpha,z) ={}}{} \pm \frac{\nu_{1}(\alpha,z)\sqrt{3\delta^{2}(\alpha,z)-128\lambda (\alpha,z)}-3\nu_{1}(\alpha,z)\delta(\alpha,z)}{8\lambda(\alpha ,z) (\sigma+C\exp[4\varkappa(\chi,\alpha,z)] )^{\frac{1}{4}}} \\& \hphantom{u_{3}(\chi,\alpha,z) ={}}{} + \frac{\mu_{4}(\alpha,z)(813\nu_{0}^{2}(\alpha,z)\sigma^{2}-8\mu _{4}^{2}(\alpha,z)\lambda(\alpha,z))}{120\nu_{1}^{2}(\alpha ,z)\sigma^{2} (\sigma+C\exp[4\varkappa(\chi,\alpha,z)] )^{\frac{1}{2}}} \\& \hphantom{u_{3}(\chi,\alpha,z) ={}}{} \pm \frac{306\mu_{4}(\alpha,z)\nu_{0}(\alpha,z)}{72\nu _{1}(\alpha,z) (\sigma+C\exp[4\varkappa(\chi,\alpha,z)] )^{\frac{3}{4}}} \\& \hphantom{u_{3}(\chi,\alpha,z) ={}}{} + \frac{\mu_{4}(\alpha,z)}{ (\sigma+C\exp[4\varkappa(\chi,\alpha ,z)] )}\biggr], \end{aligned}$$
(39)
$$\begin{aligned}& u_{4}(\chi,\alpha,z) = \frac{\sqrt[4]{\sigma+C\exp [4\varkappa(\chi,\alpha,z)]}}{\nu_{1}(\alpha,z)\pm i \nu _{0}(\alpha,z)\sqrt[4]{\sigma+C\exp[4\varkappa(\chi,\alpha,z)]}} \\& \hphantom{u_{4}(\chi,\alpha,z) ={}}{} \times \biggl[\frac{( \nu_{0}(\alpha,z)\sqrt{9\delta^{2}(\alpha,z)-384\lambda(\alpha ,z)}-3\nu_{0}(\alpha,z)\delta(\alpha,z) ) }{8\lambda(\alpha ,z)}{ } \\& \hphantom{u_{4}(\chi,\alpha,z) ={}}{} \pm i \frac{\nu_{1}(\alpha,z)\sqrt{3\delta^{2}(\alpha ,z)-128\lambda(\alpha,z)}-3\nu_{1}(\alpha,z)\delta(\alpha ,z)}{8\lambda(\alpha,z) (\sigma+C\exp[4\varkappa(\chi,\alpha,z)] )^{\frac{1}{4}}} \\& \hphantom{u_{4}(\chi,\alpha,z) ={}}{} + \frac{\mu_{4}(\alpha,z)(813\nu_{0}^{2}(\alpha,z)\sigma^{2}-8\mu _{4}^{2}(\alpha,z)\lambda(\alpha,z))}{120\nu_{1}^{2}(\alpha ,z)\sigma^{2} (\sigma+C\exp[4\varkappa(\chi,\alpha,z)] )^{\frac{1}{2}}} \\& \hphantom{u_{4}(\chi,\alpha,z) ={}}{} \pm i \frac{306\mu_{4}(\alpha,z)\nu_{0}(\alpha,z)}{72\nu _{1}(\alpha,z) (\sigma+C\exp[4\varkappa(\chi,\alpha,z)] )^{\frac{3}{4}}} \\& \hphantom{u_{4}(\chi,\alpha,z) ={}}{} + \frac{\mu_{4}(\alpha,z)}{ (\sigma+C\exp[4\varkappa(\chi,\alpha ,z)] )} \biggr], \end{aligned}$$
(40)

where

$$ \varkappa(\chi,\alpha,z)=\frac{\chi^{\varpi}}{\varpi }+ \int_{a}^{\alpha}\frac{\delta(\eta,z) (3\delta(\eta,z)-\sqrt {9\delta^{2}(\eta,z)-384\lambda(\eta,z)} )-64\lambda(\eta ,z)}{32\eta^{1-\varpi}\lambda(\eta,z)}\, d\eta, $$
(41)

provided that \(\lambda\neq0\), \(\sigma\neq0\), \(\nu_{1}\neq0\), and \(\delta^{2}\geq\frac{128\lambda}{3}\).

Case III.

$$ \textstyle\begin{cases} \mu_{0}=\mu_{0},\qquad \mu_{1}=\frac{\nu_{1} (-3\delta+\sqrt{9\delta ^{2}-528\lambda} )}{8\lambda}, \qquad \mu_{2}=\mu_{3}=\mu_{4}=\mu _{5}=0, \\ \nu_{0}=-\frac{\mu_{0}}{66} (3\delta+\sqrt{9\delta^{2}-528\lambda} ), \qquad \nu_{1}=\nu_{1}, \\ \theta=\frac{-3\delta^{2}+\delta\sqrt{9\delta^{2}-528\lambda }-88\lambda}{32\omega\lambda}, \end{cases} $$
(42)

where \(\mu_{0}\) and \(\nu_{1}\) are free integrable functions on \(\mathbb{R}_{+}\). Substituting the values (42) into (32) and using (25) produces traveling wave solutions to Eq. (28) as follows:

$$\begin{aligned}& u_{5}(\chi,\alpha,z)=\frac{ \biggl(\textstyle\begin{array}{l} 528\mu_{0}(\alpha,z)\lambda(\alpha,z) (\sigma+C\exp[4\varkappa (\chi,\alpha,z)] )^{\frac{1}{4}}\\ \quad {}\pm66\nu_{1}(\alpha,z) (-3\delta(\alpha,z)+\sqrt{9\delta ^{2}(\alpha,z)-528\lambda(\alpha,z)} ) \end{array}\displaystyle \biggr) }{ \biggl(\textstyle\begin{array}{l} -8\mu_{0}(\alpha,z)\lambda(\alpha,z) (3\delta(\alpha,z)+\sqrt {9\delta^{2}(\alpha,z)-528\lambda(\alpha,z)} )\\ \quad {}\times (\sigma+C\exp[4\varkappa(\chi,\alpha,z)] )^{\frac {1}{4}}\pm528\nu_{1}(\alpha,z)\lambda(\alpha,z) \end{array}\displaystyle \biggr) }, \end{aligned}$$
(43)
$$\begin{aligned}& u_{6}(\chi,\alpha,z)=\frac{ \biggl(\textstyle\begin{array}{l} 528\mu_{0}(\alpha,z)\lambda(\alpha,z) (\sigma+C\exp[4\varkappa (\chi,\alpha,z)] )^{\frac{1}{4}}\\ \quad {}\pm66 i \nu_{1}(\alpha,z) (-3\delta(\alpha,z)+\sqrt{9\delta ^{2}(\alpha,z)-528\lambda(\alpha,z)} ) \end{array}\displaystyle \biggr) }{ \biggl(\textstyle\begin{array}{l} -8\mu_{0}(\alpha,z)\lambda(\alpha,z) (3\delta(\alpha,z)+\sqrt {9\delta^{2}(\alpha,z)-528\lambda(\alpha,z)} )\\ \quad {}\times (\sigma+C\exp[4\varkappa(\chi,\alpha,z)] )^{\frac {1}{4}}\pm528 i \nu_{1}(\alpha,z)\lambda(\alpha,z) \end{array}\displaystyle \biggr) }, \end{aligned}$$
(44)

where

$$ \varkappa(\chi,\alpha,z)=\frac{\chi^{\varpi}}{\varpi }+ \int_{a}^{\alpha}\frac{-3\delta^{2}(\eta,z)+\delta(\eta,z)\sqrt {9\delta^{2}(\eta,z)-528\lambda(\eta,z)}-88\lambda(\eta ,z)}{32\eta^{1-\varpi}\lambda(\eta,z)}\, d\eta, $$
(45)

provided that \(\lambda\neq0\) and \(\delta^{2}\geq\frac{528\lambda}{9}\).

Obviously, we can find different traveling wave solutions of Eq. (28) by applying different cases to the solutions of the algebraic system in the Appendix.

The features of exponential functions lead to the existence of an open bounded set \(\mathbf{D}\subset\mathbb{R}\times\mathbb{R}_{+}\), \(\pi<\infty \), \(\rho>0\) provided that the solution \(u(\chi,\alpha,z)\) of Eq. (28) and all its conformable derivatives that are included in Eq. (28) are uniformly bounded with respect to \((\chi,\alpha,z)\in\mathbf{D}\times\mathcal{O}_{\pi }(\rho) \), continuous for \((\chi,\alpha) \in\mathbf{D}\)\(\forall z\in\mathcal{O}_{\pi}(\rho)\), and analytic for \(z\in\mathcal {O}_{\pi}(\rho)\)\(\forall(\chi,\alpha) \in\mathbf{D}\). According to Theorem 2.3, \(\exists U(\chi,\alpha) \in(\mathcal{D})_{-1}\) such that \(u(\chi,\alpha,z)=\widetilde{U}(\chi,\alpha) (z)\)\(\forall (\chi,\alpha,z)\in \mathbf{D}\times\mathcal{O}_{\pi}(\rho)\) and \(U(\chi,\alpha) \) solves Eq. (26) in \((\mathcal{D})_{-1}\). Hence, by taking the inverse Hermite transform to Eqs. (34)–(37), (39)–(41), and (43)–(45), we obtain the stochastic solutions of Eq. (26) as follows:

$$\begin{aligned}& U_{1}(\chi,\alpha) = \frac{\sqrt[4]{\sigma+C\exp ^{\diamond}[4\varkappa_{1}(\chi,\alpha)]}}{\nu_{1}(\alpha)\pm\nu _{0}(\alpha)\diamond\sqrt[4]{\sigma+C\exp^{\diamond}[4\varkappa _{1}(\chi,\alpha)]}} \diamond\biggl[\frac{\mu_{0}(\alpha)+A(\alpha)}{102\nu _{1}^{\diamond2}(\alpha)\diamond\sqrt{6\varLambda(\alpha) }} \\& \hphantom{U_{1}(\chi,\alpha) ={}}{} \pm {\frac{155\nu_{0}^{\diamond3}(\alpha)}{ (\sigma+C\exp ^{\diamond}[4\varkappa_{1}(\chi,\alpha)] )^{\diamond\frac {1}{2}}}}+ {\frac{255\nu_{1}^{\diamond3}(\alpha)}{ (\sigma+C\exp ^{\diamond}[4\varkappa_{1}(\chi,\alpha)] )^{\diamond\frac{3}{4}}}} \\& \hphantom{U_{1}(\chi,\alpha) ={}}{} + {\frac{2448\sigma\nu_{1}^{\diamond3}(\alpha)}{ (\sigma+C\exp ^{\diamond}[4\varkappa_{1}(\chi,\alpha)] )^{\diamond\frac{5}{4}}}} \biggr], \end{aligned}$$
(46)
$$\begin{aligned}& U_{2}(\chi,\alpha) = \frac{\sqrt[4]{\sigma+C\exp ^{\diamond}[4\varkappa_{1}(\chi,\alpha)]}}{\nu_{1}(\alpha)\pm i \nu_{0}(\alpha)\diamond\sqrt[4]{\sigma+C\exp^{\diamond }[4\varkappa_{1}(\chi,\alpha)]}} \diamond\biggl[\frac{\mu_{0}(\alpha)+A(\alpha)}{102\nu _{1}^{\diamond2}(\alpha)\diamond\sqrt{6\varLambda(\alpha) }} \\& \hphantom{ U_{2}(\chi,\alpha) ={}}{} \pm i {\frac{155\nu_{0}^{\diamond3}(\alpha)}{ (\sigma+C\exp ^{\diamond}[4\varkappa_{1}(\chi,\alpha)] )^{\diamond\frac {1}{2}}}}+i {\frac{255\nu_{1}^{\diamond3}(\alpha)}{ (\sigma+C\exp ^{\diamond}[4\varkappa_{1}(\chi,\alpha)] )^{\diamond\frac{3}{4}}}} \\& \hphantom{ U_{2}(\chi,\alpha) ={}}{} + i {\frac{2448\sigma\nu_{1}^{\diamond3}(\alpha)}{ (\sigma+C\exp ^{\diamond}[4\varkappa_{1}(\chi,\alpha)] )^{\diamond\frac{5}{4}}}} \biggr], \end{aligned}$$
(47)

where

$$ A(\alpha)=\frac{ \biggl(\textstyle\begin{array}{l} 36\mu_{0}(\alpha)\diamond\nu_{0}^{\diamond2}(\alpha)\diamond\nu _{1}(\alpha)-180\mu_{0}^{\diamond2}(\alpha)\diamond\nu_{0}(\alpha )\diamond\nu_{1}(\alpha)\diamond\Delta(\alpha) \\ \quad {}+12\mu_{0}^{\diamond2}(\alpha)\diamond\nu_{1}(\alpha)\diamond (3\nu_{0}(\alpha)\diamond\Delta(\alpha)+2\mu_{0}(\alpha)\diamond \varLambda(\alpha) ) \end{array}\displaystyle \biggr) }{ \biggl(\textstyle\begin{array}{l} 6(\mu_{0}^{\diamond2}(\alpha)\diamond\varLambda(\alpha) +\nu _{0}^{\diamond2}(\alpha)+\mu_{0}(\alpha)\diamond\nu_{0}(\alpha )\diamond\Delta(\alpha))\\ \quad {}-\mu_{0}(\alpha)\diamond(3\nu_{0}(\alpha)\diamond\Delta(\alpha )+2\mu_{0}(\alpha)\diamond\varLambda(\alpha) ) \end{array}\displaystyle \biggr) } $$
(48)

and

$$ \varkappa_{1}(\chi,\alpha)=\frac{\chi^{\varpi}}{\varpi}+ \int_{a}^{\alpha}\frac{\mu_{0}(\eta)\diamond(3\nu_{0}(\eta )\diamond\Delta(\eta)+2\mu_{0}(\eta)\diamond\varLambda(\eta ))}{6\eta^{1-\varpi}\nu_{0}^{\diamond2}(\eta)}\, d\eta $$
(49)

such that \(\lambda>0\) and \(\nu_{0}\neq0\).

$$\begin{aligned}& U_{3}(\chi,\alpha) = \frac{\sqrt[4]{\sigma+C\exp ^{\diamond}[4\varkappa_{2}(\chi,\alpha)]}}{\nu_{1}(\alpha)\pm\nu _{0}(\alpha)\diamond\sqrt[4]{\sigma+C\exp^{\diamond}[4\varkappa _{2}(\chi,\alpha)]}} \\& \hphantom{U_{3}(\chi,\alpha) = {}}{} \diamond \biggl[\frac{ ( \nu_{0}(\alpha)\diamond\sqrt{9\Delta^{\diamond2}(\alpha )-384\varLambda(\alpha) } -3\nu_{0}(\alpha)\diamond\Delta(\alpha) ) }{8\varLambda(\alpha) } \\& \hphantom{U_{3}(\chi,\alpha) = {}}{} \pm \frac{\nu_{1}(\alpha)\diamond\sqrt{3\Delta^{\diamond 2}(\alpha)-128\varLambda(\alpha) }-3\nu_{1}(\alpha)\diamond\Delta (\alpha)}{8\varLambda(\alpha) \diamond (\sigma+C\exp^{\diamond }[4\varkappa_{2}(\chi,\alpha)] )^{\diamond\frac{1}{4}}} \\& \hphantom{U_{3}(\chi,\alpha) = {}}{} + \frac{\mu_{4}(\alpha)\diamond(813\sigma^{2}\nu_{0}^{\diamond 2}(\alpha)-8\mu_{4}^{\diamond2}(\alpha)\diamond\varLambda(\alpha) )}{120\sigma^{2}\nu_{1}^{\diamond2}(\alpha)\diamond (\sigma+C\exp ^{\diamond}[4\varkappa_{2}(\chi,\alpha)] )^{\diamond\frac{1}{2}}} \\& \hphantom{U_{3}(\chi,\alpha) = {}}{} \pm \frac{306\mu_{4}(\alpha)\diamond\nu_{0}(\alpha)}{72\nu _{1}(\alpha)\diamond (\sigma+C\exp^{\diamond}[4\varkappa_{2}(\chi ,\alpha)] )^{\diamond\frac{3}{4}}} \\& \hphantom{U_{3}(\chi,\alpha) = {}}{} + \frac{\mu_{4}(\alpha)}{ (\sigma+C\exp^{\diamond}[4\varkappa _{2}(\chi,\alpha)] )} \biggr], \end{aligned}$$
(50)
$$\begin{aligned}& U_{4}(\chi,\alpha) = \frac{\sqrt[4]{\sigma+C\exp ^{\diamond}[4\varkappa_{2}(\chi,\alpha)]}}{\nu_{1}(\alpha)\pm i \nu_{0}(\alpha)\diamond\sqrt[4]{\sigma+C\exp^{\diamond }[4\varkappa_{2}(\chi,\alpha)]}} \\& \hphantom{U_{4}(\chi,\alpha) ={}}{} \diamond \biggl[\frac{ ( \nu_{0}(\alpha)\diamond\sqrt{9\Delta^{\diamond2}(\alpha )-384\varLambda(\alpha) } -3\nu_{0}(\alpha)\diamond\Delta(\alpha) ) }{8\varLambda(\alpha) } \\& \hphantom{U_{4}(\chi,\alpha) ={}}{} \pm i \frac{\nu_{1}(\alpha)\diamond\sqrt{3\Delta^{\diamond 2}(\alpha)-128\varLambda(\alpha) }-3\nu_{1}(\alpha)\diamond\Delta (\alpha)}{8\varLambda(\alpha) \diamond (\sigma+C\exp^{\diamond }[4\varkappa_{2}(\chi,\alpha)] )^{\diamond\frac{1}{4}}} \\& \hphantom{U_{4}(\chi,\alpha) ={}}{} + \frac{\mu_{4}(\alpha)\diamond(813\sigma^{2}\nu_{0}^{\diamond 2}(\alpha)-8\mu_{4}^{\diamond2}(\alpha)\diamond\varLambda(\alpha) )}{120\sigma^{2}\nu_{1}^{\diamond2}(\alpha)\diamond (\sigma+C\exp ^{\diamond}[4\varkappa_{2}(\chi,\alpha)] )^{\diamond\frac{1}{2}}} \\& \hphantom{U_{4}(\chi,\alpha) ={}}{} \pm i \frac{306\mu_{4}(\alpha)\diamond\nu_{0}(\alpha)}{72\nu _{1}(\alpha)\diamond (\sigma+C\exp^{\diamond}[4\varkappa_{2}(\chi ,\alpha)] )^{\diamond\frac{3}{4}}} \\& \hphantom{U_{4}(\chi,\alpha) ={}}{} + \frac{\mu_{4}(\alpha)}{ (\sigma+C\exp^{\diamond}[4\varkappa _{2}(\chi,\alpha)] )} \biggr], \end{aligned}$$
(51)

where

$$\begin{aligned}& \varkappa_{2}(\chi,\alpha) \\& \quad =\frac{\chi^{\varpi}}{\varpi}+ \int_{a}^{\alpha}\frac{\Delta(\eta,z)\diamond (3\Delta(\eta ,z)-\sqrt{9\Delta^{\diamond2}(\eta,z)-384\varLambda(\eta,z)} )-64\varLambda(\eta,z)}{32\eta^{1-\varpi}\varLambda(\eta,z)}\, d\eta \end{aligned}$$
(52)

such that \(\lambda\neq0\), \(\sigma\neq0\), \(\nu_{1}\neq0\), and \(\delta^{2}\geq\frac{128\lambda}{3}\).

$$\begin{aligned}& U_{5}(\chi,\alpha)=\frac{ \biggl(\textstyle\begin{array}{l} 528\mu_{0}(\alpha)\diamond\varLambda(\alpha) \diamond (\sigma+C\exp [4\varkappa_{3} (\chi,\alpha)] )^{\diamond\frac{1}{4}}\\ \quad {}\pm66\nu_{1}(\alpha)\diamond (-3\Delta(\alpha)+\sqrt{9\Delta ^{\diamond2}(\alpha)-528\varLambda(\alpha) } ) \end{array}\displaystyle \biggr) }{ \biggl(\textstyle\begin{array}{l} -8\mu_{0}(\alpha)\diamond\varLambda(\alpha) \diamond (3\Delta (\alpha)+\sqrt{9\Delta^{\diamond2}(\alpha)-528\varLambda(\alpha) } )\\ \quad {}\diamond (\sigma+C\exp[4\varkappa_{3} (\chi,\alpha)] )^{\diamond \frac{1}{4}}\pm528\nu_{1}(\alpha)\diamond\varLambda(\alpha) \end{array}\displaystyle \biggr) }, \end{aligned}$$
(53)
$$\begin{aligned}& U_{6}(\chi,\alpha,z)=\frac{ \biggl(\textstyle\begin{array}{l} 528\mu_{0}(\alpha)\diamond\varLambda(\alpha) \diamond (\sigma+C\exp [4\varkappa_{3} (\chi,\alpha)] )^{\diamond\frac{1}{4}}\\ \quad {}\pm66 i \nu_{1}(\alpha)\diamond (-3\Delta(\alpha)+\sqrt{9\Delta ^{\diamond2}(\alpha)-528\varLambda(\alpha) } ) \end{array}\displaystyle \biggr) }{ \biggl(\textstyle\begin{array}{l} -8\mu_{0}(\alpha)\diamond\varLambda(\alpha) \diamond (3\Delta (\alpha)+\sqrt{9\Delta^{\diamond2}(\alpha)-528\varLambda(\alpha) } )\\ \quad {}\diamond (\sigma+C\exp[4\varkappa(\chi,\alpha,z)] )^{\diamond \frac{1}{4}}\pm528 i \nu_{1}(\alpha)\diamond\varLambda(\alpha) \end{array}\displaystyle \biggr) }, \end{aligned}$$
(54)

where

$$\begin{aligned}& \varkappa_{3} (\chi,\alpha) \\& \quad =\frac{\chi^{\varpi}}{\varpi}+ \int_{a}^{\alpha}\frac{-3\Delta^{\diamond2}(\eta,z)+\Delta(\eta ,z)\diamond\sqrt{9\Delta^{\diamond2}(\eta,z)-528\varLambda(\eta ,z)}-88\varLambda(\eta,z)}{32\eta^{1-\varpi}\varLambda(\eta,z)}\, d\eta \end{aligned}$$
(55)

such that \(\lambda\neq0\) and \(\delta^{2}\geq\frac{528\lambda}{9}\).

5 Discussions and numerical simulations

This section is devoted to some discussions and numerical simulations to the obtained solutions.

From the equality \(\exp^{\diamond}(\varphi)=\cosh^{\diamond }(\varphi)+\sinh^{\diamond}(\varphi)\), our stochastic traveling wave solutions (46), (47), (50), (51), (53), and (54) of Eq. (26) can be handily altered to stochastic solitary wave solutions. Especially, the solution \(U_{1}(\chi,\alpha)\) can be altered to a solitary stochastic wave solution of the form

$$\begin{aligned} U^{*}_{1}(\chi,\alpha) =& \frac{\sqrt[4]{\sigma+C(\cosh^{\diamond}[4\varkappa_{1} (\chi ,\alpha)]+\sinh^{\diamond}[4\varkappa_{1} (\chi,\alpha)])}}{\nu _{1}(\alpha)\pm\nu_{0}(\alpha)\diamond\sqrt[4]{\sigma+C(\cosh ^{\diamond}[4\varkappa_{1} (\chi,\alpha)]+\sinh^{\diamond }[4\varkappa_{1} (\chi,\alpha)])}} \\ &{}\diamond \biggl[\frac{\mu_{0}(\alpha)+A(\alpha)}{102\nu _{1}(\alpha)^{\diamond2}\diamond\sqrt{6\varLambda(\alpha) }} \\ &{}\pm{\frac {155\nu_{0}^{\diamond3}(\alpha)}{ (\sigma+C(\cosh^{\diamond }[4\varkappa_{1} (\chi,\alpha)]+\sinh^{\diamond}[4\varkappa_{1} (\chi,\alpha)]) )^{\diamond\frac{1}{2}}}} \\ &{}+ {\frac{255\nu_{1}^{\diamond3}(\alpha)}{ (\sigma+C(\cosh ^{\diamond}[4\varkappa_{1} (\chi,\alpha)]+\sinh^{\diamond }[4\varkappa_{1} (\chi,\alpha)]) )^{\diamond\frac{3}{4}}}} \\ &{}+{\frac{2448\sigma\nu_{1}^{\diamond3}(\alpha)}{ (\sigma+C(\cosh ^{\diamond}[4\varkappa_{1} (\chi,\alpha)]+\sinh^{\diamond }[4\varkappa_{1} (\chi,\alpha)]) )^{\diamond\frac{5}{4}}}} \biggr], \end{aligned}$$
(56)

where \(A(\alpha)\) and \(\varkappa_{1} (\chi,\alpha)\) are given in Eqs. (48), (49) and \(\varLambda>0\). Also, from the equality \(\exp^{\diamond }(i\varphi)=\cos^{\diamond}(\varphi)+i \sin^{\diamond}(\varphi )\), our stochastic traveling wave solutions (46), (47), (50), (51), (53), and (54) of Eq. (26) can be easily altered to stochastic periodic wave solutions. Especially, the solution \(U_{1}(\chi,\alpha)\) can be altered to a periodic stochastic wave solution of the form

$$\begin{aligned} U^{**}_{1}(\chi,\alpha) =& \frac{\sqrt[4]{\sigma+C(\cos^{\diamond}[4\varkappa_{1}^{**}(\chi ,\alpha)]+i \sin^{\diamond}[4\varkappa_{1}^{**} (\chi,\alpha )])}}{\nu_{1}(\alpha)\pm\nu_{0}(\alpha)\diamond\sqrt[4]{\sigma +C(\cos^{\diamond}[4\varkappa_{1}^{**} (\chi,\alpha)]+i \sin ^{\diamond}[4\varkappa_{1}^{**} (\chi,\alpha)])}} \\ &{}\diamond \biggl[\frac{\mu_{0}(\alpha)+A(\alpha)}{102\nu _{1}(\alpha)^{\diamond2}\diamond\sqrt{6\varLambda(\alpha) }} \\ &{}\pm{\frac {155\nu_{0}^{\diamond3}(\alpha)}{ (\sigma+C(\cos^{\diamond }[4\varkappa_{1}^{**} (\chi,\alpha)]+i \sin^{\diamond}[4\varkappa _{1}^{**} (\chi,\alpha)]) )^{\diamond\frac{1}{2}}}} \\ &{}+ {\frac{255\nu_{1}^{\diamond3}(\alpha)}{ (\sigma+C(\cos ^{\diamond}[4\varkappa_{1}^{**} (\chi,\alpha)]+i \sin^{\diamond }[4\varkappa_{1}^{**} (\chi,\alpha)]) )^{\diamond\frac{3}{4}}}} \\ &{}+{\frac{2448\sigma\nu_{1}^{\diamond3}(\alpha)}{ (\sigma+C(\cos ^{\diamond}[4\varkappa_{1}^{**} (\chi,\alpha)]+i \sin^{\diamond }[4\varkappa_{1}^{**} (\chi,\alpha)]) )^{\diamond\frac{5}{4}}}} \biggr], \end{aligned}$$
(57)

where \(A(\alpha)\) is given in Eq. (48) and

$$ \varkappa_{1}^{**}(\chi,\alpha)=-i \biggl( \frac{\chi^{\varpi}}{\varpi}+ \int_{a}^{\alpha}\frac{\mu_{0}(\eta)\diamond(3\nu_{0}(\eta )\diamond\Delta(\eta)+2\mu_{0}(\eta)\diamond\varLambda(\eta ))}{6\eta^{1-\varpi}\nu_{0}^{\diamond2}(\eta)}\, d\eta \biggr),\quad \varLambda>0. $$
(58)

We notice that solutions (46), (47), (50), (51), (53), and (54) of Eq. (26) robustly rely on the given functions \(\mu _{0}(\alpha)\), \(\nu_{0}(\alpha)\), \(\nu_{1}(\alpha)\), \(\beta _{4}(\alpha)\), \(\Delta(\alpha)\), and \(\varLambda(\alpha) \). So, for diverse shapes of these functions, we can get diverse solutions of Eq. (26), which can be constructed from Eqs. (46), (47), (50), (51), (53), and (54). We explain this by the following example. We focus our work in this example on the stochastic traveling wave solution \(U_{1}\). For the other solutions \(U_{2}-U_{6}\), \(U_{1}^{*}\), and \(U_{1}^{**}\), the proceedings are similar.

Example 5.1

Assume that

$$ \textstyle\begin{cases} a=0,\qquad \nu_{0}(\alpha)=a_{0}\mu_{0}(\alpha), \qquad \nu _{1}(\alpha)=a_{1}\mu_{0}(\alpha), \\ \Delta(\alpha)=a_{2}\mu_{0}(\alpha),\qquad \varLambda(\alpha) =a_{3}\mu _{0}(\alpha),\qquad \mu_{0}(\alpha)=\zeta(\alpha)+a_{4}s^{1-\varpi }W(\alpha), \end{cases} $$
(59)

where \(a_{i}\) (\(i=0,1,\ldots,a\)) are arbitrary constants, \(\zeta(\alpha )\) is a ϖ-conformable integrable map on \(\mathbb{R}_{+}\), and \(W(\alpha)\) is the Gaussian white noise, which is the derivative of the Brownian motion \(B(\alpha)\) with respect to α. The Hermite transform of \(W(\alpha)\) is known as \(\widetilde{W}(\alpha,z)=\sum_{i=1}^{\infty}z_{i}\int_{0}^{\alpha }\varrho_{i}(\eta)\, d\eta\) [52].

Using the identity \(\exp^{\diamond}(B(\alpha))=\exp (B(\alpha )-\frac{s^{2}}{2} )\) [52], the definition of \(\widetilde{W}(\alpha,z)\), and Eq. (46) gives the functional solution of Brownian motion and white noise type of Eq. (26) as follows:

$$\begin{aligned} U_{BW}(\chi,\alpha) =&\frac{\sqrt[4]{\sigma+C\exp [4\varUpsilon(\chi,\alpha)]}}{a_{1}\pm a_{0}\sqrt[4]{\sigma+C\exp[4\varUpsilon(\chi,\alpha)]}} \\ &{}\times \biggl[\frac{1+A_{1}(\alpha)}{102a_{1}^{2}\sqrt{6a_{3} (\zeta(\alpha)+a_{4}s^{1-\varpi}W(\alpha) )^{\diamond5}}} \\ &{}\pm\frac{155a_{3}^{3}}{ (\sigma+C\exp[4\varUpsilon(\chi,\alpha)] )^{\frac{1}{2}}}+\frac{255a_{1}^{3}}{ (\sigma+C\exp[4\varUpsilon(\chi ,\alpha)] )^{\frac{3}{4}}} \\ &{}+\frac{2448\sigma a_{1}^{3}}{ (\sigma+C\exp[4\varUpsilon(\chi,\alpha )] )^{\frac{5}{4}}} \biggr], \end{aligned}$$
(60)

where

$$ A_{1}(\alpha)=\frac{ \biggl(\textstyle\begin{array}{l} 36a_{2}^{2}a_{1} (\zeta(\alpha) +a_{4}s^{1-\varpi}W(\alpha) )\\\quad {}+(24a_{1}a_{3}-144a_{0}a_{1}a_{2}) (\zeta(\alpha)+a_{4}s^{1-\varpi}W(\alpha) )^{\diamond2} \end{array}\displaystyle \biggr) }{6a_{0}^{2}+(4a_{3}+3a_{0}a_{2}) (\zeta(\alpha)+a_{4}s^{1-\varpi }W(\alpha) ))} $$
(61)

and

$$ \varUpsilon(\chi,\alpha)=\frac{\chi^{\varpi}}{\varpi}+\frac {3a_{0}a_{2}+2a_{3}}{6a_{0}^{2}} \biggl[ \int_{0}^{\alpha}\frac{\zeta(\eta)}{\eta^{1-\varpi}}\, d\eta +a_{4} \biggl(B(\alpha)-\frac{\alpha^{2}}{2} \biggr) \biggr]. $$
(62)

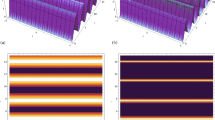
For \(\varpi=0.01, 0.1\), and 1, the numerical simulation of wave solution (60) is shown in Figs. 1 and 2, when \(C=\sigma=a_{1}=a_{3}=1\), \(a_{0}=a_{2}=a_{4}=-1\), \(\zeta(\alpha)=e^{\alpha}\), \(0\leq\alpha \leq4\), and \(0\leq\chi\leq4\). Figure 1 represents the evolutional behaviors of solution (60) without stochastic effect (\(B(\alpha)=W(\alpha)=0\)), and Fig. 2 presents the behavior of solution (60) with the noise effect \(B(\alpha)=\operatorname {Random}[0,1]\times\tan(1.7\alpha)\) and \(W(\alpha)=1.7 \operatorname{Random}[0,1]\times\sec^{2}(1.7\alpha )\). From Figs. 1 and 2, it is concluded that the stochastic forcing terms lead to the uncertainty of the traveling wave amplitudes.

Figure 1
figure 1

(a), (b), and (c) 3D plots of solution (60) without the noise effect, when \(\varpi=0.01, 0.1\), and 1, respectively

Full size image
Figure 2
figure 2

(a), (b), and (c) 3D plots of solution (60) under the noise effect, when \(\varpi=0.01, 0.1\), and 1, respectively

Full size image

6 Conclusion

In fact, the stochastic physical models are more sensible than the deterministic models. Thus, right now, we focus the investigation on the SPDEs with conformable derivatives. Foremost, the general Kudryashov method [45] is improved by the novel auxiliary equation (4), which has numerous general solutions depending on the natural number n (see Eq. (25)). Thus, a novel technique to build exact solutions for nonlinear evolution equations is obtained. This technique is called the GIKM. The major feature of the GIKM over the others lies in the way that it utilizes an especially clear and powerful algorithm to obtain exact solutions for a large family of nonlinear evolution equations. Also, a large set of exact solutions can be determined effectively on picking the parameters that showed up. Besides, the proposed GIKM generalizes some previous techniques. It depends on improving the general Kudryashov technique by the general auxiliary equation (4) which has various general solutions. Moreover, we apply the GIKM and white noise topics to construct exact solutions for the Wick-type stochastic combined KdV–mKdV equation with conformable derivatives. Also, numerical simulations with 3D profiles are provided to the obtained exact solutions. Eventually, the overall approach proposed in this paper can be utilized for solving diverse nonlinear evolution equations in physics and engineering, both deterministic and stochastic types.