1 Introduction

Some nonlinear waves in dynamical systems are of substantial importance and receive much attention, most particularly in the field of wave propagation in nonlinear systems [1]. They are expressed by nonlinear partial differential equations (NLPDEs) [2]. Application of nonlinear waves cuts across many fields, which include mixture of gas bubble in liquid [3], waves in elastic tubes [4], systems incorporating damping and dispersion [5], KP lump in ferrimagnets [6], chemical physics, and geochemistry [7]. However, the quest for exact explicit solutions of these equations remains a hot topic. Moreover, looking for localized solutions and, more specifically, solitary wave solutions, many methods of solving nonlinear wave developed by researchers over the years, including [8–16], lump-type solutions [17–32], interaction soliton–soliton, soliton–kink, and kink–kink [33, 34], interactions between solitary wave solutions and lump solutions [35, 36], as well as periodic wave solutions [37–40] remain a very interesting subject for researchers. Several mathematical methods are used in the search for these solutions. For example, the exp-function method [41, 42], the homotopy perturbation technique [43], inverse scattering method [44], and so on.

The Hirota bilinear method for finding the lump soliton solutions and interaction of a lump solution with some of one-line, two-line, and three-line and even kink-breather-soliton solutions of evolution equations was initially introduced by Ma [45] by assuming the solution to be a series of functions including lump (combination of two positive functions as polynomial), lump-kink (combination of two positive functions as polynomial and exponential functions), called the interaction between a lump and one-line soliton, lump-soliton (combination of two positive functions as polynomial and hyperbolic cos functions), called the interaction between lump and two-line solitons, kinky breather-soliton (combination of two exponential functions and trigonometric cos function), and finally the stripe soliton function only with exponential solution function. The method received considerable attention and underwent through many improvements. It is important to note that the later improvements were given different names by different authors. For getting the lump solutions and their interactions, the authors have conjugated sufficient time to search the exact rational soliton solutions, for example, the Kadomtsev–Petviashvili (KP) equation [23], the B-Kadomtsev–Petviashvili equation [42], the reduced p-gKP and p-gbKP equations [25], the \((2+1)\)-dimensional KdV equation [26], the \((2+1)\)-dimensional generalized fifth-order KdV equation [33], the \((2+1)\)-dimensional Burger equation [34], the nonlinear evolution equations [22], the generalized \((3+1)\)-dimensional Shallow water-like equation [35], the \((2+1)\)-dimensional Sawada–Kotera equation [30], and the \((2 + 1)\)-dimensional bSK equation [31, 32]. Various types of work for finding the periodic solitary wave solutions of the \((2+1)\)-dimensional extended Jimbo–Miwa equations [37], interaction between lump and other kinds of solitary, periodic and kink solitons for the \((2+1)\)-dimensional breaking soliton equation [27], lump and interaction between different types of those on the variable-coefficient Kadomtsev–Petviashvili equation [28], and periodic type and periodic cross-kink wave solutions [29] are achieved through the Hirota bilinear operator.

Nowadays NLPDEs have been created significant opportunity for the researchers to explain the tangible incidents. Therefore mathematicians and scientists work tirelessly to bring out different kinds of soliton solutions. As a result, in the past few years, several effective, rising, and realistic methods have been initiated and dilated to extract closed-form solutions to the NLPDEs, such as the generalized higher-order variable-coefficient Hirota equation [46], a higher-order nonlinear Schrödinger system [47], a \((3+1)\)-dimensional B-type KP equation [48], the \((3+1)\)-dimensional Zakharov–Kuznetsov–Burgers equation [49], the coherently coupled nonlinear Schrödinger equations [50], the coupled variable-coefficient fourth-order nonlinear Schrödinger equations [51], the \((2+1)\)-dimensional Konopelchenko–Dubrovsky equations [52], a generalized KP equation [53], a \((2+1)\)-dimensional Davey–Stewartson system [54], and the \((2+1)\)-dimensional generalized variable-coefficient KP-Burgers-type equation [55]. Various types of studies on solving NLPDEs were investigated by capable authors, for example, the space-time fractional nonlinear Schrödinger equation [56], the complex cubic-quintic Ginzburg–Landau equation [57], symmetric nonlinear Schrödinger equations with the second- and fourth-order diffractions [58], the \((2+1)\)-dimensional Korteweg–de Vries equation [59], and the \((1+1)\)-dimensional coupled integrable dispersionless equations [60].

Take the third-order evolution equation of the form

$$ \mathbb{P}_{\mathrm{TOE}}(\varPsi ):=\varPsi _{t}+\varPsi _{x}+\frac{\alpha }{2} (3 \varPsi \varPsi _{x}+a \varPsi _{y} )+\frac{\varepsilon }{6}(1-3\tau )\varPsi _{xxx}- \frac{\varepsilon }{4}(1+2\tau )\varPsi _{xyy}=0, $$
(1.1)

where α, ε are small parameters, τ is the Bond number, and o Ψ is the surface elevation in the x-direction, which is a model for the unidirectional propagation of long waves over shallow water, obtained via asymptotic expansion around simple wave motion of the Euler equations up to first-order in the small-wave amplitude [61, 62]. Assume the Hirota derivatives based on the functions \(\rho (x)\) and \(\varrho (x)\) given as

$$ \prod_{i=1}^{3}D_{\lambda _{i}}^{\pi _{i}} \rho .\varrho = \prod_{i=1}^{3} \biggl( \frac{\partial }{\partial \lambda _{i}}- \frac{\partial }{\partial \mu _{i}} \biggr)^{o_{i}}\rho (\lambda ) \varrho (\mu )\bigg|_{\mu =\lambda }, $$
(1.2)

where the vectors \(\lambda =(\lambda _{1},\lambda _{2},\lambda _{3})\), \(\mu =(\mu _{1},\mu _{2},\mu _{3})\), and \(o_{1}\), \(o_{2}\), \(o_{3}\) are arbitrary nonnegative integers. It is known that this third-order evolution equation possesses a Hirota bilinear form

$$\begin{aligned} \mathbb{B}_{\mathrm{TOE}}(\rho ) :=& \biggl(D_{x}D_{t}+D_{x}^{2}+ \frac{a}{2} \alpha D_{y}D_{x}+ \frac{\varepsilon }{6}(1-3\tau )D_{x}^{4}- \frac{\varepsilon }{4}(1+2\tau )D_{x}^{2}D_{y}^{2} \biggr)\rho .\rho \\ =&2 \biggl[\rho \rho _{xt}-\rho _{x}\rho _{t}+\rho \rho _{xx}-\rho _{x}^{2}+ \frac{1}{2}a\alpha (\rho \rho _{xy}-\rho _{x} \rho _{y}) \\ &{}+ \frac{\varepsilon }{6}(1-3\tau ) \bigl(\rho \rho _{xxxx}-4\rho _{x}\rho _{xxx}+3 \rho _{xx}^{2}\bigr) \\ &{}-\frac{\varepsilon }{4}(1+2\tau ) \bigl(\rho \rho _{xxyy}-2\rho _{x} \rho _{xyy}+\rho _{xx}\rho _{yy}-2\rho _{y}\rho _{xxy}+2\rho _{xy}^{2}\bigr) \biggr]. \end{aligned}$$
(1.3)

We utilize the following relation between the functions \(\phi (x,y,t)\) and \(\varPsi (x,y,t)\):

$$ \varPsi (x,y,t)=R\bigl(\ln \rho (x,y,t)\bigr)_{x}, $$
(1.4)

where \(R=\frac{1}{18} \frac{\varepsilon (6\tau (k_{1}^{3}+k_{1}k_{2}^{2})+3k_{1}k_{2}^{2} -2k_{1}^{3}-6a\alpha k_{2}-(k_{3}-k_{1}))}{\alpha k_{1}^{2}}\). Based on the Bell polynomial theories of soliton equations, we get to the relation

$$ \mathbb{P}_{\mathrm{TOE}}(\varPsi )= \biggl[\frac{\mathbb{B}_{\mathrm{TOE}}(\rho )}{\rho } \biggr]_{x}. $$
(1.5)

Theorem 1.1

\(\varPsi =R(\ln \rho )_{x}\)is a solution to Eq. (1.1) if and only ifρsatisfies the equation

$$\begin{aligned}& \biggl(D_{x}D_{t}+D_{x}^{2}+ \frac{a}{2}\alpha D_{y}D_{x}+ \frac{\varepsilon }{6}(1-3\tau )D_{x}^{4}- \frac{\varepsilon }{4}(1+2 \tau )D_{x}^{2}D_{y}^{2} \biggr)\rho .\rho \\& \quad =2 \biggl[\rho \rho _{xt}-\rho _{x}\rho _{t}+\rho \rho _{xx}-\rho _{x}^{2}+ \frac{1}{2}a\alpha (\rho \rho _{xy}-\rho _{x} \rho _{y}) \\& \qquad {}+ \frac{\varepsilon }{6}(1-3\tau ) \bigl(\rho \rho _{xxxx}-4\rho _{x}\rho _{xxx}+3 \rho _{xx}^{2}\bigr) \\& \qquad {}-\frac{\varepsilon }{4}(1+2\tau ) \bigl(\rho \rho _{xxyy}-2\rho _{x} \rho _{xyy}+\rho _{xx}\rho _{yy}-2\rho _{y}\rho _{xxy}+2\rho _{xy}^{2}\bigr) \biggr]. \end{aligned}$$
(1.6)

Proof

Denoting \(\varGamma =\partial _{x}(\ln \rho )\), from expression (1.4) we get

$$ \varPsi =R \varGamma\quad \Longleftrightarrow \quad \rho =\exp \biggl( \frac{1}{R} \int \varPsi \,dx \biggr). $$
(1.7)

Then, by considering \(\rho =\exp (\partial _{x}^{-1}\varGamma )>0\), the derivatives \(\rho _{x}\), \(\rho _{y}\), \(\rho _{t}\), \(\rho _{xx}\), \(\rho _{yy}\), \(\rho _{xy}\), \(\rho _{xt}\), \(\rho _{xxy}\), \(\rho _{xyy}\), \(\rho _{xxx}\), \(\rho _{xxyy}\), and \(\rho _{xxxx}\) can be written as

$$\begin{aligned}& \rho _{x}=\varGamma \exp \bigl(\partial _{x}^{-1}\varGamma \bigr), \end{aligned}$$
(1.8)
$$\begin{aligned}& \rho _{y}=\partial _{x}^{-1} \varGamma _{y}\exp \bigl(\partial _{x}^{-1} \varGamma \bigr), \end{aligned}$$
(1.9)
$$\begin{aligned}& \rho _{t}=\partial _{x}^{-1} \varGamma _{t}\exp \bigl(\partial _{x}^{-1} \varGamma \bigr), \end{aligned}$$
(1.10)
$$\begin{aligned}& \rho _{xx}=\bigl(\varGamma ^{2}+\varGamma _{x}\bigr)\exp \bigl(\partial _{x}^{-1} \varGamma \bigr), \end{aligned}$$
(1.11)
$$\begin{aligned}& \rho _{yy}=\bigl(\bigl(\partial _{x}^{-1}\varGamma _{y}\bigr)^{2}+ \partial _{x}^{-1} \varGamma _{yy}\bigr)\exp \bigl(\partial _{x}^{-1}\varGamma \bigr), \end{aligned}$$
(1.12)
$$\begin{aligned}& \rho _{xy}=\bigl(\varGamma \partial _{x}^{-1}\varGamma _{y}+\theta _{y}\bigr)\exp \bigl(\partial _{x}^{-1} \varGamma \bigr), \end{aligned}$$
(1.13)
$$\begin{aligned}& \rho _{xt}=\bigl(\varGamma \partial _{x}^{-1}\varGamma _{t}+\varGamma _{t}\bigr)\exp \bigl(\partial _{x}^{-1} \varGamma \bigr), \end{aligned}$$
(1.14)
$$\begin{aligned}& \rho _{xxx}=\bigl(\varGamma ^{3}+3\varGamma \varGamma _{x}+\varGamma _{xx}\bigr)\exp \bigl( \partial _{x}^{-1}\varGamma \bigr), \end{aligned}$$
(1.15)
$$\begin{aligned}& \rho _{xxy}= \bigl[\bigl(\varGamma ^{2}+ \varGamma _{x}\bigr)\partial _{x}^{-1}\varGamma _{y}+2 \varGamma \varGamma _{y}+\varGamma _{xy} \bigr]\exp \bigl(\partial _{x}^{-1} \varGamma \bigr), \end{aligned}$$
(1.16)
$$\begin{aligned}& \rho _{xyy}= \bigl[\varGamma \bigl(\partial _{x}^{-1}\varGamma _{y}\bigr)^{2}+ \varGamma \partial _{x}^{-1}\varGamma _{yy}+ 2\varGamma _{y}\partial _{x}^{-1}\varGamma _{y}+ \varGamma _{yy} \bigr]\exp \bigl(\partial _{x}^{-1}\varGamma \bigr), \end{aligned}$$
(1.17)
$$\begin{aligned}& \rho _{xxxx}= \bigl[\varGamma ^{4}+6\varGamma ^{2}\varGamma _{x}+4\varGamma \varGamma _{xx}+3( \varGamma _{x})^{2}+\varGamma _{xxx} \bigr] \exp \bigl( \partial _{x}^{-1}\varGamma \bigr), \end{aligned}$$
(1.18)
$$\begin{aligned}& \rho _{xxyy}= \bigl[\bigl(\varGamma ^{2}+ \varGamma _{x}\bigr) \bigl(\bigl(\partial _{x}^{-1} \varGamma _{y}\bigr)^{2}+\partial _{x}^{-1} \varGamma _{yy}\bigr)+4\varGamma \varGamma _{y} \partial _{x}^{-1}\varGamma _{y} \\& \hphantom{\rho _{xxyy}={}}{}+ 2\varGamma _{xy}\partial _{x}^{-1}\varGamma _{y}+2 \varGamma \varGamma _{yy}+2(\varGamma _{y})^{2}+ \varGamma _{xyy} \bigr] \exp \bigl(\partial _{x}^{-1} \varGamma \bigr). \end{aligned}$$
(1.19)

Plugging (1.8)–(1.19) into (1.3) yields the bilinear form of Eq. (1.3):

$$\begin{aligned}& 2 \biggl[\rho \rho _{xt}-\rho _{x}\rho _{t}+\rho \rho _{xx}-\rho _{x}^{2}+ \frac{1}{2}a\alpha (\rho \rho _{xy}-\rho _{x} \rho _{y})+ \frac{\varepsilon }{6}(1-3\tau ) \bigl(\rho \rho _{xxxx}-4\rho _{x}\rho _{xxx}+3 \rho _{xx}^{2}\bigr) \\& \qquad {}-\frac{\varepsilon }{4}(1+2\tau ) \bigl(\rho \rho _{xxyy}-2\rho _{x} \rho _{xyy}+\rho _{xx}\rho _{yy}-2\rho _{y}\rho _{xxy}+2\rho _{xy}^{2}\bigr) \biggr] \\& \quad =-\frac{1}{6}\exp \bigl(2\partial _{x}^{-1} \varGamma \bigr) \biggl[12 \int {\frac{{\mathrm{d}}^{2}}{{\mathrm{d}}{y}^{2}}}\varGamma {\mathrm{d}}x \biggl( { \frac{\mathrm{d}}{{\mathrm{d}}x}}\varGamma \biggr) \epsilon \tau +24 \biggl( { \frac{\mathrm{d}}{{\mathrm{d}}y}}\varGamma \biggr) ^{2}\epsilon \tau \\& \qquad {}+36 \biggl( { \frac{\mathrm{d}}{{\mathrm{d}}x}}\varGamma \biggr) ^{2}\epsilon \tau +6 \biggl( { \frac{{\mathrm{d}}^{3}}{{\mathrm{d}}{x}^{3}}}\varGamma \biggr) \epsilon \tau +6 \int {\frac{{\mathrm{d}}^{2}}{{\mathrm{d}}{y}^{2}}} \varGamma {\mathrm{d}}x \biggl( { \frac{\mathrm{d}}{{\mathrm{d}}x}}\varGamma \biggr) \epsilon \\& \qquad {}+6 \biggl( { \frac{{\mathrm{d}}^{3}}{{\mathrm{d}}x{\mathrm{d}}{y}^{2}}} \varGamma \biggr) \epsilon \tau +12 \biggl( { \frac{\mathrm{d}}{{\mathrm{d}}y}}\varGamma \biggr) ^{2}\epsilon - 6 a\alpha { \frac{\mathrm{d}}{{\mathrm{d}}y}}\varGamma -12 \biggl( { \frac{\mathrm{d}}{{\mathrm{d}}x}}\theta \biggr) ^{2}\epsilon \\& \qquad {}-2 \biggl( { \frac{{\mathrm{d}}^{3}}{{\mathrm{d}}{x}^{3}}}\varGamma \biggr) \epsilon +3 \biggl( {\frac{{\mathrm{d}}^{3 }}{{\mathrm{d}}x{\mathrm{d}}{y}^{2}}}\varGamma \biggr) \epsilon -12 { \frac{\mathrm{d}}{ {\mathrm{d}}t}}\varGamma -12 {\frac{\mathrm{d}}{{\mathrm{d}}x}}\varGamma \biggr] \\& \quad =-\frac{1}{6}\phi ^{2} \bigl[12\epsilon \tau \varGamma _{x}\partial _{x}^{-1} \varGamma _{yy} +24\epsilon \tau (\varGamma _{y} ) ^{2}+36 \epsilon \tau (\varGamma _{x} ) ^{2}+6 \epsilon \tau \varGamma _{xxx}+6 \epsilon \varGamma _{x}\partial _{x}^{-1}\varGamma _{yy} \\& \qquad {}+6\epsilon \tau \varGamma _{xyy} +12\epsilon (\varGamma _{y} ) ^{2}- 6 a\alpha \varGamma _{y}-12\epsilon ( \varGamma _{x} ) ^{2}-2 \epsilon \varGamma _{xxx} \\& \qquad {}+3 \epsilon \varGamma _{xyy} -12 \varGamma _{t}-12\varGamma _{x} \bigr], \end{aligned}$$
(1.20)

which can be rewritten as

$$\begin{aligned}& \frac{1}{\phi ^{2}} \biggl[\rho \rho _{xt}-\rho _{x}\rho _{t}+\rho \rho _{xx}-\rho _{x}^{2}+\frac{1}{2}a\alpha (\rho \rho _{xy}-\rho _{x} \rho _{y})+ \frac{\varepsilon }{6}(1-3\tau ) \bigl(\rho \rho _{xxxx}-4\rho _{x} \rho _{xxx}+3\rho _{xx}^{2} \bigr) \\& \qquad {}-\frac{\varepsilon }{4}(1+2\tau ) \bigl(\rho \rho _{xxyy}-2\rho _{x} \rho _{xyy}+\rho _{xx}\rho _{yy}-2\rho _{y}\rho _{xxy}+2\rho _{xy}^{2}\bigr) \biggr] \\& \quad =\frac{ (D_{x}D_{t}+D_{x}^{2}+\frac{a}{2}\alpha D_{y}D_{x} +\frac{\varepsilon }{6}(1-3\tau )D_{x}^{4}-\frac{\varepsilon }{4} (1+2\tau )D_{x}^{2}D_{y}^{2} )\rho .\rho }{2\rho ^{2}}, \end{aligned}$$
(1.21)

where \(\varGamma =\frac{1}{R}\varPsi =\partial _{x}(\ln \rho )\) and \(\partial _{x}^{-1}(\cdot )=\int (\cdot )\,dx\). Therefore Eq. (1.21) is the third-order evolution-type equation, and the theorem has been proved. □

We clearly confirm that other published papers do not cover ours, and made work is really new. Here our purpose is discovering the exact solutions of the third-order evaluation equation under consideration by the Hirota bilinear method for gaining the M lump, the interaction between 1-lump and two-stripe solutions, and the interaction between 2-lump and one-stripe solutions, which arise in more classes. We give a discussion about the third-order evaluation equation and the Hirota bilinear method. We also offer graphical illustrations of some solutions of the considered model along with the obtained solutions. After that, we deal with the probe of solutions and finish by conclusion.

2 New M-lump solutions of the third-order evolution equation

According to analysis in [39], based on the Hirota operator, the solution of nonlinear differential equation (1.3) can be written as

$$ \rho =\rho _{N}=\sum_{\sigma =0,1} \exp \Biggl(\sum_{i< j}^{N}\sigma _{i} \sigma _{j}F_{ij}+\sum _{i=1}^{N}\sigma _{i}\eta _{i} \Biggr), $$
(2.1)

where

$$\begin{aligned}& \eta _{i}=k_{i} \biggl(x+p_{i}y- \biggl[1+\frac{1}{2}a\alpha p_{{i}}- \frac{1}{4} \epsilon {k_{{i}}}^{2}{p_{{i}}}^{2} ( 2\tau +1 ) -\frac{1}{6}\epsilon {k_{{i}}}^{2} ( 3\tau -1 ) \biggr] t \biggr)+\eta _{i}^{(0)}, \end{aligned}$$
(2.2)
$$\begin{aligned}& \exp F_{ij}={ \frac{ ( k_{{i}}-k_{{j}} ) ( 2 ( k_{{i}}-k_{ {j}} ) ( 2 \tau p_{{i}}p_{{j}}+3 \epsilon \tau +p_{{i}} p_{{j}}-\epsilon ) + ( k_{{i}}{p_{{i}}}^{2}-k_{{j}}{p_{{j}} }^{2} ) ( 2 \tau +1 ) ) }{ ( k_{{i}}+k_{ {j}} ) ( 2 ( k_{{i}}+k_{{j}} ) ( 2 \tau p_{{i}}p_{{j}}+3 \epsilon \tau +p_{{i}}p_{{j}}-\epsilon ) + ( k_{{i}}{p_{{i}}}^{2}+k_{{j}}{p_{{j}}}^{2} ) ( 2 \tau +1 ) ) }}. \end{aligned}$$
(2.3)

The notation \(\sigma =0,1\) shows summation over all conceivable compositions of \(\sigma _{1}=0, 1,\sigma _{2}=0, 1,\ldots,\sigma _{N}=0,1\); the summation \(\sum_{i< j}^{N}\) is over all conceivable compositions of N values of \(i < j\). For example, the first three expressions of (2.1) are as follows:

$$\begin{aligned}& \rho _{1}=1+e^{\eta _{1}}, \end{aligned}$$
(2.4)
$$\begin{aligned}& \rho _{2}=1+e^{\eta _{1}}+e^{\eta _{2}}+a_{12}e^{\eta _{1}+\eta _{2}}, \end{aligned}$$
(2.5)
$$\begin{aligned}& \rho _{3}=1+e^{\eta _{1}}+e^{\eta _{2}}+e^{\eta _{3}}+a_{12}e^{\eta _{1}+ \eta _{2}}+a_{13}e^{\eta _{1}+\eta _{3}} +a_{23}e^{\eta _{2}+\eta _{3}}+a_{12}a_{13}a_{23}e^{ \eta _{1}+\eta _{2}+\eta _{3}}, \end{aligned}$$
(2.6)

where \(a_{ij}=\exp (F_{ij})\), \(i< j\). To find M lump solutions of Eq. (1.1), by catching \(\exp (\eta _{i}^{(0)})=-1\) in (2.2), \(\rho _{N}\) will be as follows:

$$ \rho _{N}=\sum_{\sigma =0,1} \Biggl(\prod_{i=1}^{N}(-1)^{\sigma _{i}} \exp (\sigma _{i}\zeta _{i}) \prod _{i< j}^{N}\exp (\sigma _{i}\sigma _{j} F_{ij}) \Biggr), $$
(2.7)

where

$$ \zeta _{i}=k_{i} \biggl(x+p_{i}y- \biggl[1+\frac{1}{2}a\alpha p_{{i}}- \frac{1}{4} \epsilon {k_{{i}}}^{2}{p_{{i}}}^{2} ( 2\tau +1 ) -\frac{1}{6}\epsilon {k_{{i}}}^{2} ( 3\tau -1 ) \biggr] t \biggr). $$

Taking the limit as \(k_{i}\rightarrow 0\) with all the \(k_{i}\) of the same asymptotic order, we get:

$$ \rho _{N}=\sum_{\sigma =0,1} \Biggl(\prod_{i=1}^{N}(-1)^{\sigma _{i}}(1+ \sigma _{i}k_{i}\xi _{i}) \prod _{i< j}^{N}(1+\sigma _{i}\sigma _{j} k_{i}k_{j}G_{ij}) \Biggr)+O\bigl(k^{N+1}\bigr). $$
(2.8)

In (2.8), we can see that \(\rho _{N}\) is factorized by \(\prod_{i=1}^{N}k_{i}\). By transformation \(\varPsi = R(\ln \rho )_{x}\) we get a rational solution of Eq. (1.5). The reduced \(\phi _{N}\) is

$$\begin{aligned} \rho _{N} =&\prod_{i=1}^{N} \xi _{i}+\frac{1}{2}\sum_{i,j}^{N}G_{ij} \prod_{l\neq i,j}^{N}\xi _{l}+ \frac{1}{2!2^{2}}\sum_{i,j,s,r}^{N}G_{ij}G_{sr} \prod_{l\neq i,j,s,r}^{N}\xi _{l}+ \cdots \\ &{}+\frac{1}{M!2^{M}}\sum_{i,j,\ldots,m,n}^{N}G_{ij}G_{kl}\cdots G_{mn} \prod_{p\neq i,j,k,l,\ldots,m,n}^{N}\xi _{p}, \end{aligned}$$
(2.9)

where

$$ \xi _{i}=x+p_{i}y- \biggl(1+\frac{1}{2}a \alpha p_{{i}} \biggr) t. $$

Analytical behavior of the solution function \(\rho _{1}\) as a 1-soliton is presented with \(p_{1}=a+ib\) in Fig. 1. From (2.9) we usually get a singular solution. As regards, if we take \(p_{M+i}=p_{i}^{*}\) (\(i = 1, 2,\ldots ,M\)) for \(N = 2M\), then we obtain a class of nonsingular rational solutions called M lump solutions, which were established in [17]. Continuing, we bring 1-lump and multiple-lump solutions of Eq. (1.1) in the following subsections.

Figure 1
figure 1

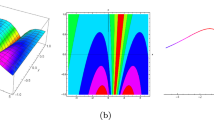
Diagram of 1-waves (2.4) using values \(a = 1.5\), \(b = 1\), \(k_{1} = 1\), \(\alpha = 0.2\), \(\epsilon = 0.3\), \(\tau = 2\), \(\eta _{0} = 0\), \(R = 2\), \(y = -2\). (f1) 3D plot, (f2) contour plot, (f3) density plot, and (f4) 2D plot with (red \(x=-1\), blue \(x=0\), and green \(x=1\))

Full size image

2.1 1-lump solutions for Equation (1.1)

By considering \(\exp (\eta _{i}^{(0)})=-1\), \(i=1,2\), 1-lump solutions of equation (1.1) for discovering 2-soliton solutions can be found in the form

$$ \rho _{2}=1-e^{\zeta _{1}}-e^{\zeta _{2}}+e^{\zeta _{1}+\zeta _{2}+F_{12}}, $$
(2.10)

where

$$\begin{aligned}& \zeta _{i}=k_{i} \biggl(x+p_{i}y- \biggl[1+\frac{1}{2}a\alpha p_{{i}}- \frac{1}{4} \epsilon {k_{{i}}}^{2}{p_{{i}}}^{2} ( 2\tau +1 ) -\frac{1}{6}\epsilon {k_{{i}}}^{2} ( 3\tau -1 ) \biggr] t \biggr),\quad i=1,2, \\& \exp F_{12} \\& \quad ={ \frac{ ( k_{{1}}-k_{{2}} ) ( 2 ( k_{{1}}-k_{ {2}} ) ( 2 \tau p_{{1}}p_{{2}}+3 \epsilon \tau +p_{{1}} p_{{2}}-\epsilon ) + ( k_{{1}}{p_{{1}}}^{2}-k_{{2}}{p_{{2}} }^{2} ) ( 2 \tau +1 ) ) }{ ( k_{{1}}+k_{ {2}} ) ( 2 ( k_{{1}}+k_{{2}} ) ( 2 \tau p_{{1}}p_{{2}}+3 \epsilon \tau +p_{{1}}p_{{2}}-\epsilon ) + ( k_{{1}}{p_{{1}}}^{2}+k_{{2}}{p_{{2}}}^{2} ) ( 2 \tau +1 ) ) }} \\& \quad =1-{ \frac{2k_{{1}}k_{{2}} ( ( {p_{{1}}}^{2}+4 p_{{1}}p_{{ 2}}+{p_{{2}}}^{2} ) ( 2 \tau +1 ) +4 ( 3 \tau -1 ) \epsilon ) }{ ( k_{{1}}+k_{{2}} ) ( ( k_{{1}}{p_{{1}}}^{2}+2 k_{{1}}p_{{1}}p_{{2}}+2 k_{{2 }}p_{{1}}p_{{2}}+k_{{2}}{p_{{2}}}^{2} ) ( 2 \tau +1 ) +2 \epsilon ( k_{{1}}+k_{{2}} ) ( 3 \tau -1 ) ) }}, \end{aligned}$$
(2.11)

and

$$\begin{aligned} \rho _{2}&=1-e^{\zeta _{1}}-e^{\zeta _{2}}+e^{\zeta _{1}+\zeta _{2}} \\ &\quad {}- \frac{2k_{{1}}k_{{2}} ( ( {p_{{1}}}^{2}+4 p_{{1}}p_{{ 2}}+{p_{{2}}}^{2} ) ( 2 \tau +1 ) +4 ( 3 \tau -1 ) \epsilon )e^{\zeta _{1}+\zeta _{2}} }{ ( k_{{1}}+k_{{2}} ) ( ( k_{{1}}{p_{{1}}}^{2}+2 k_{{1}}p_{{1}}p_{{2}}+2 k_{{2 }}p_{{1}}p_{{2}}+k_{{2}}{p_{{2}}}^{2} ) ( 2 \tau +1 ) +2 \epsilon ( k_{{1}}+k_{{2}} ) ( 3 \tau -1 ) ) }. \end{aligned}$$
(2.12)

By considering the “long wave” limit as \(k_{i}\rightarrow 0\) for \(i = 1, 2\) with \(\frac{k_{1}}{k_{2}}=2\), we conclude

$$ \rho _{2}=1-e^{\zeta _{1}}-e^{\zeta _{2}}+ \biggl(\frac{1}{3}{ \frac{ ( 2 {p_{{1}}}^{2}+2 p_{{1}}p_{{2}}-{p_{{2}}}^{2} ) ( 2 \tau +1 ) +2 ( 3 \tau -1 ) \epsilon }{ ( 2 {p_{{1}}}^{2}+6 p_{{1}}p_{{2}}+{p_{{2}}}^{2} ) ( 2 \tau +1 ) +6 ( 3 \tau -1 ) \epsilon }} \biggr)e^{\zeta _{1}+\zeta _{2}}, $$
(2.13)

where

$$ \zeta _{j}=x+p_{j}y- \biggl(1+ \frac{1}{2}a\alpha p_{{j}} \biggr) t, \quad j=1,2. $$
(2.14)

Putting \(p_{2}=p_{1}^{*}=a-ib\) into (2.13) and (2.14), we attain a nonsingular solution

$$\begin{aligned} \rho _{2} =&1-e^{\zeta _{1}}-e^{\zeta _{2}} \\ &{}+ \biggl(\frac{1}{3}{ \frac{ ( 6 iab+3 {a}^{2}+{b}^{2} ) ( 2 \tau +1 ) +2 ( 3 \tau -1 ) \epsilon }{ ( 2 iab+9 { a}^{2}+3 {b}^{2} ) ( 2 \tau +1 ) +6 ( 3 \tau -1 ) \epsilon }} \biggr)e^{\zeta _{1}+\zeta _{2}},\quad i= \sqrt{-1}, \end{aligned}$$
(2.15)

where

$$ \begin{aligned} &\zeta _{1}=x+(a+ib)y- \biggl(1+ \frac{1}{2}a\alpha (a+ib) \biggr) t, \\ &\zeta _{2}=x+(a-ib)y- \biggl(1+\frac{1}{2}a\alpha (a-ib) \biggr) t . \end{aligned} $$
(2.16)

Plugging (2.17) and (2.18) into \(\varPsi =R(\ln \rho _{2})_{x}\) and putting \(p_{1} = a + bi\), we obtain

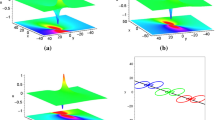
$$\begin{aligned}& \varPsi =-2\varGamma _{1}R \\& \hphantom{\varPsi ={}}{}\times \frac{ ( ( 6 iab+3 {a}^{2}+{b}^{2} ) ( 2 \tau +1 ) +2 \epsilon \varGamma _{{1}} ( 3 \tau -1 ) ) \varGamma _{{1}}-3 ( ( 2 iab+9 {a}^{2}+3 {b}^{2} ) ( 2 \tau +1 ) +6 ( 3\tau -1 ) \epsilon ) \varGamma _{{5}} }{\varGamma _{{6}}- ( ( 6iab+3{a}^{2}+{b}^{2} ) ( 2\tau +1 ) +2 ( 3\tau -1 ) \epsilon ) {\varGamma _{{1}}}^{2}+3 ( ( 2iab+9{a}^{2}+3{ b}^{2} ) ( 2\tau +1 ) +6 ( 3\tau -1 ) \epsilon ) ( \varGamma _{{3}}+\varGamma _{{4}} ) }, \\& \varGamma _{{1}}={{\mathrm{e}}^{x+ay-t-\frac{1}{2}t{a}^{2}\alpha }},\qquad \varGamma _{{2}}={{\mathrm{e}}^{x+ay-t-\frac{1}{2}t{a}^{2}\alpha }}, \\& \varGamma _{{3}}={{\mathrm{e}}^{x+iby+ay-t-\frac{1}{2}ita\alpha b- \frac{1}{2}t{a}^{2}\alpha } },\qquad \varGamma _{{4}}={{\mathrm{e}}^{x-iby+ay-t+ \frac{1}{2}ita\alpha b-\frac{1}{2}t{a}^{2}\alpha } }, \\& \varGamma _{{5}}=\cos \biggl( \frac{1}{2}b ( ta\alpha -2 y ) \biggr),\qquad \varGamma _{{6}}=-3 \bigl( 2 iab+9 {a}^{2}+3 {b}^{2} \bigr) ( 2 \tau +1 ) -18 ( 3 \tau -1 ) \epsilon . \end{aligned}$$
(2.17)

We can see that solution (2.17) decays as \(|x| \rightarrow \infty \) with amplitude 2R. In Figs. 1–2, solution (2.17) is plotted for an appropriate choice of diverse values and ρ at space \(x=-1, 0, 1\). From (2.17) we see that \(\rho _{2}\) is a positive quadratic function compatible with the findings in [19]. By selecting suitable values of the parameters \(p_{1}= a+ib\) and \(p_{2} = a-ib\) the analytical treatment of 1-lump solution is presented in Fig. 2, including the 3D plot, density plot, and 2D plot when three spaces arise at spaces \(x=-1\), \(x=0\), and \(x=1\). Also, choosing suitable values of the parameters \(p_{1}= a+ib\), \(p_{2} = c+id\), the graphic representation of 1-lump solution is presented in Fig. 3, including the 3D plot, density plot, and 2D plot when three spaces arise at spaces \(x=-1\), \(x=0\), and \(x=1\). Likewise, selecting suitable values of the parameters \(p_{1}= a+ib\) and \(p_{2} =2\), the analytical treatment of 1-lump solution is presented in Fig. 4, including the 3D plot, density plot, and 2D plot when three spaces arise at spaces \(x=-1\), \(x=0\), and \(x=1\). Finally, selecting suitable values of the parameters \(p_{1}= 3\) and \(p_{2} =2\), the graphic representation of 1-lump solution is presented in Fig. 5, including the 3D plot, density plot, and 2D plot when three spaces arise at spaces \(x=-1\), \(x=0\), and \(x=1\).

Figure 2
figure 2

Diagram of 1-lump (2.17) by taking \(a = 1.5\), \(b = 1\), \(k_{1} = 1\), \(k_{2}=2\), \(\alpha =1\), \(\epsilon =-1\), \(\tau = 2\), \(\eta _{10} = \eta _{20} =0\), \(R = 2\), \(y = -2\) at space (red \(x=-1\), blue \(x=0\), and green \(x=1\))

Full size image
Figure 3
figure 3

Diagram of 1-lump (2.17) by taking \(a = 1.5\), \(b = 1\), \(c=2\), \(d=3\), \(k_{1} = 1\), \(k_{2}=2\), \(\alpha =1\), \(\epsilon =-1\), \(\tau = 2\), \(\eta _{10} = \eta _{20} =0\), \(R = 2\), \(y = -2\) at space (red \(x=-1\), blue \(x=0\), and green \(x=1\))

Full size image
Figure 4
figure 4

Diagram of 1-lump (2.17) by taking \(a = 1.5\), \(b = 1\), \(k_{1} = 1\), \(k_{2}=2\), \(\alpha =1\), \(\epsilon =-1\), \(\tau = 2\), \(\eta _{10} = \eta _{20} =0\), \(R = 2\), \(y = -2\) at space (red \(x=-1\), blue \(x=0\), and green \(x=1\))

Full size image
Figure 5
figure 5

Diagram of 1-lump (2.17) by taking \(k_{1} = 1\), \(k_{2}=2\), \(\alpha =1\), \(\epsilon =-1\), \(\tau = 2\), \(\eta _{10} = \eta _{20} =0\), \(R = 2\), \(y = -2\) at space (red \(x=-1\), blue \(x=0\), and green \(x=1\))

Full size image

2.2 Multiple-lump solutions for Equation (1.1)

For computing the multiple-lump solutions of equation (1.1) by putting \(N=4\) and \(M=2\) in (2.9), we have:

$$ \rho _{4}=1+e^{\zeta _{1}}+e^{\zeta _{2}}+e^{\zeta _{1}+\zeta _{2}+F_{12}}+e^{ \zeta _{1}+\zeta _{3}+F_{13}}+e^{\zeta _{2}+\zeta _{3}+F_{23}}+ e^{ \zeta _{1}+\zeta _{2}+\zeta _{3}+F_{12}F_{13}F_{23}}, $$
(2.18)

where

$$\begin{aligned}& \zeta _{i}=k_{i} \biggl(x+p_{i}y- \biggl[1+\frac{1}{2}a\alpha p_{{i}}- \frac{1}{4} \epsilon {k_{{i}}}^{2}{p_{{i}}}^{2} ( 2\tau +1 ) -\frac{1}{6}\epsilon {k_{{i}}}^{2} ( 3\tau -1 ) \biggr] t \biggr),\quad i=1,2,3, \\& \begin{aligned} &\exp F_{12} \\ &\quad ={ \frac{ ( k_{{1}}-k_{{2}} ) ( 2 ( k_{{1}}-k_{ {2}} ) ( 2 \tau p_{{1}}p_{{2}}+3 \epsilon \tau +p_{{1}} p_{{2}}-\epsilon ) + ( k_{{1}}{p_{{1}}}^{2}-k_{{2}}{p_{{2}} }^{2} ) ( 2 \tau +1 ) ) }{ ( k_{{1}}+k_{ {2}} ) ( 2 ( k_{{1}}+k_{{2}} ) ( 2 \tau p_{{1}}p_{{2}}+3 \epsilon \tau +p_{{1}}p_{{2}}-\epsilon ) + ( k_{{1}}{p_{{1}}}^{2}+k_{{2}}{p_{{2}}}^{2} ) ( 2 \tau +1 ) ) }}, \\ &\exp F_{13} \\ &={ \frac{ ( k_{{1}}-k_{{3}} ) ( 2 ( k_{{1}}-k_{ {3}} ) ( 2 \tau p_{{1}}p_{{3}}+3 \epsilon \tau +p_{{1}} p_{{3}}-\epsilon ) + ( k_{{1}}{p_{{1}}}^{2}-k_{{3}}{p_{{3}} }^{2} ) ( 2 \tau +1 ) ) }{ ( k_{{1}}+k_{ {3}} ) ( 2 ( k_{{1}}+k_{{3}} ) ( 2 \tau p_{{1}}p_{{3}}+3 \epsilon \tau +p_{{1}}p_{{3}}-\epsilon ) + ( k_{{1}}{p_{{1}}}^{2}+k_{{3}}{p_{{3}}}^{2} ) ( 2 \tau +1 ) ) }}, \\ &\exp F_{23} \\ &\quad ={ \frac{ ( k_{{2}}-k_{{3}} ) ( 2 ( k_{{2}}-k_{ {3}} ) ( 2 \tau p_{{2}}p_{{3}}+3 \epsilon \tau +p_{{1}} p_{{3}}-\epsilon ) + ( k_{{2}}{p_{{2}}}^{2}-k_{{3}}{p_{{3}} }^{2} ) ( 2 \tau +1 ) ) }{ ( k_{{2}}+k_{ {3}} ) ( 2 ( k_{{2}}+k_{{3}} ) ( 2 \tau p_{{2}}p_{{3}}+3 \epsilon \tau +p_{{1}}p_{{3}}-\epsilon ) + ( k_{{2}}{p_{{2}}}^{2}+k_{{3}}{p_{{3}}}^{2} ) ( 2 \tau +1 ) ) }}, \end{aligned} \end{aligned}$$
(2.19)
$$\begin{aligned}& \rho _{4}=1+e^{\zeta _{1}}+e^{\zeta _{2}} \\& \hphantom{\rho _{4}={}}{}+{ \frac{ ( k_{{1}}-k_{{2}} ) ( 2 ( k_{{1}}-k_{ {2}} ) ( 2 \tau p_{{1}}p_{{2}}+3 \epsilon \tau +p_{{1}} p_{{2}}-\epsilon ) + ( k_{{1}}{p_{{1}}}^{2}-k_{{2}}{p_{{2}} }^{2} ) ( 2 \tau +1 ) ) }{ ( k_{{1}}+k_{ {2}} ) ( 2 ( k_{{1}}+k_{{2}} ) ( 2 \tau p_{{1}}p_{{2}}+3 \epsilon \tau +p_{{1}}p_{{2}}-\epsilon ) + ( k_{{1}}{p_{{1}}}^{2}+k_{{2}}{p_{{2}}}^{2} ) ( 2 \tau +1 ) ) }}e^{\zeta _{1}+\zeta _{2}} \\& \hphantom{\rho _{4}={}}{}+{ \frac{ ( k_{{1}}-k_{{3}} ) ( 2 ( k_{{1}}-k_{ {3}} ) ( 2 \tau p_{{1}}p_{{3}}+3 \epsilon \tau +p_{{1}} p_{{3}}-\epsilon ) + ( k_{{1}}{p_{{1}}}^{2}-k_{{3}}{p_{{3}} }^{2} ) ( 2 \tau +1 ) ) }{ ( k_{{1}}+k_{ {3}} ) ( 2 ( k_{{1}}+k_{{3}} ) ( 2 \tau p_{{1}}p_{{3}}+3 \epsilon \tau +p_{{1}}p_{{3}}-\epsilon ) + ( k_{{1}}{p_{{1}}}^{2}+k_{{3}}{p_{{3}}}^{2} ) ( 2 \tau +1 ) ) }} e^{\zeta _{1}+\zeta _{3}} \\& \hphantom{\rho _{4}={}}{}+ { \frac{ ( k_{{2}}-k_{{3}} ) ( 2 ( k_{{2}}-k_{ {3}} ) ( 2 \tau p_{{2}}p_{{3}}+3 \epsilon \tau +p_{{1}} p_{{3}}-\epsilon ) + ( k_{{2}}{p_{{2}}}^{2}-k_{{3}}{p_{{3}} }^{2} ) ( 2 \tau +1 ) ) }{ ( k_{{2}}+k_{ {3}} ) ( 2 ( k_{{2}}+k_{{3}} ) ( 2 \tau p_{{2}}p_{{3}}+3 \epsilon \tau +p_{{1}}p_{{3}}-\epsilon ) + ( k_{{2}}{p_{{2}}}^{2}+k_{{3}}{p_{{3}}}^{2} ) ( 2 \tau +1 ) ) }}e^{\zeta _{2}+\zeta _{3}} \\& \hphantom{\rho _{4}={}}{}+\exp F_{12}\exp F_{13}\exp F_{23} e^{\zeta _{1}+\zeta _{2}+\zeta _{3}}, \end{aligned}$$
(2.20)

where

$$ \zeta _{j}=x+p_{j}y- \biggl(1+\frac{1}{2}a \alpha p_{{j}} \biggr) t,\quad j=1,2,3. $$

Plugging \(\rho _{4}\) into the transmutation \(\varPsi =R(\ln \rho _{4})_{x}\) and taking \(p_{1}=a+bi\), \(p_{2}=c+di\), \(p_{3}=e+fi\) such that \(\mathfrak{R}p_{i} > 0\) (\(i = 1, 2, 3\)), we obtain the 3-lump solution of equation (1.1). In Figs. 6–10 the 3-lump solution is plotted for appropriate values of \(p_{1}=a+bi\), \(p_{2}=c+di\), \(p_{3}=e+fi\). By selecting suitable values of the parameters \((p_{1}= a+ib, p_{2} = a-ib, p+3=c+id)\) in Fig. 6, \((p_{1}= a+ib, p_{2} = c+id, p+3=e+if)\) in Fig. 7, \((p_{1}= 2, p_{2} = 3, p+3=4)\) in Fig. 8, \((p_{1}= a+ib, p_{2} = 3, p+3=c+id)\) in Fig. 9, and \((p_{1}= a+ib, p_{2} = 2, p+3=3)\) in Fig. 10 the graphical representations of 2-lump (three-soliton) solution are given in Figs. 6–10 containing the 3D plot, density plot, and 2D plot when three spaces arise at spaces \(x=-1\), \(x=0\), and \(x=1\).

Figure 6
figure 6

Diagram of 3-lump (2.20) by taking \(a = 1.5\), \(b = 1\), \(c=2\), \(d=3\), \(k_{1} = 1\), \(k_{2}=2\), \(k_{3}=3\), \(\alpha =0.1\), \(\epsilon =-1\), \(\tau = 2\), \(\eta _{10} = \eta _{20}=\eta _{30} =0\), \(R = 2\), \(y = -2\) at space (red \(x=-1\), blue \(x=0\), and green \(x=1\))

Full size image
Figure 7
figure 7

Diagram of 3-lump (2.20) by taking \(a = 1.5\), \(b = 1\), \(c=2\), \(d=3\), \(e=-1\), \(f=5\), \(k_{1} = 1\), \(k_{2}=2\), \(k_{3}=3\), \(\alpha =0.1\), \(\epsilon =-1\), \(\tau = 2\), \(\eta _{10} = \eta _{20}=\eta _{30} =0\), \(R = 2\), \(y = -2\) at space (red \(x=-1\), blue \(x=0\), and green \(x=1\))

Full size image
Figure 8
figure 8

Diagram of 3-lump (2.20) by taking \(k_{1} = 1\), \(k_{2}=2\), \(k_{3}=3\), \(\alpha =0.1\), \(\epsilon =-1\), \(\tau = 2\), \(\eta _{10} = \eta _{20}= \eta _{30} =0\), \(R = 2\), \(y = -2\) at space (red \(x=-1\), blue \(x=0\), and green \(x=1\))

Full size image
Figure 9
figure 9

Diagram of 3-lump (2.20) by taking \(a = 1.5\), \(b = 1\), \(c=2\), \(d=3\), \(k_{1} = 1\), \(k_{2}=2\), \(k_{3}=3\), \(\alpha =0.1\), \(\epsilon =-1\), \(\tau = 2\), \(\eta _{10} = \eta _{20}=\eta _{30} =0\), \(R = 2\), \(y = -2\), at space (red \(x=-1\), blue \(x=0\), and green \(x=1\))

Full size image
Figure 10
figure 10

Diagram of 3-lump (2.20) by taking \(a = 1.5\), \(b = 1\), \(c=2\), \(d=3\), \(k_{1} = 1\), \(k_{2}=2\), \(k_{3}=3\), \(\alpha =0.1\), \(\epsilon =-1\), \(\tau = 2\), \(\eta _{10} = \eta _{20}=\eta _{30} =0\), \(R = 2\), \(y = -2\), at space (red \(x=-1\), blue \(x=0\), and green \(x=1\))

Full size image

3 Interaction between lumps and stripe solitons of equation (1.1)

In the following subsections, we further treat diverse solitons.

3.1 Interaction between 1-lump and 2-stripe soliton of Equation (1.1)

To treat 1-lump and 1-stripe solitons of equation (1.1), we catch f as a blend of the following functions:

$$\begin{aligned}& \rho = \Biggl(\sum_{i=1}^{4} \varOmega _{i}x_{i} \Biggr)^{2}+ \Biggl(\sum _{i=5}^{8} \varOmega _{i}x_{i} \Biggr)^{2}+ r_{1}+r_{2}e^{\sum _{i=1}^{4}\varOmega _{i}x_{i}}+r_{3}e^{ \sum _{i=5}^{8}\varOmega _{i}x_{i}}+ r_{4}e^{\sum _{i=1}^{8}\varOmega _{i}x_{i}}, \end{aligned}$$
(3.1)
$$\begin{aligned}& (x_{1}, x_{2}, x_{3}, x_{4})=(x,y,t,1),\qquad (x_{5}, x_{6}, x_{7}, x_{8})=(x,y,t,1), \\ & \varPsi =R\frac{\partial }{\partial x}\ln (\rho ) \\ & \hphantom{\varPsi}=R \frac{r_{4}(\varOmega _{1}+\varOmega _{5})e^{\sum _{i=1}^{8}\varOmega _{i}x_{i}}+ 2\varOmega _{1}\sum_{i=1}^{4}\varOmega _{i}x_{i}+2\varOmega _{5}\sum_{i=5}^{8}\varOmega _{i}x_{i}+ r_{2}\varOmega _{1}e^{\sum _{i=1}^{4}\varOmega _{i}x_{i}}+r_{3}\varOmega _{5} e^{\sum _{i=5}^{8}\varOmega _{i}x_{i}}}{\rho }, \end{aligned}$$
(3.2)

where \((x_{1},x_{2},x_{3})=(x,y,t)\), and \(\varOmega _{i}\), \(i=1,\ldots,8\), \(r_{1}\), \(r_{2}\), \(r_{3}\) are free parameters to be found later. Plugging (3.1) into Eq. (1.3), collecting the coefficients at the diverse polynomial functions including the functions \(e^{\sum _{i=1}^{4}\varOmega _{i}x_{i}}\), \(e^{\sum _{i=5}^{8}\varOmega _{i}x_{i}}\), \(e^{\sum _{i=1}^{8}\varOmega _{i}x_{i}}\) and their products, and solving the obtained algebraic system containing 26 equations, we obtain the following solutions:

Set I:

$$ \textstyle\begin{cases} \tau =-\frac{1}{6}{ \frac{6 {\varOmega _{{2}}}^{2} \sqrt{2}+2 \epsilon {\varOmega _{{5}}}^{2}-9 {\varOmega _{{2}}}^{2}}{2{\varOmega _{{2}}}^{2} \sqrt{2}- \epsilon {\varOmega _{{5}}}^{2}-3 {\varOmega _{{2}}}^{2}}} , \qquad \varOmega _{{1}}= ( 1+ \sqrt{2} ) \varOmega _{{5}}, \qquad \varOmega _{2} = \varOmega _{2}, \\ \varOmega _{{3}}=-\frac{1}{2}a\alpha \varOmega _{{2}}- ( 1+ \sqrt{2} ) \varOmega _{{5}}, \qquad \varOmega _{4}=0, \qquad \varOmega _{5}=\varOmega _{5}, \\ \varOmega _{{6}}=\varOmega _{{2}} ( \sqrt{2}-1 ),\qquad \varOmega _{{7}}=-\frac{1}{2} ( \sqrt{2}-1 ) ( a \alpha \varOmega _{{2}}+2(\sqrt{2}+1)\varOmega _{{5}} ), \qquad \varOmega _{8} = 0, \\ r_{1} = r_{1}, \qquad r_{2}=r_{2},\qquad r_{3} = 0, \qquad r_{4}=r_{4}, \end{cases} $$
(3.3)

which should satisfy the condition

$$ (2\sqrt{2}-3){\varOmega _{{2}}}^{2} - \epsilon {\varOmega _{{5}}}^{2} \neq 0. $$

Plugging (3.3) into (3.2), we achieve te following interactive wave solution of Eq. (1.1):

$$\begin{aligned}& \varPsi _{1}=R \frac{r_{4}(2+\sqrt{2})\varOmega _{5}e^{\sum _{i=1, i\neq 4}^{7}\varOmega _{i}x_{i}}+ 2\varOmega _{1}\sum_{i=1}^{3}\varOmega _{i}x_{i}+2\varOmega _{5}\sum_{i=5}^{7}\varOmega _{i}x_{i}+ r_{2}\varOmega _{1}e^{\sum _{i=1}^{3}\varOmega _{i}x_{i}}}{\rho }, \end{aligned}$$
(3.4)
$$\begin{aligned}& \rho = \Biggl(\sum_{i=1}^{3} \varOmega _{i}x_{i} \Biggr)^{2}+ \Biggl(\sum _{i=5}^{7} \varOmega _{i}x_{i} \Biggr)^{2}+ r_{1}+r_{2}e^{\sum _{i=1}^{3}\varOmega _{i}x_{i}}+ r_{4}e^{\sum _{i=1}^{7}\varOmega _{i}x_{i}}. \end{aligned}$$
(3.5)

Moreover, by selecting suitable values of the parameters the graphic representation of periodic wave solution is presented in Fig. 11, including the 3D plot, density plot, and 2D plot when three spaces arise at spaces \(x=-1\), \(x=0\), and \(x=1\).

Figure 11
figure 11

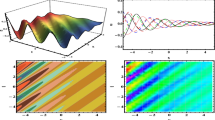
Plots of interaction between 1-lump and 1-stripe solution for (3.6) by taking \(a = 1\), \(\alpha = 0.1\), \(\epsilon = 0.3\), \(\varOmega _{2} = 1\), \(\varOmega _{5} = 1.2\), \(r_{1}= -3.5\), \(r_{2} = 1.3\), \(r_{4} = 1.4\), \(R = 2\) (first row \(t = -1\), second row \(t = 0\), and third row \(t = 1\))

Full size image

Set II:

$$ \textstyle\begin{cases} \tau =\frac{1}{6}{ \frac{2 \epsilon {\varOmega _{{1}}}^{2}-3 {\varOmega _{{2}}}^{2 }}{\epsilon {\varOmega _{{1}}}^{2}+{\varOmega _{{2}}}^{2}}} ,\qquad \varOmega _{{1}}= \varOmega _{{1}},\qquad \varOmega _{2} = \varOmega _{2}, \\ \varOmega _{{3}}=-\frac{1}{2}a\alpha \varOmega _{{2}}-\varOmega _{{1}}, \qquad \varOmega _{4}=\varOmega _{4},\qquad \varOmega _{5}=\varOmega _{5}, \qquad \varOmega _{{6}}=\frac{\varOmega _{2}\varOmega _{5}}{\varOmega _{1}}, \\ \varOmega _{{7}}=-{ \frac{ ( a\alpha \varOmega _{{2}}+2 \varOmega _{{1 }} ) \varOmega _{{5}}}{2\varOmega _{{1}}}}, \qquad \varOmega _{8} = \varOmega _{8}, \\ r_{1} = r_{1}, \qquad r_{2}=r_{2}, \qquad r_{3} = r_{3},\qquad r_{4}=r_{4} , \end{cases} $$
(3.6)

which should satisfy the condition

$$ \epsilon {\varOmega _{{1}}}^{2}+{\varOmega _{{2}}}^{2} \neq 0. $$

Plugging (3.6) into (3.2), we achieve the following interactive wave solution of Eq. (1.1):

$$\begin{aligned}& \varPsi _{2}=R \frac{r_{4}(\varOmega _{1}+\varOmega _{5}) e^{\sum _{i=1}^{8}\varOmega _{i}x_{i}}+ 2\varOmega _{1} \sum_{i=1}^{4}\varOmega _{i}x_{i}+2\varOmega _{5} \sum_{i=5}^{8} \varOmega _{i}x_{i}+ r_{2}\varOmega _{1}e^{\sum _{i=1}^{4}\varOmega _{i}x_{i}}+r_{3}\varOmega _{5} e^{\sum _{i=5}^{8}\varOmega _{i}x_{i}}}{\rho }, \end{aligned}$$
(3.7)
$$\begin{aligned}& \rho = \Biggl(\sum_{i=1}^{4} \varOmega _{i}x_{i} \Biggr)^{2}+ \Biggl(\sum _{i=5}^{8} \varOmega _{i}x_{i} \Biggr)^{2}+ r_{1}+r_{2}e^{\sum _{i=1}^{4}\varOmega _{i}x_{i}}+r_{3}e^{ \sum _{i=5}^{8}\varOmega _{i}x_{i}}+ r_{4}e^{\sum _{i=1}^{8}\varOmega _{i}x_{i}}. \end{aligned}$$
(3.8)

Likewise, by selecting suitable values of the parameters the graphic representation of periodic wave solution is presented in Fig. 12, containing the 3D plot, density plot, and 2D plot when three spaces arise at spaces \(x=-1\), \(x=0\), and \(x=1\).

Figure 12
figure 12

Plots of interaction between 1-lump and 1-stripe solutions for (3.7) by taking \(a = 1\), \(\alpha = 0.1\), \(\epsilon = 0.3\), \(\varOmega _{1}=1.5\), \(\varOmega _{2} = 1\), \(\varOmega _{4}=\varOmega _{5} = 1.2\), \(\varOmega _{8}=1\), \(r_{1}= 3.5\), \(r_{2} = 1.3\), \(r_{3}=1.2\), \(r_{4} = 1.4\), \(R = 2\) (first row \(t = -1\), second row \(t = 0\), and third row \(t = 1\))

Full size image

Set III:

$$ \textstyle\begin{cases} \tau =-\frac{1}{6}{ \frac{3 {\varOmega _{{2}}}^{2} \sqrt{17}-8 \epsilon { \varOmega _{{5}}}^{2}+9 {\varOmega _{{2}}}^{2}}{{\varOmega _{{2}}}^{2} \sqrt{17}+ 4 \epsilon {\varOmega _{{5}}}^{2}+3 {\varOmega _{{2}}}^{2}}} ,\qquad \varOmega _{{1}}=\frac{1}{2} \sqrt{-6+2 \sqrt{17}}\varOmega _{{5}}, \\ \varOmega _{2} = \varOmega _{2}, \qquad \varOmega _{{3}}=-\frac{1}{2}a\alpha \varOmega _{{2}}-\frac{1}{2} \sqrt{-6+2 \sqrt{17}} \varOmega _{{5}}, \\ \varOmega _{4}=0, \qquad \varOmega _{5}=\varOmega _{5},\qquad \varOmega _{{6}}=\frac{1}{8} \sqrt{-6+2 \sqrt{17}} ( \sqrt{17}+3 ) \varOmega _{{2}}, \\ \varOmega _{{7}}=-\frac{1}{16} \sqrt{-6+2 \sqrt{17}} ( \sqrt{17}+3 ) ( \sqrt{-6+2 \sqrt{17}}\varOmega _{{5}}+a\alpha \varOmega _{{2}} ) , \\ \varOmega _{8} = 0, \qquad r_{1} = r_{1}, \qquad r_{2}=r_{2}, \\ r_{{3}}={ \frac{ ( 912 r_{{1}}+10412+19 \sqrt{17} ( 11 r _{{1}}+124 ) +19 \sqrt{-6+2 \sqrt{17}} ( 2 \sqrt{17}+ 7 ) ( 5 \sqrt{17}+25+4 r_{{1}} ) ) r_{{4}} }{361 r_{{2}}}}, \qquad r_{4}=r_{4}, \end{cases} $$
(3.9)

which should satisfy the condition

$$ ( \sqrt{17}+3 ) {\varOmega _{{2}}}^{2}+4 \epsilon { \varOmega _{ {5}}}^{2} \neq 0. $$

Plugging (3.9) into (3.2), we achieve the following interactive wave solution of Eq. (1.1):

$$\begin{aligned}& \varPsi _{3}=R \frac{r_{4}(\varOmega _{1}+\varOmega _{5}) e^{\sum _{i=1,\neq 4}^{7}\varOmega _{i}x_{i}}+ 2\varOmega _{1} \sum_{i=1}^{3}\varOmega _{i}x_{i}+2\varOmega _{5} \sum_{i=5}^{7}\varOmega _{i}x_{i}+ r_{2}\varOmega _{1}e^{\sum _{i=1}^{3}\varOmega _{i}x_{i}}+r_{3} \varOmega _{5}e^{\sum _{i=5}^{7}\varOmega _{i}x_{i}}}{\rho }, \end{aligned}$$
(3.10)
$$\begin{aligned}& \rho = \Biggl(\sum_{i=1}^{3} \varOmega _{i}x_{i} \Biggr)^{2}+ \Biggl(\sum _{i=5}^{7} \varOmega _{i}x_{i} \Biggr)^{2}+ r_{1}+r_{2}e^{\sum _{i=1}^{3}\varOmega _{i}x_{i}}+r_{3}e^{ \sum _{i=5}^{7}\varOmega _{i}x_{i}}+ r_{4}e^{\sum _{i=1,\neq 4}^{7} \varOmega _{i}x_{i}}. \end{aligned}$$
(3.11)

Remark 3.1

By selecting suitable values of the parameters, the graphical representations of interaction solutions are presented in Figs. 11–12. These figures suggest that there are 1-lump and 2-stripe solitons, the energy of the 1-lump is more robust than that of the 2-stripe soliton; as \(t\rightarrow 0\), the 1-lump commences to be swallowed by the 2-stripe soliton gradually, its energy commences to move from one place to another into the 2-stripe soliton progressively, until it is swallowed by the stripe soliton completely. These two types of solutions move into one soliton and continue to spread.

3.2 Interaction between 2-lump and 1-stripe solitons of equation (1.1)

To search treatment between 2-lump and 1-stripe solitons of equation (1.1), we catch f as a blend of the following functions:

$$\begin{aligned}& \begin{aligned} &\rho = \Biggl(\sum_{i=1}^{4} \varOmega _{i}x_{i} \Biggr)^{4}+2 \Biggl( \sum _{i=1}^{4}\varOmega _{i}x_{i} \Biggr)^{2}+ r+ke^{\sum _{i=5}^{8} \varOmega _{i}x_{i}}, \\ &(x_{1,5}, x_{2,6}, x_{3,7}, x_{4,8})=(x,y,t,1), \end{aligned} \end{aligned}$$
(3.12)
$$\begin{aligned}& \varPsi =R\frac{\partial }{\partial x}\ln (\rho )=R \frac{4\varOmega _{1} (\sum_{i=1}^{4}\varOmega _{i}x_{i} )^{3}+4\varOmega _{1}\sum_{i=1}^{4}\varOmega _{i}x_{i}+ k\varOmega _{5}e^{\sum _{i=5}^{8}\varOmega _{i}x_{i}}}{\rho }, \end{aligned}$$
(3.13)

where \(\varOmega _{i}\), \(i=1,\ldots,4\), r, k are free elements to be defined later. Plugging (3.12) into Eq. (1.3), collecting the coefficients at the diverse polynomial functions including \(e^{\sum _{i=5}^{8}\varOmega _{i}x_{i}}\) and their products, and solving the obtained algebraic system of 11 equations, we get the following solutions:

Set I:

$$ \textstyle\begin{cases} \varOmega _{1}=\varOmega _{1}, \qquad \varOmega _{{2}}=-{ \frac{2\varOmega _{{1}} ( 3 \tau -1 ) }{ \sqrt{- ( 12 \tau +6 ) ( 3 \tau -1 ) }}}, \\ \varOmega _{{3}}=-\frac{1}{6}{ \frac{\varOmega _{{1}}\sqrt{- ( 12 \tau +6 ) ( 3 \tau -1 ) }a\alpha }{2 \tau +1}}-\varOmega _{{1}},\qquad \varOmega _{4}=\varOmega _{4}, \\ \varOmega _{5}=\varOmega _{5},\qquad \varOmega _{{6}}=\frac{1}{3}{ \frac{\sqrt{- ( 12 \tau +6 ) ( 3 \tau -1 ) }\varOmega _{{5}}}{2 \tau +1}}, \\ \varOmega _{{7}}=-\frac{1}{6}{ \frac{a\alpha \sqrt{- ( 12 \tau +6 ) ( 3 \tau -1 ) }\varOmega _{{5}}}{2 \tau +1}}- \varOmega _{ {5}}, \qquad \varOmega _{8}=\varOmega _{8}. \end{cases} $$
(3.14)

To ensure the positivity of ρ, we need the following determinant condition:

$$ (12\tau +6) (3\tau -1)< 0, \quad \tau \neq -\frac{1}{2}. $$

Plugging (3.14) into (3.13), we get the following interactive wave solution of Eq. (1.1):

$$ \varPsi _{1}=R \frac{4\varOmega _{1} (\sum_{i=1}^{4}\varOmega _{i}x_{i} )^{3} +4\varOmega _{1}\sum_{i=1}^{4}\varOmega _{i}x_{i}+ k\varOmega _{5}e^{\sum _{i=5}^{8}\varOmega _{i}x_{i}}}{\rho }, $$
(3.15)

where

$$ \rho = \Biggl(\sum_{i=1}^{4}\varOmega _{i}x_{i} \Biggr)^{4}+2 \Biggl( \sum _{i=1}^{4}\varOmega _{i}x_{i} \Biggr)^{2}+ r+ke^{\sum _{i=5}^{8} \varOmega _{i}x_{i}}. $$

Set II:

$$ \textstyle\begin{cases} \varOmega _{{1}}=\frac{3}{10}{ \frac{\varOmega _{{4}}\sqrt{- ( 12 \tau +6 ) ( 3\tau -1 ) }\varOmega _{{6}}}{3 \tau -1}}, \qquad \varOmega _{{2}}=\frac{3}{5}\varOmega _{4}\varOmega _{6}, \\ \varOmega _{{3}}=-\frac{3}{10}\varOmega _{{4}}\varOmega _{{6}} ( a \alpha +{ \frac{ \sqrt{- ( 12 \tau +6 ) ( 3 \tau -1 ) }}{3 \tau -1}} ) , \qquad \varOmega _{4}=\varOmega _{4}, \\ \varOmega _{{5}}=\frac{1}{2}{ \frac{\sqrt{- ( 12 \tau +6 ) ( 3 \tau -1 ) }\varOmega _{{6}}}{3 \tau -1}} , \qquad \varOmega _{{6}}=\varOmega _{6}, \\ \varOmega _{{7}}=-\frac{1}{2}\varOmega _{{6}} ( a\alpha +{ \frac{\sqrt{- ( 12 \tau +6 ) ( 3 \tau -1 ) }}{3 \tau -1}} ), \qquad \varOmega _{8}=\varOmega _{8}. \end{cases} $$
(3.16)

To ensure the positivity of ρ, we need the following determinant condition:

$$ (12\tau +6) (3\tau -1)< 0, \quad \tau \neq \frac{1}{3}. $$

Plugging (3.16) into (3.13), we get the following interactive wave solution of Eq. (1.1):

$$ \varPsi _{2}=R \frac{\frac{6}{5}{\frac{\varOmega _{{4}}\sqrt{- ( 12\tau +6 ) ( 3\tau -1 ) }\varOmega _{{6}}}{3\tau -1}} (\sum_{i=1}^{4}\varOmega _{i}x_{i} )^{3}+ \frac{6}{5}{\frac{\varOmega _{{4}}\sqrt{- ( 12\tau +6 ) ( 3\tau -1 ) }\varOmega _{{6}}}{3\tau -1}}\sum_{i=1}^{4}\varOmega _{i}x_{i}+ \frac{k}{2}{\frac{\sqrt{- ( 12\tau +6 ) ( 3 \tau -1 ) }\varOmega _{{6}}}{3\tau -1}}e^{\sum _{i=5}^{8}\varOmega _{i}x_{i}}}{\rho }, $$
(3.17)

where

$$ \rho = \Biggl(\sum_{i=1}^{4}\varOmega _{i}x_{i} \Biggr)^{4}+2 \Biggl( \sum _{i=1}^{4}\varOmega _{i}x_{i} \Biggr)^{2}+ r+ke^{\sum _{i=5}^{8} \varOmega _{i}x_{i}}. $$

Remark 3.2

By selecting suitable values of the parameters, the graphical representations of interaction solutions are presented in Figs. 13 and 14. By selecting suitable values of the parameters, the graphical representation of interaction between 2-lump and 1-stripe solitons is presented in Figs. 13 and 14. These figures show that there are 2-lump and a 1-stripe solitons; as \(t\rightarrow 0\), 2-lump commences to be swallowed by 2-stripe soliton gradually, its energy commences to move from one place to another into the 1-stripe soliton progressively, until it is swallowed by the 1-stripe soliton generally, and these two types of solutions move into one resonance soliton and continue to spread.

Figure 13
figure 13

Plots of interaction between 1-lump and 1-stripe solution for (3.15) by taking \(a = 1\), \(\alpha = 0.1\), \(\epsilon = 0.3\), \(\tau =-\frac{1}{5}\), \(\varOmega _{4} = 1\), \(\varOmega _{5} = 2\), \(\varOmega _{8}=-3.5\), \(r = 2\), \(k=3\), \(R = 2\) (first row \(t = -20\), second row \(t = 0\), and third row \(t = 20\))

Full size image
Figure 14
figure 14

Plots of interaction between 1-lump and 1-stripe solution for (3.17) by taking \(a = 1\), \(\alpha = 0.1\), \(\epsilon = 0.3\), \(\tau =-\frac{1}{5}\), \(\varOmega _{4} = 1\), \(\varOmega _{6} = 2\), \(\varOmega _{8}=-3.5\), \(r = 2\), \(k=3\), \(R = 2\), (first row \(t = -20\), second row \(t = 0\) and third row \(t = 20\))

Full size image

4 Conclusions

We employed the Hirota bilinear method, along with some Hirota derivatives and the Bell polynomial theories of soliton equations, to find abundantly many exact lumps and interaction lumps with two types of typical local excitations, which occurred between a lump and a stripe soliton of soliton solutions to third-order evaluation equation. We investigated M lump solutions and made different types of graphs, including the contour, density, and three- and two dimensional plots. We also obtained an interaction between 1-lump and two-stripe solutions and an interaction between 2-lump and one-stripe solutions and found more general rational exact soliton wave solutions of the third-order evaluation equation. This approach has been successfully applied to obtain some real rational soliton wave solutions to third-order evaluation equation with constant coefficients. We proved a theorem for the considered problem. We also obtained existence criteria of these solitons in the unidirectional propagation of long waves over shallow water. The attained solutions are in broad-ranging form, and the definite values of the included parameters of the attained solutions yield the soliton solutions and are helpful in analyzing the water waves mechanics, the quantum mechanics, the water waves in gravitational force, the signal processing waves, the optical fibers, and so on. This paper showed that the Hirota bilinear method, combined with Hirota derivatives, gives a unified approach to constructing the exact rational lump soliton wave solutions to many nonlinear partial differential equations. Our results allowed us to understand the dynamics of nonlinear propagation in fluid mechanics, plasma, and so on. Moreover, the established results have shown that the Hirota bilinear method is general, straightforward, and powerful and helped us to examine traveling wave solutions of NLPDEs.