Bifurcation analysis in a diffusive predator–prey system with Michaelis–Menten-type predator harvesting

Abstract

In this paper, we consider a modified predator–prey model with Michaelis–Menten-type predator harvesting and diffusion term. We give sufficient conditions to ensure that the coexisting equilibrium is asymptotically stable by analyzing the distribution of characteristic roots. We also study the Turing instability of the coexisting equilibrium. In addition, we use the natural growth rate $r_{1}$ of the prey as a parameter and carry on Hopf bifurcation analysis including the existence of Hopf bifurcation, bifurcation direction, and the stability of the bifurcating periodic solution by the theory of normal form and center manifold method. Our results suggest that the diffusion term is important for the study of the predator–prey model, since it can induce Turing instability and spatially inhomogeneous periodic solutions. The natural growth rate $r_{1}$ of the prey can also affect the stability of positive equilibrium and induce Hopf bifurcation.

1 Introduction

In nature, predation relationship plays a very important role in ecosystems. Many scholars studied predator–prey dynamic models and developed them in many ways [1–9]. Bian et al. [10] proposed a stochastic prey–predator system in a polluted environment with Beddington–DeAngelis functional response and derived sufficient conditions for the existence of boundary periodic solutions and positive periodic solutions. Zhuo and Zhang [11] considered a discrete ratio-dependent predator–prey model and obtained a new sufficient condition to ensure that the positive equilibrium is globally asymptotically stable. Liu et al. [12] proposed an impulsive stochastic infected predator–prey system with Lévy jumps and delays, and investigated the effects of time delays and impulse stochastic interference on dynamics of this predator–prey model. Liu and Cheng [13] proposed a prey–predator model with square-root response function under a state-dependent impulse and analyzed the existence, uniqueness, and attractiveness of the order-1 periodic solution.

Bifurcation phenomenon is widespread in the ecosystem, and it arouses a strong interest of researchers [14–19]. Ruan et al. [20] carried out the bifurcation analysis for a predator–prey model and showed various kinds of bifurcation phenomenon, such as the saddle-node bifurcation, the supercritical Hopf bifurcation, the homoclinic bifurcation, and so on. Huang et al. [14] considered a delayed fractional-order predator–prey model with two-competitor and nonidentical orders, focusing on the Hopf bifurcation. Jiang and Wang [15] studied global Hopf bifurcation of a predator–prey model by using the time delay as a bifurcating parameter.

Population dynamics of the predator–prey model with harvesting has been studied widely by some scholars [21–24], who suggested that the harvesting term was closely related to the long-termed stability of the population. May et al. [25] proposed the following model to describe the interaction of predator and prey with harvesting term:

$$ \textstyle\begin{cases} \dot{x} = r_{1} x ( {1 - \frac{x}{K}} ) - axy - H_{1}, \\ \dot{y} = r_{2} y ( {1 - \frac{y}{bx}} ) - H_{2}, \end{cases} $$

(1.1)

where x and y represent the densities of prey and predator at time t, respectively. All parameters involved with the model are positive, $r_{1}$ and K are the natural growth rate and carrying capacity of the prey lacking natural predators, respectively, a represents the maximum at which per capita reduction rate of the prey x can reach, $r_{2}$ plays a role of the natural growth rate of predators, bx is the carrying capacity the predators rely on the prey, and $H_{1}$ and $H_{2}$ represent the effects of the harvesting to preys and predators, respectively.

Based on model (1.1), Hu and Cao [26] proposed model (1.2) with Michaelis–Menten-type predator harvesting as follows:

$$ \textstyle\begin{cases} \dot{x} = r_{1} x ( {1 - \frac{x}{K}} ) - axy, \\ \dot{y} = r_{2} y ( {1 - \frac{y}{bx}} ) - \frac{qEy}{cE + ly}. \end{cases} $$

(1.2)

The term $\frac{qEy}{cE + ly}$ is the Michaelis–Menten-type harvesting, and E, p, c, and l are positive parameters. Hu and Cao [26] considered saddle-node bifurcation, transcritical bifurcation, Hopf bifurcation, and Bogdanov–Takens bifurcation, and suggested that the Michaelis–Menten-type harvesting was more realistic and reasonable than the constant-yield harvesting and constant effort harvesting.

In real word, diffusion phenomenon widely exists. For example, predators and their preys distribute inhomogeneously in different spatial locations at time t. To survive better, they move from a place with high competitive pressure to the place with small pressure. Compared with predator–prey models without diffusion (ordinary differential equation (ODE) type predator–prey models), the diffusion can induce more complex phenomena, such as Turing instability, spatially inhomogeneous periodic solutions, and pattern formation [27–31]. Inspired by these works, we consider the following predator–prey model with diffusion term:

$$ \textstyle\begin{cases} \frac{\partial u(x,t)}{\partial t} = r_{1} u(1 - \frac{u}{K}) - auv +d_{1}\Delta u,&x \in ( {0,l\pi } ) , t > 0, \\ \frac{\partial v(x,t)}{\partial t} = r_{2} v(1 - \frac{v}{bu+\beta })- \frac{qEv}{cE + lv} + d_{2} \Delta v,& x \in ( {0,l\pi } ) , t > 0, \\ u_{x} ( {0,t} ) = v_{x} ( {0,t} ) = 0,\qquad u_{x} ( {l\pi ,t} ) = v_{x} ( {l\pi ,t} ) = 0,& t > 0, \\ u ( {x,0} ) = u_{0} ( x ) \ge 0,\qquad v ( {x,0} ) =v_{0} ( x ) \ge 0,& x \in [ {0,l\pi } ] , \end{cases} $$

(1.3)

where $d_{1}>0$ and $d_{2}>0$ are the diffusion coefficients of prey and predator, respectively, $u(x,t)$ and $v(x,t)$ represent the densities of prey at position x and time t. The carrying capacity of the predator, denoted as β, is proportional to the prey and other food. The boundary condition is the Neumann boundary condition based on the hypothesis that the region is closed and with no prey and predator species entering and leaving the region at the boundary.

To simplify model (1.3), denote $s = \frac{a}{r_{1} }$, $m = \frac{cEr_{2} }{qE}$, and $h = \frac{lr_{2} }{qE}$. Then system (1.3) can be rewritten as

$$ \textstyle\begin{cases} \frac{\partial u(x,t)}{\partial t} = r_{1} u(1 - \frac{u}{K} - sv) + d_{1}\Delta u,&x \in ( {0,l\pi } ) , t > 0, \\ \frac{\partial v(x,t)}{\partial t} = r_{2} v(1 - \frac{v}{bu + \beta} -\frac{1}{m + hv}) + d_{2} \Delta v ,&x \in ( {0,l\pi } ) , t > 0, \\ u_{x} ( {x,t} ) = v_{x} ( {x,t} ) = 0,\qquad u_{x} ( {l\pi ,t} ) = v_{x} ( {l\pi ,t} ) = 0,&t > 0, \\ u ( {x,0} ) = u_{0} ( x ) \ge 0,\qquad v ( {x,0} ) =v_{0} ( x ) \ge 0,&x \in [ {0,l\pi } ] . \end{cases} $$

(1.4)

The rest of this paper is organized as follows. In Sect. 2, we study the local stability and Turing instability of the positive equilibrium of system (1.4). In Sect. 3, we investigate the existence and property of Hopf bifurcation. In Sect. 4, we give some numerical simulations. In Sect. 5, we give a short conclusion.

2 Stability analysis of equilibria

2.1 Existence of equilibria

Now, we discuss the existence of equilibrium of system (1.4). The equilibrium of system (1.4) is satisfied:

$$ \textstyle\begin{cases} r_{1} u(1 - \frac{u}{K} - sv) = 0, \\ r_{2} v(1 - \frac{v}{bu + \beta } - \frac{1}{m + hv}) = 0. \end{cases} $$

(2.1)

According to the first equation in Eq. (2.1), we have

$$ v = \frac{1}{s} \biggl( {1 - \frac{u}{K}} \biggr) . $$

(2.2)

If $u \in ( {0,K} )$, then $v > 0$. Thus system (1.4) has a positive equilibrium $p = ( {u_{0} ,v_{0} } )$. From Eqs. (2.1) and (2.2) we have

$$ u^{2} - u\alpha_{1} - \alpha_{2} = 0, $$

(2.3)

where

$$\begin{aligned}& \alpha_{1} = \frac{K [ {ms + h(2 - s\beta ) + bK^{2}s ( {h + ms - s} ) } ] }{h(1 + bKs)} , \\& \alpha_{2} = \frac{K^{2} [ { ( {h + ms} ) ( {s\beta - 1} ) - s^{2}\beta } ] }{h ( {1 + bKs} ) }. \end{aligned}$$

Denote

$$ \varphi (u) = u^{2} - \alpha_{1} u - \alpha_{2}. $$

(2.4)

It is easy to see that $\varphi (0) = - \alpha_{2}$ and $\varphi (K) = \frac{ - ( {m - 1} ) K^{2}s^{2}(blK + \beta )}{h ( {1 + bKs} ) }$.

Now, let us discuss $\varphi (u)$ with $u \in ( {0,K} )$ in two cases.

Case 1: $m > 1$. In this case, we have $\varphi (K) < 0$ under $\varphi (0) = - \alpha_{2} > 0$, and thus Eq. (2.4) has a unique root, whereas $\varphi (K) > 0$ under $\varphi ( 0 ) = - \alpha_{2} > 0$, and thus Eq. (2.4) has no roots.

Case 2: $m < 1$. In this case, if $\varphi ( 0 ) = - \alpha_{2} > 0$, then we get that $\varphi (K) > 0$ and $\varphi (u)$ has two roots or no root, whereas if $\varphi (0) = - \alpha_{2} < 0$, then it has a unique root.

Based on this analysis, if $( {m - 1} ) \alpha_{2} < 0$, then system (1.4) has a unique positive equilibrium $P ( {u_{0} ,v_{0} } )$. So, we always assume that system (1.4) has a positive equilibrium $P ( {u_{0} ,v_{0} } )$ in the following discussion.

2.2 Stability analysis of $P ( {u_{0} ,v_{0} } )$

To study the stability analysis of $P ( {u_{0} ,v_{0} } )$, we analyze the distribution of characteristic roots as is done in [32]. Now, we consider the characteristic equation of system (1.4). Define the real-valued Sobolev space

$$ \mathbf{X}:= \bigl\{ (u,v)\in \bigl[H^{2}(0,l\pi ) \bigr]^{2}:(u_{x},v_{x})|_{x=0.l \pi }=0 \bigr\} , $$

and the complexification of X:

$$ \mathbf{X_{\mathbb{C}}}:=\mathbf{X} \oplus i\mathbf{X}=\{x_{1}+ix_{2}:x _{1},x_{2}\in \mathbf{X}\}. $$

The linearized system of (1.4) at $(u_{0},v_{0})$ has the form

$$ \left ( \textstyle\begin{array}{@{}c@{}} u_{t} \\ v_{t} \end{array}\displaystyle \right ) =L(\rho )\left ( \textstyle\begin{array}{@{}c@{}} u \\ v \end{array}\displaystyle \right ) :=\left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} d_{1} & 0 \\ 0 & d_{2} \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{@{}c@{}} \Delta u \\ \Delta v \end{array}\displaystyle \right ) +\left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} -{r_{1}}{a_{1}} & -{r_{1}}{a_{2}} \\ {r_{2}}{b_{1}}& {r_{2}}{b_{2}} \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{@{}c@{}} u \\ v \end{array}\displaystyle \right ) , $$

where $a_{1}$, $a_{2}$, $b_{1}$, and $b_{2}$ are defined in (2.5). Then the linearized operator of the steady-state system of (1.4) evaluated at $(u_{0},v_{0})$ is

$$ L(s) = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} d_{1} \frac{\partial^{2}{}}{\partial {x^{2}}}-{r_{1}}{a_{1}} & -{r_{1}} {a_{2}} \\ {r_{2}}{b_{1}}& d_{2} \frac{\partial^{2}{}}{\partial {x^{2}}}+ {r_{2}}{b_{2}} \end{array}\displaystyle \right ) $$

with the domain $D_{L(s)}=\mathbf{X_{\mathbb{C}}}$ and

$$ {a_{1}} = \frac{{{u_{0}}}}{K},\qquad {a_{2}} = s{u_{0}}, \qquad {b_{1}} = \frac{{b{v_{0}}^{2}}}{{{{ ( {b{u_{0}} + \beta } ) } ^{2}}}},\qquad {b_{2}} = \frac{{2h{v_{0}} + m}}{{{{(h{v_{0}} + m)}^{2}}}} - 1. $$

(2.5)

It is well known that the eigenvalue problem

$$ -\varphi ''=\mu \varphi , \quad x\in (0,l\pi ); \qquad \varphi '(0)=\varphi '(l \pi )=0 $$

has the eigenvalues $\mu_{n}=\frac{n^{2}}{l^{2}}$ ($n=0,1,\ldots$) with the corresponding eigenfunctions $\varphi_{n}(x)=\cos \frac{n\pi }{l}$. Let

$$ \left ( \textstyle\begin{array}{@{}c@{}} \phi \\ \psi \end{array}\displaystyle \right ) =\sum_{n=0}^{\infty } \left ( \textstyle\begin{array}{@{}c@{}} a_{n} \\ b_{n} \end{array}\displaystyle \right ) \cos \frac{n\pi }{l} $$

be the eigenfunction of $L(\rho )$ corresponding to an eigenvalue $\beta (\rho )$, that is,

$$ L(\rho ) (\phi , \psi )^{T}=\beta (\rho ) (\phi , \psi )^{T}. $$

Then from a straightforward analysis we have

$$ L_{n}(s)\left ( \textstyle\begin{array}{@{}c@{}} a_{n} \\ b_{n} \end{array}\displaystyle \right ) =\beta (s)\left ( \textstyle\begin{array}{@{}c@{}} a_{n} \\ b_{n} \end{array}\displaystyle \right ) ,\quad n=0,1,\ldots , $$

where

$$ L_{n}(s) := \left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} -{r_{1}}{a_{1}}-\frac{d_{1}n^{2}}{l^{2}} & -{r_{1}}{a_{2}} \\ {r_{2}}{b_{1}} & {r_{2}}{b_{2}}-\frac{d_{2}n^{2}}{l^{2}} \end{array}\displaystyle \right ) . $$

It follows that the eigenvalues of $L(s)$ are given by the eigenvalues of $L_{n}(s)$ for $n=0,1,2,\ldots$ . The characteristic equation of $L_{n}(s)$ is

$$ \lambda^{2} - T_{n} \lambda + D_{n} = 0,\quad n=0,1,2,\ldots , $$

(2.6)

where

$$\begin{aligned}& \begin{aligned} &T_{n} = - ( {d_{1} + d_{2} } ) \frac{n^{2}}{l^{2}}- {r_{1}} {a_{1}} + {r_{2}} {b_{2}} , \\ &D_{n} = {d_{1}} {d_{2}} {z^{2}} + ( {{r_{1}} {a_{1}} {d_{2}} - {r _{2}} {b_{2}} {d_{1}}} ) z + {r_{1}} {r_{2}}({a_{2}} {b_{1}} - {a _{1}} {b_{2}}). \end{aligned} \end{aligned}$$

(2.7)

Thus we can obtain the eigenvalues of Eq. (2.6):

$$ \lambda_{1,2} = \frac{T_{n} \pm \sqrt{T_{n} ^{2} - 4D_{n} } }{2},\quad n = 0,1,2,3\ldots . $$

To analyze the influence of the diffusion term in model (1.4), we first study the stability of $P ( {u_{0} ,v_{0} } )$ for ODE model. If $d_{1} = d_{2} = 0$, then the characteristic roots of (2.5) are given by

$$ {\lambda_{1,2}} = \frac{{r_{2}b_{2} - r_{1}a_{1} \pm \sqrt{( {{r_{2}}{b_{2}} - {r_{1}}{a_{1}}} ) }^{2}} - 4{r_{1}} {r_{2}}({a_{2}}{b_{1}} - {a_{1}}{b_{2}}) }{2}. $$

(2.8)

We know that the positive equilibrium of a system is locally asymptotically stable when its eigenvalues all have negative real parts. Therefore we can get that both $\lambda_{1,2}$ have negative real part if and only if ${r_{2}}{b_{2}} - {r_{1}}{a_{1}} < 0$ and $a_{2} b_{1} - a_{1} b_{2} > 0$, which are guaranteed by

${\mathbf{{(H_{1} })}}$ :

$$ r_{1}>\frac{K r_{2}}{u_{0}} \biggl( \frac{1-m-(m+h v_{0}-1)^{2}}{(m+h v_{0})^{2}} \biggr) $$

and

${\mathbf{{(H_{2} })}}$ :

$$ 1+s b K>\frac{1-m}{ (m+h _{0}-1)^{2}}, $$

respectively. Summarizing the discussion, we have the following conclusions.

Theorem 2.1

For ODE system (1.4), if $\mathbf{{(H_{1} })}$ and $\mathbf{{(H_{2} })}$ hold, then the positive equilibrium $P ( {u_{0} ,v_{0} } )$ is locally asymptotically stable.

Now, we consider Turing instability of the equilibrium $P ( {u_{0} ,v_{0} } )$. For Eq. (2.6), define

$$ \textstyle\begin{cases} z = \frac{{{n^{2}}}}{{{l^{2}}}}, \\ T ( z ) = - ( {{d_{1}} + {d_{2}}} ) z - {r_{1}} {a_{1}} + {r_{2}}{b_{2}}, \\ D ( z ) = {d_{1}}{d_{2}}{z^{2}} + ( {{r_{1}}{a_{1}} {d_{2}} - {r_{2}}{b_{2}}{d_{1}}} ) z + {r_{1}}{r_{2}}({a_{2}} {b_{1}} - {a_{1}}{b_{2}}). \end{cases} $$

(2.9)

According to Theorem 2.1, under hypotheses $\mathbf{{(H_{1} })}$ and $\mathbf{{(H_{2} })}$, we have $T(0)<0$ and $D(0)>0$. Then $T ( z ) \le T ( 0 ) < 0$. For $n \ne 0$, we can gain the symmetry axis $z_{0}$ and the discriminant Δ of $D ( z )$. They are given by

$$ {z_{0}} = \frac{{{r_{2}}{b_{2}}{d_{1}} - {r_{1}}{a_{1}}{d_{2}}}}{ {2{d_{1}}{d_{2}}}} ,\qquad \Delta = { ( {{r_{1}} {a_{1}} {d_{2}} - {r_{2}} {b_{2}} {d_{1}}} ) ^{2}} - 4{d_{1}} {d_{2}} {r_{1}} {r_{2}} ( {{a_{2}} {b_{1}} - {a_{1}} {b_{2}}} ) . $$

We consider the following two cases.

Case I: ${r_{2}}{b_{2}}{d_{1}} - {r_{1}}{a_{1}}{d_{2}} \le 0$ or $\Delta < 0$. Then all the roots of Eq. (2.6) have negative real parts.

Case II: ${r_{2}}{b_{2}}{d_{1}} > {r_{1}}{a_{1}}{d_{2}}$ and $\Delta > 0$. Denote the two different roots of $D ( z ) =0$ as $z_{1}$ and $z_{2}$ $(z_{1} < z_{2} )$. By straightforward calculating we get $z_{1,2} = \frac{ - ( {r_{1} a_{1} d_{2} - r _{2} b_{2} d_{1} } ) \mp \sqrt{\Delta }}{2d_{1} d_{2} }$. Then we have the following conclusions:

• (i) For all $n \in N$, if $\frac{n^{2}}{l^{2}} \notin ( {z_{1} ,z _{2} } )$, then $D ( n ) > 0$, and all the roots of Eq. (2.6) have negative real parts.

• (ii) If there exists $k \in N$ such that $\frac{k^{2}}{l^{2}} \in ( {z_{1} ,z_{2} } )$, then $D ( k ) < 0$, and Eq. (2.6) has at least one root with positive real part.

Based on this analysis, we have the following theorem.

Theorem 2.2

For PDE system (1.4), let $\mathbf{{(H_{1} })}$ and $\mathbf{{(H_{2} })}$ hold. Then the following statements are true.

• (1) In Case I, the positive equilibrium $p ( {u_{0} ,v_{0} } )$ is locally asymptotically stable.

• (2) In Case II, $\frac{n^{2}}{l^{2}} \notin ( {z_{1} ,z_{2} } )$ for all $n \in N$, the positive equilibrium $p ( {u_{0} ,v_{0} } )$ is locally asymptotically stable.

• (3) In Case II, there exists $k \in N$ such that $\frac{k^{2}}{l^{2}} \in ( {z_{1} ,z_{2} } )$. Then the positive equilibrium $p ( {u_{0} ,v_{0} } )$ is Turing instability.

3 Analysis of Hopf bifurcation

3.1 Existence of Hopf bifurcation

In the predator–prey system, considering Hopf bifurcation is of great value and significance. In this section, we mainly study the existence of Hopf bifurcation by taking $r_{1}$ as a bifurcating parameter.

Define

$$ r_{1}^{ (n)} = \frac{r_{2} K}{u_{0} } \biggl[ \frac{2hv_{0} + m}{(hv_{0} + m)^{2}} - 1 \biggr] - \frac{K}{u_{0} } ( {d_{1} + d_{2} } ) \frac{n^{2}}{l^{2}}, \quad n = 0,1,2,\ldots ,n_{1}^{*}, $$

(3.1)

where $n_{1}^{*}$ is an integer such that $r_{1}^{ (n)}>0$ for $n\leq n_{1}^{*}$ and $r_{1}^{ (n)} \le 0$ for $n=n_{1}^{*}+1$. Obviously, $T_{n}(r_{1}^{ (n)})=0$ and ${D_{0}} ( {r_{1}^{ ( 0 ) }} ) >0$ under hypothesis $\mathbf{{(H_{2} })}$. Then there exists an integer $n_{2}^{*}\geq 1$ such that $D_{n}(r_{1}^{ (n)})>0$ when $n \leq n_{2}^{*}$ and $D_{n}(r_{1}^{ (n)})\leq 0$ when $n= n_{2}^{*}+1$. Let $n^{*}=\min \{ n_{1}^{*}, n_{2}^{*}\}$. Then Eqs. (2.6) have a part of pure imaginary roots when $r_{1}=r_{1}^{ (n)}$ where $n\leq n^{*}$. We assume that system (1.4) has a pair of complex eigenvalues $\alpha ( {{r_{1}}} ) \pm i{\omega_{0}} ( {{r_{1}}} )$ when $r_{1}$ is near $r_{1}^{n}$, where

$$ \alpha \bigl( r_{1}^{(n)} \bigr) = \frac{T_{n}}{2}, \qquad \omega \bigl( r_{1}^{(n)} \bigr) = \frac{\sqrt{4{D_{n}} - T_{n}^{2}}}{2}, \qquad \frac{d\alpha ( r_{1}) }{dr_{1} } \bigg|_{r_{1} = r_{1}^{( n )}} = -\frac{u_{0}}{2K} < 0. $$

Then the transversal condition is satisfied. System (1.4) undergoes Hopf bifurcation at $r_{1} = r_{1}^{ ( n ) }$. Hence we get the following theorem.

Theorem 3.1

If $\mathbf{{(H_{2} })}$ holds, then system (1.4) undergoes Hopf bifurcation at $r_{1} = r_{1}^{ ( n ) }$, where $n = 0,1,2, \ldots ,n^{*}$.

3.2 Property of Hopf bifurcation

By using the algorithm in [32] we will give parameters for determining the bifurcation direction and the stability of the bifurcating periodic solution. Here we just consider the case of $r_{1} = r_{1}^{ ( 0 ) }$, where ${\omega_{0}} = \frac{{ 2\sqrt{ {r_{1}}{r_{2}} ( {{a_{2}}{b_{1}} - {a_{1}}{b_{2}}} ) } }}{2}$. We have

$$ q = \left ( \textstyle\begin{array}{@{}c@{}} 1 \\ - \frac{{i{\omega_{0}}K + {r_{1}}{u_{0}}}}{{K{r_{1}}s{u_{0}}}} \end{array}\displaystyle \right ) \quad \mbox{and} \quad {q^{*} } = \left ( \textstyle\begin{array}{@{}c@{}} \frac{{{r_{1}}{u_{0}}}}{{2Kl\pi i{\omega_{0}}}} + \frac{1}{{2l\pi }} \\ \frac{{s{r_{1}}{u_{0}}}}{{2l\pi i{\omega_{0}}}} \end{array}\displaystyle \right ) . $$

(3.2)

Define

$$ \textstyle\begin{cases} f ( {{r_{1}},u,v} ) = {r_{1}}u ( {1 - \frac{u}{K} - sv} ) , \\ g ( {{r_{2}},u,v} ) = {r_{2}}v ( {1 - \frac{v}{{bu + \beta }} - \frac{1}{{m + hv}}} ) . \end{cases} $$

(3.3)

By calculating we have

$$\begin{aligned}& \begin{aligned} &{f_{uu}} = - \frac{{2{r_{1}}}}{K}, \qquad{f_{uv}} = - {r_{1}}s, \qquad f_{vv} = f_{uuu}={f_{uuv}}={f_{uvv}}={f_{vvv}} = 0, \\ &{g_{uu}} = \frac{{ - 2{r_{2}}{b^{2}}v_{0}^{2}}}{{{{ ( {b{u_{0}} +\beta } ) }^{3}}}}, \qquad {g_{uv}} = \frac{{2b{r_{2}}{v_{0}}}}{{{{ ( {b{u_{0}} + \beta } ) } ^{2}}}}, \\ &{g_{vv}} = - \frac{{2{h^{2}}{r_{2}}{v_{0}}}}{{{{(m + h{v_{0}})}^{3}}}}, \qquad {g_{uuu}}= \frac{{6{b^{3}}{r_{2}}v_{0}^{2}}}{{{{(\beta + b {u_{0}})}^{4}}}}, \\ &{g_{uuv}}= - \frac{{4{b^{2}}{r_{2}}{v_{0}}}}{{{{(\beta + b {u_{0}})}^{3}}}}, \qquad {g_{vvv}} = \frac{{2{h^{2}}{r_{2}}( - m + 2h{v_{0}})}}{{{{(m + h{v _{0}})}^{4}}}}, \qquad {g_{uvv}} = 2b{r_{2}} { ( {b{u_{0}} + \beta } ) ^{ - 2}}. \end{aligned} \end{aligned}$$

(3.4)

When $n = 0$, by a simple computation we get

$$ \begin{aligned} \bigl\langle {{q^{*} },{Q_{qq}}} \bigr\rangle = \frac{{{c_{0}}}}{2} - \frac{{{r_{1}}{u_{0}} ( {{c_{0}} + Ks{d_{0}}} ) }}{{2Ki{\omega_{0}}}}, \qquad \bigl\langle {{q^{*} },{Q_{q\bar{q}}}} \bigr\rangle = \frac{{{e_{0}}}}{2} - \frac{{{r_{1}}{u_{0}} ( {{e_{0}} + Ks{f_{0}}} ) }}{{2Ki{\omega_{0}}}}, \\ \bigl\langle {{{\bar{q}}^{*} },{Q_{qq}}} \bigr\rangle = \frac{{{c _{0}}}}{2} + \frac{{{r_{1}}{u_{0}} ( {{c_{0}} + Ks{d_{0}}} ) }}{ {2Ki{\omega_{0}}}}, \qquad \bigl\langle {{{ \bar{q}}^{*} },{C_{qq\bar{q}}}} \bigr\rangle = \frac{ {{g_{0}}}}{2} - \frac{{{r_{1}}{u_{0}} ( {{g_{0}} + Ks{h_{0}}} ) }}{ {2Ki{\omega_{0}}}}, \end{aligned} $$

(3.5)

where

$$ \begin{aligned} &{c_{0}} = - \frac{{2{r_{1}}}}{K}a_{0}^{2} - 2 {r_{1}}s{a_{0}} {b_{0}}, \qquad {e_{0}} = - \frac{{2{r_{1}}}}{K}{\vert {{a_{0}}} \vert ^{2}} - {r_{1}}s({a_{0}}\overline{{b_{0}}} + \overline{{a_{0}}} {b_{0}}), \\ &{d_{0}} = \frac{{ - 2{r_{2}}{b^{2}}v_{0}^{2}}}{{{{ ( {b{u_{0}} + \beta } ) }^{3}}}}a_{0}^{2} + \frac{{4b{r_{2}}{v_{0}}}}{{{{ ( {b{u_{0}} + \beta } ) }^{2}}}}{a_{0}} {b_{0}} - \frac{{2{h^{2}} {r_{2}}{v_{0}}}}{{{{(m + h{v_{0}})}^{3}}}}b_{0}^{2}, \qquad {g_{0}} = 0, \\ &{f_{0}} = \frac{{ - 2{r_{2}}{b^{2}}v_{0}^{2}}}{{{{ ( {b{u_{0}} + \beta } ) }^{3}}}}{\vert {{a_{0}}} \vert ^{2}} + \frac{{2b {r_{2}}{v_{0}}}}{{{{ ( {b{u_{0}} + \beta } ) }^{2}}}} ( {{a_{0}}\overline{{b_{0}}} + \overline{{a_{0}}} {b_{0}}} ) - \frac{ {2{h^{2}}{r_{2}}{v_{0}}}}{{{{(m + h{v_{0}})}^{3}}}}{ \vert {{b_{0}}} \vert ^{2}}, \\ &{h_{0}}= \frac{{6{b^{3}}{r_{2}}v_{0}^{2}}}{{{{(\beta + b{u_{0}})} ^{4}}}}{\vert {{a_{0}}} \vert ^{2}} {a_{0}} - \frac{{4{b^{2}}{r_{2}} {v_{0}}}}{{{{(\beta + b{u_{0}})}^{3}}}} \bigl( {2{{\vert {{a_{0}}} \vert } ^{2}} {b_{0}} + a_{0}^{2}\overline{{b_{0}}} } \bigr) \\ &\hphantom{{h_{0}}=}{}+\frac{{2b{r_{2}}}}{{{{ ( {b{u_{0}} + \beta } ) }^{2}}}} \bigl( {2{{\vert {{b_{0}}} \vert }^{2}} {a_{0}} + b_{0}^{2} \overline{ {a_{0}}} } \bigr) +\frac{{2{h^{2}}{r_{2}}( - m + 2h{v_{0}})}}{ {{{(m + h{v_{0}})}^{4}}}}{\vert {{b_{0}}} \vert ^{2}} {b_{0}}. \end{aligned} $$

(3.6)

We have

$$\begin{aligned}& {\omega_{20}} = { \bigl[2i{ \omega_{0}}I - L({r_{1}}) \bigr]^{ - 1}}\left [ {\left ( \textstyle\begin{array}{@{}c@{}} {c_{0}} \\ {d_{0}} \end{array}\displaystyle \right ) - \bigl\langle {{q^{*}},{Q_{q,q}}} \bigr\rangle \left ( \textstyle\begin{array}{@{}c@{}} {a_{0}} \\ {b_{0}} \end{array}\displaystyle \right ) - \bigl\langle {\overline{{q^{*}}} ,{Q_{q,q}}} \bigr\rangle \left ( \textstyle\begin{array}{@{}c@{}} \overline{{a_{0}}} \\ \overline{{b_{0}}} \end{array}\displaystyle \right ) } \right ] , \end{aligned}$$

(3.7)

$$\begin{aligned}& {\omega_{11}} = - { \bigl[ {L ( {{r_{1}}} ) } \bigr] ^{ - 1}}\left [ {\left ( \textstyle\begin{array}{@{}c@{}} {e_{0}} \\ {f_{0}} \end{array}\displaystyle \right ) - \bigl\langle {{q^{*}},{Q_{q\overline{q} }}} \bigr\rangle \left ( \textstyle\begin{array}{@{}c@{}} {a_{0}} \\ {b_{0}} \end{array}\displaystyle \right ) - \bigl\langle {\overline{{q^{*}}} ,{Q_{q\overline{q} }}} \bigr\rangle \left ( \textstyle\begin{array}{@{}c@{}} \overline{{a_{0}}} \\ \overline{{b_{0}}} \end{array}\displaystyle \right ) } \right ] , \end{aligned}$$

(3.8)

$$\begin{aligned}& {H_{20}} = \left ( \textstyle\begin{array}{@{}c@{}} {c_{0}} \\ {d_{0}} \end{array}\displaystyle \right ) - \bigl\langle {{q^{*}},{Q_{q,q}}} \bigr\rangle \left ( \textstyle\begin{array}{@{}c@{}} {a_{0}} \\ {b_{0}} \end{array}\displaystyle \right ) - \bigl\langle {\overline{{q^{*}}} ,{Q_{q,q}}} \bigr\rangle \left ( \textstyle\begin{array}{@{}c@{}} \overline{{a_{0}}} \\ \overline{{b_{0}}} \end{array}\displaystyle \right ) , \end{aligned}$$

(3.9)

$$\begin{aligned}& {H_{11}} = \left ( \textstyle\begin{array}{@{}c@{}} {e_{0}} \\ {f_{0}} \end{array}\displaystyle \right ) - \bigl\langle {{q^{*}},{Q_{q\overline{q} }}} \bigr\rangle \left ( \textstyle\begin{array}{@{}c@{}} {a_{0}} \\ {b_{0}} \end{array}\displaystyle \right ) - \bigl\langle {\overline{{q^{*}}} ,{Q_{q\overline{q} }}} \bigr\rangle \left ( \textstyle\begin{array}{@{}c@{}} \overline{{a_{0}}} \\ \overline{{b_{0}}} \end{array}\displaystyle \right ) . \end{aligned}$$

(3.10)

By calculating we get ${H_{20}} = {H_{11}} = 0$, that is, ${\omega _{20}} = {\omega_{11}} = 0$. Therefore

$$ \bigl\langle {{q^{*}},Q ( {{\omega_{11}},q} ) } \bigr\rangle = \bigl\langle {{q^{*}},Q ( {{\omega_{20}},\bar{q}} ) } \bigr\rangle = 0. $$

According to [32], we get

$$ c_{1} \bigl( {r_{1}^{ ( 0 ) } } \bigr) = \frac{i}{2\omega _{0} } \biggl( {g_{20} g_{11} - 2\vert {g_{11} } \vert ^{2} - \frac{1}{3}\vert {g_{02} } \vert ^{2}} \biggr) + \frac{g_{21} }{2}, $$

(3.11)

where

$$\begin{aligned}& g_{20} = \bigl\langle {q^{\ast },Q_{qq} } \bigr\rangle , \qquad g_{11} = \bigl\langle {q^{\ast },Q_{q\overline{q} } } \bigr\rangle , \\& g_{02} = \bigl\langle {q^{\ast },Q_{\overline{qq} } } \bigr\rangle ,\qquad g_{21} = 2 \bigl\langle {q^{\ast },Q_{\omega_{11} ,q} } \bigr\rangle + \bigl\langle {q^{\ast },Q_{\omega_{20} ,\overline{q} } } \bigr\rangle + \bigl\langle {q^{\ast },C_{q,q,\overline{q} } } \bigr\rangle . \end{aligned}$$

Through simplification, when $r_{1} = r_{1}^{ ( 0 ) }$, we obtain

$$ {c_{1}} \bigl( {r_{1}^{ ( 0 ) }} \bigr) = \frac{i}{{2{\omega _{0}}}} \bigl\langle {{q^{*}},{Q_{qq}}} \bigr\rangle \cdot \bigl\langle {{q ^{*}},{Q_{q\overline{q} }}} \bigr\rangle + \frac{1}{2} \bigl\langle {{q ^{*}},{C_{q,q,\overline{q} }}} \bigr\rangle . $$

(3.12)

Thus

$$ \operatorname{Re} \bigl\{ {{c_{1}} \bigl( {r_{1}^{ ( 0 ) }} \bigr) } \bigr\} = \operatorname{Re} \biggl\{ {\frac{i}{{2{\omega_{0}}}} \bigl\langle {{q^{*}},{Q_{qq}}} \bigr\rangle \cdot \bigl\langle {{q^{*}},{Q_{q\overline{q} }}} \bigr\rangle + \frac{1}{2} \bigl\langle {{q^{*}},{C_{q,q,\overline{q} }}} \bigr\rangle } \biggr\} . $$

(3.13)

Summarizing the discussion, we have the following conclusions.

Theorem 3.2

If $\operatorname{Re} ( {c_{1} (r_{1}^{ ( 0 ) } )} ) < 0$ (resp. >0), Hopf bifurcation at $r_{1} = r_{1}^{ ( 0 ) }$ toward the back (resp., ahead) and the bifurcating periodic solutions are asymptotically stable (resp., unstable).

The parameters determining the property of the bifurcation of the spatially inhomogeneous periodic solutions (at $r_{1} = r_{1}^{ ( j ) }$) are given in the Appendix.

4 Numerical simulations

To support the results found in the previous sections, we give some numerical simulations by Matlab. The numerical simulation of the PDE systems is implemented by pdepe function in Matlab. Fix the following parameters:

$$ \begin{aligned} &\beta = 0.2,\qquad s = 8,\qquad b = 0.1,\qquad K = 30, \\ &m = 0.99,\qquad h = 0.99,\qquad r_{2} = 2,\qquad l = 2. \end{aligned} $$

(4.1)

By computation, we get two positive equilibriums: $( {u_{0} ,v _{0} } ) _{1} \approx ( {10.341,0.082} )$ and $( u_{0} , v_{0} ) _{2} \approx ( {26.211,0.016} )$.

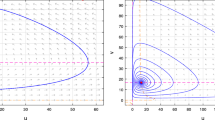
For equilibrium ${ ( {{u_{0}},{v_{0}}} ) _{2}} \approx ( {26.211,0.016} )$, we obtain ${a_{2}}{b_{1}} - {a_{1}}{b_{2}} \approx - 0.003 < 0$, so this equilibrium is unstable by Theorem 2.1. For equilibrium ${ ( {{u_{0}},{v_{0}}} ) _{1}} \approx ( {10.341,0.082} )$, we obtain ${b_{2}} < {a_{1}}$, ${r_{1}} {r_{2}}({a_{2}}{b_{1}} - {a_{1}}{b_{2}}) \approx 0.016 > 0$ when $r_{1} = 0.2$, so the positive equilibrium $p ( {{u_{0}},{v_{0}}} ) ={ ( {{u_{0}},{v_{0}}} ) _{1}}$ is locally asymptotically stable, which is shown in Fig. 1. If we choose $r_{1} = 0.029$, due to $r_{2} b_{2} > r_{1} a_{1}$, then we see that $P ( {u_{0} ,v_{0} } )$ is unstable and has a bifurcating periodic orbit.

Figure 1

Left: $r_{1} = 0.200$, the positive equilibriums $p ( {u_{0} ,v_{0} } )$ is locally asymptotically stable. Right: $r_{1} = 0.029$, $p ( {u_{0},v_{0} } )$ is unstable and has the bifurcating periodic orbit

In the following, we mainly consider the positive equilibrium $P ( {{u_{0}},{v_{0}}} ) ={ ( {{u_{0}},{v_{0}}} ) _{1}}$ and fix the parameters in (4.1). Choose $d_{1} = 0.01$, $d_{2} = 0.2$, $r_{1} =0.2$. We have $r_{2} b_{2} d_{1} - r_{1} a_{1} d_{2} \approx - 0.014 < 0$. Then $P ( {u_{0} ,v_{0} } )$ is locally asymptotically stable by Theorem 2.2, which is shown in Fig. 2.

Figure 2

The numerical simulations of system (1.4) with parameters in (4.1) and $d_{1} = 0.01$, $d_{2} = 0.2$, $r_{1} = 0.2$. Left: component u is locally asymptotically stable. Right: component v is locally asymptotically stable

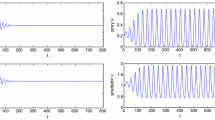
For the positive equilibrium $p ( {{u_{0}},{v_{0}}} ) ={ ( {{u_{0}},{v_{0}}} ) _{1}}$, we choose $d_{1} = 2$, $d _{2} = 0.001$, $r_{1} =0.2$. By Theorem 2.2 we have $z_{1} \approx 7.966$, $z_{2} \approx 9.996\times 10^{ - 1}$, and $4 / l^{2} = 1$, so that $z_{1} < 4 / l^{2} < z_{2}$. Hence we have Turing instability at $P ( {u_{0} ,v_{0} } )$, which is shown in Fig. 3.

Figure 3

The numerical simulations of system (1.4) with parameters in (4.1) and $d_{1} = 2$, $d_{2} = 0.001$, $r_{1} = 0.2$. Left: component u has Turing instability. Right: component v has Turing instability

For the positive equilibrium $p ( {{u_{0}},{v_{0}}} ) ={ ( {{u_{0}},{v_{0}}} ) _{1}}$, choose $d_{1} = 0.006$, $d _{2} = 0.002$. By computation we have $r_{1}^{ ( 0 ) } \approx 0.114$ and $\operatorname{Re} ( {{c_{1}}(r_{1} ^{ ( 0 ) })} ) \approx - 2.830 \times {10^{ - 3}} < 0$. So we conclude that the positive equilibriums $p ( {u_{0} ,v_{0} } )$ loses its stability, and system (1.4) undergoes a Hopf bifurcation when $r_{1}$ crosses $r_{1}^{ ( 0 ) }$. Moreover, the direction of the bifurcation is toward the back, and the bifurcating periodic solutions are asymptotically stable by Theorem 3.1, which is shown in Fig. 4.

Figure 4

The numerical simulations of system (1.4) with parameters in (4.1) and $d_{1} = 0.006$, $d_{2} = 0.002$, $r_{1} =0.02$. Left: component u is stable. Right: component v is stable

5 Conclusion

In this paper, we study a modified Michaelis–Menten harvesting predator–prey model with diffusion terms. For ODE system, we get that if hypotheses $\mathbf{{(H_{1} })}$ and $\mathbf{{(H_{2} })}$ hold, then the positive equilibrium $p ( {{u_{0}},{v_{0}}} )$ is locally asymptotically stable. For PDE system (1.4), if $r_{2} b_{2} d _{1} > r_{1} a_{1} d_{2}$ and $\Delta > 0$, then there exists $k \in N$ such that $\frac{k^{2}}{l^{2}} \in ( {z_{1} ,z_{2} } )$, $k = 0,1,2,\ldots$ , and the positive equilibrium $p(u_{0} ,v_{0} )$ of system (1.4) has Turing instability. In addition, the positive equilibrium $p(u_{0} ,v_{0} )$ is locally asymptotically stable under other conditions. Finally, we analyze Hopf bifurcation and find that if hypothesis $( \mathbf{H_{2}} )$ holds, then Hopf bifurcation occurs at $r_{1} = r_{1}^{ ( j ) }$. Moreover, if $\operatorname{Re} ( {c_{1}(r_{1}^{ ( j ) } )} ) < 0$ (resp. >0), then Hopf bifurcation is toward the back (resp., ahead), and the bifurcating periodic solutions are asymptotically stable (resp., unstable).

Appendix: Bifurcation direction of the spatially inhomogeneous periodic solutions

In this appendix, we study the bifurcation of the spatially inhomogeneous periodic solutions given in Theorem 3.1. We calculate $\operatorname{Re} ( {{c_{1}}(r_{1}^{(j)})} )$ for $j= 1, 2,\ldots , n_{0}^{*}$. Denote $r_{1}=r_{1}^{(j)}$, where $r_{1}^{(j)}$ is defined in (3.1). We get ${\omega_{j}} = \sqrt{ {D_{j}}(r_{1}^{(j)})}$, where ${D_{j}}(r_{1}^{(j)})$ is given in (2.7). We set

$$ q: = \left ( \textstyle\begin{array}{@{}c@{}} {a_{j}} \\ {b_{j}} \end{array}\displaystyle \right ) \cos \frac{j}{l}x = \left ( \textstyle\begin{array}{@{}c@{}} 1 \\ - \frac{{{r_{1}}u + i{\omega_{j}}K + {d_{1}} \frac{{{j^{2}}}}{{{l^{2}}}}K}}{{K{r_{1}}su}} \end{array}\displaystyle \right ) \cos \frac{j}{l}x $$

and

$$ {q^{*} }: = \left ( \textstyle\begin{array}{@{}c@{}} {a_{j}^{*} } \\ {b_{j}^{*} } \end{array}\displaystyle \right ) \cos \frac{j}{l}x = \left ( \textstyle\begin{array}{@{}c@{}} \frac{1}{{2l\pi }} - \frac{{{r_{1}}u + {d_{1}}\frac{{{j^{2}}}}{{{l ^{2}}}}K}}{{2l\pi i{\omega_{j}}}} \\ - \frac{{{r_{1}}su}}{{2l\pi i{\omega_{j}}}} \end{array}\displaystyle \right ) \cos \frac{j}{l}x. $$

By straightforward calculation we have

$$ { \bigl[ {2i{\omega_{j}}I - {L_{2j}} \bigl( {r_{1}^{j}} \bigr) } \bigr] ^{ - 1}} = { ( {{ \alpha_{1}} + {\alpha_{2}}i} ) ^{ - 1}} \left ( { \textstyle\begin{array}{@{}c@{\quad}c@{}} {2i{\omega_{j}} + 4{d_{2}}\frac{{{j^{2}}}}{{{l^{2}}}} - {r_{2}}{b_{2}}}& { - {r_{1}}{a_{2}}} \\ {{r_{2}}{b_{1}}}&{2i{\omega_{j}} + 4{d_{1}} \frac{{{j^{2}}}}{{{l^{2}}}} + {r_{1}}{a_{1}}} \end{array}\displaystyle } \right ) $$

with

$$\begin{aligned}& {\alpha_{1}} = 16{d_{1}} {d_{2}} \frac{{{j^{4}}}}{{{l^{4}}}} + 4 ( {{r_{1}} {a_{1}} {d_{2}} - {r_{2}} {b_{2}} {d_{1}}} ) \frac{{{j^{2}}}}{ {{l^{2}}}} + {r_{1}} {r_{2}} ( {{a_{2}} {b_{1}} - {a_{1}} {b_{2}}} ) - 4\omega_{j}^{2}, \\& {\alpha_{2}} = 2{\omega_{j}} \biggl[ {4 ( {{d_{1}} + {d_{2}}} ) \frac{ {{j^{2}}}}{{{l^{2}}}} + {r_{1}} {a_{1}} - {r_{2}} {b_{2}}} \biggr] \end{aligned}$$

and

$$ { \bigl[ {2i{\omega_{j}}I - {L_{0}} \bigl( {r_{1}^{j}} \bigr) } \bigr] ^{ - 1}} = { ( {{ \alpha_{3}} + {\alpha_{4}}i} ) ^{ - 1}} \left ( { \textstyle\begin{array}{@{}c@{\quad}c@{}} {2i{\omega_{j}} + {d_{2}}\frac{{{j^{2}}}}{{{l^{2}}}} - {r_{2}}{b_{2}}}& { - {r_{1}}{a_{2}}} \\ {{r_{2}}{b_{1}}}&{2i{\omega_{j}} + {d_{1}}\frac{{{j^{2}}}}{{{l^{2}}}} + {r_{1}}{a_{1}}} \end{array}\displaystyle } \right ) $$

with

$$\begin{aligned}& {\alpha_{3}} = {d_{1}} {d_{2}}\frac{{{j^{4}}}}{{{l^{4}}}} + ( {{r_{1}} {a_{1}} {d_{2}} - {r_{2}} {b_{2}} {d_{1}}} ) \frac{{{j^{2}}}}{ {{l^{2}}}} + {r_{1}} {r_{2}} ( {{a_{2}} {b_{1}} - {a_{1}} {b_{2}}} ) - 4\omega_{j}^{2}, \\& {\alpha_{4}} = 2{\omega_{j}} \biggl[ { ( {{d_{1}} + {d_{2}}} ) \frac{ {{j^{2}}}}{{{l^{2}}}} + {r_{1}} {a_{1}} - {r_{2}} {b_{2}}} \biggr] . \end{aligned}$$

Then we get

$$\begin{aligned}& \omega_{20} = \frac{1}{2}{ \bigl[2i{ \omega_{j}}I - L \bigl({r_{1}}^{j} \bigr) \bigr]^{ - 1}} \left [ { \biggl( {\cos \frac{{2j}}{l}x + 1} \biggr) \left ( \textstyle\begin{array}{@{}c@{}} {c_{j}} \\ {d_{j}} \end{array}\displaystyle \right ) } \right ] \\& \hphantom{\omega_{20} }= \biggl[ {\frac{{{{[2i{\omega_{j}}I - {L_{2j}}({r_{1}}^{j})]}^{ - 1}}}}{2} \cos \frac{{2j}}{l}x + \frac{{{{[2i{\omega_{j}}I - {L_{0}}({r_{1}} ^{j})]}^{ - 1}}}}{2}} \biggr] \left ( \textstyle\begin{array}{@{}c@{}} {c_{j}} \\ {d_{j}} \end{array}\displaystyle \right ) \\& \hphantom{\omega_{20}}= \frac{{{{ [ {{\alpha_{1}} + {\alpha_{2}}i} ] }^{ - 1}}}}{2} \left ( \textstyle\begin{array}{@{}c@{}} ( {2i{\omega_{j}} + 4{d_{2}}\frac{{{j^{2}}}}{{{l^{2}}}} - {r_{2}} {b_{2}}} ) {c_{j}} - {r_{1}}{a_{2}}{d_{j}} \\ ( {2i{\omega_{j}} + 4{d_{1}}\frac{{{j^{2}}}}{{{l^{2}}}} + {r _{1}}{a_{1}}} ) {d_{j}} + {r_{2}}{b_{1}}{c_{j}} \end{array}\displaystyle \right ) \\& \hphantom{\omega_{20} =}{}+ \frac{{{{ [ {{\alpha_{3}} + {\alpha_{4}}i} ] }^{ - 1}}}}{2} \left ( \textstyle\begin{array}{@{}c@{}} ( {2i{\omega_{j}} + {d_{2}}\frac{{{j^{2}}}}{{{l^{2}}}} - {r_{2}} {b_{2}}} ) {c_{j}} - {r_{1}}{a_{2}}{d_{j}} \\ ( {2i{\omega_{j}} + {d_{1}}\frac{{{j^{2}}}}{{{l^{2}}}} + {r_{1}} {a_{1}}} ) {d_{j}} + {r_{2}}{b_{1}}{c_{j}} \end{array}\displaystyle \right ) , \\& \omega_{11} = - \frac{1}{2}{ \bigl[ {L \bigl( {{r_{1}}^{j}} \bigr) } \bigr] ^{ - 1}} \left [ { \biggl( {\cos \frac{{2j}}{l}x + 1} \biggr) \left ( \textstyle\begin{array}{@{}c@{}} {e_{j}} \\ {f_{j}} \end{array}\displaystyle \right ) } \right ] \\& \hphantom{\omega_{20} }= \frac{{{\alpha_{5}}^{ - 1}}}{2}\left ( \textstyle\begin{array}{@{}c@{}} ( {4{d_{2}}\frac{{{j^{2}}}}{{{l^{2}}}} - {r_{2}}{b_{2}}} ) {e_{j}} - {r_{1}}{a_{2}}{f_{j}} \\ ( {4{d_{1}}\frac{{{j^{2}}}}{{{l^{2}}}} + {r_{1}}{a_{1}}} ) {f_{j}} + {r_{2}}{b_{1}}{e_{j}} \end{array}\displaystyle \right ) + \frac{{{\alpha_{6}}^{ - 1}}}{2}\left ( \textstyle\begin{array}{@{}c@{}} ( {{d_{2}}\frac{{{j^{2}}}}{{{l^{2}}}} - {r_{2}}{b_{2}}} ) {e_{j}} - {r_{1}}{a_{2}}{f_{j}} \\ ( {{d_{1}}\frac{{{j^{2}}}}{{{l^{2}}}} + {r_{1}}{a_{1}}} ) {f_{j}} + {r_{2}}{b_{1}}{e_{j}} \end{array}\displaystyle \right ) , \end{aligned}$$

where

$$\begin{aligned}& c_{j} = {f_{uu}} - 2{f_{uv}}\frac{{{r_{1}}u + i{\omega_{j}}K + {d_{1}}\frac{{{j^{2}}}}{{{l^{2}}}}K}}{{K{r_{1}}su}}, \\& {d_{j}} = {g_{uu}} - 2{g_{uv}}\frac{{{r_{1}}u + i{\omega_{j}}K + {d_{1}}\frac{{{j^{2}}}}{{{l^{2}}}}K}}{{K{r_{1}}su}} + {g_{vv}}\frac{ {{{ ( {{r_{1}}u + i{\omega_{j}}K + {d_{1}}\frac{{{j^{2}}}}{{{l ^{2}}}}K} ) }^{2}}}}{{{K^{2}}{r_{1}}^{2}{s^{2}}{u^{2}}}}, \\& {e_{j}} = {f_{uu}} - 2{f_{uv}} \frac{{{r_{1}}u + {d_{1}}\frac{{{j ^{2}}}}{{{l^{2}}}}K}}{{K{r_{1}}su}},\qquad {g_{j}} = 0, \\& {f_{j}} = {g_{uu}} + 2{g_{uv}}\frac{{{r_{1}}u + {d_{1}}\frac{{{j ^{2}}}}{{{l^{2}}}}K}}{{K{r_{1}}su}} + {g_{vv}}\frac{{{{ ( {{r_{1}}u + {d_{1}}\frac{{{j^{2}}}}{{{l^{2}}}}K} ) }^{2}} - \omega_{j}^{2} {K^{2}}}}{{{K^{2}}{r_{1}}^{2}{s^{2}}{u^{2}}}}, \\& {h_{j}} = {g_{uuu}} - {g_{uuv}}\frac{{3{r_{1}}u + i{\omega_{j}}K + 3 {d_{1}}\frac{{{j^{2}}}}{{{l^{2}}}}K}}{{K{r_{1}}su}} \\& \hphantom{{h_{j}} =}{} + g_{uvv}\frac{{3 [ ( {{r_{1}}u + {d_{1}}\frac{{{j^{2}}}}{{{l^{2}}}}K} ) ^{2} - {\omega_{j}}^{2}{K^{2}} ]+ 2 ( {{r_{1}}u + {d_{1}}\frac{{{j^{2}}}}{{{l^{2}}}}K} ){\omega_{j}}Ki}}{{{K^{2}}{r_{1}}^{2}{s^{2}}{u^{2}}}} \\& \hphantom{{h_{j}} =}{}- g_{vvv}\frac{{ [ {{ ( {{r_{1}}u + {d_{1}}\frac{{{j^{2}}}}{{l^{2}}}K} )^{2}} - \omega_{j}^{2}{K^{2}}} ] [{r_{1}}u + {d_{1}}\frac{{{j^{2}}}}{{{l^{2}}}}K + i{\omega_{j}}K]}}{{{K^{3}}{r_{1}}^{3}{s^{3}}{u^{3}}}}, \end{aligned}$$

and ${f_{uu}}$, ${f_{uv}}$, ${f_{vv}}$, ${g_{uu}}$, ${g_{uv}}$, ${g_{vv}}$, ${f_{uuu}}$, ${f_{uuv}}$, ${f_{uvv}}$, ${f_{vvv}}$, ${g_{uuu}}$, ${g_{uuv}}$, ${g_{uvv}}$, and ${g_{vvv}}$ are given in (3.6). Then we have

$$\begin{aligned}& {Q_{{\omega_{20}},\bar{q}}} = \left ( \textstyle\begin{array}{@{}c@{}} {f_{uu}}{\gamma_{1}} + {f_{uv}}({\gamma_{1}}{{\bar{b}}_{j}} + {\gamma _{2}}) + {f_{vv}}{\gamma_{2}}{{\bar{b}}_{j}} \\ {g_{uu}}{\gamma_{1}} + {g_{uv}}({\gamma_{1}}{{\bar{b}}_{j}} + {\gamma _{2}}) + {g_{vv}}{\gamma_{2}}{{\bar{b}}_{j}} \end{array}\displaystyle \right ) \cos \frac{{2j}}{l}x\cos \frac{j}{l}x \\& \hphantom{{Q_{{\omega_{20}},\bar{q}}}={}}{}+ \left ( \textstyle\begin{array}{@{}c@{}} {f_{uu}}{\delta_{1}} + {f_{uv}}({\delta_{1}}{{\bar{b}}_{j}} + {\delta _{2}}) + {f_{vv}}{\delta_{2}}{{\bar{b}}_{j}} \\ {g_{uu}}{\delta_{1}} + {g_{uv}}({\delta_{1}}{{\bar{b}}_{j}} + {\delta _{2}}) + {g_{vv}}{\delta_{2}}{{\bar{b}}_{j}} \end{array}\displaystyle \right ) \cos \frac{j}{l}x, \\& {Q_{{\omega_{11}},\bar{q}}} = \left ( \textstyle\begin{array}{@{}c@{}} {f_{uu}}{\varphi_{1}} + {f_{uv}}({\varphi_{1}}{{\bar{b}}_{j}} + {\varphi_{2}}) + {f_{vv}}{\varphi_{2}}{{\bar{b}}_{j}} \\ {g_{uu}}{\varphi_{1}} + {g_{uv}}({\varphi_{1}}{{\bar{b}}_{j}} + {\varphi_{2}}) + {g_{vv}}{\varphi_{2}}{{\bar{b}}_{j}} \end{array}\displaystyle \right ) \cos \frac{{2j}}{l}x\cos \frac{j}{l}x \\& \hphantom{{Q_{{\omega_{20}},\bar{q}}}={}}{}+ \left ( \textstyle\begin{array}{@{}c@{}} {f_{uu}}{\zeta_{1}} + {f_{uv}}({\zeta_{1}}{{\bar{b}}_{j}} + {\zeta _{2}}) + {f_{vv}}{\zeta_{2}}{{\bar{b}}_{j}} \\ {g_{uu}}{\zeta_{1}} + {g_{uv}}({\zeta_{1}}{{\bar{b}}_{j}} + {\zeta _{2}}) + {g_{vv}}{\zeta_{2}}{{\bar{b}}_{j}} \end{array}\displaystyle \right ) \cos \frac{j}{l}x \end{aligned}$$

with

$$\begin{aligned}& {\gamma_{1}} = \frac{{{{ [ {{\alpha_{1}} + {\alpha_{2}}i} ] } ^{ - 1}}}}{2} \biggl[ { \biggl( {2i{ \omega_{j}} + 4{d_{2}}\frac{{{j^{2}}}}{ {{l^{2}}}} - {r_{2}} {b_{2}}} \biggr) {c_{j}} - {r_{1}} {a_{2}} {d_{j}}} \biggr] , \\& {\gamma_{2}} = \frac{{{{ [ {{\alpha_{1}} + {\alpha_{2}}i} ] } ^{ - 1}}}}{2} \biggl[ { \biggl( {2i{ \omega_{j}} + 4{d_{1}}\frac{{{j^{2}}}}{ {{l^{2}}}} + {r_{1}} {a_{1}}} \biggr) {d_{j}} + {r_{2}} {b_{1}} {c_{j}}} \biggr] , \\& {\delta_{1}} = \frac{{{{ [ {{\alpha_{3}} + {\alpha_{4}}i} ] } ^{ - 1}}}}{2} \biggl[ { \biggl( {2i{ \omega_{j}} + {d_{2}}\frac{{{j^{2}}}}{ {{l^{2}}}} - {r_{2}} {b_{2}}} \biggr) {c_{j}} - {r_{1}} {a_{2}} {d_{j}}} \biggr] , \\& {\delta_{2}} = \frac{{{{ [ {{\alpha_{3}} + {\alpha_{4}}i} ] } ^{ - 1}}}}{2} \biggl[ { \biggl( {2i{ \omega_{j}} + {d_{1}}\frac{{{j^{2}}}}{ {{l^{2}}}} + {r_{1}} {a_{1}}} \biggr) {d_{j}} + {r_{2}} {b_{1}} {c_{j}}} \biggr] , \\& {\varphi_{1}} = \frac{{{\alpha_{5}}^{ - 1}}}{2} \biggl[ { \biggl( {4{d _{2}}\frac{{{j^{2}}}}{{{l^{2}}}} - {r_{2}} {b_{2}}} \biggr) {e_{j}} - {r_{1}} {a_{2}} {f_{j}}} \biggr] , \\& {\varphi_{2}} = \frac{{{\alpha_{5}} ^{ - 1}}}{2} \biggl[ { \biggl({4{d_{1}}\frac{{{j^{2}}}}{{{l^{2}}}} + {r_{1}} {a_{1}}} \biggr) {f_{j}} + {r_{2}} {b_{1}} {e_{j}}} \biggr] , \\& {\zeta_{1}} = \frac{{{\alpha_{6}}^{ - 1}}}{2} \biggl[ { \biggl( {{d_{2}} \frac{{{j^{2}}}}{{{l^{2}}}} - {r_{2}} {b_{2}}} \biggr) {e_{j}} - {r_{1}} {a _{2}} {f_{j}}} \biggr] , \\& {\zeta_{2}} = \frac{{{\alpha_{6}}^{ - 1}}}{2} \biggl[ { \biggl( {{d_{1}}\frac{{{j^{2}}}}{{{l^{2}}}} + {r_{1}} {a_{1}}} \biggr) {f_{j}} + {r_{2}} {b_{1}} {e_{j}}} \biggr] . \end{aligned}$$

For any $j \in N$, we notice that

$$ \int_{0}^{l\pi } {{{\cos }^{2}} \frac{{jx}}{l}\,dx = \frac{{l \pi }}{2}} ,\qquad \int_{0}^{l\pi } {{{\cos }^{2}} \frac{{jx}}{l} \cos \frac{{2jx}}{l}\,dx = \frac{{l\pi }}{4}} ,\qquad \int_{0}^{l \pi } {{{\cos }^{4}} \frac{{jx}}{l}\,dx = \frac{{3l\pi }}{8}}. $$

Then we get

$$\begin{aligned}& \bigl\langle {{q^{*} },{Q_{{\omega_{20}},\bar{q}}}} \bigr\rangle = \frac{{l\pi }}{4} \bigl\{ {{\bar{a}}_{j}}^{*}\bigl( {{f_{uu}} {\gamma_{1}} + {f_{uv}}({ \gamma_{1}} {{\bar{b}}_{j}} + {\gamma_{2}}) +{f_{vv}} {\gamma _{2}} {{\bar{b}}_{j}}} \bigr) \\& \hphantom{\langle {{q^{*} },{Q_{{\omega_{20}},\bar{q}}}}\rangle =}{} +{{\bar{b}}_{j}}^{*} \bigl( {g_{uu}} {\gamma_{1}} + {g_{uv}}({\gamma_{1}} {{ \bar{b}}_{j}} + {\gamma_{2}}) + g_{vv} \gamma_{2} \bar{b}_{j}\bigr) \bigr\} \\& \hphantom{\bigl\langle {{q^{*} },{Q_{{\omega_{20}},\bar{q}}}} \bigr\rangle =}{} + \frac{{l\pi }}{2} \bigl\{ {{\bar{a}}_{j}}^{*} \bigl( {{f_{uu}} {\delta_{1}} + {f_{uv}}({ \delta_{1}} {{\bar{b}}_{j}} + {\delta_{2}}) +{f_{vv}} {\delta_{2}} {{\bar{b}}_{j}}} \bigr) \\& \hphantom{\langle {{q^{*} },{Q_{{\omega_{20}},\bar{q}}}}\rangle =}{}+ \bar{b}_{j}^{*} \bigl( {{g_{uu}} { \delta_{1}} + {g_{uv}}({\delta_{1}} {{ \bar{b}}_{j}} + {\delta_{2}}) + {g_{vv}} { \delta_{2}} {{\bar{b}}_{j}}} \bigr) \bigr\} , \\& \bigl\langle {{q^{*} },{Q_{{\omega_{11}},q}}} \bigr\rangle = \frac{{l\pi }}{4} \bigl\{ {{\bar{a}}_{j}}^{*} \bigl( {{f_{uu}} {\varphi_{1}} + {f_{uv}}({ \varphi_{1}} {{\bar{b}}_{j}} + {\varphi_{2}}) + {f_{vv}} {\varphi_{2}} {{\bar{b}}_{j}}} \bigr) \\& \hphantom{\langle {{q^{*} },{Q_{{\omega_{20}},\bar{q}}}}\rangle =}{}+{\bar{b}}_{j}^{*} \bigl( {{g_{uu}} { \varphi_{1}} + {g_{uv}}({\varphi_{1}} {{ \bar{b}}_{j}} + {\varphi_{2}}) + {g_{vv}} { \varphi_{2}} {{\bar{b}}_{j}}} \bigr) \bigr\} \\& \hphantom{\langle {{q^{*} },{Q_{{\omega_{20}},\bar{q}}}}\rangle =}{}+ \frac{{l\pi }}{2} \bigl\{ {{\bar{a}}_{j}}^{*} \bigl( {{f_{uu}} {\zeta_{1}} + {f_{uv}}({ \zeta_{1}} {{\bar{b}}_{j}} + {\zeta_{2}}) + {f_{vv}} {\zeta_{2}} {{\bar{b}}_{j}}} \bigr) \\& \hphantom{\langle {{q^{*} },{Q_{{\omega_{20}},\bar{q}}}}\rangle =}{}+ \bar{b}_{j}^{*} \bigl( {{g_{uu}} { \zeta_{1}} + {g_{uv}}({\zeta_{1}} {{ \bar{b}}_{j}} + {\zeta_{2}}) + {g_{vv}} { \zeta_{2}} {{\bar{b}}_{j}}} \bigr) \bigr\} , \end{aligned}$$

and $\langle {{q^{*} },{C_{q,q,\bar{q}}}} \rangle = \frac{ {3l\pi }}{8} ( {{{\bar{a}}_{j}}^{*}{g_{j}} + {{\bar{b}}_{j}}^{*} {h_{j}}} )$. For any $j \in N$, it follows that $\langle {{q ^{*} },{Q_{qq}}} \rangle = \langle {{q^{*} },{Q_{q\bar{q}}}} \rangle = 0$. By (3.11) we have

$$ \operatorname{Re} \bigl( {{c_{j}} \bigl( {r_{1}^{j}} \bigr) } \bigr) = \frac{1}{2}\operatorname{Re} \bigl\{ {2 \bigl\langle {{q ^{*} },{Q_{{\omega_{11}},q}}} \bigr\rangle + \bigl\langle {{q^{*} }, {Q_{{\omega_{20}},\bar{q}}}} \bigr\rangle + \bigl\langle {{q^{*} }, {C_{q,q,\bar{q}}}} \bigr\rangle } \bigr\} . $$

Thus, when $c_{j}$ $(r_{1}^{j} ) > 0$ (resp., <0), the bifurcating periodic solution toward the back (resp., ahead) and the bifurcating periodic solutions are asymptotically stable (resp., unstable).